A spatiotemporal case‐crossover model of asthma exacerbation in the City of Houston

Abstract

Case‐crossover design is a popular construction for analyzing the impact of a transient effect, such as ambient pollution levels, on an acute outcome, such as an asthma exacerbation. Case‐crossover design avoids the need to model individual, time‐varying risk factors for cases by using cases as their own ‘controls’, chosen to be time periods for which individual risk factors can be assumed constant and need not be modelled. Many studies have examined the complex effects of the control period structure on model performance, but these discussions were simplified when case‐crossover design was shown to be equivalent to various specifications of Poisson regression when exposure is considered constant across study participants. While reasonable for some applications, there are cases where such an assumption does not apply due to spatial variability in exposure, which may affect parameter estimation. This work presents a spatiotemporal model, which has temporal case‐crossover and a geometrically aware spatial random effect based on the Hausdorff distance. The model construction incorporates a residual spatial structure in cases when the constant assumption exposure is not reasonable and when spatial regions are irregular.

1. INTRODUCTION

In a world with increasingly dependent data, the use of modelling frameworks enabled by conditional and hierarchical thinking is key in solving complex applied problems (Cressie & Wikle, 2011). For example, the hierarchical generalized linear model framework (Lee & Nelder, 1996) enhanced the flexibility of what could be modelled with a random effect in a generalized linear mixed modelling framework (Nelder & Wedderburn, 1972). When modelling the number of asthma exacerbations in the City of Houston, the most appropriate modelling framework would allow for an appropriate hierarchical and/or conditional structure to incorporate the individual and environmental factors known to be related to asthma exacerbation.

Originally introduced by Maclure (1991) to study myocardial infarctions, the case‐crossover design is used in to study the effect of a transient environmental exposure on an acute health outcome. In situations when a case‐control study is not possible due to lack of an appropriate control group, case‐crossover design replaces ‘controls’ with ‘crossover’, in other words, cases are used as their own controls. In addition to circumventing the difficulty in selecting a representative control group, using cases as their own controls means that subject‐dependent nuisance factors can be eliminated. These benefits are part of what makes a case‐crossover design an attractive approach for many epidemiological applications (Raun, Ensor, Pederson, Campos, & Persse, 2019; Sato et al., 2018).

A geographic constant exposure assumption is sometimes made in case‐crossover designs (Maclure & Mittleman, 2000). The benefit of assuming constant exposure is that at time t, all subjects experience the same exposure, meaning that reference windows can be selected on a global level, rather than at the subject level. In addition, the constant exposure assumption results in a case‐crossover model which is equivalent to a time series count (Poisson) regression, which has historically been seen as a competitor to case‐crossover.

The geographic constant exposure assumption cannot be made in most situations. If the study region is sized such that the exposure of interest can reasonably be expected to be the same for all subjects, the constant exposure assumption is appropriate. A constant exposure assumption should not be made when exposures vary by subject at time t. For example, if the exposure of interest is air pollution in the City of Houston, exposure should not be assumed constant because not all areas have the same amount of air quality.

Another way of viewing the geographic constant exposure assumption is that there is no spatial variability in the exposure of interest. This work examines methods of relaxing the constant exposure assumption in order to allow for spatial variability in the exposure of interest. This paper is organized as follows. Section 2 provides background on case‐crossover, the equivalence with Poisson regression, and existing methods for accounting for spatial variability in exposure. Section 3 describes a spatiotemporal, hierarchical model, which includes an analog of case‐crossover in time and a spatial random effect. Section 4 fits this model to the counts of 9‐1‐1 related asthma exacerbations for each super neighbhorhood in the City of Houston in 2015 using various reference window structures. Finally, Section 5 summarizes the methodological and application specific findings and directions for future research.

2. BACKGROUND

2.1. The case‐crossover design

The case‐crossover design constructs controls, called reference windows, by selecting periods where the transient exposure of interest is expected to be similar to exposure at the time of the event of interest.

For example, if a subject experiences a myocardial infarction at 10 AM on a Monday, the reference windows would be the previous three Mondays at 10 AM. The idea is that a subject's environment and activities are likely to be similar on Mondays at 10 AM, so it is valid to use these reference windows as controls—a time when the subject might have experienced the event, and was exposed to risk factors similar to those at the time of the event.

There are many options for the structure of reference windows, but the two most commonly used are the time‐stratified design (TSD) and the symmetric bi‐directional design (SBD). TSD divides the study period into disjoint reference windows, which avoids issues of overlap bias experienced by SBD and other designs. SBD uses windows centred on the event time and includes reference windows both before and after the event. Although the bi‐directionality accounts for the presence of trends in the number of events (unlike TSD), the implication of using control periods after the event is that subjects were not technically at risk during those times. For example, if a subject experiences an asthma exacerbation on a Wednesday, the symmetric bi‐directional design might use Monday, Tuesday, Thursday, and Friday as reference windows, but the subject may not be at risk on Thursday and Friday. For additional information on the choice of reference windows, see Levy, Lumley, Sheppard, Kaufman, and Checkoway (2001).

2.2. Equivalence of case‐crossover and Poisson regression

Lu and Zeger (2007) unified a number of existing cases of equivalence between the case‐crossover design fit with conditional logistic regression (CLR) and count time series methods. Beginning with the relative risk model

$${\lambda }_i(t,X_{it})={\lambda }_{0i}\exp (\beta X_{it}+{\gamma }_{it}),$$ (1)

where X _it is the exposure of subject i at time t, λ _0i is a constant, subject‐dependent risk, and $\exp ({\gamma }_{it})$ is the time‐varying risk for subject i. The difference in approach between the case‐crossover and time series methods is how γ _it is modelled.

To frame (1) as a time series analysis, λ _i (t, X _it ) is aggregated over all individuals i at time t which yields the expected number of events in the entire I at time t:

$${\mu }_t=\sum _{i\in I}{\lambda }_i(t,X_{it})=\exp (\beta X_t+S_t).$$ (2)

Note that (2) makes the constant exposure assumption for individuals at time t, in other words, $X_{it}=X_t$. Here, S _t represents the aggregation of individual baseline and time‐varying risk over the entire population, namely, $S_t={\sum }_{i\in I}{\lambda }_{0i}\exp ({\gamma }_{it})$. S _t is interpreted as the total population baseline risk at time t. Estimates of β are obtained using generalized linear modelling (GLM) techniques, and the nuisance term S _t can be estimated in a variety of ways, for example, a locally weighted running mean smoother, see (Lumley & Levy, 2000).

A case‐crossover analysis models the conditional probability $p_{i{t}_i}$ that individual i fails at time t _i given that the failure occurs in some pre‐specified reference window W(t _i ):

$$p_{i{t}_i}=\frac{{\lambda }_i(t_i,X_{i{t}_i})}{{\sum }_{j\in W(t_i)}{\lambda }_i(j,X_{ij})}.$$ (3)

The choice of the reference window W(t _i ) is crucial to the case‐crossover analysis because the case‐crossover assumption is that the individual, time‐varying baseline risk term is constant within the reference window or ${\gamma }_{ij}={\gamma }_{ik}$ for all j, k ∈ W(t _i ). This assumption allows the cancellation of the nuisance terms in the numerator and denominator of (3), which yields

$$p_{i{t}_i}=\frac{\exp (\beta X_{i{t}_i})}{{\sum }_{j\in W(t_i)}\exp (\beta X_{ij})}.$$ (4)

If we assume γ _it , the time‐varying subject‐specific factors, are constant for an individual within some specified reference window, we avoid the need to estimate γ _it . Conditional logistic regression (CLR) is used to estimate β .

Estimates of β using the GLM and CLR approaches can be shown to be equivalent when constant exposure at time t is assumed, and the nuisance term in the GLM S _t is chosen to capture the reference window scheme. When SBD is used, a case‐crossover fit with CLR is equivalent to a Poisson regression where S _t is estimated using a locally weighted running mean smoother; see Lu and Zeger (2007). When TSD is used, a case‐crossover fit with CLR is equivalent to a Poisson regression with indicator variables for the strata generated by the disjoint subsets formed by the TSD (Levy et al., 2001; Lu & Zeger, 2007). In Sections 3 and 4, the TSD and indicator variables for strata are used.

2.3. Spatial methods for count data

In Section 2.2, spatial variability in the number of asthma exacerbations at time t is not accounted for. Section 3 explores a strategy to incorporate a spatial error term into a spatio‐temporal analogue of case‐crossover. A brief overview of relevant spatial methods is first provided in 3.

3. METHODS

The constant exposure assumption, namely, $X_{it}=X_i$, can also be viewed as a spatial assumption. Since each individual i can be assigned a spatial location s _it at a given time t, the constant exposure assumption is stated as $X_{s_{i}t}=X_t$. A question of interest is whether the constant exposure assumption can be reasonably made in time and space, that is, $X_{s_{i}t}=X_{st}$, for all s _i , s , and t. In other words, can the constant exposure assumption be relaxed to allow for piecewise constant exposure in a spatial location s at a given time t. In Section 4, for example, exposure to ambient ozone is assumed to be constant for all individuals in a given super neighbourhood s at time t. To model the expected number of cases in region s at time t, a hierarchical generalized linear model will be applied. The model can be written as

$$Y|X,Z,\beta \sim quasiPoisson(\mu )$$ (5)

$$\mu =E(Y|X,Z,\beta )=X\beta +Z$$ (6)

$$Z\sim N(0,\mathrm{\Sigma }={(I-\rho W)}^{-1}),$$ (7)

where Y is a vector of observed counts, X a matrix of covariates with parameter β , Z is a vector of spatial random effects which follow a conditional autoregressive (CAR) model with a covariance matrix Σ , the spatial autocorrelation parameter ρ , and W is a spatial weight matrix. The autoregression is brought into the model via the spatial weight matrix W in the CAR covariance matrix. While the above model is most easily described as a hierarchical generalized linear mixed model, the model can be viewed in a GLMM context: β is the fixed effect, which in this case represents exposure (e.g., ambient ozone) as well as the temporal case‐crossover structure represented by indicator variables, and the term Z can be viewed as a spatially correlated random effect. In other words, the above model uses the spatial GLMM framework to include a temporal structure in the fixed effect, which corresponds to a time‐stratified case‐crossover model. For additional details on spatial GLMMS, including inference and specification details, see Waller and Gotway (2004).

The mean of the quasi‐Poisson distribution, μ , is a linear combination of the regression term Xβ and the spatial random effect. As can be seen in Figure 1, the data are zero‐inflated, which is why a quasi‐Poisson model was employed.

FIGURE 1.

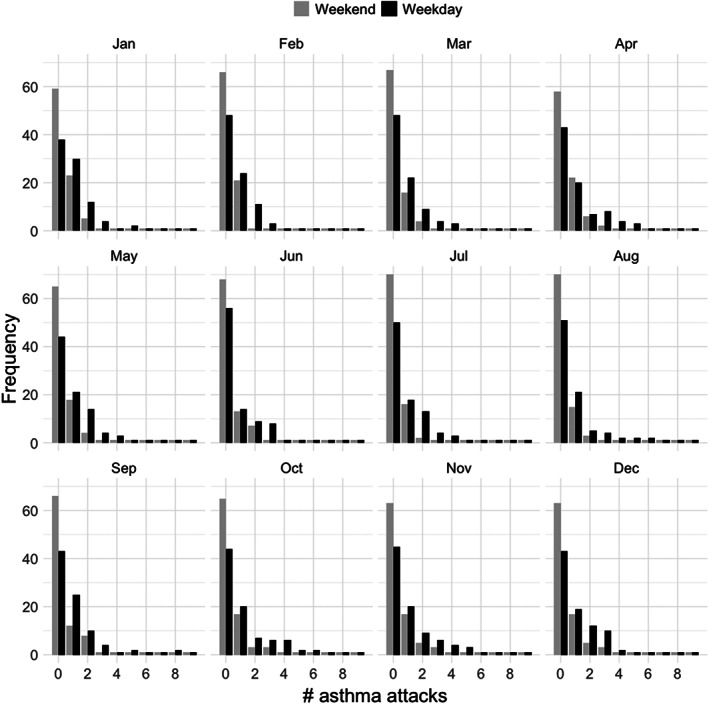
Marginal distributions of the number of asthma exacerbations by super neighbourhood, month, and weekend/weekday. The height of the black bars corresponds to the number of superneighbourhoods that experienced the given number of asthma exacerbations on a weekday for the given month, and the grey bars on weekends for a given month. Weekends tend to have fewer asthma exacerbations

The temporal case‐crossover piece is represented in the matrix of covariates X. In addition to any exposure variables, indicator variables for reference window strata are included in X. The strata are chosen based on a time‐stratified case‐crossover design. The time‐stratified design was chosen because the partitioned study periods do not induce overlap bias. The choice of strata is guided by the available data and subject‐matter expertise. Easily accessible data is often aggregated, so the resolution of the reference windows will be limited by the aggregation. In other words, if only daily data are available, hourly reference windows cannot be created. Subject‐matter expertise can guide the choice of reference windows by providing information on the exposure variables. For example, if the exposure of interest is ambient ozone, a subject‐matter expert could note that time of day is an important factor in exposure to ozone, so that daily reference windows are not sufficient.

The spatial random effect Z has a conditional autoregressive (CAR) structure, or that of a Gaussian Markov random field. The covariance matrix $\mathrm{\Sigma }={(I-\rho W)}^{-1}$ induces spatial dependence via the spatial weight matrix W. In a study with n regions, the weight matrix is n × n . Many options for W exist, such as contiguity‐based neighbours, a K nearest neighbours (KNN) structure, or a sparsified inverse distance matrix. This work utilizes a KNN structure, constructed using the knearneigh function from the spdep package (Bivand, Pebesma, & Gomez‐Rubio, 2013) in R (R Core Team, 2019), with k = 4, which was then passed to the knn2nb function with sym = T to ensure a symmetric matrix. The symmetrized matrix resulted in an average of 5.07 neighbours, meaning that enforcing symmetry resulted in some regions having greater than 4 neighbours. Symmetry is required to use a conditional autoregressive error structure.

While many KNN methods rely on distances between the centroids of the spatial regions, ‘nearest’ is defined in terms of the extended Hausdorff distance (Min, Zhilin, & Xiaoyong, 2007; Schedler, 2020). The Hausdorff distance is a distance metric defined on sets and can be thought of as the maximum of all possible shortest paths from all the points in one set to all points in the other. Use of the word ‘shortest’ in this definition hints at the flexibility of the Hausdorff distance, namely that it can be based on any underlying distance metric. This flexibility allows context of a study to be part of the definition of spatial dependence. For example, a study of commute times for all super neighbourhoods in the City of Houston might be based on a road distance rather than Euclidean or great circle distance. The extended Hausdorff distance replaces the maximum with an arbitrary percentile, for example, the 50th percentile Hausdorff distance is the median of all possible shortest paths between the two regions. In studies where the shape, size, and orientation of the regions is not constant, using the extended Hausdorff distance can mitigate these effects. The model fit to the asthma exacerbation data in Section 4 uses a spatial weight matrix which are the 4 nearest neighbours in terms of the median Hausdorff distance, although some regions may have more than two neighbours to maintain symmetry.

4. RESULTS

The spatiotemporal hierarchical model described in Section 3 is fit to the asthma exacerbation counts for the City of Houston. The hglm R package (Alam, Ronnegard, & Shen, 2015) was used, specifying family as quasipoisson and rand.family, the spatial component, to a conditional autoregressive structure based on the spatial matrix W. Code snippets and some exploratory data analysis is available in the supplemental pdf. Hourly counts of asthma exacerbation by super neighbourhood for 2015 were aggregated to varying strata; see Table 1. The data that support the findings of this study are available from the corresponding author, J.S., upon a reasonable request. The data for the super neighbourhood boundaries are available from the Kinder Urban Data platform (City of Houston, 2017).

TABLE 1.

Time variables and strata for the case‐crossover structure

Time variables	Values	Strata
	Morning: 6 AM–10 AM	Month
	Midday: 10 AM–4 PM	Month × time of day
Time of day	Afternoon/evening: 4 PM–8 PM	Month × weekday
	Night: 8 PM–6 AM	Time of day × weekday
Month	1, 2, 3, …, 12
Weekday	0 if Saturday or sunday
	1 otherwise

Figure 2 shows the parameter estimates and 95% confidence intervals for ozone and temperature for spatial and non‐spatial models for the different strata.

FIGURE 2.

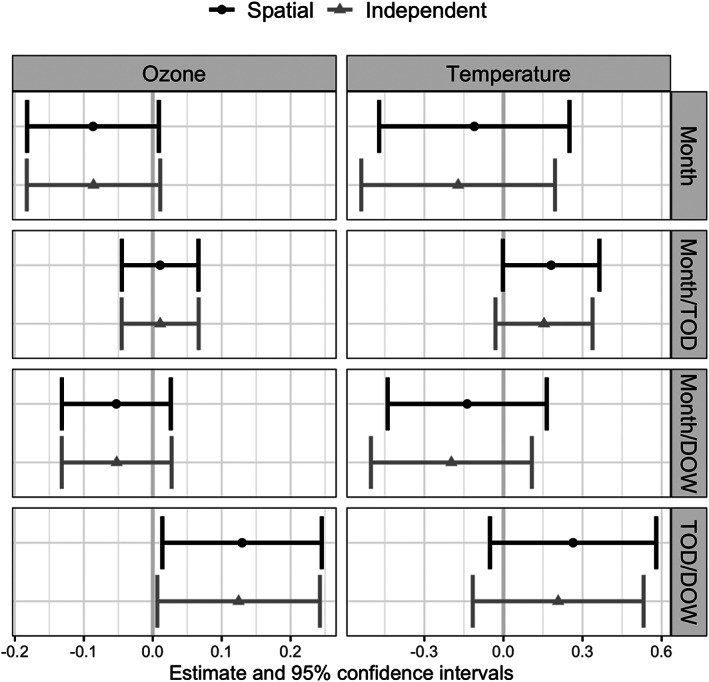
Estimates and 95% confidence intervals for the ozone and temperature exposure variables from both spatial and non‐spatial models. The labels on the right‐hand y‐axis correspond the four strata levels investigated. The panels in the left column are for the regression parameter associated with ozone, and the right is apparent temperature. With the exception of the time of day/weekday indicator strata for ozone, all the estimates are statistically insignificant at the 0.05 level

Although most parameters are not statistically significant at the 0.05 level (the 95% confidence interval captures 0), there appears to be some variability in the direction of the effect and the level of aggregation. When the strata indicates month, or the combination of month and the weekday indicator, both ozone and temperature are associated with a decrease in the average log‐odds of observing an asthma exacerbation. When the strata are either the month and time of day and the time of day combined with the weekday indicator, increase in average apparent temperature or ambient ozone was associated with an increase in the log‐odds of observing an asthma exacerbation. Apparently, including the time of day is important when considering the effect of temperature and ozone on asthma exacerbations, which is consistent with literature (Pires et al., 2018).

Finally, as seen in Figure 3, for the month/time of day strata, the spatial model fails to be statistically significant at the 0.1 level, but the independent model does not. This phenomenon is due to a failure to account for spatial autocorrelation which causes models based on the assumption of independent observations to underestimate the standard errors of parameter estimates. This known modelling fallacy causes covariates to appear statistically significant when really they are not, as the independent error assumption of the model is not met.

FIGURE 3.

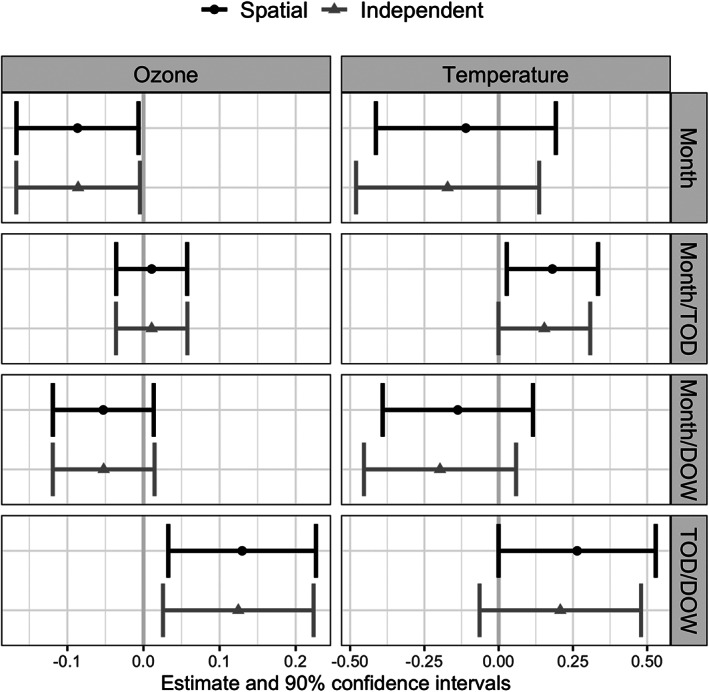
Estimates and 90% confidence intervals for the ozone and temperature exposure variables from both spatial and non‐spatial models. The labels on the right‐hand y‐axis correspond the the four strata levels investigated. The panels in the left column are for the regression parameter associated with ozone, and the right is apparent temperature

We present this example to show the relevance of our methods. However, note that the application is based on one year of data only and thereby is not as comprehensive as previous efforts.

5. DISCUSSION

Case‐crossover design and analysis has proven a fundamental method in the environmental epidemiologist's toolkit. This design is appropriate for acute health endpoints and transient environmental exposure. This paper defines a clear path forward to extend this important design to the spatiotemporal space of environmental exposure. We capitalize on the known equivalence of the case‐crossover design, coupled with conditional logistic regression, to count time series models such as Poisson time series. The methodology we present is designed to be simple in its use and interpretation, while advancing proper statistical methodology.

Our methodology is built on a time‐stratified case‐crossover design in conjunction with a spatial causal autoregressive models using the extended Hausdorff distance measure to capture the spatial dependence structure. The methodology is extendable to a wide range of count spatiotemporal processes and spatial structures. We demonstrate our method with a daily zero‐inflated count model, relating asthma exacerbations to ambient air quality that varies in both space and time.

Supporting information

Supporting Information

Schedler JC, Ensor KB. A spatiotemporal case‐crossover model of asthma exacerbation in the City of Houston. Stat. 2021;10:e357. 10.1002/sta4.357