Guide to development of compound files for PBPK modeling in the Simcyp population‐based simulator

Abstract

The Simcyp Simulator is a software platform for population physiologically‐based pharmacokinetic (PBPK) modeling and simulation. It links in vitro data to in vivo absorption, distribution, metabolism, excretion and pharmacokinetic/pharmacodynamic outcomes to explore clinical scenarios and support drug development decisions, including regulatory submissions and drug labels. This tutorial describes the different input parameters required, as well as the considerations needed when developing a PBPK model within the Simulator, for a small molecule intended for oral administration. A case study showing the development and application of a PBPK model for ondansetron is herein used to aid the understanding of different PBPK model development concepts.

INTRODUCTION

Physiologically‐based pharmacokinetic (PBPK) modeling is an approach that utilizes the knowledge of the physiological and biological elements of the human or animal body, otherwise known as “systems data” to predict the PKs of drugs when used in conjunction with relevant compound data. Within the Simcyp Simulator, the systems or population data are separated from the compound data, but these are mechanistically combined via the trial design for any simulation using in vitro in vivo extrapolation (IVIVE) techniques. ¹ This separation enables the assessment of the drug's PKs in different scenarios and to extrapolate across multiple populations. The focus of this tutorial will be on generating compound PBPK models.

The very first important step in developing a PBPK model is to consider the purpose of the model development and its context of use (e.g., is it going to be used to predict plasma concentrations, drug–drug interactions, and/or exposure in special and disease populations?) Some key considerations include “what are the mechanisms that are important to consider, to accurately describe the pharmacokinetics/dynamics (PK/PD) associated with the compound/drug,” “what input data are available to construct the PBPK model,” and “what clinical data are available to verify the developed model?” The answer to these questions will determine how complex the model can be, as generally the more mechanistic the model, the more data are required to build it.

Using ondansetron as a case study, the aim of this tutorial is to give guidance on the input parameters and model options required when developing PBPK models for compound/drug files within the Simcyp Simulator. The input parameters required for a Simcyp compound file are arranged in tabs (Figure 1a, annotation 1), thus this tutorial will go through these parameters following the layout of the different tabs.

FIGURE 1.

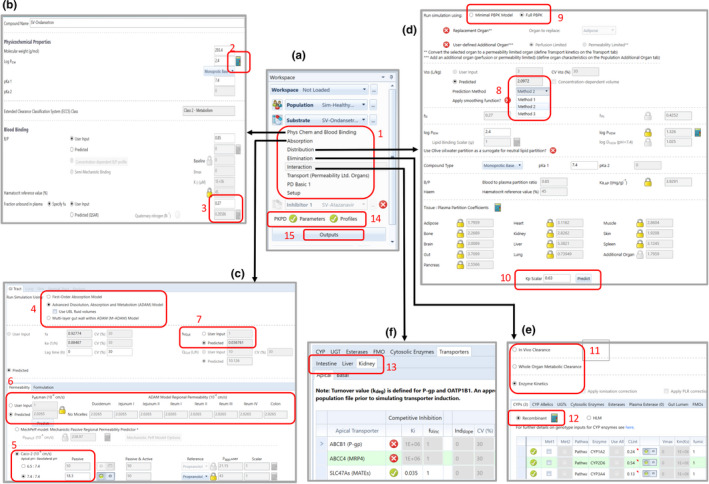
The input parameters required for a Simcyp compound file are arranged in tabs as shown in (a). The first tab (b) has the physicochemical and blood binding parameters for the compound, some of which can either be user‐input or predicted. For a drug being administered orally, the absorption parameters for the GI tract tab (c) provides the flexibility to select the absorption model to be used, a P_eff,man prediction option depending on what input parameters are available and the option to enter input parameters to describe formulation effects when applicable. The distribution tab (d) has the input parameters and the different model options that can be selected to describe the drug's distribution, whereas the elimination tab (e) has the model and input options to describe the drug's clearance from the body. When a compound is identified as a perpetrator, the interaction tab (f) is used to include input parameters in the model to enable the simulation of DDIs against either enzymes or transporters. Separate entry boxes for the same transporters in different organs are considered in the Simulator to enable independent modeling of the effect of the transporter in each organ. DDI, drug‐drug interactions; GI, gastrointestinal; P_eff,man, effective permeability of the compound in the human jejunum

Ondansetron is a serotonin 5‐HT₃ receptor antagonist, commonly given to oncology patients to prevent nausea and vomiting due to chemotherapy. Given that ondansetron is routinely co‐administered with oncology drugs, the purpose of the current PBPK model is to evaluate its liability for drug–drug interactions (DDIs), both as a victim and as a perpetrator. Following the best practice approach for PBPK modeling, ² the tutorial is split into three sections: model development, model verification, and model application.

INPUT PARAMETERS REQUIRED FOR COMPOUND MODEL DEVELOPMENT

Physicochemical and blood binding parameters

The first input parameters required when developing a PBPK model for a compound are the physicochemical and blood binding parameters. These include molecular weight (MW), compound charge type, and the related pK _a values, octanol‐buffer partition coefficient (Log p), blood‐to‐plasma partition ratio (B:P), and fraction unbound in plasma (f _u). These parameters are very important and could be influential in the choice of model parameters.

The molecular weight is calculated from the drug's chemical structure. Ondansetron has an MW of 293.4 g/mol, but most formulations are available either as the anhydrous hydrochloride salt, with an MW of 329.8 g/mol or the hydrochloride dihydrate salt, with an MW of 365.9 g/mol. The MW input required for the PBPK model is that of the free base (not including any salt form), as the free base is the moiety measured in clinical PK studies. Thus, when running simulations of clinical studies involving the salt, a dose correction is required to reflect the dose of the parent compound administered.

The pK _a of a compound describes its ionization across a range of pH values, whereas the compound type depends on the charge of the ionizable site(s) present on the molecule. Each ionizable site is assessed separately to decide whether its pK _a would be relevant in vivo. Ondansetron has two basic ionizable sites with pK _a values of 7.4 and 1.7, with no acidic ionizable sites (product monograph). However, only the nitrogen on the imidazole ring with the pK _a of 7.4 is expected to undergo ionization at physiological pH. As a rule of thumb, any basic center with a pK _a ≤ 4.4, or any acidic center with a pK _a > 10.4 will be neutral at physiological pH and may therefore not be relevant. Thus, the selected input for its compound type is monoprotic base, with a pK _a of 7.4.

Experimental B:P of 0.85, ³ f _u of 0.27 (product monograph) and Log D value of 2.12 measured at pH 7.4, ⁴ were available in the literature. The Log D gave a predicted Log p value of 2.4 using the Simcyp in‐built “Prediction Toolbox” (Figure 1b, annotation 2). These were used as input parameters in the file. In addition, its main binding protein—human serum albumin ⁵ was also defined. From the input data of f _u, the selected binding protein and the reference concentration of the selected protein (systems data), and the affinity (K _D) of the drug for the binding protein are calculated. Using the mean value for the selected plasma protein and its associated variability in the population of interest, an individual protein level is calculated for each subject. This value, together with the calculated affinity of ondansetron for the protein, is used to calculate an individualized value of f _u for each simulated subject. Using this approach, it is possible to predict the f _u of a compound in any population with altered plasma protein concentrations, assuming the affinity of the compound does not change between populations.

Experimental values are preferred for physicochemical and blood binding parameters. This is particularly important for compounds with either a high Log p or a small f _u, wherein a very small change in these values can result in a marked difference in its partitioning into tissues and hence the predicted PKs. Where these are unavailable, especially in early‐stage drug development, algorithms for predicted f _u and B:P for bases and neutrals are available in the Simulator; both of which require knowledge of the Log p and pK _a of the compound. The predicted f _u for ondansetron is 0.286, whereas the user‐input value is 0.27 (Figure 1b, annotation 3), hence the use of either value will not affect the drug's PKs. Calculated values for pK _a and Log p can be obtained from available computational tools. ⁶ Although not applicable to ondansetron, measured values of B:P and f _u at different drug concentrations can be used as user input for drugs which show nonlinearity in binding.

Oral absorption parameters

Features of the different oral absorption models available within the Simulator (Figure 1c, annotation 4) are summarized in Table 1. The choice of the absorption model to be used is dependent on the purpose of the PBPK model, its applications, the properties of the drug, and the available formulations. Oral formulations of ondansetron include tablets and solutions, available as ondansetron hydrochloride; immediate release (IR) film‐coated tablets, with the dihydrate of ondansetron hydrochloride as its active ingredient; and the oral disintegrating tablet (ODT) formulation of the free base form.

TABLE 1.

Oral absorption models available in the Simcyp Simulator

Model	f a and k a		Metabolism		Gut transporter		Handling formulations
	User defined	Predicted	Q gut	Enzymes distribution	Apical	Basolateral
First order	√	√	√
ADAM		√		√	√		√
M‐ADAM		√		√	√	√	√

Abbreviations: ADAM, advanced dissolution, absorption, and metabolism; f _a, fraction of drug absorbed; k _a, absorption rate constant; M‐ADAM, multilayer gut wall within ADAM.

Although the hydrochloride tablet is moderately soluble in water, 100% of the drug is released from the formulation within 30 min. The bioavailability of the oral tablet formulation has been shown to be equivalent to that of the oral solution in a clinical study conducted in 24 healthy male volunteers. ⁷ Solubility data for the IR tablet has also been shown to be bioequivalent to the solution and complies with the Biopharmaceutics Classification System (BCS) requirements of “highly soluble,” whereas the ODT disintegrates on the tongue within 30 s upon administration. ⁸ Given that none of the available formulations are expected to affect its oral absorption, a simplified model which assumes that ondansetron is always in solution can be utilized for its oral absorption. In addition, although identified as a P‐gp substrate, ⁹ ondansetron is rapidly and completely absorbed after oral administration at all its clinical doses, suggesting that P‐gp has a minimal impact on its bioavailability. Hence gut transporter effects do not need to be considered in the model.

Although a simple first order (FO) model would otherwise be sufficient in describing the oral absorption of ondansetron, the FO model is limited in its approach, as, given its structure, it cannot take into consideration the true physiological representation of the gastrointestinal (GI) tract, and how that in turn affects drug absorption and intestinal metabolism. With the FO model, both fraction of drug absorbed (f _a) and absorption rate constant (k _a) values can directly be entered by users. In such a case, Monte Carlo sampling is used to incorporate variability for these specific parameters, and the relevant physiological covariates are not considered. The advanced dissolution, absorption, and metabolism (ADAM) model on the other hand, divides the GI tract into nine anatomically defined segments, from the stomach through the intestine to the colon. Drug absorption from each segment is described as a function of release from the formulation, dissolution, precipitation, luminal degradation, permeability, metabolism, transport, and transit from one segment to another. ¹⁰

Given the more physiologically relevant structure and mechanistic considerations, the ADAM model offers some benefits over the FO model in modeling oral drug absorption. Its main advantages are the capability to handle formulation effects, the ability to describe regional differences in drug permeability, metabolism and transport, and other effects that cannot be modeled with FO absorption (such as enterohepatic recirculation). In addition, the intake of food prior to drug administration is known to alter the PKs of certain drugs, depending on its physicochemical properties, due to several physiological changes. These include an alteration in gastric pH, delay in gastric emptying, increase in splanchnic blood flow, stimulation of bile flow, and physical or chemical modification of the drug itself, depending on the dosage form. ¹⁰ When a drug simulation is done under fed state, by selecting the “fed state” radio button in the trial design screen, the ADAM model incorporates these physiological changes in the simulation, as these are already predefined in the Simulator as part of the systems data.

Considering the aforementioned physicochemical properties of ondansetron, selecting the ADAM model with “solution” as the formulation type would be sufficient to describe its oral absorption. For compounds with known solubility issues, a solution ADAM model would not be suitable, so alternative ADAM models “solution with precipitation” or “suspension” are available in the Simulator, which takes into consideration, the mechanics of drug release from the formulation. Thus, the required absorption input parameters for the ondansetron ADAM model are those needed for the prediction of the f _a, and those which adequately describe the fraction of the drug escaping gut metabolism (F _g), in each segment of the intestine (Table 1). Prediction of f _a is based on both biological system‐dependent parameters (radius of the small intestine, transit through each segment of the small intestine, gastrointestinal pH, fluid dynamics, etc.) and drug‐dependent parameters (solubility, formulation related parameters, effective permeability of the compound in the human jejunum [P_eff,man] etc.). In the Simulator, system‐dependent parameters are part of the population‐related library data, therefore for the ondansetron compound file, the only required compound input for fa prediction is P_eff,man, because the file is being modeled as a solution.

To account for formulation effects, additional input parameters are required to describe the dissolution of the drug in the GI tract, including intrinsic solubility, solubilization factor, pK _a, particle size, micelle partition (logK _m:w), effective diffusion coefficient (D _eff), effective diffusion layer thickness (h _eff), and parameters describing super‐saturation and precipitation. Details into modeling of such drugs are outside the scope of this tutorial, but readers are herein referred to more relevant publications describing the modeling of complex oral drug formulations. ¹⁰ , ¹¹ , ¹² For compounds with poor intrinsic solubility, it can be extremely important to include low basic pK _a(s) when present to account for drug dissolution at gastric pH, which is much lower than the physiological pH of 7.4.

Prediction of P _eff,man

The Simulator offers various options for P_eff,man prediction from in vitro permeability or physicochemical descriptors because of the experimental challenges involved in obtaining measured in vivo P_eff,man values (e.g., using the Loc‐I‐Gut technique). ¹³ These include the estimation of P_eff,man from apparent permeability (P_app) values derived in vitro in different cell lines (Caco‐2, MDCK II, and LLC‐PK₁); based on available P_app–P_eff correlations: 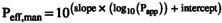, where P_app is in units of 10⁻⁶ cm/s and P_eff,man is in units of 10⁻⁴ cm/s, and the slope and intercept are specific to the in vitro system used. ¹⁴

The permeability values measured in one laboratory for compounds utilized in the P_app–P_eff correlation may sometimes differ from the original values used to establish the correlation. Thus, to account for inter‐laboratory variabilities, users should calibrate the in vitro permeability of their test compound with those measured for a series of reference compounds using the same in vitro system. This is done using the “Permeability Calibrator” located within the absorption screen, so that a scalar can be calculated to adjust the P_app value for the test compound. Alternatively, if the user has measured values for several compounds using their own in vitro system, then a user‐defined correlation can be calculated and used directly in the Simulator to scale P_app to P_eff,man.

A “passive” apparent permeability derived in Caco‐2 cells, measured at an apical and basolateral pH of 7.4, was available from the literature for ondansetron. ¹⁵ This was used as the input parameter for P_eff,man prediction in the PBPK model (Figure 1c, annotation 5). If the inhibition of any possible inherent transporter effects has not been considered in the in vitro assay (either with the use of specific transporter inhibitors or with the use of knock out cell lines), then the “Passive and Active” option should be selected in the Simulator.

Other P_eff,man prediction methods available within the Simulator are prediction from parallel artificial membrane permeability assay (PAMPA), ¹⁶ prediction from molecular descriptors‐Polar surface area (PSA) of the drug (square Ångströms) and a count of the number of hydrogen bond donors (HBDs), ¹⁷ and the MechPeff model. ¹⁸ The MechPeff model is based on the knowledge of regional gut anatomy (system parameters) and drug‐specific physicochemical parameters: MW, compound type, pK _a, and Log p. It scales the passive intrinsic membrane permeability (P_trans,0) of the drug to a passive intestinal permeability (P_eff,man), via surface area scalars derived from knowledge of the villous dimensions.

All the P_eff,man prediction methods available in the Simulator have demonstrated the ability to reasonably capture in vivo permeability for a range of compounds, especially if measured under similar experimental conditions as those in which the correlations were derived, and within the physicochemical range of the compounds studied. It should, however, be noted that there may be associated uncertainties when predicting the absorption of a particular compound with any prediction method.

When P_eff,man is uncertain, this can be adjusted or optimized using either the automated sensitivity analysis (ASA) or parameter estimation tools within the Simulator, based on clinically observed data, such as f _a, or concentration‐time profiles following oral administration. The ASA tool is particularly important where confidence in any of the required input parameters, such as in vitro P_app or Log p (required for the MechPeff prediction method) are lacking, as it can be useful in informing appropriate values for the model. There is also the option to enter user input global or region‐specific P_eff,man values (Figure 1c, annotation 6), based on either in vitro or in vivo permeability data coupled with mechanistic considerations of the GI physiology. ¹⁹

Gut metabolism

The intrinsic capability of the gut enzymes to metabolize drug molecules is one of the factors that determines F _g. This is described using the intrinsic clearance of the drug in the gut (CL_int,u,G), and is based on the drug‐specific metabolic activity mediated by each enzyme as well as the enzyme abundance at the site of metabolism. Metabolism of ondansetron is mediated by both CYP3A4 and CYP2D6, ²⁰ which are both expressed in hepatocytes and the gut enterocytes; hence ondansetron is expected to undergo gut metabolism to some extent.

Different experimental approaches can be used to determine the rate of intestinal metabolism of ondansetron. Metabolism can be measured in vitro in intestinal microsomes and then used directly as an input parameter in the Simulator. Alternatively, if the metabolism of ondansetron is defined to occur by specific enzymes, then using information about the rate of metabolism per pmol of enzyme and the abundance of the enzyme in different tissue locations allows the rate of metabolism in each tissue to be calculated. For ondansetron, the latter approach was used.

The abundance values of the gut enzymes and their distribution along the intestine are part of the population library, so the required information for the ondansetron model is the metabolic activity for each of the enzymes involved in its metabolism. This can be determined using recombinant enzyme systems or calculated based on the rate of metabolism in human liver microsomes (HLMs). When derived using HLMs, the estimated enzymatic activity is scaled down to a metabolic rate per pmol of enzyme using the mean abundance of the isozyme in question per mg of liver microsomal protein. This is then scaled up to give a CL_int by CYP3A4 and CYP2D6 in the gut, using the intestinal abundance of both enzymes in each simulated individual assigned from the mean and coefficient of variation (CV) defined for the population. This approach is based on observations that the enzyme activities mediated per unit of CYP3A4 are the same in the liver and the gut. ²¹

Based on the free drug hypothesis, only unbound drug molecules may undergo metabolism. ²² Thus, the fraction unbound in the gut (f _uGut), a parameter to account for the impact of free fraction on first pass gut metabolism is required in the model (Figure 1c, annotation 7). The f _uGut can have a big impact on F _g and the free interacting concentration of the perpetrator of a DDI at the site of metabolism. Experimental values of f _uGut have been previously reported for some compounds, ²³ however, accurately measuring f _uGut is still challenging. Several approaches have therefore been used to estimate the appropriate f _uGut value for use in a PBPK model. The default f _uGut value of one has been shown to offer the best prediction of F _g for compounds primarily metabolized by CYP3A4 in the gut based on previous reports, ¹⁴ as it gives the maximum unbound drug exposure to the gut enzymes. Alternative approaches include the use of the predicted f _uGut, which uses the physicochemical properties of the drug alongside tissue composition data (population parameter), and is estimated using the Rodgers and Rowland method for tissue‐to‐plasma coefficient (K _p) prediction (section “Distribution Parameters”). The third option is to set the f _uGut value to be the same as the free fraction of the drug in plasma or blood.

It is often advisable to perform an ASA to explore the impact of the uncertainty around f _uGut on the simulation outcome, particularly for compounds that either undergo significant gut metabolism during first pass or act as a DDI perpetrator for a gut enzyme. For victim drugs, higher f _uGut values would mean more unbound drug is available for metabolism, whereas for perpetrator drugs, a higher f _uGut would mean more unbound drug is available to inhibit the gut enzyme, thereby leading to higher DDI liabilities. Given that ondansetron is a substrate and inhibitor of gut enzymes, an ASA was done to investigate this. The simulations showed that changing the f _uGut from the default of one to the predicted value of 0.03 had little effect on the predicted F _g, and, hence, maximum concentration (C _max) and time to C _max (T _max; Figure 2). In addition, due to its low inhibitory potency against CYP2D6 and 3A4 (see section “Interaction Parameters”), the range of f _uGut values had no impact on the predicted DDI. Thus, for the ondansetron PBPK model, the predicted f _uGut was selected as the input for the file.

FIGURE 2.

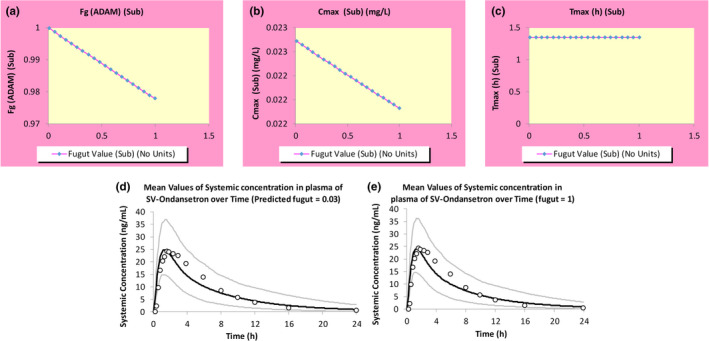
Automated sensitivity analysis (ASA) was done to investigate the impact of changing values of f _uGut on (a) the predicted fraction escaping gut metabolism (F _g), (b) the predicted C _max, and (c) the predicted T _max values. The simulations showed that changing the f _uGut from (d) the predicted value of 0.03 to (e) the default value of one had little effect on the predicted F _g, and hence C _max and T _max. ADAM, advanced dissolution, absorption, and metabolism; C _max, maximum concentration; f _uGut, fraction unbound in the gut; T _max, time to maximum concentration

Distribution parameters

Volume of distribution

Volume of distribution at steady state (V _ss) entry is needed to describe the drug's distribution and hence adequate recovery of the drug's systemic concentration profile. This can either be a user input value, derived from clinical studies with the compound dosed intravenously, or it can be predicted within the Simulator. For the predicted option, the V _ss is calculated in the Simulator from Equation 1 using a combination of the volumes for plasma (V _p), erythrocytes (V _e), and individual tissues (V _t), along with partitioning into blood cells (erythrocyte plasma partition coefficient [E:P]) and tissues (K _p). The extent of distribution to each tissue depends on tissue composition differences and the drug properties.

$$V_{\mathrm{ss}}=V_{\mathrm{p}}+V_{\mathrm{e}}\times \mathrm{E}:\mathrm{P}+\sum V_{\mathrm{t}}\times K_{\mathrm{p}}$$ (1)

Individual K _p values for any compound can be obtained experimentally. However, these data are not readily available, particularly for human tissues. Thus, K _p values are usually predicted using one of the three mechanistic methods available in the Simulator (Figure 1d, annotation 8), which in turn is used to estimate the V _ss (Equation 1).

Method 1 is based on a corrected version of the Poulin and Theil method to better account for drug partitioning between the different neutral components of the cell. ²⁴ Method 1, however, does not account for ionization of the drug at the pH of the tissue compartment and, as such, does not take into consideration the compound type. Method 2 is based on the method published by Rodgers et al. ²⁵ With the addition of an extra compartment and inclusion of acid phospholipids as cell components. Method 2 accounts for binding of the ionized fraction of the drug and has been shown to improve V _ss predictions for both acids and bases. Method 3 is derived from a combination of the Fick‐Nernst‐Planck equation with the Rodgers and Rowland's method to account for passive penetration of electrolytes across the cell membrane, together with the passive penetration of neutral molecules. ²⁶ Subcellular distribution for an organelle (e.g., lysosome) within any tissue can also be accounted for with method 3.

For neutral compounds, any of the three methods can be used, although there is a risk of overestimation of lipid binding for high Log p compounds (Log p > 4), resulting in V _ss overprediction. In general, changes in V _ss predictions are more sensitive to compounds with high Log p values. This is because a small change in Log p will result in a more than proportionate change in predicted V _ss. A lipid binding scalar option is available within the distribution tab of the Simulator for improving V _ss predictions for neutral and acidic compounds with Log p > 4. It back calculates the maximum extent of cellular lipid binding consistent with experimentally measured B:P ratios for the compound, which is then used to correct the predicted V _ss.

Distribution models

There are two broad options available for distribution modeling, either minimal PBPK (mPBPK), with or without the single adjusting compartment (SAC), or full PBPK (Figure 1d, annotation 9). All three V _ss prediction methods are available for both options. The mPBPK model has three compartments, predicting only the systemic, portal vein, and liver compartment concentrations, with the systemic compartment reflecting the measured plasma concentration. In addition to its inhibitory effect on transporters of cations, such as MATE and OCT2 in the kidneys, ondansetron is also known to cross the blood brain barrier (BBB) to exert its pharmacologic effect. ⁹ Hence, simulating either brain tissue concentrations or drug concentrations in the kidneys for adequate modeling of renal transporter inhibition would not be possible with the mPBPK model. For this reason, the mPBPK distribution model is not a suitable distribution model to be used in the development of a fully mechanistic file for ondansetron.

The Full PBPK distribution model on the other hand simulates the concentrations in various organ compartments: blood (plasma), adipose, bones, brain, gut, heart, kidneys, liver, lungs, muscles, pancreas, skin, and spleen. Interindividual variability is introduced through a covariate‐based structure in predicting tissue volumes, considering an individual's specific age, sex, weight, and height. Unlike the mPBPK model, it permits the use of permeability‐limited models available within the Simulator for several organs (liver, kidneys, brain, and lungs), thereby allowing modeling of active drug transport to be considered. Distribution is assumed to be perfusion‐limited unless any of the permeability‐limited models are activated.

For the Full PBPK model, only the predicted V _ss is available as input into the model. If the V _ss predicted from the selected method is not in line with observed data, the user has the option to manually adjust the V _ss using the “K _p scalar” (Figure 1d, annotation 10), which can be used to equally scale all predicted K _p values to adjust the predicted V _ss from any of the selected methods if required. In addition, if a drug is known to have high partitioning to a specific tissue, based on preclinical data, for instance, the tissue:plasma partition coefficient padlock for that tissue can be opened and the tissue K _p manually adjusted.

The full PBPK option with method 2 predicted V _ss was chosen for the ondansetron file. Although the method 1 predicted V _ss gave a value of 1.8 L/kg, which is close to the weighted mean observed value of 2.1 L/kg, ²⁷ , ²⁸ , ²⁹ it cannot be used when permeability‐limited distribution is required, in addition to the fact that binding of ondansetron as a base to acid phospholipids will not be considered. A K _p scalar of 0.63 was included in the model to adjust the method 2 predicted V _ss of 3.2 L/kg. Without the K _p scalar, the method 2 predicted V _ss resulted in a slight overprediction of ondansetron's observed V _ss.

Elimination parameters

As mentioned earlier, the purpose of the PBPK model is an important consideration when deciding what input parameters are required to describe the elimination of the compound. In this example, the ondansetron PBPK model is being developed to simulate both substrate (victim) and inhibitor (perpetrator) DDIs. There are three elimination options within the Simcyp Simulator: in vivo clearance, whole organ metabolic clearance, and enzyme kinetics (Figure 1e, annotation 11). Only the enzyme kinetics option is suitable for developing a substrate file. This is because it assigns drug clearance to different enzymes and transporters, thereby enabling the evaluation of potential DDIs. It is also the required option for modeling drugs that demonstrate nonlinear PKs, due to inhibition or induction of their own metabolism (auto‐inhibition or auto‐induction, respectively).

The input parameters for enzyme kinetics, either as CL_int or V _max/K _m, can be obtained from in vitro assays carried out in tissue subcellular fractions, the choice of which depends on the type of metabolism the drug undergoes and where the enzymes responsible for these reside. The V _max (maximum rate of the enzymatic reaction) and K _m (concentration of the substrate which permits the enzyme to achieve half V _max) inputs are preferable to enable modeling of enzyme saturation. The unbound fraction of the drug in the incubation system (f _u,mic or f _u,inc) is also required, which can either be measured in vitro or predicted from physicochemical properties.

In vitro kinetic data derived using both recombinant enzymes and HLMs were available in the literature for ondansetron, which confirmed the involvement of CYP1A2, 2D6, and 3A4 in its elimination in vivo. ²⁰ Input values of intrinsic clearances are scaled up in the Simulator using an IVIVE approach, which requires population parameters of enzyme abundance, microsomal protein per gram of liver (MPPGL) and liver weight, ³⁰ which are all available as part of the system parameters in the Simulator. The specifics of how these are incorporated into the well‐stirred liver model to predict hepatic clearance and, hence, fraction escaping hepatic clearance (F _h), while accounting for interindividual variability have been described previously. ³¹

When used in the PBPK model, the in vitro derived input parameters for the different ondansetron metabolic elimination routes obtained from HLMs ³² predicted a in vivo intravenous clearance (CL_iv) of 6.7 L/h, which underpredicted the weighted mean CL_iv value of 28.4 L/h. ²⁷ , ²⁸ , ²⁹ The misprediction of in vivo hepatic clearance when in vitro derived kinetic parameters are used is one of the challenges of IVIVE in PBPK modeling. Thus, the facility to derive enzyme kinetic parameters from clinically derived in vivo clearance values is available within the Simulator using the reverse translational tool (RTT).

The RTT, which is accessed via the elimination screen (Figure 1e, annotation 12), enables the estimation of in vitro CL_int values from an in vivo clearance and renal clearance (where applicable) using a reverse of the well‐stirred liver model, for compounds metabolized by CYPs and/or UGTs. It uses either information from an in vitro study about the percentage hepatic metabolism (% Hep Met), or the in vivo fraction metabolized (f _m) via different enzyme pathways, either obtained from a clinical DDI study or from a human mass balance study. ³³ The RTT also allows the use of in vivo clearance from an oral study (CL_po) if CL_iv is unavailable, but for this, additional information about the f _a and F _g of the compound is required. When CL_po is selected, only the % Hep Met CL input option is available.

The use of probe inhibitors within the Dixon study enabled an estimation of the percentage of the total hepatic metabolism mediated by each enzyme, which were given as 23%, 9%, and 36%, respectively, for CYP1A2, 2D6, and 3A4. ²⁰ This information as well as the CL_iv of 28.4 L/h and the observed renal clearance of 0.9 L/h ³⁴ were utilized in the RTT to derive more relevant in vitro kinetic parameters for the model (Table 2). The remaining 32% hepatic metabolism that was unaccounted for was assigned as “additional HLM clearance” in the model.

TABLE 2.

Input parameters used in the ondansetron PBPK model

Parameter	Value	Method/reference
Molecular weight (g/mol)	293.4	Pubchem
Log p	2.4	Pubchem
Compound type	Monoprotic base
pK a	7.4	Product Monograph 2016
B:P	0.85	3
f u	0.27	Product Monograph 2016
Main plasma binding protein	Human serum albumin	5
Absorption model	ADAM
f u,gut	0.037	Predicted
Peff,man (10−4 cm/s)	2.03	Predicted
Permeability	Predicted from Caco‐2
Apical:basolateral pH	7.4:7.4
Papp(A‐B) (10−6 cm/s)	18.3	15
Distribution model	Full PBPK model
V ss (L/kg)	2.1	Method 2 predicted
K p scalar	0.63	Optimized to V ss from meta‐analysis
Elimination	Enzyme kinetics
Enzyme	CYP2D6
Pathway	Pathway 1
CLint (μl/min/pmol)	0.54	Optimized 20
Enzyme	CYP3A4
Pathway	Pathway 1
CLint (μl/min/pmol)	0.13	Optimized 20
Enzyme	CYP1A2
Pathway	Pathway 1
CLint (μl/min/pmol)	0.24	Optimized 20
Additional clearance	HLM
CLint (HLM) (μl/min/mg protein)	14.4	RTT
CLR (L/h)	0.9	34
Interaction parameters
Enzyme	CYP2D6
K i (μM)	29	44
f u,mic	0.96	Simcyp predicted
Enzyme	CYP3A4
K i (μM)	31	44
f u,mic	0.96	Simcyp predicted
Transporter	Kidney SLC22A2‐OCT2
K i (μM)	3.85	45
Transporter	Kidney SLC47A‐MATE
K i (μM)	0.0385	45

Abbreviations: ADAM, advanced dissolution, absorption, and metabolism; B:P, blood‐to‐plasma partition ratio; CL_int, intrinsic clearance of the drug; CL_R, renal clearance; f _u, fraction unbound in plasma; f _u,gut, fraction unbound in the gut (no plasma included); f _u,mic, unbound fraction of the drug in the microsome; HLM, human liver microsome; K _i, inhibition constant; K _p, tissue‐to‐plasma coefficient; P_app, apparent permeability; PBPK, physiologically‐based pharmacokinetic; P_eff,man, effective permeability of the compound in the human jejunum; pK _a, negative log of the acid dissociation constant; V _ss, volume of distribution at steady state.

When a PBPK model for a compound is developed using only in vitro data, it is regarded as a “bottom‐up” PBPK model. If only clinical data forms the basis of the model development, it is referred to as a “top‐down” PBPK model. A “middle‐out” approach is that which combines prior in vitro information in analyzing clinical effects to determine unknown or uncertain parameters in the model. ³⁵ The ondansetron model is an example of a middle‐out PBPK model because the physchem inputs were all derived in vitro, and the in vitro derived fraction metabolized via different enzyme pathways was used to obtain in vivo relevant elimination input parameters (Figure 3). ³⁵

FIGURE 3.

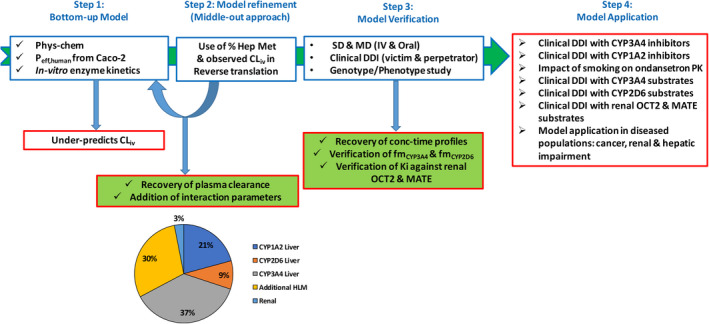
Workflow of ondansetron model development. The model was initially developed using a bottom‐up approach, incorporating physicochemical, in vitro permeability, and in vitro metabolism data. However, this base model underpredicted the reported clinical CL_iv and was refined using the RTT tool with CL_iv and the in vitro derived percentage of hepatic metabolism as inputs. The optimized model was verified with clinical studies in which ondansetron was administered as single doses both i.v. and orally as well as to a phenotyped CYP2D6 population. The model was further verified as a CYP3A4 substrate with a clinical DDI with rifampicin, as well as an inhibitor of OCT2 and MATE transporters with a clinical DDI with metformin. The verified model can be further applied in exploring other “what‐if” scenarios. CL_iv, intravenous clearance; DDI, drug‐drug interaction; Hep Met, hepatic metabolism; MD, multiple dose; RTT, reverse translational tool; SD, single dose

Transporter parameters

Several approaches are used to assess the necessity of including transporters in a PBPK model. If nonlinear PKs of a compound are observed in vivo, which cannot be explained by low solubility, saturation of metabolism, or nonlinear protein binding, or other causes, then transporters are likely to be involved. In addition, observation of a significant DDI with a known transporter inhibitor, either in vitro or in vivo, is another indication for including transporter kinetics in the compound file, using either CL_int, or J _max and K _m as input parameters. Suitable in vitro systems that can be used to derive these input parameters have been discussed previously, depending on the transporter of interest. ³⁶ In certain cases, modeling of in vitro transport data are often required to obtain appropriate input values for use in PBPK models. ³⁷

As mentioned previously, ondansetron is a P‐gp substrate and to be able to include this in the PBPK model, experiments performed in the apical‐to‐basolateral and/or basolateral‐to‐apical transport direction across cell monolayers grown on transwells, at an in vivo relevant concentration range are required for estimating J _max and K _m parameters. However, as mentioned previously, the P‐gp efflux activity in the gut does not affect the oral bioavailability of ondansetron and was therefore not included in the model. ⁸ However, the ondansetron exposure in the cerebrospinal fluid (CSF) of the brain was only recovered after a 10‐fold reduction of the passive permeability (data not shown), thereby suggesting the importance of the P‐gp efflux activity at the BBB on the drug's PKs and pharmacodynamics (PDs).

The current ondansetron model has been developed for its ability to inhibit MATEs and OCT2 present in the kidneys (section “PBPK Model Verification”). Given that these transporters share specificity with the liver OCT1 and MATE1, it is not surprising that ondansetron has also been identified as a substrate of OCT1. ³⁸ Thus, the availability of reliable in vitro data would also allow the interaction with OCT1 to be incorporated in a refined PBPK model.

When modeling transporter function, the permeability limited models for the respective organ(s) need to be activated. The overall effect of a transporter depends on its activity as well as the passive permeability of the drug into the organ. Drugs with high passive diffusion tend to have less marked effect of transporters on their distribution. It is therefore important to have robust input data for the passive permeability of the compound in the organ of interest (CL_PD in the liver, kidneys, lungs, and brain or P_eff,man in the gut), in addition to the transporter kinetics. ³⁹

Interaction parameters

Interaction parameters are required in the development of the PBPK model, when the compound has been shown, either in vitro or in vivo to inhibit or induce any of the enzymes or transporters involved in drug elimination and/or distribution. The compound thus has the potential to be a “perpetrator” of DDIs. When the perpetrator affects its own metabolism (auto‐inhibition and/or auto‐induction), incorporating the interaction parameters alongside the kinetics of its elimination (section “Elimination Parameters”) is required to accurately predict its PK profiles, specifically for multiple dosing. The magnitude of the predicted interaction depends not only on the interaction parameters, but also on the model choice for different organs. This is because the operating/interacting concentration of the perpetrator in the organ(s) of interest could be different depending on the selected model structure and components incorporated in the model (e.g., the use of a first order absorption model instead of the ADAM model).

There are four main options available in the Simulator for modeling the effect of the altered activities of various drug‐metabolizing enzymes and transporters by the perpetrator. These include competitive inhibition, mechanism‐based inhibition (MBI), ⁴⁰ induction, ⁴¹ and suppression. ⁴² Competitive inhibition of all enzyme and transporter moieties available in the Simulator can be modeled, whereas only induction/suppression of CYPs, UGTs, and transporters can be modeled using the Simulator, in a concentration and time‐dependent manner. MBI can only currently be considered for CYPs. For transporters, relevant PBPK input parameters may differ between tissues for the same probe substrate and inhibitor due to differences in membrane concentrations of the drug and its mechanism of interaction with the binding site(s) of the transporter. Therefore, separate entry boxes for the same transporters in different organs are considered in the Simulator (Figure 1f, annotation 13) to enable independent modeling of the effect of the transporter in each organ.

Static and/or dynamic PBPK models for DDI predictions are recommended by regulatory authorities, ³⁶ , ⁴³ and these two modes are available within the Simulator, identified as “PKPD Parameters” for static predictions and “PKPD Profiles” for dynamic predictions (Figure 1a, annotation 14). The static mode enables steady‐state calculations of in vivo clearance for the substrate, in the presence or absence of the “inhibitor”; while accounting for the fraction of the drug metabolized by multiple “inhibited” pathways, and “inhibition” of first pass metabolism in the gut wall. It, however, cannot consider transporter DDIs. In the dynamic mode, the time variance of the relevant interacting concentrations of the inhibitor and substrate concentrations are considered.

In an in vitro assay, ondansetron competitively inhibited the CYP2D6‐mediated O‐demethylation of dextromethorphan as well as the CYP3A4‐mediated metabolism of cyclosporin in HLMs. ⁴⁴ The inhibition constant (K _i) values of 29 and 31 μM against CYP2D6 and CYP3A4, respectively, were estimated, which were used alongside a predicted f _u,mic value of 0.96 as input values for use in the Simulator. These interaction parameters when included in the PBPK model can be used to predict clinical DDIs between ondansetron and other CYP2D6 and CYP3A4 substrates. Similarly, unbound inhibition constants (K _i,u) of 3.85 and 0.035 μM against OCT2 and MATE transporters, respectively, were obtained from an in vitro study in HEK‐293 cells with metformin as a probe. ⁴⁵ These values were included in the ondansetron PBPK model with an f _u,inc of one for the inhibition of renal OCT2 and MATE transporters only, due to lack of information on ondansetron as an inhibitor of hepatic transporters.

PBPK MODEL VERIFICATION

The final input parameters used in the ondansetron compound file, which were selected based on the model options that needed to be considered to achieve the objective of the model development, and on the availability of reliable data are summarized in Table 2 below. A schematic of the workflow for the file development is shown in Figure 3. Simulations using these parameters against clinical studies is the next step to assess the model performance and hence verify the developed PBPK model. Recovery of the clinical exposure of the drug, after single and/or multiple doses administered both i.v. and orally, is utilized as a means of ensuring that the absorption, distribution, and elimination processes are well‐described. Characteristics of the virtual subjects for the simulations are matched closely to the clinical studies (i.e., number of subjects, age range, and gender ratios) are replicated. Multiple trials of the study design (usually 10) are selected to ensure the participants used in the actual clinical study are represented in the simulated population.

A clinical study in which ondansetron was administered as a 4 mg i.v. dose to five male and seven female healthy volunteers, ⁴⁶ and another study in which an 8 mg dose of ondansetron was administered orally under both fasted and fed conditions to 12 healthy male volunteers ⁷ was simulated and used to verify the input parameters used in the model development (Figure 4a–c). The predicted results of all the simulated individuals can be viewed in an Excel workbook, by preselecting via the outputs tab (Figure 1a, annotation 15), the output sheets which correspond to the model selection(s), prior to running the simulation. These include, but are not limited to, concentration time profiles (with or without percentiles) as well as tables and charts of the summary statistics of the different PK parameters. As shown in Figure 4, the simulated concentration time profiles were all in reasonable agreement with the observed data, given that all the observed data points were within the 5th and 95th percentiles of the simulated data, and the observed values of reported PK parameters were within the range of the predicted values.

FIGURE 4.

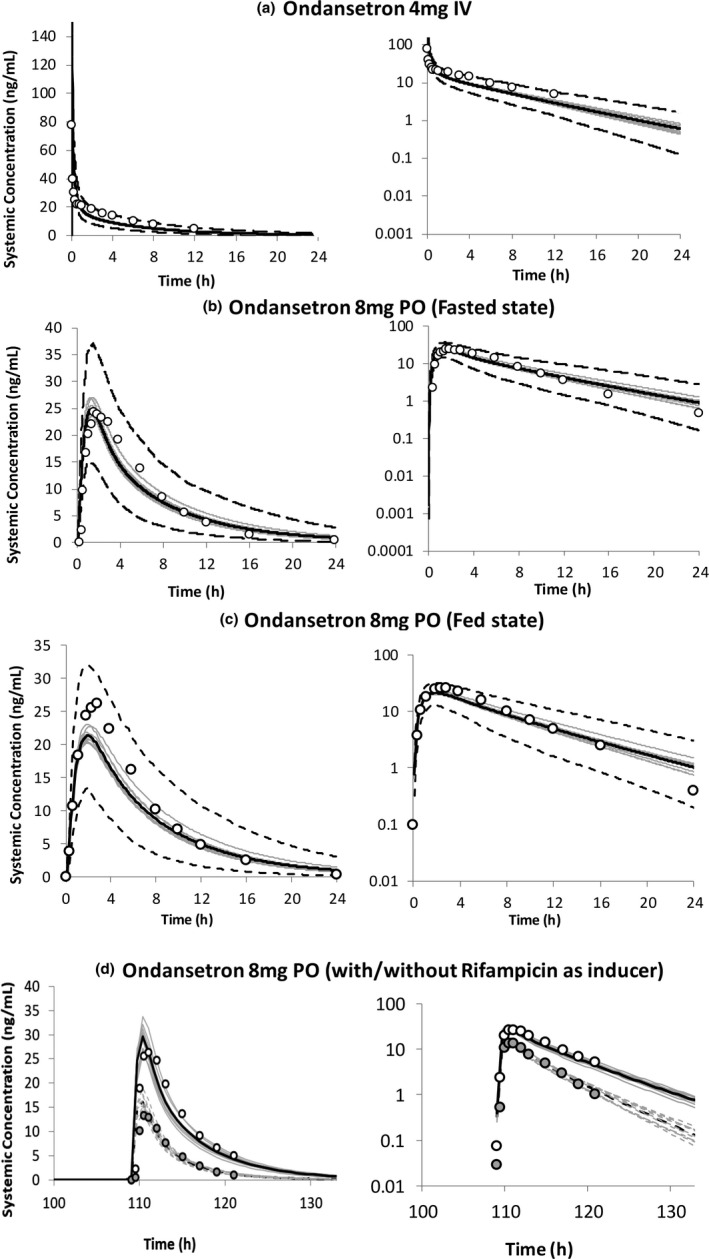
Simulated and observed (open circles) mean plasma concentration–time profiles of ondansetron after (a) single dose of 4 mg administered i.v. (10 trials × 12 HVs, 32–57 years, 0.58 women) ⁴⁶ ; (b) single dose of 8 mg administered orally under fasted and (c) fed states (10 trials × 12 male HVs, 18–40 years) ⁷ ; and (d) single dose of 8 mg administered orally before and after the administration of multiple doses of 600 mg rifampicin for 5 days (10 trials × 10 HVs, 21–41 years, 0.8 women) ⁴⁸ ; as performance verification of the developed ondansetron PBPK model. The dark lines represent the mean plasma concentration–time profiles, the gray lines represent the predictions from individual trials, whereas the dashed lines represent the 5th and 95th percentiles. The dashed lines in d represent the predictions after the administration of rifampicin. HVs, healthy volunteers

For substrate drugs, clinical DDIs with a known and verified inhibitor, or genotype studies (for enzymes with known genetic polymorphisms) can be used to verify the kinetic inputs used to define their elimination as well as the estimated f _m. A clinical study carried out in CYP2D6 phenotyped individuals after i.v. administration of 8 mg ondansetron hydrochloride dihydrate (equivalent to 6.4 mg of the free base) ⁴⁷ was reasonably recovered by the PBPK model. There was a 5% reduction in ondansetron clearance in CYP2D6 poor metabolizers (PMs) compared to extensive metabolizers (EMs) predicted by the model, which is in line with the 4% reduction obtained in the study, resulting in a marginal increase in ondansetron area under the curve (AUC) in CYP2D6 PMs compared to EMs (Table 3). This also verifies the low in vivo f _m of 9% assigned to CYP2D6 (Figure 3). There was no clinical study between ondansetron and a known CYP3A4 inhibitor available, thus the 37% f _m CYP3A4 was verified using a clinical DDI with rifampicin, which is a known CYP3A4 inducer. ⁴⁸ The model predicted a 58% (trial range 54–63%) increase in ondansetron clearance due to induction of CYP3A4 enzyme activity, which is in line with the 65% (45–76%) increase in clearance observed in the clinical study (Figure 4d and Table 3).

TABLE 3.

Summary of results of the clinical studies (observed and simulated) used to verify the final input parameters used in the ondansetron PBPK model

References	Study design	Observed (mean ± SD)		Predicted (trial range) a		Observed ratio (range) (to control study)		Predicted ratio (range) (to control study)		Predicted/observed
		C max (ng/ml)	AUC∞ (ng/ml h)	C max (ng/ml)	AUC∞ (ng/ml·h)	C max	AUC∞	C max	AUC∞	C max	AUC∞
48	8 mg Ondansetron SD p.o. on day 6 at 9 a.m. after placebo (control) and after rifampicin 600 mg q.d. at 8 p.m. × 5 days	27.2 ± 3	198 ± 24.6	30. 2 (27.5–33.9)	187 (158–213)	0.51 (0.33–0.78)	0.35 (0.24–0.55)	0.54 (0.5–0.58)	0.42 (0.37–0.46)	1.06	1.2
48	8 mg Ondansetron SD i.v. on day 6 at 9 a.m. after placebo (control) and after rifampicin 600 mg q.d. at 8 p.m. × 5 days	NS	326 ± 30	NS	299.3 (267.4–308.2)	NS	0.52 (0.39–0.78)	NS	0.65 (0.62–0.68)	NA	1.25
49	850 mg Metformin SD administered p.o. alone (control) and 12 h after administering 8 mg ondansetron q.d. p.o. at 8 p.m. for 5 days	2300 ± 520	1700 ± 325	1990 (1680–2210)	1560 (1380–1760)	1.21	1.21	1.25 (1.21–1.31)	1.33 (1.27–1.43)	1.03	1.1
47 b	8 mg s.d. Ondansetron i.v. administered to CYP2D6 EMs (control) and CYP2D6 PMs	183 (106, 315)	247 (192, 319)	268 (223, 318)	234 (157, 395)	1.09	1.04	0.99	1.03	0.91	0.99

Abbreviations: AUC∞, area under the curve to infinity; C _max, maximum concentration; DDI, drug‐drug interaction; EM, extensive metabolizer; NA, not applicable; NS, not significant; PBPK, physiologically‐based pharmacokinetic; PM, poor metabolizer; SD, single dose.

^a The healthy volunteer population in the Simcyp Simulator was used for the rifampicin clinical DDI simulations (10 trials of 12 subjects, 21–41 years, 80% women), and the simulation in CYP2D6 phenotyped subjects (10 trials of 6 subjects, 32–43 years [PMs], 35–44 years [EMs], 66.7% women); while the Chinese healthy volunteer population was used for the metformin clinical DDI (10 trials of 12 male subjects, 20–24 years).

^b Data reported as geometric mean (5th and 95th percentiles).

Verification of a drug using clinical DDI studies not only enables the assessment of the f _m (with regard to its role as a substrate), but also the assessment of the interaction parameters in the model (for its role as a perpetrator). ³⁶ Although interaction parameters for CYP2D6 and CYP3A4, as well as OCT2 and MATE transporters in the kidneys were included in the PBPK model, only a clinical DDI in Chinese healthy volunteers between ondansetron and metformin was available. ⁴⁹ This study was used to verify the inhibition constants against the renal OCT2 and MATE transporters included in the model. Results of the clinical DDIs with ondansetron, either as substrate or perpetrator are summarized in Table 3. The predictive performance of the model in recovering any DDI is assessed using predicted over observed AUC and C _max ratios, which is expected to lie between 0.8 and 1.25, or meet other predefined criteria previously described. ⁵⁰ As shown by the results, all the simulations met these criteria.

All the simulations that were carried out to verify the ondansetron file were done using the healthy volunteer population ³⁰ within the Simcyp Simulator version 20, except the DDI with metformin, wherein the Chinese healthy volunteer population ⁵¹ was used. These population files contain all the systems data referred to in this paper.

DISCUSSION, LIMITATIONS, AND FURTHER APPLICATIONS OF THE MODEL

The current ondansetron PBPK model has been developed as a substrate of CYP2D6, CYP1A2, and CYP3A4; and an inhibitor of CYP2D6 and CYP3A4 as well as renal OCT2 and MATE transporters, to enable the prediction of clinical DDIs with drugs co‐administered with ondansetron. Adequate verification of a PBPK model is often limited by what clinical data are available. In such scenarios, prospective simulations, sometimes utilizing the ASA toolkit, can help to explore various “what if scenarios” to gain confidence in the model's input parameters.

For the current model, a local sensitivity analysis (LSA) approach was used to inform the choice of the f _u,Gut input used in the model. Other areas within these can be utilized in model development have been briefly mentioned, such as in understanding the impact of different Log p values on the predicted PKs of a compound. For either of these examples, an understanding of the PK parameter(s) that would be most affected by the model input is required. Alternatively, a global sensitivity analysis (GSA) approach can be used in the first instance to identify and then rank the most influential model parameters that could affect the model outputs. ⁵² An LSA can then be carried out as a second step when specific parameters have been identified to obtain initial estimates for the model, as LSA evaluates the model parameters’ impact on a specified output by altering one parameter at a time or a few simultaneously.

Exploratory simulations coupled with sensitivity analysis can also be used to look at further applications of the developed PBPK model. With regard to CYP enzymes, a DDI with a potent CYP3A4 inhibitor like ketoconazole can be simulated to explore what the clinical impact will be if ondansetron, with an f _m CYP3A4 of 37% is co‐administered with drugs that are potent CYP3A4 inhibitors. The clinical study in CYP2D6 PMs has shown the minimal impact it has in ondansetron's metabolism. The same might not be the case for CYP1A2 with an f _m of 21%, so either a DDI with a potent CYP1A2 inhibitor or a look at the impact of smoking on the clearance of ondansetron can be explored. Given that interaction parameters against CYP2D6 and CYP3A4 are already included in the model, an exploratory simulation with ASA was carried out to assess the impact when ondansetron is co‐administered with a potent CYP3A4 and/or CYP2D6 substrate. The simulations showed that the unbound input K _is of 27.9 and 29.9 μM against CYP2D6 and CYP3A4, respectively, were not very potent, and at least a 100‐fold reduction in K _is would be required to bring about a significant decrease in intrinsic clearance both in the gut and in the liver (data not shown).

Although ondansetron has been identified as both a transporter substrate and inhibitor, the absence of relevant input data to fully develop the PBPK model as either an OCT and/or a P‐gp substrate means that prospective DDIs with potent inhibitors of either of those transporters cannot be explored and the extent of the impact of these transporters on ondansetron's distribution is currently not being considered. Polymorphism of the ABCB1 gene that encodes for P‐gp has been shown to reduce the central nervous system (CNS) penetration of ondansetron, and hence its efficacy, despite adequate systemic concentrations. ⁹ P‐gp limits the brain permeation of ondansetron and therefore DDI with P‐gp could impact the PD effect of the drug.

It has also been shown that the number of inactive OCT1 alleles is linked to higher ondansetron serum concentrations and fewer episodes of vomiting in oncology patients. ⁵³ If included in the PBPK model, it may mechanistically account for the observed interindividual variability associated with the drug. Nonetheless, the current file can be used to simulate prospective DDIs with other substrates of the renal OCT2 and MATE transporters.

Another important application of the ondansetron file would be its use in other populations. The current model was developed using a healthy volunteer population. However, simulations using a disease population, such as the Sim‐Cancer population available in the Simcyp library, or any of the cirrhosis or renal‐impaired populations can assess the impact of the physiological changes due to disease on the drug's PKs. Finally, although not incorporated in this model, there is also the possibility to link the simulated PK parameters to a PD model using any of the PD options available within the Simulator that best describes ondansetron's mechanism of action. In this way, the impact of a change in PKs, either due to drug dosing in a diseased population, or because of DDIs when co‐administered with another drug can be immediately assessed.

The use of PBPK models as part of regulatory submissions for drug approvals has grown considerably in the last decade, with simulations involving enzyme‐mediated clinical DDIs identified as the area with the highest application (~60%). ⁵⁴ Confidence in the prospective predictions of both CYP and non‐CYP mediated DDIs has increased as more robust data required to build these models have become available. It is envisaged that as research into other areas of application progress, an increase in submissions of PBPK models predicting the impact of transporter mediated DDIs, food effects, and drug exposure in special populations, such as patients with hepatic or renal impairment, pediatrics, and pregnant women are to be expected.

CONCLUSIONS

Pharmaceutical companies are increasingly using PBPK models in regulatory submissions for drugs in development, as well as academic groups for exploratory research projects. Currently, there are over 1300 Simcyp Simulator licenses being used by academic groups in their teaching and/or research, in addition to another 300 being used by pharmaceutical companies and regulatory bodies. Over the years, the utility and complexity of the Simcyp population‐based Simulator has significantly expanded, with the addition of more mechanistic models to explore various “what‐if” questions for these compounds. This tutorial is therefore a useful introductory resource to PBPK compound model development for anyone being introduced to the Simulator or PBPK modeling for the first time.

Although the development of PBPK platforms, such as the Simcyp Simulator, has been criticized in some quarters because the platform does not have an “open‐source code,” it is important to also consider the ongoing debate regarding the separation of the model from the platform and their individual “qualification”, ⁵⁵ as well as regulatory perspectives on model “credulity” ⁵⁶ , ⁵⁷ when considering the pros and cons of different platforms. As shown in this tutorial, there are many established generic models which are implemented in platforms such as Simcyp (and can be modified as needed by the user). Recent statistics on PBPK publications ⁵⁸ show that the research using PBPK modeling (applications) has overtaken the research into PBPK itself (exploring algorithms). We hope this tutorial will help the former group in furthering their efforts, while we try to keep up with the pace of novel development in the latter category and enable them to be rolled into the platform when possible and deemed necessary.

CONFLICT OF INTEREST

All authors are paid employees of Certara UK Limited (Simcyp Division) and may hold shares in Certara.

Ezuruike U, Zhang M, Pansari A, et al. Guide to development of compound files for PBPK modeling in the Simcyp population‐based simulator. CPT Pharmacometrics Syst Pharmacol. 2022;11:805‐821. doi: 10.1002/psp4.12791