Robust physiologically based pharmacokinetic model of rifampicin for predicting drug–drug interactions via P‐glycoprotein induction and inhibition in the intestine, liver, and kidney

Abstract

P‐glycoprotein (P‐gp) is an efflux transporter that plays an important role in the pharmacokinetics of its substrate, and P‐gp activities can be altered by induction and inhibition effects of rifampicin. This study aimed to establish a physiologically based pharmacokinetic (PBPK) model of rifampicin to predict the P‐gp‐mediated drug–drug interactions (DDIs) and assess the DDI impact in the intestine, liver, and kidney. The induction and inhibition parameters of rifampicin for P‐gp were estimated using two of seven DDI cases of rifampicin and digoxin and incorporated into our previously constructed PBPK model of rifampicin. The constructed rifampicin model was verified using the remaining five DDI cases with digoxin and five DDI cases with other P‐gp substrates (talinolol and quinidine). Based on the established PBPK model, following repeated dosing of 600 mg rifampicin, the deduced net effect was an approximately threefold induction in P‐gp activities in the intestine, liver, and kidney. Furthermore, in all 12 cases the predicted area under the plasma concentration–time curve ratios of the P‐gp substrates were within the predefined acceptance criteria with various dosing regimens. Intestinal effects of P‐gp–mediated DDIs had their greatest impact on the pharmacokinetics of digoxin and talinolol, with a minimal impact on the liver and kidney. For quinidine, predicted intestinal P‐gp/cytochrome P450 3A–mediated DDIs were slightly underestimated because of the complexity of nonlinearity and transporter‐enzyme interplay. These findings demonstrate that our rifampicin model can be applicable to quantitatively predict the net impact of P‐gp induction and/or inhibition on diverse P‐gp substrates and investigate the magnitude of DDIs in each tissue.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Rifampicin is an inducer and inhibitor for P‐glycoprotein (P‐gp) and can affect the pharmacokinetics of P‐gp substrates. P‐gp–mediated drug–drug interactions (DDIs) by rifampicin are considered to be caused mainly in the intestine, but the involvement for the liver and kidney is uncertain.

WHAT QUESTION DID THIS STUDY ADDRESS?

The purposes of this study are to accurately predict P‐gp–mediated DDIs with a physiologically based pharmacokinetic (PBPK) model of rifampicin; assess the DDI impact in the intestine, liver, and kidney; and estimate the P‐gp activity‐time profiles in each tissue during rifampicin treatment.

WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

Our established PBPK model of rifampicin successfully captured the clinically observed DDIs with digoxin, talinolol, and quinidine. These simulations have made it clear that the intestinal P‐gp was impacted by rifampicin‐mediated DDIs much more than hepatic or renal P‐gp.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

By incorporating the components for P‐gp induction and inhibition, our rifampicin PBPK model may enable net quantitative DDI predictions with various P‐gp substrates that are in clinical use or under development.

INTRODUCTION

Rifampicin can cause clinically relevant drug–drug interactions (DDIs) because of its induction and inhibition effects on drug metabolizing enzymes and transporters. ¹ , ² Among transporters, P‐glycoprotein (P‐gp) has been studied most extensively as an efflux transporter expressed on apical membranes of various cells such as enterocytes, hepatocytes, and renal proximal tubular cells. ³ Although rifampicin can induce and inhibit P‐gp in each tissue, an effective method for predicting the net effect of P‐gp–mediated DDIs has not been established.

Digoxin, a well‐known probe substrate of P‐gp, is absorbed in the intestine (oral bioavailability, 63%) and extensively eliminated by renal excretion (fraction of dose excreted into urine [fe] after an oral dose, 52%) and to a lesser extent biliary excretion (fraction of dose excreted into bile after an intravenous dose, 6.3%), with negligible metabolism. ⁴ , ⁵ , ⁶ , ⁷ P‐gp could play an important role in the intestinal, renal, and biliary efflux of digoxin. In clinical studies, multiple oral doses of 600 mg rifampicin reduced the area under the plasma concentration–time curve (AUC) of digoxin (AUC ratios [AUCRs] of 0.70 and 0.81) ⁶ , ⁸ when given 12 h after the last rifampicin dose. In contrast, a single oral dose of 600 mg rifampicin increased the AUC of digoxin (AUCR of 1.31) ⁹ via the inhibition of P‐gp by rifampicin. These findings demonstrate that the magnitude of P‐gp–mediated DDIs of rifampicin can be altered by the net effect of P‐gp induction and inhibition according to the dose timing, duration, and routes of P‐gp substrates and rifampicin.

To assess the P‐gp–mediated DDIs, it is essential to integrate the impact of tissue‐specific DDIs by rifampicin. Based on P‐gp protein levels, intestinal P‐gp increased 1.1‐ to 8.3‐fold with large variability after multiple doses of 600 mg rifampicin, ¹⁰ , ¹¹ but the inductions of hepatic and renal P‐gp have not been reported. ¹² Following multiple oral doses of 600 mg rifampicin, the biliary excretion rate of intravenously administered digoxin increased by 2.1‐fold, supporting hepatic P‐gp induction. ¹³ Renal clearance of digoxin remained unchanged after rifampicin treatment, ⁶ , ⁸ suggesting that renal P‐gp may not be induced or P‐gp–mediated secretion may not be a rate‐limiting step of the renal clearance. Taken together, there are limited clinical data on P‐gp induction levels by rifampicin in each tissue to support a quantitative discussion. ¹² Hence, we believe that physiologically based pharmacokinetic (PBPK) modeling can be beneficial to predict the P‐gp induction levels as well as inhibition and the DDI impact in each tissue.

We previously constructed a comprehensive PBPK model of rifampicin that can predict induction of cytochrome P450 (CYP) 3A/2C9/2C8 and organic anion transporting polypeptide (OATP) 1B and inhibition of OATP1B and multidrug resistance protein 2. ¹⁴ , ¹⁵ In this study, we aimed to establish an expanded PBPK model of rifampicin by incorporating its inductive and inhibitory effects on P‐gp into our previous PBPK model. The relevant parameters for P‐gp were estimated using blood digoxin concentration–time profiles after oral dosing of digoxin with rifampicin treatment. Our PBPK model of rifampicin was then verified by predicting different DDI scenarios with P‐gp substrates (digoxin, talinolol, and quinidine) based on the modeling network concept that mutually validates each PBPK model. ¹⁶

METHODS

Development of PBPK models

All nomenclature and physiological parameters are shown in Supplementary Material S1 and Table S1, respectively. The structures and pharmacokinetic parameters of PBPK models for rifampicin, digoxin, talinolol, and quinidine are summarized in Figure 1 and Table 1. For rifampicin, a previously developed PBPK model was used with certain modification. ¹⁵ Although the previous rifampicin model had one intestinal compartment, the present model set three compartments assuming the duodenum, jejunum, and ileum to investigate intestinal DDIs. By manually adjusting the parameters related to intestinal passive diffusion and metabolism, the updated model provided a concentration‐time profile of rifampicin in the jejunum comparable with that in the intestinal compartment of the previous model. The blood and liver concentration‐time profiles of rifampicin and the induction ratios of CYP isoforms in the liver and intestine were consistent before and after updating the PBPK model, appropriately expanding the previous PBPK model of rifampicin.

FIGURE 1.

Structures of physiologically based pharmacokinetic models of rifampicin, digoxin, talinolol, and quinidine. CD, renal collecting duct; CL_int,bile, intrinsic clearance of biliary excretion; CL_int,met, intrinsic clearance of metabolism; CL_renal, renal clearance; DT, renal distal tubule; Duo, duodenum; EHC, enterohepatic circulation; Ent, enterocytes; f _B, unbound fraction in blood; f _E, unbound fraction in enterocytes; f _H, unbound fraction in hepatocytes; f _R, unbound fraction in renal cells; GL, gut lumen; GLO, glomerulus; HC, hepatocytes; HE, hepatic extracellular space; Ile, ileum; IV, intravenous infusion; Jej, jejunum; k _bile, transit rate constant in EHC; MB, mucosal blood; P‐gp, P‐glycoprotein; PO, oral; PS_act, intrinsic clearance by transporter; PS_dif, intrinsic clearance by passive diffusion; PS_in, intrinsic clearance by passive diffusion from extracellular to intracellular space; PS_out, intrinsic clearance by passive diffusion from intracellular to extracellular space; PS_P‐gp, efflux intrinsic clearance by P‐gp; PT, renal proximal tubule; Q _tissue, blood flow rate in tissue; T _lag, lag time in intestinal absorption

TABLE 1.

Summary of fixed or initial parameters for rifampicin, digoxin, talinolol, and quinidine

Parameter	Rifampicin 15	Digoxin	Talinolol	Quinidine
T lag (h)	0.255	0	0	0
k stomach (/h)	–	–	0.8 a	5 a
R B	0.9	0.955 44	0.941 22	0.919 22
f B	0.0778	0.785 b	0.478 b	0.218 b
f hepatocytes	0.0814	0.535 c	0.893 c	–
f enterocytes	0.115	0.360 c	0.724 22	0.215 22
f renal cell	–	0.504 c	0.881 c	0.856 c
SFKp	6.65	30 a	2 a	5 a
K p,liver c	–	–	–	0.409
K p,muscle c	0.0947	–	0.861	0.434
K p,skin c	0.326	–	0.877	0.589
K p,adipose c	0.0629	–	0.383	0.229
K p,serosa c	0.200	1.25	0.908	0.523
f BCLint,all or f BCLint (L/h/kg)	0.251	0.0091 d	0.6 a	0.189 a , d
R dif,inf,liver	0.129	0.665 26	1 e	–
β liver	0.2	0.2/0.5/0.8	0.2/0.5/0.8	–
γ inf,liver	0.778	1	4.15 45	–
f bile	–	0.77 7	0.914 46	–
f m,liver or f P‐gp,liver	0.759 (UGT)	1 (P‐gp) e	1 (P‐gp) e	0.962 (CYP3A) f
PSdif,gut lumen to enterocytes (L/h/kg)	0.08 g	0.01 a	0.016 h	0.011 h
R dif,eff,duodenum i	–	1.45	1.05	1.38
R dif,eff,jejunum i	–	0.406	0.292	0.385
R dif,eff,ileum i	–	0.332	0.239	0.315
γ inf,enterocytes j	0.778	1 e	1 e	1 e
CLint,met,enterocytes (L/h/kg)	0.005 g	0 i	0 i	0.008 h
f m,enterocytes or f P‐gp,enterocytes	0.759 (UGT)	1 (P‐gp) e	1 (P‐gp) e	1 (P‐gp) e 1 (CYP3A) e
R dif,inf,kidney	–	0.002 a	0.012 k	0.02 k
R dif,eff,kidney	–	1 k	1 k	0.3 k
PSdif,proximal cells to vessels (L/h/kg) l	–	0.00125	0.000617	0.0104
PSdif,proximal cells to tubule (L/h/kg) l	–	0.00941	0.00464	0.0784
PSdif,distal cells to vessels (L/h/kg) l , m	–	0.000324	0.00016	0.0027
PSdif,collecting duct cells to vessels (L/h/kg) l , n	–	0.0000694	0.0000343	0.000579
f P‐gp,kidney	–	1 (P‐gp) e	1 (P‐gp) e	1 (P‐gp) e
K m,u (ng/mL)	146 (OATP1B)	–	4071 (P‐gp) 22	409 (P‐gp) 22 1996 (CYP3A) 22

Note: Physiologically based pharmacokinetic model parameters of rifampicin were mostly adapted from the previous report. ¹⁵ The following parameters were also used: rifampicin parameters—CL_renal (0.011 L/h/kg), E _max,UGT (1.34, autoinduction), E _max,CYP3A (4.57), EC_{50 ,u} (63.9 nmol/L); Digoxin parameters—f _muscle (0.716),^c f _skin (0.187),^c f _adipose (0.00854),^c PS_{tissue ,in} (0.3 L/h/kg),^a PS_tissue,ratio (5)^a; talinolol parameterso—R _{dif,inf,gut lumen to enterocytes} (0.5),^e γ _{inf,proximal cells} (8.95), γ _{inf,distal cells} (7.01), γ _{inf,collecting duct cells} (8.95), γ _{eff,proximal cells} (8.04), γ _{eff,distal cells} (5.07), γ _{eff,collecting duct cells} (2.72); quinidine parameterso—SF_{renal permeability} (0.1), γ _{inf,proximal cells} (7.22), γ _{inf,distal cells} (5.96), γ _{inf,collecting duct cells} (7.22), γ _{eff,proximal cells} (6.41), γ _{eff,distal cells} (4.35), γ _{eff,collecting duct cells} (2.50).

Abbreviations: β _liver, (CL_int,met + CL_int,bile)/(PS_dif,eff + CL_int,met + CL_int,bile); CL_int, hepatic intrinsic clearance; CL_int,all, overall hepatic intrinsic clearance; CL_int,bile, intrinsic clearance of biliary excretion; CL_int,met, intrinsic clearance of metabolism; CL_renal, renal clearance; CYP3A, cytochrome P450 3A; EC_50,u, unbound concentration for half maximum induction effect; E _max, maximum induction effect; f, unbound fraction in each tissue; F _a(F _g), intestinal availability after an oral dose; f _B, unbound fraction in blood; f _bile, CL_int,bile/(CL_int,bile + CL_int,met); f _m, fractional metabolism of each metabolizing enzyme to overall metabolism: f _P‐gp, fractional efflux of P‐gp to overall transpoter efflux; γ _eff, PS_dif,inf/PS_dif,eff on apical membrane; γ _inf, PS_dif,inf/PS_dif,eff on sinusoidal or basolateral membrane; K _m,u, unbound Michaelis–Menten constant; K _p, tissue/blood concentration ratio; k _stomach, transit rate constant from stomach to duodenum lumen; OATP1B, organic anion transporting polypeptide 1B; P‐gp, P‐glycoprotein; PS_act,inf, influx intrinsic clearance by transporter; PS_{dif,collecting duct cells to vessels}, intrinsic clearance by passive diffusion from collecting duct cells to vessels; PS_{dif,distal cells to vessels}, intrinsic clearance by passive diffusion from distal cells to vessels; PS_dif,eff, efflux intrinsic clearance by passive diffusion; PS_{dif,gut lumen to enterocytes}, intrinsic clearance by passive diffusion from gut lumen to enterocytes; PS_dif,inf, influx intrinsic clearance by passive diffusion; PS_{dif,proximal cells to tuble}, intrinsic clearance by passive diffusion from proximal cells to tuble; PS_{dif,proximal cells to vessels}, intrinsic clearance by passive diffusion from proximal cells to vessels; PS_P‐gp, efflux intrinsic clearance by P‐gp; PS_tissue,in, intrinsic clearance by passive diffusion from extracellular to intracellular space of each tissue; PS_tissue,out, intrinsic clearance by passive diffusion from intracellular to extracellular space of each tissue; PS_tissue,ratio, PS_tissue,in/PS_tissue,out; R _B, blood‐to‐plasma concentration ratio; R _dif,eff, PS_dif,eff/PS_P‐gp on apical membrane; R _dif,inf, PS_dif,inf/PS_act,inf on sinusoidal or basolateral membrane; SF_Kp, common scaling factor to in silico K _p values in each tissue; R_{dif,inf,kidney}, _Rdif,inf in the kidney; SF_{renal permeability}, common scaling factor to intrinsic clearance by passive diffusion in kidney; T _lag, lag time in intestinal absorption; UGT, uridine diphosphate‐glucuronosyl transferase.

^a Initial value for optimization.

^b Calculated as f _B = f _Plasma/R _B with the previous reports. ³⁷ , ,47

^c Calculated based on in silico methodology.

^d Calculated based on the previous report. ¹⁵

^e Assumption.

^f Extracted value from the Simcyp software package version 20.1.

^g Adjusted manually to be comparable to the previous model. ¹⁵

^h Adjusted manually to reproduce observed F _a F _g.

ⁱ Details are provided in the Method section.

^j Assumed to be equal to γ _{eff,enterocytes}.

^k Adjusted manually to reproduce observed CL_renal.

^l Calculated by multiplying the apparent permeability coefficient obtained from Caco‐2 cells by the surface area of each segment. ²² , ^,40

^m Assumed to be equal to PS_{dif,distal cells to tubule}.

ⁿ Assumed to be equal to PS_{dif,collecting duct cells to tubule}.

^o γ_inf and γ_eff of talinolol and quinidine in proximal cells, distal cells, and collecting duct cells were calculated according to the previous report. ¹⁷

The PBPK models of P‐gp substrates (digoxin, talinolol, and quinidine) were constructed in this study according to the previous reports. ¹⁵ , ¹⁷ , ¹⁸ Briefly, intestinal absorption was described by a segregated flow model ¹⁹ with three compartments corresponding to the duodenum, jejunum, and ileum to account for the P‐gp–mediated efflux. A stomach compartment was added for talinolol and quinidine to capture clinical blood concentration–time profiles with slow absorption, incorporating the dissolution time of each drug. Distribution volume was described by muscle, skin, and adipose compartments, adjusted with the same scaling factor to in silico tissue/blood concentration ratio values for each tissue. For digoxin, the compartments of muscle, skin, and adipose were further divided into extracellular and intracellular compartments to explain the long half‐life of digoxin in plasma based on its high affinity and slowly equilibrating binding to sodium‐potassium ATPase pump (Na,K‐ATPase). ²⁰ A five‐liver model was used to mimic the dispersion model. ²¹ In the case of a permeability‐limited condition, each liver compartment was subdivided into extrahepatic and hepatocellular compartments. Enterohepatic circulation was included for digoxin and talinolol by incorporating three transit compartments between the liver and the duodenum lumen. A previously reported kidney model consisting of the glomerulus, proximal tubule, distal tubule, and collecting duct was used. ¹⁷ Each tubule was further divided into the three subcompartments of blood vessels, cells, and urinary lumen to consider renal transporter components. The structure of the PBPK models was determined considering the pharmacokinetic characteristics of each P‐gp substrate (Table S2), with detailed parameters shown in Table 1. Talinolol and quinidine are P‐gp substrates but have different pharmacokinetics from digoxin in terms of elimination pathways and nonlinearity and were selected.

Transport and metabolism components in PBPK models of P‐gp substrates

P‐gp–mediated intestinal efflux (PS_P‐gp) and intestinal efflux intrinsic clearance by passive diffusion (PS_dif,eff) were incorporated into the PBPK models of P‐gp substrates using ratio of PS_dif,eff to PS_P‐gp (R_dif,eff [=PS_dif,eff/PS_P‐gp]) values. Although in vitro R _dif,eff values of digoxin (0.0435), talinolol (0.0313), and quinidine (0.0412) were calculated from a Caco‐2 cell permeability assay, ²² the in vivo R _dif,eff value was obtained only for digoxin (0.406) in the jejunum using an intestinal perfusion method. ¹³ In vivo R _dif,eff values of talinolol (0.292 [=0.0313 × 0.406/0.0435]) and quinidine (0.385 [=0.0412 × 0.406/0.0435]) in the jejunum were then calculated from the aforementioned in vivo and in vitro R _dif,eff values. Subsequently, in vivo R _dif,eff values of each P‐gp substrate in the duodenum and ileum were calculated from the in vivo R _dif,eff values in the jejunum by correcting PS_dif,eff and PS_P‐gp using the surface area and P‐gp expression levels, respectively, in each intestinal segment (Tables 1 and S1). The expression levels of P‐gp were obtained from Simcyp virtual population (Version 19.1; Simcyp). Intestinal metabolism was not considered for digoxin and talinolol because of the negligible metabolism, ⁶ , ²³ but CYP3A metabolism was considered for quinidine. ²⁴ Because nonlinear pharmacokinetics have been reported for talinolol and quinidine, saturation of P‐gp and CYP3A was considered (Supplementary Material S1).

In the liver, the transporter‐mediated uptake, P‐gp–mediated biliary excretion, and metabolism processes were considered for digoxin and talinolol. ²⁵ , ²⁶ In this case, the overall hepatic intrinsic clearance (CL_int,all) and hepatic β are described using Equations (1) and (2), respectively, according to the extended clearance concept. ²¹

$${\mathrm{CL}}_{\mathrm{int},\mathrm{all}}=\left({\mathrm{PS}}_{\mathrm{act},\inf }+{\mathrm{PS}}_{\mathrm{dif},\inf }\right)\times \frac{{\mathrm{CL}}_{\mathrm{int},\mathrm{met}}+{\mathrm{CL}}_{\mathrm{int},\text{bile}}}{{\mathrm{PS}}_{\mathrm{dif},\mathrm{eff}}+{\mathrm{CL}}_{\mathrm{int},\mathrm{met}}+{\mathrm{CL}}_{\mathrm{int},\text{bile}}}$$ (1)

$$\begin{array}{c}\text{hepatic}\beta =\frac{{\mathrm{CL}}_{\mathrm{int},\mathrm{met}}+{\mathrm{CL}}_{\mathrm{int},\text{bile}}}{{\mathrm{PS}}_{\mathrm{dif},\mathrm{eff}}+{\mathrm{CL}}_{\mathrm{int},\mathrm{met}}+{\mathrm{CL}}_{\mathrm{int},\text{bile}}}\hfill \end{array}$$ (2)

The values of each intrinsic clearance (active uptake intrinsic clearance on sinusoidal membrane [PS_act,inf], influx intrinsic clearance by passive diffusion on sinusoidal membrane [PS_dif,inf], efflux intrinsic clearance by passive diffusion on sinusoidal membrane [PS_dif,eff], intrinsic clearance of hepatic metabolism [CL_int,met], and intrinsic clearance of biliary excretion [CL_int,bile]) can be calculated with CL_int,all and hybrid parameters of R _dif,inf (=PS_dif,inf/PS_act,inf), β, γ _inf,liver (=PS_dif,inf/PS_dif,eff), and f _bile (=CL_int,bile/[CL_int,bile + CL_int,met]). The β values ranging from 0 to 1 can inform the rate‐limiting steps of hepatic elimination. When the sum of CL_int,met and CL_int,bile is much greater than PS_dif,eff (β close to 1), CL_int,all can be approximated as PS_inf, indicating that the hepatic uptake becomes the rate‐limiting step of CL_int,all. In contrast, when the sum of CL_int,met and CL_int,bile is negligible compared with PS_dif,eff (β close to 0), CL_int,all can be approximated as (PS_act,inf + PS_dif,inf) × (CL_int,met + CL_int,bile)/PS_dif,eff, indicating that not only hepatic uptake but also metabolism and biliary excretion become the rate‐limiting steps of CL_int,all. Because of the difficulties in estimating the hepatic β values of digoxin and talinolol experimentally, three different β values—low (0.2), moderate (0.5), and high (0.8)—were used to evaluate the DDI impact by rifampicin as sensitivity analyses.

In the kidney model of digoxin, the following transporter‐mediated uptake and efflux were considered only in the proximal tubular cells: (i) uptake into the proximal cells from the vessels via sodium‐dependent process and OATP4C1; and (ii) efflux out of cells to urinary lumen via P‐gp. ²⁷ Also for talinolol and quinidine, their renal clearances were greater than the respective values of unbound fraction in plasma × glomerular filtration rate, suggesting the presence of active renal secretion. Thus, active uptake by an unidentified transporter and P‐gp–mediated efflux were incorporated. The renal β of the P‐gp substrates in the proximal tubular cells is described using Equation (3).

$$\begin{array}{c}\text{renal}\mathit{\beta }=\frac{{\mathrm{PS}}_{\mathrm{dif},\mathrm{eff},\text{cells to lumen}}+{\mathrm{PS}}_{\mathrm{P}-\mathrm{gp}}}{{\mathrm{PS}}_{\mathrm{dif},\mathrm{eff},\text{cells to vessels}}+{\mathrm{PS}}_{\mathrm{dif},\mathrm{eff},\text{cells to lumen}}+{\mathrm{PS}}_{\mathrm{P}-\mathrm{gp}}}\hfill \end{array}$$ (3)

The renal β value can inform the rate‐limiting steps of active renal secretion, similar to the hepatic β value. When the renal β is close to 1, only the uptake process becomes rate‐limiting; when the renal β is close to 0, both the uptake and the efflux processes become rate‐limiting.

Optimization of PBPK models of P‐gp substrates

The PBPK models were constructed and optimized using Numeric Analysis Program for Pharmacokinetics (Version 2.31; available from https://plaza.umin.ac.jp/~todaiyak/download.php). ²⁸ On optimization, nonlinear least‐squares fitting was conducted, taking the square root of the weight to deal with a wide range of observed blood concentrations of drugs. Plasma concentrations of each drug reported in the literature were converted to blood concentrations using blood‐to‐plasma concentration ratio values in PBPK model analysis. Dosing regimens were matched to published clinical study designs. All P‐gp substrate parameters are shown in Table 1. Most were fixed, but several optimized parameters are shown in Table S2 according to the following procedure: for digoxin, several parameters (intrinsic clearance by passive diffusion from gut lumen to enterocytes [PS_{dif,gut lumen to enterocytes}], ratio of PS_dif,inf to PS_act,inf on basolateral membrane in the kidney [R_{dif,inf,kidney}], common scaling factor to in silico tissue/blood concentration ratio values in each tissue [SF_Kp], intrinsic clearance by passive diffusion from extracellular to intracellular space of each tissue [PS_tissue,in], and ratio of PS_tissue,in to intrinsic clearance by passive diffusion from intracellular to extracellular space (PS_tissue,out) [PS_tissue,ratio]) were optimized using blood digoxin concentration‐time profiles after single oral doses of digoxin without rifampicin treatment (i.e., the control condition). ⁸ Similarly, several parameters (transit rate constant from stomach to duodenum lumen, SF_Kp, and f _BCL_int,all) for talinolol and quinidine were optimized using their respective blood profiles under control conditions, including nonlinear profiles. ¹⁰ , ²³ , ²⁴ , ²⁹ , ³⁰ Subsequently, the pharmacokinetic parameters of P‐gp substrates (e.g., fe and intestinal availability after an oral dose [F _a F _g]) were calculated.

Optimization of DDI parameters of rifampicin

Stepwise optimization was applied to estimate the DDI parameters of rifampicin for P‐gp, similar to our previous reports. ¹⁴ , ¹⁵ Briefly, digoxin parameters obtained under control conditions and rifampicin parameters reported previously were used as fixed for optimization. The maximum induction effect (E _max) of rifampicin for P‐gp was optimized using the blood digoxin profile after repeated oral dosing of rifampicin (600 mg once daily for 15 days; i.e., DDI condition). ⁸ In this optimization, the P‐gp inhibition effect of rifampicin was not included because digoxin was administered 12 h after the last dose of the repeated rifampicin dosing and the inhibition effect appeared to be minimal. With the optimized E _max value as fixed, the inhibition constant (K _i ) value of rifampicin for P‐gp was then estimated using the blood digoxin profile, which was simultaneously administered with the last dose of rifampicin (600 mg once daily for 15 days). ⁸ The induction process of rifampicin for P‐gp was described using a turnover model, ¹⁵ , ³¹ and associated assumptions are provided as Supplementary Material S1. Briefly, rifampicin concentration in blood was set to induce the renal P‐gp instead of that in proximal tubular cells as a surrogate, assuming the free drug hypothesis. The unbound concentration for half maximum induction effect of rifampicin for P‐gp was set to be equal to that for CYP3A (63.9 nmol/L) optimized previously, ¹⁴ assuming the same concentration to activate pregnane X receptor‐mediated induction for P‐gp and CYP3A. Because of the lack of reported degradation rate constant (k _deg) values of P‐gp in the intestine, liver, and kidney, they were assumed to be equal to those of CYP3A in the intestine or liver.

Verification of the optimized rifampicin PBPK model

During multiple oral doses of 600 mg rifampicin, the relative P‐gp activities in the intestine, liver, and kidney were predicted using the optimized induction and inhibition parameters for P‐gp. The relative P‐gp activities were defined as P‐gp activities under rifampicin treatment with P‐gp activities in the absence of rifampicin set to 100%. In addition, the effects of rifampicin on the pharmacokinetics of digoxin, talinolol, and quinidine were predicted. For the DDI predictions, virtual clinical studies were performed using R (Version 4.1.1; R Foundation for Statistical Computing), taking into consideration variabilities in physiological and pharmacokinetic parameters from recent reports. ³² , ³³ The numbers, gender ratio, and body weight of the virtual subjects were matched to the published study designs, and 10 trials for each DDI study were generated. The predicted results were expressed as the blood concentration–time profiles, AUCRs, and maximum blood concentration ratios (C _maxRs) of P‐gp substrates and then compared with the observed corresponding data (mean ± SD) unless noted otherwise. To assess the prediction accuracy, Guest's criteria and the geometric mean fold error (GMFE) were used. ³⁴ Moreover, the predicted results without considering DDIs in the intestine, liver, or kidney were also presented to evaluate the DDI impact in each tissue.

RESULTS

Optimized PBPK models of P‐gp substrates

Certain PBPK model parameters for digoxin, talinolol, and quinidine were estimated using the respective blood profiles under control conditions (Table S2). The calculated values of fe, F _a F _g, and hepatic availability of each drug were in agreement with reported values (Table S2). In addition, optimized parameters were obtained for talinolol and quinidine using their nonlinear blood profiles after single oral doses of talinolol (25–400 mg) and quinidine (0.1–100 mg; Figure S1a,b and Table S2). ²³ , ²⁴ For the nonlinear analyses, the estimated dose‐normalized AUC and F _a F _g of talinolol and quinidine were within 1.8‐fold of the observed values with the in vitro unbound Michaelis–Menten constant value of talinolol for P‐gp (11.2 μmol/L) and quinidine for P‐gp (1.26 μmol/L) and CYP3A (6.15 μmol/L; Figure S1c–f). ²²

Optimized DDI parameters of rifampicin and predicted relative P‐gp activities during rifampicin treatment

The E _max value of rifampicin for P‐gp was estimated to be 4.01 using the observed blood profile of digoxin, which was given 12 h after the last dose of the repeated rifampicin dosing (Figure 2a and Table S2). ⁸ Subsequently, the K _i value of rifampicin for P‐gp was estimated to be 402 ng/ml (0.488 μmol/L) using the observed blood profile of digoxin, which was simultaneously coadministered with the last dose of the repeated rifampicin dosing (Figure 2b and Table S2). ⁸

FIGURE 2.

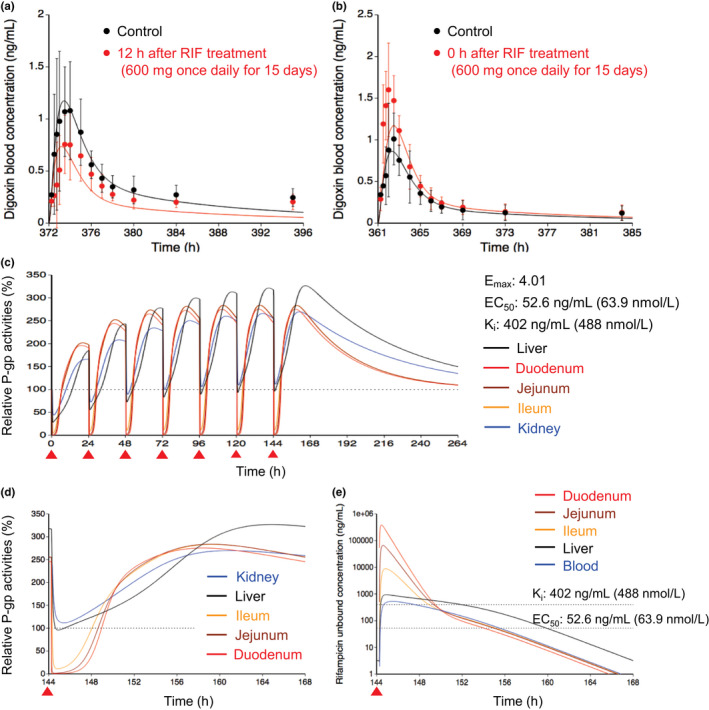
Optimized and observed blood concentration–time profiles of digoxin before and after repeated oral dosing of RIF and relative P‐gp activities in the intestine, liver, and kidney during RIF treatment. (a, b) Blood concentration–time profiles of digoxin after a single oral dose of 0.5 mg digoxin before (black) and after (red) repeated oral dosing of 600 mg RIF once daily for 15 days. ⁸ The predicted digoxin profiles were shown with the hepatic β value of 0.5 because no major differences were observed with three β values of 0.2, 0.5, and 0.8. Solid lines and closed circles represent optimized and observed blood profiles of digoxin, respectively. Observed blood concentrations were shown as mean ± SD. (c, d) Predicted time profiles of relative P‐gp activities in the first liver (black) of the five‐liver model, duodenum (red), jejunum (brown), ileum (orange), and kidney (blue) during repeated oral dosing of 600 mg RIF. Black dashed horizontal line represents unity. The E _max, EC₅₀, and K _i values of RIF for P‐gp are indicated at the right side. The degradation rate constant value for P‐gp was set to be 0.0158/h in the liver and kidney or 0.0288/h in the duodenum, jejunum, and ileum. The red closed triangles represent the timing of RIF dosing. The time window from 144 h to 168 h after the last dose of RIF was expanded and shown in Figure 2d. (e) Unbound concentration‐time profiles of RIF in the first liver (black), duodenum (red), jejunum (brown), ileum (orange), and blood (blue) under the same condition as Figure 2d. Black dashed horizontal lines represent K _i and EC₅₀ values of RIF for P‐gp. EC₅₀, concentration for the half maximum induction effect; E _max, maximum induction effect; K _i , inhibition constant; P‐gp, P‐glycoprotein; RIF, rifampicin

Using the induction and inhibition parameters of rifampicin, relative P‐gp activities in the liver, intestine, and kidney were predicted during repeated oral dosing of 600 mg rifampicin (Figure 2c). With a single dose of 600 mg rifampicin, the P‐gp activities decreased to 28% in the liver, ≤5% in the intestine, and 44% in the kidney at the trough because of the inhibition of P‐gp. At steady state, following repeated dosing of rifampicin, the P‐gp activities increased to 321% in the liver, 276%–284% in the intestine, and 266% in the kidney. Upon the administration of the next rifampicin dose, the P‐gp activities decreased to 93% in the liver, ≤11% in the intestine, and 109% in the kidney at the trough and then recovered with the decrease of rifampicin concentration in each tissue (Figure 2d,e).

Verification of the PBPK models by comparing DDIs between rifampicin and P‐gp substrates

Case 1: digoxin

The effects of rifampicin on the pharmacokinetics of digoxin were predicted in seven cases with varying dosing regimens. ⁶ , ⁸ , ⁹ , ³⁵ , ³⁶ The PBPK model of rifampicin including the P‐gp inductive and inhibitory effects reasonably captured the observed blood profiles of digoxin (Figure 3). The predicted AUCRs and C _maxRs for digoxin met Guest's criteria in all seven cases (Figure 4 and Table S3). In addition, the predictive accuracy of the digoxin AUCR was reduced when the intestinal induction and inhibition of P‐gp were not taken into account (Figure S2, orange symbols). Because the hepatic clearance of digoxin was approximately 10 times lower than the total clearance, ⁶ the hepatic β value could not be determined by sensitivity analyses (Figure S2 and Table S3).

FIGURE 3.

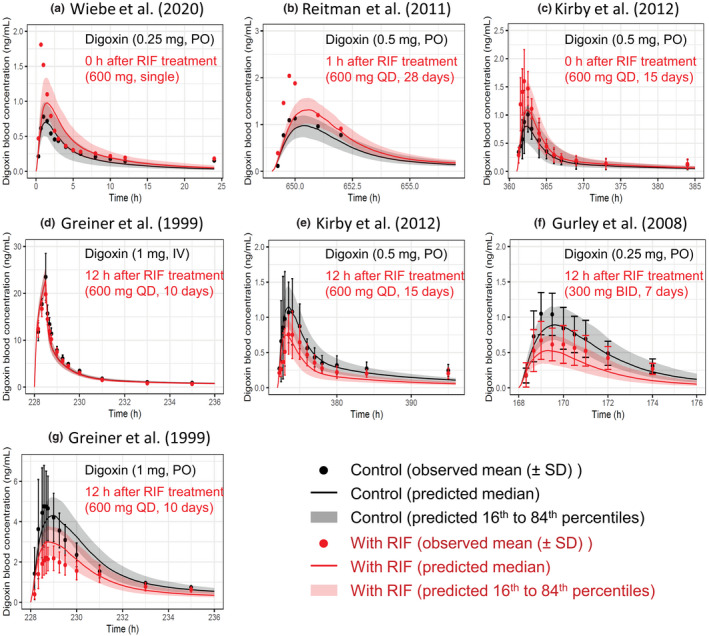
Predicted and observed blood concentration–time profiles of digoxin with various dosing regimens of RIF. Solid lines and closed circles represent predicted and observed blood concentration–time profiles of digoxin before (black) and after (red) RIF treatment. The shaded areas illustrate the respective 68% prediction intervals. The predicted digoxin profiles were shown with the hepatic β value of 0.5 because no major differences was observed with three β values of 0.2, 0.5, and 0.8. For drug–drug interaction predictions, P‐glycoprotein induction and inhibition effects of RIF in the intestine, liver, and kidney were incorporated. Detailed dosing regimens of digoxin and RIF are indicated on each figure. (a) Digoxin was orally dosed with a single PO dose of 600 mg RIF. ⁹ (b, c, e, g) Digoxin was orally dosed simultaneously (c), 1 h (b), or 12 h (e, g) after the last dose of repeated oral dosing of 600 mg RIF once daily. ⁶ , ⁸ , ³⁵ (d) Digoxin was intravenously dosed 12 h after the last dose of repeated oral dosing of 600 mg RIF once daily. ⁶ (f) Digoxin was orally dosed 12 h after the last dose of repeated oral dosing of 300 mg RIF twice daily. ³⁶ BID, twice daily; IV, intravenous infusion; PO, oral; QD, once daily; RIF, rifampicin

FIGURE 4.

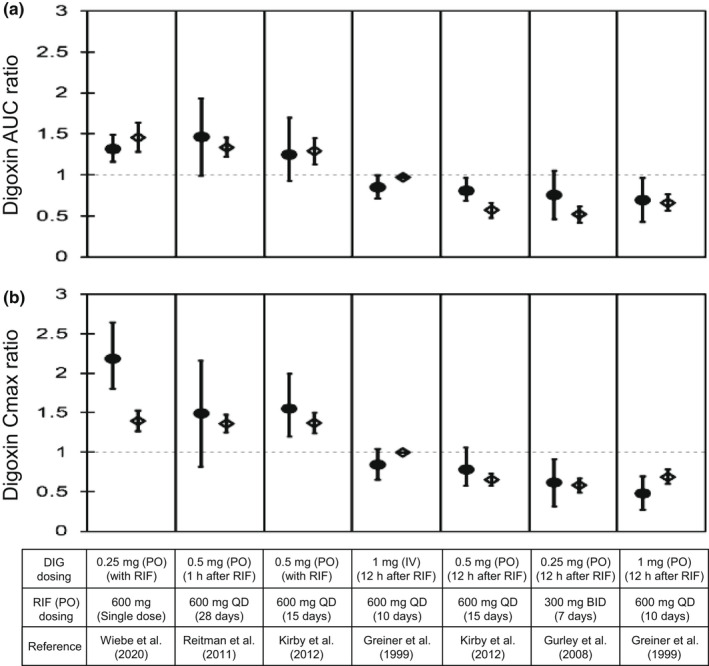
Predicted and observed AUC and C _max ratios of DIG with various dosing regimens of RIF. Closed circles and open diamonds represent the observed and predicted DIG AUC ratios (a) and C _max ratios (b) that were obtained from Figure 3. The predicted values of DIG with the hepatic β value of 0.5 were shown because no major differences were observed with three β values of 0.2, 0.5, and 0.8. Dosing regimens of DIG and RIF are indicated at the bottom. The observed data are shown as mean ± SD or mean (90% confidence interval; first, third, and fifth boxes from the left). The predicted data are shown as mean ± SD. AUC, area under the plasma concentration–time curve; BID, twice daily; C _max, maximum blood concentration; DIG, digoxin; IV, intravenous infusion; PO, oral; QD, once daily; RIF, rifampicin

Case 2: talinolol

The effects of rifampicin on the pharmacokinetics of talinolol were predicted in two dosing routes of talinolol using the components for P‐gp induction and inhibition (Figure 5a,b). When an intravenous 30‐min infusion dose of talinolol was given 13 h after rifampicin treatment (600 mg once daily for 9 days), the predicted AUCR (0.82 ± 0.07) and C _max R (0.97 ± 0.01) of talinolol with the hepatic β value of 0.8 were in agreement with the observed AUCR (0.79 ± 0.15) and C _max R (0.81 ± 0.19; Figure 6a,c). ¹⁰ When talinolol was orally dosed 13 h after rifampicin treatment (600 mg once daily for 7 days), the predicted AUCR (0.73 ± 0.15) and C _max R (0.73 ± 0.11) of talinolol with the hepatic β values of 0.8 were comparable with the observed AUCR (0.65 ± 0.32) and C _max R (0.62 ± 0.36; Figure 6a,c). ¹⁰ The hepatic β value of 0.5 and 0.8 gave the higher prediction accuracy (GMFE of 1.10 and 1.04 for AUCR, respectively) compared with the β value of 0.2 (GMFE of 1.35; Table S3). With the hepatic β value of 0.5 and 0.8, the prediction accuracy of talinolol AUCR was reduced when the intestinal induction and inhibition for P‐gp were not taken into account (Figure S3a,c, orange symbols).

FIGURE 5.

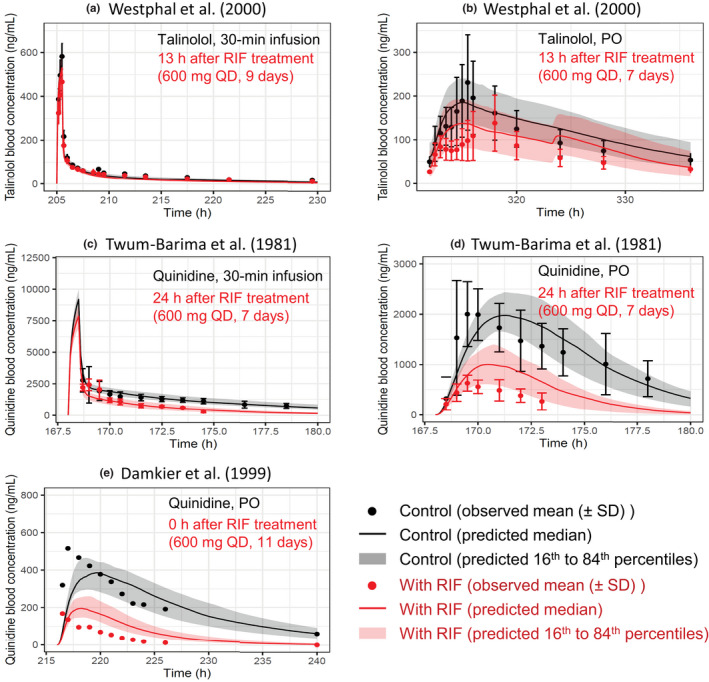
Predicted and observed blood concentration–time profiles of talinolol and quinidine with various dosing regimens of RIF. Solid lines and closed circles represent predicted and observed blood concentration–time profiles of talinolol (a, b) and quinidine (c–e) before (black) and after (red) RIF treatment. The shaded areas illustrate the respective 68% prediction intervals. The predicted talinolol profiles were shown with the hepatic β value of 0.8. For drug–drug interaction predictions with talinolol, P‐glycoprotein induction and inhibition effects of RIF in the intestine, liver, and kidney were incorporated. For drug–drug interaction predictions with quinidine, the following RIF effects were incorporated: (i) P‐glycoprotein induction and inhibition effects in the intestine and kidney; and (ii) cytochrome P450 3A induction effect in the intestine and liver. Dosing regimens of victim drugs and RIF are indicated on each figure. Talinolol was dosed intravenously (a) or orally (b) 13 h after the last dose of repeated oral dosing of 600 mg RIF once daily. ¹⁰ Quinidine was intravenously dosed (c) or orally dosed (d) 24 h after the last dose of repeated oral dosing of 600 mg RIF once daily. ²⁹ (e) Quinidine was orally dosed simultaneously with the last dose of repeated oral dosing of 600 mg RIF once daily. ³⁰ PO, oral; QD, once daily; RIF, rifampicin

FIGURE 6.

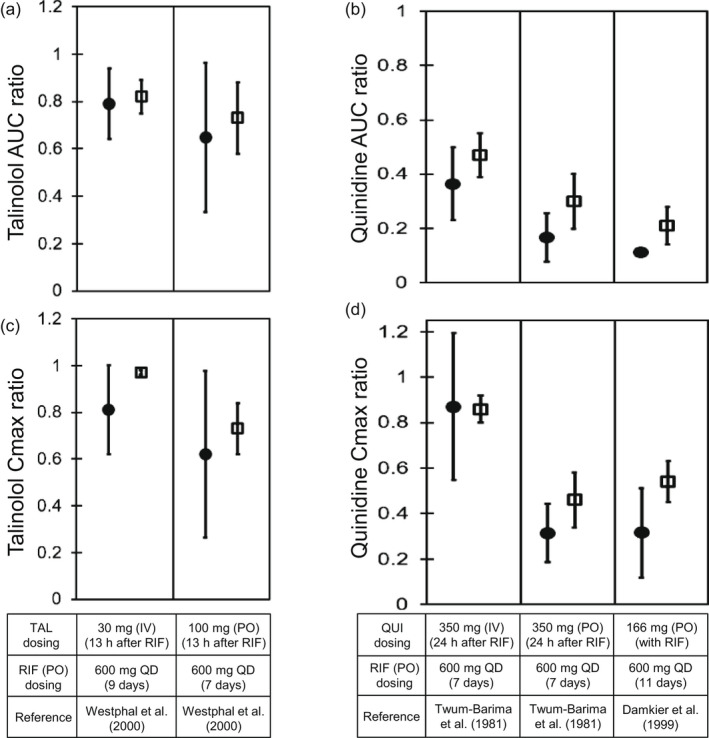
Predicted and observed AUC and C _max ratios of TAL and QUI with various dosing regimens of RIF. Closed circles and open diamonds represent the observed and predicted AUC ratios (a, b) and C _max ratios (c, d) of TAL (a, c) and QUI (b, d). The AUC ratios and C _max ratios were obtained from Figure 5. The predicted values of TAL with the hepatic β value of 0.8 were shown. Dosing regimens of TAL, QUI, and RIF are indicated at the bottom. The observed and predicted data are shown as mean ± SD. AUC, area under the plasma concentration–time curve; C _max, maximum blood concentration; IV, intravenous infusion; PO, oral; QD, once daily; QUI, quinidine; RIF, rifampicin; TAL, talinolol

Case 3: quinidine

The effects of rifampicin on the pharmacokinetics of quinidine were predicted in three cases using the components for P‐gp/CYP3A induction and P‐gp inhibition (Figure 5c–e). When an intravenous 30‐min infusion dose of quinidine was given 24 h after rifampicin treatment (600 mg once daily for 7 days), the predicted AUCR (0.47 ± 0.08) and C _max R (0.86 ± 0.06) of quinidine were in agreement with the observed AUCR (0.36 ± 0.13) and C _max R (0.87 ± 0.32; Figure 6b,d). ²⁹ When quinidine was orally dosed simultaneously or 24 h after the last dose of rifampicin treatment (600 mg once daily for 7 or 11 days), the predicted AUCRs and C _maxRs of quinidine met Guest's criteria (Figure 6b,d). ²⁹ , ³⁰ The prediction accuracy was reduced when the hepatic CYP3A induction was not taken into account (Figure S3b,d, green symbols).

DISCUSSION

To predict P‐gp–mediated DDIs by rifampicin, it is crucial to integrate the effects of P‐gp induction and inhibition as well as DDI effects in the intestine, liver, and kidney. Because previously reported PBPK models of rifampicin did not predict P‐gp inhibition, we considered all such reports in this study. ¹⁶ , ³⁷ , ³⁸ Our established PBPK model of rifampicin successfully predicted P‐gp–mediated DDIs with three P‐gp substrates (digoxin, talinolol, and quinidine), each with different pharmacokinetic properties. Overall, in all 12 cases the predicted AUCRs and C _maxRs met Guest's criteria.

The optimized E _max (4.01) and K _i (0.488 μmol/L) values of rifampicin for P‐gp successfully predicted the blood digoxin profiles across the seven different dosing regimens with a range of AUCRs (0.70–1.31; Figures 3 and 4). Importantly, the greatest impact of the P‐gp–mediated DDIs was in the intestine, with minimal impacts in the liver and kidney when predicting the effects on DDIs in each tissue (Figure S2). The predicted maximum blood concentrations of digoxin, where digoxin was given simultaneously or 1 h after oral dosing of rifampicin, were underestimated relative to the observed values (Figure 3a–c). The reason for this discrepancy is unclear but may include an inhibitory effect of rifampicin on the binding of digoxin to Na,K‐ATPase, the pharmacological target of digoxin, considering that digoxin has a large distribution volume (5 L/kg) and its tissue distribution is governed principally by its binding to Na,K‐ATPase as cardiac glycosides. ²⁰ , ³⁹

Our PBPK model of rifampicin predicted the inductive and inhibitory effects on the P‐gp activities during multiple doses of 600 mg rifampicin (Figure 2c). The predicted increases in intestinal P‐gp activities (approximately 2.8‐fold) were comparable with the following induction levels after repeated oral dosing of 600 mg rifampicin: (i) the intestinal P‐gp protein levels increased to 3.0‐fold (average value of six reports ranged from 1.1‐ to 8.3‐fold; Table S4) and (ii) the estimated increases of intestinal P‐gp protein levels were three‐ to four‐fold by the recent PBPK analyses. ³⁷ Moreover, our predicted induction level of hepatic P‐gp (3.2‐fold) was comparable with the increase (2.1 ± 2.1 fold) of biliary excretion of digoxin after multiple doses of 600 mg rifampicin. ¹³ These results indicate the utility of the optimized E _max value to predict intestinal and hepatic P‐gp–mediated DDIs by rifampicin with diverse P‐gp substrates.

Regarding the renal P‐gp induction, because there have not been clinical data that can be compared with our predicted increase level (2.6‐fold), further investigation will be needed. However, it is worth emphasizing that the renal P‐gp induction and inhibition by rifampicin had little effect on digoxin AUCRs and C _maxRs (Figure S2, gray symbols). The modeling results suggested that renal clearance of digoxin, the primary elimination pathway, was not changed by rifampicin treatment, which was consistent with clinical data. ⁶ , ⁸ This may be because P‐gp–mediated efflux of digoxin was not a rate‐limiting step of the active renal secretion. Considering that the surface area of the apical membrane in the renal proximal tubule is 7.5 times that of the basolateral membrane, ⁴⁰ intracellular digoxin is mostly excreted into the urinary lumen even when passive diffusion alone is considered, resulting in the calculated renal β value of 0.88. Thus, we reasoned that renal P‐gp–mediated DDIs by rifampicin did not impact the pharmacokinetics of digoxin.

Although the k _deg values of P‐gp in the intestine, liver, and kidney were set to be equal to those of CYP3A, this assumption did not affect the optimized E _max value for P‐gp because of the fact that a 0.5‐ to 2‐fold change in the k _deg values in each tissue resulted in only a 0.94‐ to 1.04‐fold change in the E _max value (data not shown). Of note, the optimized K _i value (0.488 μmol/L) of rifampicin for P‐gp differed by approximately ninefold from the lowest K _i value (4.3 μmol/L) reported in vitro (Table S4). ⁴¹ For further validation of the optimized K _i value, clinical evaluation of the inhibitory effect may be needed by changing the rifampicin dose or dosing intervals between rifampicin and the P‐gp substrate. Recently, the in vitro and in vivo K _i values for intestinal P‐gp by itraconazole and verapamil were reported to be consistent. ⁴² In the literature, the following parameters were optimized or assumed, unlike our analysis method: (i) fractional P‐gp efflux to overall efflux, including passive permeability for P‐gp substrates; and (ii) unbound fraction in the enterocytes for P‐gp substrates and perpetrators. Further studies on the setting of these parameters will be needed to successfully predict P‐gp–mediated DDIs.

For the PBPK model of talinolol, predictive accuracy for P‐gp‐mediated DDIs by rifampicin was higher when the hepatic β value of talinolol was 0.5 or 0.8 compared with 0.2, suggesting that the in vivo β value could be moderate or high (Figure S3a,c and Table S3). Further investigations may be necessary to account for the slight discrepancies between the predicted and observed talinolol profiles (Figure 5b). Grapefruit juice is reported to inhibit the intestinal uptake of talinolol and decrease the AUC of talinolol (AUCRs of 0.56 and 0.64). ⁴³ In our simulation, 80% inhibition of the intestinal uptake transporter resulted in a talinolol AUCR of 0.58 (data not shown). Considering the well‐predicted results of the nonlinearity and interactions with rifampicin and grapefruit juice, our constructed PBPK model of talinolol could reflect in vivo situations.

Regarding the nonlinearity of quinidine, the contributions of intestinal CYP3A and P‐gp to the dose‐dependent F _a F _g values were similar to the previous report (Figure S1f). ²² Regarding the DDIs with multiple dosing of rifampicin, our quinidine model was comparatively predictive of the blood profiles after an intravenous dose of quinidine, but overestimated the blood profiles after oral doses of quinidine (Figure 5c–e). The modeling results suggested that the hepatic CYP3A induction by rifampicin was well predicted but slightly underestimated the intestinal P‐gp/CYP3A‐mediated DDIs (Figure 6). We hypothesize that overestimated saturation of intestinal P‐gp(CYP3A) attributed to the high doses of quinidine may result in underestimation of the P‐gp(CYP3A) inductive effects of rifampicin from the calculated F _a(F _g) values (Figure S1f and Table S2). Further assessment may be warranted to understand the complex intestinal disposition of quinidine, including the nonlinearity and transporter‐enzyme interplay.

In conclusion, the present study established a robust PBPK model of rifampicin that can predict P‐gp induction‐ and inhibition‐mediated DDIs. The established PBPK model successfully predicted the P‐gp‐mediated DDIs with digoxin, talinolol, and quinidine under various conditions with different doses, timing, duration, and administration routes. These findings demonstrate that our rifampicin PBPK model can be useful for predicting DDIs with various P‐gp substrates and investigating the magnitude of DDIs in the intestine, liver, and kidney.

CONFLICT OF INTEREST

The authors declared no competing interests for this work.

AUTHOR CONTRIBUTIONS

R.A., K.N., Y.Y., K.S.T., and Y.S. wrote the manuscript. R.A. and Y.S. designed and performed the research and analyzed the data.

Supporting information

Appendix S1

Table S1

Table S2

Table S3

Table S4

Figure S1

Figure S2

Figure S3

Asaumi R, Nunoya K, Yamaura Y, Taskar KS, Sugiyama Y. Robust physiologically based pharmacokinetic model of rifampicin for predicting drug–drug interactions via P‐glycoprotein induction and inhibition in the intestine, liver, and kidney. CPT Pharmacometrics Syst Pharmacol. 2022;11:919‐933. doi: 10.1002/psp4.12807