Abstract
We present the application of ReconGAN, introduced in a previous study, for simulating the vertebroplasty (VP) operation and its impact on the fracture response of a vertebral body. ReconGAN consists of a Deep Convolutional Generative Adversarial Network (DCGAN) and a finite element based shape optimization algorithm to virtually reconstruct the trabecular bone microstructure. The VP procedure involves injecting shear‐thinning liquid bone cement through a needle in the trabecular region to reinforce a diseased or fractured vertebra. To simulate this treatment modality, computational fluid dynamics (CFD) is employed to predict the morphology of the injected cement within the bone microstructure. A power‐law equation is utilized to characterize the non‐Newtonian shear‐thinning behavior of the polymethyl methacrylate (PMMA) bone cement during injection simulations. The CFD model is coupled with the level‐set method to simulate the motion of the interface separating bone cement and bone marrow. After predicting the cement morphology, a data co‐registration algorithm is employed to transform the CFD model to a high‐fidelity continuum damage mechanics (CDM) finite element model of the augmented vertebra for predicting the fracture response. A feasibility study is presented to demonstrate the ability of this CFD‐CDM framework to investigate the effect of VP on the mechanical integrity of the vertebral body in a cancer patient with a lytic metastatic tumor.
Keywords: computational fluid dynamics, finite element method, spinal metastasis, vertebral fracture, Vertebroplasty
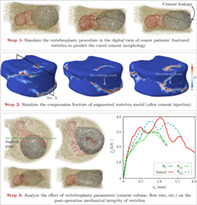
An integrated computational framework is presented to simulate the vertebroplasty operation in spinal metastasis cancer patients with fractured vertebra and studying its impact on restoring the mechanical integrity of vertebra. The cement injection process is simulated in a realistic digital twin of vertebra using computational fluid dynamics to predict the cured cement morphology, followed by performing high fidelity finite element analysis to simulate the vertebral compression fracture. This predictive capability is employed to study the effect of various parameters such as the needle tip location, injection flow rate, and cement volume on the risk of cement leakage through pedicles, as well as the mechanical stability of the augmented vertebra.
1. INTRODUCTION
Vertebroplasty (VP) is a common treatment modality that helps to stabilize the vertebra in metastatic cancer or osteoporotic patients suffering from vertebral fracture (VF). 1 , 2 , 3 This minimally invasive procedure involves injecting a polymeric material such as polymethyl methacrylate (PMMA) bone cement via a needle to fill the trabecular regions of the diseased/fractured vertebra. The in‐situ polymerization, that is, hardening of the bone cement, mechanically stabilizes the affected vertebra, which can significantly reduce pain and improve the quality of life in VF patients. However, based on the clinical follow‐up observations in such patients, the augmented vertebral body or its adjacent bodies could be subjected to new fractures. 4 , 5 These secondary fractures are often associated with the natural history of osteoporosis, 6 or the increased stiffness of the augmented bone, inducing fracture on adjacent vertebra. 7 , 8 Further, the injection of bone cement may come with adverse risks such as thermal necrosis of the bone tissue (due to high polymerization temperatures) 9 or intraspinal cement leakage. 10 , 11 Although most leakages are asymptomatic, serious complications may emerge if the cement injection causes pulmonary embolism or compression of the spinal cord. 12 As VP is widely available and could help thousands of patients each year (e.g., 24,316 operations from 2012 to 2017 in the Medicare population 13 ), prospective data on proper use of VP is vital for managing high‐risk cases.
The recovery of the vertebra's mechanical stability after the VP procedure, as well as the side effects discussed above, are directly linked to the morphology of the polymerized cement. Several biomechanical factors, such as the cement viscosity, injection flow rate, injected volume, and trabecular tissue architecture, affect the cement shape and, thereby, the VP efficacy. The anisotropic permeability of the underlying tissue, which consists of the trabecular bone, pre‐existing cracks, and potential tumors, leads to high variability in the cement infiltration pattern. In a successful VP procedure, the bone cement uniformly infiltrates trabecular cavities, and its volume is sufficient to recover the mechanical strength of the vertebral body. It is suggested to keep the maximum injection pressure below 2 MPa to reduce micro‐scale damages associated with the injection process. 14 Cement viscosity has been identified as a crucial parameter affecting the uniformity of the filling pattern, and thereby the risk of cement leakage. 14 , 15 Experimental studies have shown that polymeric‐based bone cements such as PMMA are shear‐thinning non‐Newtonian fluids. 16 Therefore, the cement viscosity decreases at higher fluid shear rates, which in turn increases the risk of cement leakage.
Besides in vivo and in vitro studies, computational modeling can be used to study the VP procedure. The cement injection process, which is a fluid dynamics problem from a physical point of view, has been numerically investigated using various computational techniques. 17 , 18 , 19 These studies are based on the solution of Darcy's law in conjugation with effective underlying permeabilities, directly estimated from imaging data. For example, a computational homogenization (CH) approach is employed to upscale micro‐scale rheological properties of PMMA to the macroscale. 19 However, such models overlook the complex porous microstructure of the vertebra, which is crucial for predicting the cement infiltration pattern. An accurate simulation of this process requires creating a realistic geometrical model of the vertebra that captures its intricate microstructure. Incorporating local tissue architecture in the CFD model of a patient's vertebra could be a challenging task, as current diagnostic imaging technologies such as computed tomography (CT) lack the required resolution to capture such microstructural details. As an alternative approach, micro‐CT imaging can provide a high‐resolution visualization of the 3D bone microstructure with sub‐micron accuracy. Numerical studies based on the microscale flow through trabecular cavities extracted from micro‐CT data are carried out using techniques such as the lattice Boltzmann method 20 and the finite volume method. 21 However, such studies are limited to only a small trabecular sample, which does not provide a sufficiently sizable geometrical model that takes into account microstructural features of the whole vertebra. Moreover, micro‐CT data can only be acquired from small cadaveric samples, which does not allow the reconstruction of a patient‐specific model.
Among numerical studies currently available in the literature, the main focus is on the simulation of the treated vertebra's mechanical behavior after performing VP through finite element (FE) simulations. 22 , 23 , 24 Such studies enable virtually evaluating the impact of various underlying parameters such as pre‐existing defects, 23 cement distribution, 22 and the cement stiffness 24 on the efficacy of VP. However, most of these investigations assume a pre‐determined bone cement distribution, 23 which is not necessarily specific to the subject's underlying vertebral body microstructure. Some studies use a geometrical model of the vertebra directly reconstructed from CT data, although this approach limits the scope of the study to one injection scenario at a time, as well as the time/cost associated with experimental and imaging procedures. 22 To address this limitation, a combination of CFD simulations to predict the cement injection pattern after VP and high‐fidelity FE simulations to predict the corresponding VF response of the augmented vertebra simulations is presented in Reference 17. However, this study does not take into account the complex microstructural features of the whole vertebra, which could affect the accuracy of the resulting predictions.
The challenges outlined above have motivated the implementation of a CFD model to simulate the injected cement morphology within the ReconGAN framework, 1 which enables reconstructing a realistic geometrical model of the vertebra and predicting its post‐VP fracture response. The knowledge gained from this effort will provide insights on optimizing VP and maximize its clinical benefit. The ReconGAN model relies on a deep convolutional generative adversarial network (DCGAN) 25 learning algorithm to synthesize realistic gray‐scale microstructural models of the trabecular tissue. The main reason for using this model to synthesize the trabecular microstructure rather than a direct reconstruction from quantitative micro‐CT (micro‐QCT) data is the unique ability of DCGAN to enlarge the size of the virtual microstructure. Given the small size of cadaveric samples used for preparing micro‐QCT imaging data, this scalability is essential for synthesizing a sufficiently large model of the trabecular bone microstructure that can subsequently be embedded in a whole vertebra model (cortical shell) using a shape optimization‐based approach. The resulting digital twin of the vertebral body can then be transformed into a high‐fidelity FE model to analyze vertebra's mechanical stability under different loading conditions. Using CFD to simulate the injected cement morphology within the trabecular region of this digital twin not only allows for predicting its fracture response after the VP but also enables linking this response to operation parameters such as needle tip location, cement volume, and injection rate.
After synthesizing the vertebral geometrical model and simulating the VF response, image segmentation is performed to isolate the porous phase of the fractured vertebra and convert that into a high‐fidelity mesh for cement injection CFD simulations. In these simulations, the level‐set method 26 is employed to track the interface separating the injecting PMMA cement and the bone marrow under the assumption of a two‐phase immiscible flow. 27 This assumption is justified by the non‐zero surface tension at the interface between cement and the bone marrow, which results in a distinct fluid–fluid interface separating these phases in the porous trabecular microstructure. 28 After the injection simulation, the cured cement morphology is embedded in vertebra's FE model to simulate its VF response and compare that with that of the original vertebra before the VP operation. Because the meshes used in CFD and continuum damage mechanics (CDM) simulations do not precisely coincide, an image co‐registration approach is employed to accomplish this task. Note that, due to the shrinkage of the cement during the polymerization process, the cement‐bone interface is debonded in some regions. 29 Therefore, the interdigitation between the PMMA cement and trabecular microstructure is an important factor on the mechanical stability of augmented vertebra, 30 which must properly be reflected in the FE model used for the VF simulation. It is noteworthy that this simulation is carried out using a phenomenological strain‐based damage model, accounting for stress triaxiality in the bone tissue. 31 The stress triaxiality, which is the ratio of the hydrostatic stress to the von‐Mises stress, 32 accounts for tension‐compression asymmetry and loading mode dependency of the bone response. 33
The remainder of this manuscript is structured as follows: Constitutive equations and material properties associated with the flow of PMMA cement are presented in Section 2. Section 3 provides a detailed description of the CFD model, as well as the reconstruction of FE models used for CFD and CDM simulations. A thorough feasibility study is presented in Section 4 on the ability of the integrated CFD‐CDM framework for investigating the effect of three VP parameters, namely the cement flow rate, cement volume, and the needle tip location on the cured cement morphology and its subsequent impact on the risk of VF in the augmented vertebra. Final concluding remarks are summarized in Section 5.
2. CONSTITUTIVE MODELS AND MATERIAL PROPERTIES
PMMA‐based bone cements used for clinical applications are composed of a polymeric powder and a liquid monomer. 34 Upon mixing, the cement shows a non‐Newtonian flow behavior with properties recorded through rheological measurements. 35 , 36 Studies have shown that in addition to the time‐dependency of viscosity, PMMA‐based cements are shear‐thinning, 36 meaning the viscosity decreases at higher fluid shear rates. In the current study, the rheological behavior of PMMA is defined using a power‐law relationship as 16
| (1) |
where is the dynamic viscosity, is the fluid shear rate, 60 s is the characteristic time, and 1.0 is the characteristic shear rate. Also, and are PMMA viscosity parameters adopted from Reference 16 as Pa.s, Pa.s, , and . Note that the parameters used in the equation above are validated for Simplex bone cement, which is a widely used bone cement for orthopedic applications.
In the CFD simulations presented in this work, the scripting interface of COMSOL Multiphysics software package 37 is employed to evaluate the cement viscosity as a function of time and shear rate. The shear rate is given by
| (2) |
where is the strain rate tensor. The cement and bone marrow flows are governed by the Navier–Stokes equations as
| (3) |
where is the pressure, is the velocity, is the density, and is the force vector associated with the surface tension between the bone marrow and the cement. Here, and represent inertial and viscous components deriving the fluid flow. In the current study, we assume , 20 , 18 and . 38
The cement flow in trabecular cavities is characterized using the Reynolds number,
| (4) |
where is the characteristic length scale associated with the internal microstructure. It is well‐known that at low Reynolds numbers, viscous forces are significantly higher than inertial forces, which is also known as a creeping flow. 39 In this work, a preliminary simulation was carried out that showed the maximum Reynolds number during the injection process was , meaning the creeping flow regime is in place and the effect of in (3) can be neglected.
3. VIRTUAL RECONSTRUCTION OF AUGMENTED VERTEBRA
As outlined in Section 1, the goal of the present work is to simulate the VP procedure and quantitatively understand its impact on the mechanical stability of the vertebra. In this section, we present a CFD‐assisted algorithm for reconstructing a realistic geometrical model of an augmented vertebra after performing this procedure. This framework consists of four main phases: (i) generating a 3D geometrical model of the vertebra using the ReconGAN framework 1 ; (ii) simulating the fractured vertebra geometry through continuum damage mechanics (CDM) FE simulations; (iii) predicting the injected cement morphology via CFD simulations, which requires using the level‐set algorithm to track the cement‐marrow interface during the injection process; (iv) performing CFD‐CDM data integration to incorporate the cement morphology in a second FE model to predict its mechanical stability via CDM simulations.
As described in Reference 1, ReconGAN relies on a 3D deep convolutional generative adversarial network (DCGAN) to generate a realistic microstructural model of the trabecular bone tissue after being trained with micro‐QCT images obtained from cadaveric samples. Classic Generative Adversarial Networks (GANs) use two independent networks (generator and discriminator) in an adversarial manner such that the generator aims to produce fake samples while the discriminator determines if these samples are sufficiently realistic or not through comparison with reference data. From a mathematical perspective, these networks play a two‐player min‐max game with the objective of generating very good fake images (here, bone microstructure) that are indistinguishable from real ones. The resulting virtual microstructure is infused into the vertebra cortical shell extracted from the patient's CT data to fill the interior region. Additionally, an FE‐based shape optimization algorithm is employed to locally (along trabecular‐cortical interfaces) evolve the initial synthetic model into an optimal digital design, with a smooth transition from the tubercular tissue to the cortical shell. This is a crucial step to avoid unrealistic stress concentrations in this region that lead to premature damage (and thus under‐estimating the strength) when simulating the fracture response of the vertebra. To track the progression of damage in the bone tissue, a continuum damage model is implemented that relies on the von‐Mises yield criterion with the hardening law
| (5) |
where is the von‐Mises stress, is the equivalent plastic strain, and represents the yield stress function. Damage initiation and progression are then triggered based on a strain‐driven criterion given by
| (6) |
where is the threshold value and is a function of stress‐triaxiality . From theories of continuum mechanics, it is well‐known that incorporating the stress‐triaxiality in damage formulation accounts for tension‐compression asymmetry in mechanical behavior of the bone tissue. Next, we describe the CFD model and the integration of CFD‐CDM data for re‐assessing the vertebra fracture response post‐VP procedure.
3.1. Prediction of injected cement morphology
To simulate the cement injection into the trabecular region of the vertebral body, Navier–Stokes equations governing the bone marrow and cement are combined with the level‐set method to track the moving interface between these phases. In the level‐set algorithm, the interface location is implicitly tracked using a smooth step function, , which varies between zero in one fluid (bone marrow) to one in the other (cement) over the thickness . Typically, it is assumed that , where is the maximum element size of the CFD mesh. The following governing equation, coupled with Navier–Stokes equations, is solved during the cement injection simulation to evaluate
| (7) |
where is the interface velocity and is a problem‐specific stabilization parameter. It is suggested that an appropriate value for is the maximum magnitude of . To ensure numerical stability, the dynamic viscosity in the domain is defined as a function of the level‐set variable as
| (8) |
where and are dynamic viscosities of cement and bone marrow, respectively. Moreover, the level‐set variable is employed to evaluate the volumetric surface tension force vector given in (3) as 26
| (9) |
where is the surface tension coefficient. 40 To calculate the interface velocity, the Navier–Stokes and level‐set equations are solved as a fully coupled nonlinear system of equations using a staggered approach. 41 , 42 In this approach, the fully coupled system is divided into multiple uncoupled equations (Navier–Stokes and level‐set) solved separately. In this iterative process, the continuity of velocity and level‐set variable in the domain is ensured by exchanging information at the cement‐bone interface. For more details on the physics governing the two‐phase flow using the level‐set method, refer to Reference 43.
3.2. Creating augmented vertebral FE model
As shown in Figure 1, after simulating the cement injection process using a CFD model, the predicted cement morphology must be incorporated into the vertebra model to analyze its mechanical stability post‐VP operation. Note that while the FE models used for CFD and CDM simulations are completely different, the former requires simulating the cement injection into the bone marrow space and, therefore, the bone tissue is not incorporated in the FE model (cf. Figure 2A). On the other hand, Given the negligible mechanical stiffness of the bone marrow compared to the bone tissue, the bone marrow is not considered in the CDM FE model used for the VF simulation and is instead modeled as a porous region (cf. Figure 2B). Therefore, it is necessary to transform the cement morphology simulated using the CFD model (mesh 1) into mesh used for a subsequent CDM simulation (mesh 2) for the augmented vertebra.
FIGURE 1.
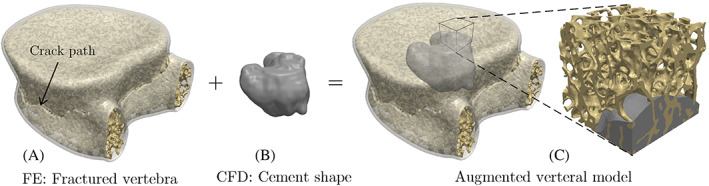
Creating the geometrical model of the augmented vertebra by infusing the cement morphology generated using CFD simulations within the fractured vertebral model generated using FE simulation. CFD, computational fluid dynamics; FE, finite element
FIGURE 2.
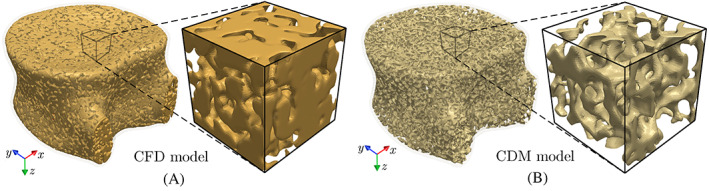
(A) CFD and (B) CDM models of the vertebra generated by segmenting bone marrow and bone tissue from imaging data to simulate cement injection and vertebral fracture, respectively. CDM, continuum damage mechanics; CFD, computational fluid dynamics
To incorporate the cement shape in the vertebra's FE model used for the VF simulation (mesh 2), we first convert this mesh into a voxelated geometrical model (volumetric image) represented in the VTK format. 44 The CFD simulation result (mesh 1) is converted into a binary image according to the level set variable assigned to each element, where the bone marrow and cement are identified as and , respectively. The injected cement morphology is then extracted from this volumetric binary image by performing image segmentation using the scikit‐image python package. 45 As shown in Figure 1C, the resulting cement shape can then be embedded in the voxelated model of mesh 2 to generate a geometrical model of the augmented vertebra.
A smooth transition between these geometrical models (vertebral trabecular tissue and cement) requires several additional considerations. First and foremost, it is crucial to use similar input parameters for generating mesh 1 and mesh 2 (i.e., similar element sizes, types, and local refinement levels) to avoid a significant mismatch between the trabecular geometry and cement shape along their interface. However, given that two distinct domains are modeled in mesh 1 and mesh 2 (the bone marrow versus the bone tissue; see Figure 3A,B), it would practically be impossible to avoid small mismatches between the cement morphology extracted from the former and the trabecular tissue (cf. Figure 3C).
FIGURE 3.
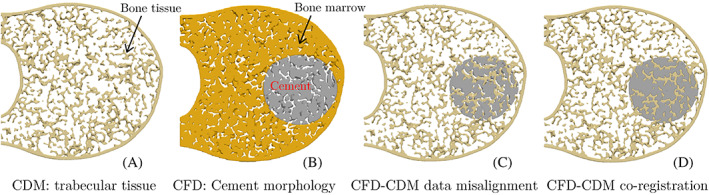
Cross sections of the vertebral body showing the process of stitching the CDM FE model (mesh 1) and the CFD simulation result (mesh 2) to generate an FE model of the augmented vertebra. CDM, continuum damage mechanics; CFD, computational fluid dynamics; FE, finite element
An image co‐registration approach is employed to address this issue by aligning the position and orientation of the two voxelated data. The co‐registration process involves identifying paired landmark points to generate the coordinate transformation function that puts (registers) both data sets in the same coordinate system. In the current work, a semi‐automatic co‐registration algorithm used in the 3DSlicer software package 46 is employed to stitch the vertebra model and the cement morphology obtained from CFD simulations (cf. Figure 3D). A conforming FE mesh is then generated for the resulting voxelated image of the augmented vertebra to simulate its fracture response and analyze its mechanical stability post VP operation. Note that the mesh size was selected after performing a mesh‐sensitivity analysis on fracture response of trabecular bone samples subjected to a compressive load.
Elastoplastic and damage properties of the bone tissue used in this FE model, as well as the process of mapping density‐dependent bone elastic modulus from voxelated model to the FE mesh, were presented in Reference 1. The workflow for evaluating the elastic modulus of the bone tissue from gray‐scale imaging data can be written as
| (10) |
where is the volume‐averaged gray‐scale value corresponding to each element of the FE mesh. The bone mineral density is calculated based on a linear curve interpolated between and parameters, which are calibrated using phantoms with known density scanned alongside the tissue sample. Finally, the elastic modulus is computed using a power law, with GPa and , which are calibrated for vertebral trabecular specimens subjected to compression. 47 Note that the bone cement (PMMA) is modeled as a linear elastic material with elastic modulus MPa and Poisson's ratio . 48
4. RESULTS AND DISCUSSIONS
In this section, we study the effect of three VP parameters, namely the cement flow rate, cement volume, and the needle location on the injected cement morphology and its subsequent impact on the fracture response of the augmented vertebra. As shown in Figure 4, four vertebral models virtually reconstructed using the ReconGAN framework are used in this study. The first model, , has no metastatic tumor or pre‐existing fracture, which is used as a benchmark to compare its response with three other models all having the same lytic tumor but different pre‐existing fracture patterns; : no cortical fracture and only minor cracks in the trabecular bone under uniform compression; : major cortical fracture caused by a higher uniform compressive load; and : cortical fracture caused by a flexion load (combined bending and compression). These pre‐existing fracture patterns are simulated using the FE CDM model, and the behavior of each case was previously studied in Reference 1. It is also worth mentioning that in addition to pre‐existing fractures, the presence of the lytic lesion significantly compromises the vertebra mechanical stability due to the deterioration of bone tissue and loss of its load‐bearing capacity within the tumor.
FIGURE 4.
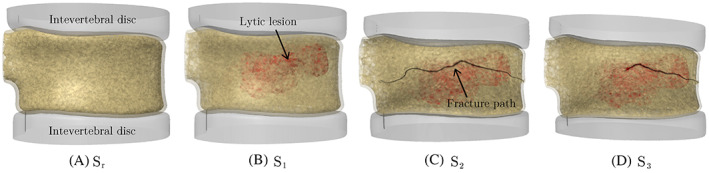
Geometrical models of vertebral bodies with (A) no lytic metastasis or pre‐existing fracture; (B) lytic tumor but no cortical fracture; (C) lytic tumor and pre‐existing cortical fracture under pure compression; and (D) lytic tumor and pre‐existing cortical fracture under a flexion load
CFD simulations were carried out using COMSOL for each vertebral model to predict the injected cement morphology corresponding to different needle locations, cement volumes, and flow rates. The lytic lesion is assumed to be surgically removed or irradiated in these models, meaning cement can flow into the resulting cavity without any resistance. In all CFD simulations, we assume the cortical shell pressure is , 49 with a zero‐shear slip boundary condition () along bone tissue surfaces, where is the unit normal vector to the surface. During a VP operation, the injection pressure of the surgical needle is monitored to ensure it is well below the trabecular strength ( MPa 14 ). In this study, we simulate a uni‐pedicular injection using a 13‐gauge needle for injecting cement into the anterior portion of the vertebra (cf. Figure 5). Given the large number of tetrahedral elements in the CFD models (: 11.8 million, : 10.3 million, : 10.1 million, and : 9.8 million), the simulations were conducted in parallel on 48 processors using the computing resources at the Ohio Supercomputer Center. The simulation times ranged from 32 to 54 h, depending on the flow rate and injected volume of the cement.
FIGURE 5.
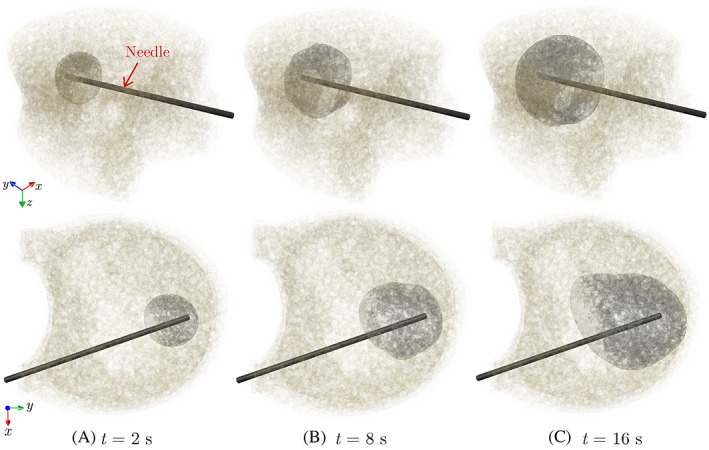
Different snapshots of the simulated cement morphology injected into the model for an injection flow rate of
Figure 5 shows three snapshots of the cement morphology at different stages of simulating the cement injection into the model for a flow rate of . The propagation front of the cement‐bone marrow interface is visualized by an iso‐surface representing a level‐set variable of . Note that the resulting cured cement shape depends on various parameters such as the bone microstructure, tumor morphology, injection site, injection flow rate, and cement volume. Unlike the first two parameters that are patient‐specific in nature, the other three parameters can be controlled by the surgeon to achieve the desired cement shape that maximizes the mechanical stability of the bone. As shown next, studying the impact of these three parameters on the cement morphology and the VF response of the augmented vertebra requires using a realistic patient‐specific model of the vertebra generated using the ReconGAN framework. We also aim to study the risk of cement leakage into the spinal canal associated with each parameter, which is one of the most serious side effects of the VP operation that causes pain and may necessitate follow‐up surgeries.
The first parametric study in this section focuses on the impact of the injection flow rate on the shape of the cured cement, where we simulated the injection of 4.0 ml of cement with three different flow rates (, 0.1, and 0.25 ) into the model (needle location similar to Figure 5). The cured cement shape corresponding to each case is illustrated in Figure 6, indicating a highly uniform (nearly ical) distribution of cement in the trabecular region for the lowest flow rate ( ). Increasing the injection flow rate leads to a more irregular cement pattern due to its accelerated flow in the path of least resistance (i.e., the lytic lesion). This irregular pattern is especially evident for the highest flow rate, , which also shows the cement intrusion into one of the pedicles indicating a higher risk of cement leakage. A similar phenomenon is observed in experimental studies, 14 where it has been shown that a higher injection flow rate reduces the ratio of the pressure needed to inject the cement into the lytic defect to the pressure required to expand that uniformly. While this magnified pressure reduces the cement viscosity and thereby helps filling the removed tumor regions more effectively, as shown in Figure 5C, it also leads to a more tortuous cement path that amplifies the risk of cement leakage through pedicels.
FIGURE 6.
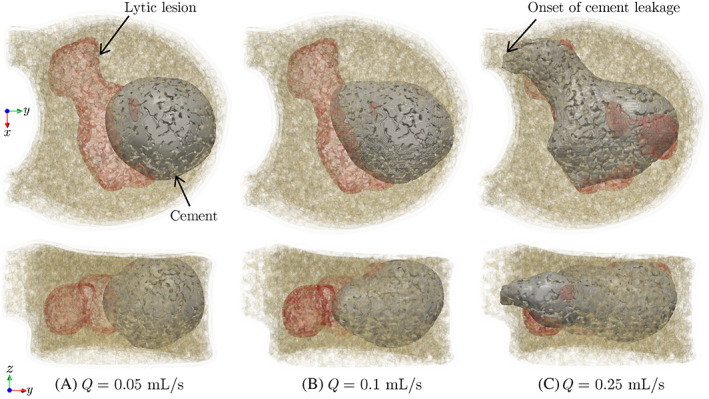
Morphologies of 4.0 ml of cement injected into the vertebra model at different flow rates. Top and bottom rows show top and side views of the vertebral body, respectively
According to the results presented above, an injection flow rate of is selected in the remainder of this study due to the uniform distribution of cement in the anterior region of the vertebra and the low risk of cement leakage associated with that. Figure 7 illustrates the top and side views of 4.0 ml of cement injected into , , , and vertebrae models (same needle location as Figure 5) at this flow rate. As shown in this figure, the injected cement properly fills the anterior region of all vertebra models, with the most ideal (spherical) pattern observed in the model. Note that in the VP procedure, from a clinical perspective, it is desirable that the injected cement cures into the shape of a uniformly expanding cloud 50 to minimize complications such as cement leakage through pedicles. However, the presence of tumors and pre‐existing fracture vertebrae such as those modeled in – lead to more irregular cement patterns, which is attributed to the fact that the cement tends to flow into the path of least resistance with the highest permeability (e.g., the large cavity caused by the lytic lesion) compared to the more intricate network of trabecular cavities in these models. Also, note the small cement leakage into the anterior cortical opening in the model due to a pre‐existing cortical fracture. While this leakage is not into the spinal canal and is not of particular concern compared to leakage through pedicels, this observation suggests that further increasing the injection flow rate could increase the side effects of the VP operation. While in practice, the healthy vertebral model () is not a candidate for the VP operation, comparing this benchmark model with the other three vertebral models in this study clearly shows the impact of the tumor and pre‐existing fracture (patient‐specific parameters) on the cement pattern.
FIGURE 7.
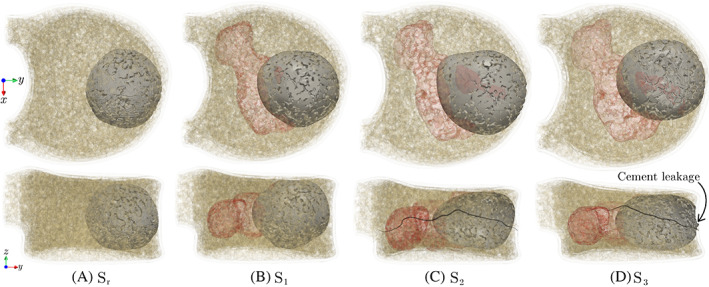
Morphologies of 4.0 ml of injected cement into (A) : intact vertebra, (B) : lytic vertebra with no cortical damage, (C) : lytic vertebra with pre‐existing crack under pure compression, and (D) : lytic vertebra with pre‐existing crack under flexion. Top and bottom rows show top and side views of the vertebral body, respectively
It is worthwhile to study the variation of the injection pressure during each of the CFD simulations with presented above. As shown in Figure 8A, in all four vertebra models, high injection pressure is initially required to enable the cement flow into trabecular cavities and push out the bone marrow. This initial pressure is particularly high in the model, where the trabecular microstructure is intact. On the other hand, the cavity (higher permeability) caused by the removal of the lytic tumor causes a much lower pressure threshold for injecting the cement into the vertebra. After this initial phase of the rapid surge in pressure, the injection pressure increases at a much lower rate in all models remotely mimicking a steady‐state flow condition, although the increasing viscosity associated with the progressive polymerization of the cement during the injection process does not allow reaching this condition in practice. It is worth noting that the pressure needed to inject the cement into the fractured vertebrae ( and ) is higher than that of the lytic vertebra with no cortical fracture ( model), which is due to the reduced height of fractured vertebrae and partial collapse of the tumor cavity that reduces permeability in and models. Nevertheless, in all four vertebral models, the injection pressure is well below the 2.0 MPa threshold that might cause mechanical damage to the trabecular microstructure.
FIGURE 8.
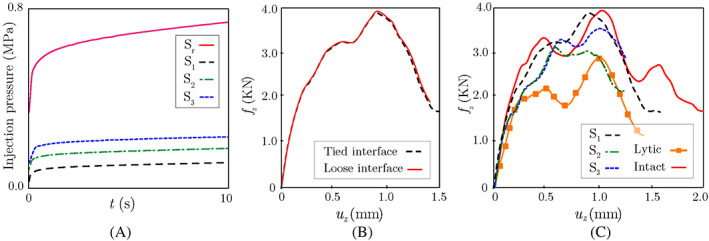
(A) Variation of the cement injection pressure versus time during VP CFD simulations; (B) Comparison between force‐displacement responses of augmented model with tied (strong bonding) and loose (hard contact) cement‐bone interfaces in the CDM model; (C) Simulated force‐displacement responses of augmented vertebrae , , and , as well as two non‐augmented vertebrae (intact and lytic) subjected to uniform compression. CDM, continuum damage mechanics; CFD, computational fluid dynamics
The ability to predict the injected cement morphology via CFD simulations allows for analyzing the VF response of the augmented vertebra via CDM simulations to quantify its restored mechanical stability post‐operation. Before performing such study, it is crucial to determine the impact of the cement‐bone interface bonding strength in the FE damage models on the VF simulation results. To quantify this effect, we consider two extreme cases in the FE damage model generated for the vertebra (lytic vertebra with no cortical fracture): loose interface (no bonding, only contact) and perfect bonding (tied interface) between the cement and trabecular bone. Figure 8B illustrates the simulated force‐displacement response of each model under uniform compression, which shows a negligible difference between these results. It is worth mentioning that the effect of cement‐bone interface bonding strength on the VF strength might depend on a variety of parameters such as the loading condition and the fracture mode. In the CFD simulations presented in this study, it is assumed that cement is fully infiltrated within the trabecular tissue, which provides a physical interlocking between cement and bone phases. Our numerical studies have shown that this interlocking is the dominant factor in stabilizing the vertebra compared to the cement‐bone bonding strength. Therefore, in the simulations presented next, a perfect bonding condition is assumed along the cement‐bone interface in the FE models used to study the VF response of augmented vertebrae.
To study the impact of the VP operation on restoring the mechanical stability of the vertebra, we simulated VF responses of three augmented vertebral models (, , and ) with 4.0 ml cement injection, as well as two non‐augmented vertebrae (lytic and intact) subjected to a uniform compression of mm/s. Figure 8C illustrates force‐displacement responses of the three augmented vertebrae generated using the CFD model and their comparison with responses of the intact and lytic models. As shown in this figure, the cement injection can considerably recover the mechanical stability of all augmented vertebrae, where the force‐displacement curves show a significant improvement compared to the lytic (un‐treated) model. Among the three treated vertebrae, the model (lytic cavity, no pre‐existing cortical fracture) shows a nearly complete restoration of mechanical stability compared to the intact model. This observation suggests that performing VP as a preventive measure before the emergence of cortical fracture could significantly reduce the risk of VF, although clinically, this is not often the case, and VP is mainly performed in patients with a fractured vertebra. Unlike the , the presence of cortical fracture in and only leads to 19.2% and 57.1% restoration of the strength, respectively. This can be attributed to the fact that at a low injection flow rate, the cement can only partially penetrate the crack surface, leading to a partial recovery of mechanical stability, although as shown previously, increasing the flow rate would increase the risk of cement leakage. It is also worth mentioning that despite a partial recovery of mechanical stability after the cement injection, minimizing the relative motion of fractured segments in these treated vertebrae could still significantly reduce the patient's pain after the VP operation.
To better understand the impact of injected cement on the VF response of the treated vertebra, damage patterns after failure in augmented , , and models are depicted in Figure 9. As shown in these figures, the final fracture path does not completely match the pre‐existing cortical fracture in these vertebrae. Instead, the damage often initiates and propagates from a site of high‐stress concentration in the trabecular bone adjacent to the cured cement. Figure 10 illustrates the damage propagation along Section A of the treated vertebra (cf. Figure 9A), showing that the trabecular tissue surrounded by the cement is practically immune to damage. Referring back to Figure 9, another key feature of damage pattern in all three models is damage on the upper surface of the vertebra, caused by pressing a thin layer of cortical bone on the cement in this region (also see Figure 10). In other words, compared to a healthy vertebra, the presence of cement in the treated vertebra disturbs the uniform stress distribution from the intervertebral disc to the treated vertebral body and causes damage accumulation on its upper and lower surfaces. Although only one vertebra is simulated in this work, we hypothesize that this behavior also explains the fractures commonly observed in adjacent vertebrae after the VP operation, 48 although further studies are required to verify this assumption.
FIGURE 9.
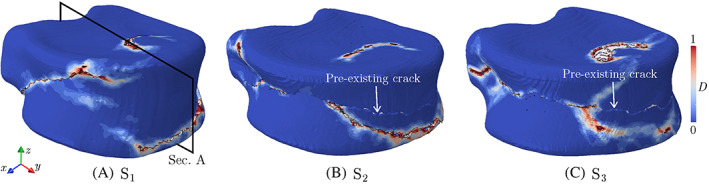
Damage pattern at the failure point in augmented , , and vertebra models subjected to uniform compression
FIGURE 10.
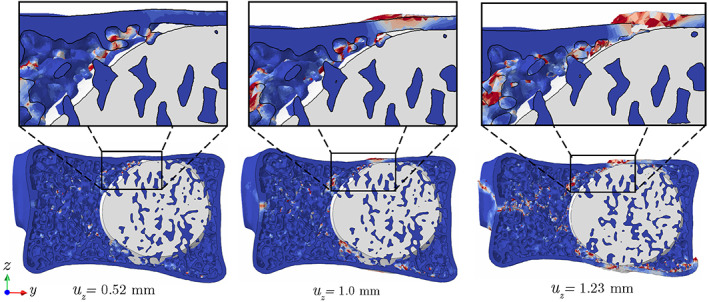
Damage propagation patterns on Section A of the vertebra (cf. Figure 9) under uniform compression
We also studied the impact of the needle location on the shape of the injected cement and corresponding VF response of the augmented vertebra. As shown in Figure 11A, in the first study, the needle was placed on the lower side of the sagittal plane to simulate the injection of the same volume of cement (4.0 ml) into the vertebral model. While the resulting cement location is notably different than the original shape of cement (cf. Figure 7) in this case, as shown in Figure 11C, both augmented vertebrae have similar VF responses, and no considerable difference is observed between their fracture strength and ductility. Note that, while at different locations, the needle tip was kept in the anterior region of the vertebra in both simulations to avoid the cement leakage into pedicels, which is a common practice during VP operations.
FIGURE 11.
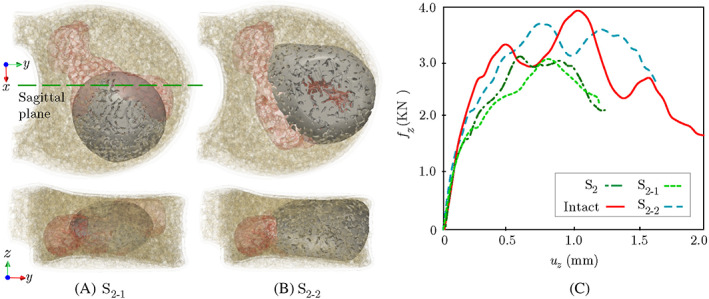
(A) Augmentation of the vertebra with cement filling the lower side of the sagittal plane (); (B) An endplate‐to‐endplate injection scenario for the vertebra (); (C) Comparison of force‐displacement plots of and with the original injection scenario
Finally, it is worthwhile to study the impact of the injected cement volume on the VF response of the treated vertebra. It is postulated that in a clinical setting, an end plate‐to‐end plate cement augmentation can significantly increase the post‐operative mechanical stability of the vertebra compared to a partial augmentation. 51 To quantify this effect, we simulated the injection of 6.0 ml cement (50% increase in volume) into the model while preserving the original needle tip location. Note that the augmentation of this vertebra with 4.0 ml of cement leads to only 19.2% recovery in fracture strength, which was the lowest among all models studied thus far. Figure 11B shows the simulated morphology of 6.0 ml cement injected into this vertebra, which provides an end plate‐to‐end plate augmentation with no leakage into pedicels due to the low injection flow rate ( ).
The CDM approximation of the force‐displacement response of the augmented vertebra with 6.0 ml of cement injection is depicted in Figure 11C, showing a considerably better restoration of mechanical stability (72% strength recovery) compared to only 19.2% in the case of partial augmentation. This figure also shows that the end plate‐to‐end plate augmentation of this vertebra increases the ductility (absorbed energy) compared to the vertebra with 4.0 ml cement injection. The von‐Mises stress field in the elastic zone for each case scenario is depicted in Figure 12, where the end plate‐to‐end plate augmentation provides a more uniform distribution of stresses within the vertebra. This pilot study verifies that the end plate‐to‐end plate augmentation of the vertebra could significantly improve its mechanical stability in clinically relevant anterior wedge fractures, although further studies are necessary to investigate the impact on adjacent vertebral bodies.
FIGURE 12.
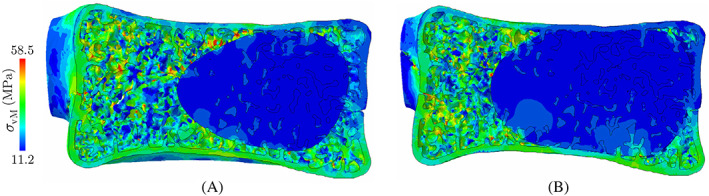
von‐Mises stress distribution in the elastic zone along the sagittal plane of the vertebra with (A) partial, and (B) end plate‐to‐end plate cement augmentation
5. CONCLUSIONS
An integrated CFD‐assisted framework was introduced for simulating the vertebroplasty (VP) procedure and predicting its impact on the fracture response of augmented vertebrae, considering realistic microstructure of the bone tissue generated using an AI‐enhanced algorithm. After performing CFD injection simulation to predict the cured cement morphology, an imaging data co‐registration approach was employed to generate a high‐fidelity FE damage model to study the VF response of the augmented vertebra. A feasibility study relying on virtual geometrical models of a cancer patient with a lytic metastatic tumor and pre‐existing fractures was conducted to demonstrate the ability of the proposed framework to investigate the effect of VP on the mechanical integrity of treated vertebrae. Main outcomes of the study are summarized below:
Under higher injection flow rates, the cement tends to form into a more irregular pattern due to its accelerated flow in the path of least resistance (i.e., lytic lesion). The study shows that increasing the injection flow rate leads to a higher risk of intra‐spinal cement leakage during the injection process.
Simulating the compression fracture responses of two augmented vertebral models with a weak (no bonding, only contact) and a perfectly bonded (tied) cement‐bone interface showed the negligible impact of bonding strength in force‐displacement curves.
Force‐displacement responses of the three augmented lytic vertebrae, with cement shapes predicted via CFD simulations, showed the strength recovery of for the vertebra with no pre‐existing cortical fracture, while only and recovery where achieved for cases with pre‐existing fractures caused by pure compression and flexion loadings, respectively.
Under a uniform compression, the damage often initiates from sites of high‐stress concentrations adjacent to the injected cement. However, the final propagation pattern does not completely match the pre‐existing cortical fracture (no healing) in the augmented vertebra.
An end plate‐to‐end plate cement augmentation is shown to considerably improve the mechanical strength of the treated vertebra (~72% strength recovery) compared to only ~19.2% in the case of partial augmentation.
The feasibility study presented in this manuscript aimed at demonstrating the capability of an AI‐enhanced digital twin to provide an end‐to‐end modeling framework for simulating the vertebroplasty procedure. A more comprehensive in‐vitro study must be conducted to calibrate/validate the cement injection CFD simulation and corresponding CDM simulations used to analyze the mechanical stability of augmented vertebrae. Furthermore, a better understanding of variations in the bone tissue properties in the presence of metastatic tumor lesions may be necessary to study the impact of vertebroplasty in stabilizing the vertebra in such patients. Such studies require incorporating a three‐phase flow model, as well as understanding/incorporating mechano‐biological factors such as the stress‐induced metastatic tumor response. Nevertheless, the preliminary studies presented in this work show the ability of the applicability of the digital twin for performing a variety of clinically relevant studies.
ACKNOWLEDGMENTS
This work has been supported by the Center for Cancer Engineering through combined funding from College of Engineering and Comprehensive Cancer Center at the Ohio State University. The authors also acknowledge the allocation of computing resources from the Ohio Supercomputer Center.
Ahmadian H, Mageswaran P, Walter BA, et al. A digital twin for simulating the vertebroplasty procedure and its impact on mechanical stability of vertebra in cancer patients. Int J Numer Meth Biomed Engng. 2022;38(6):e3600. doi: 10.1002/cnm.3600
DATA AVAILABILITY STATEMENT
Research data are not shared.
REFERENCES
- 1. Ahmadian H, Mageswaran P, Walter B, et al. AI‐assisted reconstruction of digital twin for predicting the vertebral fracture response. Int J Numer Meth Biomed Eng. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Burton AW, Rhines LD, Mendel E. Vertebroplasty and kyphoplasty: a comprehensive review. Neurosurg Focus. 2005;18(3):1‐9. [DOI] [PubMed] [Google Scholar]
- 3. Mendel E, Bourekas E, Gerszten P, Golan JD. Percutaneous techniques in the treatment of spine tumors: what are the diagnostic and therapeutic indications and outcomes? Spine. 2009;34(22S):S93‐S100. [DOI] [PubMed] [Google Scholar]
- 4. Trout AT, Kallmes DF, Kaufmann TJ. New fractures after vertebroplasty: adjacent fractures occur significantly sooner. Am J Neuroradiol. 2006;27(1):217‐223. [PMC free article] [PubMed] [Google Scholar]
- 5. Fahim DK, Sun K, Tawackoli W, et al. Premature adjacent vertebral fracture after vertebroplasty: a biomechanical study. Neurosurgery. 2011;69(3):733‐744. [DOI] [PubMed] [Google Scholar]
- 6. Jensen ME, Dion JE. Percutaneous vertebroplasty in the treatment of osteoporotic compression fractures. Neuroimaging Clin N Am. 2000;10(3):547‐568. [PubMed] [Google Scholar]
- 7. Wilcox RK. The biomechanical effect of vertebroplasty on the adjacent vertebral body: a finite element study. Proc Inst Mech Eng Part H. 2006;220(4):565‐572. [DOI] [PubMed] [Google Scholar]
- 8. Polikeit A, Nolte LP, Ferguson SJ. The effect of cement augmentation on the load transfer in an osteoporotic functional spinal unit: finite‐element analysis. Spine. 2003;28(10):991‐996. [DOI] [PubMed] [Google Scholar]
- 9. Anselmetti GC, Manca A, Kanika K, et al. Temperature measurement during polymerization of bone cement in percutaneous vertebroplasty: an in vivo study in humans. Cardiovasc Intervent Radiol. 2009;32(3):491‐498. [DOI] [PubMed] [Google Scholar]
- 10. Teng MMH, Cheng H, Ho DM, Chang CY. Intraspinal leakage of bone cement after vertebroplasty: a report of 3 cases. Am J Neuroradiol. 2006;27(1):224‐229. [PMC free article] [PubMed] [Google Scholar]
- 11. Baumann C, Fuchs H, Kiwit J, Westphalen K, Hierholzer J. Complications in percutaneous vertebroplasty associated with puncture or cement leakage. Cardiovasc Intervent Radiol. 2007;30(2):161‐168. [DOI] [PubMed] [Google Scholar]
- 12. Laredo JD, Hamze B. Complications of percutaneous vertebroplasty and their prevention. Skeletal Radiol. 2004;33(9):493‐505. [DOI] [PubMed] [Google Scholar]
- 13. Lopez CD, Boddapati V, Lombardi JM, et al. Medicare utilization and reimbursement for vertebroplasty and kyphoplasty: a national analysis from 2012–2017. Spine. 2020;45(24):1744‐1750. [DOI] [PubMed] [Google Scholar]
- 14. Baroud G, Bohner M, Heini P, Steffen T. Injection biomechanics of bone cements used in vertebroplasty. Biomed Mater Eng. 2004;14(4):487‐504. [PubMed] [Google Scholar]
- 15. Loeffel M, Ferguson SJ, Nolte LP, Kowal JH. Vertebroplasty: experimental characterization of polymethylmethacrylate bone cement spreading as a function of viscosity, bone porosity, and flow rate. Spine. 2008;33(12):1352‐1359. [DOI] [PubMed] [Google Scholar]
- 16. Baroud G, Yahia FB. A finite element rheological model for polymethylmethacrylate flow: analysis of the cement delivery in vertebroplasty. Proc Inst Mech Eng Part H. 2004;218(5):331‐338. [DOI] [PubMed] [Google Scholar]
- 17. Teo J, Wang SC, Teoh SH. Preliminary study on biomechanics of vertebroplasty: a computational fluid dynamics and solid mechanics combined approach. Spine. 2007;32(12):1320‐1328. [DOI] [PubMed] [Google Scholar]
- 18. Bleiler C, Wagner A, Stadelmann VA, et al. Multiphasic modelling of bone‐cement injection into vertebral cancellous bone. Int J Numer Meth Biomed Eng. 2015;31(1):37‐57. [DOI] [PubMed] [Google Scholar]
- 19. Soyka RPW, López A, Persson C, Cristofolini L, Ferguson SJ. Numerical description and experimental validation of a rheology model for non‐Newtonian fluid flow in cancellous bone. J Mech Behav Biomed Mater. 2013;27:43‐53. [DOI] [PubMed] [Google Scholar]
- 20. Zeiser T, Bashoor‐Zadeh M, Darabi A, Baroud G. Pore‐scale analysis of Newtonian flow in the explicit geometry of vertebral trabecular bones using lattice Boltzmann simulation. Proc Inst Mech Eng Part H. 2008;222(2):185‐194. [DOI] [PubMed] [Google Scholar]
- 21. Teo J, Teoh SH. Permeability study of vertebral cancellous bone using micro‐computational fluid dynamics. Comput Methods Biomech Biomed Engin. 2012;15(4):417‐423. [DOI] [PubMed] [Google Scholar]
- 22. Chevalier Y, Pahr D, Charlebois M, Heini P, Schneider E, Zysset P. Cement distribution, volume, and compliance in vertebroplasty: some answers from an anatomy‐based nonlinear finite element study. Spine. 2008;33(16):1722‐1730. [DOI] [PubMed] [Google Scholar]
- 23. Rohlmann A, Boustani HN, Bergmann G, Zander T. A probabilistic finite element analysis of the stresses in the augmented vertebral body after vertebroplasty. Eur Spine J. 2010;19(9):1585‐1595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Peng Y, Du X, Huang L, et al. Optimizing bone cement stiffness for vertebroplasty through biomechanical effects analysis based on patient‐specific three‐dimensional finite element modeling. Med Biol Eng Comput. 2018;56(11):2137‐2150. [DOI] [PubMed] [Google Scholar]
- 25. Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434. 2015.
- 26. Olsson E, Kreiss G. A conservative level set method for two phase flow. J Comput Phys. 2005;210(1):225‐246. [Google Scholar]
- 27. Baroud G, Falk R, Crookshank M, Sponagel S, Steffen T. Experimental and theoretical investigation of directional permeability of human vertebral cancellous bone for cement infiltration. J Biomech. 2004;37(2):189‐196. [DOI] [PubMed] [Google Scholar]
- 28. Widmer RP, Ferguson SJ. A mixed boundary representation to simulate the displacement of a biofluid by a biomaterial in porous media. J Biomech Eng. 2011;133(5):051007. [DOI] [PubMed] [Google Scholar]
- 29. Gilbert JL, Hasenwinkel JM, Wixson RL, Lautenschlager EP. A theoretical and experimental analysis of polymerization shrinkage of bone cement: a potential major source of porosity. J Biomed Mater Res. 2000;52(1):210‐218. [DOI] [PubMed] [Google Scholar]
- 30. Krüger A, Oberkircher L, Kratz M, Baroud G, Becker S, Ruchholtz S. Cement interdigitation and bone‐cement interface after augmenting fractured vertebrae: a cadaveric study. Int J Spine Surg. 2012;6:115‐123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Fiedler B, Hojo M, Ochiai S, Schulte K, Ando M. Failure behavior of an epoxy matrix under different kinds of static loading. Compos Sci Technol. 2001;61(11):1615‐1624. [Google Scholar]
- 32.de Souza Neto EA, Peric D, Owen DRJ. Computational Methods for Plasticity: Theory and Applications. John Wiley & Sons; 2011. [Google Scholar]
- 33. Niebur GL, Feldstein MJ, Yuen JC, Chen TJ, Keaveny TM. High‐resolution finite element models with tissue strength asymmetry accurately predict failure of trabecular bone. J Biomech. 2000;33(12):1575‐1583. [DOI] [PubMed] [Google Scholar]
- 34. Webb JCJ, Spencer RF. The role of polymethylmethacrylate bone cement in modern orthopaedic surgery. J Bone Joint Surg British. 2007;89(7):851‐857. [DOI] [PubMed] [Google Scholar]
- 35. Krause WR, Miller J, Ng P. The viscosity of acrylic bone cements. J Biomed Mater Res. 1982;16(3):219‐243. [DOI] [PubMed] [Google Scholar]
- 36. Farrar DF, Rose J. Rheological properties of PMMA bone cements during curing. Biomaterials. 2001;22(22):3005‐3013. [DOI] [PubMed] [Google Scholar]
- 37. COMSOL . Multiphysics v. 5.4. https://www.comsol.com; 2018.
- 38. Bryant JD, David T, Gaskell PH, King S, Lond G. Rheology of bovine bone marrow. Proc Inst Mech Eng Part H. 1989;203(2):71‐75. [DOI] [PubMed] [Google Scholar]
- 39. Lautrup, B . Physics of Continuous Matter: Exotic and Everyday Phenomena in the Macroscopic World. CRC press; 2011. [Google Scholar]
- 40. van Ness KE. Surface tension and surface entropy for polymer liquids. Polym Eng Sci. 1992;32(2):122‐129. [Google Scholar]
- 41. Haroutunian V, Michael SE, Isaac H. Segregated finite element algorithms for the numerical solution of large‐scale incompressible flow problems. Int J Numer Meth Fluids. 1993;17(4):323‐348. [Google Scholar]
- 42. Tao WQ, Qu ZG, He YL. A novel segregated algorithm for incompressible fluid flow and heat transfer problems—Clear (coupled and linked equations algorithm revised) part I: Mathematical formulation and solution procedure. Numer Heat Transf Part B: Fundam. 2004;45(1):1‐17. [Google Scholar]
- 43. Multiphysics C. Comsol multiphysics reference manual. COMSOL: Grenoble, France 2013:1084.
- 44.Schroeder WJ, Martin KM, Lorensen WE. The Visualization Toolkit an Object‐Oriented Approach to 3D Graphics. Prentice‐Hall, Inc; 1998. [Google Scholar]
- 45. Walt V dS, Schönberger JL, Nunez‐Iglesias J, et al. Scikit‐image: image processing in python. PeerJ. 2014;2:e453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kikinis R, Pieper SD, Vosburgh KG. 3D Slicer: a platform for subject‐specific image analysis, visualization, and clinical support. In Intraoperative imaging and image‐guided therapy. Springer, New York, NY; 2014. pp. 277‐289.
- 47. Nicholson PH, Cheng X, Lowet G, et al. Structural and material mechanical properties of human vertebral cancellous bone. Med Eng Phys. 1997;19(8):729‐737. [DOI] [PubMed] [Google Scholar]
- 48. Baroud G, Bohner M. Biomechanical impact of vertebroplasty. Joint Bone Spine. 2006;73(2):144‐150. [DOI] [PubMed] [Google Scholar]
- 49.MLA Weikopf M, Ohnsorge JAK, Niethard FU. Intravertebral pressure during vertebroplasty and balloon kyphoplasty: an: in vitro: study. Spine. 2008;33(2):178‐182. [DOI] [PubMed] [Google Scholar]
- 50. Baroud G, Crookshank M, Bohner M. High‐viscosity cement significantly enhances uniformity of cement filling in vertebroplasty: an experimental model and study on cement leakage. Spine. 2006;31(22):2562‐2568. [DOI] [PubMed] [Google Scholar]
- 51. Steens J, Verdonschot N, Aalsma A, Hosman A. The influence of endplate‐to‐endplate cement augmentation on vertebral strength and stiffness in vertebroplasty. Spine. 2007;32(15):E419‐E422. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Research data are not shared.


