An agent-based model to assess large-scale COVID-19 vaccination campaigns for the Italian territory: The case study of Lombardy region

Abstract

Background

In Italy, the administration of COVID-19 vaccines began in late 2020. In the early stages, the number of available doses was limited. To maximize the effectiveness of the vaccine campaign, the national health agency assigned priority access to at-risk individuals, such as health care workers and the elderly. Current vaccination campaign strategies do not take full advantage of the latest mathematical models, which capture many subtle nuances, allowing different territorial situations to be analyzed aiming to make context-specific decisions.

Objectives

The main objective is the definition of an agent-based model using open data and scientific literature to assess and optimize the impact of vaccine campaigns for an Italian region. Specifically, the aim is twofold: (i) estimate the reduction in the number of infections and deaths attributable to vaccines, and (ii) assess the performances of alternative vaccine allocation strategies.

Methods

The COVID-19 Agent-based simulator Covasim has been employed to build an agent-based model by considering the Lombardy region as case study. The model has been tailored by leveraging open data and knowledge from the scientific literature. Dynamic mobility restrictions and the presence of Variant of Concern have been explicitly represented. Free parameters have been calibrated using the grid search methodology.

Results

The model mimics the COVID-19 wave that hit Lombardy from September 2020 to April 2021. It suggests that 168,492 cumulative infections 2,990 cumulative deaths have been avoided due to the vaccination campaign in Lombardy from January 1 to April 30, 2021. Without vaccines, the number of deaths would have been 66% greater in the 80–89 age group and 114% greater for those over 90. The best vaccine allocation strategy depends on the goal. To minimize infections, the best policy is related to dose availability. If at least 1/3 of the population can be covered in 4 months, targeting at-risk individuals and the elderly first is recommended; otherwise, the youngest people should be vaccinated first. To minimize overall deaths, priority is best given to at-risk groups and the elderly in all scenarios.

Conclusions

This work proposes a methodological approach that leverages open data and scientific literature to build a model of COVID-19 capable of assessing and optimizing the impact of vaccine campaigns. This methodology can help national institutions to design regional mathematical models that can support pandemic-related decision-making processes.

1. Introduction

The COVID-19 pandemic has hit the entire planet severely since the beginning of 2020. As of June 24, 2022, more than 539 million cases and more than 6.3 million deaths due to SARS-CoV-2 have been officially reported worldwide [1]. In 2020, the only tools to counter the spread of the disease were non-pharmaceutical interventions (NPIs), as vaccines were being developed and tested. These intervention strategies included preventive care (e.g., social distancing, hand washing, and face masks), lockdowns (e.g., travel restrictions, school closures, and remote work), and logistics associated with testing (e.g., contact tracing and quarantine). Starting from the beginning of January 2021, the main pharmaceutical companies have supplied vaccines for COVID-19. To support countries in vaccine prioritization decisions, the World Health Organization (WHO) proposed a guideline [2] that prioritizes vaccine access to at-risk groups such as health care workers and older adults. International and national public health organizations have proposed similar approaches [3]. The availability of vaccines has been limited for several months and thus, each national health administration decided to distribute the vaccines in different ways to the different categories of the population. The proposed campaigns of vaccination are based on traditional decision-making methods that usually exploit the experience and the knowledge of experts to evaluate the efficiency of an applied strategy [4].

Mathematical modeling, such as compartmental and agent-based models, has been extensively used to simulate the spread of disease and support decision-making in the pandemic setting. The main advantage is that models can be built to capture subtle nuances, allowing them to be adapted to different territories, with the goal of analyzing and making context-specific informed decisions based on strong mathematical support. These tools can be applied to analyze vaccination strategies in the context of limited supplies. The innovative methods of modeling allow a better prediction on the impact of each specific strategy and compare them to find the optimal one by considering new information and data obtained during the COVID-19 outbreak [5].

The paper concerns the definition of a retrospective analysis to simulate the effect of several prioritization strategies for the vaccination campaign. A stochastic agent-based model of COVID-19 has been built using the available knowledge in the scientific literature, publicly available open data, decrees and ordinances of local and national authorities. Differently from other publications, the model has been tailored to reproduce the infection trend in the Italian region of Lombardy instead of considering the whole national territory. First, the paper describes the scientific background of mathematical and stochastics models exploited in literature, then the methodological approach and its application for the Lombardy region are described. The obtained results are presented and discussed. Finally, the conclusions are drawn.

2. Scientific background

There are two main categories of mathematical models that are widely used to model the COVID-19 pandemic and assess the effectiveness of different vaccine allocation strategies in a context of limited supply: (i) compartmental models and (ii) agent-based models (ABMs), also known as individual-based models (IBMs).

The vast majority of models that proliferated in response to the COVID-19 pandemic have been compartmentalized models. These models have relatively simple developmental requirements and a longstanding body of work available, making them the most accessible to epidemiologists. Zhou et al. [6] used a SEIR (susceptible, exposed, infectious, recovered) model to estimate the basic reproduction number (R ₀) in Wuhan, China. Giordano et al. [7] and Zhao and Chen [8] extended classical compartmental models to simulate more nuances of progression across different disease states in order to investigate the effects of various interventions such as social distancing and testing. Various research works focused on vaccination strategies in the context of limited supply. Suzan et al. [9] compared the two modes to supply vaccines by modeling an ODE based on biological signals. They simulated the impact to distribute two doses of vaccine with either different time intervals or different quantities of vaccine. The results highlighted that several aspects should take into account also cultural and social behaviors to better simulate the evolution of the pandemic situation. Libotte et al. [10] defined a multi-objective optimization model to control the distribution of vaccines using the available data of China. They used a SIR (susceptible, infectious, removed) model to design the optimization method. In this case, the results and the discussion of authors highlighted a poor quality of the data initially adopted to model more realistic management of vaccines. Jentsch et al. [11] employed a Bayesian particle filtering approach to fit a SEPAIR (susceptible, exposed, presymptomatic, asymptomatic, symptomatic, removed) model for age and structure to Ontario. They exploited the model to predict pandemic curves under hypothetical scenarios of different levels of vaccine availability and non-pharmaceutical interventions. Their results suggest that if SARS-CoV-2 vaccines would have become available late enough in the pandemic, the use of such vaccines to interrupt transmission could prevent more deaths from COVID-19 than the use of vaccines to target people aged 60 and older. Their findings are highly dependent on the context at the time the work was done. The rising prevalence of variants with different transmissibility and infection-fatality ratios, such as Omicron, could lead to different conclusions. Matrajt et al. [12] found a similar result using a deterministic age-structured mathematical model with a population stratified into 16 age groups. According to their work, the level of pre-existing immunity strongly dictates outcomes: when pre-existing immunity is high, strategies that distribute the vaccine more evenly across age groups can be more effective than prioritizing older age groups. Buckner et al. [13] focused on scenarios where social distancing is limited for essential workers. Using an age-stratified SEIR model, they found out that in most cases it is better to target first older essential workers. However, depending on the objective and alternative model scenarios considered, younger essential workers may be prioritized to control spread or seniors to directly control mortality. Giordano et al. [14] used an ODE model to describe the evolution of outbreaks with the introduction of vaccines in Italy. They combined the ODE model with a data-based model to evaluate the impact of the vaccines on the cost relative to the Italian public health service. The management of the vaccine distribution is described by a single parameter and the authors highlighted the need for a more complex model to better simulate the vaccine supply by means of ABMs.

ABMs are characterized by a high degree of flexibility that allows them to evaluate micro-level policies much more accurately than compartmental models. These models can be used to study detailed interventions with maximum realism because they can account for detailed information about population structure, including the number of households and non-family contacts, the age and clustering of contacts within households, and the microstructure in schools and workplace settings informed by census and time-use data [5]. A significant disadvantage of ABMs is the high computational cost. In addition, the lack of an adequate amount of data for validation can severely affect the acceptability of model results. Lastly, defining the parameters and calibrating the model are a major challenge [15]. Despite that, researchers have exploited extensively ABMs to model the SARS-CoV-2 pandemic. In March 2020, Ferguson et al. [16] expanded an ABM of influenza to investigate COVID-19. At that time, there had been only 6000 COVID-19 deaths globally, but this ABM predicted half a million deaths in the United Kingdom and over 2 million deaths in the United States if strong interventions were not implemented. Panovska-Griffiths et al. [17] used the open-source framework Covasim [18] to develop an ABM on the UK to predict the impact of two possible strategies for reopening schools from September 2020, considering different assumptions on the relaxation of physical distancing measures and the scale-up of testing. Several studies have investigated the impact of vaccination campaigns and the optimal vaccine allocation strategy by means of ABMs. Zhou et al. [19] exploited data on mobile phone trajectories to build an integrated spatial ABM over the city of Guangzhou, China. According to their simulations, the most efficient strategy is to prioritize vaccine access to areas with lower rates of herd immunity and at the same time to older people. The simulations performed using an ABM by Zachreson et al. [20] suggest that in Australia no combination of realistic vaccine efficacy values is likely to eliminate the pandemic threat. Additional refinements to the current Australian vaccination campaign, such as vaccinating those under 18 years of age, may be necessary to achieve herd immunity and further reduce, or eliminate, the need for subsequent restrictions and lockdowns. In a preprint, Hoertel et al. [21] tailored a stochastic ABM over France. Their results suggest that proceeding by vaccinating only the elderly would require 35.3 million doses to lift all NPIs without triggering the resurgence of the pandemic, whereas 57 million doses would be needed if vaccinating the population uniformly. This work is based on optimistic assumptions, such as that vaccines give sterilizing immunity and that no reinfection is possible following recovery. Romero-Brufau et al. [22] estimated the health outcome of delaying the second dose of SARS-CoV-2 mRNA vaccines in the US. Simulations carried out with an ABM show that delaying the second dose, at least for people younger than 65 years, could result in reduced cumulative mortality under certain conditions. Giacopelli [23] exploited a collision detection algorithm to develop a full-scale ABM over Lombardy (10 million agents) capable of running on a commercial PC. Assuming fully sterilizing immunity, his model suggests that herd immunity against COVID-19 can be achieved when 70% of the population is vaccinated. Li & Giabbanelli [24] compared Trump's vaccination plan (Operation Warp Speed) to Biden's vaccination plan (‘100-day’ goal) by means of an ABM built using the open-source framework Covasim [18]. The simulations were run under 7 different scenarios of NPIs. Authors suggest that the Biden plan showed more power in controlling infection under all scenarios than the plan created under the previous administration and that vaccines alone cannot effectively end the pandemic without the enforcement of NPIs. Similarly, Kou et al. [25] highlighted the importance of maintaining interventions alongside vaccination. They leveraged real-world data on traffic patterns and demographic parameters to build an ABM on four Chinese cities. Their model predicts that peak infections will decrease by 67.37% with an 80% vaccination rate, compared to an 89.56% decrease when isolation and quarantine measures are also in place. The ABM-based research works described above do not fully exploit the potential of these models. In particular, three limitations emerge: (i) they all assume that vaccination and recovery from COVID-19 confer perfect sterilizing immunity for an unlimited time, although it is known that reinfection can still occur [26]; (ii) they all consider the characteristics of SARS-CoV-2 to be fixed, but the emergence of more transmissible and deadly variants has changed the spread of infection over time [27] and reduced the effectiveness of vaccines [28]; (iii) they all model the level of protection given by non-pharmaceutical interventions as fixed over time, while governments tighten or weaken the restrictive measures in place as pandemic curves change [29].

The aim of this research work is the definition of a retrospective analysis of the impact of the vaccination campaign and simulating the effect of several prioritization strategies by means of the definition of a stochastic ABM. The retrospective analysis considers (i) the limited effect of vaccination, (ii) the generation of new COVID-19 variants, and (iii) the variability of non-pharmaceutical intervention when the pandemic curve changes. The stochastic ABM of COVID-19 has been built exploiting the open-source framework Covasim [18] using the available knowledge in the scientific literature, publicly available open data, and decrees and ordinances of local and national authorities. According to the organization of the Italian national health system, which allows the regions to manage their own health service in an autonomous way, the ABM has been designed to reproduce the infection trend in Lombardy from September 1, 2020, to April 30, 2021.

3. Method and tools

The proposed method allows the definition of an ABM to examine the performance of alternative vaccination strategies in an Italian region. Fig. 1 shows the main steps of the methodological approach. First, open data from the scientific literature and open data publicly available have been exploited to shape the model on the specific region. Then, a stochastic agent-based model of COVID-19 has been implemented using the open-source framework Covasim; the model has been calibrated to fit the reported number of diagnoses and deaths. The calibrated model simulates the spread of COVID-19 under different scenarios: multiple vaccine allocation strategies and doses availability may be considered. Finally, results can be analyzed to identify the impact of vaccine allocation strategies.

Fig. 1.

Outline of the procedure performed.

3.1. Open data and scientific literature

For the creation of the ABM relative to Lombardy, open data and literature about the pandemic evolution have been selected. In the following, all the exploited databases and information are described and referenced. In the early stages of the COVID-19 pandemic, Lombardy was the first western area to rise to the headlines for the rapid spread of the disease. The COVID-19 open data from the Italian Civil Protection Department [30] have been exploited in this study.

3.1.1. Serological data

The serological survey conducted by the Italian National Institute of Statistics (ISTAT) reported that, as of July 2020, 7.5% (C.I. 6.8% to 8.3%) of Lombardy citizens had come into contact with SARS-CoV-2 and developed an antibody response capable of protecting them from reinfection [31].

3.1.2. Variants of concern data

Part of the increase in cases of COVID-19 in the second wave may be attributed to the emergence of new variants of SARS-CoV-2. The strain B.1.1.7, named Alpha Variant of Concern (VoC), has been detected in Lombardy starting in December 2020 and has become predominant in February 2021 [32]. To model the variant within the simulation, the parameters from the scientific literature represented in Table 1 have been used.

Table 1.

Characteristics of the Alpha VoC within the model. Data are expressed relative to the wild strain.

Parameter	Relative change	Source
Transmissibility (β)	+56%	Midpoint of the range (1.55–1.57) reported in Italy [33].
Symptomatic disease	–	Inconclusive evidence on the likelihood of symptom development [34].
Severe disease	+64%	Reported in Denmark [35], consistent with analysis from the EU and UK [36].
Critical disease	–	Various studies have found increased mortality for B.1.1.7, but not necessarily when conditioned on having developed severe disease [37].
Death	–	Same as above.

3.1.3. Mobility restrictions data

To counteract the second wave of COVID-19 that has affected Italy starting in the fall of 2020, on October the 14th the government first introduced tighter restrictions at the national level. Effective November 6, 2020, the containment measures were upgraded to a protocol of regionally-based tiered restrictions [29]. Each week an epidemiological risk assessment on each region is performed and the restrictions are updated accordingly. Restrictions, coded as yellow, orange, and red, ranged from a curfew between 10 pm and 5 am to a full-day stay-home mandate with a ban on interregional mobility and closure of nonessential activities. Manica et al. [27] employed Google mobility data to quantitatively compute the impact on human activities of those restrictions. Their work has been integrated with the ratio of students in distance learning (Table 2 ) and has been exploited to build the model.

Table 2.

Relative changes in time spent in human interactions across different tiers of restrictions applied in Lombardy. Data are expressed as relative to pre-pandemic values.

Contact network	Restriction tier	Relative change	Source
Households	National (Oct 14 – Nov 5)	+6.90%	Relative change in the per-contact transmission probability, based on the change in time spent in residential locations [27].
	Yellow	+10.60%
	Orange	+14.70%
	Red	+16.90%
Workplaces	National (Oct 14 – Nov 5)	−16.70%	Relative change in the number of contacts, based on the reduction in the number of visitors in workplaces [27].
	Yellow	−23.40%
	Orange	−28.20%
	Red	−32.60%
Community	National (Oct 14 – Nov 5)	−7.57%	Relative change in the number of contacts, based on the average reduction in the number of visitors over grocery/pharmacy, parks, retail/recreation, and transit stations [27].
	Yellow	−16.35%
	Orange	−30.87%
	Red	−40.52%
Schools	National (Oct 14 – Oct 25)	–	Relative change in the number of contacts, based on the number of students in distance learning [39].
	Regional decree (Oct 25 – Nov 5)	−45.48%
	Yellow	−45.48%
	Orange	−45.48%
	Red	−51.67%

3.1.4. Vaccination campaign open data

The vaccination campaign open data from the Italian Special Commissioner for the COVID-19 emergency [40] have been exploited in this study. Following the first approval of a SARS-CoV-2 vaccine by the European Medicines Agency (EMA) in late December 2020, Italy initiated its national vaccination program. Priority in vaccine access was given to at-risk groups, such as health care workers, and the elderly. At the end of April 2021, a total of four vaccines were in use in Italy, each with different dosages and efficacy to different strains of the virus.

3.2. Design of ABM with Covasim

The ABM has been built using the open-source framework Covasim (version 3.0.7). Covasim simulates the spread of COVID-19 over time across networks of individuals. It can model the effects of interventions such as vaccine campaigns, as well as non-pharmaceutical interventions including testing, contact tracing, quarantine, partial or full lockdowns, social distancing, and mask usage. The model's mutually exclusive disease states are represented in Fig. 2 . Individuals who have never contracted the virus are placed in the naive compartment. Once exposed to infection, they can become asymptomatic or symptomatic with varying levels of severity. Progression is stochastic and depends on the age of the individual. The model includes individual heterogeneity in infectiousness and time spent in each disease state. Individuals who recover from the disease develop neutralizing antibodies (NAbs) that protect them against reinfection. NAbs can also be acquired through vaccination. The presence of several strains of SARS-CoV-2 with different transmissibility and severity can be represented within the simulation. Further details are available in Kerr et al. [18].

Fig. 2.

Diagram illustrating the mutually exclusive states and the disease progression within the model.

To analyze the spread of COVID-19 in Lombardy from September 1, 2020, to April 30, 2021, a synthetic population of 100,000 agents interacting over four transmission networks (households, schools, workplaces, community) has been generated. The age structure of the population and the households’ network was built based on data from the Italian National Institute of Statistics, while the other contact networks were built based on the default parameters of Covasim. To ensure a smooth take-off, the simulation has been initialized by seeding infections from 1 to 15 September according to the official number of diagnoses reported [30].

3.2.1. Testing and contact tracing

Within the simulation, individuals who are tested positive to COVID-19 are placed in the isolation state, and their known contacts can be traced and placed in the quarantine state. People in isolation or quarantine have a lower probability of infecting others (if they are infectious) or of acquiring COVID-19 (if they are quarantined and susceptible). For isolation, the reduction is assumed to be 70% in the household and 90% in school, work, and community layers, while quarantine is assumed to have lower compliance (40% reduction in the household and 80% in other layers). The employed reduction has been set according to the default parameters of Covasim [18]. The number of daily SARS-CoV-2 tests carried out in the simulation is equal to the official number of swabs carried out in Lombardy. Symptomatic individuals are assumed to be 100 times more likely to receive a swab than healthy and asymptomatic people, as in Kerr et al. [18]. Furthermore, the sensitivity of the test is assumed to be 100%, following again Kerr et al. [18]. The probability to contact trace an individual is assumed to be 99.5% within the same date of diagnosis for households’ contacts, 85% within 2 days for school places contacts, 60% within 2 days for workplaces contacts, and 10% within 3 days for community contacts.

3.2.2. Fading immunity

Immune protection from SARS-CoV-2 is closely linked to NAbs levels [41]. Thus, immunity has been handled by simulating fading NAbs through the Covasim immunity module [42]. Upon the first infection, individuals draw an initial NAbs level from a log-normal distribution ${\log }_2\left(NA{b}_0\right)\sim N\left(0,2\right)$, following the distribution used by Khoury et al. [13]. Initial NAbs are adjusted based on the severity of symptoms individuals experience throughout the infection, again following [13]. NAbs grow linearly until they reach their peak after three weeks and then follow a two-part exponential decay. For individuals who have some prior immunity, reinfection boosts the level of NAbs by a factor of 1.5, as described in [42].

To link NAbs and protective efficacy, the function identified by Cohen et al. [42] has been used. First, the authors used data from vaccine efficacy and re-infection studies to fit four linear regressions on a logit-log scale using linear optimization. The output has been a continuous function relating NAbs to the reduction of SARS-CoV-2 infection risk. Subsequently, this function has been exploited to infer the relationship between NAbs and the reduction of moderate and severe symptoms for individuals with asymptomatic and symptomatic infections.

3.2.3. Seroprevalence

The population in the simulation has been initialized by accounting for the presence of individuals who contracted SARS-CoV-2 before September 2020. As of July 15, 2020, 0.95% of Lombardy citizens tested positive for SARS-CoV-2 [30], against the 7.5% infections estimated by the serological survey [31]. The number of diagnoses drastically underestimates the real number of infections, thus it can't be used to initialize the simulation. To overcome this, the test yield ratio curve has been rescaled and used as a proxy to estimate the actual infections. In detail, the infection curve has been estimated as follows:

$$\widehat{i}\left(t\right)=k\frac{t_y\left(t\right)}{{\int }_u{t}_y\left(u\right)du}$$

where $\widehat{i}\left(t\right)$: estimation of actual infections, t_y(t): ratio of positive swabs / total swabs, $\underset{u}{\int }{t}_y\left(u\right)du$: integral of t_y between February 24 and July 15, 2020, and k: cumulative infection as of July 15, 2020, estimated by the serological survey. The ratio of asymptomatic infections is assumed to be 42.5% (midpoint of the range reported by Oran and Topol [16]), severe infections are assumed to be 3.9% (average severity ratio over all age groups reported by Verity et al. [17]), and the severity of the remaining infections are assumed to be mild.

3.2.4. Vaccinations

Vaccine protection has been modeled by simulating the antibodies response in individuals, exploiting the previously described fading-NAbs methodology. Vaccination is assumed to generate an initial NAbs level drawn from a lognormal distribution ${\log }_2\left(NA{b}_0\right)\sim N\left({\mu }_{vax},2\right)$, where μ_vax depends on the vaccine administered, following [13]. Second doses boost NAbs by B_vax, where B_vax is a vaccine-specific factor.

In the simulation, vaccines have been administered following the numbers and the proportions of inoculations by age group reported in the official data [40]. In the period from December 27, 2020, to April 30, 2021, a slight difference between expected second doses administered based on the number of first doses and actual second doses administered has been noticed. Nonetheless, it was decided to use official data on the number of second doses administered for simulation purposes.

3.2.5. Alpha VoC

Within the model, agents are infected and can transmit either the wild strain or the B.1.1.7 strain. The probability that a susceptible agent in contact with an infectious agent will become infected is proportional to the strain-specific β_v parameter. Each strain is also characterized by parameters that influence the stochastic progression of the disease. Parameters of the B.1.1.7 strain have been expressed relative to the wild strain and have been chosen according to the literature (Table 1). In addition, the immunity acquired through infection with the wild-type strain is assumed to be less effective against the B.1.1.7 strain, and vice versa. The efficacy of cross-immunity is computed by scaling the NABs level by a factor of 0.5, following Cohen et al. [42].

In the simulation, the B.1.1.7 strain has been introduced starting from December 1, 2020. A total of 1000 individuals chosen at random have been infected. To ensure a smooth ramp-up, the seeding of the B.1.1.7 strain has been distributed from December 1 to 15, 2020.

3.2.6. Tiered restrictions

From November, 15th to April, 30th the containment measures of Lombardy have been updated 16 times [45]. Manica et al. [27] quantitatively computed the impact on human activities for each of the tiered restrictions (yellow, orange, red) and for the national restrictions introduced on October 14. Based on their work, pattern variation in human activities has been represented within the model (Table 2). Changes in the time spent in residential locations have been modeled as a change in the per-contact transmission probability between household members; changes in the number of visitors in workspaces and community locations have been modeled as a reduction in the number of contacts in the layer.

3.3. Calibration of the ABM

The model has been calibrated following the methodology previously exploited by Pham et al. [46] to tailor a Covasim model over Vietnam.

The cost function that has been minimized is the following:

$$\begin{array}{ccc}\hfill g\left(\theta \right)& =& \sum _t[k_1·NA{E}_t\left({\mathcal{M}}^{diagn}\left(\theta \right),{\mathcal{D}}^{diagn}\right)\hfill \\ & & +k_2·NA{E}_t\left({\mathcal{M}}^{deaths}\left(\theta \right),{\mathcal{D}}^{deaths}\right)]\hfill \end{array}$$

$\text{where}\mathit{NA}{E}_t(X,Y)=\frac{\left|Y\right(t)-X(t\left)\right|}{\max \left(\max \right(X),\max (Y\left)\right)}$

${\mathcal{D}}^{diagn}$, ${\mathcal{D}}^{deaths}$ are the cumulative reported diagnoses and deaths, ${\mathcal{M}}^{diagn}$, ${\mathcal{M}}^{deaths}$ the model predictions of cumulative diagnoses and deaths, θ = (β,  s) the model parameters (the overall transmission rate and the seed used to initialize the random number generation, respectively), NAE(…) the normalized absolute error, and k ₁, k ₂ > 0 the weights used to shift the relevance of the two terms.

The cost function g(θ) has been optimized using the grid search method, again following [46]. The overall transmission rate β ranged from 0.01875 to 0.01975 with an increment of 0.0001, and the seed s ranged from 0 to 499 with an increment of 1. The best 30 combinations of parameters out of 5500 trials have been selected and included in the final model. Diagnoses vs. deaths data have been weighted in the ratio 2:1, which has been found to be the best tradeoff between curve fitting of deaths and diagnoses. The final calibration process result is not sensitive to small changes in the ratio of the weights. Consistently with various works based on Covasim ([46], [47], [48]), all the data points available have been used within the calibration process.

3.4. Scenarios

The overall effect of the vaccination campaign carried out in Lombardy can be investigated using the calibrated ABM. First, a simulation has been performed assuming that no vaccine has been administered to the population. Then, the impact of the vaccine allocation strategy has been investigated and compared with a scenario without vaccines. Four vaccinations strategies have been considered:

• aAt-risk & oldest first: priority is given to health care workers, followed by the elderly. This strategy is consistent with the one actually employed in Lombardy;
• bOldest first: priority is given to the elderly;
• cUniform: vaccines are administered uniformly in all individuals;
• dYoungest first: priority is given to youngest individuals.

Consistent with the indications of the Italian Medicines Agency (AIFA), in all strategies considered it is assumed that individuals under 12 years of age are excluded from vaccination. The study has been performed by evaluating the performance of the vaccine strategy as dose availability ranged. The simulations have been performed considering up to a maximum of a 10-fold increase in inoculations compared with the number of vaccines administered, with a distribution over time consistent with the actual number of inoculations carried out in Lombardy. The protocol of tiered restrictions applied in Lombardy establishes that the level is established based on a series of epidemiological parameters, where the one with the greatest weight is the net reproduction index R_t [38]. In the simulations, the restriction level has been dynamically changed as the R_t index changed, based on the thresholds established by the protocol. Consistent with what occurred in reality, the update of the level has been performed every Monday.

The scenarios have been emulated with the calibrated ABM and the results are used for a vaccine allocation analysis that will be explained in the next section.

4. Results

The section describes the quality of the calibrated ABM, the data obtained by the simulation of the different vaccination campaigns and the effect of the vaccination strategies.

4.1. Calibration results

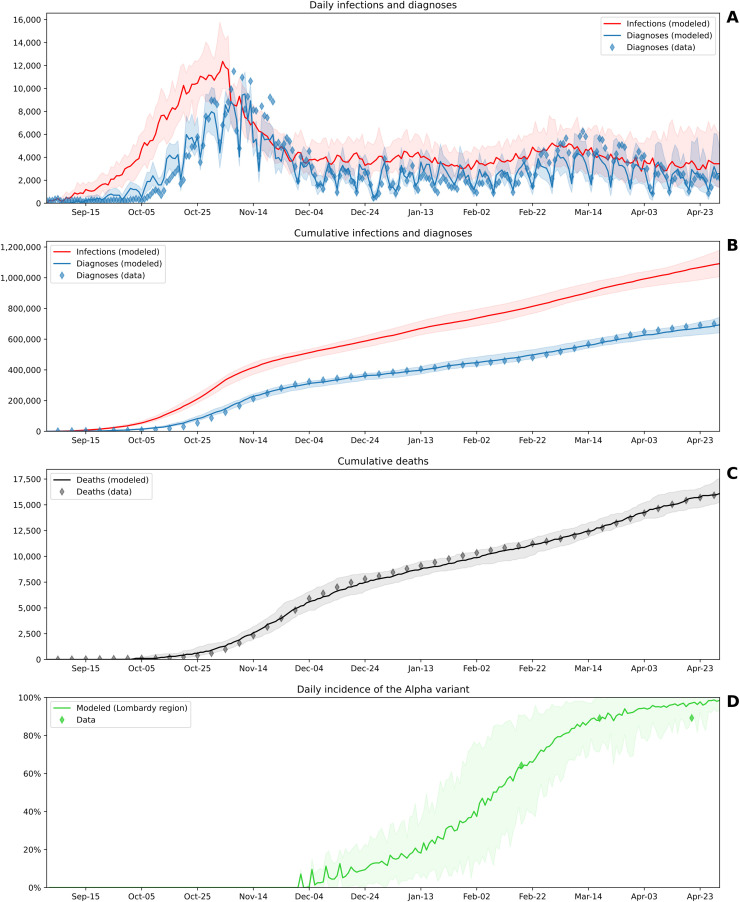
The calibrated model captures the COVID-19 wave that hit Lombardy in autumn 2020 and the progression over the following months (Fig. 3 ). According to the simulation, from September 1, 2020, to April 30, 2021, in Lombardy a total of 1091,784 COVID-19 infections have been estimated, 36.5% of which remained undiagnosed.

Fig. 3.

Fitting of the calibrated model to the COVID-19 infection in Lombardy from September 1, 2020, to April 30, 2021. (A) Daily trajectories. (B)(C) Cumulative trajectories. (D) Daily incidence of the SARS-CoV-2 Alpha variant (lineage B.1.1.7). Solid lines indicate the median model across 30 simulations, shaded areas indicate 90% projection intervals, and diamonds indicate data. For ease of visualization, the data in (B) and (C) are plotted at 5-day intervals, although daily data have been used for calibration. Data sources: Italian Civil Protection [30] for diagnoses and deaths; Italian National Institute of Health [32] for the incidence of the Alpha variant.

The progression of the daily incidence of Variant Alpha is consistent with nationwide data reported by the Italian National Institute of Health [32], although these data are not explicitly accounted for by the cost function used for the optimization. Furthermore, the attack rate among individuals identified through contact tracing is consistent with the one reported for Italy. Between September 1, 2020, and December 31, 2020, the attack rate found in 30 runs of the model ranged from 15.2% to 20.8% (median: 17.6%), while it has been reported to be 20.3% in Italy between July and December 2020 [49].

The calibration process has been performed on a Windows laptop equipped with an Intel i7–7700HQ CPU, 16 GB RAM, and an NVIDIA GeForce GTX 1050. The parallelized execution of the calibrated model (30 simulations with different seeds) takes approximately 12 min.

4.2. Effect of the vaccination campaign

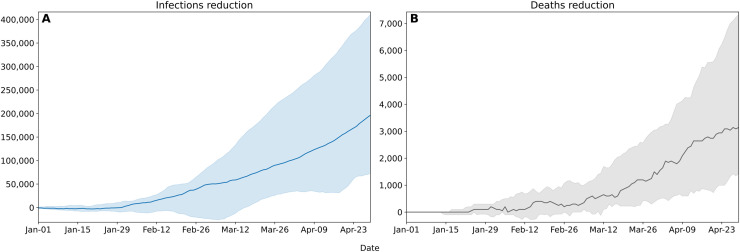
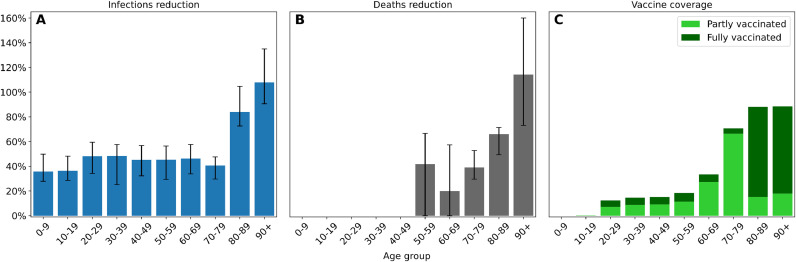
The model estimates that 2990 cumulative deaths and 168,492 cumulative infections have been avoided due to the vaccination campaign in Lombardy from January 1 to April 30, 2021 (Fig. 4 ). The interquartile ranges for cumulative infections and cumulative deaths are 72,759–411,064 and 1420–7326, respectively, as of April 30, 2021. The magnitude of these intervals is consistent with the nature of stochastic ABMs. Most of the deaths have been avoided in the older age groups of the population (Fig. 5 ). Notably, it is estimated that the number of deaths could have been 66% greater in the 80–89 age group and 114% greater for those over 90. A greater reduction in the number of deaths is reported in the 50–59 bracket than in the 60–69 bracket (42% vs 20%), attributable to the fact that in the first segment a greater percentage of individuals completed the vaccination cycle. The greatest reduction in the number of infections involves the age groups that received the most vaccines (84% for 80–90, 108% for 90+), but the effect of immunization given by the drugs is reflected in the spread across all age's groups. For performance concerns, it has been chosen to run the simulations with an agent-to-population ratio of approx. 1:100. This resolution may account for the fact that minute variations in the number of deaths may not have been captured by the model for the 0–49 age groups.

Fig. 4.

Cumulative infections (A) and deaths (B) reduction attributable to the vaccination campaign in Lombardy from January 1 to April 30, 2021. Solid lines indicate the median model across 30 simulations, shaded areas indicate the interquartile range.

Fig. 5.

Percentage reduction in the number of cumulative infections (A) and deaths (B) by age group attributable to the vaccination campaign in Lombardy from January 1 to April 30, 2021. Vaccine coverage as of April 30, 2021, is shown in (C); light green represents the fraction of individuals partially vaccinated, while light green represents individuals who have completed the vaccination cycle. The bars represent the median values across 30 simulations and the black lines depict the interquartile ranges.

4.3. Effect of vaccine allocation strategy

The effect of different prioritization strategies in Lombardy on varying dose availability has been estimated. The interval considered is the first four months of inoculation.

To minimize the number of overall deaths, the results of the simulations indicate that the best allocation strategy is the "at-risk & oldest first" in each vaccine availability scenario (Fig. 6 ). Despite the death-to-infection ratio is better with the "oldest first" strategy, proceeding with an age-only criterion results in the greatest number of deaths per vaccine availability condition. This can be explained by the fact that the elderly have fewer social interactions than younger people: vaccinating only the elderly has less effect on slowing the spread of infection, thus leading to a higher number of overall deaths. Vaccinating the population uniformly results in performance similar to "at-risk & oldest first" in terms of the number of infections but leaving more frail individuals uncovered from vaccine protection causes more deaths overall.

Fig. 7.

Detail of the estimated cumulative infections and deaths for various vaccine allocation strategies as the number of vaccinations administered varied between January 1 and April 30, 2021, in Lombardy. (A), (B) show the vaccine allocation strategy employed Lombardy, based on the prioritization of groups at-risk & elderly; (C), (D) show an age-based policy that prioritizes the elderly; (E), (F) shows a no-priority policy in which anyone has the same probability of being vaccinated; (G), (H) shows the prioritization of young individuals. Dots have been obtained by assuming different numbers of doses administered in steps of 850,000. For each step, 30 simulations have been performed and the median value has been selected. Continuous lines represent a second-degree polynomial fitted on dots employing least-squares polynomial optimization.

Fig. 6.

Simulation of cumulative infections (A) and deaths (B) for various vaccine allocation strategies as the number of vaccinations administered varied between January 1 and April 30, 2021, in Lombardy. Red lines represent the vaccine allocation strategy employed Lombardy, based on the prioritization of groups at-risk & elderly; orange lines represent an age-based policy that prioritizes the elderly; light blue lines represent a no-priority policy in which anyone has the same probability of being vaccinated; dark blue lines represent the prioritization of young individuals. Within the simulation, the level of the tiered restriction has been updated as the Rt index changed, as described in the text. The curves have been obtained by fitting a second-degree polynomial via least-squares optimization to data points calculated through different simulations assuming different numbers of doses administered. The individual data points are shown in Fig. 7.

On the other hand, to minimize infections, the model suggests that the best strategy depends on vaccine availability. Below a certain threshold (in Lombardy estimated at 6.7 million doses) the best allocation strategy is "youngest first". Beyond that, the "at-risk & oldest first" is the most effective. In other words, in the Lombardy context, the model suggests that if the number of doses is not available to fully cover at least 1/3 of the population in 4 months, to exclusively minimize the number of infections it is better to vaccinate younger people first. Beyond this threshold, it is more effective to prioritize the elderly and those at risk.

5. Discussion

The reached results confirmed that the designed ABM fits the data relative to the pandemic situation in Lombardy. The simulations of the vaccination campaign can help to understand the impact of specific choices for potential future waves of the COVID outbreak. The methodological approach based on the open data may help the Italian national institutions to design new ABMs for the other Italian regions.

The nature of ABMs makes it possible to capture complex interactions between system elements, such as higher-order interactions. Despite this, the expressive power is still limited by the level of detail of the modeling. One element that has not been considered in this work is the link between the number of vaccinations, the burden on health facilities, and the resulting variation in vaccine administration rates. However, the bottleneck in the first phase of the vaccination campaign in Lombardy was the pace of dose production by pharmaceutical companies. Therefore, future scientific studies should investigate that this relationship did not have a significant impact on the final outcome. One element that could have an influence on the results is the willingness of the population to receive a vaccine. In particular, the percentage of the population opposed to the vaccine may vary depending on environmental factors, such as the trend of the pandemic curve, the incidence of vaccine adverse effects, media attention, and the spread of fake news. To date, this link has not yet been clearly quantified. Therefore, it has not been considered in this research study. Future works may investigate this relationship further.

The proposed approach can be also further improved by means of a more customized ABM. First, although an attempt has always been made to identify the parameters that characterize the pandemic in Lombardy, some of the sources used refer to other contexts [35,43,44]. However, the main aspects used in the modeling and calibration, namely the characterizations of contagiousness in the different levels of tiered restrictions, the seropositivity of the population, and the description of the vaccination campaign, have been modeled using data referring to Lombardy [30,31,38,40]. Secondly, some phenomena about the spread of infection can be specifically modeled, such as periods of mass vacation that alter the normal activities of individuals [50], and the so-called "pandemic fatigue" that can occur over time [51]. Third, as with any modeling study, some assumptions have been made when simulating the epidemic. Unlike other countries [52], no detailed data are available on contact tracing performance in Italy. Thus, it has not been possible to do directly data-driven modeling of contact tracing, but assumptions had to be made. Nevertheless, the attack rate between primary contacts found in the calibrated model is consistent with the one reported by the European centre for Disease Prevention and Control [49]. Finally, only the variant of concern labeled as "Alpha" has been accounted for in this work, although other variants have been detected in Lombardy during the period considered, albeit with a prevalence of no more than 1.4% [32].

6. Conclusions

The paper presents a methodological approach to define an ABM about the COVID-19 outbreak and several scenarios of vaccination campaigns specifically for an Italian region. In particular, the effect of the vaccination campaign and the impact of alternative vaccine allocation strategies have been estimated over Lombardy, Italy. To perform the study, publicly available data and parameters from the scientific literature have been exploited to tailor a stochastic ABM of COVID-19 to Lombardy. The model has been calibrated through grid search optimization. Firstly, it has been shown that the model fits the reported diagnoses, deaths, and the incidence of the Alpha VoC from 1 September 2020 to 30 April 2021. Secondly, the calibrated model has been exploited to evaluate the effect of the COVID-19 vaccination campaign carried out in Lombardy. It was estimated that 168,492 infections and 2990 deaths were prevented by the vaccines. In particular, the number of deaths would have been 114% greater among the over-90 s and 66% greater in the 80–89 s. Finally, the calibrated model was exploited to evaluate the performance of alternative vaccine allocation strategies. It was shown that the strategy applied in Lombardy, based on the prioritization of at-risk individuals and the elderly, is the most efficient in reducing the number of deaths under any scenario of vaccine availability. The methodological approach based on the open data may help the Italian national institutions to design new ABMs for each Italian region to take the best decisions. Furthermore, the proposed approach should allow further customization of the ABM for a specific region by employing epidemic parameters relative to the local context, considering changes in daily practices related to holiday periods, and modeling individuals' willingness to vaccinate.

Funding

Part of this work was supported by Regione Lombardia, ITALY, within the research grant n. 1847162 - “Linea 2 della Misura Covid di cui alla DGR n. 3015/2020: Sviluppo di strumenti software e servizi a supporto dell'individuazione precoce e il successivo contenimento del contagio da SARS-CoV-2”.

Declaration of Competing Interest

We confrim that this work is not currently under consideration for publictaion elsewhere. We have no conflicts of interest to disclose.