Multiscale Kinetic Analysis of Proteins

Abstract

The stochasticity of molecular motion results in the existence of multiple kinetically relevant pathways in many biomolecular mechanisms. Because it is highly demanding to characterize them for complex systems, mechanisms are often described with a single-pathway perspective. However, kinetic network analysis and sub-ensemble experimental insight are increasingly demonstrating not only the existence of competing pathways, but also the importance of kinetic selection in biology. This review focuses on advances in multiscale kinetic analysis of proteins, which connects molecular level information from simulations to macroscopic data to characterize mechanistic reaction networks and the reactive flux through them. We describe a range of methods used and highlight several examples where kinetic modeling has revealed functional importance of pathway heterogeneity.

INTRODUCTION

Protein mechanisms are often described as a series of transitions between intermediates (Figure 1). This single-pathway perspective can be helpful for envisioning how a process might proceed. However, it can also be qualitatively wrong, missing the mechanistic heterogeneity exemplified in single-molecule experiments [2]. The relevance of competing pathways is obvious in heterogeneous catalysis, where percent yields quantify the dominance of particular pathways in a reaction network. While the same principles hold for biomolecular transformations [3], pathway heterogeneity has been especially challenging to discern because it requires identifying not only all relevant intermediates, but also the transition rates between them and reactive flux through them under a given set of conditions. Kinetic network analysis aims to do just this, and its multiscale application to proteins, wherein molecular-level information is combined with experimental restraints, is the focus of this review.

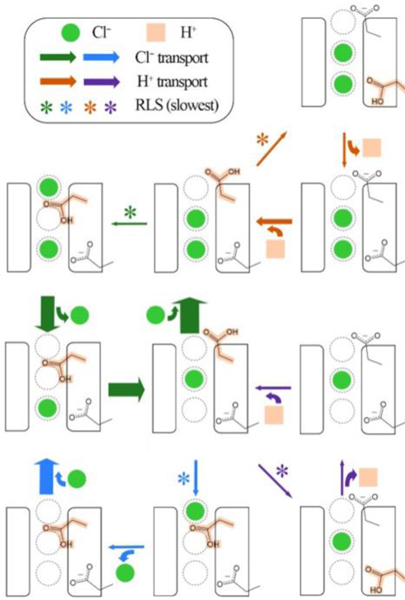
Figure 1.

Single pathway mechanism proposed for Cl-/H+ antiporter [1].

We open with several biological contexts in which mechanistic heterogeneity has been demonstrated. This discussion is far from exhaustive, but intended to provide key examples of cases where kinetic selection is functionally important. We then summarize several methodological approaches to kinetic analysis to provide context for our efforts to advance multiscale kinetic modeling (MKM). Despite fruitful methodological overlap [4], we retain a molecular perspective for space reasons and refer the reader to recent reviews and method development in the network modeling central to systems biology [5–8]. We close with the insights gained on secondary active ion transport and a perspective on future directions for multiscale kinetic analysis of proteins.

KINETIC SELECTION IN BIOLOGY

The importance of kinetic selection in biology was poignantly brought to light by the independent work of Hopfield and Ninio circa 1974 [9, 10], who proposed the concepts of kinetic proofreading (or kinetic amplification) during replication and translation. Their work revealed how substrate specificity can be increased by introducing a delay following binding (e.g., tRNA-ribosome association followed by slow ATP hydrolysis), such that incorrect substrates have time to dissociate prior to product formation. In this case, kinetic selection between competing pathways, one with the correct substrate and one with the incorrect substrate, is driven by phosphate hydrolysis. This results in a lower error rate than would be possible based on relative substrate binding affinities alone. Hopfield noted then that, ‘Understanding the meaning of biosynthetic pathways in such cases will involve the nuances of minor pathways, competitive rates, and side reactions.’ [10]. Kinetic proofreading has since been demonstrated in other processes, including transcription [11], signal transduction [12, 13] and pathogen recognition [14]. A fascinating recent extension to the concept of kinetic proofreading is the replacement of slow enzymatic steps with slow diffusion such that spatial localization affects the same substrate discrimination [15]•. Additionally, the concept that relative steady state fluxes are kinetically controlled has been proposed more broadly based on flux ratios that are not altered by the thermodynamic stability of intermediates in the absence of altered rates[16].

Branched pathways have also been demonstrated in motor proteins. In 2007 Liepelt and Lipowsky proposed a network theory to describe the chemomechanical coupling (i.e., coupling between ATP hydrolysis and mechanical motion) of the molecular motor kinesin [17]. Their work and subsequent work on other motor proteins detail the functional relevance of branched pathways that dominate under specific conditions. For example, myosin V was shown to proceed with both ATP-dependent force-generating mechanical steps and ATP-independent high-speed backward steps induced by superstall loading, consistent with single-molecule observations under varying ATP/ADP concentrations [18]•. F₁-ATPase was shown to function with a forward rotary motor, driven by ATP hydrolysis, and reverse ATP synthesis, driven by forced rotation, revealing that high torque conditions can induce mechanical slip (rotation) without coupled chemistry (ATP synthesis) [19]•.

The role of kinetic selection is also increasingly apparent in membrane transporters, where inconsistent ratios of transported substrates can only be explained by competing transport pathways. Our work, summarized below, demonstrates how multiple pathways (Figure 2) explain the non-integer stoichiometry of ion exchange (2.2 Cl⁻ to 1 H⁺) in Cl⁻/H⁺ antiporters [20]. Variable coupling under different conditions has been demonstrated in multiple transporters[21–23]••, perhaps most strikingly in the multidrug efflux pump EmrE [24]••. This mechanistic heterogeneity can confer biological advantage, such as toxin discrimination in symporters [25, 26]••. It is likely that mechanistic heterogeneity from kinetic selection is much more widespread than the examples given above. However, discerning this requires a more detailed and nuanced understanding of biomolecular processes than has traditionally been achievable. The methodological advances described next are getting us closer to this goal.

Figure 2.

Competing ion transport pathways in ClC-ec1.

METHODOLOGICAL APPROACHES

Kinetic modeling is carried out in a vast array of research fields, each with its own nuances and domain-specific challenges. The most common approaches are phenomenological kinetic models employing physics-based theoretic analyses. These ‘top-down’ approaches fit unknown transition rates to known macroscopic data. Because the kinetic solution space (i.e., all sets of transition rates that fit the few known observables) is generally vast, it has traditionally been essential to simplify the reaction network. Consequently, a central challenge has been making sense of the wide range of possible solutions and understanding solution dependence on the selected network representation [18]•. Despite these challenges, most of the insights described above have used this top-down approach. Valuable trends can be extracted, and the models improved with increasing experimental data. Moreover, advances in sampling are enabling more systematic exploration of solution space leading to increased network complexity and the generation of solution sets that can be experimentally tested [26]••.

In contrast, Markov state models (MSMs) can be built directly from molecular-level data and have become a powerful approach for understanding biomolecular processes [27, 28]. They are most often used to characterize molecular dynamics (MD) simulations, coarse-graining the captured phase space into metastable intermediates (states) and quantifying the transition probabilities between them. Configurations must be sampled beyond the state correlation times (lag times) to achieve Markovian transitions, which can create MSMs with a large number of microstates, each with sufficiently fast relaxation dynamics, and complex resulting networks. The benefit of this is that the multiplicity of pathways is retained; the challenge is in adequately sampling and reducing phase space to resolve them. MSM-associated methods to address these challenges are rapidly advancing (see, e.g., [29]•), lending hope to our future prospects for rigorous kinetic modeling of complex systems (see Conclusions). Already, MSM is revealing novel mechanistic insight from kinetic modeling. As just one example, sequence changes in myosin motor domains were shown to shift pathway flux to explain ADP release rates [30].

Finally, microkinetic modeling must be mentioned. Although applied in heterogeneous catalysis, the advanced methodolgy [31] may lead to promising new avenues for biomolecular kinetic modeling. In ‘bottom-up’ approaches, rates for chemical reactions are calculated with ab initio methods and then factored into a kinetic master equation. Consistent with our findings [20], pure bottom-up models generally do not produce physically meaningful solutions and must be combined with a top-down optimization of rate coefficients. Increasingly sophisticated methods are being developed for parameter refinement, including Bayesian and other stochastic optimization methods [32, 33]. Solution refinement can be further improved with sensitivity analysis and the removal of transitions that have little impact on macroscopic flow rates [31]. Correlative global sensitivity analysis additionally accounts for co-variance of parameters [34].

MULTISCALE KINETIC MODELING

Similar to some MSMs [11] and to microkinetic modeling, the MKM we have been developing also combines bottom-up quantification of transition rates with top-down refinement based on experimental data. Distinct from these approaches has been the need for enhanced free energy sampling, sometimes at multiscale resolution, to obtain calculated transition rates [35–37] and the refinement of all calculated or measured rates within estimated error [20]. Additional differences from microkinetic modeling that motivated our efforts include cyclic mechanisms as opposed to a series of chemical transformations; the condensed phase medium (often including spatial relevance such as membrane transport) instead of gas-phase surface adsorption; diverse transitions (e.g., enzymatic reactions, noncovalent association, ion transport) often coupled with intermediate-distinguishing hydration and conformational changes as opposed to chemical reactions; and diverse experimental conditions beyond concentrations and temperature, such as localization, orientation, pH, ion gradients, transmembrane voltage and more.

MKM can be broken down into 6 steps, each of which can be a formidable challenge:

1. Intermediate Determination: This can be the crux of a model as the fidelity of the solution depends on inclusion of all relevant intermediates, which requires extensive system characterization. In principle, any state separated from others by rate-influencing barriers that contributes to the total flux should be included. In practice, fast transitioning states can be grouped together (see Network Reduction).

2. Rate Determination: Initial rate coefficients can be measured in experiment, as nicely demonstrated on EmrE [24]••, or calculated in silico. This significantly reduces the kinetic solution space compared to top-down approaches. Depending on the transition, this step alone can require multiscale treatment (e.g., QM/MM for an enzymatic reaction or reactive MD for charge transport [37]).

3. Kinetic Modeling: Obtained rate coefficients are mapped into a kinetic master equation, a set of differential equations describing the conversion between intermediates over time that can be solved for the steady-state solution or for the evolution of populations over time given initial concentrations [38].

4. Solution Refinement: Given the exponential in the Eyring-Polanyi relationship (k_i =A_ie^−βΔG‡), even small errors in calculated ΔG^‡ values result in large rate deviations. Solutions consistent with established data thus require parameter refinement [32, 33] and can be improved by focusing on the important transitions with sensitivity analysis [31].

5. Network Reduction: Kinetic networks can be large, complex and sparse. Reducing their dimensionality by lumping states together can alleviate numerical challenges and reveal important pathways. The simplest approach is to combine states separated by fast transitions with a local equilibrium approximation. More rigorous approaches utilize methods like the graph transformation algorithm, which computes mean first passage times [39], to group states and reweight rates while retaining the network dynamic properties [40, 41].

6. Network Analysis: Once a solution is obtained, the network must be analyzed by quantifying dominant flow cycles, identifying rate-influencing steps, tracking time-dependent populations, and testing condition-dependent behavior. Again, there are domain-specific challenges. Since many biomolecular mechanisms must be described in a cyclic manner, we used Markov cycle theory [42] to develop a method that quantifies the flux through cyclic pathways in a closed network [43].

CHLORIDE CHANNEL ANTIPORTERS

Our work in this field was motivated by a long-standing effort to characterize the coupled Cl⁻/H⁺ exchange mechanism in the chloride channel, ClC-ec1. Different multiscale approaches, including QM/MM, multiscale reactive MD, polarizable MD, and Brownian dynamics simulations, were employed to determine free energy profiles for each involved transition [35–37, 44]. Even with these, a full mechanistic description was undecipherable without a kinetic model. The above methodology was developed for this purpose. The calculated rate coefficients were refined with macroscopic restraints (experimental Cl^– transport rates and Cl⁻:H⁺ exchange ratios [45, 46]) in a kinetic master equation to generate physically meaningful solutions [44].

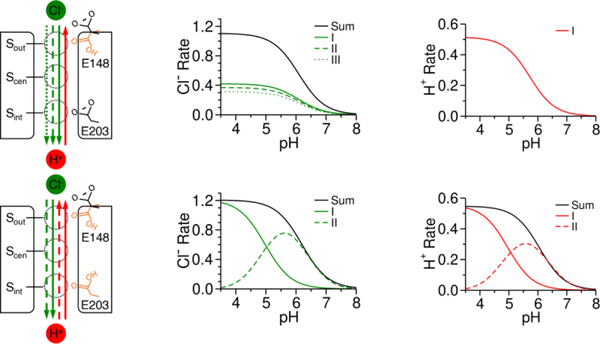
In contrast to the many single-pathway Cl⁻/H⁺ exchange mechanisms proposed (e.g., Figure 1), our work revealed multiple pathways contribute to the flux of each ion (Figure 2). This explains how the exact exchange stoichiometry is consistently non-integer, 2.2 Cl⁻ to every 1 H⁺, for the wildtype system. This facet alone is indicative of pathway heterogeneity. The kinetic solutions also resolve how the upper glutamic acid, E148, couples ion exchange through protonation-dependent blockage of Cl⁻ transport and anion-dependent release of the excess proton. We next probed how flux varies with pH [47], a reactant concentration in this case. Similar to the findings for molecular motors, the mechanism changes under different reaction conditions as the dominance of various pathways shifts (Figure 3) [47]. Interestingly, the lower glutamic acid, which has had questionable importance in the transport cycle to date, determines the distribution between various pathways. Increased back flux through this residue enables stabilization of the ion exchange rates and stoichiometry at lower pH values. This could explain the importance of a lower glutamic acid in the evolution of ClC antiporters.

Figure 3.

Shift in dominant pathways controlled by lower glutamic acid protonation state

CONCLUSIONS/PERSPECTIVE

The examples above highlight an increasing recognition of the fascinating and important role pathway heterogeneity can play in biology. Despite this, it remains a significant challenge to characterize kinetic networks for most complex biomolecular processes. With continued method development and increasing sub-ensemble experimental data, we are optimistic that kinetic analysis will someday be a standard tool used to query any biomolecular mechanism. The rapid evolution of kinetic analysis methods is encouraging in this sense. From phase space exploration with improved adaptive sampling [48–50] to feature extraction and phase space reduction with machine-learned and nonlinear collective variable discovery [51], each of the sub-domains discussed herein is quickly improving. Combining these rate-determining methods with effective kinetic solution space sampling [26]•• could offer a promising paradigm. The impressive experimental characterization for systems like EmrE additionally offers system-specific insight and an essential training ground for method development and benchmarking [24]••. Collectively, the field is progressing toward the ability to understand when and how kinetic selection influences any mechanism. This, in turn, may give us new ways to control biological systems and affect changes in mechanistic outcomes.