Hunting for protective drugs at the break of a pandemic: Causal inference from hospital data

Abstract

At the break of a pandemic, the protective efficacy of therapeutic interventions needs rapid evaluation. An experimental approach to the problem will not always be appropriate. An alternative route are observational studies, whether based on regional health service data or hospital records. In this paper, we discuss the use of methods of causal inference for the analysis of such data, with special reference to causal questions that may arise in a pandemic. We apply the methods by using the aid of a directed acyclic graph (DAG) representation of the problem, to encode our causal assumptions and to logically connect the scientific questions. We illustrate the usefulness of DAGs in the context of a controversy over the effects of renin aldosterone system inhibitors (RASIs) in hypertensive individuals at risk of (or affected by) severe acute respiratory syndrome coronavirus 2 disease. We consider questions concerning the existence and the directions of those effects, their underlying mechanisms, and the possible dependence of the effects on context variables. This paper describes the cognitive steps that led to a DAG representation of the problem, based on background knowledge and evidence from past studies, and the use of the DAG to analyze our hospital data and assess the interpretive limits of the results. Our study contributed to subverting early opinions about RASIs, by suggesting that these drugs may indeed protect the older hypertensive Covid-19 patients from the consequences of the disease. Mechanistic interaction methods revealed that the benefit may be greater (in a sense to be made clear) in the older stratum of the population.

1. Introduction

At the break of a pandemic, the protective efficacy of the proposed therapeutic interventions needs rapid evaluation. An experimental approach to the problem may sometimes be impossible or discouraged by excessive duration, cost, local and national regulatory requirements, delays in approval and potential non-necessity. An alternative route are observational studies, whether based on regional health service data or hospital record data. In this paper, we discuss the role of methods of causal inference for the analysis of such data, with special reference to scientific questions that may arise in a pandemic.

There are two main frameworks for causal inference. One is the potential outcome framework associated with the work by Rubin.¹ The second framework, which we here adopt, uses causal directed acyclic graphs (DAGs), endowed with causal semantics, for example, as proposed by Dawid.² The latter approach involves the construction of a DAG that links the variables in the problem (some observed and some unobserved), and codes the researcher’s causal assumptions. The DAG will help the researcher decide which questions can be meaningfully addressed on the basis of the available data. It will then help the researcher get answers to those questions. We illustrate this with the aid of a collection of studies that jointly examined the effects of renin aldosterone system inhibitors (RASIs) in individuals at risk of (or affected by) Covid-19. Of inferential interest were the existence and the directions of the putative effects, their underlying mechanisms and possible dependence on context variables.

We have seen many papers where the focus is on getting answers from a given DAG. They often take the particular DAG as a starting point for discussing the identification or estimation problems posed by that particular model structure. Papers illustrating the usefulness of DAGs in the process of construction (formulation) of the model in a real-world scientific context are much less frequent. There would be no issue if we, from the start, knew how the world works, and could immediately represent this knowledge in the form of a DAG. But this is not always the case. Motivated by these considerations, this paper gives equal emphasis to aspects of model formulation in the light of the available knowledge (i.e. construction of the DAG) and the use of the obtained DAG for a causally aware analysis of the data.

Of the several scientific questions tackled in our RASI study, some have been addressed by previous studies. The DAG we came up with encodes the causal assumptions at the basis of our analysis and reveals the way in which those questions relate to each other. It allowed us to harmonise the pieces of evidence generated by the relevant studies and to highlight the limits of interpretation of the results. Our study contributed to subverting early opinions about RASIs, by suggesting that these drugs may indeed protect the older hypertensive Covid-19 patients from the consequences of the disease. In addition, mechanistic interaction methods proposed by Berzuini and Dawid^3,4 revealed that the benefit may be greater (in a sense to be made clear) in the older stratum of the population.

The paper consists of three sections. Section 2 presents an account of the medical controversy that sparked interest in RASIs. Section 3 reviews early studies relevant to the topic. Section 4 is based on an analysis of our data, with emphasis on causal inference aspects. Methodological diversions are included as required at various points in the text, with details moved into two Appendices.

2. The medical controversy

The story begins with a worldwide 2020 controversy over the effects of RASIs in Covid-19. Biologists had claimed that RASIs might increase the expression of the angiotensin-converting enzyme 2 (ACE2) receptor, which is responsible for the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) entering human cells. They had deduced from this that exposure to RASIs could harm individuals at risk of, or infected by, Covid-19. Many elderly hypertensives worldwide reacted to the news by stopping RASIs – a decision that may actually have harmed them.

Animal studies show that ACE2, a membrane-bound aminopeptidase primarily expressed in the lungs and in the heart, is used by the SARS-CoV-2, which is responsible for Covid-19, as a functional receptor for its entrance into the cells. ACE2 is a main player in the renin-aldosterone system (RAS), which regulates the long-term evolution of blood pressure, and plays a key role in cardiovascular pathophysiology.

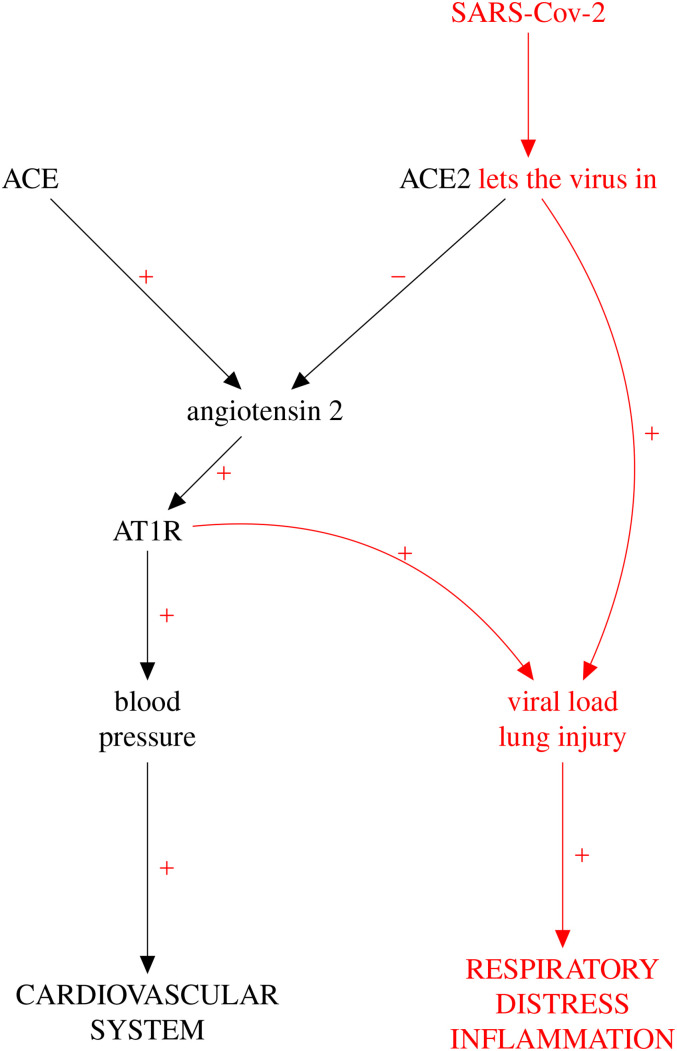
The schematic diagram of RAS in Figure 1 includes receptors ACE and ACE2, located on the membrane of the Covid-susceptible cell. ACE converts angiotensin to angiotensin 2, which in turn, through AT1R receptor binding, stimulates oxidative stress via vasoconstriction, with general pathologic consequences on the cardiovascular system. The figure also shows that ACE2, in contrast with ACE, has the capacity of inhibiting the pathogenic action exerted by angiotensin 2.

Figure 1.

Schematic representation of the RAS pathway. Coloured in red are the links operating when the cell is infected by SARS-CoV-2. (This is not intended to be a causal DAG in the technical sense of this paper.) RAS: renin-aldosterone system; SARS-CoV-2: severe acute respiratory syndrome coronavirus 2; DAG: directed acyclic graph. (Colour figure available online)

The first-choice class of drugs for treating hypertension and a variety of heart and kidney conditions are ACE inhibitors (ACEIs). They exert their beneficial action by inhibiting ACE and, in this way, preventing the vasoconstrictive action of the ACE $\to$ Angiotensin 2 $\to$ AT1R axis. Another class of anti-hypertensives, the angiotensin receptor blockers (ARBs), exert their anti-hypertension effect via inhibition of AT1R. ACEIs and ARBs are subclasses of the larger class of RASIs.

The advent of Covid-19 brought RASIs under the spotlight. Biologists, for example Hoffmann et al.,⁵ sparked early concern that RASIs, which are widely used by the elderly, might upregulate ($=$ increase the expression of) ACE2, thereby helping SARS-CoV-2 invade human cells in this most Covid-vulnerable stratum of the population, as suggested by Reynolds et al.⁶ These concerns surfaced to public notice, causing a worldwide rush of the elderly to stop their RASI therapy, with potentially harmful consequences.

Soon a group of researchers, for example, Liu et al.,⁷ questioned the above concerns. RASIs – they claimed – might protect the Covid-19 patient by countering the adverse effects of the disease on a dysregulated RAS. This could happen via RASI antagonism of the deleterious effects of Angiotensin 2, whether through inhibition of ACE (in the case of ACEIs), or, in the case of ARBs, through inhibition of AT1R. The latter mechanism – it was suggested by Ferrario et al.⁸ – could prevent virus/ACE2 interaction, and hence SARS-CoV-2 cells entry. There were also speculations that prolonged RASI use in the healthy population might confer a prophylactic protection against severe Covid-19 via long-lasting structural and functional effects on kidneys and cardiovascular system.

3. Early studies of the effect of RASIs in Covid-19

3.1. Health registry data

In the study by Mancia et al.,⁹ 6000+ Lombardy residents with severe SARS-CoV-2 infection were 1:5 perfectly matched to 30,000+ beneficiaries of the Lombardy Regional Health Service (RHS) according to sex, age, and municipality of residence. Information about the use of selected drugs and patients’ clinical profiles were obtained from RHS databases.

The 617 infected who received assisted ventilation or died were classified as having a ‘critical’ infection; the remaining infected were put in the ‘moderate Covid-19’ category. Table 4 of the mentioned paper reports no significant evidence of an effect of RASIs on the development of either a moderate Covid-19 disease (ACEIs: odds ratio (OR)$=$0.97; 95% confidence interval (CI) 0.88–1.07) (ARBs: OR$=$0.96, 95% CI 0.87–1.07) or a critical Covid-19 disease (ACEIs: OR$=$0.91; 95% CI 0.69–1.21) (ARBs: OR$=$0.83, 95% CI 0.63–1.10). These results do not distinguish between the patient’s initial Covid-19 respiratory failure (that leads to the decision to ventilate them) from the worsening organ dysfunction process that may hit the patients irrespective of baseline severity, and be lethal.

3.2. Clinical experiments

The BRACE CORONA randomised study of Lopes¹⁰ investigated the effect of in-hospital administration of RASIs on the number of days alive and out of the hospital (NDAOH) through 30 days. It involved 659 hypertensive patients who had been long time taking ACEIs or ARBs prior to being hospitalised for mild to moderate Covid-19 disease. The patients were randomised between continuation versus discontinuation of RASIs upon admission. The sample median age was 55.1 years, with 14.7% of the sample aged 70 years or more. The between-group median difference in NDAOH was 0 days (95% CI: $-1$ to 1). The authors conclude that there is no significant difference in the outcome for those who discontinued versus those who continued these medications.

Lopes¹⁰ report that the effect of ‘discontinuation’ on NDAOH was ‘overall consistent’ across major predefined subgroups. In particular, there was no significant interaction between this effect and that of ‘age above or below 65’ ($p=$0.18). However, it appears from Figure 3 of the cited paper that within the over-65 subgroup, the 74 individuals in the ‘discontinuation’ arm had a mean NDAOH of 17.9 (SD$=10$), which should be compared with the mean NDAOH of 20.7 (SD$=8.3$) estimated from the 95 remaining individuals. The comparison gives a 95% CI of (0.73–1.01) for the mean effect ratio, which is consistent with a non-negligible effect of RASI continuation in this age group.

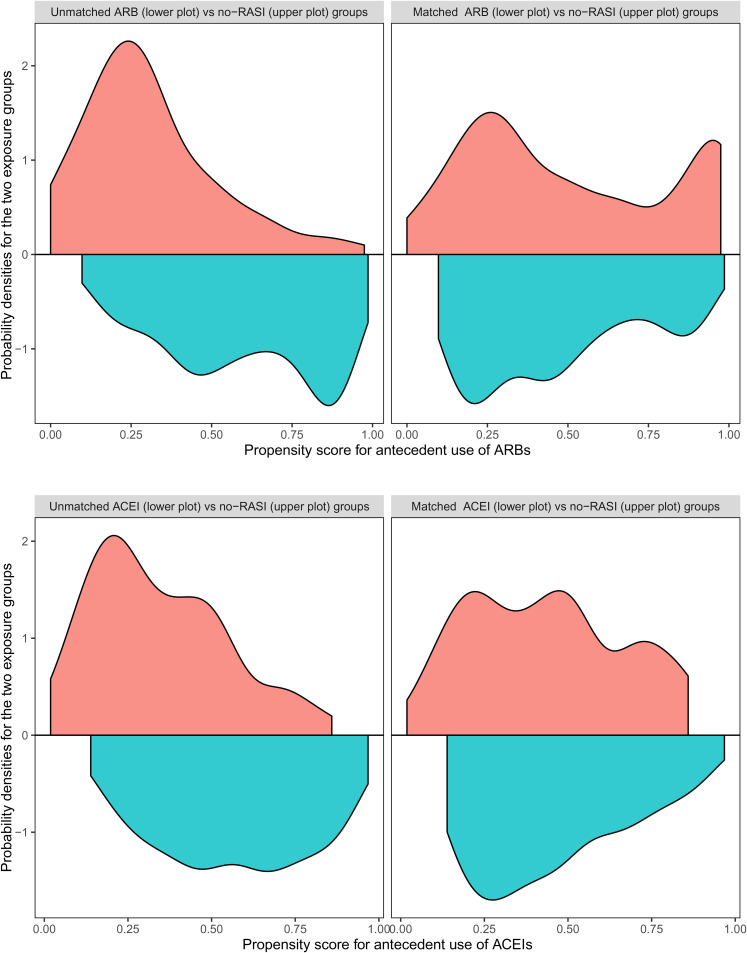
Figure 3.

Upper left plot: Comparison of the probability densities of the ARB-users (lower half of the plot) vs the no-RASI-users (upper half of the plot) group over the propensity score for antecedent use of ARBs, as they have been estimated before the matching. Upper right plot: Comparison of the same groups after the matching. Note the balance improvement achieved by the matching. Lower left plot: Comparison of the probability densities for the ACE-users (lower half of the plot) versus no-RASI-users group (upper half of the plot) over the propensity score for antecedent use of ACEIs, as they have been estimated before the matching. Lower right plot: Comparison of the same groups after the matching. Note the balance improvement achieved by the matching. ARB: angiotensin receptor blocker; RASI: renin aldosterone system inhibitor; ACE: angiotensin-converting enzyme; ACEI: ACE inhibitor. (Colour figure available online)

3.3. Transcriptomics study

Jiang et al.¹¹ find no evidence of RASIs upregulating ACE2, based on a sample of RNA-sequenced kidney transcriptomes, which significantly mitigates fears of a possible harmful RASI effect in Covid-19. The authors find kidney expression of ACE2 to increase with age but not as an effect of RASI exposure.

4. Our RASI study

4.1. Motivation

After the results from BRACE CORONA became public, the debate over the effects of RASIs in Covid-19 seemed to rest on the back burner. But there were reasons not to do so. After all, those results were based on very few patients, few of whom had developed a severe outcome. Thus, BRACE CORONA could not be regarded as the last pronouncement on the problem.

No epidemiologic study had provided conclusive evidence of either a beneficial or harmful effect of RASIs in Covid-19. At the same time, there were opinions in support of the former hypothesis. Sackin¹² described cellular mechanisms that could enable RASIs to mitigate both viral infection and disease severity by altering a cell–surface interaction between ACE2 and the angiotensin receptor type one. To the best of our knowledge, Cippá et al.¹³ were the first to publish an epidemiological study pointing to a beneficial effect of exposure to RASIs on the outcome of Covid-hospitalisation. This was an observational study involving regression adjustment for a large collection of patient profile variables. But more evidence was needed. Our own group had also found evidence of a beneficial effect of RASIs in old age hypertensive Covid-19 patients, by using the causal inference methods that are the focus of the present paper. The fact that ACEIs and ARBs turned out in our study to exert similar and significant effects increased confidence in the results. In the remaining part of this paper, we describe this study of ours, which we shall refer to as the ‘RASI Study’.

4.2. RASI study setting

This investigator-initiated study was based on hospital data from the place that was worst hit by Covid-19: the city of Bergamo, in the northern Italian region called Lombardy. In April 2020, we found evidence of a beneficial effect of antecedent RASIs on mortality from SARS-CoV-2 in a sample of consecutive Covid-affected hypertensive patients. The beneficial effect was found to increase with age, as described by Gori et al.¹⁴

4.3. Data

Our analysis considered all hypertensive patients older than 18 years, who were admitted between 10 February and 7 April 2020, for a total of 712 patients (a small fraction of these were eliminated due to ambiguous coding of the outcome). Hypertension was defined as having a diastolic blood pressure $\ge$90 mmHg and/or a systolic blood pressure $\ge$140 mmHg and/or a history of antihypertensive medications. Laboratory molecular confirmation of SARS-CoV-2 infection was obtained by using methods by GeneFinder COVID-19-Elitech Group and Allplex^TM2019-nCoV Assay-Seegene Inc. Patient follow-up ended on 5 May 2020, for a median post-hospitalisation follow-up time of 34 days. The main pre-hospitalisation patient characteristics are listed in Table 1. They include age at hospitalisation, sex, smoking status, obesity, comorbidities, chronic use of drugs, home therapies and date of symptoms’ onset. Analyses were conducted by using software from the R Core Team.¹⁵

Table 1.

Main pre-hospitalisation characteristics for the RASI study sample of hypertensive Covid-19 patients.

Characteristic	N$=$712
Sex
Female	209 (29%)
Male	503 (71%)
Age (years)
25%,75%	62, 78
Min, Max	35, 95
Obesity (BMI >30)	151 (21%)
Cerebrovascular disease	60 (8.4%)
Atrial fibrillation	97 (14%)
Previous myocardial infarction	104 (15%)
Vasculopathy	96 (13%)
Rheumatic pathology	41 (5.8%)
Peptic ulcer	11 (1.5%)
Immunosuppression	40 (5.6%)
Cirrhosis	13 (1.8%)
Diabetes	192 (27%)
Coronary artery disease	111 (16%)
Chronic heart failure	50 (7.0%)
Chronic kidney failure	87 (12%)
Chronic obstructive pulmonary disease	63 (8.8%)
Exposure to ACEIs	249 (35%)
Exposure to ARBs	215 (30%)
Pulmonary hypertension	261 (37%)
Oral anti-diabetics	140 (20%)
Insulin	49 (6.9%)
Exposure to inhalers	48 (6.7%)
Loop diuretics	135 (19%)
Other diuretics	131 (18%)
Long-term oxygen therapy	18 (2.5%)
Beta-blockers	266 (37%)
Mineralocorticoid Receptor Antagonists	45 (6.3%)
Other	327 (46%)
Statins	240 (34%)
Steroids	36 (5.1%)
Antiplatelets	252 (35%)

RASI: renin aldosterone system inhibitor; BMI: body mass index; ACEI: angiotensin-converting enzyme inhibitor.

4.4. Graphical model

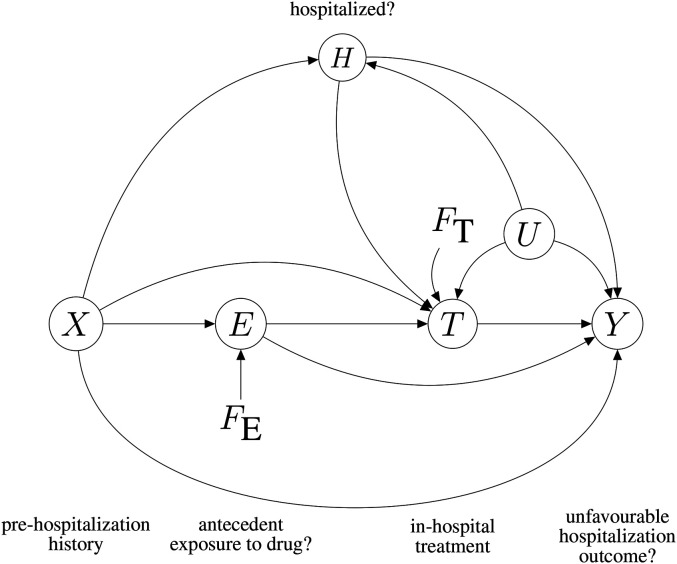
We take our RASI data generating process to be represented by the DAG in Figure 2. The graph is ‘directed’ because each edge, connecting a pair of nodes, has a direction; it is ‘acyclic’ because it is impossible to start from a node and get back to it by following edge directions.

Figure 2.

Causal graphical model of the RASI study. See the main text for an explanation of the symbols. ‘Antecedent’ here means ‘prior to possible hospitalisation’.

The graph describes the generic, initially uninfected, individual of the population, who may ($E=1$) or may not ($E=0$) be exposed to RASIs and may ($H=1$) or may not ($H=0$) end up being Covid-hospitalised. Symbol $T$ denotes a specific post-hospitalisation treatment that the patient may ($T=1$) or may not ($T=0$) undergo, for example, in-hospital continuation of RASI therapy. Hospitalisation outcome may be favourable ($Y=0$) or unfavourable ($Y=1$). Variable $E$ represents antecedent exposure, that is, use of RASIs before a possible hospitalisation. Here is a more detailed description of the variables in the graph:

• $E$: observed binary variable indicating whether the individual experiences ($E=1$) or does not experience ($E=0$) exposure to RASIs prior to suffering any possible consequences from the pandemic;
• $H$: binary indicator, with $H=1$ indicating that the individual gets Covid-hospitalised;
• $X$: a collection of observed variables summarising the individual’s medical history prior to suffering any possible consequences from the pandemic;
• $Y$: for a hospitalised individual, this is the binary indicator of hospitalisation outcome: either favourable ($Y=0$) or unfavourable ($Y=1$);
• $T$: this variable is defined for the hospitalised individual, and indicates whether they were subjected to a hospital treatment of interest ($T=1$) or not ($T=0$);
• $U$: unrecorded information that may have simultaneously influenced the value of $T$ and of the outcome, thereby introducing confounding of the $T$–$Y$ relationship;
• $Z$: for a hospitalised individual, age at hospitalisation (not represented in the graph).

Symbols $F_{\mathrm{E}}$ and $F_{\mathrm{T}}$ represent (non-stochastic) regime indicators. They enable a causal interpretation of the graph, as in Dawid.^2,16 First consider $F_{\mathrm{E}}$. Imagine a (perhaps hypothetical) situation where a public health intervention has imposed the drug on everyone. This corresponds to setting the value of $E$ to be 1 for everybody, by intervention. Let this situation be called the ‘all exposed’ regime. Then imagine a (perhaps hypothetical) situation where the drug is unavailable, as if there had been an intervention to banish it, which corresponds to setting the value of $E$ to be 0 for everybody, by intervention. Call this the ‘nobody exposed’ regime. Add a third regime called ‘observational’, representing the circumstances under which the data were actually collected, that is, by passive observation. Let the three regimes now be indexed by $F_{\mathrm{E}}$. This we can do by defining $F_{\mathrm{E}}$ to take the same values as $E$, plus a special value $\mathrm{\varnothing }$. More precisely, let $F_{\mathrm{E}}=0$ indicate ‘nobody exposed’; let $F_{\mathrm{E}}=1$ indicate ‘all exposed’, and let $F_{\mathrm{E}}=\mathrm{\varnothing }$ indicate the observational regime. With these definitions, the conditioning on $F_{\mathrm{E}}=e$, with $e\in (0,1)$, is equivalent to specifying that the exposure variable $E$ has been set to $e$ by intervention or external circumstances, whereas the conditioning on $F_{\mathrm{E}}=\mathrm{\varnothing }$ is equivalent to specifying that the value of $E$ has arisen naturally, that is, passively observed.

Define $F_{\mathrm{T}}$ analogously, with $F_{\mathrm{T}}=1$ indicating a regime where everybody undergoes treatment $T$, $F_{\mathrm{T}}=0$ a regime where the rule is ‘never administer in-hospital treatment $T$’, and $F_{\mathrm{T}}=\mathrm{\varnothing }$ the observational regime where the decision to treat is not subject to any external intervention.

A full description of the assumptions in the graph of Figure 2 would take long. For the time being, let us focus on the two causal paths that lead from $E$ to $Y$: a direct path, $E\to Y$, and an indirect path, $E\to T\to Y$. The presence of these two paths is equivalent to stating that antecedent use of RASIs could exert a causal influence on $Y$. As we shall see, the two paths have different medical interpretations and implications as far as public health policy is concerned. Unfortunately, if we believe in Figure 2, the effect components they represent cannot be separately estimated on the basis of our RASI data, but their sum, called the total effect of $E$ on $Y$, can be estimated. Further aspects of the graph will be discussed as required.

4.5. Interpretations of the graph

In statistics, we often use DAGs to represent the assumption that the data are generated by a probability distribution we can express as a product of conditional distributions of each node given its parent nodes in the graph. Such a distribution is said to be Markov with respect to the DAG, and the conditional independence relationships it embodies can be read off the graph by using the $d$-separation criterion of Geiger et al.¹⁷ or, equivalently, the moralisation criterion of Lauritzen et al.¹⁸ These relationships are conveniently expressed by using the conditional independence notation of Dawid,¹⁹ where $A\perp \perp B\mid C$ reads: ‘$A$ is independent of $B$, given $C$’, asserting that the conditional distribution of the random variable $A$, given the value of the random variable $C$, does not further depend on $B$. Appendix 1 provides details about the $d$-separation properties of a DAG and their interpretation in terms of conditional independence relationships. For example, Figure 2 tells us that $Xd$ -separates $E$ from $H$, and this can be interpreted as saying that, in all distributions that are Markov with respect to the graph of Figure 2, $E$ is independent of $H$ given $X$, written $E\perp \perp H\mid X$, meaning that two individuals with identical $X$ have identical risks of being hospitalised for Covid-19, whatever their values of $E$.

The generic relationship $A\perp \perp B\mid C$, as read off a DAG, makes sense also when $B$ or $C$ is a regime indicator, as discussed by Dawid² and Constantinou and Dawid.²⁰ For example, one relationship that follows from Figure 2, $F_{\mathrm{E}}\perp \perp H$, can be interpreted as saying that if there was a hypothetical switch from the ‘nobody exposed’ to the ‘all exposed’ regime, the distribution of $H$, that is, the population Covid-hospitalisation rate, would remain unchanged. In other words, that relationship represents the assumption that setting the value of $E$ by intervention (e.g. imposing the drug on an individual) will not affect their risk of Covid-hospitalisation. This is an untestable assumption, were it only for the fact that we are not able to collect data under hypothetical regimes. Here is a more tortuous example: the relationship $F_{\mathrm{E}}\perp \perp Y\mid (E,X)$, implicit in Figure 2, can be interpreted as stating that the probability of an adverse outcome ($Y=1$) in an individual with pre-hospitalisation history $X$ and exposure E does not depend on how the value of E has arisen, whether observationally or exogenously (eg., by intervention) – which we shall find to be a crucial assumption as far as the identifiability of the effect of E on Y is concerned.

4.6. Does age modify the effect of RASIs?

The first question we intended to address is whether the effect of RASIs in hypertensive Covid-19 patients is modified (in a sense to be clarified) by age (not included in the graph). The question seemed to be a sensible one. The study of Jiang et al.¹¹ confirmed that an older age favours the SARS-CoV-2 infection process by upregulating ACE2. A possible explanation being that RASIs could counterbalance this process through alteration of the cell surface interaction mechanism between this receptor and the angiotensin receptor type one. RASIs could also mitigate the consequences of an age-related impairment of immune function. One only needs to connect a few dots to compose a picture where RASIs exert the best of their effect in older patients, as we are going to show on the basis of our data.

Our data appear to confirm the hypothesis. In our population of hypertensive Covid-19 patients, relative mortality for RASI users versus no-RASI users was 0.8. In the over-68 stratum, it was 0.68, which suggests that the older, more than the young, may be in need of the protective effect of RASIs.

The discussion here begs a methodological digression. How can we rigorously define the idea of a drug having a stronger effect in some stratum of the population? In other words, what is a causally rigorous definition of ‘effect modification’? Let us talk about this. Let $Z$ represent ‘age’ on a continuous scale, and let $E=1$ indicate antecedent exposure to RASIs. Define a dichotomised version of the variable ‘age’, called $A$, by writing $A\equiv {\mathrm{I}}_{Z>\tau }$, with $\tau$ an arbitrary age threshold, so that $A=0$ stands for ‘young’ and $A=1$ for ‘old’. Let the adverse outcome (Y = 1) be defined to represent death. Let $P_{\mathrm{eax}}$ denote the observationally estimated probability of death for a Covid-19 patient with $(E=1-e,A=a,X=x,H=1)$, that is

$$P_{\mathrm{eax}}\equiv P(Y=1\mid E=1-e,A=a,X=x,H=1,F_E=\mathrm{\varnothing }).$$

Let

$$P_{\mathrm{eax}}^{‘}\equiv P(Y=1\mid E=1-e,A=a,X=x,H=1,F_{\mathrm{E}}=1-e)$$

be the corresponding probability when the value of $E=1-e$ is set by intervention, that is, $e=0$ (in the ‘all exposed’ regime) or $e=1$ (in the ‘nobody exposed’ regime).

It is important to understand the difference between $P_{eax}$ and $P_{eax}^{{}^{\prime }}$. For example, both $P_{00\mathrm{x}}$ and $P_{00x}^{‘}$ are probabilities of post-hospitalisation death for a young RASI user with hospital-free history $X=x$. However, the former is defined in the observational regime, and can thus be estimated from the data, whereas the latter is defined in the interventional, ‘all exposed’, regime, and is therefore generally unknown.

We are getting close to the definition of ‘effect modification’ we are aiming at. Let us measure the causal effect of the drug (i.e. antecedent RASI exposure) on the outcome $Y$ in terms of the expected percentage of additional lives we would hypothetically save in a population living under the ‘nobody exposed’ regime if we imposed a transition to the ‘all exposed’ regime. Within the group of young patients with history $X=x$, this percentage is proportional to ${\pi }_{A=0,x}\equiv P_{00x}^{{}^{\prime }}-P_{10x}^{{}^{\prime }}$, whereas among old patients with history $X=x$ it is proportional to ${\pi }_{A=1,x}\equiv P_{01x}^{‘}-P_{11x}^{‘}$. Assuming that the effect of antecedent RASI use is not harmful, we shall define to be a modifier of the effect of RASIs on the outcome (in the sense of the effect being higher in old patients than in the young ones) when ${\pi }_{A=1,x}>{\pi }_{A=0,x}$. Appendix 2 shows that, under the assumptions of Figure 4, we have $P_{eax}=P_{eax}^{{}^{\prime }}$ for all values of $(e,a,x)$. In this situation, the causal effect of RASIs on the outcome in terms of an additional number of lives saved, will be greater in the old (as compared with the young) when the following (observationally testable) property, called superadditivity, holds in the data:

$${\mathrm{RERI}}_x\equiv P_{11x}-P_{10x}-P_{01x}+P_{00x}>0$$ (1)

where RERI is the acronym for relative excess risk due to interaction. When the above superadditivity condition holds, we also say that E and Z interact mechanistically, or causally, in their effects on Y. In the light of these considerations, we proceeded by checking whether the above superadditivity condition holds in our data. To do this, we dichotomised age by using the cutoff threshold $\tau$ to equal the sample median age (68 years) so as to define $A$ as in $A\equiv {\mathrm{I}}_{Z>68years}$. Then we fitted the following model to our sample of hospitalised patients

$$\mathrm{logit}p(Y=1\mid E,A,X)={\gamma }_0+{\gamma }_E(1-E)+{\gamma }_{A}A+{\gamma }_{EA}(1-E)A+{\gamma }_X^{\mathrm{T}}X$$

where vector ${\gamma }_X^{\mathrm{T}}$ represents the unknown effects associated with the components of the patient’s history $X$. Under a ‘rare disease’ assumption, RERI${}_x$ could be re-expressed in terms of ORs. We thus obtained the following approximate version of the superadditivity condition:

$${RERI}^{OR}\approx exp({\gamma }_E+{\gamma }_A+{\gamma }_{EA})-exp({\gamma }_E)-exp({\gamma }_A)+1>0.$$

which eliminates the problematic dependence on $x$. A credible interval for ${RERI}^{OR}$ was calculated in our study via Markov chain Monte Carlo within a Bayesian approach to the logistic regression model. We obtained a posterior mean of 1.15 for ${RERI}^{OR}$, with a credible interval $(0.97,1.5)$. To conclude, our data support the hypothesis that age and antecedent RASI exposure interact causally in their effects on mortality of hypertensive Covid-19 patients, with old Covid-19 patients getting a greater advantage from the exposure than the young.

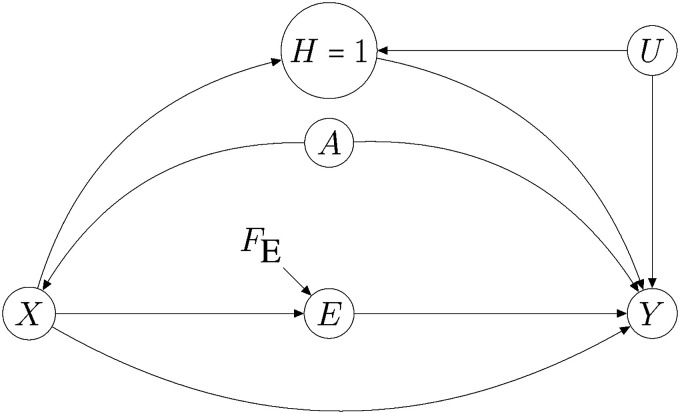
Figure 4.

Assumptions for assessing Age as a modifier of the effect of antecedent renin aldosterone system inhibitor (RASI) use ($E$) on $Y$. Symbol A represents a dichotomized version of variable Age. See text for details.

A more rigorous justification of the procedure can be formulated within the theory of mechanistic interaction proposed by Berzuini and Dawid.^3,4 Related work is described by Blot and Day,²¹ Rothman,²² Walker et al.,²³ Saracci,²⁴ Knol and VanderWeele²⁵ and Vanderweele and Robins.²⁶

4.7. Is the $E\to Y$ causal effect identifiable?

Consider estimation of the conditional causal effect of $E$ on $Y$ in the $H=1$ population, given pre-hospitalisation history $X$. Let this effect be defined by the following conditional causal OR (see, e.g. Hernan²⁷):

$$\begin{array}{r}\mathrm{CCOR}\equiv \frac{P(Y=1\mid E=1,X=x,H=1,F_{\mathrm{E}}=1)}{P(Y=0\mid E=1,X=x,H=1,F_{\mathrm{E}}=1)}/\\ \frac{P(Y=1\mid E=0,X=x,H=1,F_{\mathrm{E}}=0)}{P(Y=0\mid E=0,X=x,H=1,F_{\mathrm{E}}=0)}\end{array}$$

The above expression involves probabilities that are specific to hypothetical regimes $F_{\mathrm{E}}=1$ and $F_{\mathrm{E}}=0$, and hence non-estimable. However, subject to the well-known ‘back door’ conditions of Pearl,²⁸ those non-estimable probabilities can safely be replaced by the corresponding, estimable, observational probabilities, so that CCOR can be safely replaced by:

$$\begin{array}{r}{\mathrm{CCOR}}^{{}^{\prime }}\equiv \frac{P(Y=1\mid E=1,X=x,H=1,F_{\mathrm{E}}=\mathrm{\varnothing })}{P(Y=0\mid E=1,X=x,H=1,F_{\mathrm{E}}=\mathrm{\varnothing })}/\\ \frac{P(Y=1\mid E=0,X=x,H=1,F_{\mathrm{E}}=\mathrm{\varnothing })}{P(Y=0\mid E=0,X=x,H=1,F_{\mathrm{E}}=\mathrm{\varnothing })}\end{array}$$

The relevant back-door conditions are

1. $X$ and $H$ must not be descendants of $F_{\mathrm{E}}$ in the graph, formally: $(X,H)\perp \perp F_{\mathrm{E}}$,

2. once we are told the values of $(E,X,H)$, the probability distribution of $Y$ does not further depend on the way the value of $E$ has arisen, formally: $Y\perp \perp F_{\mathrm{E}}\mid (E,X,H)$.

Both these conditions follow from Figure 2. The observationally estimated quantity ${\mathrm{CCOR}}^{{}^{\prime }}$ can therefore be used to quantify the causal effect of $E$ on $Y$ on the basis of $(X,E,Y)$ data. Practical aspects of the estimation are discussed in Section 4.9 The following consideration concerns the potential truncation bias (in the sense of Wang et al.²⁹) incurred by our analysis. We have just seen that we are able to estimate the causal effect of variable $E$, which is defined in the general population, on the variable $Y$, despite the latter being defined only in the subpopulation of the hospitalised. How is it that we are able to do this by avoiding the truncation bias that typically arises in situations of this kind? The reason why truncation bias does not bite in our situation is the absence of an $E\to H$ arrow in the graph. If this arrow were present, then the back-door criterion would no longer be applicable. Moreover, the conditioning on $H=1$ would unblock the bias-inducing, noncausal, path $E\to H\leftarrow U\to Y$ between exposure and outcome, resulting in a likely departure of ${\mathrm{CCOR}}^{{}^{\prime }}$ from the null even in the absence of a causal effect of $E$ on $Y$.

A justification for the missing $E\to H$ arrow follows from the previously discussed NEJM study by Mancia et al.,⁹ which was carried out in the same region of Italy as our RASI study, and found no evidence of a causal effect of RASI exposure on Covid-related hospitalisation.

In situations different from ours, truncation bias will have to be properly (and sometimes laboriously) tackled. See discussions by Frangakis and Rubin,³⁰ Rubin¹ and Wang et al.²⁹

4.8. The two components of the causal effect of $E$ on $Y$

The graph of Figure 2 contains two non-overlapping, directed, paths from $E$ to $Y$. This means that, if a causal effect of $E$ on $Y$ exists at all then, according to the graph, this effect will have two distinct, but not exclusive, potential explanations. What are these? Consider the following example, where we go on taking $E=1$ to indicate antecedent (hospital-free) exposure to RASIs, and $T=1$ in-hospital administration of RASIs. Then, were a beneficial effect of $E$ on $Y$ detected, the $E\to Y$ would correspond to explaining the effect in terms of RASIs inducing beneficial physiologic changes that persist long enough for the individual, once hospitalised, to be protected from an adverse outcome. The other path, $E\to T\to Y$, would in that case point to a different explanation: that antecedent exposure to RASIs exhorts the hospital staff to continue RASI administration once the individual has been hospitalised, in which case the benefit would be better explained as an effect of in-hospital (as opposed to antecedent) exposure to RASIs. There will also, a priori, be a possibility of cancellation between the two components of the effect, so-called path-cancellation, although it seems that this can be safely excluded in the present application. The two paths from $E$ to $Y$ can be conveniently referred to as the direct and the indirect component of the total causal effect of $E$ to $Y$.

Unfortunately, the presence of the unobserved confounder $U$, representing unrecorded information bearing on in-hospital decisions about $T$, introduces potential confounding, thereby preventing us from estimating the $T\to Y$ effect, and ultimately from separately quantifying the two (above-mentioned) components of the effect of $E$ on $Y$, except in any of the following situations: (1) when we can randomise $T$ via a clinical experiment, corresponding to ‘cutting’ the $U\to T$ link, (2) when we have an appropriate instrumental variable for $T$, (3) when we can safely assume that the decision about $T$ has been unaffected by $E$, whether due to external imposition of $T=0$, or to clinicians being unable to consult the value of $E$, and (4) when $U$ can be safely summarised by the recorded variables.

4.9. Estimation of the total $E\to Y$ causal effect

The crude statistics of Table 2 presents prima facie evidence of over-68 hypertensive Covid-19 patients with antecedent exposure to ARBs or ACEIs having a lower all-cause mortality than similar patients who did not use RASIs. Table 3 presents prima facie evidence of antecedent use of ACEIs and ARBs being both beneficial in older patients when compared with no-RASI use. Because RASI users were generally in worse health conditions than non-RASI users in the general population, these tables are likely to underestimate the effects of interest, which motivates the ensuing, more formal, analysis of the effect of antecedent RASI use on Covid-19 mortality of hypertensive patients.

Table 2.

The table reports sample numerosities stratified by age (all ages, 68+), survival status and exposure (renin aldosterone system inhibitor (RASI) use, no RASI use). Reported in brackets are stratum-specific mortalities.

	Whole population		Hypertensives all ages		Hypertensives 68+
		Decedents		Decedents		Decedents
Exposure	Surv	(mortality)	Surv	(mortality)	Surv	(mortality)
no RASI	690	221 (24%)	154	106 (40%)	63	89 (58%)
RASI	324	155 (32%)	304	148 (32%)	153	106 (40%)

Table 3.

Over-68 hypertensive Covid-19 patients cross-stratified by outcome status (rows) and according to as they do not use RASIs (column 2), or use ACEIs but not ARBs (column 3), or use ACEIs but not ARBs (column 4). Reported in brackets are stratum-specific crude mortality estimates.

Outcome	RASI non-users	ACEIs	ARBs
	(mortality)	(mortality)	(mortality)
Survived	69	83	74
Decedent	90	61	46
	(56%)	(42%)	(38%)

RASI: renin aldosterone system inhibitor; ACEI: angiotensin-converting enzyme inhibitor; ARB: angiotensin receptor blocker.

Within the stratum of older patients, ARB-only and ACEI-only users were separately compared with matched no-RASI users in terms of their outcome distribution in order to assess the effects of antecedent use of those two drugs in that stratum. With $E$ representing in turn ‘use of ARBs-only vs no-RASI’ and ‘use of ACEIs-only vs no-RASI’, we selected a subsample of individuals with $E=1$ and one with $E=0$, in such a way that the two subsamples would hopefully be comparable in terms of $X$, for comparison in terms of the mortality outcome $Y$. Following Rosenbaum and Rubin,³¹ we did this by constructing a propensity score, $S_E(X)$, such that $E$ could be assumed to depend on $X$ only through $S_E(X)$ in the studied population, formally $E\perp \perp X\mid (S_E,F_{\mathrm{E}}=\mathrm{\varnothing })$. We estimated the score via logistic regression of $E$ on $X$, although nothing prevents the use of more sophisticated models of dependence, including machine learning methods, as in Lee et al.³²We then extracted the $E=0$ and $E=1$ subsamples in such a way that their distributions along $S_E(X)$ were similar; said differently, that they were ‘balanced’. For this purpose, we used the stochastic matching procedure proposed by Rosenbaum.³³

We obtained a good balance thanks to $E$ representing in our case exposure to a drug whose prescription in the population was free of precise guidelines. A good balance would not have been achieved had the data markedly departed from the positivity condition: that the inequality $P(E=e\mid X,F_{\mathrm{E}}=\mathrm{\varnothing })>0$ be satisfied for both $e=0$ and $e=1$ with probability 1, as noted by Guo and Dawid.³⁴

Our results in Table 4 highlight a protective total effect of antecedent use of ACEIs ($p=0.018$, $\mathrm{OR}=0.57$, 95% CI 0.36–0.91) on mortality of over-68 hypertensive Covid-19 patients, and in the same stratum of patients, an even stronger protective total effect of antecedent use of ARBs ($p=0.006$, $\mathrm{OR}=0.49$, 95% CI 0.29–0.82).

Table 4.

Estimated ORs of adverse outcome for antecedent use of ARBs/no-ACEIs and antecedent use of ARBs/no-ACEIs within the population of over-68 hypertensive Covid-19 patients, expressed relative to the RASI-free group (which therefore acts as reference). All the ORs are adjusted for pre-hospitalisation variables via propensity-score matching.

		OR
Exposure	$N$ (decedents)	(95% CI)	P
no RASIs	120 (67)	1.0 (ref)
	144 (81)
ARBs	120 (46)	0.49	.006
		(0.29,0.82)
ACEIs	144 (61)	0.57	.018
		(0.36,0.91)

OR: odds ratio; ARB: angiotensin receptor blocker; RASI: renin aldosterone system inhibitor; ACEI: angiotensin-converting enzyme inhibitor.

Within the stratum of younger patients, no-RASI users were compared with RASI users in terms of mortality in order to assess the effects of RASIs in that stratum. Again, propensity score-based subselection and matching were used to adjust for observed potential confounders. The data provided no evidence of an effect of antecedent use of RASIs in this age stratum. The estimated odds ratio is reported in Table 5 ($p\approx 1$, $\mathrm{OR}\approx 1$, 95% CI 0.47–2.13). Table 5 reports OR estimates for the effects of antecedent RASI on the risk of an adverse outcome among under-68 hypertensive Covid-19 patients, none of these effects turning out to be significant.

Table 5.

Estimated OR of adverse outcome for antecedent use of RASIs versus no-RASIs use within the population of hypertensive Covid-19 patients of age 68 or less. The OR is adjusted for pre-hospitalisation variables via propensity-score matching.

		OR
Exposure	$N$ (decedents)	(95% CI)	P
no RASIs	108 (17)	1.0 (ref)
RASIs use	193 (42)	$\approx 1$	$\approx$ 1
		(0.47,2.12)

OR: odds ratio; CI: confidence interval; RASI: renin aldosterone system inhibitor.

4.10. Analysis diagnostics

A check of the degrees of balance (with respect to the propensity score) achieved in the above analysis can be performed with the aid of Figure 3. This figure contains four plots. The upper left plot compares the probability densities of the ARB-users (lower half of the plot) versus the no-RASI-users (upper half of the plot) groups over the propensity score for antecedent use of ARBs, as they have been estimated before the matching. The upper right plot presents the same comparison, with the densities estimated after the matching. Note the balance improvement achieved by the matching. The lower left plot compares the probability densities for the ACE-users (lower half of the plot) versus the no-RASI-users (upper half of the plot) groups over the propensity score for antecedent use of ACEIs, as they have been estimated before the matching. Finally, the lower right plot performs the same comparison as the plot on its left side, with densities estimated after the matching. Again, note the balance improvement achieved by the matching.

5. Discussion

We hope we have provided a convincing example of the usefulness of causal DAGs in complex problems of assessment of medical interventions on the basis of observational data. Our example involved multiple interrelated questions about the effects of anti-hypertensive RASI drugs. A most important step of the analysis was the construction of a proper DAG representation of the available knowledge and of the relevant questions, prior to using the DAG for getting the desired answers. In order to help the reader gain an insight into this aspect of the study, we have provided a detailed description of the scientific context.

As concerns the substantive aspect of our work, we think we now have enough evidence to motivate an experimental confirmation of a protective RASI effect. This would also be the best way of answering the (practically important) question of whether the beneficial RASI effect operates via antecedent (pre-hospital) exposure or in hospital administration. The resolution to continue research in this direction may now have lost momentum as a consequence of the increasing attention devoted by the scientific community to the development of Covid-19 vaccination programmes.

Appendix 1. $d$-separation and conditional independence

In a DAG, when an arrow leads from a generic node $A$ to a generic node $B$, we say that $A$ is a parent node of $B$. If we are able to reach node $B$ by starting from $A$ and by moving along the graph edges in accord with their directions, then $B$ is a descendant of $A$. Having taken the DAG to represent a specific family of probability distributions over its variables (see Section 4.5), the previously mentioned $d$-separation and moralisation criteria help us to read off the graph the conditional independence relationships implied by that distributional family.

In this paper, we adopt the $d$-separation criterion, which rests on the concept of path along a graph, defined as consisting of a consecutive sequence of edges, regardless of their directions. An example of path in Figure 2 is $X\to H\leftarrow U\to Y$. Because this example of path does not lead from $X$ to $Y$ (or vice versa) in accord with arrow directions we call it noncausal. We would otherwise call it causal.

A path is unconditionally unblocked if it does not contain a pair of arrows that collide head-to-head, $\to \circ \leftarrow$, so called collider. The path $X\to H\leftarrow U\to Y$, for example, is not unconditionally unblocked, because node $\to H\leftarrow$ acts as a collider relative to this path. We therefore call this an unconditionally blocked path. Two generic graph nodes, $A$ and $B$, are said to be unconditionally $d$-connected if there is at least an unconditionally unblocked path between them. With reference to Figure 2, for example, $X,E,Y$ and $T$ are all unconditionally $d$-connected with each other, whereas $X$ and $U$ are not.

A path is conditionally unblocked, given a generic set $C$ of nodes, if no non-collider in the path is in $C$, and all the colliders in the path are either in $C$ or have a descendant in $C$. We may, in this case, equivalently say that conditioning on $C$unblocks the path. In Figure 2, for example, conditioning on $H$ or $T$ unblocks the $X\to H\leftarrow U\to Y$ path (hint: note that $T$ is a descendant of $H)$.

If, conditional on a generic node $C$, no unblocked path exists between generic nodes $A$ and $B$, then we say that conditional on $C$, nodes $A$ and $B$ are $d$-separated. In Figure 2, for example, node $X$$d$-separates $E$ from $H$. If a generic node $C$$d$-separates the generic node $A$ from the generic node $B$ then, under all the probability distributions represented by the graph, $A$ and $B$ are conditionally independent given $C$. If, instead, $C$ does not$d$-separate $A$ from $B$, then there may exist, within the family of distributions represented by the DAG, one particular distribution where $A$ and $B$ are not conditionally independent given $C$.

$d$-separation allows us to examine whether a given conditional independence relationship follows from a given DAG. In Figure 2, for example, we prove that $E$ is independent of $H$ given $X$, written $E\perp \perp H\mid X$. This is because the conditioning on $X$ blocks the $E\leftarrow X\to H$ path without unblocking the remaining paths between $E$ and $H$. Hence $X$$d$-separates $E$ from $H$, from which $E\perp \perp H\mid X$ follows, implying that two individuals with identical $X$ have identical risks of being hospitalised for Covid-19, whatever their values of $E$.

Appendix 2. A closer look at superadditivity

In the graph of Figure 4, the symbol $A$ denotes a dichotomised version of variable Age, with $A\equiv I_{\mathrm{Age}>68\mathrm{years}}$. The effect of this variable on the probability of hospitalisation for Covid-19 appears in the graph to be completely mediated by pre-hospitalisation history $X$. Node $H=1$ indicates that we are conditioning on the individual having been hospitalised for Covid-19, which accounts for the fact that analysis is carried out on hospitalised individuals. Under the assumptions coded by this graph, we can interpret the superadditivity condition (1) given in Section 4.6 in a causal way. This is because the graph implies $Y\perp \perp F_{\mathrm{E}}\mid E,X,A,H=1$, and hence

$$\begin{array}{r}{P}_{eax}^{‘}\equiv P(Y=1\mid E=1-e,A=a,X=x,H=1,F_E=1-e)\\ =P(Y=1\mid E=1-e,A=a,X=x,H=1,F_E=\mathrm{\varnothing })=P_{eax}\end{array}$$