Abstract
In the last decade, Bayesian networks (BNs) have been widely used in engineering risk assessment due to the benefits that they provide over other methods. Among these, the most significant is the ability to model systems, causal factors, and their dependencies in a probabilistic manner. This capability has enabled the community to do causal reasoning through associations, which answers questions such as: “How does new evidence about the occurrence of event change my belief about the occurrence of event ?” Associative reasoning has helped risk analysts to identify relevant risk‐contributing factors and perform scenario analysis by evidence propagation. However, engineering risk assessment has yet to explore other features of BNs, such as the ability to reason through interventions, which enables the BN model to support answering questions of the form “How does doing change my belief about the occurrence of event ?” In this article, we propose to expand the scope of use of BN models in engineering risk assessment to support intervention reasoning. This will provide more robust risk‐informed decision support by enabling the modeling of policies and actions before being implemented. To do this, we provide the formal mathematical background and tools to model interventions in BNs and propose a framework that enables its use in engineering risk assessment. This is demonstrated in an illustrative case study on third‐party damage of natural gas pipelines, showing how BNs can be used to inform decision‐makers about the effect that new actions/policies can have on a system.
Keywords: Bayesian Network, Causality, Decision Support, Engineering Risk Assessment, Intervention Reasoning
1. INTRODUCTION
Bayesian networks (BNs) have gained wide popularity over the last two decades in engineering systems risk assessment for decision support (Langseth & Portinale, 2007; Fenton & Neil, 2012) due to its capability of computing complex multi‐variate joint distributions in an efficient way (Khakzad, 2018). This is accomplished by representing an engineering system as a directed acyclic graph (DAG) (also called BN structure), where nodes represent the modeled variables of interest, and edges encompass dependency relationships between nodes. This interpretation of BNs as a description of complex joint distributions describing an engineering system have been studied for the reliability modeling of levee systems (Roscoe, Hanea, Jongejan, & Vrouwenvelder, 2020) and fire safety modeling of oil terminals (Khakzad, 2018), among others (Chemweno, Pintelon, Muchiri, & Van Horenbeek, 2018).
However, a causal interpretation of BNs is usually adopted for the risk assessment of high consequence industries and activities (Lewis & Groth, 2019). Here, the edges of a BN represent the causal relationships between variables instead of just dependencies. By doing this, causal reasoning with BNs is enabled, which has been studied in the form of association queries to enhance risk‐informed decision support (i.e., answering how the probability of a variable of interest change given new evidence on other variables of the studied BN. We call this type of reasoning as associative reasoning). For example, Groth, Denman, Darling, Jones, and Luger (2020) represented the causal relationships between accident sequences, reactor system components, and plant parameters of a nuclear power plant in a dynamic BN structure for fault diagnosis in accident scenarios, facilitating the interpretability of the system behavior for operators to manage an accident better. Another example is seen in Zhang, Wu, Qin, Skibniewski, and Liu (2016) work on tunneling‐induced pipeline damages, where the causal relationships between risk factors of pipeline safety in a tunnel construction are represented in a fuzzy BN structure. Then, evidence‐based sensitivity analyses are performed to identify which pipeline safety risk factors need to be addressed for damage mitigation. The reader is referred to Weber, Medina‐Oliva, Simon, & Iung (2012), Mkrtchyan, Podofillini, and Dang (2015), Brito and Griffiths (2016), Groth, Smith, and Moradi (2019), and Ayele, Barabady and Droguett (2016) for other examples on BN‐based associative reasoning in engineering systems risk assessment.
As shown above, causal reasoning in BNs has proved to be highly beneficial for engineering systems risk assessment, being associative reasoning the primary tool used for risk‐informed decision support. Taking excavation activities as an example, associative reasoning has allowed analysts to provide decision‐makers with insights such as “evidence shows that untrained excavators are involved in 50% more pipeline damage incidents than trained excavators.” However, Pearl (2009) proposed BNs as causal models capable of addressing much more complex causal inferences based on the modeling of interventions on a system. This type of inferences is based on intervention reasoning, which enables the proper quantification of the effect that a hypothetical intervention on a system variable can have on another variable of interest . Then, decision support with BNs can be further enhanced by adding intervention reasoning to the current BN causal reasoning toolbox, enabling the estimation of causal insights such as “if excavators are trained, pipeline damage incidents caused by them are expected to decrease in a 50%.”
In the risk analysis field, causal reasoning through interventions has been promoted by authors such as Cox Jr (2013) and Broniatowski and Tucker (2017) for decision support, arguing that its use can be highly beneficial by enabling the estimation of the effect that a certain action or policy can have on a system behavior. However, an exhaustive literature review showed us no works on intervention reasoning with BNs for engineering systems risk assessment.
The conducted literature review was performed on the journals Risk Analysis (RA), Reliability Engineering and System Safety (RESS), and Journal of Risk and Reliability (JRR), filtering works from the year 2000 to the present using different Boolean combinations for the keywords “Causality,” “Causal Inference,” “Intervention,” “Engineering,” and “Bayesian Network.” A total of 79 papers (8 from RA, 18 from JRR, and 53 from RESS) were identified as having causal reasoning with BNs in engineering systems as its main topic; however, only two works were found that dealt with intervention reasoning. The first was Langseth and Portinale (2007) review on the use of BNs in reliability, dedicating a section to intervention reasoning tools and showing qualitatively how planned maintenance decision‐making can benefit from these. The second is Hund and Schroeder (2020), who worked on a battery performance simulated data set, where they exemplify how reliability estimations can be strongly biased if interventions are not properly addressed. Nevertheless, both works were in the context of engineering reliability, not risk assessment.
Even though intervention reasoning benefits are known and studied in other disciplines (Joffe, Gambhir, Chadeau‐Hyam, & Vineis, 2012; Hünermund & Bareinboim, 2019) and suggested by authors in the risk analysis field, a gap of knowledge is identified for engineering systems risk assessment. To address this gap, this article's objective is to expand the scope of engineering systems BN models to support causal reasoning through interventions, with emphasis on its benefits on risk‐informed decision support by estimating the effect that policies and actions can have on a system before being implemented.
To address the aforementioned objective, we will first introduce causal reasoning through interventions and its relevance in engineering risk assessment in Section 2. The formal concepts, mathematical background, and techniques to perform risk assessment through intervention reasoning in BNs are presented in Section 3. Then, in Section 4, we present a BN‐based framework that enables risk analysts to properly model actions/policies as interventions in BNs, intending to improve risk‐informed decision support. This framework is exemplified through an illustrative case study on third‐party damage (TPD) on natural gas pipelines in Section 5. Lastly, concluding remarks on the benefits of performing causal reasoning through interventions are presented in Section 6.
2. A PRIMER ON CAUSALITY AND INTERVENTIONS IN ENGINEERING RISK ASSESSMENT BNs
To introduce proper causal modeling and language in the artificial intelligence community, Pearl and Mackenzie (2018) defined the Ladder of Causation (as shown in Fig. 1); a metamodel that separates causal reasoning into three different levels: association, intervention, and counterfactual. It can be seen that the rungs of the ladder are defined to answer different causal queries, which will be denoted as . To understand Fig. 1, we denote as a random variable that can take on values and (i.e., ). In addition, represents the estimated value of in an intervened BN with .
Fig 1.

Ladder of causation. Figure derived from Pearl and Mackenzie (2018).
Rung 1: Associative reasoning. Answers associative queries of the form “How does new evidence about the occurrence of event change my belief about the occurrence of event ?” Mathematically, these are expressed as . The gross body of work on engineering systems BN studies uses this type of reasoning. Using associative reasoning, risk analysts can inform decision‐makers about how the probability of an outcome changes for a particular event; this occurs by performing evidence propagation. For example, Hegde, Utne, Schjølberg, and Thorkildsen (2018) developed a BN model to help supervisors to determine when an autonomous underwater vehicle mission should be aborted. This model connects 41 technical, organizational, and operational causal factors to a target node that represents the probability of aborting a mission. Then, by setting evidence on the state of the system operational conditions in the model nodes, and propagating that evidence through the rest of the BN, the mission abortion probability is calculated and informed to supervisors to decide on continuing or aborting operations.
Rung 2: Intervention reasoning. Answers intervention queries of the form “How does doing change my belief about the occurrence of event ?” Mathematically, these are expressed as , where is an operator that represents an hypothetical intervention on . As shown in Section 1, we only found two works on engineering systems using intervention reasoning. Taking Langseth and Portinale (2007) qualitative BN example on component reliability to explain this rung, they showed that association reasoning‐based causal insights are restricted to claims such as “In this data set, we find that components that are maintained once a year fail twice as often as those maintained twice a year.” However, Langseth and Portinale showed that the effect that different planned maintenance () interval values alternatives has on a component remaining life (), such as months, can be modeled in a BN by the intervention queries and , and thus enabling more potent causal insights such as: “If we change the PM interval of a component from 12 to 6 months, we can expect an increase in its remaining life by a factor of about 2.”
Rung 3: Counterfactual reasoning. Answers counterfactual queries of the form “How does my belief in the occurrence of event change had event been instead of .” Mathematically, these are expressed as . Although out of the scope of this study, this type of causal reasoning can be very useful for analyzing postintervention scenarios. An example of this can be seen in Johnson and Holloway (2003) work on incident investigation, showing that investigators usually guide their analysis by counterfactuals, being assertions of the form “If had not occurred, the incident would have been avoided” used and promoted in handbooks (Johnson, 2003).
As shown above, given that BNs are used in engineering risk assessment to make causal claims when providing information to decision‐makers (Lam & Cruz, 2019), distinguishing the causal query to be solved is highly important. By introducing the ladder of causation to the engineering risk assessment community, causal queries made to BN models can now be properly defined and expressed mathematically.
2.1. The Importance of Intervention Reasoning in Engineering Risk Assessment BN Models
When a risk assessment is performed on an engineering system, BN models are used to identify possible risk sources and causal factors that should be intervened on to mitigate risks. Then, this information is given to decision‐makers to implement new actions and policies to improve system safety. Until now, the extension of causal insights from BNs in risk assessment stops here. However, by introducing intervention reasoning, causal inference in BNs will enable risk analysts to also estimate and inform the magnitude that a considered decision can have on the system behavior, enhancing risk‐informed decision support.
Taking Kabir, Balek, and Tesfamariam (2018) work on buried infrastructure risk as an example, we can see that, using a BN model sensitivity study, they identified both diameter and burial depth as critical risk factors that can lead to highly undesirable consequences. To improve safety, this information can be used by authorities to implement new regulations on the design features of newly constructed underground facilities. Kabir's BN model risk‐informed decision support can be further enhanced by using intervention reasoning, enabling the estimation of the effect that different infrastructure design alternative values can have in its failure likelihood.
In this article, we intend to open a new research direction for BNs in engineering risk assessment, being the above just one example of how adding intervention reasoning to the engineering risk assessment BN toolbox can improve risk‐informed decision support. To do this, we will provide in the following section the formal mathematical background and tools needed to estimate the effect that actions and policies can have in an engineering system before being implemented.
3. MATHEMATICAL BACKGROUND AND TOOLS
In this section, the formal mathematical background and tools needed to model hypothetical intervention in BNs are introduced.
3.1. Bayesian Networks as Structural Causal Models
A BN model represents a set of variables and conditional dependencies in the nodes and arcs, respectively, of a DAG (also called BN structure) . The strength of the dependencies among nodes is quantified by the conditional probabilities between them. In this work, we will use the following nomenclature and definitions to define a BN:
as the set of nodes present in a BN with graph G. Also, are going to be used later for clearer explanations.
The set of states of a node are represented by {}.
as the set of parents of , i.e., all nodes with an outgoing edge to .
as the set of descendants of , i.e., all nodes with an ingoing edge from .
as the conditional probability table (CPT) of discrete variable or conditional probability function (CPF) of a continuous variable .
as a path between and , i.e., a unique set of nodes and edges that connects to .
The main feature that enables causal reasoning in BNs is the independence properties embedded in its structure, which are denoted by , (i.e., is conditionally independent of given ). There are three basic junction patterns that define conditional independence among nodes in a BN (Pear, 1985): chains, forks, and colliders. As shown in Fig. 2, both chains and forks embed , whereas colliders show that (i.e., is not conditionally independent of given ). If multiple junction patterns are present in a BN structure, the d‐separation criterion (Pearl, 1988) can be used to extract node independence properties from a BN structure.
Fig 2.
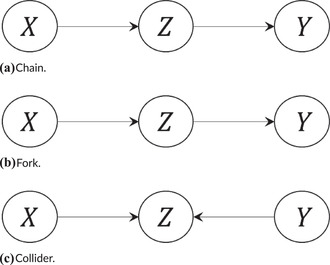
Basic junctions patterns in a BN.
Definition 1
(d‐separation) and are d‐separated conditional on a set of nodes (i.e., ) if blocks every path between and . blocks a path if either:
contains a chain or a fork such that is in .
contains a collider such that or its descendants are not in .
d‐Separation enables factoring high‐dimensional joint distributions in BNs by the product of local conditionally independent distributions present in its structure. Then, any joint distribution in a BN can be expressed by the factorization formula:
| (1) |
In engineering risk assessment BN models, Equation (1) is widely used to answer association queries of the form . To do this, new evidence on the state of a set of variables of interest can be propagated through the BN model to obtain an updated probability on the states of a set of variables of interest (Fenton & Neil, 2012).
3.2. Interventions and the do‐operator
To move from association to intervention reasoning in the ladder of causation, hypothetical interventions in BNs needs to be modeled, for which the do‐operator is introduced. Given a BN model , the effect of an intervention on a node can be represented by (Pearl, 2012):
| (2) |
were is the postintervention BN model. In terms of the original DAG , the equivalent postintervention DAG is , where corresponds to with all ingoing edges to removed, as shown, for example, in Fig. 3(b). In addition, CPTs (or CPFs) of are modified in to represent .
Fig 3.
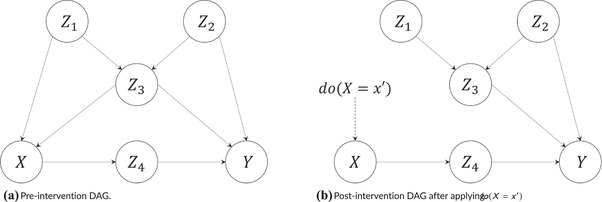
Illustrative BN DAG.
Combining Equations (1) and (2), the joint distribution generated by an intervention on a set of nodes that represents the changes made by an action/policy in an engineering system can be expressed by the truncated factorization formula as:
| (3) |
where are preintervention conditional distributions present in . Then, it can be seen that the use of Equation (3) to represent an intervention on a BN model with DAG is equivalent to applying the factorization formula (1) to find the joint distribution of a postintervention BN DAG , which is then conditioned on , resulting in .
As an example, applying Equation (3) in Fig. 3(a), the postintervention joint distribution of performing can be computed by:
| (4) |
Then, the effect of the intervention on can be identified from Equation (4) just by marginalizing over , and as:
| (5) |
3.3. Adjusting for Confounding Bias
When computing intervention queries on BN models, disentangling correlational from causal relationships between the intervened variable and the studied outcome due to common causes is critical. If not done, the obtained postintervention distribution can be highly biased. In other words, this means that usually do not coincide with due to the presence of common causes. For an engineering system, this phenomenon was discussed by Hund and Schroeder (2020), where they show that the mistreatment of common causes can lead to incorrect results and insights from a BN model. Bias‐inducing common cause nodes between and are called confounders, and are defined by VanderWeele and Shpitser (2013) as follows.
Definition 2
(Confounder) A preintervention node is a confounder of the effect of on if conditioning over it blocks a backdoor path from to .
A backdoor path between and is any noncausal path between them (i.e., a path with an ingoing edge to that starts with an ingoing edge to ). Evidence propagation through unblocked backdoor paths is the reason of possible spurious associations between and when addressing causal claims, a bias called as confounding bias (Pearl, 2009).
The simplest graphical representation of confounding bias is shown in Fig. 4, where confounds the effect of on . Then, to compute the effect of on , Equation (3) can be used as and marginalized over , obtaining:
| (6) |
and thus blocking the backdoor path by conditioning on .
Fig 4.
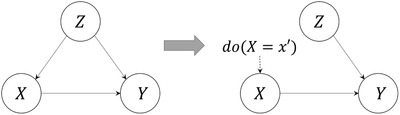
Basic confounding BN structure and its postintervention DAG.
The process of conditioning the causal effect of on over a bias‐inducing confounder is called adjusting for confounding. Cases like Fig. 4 are easy to adjust for, but real‐life BN structures are usually more complex, requiring the adjustment of multiple confounders to properly compute postintervention distributions. To address this difficulty, a first option is just to marginalize over all non‐ and non‐ nodes identified by Equation (3) (being not all necessarily confounders). This first option is viable only if the risk analyst has a completely parameterized BN model. A second option is to find a sufficient admissible set of confounders in the BN model that ensures that no unblocked backdoor paths exist between and if they are adjusted for confounding, generating an unbiased estimation of the intervention query by making dependent on only for the direct paths between them (which is analogous to removing the incoming edges to as done by applying the truncated factorization formula). The set can be found using the backdoor criterion, defined by Pearl (1995) as follows.
Definition 3
(Backdoor criterion) Given an ordered pair of nodes in a BN model, a set of variables is sufficient admissible for adjustment relative to if:
no node in is a descendant of and
blocks every backdoor path between and .
Then, Equation (6), which we will now call as the backdoor formula, can be used to estimate the causal effect of intervening on if is considered to be a set of nodes that satisfies the backdoor criterion.
The backdoor criterion is one of the most powerful tools present in BNs, enabling risk analysts to compute confounding‐unbiased intervention queries on a model even though it is not fully parameterized. To exemplify the latter, consider an analyst who represented an engineering process by the BN shown in Fig. 3(a) and have access to data on , and . If he is interested on estimating the effect that intervening on will have on , the intervention query needs to be identified. Given that there is no data on nodes nor , the analyst uses the backdoor criterion and identified as a sufficient adjustment set for confounding, enabling the use of backdoor formula (6) as to estimate the intervention query .
Sometimes, in the presence of nonparameterized nodes, it is not possible to quantify a sufficient adjustment set for confounding, and thus, Equations (3) and (6) cannot be used to compute an intervention query . To generalize the identifiability of causal queries in BN models, Pearl (1995) defined the do‐calculus rules by which a postintervention distribution in can be computed from preintervention data in . These are defined as follows.
Theorem 1
(Do‐calculus rules) Let X, Y, Z, and W be a disjoint set of nodes in . Let and be the graph obtained by deleting the ingoing and outgoing edges of X, respectively. Let be the DAG resulting from deleting ingoing edges to X and outgoing edge from Z. The following rules are defined for .
Rule 1 (Insertion / deletion of observations):
if .
Rule 2 (Intervention / observation exchange):
if .
Rule 3 (Insertion / deletion of interventions):
if , where is the set of Z‐nodes that are not ancestors of any W node in .
A sequential application of these rules guarantees the identifiability of an intervention query, if possible, by providing a do‐free postintervention distribution expression (Shpitser & Pearl, 2006). However, it should be noticed that in the presence of a nonfully parameterized BN model, the estimation of the intervention query by using the backdoor criterion or the do‐calculus rules is only possible if data on the variable of interest have been collected. If this is not the case, the intervention query cannot be estimated.
Applying the do‐calculus rules to identify an intervention query is not trivial and can become very demanding in large graphs. Given this, Shpitser and Pearl (2006) automated this process, making causal identification straightforward by publicly available libraries such as the R package causaleffect (Tikka & Karvanen, 2017).
4. A BN‐BASED FRAMEWORK FOR CAUSAL REASONING THROUGH INTERVENTIONS IN ENGINEERING RISK ASSESSMENT
To create a comprehensive BN model that represents the behavior of an engineering system when intervened, the full spectrum of contexts and causal factors relevant to it should be taken into account. This not only enables risk analysts to fully express their knowledge and assumptions, but also to properly inform them to decision‐makers.
To address these requirements, we propose the three‐step BN‐based framework, as shown in Fig. 5. This will enable risk analysts to use the BN mathematical tools presented in Section 3 to properly estimate and inform the effect that a new action/policy can have on an engineering system.
Fig 5.

Proposed BN‐based framework for causal reasoning through interventions.
BN‐based frameworks for risk‐informed decision support such as influence diagrams (IDs) are similar to the proposed framework by sharing a node representing a decision to be made by a decision‐maker (i.e., decision node in IDs and treatment node in the proposed framework). However, our framework differs from IDs in that they solve different problems. In the proposed framework, a probabilistic inference problem is solved by estimating the effect that an intervention can have on the belief in which a system behavior will change, given our prior data and knowledge on the system. In contrast, IDs solve a decision making problem by identifying the decision that should be made to maximize a certain cost or utility function. It is important to notice that the proposed framework does not try to determine an optimal decision but just express and inform the probabilistic effect of a decision on a system.
The steps of the proposed framework are defined below.
4.1. Frame the Problem
First, the risk analyst frames the problem in terms of an intervention query, taking both the action/policy of study and available data into consideration. In order to do this, the following practices are suggested:
-
(i)
Frame the action/policy. The risk analyst understands and contextualizes both the objective of the decision‐maker and the different action/policy changes that are being considered to achieve it. To guide this process, the following questions are suggested:
What action/policy changes are being considered? (intervention)
What is the objective of the action/policy? (outcome)
What is the context of the action/policy with respect to the problem?
-
(ii)
Frame the data. In addition, a broad understanding of the available data to model the studied query is needed. This will help with the identification of candidate data set variables that represent the action/policy and its objective. To guide this process, the following questions are suggested:
What data are available?
Is the quantity and quality of the data comprehensive enough to support modeling the action/policy?
Is the considered action/policy change present in the data? if not, it is possible to model?
Is the action/policy objective present in the data? if not, it is possible to model?
4.2. Perform Intervention Reasoning
Second, the studied action/policy is modeled and quantified using a BN model and the tools shown in Section 3. This is done to estimate the intervention query outlined in the previous step in a way that all assumptions used by the risk analyst to compute it are explicit and properly communicated to the decision‐maker. To ensure this, the following methodology is proposed:
-
(i)Define the intervention query. The intervention query is defined in a general form by:
(7) Equation (7) will explicitly express the target and intervention to be modeled in the BN.
-
(ii)
Build the BN model. The risk analyst expresses his or her understanding of the system behavior as a BN model, defining its nodes, states, parameterization strategy, and quantification. This is essential to later express Equation (7) in terms of the available data.
To guide the construction of a BN that allows the use of the tools presented in Section 3, we propose the meta‐BN structure shown in Fig. 6. Here, dashed bidirected edges represent causal assumptions between nodes that are not imposed in this metamodel. On the other hand, directed edges should be used as shown in the figure. Note that all nodes considered as relevant by the risk analyst should be included in the BN structure, even if they are not observed in the available data.
Given an intervention query , the nodes in Fig. 6 are defined as:- Treatment nodes (). Corresponds to the set of nodes that the risk analyst wants to intervene on (applying the do‐operator) to estimate its effect on an outcome node . These nodes should reflect the action/policy changes that the decision‐maker wants to implement on a system.
- Outcome nodes (). Corresponds to the set of target nodes in that the risk analyst is interested in estimating. These nodes should represent the variables of interest that a decision‐maker is taking into consideration to make a decision (i.e., indicate if the action/policy objective is achieved).
- Confounder nodes (). Corresponds to the set of nodes that the risk analyst considers that can confound and thus bias the estimation of . These nodes should be identified and informed to the decision‐maker to clarify how the risk analyst interpreted the system behavior against an intervention made on it.
- Mediation nodes (). Corresponds to the set of nodes that the risk analyst considers that can mediate (i.e., increase or decrease) the direct effect that an intervention on has on . Structurally, mediation nodes are represented in the causal path between the treatment and outcome nodes. It should be noted that mediation nodes can also be confounders if they comply with Definition 2.
- Structural nodes (). Corresponds to the set of nodes that are not identified by any of the definitions above, but that contributes to the representation of the risk analyst knowledge of the system.
-
(iii)
Identify the intervention query. The defined from (step 2.i) is now mapped to the BN defined in (step 2.ii), where the action/policy and objective are represented by and , respectively. Then, an expression for can be obtained using either Equation (3), the backdoor criterion or by a systematic application of the ‐calculus rules.
-
(iv)
Estimate the intervention query. Using the expression found in the previous step, is estimated using the available data. The BN structure should be revised if the implications of the obtained result are unfeasible or unreasonable.
Fig 6.
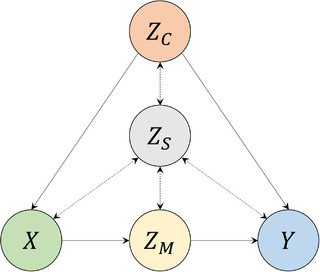
Proposed meta‐BN structure for intervention reasoning.
4.3. Inform the Decision‐Maker
Finally, the results obtained in the previous step of the framework have to be expressed in the best way possible to inform the decision‐maker. The estimated value of the intervention query does not give much information on its own, so the following intervention‐based causal metrics are suggested to provide relevant information on the causal effect that an intervened variable has on an outcome :
-
(i)
Intervention Effect (IE). This metric is used to express the difference in the outcome likelihood between the pre‐ and postintervention distributions given the risk analyst's knowledge of the system.
Given the preintervention marginal distribution of an outcome variable , the effect of the intervention on a specific value of can be expressed as:(8) -
(ii)
Comparative Causal Effect (CCE). This metric is used to express how an outcome changes relatively to different actions/policies, enabling the risk analyst to rigorously compare all action/policy alternatives considered by the decision‐maker.
The comparative effect of two different intervention queries and on an specific value of an outcome variable can be expressed as:(9) -
(iii)
Controlled Direct Effect (CDE). This metric provides decision‐makers with insights on how much of the system postintervention behavior was directly affected by the performed intervention, and not on its consequences. Similar values of IE and CDE suggest that the effect of the interventions is mostly direct. If not, the effect is considerably mediated.
Given the presence of a mediation node , the direct effect of the intervention on can be computed by controlling for different relevant values of as
which requires the computation of the queries and .(10)
Both CCE and CDE metrics require the identification and estimation of multiple intervention queries on the built BN model. These can be identified and estimated by following steps (2.iii) and (2.iv) from Section 4.2.
5. ILLUSTRATIVE CASE STUDY: THIRD‐PARTY DAMAGE IN NATURAL GAS PIPELINES
In this section, the proposed BN‐based framework for causal reasoning through interventions is demonstrated in a case study regarding TPD on natural gas pipelines (i.e., damage done by personnel not associated with the pipeline operation). In addition, the limitations of using associative reasoning to answer intervention queries are discussed. It is important to state that this case study is meant to be illustrative for the proposed framework and not conclusive in its results.
The natural gas pipeline network in the United States consists of more than 4 million kilometers of pipelines, which are used to gather, transmit, and distribute natural gas to customers across the United States (U.S. Pipeline and Hazardous Materials Safety Administration (PHMSA), 2020). The PHMSA has collected data on natural gas pipeline incidents and accidents since 1970, and data indicate that TPD is a leading cause of failures (U.S. Pipeline and Hazardous Materials Safety Administration (PHMSA), 2020). Between 2015 and 2020, TPD caused on average of the PHMSA incident reports for transmission and distribution lines. These incidents have had severe consequences, involving $125 million in costs, 13 fatalities, and 67 injuries (U.S. Pipeline and Hazardous Materials Safety Administration (PHMSA), 2020).
In an effort to mitigate TPD, the Common Ground Alliance (CGA), a nonprofit organization dedicated to preventing damage to underground infrastructure, provides the following dig‐in best practices steps in the excavation process (Santarelli, 2019):
The excavator delineates the digging area.
The excavator provides notice on intent to dig to a One Call center (e.g., 811) or submits an online form providing dig and site information.
The utility operator locates and marks (L&M) their underground facilities in the area of the request in an accurate and timely manner. When done, One Call will notify the excavator.
The excavator proceeds to dig safely by exposing underground utilities using proper tools to avoid accidental damage.
TPD can occur when one of these practices fails to be properly executed.
According to the 2018 CGA DIRT report (DIRT, 2020), “Notification Issues,” “Locating Issues,” and “Excavation Issues” are the leading root cause groups for excavation damage, corresponding to an improper execution of steps 2–4, respectively. Between 2015 and 2019, “Excavation Issues” represented the of damage causes, with “failure to test hole (pothole)” (i.e., not exposing underground facilities using hand tools before digging) its leading contributor (DIRT, 2020). Given this, one of the major recommendations provided in the 2018 CGA DIRT report is the promotion of potholing as a best practice for excavators.
In this illustrative case study, we will answer the question: “how does making potholing mandatory will affect the sufficiency of TPD preventive measures?” based on pipeline damage databases of a partner utility company. In order to do this, the proposed framework presented in Section 4 is applied as follows.
5.1. Frame the Problem
First, the problem of modeling and estimating the effect of making potholing mandatory can have on TPD prevention is framed in terms of an intervention query. Both the action and available data are framed as follows.
-
(i)
Frame the action/policy
What action/policy changes are being considered? Evaluate making potholing a mandatory practice in excavation activities.
What is the objective of the action/policy? To ensure that sufficient preventive measures are taken to avoid TPD. The idea behind this objective is that preventive measures insufficiency drops by a if two out of three main risk factors for TPD (i.e., “Notification Issues,” “Locating Issues,” and “Excavation Issues”) mitigating best practices were sufficient (Peng, 2019).
What is the context of the action/policy with respect to the problem? Reduce third‐party excavation damage to natural gas pipelines. The CGA (CGA, 2019) recognizes that excavators have limited knowledge about best practices beyond the need to notify before beginning work. The 2018 CGA DIRT report (DIRT, 2020) suggests promoting potholing, given that DIRT data show that the lack of it is highly correlated with excavation‐related damages.
-
(ii)
Frame the data
What data are available? Natural gas pipelines third party caused damage reports from 2015 to January 2020 from a partner utility company. To protect the proprietary information of our partner, we have created a simulated data set using the same variables. In addition, we have access to an industry‐validated fully parameterized TPD BN model, which is described in Peng (2019).
Is the quantity and quality of the data comprehensive enough to support modeling the action/policy? From the data, we see that, in terms of quantity, there are approximately 9,000 damage reports available with more than 40 different context and root cause related fields (such as “root cause” and “root cause group,” “excavation tools,” “dig‐in description,” among others). Regarding quality, only of the data are missing, on average, in three relevant context fields. In addition, high granularity and low redundancy make the data comprehensive enough to develop a criteria for quantifying possible relevant variables that are not explicitly reported.
Is the considered action/policy change present in the data? if not, it is possible to model? Potholing is not reported explicitly, but it is possible to quantify it from the type of tools used in the excavation in addition to a cross‐validation with written dig‐in descriptions. Moreover, to validate our quantification, we can compare it with Peng (2019) industry‐validated TPD BN model observations on potholing.
Is the action/policy objective present in the data? if not, it is possible to model? There is no field in the data that directly quantify if preventive measures were taken. However, we can use the same parameterization strategy performed in Peng (2019) TPD BN model to quantify this variable in our model. The details of this strategy are shown in Section 5.2.
5.2. Perform Intervention Reasoning
To model and estimate the effect of making potholing mandatory can have on TPD prevention, the following steps are followed.
-
(i)Define the intervention query. For this problem, the intervention query can be expressed by:
(11) -
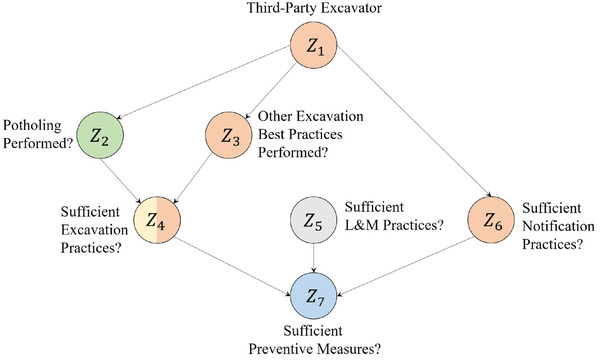
(ii)Build the BN model. When performing excavation damage risk assessment, three leading root cause groups are identified: “Notification Issues,” “Locating Issues,” and “Excavation Issues.” The latter can be mitigated by performing multiple excavation best practices (CGA, 2020), from which potholing is isolated to be the focus of this study. Performing sufficient excavation, L&M, and notification practices are considered to be the main factors that contribute to TPD preventive measures. Also, the specific type of third party that performed the excavation is considered to be the cause of differences in notification practices and likelihood on following recommended excavation best practices. These assumptions are expressed in the discrete BN model shown in Fig. 7. The nodes definition based on the meta‐BN structure presented in Section 4.2 and parameterization strategy are shown below. After parameterization, each node CPT can be found in the Appendix A (Tables A1, A2, A3, A4, A5, A6, A7). Node states and preintervention probabilities are shown in Table I.
- Third‐Party Excavator (). Identifies the type of excavator that performed the excavation. These can be “Property Owner,” “Contractor,” or “Government Entity.” This node is explicitly reported in the used damage reports data set, so its CPT is parameterized directly from it.
- Potholing Performed? (). Identifies if potholing was performed in an excavation activity. Although not explicit in the data set, we created a new field identifying potholing based on the type of tools used in the excavation (such as shovel, air vacuum excavator, and hydro vacuum excavator) in addition to a cross‐validation with written dig‐in descriptions for each damage report data set entry. Given this parameterization, we found that potholing was performed in of excavations. We validated this result with the partner company TPD BN model in Peng (2019), which shows that potholing is performed on of excavations.
- Other Excavation Best Practices Performed? (). Identifies if any CGA excavation best practices aside from potholing are performed. These are “maintain clearance after verifying marks,” “protect/shore/support marked and exposed facilities,” “proper backfilling practices,” and “maintain marks or request remarking if faded” (CGA, 2020). This node is explicitly reported in the used damage reports data set, so its CPT is parameterized directly from it.
- Sufficient Excavation Practices? (). Identifies if there were insufficient excavation practices in general, becoming a contributor to TPD in the damage report. In addition to CGA excavation best practices, this node includes all other excavation issues that are not directly dependant on the specific excavator, such as failing to dig with care. This node is explicitly reported in the used damage reports data set, so its CPT is parameterized directly from it.
- Sufficient L&M Practices? (). Identifies if there were insufficient L&M practices by part of the utility operator, becoming a contributor for TPD. Inaccurate and lack of marks are considered as bad L&M practices. This node is explicitly reported in the used damage reports data set, so its CPT is parameterized directly from it.
- Sufficient Notification Practices? (). Identifies if there were insufficient notification practices by part of the excavator, becoming a contributor for TPD. Excavation activities without notification or made different from the information notified are considered as bad notification practices. This node is explicitly reported in the used damage reports data set, so its CPT is parameterized directly from it.
- Sufficient Preventive Measures? (). Indicates if sufficient preventive measures were taken to avoid TPD, which depends on the sufficiency of three factors: excavation, L&M, and notification practices. This node is not explicitly reported in the data set. To parameterize this node CPT, we used the same parameterization strategy present our partner company industry‐validated TPD BN model (Peng, 2019), which is shown in Table II. The three unknown parameters , and in the CPT represents a drop of a in preventive measures insufficiency if two out of three factors were sufficient. These parameters can be found using damage reports mapping of and to .
Given Section 5.1 identified action/policy changes and objectives, “Potholing Performed?” and “Sufficient Preventive Measures?” are considered as treatment and outcome nodes, respectively, in the proposed meta‐BN structure shown in Fig. 6 (i.e., and ). Then, given the context of the action/policy, are identified as confounder nodes and as a structural node. In addition, is also identified as a mediation node of the effect of on .
-
1.Identify the intervention query. Mapping the intervention query defined in (i) to the BN built in (ii), we can express as:
with subsequent postintervention BN DAG, as shown in Fig. 8.(12) Given that we have a fully parameterized BN model for the case study, the truncated factorization formula (3) is applied to identify the intervention query Q in (12). Marginalizing over the nodes , and , can be computed by:(13) It is important to highlight that Equation (13) is possible to be used only because we have a fully parameterized BN model. However, a more common scenario is one in which a risk analyst has data on the treatment and outcome nodes but not for the other variables that compose their BN model. Nevertheless, as shown in Section 3.3, it is still possible to identify an intervention query using the backdoor criterion or a sequential application of the do‐calculus rules. This scenario will be further discussed in Section 5.4.
-
2.Estimate the intervention query. Using the available data for this case study, Equation (13) is estimated as:
which shows that the postpolicy probability of sufficiency of preventive measures to mitigate TPD in an excavation activity if potholing is made mandatory.(14) In addition, postintervention probabilities for all nodes of the BN model are shown in Table I.
Fig 7.
Built BN model for TPD with focus on potholing practices. Colors denote node type as done in Fig. 6.
Table I.
TPD BN Model Nodes, States, Pre‐ and Postintervention Probabilities, and Node Types
| Node | Node State | Preintervention Probability [%] | Postintervention Probability [%] | Node Type | |
|---|---|---|---|---|---|
| : Third‐Party Excavator | Property Owner | 19.41 | 19.41 |
|
|
| Contractor | 74.81 | 74.81 | |||
| Government Entity | 5.78 | 5.78 | |||
| : Potholing Performed? | Yes | 22.07 | 100.00 |
|
|
| No | 77.93 | 0.00 | |||
| : Other Excavation Best Practices Performed? | Yes | 71.60 | 71.60 |
|
|
| No | 28.40 | 28.40 | |||
| : Sufficient Excavation Practices? | Yes | 54.57 | 94.30 |
|
|
| No | 45.43 | 5.70 | |||
| : Sufficient L&M Practices? | Yes | 87.66 | 87.66 |
|
|
| No | 12.34 | 12.34 | |||
| : Sufficient Notification Practices? | Yes | 54.54 | 53.02 |
|
|
| No | 45.46 | 46.98 | |||
| : Sufficient Preventive Measures? | Yes | 77.17 | 78.35 |
|
|
| No | 22.83 | 21.65 |
Table II.
CPT Formulation for Node : “Sufficient Preventive Measures?”
|
|
Yes | No | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
Yes | No | Yes | No | |||||||
|
|
Yes | No | Yes | No | Yes | No | Yes | No | |||
| Yes | 1.0 | 1‐ | 1‐0.1 | 1‐ | 1‐0.1 | 1‐ | 0.9 | 0.0 | |||
| No | 0.0 |
|
0.1 |
|
0.1 |
|
0.1 | 1.0 | |||
Fig 8.
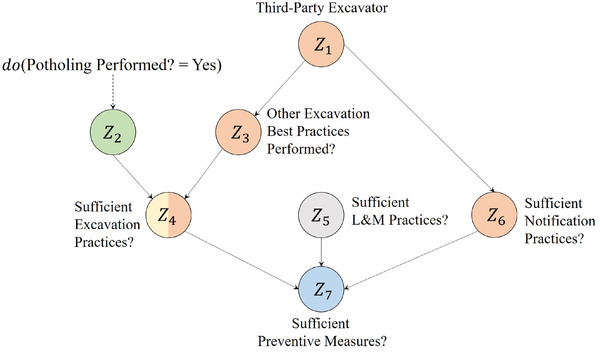
Postintervention DAG for the TPD BN model shown in Fig. 7.
5.3. Inform the Decision‐Maker
To better inform a decision‐maker about the effect of making potholing mandatory on the sufficiency of TPD preventive measures, the following IE, CCE, and CDE metrics are calculated.
-
(i)Intervention Effect (IE). Using the estimated intervention query in Equation (14) and the preintervention probability of shown in Table I, IE can be estimated as:
This result informs decision‐makers that making potholing mandatory can increase the likelihood of preventive measures sufficiency by a over prepolicy conditions.(15) -
(ii)CCE. To put the studied policy in perspective for decision‐makers, the CCE of making potholing mandatory over the rest of CGA excavation best practices is calculated. In order to do this, the intervention query is going to be compared with . The latter can be estimated using Equation (3), obtaining:
Then, the CCE can be computed by:(16)
This result shows that making all CGA excavation best practices mandatory can increase the likelihood of preventive measures sufficiency by over the effect of just making potholing mandatory with respect to prepolicy conditions. Decision‐makers can use this result to put their decisions in perspective by comparing different policy alternatives effect on the system.(17) -
(iii)Comparative Direct Effect (CDE). Finally, to understand how much the effect of making potholing mandatory is mediated by doing proper excavation practices in general, we can control for and calculate the CDE by
The CDE is estimated using Equation (3) for and the backdoor criterion for (using as a sufficient admissible set), obtaining:(18)
Comparing this value to , it shows that the effect of making potholing mandatory over prepolicy conditions is completely mediated by performing proper excavation practices in general. This result shows that performing sufficient excavation practices is what mostly affect the sufficiency of preventive measures in the context of excavation practices.(19)
As shown above, IE, CCE, and CDE metrics give the decision‐maker information on the magnitude of the effect that making potholing mandatory can have in the sufficiency of preventive measures. Furthermore, it also enables them to put this policy in perspective to other possible actions, such as making all CGA excavation best practices mandatory. In addition, it is possible to inform decision‐makers that performing sufficient excavation practices is what mostly affect the sufficiency of preventive measures in the context of excavation practices.
5.4. The Limitations of Relying on Associative Reasoning to Answer Intervention Queries
As stated in Section 3.3, usually, due to the presence of confounders between and . This shows that intervention queries cannot be properly estimated using associative reasoning by evidence propagation, which is the main BN tool used in engineering risk assessment. A clear example of this limitation can be shown in this case study.
Indeed, if the intervention query defined in Section 5.2 (i) is estimated by associative reasoning as (instead of Equation (12)) using Equation (1) on the BN structure shown in Fig. 7, we get the prior and posterior probabilities of sufficiency of TPD preventive measures presented in Table III.
Table III.
Prior and Posterior Probabilities of “Sufficient Preventive Measures?” by Associative Reasoning with Evidence on “Potholing Performed? = Yes”
| Sufficient | ||
|---|---|---|
| Preventive Measures? | ||
| [%] | 77.17 | |
| [%] | 76.40 | |
|
|
−0.77 |
Table III shows a 0.77% decrease in the probability of sufficiency of preventive measures if potholing is performed, which is counterintuitive given that potholing is a recommended excavation best practice. However, an associative reasoning approach was employed, so it is essential to interpret this result as just the evidential association that potholing has on TPD preventive measures' sufficiency in the used data set given the assumed BN model structure.
If we want to estimate the effect that potholing has on TPD preventive measures' sufficiency (which is an intervention query), spurious associations due to confounding between these two variables need to be adjusted to obtain an unbiased estimation. Based on the assumed BN structure shown in Fig. 7, an unbiased estimate of the effect that “” has on “” can be obtained by blocking all confounding‐inducing backdoor paths between these two variables. Using the backdoor criterion in Fig. 7, we found that conditioning on the type of third‐party excavator blocks all backdoor paths between and . The latter means that for the paths and , which is equivalent to eliminating the incoming edges to as done when the truncated factorization formula (3) is used for intervention reasoning. Then, is computed using the factorization formula (1) shown in Fig. 7 and in Table IV.
Table IV.
Prior and Posterior Probability of “Sufficient Preventive Measures?” by Associative Reasoning with Evidence on “Potholing Performed? = Yes” and Conditioned on Each Specific Type of Third‐Party Excavator
| : Third‐Party Excavator | ||||
|---|---|---|---|---|
| Sufficient Preventive Measures? | Property Owner | Contractor | Government Entity | |
| [%] | 61.20 | 80.40 | 89.00 | |
| [%] | 61.75 | 81.69 | 90.86 | |
|
|
+0.55 | +1.29 | +1.86 | |
Table IV shows, as expected, an increase in the probability of sufficiency of preventive measures if potholing is performed for each type of third‐party excavator. Now, for the aggregated population of excavators, the causal effect that potholing has on the sufficiency of TPD preventive measures can be calculated using intervention reasoning by applying backdoor formula (6) as:
| (20) |
which is analogous to the result obtained using the truncated factorization formula (3) in Section 5.2 (iii). It is important to notice that the difference between the result shown for associative reasoning in (20) and the one in Table III is that the former contains only information on the causal path , whereas the latter also contains information on the spurious backdoor paths between and .
Misleading causal effect estimations based on associative reasoning as the one encountered between Tables III and IV, where a positive association between the studied intervention and outcome for each type of excavator reverses for the combined population, is a widely studied phenomenon called “Simpson's Reversal” (Blyth (1972)). Pearl (2014a) used this phenomenon as an extreme example of the type of biases that improper handling of confounding variables can have on estimating an intervention query, demonstrating that it is possible to remediate it by adjusting for confounders that can bias the causal effect being estimated. For our case study, given that a fully parameterized BN was used, confounding adjustment is naturally made by using the truncated factorization formula (3) as done in Section 5.2 (iii). However, in the much more common scenario where a data set does not contain information on all of the considered BN model variables, an intervention query can still be estimated using the backdoor criterion or the do‐calculus rules. For example, our case study query can still be properly estimated using the backdoor criterion as shown in (20), where only data on the treatment and outcome variables and the confounder are needed to compute it.
As demonstrated in this section, intervention queries cannot be properly estimated nor informed to decision‐makers by just using associative reasoning, highlighting the importance of using intervention reasoning tools if an intervention query wants to be properly answered.
6. CONCLUDING REMARKS
To date, engineering risk assessment BN models have used associative reasoning to support risk‐informed decision making. However, BNs also have the ability to model interventions; an unexplored feature that enables risk analysts to estimate the effect of policies and actions before being implemented. In this article, we provided the mathematical background and tools needed to model interventions in BNs, showing how to properly express their postintervention joint probability distribution by means of the do‐operator. Furthermore, it was shown that the application of this operator ensures unbiased estimations of the effect of interventions on outcome variables of interest, even in the presence of confounders.
In this work, a BN‐based framework capable of modeling actions/policies as interventions to inform their effect on a system was proposed. Furthermore, the framework was exemplified by means of an illustrative case study on TPD of natural gas pipelines. The obtained results show the following contributions on risk‐informed decision support for engineering systems:
Enable risk analysts to properly model, estimate, and inform decision‐makers on the magnitude of the effect that a studied action/policy can have on a system behavior.
Enable risk analysts to inform the studied policy effect in perspective to the system' preintervention behavior and compare it with other policy alternatives effect by using intervention‐based causal metrics. Furthermore, we showed that this effect can be isolated from any other possible mediating effect of other variables of interest.
To the best of the authors' knowledge, this article is the first attempt to expand BNs causal reasoning capabilities by means of interventions to support engineering systems risk assessment. As demonstrated in this work, interventions can be used to estimate the effect of actions and policies before being implemented. Then, a natural next step of this research will be to analyze postintervention scenarios by counterfactual reasoning in BNs. Taking excavation near buried facilities damages as an example, counterfactuals can be used to address and estimate causal claims such as “If vacuum excavators are used instead of hand‐tools, the likelihood of excavation damage would be less.”
Additionally, further efforts should be made on improving the proposed case study TPD BN model and study how intervention reasoning tools scale for a larger and more complex model. In order to do this, the granularity of risk factors should be increased (Guo, Zhang, Liang, & Haugen, 2018) and parameterization techniques enhanced (Jackson & Mosleh, 2018). Moreover, further research should explore adding temporal‐dependent variables (e.g., weather and excavation time) to our case study by the use of dynamic BNs, which, given that they are unwrapped static BNs in a temporal dimension, accept all the intervention reasoning tools presented in this article. The latter two improvements will allow the model to be queried on a wider range of actions/policies and understand their temporal effect on a system behavior, enhancing its use for risk‐informed decision support.
ACKNOWLEDGMENTS
The authors would like to thank the two anonymous reviewers for their insightful comments and suggestions. This research received no specific grant from any funding agency in the public, commercial, or not‐for‐profit sectors.
APPENDIX A.
The tables below presents each node CPTs from the BN model used in the case study.
Table A1.
: Third‐Party Excavator CPT
| Property Owner [%] | 19.4 |
| Contractor [%] | 74.8 |
| Government Entity [%] | 5.8 |
Table A2.
: Potholing Performed? CPT
| : Third‐Party Excavator | |||
|---|---|---|---|
| Property Owner | Contractor | Government Entity | |
| Yes [%] | 30.9 | 21.1 | 5.3 |
| No [%] | 69.1 | 78.9 | 94.7 |
Table A3.
: Other Excavation Best Practices Performed? CPT
| : Third‐Party Excavator | |||
|---|---|---|---|
| Property Owner | Contractor | Government Entity | |
| Yes [%] | 94.7 | 66.4 | 61.1 |
| No [%] | 5.3 | 33.6 | 38.9 |
Table A4.
: Sufficient Excavation Practices? CPT
| Z2: Potholing Performed? | ||||
|---|---|---|---|---|
| Yes | No | |||
| Z3: Other Excavation | ||||
| Best Practices Performed? | ||||
| Yes | No | Yes | No | |
| Yes [%] | 100.0 | 79.9 | 60.9 | 0.0 |
| No [%] | 0.0 | 20.1 | 39.1 | 100.0 |
Table A5.
: Sufficient L&M Practices? CPT
| Yes [%] | 87.7 |
| No [%] | 12.3 |
Table A6.
: Sufficient Notification Practices? CPT
| : Third‐Party Excavator | |||
|---|---|---|---|
| Property Owner | Contractor | Government Entity | |
| Yes [%] | 17.9 | 61.9 | 82.2 |
| No [%] | 82.1 | 38.1 | 17.8 |
Table A7.
: Sufficient Preventive Measures? CPT
| : Sufficient Excavation Practices? | ||||||||
|---|---|---|---|---|---|---|---|---|
| Yes | No | |||||||
| : Sufficient L&M Practices? | ||||||||
| Yes | No | Yes | No | |||||
| : Sufficient Notification Practices? | ||||||||
| Yes | No | Yes | No | Yes | No | Yes | No | |
| Yes [%] | 100.0 | 55.2 | 94.2 | 42.3 | 95.9 | 59.5 | 90.0 | 0.0 |
| No [%] | 0.0 | 44.8 | 5.8 | 57.7 | 4.1 | 40.5 | 10.0 | 100.0 |
REFERENCES
- Ayele, Y. Z. , Barabady, J. , & Droguett, E. L. (2016). Dynamic Bayesian network‐based risk assessment for arctic offshore drilling waste handling practices. Journal of Offshore Mechanics and Arctic Engineering, 138(5), 051302‐1–051302‐12. [Google Scholar]
- Blyth, C. R. (1972). On Simpson's paradox and the sure‐thing principle. Journal of the American Statistical Association, 67(338), 364–366. [DOI] [PubMed] [Google Scholar]
- Brito, M. , & Griffiths, G. (2016). A Bayesian approach for predicting risk of autonomous underwater vehicle loss during their missions. Reliability Engineering & System Safety, 146, 55–67. [Google Scholar]
- Broniatowski, D. A. , & Tucker, C. (2017). Assessing causal claims about complex engineered systems with quantitative data: Internal, external, and construct validity. Systems Engineering, 20(6), 483–496. [Google Scholar]
- CGA . (2019). Data‐informed insights and recommendations for more effective excavator outreach. CGA White Paper, Common Ground Alliance, Alexandria, VA. [Google Scholar]
- CGA . (2020). The definitive guide for underground safety & damage prevention. Technical Report, Common Ground Alliance, Alexandria, VA. [Google Scholar]
- Chemweno, P. , Pintelon, L. , Muchiri, P. N. , & Van Horenbeek, A. (2018). Risk assessment methodologies in maintenance decision making: A review of dependability modelling approaches. Reliability Engineering & System Safety, 173, 64–77. [Google Scholar]
- Cox Jr, L. A. (2013). Improving causal inferences in risk analysis. Risk Analysis, 33(10), 1762–1771. [DOI] [PubMed] [Google Scholar]
- DIRT . (2020). Dirt annual report for 2018. Technical Report, Common Ground Alliance, Alexandria, VA. [Google Scholar]
- Fenton, N. , & Neil, M. (2012). Risk assessment and decision analysis with Bayesian networks. Boca Raton, FL: CRC Press. [Google Scholar]
- Groth, K. M. , Denman, M. R. , Darling, M. C. , Jones, T. B. , & Luger, G. F. (2020). Building and using dynamic risk‐informed diagnosis procedures for complex system accidents. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 234(1), 193–207. [Google Scholar]
- Groth, K. M. , Smith, R. , & Moradi, R. (2019). A hybrid algorithm for developing third generation HRA methods using simulator data, causal models, and cognitive science. Reliability Engineering & System Safety, 191, 106507. [Google Scholar]
- Guo, X. , Zhang, L. , Liang, W. , & Haugen, S. (2018). Risk identification of third‐party damage on oil and gas pipelines through the Bayesian network. Journal of Loss Prevention in the Process Industries, 54, 163–178. [Google Scholar]
- Hegde, J. , Utne, I. B. , Schjølberg, I. , & Thorkildsen, B. (2018). A Bayesian approach to risk modeling of autonomous subsea intervention operations. Reliability Engineering & System Safety, 175, 142–159. [Google Scholar]
- Hund, L. , & Schroeder, B. (2020). A causal perspective on reliability assessment. Reliability Engineering & System Safety, 195, 106678. [Google Scholar]
- Hünermund, P. , & Bareinboim, E. (2019). Causal inference and data‐fusion in econometrics. arXiv preprint arXiv:1912.09104. [Google Scholar]
- Jackson, C. , & Mosleh, A. (2018). Oil and gas pipeline third party damage (tpd)‐a new way to model external hazard failure. In The Probabilistic Safety Assessment and Management Conference. [Google Scholar]
- Joffe, M. , Gambhir, M. , Chadeau‐Hyam, M. , & Vineis, P. (2012). Causal diagrams in systems epidemiology. Emerging Themes in Epidemiology, 9(1), 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, C. (2003). Failure in Safety‐Critical Systems: A Handbook of Accident and Incident Reporting. Glasgow, Scotland: University of Glasgow Press. [Google Scholar]
- Johnson, C. , & Holloway, C. M. (2003). A survey of logic formalisms to support mishap analysis. Reliability Engineering & System Safety, 80(3), 271–291. [Google Scholar]
- Kabir, G. , Balek, N. B. C. , & Tesfamariam, S. (2018). Consequence‐based framework for buried infrastructure systems: A Bayesian belief network model. Reliability Engineering & System Safety, 180, 290–301. [Google Scholar]
- Khakzad, N. (2018). Which fire to extinguish first? A risk‐informed approach to emergency response in oil terminals. Risk Analysis, 38(7), 1444–1454. [DOI] [PubMed] [Google Scholar]
- Lam, C. Y. , & Cruz, A. M. (2019). Risk analysis for consumer‐level utility gas and liquefied petroleum gas incidents using probabilistic network modeling: A case study of gas incidents in Japan. Reliability Engineering & System Safety, 185, 198–212. [Google Scholar]
- Langseth, H. , & Portinale, L. (2007). Bayesian networks in reliability. Reliability Engineering & System Safety, 92(1), 92–108. [Google Scholar]
- Lewis, A. , & Groth, K. (2019). A review of methods for discretizing continuous‐time accident sequences. In Proceedings of the 29th European Safety and Reliability Conference, 754–761. [Google Scholar]
- Mkrtchyan, L. , Podofillini, L. , & Dang, V. N. (2015). Bayesian belief networks for human reliability analysis: A review of applications and gaps. Reliability Engineering & System Safety, 139, 1–16. [Google Scholar]
- Pearl, J. (1985). Bayesian networks: A model of self‐activated memory for evidential reasoning. In Proceedings of the 7th Conference of the Cognitive Science Society, (pp. 329–334). [Google Scholar]
- Pearl, J. (1995). Causal diagrams for empirical research. Biometrika, 82(4), 669–688. [Google Scholar]
- Pearl, J. (2009). Causality. Cambridge: Cambridge University Press. [Google Scholar]
- Pearl, J. (2012). The do‐calculus revisited. arXiv preprint arXiv:1210.4852. [Google Scholar]
- Pearl, J. (2014a). Comment: Understanding Simpson' paradox. The American Statistician, 68(1), 8–13. [Google Scholar]
- Pearl, J. (1988). Probabilistic reasoning in intelligent systems: Networks of plausible inference. Amsterdam, Netherlands: Elsevier. [Google Scholar]
- Pearl, J. , & Mackenzie, D. (2018). The book of why: The new science of cause and effect. London, England: Penguin Books. [Google Scholar]
- Peng, T. (2019). Modernizing tools for 3rd party damage. Technical Report 22412, Gas Technology Institute (GTI). [Google Scholar]
- Roscoe, K. , Hanea, A. , Jongejan, R. , & Vrouwenvelder, T. (2020). Levee system reliability modeling: The length effect and Bayesian updating. Safety, 6(1), 7. [Google Scholar]
- Santarelli, J. S. (2019). Risk analysis of natural gas distribution pipelines with respect to third party damage [Master's thesis] . University of Western Ontario. [Google Scholar]
- Shpitser, I. , & Pearl, J. (2006). Identification of conditional interventional distributions. In Proceedings of the Twenty‐Second Conference on Uncertainty in Artificial Intelligence (UAI2006), pp. 437–444. [Google Scholar]
- Tikka, S. , & Karvanen, J. (2017). Identifying causal effects with the R package causal effect. Journal of Statistical Software, 76(12), 1–30. [Google Scholar]
- U.S. Pipeline and Hazardous Materials Safety Administration (PHMSA) . (2020). Annual report mileage summary statistics. Technical Report, U.S. Department of Transportation. [Google Scholar]
- U.S. Pipeline and Hazardous Materials Safety Administration (PHMSA) (2020). Pipeline incident 20 year trends. Technical Report, U.S. Department of Transportation. [Google Scholar]
- VanderWeele, T. J. , & Shpitser, I. (2013). On the definition of a confounder. Annals of Statistics, 41(1), 196–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber, P. , Medina‐Oliva, G. , Simon, C. , & Iung, B. (2012). Overview on Bayesian networks applications for dependability, risk analysis and maintenance areas. Engineering Applications of Artificial Intelligence, 25(4), 671–682. [Google Scholar]
- Zhang, L. , Wu, X. , Qin, Y. , Skibniewski, M. J. , & Liu, W. (2016). Towards a fuzzy Bayesian network based approach for safety risk analysis of tunnel‐induced pipeline damage. Risk Analysis, 36(2), 278–301. [DOI] [PubMed] [Google Scholar]


