Identifying robust strategies for assisted migration in a competitive stochastic metacommunity

Abstract

Assisted migration (AM) is the translocation of species beyond their historical range to locations that are expected to be more suitable under future climate change. However, a relocated population may fail to establish in its donor community if there is high uncertainty in decision‐making, climate, and interactions with the recipient ecological community. To quantify the benefit to persistence and risk of establishment failure of AM under different management scenarios (e.g., choosing target species, proportion of population to relocate, and optimal location to relocate), we built a stochastic metacommunity model to simulate several species reproducing, dispersing, and competing on a temperature gradient as temperature increases over time. Without AM, the species were vulnerable to climate change when they had low population sizes, short dispersal, and strong poleward competition. When relocating species that exemplified these traits, AM increased the long‐term persistence of the species most when relocating a fraction of the donor population, even if the remaining population was very small or rapidly declining. This suggests that leaving behind a fraction of the population could be a robust approach, allowing managers to repeat AM in case they move the species to the wrong place and at the wrong time, especially when it is difficult to identify a species’ optimal climate. We found that AM most benefitted species with low dispersal ability and least benefited species with narrow thermal tolerances, for which AM increased extinction risk on average. Although relocation did not affect the persistence of nontarget species in our simple competitive model, researchers will need to consider a more complete set of community interactions to comprehensively understand invasion potential.

Short abstract

Article impact statement: Relocating a fraction of declining dispersal‐limited populations can allow managers to repeat assisted migration if it fails.

INTRODUCTION

Global biodiversity is expected to decline with projected climate change (Urban, 2015). Among the species at risk of extinction are those with limited dispersal, narrow ranges, narrow climate tolerance, and low population sizes (Pearson, 2006; Tewksbury et al., 2008). Competition and other community interactions could increase extinction risk because negative interactions can limit the dispersal of species that might be otherwise adequate dispersers (Urban et al., 2012). Many of these climate‐threatened species face a high likelihood of extinction without human intervention, prompting scientists and managers to consider a variety of novel approaches to conservation. Among these is assisted migration (AM), in which managers relocate individuals from a threatened population to a location outside their historical range that is expected to be more suitable under future climates (McLachlan et al., 2007). By allowing species to reach favorable climates in densities that they would not be able to reach on their own, AM could increase the likelihood of persistence for climate‐threatened species or protect species with high ecological and socioeconomic value in ways that traditional conservation strategies might not (Lawler & Olden, 2011; McLachlan et al., 2007; Schwartz et al., 2012).

Moving a species into a novel ecosystem could also incur many risks (Hewitt et al., 2011; Ricciardi & Simberloff, 2009), including invasion (Mueller & Hellmann, 2008), spread of pathogens and parasites (Simler et al., 2018), elevated stress on relocated individuals (Dickens et al., 2010), and decreased genetic diversity (Kekkonen & Brommer, 2015). Demographic and genetic risks may contribute to the risk of a species failing to establish after relocation (Chauvenet et al., 2013; Peterson & Bode, 2020; Plein et al., 2016), as seen with the low‐to‐intermediate success of previous conservation translocations across a wide range of taxa (Bubac et al., 2019; Fischer & Lindenmayer, 2000; Godefroid et al., 2011). Establishment failure could accelerate the negative impacts on climate‐threatened species by reducing the population size and genetic diversity while diverting the limited resources available to conservation (Hewitt et al., 2011; McDonald‐Madden et al., 2008). This risk also depends on uncertainties that could lead managers to relocate a species to the wrong place at the wrong time, especially if the species can only persist under a narrow range of climates. A major source of uncertainty stems from the difficulty in quantifying and differentiating between the abiotic and biotic drivers of species’ ranges (Case et al., 2005). For example, a species with narrow climate tolerance and limited competition in its historical range may be a poor candidate for AM if the recipient community becomes highly competitive as other species shift with climate change. Given these uncertainties, a key management challenge is developing robust approaches over a range of conditions (McDonald‐Madden et al., 2008) for the array of decisions involved in AM. This involves evaluating which species are vulnerable to climate‐threatened extinction, which species will likely benefit from AM, when and where to move a species, and how many individuals to move (McDonald‐Madden et al., 2011; Rout et al., 2013).

Despite a lack of consensus among the scientific community and the public about the benefits and risks of AM (Hewitt et al., 2011; Javeline et al., 2015), several species are already being relocated (Seddon et al., 2015). Scientific guidance for AM is available from existing decision‐making frameworks, which typically focus on optimizing a species’ persistence under climate change based on single‐species models (McDonald‐Madden et al., 2011; Rout et al., 2013). Extending these to a multispecies framework is a crucial next step to account for the species interactions that give rise to the risks of invasiveness and uncertainty in the drivers of species range (Peterson & Bode, 2020).

We quantified the benefit to target species’ persistence, risk of failed translocation, and risk of nontarget species’ response to AM given competitive interactions, multiple sources of uncertainty, and an array of management decisions. We built a stochastic metacommunity model to simulate competing species undergoing climate change to estimate which species were vulnerable to extinction, which species were likely to benefit from AM, and what fraction of the population to relocate. Though the dynamics of interacting communities that give rise to the risk of invasiveness are often complex, involving many direct and indirect trophic interactions (Chesson & Kuang, 2008; Holt, 1984), we focused on competition. Competition is an extensively studied species interaction that drives range limits (Sexton et al, 2009), and knowledge of this role is rooted in long‐standing ecological theory (Connell, 1972). Due to its role in affecting species’ ranges generally, competition has a significant potential to affect range shifts and persistence under climate change (Ettinger & HilleRisLambers, 2013; Urban et al., 2012), the dynamic central to the AM decisions on which we focused. Another potential source of uncertainty comes from abiotic drivers of species’ ranges. Because managers will have limited knowledge of a species’ optimal climate (a reducible uncertainty), we simulated relocation with uncertainty in estimating species’ thermal optima. By repeating these simulations under different levels of environmental stochasticity (an irreducible uncertainty), we sought to identify characteristics of successful AM approaches that are robust over a wide variety of uncertainty scenarios.

METHODS

Model overview

To compare AM strategies, we modeled metacommunity dynamics of multiple species competing on a one‐dimensional linear temperature gradient subjected to climate change, analogous to a previous model by Urban et al. (2012) with environmental stochasticity. For simplicity, all species in this metacommunity were annuals competing over the same resources at the same trophic level. The model cycled through reproduction, dispersal, and competition, all with demographic stochasticity, over each time step (Figure 1). Each species $i$ had a unique dispersal distance (${\gamma }_i$), thermal optimum ($z_i$), thermal tolerance breadth (${\sigma }_i$), and a reproductive strength parameter ($r_i$) that scaled the birth rate with ${\sigma }_i$ to create a specialist versus generalist trade‐off with temperature (Levins, 1968). We simulated AM by selecting one target species and relocating a fraction of its total population toward its thermal optimum each time the population fell below a threshold population size. We compared outcomes when relocating different target species with different fractions of the population into different locations.

FIGURE 1.

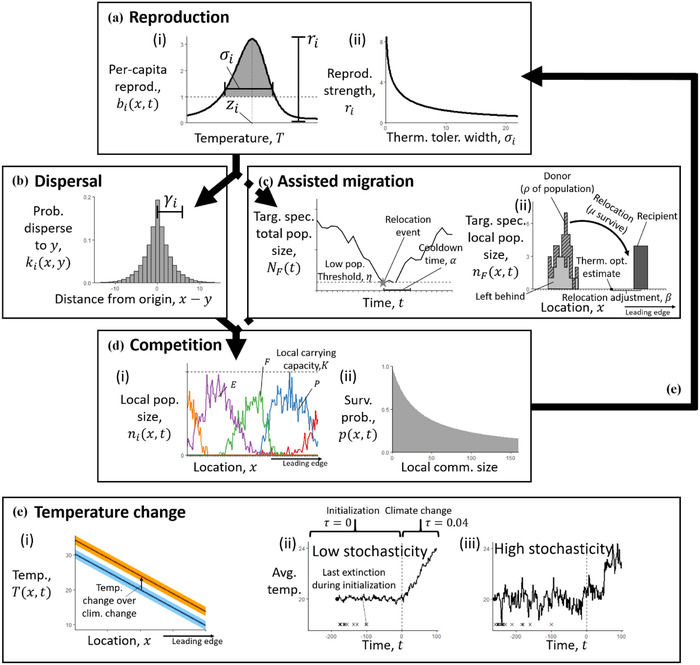
All extant species in the metacommunity model cycle through (a) reproduction, (b) dispersal, and (d) competition before (e) the temperature changes stochastically, and the next time step repeats this process. The target species is also moved through (c) assisted migration during certain time steps

Symbol definitions: t, time; x, space; $T(x,t)$, temperature; $b_i[T(x,t)]$, per capita reproductive output; z_i , species’ thermal optimum;${\sigma }_i,$ thermal tolerance breadth; r_i , reproductive strength; ${\gamma }_i$, mean dispersal distance; $\eta$, low population threshold for assisted migration; $\alpha$, cooldown time before another relocation can happen; $\rho$, fraction of the population removed from original distribution and moved to a new location; $\mu$, fraction that survive relocation; $\beta$, when relocating the population, the number of patches ahead of the thermal optimum estimate to move the relocated population; F, target species; E, equatorward species; P, poleward species; K, carrying capacity; $p(x,t)$, individual survival probability; lower line in panel e, $t=0$; upper line in panel e, $t=100$; vertical dashed line, model changes from the initialization phase (average temperature change $\tau =0$) to the climate change phase ($\tau =0.04$). Climate change occurs only after a relatively stable metacommunity has been assembled (i.e., after 100 time steps with no extinctions)

We analyzed the potential benefit of AM based on the target species’ persistence likelihood throughout all locations. Persistence likelihood also indicates the risk of translocation failure due to uncertainty and stochasticity. We measured the risk of invasiveness from competitive interactions based on the persistence likelihood of nontarget species as well as the overall gamma diversity. Though this metric represents only an extreme outcome on the continuum of possible invasive impacts on community structure and ecosystem function (Blackburn et al., 2014), other metrics would require investigation beyond competitive interactions within a trophic level.

Population dynamics

In our model, each species $i$ had a local population size of $n_i(x,t)$ individuals in discrete patch $x$ and a total metapopulation size over all space $X$ of $N_i(t)={\sum }_{x\in X}{n}_i(x,t)$ at discrete time $t$. All individuals reproduced (Figure 1a) with a reproductive output $b_i[T(x,t)]$ that depended on local temperature $T(x,t)$. Temperature dependence was skew‐normal, given skewness constant $\lambda$, and the highest values were around the thermal optimum $z_i$. There was a sharp decrease above $z_i$ (Norberg, 2004). Thermal tolerance breadth ${\sigma }_i$ and reproductive strength $r_i$ determined the breadth and height of the temperature dependence. Thus, $b_i[T(x,t)]$ is

$$\begin{array}{ccc}& & b_i\left[T\left(x,t\right)\right]\hfill \\ & & =\exp \left[r_i\left(\exp \left\{-{\left[\frac{T\left(x,t\right)-z_i}{{\sigma }_i}\right]}^2\right\}·\left\{1+\text{erf}\left[\lambda \frac{T\left(x,t\right)-z_i}{{\sigma }_i}\right]\right\}-1\right)\right]\hfill \end{array}$$ (1)

(following Urban et al., 2012). To incorporate demographic stochasticity, the number of propagules produced by species $i$ in patch $x$ was a Poisson random variable with mean equal to the reproductive output, $n_i^{\ast }(x,t)\sim \mathrm{Poisson}(n_i(x,t)b_i)$ (Melbourne & Hastings, 2008).

Each propagule dispersed from its origin (Figure 1b). We adapted the Laplace dispersal kernel to a discrete‐space analog (Appendix S1). We defined ${\gamma }_i$ as the mean absolute distance (in patches) that species $i$ moves from its origin and let kernel parameter $q_i=\frac{{\gamma }_i+1-\sqrt{{\gamma }_i^2+1}}{{\gamma }_i}$. Thus, the probability of a propagule from patch $x$ moving to patch $y$ is

$$k_i\left(x,y\right)=\left(\frac{q_i}{2-q_i}\right){\left(1-q_i\right)}^{\left|x-y\right|}.$$ (2)

All propagules of species $i$ dispersed from patch $x$ throughout all space $X$ with the random vector $M_i(n_i^{*}(x,t),x,X,t)\sim \mathrm{M}\mathrm{ultinomial}(n_i^{*}(x,t),k_i(x,X))$, and the vector of local populations after dispersal was $n_i^{\ast \ast }(X,t)={\sum }_{y\in X}{M}_i(n_i^{\ast }(y,t),y,X,t)$.

Dispersed propagules competed in each patch $x$ given community‐wide carrying capacity $K$ (Figure 1d). We assumed a variation on lottery competition (Chesson & Warner, 1981; Sale, 1978); each individual had an equal probability of surviving:

$$p\left(x,y\right)={\left(1+\frac{{\sum }_{j=1}^S{n}_j^{\ast \ast }\left(x,t\right)}{K}\right)}^{-1}.$$ (3)

The total number of propagules of species $i$ in patch $x$ that survived after competition was a binomial random variable $n_i(x,t+1)\sim \mathrm{Binomial}(n_i^{**}(x,t),p(x,t))$ (Melbourne & Hastings, 2008). Therefore, the overall quality of a location depended on the constant carrying capacity $K$ and match between the local environment and species thermal tolerance.

Spatial structure

Metacommunity dynamics occurred across a one‐dimensional, linear temperature gradient of$L$ patches (Figure 1e), representing gradual latitudinal or sharp elevational change (Urban et al., 2012). We removed propagules that dispersed outside the spatial gradient. Because these absorbing boundary conditions could bias our analyses, we disregarded the first $\frac{L}{8}$ patches on the poleward edge and the last $\frac{3L}{8}$ patches on the equatorward edge for community metrics.

Temperature changed each time step by mean $\tau$ with autocorrelation $\kappa$ and standard deviation $\psi$ around white noise $\omega (t)$. The stochastic component of yearly temperature change was $\epsilon \left(t+1\right)=\kappa \epsilon \left(t\right)+\omega \left(t\right)\sqrt{1+{\kappa }^2}$. The square root term removed the effect of autocorrelation on the variance (Wichmann et al., 2005). The temperature in patch $x$ changed over time as

$$T\left(x,t+1\right)=T\left(x,t\right)+\tau +\psi \epsilon \left(t\right).$$ (4)

Assisted migration

AM focused on a single target species $F$ (Figure 1c). We relocated species $F$ if its total metapopulation size $N_F(x,t)$ was below a threshold $\eta$ at the beginning of a time step. Though population size would realistically need to be estimated, we assumed perfect knowledge of population size to focus on uncertainty in the drivers of a species’ range. To avoid repeating AM before species $F$ recovered, we relocated only if we did not previously relocate in the last $\alpha$ time steps. After reproduction, we selected a fraction of propagules $\rho$ for AM, randomly chosen from throughout the species’ range. The remaining propagules were left behind to disperse naturally (the donor population). From the propagules chosen for AM, only a proportion $\mu$ survived relocation. This proportion was relocated uniformly among five connected patches around a patch that was $\beta$ poleward of the patch that most closely matched the species’ estimated thermal optimum (the recipient population).

We considered three methods of estimating the thermal optimum of species $F$. The perfect knowledge estimate was the exact value of the true thermal optimum $z_F$. The realized niche estimate was the temperature in the median patch of the target species’ distribution at $t=0$. The fundamental niche estimated measures species’ limits without competition by simulating 100 time steps with $\tau =0$ °C/year and only species $F$. This estimate was the temperature in the median patch of the resulting distribution.

Parameterization and implementation

Simulations occurred on a temperature gradient with $L=512$ patches, where initial temperatures linearly varied over space from 9.78 to 30.22 °C. We considered two types of environments, defined by the degree of stochasticity. Low‐stochasticity environments had an annual temporal SD of $\psi =0.1639{}^{\circ }\mathrm{C}$, equal to the SD of mean combined global land‐surface air and sea‐surface water temperature anomalies from 1880 to 1979 (GISTEMP Team, 2019; Lenssen et al., 2019), and high‐stochasticity environments had four times that amount. Both had an annual temporal autocorrelation of $\kappa =0.767$, also from temperature anomalies from 1880 to 1979. We used skewness constant $\lambda =-2.7$ (Urban et al., 2012) and a carrying capacity (K) of 30 individuals. We chose this parameter space, including low values for K, so that extinctions would not occur for some species and AM was a relevant management consideration (Appendix S3).

Before simulating climate change, we initialized the model to assemble a metacommunity with multidecadal coexistence under background environmental stochasticity. We generated a pool of$S=32$ species, each with uniquely randomized dispersal distances ${\gamma }_i$, thermal optima $z_i$, and thermal tolerance breadths ${\sigma }_i$, (based on Urban et al. [2012]) (Table 1). We numerically derived the reproductive strength $r_i$ from ${\sigma }_i$, such that each species had the same overall reproductive potential $B=5$ when integrating over temperature, emulating a jack‐of‐all‐trades–master‐of‐none trade‐off (Levins, 1968). We placed 25 individuals from each species into five adjacent patches that most closely matched each species’ thermal optimum and iterated through the model with mean temperature change $\tau =0$ °C/year until 100 time steps passed without extinction. The remaining communities set initial conditions for subsequent climate change simulations (Appendix S4).

TABLE 1.

Definitions of the symbols used in the stochastic metacommunity model for assisted migration, including biotic, environmental, and management parameters

Parameter	Symbol	Value	Units
Total species	$S$	32	Species
Dispersal distance of species $i$	${\gamma }_i$	Lognormal, mean = 2.5, SD = 2.5	Patches
Thermal optimum of species $i$	$z_i$	Uniform, 9.78–30.22	°C
Thermal tolerance breadth of species $i$	${\sigma }_i$	Lognormal, mean = 5, SD = 5	°C
Reproductive strength of species $i$	$r_i$	Derived from ${\sigma }_i$	–
Skewness constant	$\lambda$	−2.7	–
Fraction of population relocated	$\rho$	0, 0.05, 0.1, …, 1	–
Assisted migration survival probability	$\mu$	0.8	–
Low population threshold	$\eta$	42	Individuals
Cooldown time between relocations	$\alpha$	5	Years
Relocation adjustment (relative to optimum)	$\beta$	10	Patches
Total patches	$L$	512	Patches
Patch carrying capacity	$K$	30	Individuals
Mean annual temperature change	$\tau$	0.04	°C/year
Annual temporal autocorrelation	$\kappa$	0.767	–
Annual temporal standard deviation	$\psi$	low = 0.1639, high = 0.6556	°C
Initial total population size of species $i$	$N_i(0)$	–	Individuals
Difference in thermal optimum with species $i$	$z_{\mathrm{diff},i}$	–	°C
Inverse Simpson's index of region $W$	$D_W$	–	–
Measured temperature change	$c_T$	–	°C
Measured SD in temperature	$s_T$	–	°C
Deviation in thermal optimum estimate	$z_{\mathrm{est},\mathrm{dev}}$	–	°C

We modeled metacommunity dynamics under climate change with AM to test the success of a suite of potential relocation decisions. We initialized 10,000 metacommunities under both low and high stochasticity before iterating through 100 time steps with mean annual temperature change $\tau =0.04$ °C/year to reflect projected temperature changes under RCP8.5 (IPCC, 2014; Urban et al., 2012). For AM, we chose several target species that could be considered vulnerable to climate change, including species with the shortest dispersal, species with the narrowest thermal tolerance breadth, species with the closest poleward neighbor, species with the lowest initial population size, and a randomly selected species. All target species were initially extant in an interior region of the temperature gradient, $W\in [65,320]$, ensuring that their thermal optimum would likely exist after climate change and that there was competitive pressure on both the trailing and leading edges. We simulated each combination of target species type, fraction relocated $\rho$ from 0 to 1 (by 0.05), and thermal optimum estimate while keeping consistent values for AM survival probability (μ) of 0.8, cooldown time (α) of 5, and relocation adjustment (β) of 10. From baseline simulations without AM (Appendix S2), we chose low‐population threshold for AM of 42, high enough that relocation could occur before extinction but low enough to avoid relocating species that would have persisted even without AM.

To determine what types of species and communities are conducive to AM success (increased persistence likelihood with AM), we ran random forest classifications (randomForest 4.6‐14 package, R version 3.5.1) separately for low and high stochasticity. (Analogous analysis for simulations without AM is in Appendix S2.) The dependent variable was the fate of the target species: global extinction or persistence throughout all locations, disregarding the fate in the original range. The independent variables were target species’ thermal optimum ($z_F$), difference in thermal optimum between target species and neighbors $(z_{\mathrm{diff},P}$, $z_{\mathrm{diff},E}$), target and neighbor species’ dispersal (${\gamma }_F$, ${\gamma }_P$, ${\gamma }_E$), target and neighbor species’ thermal tolerance breadths (${\sigma }_F$, ${\sigma }_P$, ${\sigma }_E$), target and neighbor species’ initial population sizes ($N_F[0]$, $N_P[0]$, $N_E[0]$), inverse Simpson's diversity index of the initial community ($D_W$), measured temperature change ($c_T$), measured standard deviation in temperature ($s_T$), and the deviation between the estimated and true thermal optimum ($z_{\mathrm{est},\mathrm{dev}}$). To focus on cases where target species specifically benefited from AM, we included only simulations in which the target species went extinct without AM. To simplify analyses, we focused random forest classifications on simulations with fraction‐moved $\rho =0.5$, the shortest dispersers, and realized niche estimates.

RESULTS

Under all scenarios, relocated species had a higher chance of persisting when relocating an intermediate fraction of the total population during AM (Figures 2, 3a, and 3b). Relocating an intermediate fraction of the total population usually allowed the target species to exist in higher densities relative to interacting species in both the donor and recipient communities (Figures. 3c and 3d). On average, this increased the likelihood of long‐term persistence of both the donor and recipient populations (Figures 3e and 3f) and overall persistence relative to no management action (Figure 2). Moreover, target species’ persistence was typically lower when relocating 100% of the total population than without relocation (except when relocating the shortest disperser). Often, AM involved multiple relocations (Figures 4a and 4b), and the higher AM success when relocating intermediate fractions came with more individual relocation events (Figures 4c and 4d). AM had little effect on the persistence of nontarget species and final community diversity (Appendix S5), so the remaining results focus on persistence instead of invasion risk arising from the competitive interactions modeled here.

FIGURE 2.

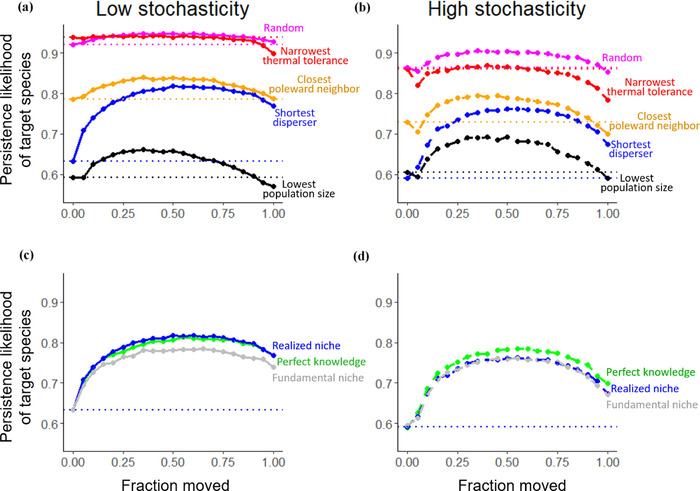
Persistence likelihood of a species chosen for assisted migration (AM) relative to fraction of that population that was relocated and the level of environmental stochasticity (dotted horizontal lines, persistence likelihood without AM [0 moved or no management action]; colors, match each comparison: [a and b] how target species was chosen for relocation [at random, narrowest thermal tolerance, closest poleward neighbor, shortest dispersal distance, lowest population size] when thermal optimum estimate is realized niche and [c and d] which type of thermal optimum estimate was for relocation decisions [realized niche, fundamental niche, perfect knowledge] when target species is shortest disperser)

FIGURE 3.

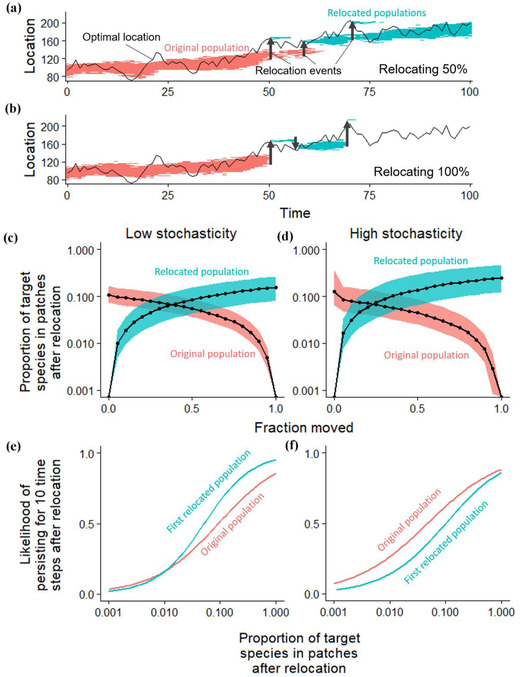
Dynamics and fate of original and relocated populations relative to fraction of the total population relocated: (a and b) example simulations showing change in shortest dispersing species’ range over time in a high stochasticity environment (x‐axis, time; y‐axis, space with higher values further poleward; lines, location of optimal climate as it changes over time; shaded region, population range [colored separately for pre‐ and postrelocation]; arrows, total population size falls below a low threshold ($\eta$) after which a fraction is relocated based on the estimated thermal optimum); (c and d) composition of donor and recipient communities after relocation (lines, median value for the fraction of propagules in the community that are target species; shading, 25% and 75% quantiles); and (e and f) likelihood of persisting for at least 10 time steps for both donor and recipient populations relative to their proportion in the community (x‐axes) (lines, predictions from logistic regression)

FIGURE 4.

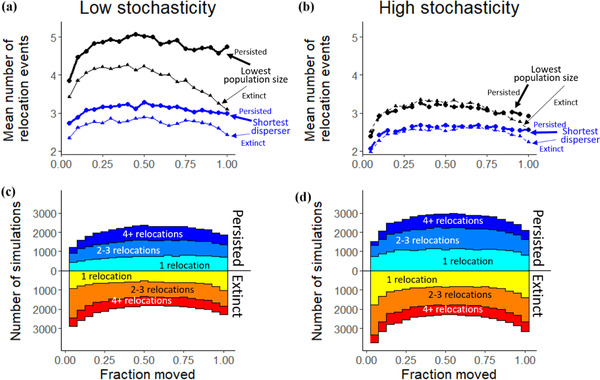
The number of independent relocation events that occurred during assisted migration simulations for low stochasticity and high stochasticity environments: (a and b) mean number of independent relocation events that occurred under a range of values relative to the fraction of the population that was relocated each time (relocated at least once) (black and blue, different target species; thick line, target species persists; thin line, target species went extinct; thermal optimum estimate, realized niche) and (c and d) fate of the species (persistence or extinction) and number of independent relocation events that occurred over the course of the simulation relative to the fraction of the population moved during assisted migration and number of relocations (target species, shortest disperser; thermal optimum estimate, realized niche)

Of the possible target species, the shortest dispersers benefited the most from AM (Figures 2a and 2b). For most combinations, AM also increased persistence of target species with the lowest population sizes, species with the closest poleward neighbors, and randomly picked species. However, AM usually decreased persistence of species with the narrowest thermal tolerances (specialists).

On average, AM had a similar effect on persistence regardless of how we estimated the species’ thermal optimum (Figures 2c and 2d). Under high stochasticity, AM was most successful with perfect knowledge of species’ thermal optima, but under low stochasticity, AM was most successful with realized niche estimates. This difference suggests stronger competition in low‐stochasticity environments such that competition set species limit more than species’ inherent thermal tolerances.

For both levels of stochasticity, three of the top four most important variables for predicting AM success of the shortest disperser were the target species’ initial population size, target species’ thermal tolerance breadth, and the difference in thermal optimum between the target species and its poleward neighbor (random forest classifications) (out‐of‐bag error: 25.27% low stochasticity, 30.56% high stochasticity) (Figures 5a and 5b). AM was most successful when the values of these characteristics were high (Figure 5c–e), suggesting that AM is most likely to benefit generalists with higher population sizes and less poleward competition. Under low stochasticity, AM was less successful when the poleward neighbor was a specialist with narrow thermal tolerance breadth (Figure 5f), implying that poleward competition limited AM success under low stochasticity but not as much under high stochasticity. AM was also more successful when thermal optimum estimates were warmer than the true value (positive deviation of $z_{\mathrm{est},\mathrm{dev}}$) (Figure 5g), and this effect was stronger under high stochasticity. Colder estimates placed target species further along the climate gradient, often beyond temperatures under which they can survive, so extreme year‐to‐year temperature change under high stochasticity would be more likely to drive the relocated population to extinction if they were placed into the wrong location.

FIGURE 5.

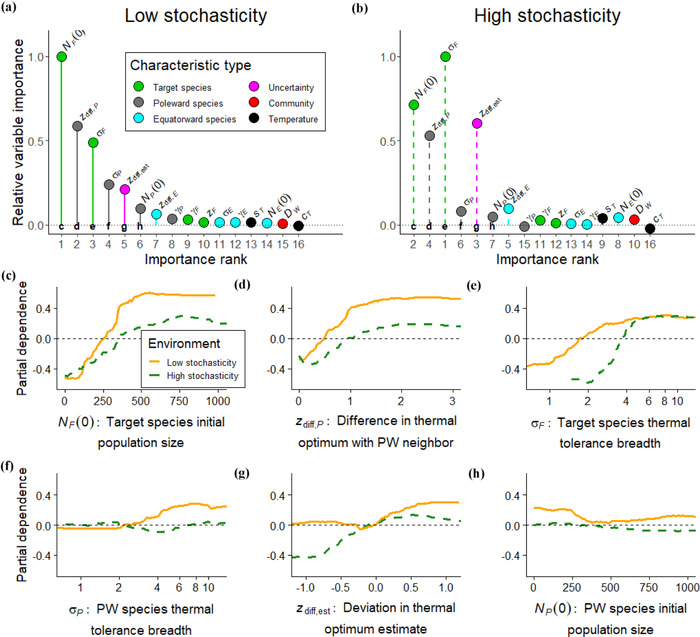
Importance of ecological characteristics from random forest classifications in determining whether assisted migration was successful for the target species (relocating 50% of the shortest dispersing species population with a realized niche estimate thermal optimum): (a and b) relative unscaled permutation importance of independent variables of whether or not assisted migration improved species’ persistence under low stochasticity and high stochasticity (importance rank, variable importance compared with other variables [1 most important]; colors, characteristic of target species, target species’ neighbors, full community, environment, or uncertainty) and (c–h) partial dependence of six independent variables (partial dependence, log probability of whether assisted migration increases persistence of a species [higher the value, the more likely to persist]; solid lines, low stochasticity; dashed lines, high stochasticity). Symbols defined in Table 1

DISCUSSION

Our model results suggest that AM can effectively increase species’ persistence under climate change if the species is limited by short dispersal, small population sizes, and competition. However, like many related conservation translocations (Fischer & Lindenmayer, 2000), we found that the relocated population often did not establish, especially for narrow thermal tolerance species. Relocating an intermediate fraction of the population was consistently an optimal strategy due to multiple possible drivers, such as allowing additional relocation attempts after establishment failure and reducing the degree of negative density dependence in both the donor and recipient populations.

Fractional relocation

Our modeling results suggest that species are more likely to persist through climate change if an intermediate fraction of the total population is relocated through AM (typically around 50–60% because this was most robust to uncertainty that could cause AM actions to fail). By leaving donor populations to persist temporarily, this approach retains a source for future conservation actions in case relocation occurs at the wrong time or place. Though a fractional relocation method would not reduce the failure rate of individual translocation events, it could increase the overall persistence of the species through multiple relocation events. Fractional relocation also buffered the risk of falsely identifying a target species for AM, in which case leaving some individuals behind could allow the species to recover those individuals that might be lost during AM.

In practice, translocations continue to have high failure rates despite increased awareness of the problem and scientific insight into potential solutions (Bubac et al., 2019), and these failures are likely to extend to AM (Peterson & Bode, 2020; Skikne et al., 2020). Although the expectation of several failures before establishment may not be appealing to some decision makers and stakeholders, there is some precedent in other conservation translocations. For a variety of animals and fungi in Australia and New Zealand, managers might release pioneers to test for behaviors and survival following release events (Seddon et al., 2015). For bird translocations, individual survival often improves after the first year, possibly because later released birds learn from previously released birds (Skikne et al., 2020). Maintenance of the donor population occurs largely by default in cases where relocation occurs through seeds or clonal offshoots because adults would be left in their original location (e.g., forests trees with AM through adjusting seed transfer guidelines and zones and tropical corals where clonal fragments can supply transplants [Rinkevich, 2019; Williams & Dumroese, 2013]), allowing for larger releases without affecting the fate of the donor population.

Though relocating more individuals should increase the chances that a species establishes (Blackburn et al., 2015; Godefroid et al., 2011), this could have diminishing returns with negative density dependence (Fischer & Lindenmayer, 2000). However, creating two smaller populations could increase extinction risk in some situations. Though our model accounted for the extinction risk through demographic and environmental stochasticity (Lande, 1998), we did not include additional extinction risks from Allee effects or explicit genetic factors that could cause inbreeding depression (Gilpin & Soulé, 1986). In practice, small populations are challenging to translocate because of the difficulty of predicting Allee effects and the potential for translocations to cause both source and target populations to fall below Allee thresholds (Deredec & Courchamp, 2007). Avoiding Allee effects may require decision makers to take a proactive approach to fractional AM, making sure to maintain a relatively large population source in remnant donor population is still feasible. This conclusion is robust to different values of threshold population size for movement and carrying capacity that influence the likelihood of engaging in AM and degree of density dependence, respectively (Appendix S3).

Fractional relocation could also be robust to other risks that we did not directly model, such as the risk of invasion beyond that arising from competitive interactions. Though fractional relocation relies largely on multiple translocations, which repeatedly expose the recipient ecosystem to potential invasion events (Kolar & Lodge, 2001), intentionally relocating fewer individuals into a well‐monitored ecosystem could also make it easier to detect and prevent invasions before they occur. Similarly, smaller releases could be easier to control if funding, planning, or societal opinions change and reversal is necessary (Haight et al., 2000).

Choosing species for AM

Species are vulnerable to climate change for a variety of reasons, ranging from dispersal limitation (Pearson, 2006), to narrow thermal tolerance (Tewksbury et al., 2008), to competitive interactions (Urban et al., 2012). Our model suggests that the effectiveness of AM as a management strategy depends on the driver of vulnerability. In particular, AM may not be appropriate for specialist, narrow‐tolerance species, such as tropical ectotherms (Tewksbury et al., 2008). With only a narrow range of temperatures under which specialists can replace themselves, any error in identifying a species’ optimal climate would disproportionately affect specialists. However, because of our assumption of a jack‐of‐all‐trades–master‐of‐none trade‐off (Levins, 1968), specialist species usually persisted under climate change without AM. With this trade‐off, specialists were stronger competitors under lottery competition (Chesson & Warner, 1981), outweighing the costs of narrow thermal tolerance in our model. Removing this trade‐off would reduce specialists’ competitiveness, making them potentially more vulnerable to climate change, but also more vulnerable to having smaller, divided populations with AM.

AM was most successful for dispersal‐limited species because, in these cases, AM directly mitigated the driver of their vulnerability to climate change. Short dispersal was a strong predictor of extinction, and the shortest dispersers had the strongest proportional increase in persistence with AM. Moreover, the shortest dispersers were the only target species with increased average persistence in every variation of AM that we modeled. We also found that species with low initial population sizes and species with close poleward competitors were also likely to be vulnerable to climate change and to benefit from AM. In our model, species with low population sizes and high competition also had lower‐than‐average dispersal (Appendix S6), suggesting they were likely to be strong AM candidates because of multiple vulnerabilities (Thompson & Gonzalez, 2017). Therefore, AM is more likely to be a relevant tool for species that face several climate limitations, such as trees with short dispersal and stronger poleward competition (Ettinger & HilleRisLambers, 2013), which comprise the majority of taxon‐specific AM studies (Hewitt et al, 2011). However, there is debate about whether plant distributions are driven by climate limitations or species interactions (Early & Sax, 2014), which could become important in evaluating whether a particular species would be a strong candidate for AM. Our results suggest that AM may be more effective for a plant population that is small with a narrow range because of species interactions than for a plant population that is limited by climate tolerance alone.

Given the possibility that climate change could select for increased dispersal, fecundity, and climate tolerance in relatively short time frames (Nadeau & Urban, 2019), the traits associated with AM success could change over time. This rapid evolution may act as another source of uncertainty that can affect AM decisions, such as the choice of source locations or whether declining populations reliably indicate the persistence risk (because the “evolutionary rescue” process of adapting to novel environments often entails a period of population decline before eventual adaptation and growth [Carlson et al, 2014]). Though close poleward competitors also increased extinction risk, our focus on lottery competition (among many possible drivers of competitive coexistence [Chesson, 2000]) ignored the niche differentiation for environmental characteristics beyond temperature, which might reduce the impact of poleward competitors. While acknowledging these assumptions inherent to our simple model, our results suggest that AM might be an option for conserving a variety of species beyond those that are directly dispersal limited.

Even under optimal conditions, AM did not prevent the extinction of nearly 20% of short‐dispersing species in our model. In these cases, managers might combine alternative management strategies, such as increasing connectivity, removing barriers, or creating new reserves (Lawler & Olden, 2011). For example, we found that species persisted more often after being relocated into low‐density communities, suggesting that managers could prepare the recipient ecosystems by controlling the populations of resident species (Godefroid et al., 2011). This approach might limit competitive pressure, reduce the risk of establishment failure, and temporarily increase the realized niche of the relocated species, but it would come with additional risks to resident species. To be able to compare AM to alternative management strategies, such as increasing connectivity, protection, and restoration, our next step is extending our model to incorporate variable carrying capacity and a two‐dimensional landscape.

Community ecology of AM

Our model builds on past research that suggests competition can prevent some species from tracking climate change (Urban et al., 2012). Though species were vulnerable to extinction if poleward species were strong competitors, AM was also less successful when we relocated species into an area occupied by stronger competitors. Empirically, Seddon et al. (2015) found that past AM efforts with animals in Australia and New Zealand were more likely to fail when non‐native predators and competitors were in the recipient location. Our theoretical results extend this insight to suggest that strong competition from native species could also impede AM efforts. Moreover, the effect of competition was higher in competition‐driven, low‐stochasticity communities where AM success depended on characteristics of the poleward species than in dispersal‐driven, high‐stochasticity communities where success depended more on the ability to accurately place species in their optimal climates. This difference suggests that historical climate variability and community assembly could inform management decisions about AM. For example, limiting competitive interactions (Godefroid et al., 2011) might be more effective for species from environments with low historical variability, whereas relocating species into climate refugia (Morelli et al., 2016) might be more effective for species from environments with higher historical variability.

Though we did not find any substantial negative effects of relocated species on the persistence of species in recipient communities, we made several simplifications to our model that could have limited the capacity for invasion impacts to occur. First, due to simple spatial structure we assumed that a single contiguous community assembled without distinct barriers, making the AM in our model analogous to intracontinental relocations that are less likely to cause invasions (Mueller & Hellmann, 2008). Second, for the sake of simplicity, we considered only intraguild lottery competition without the wider web of species interactions that would naturally occur. Biological invasions usually involve more complex ecological dynamics, many of which are taxon specific and difficult to generalize (Kolar & Lodge, 2001). Moreover, enemy‐release effects would occur if relocated species escape antagonistic interactions within their original range (Prenter et al., 2004), and relocated species might carry pathogens or parasites that spread (Simler et al., 2018). A richer set of interactions could also complicate AM success because relocating a species without a mutualist might limit establishment (Plein et al., 2016). In particular, Spasojevic et al. (2014) found that experimental transplants of certain plant species were more successful when facilitated by neighboring plants. In comparison with our competition‐driven model, local extinctions often occurred after relocation in another AM community model with generalized Lotka–Volterra interactions that incorporate predation and mutualism as well as competition (Peterson & Bode, 2020). However, a simpler spatial structure did not account for the natural range shifting of recipient communities along the temperature gradient. Overall, although our simple competitive framework provides a first step toward exploring the uncertainties and community context of AM, analyzing more interactions will help understanding of the outcomes following a relocation event, from establishment failure, to invasion, to the wide‐scale restructuring of ecological communities that is already taking place with climate change.

Supporting information

Figure S2.1: Species’ persistence and the characteristics that predicted persistence varied with environmental stochasticity.

Figure S2.2: Importance of species, community, and environmental characteristics in determining whether the target species will persist with climate change without assisted migration.

Figure S2.3: Comparison of the thermal tolerances of target that went extinct during simulations without assisted migration and with the species on their pole‐ward side (a) under low stochasticity and (b) under high stochasticity. Target species are grouped into 10% quantiles of their thermal tolerances with the bottom and top quantiles removed to limit the scale of the figure.

Figure S2.4: When simulated under climate change without assisted migration, species fell into three categories (shaded) depending on their fate following the first time they fell below a low population threshold.

Appendix S3: Global sensitivity of

$\eta$

and

$K$

Appendix S4: Initialized community data

Figure S3: Based on 10,000 climate change simulations, the persistence likelihood of a target species chosen for assisted migration (vertical axis) depended on the fraction of that population that was relocated (horizontal axis).

Figure S4: Distribution of initialized community characteristics before 2¹⁶ climate change simulations, comparing between low stochasticity (salmon colored with solid line) and high stochasticity (teal colored with dashed line).

Appendix S5: Effects of assisted migration on nontarget species and community

Figure S4.1: During climate change simulations, the persistence likelihood of nontarget species that were not chosen for assisted migration (vertical axis) did not depend on the fraction of that population that was relocated (horizontal axis). The dotted lines correspond to persistence with no management action and are shaded to match each comparison.

Figure S4.2: During climate change simulations, the relative change in gamma inverse Simpson's diversity index (vertical axis) depended on the fraction of the target population that was relocated (horizontal axis).

Appendix S6: Table of relative values of target species

Table S5: Mean value of characteristic values for different types of target species relative to mean values from randomly chosen species in both low and high stochasticity environments.

Appendix S7: R code

Backus GA. & Baskett ML. Identifying robust strategies for assisted migration in a competitive stochastic metacommunity Conservation Biology, 2021;35:1809−1820. 10.1002/cobi.13736