Summary
The most productive C4 food and biofuel crops, such as Saccharum officinarum (sugarcane), Sorghum bicolor (sorghum) and Zea mays (maize), all use NADP‐ME‐type C4 photosynthesis. Despite high productivities, these crops fall well short of the theoretical maximum solar conversion efficiency of 6%. Understanding the basis of these inefficiencies is key for bioengineering and breeding strategies to increase the sustainable productivity of these major C4 crops. Photosynthesis is studied predominantly at steady state in saturating light. In field stands of these crops light is continually changing, and often with rapid fluctuations. Although light may change in a second, the adjustment of photosynthesis may take many minutes, leading to inefficiencies. We measured the rates of CO2 uptake and stomatal conductance of maize, sorghum and sugarcane under fluctuating light regimes. The gas exchange results were combined with a new dynamic photosynthesis model to infer the limiting factors under non‐steady‐state conditions. The dynamic photosynthesis model was developed from an existing C4 metabolic model for maize and extended to include: (i) post‐translational regulation of key photosynthetic enzymes and their temperature responses; (ii) dynamic stomatal conductance; and (iii) leaf energy balance. Testing the model outputs against measured rates of leaf CO2 uptake and stomatal conductance in the three C4 crops indicated that Rubisco activase, the pyruvate phosphate dikinase regulatory protein and stomatal conductance are the major limitations to the efficiency of NADP‐ME‐type C4 photosynthesis during dark‐to‐high light transitions. We propose that the level of influence of these limiting factors make them targets for bioengineering the improved photosynthetic efficiency of these key crops.
Keywords: photosynthetic induction, C4 photosynthesis, Zea mays, Sorghum bicolor, Saccharum officinarum, mathematical model, Rubisco activase, PPDK regulatory protein, stomatal conductance
Significance Statement
Despite high productivities, the photosynthetic efficiency of C4 crops is well below the theoretical value. Analyses of limitations have focused on constant conditions, but fluctuating light prevails in crop canopies in the field. A combined dynamic metabolic, stomatal and leaf microclimate model is developed and parameterized for maize, sorghum and sugarcane. The model shows that stomatal opening and the proteins activating Rubisco and PPDK are the major limitations to photosynthesis under fluctuating light. The findings indicate new targets for increasing the productivity of these key crops.
INTRODUCTION
Increasing crop genetic yield potential during the Green Revolution proved critical both to global food security and reducing the land‐use change that would otherwise have been necessary to support the growing world population. The biggest contribution from this period was from new genotypes of major grain crops, which had greatly improved harvest indices and, coupled with improved agronomy, provided increased yield (FAO, IFAD and UNICEF, 2018, 2020). However, after rapid increases in yield over the 45 years from 1960, the growth in productivity of the world’s major crops is stagnating (Ray et al., 2012). With a forecast 60% increase in global demand for primary foodstuffs by mid‐century there is an urgent need to find new means to sustainably increase the productivity of these key crops (FAO, IFAD and UNICEF, 2020).
In parallel, a second global challenge is how to provide sustainable sources of energy and bioproducts to meet increasing societal pressures to achieve zero net glasshouse gas emissions. Displacing 55–70% of the petroleum demand in the USA with cellulosic biofuels would require about 109 Mg of biomass (Langholtz et al., 2016; Robertson et al., 2017). Saccharum officinarum (sugarcane) and Zea mays (maize) are the largest current sources of biofuels, whereas Sorghum bicolor (sweet and fiber sorghum) and the sugarcane‐derivative fiber crop, energycane, have emerged as major potential bioenergy and bioproduct feedstocks (Crow et al., 2020; Gautam et al., 2020; Jaiswal et al., 2017; Long et al., 2015; Parajuli et al., 2020). All belong to the monophyletic grass tribe Andropogoneae and all predominantly use the C4 NADP‐ME metabolic pathway (Bianconi et al., 2019). Increasing crop photosynthetic efficiency is one means to meet the need to increase the yields of food, biofuels and bioproduct crops and so avoid a need to bring more land into agriculture.
The yield potential of a given genotype at a given location is the product of the incident photosynthetically active radiation over the growing season, the efficiency of the crop in intercepting that radiation (ɛi), the efficiency of the conversion of intercepted radiation into plant mass (ɛc) and the efficiency of partitioning that mass into the harvested product (ɛp), also termed harvest index (Zhu et al., 2010); see Table 1 for a list of abbreviations, their definitions and units. Plant breeding has optimized ɛi and ɛp to the point where there is little opportunity for further improvement of these efficiencies in the major crops (Long et al., 2019; Zhu et al., 2010). Harvest indices are now as high as 0.6 in modern crop cultivars, with little scope for further improvement in this trait (Evans, 1997; Murchie et al., 2009; Zhu et al., 2010). Under optimal conditions the ɛp of maize hybrids is about 0.52, which has remained unchanged for the last two decades (Di Matteo et al., 2016), whereas sugarcane has an already high ɛp of 0.8, as the majority of the plant is the harvested product (i.e. stem) (Waclawovsky et al., 2010). By contrast, the third factor ɛc (also known as light‐use efficiency) of C3 and C4 crops, governed by photosynthesis, falls well below its theoretical maximum (Zhu et al., 2008). Theoretical analysis and genetic engineering have shown considerable potential to increase photosynthetic efficiency in both C3 and C4 crops (Kromdijk et al., 2016; Long et al., 2019; López‐Calcagno et al., 2020; Murchie et al., 2009; Salesse‐Smith et al., 2018; South et al., 2019; Yoon et al., 2020). Although increasing the stress tolerance of crops is another important route to increasing productivity, experience shows that increasing genetic yield potential can address both of these factors, thereby increasing the average yields achieved under both optimal and stress conditions (Wu et al., 2019). For example, a detailed analysis of progressive gains in yield potential through soybean breeding have resulted in achieved yield increases in years with both good and suboptimal production conditions (Koester et al., 2014).
Table 1.
Abbreviations
| Parameter | Full name | Unit |
|---|---|---|
| ϕ | CO2 leakiness | Dimensionless |
| A | Net CO2 uptake rate | µmol m−2 sec−1 |
| C i | Intercellular CO2 concentration | μmol mol– 1 |
| E | Transpiration rate | mol m−2 sec−1 |
| f VmRubisco | The ratio between measured V cmax and the maximal Rubisco activities in the model | Unitless |
| f VmPEPC | The slope of the linear relationship between measured V pmax and the maximal PEPC activities in the model | Unitless |
| g s | Stomatal conductance | |
| g s_Kd | Rate constant of decreasing stomatal conductance | min−1 |
| g s_Ki | Rate constant of increasing stomatal conductance | min−1 |
| J max | Maximum electron transport capacity | μmol m−2 sec−1 |
| K o | Michaelis–Menten constant of Rubisco for O2 | mbar |
| K c | Michaelis–Menten constant of Rubisco for CO2 | μbar |
| PAR | Photosynthetically active photon flux | μmol m−2 sec−1 |
| PEPC | Phosphoenolpyruvate carboxylase | |
| PDRP | Pyruvate phosphate dikinase regulatory protein | |
| PPDK | Pyruvate phosphate dikinase | |
| Rca | Rubisco activase | |
| R d | Mitochondria respiration | μmol m−2 sec−1 |
| τRubisco | Time constant of Rubisco activation | min |
| V cmax | Maximum rubisco activity estimated from measured A–C i curve | μmol m−2 sec−1 |
| V pmax | Maximum PEPC activity estimated from measured A–C i curve | μmol m−2 sec−1 |
| V max | Maximum activity of enzyme | μmol m−2 sec−1 |
| WUE | Water‐use efficiency (A/E) | mmol (CO2)/mol (H2O) |
Mathematical modeling of the photosynthetic process and the application of optimization methods have proven valuable in identifying targets for the bioengineering of increased efficiency and sustainability (Wang et al., 2014; Zhu et al., 2007, 2004). They have led to proof‐of‐concept improvements in productivity in replicated field trials with genetically engineered Nicotiana tabacum (tobacco) (Kromdijk et al., 2016; López‐Calcagno et al., 2020; South et al., 2019). However, these models have focused largely on the steady state and often on light‐saturated conditions, as have most measurements and analyses of the limitations of leaf photosynthesis.
In the field, however, leaves are rarely in steady state, and are subject to frequent fluctuations in light intensity. There has been a growing awareness of the need to address photosynthetic efficiency in fluctuating light conditions, as well as under constant light (Acevedo‐Siaca et al., 2020b; De Souza et al., 2020; Deans et al., 2019; Hubbart et al., 2012; McAusland and Murchie, 2020; McAusland et al., 2016; Murchie and Ruban, 2020).
A great deal of progress has been made towards understanding the dynamic response to light in C3 plants. The non‐steady‐state photosynthetic rate of C3 plants under fluctuating light is mainly affected by the speed of the following responses: the relaxation of non‐photochemical quenching; the activation and de‐activation of Rubisco; the activation of ribulose 1,5‐bisphosphate (RuBP) regeneration enzymes; metabolite pool sizes; mesophyll conductance and stomatal conductance (Deans et al., 2019; Kaiser et al., 2016; Mott and Woodrow, 2000; Pearcy, 1994; Slattery et al., 2018). However, the major limitations vary with species (Acevedo‐Siaca et al., 2020; De Souza et al., 2020; McAusland et al., 2016; Taylor and Long, 2017).
Dynamic photosynthetic models infer that faster responses of photosynthesis to light fluctuations within canopies could increase the productivity of C3 crops by 13–32% (Taylor and Long, 2017; Wang et al., 2020; Zhu et al., 2004). A bioengineered increase in the speed of the relaxation of non‐photochemical quenching, upon transition from high light to low light, significantly increased the quantum yield of photosynthesis in tobacco grown under fluctuating light, and also resulted in an approximately 20% increase in productivity in replicated field trials (Kromdijk et al., 2016).
Few experimental studies of photosynthesis under fluctuating light conditions in C4 plants have been published, however. The loss of productivity in fluctuating light, relative to constant light, in two C4 species (Amaranthus caudatus and Setaria macrostachya) was greater than in two C3 species (Celosia argentea and Triticum aestivum), implying a greater impact on C4 plants (Kubásek et al., 2013). Aside from this experiment, two early sets of gas‐exchange measurements suggested that stomatal conductance is not a limiting factor during photosynthetic induction in maize (Furbank and Walker, 1985; Usuda and Edwards, 1984).
Energy‐use efficiency limitations of C4 photosynthesis under steady‐state conditions have been analyzed via a number of empirical analyses and biochemical models (Bellasio and Griffiths, 2014; Laisk and Edwards, 2000; Wang et al., 2014a,b; Yin and Struik, 2018; Yin and Struik, 2021). However, no mechanistic modeling studies have analyzed the limitations of non‐steady‐state C4 photosynthesis. Here, we developed a dynamic model to predict the potential limitations within C4 photosynthesis in fluctuating light to suggest feasible targets to improve the energy‐use efficiency of C4 crops. As the major food and fiber C4 crops maize, sorghum, sugarcane and Miscanthus predominantly use the NADP‐ME form of C4 photosynthesis, we previously developed a kinetic metabolic model of this form of C4 photosynthesis. It represented all discrete metabolic reactions of photosynthesis within the different cellular compartments of a C4 leaf, and transfer between the compartments, as a system of ordinary differential equations (ODEs). Each individual reaction and transfer between compartments is described using either enzyme kinetics or metabolite diffusion kinetics (Wang et al., 2014). This metabolic model was used to predict the limitations of C4 photosynthesis under steady‐state lighting at 25°C.
To predict limitations under non‐steady‐state conditions, this metabolic model was extended to capture the key factors affecting non‐steady‐state photosynthesis during transitions from low light to high light, and vice versa. Specifically, we included the post‐translational regulation of key photosynthetic enzymes, temperature responses of the enzyme activities, dynamic stomatal conductance and leaf energy balance. We then parameterized the model using gas‐exchange data for the three most widely grown NADP‐ME C4 crops: maize, sorghum and sugarcane. From this, the major factors limiting photosynthesis during transitions from the dark to high light for these crops were predicted to be Rubisco activase (Rca), the pyruvate, phosphate dikinase (PPDK) regulatory protein and stomatal conductance.
RESULTS
Factors influencing induction of C4 photosynthesis in transitions from dark to high light
The dynamic model presented here extends a previous C4 metabolic model (Wang et al., 2014a,b) to include post‐translational regulation, temperature responses of enzymes, dynamic stomatal conductance and leaf energy balance (Figure 1). The model was built by superimposing the dynamic regulation of enzyme activation and stomatal conductance on the metabolic NADP‐ME C4 leaf photosynthesis model of Wang et al. (2014). This was initially parameterized from the literature (Table 2). During induction some C4 metabolic pools, in particular malate in the bundle sheath cytoplasm, rise to very high concentrations (Leegood, 1997). To assess the role of this accumulation of photosynthetic metabolites during induction, the model was first run assuming that all enzymes were fully activated and the stomata open. Termed scenario 1, this resulted in a rapid induction to near steady state within 120 sec (Figure 2a). The major limitation over this period was the time taken for C4 metabolites to accumulate and approach steady state, lagging C3 metabolites (Figure S1). Leakiness (ϕ), that is the proportion of CO2 released by decarboxylation in the bundle sheath that diffused back to the mesophyll, reached a minimum at 30 sec, gradually climbing to a steady‐state value of approximately 0.22 at approximately 600 sec, indicating that the flux through the C4 cycle continued to limit photosynthesis (Figure 2b). This limitation was affected by the activity of mutase and enolase, the enzymes that convert PGA to PEP. Increasing the maximum activity of mutase and enolase accelerated induction in scenario 1 (Figure S2).
Figure 1.
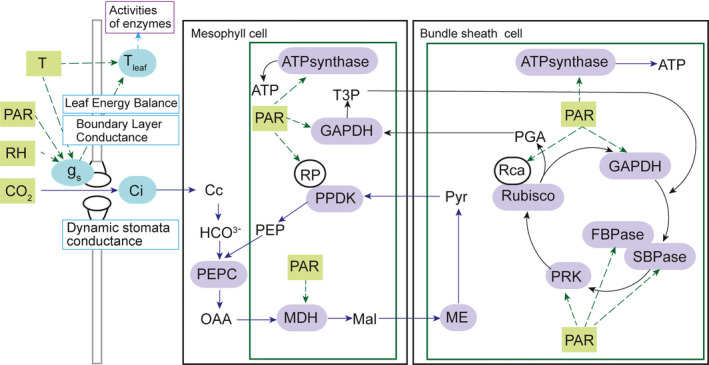
Metabolic model schematic of C4 photosynthesis. The model includes all metabolites and enzymes of photosynthetic carbon metabolism, as detailed previously (Wang et al., 2014). Here, only enzymes that are light modulated and therefore modified in this new dynamic model are indicated. Green rectangles are driving environmental variables affecting enzyme activities (purple) and stomatal conductance. Blue blocks are state variables calculated from leaf energy balance for T leaf, dynamic stomatal response model for stomatal conductance (gs ), and from the external [CO2], gs and predicted leaf CO2 uptake rate for Ci .
Table 2.
Input parameters for the dynamic C4 photosynthesis model
| Parameters | Original value | Reference | Maize | Sorghum | Sugarcane | Method of measurement |
|---|---|---|---|---|---|---|
| SlopeBB | 4.53 | Miner et al. (2017) | 5.183 ± 0.419 | 4.843 ± 0.211 | 4.941 ± 0.177 | A–Q curve |
| InterceptBB | 0.020 | Miner et al. (2017) | 0.036 ± 0.020 | 0.019 ± 0.013 | 0.027 ± 0.007 | A–Q curve |
| g s_ki (min−1) | 0.227 | McAusland et al. (2016) | 0.127 ± 0.016 | 0.257 ± 0.063 | 0.204 ± 0.031 | Shade–light dynamics |
| g s_kd (min−1) | 0.071 | McAusland et al. (2016) | 0.123 ± 0.026 | 0.377 ± 0.055 | 0.221 ± 0.023 | Shade–light dynamics |
| V pmax (µmol m−2 sec−1) | 120 | Von Caemmerer (2000) | 124.128 ± 9.253 | 133.626 ± 5.678 | 83.840 ± 4.140 | A–C i curve |
| V cmax (µmol m−2 sec−1) | 60 | Von Caemmerer (2000) | 49.919 ± 1.847 | 51.082 ± 2.001 | 52.783 ± 1.975 | A–C i curve |
| τRubisco (min) | 5 | Woodrow and Mott (1989) | 3.881 ± 1.117 | 9.714 ± 2.338 | 4.776 ± 0.316 | Dark–light dynamics |
| f VmPEPC | 1 | Assumed | 0.72 | 0.68 | 0.92 | A–C i curve |
| f VmRubisco | 0.85 | Assumed | 0.67 | 0.56 | 0.67 | A–C i curve |
| [PDRP] (µmol) | 0.04 | Assumed | 0.058 | 0.038 | 0.037 | Dark–light dynamics |
| Rd (µmol m−2 sec−1) | 1 | Von Caemmerer (2000) | 2.282 | 0.979 | 1.446 | Dark–light dynamics |
The values were collected from literature or calculated from gas exchange measurements.
Figure 2.

Simulated induction of: (a) leaf CO2 uptake (A); and (b) bundle‐sheath leakiness (ϕ), with various dynamic regulation settings. Scenario 1 uses the original metabolic model (Wang et al., 2014), which assumes steady‐state light activated enzyme activity and stomatal conductance from time zero, that is, throughout. In scenarios 2 and 3, DyPPDK and DyRubisco are added to the steady‐state model of scenario 1 to model the induction responses of pyruvate phosphate dikinase (PPDK) and Rubisco, respectively, regulated by the action of the PPDK regulatory protein (PDRP) and by the action of Rubisco activase (Rca) for Rubisco, respectively. Scenario 4 combines scenarios 2 and 3, and scenario 5 includes all light‐regulated enzymes. Scenario 6 superimposes stomatal opening on scenario 5. The induction simulates transfer from darkness to full sunlight: 1800 µmol m−2 sec−1. The input parameters are those listed in Table 2: ‘Original values’.
In scenario 2, the regulation of PPDK by its regulatory protein (PDRP) substantially slowed the rate of induction (dA/dt) of the CO2 assimilation rate (A) (Figure 2a) by limiting the synthesis of phosphoenolpyruvate (PEP), and thus lowering the predicted ϕ (Figure 2b). In scenario 3, Rubisco regulation alone is added and resulted in a similar decrease in the rate of induction of (dA/dt) to that of scenario 2. It reduced the final steady‐state level of A, as a greater proportion of Rubisco now remained inactive (Figure 2a). As would be expected, in contrast to scenario 2, leakiness is high in scenario 3 throughout induction, as the C4 cycle is delivering CO2 to the bundle sheath, but Rubisco is not fully activated and so is less able to use the CO2 being released by malate decarboxylation (Figure 2b). Combining the activation of both PPDK and Rubisco to give scenario 4 results in a yet slower rate of induction (Figure 2a), but the closer coordination of the activation of the two enzymes results in less bundle‐sheath leakiness during induction. The simulated leakiness increases for the first 600 sec and then declines to a steady‐state value of approximately 0.28 by 1200 sec, reflecting the predicted faster activation of PPDK than Rubisco (Figure 2b). The addition of dynamic control of the other light‐activated enzymes of photosynthetic carbon metabolism (Figure 1) in scenario 5 produces dynamic responses of A and ϕ that are almost identical to those of scenario 4 (Figure 2). Finally, superimposing the response of stomatal conductance (g s) in scenario 6 on the dynamics of A and intercellular CO2 concentration (C i) further slows the speed of induction, but dampens the bundle‐sheath leakage that would otherwise occur (Figure 2a,b).
The model is shown to predict typical dynamic responses of A and g s, both with respect to pattern and magnitude during induction. The simulation predicts PPDK activation, Rubisco activation and stomatal dynamics as the major limitations, whereas the activation of other enzymes of carbon metabolism and metabolic pool size adjustment had little effect (Figure 3). The concentration of PDRP regulates the initial phase of the photosynthetic induction curve (Figure 3a), whereas the speed of Rubisco activation affects the later phase of the induction (Figure 3b). During the mid‐phase of induction, g s is shown to limit A (Figure 3c).
Figure 3.
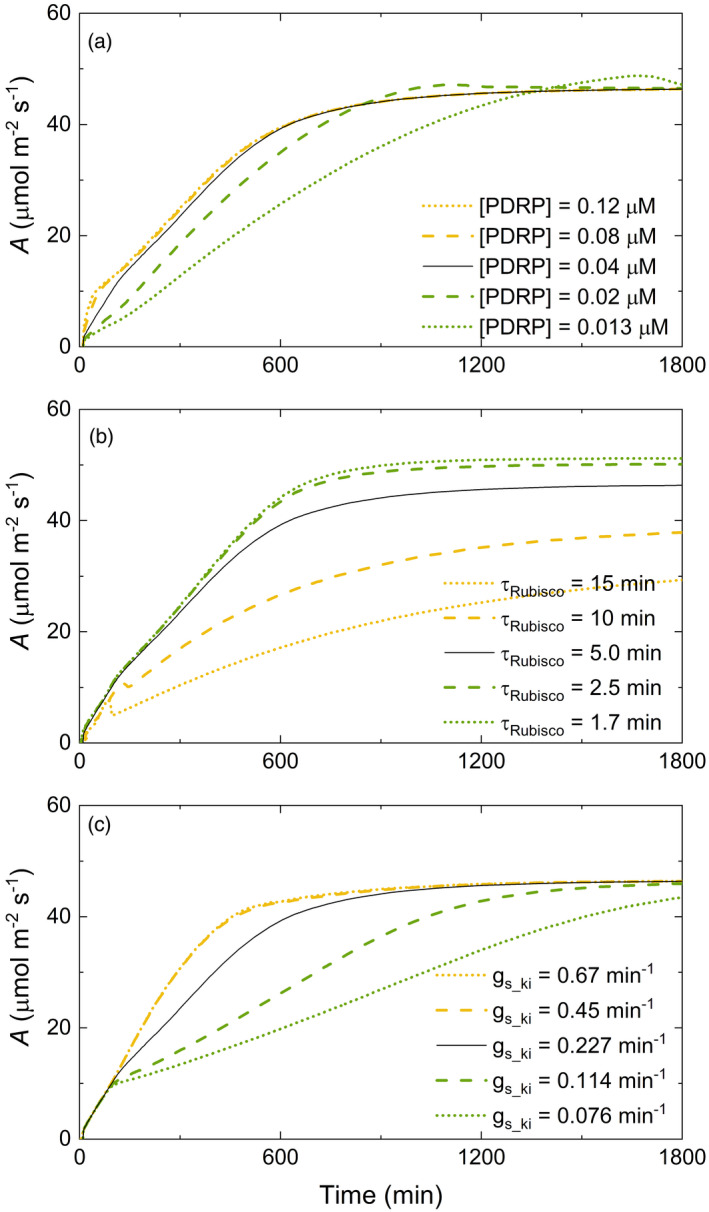
Simulated induction of leaf CO2 uptake (A) from dark to high light with variation in (a) the concentration of pyruvate phosphate dikinase regulatory protein (PDRP), (b) the time constant for the activation of Rubisco by Rubisco activase (τRubisco), and (c) the speed of stomatal opening (g s_ki ); k i is the rate constant for increase in stomatal conductance. After dark adaptation, and at time 0 above, the light intensity was raised to 1800 µmol m−2 sec−1 to initiate induction. The input parameters and 'Original values' are listed in Table 2; symbols are defined in Table 1.
Measured photosynthetic induction of maize, sorghum and sugarcane
To further analyze the limitations for different C4 crop species, the steady‐state and dynamic gas exchange of three major C4 crops were measured, using one widely grown or well‐studied genotype for each species: maize B73, sugarcane CP88‐1762 and sorghum Tx430. During the transition from dark to high light, the CO2 assimilation rate of maize rose the fastest, followed by sorghum and then by sugarcane (Figure 4a). The time required to reach 50% of the steady‐state rate (IT50) for the three crops was 196, 237 and 316 sec, respectively. The average CO2 assimilation rate in the 30‐min induction was reduced by 17.7, 20.6 and 24.2% in maize, sorghum and sugarcane, respectively, compared with the steady‐state CO2 assimilation rate. However, maize had a slower rate of increase in g s compared with sorghum and sugarcane (Figure 4c; Table 2). The C i value dropped rapidly in the first approximately 100 sec, and then slowly increased to the steady‐state level. The lowest C i values were 66, 86 and 107 µmol mol−1 in maize, sorghum and sugarcane, respectively, which are 53, 21 and 22% lower than their steady‐state C i values (Figure 4b). The low C i values would appear to be insufficient to fully saturate photosynthesis from about 180 to 600 sec after illumination began. Maize showed the highest intrinsic water‐use efficiency (iWUE) in the first 600 sec, whereas sorghum had the highest iWUE after 600 sec (Figure 4e). iWUE is the ratio of A to g s. Non‐photochemical quenching (NPQ) of the three species rose to a peak at approximately 60 sec and then declined to a steady state at approximately 600 sec, largely in concert with assimilation (Figure 4d).
Figure 4.
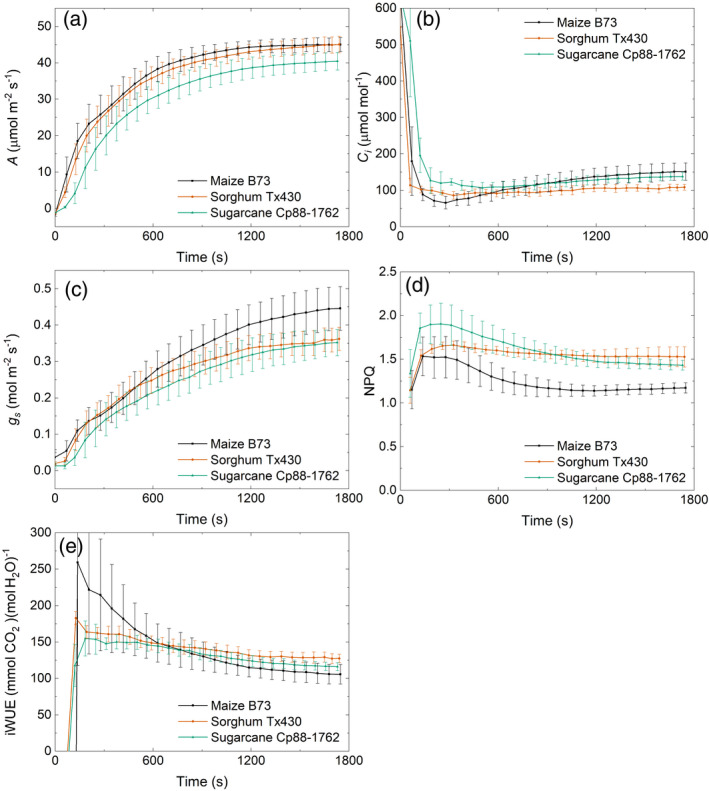
Measured gas exchange parameters upon transition from dark to high light (1800 µmol m−2 sec−1) after 30 min of dark adaptation: (a) leaf CO2 uptake rate (A); (b) intercellular CO2 concentration (Ci ); (c) stomata conductance (gs ); (d) non‐photochemical quenching (NPQ); and (e) intrinsic water‐use efficiency (iWUE). Bars represent ±1 SEMs for six plants. Leaf CO2 uptake (A) of the youngest fully expanded leaf was measured on 30‐day‐old maize B73, sugarcane CP88‐1762 and sorghum Tx430 plants with a gas exchange system (LI‐6800, LI‐COR).
Model parameterization and validation
Using the measured steady‐state and dynamic gas exchange data (Figures 4, 5 and Figure S6), we estimated the following photosynthetic parameters: maximum Rubisco activity (V cmax); maximum PEP carboxylase activity (V pmax); rate constants for stomatal conductance on dark‐to‐light and light‐to‐dark transitions (k i and k d, respectively); time constant of Rubisco activation (τRubisco); mitochondrial respiration (R d); concentration of PDRP; and the slope and intercept for the model described by Ball et al. (1987) (Figures S3–S7; Table 2). Using these species‐specific parameters alone, the model was able to closely replicate the measured dynamics of A and g s in all three C4 crops under fluctuating light (Figure 5). This consisted of 30 min of dark adaptation, followed by 30‐min intervals of high light, low light and high light again (Figure 5).
Figure 5.
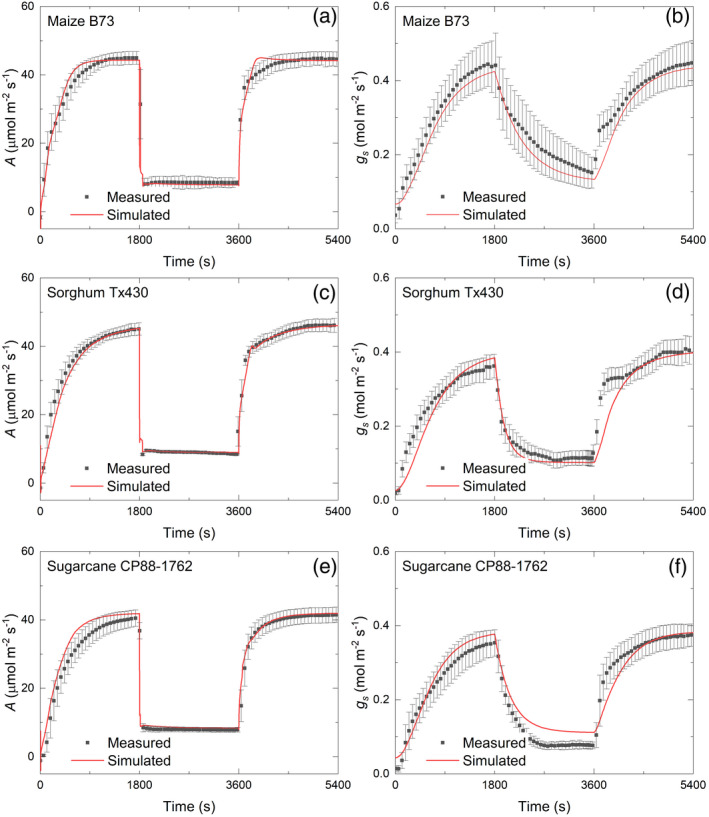
Simulated dynamic (a, c, e) photosynthesis (A) and (b, d, f) stomatal conductance (g s ) under fluctuating light conditions, for (a, b) maize, (c, d) sorghum and (e, f) sugarcane. The simulation used the parameters of non‐steady‐state photosynthesis from scenario 6 in Figure 2, but calibrated to the measured steady‐state photosynthesis of Figure 4. The measurements were made on six replicate plants. Red lines are the simulated results and black dots are the means of the measured data ±1 SE. After 30 min of dark adaptation, the leaves underwent three light change steps beginning at time 0 in above Figures, with the light intensity set to 1800, 200 and 1800 µmol m−2 sec−1 for each 1800 sec (30 min) step. The input parameters are listed in Table 2.
Factors limiting the speed of photosynthetic induction
Sensitivity analysis of PDRP and Rca concentrations and the speed of the stomatal response indicated that all three limit the rate of photosynthetic induction upon transition from dark to light in the three C4 crops (Figure 6). However, the strength of each limitation varied between species and with time into induction. In maize B73, sensitivity analysis suggested that PDRP exerts the highest limitation in the first 200 sec of induction, followed by stomatal opening over the next 400 sec and then Rca slightly limits the remaining phase of induction (Figure 6a). In sorghum Tx430 and sugarcane CP88‐1762, the concentration of PDRP limits the rate of induction in the first 240 sec, a little longer than in maize (Figure 6b,c). Rca exerts more influence in sorghum, with a peak at around 420 sec (Figure 6b), whereas the Rca limitation in maize and sugarcane remains approximately constant over this time period (Figure 6a,c). Stomatal limitation was greater in maize and sugarcane compared with sorghum (Figure 6).
Figure 6.
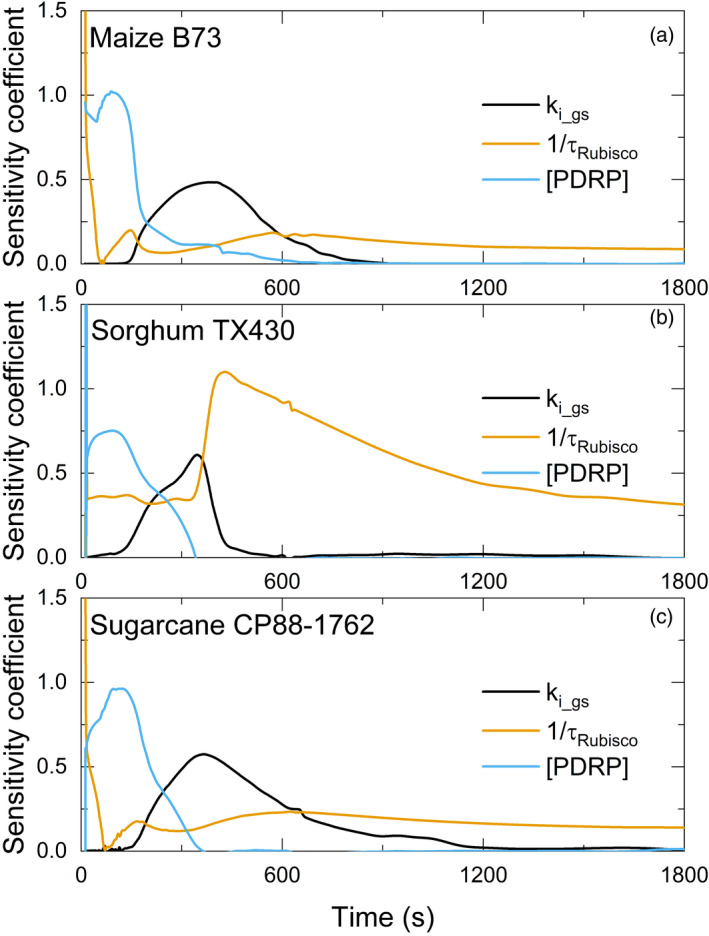
Simulated changes in the sensitivity coefficients of key parameters through photosynthetic induction for (a) maize, (b) sorghum and (c) sugarcane. After dark adaptation, light intensity was raised to 1800 µmol m−2 sec−1; time 0 above. To determine which steps in the system exert the strongest control on dynamic photosynthesis rate, a sensitivity analysis was performed by varying each parameter ±1%. Sensitivity coefficients are calculated as the ratio of change in the value of the parameter divided by change in leaf CO2 uptake rate (A), individually. If a 1% change in a parameter results in a 1% change in A, the sensitivity coefficient is 1, whereas if the change in A is zero, then the sensitivity coefficient is 0, meaning that no effect is exerted by that parameter. k i_gs is the time constant of stomata opening, τRubisco is the time constant of Rubisco activation, and [PDRP] is the concentration of the pyruvate phosphate dikinase (PPDK) regulatory protein.
In general, PPDK and Rubisco have high control coefficients in the first few minutes; whereas that of PPDK then declines, Rubisco continues to exert control through the mid and final stages of the induction. PEPC also has a high control coefficient from the middle of the induction in sugarcane (Figure 7e). PPDK and ME have some control in the later stage in maize and sorghum (Figure 7c). A control coefficient in the present context quantifies the relative influence of a single metabolic step on the rate of CO2 assimilation. A control coefficient of 1 indicates that the step has complete control and a control coefficient of zero indicates that the step has no control. Except for Rubisco, other light‐regulated enzymes of the Calvin–Benson cycle, including glyceraldehyde‐3‐phosphate dehydrogenase (GAPDH), sedoheptulose‐bisphosphatase (SBPase) and phosphoribulokinase (PRK), exerted only mild control in the first 150 sec of the induction (Figure 7b,d,f).
Figure 7.
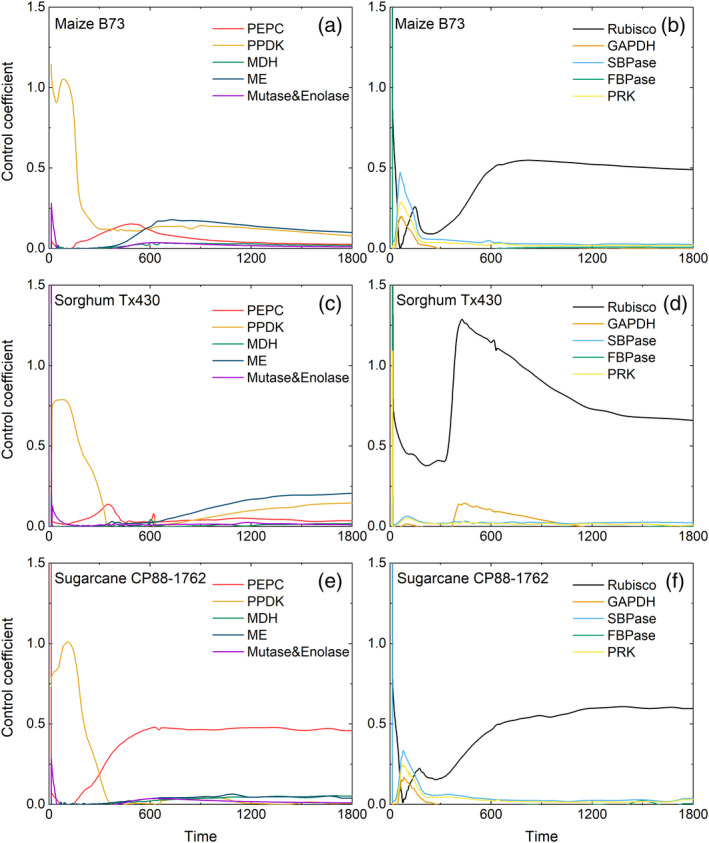
The control coefficient of the maximum activity of photosynthetic enzymes (V max) through time(s) of induction. After dark adaptation, the light intensity was raised to 1800 µmol m−2 sec−1. The photosynthetic enzymes shown here include: PEPC, phosphoenolpyruvate carboxylase; PPDK, pyruvate phosphate dikinase; MDH, malate dehydrogenase (NADP+); ME, NADP‐malic enzyme; mutase and enolase; Rubisco, ribulose‐bisphosphate carboxylase; GAPDH, glyceraldehyde‐3‐phosphate dehydrogenase (NADP+); SBPase, sedoheptulose‐bisphosphatase; FBPase, fructose‐bisphosphatase; PRK, phosphoribulokinase. (a, c, e) The predicted control coefficients of the C4 cycle enzymes. (b, d, f) The predicted control coefficients of the Calvin–Benson cycle enzymes.
Predicted CO2 leakiness (ϕ) during photosynthetic induction
Predicted ϕ shows an increase as PPDK becomes activated and then declines as simulated Rubisco activity catches up for the three C4 crops. This suggested a loss of coordination between the C4 and Calvin–Benson cycles during induction (Figure 8). The simulated ϕ of sorghum declines more slowly than that of maize and sugarcane, because of the slower rate of Rubisco activation (Figure S4; Table 2).
Figure 8.
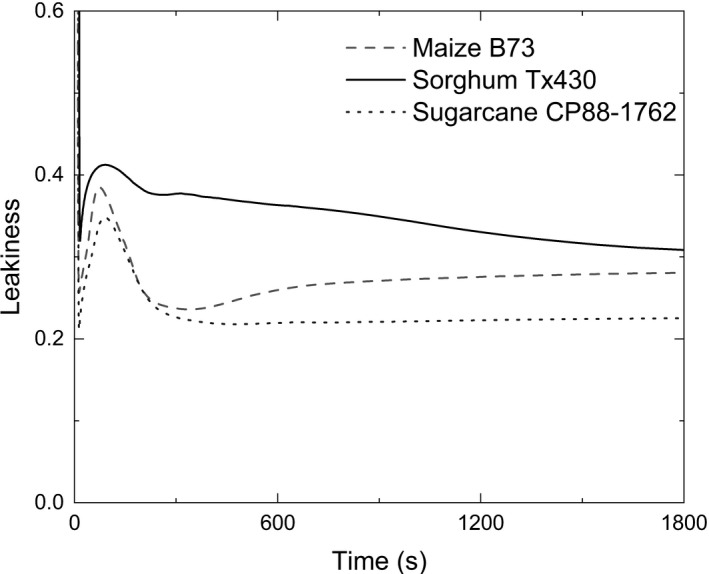
Simulated CO2 leakiness (ϕ) dynamics for maize, sorghum and sugarcane during photosynthetic induction following 30 min of dark adaptation. The light intensity was set to 1800 µmol m−2 sec−1. The input parameters are listed in Table 2: ‘Maize, sorghum and sugarcane’.
DISCUSSION
The energy‐use efficiency of C4 leaves is impacted under fluctuating light
In this study, the average photosynthetic rate through the 30‐min induction was reduced by 18, 21 and 24% in maize, sorghum and sugarcane, respectively, as compared with the steady‐state photosynthetic rate (Figure 4a). This reduction has a very significant effect on the energy‐use efficiency and net carbon assimilation of crops in the field, as clouds, wind and the movement of the sun cause frequent light fluctuations within leaf canopies (Kaiser et al., 2018; Tanaka et al., 2019; Wang et al., 2020; Zhu et al., 2004). In sunny conditions, C4 crops have a higher light energy‐use efficiency compared with C3 crops as a result of the CO2 concentrating mechanism, which largely removes the energy cost of photorespiration (Zhu et al., 2010). However, C4 crops may be less resilient to fluctuating light levels, resulting in a decrease in productivity in dynamic light environments (Kubásek et al., 2013). This indicates a significant potential for yield improvement of C4 food and biofuel crops by engineering or breeding for improved speeds of adjustment to fluctuating light.
Including post‐translational regulation, the temperature response of enzyme activities, dynamic stomatal conductance and a leaf energy balance module, the model closely simulated the measured photosynthetic responses of these crops under fluctuating light (Figure 5), in contrast to the original metabolic model (Figure 2). This suggests that the model captured the key factors affecting the speed of induction upon light fluctuations (Figure 5). Using this model, we determined the factors influencing the speed of induction. With the species‐specific input parameters (Table 2), the model is able to predict the limiting factors under conditions of fluctuating light (Figures 6 and 7). This has identified potential targets for the improvement of energy‐use efficiency in maize, sorghum and sugarcane. Namely, the coordinated upregulation of Rca and the PPDK regulatory protein, as well as increased rates of stomatal adjustment.
Limiting factors during photosynthetic induction
In C3 plants, the rate of photosynthetic induction is mainly limited by the activation of Rubisco, the activation of the enzymes affecting RuBP regeneration and the speed of stomata opening, with the major limitations varying between species (Acevedo‐Siaca et al., 2020; De Souza et al., 2020; McAusland et al., 2016; Taylor and Long, 2017). However, the limitations to C4 photosynthetic efficiency under fluctuating light have received little attention. Through a combination of model simulation and gas‐exchange experiment, we identified the following limiting factors in photosynthetic induction: (i) the accumulation of C4 photosynthetic intermediates to drive intercellular flux; (ii) the activation of PPDK; (iii) stomata opening; and (iv) the activation of Rubisco.
In our simulations, C4 cycle metabolites took longer to reach a steady state compared with Calvin–Benson cycle enzymes (Figure S1c,d), although the influence on the induction of photosynthesis was limited to the first 120 sec (Figure S1a). Also, accelerating the exchange of metabolites between the Calvin–Benson cycle and the C4 cycle, that is, increasing the activity of mutase and enolase, which catalyze the conversion of PGA to PEP, can further reduce the limitation of metabolites during this initial period of induction (Figure S2). We noted that mutase and enolase exerted higher control at the beginning of the induction and dropped to zero after about 60 sec, based on our control analysis for the three C4 crops (Figure 7). However, if the leaves experience a short‐term sun fleck, increased rates of photosynthetic metabolite accumulation would improve efficiency. The high concentration of C4 metabolites in NADP‐ME species at light saturation results in a slower decline in leaf CO2 uptake upon transitions from high light to shade, as the decarboxylation of malate continues to provide NADPH, compensating for the decline in NADPH from whole‐chain electron transport for a few minutes (Stitt and Zhu, 2014).
Our results infer that increasing the concentration of PDRP will increase the photosynthetic efficiency of these C4 plants under the fluctuating light conditions of field crop canopies. This is based on the simulation using the dynamic model developed in this study, which suggested that the concentration of PDRP is a major limitation during the first 180 sec of induction for maize, and for roughly the first 250 sec of induction for sorghum and sugarcane (Figure 6). It regulates both dark‐induced inactivation and light‐induced activation of PPDK by catalyzing the reversible phosphorylation of a threonine residue (Ashton et al., 1984; Budde et al., 1985; Burnell and Hatch, 1983, 1985; Chastain, 2010; Chastain et al., 2018). Although these studies elucidated the molecular mechanism for the activation of PPDK by PDRP, the direct effect of PDRP on photosynthetic efficiency has not been analyzed previously. The present analysis suggests that overexpression of PDRP would increase photosynthetic efficiency under field conditions.
The sensitivity coefficient of the time constant of stomata opening (k i) indicated that the speed of stomatal opening was rate limiting from 180 to 600 sec after illumination in maize (Figure 6). This differed from two previous studies indicating that stomatal conductance was not limiting in maize because C i was always higher than 100 µmol mol−1 during photosynthetic induction (Furbank and Walker, 1985; Usuda and Edwards, 1984). A meta‐analysis of responses of A to C i across a number of studies in maize indicated that A was only CO2 saturated at C i ≥ 100 µmol mol−1 (Pignon and Long, 2020). In the measurements here, C i dropped as low as 66 µmol mol−1, suggesting that g s was a limitation (Figure 4). However, our study used a higher inducing light intensity of 1800 µmol m−2 sec−1, as compared with 1400 µmol m−2 sec−1 (Usuda and Edwards, 1984) and 115–1150 µmol m−2 sec−1 (Furbank and Walker, 1985), and a longer dark treatment time of 30 min, in comparison with 10 and 20 min, respectively. The higher the light intensity used, the lower C i appeared during the induction (Furbank and Walker, 1985). The longer dark treatment time used here, was to allow sufficient time for stomata to close and for Rubisco to deactivate.
The present analysis indicated that the activation of Rubisco by Rca is the most important limiting factor after the first few minutes of induction, especially in sorghum with slower Rubisco activation (Figures 5 and 6). In Oryza sativa (rice), Rca has been demonstrated to play a crucial role in the regulation of non‐steady‐state photosynthesis (Yamori et al., 2012). Rubisco is arguably the major limiting enzyme of light‐saturated C4 photosynthesis (von Caemmerer, 2000; von Caemmerer et al., 2005; Furbank et al., 1997; Kubien et al., 2003; Wang et al., 2014), and increasing both Rca and Rubisco content have been shown to increase grain yield in maize (Salesse‐Smith et al., 2018; Yin et al., 2014). Hence, based on our simulation and previous studies, increasing the activity of Rubisco and Rca in tandem will increase the photosynthetic efficiency under constant and fluctuating light.
Phosphoenolpyruvate carboxylase (PEPC) appears not to restrict photosynthesis under steady‐state conditions, except under conditions inducing a low C i, such as drought (Pignon and Long, 2020). However, as C i dropped below 100 µmol mol−1 during induction (Figure 4b), sensitivity analysis indicated that increasing PEPC would increase photosynthetic efficiency from 180 sec to about 600 sec during induction in maize and sorghum (Figure 7a,c). In sugarcane, however, PEPC limits the steady‐state photosynthetic rate of sugarcane, through its lower V pmax compared with maize and sorghum (Figure 7e; Table 2).
Differences in the limiting factors of photosynthetic induction among species
Furbank et al. (1997) concluded from antisense manipulations that PPDK and Rubisco shared metabolic control of steady‐state light‐saturated photosynthesis in the C4 dicot Flaveria bidentis. The limited studies of C4 photosynthesis under fluctuating light have focused on maize. Two early studies indicated that photosynthesis reached a maximum rate after about 15–25 min in maize (Furbank and Walker, 1985; Usuda and Edwards, 1984), which is comparable with the observations and simulations here (Figures 4a and 5).
This study is limited to single accessions of each of three NADP‐ME C4 species. Therefore, it cannot be generalized to the species studied here. However, the examination of individuals from three distinct species of the monophyletic Andropogonae, all C4‐NADPME plants, is likely to have revealed limitations that apply across this key clade of food and energy crops. They therefore point to manipulations that could improve photosynthetic efficiency and yields across the clade. Although there were many similarities, some differences were found. Maize, as perhaps the species most intensively bred for productivity, showed the fastest induction and greatest efficiency of carbon gain over the period of induction, whereas sugarcane was the slowest (Figure 4). Whether these are species characteristics can only be determined by analyzing a wider range of genotypes of each crop. Characterizing within‐species variation would also show the potential for improving non‐steady‐state photosynthesis through breeding. In rice, intraspecific genetic variation in non‐steady‐state photosynthetic efficiency was found to be substantially greater than in the steady state, suggesting an overlooked target for improvement that might similarly be available in these crops (Acevedo‐Siaca et al., 2020a,b).
Maize showed the fastest induction, because of more PDRP and faster τRubisco (Table 2), which indicated that maize has faster PPDK and Rubisco activation capacity. However, the stomatal response of maize is slow (Table 2). Here the stomata were one of the major limiting factors during the induction process (Figure 6). This conclusion is different from previous studies (Furbank and Walker, 1985; Usuda and Edwards, 1984), and the possible reasons were explained in the previous section. Speeding up stomatal opening and closing is the key to speed up the photosynthetic response while maintaining water‐use efficiency. New combined thermal and modulated fluorescence techniques now provide a potential high‐throughput means to screen germplasm for this trait (Pignon et al., 2021; Vialet‐Chabrand and Lawson, 2019; Vialet‐Chabrand and Lawson, 2020). Bioengineering for more and smaller stomatal complexes would be another approach (Drake et al., 2013).
For sorghum, the speed of stomatal opening had little effect on A during induction (Figure 6). Enzyme activities were the main limiting factors, that is, the concentration of PDRP (i.e. the activation rate of PPDK), the activation rate of Rubisco (τRubisco) and Rubisco activity (V cmax) (Figures 6 and 7). Thus, increasing the activity of PDRP, Rca and Rubisco would lead to higher dynamic photosynthesis. However, analysis of water‐use efficiency across a wide range of sorghum germplasm suggests at the species level that the speed of stomatal adjustment is also important (Pignon et al., 2021).
For sugarcane, its dynamic photosynthetic efficiency was co‐limited by many factors, including the rate of stomatal opening, the concentration of PDRP, the activation rate of Rubisco (τRubisco) and Rubisco activity (V cmax). In addition, a high control coefficient of PEPC, relative to the other species, was found in sugarcane during induction and in the steady state (Figure 7). Therefore, to improve dynamic photosynthesis, all the limiting factors above may need to be considered. However, with only one accession of each species, our study cannot determine whether these are actual species differences or simply the result of the accessions that were chosen.
Imbalances in the regulation of C3 and C4 cycles
Coordination between the C3 and C4 cycles is essential to the efficiency of C4 photosynthesis. Leakiness (ϕ) describes the proportion of carbon fixed by PEPC that retrodiffuses back out of bundle‐sheath cells into the mesophyll (Equation 30). It was estimated to be about 0.2 in several C4 species under various environmental conditions (Henderson et al., 1992) and between 0.20 and 0.22 in a recent study of maize (Salesse‐Smith et al. 2018). Our simulated steady‐state ϕ values of the three species lie between 0.2 and 0.3 (Figure 8). In our simulation, the leakiness is predicted to change during the induction through an imbalance in the regulation of the Calvin–Benson cycle and the C4 cycle, especially when the activation of Rubisco is slower (Figure 8, Sorghum). Thus, increasing the activation speed of Rubisco is the first choice to improve efficiency during transitions from dark to light. Although the activation of PPDK is also one of the main limiting factors, increasing the PDRP concentration could not significantly improve photosynthetic efficiency without a larger increase in the speed of Rubisco activation. Overall, this study has identified several potential opportunities for increasing photosynthetic efficiency in these major crops during the frequent light fluctuations that occur in field canopies.
EXPERIMENTAL PROCEDURES
Model development
We developed a generic dynamic systems model of C4 photosynthesis from the previous NADP‐ME metabolic model for maize (Wang et al., 2014a,b, Appendix S2). The NADP‐ME metabolic model is an ordinary differential equation model including all individual steps in C4 photosynthetic carbon metabolism. Here, we extended the model to include the post‐translational regulation and temperature response of enzyme activities, together with the dynamics of stomatal conductance and leaf energy balance. The model was implemented in matlab. To save space and make the text more readable, abbreviations have been introduced throughout this section. They can be seen in Table 1.
Post‐translational regulation of enzyme activity
PPDK activation state
The activity of PPDK is regulated by PDRP, which is affected by the level of incident light via ADP concentration (Ashton et al., 1984; Burnell and Hatch, 1985; Chastain, 2010). PDRP is a bifunctional protein kinase/protein phosphatase, catalyzing the reversible phosphorylation of PPDK. The inactivation rate ( and activation rate ( were calculated by the following equations:
| (1) |
| (2) |
where [PDRP]Mchl is the PDRP concentration in the mesophyll cell chloroplasts, and and are the turnover number of PDRP for the inactivation and activation reaction, respectively. is the concentration of active PPDK in the mesophyll chloroplasts; is the concentration of inactive PPDK in the mesophyll chloroplasts.
Differential equations, parameters and their sources are listed in Appendix S1.
Rubisco activation state
The time constant of Rubisco activation was determined from the measured kinetics of photosynthetic gas exchange following transitions from dark to high light, using the method given by Woodrow and Mott (1989) (Equation 27; Figure S4). The differential equation for the transient maximal Rubisco activity is:
| (3) |
where τRubisco is the rate constant of Rubisco activation catalyzed by Rca. V max_Rubisco_i is the transient maximal Rubisco activity; V max_Rubisco_s is the steady‐state maximal Rubisco activity, which is related to the Rca concentration, [Rca] (Mott and Woodrow, 2000). The total [Rca] is calculated using measured τRubisco (Equation 25; Table 2):
| (4) |
where k is a constant, which is 216.9 min mg m−2 (Mott and Woodrow, 2000).
Steady‐state maximal Rubisco activity is calculated with the following equations:
| (5) |
| (6) |
where is the theoretical maximum activity of Rubisco. [Rca]A is the concentration of active Rca, which is regulated by light intensity (Appendix S1). is a constant, which equals 12.3 mg m−2 (Mott and Woodrow, 2000).
Activation of enzymes regulated via light intensity
The model used a simplified equation for the light regulation of ATP synthase (ATPase), fructose‐1:6‐bisphosphatase (FBPase), glyceraldehyde‐3‐phosphate dehydrogenase (GAPDH), phosphoribulose kinase (PRK), rubisco activase (Rca) and sedoheptulose‐1:7‐bisphosphatase (SBPase):
| (7) |
| (8) |
| (9) |
where V max_E_i is the transient maximal enzyme activity, τE is the rate constant of the activation of each enzyme and is the steady‐state maximal enzyme activity, as affected by light intensity (I). k E_A and c E_A are two constants, that is, the slope and intercept of the linear relationship of the proportion of activated enzyme () as a function of I. is the activity of the enzyme when fully activated.
Although the activation of PEPC is regulated by light via phosphorylation, the whole pathway and parameters of this regulation have not been measured quantitatively. Thus, the dynamics of PEPC activity was as described by Equations (7), (8), (9). Parameters and their sources are listed in Appendix S1.
Temperature response of enzymes
In order to simulate the effects of fluctuating leaf temperature with fluctuations in light, the Arrhenius equation (Johnson et al., 1942) and Q 10 function were used to adjust the enzymatic parameters to the actual leaf temperature (T leaf). The formula used for each parameter was determined based on the availability of experimental data.
The temperature response of the maximum activity of carbonic anhydrase (CA) and PEPC (V max_CA and V max_PEPC) were incorporated into the model using a peaked Arrhenius function (Johnson, Eyring and Williams, 1942):
| (10) |
where E a is the exponential rate of the rise, H d describes the rate of decrease at supraoptimal temperatures and ΔS is the entropy factor.
The remperature response of enzymatic parameters of pyruvate phosphate dikinase (V max_PPDK), electron transport capacity (J max) and Rubisco (V max_Rubisco_CO2, V max_Rubisco_O2/V max_Rubisco_CO2, K o and K c) were incorporated into the model using an Arrhenius function:
| (11) |
Parameters and sources are listed in Appendix S1.
For other enzymes, a Q 10 function was used to estimate the temperature response of the maximum activity, as described previously (Woodrow and Berry, 1988). Q10 was set as 2:
| (12) |
Dynamic stomatal response
Ball–Berry model parameters for predicting steady‐state stomatal conductance (Ball et al., 1987) were obtained from light response curves measured for each C4 crop evaluated in this study. In the Ball–Berry model, stomatal conductance was with a function of A, relative humidity (RH) and CO2 concentration at the leaf surface (C a):
| (13) |
where SlopeBB is the slope of the relationship between g s_steady and A × RH/C a and InterceptBB is the residual stomatal conductance. SlopeBB and InterceptBB were estimated by linear regression of and g s_steady from the light response curve (A–Q curve) measurement.
Dynamic stomatal conductance (g s) was estimated with the following equation:
| (14) |
where g s_steady is the steady‐state stomatal conductance calculated by the Ball–Berry model (Equation 13; Ball et al., 1987); k (k i or k d) is the rate constant of the stomata conductance response calculated from the measured stomata dynamics of the three C4 crops, and k i and k d represent the rate constants of stomata conductance increasing and decreasing, respectively (Table 2; Equation 26).
Dynamic leaf energy balance
For leaf energy balance, the equations used in our model were based on the method of Nikolov et al. (1995). According to this model, leaf energy balance takes account of intercepted short‐ and long‐wave radiation, radiative energy loss from the leaf, convection and latent heat loss in transpiration. The net photosynthesis rate (A), stomatal conductance and leaf temperature are interdependent. For example, A affects stomatal conductance, stomatal conductance affects leaf temperature and leaf temperature affects A. Instead of solving these steady‐state circular connections iteratively (Nikolov et al., 1995), a differential equation describes leaf temperature (T leaf) change (Equation 15):
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
where is the absorbed photosynthetic active radiation, assuming that 85% of PAR is absorbed by the leaf, NIR is the absorbed near‐infrared radiation and LR is the absorbed long‐wave radiation. Both NIR and LR were set to zero. C p is the specific heat capacity of the leaf, and here we assumed it is the same as the specific heat capacity of water (4.184 J g−1 °C−1). m leaf is the specific leaf fresh weight (g m−2) and was set as 198 g m−2 for all species based on the measured value of maize leaves (197.9 ± 4.5 g m−2). Humidity in the leaf internal air space is assumed to be saturated at the temperature of the leaf. H and LE are the sensible and latent heat fluxes, respectively. E is the emitted long wave radiation and M e is the energy consumed in photosynthesis (Nikolov et al., 1995). The boundary layer conductance to heat is calculated as g bh = 0.924g b (Nikolov et al., 1995). C P_air is the specific heat capacity of air (29.3 J mol−1 °C−1), C lv is the latent heat of vaporization of water (44 000 J mol−1) and g l is the total conductance of the stomata and the boundary layer. is the leaf emisivity of long‐wave radiation and is the Boltzman constant.
Boundary layer conductance
Boundary layer conductance was calculated following Nikolov et al. (1995), and both free and forced convection was considered in determining the boundary layer conductance of the leaf. The leaf boundary layer conductance to vapor transport is the maximum of g bf and g br:
| (20) |
The forced‐convective and free‐convective leaf boundary layer conductance is computed as:
| (21) |
| (22) |
where d o is the characteristic dimension of a leaf (leaf width), ΔT is the temperature difference between the leaf and the local air (Monteith and Unsworth, 1990), u is the wind velocity, and c f and c e are two constants.
Gas exchange measurement and parameter estimation
Gas exchange measurements of Maize B73, sugarcane CP88‐1762 and sorghum Tx430 were used to calculate the values of the following photosynthetic parameters: maximum Rubisco activity; maximum PEPC activity; rate constants for stomatal conductance during opening and closing; time constants for Rubisco activation; mitochondrial respiration; concentration of PPDK regulatory protein; and the Ball–Berry slope and intercept (Table 2).
Plant material and growth conditions
Maize B73, sugarcane CP88‐1762 and sorghum Tx430 were grown in a controlled‐environment glasshouse at 28°C (day)/24°C (night). Maize and sorghum were grown from seed and sugarcane CP88‐176 was grown from stem cuttings. The positions of the plants in the glasshouse were re‐randomized every week to avoid the influence of environmental variations within the glasshouse. From 25 July to 8 August 2019, six biological replicates were measured in a randomized experimental design for each species in each measurement.
Steady‐state gas exchange measurements and parameter estimation
Leaf gas exchange of the youngest fully expanded leaf was measured on plants at 30–35 days old with a gas exchange system (LI‐6800; LI‐COR, Lincoln, NE, USA). The leaf chamber temperature was set at 28°C, with a water vapor pressure deficit of 1.32 KPa and a flow rate of 500 µmol sec−1 for all gas exchange measurements.
For the response of A to intracellular CO2 concentration curves (A–C i curves), the leaf was acclimated to a light intensity of 1800 µmol m−2 sec−1 and a CO2 concentration of 400 µmol mol−1. After both A and g s reached steady state, the CO2 concentration of the influent gas was varied in the following sequence: 400, 300, 200, 120, 70, 40, 20, 10, 400, 400, 400, 600, 800, 1200 and 1500 µmol mol−1.
The maximum Rubisco activity (V cmax) and maximum PEPC activity (V pmax) were estimated from the A–C i curves using the equations of von Caemmerer (2000). In order to obtain the relationship between estimated V pmax and the theoretical maximal PEPC activity (V max_PEPC) in our model, and similarly the relationship between V cmax and the theoretical maximal Rubisco activity (V max_Rubisco), we introduced two variables (f vpmax and f vcmax) into the simulation:
| (23) |
| (24) |
Both f vpmax and f vcmax were estimated by minimizing the sum () of the squared differences between the estimated A (A e _C i) from the dynamic model and the measured A (A m _C i), in response to intercellular CO2 (A–C i curve), using the least‐squares method for each species:
| (25) |
| (26) |
f vPEPC was estimated using the initial slope () of the measured A–C i curve (CO2 air = 120, 70, 40, 20, 10 µmol mol−1); f vcmax was estimated using CO2‐saturated A m_Ci (CO2 air = 800, 1200 and 1500 µmol mol−1) (Figure S3). The steady‐state V max of the other enzymes of C4 and C3 metabolism in Figure 1 were scaled for each species with f vpmax and f vcmax, respectively.
To define the response of A to light intensity (A–Q curves), the leaf was acclimated to a light intensity of 1800 µmol m−2 sec−1 and a CO2 concentration of 400 µmol mol−1. After leaf gas exchange reached the steady state, the light intensity in the chamber was changed in the following sequence: 2000, 1500, 1000, 500, 300, 200, 100 and 50 µmol m−2 sec−1. The gas exchange data were logged after 5 min to ensure that there was enough time for the transpiration, and therefore stomatal condcutance, to reach the steady state at each light level. Ball–Berry model parameters (Ball et al., 1987) were estimated by the linear regression of and g s_steady from data from the A–Q curves, including the prediction of steady‐state stomatal conductance (g s_steady) for each species (Equation 13).
Dynamic gas exchange measurements and parameter estimation
Gas exchange during photosynthetic induction was measured in the transition from darkness to high light (1800 μmol m−2 sec−1) to determine the kinetics of Rubisco activation in these C4 crops (). The leaf was first acclimated to darkness for 30 min, with a CO2 concentration of 400 µmol mol−1 and then the light intensity was changed to 1800 μmol m−2 sec−1 for 30 min, which was more than sufficient time for leaf CO2 uptake and stomatal conductance to reach the steady state. Leaf gas exchange was logged before the light was turned on, and then logged every 10 sec for the following 30 min. The time constant of Rubisco activation (τRubisco) was estimated from the linear portion of the semi‐logarithmic plot of photosynthesis with time (Woodrow and Mott, 1989, 1993; Figure S4). The slope of this portion was determined by the linear regression of the data between 3 and 7 min. The value of was calculated as:
| (27) |
The calculated values of the three C4 species are listed in Table 2.
To further evaluate the response of gas exchange in C4 plants under fluctuating light, following this 30 min of induction the responses to the transition from high to low and back to high light (i.e. relaxation curves followed by induction curves) were measured. This involved decreasing light to 200 µmol m−2 sec−1 PPFD for 30 min and then returning to 1800 µmol m−2 sec−1 PPFD for an additional 30 min. Gas exchange was recorded every 10 sec.
Rate constants were calculated for g s increase on transfer from low light (200 µmol m−2 sec−1 PPFD) to high light (k i), and again for the decrease in g s on return to low light (k d). The measured time series for stomatal conductance changes were fitted with the following equation (Vialet‐Chabrand et al., 2017):
| (28) |
where g max is the maximum stomata conductance, g 0 is the minimum stomata conductance, t is time and k (k i or k d) is the rate constant of g s. g max, g 0 and k were estimated using Equation 28 by the curve fitting function (fit) in matlab (MathWorks, https://www.mathworks.com).
Mitochondrial respiration (R d) was estimated from the measured CO2 efflux after 30 min of dark adaptation. The concentration of PDRP was estimated by minimizing the difference between the estimated A (A e_t) from the dynamic model and the measured A (Am_t) at the beginning of the induction using the least‐squares method, which minimizes the sum () of the squared difference between estimated and measured A in the beginning of the photosynthetic induction (Figure S5). Data points from 1–3 min of the induction were used.
| (29) |
Model parameterization
The model took the following 11 photosynthetic parameters estimated from measured gas exchange data as input variables: maximum Rubisco activity (V cmax and f vcmax); maximum PEPC activity (V pmax and f vpmax); the rate constant of stomata conductance increase and decrease (k i and k d); the time constant of Rubisco activation (τRubisco); mitochondrial respiration (R d); [PDRP]; and the Ball–Berry slope (SlopeBB) and intercept (InterceptBB) (Table 2). The estimation methods of the input variables were described in the previous section (Gas exchange measurement and parameter estimation). Parameters and equations affected by the input variables are listed in Appendix S1.
Model prediction
CO2 uptake rate (A) and leakiness (ϕ) calculation
During the simulation, metabolite concentrations and reaction rates were extracted from the model. The velocity of CO2 flowing into the leaf via stomata was used to represent A. Leakiness (ϕ) describes the proportion of carbon fixed by PEPC that subsequently leaks out of the bundle sheath cells. Thus, ϕ was calculated as:
| (30) |
where the CO2 leak rate (v CO2_leak) is determined by the permeability of CO2 through plasmodesmata (P CO2_pd) and the concentration gradient of CO2 between bundle sheath cytosol and mesophyll cytosol, [CO2]BSC–[CO2]MC, and v PEPC is the velocity of carbon fixation by PEPC.
Sensitivity analysis
The sensitivity coefficient (SC p) gives the relative fractional change in the simulated result with a fractional change in the input variable (p), SC p is the partial derivative used to describe how the output estimate varies with changes in the values of the input parameter (p), where the output in this study is the estimated leaf CO2 uptake rate (A):
| (31) |
where the variable (p) was both increased and decreased by 1% individually in the model to calculate the new value of A (A + and A −, respectively) in order to identify the parameters influencing A.
The flux control coefficient of each enzyme (FCC) was also estimated by Equation 31, using the maximal activity (V max_E) of the enzyme as the variable (p).
AUTHOR CONTRIBUTIONS
SPL and YW designed the study. YW performed the computational analysis. YW conducted the gas exchange measurements. YW and KC implemented the literature data collection. SPL, YW and KC wrote the article.
CONFLICT OF INTEREST
The authors declare that they have no conflicts of interest associated with this work.
Supporting information
Figure S1. Simulated photosynthetic induction using metabolic model without post‐translational regulation of enzymes and delay of stomata conductance.
Figure S2. Estimated influence of mutase and enolase on photosynthetic induction.
Figure S3. Estimation of f vPEPC and f vRubisco using least‐squares method.
Figure S4. Semilogarithmic plot of the difference between photosynthesis (A) and maximum photosynthesis (A f) as a function of time.
Figure S5. Estimation of PPDK regulatory protein concentration, [PDRP], using measured photosynthetic induction curves.
Figure S6. Measured CO2 response curves and light response curves of maize B73, sorghum Tx430 and sugarcane CP88‐1762.
Figure S7. Calculated Ball–Berry slope and intercept using gas exchange data from the light response curves of maize, sorghum and sugarcane.
Appendix S1. New modules of the dynamic photosynthesis model.
Appendix S2. Equations and parameters of the C4 metabolic model (Wang et al., 2014).
ACKNOWLEDGMENTS
We thank Nikhil Jaikumar for providing the propagules of sugarcane CP88‐176. This work was supported by the DOE Center for Advanced Bioenergy and Bioproducts Innovation (US Department of Energy, Office of Science, Office of Biological and Environmental Research under award number DE‐SC0018420) and the project Realizing Increased Photosynthetic Efficiency (RIPE), which is funded by the Bill & Melinda Gates Foundation, Foundation for Food and Agriculture Research (FFAR) and the UK Foreign, Commonwealth and Development Office, under grant number OPP1172157.
Linked article: This paper is the subject of a Research Highlight article. To view this Research Highlight article visit https://doi.org/10.1111/tpj.15408
[Correction added on 23 September 2021, after first online publication: the name of the second author has been corrected to Kher Xing Chan.]
DATA AVAILABILITY STATEMENT
All measurements made here are freely available from the Illinois DataBank at https://doi.org/10.13012/B2IDB‐2694900_V1. All scripts for the model and associated files are available at https://github.com/yuwangcn/C4_dynamic_model.
REFERENCES
- Acevedo‐Siaca, L.G. , Coe, R. , Quick, W.P. & Long, S.P. (2020a) Variation between rice accessions in photosynthetic induction in flag leaves and underlying mechanisms. Journal of Experimental Botany, 72(4), 1282–1294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Acevedo‐Siaca, L.G. , Coe, R. , Wang, Y. , Kromdijk, J. , Quick, W.P. & Long, S.P. (2020b) Variation in photosynthetic induction between rice accessions and its potential for improving productivity. New Phytologist, 227(4), 1097–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashton, A. , Burnell, J. & Hatch, M. (1984) Regulation of C4 photosynthesis: inactivation of pyruvate, Pi dikinase by ADP‐dependent phosphorylation and activation by phosphorolysis. Archives of Biochemistry and Biophysics, 230, 492–503. [DOI] [PubMed] [Google Scholar]
- Ball, J. , Woodrow, I. & Berry, J. (1987) A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. In: Biggins, J. (Ed.) Progress in Photosynthesis Research. Dordrech: Springer, pp. 221–224. [Google Scholar]
- Bellasio, C. & Griffiths, H. (2014) The operation of two decarboxylases, transamination, and partitioning of C4 metabolic processes between mesophyll and bundle sheath cells allows light capture to be balanced for the maize C4 pathway. Plant Physiology, 164, 466–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bianconi, M.E. , Hackel, J. , Vorontsova, M.S. , Alberti, A. , Arthan, W. , Burke, S.V. et al. (2019) Continued adaptation of c4 photosynthesis after an initial burst of changes in the andropogoneae grasses. Systematic Biology, 69, 445–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budde, R.J. , Holbrook, G.P. & Chollet, R. (1985) Studies on the dark/light regulation of maize leaf pyruvate, orthophosphate dikinase by reversible phosphorylation. Archives of Biochemistry and Biophysics, 242, 283–290. [DOI] [PubMed] [Google Scholar]
- Burnell, J. & Hatch, M. (1983) Dark‐light regulation of pyruvate, Pi dikinase in C4 plants: evidence that the same protein catalyses activation and inactivation. Biochemical and Biophysical Research Communications, 111, 288–293. [DOI] [PubMed] [Google Scholar]
- Burnell, J. & Hatch, M. (1985) Regulation of C4 photosynthesis: purification and properties of the protein catalyzing ADP‐mediated inactivation and Pi‐mediated activation of pyruvate, Pi dikinase. Archives of Biochemistry and Biophysics, 237, 490–503. [DOI] [PubMed] [Google Scholar]
- Chastain, C.J. (2010) Structure, function, and post‐translational regulation of C 4 pyruvate orthophosphate dikinase. In: Raghavendra, A.S. & Sage, R.F. (Eds.) C4 Photosynthesis and Related CO2 Concentrating Mechanisms. Dordrect: Springer, pp. 301–315. [Google Scholar]
- Chastain, C.J. , Baird, L.M. , Walker, M.T. , Bergman, C.C. , Novbatova, G.T. , Mamani‐Quispe, C.S. et al. (2018) Maize leaf PPDK regulatory protein isoform‐2 is specific to bundle sheath chloroplasts and paradoxically lacks a Pi‐dependent PPDK activation activity. Journal of Experimental Botany, 69, 1171–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow, S.E. , Wells, J.M. , Sierra, C.A. , Youkhana, A.H. , Ogoshi, R.M. , Richardson, D. et al. (2020) Carbon flow through energycane agroecosystems established post‐intensive agriculture. GCB Bioenergy, 12, 806–817. [Google Scholar]
- De Souza, A.P. , Wang, Y. , Orr, D.J. , Carmo‐Silva, E. & Long, S.P. (2020) Photosynthesis across African cassava germplasm is limited by Rubisco and mesophyll conductance at steady state, but by stomatal conductance in fluctuating light. New Phytologist, 225, 2498–2512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deans, R.M. , Farquhar, G.D. & Busch, F.A. (2019) Estimating stomatal and biochemical limitations during photosynthetic induction. Plant, Cell & Environment, 42, 3227–3240. [DOI] [PubMed] [Google Scholar]
- Di Matteo, J.A. , Ferreyra, J. , Cerrudo, A.A. , Echarte, L. & Andrade, F.H. (2016) Yield potential and yield stability of Argentine maize hybrids over 45 years of breeding. Field Crops Research, 197, 107–116. [Google Scholar]
- Drake, P.L. , Froend, R.H. & Franks, P.J. (2013) Smaller, faster stomata: scaling of stomatal size, rate of response, and stomatal conductance. Journal of Experimental Botany, 64, 495–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans, L. (1997) Adapting and improving crops: the endless task. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 352, 901–906. [Google Scholar]
- FAO, IFAD and UNICEF (2018) The State of Food Security and Nutrition in the World 2018. Rome: FAO. [Google Scholar]
- FAO, IFAD and UNICEF (2020) The State of Food Security and Nutrition in the World 2020. Rome: FAO. [Google Scholar]
- Furbank, R.T. , Chitty, J.A. , Jenkins, C.L.D. , Taylor, W.C. , Trevanion, S.J. , von Caemmerer, S. et al. (1997) Genetic manipulation of key photosynthetic enzymes in the C‐4 plant Flaveria bidentis. Australian Journal of Plant Physiology, 24, 477–485. [Google Scholar]
- Furbank, R. & Walker, D. (1985) Photosynthetic induction in C4 leaves. Planta, 163, 75–83. [DOI] [PubMed] [Google Scholar]
- Gautam, S. , Mishra, U. , Scown, C.D. & Zhang, Y. (2020) Sorghum biomass production in the continental United States and its potential impacts on soil organic carbon and nitrous oxide emissions. GCB Bioenergy, 12, 878–890. [Google Scholar]
- Henderson, S.A. , Caemmerer, S. & Farquhar, G.D. (1992) Short‐term measurements of carbon isotope discrimination in several C4 species. Functional Plant Biology, 19, 263–285. [Google Scholar]
- Hubbart, S. , Ajigboye, O.O. , Horton, P. & Murchie, E.H. (2012) The photoprotective protein PsbS exerts control over CO2 assimilation rate in fluctuating light in rice. The Plant Journal, 71, 402–412. [DOI] [PubMed] [Google Scholar]
- Jaiswal, D. , De Souza, A.P. , Larsen, S. , LeBauer, D.S. , Miguez, F.E. , Sparovek, G. et al. (2017) Brazilian sugarcane ethanol as an expandable green alternative to crude oil use. Nature Climate Change, 7, 788–792. [Google Scholar]
- Johnson, F.H. , Eyring, H. & Williams, R. (1942) The nature of enzyme inhibitions in bacterial luminescence: sulfanilamide, urethane, temperature and pressure. Journal of Cellular and Comparative Physiology, 20, 247–268. [Google Scholar]
- Kaiser, E. , Morales, A. & Harbinson, J. (2018) Fluctuating light takes crop photosynthesis on a rollercoaster ride. Plant Physiology, 176, 977–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser, E. , Morales, A. , Harbinson, J. , Heuvelink, E. , Prinzenberg, A.E. & Marcelis, L.F. (2016) Metabolic and diffusional limitations of photosynthesis in fluctuating irradiance in Arabidopsis thaliana. Scientific Reports, 6, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koester, R.P. , Skoneczka, J.A. , Cary, T.R. , Diers, B.W. & Ainsworth, E.A. (2014) Historical gains in soybean (Glycine max Merr.) seed yield are driven by linear increases in light interception, energy conversion, and partitioning efficiencies. Journal of Experimental Botany, 65, 3311–3321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kromdijk, J. , Głowacka, K. , Leonelli, L. , Gabilly, S.T. , Iwai, M. , Niyogi, K.K. et al. (2016) Improving photosynthesis and crop productivity by accelerating recovery from photoprotection. Science, 354, 857–861. [DOI] [PubMed] [Google Scholar]
- Kubásek, J. , Urban, O. & Šantrůček, J. (2013) C4 plants use fluctuating light less efficiently than do C3 plants: a study of growth, photosynthesis and carbon isotope discrimination. Physiologia Plantarum, 149, 528–539. [DOI] [PubMed] [Google Scholar]
- Kubien, D.S. , von Caemmerer, S. , Furbank, R.T. & Sage, R.F. (2003) C4 photosynthesis at low temperature. A study using transgenic plants with reduced amounts of Rubisco. Plant Physiology, 132, 1577–1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laisk, A. & Edwards, G.E. (2000) A mathematical model of C4 photosynthesis: the mechanism of concentrating CO2 in NADP‐malic enzyme type species. Photosynthesis Research, 66, 199–224. [DOI] [PubMed] [Google Scholar]
- Langholtz, M.H. , Stokes, B.J. & Eaton, L.M. (2016) 2016 Billion‐ton report: Advancing Domestic Resources for a Thriving Bioeconomy, Volume 1: Economic Availability of Feedstock. Oak Ridge, TN: Oak Ridge National Laboratory. [Google Scholar]
- Leegood, R.C. (1997) The regulation of C‐4 photosynthesis. Advances in Botanical Research, 26, 251–316. [Google Scholar]
- Long, S.P. , Burgess, S. & Causton, I. (2019) Redesigning crop photosynthesis. In: Zeigler, R.S. (Ed.) Sustaining Global Food Security: The Nexus of Science and Policy. Clayton: CSIRO Publishing, pp. 128–143. [Google Scholar]
- Long, S.P. , Karp, A. , Buckeridge, M. , Davis, S. , Jaiswal, D. , Moore, P. et al. (2015) Feedstocks for biofuels and bioenergy. In: Souza, G.M. , Victoria, R. , Joly, C. & Verdade, L.M. (Eds.) Bioenergy & Sustainability: Bridging the Gaps ‐ SCOPE 72. São Paulo: SCOPE, pp. 302–347. [Google Scholar]
- López‐Calcagno, P.E. , Brown, K.L. , Simkin, A.J. , Fisk, S.J. , Vialet‐Chabrand, S. , Lawson, T. et al. (2020) Stimulating photosynthetic processes increases productivity and water‐use efficiency in the field. Nature Plants, 6, 1054–1063. [DOI] [PubMed] [Google Scholar]
- McAusland, L. & Murchie, E.H. (2020) Start me up; harnessing natural variation in photosynthetic induction to improve crop yields. New Phytologist, 227, 989–991. [DOI] [PubMed] [Google Scholar]
- McAusland, L. , Vialet‐Chabrand, S. , Davey, P. , Baker, N.R. , Brendel, O. & Lawson, T. (2016) Effects of kinetics of light‐induced stomatal responses on photosynthesis and water‐use efficiency. New Phytologist, 211, 1209–1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miner, G.L. , Bauerle, W.L. & Baldocchi, D.D. (2017) Estimating the sensitivity of stomatal conductance to photosynthesis: a review. Plant, Cell & Environment, 40, 1214–1238. [DOI] [PubMed] [Google Scholar]
- Monteith, J.L. & Unsworth, M.H. (1990) Principles of Environmental Physics. 2nd edition. Oxford, UK: Elsevier, p. 291. [Google Scholar]
- Mott, K.A. & Woodrow, I.E. (2000) Modelling the role of Rubisco activase in limiting non‐steady‐state photosynthesis. Journal of Experimental Botany, 51, 399–406. [DOI] [PubMed] [Google Scholar]
- Murchie, E. , Pinto, M. & Horton, P. (2009) Agriculture and the new challenges for photosynthesis research. New Phytologist, 181, 532–552. [DOI] [PubMed] [Google Scholar]
- Murchie, E.H. & Ruban, A.V. (2020) Dynamic non‐photochemical quenching in plants: from molecular mechanism to productivity. The Plant Journal, 101, 885–896. [DOI] [PubMed] [Google Scholar]
- Nikolov, N.T. , Massman, W.J. & Schoettle, A.W. (1995) Coupling biochemical and biophysical processes at the leaf level: an equilibrium photosynthesis model for leaves of C3 plants. Ecological Modelling, 80, 205–235. [Google Scholar]
- Parajuli, S. , Kannan, B. , Karan, R. , Sanahuja, G. , Liu, H. , Garcia‐Ruiz, E. et al. (2020) Towards oilcane: engineering hyperaccumulation of triacylglycerol into sugarcane stems. GCB Bioenergy, 12, 476–490. [Google Scholar]
- Pearcy, R.W. (1994) Photosynthetic utilization of sunflecks: a temporally patchy resource on a time scale of seconds to minutes. In: Caldwell, M.M. & Pearce, R. (Eds.) Exploitation of Environmental Heterogeneity by Plants, 1st edition. New York: Academic Press, pp. 175–208. [Google Scholar]
- Pignon, C.P. , Leakey, A.D.B. , Long, S.P. & Kromdijk, J. (2021) Drivers of natural variation in water‐use efficiency under fluctuating light are promising targets for improvement in sorghum. Frontiers in Plant Science, 12, 627432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pignon, C.P. & Long, S.P. (2020) Retrospective analysis of biochemical limitations to photosynthesis in 49 species: C4 crops appear still adapted to pre‐industrial atmospheric [CO2]. Plant, Cell & Environment, 43, 2606–2622. [DOI] [PubMed] [Google Scholar]
- Ray, D.K. , Ramankutty, N. , Mueller, N.D. , West, P.C. & Foley, J.A. (2012) Recent patterns of crop yield growth and stagnation. Nature Communications, 3, 1–7. [DOI] [PubMed] [Google Scholar]
- Robertson, G.P. , Hamilton, S.K. , Barham, B.L. , Dale, B.E. , Izaurralde, R.C. , Jackson, R.D. et al. (2017) Cellulosic biofuel contributions to a sustainable energy future: choices and outcomes. Science, 356, eaal2324. [DOI] [PubMed] [Google Scholar]
- Salesse‐Smith, C.E. , Sharwood, R.E. , Busch, F.A. , Kromdijk, J. , Bardal, V. & Stern, D.B. (2018) Overexpression of Rubisco subunits with RAF1 increases Rubisco content in maize. Nature Plants, 4, 802–810. [DOI] [PubMed] [Google Scholar]
- Slattery, R.A. , Walker, B.J. , Weber, A.P. & Ort, D.R. (2018) The impacts of fluctuating light on crop performance. Plant Physiology, 176, 990–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- South, P.F. , Cavanagh, A.P. , Liu, H.W. & Ort, D.R. (2019) Synthetic glycolate metabolism pathways stimulate crop growth and productivity in the field. Science, 363, eaat9077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stitt, M. & Zhu, X.G. (2014) The large pools of metabolites involved in intercellular metabolite shuttles in C4 photosynthesis provide enormous flexibility and robustness in a fluctuating light environment. Plant, Cell & Environment, 37, 1985–1988. [DOI] [PubMed] [Google Scholar]
- Tanaka, Y. , Adachi, S. & Yamori, W. (2019) Natural genetic variation of the photosynthetic induction response to fluctuating light environment. Current Opinion in Plant Biology, 49, 52–59. [DOI] [PubMed] [Google Scholar]
- Taylor, S.H. & Long, S.P. (2017) Slow induction of photosynthesis on shade to sun transitions in wheat may cost at least 21% of productivity. Philosophical Transactions of the Royal Society B: Biological Sciences, 372, 20160543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usuda, H. & Edwards, G.E. (1984) Is photosynthesis during the induction period in maize limited by the availability of intercellular carbon dioxide? Plant Science Letters, 37, 41–45. [Google Scholar]
- Vialet‐Chabrand, S. & Lawson, T. (2019) Dynamic leaf energy balance: deriving stomatal conductance from thermal imaging in a dynamic environment. Journal of Experimental Botany, 70, 2839–2855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vialet‐Chabrand, S. & Lawson, T. (2020) Thermography methods to assess stomatal behaviour in a dynamic environment. Journal of Experimental Botany, 71, 2329–2338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vialet‐Chabrand, S.R. , Matthews, J.S. , McAusland, L. , Blatt, M.R. , Griffiths, H. & Lawson, T. (2017) Temporal dynamics of stomatal behavior: modeling and implications for photosynthesis and water use. Plant Physiology, 174, 603–613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Caemmerer, S. (2000) Biochemical Models of Leaf Photosynthesis. Collingwood: CSIRO Publishing. [Google Scholar]
- von Caemmerer, S. , Hendrickson, L. , Quinn, V. , Vella, N. , Millgate, A. & Furbank, R.T. (2005) Reductions of Rubisco activase by antisense RNA in the C4 plant Flaveria bidentis reduces Rubisco carbamylation and leaf photosynthesis. Plant Physiology, 137, 747–755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waclawovsky, A.J. , Sato, P.M. , Lembke, C.G. , Moore, P.H. & Souza, G.M. (2010) Sugarcane for bioenergy production: an assessment of yield and regulation of sucrose content. Plant Biotechnology Journal, 8, 263–276. [DOI] [PubMed] [Google Scholar]
- Wang, Y. , Bräutigam, A. , Weber, A.P. & Zhu, X.‐G. (2014a) Three distinct biochemical subtypes of C4 photosynthesis? A modelling analysis. Journal of Experimental Botany, 65, 3567–3578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, Y. , Burgess, S.J. , de Becker, E.M. & Long, S.P. (2020) Photosynthesis in the fleeting shadows: an overlooked opportunity for increasing crop productivity? The Plant Journal, 101, 874–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, Y. , Long, S.P. & Zhu, X.‐G. (2014b) Elements required for an efficient NADP‐malic enzyme type C4 photosynthesis. Plant Physiology, 164, 2231–2246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodrow, I.E. & Berry, J. (1988) Enzymatic regulation of photosynthetic CO2, fixation in C3 plants. Annual Review of Plant Physiology and Plant Molecular Biology, 39, 533–594. [Google Scholar]
- Woodrow, I. & Mott, K. (1989) Rate limitation of non‐steady‐state photosynthesis by ribulose‐1, 5‐bisphosphate carboxylase in spinach. Functional Plant Biology, 16, 487–500. [Google Scholar]
- Woodrow, I.E. & Mott, K.A. (1993) Modelling C 3 photosynthesis: a sensitivity analysis of the photosynthetic carbon‐reduction cycle. Planta, 191, 421–432. [Google Scholar]
- Wu, J.R. , Lawit, S.J. , Weers, B. , Sun, J.D. , Mongar, N. , Van Hemert, J. et al. (2019) Overexpression of zmm28 increases maize grain yield in the field. Proceedings of the National Academy of Sciences of United States of America, 116, 23850–23858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamori, W. , Masumoto, C. , Fukayama, H. & Makino, A. (2012) Rubisco activase is a key regulator of non‐steady‐state photosynthesis at any leaf temperature and to a lesser extent, of steady‐state photosynthesis at high temperature. The Plant Journal, 71, 871–880. [DOI] [PubMed] [Google Scholar]
- Yin, X. & Struik, P.C. (2018) The energy budget in C4 photosynthesis: insights from a cell‐type‐specific electron transport model. New Phytologist, 218, 986–998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin, X. & Struik, P.C. (2021) Exploiting differences in the energy budget among C4 subtypes to improve crop productivity. New Phytologist, 229, 2400–2409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin, Z. , Zhang, Z. , Deng, D. , Chao, M. , Gao, Q. , Wang, Y. et al. (2014) Characterization of RuBisCo activase genes in maize: an α‐isoform gene functions alongside a β‐isoform gene. Plant Physiology, 164, 2096–2106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoon, D.‐K. , Ishiyama, K. , Suganami, M. , Tazoe, Y. , Watanabe, M. , Imaruoka, S. et al. (2020) Transgenic rice overproducing Rubisco exhibits increased yields with improved nitrogen‐use efficiency in an experimental paddy field. Nature Food, 1, 134–139. [DOI] [PubMed] [Google Scholar]
- Zhu, X.‐G. , De Sturler, E. & Long, S.P. (2007) Optimizing the distribution of resources between enzymes of carbon metabolism can dramatically increase photosynthetic rate: a numerical simulation using an evolutionary algorithm. Plant Physiology, 145, 513–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, X.‐G. , Long, S.P. & Ort, D.R. (2008) What is the maximum efficiency with which photosynthesis can convert solar energy into biomass? Current Opinion in Biotechnology, 19, 153–159. [DOI] [PubMed] [Google Scholar]
- Zhu, X.‐G. , Long, S.P. & Ort, D.R. (2010) Improving photosynthetic efficiency for greater yield. Annual Review of Plant Biology, 61, 235–261. [DOI] [PubMed] [Google Scholar]
- Zhu, X.G. , Ort, D.R. , Whitmarsh, J. & Long, S.P. (2004) The slow reversibility of photosystem II thermal energy dissipation on transfer from high to low light may cause large losses in carbon gain by crop canopies: a theoretical analysis. Journal of Experimental Botany, 55, 1167–1175. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Simulated photosynthetic induction using metabolic model without post‐translational regulation of enzymes and delay of stomata conductance.
Figure S2. Estimated influence of mutase and enolase on photosynthetic induction.
Figure S3. Estimation of f vPEPC and f vRubisco using least‐squares method.
Figure S4. Semilogarithmic plot of the difference between photosynthesis (A) and maximum photosynthesis (A f) as a function of time.
Figure S5. Estimation of PPDK regulatory protein concentration, [PDRP], using measured photosynthetic induction curves.
Figure S6. Measured CO2 response curves and light response curves of maize B73, sorghum Tx430 and sugarcane CP88‐1762.
Figure S7. Calculated Ball–Berry slope and intercept using gas exchange data from the light response curves of maize, sorghum and sugarcane.
Appendix S1. New modules of the dynamic photosynthesis model.
Appendix S2. Equations and parameters of the C4 metabolic model (Wang et al., 2014).
Data Availability Statement
All measurements made here are freely available from the Illinois DataBank at https://doi.org/10.13012/B2IDB‐2694900_V1. All scripts for the model and associated files are available at https://github.com/yuwangcn/C4_dynamic_model.


