A modern network approach to revisiting the Positive and Negative Affective Schedule (PANAS) construct validity

Abstract

Introduction

The factor structure of the Positive and Negative Affective Schedule (PANAS) is still a topic of debate. There are several reasons why using Exploratory Graph Analysis (EGA) for scale validation is advantageous and can help understand and resolve conflicting results in the factor analytic literature.

Objective

The main objective of the present study was to advance the knowledge regarding the factor structure underlying the PANAS scores by utilizing the different functionalities of the EGA method. EGA was used to (1) estimate the dimensionality of the PANAS scores, (2) establish the stability of the dimensionality estimate and of the item assignments into the dimensions, and (3) assess the impact of potential redundancies across item pairs on the dimensionality and structure of the PANAS scores.

Method

This assessment was carried out across two studies that included two large samples of participants.

Results and Conclusion

In sum, the results are consistent with a two‐factor oblique structure.

1. INTRODUCTION

The study of the structure of affect has been particularly important in increasing psychopathological and clinical knowledge about mental disorders. Anxiety and depression are among the most prevalent mental problems, and although the role of temperamental traits (i.e., Positive and Negative Affect) seems to play a role of relevance, it continues to be a topic of controversy and debate among clinicians and researchers. A large number of studies suggest that low levels of Positive Affect are related to the onset of depression and that higher levels of Positive Affect (PA) are associated with greater well‐being. Likewise, low levels of Negative Affect (NA) indicate a state of calm and serenity, whereas high levels of NA are a characteristic of anxiety (Díaz‐García et al., 2020). Much remains to be known about the mechanisms underlying the relationship between affect and emotional disorders. It is important to note that without adequate and reliable measurement of affect, it is not feasible to conduct research that provides empirical support in this field. Likewise, having these instruments with solid psychometric properties is indispensable for an adequate clinical evaluation.

The original version of the Positive and Negative Affective Schedule (PANAS) developed by Watson et al. (1988) is an instrument that was constructed to measure two orthogonal or relatively independent latent factors (Watson, 2000) named Positive and Negative Affect. Since its initial development, the PANAS become a widely used instrument in clinical and research fields (Flores‐Kanter et al., 2019; Rush & Hofer, 2014). However, a considerable heterogeneity in the scale structure is evidenced in past research. In one of the developed studies, the timeframes used in their instructions differ considerably (i.e., affective‐state version vs. trait‐like version). Moreover, other inconsistencies are found in the adapted versions, including English, German, French, Italian, Canadian, Spanish, and, to a lesser extent, those developed in Latin American countries (Flores‐Kanter & Medrano, 2018; Heubeck & Wilkinson, 2019). In the present study, we will first overview the available literature on the observed variability in the dimensionality obtained from the PANAS scores and the discussion around its internal structure.

From the search made in the SCOPUS and WoS databases, we found 49 previous studies on the internal structure and construct validity of the PANAS. Of these, 9 (18.36%) exclusively applied Exploratory Factor Analysis (EFA); 10 (20.40%) developed EFA and Confirmatory Factor Analysis (CFA); 2 (4.08%) used Exploratory Structural Equation Modeling analysis (ESEM); and the rest exclusively used CFA (n = 28; 57.14%). In the case of EFA, most studies (n = 10; 52.63%; Dahiya & Rangnekar, 2019; Dufey & Fernandez, 2012; Krohne et al., 1996; Melvin & Molloy, 2000; Pires et al., 2013; Robles & Páez, 2003; Sandín et al., 1999; Terraciano et al., 2003; Thompson, 2007; Watson et al., 1988) have applied the criticized the Little Jiffy procedure (i.e., the use of the principal component analysis, with varimax rotation and factor selection based on subjective or poor performing criteria such as scree plot or eigenvalues greater than 1). In particular, the use of the principal component analysis estimation method has been strongly criticized as it does not respond to the general objectives and postulates of EFA (Lloret‐Segura et al., 2014). However, principal axis factoring has been applied in 4 of the 19 antecedents that have applied EFA (21.05%; Huebner & Dew, 1995; Kwon et al., 2010; López‐Gómez et al., 2015; Nunes et al., 2019). It is relevant to note that of the remaining EFA studies in the literature, three have applied the maximum likelihood estimation method (ML) that assumes quantitative indicators and normal distributions of scores (n = 5; 26.31%; Arancibia‐Martini, 2019; Killgore, 2000; Moriondo et al., 2011; Mota de Sousa et al., 2016; Santángalo et al., 2019).

Regarding the CFA studies, the ML method was the most employed, appearing in eight of the twenty‐six studies that made explicit the estimation method applied (30.76%; Allan et al., 2015; Crawford & Henry, 2004; Flores Kanter & Medrano, 2016; Hansdottir et al., 2004; López‐Gómez et al., 2015; Melvin & Molloy, 2000; Molloy et al., 2001; Serafini et al., 2016). In addition to ML, other methods more in line with the distribution of PANAS scores and the categorical nature of its indicators have been used. Among these, a method widely used in previous PANAS CFAs is the WLSMV estimator, employed in 6 of the 26 previous studies (23.07%; Caicedo Cavagnis et al., 2018; Díaz‐García et al., 2020; Heubeck & Boulter, 2020; Heubeck & Wilkinson, 2019; Ortuño‐Sierra et al., 2015; Vera‐Villarroel et al., 2017). Another categorical variable estimator approximately equal to WLSMV, Diagonal Weighted Least Squares (DWLS), was used in 4 of the 26 previous studies (15.38%; Buz et al., 2015; Leue & Beauducel, 2011; Santángalo et al., 2019; Tuccitto et al., 2010). However, the Robust Maximum likelihood (RML) method, appropriate for nonnormal continuous variables, was applied in 6 out of 26 previous studies (23.07%; Jovanović & Gavrilov‐Jerković, 2015; Lim et al., 2010; Merz & Roesch, 2011; Merz et al., 2013; Narayanan et al., 2019; Seib‐Pfeifer et al., 2017); and finally, in the case of ESEM, of the two studies carried out with this approach, only one indicated the estimation method applied, which is WLSMV (Ortuño‐Sierra et al., 2019).

It can be seen that, even within the same factorial approaches (e.g., EFA), the results obtained on the internal structure of the PANAS are not homogeneous. Thus, from the studies considered that have applied EFA (n = 19), it is evidenced that eight (42.10%) present items with low factor loadings in their respective factor and/or low communities (Alert factor loading = 0.09 in Pires et al., 2013; Excited factor loading = 0.332 in Mota de Sousa et al., 2016; Distressed communality estimate = 0.08 in Villodas et al., 2011; Distressed factor loading = 0.28 in Thompson, 2007; Ashamed factor loading = 0.31 in Santángalo et al., 2019; Excited factor loading = 0.35 and Proud factor loading < 0.30 in Moriondo et al., 2011; Alert factor loading = 0.19, Upset factor loading = 0.11, and Afraid factor loading = −0.11 in Castillo et al. (2017); Interested factor loading = 0.22 and Hostile factor loading = 0.36 in Masculine Sample, and Alert factor loading = 0.04 and Afraid factor loading = 0.13 in Female Sample in Dufey & Fernandez, 2012). In addition, five EFA studies (26.31%) show salient cross‐loadings (>0.30; Proud, Alert, Jittery in Villodas et al., 2011; Jittery in Santángalo et al., 2019; Alert in Pires et al., 2013; Proud in Moriondo et al., 2011; Alert in Dufey & Fernandez, 2012). Furthermore, five EFA studies (26.31%) found evidence of the presence of a third factor (i.e., Negative Affect separated in two factors; Huebner & Dew, 1995; Killgore, 2000; Nolla et al., 2014; Pires et al., 2013; Vera‐Villarroel et al., 2017).

A similar heterogeneity is seen in the studies that have applied ESEM or CFA (n = 30). Within the ESEM models (n = 2), one of the antecedents has found better fit rates for the two‐factor orthogonal solution (RMR = 0.04, RMSEA = 0.08; Carvalho et al., 2013), whereas another study found better fit for the three‐factor solution (i.e., hierarchical model suggested by Mehrabian, 1997 ¹; over the 0.95 CFI criterion; Ortuño‐Sierra et al., 2019). In the case of the CFA studies that have compared the fit of a two‐factor model with other factor solutions (e.g., tree factor or bifactor models; n = 17), the same inconsistencies are observed, with six (35.29%) finding better fit for the three‐factor model (i.e., suggested by Mehrabian, 1997 or Gaudreau et al., 2006;² Allan et al., 2015; Caicedo Cavagnis et al., 2018; Flores Kanter & Medrano, 2016; Merz et al., 2013; Ortuño‐Sierra et al., 2015; Graudeau et al., 2006) and four (23.52%) reporting better fit for alternative hierarchical two‐factor or bifactor models³ (Leue & Beauducel, 2011; Mihić et al., 2014; Ortuño‐Sierra et al., 2015; Seib‐Pfeifer et al., 2017). It is important to mention that in the case of bifactor models, although they obtain higher fit indexes in most of the cases when they are applied, analysis of complementary rates has shown that these types of models present poor fit for the PANAS (see Flores‐Kanter et al., 2018). The remaining CFA studies (41.17%) show fit indexes in favor of the original two‐factor model (oblique or orthogonal). In addition, it has been shown in the previous PANAS history of applying CFAs (n = 27) that some items present a complex behavior (i.e., cross‐load). This situation has been evidenced in six of the previous studies (22.22%), involving the items Alert, Excited, Strong, Nervous, Jittery, Hostile, and Active (Caicedo Cavagnis et al., 2018; Flores Kanter & Medrano, 2016; Heubeck & Boulter, 2020; Graudeau et al., 2006; Nunes et al., 2019). It is also relevant to note that in the remaining 11 studies that have used CFA (39.28%), only the fit of the two‐factor model has been ascertained. However, beyond the fit obtained by this factor structure, it is not possible to rule out a priori that alternative models could have achieved a similar or better fit (e.g., three‐factor models).

Finally, considering all the ESEM and CFA PANAS studies (n = 30), it is relevant to highlight that only 10 studies (33.33%) achieved acceptable fit indexes without correlating residual errors. In all the remaining cases, errors had to be correlated to achieve an acceptable fit. A detailed analysis of this allows us to observe that the pairs of items whose errors have been most frequently correlated are as follows: scared and afraid; excited and enthusiastic; guilty and ashamed; attentive and alert; hostile and irritable; nervous and jittery; enthusiastic and inspired; distressed and upset; strong and active; excited and inspired; interested and alert; interested and attentive; and proud and determined. In all the cases, the modification rates and/or alluding to Zevon and Tellegen's (1982) mood content categories (e.g., as in Crawford & Henry, 2004) have been used to guide the correlation of these errors.

In conclusion, it can be stated that the factorial structure of the PANAS scores has not been consistent throughout previous studies, considering this heterogeneity is independent of the factorial approach implemented. These inconsistencies between different factor solutions and the lack of clarity concerning the items that make up the factors impede clear interpretations of PANAS scores in clinical and research contexts. It becomes necessary to propose novel psychometric approaches to advance the knowledge of the latent structure underlying the PANAS scores (Rush & Hofer, 2014). A new and robust methodology that has not yet been applied in PANAS is the Network approach called Exploratory Graph Analysis (EGA: Golino & Epskamp, 2017).

There are several reasons why using EGA for scale validation is advantageous and can help understand and resolve conflicting results in the factor analytic literature. The benefits of using EGA are particularly relevant for data with complex underlying structures that include correlated residuals, factors composed of a few variables, and highly correlated factors, all of which are potentially relevant for the PANAS. We highlight the most important benefits of using EGA for scale validation next.

2. ADVANTAGES OF USING EXPLORATORY GRAPH ANALYSIS FOR SCALE VALIDATION

First, a common strategy used to determine the optimal dimensional structure underlying a set of observed variables is to assess model fit. Despite the appeal of this approach (Preacher et al., 2013), multiple simulation studies have shown that fit indexes do not perform well in establishing latent dimensionality (Clark & Bowles, 2018; Garrido et al., 2016; Montoya & Edwards, 2021). In contrast, EGA has emerged as one of the most accurate methods to determine latent dimensionality (Golino & Demetriou, 2017; Golino & Epskamp, 2017; Golino et al., 2020a), while also providing an especially useful visual guide—network plot—that shows which items cluster together and their level of association.

Second, researchers typically report their choice for optimal model as a result of several analyses but are often unaware of how stable this structure might be across different samples. Although bootstrapping has proven advantageous in the estimation of the point estimates, standard errors, and confidence intervals (CIs) of EFA, CFA, and Structural Equation Models (SEMs; e.g., Lai, 2018; Zhang et al., 2010), it is generally applied in this context by estimating the same model across the bootstrap samples. This is a notable limitation because the factor analytic bootstrap procedures do not inform whether different dimensional models might have been chosen as optimal across the bootstrap samples. Obtaining this information of dimensional and structural stability could help researchers better understand discrepancies across studies that suggest different latent structures for the same instrument. Also, it would provide a more nuanced and complete view of the merits of competing structures underlying the scores of a particular instrument. Regarding this point, EGA provides a bootstrap function that informs of the stability of the dimensionality estimate as well as of the item assignments into the dimensions (Christensen & Golino, 2019), thus giving researchers greater insight into the robustness and reproducibility of their latent solutions.

Third, the latent structures of empirical data are likely to contain, aside from a number of major common factors, numerous minor factors, or systematic error variance that is generally not accounted for by the parsimonious factor models specified by researchers. One frequent source for this systematic error variance is the correlation between the residuals of items that have similar wording or overlapping content (Heene et al., 2012; Montoya & Edwards, 2021). When unaccounted for, large, correlated residuals can have a substantial impact on the estimation of the dimensionality and factor structure of empirical data (Christensen et al., 2021; Garrido et al., 2018; Yang et al., 2018). The typical procedure for identifying correlated residuals in factor analysis is by using the information provided by the modification index and standardized expected parameter change statistics (Saris et al., 2009; Whittaker, 2012). However, the values of these local fit statistics are dependent on the number of factors specified by the researchers (Heene et al., 2012), creating a problem of conflation if what the researchers are trying to establish in the first place is the dimensionality of the data. With the EGA method, this issue is resolved because it provides measures of redundancy between pairs of items that do not require the specification of a particular latent structure (Christensen et al., 2021). This way, researchers can identify potential sets of redundant items and test their impact on the dimensionality and latent structure of the data (Christensen et al., 2021; Rozgonjuk et al., 2020), without having to worry that their findings are an artifact of a misspecified factorial structure.

Fourth, when deciding on an optimal factor structure, researchers often estimate competing structures with adjacent numbers of factors and evaluate their interpretability. This strategy can be problematic in certain scenarios, because if researchers specify more major factors than those that are present at the population, the true factors can split, giving the impression that more substantive factors are present than those that exist (Auerswald & Moshagen, 2019; Wood et al., 1996). By using EGA for scale validation, researchers can have not just a good estimate of the dimensionality of their data, but also information regarding the robustness of this estimate that can suggest when to give credence to potential adjacent solutions.

Fifth, conflicting results across scale validation studies can arise due to the instability of the factorial structure across samples, which is related to various characteristics of the data such as the level of factor loadings, the number of variables per factor, and the size of the factor correlations (de Winter et al., 2009; Hogarty et al., 2005; Wolf et al., 2013). Incorporating EGA for scale validation is especially advantageous in this regard, because this method has been shown to be notably accurate, in comparison to competing procedures, when estimating dimensionality in the presence of difficult conditions such as with a few variables per factor, high factor correlations, or weak factor loadings, given that there is a large enough sample size (Golino & Demetriou, 2017; Golino & Epskamp, 2017; Golino et al., 2020a).

2.1. The present study

The main objective of the present study was to advance the knowledge regarding the factor structure underlying the PANAS scores by utilizing the different functionalities of the EGA method. Despite the widespread use of this instrument (Heubeck & Wilkinson, 2019), there is controversy regarding its factor structure. In light of this, EGA was used to (1) estimate the dimensionality of the PANAS scores, (2) establish the stability of the dimensionality estimate and of the item assignments into the dimensions, and (3) assess the impact of potential redundancies across item pairs on the dimensionality and structure of the PANAS scores. This assessment was carried out across two studies that included two large samples of participants that varied across a wide range of ages and that included persons in treatment for psychological disorders. To reduce the possibility of capitalization on chance, the sample for Study 1 was split into two halves, as recommended in the literature (Anderson & Gerbing, 1988), with the first half used to derive the optimal structure for the PANAS using EGA and ESEM (Asparouhov & Muthén, 2009), and the second half used to cross‐validate it with EGA, ESEM, and CFA (Jöreskog, 1969). The sample for Study 2 was then employed to confirm the dimensionality and latent structure of the PANAS scores using both EGA and CFA. In addition, the measurement invariance of the PANAS factor structure across sex, age, and treatment status was assessed in Study 2 for both samples, as well as the reliability of the confirmed scales. Overall, these analyses aimed to offer more clarity to the lingering debate regarding the optimal factorial structure for the PANAS scores and to provide a framework that other researchers can use for scale validation of the scores of this or other instruments.

The data for both studies were collected in November–December 2018 and January–February 2019. In these investigations, several scales were administered with the aim of verifying the relationship between affective variables, emotional regulation, and indicators of mood disorders. Among the scales included, the PANAS was administered together with the General Anxiety Disorder‐7 (GAD‐7) and the Patient Health Questionnaire‐9 (PHQ‐9).

3. STUDY 1

3.1. Derivation and cross‐validation of the PANAS factor structure

The aim of Study 1 was to establish an optimal factor structure for the PANAS’ item scores through an in‐depth process of derivation, cross‐validation, and criterion validity analyses. To carry out these objectives, we used various functions and capabilities of EGA, and complemented them with ESEM, CFA, and SEM analyses across a large sample of Argentinian children and adults. We hypothesized that the dimensionality estimates of the PANAS scores would be affected by correlated residuals emerging from unmodeled lower order facets corresponding to Zevon and Tellegen's (1982) mood content categories. Specifically, we hypothesized that the systematic variance resulting from these correlated residuals, when not taken into account, would lead to factor splitting (Auerswald & Moshagen, 2019; Wood et al., 1996). Furthermore, we hypothesized that models that contained factor splitting as a result of unmodeled redundancies could also be identified by similarities in the nomological networks of the factors involved in the split.

For the derivation and cross‐validation analyses, the sample of this study, “sample A,” was divided into two halves. With the first half of sample A, the “derivation sample,” a series of EGA and ESEM analyses were performed to tentatively select an optimal structure for the PANAS’ scores. First, redundancy analyses were carried out with EGA to determine potential overlaps/redundancies between item pairs. Indeed, previous research with the PANAS has shown that several item pairs produce correlated residuals within the context of factor modeling (Buz et al., 2015; Crawford & Henry, 2004; Ortuño‐Sierra et al., 2015; Thompson, 2007; Tuccitto et al., 2010). Second, EGA with both the graphical least absolute shrinkage and selection operator (GLASSO) and the triangulated maximally filtered graph (TMFG) estimators were used to determine the dimensionality and structure for the PANAS. Third, bootEGA was used to assess the stability of the EGA dimensionality estimates and item factor assignments across many bootstrap samples. Fourth, to see if the item redundancies affected the EGA estimates and their stability, the second and third steps were repeated by taking into account the largest item redundancies found on the first step. Fifth, a series of one‐ to four‐factor ESEM models were estimated and evaluated, each with an increasing number of correlated errors that were identified using the standardized expected parameter change (SEPC) local fit statistic (Saris et al., 2009; Whittaker, 2012). Finally, the EGA and ESEM results were evaluated in conjunction to determine the optimal structure of the PANAS for this sample.

The second half of sample A, the “cross‐validation sample,” was used to, first, assess the replicability of the EGA estimates from the derivation sample, second, to assess the replicability of the optimal ESEM model from the derivation sample, third, to determine if the PANAS’ scores could be adequately modeled as a simple structure using CFA, fourth, to compare the results of the optimal derived model with two alternative CFA models from the literature, one that hypothesized two orthogonal factors of Positive and Negative Affect (e.g., Heubeck & Wilkinson, 2019; Tuccitto et al., 2010), and Mehrabian's (1997) oblique three‐factor model of Positive Affect, Upset, and Afraid.

The final analyses of Study 1 involved an evaluation of the criterion validity of the PANAS factors from the different models considered in the previous steps. For these criterion validity analyses, we used the complete sample A and estimated SEM models with the PANAS factors as predictors, and factors of Generalized Anxiety Disorder and Major Depression as the outcomes.

4. METHODS

4.1. Participants and procedure

The sample for Study 1 was composed of 4909 Argentine children and adults with ages ranging from 10 to 81 years (M = 27.14, SD = 9.86). In terms of age groups, there were 757 participants in the 10–19 age group, 2810 in the 20–29 group, 704 in the 30–39 group, and 638 were in the age group of 40 years or more. Of the total sample, 3358 (68.4%) were composed of females, with the remaining 1551 (31.6%) composed of males. In addition, 640 participants (13.0%) reported to be undergoing psychological and/or psychiatric treatment at the moment they responded to the survey.

All participants were adequately informed of the research objectives, the anonymity of their responses, and their voluntary participation. Likewise, it was clarified that participation would not cause any harm and that they could leave the study whenever they wished. International ethical guidelines for studies with human beings were considered (American Psychological Association [APA], 2017). In this study, no specific incentive was used for participation in the study. In the case of minors under 18 years of age, prior parental consent was additionally requested. The ethics committee of the Research Secretariat of the 21st Century University previously approved the research protocol following APA ethical guidelines. The sample was obtained through an open mode online sample method (The International Test Commission, 2006). This methodology of data collection has proven to be equivalent to traditional forms of collection (i.e., face to face, Weigold et al., 2013), producing equal means, internal consistencies, intercorrelations, response rates, and comfort level when completing questionnaires. The sample for this observational, cross‐sectional study was collected using an online survey format to gather information through the Google Forms platform and was delivered by Facebook social media. The data were collected in November and December 2018.

4.2. Measures

4.2.1. Positive and Negative Affect Schedule (PANAS; Watson et al., 1988)

The PANAS consists of 20 terms that describe different positive (e.g., active, strong, inspired) and negative (e.g., irritated, scared, nervous) feelings and emotions. The participant being evaluated must indicate what level of intensity is felt for each one of the emotions presented. For this study, the online version validated in Argentina by Flores Kanter and Medrano (2016) was applied. In this study, Flores Kanter and Medrano (2016) obtained better fit for a structure of three latent factors. The reliability indicators obtained were acceptable in all cases (PANAS state: Positive Affect ρ = 0.84, α = 0.87; Disgusted Affect ρ = 0.77, α = 0.70—including the items aroused and alert—and = 0.74—without the items aroused and alert; Fearful Affect ρ = 0.85, α = 0.86; PANAS trait: Positive Affect ρ = 0.85, α = 0.88; Disgusted Affect ρ = 0.79, α = 0.68—including aroused and alert items—and α = 0.76—without aroused and alert items; Fearful Affect ρ = 0.85, α = 0.86). This online version was based on the Argentine translated adaptation version of the 20‐item PANAS (Medrano et al., 2015). In the Argentine adaptation of the PANAS, Medrano et al. (2015) and Moriondo et al. (2011) presented evidence of validity of a two‐factor structure through EFA, evidencing acceptable reliability indicators (Positive Affect α = 0.73; Negative Affect α = 0.82, in Moriondo et al., 2011; Positive Affect α = 0.82; Negative Affect α = 0.83, in Medrano et al., 2015). In the paper‐and‐pencil and online versions of the Argentine PANAS validations, the alert and excited items were removed due to their cross‐loading patterns and interpretation ambiguity. The same was done for this study, so that the 18‐item Spanish language version of the PANAS was administered. The PANAS items were responded via a 5‐point Likert scale. The “state” form of the PANAS was applied in Study 1, which probes into the intensity of emotions in the present moment.

4.2.2. Generalized Anxiety Disorder‐7 (GAD‐7; Spitzer et al., 2006)

This scale was used to detect the symptoms of GAD described in the DSM‐IV: nervousness, agitation, fatigue, muscle pain or tension, sleep problems, attention problems, and irritability. In the present study, the Spanish version validated by García‐Campayo et al. was used. As in its original English version, the Spanish version of the GAD‐7 includes a 4‐point response scale ranging from 0 (never) to 3 (almost every day), with a score ranging from 0 to 21. This scale was applied only for sample A, for which a Cronbach's α coefficient of 0.87 was obtained for the observed scores.

4.2.3. Patient Health Questionnaire‐9 (PHQ‐9; Kroenke et al., 2001)

This scale consists of nine items based on the presence of nine diagnostic criteria for major depression according to the DSM‐IV: (a) depressed mood, (b) anhedonia, (c) sleep problems, (d) fatigue, (e) changes in appetite or weight, (f) feelings of guilt or worthlessness, (g) difficulty concentrating, (h) feelings of slowness or worry, and (i) suicidal ideation. Items are answered on a 5‐point Likert scale: 0 (never), 1 (several days), 2 (more than half the days), and 3 (most days). In the present investigation, the Spanish and computerized version of the PHQ‐9 was applied. This scale was applied only in sample A, for which a Cronbach's α coefficient of 0.86 was obtained for the observed scores.

4.3. Statistical analyses

4.3.1. Dimensionality and latent structure assessment

Dimensionality and latent structure assessment was performed with EGA (Golino & Epskamp, 2017; Golino et al., 2020a). As recommended by Golino et al. (2020a) and Golino et al. (2020b), EGA was estimated using both the GLASSO and the TMFG methods, with the total entropy fit index with Von Neumann entropy (TEFI.vn) used to select the optimal solution in case they differed (Golino et al., 2020b). The stability of the dimensionality and latent structure estimates across bootstrap samples and potential redundancies between item pairs were also evaluated using EGA.

4.3.2. Factor modeling specifications

The PANAS item scores were modeled using ESEM, CFA, and SEM. As the factor indicators were categorical, the weighted least squares with mean‐ and variance‐adjusted standard errors (WLSMV) estimator was employed, which is widely recommended for models composed of ordinal–categorical variables (Rhemtulla et al., 2012). In the case of the ESEM models, the factors were rotated using Geomin and Oblimin rotations (Browne, 2001; Izquierdo Alfaro et al., 2014; Sass & Schmitt, 2010). To interpret the factor solutions, loadings of 0.40, 0.55, and 0.70 were considered as low, medium, and high, respectively (Garrido et al., 2011, 2013). Regarding the size of the factor correlations, values of 0.10, 0.30, and 0.50 were considered as small, medium, and large, respectively (Cohen, 1992).

To determine the plausibility of simple structure for the PANAS’ scores, we used the following guidelines: If the model parameters of the ESEM and corresponding CFA (with cross‐loadings fixed to zero) were roughly equivalent, and the fit of the CFA was similar or better to that of the ESEM, simple structure would be supported and the CFA would be selected as the optimal model. In contrast, if the model parameters of the ESEM and CFA were different, and the fit of the ESEM was better to that of the CFA, the factor structure would be deemed complex and the ESEM would be chosen as the optimal model. In the latter case, the ESEM would typically show significant nontrivial cross‐loadings, as well as different primary loadings and lower factor correlations than those of the CFA, which would generally overestimate the factor correlations due to omitted cross‐loadings (Asparouhov & Muthén, 2009; Garrido et al., 2018; Marsh et al., 2014).

4.3.3. Fit criteria

The fit of the factor models was assessed with three complimentary indices: the comparative fit index (CFI), the root mean square error of approximation (RMSEA), and the standardized root mean square residual (SRMR). The Tucker–Lewis index (TLI) was not reported because its values are generally redundant (correlate near perfectly) in comparison to the CFI index (Garrido et al., 2016). Values of CFI greater than or equal to 0.90 and 0.95 have been suggested to reflect acceptable and excellent fits to the data, whereas values of RMSEA less than 0.08 and 0.05 may indicate reasonable and close fits to the data, respectively (Hu & Bentler, 1999; Marsh et al., 2004; Schreiber et al., 2006). In the case of SRMR, a value less or equal to 0.08 has been found to indicate a good fit to the data (Hu & Bentler, 1999; Schreiber, 2017). For the RMSEA index, a 90% CI was also estimated and reported. It should be noted that as the values of these fit indices are also affected by incidental parameters not related to the size of the misfit (Beierl et al., 2018; Garrido et al., 2016; Shi et al., 2018), they should not be considered golden rules and must be interpreted with caution (Greiff & Heene, 2017; Marsh et al., 2004). Local misfit related to correlated residuals was evaluated with the standardized expected parameter change (SEPC) statistic in conjunction with the significance test of its associated modification index (Saris et al., 2009; Whittaker, 2012). SEPCs above 0.20 in absolute have been suggested as potentially large enough to consider freeing the parameter (Whittaker, 2012).

4.3.4. Missing data handling

There were zero missing values in the responses to the PANAS’ items, removing the need to consider missing data handling methods.

4.3.5. Analysis software

Data handling and descriptive statistics were computed with the IBM SPSS software version 25. Dimensionality estimates were computed with the EGA function of the EGAnet R package version 0.9.7 (Golino & Christensen, 2020). The stability of the dimensionality estimates was evaluated across 1000 bootstrap samples with the bootEGA function contained in the EGAnet R package version 0.9.7 (Golino & Christensen, 2020). Potential redundancies between item pairs were evaluated using the UVA function of the EGAnet R package version 0.9.7 (Golino & Christensen, 2020). The R codes for the analyses with the EGAnet package are included in the Supporting Information. Factor modeling with ESEM and CFA was performed with the Mplus program version 8.3. Internal consistency reliability with the categorical omega and alpha coefficients was estimated with the ci.reliability function contained in the R package MBESS version 4.6.0 (Kelley, 2019).

5. RESULTS AND DISCUSSION

5.1. Derivation of the PANAS factor structure

The first step in the analyses of the PANAS’ scores was performed on the derivation sample using the UVA function contained in the EGAnet package. These analyses aimed to explore potential redundancies between item pairs based on the similarity between their connections and weights with other nodes (variables). On the basis of the weighted topological overlaps (wTO) statistic, five item pairs were identified to have significant redundancies; their network redundancy plot is depicted in Figure 1. In decreasing order of magnitude, these were as follows: afraid–scared (wTO = 0.32), upset–distressed (wTO = 0.26), enthusiastic–inspired (wTO = 0.25), nervous–jittery (wTO = 0.23), and determined–attentive (wTO = 0.19). Four of these five item pairs (all except determined–attentive, which had the lowest wTO) correspond to Zevon and Tellegen's (1982) mood content categories and are in congruence with previous factor analytic studies of the PANAS (Buz et al., 2015; Crawford & Henry, 2004; Tuccitto et al., 2010).

Figure 1.

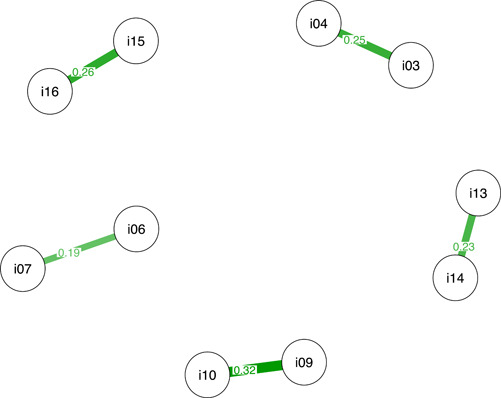
EGA item redundancy analyses for the derivation sample (N = 2455). Note: i03 = enthusiastic; i04 = inspired; i06 = determined; i07 = attentive; i09 = afraid; i10 = scared; i13 = nervous; i14 = jittery; i15 = upset; i16 = distressed. The values shown on the edges are the weighted topological overlaps (WTOs). Higher WTO values indicate greater redundancy or overlap. Only significant overlaps are shown in the plot. EGA, Exploratory Graph Analysis [Color figure can be viewed at wileyonlinelibrary.com]

The second step in the analyses involved using the EGA function of the EGAnet package to estimate the PANAS’ dimensionality and item clusterings using the GLASSO and TMFG methods. These results are presented in the top panel of Figure 2 (zero redundancies). As can be seen in the figure, the GLASSO and TMFG methods produced identical three‐dimension solutions. As the solutions were identical both in the number of dimensions and items assigned to each dimension, there was no need to use TEFI.vn index to determine which was optimal. According to the network plots, one of the dimensions was composed of the Positive Affect items, another contained the items afraid, scared, ashamed, nervous, and jittery, and the last dimension was composed of the items guilty, upset, distressed, hostile, and irritable. With the exception of the guilty item, this solution corresponds to Mehrabian's (1997) oblique three‐factor model of Positive Affect, Afraid, and Upset.

Figure 2.

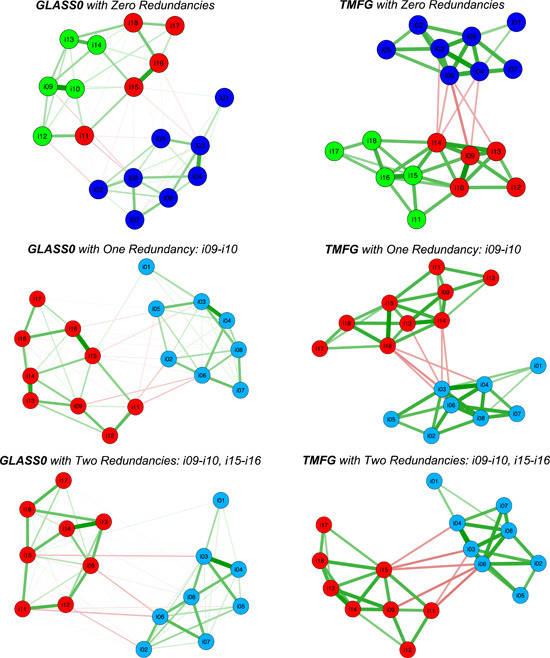
EGA network plots for the derivation sample (N = 2455). Note: i01 = interested; i02 = strong; i03 = enthusiastic; i04 = inspired; i05 = proud; i06 = determined; i07 = attentive; i08 = active; i09 = afraid; i10 = scared; i11 = guilty; i12 = ashamed; i13 = nervous; i14 = jittery; i15 = upset; i16 = distressed; i17 = hostile; i18 = irritable. Redundant item pairs were summed. EGA, Exploratory Graph Analysis [Color figure can be viewed at wileyonlinelibrary.com]

The third step in the analyses of the PANAS with derivation sample involved using the bootEGA function of the EGAnet package to assess the stability of the dimensionality estimate and item assignments. According to these results, the stability of the dimensionality estimate was very poor for both the GLASSO and TMFG methods (Table 1, zero redundancies). In the case of GLASSO, it suggested three dimensions for 60.5% of the bootstrap samples and two dimensions for 38.7%. In the case of TMFG, the two‐dimensional solution was suggested for 54.3% of the bootstrap samples and three‐dimensional solution for the remaining 45.7%. Regarding the stability of the item assignments to the dimensions from the single solution using the complete derivation sample (Table 2, zero redundancies), they were excellent for the Positive Affect items (100%), mostly good to excellent for the Afraid factor (97%–100% for GLASSO and 72%–100% for TMFG), and poor for the Upset dimension (61% for GLASSO and 45%–46% for TMFG). Therefore, these results indicated that the Upset dimension was extremely unstable across the bootstrap samples.

Table 1.

Stability of the EGA dimensionality estimates across bootstrap samples

Sample
Redundant item pairs	Dimensions
Estimator	2	3	4
Sample A: Derivation (N = 2455)
No redundancies
GLASSO	0.387	0.605	0.008
TMFG	0.543	0.457	0.000
One redundancy (i09–i10)
GLASSO	0.995	0.005	0.000
TMFG	0.977	0.023	0.000
Two redundancies (i09–i10, i15–i16)
GLASSO	1.000	0.000	0.000
TMFG	1.000	0.000	0.000
Sample A: Cross‐validation (N = 2454)
Two redundancies (i09–i10, i15–i16)
GLASSO	1.000	0.000	0.000
TMFG	0.998	0.002	0.000
Sample B: Confirmation (N = 2166)
Two redundancies (i09–i10, i15–i16)
GLASSO	1.000	0.000	0.000
TMFG	1.000	0.000	0.000

Note: i09 = afraid; i10 = scared; i15 = upset; i16 = distressed. Values above 0.95 are bolded. Redundant item pairs were summed. Values in the table indicate the proportion of times each dimensionality estimate was obtained.

Abbreviations: EGA, Exploratory Graph Analysis; GLASSO, graphical least absolute shrinkage and selection operator; TMFG, triangulated maximally filtered graph.

Table 2.

Stability of the EGA item‐dimension assignments for the derivation sample (N = 2455)

	Zero redundancies						One redundancy				Two redundancies
	GLASSO			TMFG			GLASSO		TMFG		GLASSO		TMFG
Item/composite	F1	F2	F3	F1	F2	F3	F1	F2	F1	F2	F1	F2	F1	F2
i01. Interested	1.00			1.00			1.00		1.00		1.00		1.00
i02. Strong	1.00			1.00			1.00		1.00		1.00		1.00
i03. Enthusiastic	1.00			1.00			1.00		1.00		1.00		1.00
i04. Inspired	1.00			1.00			1.00		1.00		1.00		1.00
i05. Proud	1.00			1.00			1.00		1.00		1.00		1.00
i06. Determined	1.00			1.00			1.00		1.00		1.00		1.00
i07. Attentive	1.00			1.00			1.00		1.00		1.00		1.00
i08. Active	1.00			1.00			1.00		1.00		1.00		1.00
i09. Afraid		1.00			1.00		–	–	–	–	–	–	–	–
i10. Scared		1.00			1.00		–	–	–	–	–	–	–	–
i11. Guilty			0.42			0.17		1.00		0.98		1.00		1.00
i12. Ashamed		0.97			1.00			1.00		0.99		1.00		1.00
i13. Nervous		0.97			0.86			1.00		1.00		1.00		1.00
i14. Jittery		0.97			0.72			1.00		1.00		1.00		1.00
i15. Upset			0.61			0.45		1.00		0.98	–	–	–	–
i16. Distressed			0.61			0.46		1.00		0.99	–	–	–	–
i17. Hostile			0.61			0.45		1.00		0.99		1.00		1.00
i18. Irritable			0.61			0.45		1.00		0.99		1.00		1.00
i09 + i10	–	–	–	–	–	–		1.00		0.99		1.00		1.00
i15 + i16	–	–	–	–	–	–	–	–	–	–		1.00		1.00

Note: F1–F3 = factors; First redundancy: i09–i10. Second redundancy: i15–i16. Redundant item pairs were summed. Values in the table indicate the proportion of times an item was assigned to its dimension from the single estimate using the complete sample.

Abbreviations: EGA, Exploratory Graph Analysis; GLASSO, graphical least absolute shrinkage and selection operator; TMFG, triangulated maximally filtered graph.

The fourth step in the analyses of the PANAS’ scores with the derivation sample aimed to evaluate if the EGA estimates would change if the item redundancies were taken into account. To carry out this objective, steps two and three were repeated using the information obtained in the first step. Specifically, the item pairs with the largest redundancies were summed in succession to create composite scores that replaced the original items in the data set. These results are shown in the one and two redundancies sections of Figure 2 (network plots), Table 1 (stability of the dimensionality estimates), and Table 2 (stability of the item assignments). When the afraid–scared item pair was summed to create a composite, both the GLASSO and TMFG methods suggested a structure composed of two factors corresponding to Positive and Negative Affect (Figure 2, one redundancy). In addition, the stability of the dimensionality estimates was excellent, with GLASSO suggesting two factors for 99.5% of the bootstrap samples and TMFG for 97.7% (Table 1, one redundancy). Similarly, the stability of the item assignments was also excellent, 100% for GLASSO for all items, and between 98% and 100% for TMFG. When a second item pair, upset–distressed, was summed to create an additional composite, both GLASSO and TMFG again suggested two dimensions (Figure 2, two redundancies), with perfect stability of 100% for both the dimensionality estimates (Table 1, two redundancies) and item assignments (Table 2, two redundancies). Due to the stability of these results, no further item redundancies were considered.

In all, these EGA analyses conducted in steps one to four suggested that the three‐factor solutions indicated by EGA initially, though in line with Mehrabian's (1997) model, were an artifact produced by redundant item pairs. Once a single redundancy was considered, both EGA methods suggested unequivocally the two‐dimensional model of Positive and Negative Affect. Given the accuracy of EGA with large samples such as this one (>2000 observation; Golino & Epskamp, 2017), if a third dimension truly underlid the data in the population, it is highly likely that it would have been detected by the method, at least in some of the bootstrap samples. The absence of this third factor in the results, when at least one redundancy was considered, is a strong indication that such a factor does not exist for this data.

The fifth step in the analyses with the derivation sample involved the estimation of ESEM models that specified one to four factors and that had an increasing number of correlated errors estimated, which were identified using the SEPC statistic. Table 3 shows the fit of these ESEM models from the derivation sample, as well as the correlated errors that were identified for each model and their estimates in the subsequent models. The different models were named using the modeling approach (ESEM), the number of factors (#F), and the number of correlated errors that were freely estimated (#θ). So, for example, model ESEM.3F.2θ was an ESEM model that estimated three factors and two correlated errors. The correlated errors that were estimated for this model can be identified by looking at the highest SEPCs that were obtained from the previous models. In the case of ESEM.3F.2θ, the previous models were ESEM.3F.0θ, which suggested the error correlation between items afraid–scared (i09–i10), and ESEM.3F.1θ, which suggested the error correlation between items upset–distressed (i15–i16).

Table 3.

Fit statistics for the ESEM‐ and CFA‐estimated models

Sample/model	χ 2	df	CFI	SRMR	RMSEA (90% CI)	θ1	θ2	θ3	θ4	SEPC
Sample A: Derivation (N = 2455)
1 Factor
ESEM.1F.0θ	9322.49	135	0.679	0.110	0.166 (0.164–0.169)					θ09,10 = 0.71
ESEM.1F.1θ	8575.87	134	0.705	0.107	0.160 (0.157–0.163)	0.55				θ03,04 = 0.57
ESEM.1F.2θ	8107.28	133	0.721	0.104	0.156 (0.153–0.159)	0.54	0.48			θ15,16 = 0.51
ESEM.1F.3θ	7738.56	132	0.734	0.102	0.153 (0.150–0.156)	0.54	0.47	0.43		θ08,14 = 0.51
ESEM.1F.4θ	7556.10	131	0.741	0.101	0.152 (0.149–0.155)	0.54	0.47	0.44	0.55	θ08,13 = 0.53
2 Factors
ESEM.2F.0θ	2756.43	118	0.908	0.041	0.095 (0.092–0.099)					θ09,10 = 0.71
ESEM.2F.1θ	2138.04	117	0.929	0.038	0.084 (0.081–0.087)	0.47				θ15,16 = 0.43
ESEM.2F.2θ	1819.27	116	0.941	0.035	0.077 (0.074–0.080)	0.46	0.36			θ03,04 = 0.31
ESEM.2F.3θ	1726.30	115	0.944	0.035	0.076 (0.072–0.079)	0.46	0.36	0.26		θ16,18 = 0.28
ESEM.2F.4θ	1559.29	114	0.950	0.033	0.072 (0.069–0.075)	0.45	0.39	0.26	0.26	θ17,18 = 0.26
3 Factors
ESEM.3F.0θ	1415.30	102	0.954	0.029	0.072 (0.069–0.076)					θ09,10 = 0.82
ESEM.3F.1θ	1288.48	101	0.959	0.028	0.069 (0.066–0.073)	0.40				θ15,16 = 0.60
ESEM.3F.2θ	1163.02	100	0.963	0.027	0.066 (0.062–0.069)	0.39	0.37			θ03,04 = 0.29
ESEM.3F.3θ	1100.35	99	0.965	0.026	0.064 (0.061–0.068)	0.38	0.37	0.24		θ13,14 = 0.27
ESEM.3F.4θ	1011.00	98	0.968	0.025	0.062 (0.058–0.065)	0.34	0.36	0.23	0.23	θ13,18 = 0.30
4 Factors
ESEM.4F.0θ	1011.58	87	0.968	0.024	0.066 (0.062–0.069)					θ09,10 = 0.96
ESEM.4F.1θ	853.40	86	0.973	0.022	0.060 (0.057–0.064)	0.43				θ15,16 = 0.63
ESEM.4F.2θ	709.81	85	0.978	0.021	0.055 (0.051–0.058)	0.43	0.37			θ13,18 = 0.30
ESEM.4F.3θ	645.13	84	0.980	0.020	0.052 (0.048–0.056)	0.43	0.35	0.30		θ13,14 = 0.28
ESEM.4F.4θ	628.29	83	0.981	0.019	0.052 (0.048–0.056)	0.40	0.33	0.29	0.22	θ03,12 = 0.29
Sample A: Cross‐validation (N = 2454)
ESEM.2F.2θ	1697.04	116	0.945	0.034	0.075 (0.071–0.078)	0.41	.33
CFA.2F.0θ	2152.28	134	0.930	0.048	0.078 (0.075–0.081)
CFA.2F.0θ. orth	5,372.23	135	0.819	0.117	0.126 (0.123–0.129)
CFA.2F.2θ	1709.15	132	0.945	0.044	0.070 (0.067–0.073)	0.42	0.31
CFA.2F.2θ. orth	5106.99	133	0.828	0.116	0.123 (0.121–0.126)	0.41	0.34
CFA.3F.0θ	1820.73	132	0.942	0.044	0.072 (0.069–0.075)
CFA.3F.2θ	1606.68	130	0.949	0.042	0.068 (0.065–0.071)	0.39	0.17
Sample B: Confirmation (N = 2166)
CFA.2F.2θ	1362.80	132	0.966	0.044	0.066 (0.062–0.069)	0.45	0.35

Note: ESEM = exploratory structural equation modeling; CFA = confirmatory factor analysis; #F = number of factors; #θ = number of error correlations; orth = orthogonal; χ2 = chi‐square; df = degrees of freedom; CFI = comparative fit index; SRMR = standardized root mean square residual; RMSEA = root mean square error of approximation; SEPC = highest absolute standardized expected parameter change; i03 = enthusiastic; i04 = inspired; i08 = active; i09 = afraid; i10 = scared; i12 = ashamed; i13 = nervous; i14 = jittery; i15 = upset; i16 = distressed; i17 = hostile; i18 = irritable. For the derivation sample, the error correlations were specified according to the SEPCs of the previous models with the same number of factors. For the cross‐validation and confirmation samples, the two error correlations specified were the two highest identified for the multidimensional models of the derivation sample: i09–i10 (θ1) and i15–i16 (θ2). Model CFA.3 F.2θ corresponds to Mehrabian's (1997) three factors of Positive Affect, Upset, and Afraid. p < 0.001 for all chi‐square tests of model fit and SEPCs.

The results in Table 3 for the derivation sample indicated that a single factor was not able to account for the PANAS item scores, as all the ESEM.1 F models produced a very poor fit to the data (CFI < 0.75, SRMR > 0.10, RMSEA > 0.15). However, all models that specified three‐ and four‐factor solutions had adequate levels of fit (CFI > 0.95, SRMR < 0.03, RMSEA < 0.08). In the case of the two‐factor models, they benefited the most in terms of fit from the estimation of error correlations, in particular for the first two included. Although the ESEM.2F.0θ model had a marginally adequate level of fit (CFI = 0.908, SRMR = 0.041, RMSEA = 0.095), the fit improved notably with the inclusion of one correlated error (CFI = 0.929, SRMR = 0.038, RMSEA = 0.084) and with the inclusion of a second correlated error (CFI = 0.941, SRMR = 0.035, RMSEA = 0.077). The inclusion of additional correlated errors for the two‐factor models produced less substantial gains in fit, similar to those obtained for the three‐ and four‐factor ESEM models. In terms of the item pairs that were identified with the highest correlated residuals, these varied depending on the number of factors estimated. However, for the two‐ to four‐factor models, the two highest were always afraid–scared (i09–i10) and upset–distressed (i15–i16), which is congruent with the two highest identified through the EGA redundancy analyses.

The factor loadings and factor correlations for the two‐ to four‐factor ESEM models for the derivation sample are shown in Tables S4–S9 using both Geomin and Oblimin rotations. In addition, Table S2 shows the congruence of sequential ESEM solutions, so as to assess if adding error correlations changed the loading structure meaningfully. Also, Table S3 shows the congruence between the two rotations for the same ESEM model, to evaluate if changing the factor rotation algorithm had a notable impact in the estimated factor structure. The most notable results from these tables are presented next.

First, there was no support for a four‐factor solution (Tables S8 and S9), as the fourth factor for all models was made up of only a few variables (in the case Oblimin never more than two) that also loaded saliently (and oftentimes higher) on other factors.

Second, the level of congruence between Geomin and Oblimin for the three‐factor solutions was mostly unsatisfactory (Table S3), except for the ESEM.4F.4θ model. The Oblimin three‐factor solutions generally resembled Mehrabian's model (in particular for model ESEM.3F.1θ) and were not greatly impacted by the estimation of the error correlations (Table S2); the coefficient of congruence was above 0.95 for all cases except for the third factor of the ESEM.3F.1θ and ESEM.3F.2θ solutions, where it was 0.944. In the case of Geomin, the three‐factor solutions changed substantially when error correlations were added to the models, up to the last model estimated, which most closely resembled Mehrabian's model. It is worth noting that when no error correlations were estimated, upset and distressed loaded very highly on the third factor of both rotations, but their loadings were dramatically reduced once their error correlation was estimated (models ESEM.3F.2θ to ESEM.3F.4θ).

Third, as shown in Table 2, the two‐factor solutions remained very stable as error correlations were incorporated into the models (the coefficient of congruence was always above 0.99). Similarly, the congruence between the Geomin and Oblimin solutions was very high (>0.99) for all the models (Table S3). All estimated two‐factor solutions reproduced perfectly the theoretical PANAS structure of Positive and Negative Affect, with medium factor correlations that ranged between −0.36 and −0.41 (Tables S4 and S5).

Taken together, the results from the ESEM analyses for the derivation sample support the findings from the EGA analyses. The one‐factor solutions were discarded due to very poor fit and the four‐factor solutions due to insufficient primary loadings on the fourth factor. In the case of the three‐factor solutions, these were shown to be mostly unstable across rotation algorithms and error correlations estimated. Coupled with the clear indications from EGA that the PANAS’ scores contained only two dimensions, it appears that these variable three‐factor solutions were mostly due to factor splitting as a result of the estimation of too many factors (Auerswald & Moshagen, 2019; Wood et al., 1996). In contrast, the two‐factor ESEM models were very stable across rotation algorithms and error correlations estimated, perfectly reproducing the theoretical Positive and Negative Affect factor structure. Given how the item redundancies affected the dimensionality estimates with EGA, as well as the fit of the ESEM models, we chose the ESEM.2F.2θ as the optimal model, with error correlations between the item's pairs of afraid–scared (θ = 0.46) and upset–distressed (θ = 0.36). These error correlations were both above the threshold of 0.20 suggested by Whittaker (2012).

5.2. Cross‐validation of the PANAS factor structure

To cross‐validate, the EGA estimates obtained with the derivation sample, the EGA dimensionality and stability analyses were conducted for the data set that included the two composites of afraid–scared and upset–distressed, which is consistent with the optimal ESEM.2F.2θ model previously identified. On the basis of this data set with these two composites, EGA with both GLASSO and TMFG again provided an estimate of two dimensions that perfectly reproduced the Positive and Negative Affect factors (Figure 3, top panel). In terms of the stability of the estimates, GLASSO and TMFG estimated two dimensions for approximately 100% of the bootstrap samples (Table 1), and the items were assigned to the same dimensions in approximately 100% of the bootstrap samples as well (Table S1). In all, these results indicate that the structure obtained with EGA for the derivation sample perfectly cross‐validated for the other half of the sample.

Figure 3.

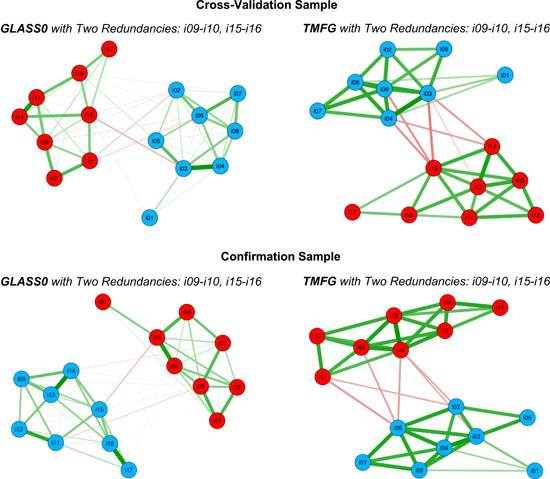
EGA network plots for the cross‐validation (N = 2454) and confirmation (N = 2166) samples. Note. i01 = interested; i02 = strong; i03 = enthusiastic; i04 = inspired; i05 = proud; i06 = determined; i07 = attentive; i08 = active; i09 = afraid; i10 = scared; i11 = guilty; i12 = ashamed; i13 = nervous; i14 = jittery; i15 = upset; i16 = distressed; i17 = hostile; i18 = irritable. Redundant item pairs were summed. EGA, Exploratory Graph Analysis

Next, the optimal ESEM.2F.2θ model was estimated for the cross‐validation sample, and it obtained a good fit (CFI = 0.945, SRMR = 0.034, RMSEA = 0.075) that was similar to the one for the derivation sample (Table 3). Also, the factor solution (Table 4) was remarkably similar to that of the derivation sample, with a coefficient of congruence of 0.998 for both Positive Affect and Negative Affect (Geomin rotation). The average primary loadings of the ESEM.2F.2θ model for the cross‐validation sample were high, with a mean of 0.65 (0.37–0.78) for Positive Affect and a mean of 0.63 (0.47–0.78) for Negative Affect. The cross‐loadings, for their part, were small and ranged from −0.13 to 0.14. Regarding the factor correlation, it was −0.40, very similar to the −0.36 obtained for the derivation sample. Moreover, the error correlations were 0.41 for afraid–scared and 0.33 for upset–distressed, approximately equal to those obtained for the derivation sample (Table 3).

Table 4.

Two‐ and three‐factor solutions for the cross‐validation and confirmation samples

	Sample A: Cross‐validation (N = 2454)										Sample B: Confirmation (N = 2166)
	ESEM.2 F.2θ			CFA.2 F.2θ			CFA.3 F.2θ				CFA.2 F.2θ
Item/factor	F1	F2	h 2	F1	F2	h 2	F1	F2	F3	h 2	F1	F2	h 2
i01. Interested	0.37	0.14	0.11	0.26	0.00	0.07	0.26	0.00	0.00	0.07	0.33	0.00	0.11
i02. Strong	0.59	−0.13	0.43	0.68	0.00	0.47	0.68	0.00	0.00	0.46	0.72	0.00	0.51
i03. Enthusiastic	0.78	0.01	0.60	0.76	0.00	0.58	0.76	0.00	0.00	0.58	0.79	0.00	0.62
i04. Inspired	0.77	0.03	0.58	0.75	0.00	0.56	0.75	0.00	0.00	0.56	0.78	0.00	0.61
i05. Proud	0.61	0.06	0.35	0.56	0.00	0.32	0.56	0.00	0.00	0.32	0.64	0.00	0.41
i06. Determined	0.71	−0.09	0.57	0.77	0.00	0.59	0.77	0.00	0.00	0.59	0.81	0.00	0.66
i07. Attentive	0.63	−0.03	0.41	0.64	0.00	0.41	0.64	0.00	0.00	0.41	0.69	0.00	0.48
i08. Active	0.73	−0.01	0.54	0.74	0.00	0.54	0.74	0.00	0.00	0.54	0.75	0.00	0.56
i09. Afraid	0.02	0.71	0.50	0.00	0.69	0.48	0.00	0.71	0.00	0.51	0.00	0.75	0.57
i10. Scared	−0.02	0.67	0.46	0.00	0.68	0.46	0.00	0.70	0.00	0.48	0.00	0.74	0.55
i11. Guilty	−0.11	0.60	0.42	0.00	0.67	0.44	0.00	0.68	0.00	0.46	0.00	0.70	0.49
i12. Ashamed	−0.02	0.61	0.38	0.00	0.62	0.38	0.00	0.63	0.00	0.39	0.00	0.69	0.47
i13. Nervous	0.11	0.78	0.55	0.00	0.70	0.50	0.00	0.72	0.00	0.51	0.00	0.78	0.61
i14. Jittery	0.02	0.73	0.52	0.00	0.71	0.50	0.00	0.72	0.00	0.52	0.00	0.81	0.66
i15. Upset	−0.10	0.60	0.42	0.00	0.66	0.44	0.00	0.00	0.74	0.54	0.00	0.72	0.51
i16. Distressed	−0.10	0.56	0.36	0.00	0.63	0.39	0.00	0.00	0.69	0.48	0.00	0.74	0.54
i17. Hostile	0.09	0.47	0.19	0.00	0.41	0.17	0.00	0.00	0.43	0.19	0.00	0.62	0.39
i18. Irritable	−0.01	0.58	0.34	0.00	0.58	0.34	0.00	0.00	0.62	0.38	0.00	0.72	0.52
F1	1.00			1.00			1.00				1.00
F2	−0.40	1.00		−0.45	1.00		−0.42	1.00			−0.27	1.00
F3							−0.44	0.84	1.00

Note: ESEM = exploratory structural equation modeling; CFA = confirmatory factor analysis; #F = number of factors; #θ = number of error correlations; i01–i18 = items; F1–F3 = factors; h2 = communality. The error correlations between items i09–10 and i15–i16 were estimated for all models The geomin rotation is shown for the ESEM solution. Factor loadings ≥ 0.30 in absolute value are in bold. Cross‐loadings fixed to zero appear in italics. Model CFA.3F.2θ corresponds to Mehrabian's (1997) three factors of positive affect, upset, and afraid, with the addition of the two error correlations. p < 0.05 for all factor loadings, factor correlations, and communalities, except those underlined.

To determine if a simple structure could account for the PANAS’ item scores in the cross‐validation sample, the CFA.2F.2θ model with all cross‐loadings fixed to zero was estimated and compared with the ESEM.2F.2θ model. In terms of fit, the CFA.2F.2θ model attained a good fit (CFI = 0.945, SRMR = 0.044, RMSEA = 0.070), which was similar to that of the ESEM.2F.2θ model (Table 3). The loadings of the CFA.2F.2θ model were also remarkably similar to those from the ESEM.2F.2θ (Table 4), with a coefficient of congruence of 0.989 for Positive Affect and 0.991 for Negative Affect. Likewise, the factor correlation for the CFA.2F.2θ model was −0.45, just slightly stronger than that for the ESEM.2F.2θ model, which was −0.40. Finally, the error correlations for the CFA.2F.2θ model were 0.42 for afraid–scared and 0.31 for upset–distressed, almost identical to those obtained for the ESEM.2F.2θ model (Table 3). Taken together, these results indicate that a simple structure two‐factor model (with two error correlations) was appropriate to model the PANAS’ item scores.

The final analyses with the cross‐validation sample involved the estimation of alternative PANAS factor models from the literature. First, two orthogonal CFA models were estimated: one with two factors and no correlated errors (CFA.2F.0θ.orth) and one with two factors and the two correlated errors identified previously (CFA.2F.2θ.orth). Both of these models produced a very poor fit to the data (Table 3; CFI < 0.83, SRMR >0.11, RMSEA >0.12). In addition, a two‐factor oblique CFA model with no correlated errors was also estimated (CFA.2F.0θ), which produced a moderately poorer fit (CFI =0.930, SRMR = 0.048, RMSEA = 0.078) than that of the same model but with the two error correlations (CFA.2F.2θ). Aside from the two‐factor Positive and Negative Affect models, two three‐factor models were estimated according to Mehrabian's (1997) model: one without correlated errors (CFA.3F.0θ) and the other with the two error correlations (CFA.3F.2θ). Both three‐factor models produce a good fit to the data (Table 3), with the former (CFI = 0.942, SRMR = 0.044, RMSEA = 0.072) obtaining somewhat poorer fit in comparison to the latter (CFI = 0.949, SRMR = 0.042, RMSEA = 0.068).

The models that specified orthogonal factors were discarded due to poor fit, whereas the models without error correlations were considered less optimal due to poorer fit in comparison to those with the two error correlations. The factor solutions of these discarded models can be found in Table S10. The factor solutions for the remaining competing models, the two‐factor and three‐factor models, with two error correlations (CFA.2F.2θ and CFA.3F.2θ) are shown in Table 5. Whereas both produced an adequate loading pattern, the Afraid (F2) and Upset (F3) factors of Mehrabian's (1997) three‐factor model had an extremely high factor correlation of 0.84, which questions their discriminant validity and further supports the notion that these, in fact, constitute a single Negative Affect factor. Other authors have found extremely high correlations between the Afraid and Upset factors, like Heubeck and Wilkinson (2019), who obtained factor correlations between 0.79 and 0.85. Moreover, Afraid had almost the same correlation with Positive Affect (−0.42) as did Upset (−0.44), adding further support to the previous argument. In all, the various cross‐validation analyses that were conducted indicate that the results from the derivation sample replicated well, and that a two‐factor simple structure model of Positive and Negative Affect with two error correlations (afraid–scared and upset–distressed) optimally accounted for PANAS's item scores.

Table 5.

Factorial invariance analyses across sex, age, and treatment status

Sample
Variable	Overall model fit					Change in model fit
Invariance model	χ 2	df	CFI	SRMR	RMSEA	Δχ 2	Δdf	ΔCFI	ΔSRMR	ΔRMSEA
Sample A (N = 4909)
Sex
MI1. Configural	3778.9	264	0.939	0.048	0.074
MI2. Metric (FL)	3681.6	280	0.941	0.048	0.070	54.1	16	0.002	0.000	−0.004
MI3. Scalar (FL,Th)	3688.9	332	0.941	0.048	0.064	234.8	68	0.002	0.000	−0.010
Age
MI1. Configural	4095.0	528	0.937	0.050	0.074
MI2. Metric (FL)	4017.6	576	0.939	0.050	0.070	132.1	48	0.002	0.000	−0.004
MI3. Scalar (FL,Th)	4465.7	732	0.934	0.051	0.064	762.7	204	−0.003	0.001	−0.010
Treatment status
MI1. Configural	3494.9	264	0.941	0.047	0.071
MI2. Metric (FL)	3373.9	280	0.943	0.047	0.067	29.7	16	0.002	0.000	−0.004
MI3. Scalar (FL,Th)	3329.8	332	0.945	0.047	0.061	169.9	68	0.004	0.000	−0.010
Sample B (N = 2166)
Sex
MI1. Configural	1516.5	264	0.965	0.047	0.066
MI2. Metric (FL)	1536.3	280	0.965	0.047	0.064	29.4	16	0.000	0.000	−0.002
MI3. Scalar (FL,Th)	1614.1	332	0.965	0.047	0.060	150.5	68	0.000	0.000	−0.006
Age
MI1. Configural	1848.6	528	0.961	0.053	0.068
MI2. Metric (FL)	1899.8	576	0.961	0.053	0.065	78.1	48	0.000	0.000	−0.003
MI3. Scalar (FL,Th)	2215.7	732	0.956	0.054	0.061	473.1	204	−0.005	0.001	−0.007
Treatment status
MI1. Configural	1435.4	264	0.966	0.045	0.064
MI2. Metric (FL)	1422.2	280	0.967	0.045	0.061	12.9	16	0.001	0.000	−0.003
MI3. Scalar (FL,Th)	1430.0	332	0.968	0.046	0.055	78.9	68	0.002	0.001	−0.009

Note: Sample A group sizes: (a) sex: female = 3358, male = 1551; (b) age: 10–19 years = 757, 20–29 years = 2810, 30–39 years = 704, 40 or more years = 638. Sample B group sizes: (a) sex: female = 1561, male = 605; (b) age: 10–19 years = 426, 20–29 years = 1086, 30–39 years = 210, 40 or more years = 442; (c) treatment status: not in treatment = 1853, in treatment = 313. χ² = chi‐square; df = degrees of freedom; CFI = comparative fit index; SRMR = standardized root mean square residual; RMSEA = root mean square error of approximation; MI = measurement invariance; FL = factor loadings; Th = thresholds. The parameters constrained to be equal across groups are shown in the parentheses next to the invariance models. The chi‐square difference tests between nested models were conducted using Mplus' DIFFTEST option. p < 0.001 for all chi‐square tests. Changes in model fit were computed against the configural model.

5.3. Criterion validity of the PANAS factors

The evaluation of the criterion validity of the PANAS factors involved the estimation of two SEM models: one that included the two‐factor model of the PANAS and another for Mehrabian's three‐factor representation of the PANAS that split the Negative Affect factor into Afraid and Upset. Both models posited as outcomes the factors for Generalized Anxiety Disorder and Major Depression. For the estimation of the SEM models, three residual correlations were freed: the two identified in the derivation and cross‐validation analyses of the PANAS (afraid–scared and upset–distressed) and a third one corresponding to the PANAS item irritable and the GAD‐7 item becoming easily annoyed or irritable, which shared similar content.

The SEM model with the original two‐factor representation of the PANAS (SEM.4F.3θ; Figure 4) produced a good fit to the data (χ ² = 11,924.93, df = 518, p < 0.001, CFI = 0.923, SRMR =0.047, RMSEA = 0.067 [90% CI = 0.066–0.068]). Likewise, the fit for the SEM model with Mehrabian's three‐factor PANAS representation (SEM.5F.3θ; Figure 4) was also good and approximately equal to the former model (χ ² = 11,720.57, df = 514, p < 0.001, CFI = 0.924, SRMR = 0.047, RMSEA = 0.067 [90% CI = 0.066–0.068]). The factors posited in both SEM models were well defined with generally high factor loadings (Table S11). Specifically, the mean factor loadings were 0.64 for Positive Affect (both models), 0.75 for Generalized Anxiety Disorder (both models), 0.71 for Major Depression (both models), 0.63 for Negative Affect (SEM.4F.3θ), and 0.68 and 0.64 for Afraid and Upset, respectively (SEM.5F.3θ). Regarding the three error correlations estimated for each model, they were all significant and mostly of substantial magnitude, ranging between 0.16 and 0.60 (Table S11).

Figure 4.

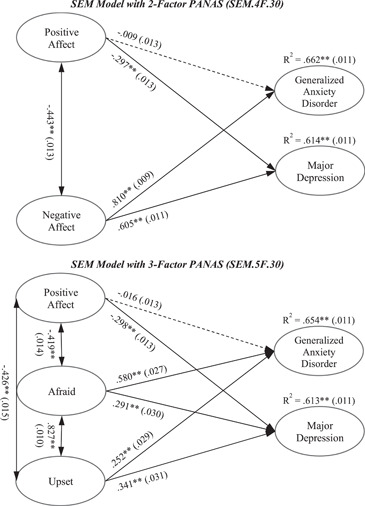
Structural equation models (SEMs) for the criterion validity analyses. Note: Ovals represent latent factors; unidirectional lines represent regression paths; bidirectional lines represent factor correlations; R ² = variance explained. Standard errors are shown in parenthesis. All values represent standardized coefficients. Lines for nonsignificant coefficients appear dashed. **p < 0.001

The standardized regression coefficients and factor correlations for the estimated SEM models are shown in Figure 4. Regarding the criterion validity of the PANAS factors, the main results were as follows: first, Positive Affect did not significantly explain the variance of Generalized Anxiety Disorder but did explain that of Major Depression with a medium‐sized coefficient (−0.297 for SEM.4F.3θ and −0.298 for SEM.5F.3θ, p < 0.001). Second, Negative Affect significantly explained the variance of both Generalized Anxiety Disorder and Major Depression, with large coefficients of 0.810 (p < 0.001) and 0.605 (p < 0.001), respectively. Third, both Afraid and Upset explained Generalized Anxiety Disorder, but Afraid (0.580, p < 0.001) had a larger standardized coefficient than Upset (0.252, p < 0.001). Fourth, both Afraid (0.291, p < 0.001) and Upset (0.341, p < 0.001) significantly explained Major Depression with similar medium‐sized regression coefficients. Fifth, and most important, the total variance explained of Generalized Anxiety Disorder (66.2% vs. 65.4%) and Major Depression (61.4% vs. 61.3%) was approximately equal for both SEM models.

Taken together, the results from the SEM models indicate that splitting Negative Affect into Afraid and Upset did not result in a better fitting model or in greater capacity to explain the criterion variables. In addition, estimates from the corresponding correlated factors CFA model (which has the same fit, degrees of freedom, and factor loadings as the SEM.5F.3θ model) revealed that the Afraid and Upset factors had approximately equal correlations with the remaining factors. In the case of Positive Affect, Afraid had a correlation of −0.419 (p < 0.001), whereas Upset had a correlation of −0.426 (p <0.001). Regarding Major Depression, the factor correlations were 0.698 (p < 0.001) and 0.708 (p < 0.001) for Afraid and Upset, respectively. Also, Afraid had a correlation of 0.796 (p < 0.001) with Generalized Anxiety Disorder, whereas Upset had a correlation of 0.739 (p < 0.001). Having approximately equal nomological networks further suggests that Afraid and Upset do not constitute distinct latent dimensions. However, the factor correlations for the CFA model corresponding to the two‐factor representation of the PANAS were as follows: Major Depression had correlations of −0.565 (p < 0.001), and 0.737 (p < 0.001) with Positive Affect and Negative Affect, respectively. Generalized Anxiety Disorder, for its part, had correlations of −0.367 (p < 0.001) and 0.814 (p < 0.001) with Positive Affect and Negative Affect, respectively. Finally, Generalized Anxiety Disorder and Major Depression had a correlation of 0.808 (p < 0.001).

6. STUDY 2

6.1. Confirmation and measurement invariance of the PANAS factor structure

The aim of Study 2 was to confirm the optimal PANAS factor structure from Study 1 (CFA.2F.2θ) using both EGA and CFA in a new sample, “sample B” or the “confirmation sample.” Sample B was composed of a large number of Argentinian children and adults with a wide age range that included some persons in therapy treatment for psychological or psychiatric disorders. Also, the measurement invariance of the PANAS factor structure across sex, age, and treatment status was assessed in Study 2 for both samples A and B. After measurement invariance was established, the latent means of the different groups were compared. Finally, the reliability of the sum scores for the PANAS scales of Positive and Negative Affect was evaluated for both samples. Given the excellent dimensional and structural stability of the two‐factor model suggested in Study 1 by the bootstrap EGA (when the item redundancies were taken into account), we hypothesized that this structure would be adequately confirmed (in terms of dimensionality, item assignments into the dimensions, and parameter estimates), with sample B.

7. METHODS

7.1. Participants and procedure

The sample for Study 2 was composed of 2166 Argentine children and adults with ages ranging from 13 to 78 years (M = 29.88, SD = 14.89). In terms of age groups, there were 426 participants in the 10–19 age group, 1086 in the 20–29 group, 210 in the 30–39 group, and 442 in age group of 40 years or more (2 participants did not provide their ages). Of the total sample, 1561 (72.1%) were females and the remaining 605 (27.9%) were males. In addition, 313 participants (14.5%) reported to be undergoing psychological and/or psychiatric treatment at the moment they responded to the survey. The procedure followed to collect the sample of this study was the same as the one described for Study 1, including data collection methodology, online platform employed, and dissemination strategy for the survey. The data were collected in January and February 2019.

7.2. Measures

7.2.1. Positive and Negative Affect Schedule (PANAS; watson et al., 1988)

A description of the 18‐item Spanish language version of the PANAS used for this study can be found in Study 1. The only difference is that for Study 1, the “state” form of the PANAS was employed, whereas for this study, the “trait” form was administered. The trait form probes into the intensity of the emotions in general (not only in the present moment).

7.3. Statistical analyses

The dimensionality and latent structure assessments, factor modeling specifications, fit criteria, and analysis software employed were the same as those described for Study 1. In addition, as in Study 1, there were no missing values in the PANAS’ item scores, so there was no need to consider missing data handling methods.

7.3.1. Measurement invariance analyses

Analyses of factorial invariance were performed across sex, age, and treatment status, according to three sequential levels of measurement invariance (Marsh et al., 2014): (a) configural invariance, (b) metric (weak) invariance, (c) and scalar (strong) invariance. Configural invariance implies that the same number of factors and item factor relationships hold across groups. Metric invariance indicates that, aside from configural invariance, the factor loadings are equal across groups. Scalar invariance implies that both the factor loadings and the thresholds are invariant across groups. It was considered that a particular invariance level was supported if the fit for the more restricted model, when compared with the configural model, did not decrease by more than 0.01 in CFI or increase by more than 0.015 in RMSEA (Chen, 2007). The delta parameterization was used for all measurement invariance models. When scalar invariance was supported, the latent means across groups were compared for the scalar model using the Wald test. The Wald statistic (W) follows an asymptotic chi‐square distribution. For the cases where there were more than two groups, an omnibus Wald test was first conducted where all latent means were specified to be equal. If the omnibus Wald test was significant, post hoc tests were subsequently conducted using the Bonferroni correction for multiple comparisons. Cohen's d statistic was used to measure the effect size of the latent mean differences between the groups. According to Cohen (1992), values of d of 0.20, 0.50, and 0.80 can be considered as indicative of small, medium, and large effects, respectively.

7.3.2. Reliability analyses

The internal consistency reliabilities of the observed scale scores were evaluated with Green and Yang's (2009) categorical omega coefficient. Categorical omega takes into account the ordinal nature of the data to estimate the reliability of the unit‐weighted scale scores, and as such, it is recommended for Likert‐type item scores (Viladrich et al., 2017; Yang & Green, 2015). To provide common reference points with the previous literature, Cronbach's (1951) alpha with the items treated as continuous was also computed and reported. For all coefficients, 95% CIs were computed across 1000 bootstrap samples using the percentile method (Kelley & Pornprasertmanit, 2016). According to George and Mallery (2003), reliability coefficients can be interpreted using the following guide: ≥0.90 excellent, ≥0.80 and <0.90 good, ≥0.70 and <0.80 acceptable, ≥0.60 and <0.70 questionable, ≥0.50 and <0.60 poor, and <0.50 unacceptable.

8. RESULTS AND DISCUSSION

To confirm the EGA estimates obtained in Study 1, the EGA dimensionality and stability analyses were conducted for the confirmation data set that included the two composites of afraid–scared and upset–distressed. On the basis of this data set with these two composites, EGA with both GLASSO and TMFG provided an estimate of two dimensions that perfectly reproduced the Positive and Negative Affect factors (Figure 3, bottom panel). In terms of the stability of the estimates, GLASSO and TMFG estimated two dimensions for 100% of the bootstrap samples (Table 1), and the items were assigned to the same dimensions in 100% of the bootstrap samples as well (Table S1). In all, these results indicate that the structure obtained with EGA in Study 1 was confirmed in sample B.

The fit of the optimal CFA.2F.2θ model from Study 1 for the confirmation sample is shown in Table 3. As can be seen in the table, the model provided a good fit to the data (CFI = 0.966, SRMR = 0.044, RMSEA = 0.066). In addition, the two error correlations were significant and of very similar magnitude (0.45 for afraid–scared and 0.35 for upset–distressed) to the values obtained for the cross‐validation sample. The factor solution for this model is shown in Table 4. According to the results in Table 4, the primary loadings for both factors were very high, with a mean of 0.69 (0.33–0.81) for Positive Affect and a mean of 0.73 (0.62–0.81) for Negative Affect. In terms of the factor correlation, it was −0.27, which was notably weaker than the correlation of −0.45 obtained for the cross‐validation sample.

The fit of the measurement invariance models is shown in Table 5. Three measurement invariance levels were tested: configural (the number of factors and loading configurations were equal across groups), metric (the factor loadings were equal across groups), and scalar (the factor loadings and thresholds were equal across groups). As can be seen in the table, all configural models provided an adequate fit to the data (CFI > 0.93, SRMR < 0.06, RMSEA < 0.08). In addition, the levels of metric and scalar invariance were supported for all the evaluated variables, as the fit of the models according to CFI never deteriorated more than 0.01 from the fit attained by the configural model (the largest decrease in CFI fit was 0.005). In fact, many of the metric and scalar models showed equal or a slight improvement in CFI fit in comparison to the configural models. According to RMSEA, the metric and scalar levels of invariance were also supported, as the more stringent models (metric and scalar) always attainted better fit (lower RMSEA) in comparison to the configural model. In the case of the SRMR index, the fit of the metric and scalar models was generally equal to the fit obtained for the corresponding configural models. In all, these results across two samples indicate that the PANAS’ factor structure was found to be invariant across sex, age, and treatment status. These results are congruent with previous research with the PANAS that has also found its structure to be invariant across sex and age, including comparisons between children and adults (Buz et al., 2015; Heubeck & Wilkinson, 2019; Ortuño‐Sierra et al., 2015, 2019).

Having established measurement invariance, the latent means for the groups according to sex, age, and treatment status were compared. Regarding sex, the results revealed that for sample A, women, on average, scored 0.24 standardized units lower than men in the Positive Affect factor (W = 44.875, df = 1, p < 0.001) and 0.13 standardized units higher than men in the Negative Affect factor (W = 14.334, df = 1, p < 0.001). The mean comparisons for sex for sample B were very similar, with women scoring, on average, 0.23 standardized units lower than men in Positive Affect (W = 18.828, df = 1, p < 0.001) and 0.12 standardized units higher in Negative Affect (W = 5.285, df = 1, p = 0.022). According to Cohen (1992), these differences could be categorized as small. In terms of treatment status, the results with sample A revealed that those in psychological and/or psychiatric treatment scored, on average, 0.31 standardized units lower in Positive Affect than those not in treatment (W = 43.110, df = 1, p < 0.001) and 0.43 standardized units higher in Negative Affect than those not in treatment (W = 83.739, df = 1, p < 0.001). The mean comparisons for sample B produced smaller differences, with those in psychological and/or psychiatric treatment scoring, on average, 0.10 standardized units lower in Positive Affect than those not in treatment, a nonsignificant difference (W = 2.244, df = 1, p = 0.134), and 0.19 standardized units higher in Negative Affect than those not in treatment (W = 8.976, df = 1, p = 0.003). The difference in Negative Affect across treatment status could be categorized as small.

The mean comparisons across age revealed similar trends for samples A and B. For the standardized solutions, the means for Positive Affect for sample A were 0.00, 0.11, 0.28, and 0.48, for the age groups 10–19, 20–29, 30–39, and 40 or more, respectively. The omnibus Wald test indicated that these differences were significant (W = 71.063, df = 3, p < 0.001). For sample B, the Positive Affect scores also increased with age, with latent means in the standardized solutions of 0.00, 0.15, 0.48, and 0.70, for the age groups 10–19, 20–29, 30–39, and 40 or more, respectively. Again, the omnibus Wald test indicated that these differences were significant (W = 72.714, df = 3, p < 0.001). For the pairwise post hoc tests, a Bonferroni correction was applied to the significance threshold. As there were six pairwise comparisons across the four age groups, the threshold for statistical significance was set at 0.008 (0.05/6). All pairwise comparisons for Positive Affect were significant except between 10–19 and 20–29, which were nonsignificant for both samples A (W = 5.951, df = 1, p = 0.015) and B (W = 5.521, df = 1, p = 0.019). The largest latent mean differences, which were obtained when comparing the age groups 10–19 and 40 or more, could be categorized as approximately medium (0.48) for sample A (W = 60.408, df = 1, p < 0.000) and medium (0.70) for sample B (W = 62.316, df = 1, p < 0.000).

In the case of Negative Affect, the latent means decreased with age, with values of 0.00, −0.02, −0.08, and −0.37 for the age groups 10–19, 20–29, 30–39, and 40 or more, respectively, of sample A. The omnibus Wald test indicated that these differences were significant (W = 62.937, df = 3, p < 0.001). Similarly, the latent means in the standardized solutions of sample B were 0.00, −0.05, −0.22, and −0.50 for the age groups 10–19, 20–29, 30–39, and 40 or more, respectively. As with sample A, these differences were significant (W = 61.014, df = 3, p < 0.001). Regarding the pairwise comparisons, as with Positive Affect, the significance threshold was set at 0.008. The results of the Wald tests for the pairwise comparisons revealed that the 40 or more group had lower Negative Affect means than the rest of the age groups. Specifically, the 40 or more group had lower means than the 30–39 group (sample A: W = 27.450, df = 1, p < 0.000; sample B: W = 8.466, df = 1, p = 0.004), the 20–29 group (sample A: W = 59.795, df = 1, p < 0.000; sample B: W = 53.144, df = 1, p < 0.000), and the 10–19 group (sample A: W = 48.834, df = 1, p < 0.000; sample B: W = 44.859, df = 1, p < 0.000). The largest latent mean differences, which were obtained when comparing the age groups 10–19 and 40 or more, could be categorized as small (−0.37) for sample A and medium (−0.50) for sample B.

The final analyses were conducted to evaluate the reliability of the sum scores of Positive and Negative Affect for samples A and B. In the case of Positive Affect, the categorical omega coefficient (also known as the nonlinear SEM reliability coefficient) estimated an internal consistency reliability of 0.842 (95% CI = 0.835–0.850) for sample A and of 0.875 (95% CI = 0.866–0.883) for sample B. As expected, the suboptimal alpha coefficient produced lower estimates of 0.825 (95% CI = 0.817–0.833) for sample A and 0.857 (95% CI = 0.848–0.866) for sample B. Regarding the sum scores of Negative Affect, the categorical omega coefficient estimated reliabilities of 0.885 (95% CI = 0.879–0.891) for sample A and 0.927 (95% CI = 0.921–0.933) for sample B. Again, the suboptimal alpha produced lower estimates of reliability, with values of 0.848 (95% CI = 0.841–0.854) for sample A and 0.897 (95% CI = 0.889–0.903) for sample B. According to the guide of George and Mallery (2003), the reliabilities of the PANAS sum scale scores can be considered as good to excellent.

9. GENERAL DISCUSSION

Despite the widespread use of the PANAS, there is controversy regarding its factor structure (Flores‐Kanter et al., 2018; Heubeck & Wilkinson, 2019). The determination of latent factors and their respective items is a topic of great importance, which currently has new developments coming from graphics models. The main objective of the present study was to advance the knowledge regarding the factor structure underlying the PANAS scores by utilizing the different functionalities of the EGA method. In light of this, EGA was used to (1) estimate the dimensionality of the PANAS scores, (2) establish the stability of the dimensionality estimate and of the item assignments into the dimensions, and (3) assess the impact of potential redundancies across item pairs on the dimensionality and structure of the PANAS scores.

In sum, the results are consistent with a two‐factor oblique structure. This dimensionality proved to be reliable; invariant in terms of gender, age, and treatment; and stable according to the different samples analyzed and contemplating the bootstrapping analyses applied. It could also be verified that solutions of more than two dimensions, specifically three‐factor structures, were a methodological artifact resulting from unaccounted item redundancies, particularly those of the item pairs scared–afraid and upset–distressed. This latter finding is of great importance as it helps explain some of the divergences evidenced in previous studies regarding the dimensionality of the PANAS.

This investigation has some limitations that need to be noted. First, the use of a cross‐sectional design and retrospective self‐report scale formats are issues of concern. Therefore, we consider that future research should also focus on a just‐in‐time or ecological momentary assessment and longitudinal measures. In this sense, future studies have to choose more appropriate analysis for the study of the validity of the PANAS. Nevertheless, it is important to note that previous research that has implemented these types of methodologies has found results that are consistent with our findings (Merz & Roesch, 2011; Rush & Hofer, 2014). In other words, the optimal structure is one in which there are two relatively independent Positive and Negative Affect factors.

Finally, it is noteworthy that this study was carried out applying the Spanish adaptation of PANAS made in Argentina by Medrano et al. (2015), Moriondo et al. (2011), and Flores Kanter and Medrano (2016). In these adaptations and validations of the PANAS, it was verified that 2 of the 20 items of the original scale presented complex behavior. Specifically, the Alert and Excited items presented high cross‐loadings (>0.30) on the Positive and Negative Affect factors. In the original scale, these items were constructed as indicators of Positive affect (Watson et al., 1988). However, the translation of these adjectives into other languages has presented serious difficulties (López‐Gómez et al., 2015). Research conducted in different parts of the world evidences that these terms are associated or connote in their meaning both a positive and a negative mood. As a result of the attempt to remedy this difficulty, there is great variability in the way these items have been translated. For example, in Spain, the adjective “excited” was translated as “ilusionado o emocionado,” and the term “alert” was translated as “despierto” (Lopez‐Gómez et al., 2015). In Argentina, the translation was more literal, translating these adjectives as “alerta” and “excitado” (Medrano et al., 2015). In Chile, the term “excited” was changed to “optimistic” (Dufey & Fernandez, 2012). In Serbia, the item “excited” had an ambivalent valence and was substituted with “elated” (Mihić et al., 2014). In an Arabic Sample, a challenge arose with “excited,” which was initially translated into the literal term “aroused.” However, some other translators believed an appropriate and adequate Arabic translation was “Farhan.” In specific Arabic contexts, it can be read and understood as “happy” rather than “excited” (Narayanan et al., 2019). In the Italian version, the item “alert” (allerta) was substituted for “concentrating” (concentrato), because in Italian, the valence of alert is ambivalent, whereas concentrating has a clear positive valence (Terraciano et al., 2003). The above considerations are true even in the same countries. Within Argentina, for example, there is another adaptation where the term “excited” has been translated as “exaltado/a,” whereas the term “alert” has been translated as “alerta ‐ dispuesto/a” (Santángalo et al., 2019). Therefore, the inclusion of these and other items in the case of PANAS continues to be a topic of discussion and diverse resolutions.

It has been suggested that maintaining the original format of the PANAS can often be ambiguous for certain affective descriptions (i.e., the same adjective might be interpreted differently by different subjects), thus running the risk of reducing the construct validity of the questionnaire (Sandín et al., 1999). As described above, there is evidence in different contexts that supports this possibility. In the present investigation, we have found only one study that directly investigated the meaning given by the participants to the different adjectives of the PANAS, obtaining relevant results for the present discussion. In this study developed by Thompson (2007), there is evidence that some items were considered easy to understand but to have multiple meanings. In the case of the adjective Excited, this item was thought to incorporate both positive and negative connotations. For some participants, this item might be interpreted as close to agitated, whereas for others, it is similar to importunate. For other participants, the excited item had a clear positive connotation. Given the current controversy and lack of consensus on how to translate these and other adjectives from the original PANAS scale, we have chosen here not to include the Alert and Excited items in the data collection. This way of proceeding is similar to that applied in other research in different contexts, such is the case of the USA where three items with relatively high cross‐loadings (i.e., proud, alert, jittery) as well as the item with the lowest communality estimate (i.e., distressed) were removed, because the goal was to develop a relatively pure measure of Positive Affect and Negative Affect (Villodas et al., 2011). However, this does not rule out the possibility that the inclusion of these two items may have an impact on the internal structure seen for the PANAS scores. For example, it would be interesting to verify whether the results evidenced in the present research are replicated with the inclusion of the Alert and Excited items. Beyond these considerations, it is relevant to indicate that the evidence obtained here on the internal structure of the PANAS is consistent with data previously obtained for Argentine population using the 20‐item version (see Flores‐Kanter & Medrano, 2018; Medrano et al., 2015; Moriondo et al., 2011).

In conclusion, we show how alternative factor models from the PANAS literature, such as Mehrabian's (1997) or Gaudreau's et al. (2006) three‐factor models of Positive Affect, Afraid, and Upset, which from a purely factor‐analytic perspective can appear appropriate for the PANAS (including for our data), could be discarded with confidence when the information provided by EGA was taken into account. These analyses not only help to decide the optimal factor structure for the population of our study, but can provide a framework to other researchers showing how to analyze the data more richly and to be able to make optimal decisions with such complicated data.

CONFLICT OF INTERESTS

The authors declare that there are no conflict of interests.

PEER REVIEW

The peer review history for this article is available at https://publons.com/publon/10.1002/jclp.23191

Supporting information

Supporting information.

Flores‐Kanter, P. E. , Garrido, L. E. , Moretti, L. S. , & Medrano, L. A. (2021). A modern network approach to revisiting the Positive and Negative Affective Schedule (PANAS) construct validity. J Clin Psychol, 77, 2370–2404. 10.1002/jclp.23191

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available in “Mendeley Data” at 10.17632/rjgtbhsnfc.3, reference number V3.