Assessment of the global noise algorithm for automatic noise measurement in head CT examinations

Abstract

Purpose

The global noise (GN) algorithm has been previously introduced as a method for automatic noise measurement in clinical CT images. The accuracy of the GN algorithm has been assessed in abdomen CT examinations, but not in any other body part until now. This work assesses the GN algorithm accuracy in automatic noise measurement in head CT examinations.

Methods

A publicly available image dataset of 99 head CT examinations was used to evaluate the accuracy of the GN algorithm in comparison to reference noise values. Reference noise values were acquired using a manual noise measurement procedure. The procedure used a consistent instruction protocol and multiple observers to mitigate the influence of intra‐ and interobserver variation, resulting in precise reference values. Optimal GN algorithm parameter values were determined. The GN algorithm accuracy and the corresponding statistical confidence interval were determined. The GN measurements were compared across the six different scan protocols used in this dataset. The correlation of GN to patient head size was also assessed using a linear regression model, and the CT scanner's X‐ray beam quality was inferred from the model fit parameters.

Results

Across all head CT examinations in the dataset, the range of reference noise was 2.9–10.2 HU. A precision of ±0.33 HU was achieved in the reference noise measurements. After optimization, the GN algorithm had a RMS error 0.34 HU corresponding to a percent RMS error of 6.6%. The GN algorithm had a bias of +3.9%. Statistically significant differences in GN were detected in 11 out of the 15 different pairs of scan protocols. The GN measurements were correlated with head size with a statistically significant regression slope parameter (p < 10^‒7). The CT scanner X‐ray beam quality estimated from the slope parameter was 3.5 cm water HVL (2.8–4.8 cm 95% CI).

Conclusion

The GN algorithm was validated for application in head CT examinations. The GN algorithm was accurate in comparison to reference manual measurement, with errors comparable to interobserver variation in manual measurement. The GN algorithm can detect noise differences in examinations performed on different scanner models or using different scan protocols. The trend in GN across patients of different head sizes closely follows that predicted by a physical model of X‐ray attenuation.

1. INTRODUCTION

Diagnostic CT imaging is well established as an important tool in patient care, due to its excellent combination of image contrast, spatial and temporal resolution. Although the carcinogenic risk from CT radiation exposure is small, it is not negligible. ¹ Maximizing the diagnostic utility of any imaging examination is an important objective; it follows that the quality of the images produced in any examination are suited to the diagnostic task. Expert advisory organizations have stated the need for optimizing imaging to balance the risk from radiation exposure with the image quality needed for a diagnostic task. ² , ³ To this end, the registries of radiation exposure in common CT examinations have been established. However, similarly well‐established quantitative benchmarks of image quality have not been established to date. It is important to tabulate benchmark values of noise and other image quality metrics in CT examinations, as these normative data would allow a comparison of quality in CT examinations at one hospital or institution against a benchmark value.

The traditional, objective method for evaluating CT image quality involves imaging of test objects (phantoms). In fact, accrediting bodies ⁴ (Chapter 12) require routine testing of CT image quality using phantoms. However, there is no standard phantom for image quality assessment of head CT examinations. Although the ACR CT QC and CATPHAN® (The Phantom Laboratory) phantoms are widely used for CT image quality assessment, these phantoms do not resemble the human head. Specifically, the skull hardens and rapidly attenuates an X‐ray beam, and ultimately affects the image noise properties. Therefore, image quality metrics measured using the ACR QC or other standard phantoms may not be the best surrogates for head CT examination image quality. Direct image quality assessment of patient examinations may produce more relevant and comparable metrics.

Image noise depends not only on the examination radiation dose, which is often fixed in head CT, but also on patient anatomy, patient positioning, acquisition parameters such as X‐ray beam filtration, collimation, detector sensitivity, and image reconstruction parameters such as reconstruction algorithm, image slice thickness, and reconstruction field‐of‐view diameter. Therefore, an objective method is needed to detect noise differences between head CT examinations performed using differing scanners and imaging protocols.

Another important component of quality control is subjective evaluation of clinical images by end user, typically the radiologist. Radiologist feedback is holistic and accounts for the complex interdependence of noise, resolution, contrast, and artifacts; however, this feedback is subjective, susceptible to bias, and may be difficult to obtain in a systematic manner or frequency. Recently, methods have become available for objective quantitative assessment of clinical CT images. ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² In particular, Christianson et al presented the global noise (GN) algorithm as a method for automatic noise measurement in CT examinations. ⁶ The algorithm has received considerable attention: Ria et al measured noise in nearly 3000 routine CT examinations using the GN algorithm ¹³ ; and Lacy et al used GN measurements as part of detectability index, a task‐based image quality metric, and used this metric to evaluate image quality in more than 500 CT examinations. ¹⁰

Despite these encouraging advances, there is a general lack of assessments of the accuracy of the GN algorithm with statistical confidence estimates. A major obstacle is obtaining comparison ground truth noise values in clinical CT images. The GN algorithm has been previously validated with statistical estimates of accuracy in abdomen CT examinations, ¹⁴ but to date has not been validated as such in CT examinations of other body sites. An issue specific to the GN algorithm is that there is an implicit algorithmic assumption of some degree of piecewise constancy in the imaged object. Although the GN algorithm has been previously shown to be accurate in the abdomen (likely due to the liver as a large, mostly homogeneous organ), there is no general principle that guarantees the GN algorithm is equally accurate in other body parts. Therefore, the GN algorithm requires validation in CT examinations of different body parts. The brain, specifically, is comprised mostly of two different globally distributed soft tissue components: gray and white matter. (The ventricles are a separate large, homogeneous component, but noise is lower in the ventricles than in soft tissue.) When multiple tissue components are present, the GN algorithm is susceptible to the degree of heterogeneity or “marbling” of components, even if the components themselves are perfectly homogeneous materials. Thus the accuracy and bias of the GN algorithm in head CT is unclear.

This work determines the global noise algorithm accuracy in head CT examinations, and validates the algorithm for this application. Noise was measured using both a reference manual measurement procedure and the automatic GN algorithm, and the GN algorithm accuracy was determined in comparison to the reference noise values. The procedure used to acquire the reference noise values mitigated the influence of intra‐ and interobserver variation by using multiple observers and a consistent set of measurement instructions.

2. MATERIALS AND METHODS

2.1. Head CT dataset

Image noise was measured in a dataset of 99 noncontrast head CT examinations. The examinations were performed to assess acute cognitive or motor deficit and are publicly available in The Cancer Imaging Archive ¹⁵ as the “Low Dose CT Image and Projection Data (LDCT and Projection data)” collection. ¹⁶ The primary purpose of this public dataset is to provide public raw projection data for the purpose of testing experimental image reconstruction technologies, especially using deep learning. Along with the raw projection data, this dataset includes the clinical tomographic images using the scanner vendor's commercial reconstruction algorithm.

Examinations were performed on scanners from two different vendors, General Electric and Siemens, with two different scanner models used according to the DICOM metadata in the public dataset. Forty‐nine examinations were performed using a GE Discovery CT750i model using a mean dose of 56.8 mGy ${\text{CTDI}}_{\text{vol}}$, and 50 examinations were performed using the Siemens SOMATOM Definition Flash model using a mean dose of 43.7 mGy ${\text{CTDI}}_{\text{vol}}$. ¹⁶

Imaging parameters were extracted from the DICOM metadata. The examinations performed on GE scanners arise from two distinct scan protocols performed in either axial or helical mode. The DICOM metadata showed that 42 examinations were performed using axial acquisition mode with fixed 300 mA tube current, and seven examinations were performed using helical acquisition mode with fixed 550 mA tube current. Here, these two groups are called “GE Protocol 1” and “GE Protocol 2,” respectively. The image field‐of‐view (FOV) diameter ranged from 20.0 to 25.4 cm across both protocols.

The examinations performed on Siemens scanners also appear to arise from two distinct scan protocols, referred to here as “Siemens Protocol 1” and “Siemens Protocol 2”, respectively. The Siemens protocols showed two different sets of tube current used, sharply clustered around 150 mA and 205 mA, respectively. The FOV diameter was fixed for these examinations at 25.0 cm.

All examinations used a 120 kV tube voltage and all images were reconstructed with a thickness and spacing of 5 mm. Other examination parameters can found in the article describing the public dataset. ¹⁷

The TCIA LDCT and Projection data collection also includes simulated low‐dose examinations at 25% of full dose, obtained by adding noise to the raw projection data using a validated physical noise model. ¹⁸ At the time of this manuscript, the low‐dose simulated examinations were available for only the 50 examinations performed on Siemens scanners. “Siemens Low‐dose Protocol 1” and “Siemens Low‐dose Protocol 2” were simulated from the raw projection data of Siemens Protocol 1 and Siemens Protocol 2 examinations, respectively. The protocol parameters for these scan protocols are summarized in Table 1. The public dataset serves as good test case for assessing the GN algorithm as it contains variable noise, especially across the full and low‐dose image sets.

TABLE 1.

Summary of imaging parameters across scan protocols

Protocol	N	Scan Mode	Tube current (mA)	CTDIvol (mGy)	Recon. filter	FOV (cm)
GE Protocol 1	42	axial	300	56.8	Standard	20.0–25.4
GE Protocol 2	7	helical	550	56.8	Standard	20.6–21.3
Siemens Protocol 1	30	(unverified)	149 or 151	43.7	H40	25.0
Siemens Protocol 2	20	(unverified)	202–211	43.7	H40	25.0
Siemens Low dose Protocol 1	30	(unverified)	37 (approx.)	10.9 (approx.)	H40	25.0
Siemens Low dose Protocol 2	20	(unverified)	51 (approx.)	10.9 (approx.)	H40	H40

2.2. Manual noise measurement

Manual noise measurements were taken by three observers (one board‐certified diagnostic medical physicist and two undergraduate research assistants). These observers measure noise in the white matter brain parenchyma in each CT examination according to an instruction protocol. The white matter tissue component was chosen due to relative homogeneity compared to other tissue components in the head.

The measurement instruction protocol was used to mitigate inter‐ and intraobserver measurement variation. Specifically, the instruction protocol specified a standard anatomical measurement location, use of multiple regions‐of‐interest (ROIs), and consistent image display settings. The observers were blinded to each other's measurements and to the GN measurement. The ImageJ software (National Institutes of Health, Bethesda, MD, USA) was used for image display and manual measurements.

The protocol specified image display using a window width/level setting of 100/40 HU. In each CT examination, the observer determined the slice that most prominently displayed both the frontal and occipital horns of the lateral ventricles. In each examination, the standard deviation of selected slice locations across observers was calculated as the slice location variation; the average over all examinations of the slice location variation was taken as an indicator of observer agreement in the measurement location.

Each observer placed four circular regions‐of‐interest (ROIs) in homogeneous regions of the cerebral white matter, with one ROI in each of the right anterior, right posterior, left anterior, and left posterior quadrants of the brain. The ROIs were place according to the observers’ determination of image homogeneity. The ROI diameter was specified at 6.5 mm. The protocol instructed observers to avoid ROI placement on gross pathology. Figure 1 displays an example of ROI placement. The pixel standard deviation of each ROI was recorded, and the average of the four ROI standard deviation values were taken as the observer's measurement of image noise.

FIGURE 1.

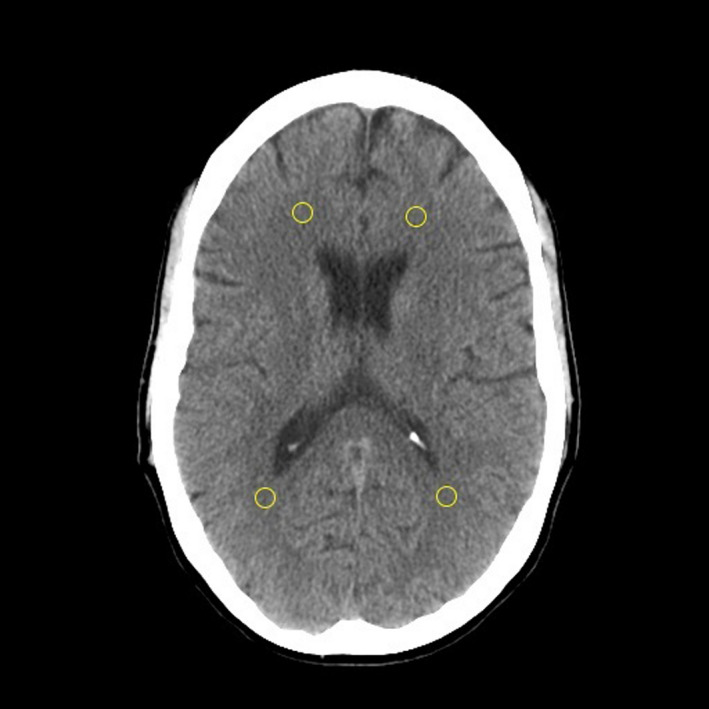
Example manual noise measurement using ROI placement in cerebral white matter. The slice location containing all four lateral ventricle horns was used in the manual measurements. Four quadrant ROI locations were used

For each CT examination, all observers’ noise measurements were averaged together and taken as the reference noise value. The standard error of the mean across observers was used to calculate a 95% confidence interval for the reference noise value. The standard deviation of observers’ noise measurements within each examination was taken as the interobserver variation. As the number of observers increases, the standard error of the mean decreases; therefore, the study design of multiple observers helps mitigate the influence of interobserver variation. Finally, the spatial noise variation was calculated by taking the standard deviation of the four ROI noise values, and then by averaging this quantity over all observers and examinations.

2.3. Automatic noise measurement

Noise was measured automatically in each examination using the GN algorithm. The slice locations selected by the observers were averaged together; the slice image closest to this location was selected for GN analysis. The GN algorithm was used to analyze only this selected slice image, and not any other image in the CT examination. Presumably, the observers selected similar slice locations (and therefore approximately similar noise) by using the lateral ventricles as anatomical landmarks for slice selection. This assumption was tested by measuring the variation of selected slice location across observers.

The difference between the GN and reference measurements was taken as the GN algorithm error; The root‐mean‐square (RMS) error was calculated over all CT examinations, and was taken as an indicator of the GN algorithm accuracy. The 95% confidence interval value in the RMS error was calculated. Percent RMS error was calculated as RMS error divided by mean reference noise over the set of examinations.

2.4. Optimization of the GN algorithm parameters

The GN algorithm parameter values were optimized for application to head CT examinations as follows. The dataset of head CT examinations was divided into optimization and validation datasets, with 75 and 74 CT image sets in the optimization and test datasets. There was an equal split of the low‐ and high‐dose CT examinations. Global noise algorithm parameters were optimized by finding the set of parameter values with minimum RMS error in the optimization dataset. These fixed optimal parameter values were used for the algorithm evaluation in the test dataset. A grid search method was used for parameter optimization. Grid parameter values were as follows: kernel size of 5 × 5, 7 × 7, or 9 × 9 pixels, a soft tissue mask upper threshold of 50 or 100 HU, and the histogram bin size of 0.1 or 0.2 HU. The soft tissue mask lower threshold was fixed at 0 HU. This optimization search space was informed by results of the previous GN algorithm validation study as an optimal range. ¹⁴

2.5. Role of gray versus white matter in reference noise measurement

Since gray and white matter tissue components appear to have different image homogeneity, the choice of tissue component in manual measurement may affect the reference noise value. An additional analysis was performed to assess how the reference noise value is affected. One of the authors (M.A.) measured noise in gray matter using four ROIs, one per each quadrant of the brain as before. This observer's measurements were not averaged together with the two other observers, in order to maintain a similar procedure for the white and gray matter reference noise values. The reference noise values using gray and white matter were compared using paired t‐test. The biases of the GN measurement relative to both gray and white matter reference noise values were calculated. For this subanalysis, data from only Siemens Protocol 1 was used, as this was considered to be the most controlled protocol in terms of both acquisition and image reconstruction parameters.

2.6. Global noise measurements across scan protocols

One proposed application of the GN automatic noise measurement is detection of noise differences between different scan protocols, either within a scanner or across scanner models. The GN measurements were compared between the six scan protocols in this dataset. Student's t‐tests between each of the various pairs of protocols were performed.

2.7. Global noise versus head size

An analysis was performed to assess whether the GN variation among CT examinations can be explained by different patient head sizes. For this analysis, only Siemens Protocol 1 was used, as it is the most controlled, especially the fixed FOV compared to the image data from the GE examinations. For each CT examination in this subset, the water equivalent diameter (WED) of the patient's head was automatically calculated using the method of AAPM Report 220 ¹⁹ . The WED was calculated on the consensus image slice determined by the three observers.

The physical model relating WED to CT image noise is:

$$\text{Noise}=\frac{1}{\sqrt{I}}=\frac{1}{\sqrt{I_0{e}^{\frac{‐\text{log}2\left(\text{WED}\right)}{\text{HVL}}}}},$$ (1)

where I is the intensity of X‐rays transmitted through the imaged object predicted by the Beer–Lambert law of attenuation, I ₀ is an unattenuated X‐ray intensity, $\text{WED}$ is the water equivalent diameter of the object, and $\text{HVL}$ is the X‐ray beam's water half‐value layer. Taking the natural logarithm of this equation,

$$\text{log}\left(\text{Noise}\right)=‐\frac{1}{2}{\text{logI}}_0+\frac{\text{log}2}{2·\text{HVL}}·\text{WED}=\mathrm{a}+\mathrm{b}·\text{WED}$$ (2)

Equation 2 represents a linear model relating patient head size (WED) to the log‐transformed image noise with intercept and slope parameters a and b, respectively. Linear regression was used to fit a model of log‐transformed GN to WED. The R ² correlation statistic of GN to head size was determined. The slope b of the linear regression model was used to estimate the beam quality (water HVL) of the CT scanner's X‐ray beam using:

$$\text{HVL}=\frac{\text{log}2}{2b}$$ (3)

3. RESULTS

3.1. Reference noise measurements

The mean and standard deviation of the reference noise values in the head CT dataset were 5.1 and 1.7 HU, respectively. The range of reference noise values was 2.9–10.2 HU. The reference noise values in this dataset are bi‐modal, since the data are from either full‐dose or low‐dose examinations. The summary statistics of reference noise for all examinations, full‐dose examinations, and low‐dose examinations are presented in Table 2. The raw data of the reference and global noise measurements in each CT examination are provided in the supplementary materials.

TABLE 2.

Summary statistics of reference noise measurements

Set of examinations	Mean noise (95% CI)	Minimum	Maximum	Standard deviation	Spatial variation
All	5.1 HU (4.5–5.8 HU)	2.9 HU	10.2 HU	1.7 HU	0.5 HU
Full dose	4.0 HU (3.7–4.7 HU)	2.9 HU	5.6 HU	0.4 HU	0.4 HU
Low dose	7.3 HU (6.6–7.9 HU)	6.0 HU	10.2 HU	0.9 HU	0.7 HU

The average variation among selected slice locations was 4.8 mm, nearly equal to the image slice thickness; therefore, the observers mostly selected the same or adjacent slice locations. The interobserver noise measurement variation was 0.29 HU (5.7%), on average across all examinations. The reference noise value uncertainty was ±0.33 HU (95% CI), on average across examinations. The spatial noise variation was 0.49 HU (9.6%), on average across examinations and observers.

3.2. Optimization of algorithm parameters

The optimal GN algorithm parameters were as follows: a kernel size of 7 × 7 pixels, a soft tissue mask upper threshold of 100 HU, and a histogram bin width of 0.1 HU. In the optimization dataset, The RMS error was 0.38 HU using optimal parameter values. The maximum RMS error and the RMS error standard deviation over the parameter search space were 0.65 HU and 0.10 HU, respectively.

3.3. Global noise algorithm accuracy

The accuracy of the GN algorithm was assessed on the 74 examinations in the validation dataset using the optimized parameters. The RMS error (and 95% confidence interval) was 0.34 HU (0.24–0.46 HU) over all examinations. Converted to percentages by dividing by mean noise, the percent RMS error (and 95% confidence interval) was 6.6% (4.7%–9.0%). The GN accuracy analysis was also performed for the full and low‐dose sets separately. The full accuracy results are tabulated in Table 3.

TABLE 3.

Summary of results for GN algorithm error and bias

Set of examinations	RMS error	Percent RMS error	Percent bias
All	0.34 HU (0.24–0.46 HU)	6.6% (4.7%–9.0%)	+3.9% (+2.6%–+5.1%)
Full dose	0.25 HU (0.16–0.35 HU)	6.0% (3.9%–8.8%)	+3.1% (+1.7%–+4.6%)
Low dose	0.47 HU (0.25–0.79 HU)	6.5% (3.5%–10.8%)	+4.6% (+2.8%–+6.4%)

95% confidence intervals indicated in parentheses.

The differences between GN and reference noise measurements in the validation dataset are displayed in a Bland–Altman analysis plot (Figure 2). The plot is coded for data points corresponding to the different scan protocols. There is no clear difference in the accuracy of the GN algorithm across scan protocols. The GE Protocol 2 data points all fall below mean difference line, but this sample size (n = 4) in the validation set was too small to draw conclusions. Overall, the range of differences between GN and reference values was −0.34 to +0.73 HU (95% interval). The mean difference was +0.2 HU (+4%), indicating a positive bias of the GN measurements over than the reference values. The data points are clearly separated into two clusters corresponding to full and low‐dose examinations. The bias was +0.13 HU (+3%) and +0.34 HU (+5%) for full and low‐dose examinations, respectively. The overall bias of +4% was statistically significant (p < 10^‒7, two‐sided paired t‐test).

FIGURE 2.

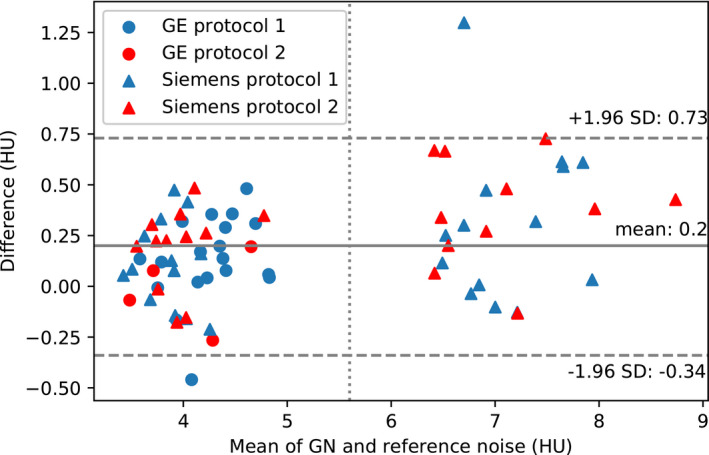
Differences between GN and reference noise values shown in a Bland–Altman plot. Data points to the right of the vertical dashed line are from simulated low‐dose examinations from Siemens Protocols 1 and 2

3.4. Role of gray versus white matter in reference noise measurement

When the gray matter tissue component was used for reference noise measurement, the mean noise was 4.17 HU. In comparison, the mean white matter noise was 3.78 HU. These means are significantly different (p < 0.001). The bias between GN and reference gray matter noise values was −0.21 (−4.9%); the bias between GN and reference white matter noise values was +0.19 HU (+4.9%). The lower reference noise in white matter indicates lower sensitivity to tissue heterogeneity; therefore, reference noise measured in white matter is a better indicator of stochastic noise. Furthermore, it was more difficult to place an ROI in homogeneous regions of gray matter while avoiding an intersection of the ROI with anatomical boundaries. Taken together, these results support the choice of white matter for reference manual noise measurements. The GN value was intermediate between white and gray matter reference noise. This is likely due to some gray matter inhomogeneity sensitivity on GN.

3.5. Global noise measurements across scan protocols

A plot of global noise measurements across scan protocols is shown in Figure 3. The GN algorithm clearly measures higher noise in the low‐dose protocols. Within the full‐dose examinations, GE examinations had higher GN measurement than the Siemens examinations with statistical significance, even though the programmed dose was higher in the GE examinations. The difference is likely due to the different reconstruction filters. Interestingly, a statistically significant difference in GN was also discovered between Siemens Protocols 1 and 2 (p = 0.026); however, this difference is only weakly significant (p = 0.156) when the Bonferroni correction for multiple hypothesis testing is applied. (A multiplicity number n = 6 was used for the Bonferroni correction, taking into account that only four different scan protocols were independent, leading to six unique pairwise combinations.) A matrix of t‐test statistics for pairwise comparison of the different scan protocols is presented in Table 4.

FIGURE 3.

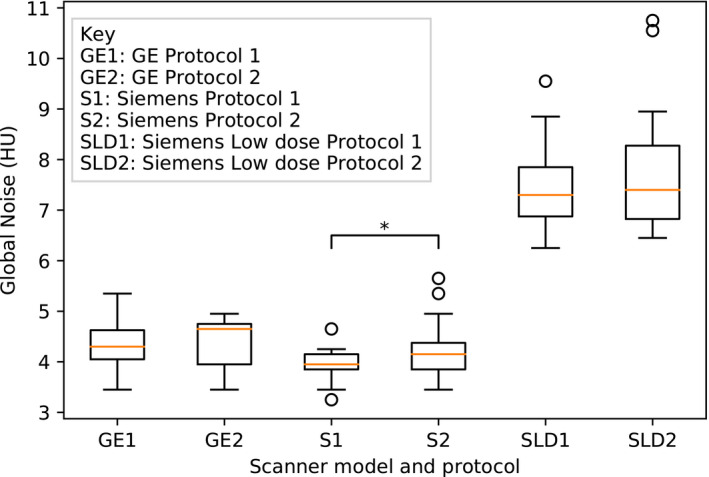
Boxplot of automatic global noise measurements. * p < 0.05

TABLE 4.

p test statistics for pairwise differences of mean GN between protocols

Scan Protocol	GE1	GE2	S1	S2	SLD1	SLD2
GE Protocol 1 (GE1)	—	0.95	***	0.45	****	****
GE Protocol 2 (GE2)		—	**	0.64	****	****
Siemens Protocol 1 (S1)			—	*0.026	****	****
Siemens Protocol 2 (S2)				—	****	****
Siemens Low‐dose Protocol 1 (SLD1)					—	0.24
Siemens Low‐dose Protocol 2 (SLD2)						—

^* p < 0.05

^** p < 0.01

^*** p < 0.001

^**** p < 0.0001.

3.6. Global noise versus head size

A scatterplot of log‐transformed GN versus head size (in terms of WED) is shown in Figure 4 with a linear regression fit overlayed on the plot. The GN is sensitive to head size with a fit slope parameter significantly different from zero (p < 10^‒7). The correlation coefficient R ² = 0.68 indicates that more than half of the variation in GN is explained by head size.

FIGURE 4.

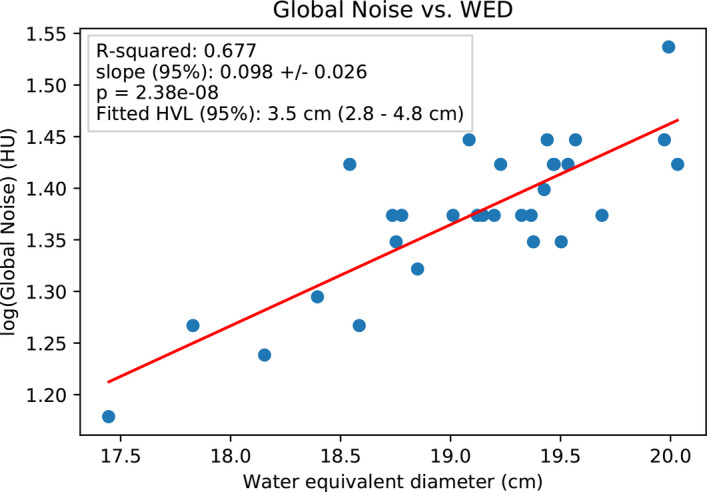
Scatterplot of GN versus head size

Furthermore, the slope parameter was used to estimate a beam quality of 3.5 cm water HVL (2.8–4.8 cm 95% confidence interval) for the X‐ray beam used in this group of examinations. A reference value for X‐ray beam quality for a CT scanner operating at 120 kV tube voltage was taken to be 3.4 cm water HVL. This approximation arises from the water mass attenuation coefficient of 0.21 cm²/g at 60 keV X‐ray effective energy. ²⁰ Given the reference value, the GN‐based beam quality procedure was accurate within 3%.

4. DISCUSSION

The public availability of the image dataset used here means that this analysis is repeatable and verifiable. To date, no other study has assessed the accuracy of the global noise algorithm in head CT with statistical confidence in a large dataset. The procedure used to obtain the nose reference values was critical in establishing precise reference values. It was found that spatial noise variation was greater than interobserver variation, highlighting the importance of using anatomical landmarks and consistent ROI placement. It is likely that intraobserver variation would be higher in an alternative single ROI measurement procedure than in the multiple ROI procedure used here. Another important aspect of this study was that the influence of interobserver variation on reference noise values was reduced by averaging over observers.

The uncertainty in the reference noise measurements was ±0.33 HU. Therefore, the accuracy assessment of the GN algorithm is bound by this lower limit. The reference value uncertainty was itself dependent on the study design in obtaining the reference values, particularly on the number of observers. In comparison, had this study used only a single observer, each reference noise value would have an uncertainty of approximately ±0.57 HU. The GN algorithm RMS error (0.34 HU) was below this value, demonstrating the importance of the multiple observer design. The GN RMS error was nearly equal to the uncertainty of the reference measurements, providing strong evidence that the GN accuracy was likely limited by the uncertainty of the reference noise measurements in this study, not by the performance of GN algorithm itself. The true accuracy of the GN algorithm compared to a reference value obtained by consensus from an even larger number of observers may be better than reported here.

The GN algorithm parameter optimization was guided by the results of the previous validation study in abdomen CT. ¹⁴ The sensitivity of the GN algorithm to parameter values in the search space was relatively small compared to that observed in the previous study.

The percent RMS error in this study was 6.6%. The percent RMS difference in this present study was similar between the full‐ and low‐dose groups, indicating applicability of the GN algorithm over a broad range of noise magnitudes. To put the RMS error in context, the percent variation in reference noise ($\pm 2\sigma$) in the set of full‐dose examinations was 22%. This comparison demonstrates that the GN algorithm can detect noise differences in a population of routine head CT examinations. The GN algorithm accuracy found in this study is more or less consistent with previous studies: Ahmad et al reported a percent RMS error of 8.6% in the validation study of the GN algorithm applied to abdomen CT examinations. ¹⁴ Christianson et al found a percent RMS error of 3.9%, albeit in a small validation sample of three abdomen CT examinations. ⁶

The GN algorithm is somewhat biased in comparison to reference noise because reference noise was measured in white matter. As the GN algorithm name implies, noise is measured globally throughout the image, limited to soft tissue using pixel threshold values. Therefore, the GN algorithm considers both gray and white matter. The GN algorithm is susceptible to the inherently higher inhomogeneity of the cerebral cortex compared to the white matter. This explains the positive bias in the GN measurements compared to the reference measurements manually obtained in the white matter of the brain. Future refinement of the GN algorithm may segment the white matter and restrict the GN calculation to this tissue component.

Nevertheless, the GN bias was smaller than the uncertainty in manual measurements. Although it was not done here, the known bias of the GN algorithm could be used to adjust the GN measurement to improve accuracy. The previous validation of the GN algorithm in abdomen CT did not show a bias. The potential differences in accuracy and bias of the GN algorithm in different body parts highlight the importance of validating the GN algorithm in each body part. Future work will assess the GN algorithm in other examinations such as chest CT and neck CT.

The GN algorithm was applied to detect noise differences between scan protocols both within and across scanner models. The GN algorithm detected clear differences between full‐dose and simulated low‐dose protocols, and between Siemens Protocol 1 and the GE protocols. This demonstrates the utility of the method in standardizing image quality across different scanner models. On the Siemens scanner model, examination of the metadata revealed two distinct protocols with different acquisition parameters, even though the authors of the public dataset describe the Siemens data as arising from one protocol. The application of the GN analysis revealed noise differences between the two protocols. (The DICOM metadata did not appear to have sufficient information to determine whether there were programmed dose differences between the two protocols.) Nevertheless, this example shows how the GN method could be useful in characterizing image quality variation within a protocol. This is significant because modern CT scanners customize image acquisition parameters to the patient.

The GN and head size measurements together were used to accurately measure a CT scanner X‐ray beam quality using a population of human heads as X‐ray attenuators. This remarkable result indicates that the GN measurement truly corresponds to stochastic noise. It should be noted though, the beam quality measurement uncertainty using GN was relatively large in comparison to conventional methods of beam quality measurement.

Given the demonstrated level of GN accuracy, nearly on par with interobserver variation, the results validate the GN method as an automated alternative to manual noise measurement. Furthermore, aside from any reference or ground truth noise, the GN response to differing head size corresponds to the physical model of image noise.

The GN algorithm can be used to automatically measure CT image noise nearly instantly, and the result can be archived in a database of all CT examinations performed at a hospital/clinic. This tool can be used in a QA program to detect noise differences attributable to patient, image acquisition, or image reconstruction differences. Traditional phantom testing (such as using ACR or CATPHAN phantom) can determine relative noise differences between different scanner hardware, acquisition, and reconstruction parameters; however, standard phantoms cannot capture the absolute noise properties of a CT image of the head due to the great differences between the phantom and the human head. Furthermore, the effects of nonlinear or deep learning‐based image reconstruction may be entirely different in the head compared to a standard phantom. Whether phantom‐based image quality tests of deep learning reconstruction are even relevant is an open question. A broader discussion of potential applications in quality control and standardization enabled by the automatic noise measurement is presented elsewhere. ¹⁴

The limitations of this study are as follows. The reference noise values obtained in this study are not strictly ground truth values, even though they were acquired with high precision. A ground truth value of noise may be obtained by multiple scans of the patient, but it would generally be unethical to perform such measurements. Second, only routine noncontrast head CT examinations were analyzed in this study. It is unclear whether the GN algorithm would be equally accurate in contrast‐enhanced head CT examinations or CT angiography examinations of the head.

It is emphasized that noise magnitude is only one component of image quality. Noise texture, tissue contrast, spatial and temporal resolution, and image artifacts are other important metrics that must be considered in the overall image quality assessment. Nevertheless, the accurate assessment of noise magnitude across patients is important since this can be sensitive to patient variation. The GN measurement may be combined with noise texture and spatial resolution measurements (either in patient or phantom data) to produce a more patient‐specific task‐based image quality metric.

5. CONCLUSION

The global noise algorithm was validated as method for automatic noise measurement in head CT examinations. This conclusion is supported by two independent results.

First, the accuracy of automatically calculated values was found to be accurate against reference noise values acquired by manual measurement. A measurement instruction protocol and participation of multiple observers were key elements in mitigating the effects of intra‐ and interobserver variation, thereby resulting in precise reference values. With comparison to these reference values, the accuracy of the GN algorithm was determined with statistical confidence limits. The RMS error of the GN algorithm is small compared to actual noise variation across examinations, indicating that the method can detect true noise difference among examinations.

Second, it was shown that the GN measurement follows the expected physical model of noise across different patient sizes. This result demonstrates that the global noise measurement is grounded in reality with results that are explained by physics.

CONFLICT OF INTEREST

The authors have no conflict to disclose.

Supporting information

Table S1

Ahmad M, Tan D, Marisetty S. Assessment of the global noise algorithm for automatic noise measurement in head CT examinations. Med Phys. 2021;48:5702–5711. 10.1002/mp.15133

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available in the supplementary material of this article (Table S1). These data were derived from the following resources available in the public domain: The Cancer Imaging Archive, LDCT‐and‐Projection‐data Collection: https://doi.org/10.7937/9npb‐2637