Abstract
Landmark‐based geometric morphometrics has emerged as an essential discipline for the quantitative analysis of size and shape in ecology and evolution. With the ever‐increasing density of digitized landmarks, the possible development of a fully automated method of landmark placement has attracted considerable attention. Despite the recent progress in image registration techniques, which could provide a pathway to automation, three‐dimensional (3D) morphometric data are still mainly gathered by trained experts. For the most part, the large infrastructure requirements necessary to perform image‐based registration, together with its system specificity and its overall speed, have prevented its wide dissemination.
Here, we propose and implement a general and lightweight point cloud‐based approach to automatically collect high‐dimensional landmark data in 3D surfaces (Automated Landmarking through Point cloud Alignment and Correspondence Analysis). Our framework possesses several advantages compared with image‐based approaches. First, it presents comparable landmarking accuracy, despite relying on a single, random reference specimen and much sparser sampling of the structure's surface. Second, it can be efficiently run on consumer‐grade personal computers. Finally, it is general and can be applied at the intraspecific level to any biological structure of interest, regardless of whether anatomical atlases are available.
Our validation procedures indicate that the method can recover intraspecific patterns of morphological variation that are largely comparable to those obtained by manual digitization, indicating that the use of an automated landmarking approach should not result in different conclusions regarding the nature of multivariate patterns of morphological variation.
The proposed point cloud‐based approach has the potential to increase the scale and reproducibility of morphometrics research. To allow ALPACA to be used out‐of‐the‐box by users with no prior programming experience, we implemented it as a SlicerMorph module. SlicerMorph is an extension that enables geometric morphometrics data collection and 3D specimen analysis within the open‐source 3D Slicer biomedical visualization ecosystem. We expect that convenient access to this platform will make ALPACA broadly applicable within ecology and evolution.
Keywords: automation, biological structures, image registration, open source, phenomics, phenotyping
1. INTRODUCTION
In the past 10 years, volumetric (3D) imaging has been used with increasing frequency to characterize morphological variation in complex biological structures in ecological and evolutionary contexts (Boyer et al., 2011; Falkingham, 2012; Goswami et al., 2019; Marcy et al., 2018). The general approach has been to capture high‐resolution specimen images (but see Marcy et al., 2018) and posteriorly collect the position of several anatomical landmarks of interest. These anatomical landmarks are then used in multivariate shape analyses, allowing researchers to test specific functional/developmental hypotheses regarding the ecology or evolution of complex phenotypes (e.g. Felice et al., 2019; Sanger et al., 2013; Sherratt et al., 2014).
While the quality of imaging techniques (e.g. Gignac et al., 2016) and the density of landmarks (e.g. Goswami et al., 2019) have continuously increased during the last decade, the gold standard method for landmark data collection has remained largely the same, that is, manual annotation by a trained expert. Manual annotation of landmarks is, however, both time and labour intensive, low throughput and subject to significant amounts of intra‐ and inter‐observer bias, precluding datasets from different laboratories (or even multi‐year datasets) from being confidently combined (Percival et al., 2019).
Recently, several approaches have been developed to automate and standardize landmark data collection in the context of volumetric imaging. While deep learning approaches are starting to emerge (e.g. Devine et al., 2020), most studies approach the problem using image‐based registration techniques developed in biomedical contexts (Bromiley et al., 2014; Maga et al., 2017; Young & Maga, 2015). Image registration represents the alignment of images that belong to the same anatomical structure of interest and provides researchers with a powerful framework for workflow automation, allowing morphometric research to truly enter the age of big data (Maga et al., 2017).
However, attempts to translate these biomedically oriented approaches to more ecological and evolutionary contexts have remained rather elusive and have faced substantial practical and technical barriers. For example, most image‐based registration approaches depend on high‐end hardware, all the while producing results in a timeframe that greatly exceeds the amount of time required for manual annotation (e.g. 10 CPU hours per specimen; Devine et al., 2020). While computing clusters have made high‐end hardware more accessible at the institutional level, the cost‐benefit ratio of implementing such approaches is still highly skewed against automation. Additionally, these algorithms are highly system specific and difficult to generalize to different study systems. Finally, image registration techniques rely on specialized labour, which include a dedicated programmer for algorithmic development and an imaging technician capable of developing and troubleshooting high‐resolution anatomical ‘reference maps’ representing the structure of interest, also known as anatomical atlases (Joshi et al., 2004).
Here we propose a new and general approach to automated three‐dimensional (3D) landmarking based on point cloud registration. Starting with 3D surface meshes, the procedure performs pairwise registration of subjects to the specified template using a sequential procedure with four steps. Initially, the edge information in individual meshes is discarded and the resulting point clouds are downsampled to facilitate the initial alignment and increase the speed of calculation. These point clouds are then subjected to a global registration step (Rusu et al., 2009), in which there is an initial alignment of the source and target point clouds. This initial alignment is followed by a local registration step (Rusinkiewicz & Levoy, 2001), in which the initial alignment is refined. Finally, the two rigidly aligned point clouds are subjected to a deformable registration step (Myronenko & Song, 2010), in which the source point cloud is deformed to match the target point cloud. As a result of the deformable registration step, the landmark correspondences across meshes gets established and landmark positions can be transferred across specimens.
Point cloud registration provides a simpler and more general alternative to image‐based registration, since it not only requires less preprocessing, but is also of much lighter implementation, therefore eliminating many of the challenges listed above. Point cloud registration has three main requirements: (a) a single reference (source) specimen; (b) one or multiple target specimens; and (c) that the meshes being aligned represent the same biological structure (i.e. there are no extraneous morphological elements). Since the source specimen will be deformed to match all target specimens, some care in the choice of source mesh is advisable (e.g. avoid using individuals with extreme morphologies). However, that is not a strict requirement of the ALPACA pipeline, which allows for any individual to be chosen as the source. We provide an efficient implementation of the single‐template ALPACA pipeline in the most recent version of SlicerMorph (Rolfe et al., 2020), the 3D morphometrics extension to the open‐source biomedical visualization software 3D Slicer (Fedorov et al., 2012; Kikinis et al., 2014). This implementation is specifically targeted at intraspecific studies in ecology, evolution and biomedicine.
2. MATERIALS AND METHODS
Below, we present and describe in detail: (a) the set of images and landmarks used to explore the performance of the method, (b) the proposed pipeline and (c) the metrics employed to validate the approach and to quantify how reliable it is in comparison with manual digitization and other image‐based registration methods that have been published in the literature.
2.1. Samples
When developing automated landmarking methods, it is often useful to have a dataset of manually digitized samples to serve as a reference set (i.e. a gold standard for performance). We have developed and tested our approach on a standard dataset used in many image‐based automated landmarking approaches, namely the laboratory mouse skull (Devine et al., 2020; Maga et al., 2017; Percival et al., 2019). For the sake of generality, we also test it on three separate datasets belonging to non‐human primates (Pongo, Pan and Gorilla). Figure S1 presents the anatomical landmarks used in this study. We note, however, that our approach should work for any other biological structure of interest, and it is not restricted to craniofacial research.
2.1.1. Mice
More specifically, we developed and initially tested the ALPACA framework on a published dataset containing 51 wild‐ and laboratory‐derived inbred strains of mice (Table S1, Maga et al., 2017). In short, 8‐week‐old females, each derived from a total of 25 inbred and 5 F1 crosses, were commercially acquired from Jackson Laboratories and then sacrificed at 56 ± 3 days of age via CO2 asphyxiation followed by decapitation. Heads were imaged using a Skyscan 1076C micro‐CT using a standardized imaging protocol. These images were then processed following Maga et al. (2017). All animal procedures used in the study were reviewed and approved by the Institutional Animal Care and Use Committee of the Seattle Children's Research Institute (protocol # 13733).
2.1.2. Hominoids
We also applied the ALPACA framework to skull meshes belonging to three other mammalian datasets, all of them great apes: Pan troglodytes (N = 11), Gorilla gorilla (N = 22) and Pongo pygmaeus (N = 18). These meshes were generated from CT scans of dry crania of specimens housed in the National Museum of Natural History (NMNH). We present the list of specimens used in this study as Table S1. More details can be found on Rolfe et al. (2021). We should note that all three ape datasets were analysed separately from each other, at the intraspecific level. We should also note that specimen choice was based purely on availability of dry crania 3D volumes.
2.2. Overview of the pipeline—ALPACA
We approach the problem of automated 3D landmarking using a lightweight point cloud registration approach based on surface meshes. In this approach, a reference mesh (here, the source mesh) is aligned and posteriorly deformed to match a target mesh for which we want to predict the landmark positions for. Using the transformation parameters used to deform one mesh into another, we project the landmark positions of the source mesh into the target one. In other words, we approach the problem of automated landmarking by transferring the landmark position of a single specimen (or template) into another (Figure 1).
FIGURE 1.
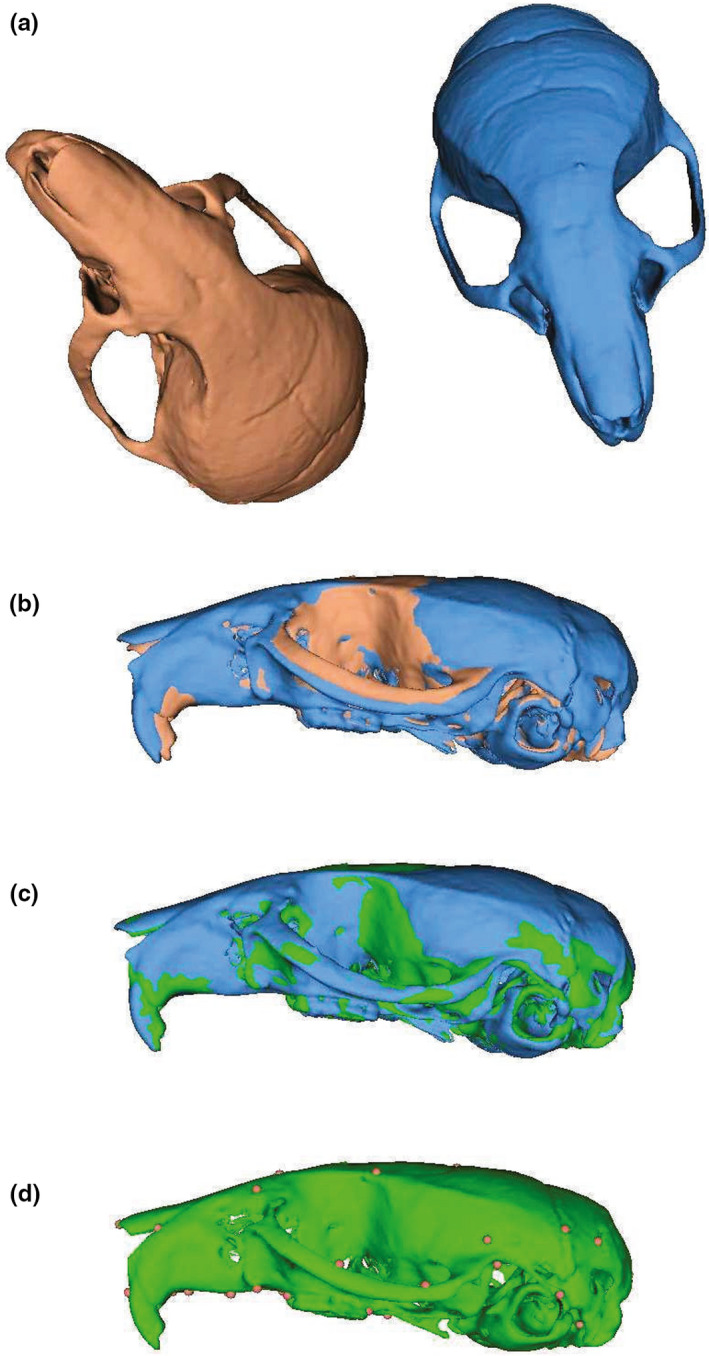
Visual representation of the ALPACA pipeline. Starting with a source (red) and target (blue) meshes representing the same biological structure and lying at arbitrary positions in XYZ axes (a), the pipeline starts with an initial downsampling of the two meshes into point clouds that are then rigidly aligned (b) to each other. Note the differences between the two meshes in terms of the angle of the nasal bone relative to the neurocranium and in terms of the position of the zygomatic arch. Once rigidly aligned, these point clouds are then subjected to a deformable registration step (c) in which the source mesh is warped (green) to match the target one (blue). Note how the nasal bone and zygomatic arch are much more closely aligned. Finally, after the deformable registration step, the landmark positions (dots) in the source mesh are projected into the target one (d) using point correspondence
Note that the source sample does not necessarily need to be aligned to the target one (i.e. meshes can be oriented in opposite directions). Similarly, one could choose the surface mesh of any specimen for which landmark data are available as the source mesh. The same is true for the target sample. However, it is advisable to carefully consider which specimen should be chosen as the reference specimen to annotate new samples with, as the template choice may itself influence the quality of the prediction (Young & Maga, 2015). This is particularly true when the reference sample is not near the species/population average shape (see Figure 2a). The speed and ease of ALPACA pipeline is meant to greatly facilitate an initial exploration of the automation parameters, including the choice of template specimen. The user can quickly change the source sample and compare how resultant landmarks differ across samples. Overall, this initial exploration of parameters is best done using target specimens that are highly divergent in shape, therefore lying near the edge of the shape distribution. In particular, target specimens near the edge of the shape distribution will be the furthest away from the centre of the deformation space, and therefore will require the largest deformation magnitude (Young & Maga, 2015). Based on the two initial samples, the pipeline then proceeds as follows.
FIGURE 2.
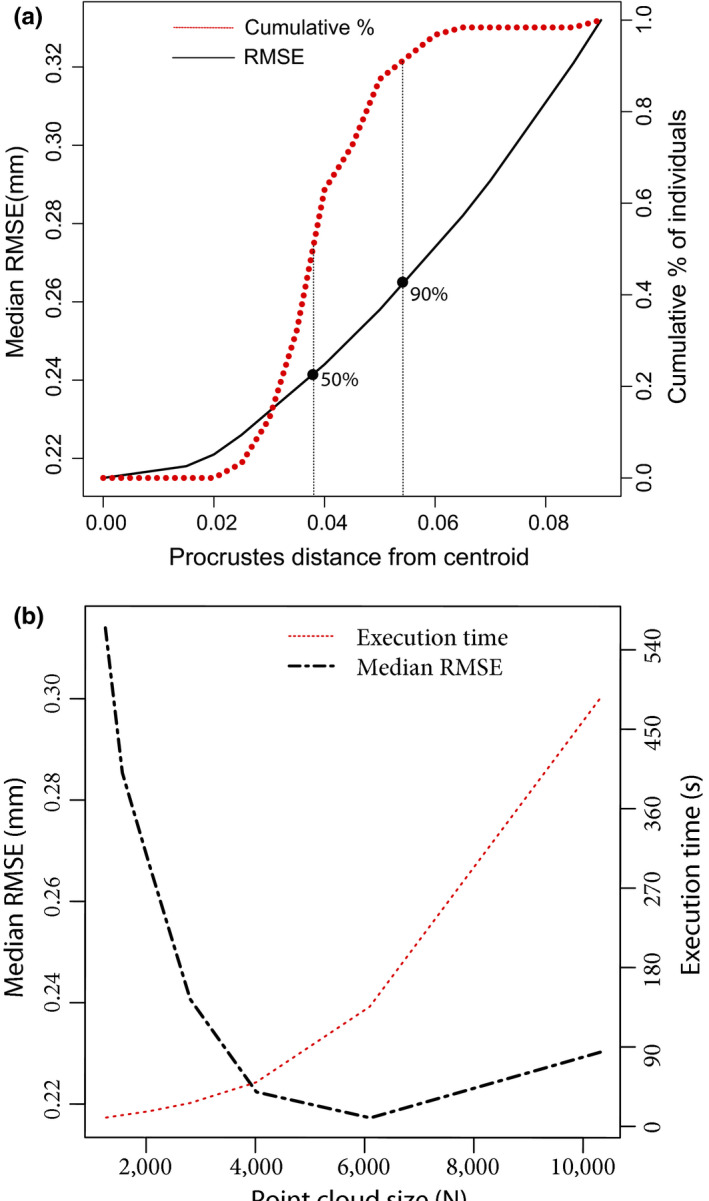
(a) Prediction error (black solid line) and cumulative percentage of individuals (red dotted line) as a function of the template's Procrustes distance from the centroid. Note that prediction error, measured in terms of the root mean squared error, has a nonlinear relationship with the template's distance from the centroid and is minimized at 0 (synthetic template). The cumulative percentage of individuals at a certain distance from the centroid is also nonlinearly related to the distance from the centroid, with 50% of the specimens being <0.04 units away from the centroid and 90% of the specimens being <0.06 units away from the centroid. In other words, if one was to choose a random sample as template, one would have a 50% chance of obtaining RMSE values around (or lower than) ~0.24 mm and a 90% chance of obtaining RMSE values around (or lower than) ~0.27 mm. (b) Prediction error (black dashed line) and execution time (red dotted line) of the ALPACA pipeline at different point cloud sizes based on the mouse dataset. Note that prediction error, measured in terms of the root mean squared error, has a nonlinear relationship with point cloud size and is minimized on point clouds in the 5,000–6,000 points range. Execution time, measured in seconds, is also nonlinearly related to point cloud size, increasing exponentially with increasing point cloud size
2.2.1. Step 1—Scaling and downsampling
The ALPACA pipeline starts with an optional step. In this step, the source mesh is isotropically scaled to match the target mesh. Following the optional scaling procedure, the source and target meshes are then uniformly downsampled to simplify the initial alignment and increase the speed of calculation. The downsampling procedure occurs in units of physical space and discards the edge information, transforming the mesh into a point cloud. In our case, we downsampled each mesh using a voxel grid (Zhou et al., 2018) to a point cloud of approximately 5,000 points. Voxel grid downsampling occurs through the regular subdivision of 3D space at a user‐defined voxel size, and in which mesh vertices falling within the same voxel get replaced by their centroid. The 5,000‐point standard was empirically determined to be a good compromise between accuracy and computational burden (Figure 2b), based on an initial exploration of hyperparameters using the mouse dataset, and has been independently observed in the literature in other contexts and datasets (Hirose, 2020a). Once downsampled, the two point clouds are then subjected to a global registration procedure that aligns these two samples in physical space (see Figure 1).
2.2.2. Step 2—Global registration
Similar to Procrustes superimposition techniques, global registration techniques aim to find the optimal rotation, translation and scaling transformations required to align two 3D shapes starting from arbitrary initial positions (Gelfand et al., 2005). In other words, they aim to find a transformation that correctly registers a source point cloud or image to a target one. Usually, approaches to global registration use iterative procedures that either (a) exhaustively search hyperparameter space for optimal combinations of parameters, or (b) run until some convergence criteria are met (Zhou et al., 2016). As such, they are often plagued by the curse of dimensionality, making them inefficient and more error prone at increasing image sizes. These approaches, however, perform well when using semantically rich local geometric descriptors, which greatly decrease the false correspondence rate when comparing two point clouds (Chen et al., 2019). In our case, we used a feature‐based random sample consensus algorithm (RANSAC) to estimate the optimal transform (Rusu et al., 2009). Essentially, in each RANSAC iteration, a user‐defined number of points are sampled from the source point cloud and their corresponding points in the target point cloud are identified through finding their nearest neighbour in a space of geometric features. The features, in this case, are fast point feature histograms (FPFHs; Rusu et al., 2009). FPFHs are 33‐dimensional vectors that provide a description of the local geometric properties around a point and that are scale invariant, providing the RANSAC algorithm with good discriminative power in the search for point correspondence across point clouds.
Aside from the number of iterations and the number of validation steps typical of iterative algorithms, ALPACA's implementation of the FPFH‐based RANSAC has three main parameters that can be defined by the user. The first one is the normal search radius that defines the neighbourhood of points used when calculating the surface normals in each point cloud. The second is FPFH search radius, which defines the neighbourhood of points used when computing the FPFH features. Lastly, users have the option of controlling the maximum distance between two points up to which the points can be considered corresponding to each other (in voxel size units).
Once the rigid transforms are obtained from the FPFH‐based RANSAC, they are then fed to the third step of our pipeline, representing a local registration step.
2.2.3. Step 3—Local registration
While the FPFH‐based RANSAC algorithm provides an approximation of the rigid transform, its alignment is performed using broad geometric features, which lead to an imperfect alignment. To refine the initial alignment, we then proceeded with a local registration algorithm.
The alignment of the two point clouds was improved upon through an iterative procedure that assigns, to each point in the source point cloud, its closest point in the target point cloud. In our case, we opted to using the point‐to‐plane iterative closest point algorithm (point‐to‐plane ICP) to do so (Rusinkiewicz & Levoy, 2001). ICP represents a family of widely used local registration algorithms, with applications in a variety of computer vision problems (Rusinkiewicz & Levoy, 2001). Essentially, given the target and source point clouds, the ICP algorithm calculates, at each iteration, the squared distance between each source point and the tangent plane at its corresponding target point. The algorithm proceeds iteratively until the distance between the two point clouds is minimized. The main advantage of the point‐to‐plane version of ICP is the speed of convergence relative to point‐to‐point error (Rusinkiewicz & Levoy, 2001).
Similar to the global registration step, the result of the point‐to‐plane ICP is a rigid transform, corresponding to the optional rigid alignment of the source and target point clouds. Also, similar to the global registration step, users have the option to control a maximum distance between points (in voxel size units) up until which they still can be considered corresponding to each other.
Once the optimal rigid alignment is obtained, we then proceed to the deformable registration step of the pipeline.
2.2.4. Step 4—Deformable registration and point projection
The final step of the ALPACA pipeline is the deformation of the rigidly aligned source point cloud to match the target point cloud. We use a low‐rank implementation of Coherent Point Drift (CPD) algorithm to do so (Dupej et al., 2015; Myronenko & Song, 2010). CPD is a probabilistic procedure for point cloud registration, in which the alignment of two point clouds is framed in terms of a probability density estimation. The source point cloud represents Gaussian mixed model (GMM) centroids that are fitted to the target set using maximum likelihood (Myronenko & Song, 2010). The main benefit of CPD is that it imposes a constraint in the form of motion coherence among neighbouring points, leading to deformations that preserve the topology of the structure of interest. It also makes no other underlying assumption about the nature of the transformation itself, allowing for a wealth of possible deformation models to be true. Finally, it has the additional benefit of being one of the few methods for non‐rigid registration that can accommodate large point clouds (5,000+ points) with slightly different numbers of points (Myronenko & Song, 2010).
ALPACA's implementation of CPD contains two free parameters (β and α), and uses a partial eigenvector decomposition of large matrices during the M‐step of the Expectation–maximization (EM) algorithm to improve speed (following Myronenko & Song, 2010). Parameter β refers to the width of the Gaussian filter used when applying smoothness constraints, representing one approach to regularization. High values of β create large directional correlation among the displacement vectors of neighbouring points during deformation, and vice versa (Hirose, 2020b). Parameter α, on the other hand, represents a trade‐off between goodness‐of‐fit and model regularization, with high values leading to overall structural rigidity and low values to more structural fluidity (Hirose, 2020b).
Following the deformation, ALPACA has a final and optional post‐processing step in which the predicted landmarks are projected to the target surface mesh. This step guarantees that the landmarks will lay on the most exterior surface of the original mesh, limited by a user‐adjustable point displacement (the default being 1% of the diagonal size of the image). Each point is projected from the deformed model to the original surface using the following steps: (a) cast a ray from a landmark point on the deformed model in the direction of its normal vector. Select the final intersection with the original model as the intersection point; (b) If there is no intersection, reverse the direction of the normal vector and select the first intersection with the original model; (c) In the case no intersection is found, select the closest point on the original model.
2.3. Prediction parameters
The parameters used when running ALPACA on all four datasets are present in Table 1. When running the pipeline for the mouse dataset, we have used the synthetic population template presented in Maga et al. (2017) as the initial source mesh. While the ALPACA pipeline does not require a synthetic source template, that is the recommended single‐template approach given its demonstrated ability to maximize the performance of registration methods by minimizing the average deformation magnitude (Young & Maga, 2015). Additionally, by using the same template used for another automated landmarking approach, we can directly compare the results obtained by each method.
TABLE 1.
Point cloud registration parameters used for each dataset. Parameters are divided according to the corresponding step of the pipeline. See main text for details
| Dataset | Source | Subsampling | RANSAC a | ICP a | CPD | |||
|---|---|---|---|---|---|---|---|---|
| Voxel size (mm) | Normal search radius | FPFH search radius | Max distance | Max distance | α | β | ||
| Mus | Template | 0.5 | 2 | 5 | 1.5 | 0.4 | 2 | 2 |
| Pan | USNM220063 | 5.4 | 2 | 5 | 1.5 | 0.4 | 1 | 6 |
| Pongo | USNM588109 | 6.5 | 2 | 5 | 1.5 | 0.4 | 1 | 6 |
| Gorilla | USNM176211 | 7.5 | 2 | 5 | 1.5 | 0.4 | 1 | 6 |
Abbreviations: CPD, coherent point drift; ICP, iterative closest point; RANSAC, random sample consensus.
Parameters are defined relative to voxel size.
To provide users with a clearer picture of the impact of template choice on the pipeline's performance, we also ran the pipeline with five extra template specimens (A/J, SF/CamEiJ, CB6F1/J, SPRET/EiJ and C3H/HeJ), representing specimens that are increasingly distant from the population centroid (in 0.01 Procrustes units). These extra templates were used to estimate the relationship between distance from the centroid and pipeline performance, in such a way as to provide users with useful parameters regarding the impact of template choice on the outcome of the analysis (Figure 2a).
When running the pipeline on the three non‐human primate datasets, a randomly chosen specimen was used to generate the predictions for the remaining ones. Specimens with missing skull elements (e.g. teeth) or damaged skulls were not added to the pool of specimens from which random samples were drawn, as the algorithm assumes the presence of corresponding structures in the source and target meshes.
Note that all datasets used here to test the performance of the method are intraspecific datasets represented by adult specimens at similar ontogenetic stages. As such, caution is advisable when extrapolating the pipeline's performance reported here to, for example, interspecific study questions. We anticipate, however, that the ALPACA pipeline could be confidently used in interspecific contexts involving topologically simple skeletal elements, such as long bones or mandibles.
2.4. Evaluating performance
We evaluated the performance of ALPACA's approach not only in terms of the Euclidean distance between the manual and predicted landmark locations, but also in terms of the patterns of morphological variation and covariation among landmarks. Note that the underlying assumption in doing so is that the manual dataset represents the ground truth, which is almost certainly incorrect (e.g. Robinson & Terhune, 2017). For that reason, the term accuracy, as used in the remaining of this manuscript, should be understood in that context.
2.4.1. Euclidean distance
One way in which automated landmarking datasets can be evaluated is through the calculation of the root mean squared error (RMSE) between the landmark positions as predicted by the pipeline and as manually annotated (e.g. Percival et al., 2019). RMSE values calculated for such datasets include not only the errors committed by the automated pipeline, but also observation errors committed by the anatomical expert. While the pipeline error can be minimized, intra‐observer error is unavoidable. Therefore, the error produced by the pipeline should always be evaluated on a relative basis (Percival et al., 2019). We here consider the intra‐observer error as the minimum possible error the approach could hope to achieve and, therefore, use it to evaluate relative performance. While measurements of intra‐observer error are difficult to be obtained for most datasets, the mouse skull and mandible have become a standard dataset in many automated landmarking algorithms (e.g. Devine et al., 2020; Maga et al., 2017; Percival et al., 2019; Young & Maga, 2015). Consequently, there are precise published estimates of intra‐observer error for most of our landmarks (35 of 45; Percival et al., 2019). We here assume that the intra‐observer manual annotation errors reported by Percival et al. (2019) are, to a large extent, representative of the morphometric community at large.
Since the non‐human primate datasets have not been measured repeatedly, we report their overall RMSE values but evaluate these datasets purely in terms of their ability to accurately characterize size and shape variation.
2.4.2. Size and shape
To quantify the impact of the choice of method on the results of size and shape analyses, we performed a joint generalized Procrustes superimposition across datasets (Rohlf & Slice, 1990). We then performed a Procrustes ANOVA (Anderson, 2001, 2014; Goodall, 1991) with landmarking method as a factor using the procD.lm function in geomorph 4.0 (Adams et al., 2021). This led us to quantify the percentage of the total variance in shape that is associated with the choice of landmarking methodology and its corresponding standard score (Z).
We also use the joint superimposition to test whether Procrustes variances obtained by each method are significantly different from one another using a permutation procedure where the vectors of residuals are randomized among groups, as implemented in the morphol.disparity function in the geomorph R package (Adams et al., 2021).
To evaluate the ordination of specimens in size and shape space, we correlate the manual predictions with the automated ones in terms of size (centroid size) and shape, represented here by the pairwise Euclidean distances between specimens in the tangent shape space.
Finally, to evaluate the similarity in the distribution of morphological variation in multivariate space, we perform a principal component analysis of the manual dataset and project the automated landmark configurations into the manual PC space. We then reduce the Procrustes shape coordinates to the first six principal components to avoid collinearities, following Le Maître and Mitteroecker (2019). After that, we calculate variance/covariance matrices for both automated and manual configurations in this shared space and test the proportionality of these matrices using a maximum likelihood method as implemented in the vcvComp R package (Le Maître & Mitteroecker, 2019). Finally, we compare the trace (i.e. overall shape variance) of these matrices using a resampling procedure following Devine et al. (2020), therefore testing whether observed differences in overall shape variance are larger than differences that should be expected solely based on sampling error. The rationale used when comparing measurement error to sampling error is simple. Automated methods allow for substantial increases in the sample sizes of most studies (e.g. Porto & Voje, 2020). Consequently, the smaller the error produced by the pipeline relative to sampling error, the less significant measurement error becomes in terms of its effect on the study's outcome, depending on the hypothesis being tested.
2.5. Bias correction
In many situations, researchers might be interested in combining datasets generated by automated landmarking methods with manually annotated ones (Percival et al., 2019). That is often a challenging task, since there is the possibility that both the means and error variances are different across landmarking methods. Hence, when possible, it is generally not advisable to do so. However, there are a few situations in which such interest might be justified. For example, a researcher might be interested in combining multi‐year (large) datasets that were acquired using different methods by a laboratory producing advanced intercross lines (e.g. Cheverud et al., 2014). In another example, a researcher might have detected a consistent bias in the way ALPACA has predicted landmark positions for their specimens. In that case, we here propose the usage of a parametric empirical Bayes framework (ComBat model, Fortin et al., 2018) to robustly adjust the tangent space coordinates for these effects. This batch‐effect correction framework assumes that the expected values of the tangent space coordinates can be modelled as linearly dependent on (landmarking) method‐specific effects, and whose errors are also method specific. The underlying assumption is that the landmarking method has both additive and multiplicative effects on the tangent space coordinates (Fortin et al., 2018).
The outputs of this linear model represent the bias‐corrected tangent space coordinates, if we assume the manual landmarking method to be the reference one.
In our case, the only dataset large enough to apply bias correction was the mouse dataset. To do so, we selected a small percentage of the original samples (20%) to estimate the ComBat model parameters and use such parameters to correct the automated predictions for all remaining samples (80%), we then evaluate the impact that such procedure has on RMSE estimates and overall mean configuration plots.
2.6. Implementation—SlicerMorph module
All algorithms were implemented as a SlicerMorph (Rolfe et al., 2020) module using the following external python libraries: open3d v.0.10.0 (Zhou et al., 2018) and pycpd 2.0.0. Source code for SlicerMorph is Python based and can be found at https://github.com/SlicerMorph/SlicerMorph or downloaded directly from the 3D Slicer Extension Manager. The ALPACA module provides a graphical user interface, and it can be run on any operating system. As Supporting Information, we provide installation instructions and links to a detailed ALPACA tutorial. The ALPACA pipeline was implemented with two different modes of functionality: a pairwise and a batch processing. The pairwise branch should largely be used to perform a user‐guided search for the best combination of parameters (including template) for their dataset, which can then be applied to a larger array of samples in batch mode. Note, however, that SlicerMorph module was developed with a larger array of use cases than the four datasets we present here and, therefore, presents default parameters that might not be necessarily ideal for all study systems. While rigid registration parameters are robust to a large array of scenarios and are unlikely to require change, deformation parameters often need to be slightly adjusted across study systems for maximal performance. Similarly, largely due to the underlying RANSAC implementation, ALPACA is not strictly deterministic, due to one of its python dependencies. In the mouse dataset, repeated runs using the same specimens and the same hyperparameters will produce final predictions that are 0.03 mm apart, on average. Note, however, that all results presented in this manuscript are robust to multiple independent runs of the pipeline and yield, at the population scale, virtually identical qualitative and quantitative results on each run. For example, multiple runs of the pipeline for the mouse dataset result in average RMSE values that are identical up to the third decimal (1/1,000th of a millimetre). In other words, imprecision at the single landmark level does not imply the same level of imprecision in the population mean RMSE.
3. RESULTS
3.1. Implementation speed
We used the mouse dataset (N = 51) to benchmark the speed of the pipeline, using a Linux Mint OS laptop with an Intel Core i7‐6700HQ 2.7Ghz CPU and with 16 GB of RAM. The complete ALPACA workflow for 51 samples took approximately 1.47 hr. Most of the time (>50%) was spent on the deformable registration step. When run pairwise, the breakdown per specimen (on average) is as follows: 0.67 s for downsampling, 1.42 s for global registration, 8.27 s for local registration (2.23 s of which are devoted to the calculation of surface normals) and 105 s for deformable registration.
3.2. Manual landmarks versus ALPACA landmarks
3.2.1. Euclidean distances
In terms of their Euclidean distances to manual landmarks, which we treat as the gold standard, the majority of ALPACA's landmarks were accurately placed by the pipeline. We here report the observed RMSE values both in millimetres and as percentages relative to the maximum skull length.
In the mouse dataset, median RMSE values varied from 0.12 mm (0.5%) to 0.87 mm (3.8%; Figure 3a), with an average of 0.22 mm (0.95%). These RMSE values are within the same range as to those obtained by other image‐based registration methods (Figure 3, blue dots, Percival et al., 2019), and also within 0.03 mm of the manual (intra‐observer) error (Figure 3, green squares). Note that intra‐observer error represents the theoretical minimum error the pipeline could hope to achieve. Only landmarks 2 and 3 present much higher than average error (>2 SD from mean) when compared to the manual dataset and those are associated with a methodological bias in the estimate of the population mean, as it will be further explored in the Procrustes analysis section.
FIGURE 3.
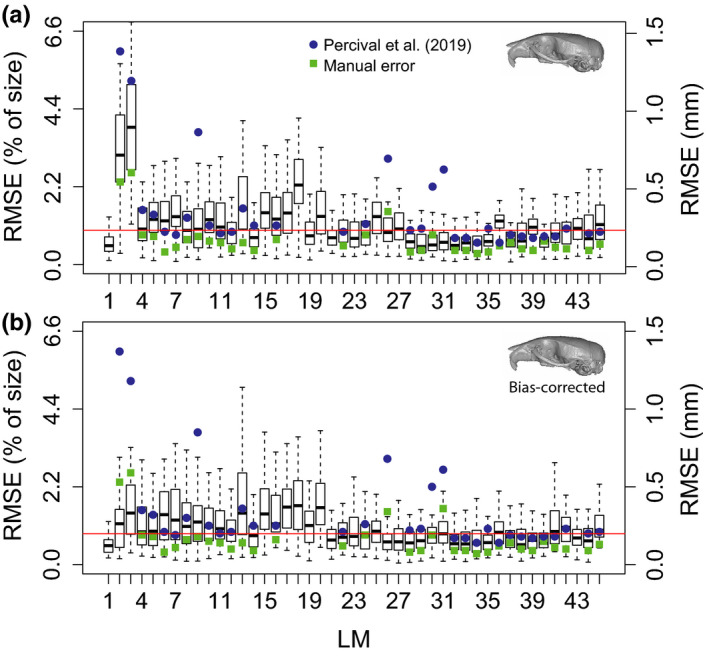
Boxplots illustrating the landmark‐specific distribution of prediction errors for the mouse dataset, measured as root mean squared error (RMSE). (a) Initial predictions. (b) Bias‐corrected predictions. RMSE values are calculated based on the difference between the predicted landmark positions and their manually annotated counterparts (in mm). The median error across landmarks is illustrated with a red line. Prediction errors calculated for an image‐based registration approach are illustrated with blue circles (Percival et al., 2019). Intra‐observer errors calculated by Percival et al. (2019) are presented as green squares
Bias correction considerably reduced mouse RMSE values for most landmarks and effectively corrects it for the biases on the population means (Figure 3b). On average, mouse RMSE values after correction are 0.032 mm lower than the uncorrected ones (Figure 3b), resulting in a mean value of 0.188 mm (0.82%).
Finally, we should also highlight that the maximum improvement that could be expected in any future automated algorithm is in the order of 0.03 mm, given the difference between bias‐corrected RMSE values (~0.19 mm) and manual RMSE values (0.16 mm).
Among the great apes, median RMSE values were generally more homogeneous across landmarks and largely comparable across species relative to their overall skull size (Figure 4). Gorilla median RMSE values varied from 1.41 mm (0.4%) to 7.57 mm (2.3%), with an average of 3.12 mm (0.95%). Pan median RMSE values varied from 1.7 mm (0.87%) to 6.11 mm (3.13%), with an average of 2.42 mm (1.24%). Finally, Pongo median RMSE values varied from 1.58 mm (0.65%) to 5.43 mm (2.26%), with an average of 3.13 mm (1.3%).
FIGURE 4.
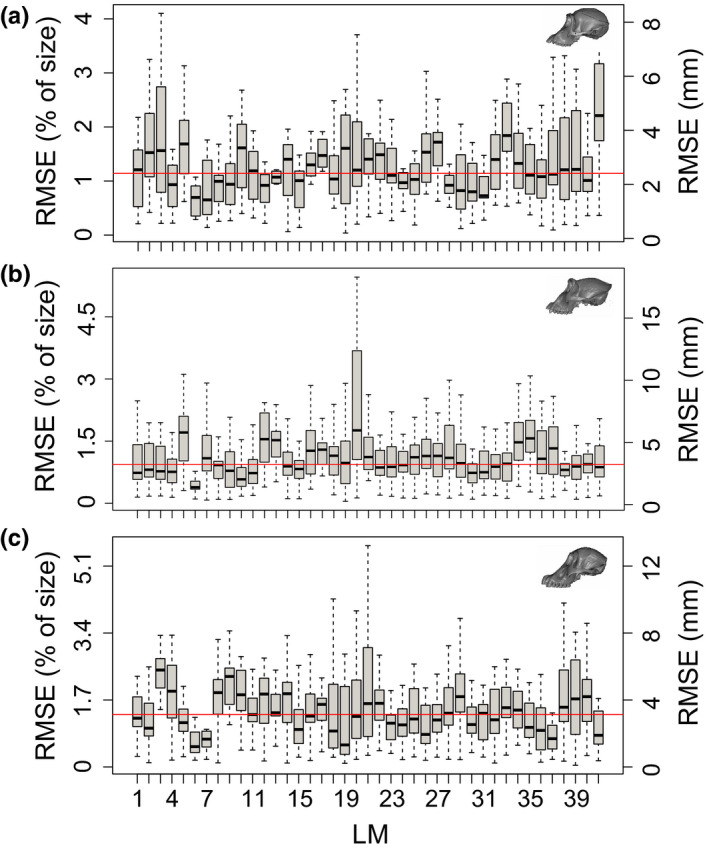
Boxplots illustrating the landmark‐specific distribution of prediction errors for all three great ape datasets, measured as root mean squared error (RMSE). RMSE values are calculated here based on the difference between the predicted landmark positions and their manually annotated counterparts (in mm). The median error across landmarks is illustrated with a red line. (a) Pan; (b) Gorilla; (c) Pongo
When standardized by the maximum skull length, median RMSE values observed across species are equivalent to 0.95% (Mus), 0.95% (Gorilla), 1.24% (Pan) and 1.3% (Pongo), indicating similar performance of ALPACA across different organisms.
3.2.2. Procrustes analysis
In Figure 5, we report a joint generalized Procrustes analysis (joint GPA) of manual‐ and ALPACA‐based landmark datasets. ALPACA‐based landmark configurations broadly overlap (>0.7 intersection over union) with those obtained through manual digitization (blue vs. red, Figure 5a,d–f). On the mouse dataset, the manually digitized dataset possesses larger Procrustes variances than ALPACA dataset, as revealed by the morphological disparity test (p < 0.001). This difference is particularly noticeable for landmarks in the lateral parts of the nasal/premaxilla sutures (Figure 5a, landmarks 2 and 3) and is effectively removed by the bias‐correction procedure (Figure 5c, p = 0.124). No other dataset presents significant differences in the degree of morphological disparity (p = 0.147 for Pan, p = 0.246 for Pongo and p = 0.174 for Gorilla).
FIGURE 5.
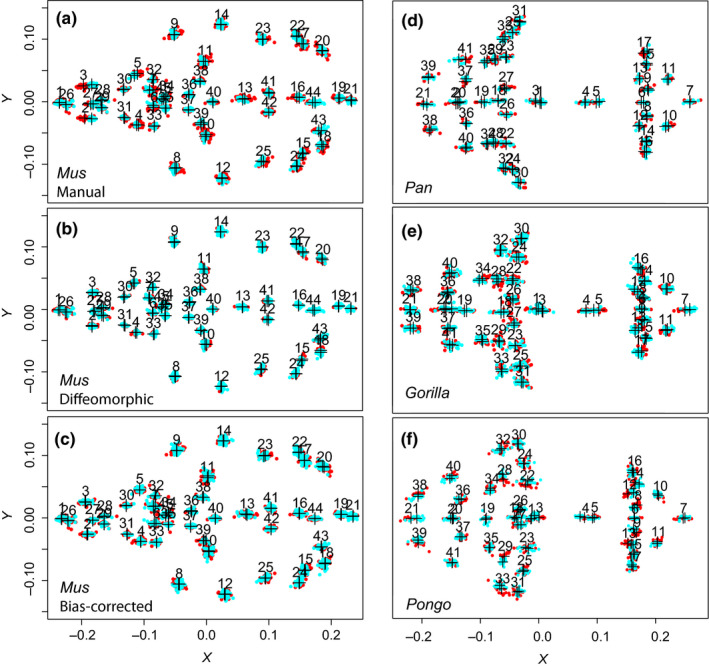
Two‐dimensional projection (XY) comparing the ALPACA landmark predictions (light blue) with other methods (red) after joint GPA superimposition. Crosshairs indicate the consensus shapes of each method under the joint superimposition. Other methods are, in order: (a) Manual landmarking (Mus); (b) Diffeomorphic approach described in Maga et al. (2017) (Mus); (c) Manual landmarking after bias correction (Mus); (d) Manual landmarking (Pan); (e) Manual landmarking (Gorilla); and (f) Manual landmarking (Pongo)
A Procrustes ANOVA conducted in the joint GPA data reveals that the landmark placement method (ALPACA vs. Manual) explains around 15% of the total variation around the mean shape in the mouse dataset (p < 0.001, Z = 4.8, Table S2). After bias correction, the landmark placement method loses its explanatory power (p = 0.49, R 2 = ~1%, Z = −0.001, Table S2). Landmark placement method explains comparable percentages of variation in all three ape datasets (R 2 = 14.4% and Z = 3.47 for Pan; R 2 = 12.4% and Z = 3.67 for Pongo; R 2 = 8.2% and Z = 2.94 for Gorilla; Table S2).
Automated‐manual correlations of specimen ordinations in terms of centroid size were high in all four datasets, varying from 0.98 (Pan) to 0.99 (Figure 6, first column). The correlations between the Euclidean distances in shape space, on the other hand, were moderate–high and less homogeneous than for centroid size, with correlations varying from 0.76 (Pan) to 0.87 (Mus; Figure 6, second column). Note, however, that Pan contains the smallest sample size (N = 11) of all four datasets.
FIGURE 6.
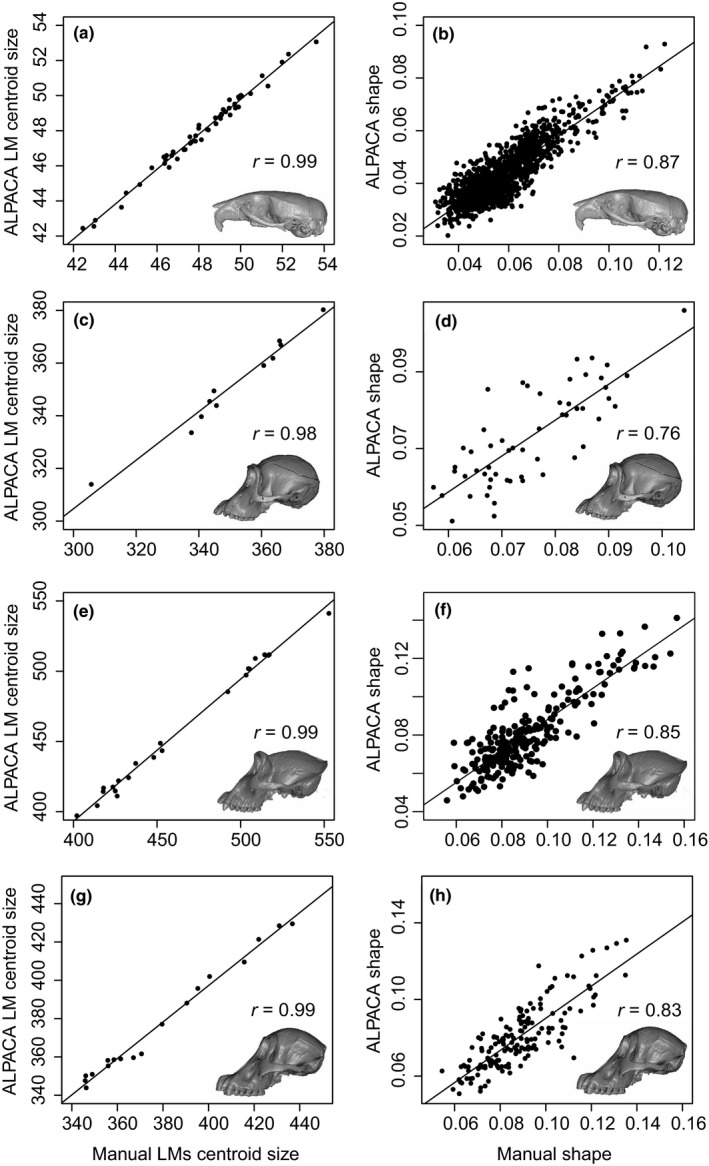
Comparison of centroid size (a–c–e–g) and shape (b–d–f–h) measures as predicted by ALPACA and by manual annotation. Note the high and statistically significant correlations (p < 0.001) across all datasets. Correlation values for each PC are presented in Figure 7. (a, b) Mus; (c, d) Pan; (e, f) Gorilla, (g, h) Pongo
When measured in terms of covariance matrix trace, automated shape variances were consistently and significantly lower than their manual counterparts (Figure 7, first column), with variance reductions varying from 35.2% (Mus, after bias correction) to 48% (Pan). Despite the difference in overall variances, we could not reject the proportionality of automated‐manual matrices in either of the ape datasets (p = 0.96, Pan; p = 0.64, Gorilla; p = 0.65, Pongo). The only dataset to present significant differences across manual‐automated matrices was the mouse dataset prior to bias correction (p = 6.5 × 10−5). After bias correction, however, we could not reject the proportionality of automated‐manual matrices in the mouse (p = 0.14).
FIGURE 7.
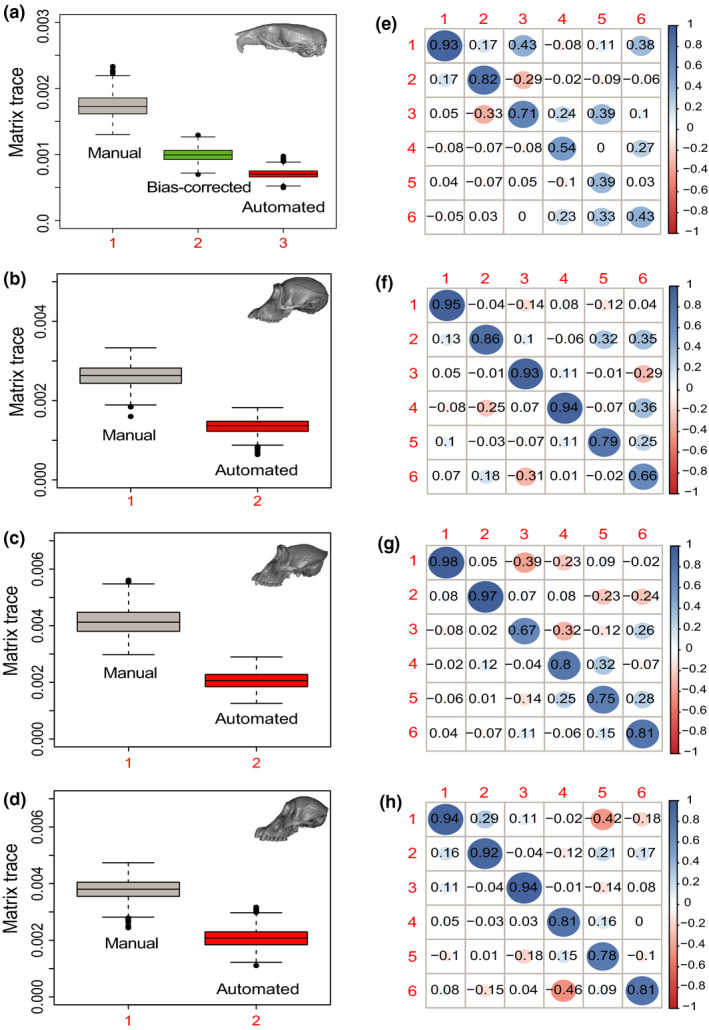
(a–d) Estimates of overall craniofacial variance obtained by bootstrap resampling the trace of each covariance matrix. (e–h) Correlation between the automated and manual PC scores for the first six PCs in the manual PC space. First row = Mus; Second row = Pan; Third row = Gorilla; Fourth row = Pongo
Finally, automated‐manual PC correlations were generally high (>0.8) for most higher ranking PCs (Figure 7, second column). Correlations varied from 0.93 to 0.98 for PC1, 0.82 to 0.97 for PC2 and 0.67 to 0.94 for PC3. Correlations between PCs ranking 4 and lower varied more widely across datasets, with the mouse dataset presenting correlations as low as 0.39 for PC5. Note that PC scores were calculated in the PC space of the manual dataset.
3.3. ALPACA landmarks versus diffeomorphic landmarks
Since the mouse dataset reported in this study has been used to develop an image registration pipeline (Maga et al., 2017), we also report a joint GPA comparing ALPACA to more traditional image registration workflows.
The ALPACA‐based landmarks show broadly overlapping (>0.7 intersection over union) distribution relative to the diffeomorphic ones after a joint superimposition (Figure 5b).
A Procrustes ANOVA conducted in the joint GPA reveals that there is a significant difference between the multivariate means obtained for both datasets (p < 0.001). However, contrary to manual datasets, the morphological disparity test indicates that one could not distinguish such approaches in terms of the level of morphological disparity (p = 0.797), with ALPACA having higher PC score correlations to the diffeomorphic dataset (Figure 8). Finally, both the centroid sizes and the pairwise Euclidean distances between specimens in shape space are also highly correlated across the two methods (Figure 8).
FIGURE 8.
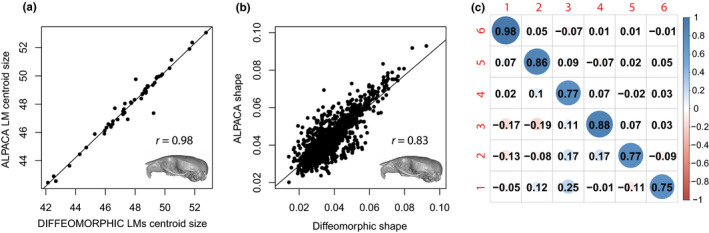
Comparison of centroid size (a) and shape (b) measures as predicted by ALPACA and by the diffeomorphic method of Maga et al. (2017) based on the mouse dataset. Note the high and statistically significant correlations (p < 0.001) between the two methods. (c) ALPACA and diffeomorphic PC score correlations for the first six PCs
4. DISCUSSION
Dense morphometric characterizations of biological structures have become an essential component of morphological studies in ecology and evolution (Bardua et al., 2019; Collins et al., 2019; Goswami et al., 2019; Souter et al., 2010). Consequently, the gold standard for morphometric data collection (i.e. manual digitization) has become an important bottleneck for morphometric research pipelines. Here, we propose a fast and accurate intraspecific pipeline for automated landmarking in any 3D biological structure. Our approach is based on a lightweight point cloud registration approach, which can be used to transfer landmarks from a single source specimen to one or multiple targets, accurately placing landmarks of interest on unmeasured specimens.
4.1. ALPACA advantages
One main benefit of our approach relative to other automated methods is that it is more broadly applicable to intraspecific studies in ecology and evolution, for two main reasons. First, it works directly on surface meshes. While one can always generate a mesh from a volume, the same is not true when starting with a mesh. Since a substantial amount of 3D work utilizes surface scanners (both laser and lidar), ALPACA tends to be more generally applicable than volume‐based methods. Similarly, ALPACA allows for the use of a single reference specimen as the source mesh. While anatomical atlases are available for mouse datasets (e.g. Maga et al., 2017), they are rare for non‐model organisms and represent an important constraint for image‐based approaches. As demonstrated in the mouse dataset (Figure 2a), around 50% of the individuals in the population could be used as template and still yield results that are only 10% less accurate than using a synthetic template.
Other advantages of our framework are its accuracy, speed, consistency and its low hardware requirements.
4.1.1. Accuracy
When applied to the mouse dataset, our approach obtains results that are as accurate (or more) than other image‐based registration techniques (Figure 3) and recovers patterns of morphological variation that are statistically indistinguishable from those obtained by manual digitization (p = 0.14), provided bias correction is performed. While we observe greater Procrustes variances in the manually annotated mouse dataset when compared to automated one, this is a common observation in many image registration‐based approaches (e.g. Boyer et al., 2011; Devine et al., 2020; Maga et al., 2017; Percival et al., 2019) and is partially explained by the intra‐observer error present in manually annotated ones. As a matter of fact, we can calculate how much room still exists for methodological improvement based on the mouse dataset and this value seems to be in the order of 0.03 mm, given the small difference between bias‐corrected RMSE values and manual error values (Figure 3). Furthermore, since we have produced a SlicerMorph module that has a graphical user interface, any apparent error produced by the pipeline can be instantly corrected using the 3D Slicer's fiducial tools (Fedorov et al., 2012; Kikinis et al., 2014).
4.1.2. Speed and consistency
The other large benefit of automation is its overall speed and consistency. Calculating speed in morphometric data collection is fraught with difficulty, since both manual and automated approaches require some pre‐processing steps whose speed is hard to quantify. For manual landmarking, the researcher annotating the dataset will need to spend time getting used to the order of landmarks and the overall layout of the annotation software. These steps are not necessary in automated approaches. Automated approaches will require, on the other hand, a more thorough cleaning of each sample's mesh, due to the need for structural correspondence across samples. This cleaning step will often require segmentation of the morphological elements of interest and removal of any extraneous information (e.g. removal of neck vertebrae from a skull mesh). In other words, if sample pre‐processing cannot be automated, the speed of the algorithmic pipeline can be counterbalanced by bottlenecks in sample preparation. Cleaning steps are often much simpler for manual landmarking, since the user can start from an image sequence containing a myriad of extraneous morphological elements. As such, ALPACA's speed, as reported below, should be evaluated with this caveat in mind.
The ALPACA pipeline performs landmark prediction for the entire mouse dataset (N = 51) in 1.47 hr. Note that the number of landmarks annotated in each mouse skull is on the smaller side of current morphometric approaches (Bardua et al., 2019; Collins et al., 2019; Goswami et al., 2019; Souter et al., 2010) and that ALPACA's execution time is largely independent on the number of landmarks. Given the recent popularization of high‐density semi‐landmark approaches in ecology and evolution (Gunz & Mitteroecker, 2013), ALPACA would allow high‐density morphometric characterizations of numerous specimens in a matter of hours.
More importantly, ALPACA's main advantage over manual annotation is its consistency. As mentioned before, manual annotation is subject to significant amounts of intra‐ and inter‐observer bias. These biases are often in the same order of magnitude as intraspecific differences (Robinson & Terhune, 2017) and represent an important and understudied issue in the field. Currently, the only way to address concerns about bias in morphometric studies is through the use of multiple expert annotators. By using ALPACA, a single template can be used by a research group throughout the years, allowing for a better standardization of landmarking protocols and increasing its reproducibility. Similarly, even multiple research groups can use the same template, allowing for data to be combined across studies from different laboratories.
4.1.3. Hardware and ease‐of‐use
Finally, another major advantage of our framework is the ability to obtain high‐throughput phenotyping with consumer‐grade, off‐the‐shelf hardware. As currently implemented, the SlicerMorph module can be run on any machine with Windows 7 64‐bit, MacOS X Lion, or recent Linux distribution, 8 GB of RAM memory, 1,280 × 1,024 monitor resolution, and graphics card with at least 1 GB memory. For ease‐of‐use, the pipeline was implemented with two branches: pairwise and batch processing. The pairwise branch can be used to explore and fine‐tune the registration parameters by going through the process of registering a single (target) sample to its reference (source), step‐by‐step. This step‐by‐step approach allows users to find the best combination of parameters for their task, which can then be applied to a larger array of samples in batch mode. In other words, the batch processing branch opens up the possibility of a simple automated pipeline for high‐throughput high‐dimensional phenotyping, which will greatly increase the scale morphometric approaches in ecology and evolution.
4.2. ALPACA limitations
The main limitation of the proposed pipeline, which is largely shared with other deformable registration approaches, is that it can lead to spurious results when the initial shapes are too dissimilar and/or registration parameters are poorly chosen (Boyer et al., 2011; Percival et al., 2019). In other words, when working in a broad phylogenetic context, with species that are highly divergent in shape and form, the ability to find corresponding landmarks can breakdown. In our view, the proposed pipeline is better employed within species or among closely related species. In broad phylogenetic contexts, a more careful consideration of the source meshes will likely be necessary. One possible approach would be to use multiple source meshes, each corresponding to a clade or morphotype. In that case, ALPACA would still increase the speed and reproducibility of morphometric data collection, but it would have to be applied separately for each clade or morphotype. The application of ALPACA in this context would, as a consequence, allow researchers to sample more deeply within a clade or morphotype, thus increasing the overall sample size and improving the robustness of the morphometric results. Another possibility would be to use homology‐free landmark approaches (Boyer et al., 2015). One should note, however, that homology‐free approaches, such as Auto3DGM (Boyer et al., 2015), generally do not allow for the addition of samples post‐hoc. In other words, if a new sample needs to be incorporated into the dataset, the pipeline has to be rerun for all samples. This limitation is not present in ALPACA, since the use of a reference specimen (or template) allows for the addition of new samples post‐hoc, giving the user more flexibility.
Another limitation of the ALPACA is its sensitivity to the presence of noise in the form of additional skeletal structures or damaged parts (Myronenko & Song, 2010). In mouse datasets, for example, neck vertebrae and limbs are often still attached to the base of the skull. If skull segmentation is not properly carried out and rigidity constraints in the deformable step are not correctly fine‐tuned, the addition of such skeletal elements to the 3D surface can lead to spurious results. Similarly, primate skulls frequently present missing canines/incisors and males tend to present largely developed sagittal crests. Such missing, extremely dimorphic or damaged skeletal elements can potentially lead to increased prediction error. Note, however, that several of the primate skulls used in the current manuscript do present such artefacts and, therefore, the results presented here represent the actual performance of the method even when faced with significant challenges. In other words, due to the rigidity constraints in the deformable step, damaged or missing skeletal structures can be overcome (to some extent) by the pipeline when properly tuned (Figure S2). At some point, however, the differences will be too extensive for rigidity constraints to account for them. ALPACA is not unique in this sense, since these constraints (i.e. completeness, and sensitivity to additional objects) are common in almost all automated morphometric analysis.
A significant limitation of ALPACA that is also shared with other image registration approaches is its inability to respect qualitative boundaries. While ALPACA is quantitatively accurate (Figure 3), it does not impose qualitative constraints in landmark placement. For example, craniofacial researchers will often want their landmarks to fall precisely at suture lines. However, it is not uncommon to have automated approaches predict landmarks slightly off‐suture. To a large extent, this limitation embedded in image registration approaches is a direct consequence of the concept of homology underlying deformation‐based approaches. In such approaches, the ability to maintain homology is dependent on the ability of statistical deformations to mimic biological deformations. Certain disorders, such as the formation of the interfrontal bone in specific mice strains, will lead to spurious results due to a breakdown of equivalency between structures. In such cases, we suggest the use of Slicer fiducial tools to correct ALPACA predictions. Slicer has click‐and‐drag functionality for objects loaded into the scene, allowing the user to slide each landmark along the surface of the target mesh, and therefore allowing for an immediate correction of ALPACA predictions.
4.3. Future directions
While the current version of ALPACA is geared towards intraspecific studies in ecology and evolution, we have plans to expand the ALPACA pipeline to more diverse datasets. Currently, there are two expansions under development. In one, we are developing a multi‐template version of ALPACA. The multi‐template version will eliminate many of the issues associated with template choice, since the use of multiple templates has been demonstrated to greatly decrease template bias in similar contexts (e.g. Devine et al., 2020). Likewise, we are working towards a closest‐template approach that is geared towards interspecific datasets. Given a group of templates, the closest‐template approach allows the user to automatically choose the source sample that is closest in shape to the specimen at hand when generating the predictions. In other words, we want ALPACA to be viewed as an extensible platform from which more targeted pipelines can be developed.
5. CONCLUSIONS
We have developed a lightweight point cloud registration approach (ALPACA) for automated landmarking of 3D biological structures represented by surface meshes. The method is implemented as a SlicerMorph module and provides fast landmark transfer from a 3D model and its associated landmark set to target 3D models through point cloud alignment and deformable point cloud registration.
ALPACA's main strengths are its speed, which is at least an order of magnitude faster than other automated approaches, and accuracy, given its ability to replicate results obtained through manual digitization. It is, however, sensitive to missing, damaged or strongly dimorphic morphological elements.
We expect that ALPACA will greatly increase the scale of 3D geometric morphometrics, and that it will open up new research avenues for morphometric research.
CONFLICT OF INTEREST
None of the authors have a conflict of interest to declare.
AUTHORS' CONTRIBUTIONS
A.P. and A.M.M. conceived the project, collected the data and designed the methodology; A.P. analysed the data and developed the initial pipeline. A.M.M. acquired funding; A.P. and S.R. refined the pipeline and wrote the code, with S.R. leading the development of the SlicerMorph module. All authors contributed to writing the manuscript, with A.P. having the lead on the writing.
Supporting information
Fig S1‐S2
Table S1‐S2
Supplementary Material
ACKNOWLEDGEMENTS
This project is funded by an NSF grant (An Integrated Platform for Retrieval, Visualization and Analysis of 3D Morphology From Digital Biological Collections, award number 1759883) and by a NIH/NIDCR grant (Inbred Mice Strains: Untapped Resource For Genome‐Wide Quantitative Association Study For Craniofacial Shape, DE027110) to A.M.M. We thank participants of the Spring 2020 SlicerMorph Workshop for their valuable feedback on initial iterations of ALPACA. We thank the Smithsonian's Division of Mammals and Human Origins Program as well as Dr Matt Tocheri and Dr Kristofer Helgen for the scans of USNM specimens used in this research (http://humanorigins.si.edu/evidence/3d‐collection/primate). These scans were acquired through the generous support of the Smithsonian 2.0 Fund and the Smithsonian's Collections Care and Preservation Fund.
Porto, A. , Rolfe, S. , & Maga, A. M. (2021). ALPACA: A fast and accurate computer vision approach for automated landmarking of three‐dimensional biological structures. Methods in Ecology and Evolution, 12, 2129–2144. 10.1111/2041-210X.13689
Handling Editor Natalie Cooper
DATA AVAILABILITY STATEMENT
The mouse dataset is freely available as part of https://doi.org/10.1111/joa.12645 and is also available through Open Science Framework (https://osf.io/xzj4t/). The raw DICOM sequences of hominoids used here are freely available for non‐commercial use from the Smithsonian Institution's National Museum of Natural History (NMNH). From their main page (https://humanorigins.si.edu/evidence/3d‐collection/primates), select ‘Contact us’ and paste ‘3D model download access’ in your subject line.
REFERENCES
- Adams, D. , Collyer, M. , Kaliontzopoulou, A. , & Baken, E. (2021). Geomorph: Software for geometric morphometric analyses. R package version 4.0. Retrieved from https://cran.r‐project.org/package=geomorph [Google Scholar]
- Anderson, M. J. (2001). A new method for non‐parametric multivariate analysis of variance. Austral Ecology, 26, 32–46. [Google Scholar]
- Anderson, M. J. (2014). Permutational multivariate analysis of variance (PERMANOVA) (pp. 1–15). Wiley statsref: Statistics reference online. [Google Scholar]
- Bardua, C. , Felice, R. N. , Watanabe, A. , Fabre, A.‐C. , & Goswami, A. (2019). A practical guide to sliding and surface semilandmarks in morphometric analyses. Integrative Organismal Biology, 1(1). 10.1093/iob/obz016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyer, D. M. , Lipman, Y. , St. Clair, E. , Puente, J. , Patel, B. A. , Funkhouser, T. , Jernvall, J. , & Daubechies, I. (2011). Algorithms to automatically quantify the geometric similarity of anatomical surfaces. Proceedings of the National Academy of Sciences of the United States of America, 108(45), 18221–18226. 10.1073/pnas.1112822108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyer, D. M. , Puente, J. , Gladman, J. T. , Glynn, C. , Mukherjee, S. , Yapuncich, G. S. , & Daubechies, I. (2015). A new fully automated approach for aligning and comparing shapes. The Anatomical Record, 298(1), 249–276. 10.1002/ar.23084 [DOI] [PubMed] [Google Scholar]
- Bromiley, P. A. , Schunke, A. C. , Ragheb, H. , Thacker, N. A. , & Tautz, D. (2014). Semi‐automatic landmark point annotation for geometric morphometrics. Frontiers in Zoology, 11(1), 61. 10.1186/s12983-014-0061-1 [DOI] [Google Scholar]
- Chen, J. , Zhou, F. , Liu, B. , Bai, X. , Zhang, Y. , Zhao, T. , & Zhou, Y. (2019). 3D rigid registration of patient body surface point clouds by integer linear programming. In 2019 International Conference on Image and Vision Computing New Zealand (IVCNZ) (pp. 1–6). 10.1109/IVCNZ48456.2019.8960993 [DOI] [Google Scholar]
- Cheverud, J. M. , Lawson, H. A. , Bouckaert, K. , Kossenkov, A. V. , Showe, L. C. , Cort, L. , Blankenhorn, E. P. , Bedelbaeva, K. , Gourevitch, D. , Zhang, Y. , & Heber‐Katz, E. (2014). Fine‐mapping quantitative trait loci affecting murine external ear tissue regeneration in the LG/J by SM/J advanced intercross line. Heredity, 112(5), 508–518. 10.1038/hdy.2013.133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins, K. S. , Edie, S. M. , Gao, T. , Bieler, R. , & Jablonski, D. (2019). Spatial filters of function and phylogeny determine morphological disparity with latitude. PLoS ONE, 14(8), e0221490. 10.1371/journal.pone.0221490 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devine, J. , Aponte, J. D. , Katz, D. C. , Liu, W. , Vercio, L. D. L. , Forkert, N. D. , Marcucio, R. , Percival, C. J. , & Hallgrímsson, B. (2020). A registration and deep learning approach to automated landmark detection for geometric morphometrics. Evolutionary Biology, 47(3), 246–259. 10.1007/s11692-020-09508-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupej, J. , Krajíček, V. , & Pelikán, J. (2015). Low‐rank matrix approximations for coherent point drift. Pattern Recognition Letters, 52, 53–58. [Google Scholar]
- Falkingham, P. (2012). Acquisition of high resolution three‐dimensional models using free, open‐source, photogrammetric software. Palaeontologia Electronica., 10.26879/264 [DOI] [Google Scholar]
- Fedorov, A. , Beichel, R. , Kalpathy‐Cramer, J. , Finet, J. , Fillion‐Robin, J.‐C. , Pujol, S. , Bauer, C. , Jennings, D. , Fennessy, F. , Sonka, M. , Buatti, J. , Aylward, S. , Miller, J. V. , Pieper, S. , & Kikinis, R. (2012). 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magnetic Resonance Imaging, 30(9), 1323–1341. 10.1016/j.mri.2012.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felice, R. N. , Watanabe, A. , Cuff, A. R. , Noirault, E. , Pol, D. , Witmer, L. M. , Norell, M. A. , O'Connor, P. M. , & Goswami, A. (2019). Evolutionary integration and modularity in the archosaur cranium. Integrative and Comparative Biology, 59(2), 371–382. 10.1093/icb/icz052 [DOI] [PubMed] [Google Scholar]
- Fortin, J.‐P. , Cullen, N. , Sheline, Y. I. , Taylor, W. D. , Aselcioglu, I. , Cook, P. A. , Adams, P. , Cooper, C. , Fava, M. , McGrath, P. J. , McInnis, M. , Phillips, M. L. , Trivedi, M. H. , Weissman, M. M. , & Shinohara, R. T. (2018). Harmonization of cortical thickness measurements across scanners and sites. NeuroImage, 167, 104–120. 10.1016/j.neuroimage.2017.11.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelfand, N. , Mitra, N. J. , Guibas, L. J. , & Pottmann, H. (2005). Robust global registration. The Eurographics Association. 10.2312/SGP/SGP05/197-206 [DOI] [Google Scholar]
- Gignac, P. M. , Kley, N. J. , Clarke, J. A. , Colbert, M. W. , Morhardt, A. C. , Cerio, D. , Cost, I. N. , Cox, P. G. , Daza, J. D. , Early, C. M. , Echols, M. S. , Henkelman, R. M. , Herdina, A. N. , Holliday, C. M. , Li, Z. , Mahlow, K. , Merchant, S. , Müller, J. , Orsbon, C. P. , … Witmer, L. M. (2016). Diffusible iodine‐based contrast‐enhanced computed tomography (diceCT): An emerging tool for rapid, high‐resolution, 3‐D imaging of metazoan soft tissues. Journal of Anatomy, 228(6), 889–909. 10.1111/joa.12449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodall, C. (1991). Procrustes methods in the statistical analysis of shape. Journal of the Royal Statistical Society: Series B, 53(2), 285–321. [Google Scholar]
- Goswami, A. , Watanabe, A. , Felice, R. N. , Bardua, C. , Fabre, A.‐C. , & Polly, P. D. (2019). High‐density morphometric analysis of shape and integration: The good, the bad, and the not‐really‐a‐problem. Integrative and Comparative Biology, 59(3), 669–683. 10.1093/icb/icz120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunz, P. , & Mitteroecker, P. (2013). Semilandmarks: A method for quantifying curves and surfaces. Hystrix, the Italian Journal of Mammalogy, 24(1), 103–109. 10.4404/hystrix-24.1-6292 [DOI] [Google Scholar]
- Hirose, O. (2020a). Acceleration of non‐rigid point set registration with downsampling and Gaussian process regression. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1. 10.1109/TPAMI.2020.3043769 [DOI] [PubMed] [Google Scholar]
- Hirose, O. (2020b). A Bayesian formulation of coherent point drift. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1. 10.1109/TPAMI.2020.2971687 [DOI] [PubMed] [Google Scholar]
- Joshi, S. , Davis, B. , Jomier, M. , & Gerig, G. (2004). Unbiased diffeomorphic atlas construction for computational anatomy. NeuroImage, 23, S151–S160. 10.1016/j.neuroimage.2004.07.068 [DOI] [PubMed] [Google Scholar]
- Kikinis, R. , Pieper, S. D. , & Vosburgh, K. G. (2014). 3D Slicer: A platform for subject‐specific image analysis, visualization, and clinical support. In Jolesz F. A. (Ed.), Intraoperative imaging and image‐guided therapy (pp. 277–289). Springer. [Google Scholar]
- Le Maître, A. , & Mitteroecker, P. (2019). Multivariate comparison of variance in R. Methods in Ecology and Evolution, 10(9), 1380–1392. 10.1111/2041-210X.13253 [DOI] [Google Scholar]
- Maga, A. M. , Tustison, N. J. , & Avants, B. B. (2017). A population level atlas of Mus musculus craniofacial skeleton and automated image‐based shape analysis. Journal of Anatomy, 231(3), 433–443. 10.1111/joa.12645 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcy, A. E. , Fruciano, C. , Phillips, M. J. , Mardon, K. , & Weisbecker, V. (2018). Low resolution scans can provide a sufficiently accurate, cost‐ and time‐effective alternative to high resolution scans for 3D shape analyses. PeerJ, 6, e5032. 10.7717/peerj.5032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myronenko, A. , & Song, X. (2010). Point‐set registration: Coherent point drift. IEEE Transactions on Pattern Analysis and Machine Intelligence, 32(12), 2262–2275. 10.1109/TPAMI.2010.46 [DOI] [PubMed] [Google Scholar]
- Percival, C. J. , Devine, J. , Darwin, B. C. , Liu, W. , van Eede, M. , Henkelman, R. M. , & Hallgrimsson, B. (2019). The effect of automated landmark identification on morphometric analyses. Journal of Anatomy, 234(6), 917–935. 10.1111/joa.12973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porto, A. , & Voje, K. L. (2020). ML‐morph: A fast, accurate and general approach for automated detection and landmarking of biological structures in images. Methods in Ecology and Evolution, 11(4), 500–512. 10.1111/2041-210X.13373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson, C. , & Terhune, C. E. (2017). Error in geometric morphometric data collection: Combining data from multiple sources. American Journal of Physical Anthropology, 164(1), 62–75. 10.1002/ajpa.23257 [DOI] [PubMed] [Google Scholar]
- Rohlf, F. J. , & Slice, D. (1990). Extensions of the procrustes method for the optimal superimposition of landmarks. Systematic Biology, 39(1), 40–59. 10.2307/2992207 [DOI] [Google Scholar]
- Rolfe, S. , Davis, C. , & Maga, A. M. (2021). Comparing semi‐landmarking approaches for analyzing three‐dimensional cranial morphology. American Journal of Physical Anthropology, 175(1), 227–237. 10.1002/ajpa.24214 [DOI] [PubMed] [Google Scholar]
- Rolfe, S. , Pieper, S. , Porto, A. , Diamond, K. , Winchester, J. , Shan, S. , Kirveslahti, H. , Boyer, D. , Summer, A. , & Maga, A. M. (2020). SlicerMorph: An open and extensible platform to retrieve, visualize and analyze 3D morphology. bioRxiv.
- Rusinkiewicz, S. , & Levoy, M. (2001). Efficient variants of the ICP algorithm. In Proceedings third international conference on 3‐D digital imaging and modeling (pp. 145–152). IEEE Computer Society. 10.1109/IM.2001.924423 [DOI] [Google Scholar]
- Rusu, R. B. , Blodow, N. , & Beetz, M. (2009). Fast point feature histograms (FPFH) for 3D registration. In 2009 IEEE international conference on robotics and automation (pp. 3212–3217). IEEE. 10.1109/ROBOT.2009.5152473 [DOI] [Google Scholar]
- Sanger, T. J. , Sherratt, E. , McGlothlin, J. W. , Brodie, E. D. , Losos, J. B. , & Abzhanov, A. (2013). Convergent evolution of sexual dimorphism in skull shape using distinct developmental strategies. Evolution, 67(8), 2180–2193. 10.1111/evo.12100 [DOI] [PubMed] [Google Scholar]
- Sherratt, E. , Gower, D. J. , Klingenberg, C. P. , & Wilkinson, M. (2014). Evolution of cranial shape in caecilians (Amphibia: Gymnophiona). Evolutionary Biology, 41(4), 528–545. 10.1007/s11692-014-9287-2 [DOI] [Google Scholar]
- Souter, T. , Cornette, R. , Pedraza, J. , Hutchinson, J. , & Baylac, M. (2010). Two applications of 3D semi‐landmark morphometrics implying different template designs: The theropod pelvis and the shrew skull. Comptes Rendus Palevol, 9(6), 411–422. 10.1016/j.crpv.2010.09.002 [DOI] [Google Scholar]
- Young, R. , & Maga, A. M. (2015). Performance of single and multi‐atlas based automated landmarking methods compared to expert annotations in volumetric microCT datasets of mouse mandibles. Frontiers in Zoology, 12(1), 33. 10.1186/s12983-015-0127-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, Q.‐Y. , Park, J. , & Koltun, V. (2016). Fast global registration. In Leibe B., Matas J., Sebe N., & Welling M. (Eds.), Computer vision – ECCV 2016 (pp. 766–782). Springer International Publishing. 10.1007/978-3-319-46475-6_47 [DOI] [Google Scholar]
- Zhou, Q.‐Y. , Park, J. , & Koltun, V. (2018). Open3D: A modern library for 3D data processing. Retrieved from http://arxiv.org/abs/1801.09847 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig S1‐S2
Table S1‐S2
Supplementary Material
Data Availability Statement
The mouse dataset is freely available as part of https://doi.org/10.1111/joa.12645 and is also available through Open Science Framework (https://osf.io/xzj4t/). The raw DICOM sequences of hominoids used here are freely available for non‐commercial use from the Smithsonian Institution's National Museum of Natural History (NMNH). From their main page (https://humanorigins.si.edu/evidence/3d‐collection/primates), select ‘Contact us’ and paste ‘3D model download access’ in your subject line.


