Fifty years of nucleophilic substitution in the gas phase

Abstract

Bimolecular nucleophilic substitution (${\mathrm{S}}_{\mathrm{N}}2$) reactions have become a model system for the investigation of structure–reactivity relationships, stereochemistry, solvent influences, and detailed atomistic dynamics. In this review, the progress during five decades of experimental and theoretical research on gas phase ${\mathrm{S}}_{\mathrm{N}}2$ reactions is discussed. Many advancements of the employed methods have led to a tremendous increase in our understanding of the properties and the dynamics of these reactions. For reactions involving six atoms a quantitative agreement of the differential reactive scattering cross sections has already been achieved, in the future it is expected that even larger polyatomic reactions systems become tractable. Furthermore, studies with higher precision, improved reactant control, and a more accurate theoretical treatment of quantum effects are envisioned.

1. INTRODUCTION

Nucleophilic substitution reactions are one of the important classes of chemical reactions in organic synthesis. Being widely used in chemistry, the properties of substitution reactions have been investigated since the 19th century and they have played important roles in the development of an understanding how energetics, steric, or solvent effects affect chemical reactions. Here we focus on bimolecular nucleophilic substitution (${\mathrm{S}}_{\mathrm{N}}2$) reactions, which occur in the simplest form at a saturated carbon atom and can be written as

$${\mathrm{X}}^{-}+{\text{CH}}_3\mathrm{Y}\to {\mathrm{Y}}^{-}+{\text{CH}}_3\mathrm{X}.$$ (1)

X and Y may be individual halogen atoms or various molecular compounds. In practical applications, one or more of the hydrogen atoms at the central carbon in Equation (1) are often replaced by side groups.

Back in 1896 Paul Walden investigated reactions of optically active halogen compounds. Studying chiral organic acids, specifically malic acid and chlorine or bromine substituted succinic acid, he found that upon reaction with silver oxide and phosphorous pentachloride one enantiomer could be transformed into the opposite enantiomer and back again (Walden, 1896), a process referred to as Walden cycle. In extensive work during the 1930s Hughes, Ingold, and coworkers (see Cowdrey et al., 1937; Hughes & Ingold, 1935) discussed first and second order nucleophilic substitution reactions, ${\mathrm{S}}_{\mathrm{N}}1$ and ${\mathrm{S}}_{\mathrm{N}}2$. They explained Walden's results by a steric inversion at the central carbon atom that occurs during ${\mathrm{S}}_{\mathrm{N}}2$ reactions and is now known as Walden inversion. In contrast, ${\mathrm{S}}_{\mathrm{N}}1$ reactions lead to a racemic mixture of products due to the formation of a detectable intermediate carbocation. This study shaped the notion that ${\mathrm{S}}_{\mathrm{N}}2$ reactions occur by concerted bond‐formation and bond‐cleavage following the approach of a nucleophile ${\mathrm{X}}^{-}$ towards the backside of the ${\text{CH}}_3\mathrm{Y}$ reactant. This description of ${\mathrm{S}}_{\mathrm{N}}2$ reactions has since found entry in the standard organic chemistry textbooks.

If second order nucleophilic substitution (${\mathrm{S}}_{\mathrm{N}}2$) reactions, also referred to as nucleophilic displacement reactions, occur in a bimolecular collision process, they may be investigated in the absence of solvent molecules in gas phase experiments. This started 50 years ago (Bohme & Young, 1970) and led to numerous surprising discoveries until the present time (Xie & Hase, 2016). In the present review we discuss the results that have been obtained on gas phase ${\mathrm{S}}_{\mathrm{N}}2$ reactions during the last five decades. Different gas phase physical chemistry and chemical physics methods have been used since the first ion flow tube experiment in 1970. During this time, nucleophilic substitution reactions have possibly become the most intensely studied ion–molecule reaction. It is the aim of this review to present how the development and improvement of experimental and computational methods has allowed for more and more insight into these reactions. There certainly have been more publications on this topic than can be cited here, but we have tried to include reference to all important contributions that advanced the understanding of gas phase nucleophilic substitution reactions. Many reviews have discussed ${\mathrm{S}}_{\mathrm{N}}2$ reactions in the past, most notably the reviews by Laerdahl and Uggerud (2002), Mikosch et al. (2010), Xie et al. (2014), and most recently Uggerud (2017). Our reviews on crossed‐beam reaction dynamics experiments also contained major parts on ${\mathrm{S}}_{\mathrm{N}}2$ reactions (Carrascosa, Meyer, & Wester, 2017; Meyer & Wester, 2017; Wester, 2014).

In Section 2 of this review the early experimental work on gas phase ${\mathrm{S}}_{\mathrm{N}}2$ reactions is discussed. The following section covers the mostly kinetics oriented focus of the work until about the year 2000 (Section 3). In the subsequent section (Section 4) spectroscopic studies of the reaction complex are discussed. This is followed by a section that presents the reaction dynamics research that started in the “zero years” of the present century (Section 5). Finally an outlook (Section 6) on probably several more decades of gas phase studies of ${\mathrm{S}}_{\mathrm{N}}2$ reactions is given.

2. THE EARLY YEARS

Gas phase experiments on nucleophilic substitution reactions started fifty years ago with the work by Bohme and Young (1970). Using the flowing afterglow technique developed by Fehsenfeld and others, Bohme and Young measured the thermal reaction rate coefficients for a number of negative ion reactions with ${\text{CH}}_3\text{Cl}$. The focus of their work was on testing capture theory, which predicts ion–molecule reaction rates based on the long‐range ion‐induced dipole and ion‐permanent dipole interaction. The former leads to the Langevin rate coefficient $k_L\propto \sqrt{\alpha ∕\mu }$, while the latter term is proportional to the permanent dipole moment of the neutral ($\alpha$ is the polarizability of the neutral reactant and $\mu$ the reduced mass of the collision system). The experimental reaction efficiencies provided evidence to which extent dipole‐locking occurs during a collision.

The Bohme group at York University continued to investigate the kinetics, equilibrium constants, and thermodynamics of ${\mathrm{S}}_{\mathrm{N}}2$ reactions of negative ions with ${\text{CH}}_3\text{Cl}$ and ${\text{CH}}_3\mathrm{F}$ and also included combustion‐relevant reactions, such as the reactions of ${\mathrm{C}}_2^{-}$ and ${\text{CN}}^{-}$ with ${\text{CH}}_4$ or ${\mathrm{C}}_2{\mathrm{H}}_2$ (Schiff & Bohme, 1975). Later they moved to reactions of negative ions with silane, ${\text{SiH}}_4$, and compared this to reactions with methane (Payzant et al., 1976). While reactions of anions with methane were quite unreactive, reactions with silane showed large rate coefficients and many different reaction channels, which is attributed to the more favorable thermodynamics in reactions of ${\text{SiH}}_4$.

In parallel also first results for cationic nucleophilic displacement reactions in the gas phase were reported (Holtz et al., 1970). In this case the ion cyclotron resonance (ICR) technique was employed. This technique was also chosen by Brauman and coworkers, who investigated reactions of ${\mathrm{F}}^{-},{\text{Cl}}^{-}$, and ${\text{CH}}_3{\mathrm{S}}^{-}$ anions with ${\text{CH}}_3\text{Cl}$ and ${\text{CH}}_3\text{Br}$ (Brauman et al., 1974), which also allowed them to detect the neutral products (Lieder & Brauman, 1974). They measured changes in the reaction rate coefficients that were found to be small, but important, given the fact that barrier‐less ion–molecule reactions usually proceed with very similar capture rate coefficients. This led to the conclusion that an intermediate barrier is modifying nucleophilic displacement reactions.

Further experiments, where they obtained thermal rate coefficients for more than 30 different ${\mathrm{S}}_{\mathrm{N}}2$ reactions, led Brauman and coworkers to predict a double‐well potential energy landscape for gas phase nucleophilic substitution reactions (Olmstead & Brauman, 1977) (see also Section 3.4). Two potential energy minima describe the entrance and exit channel complexes of reaction (1), ${\mathrm{X}}^{-}\left({\text{CH}}_3\mathrm{Y}\right)$ and $\left({\text{XCH}}_3\right){\mathrm{Y}}^{-}$, separated by an intermediate barrier that represents the transition state of the reaction (see Figure 1). The energy of this transition state is often found to be submerged with respect to the energy of the reactants, nevertheless it profoundly influences the reaction as a dynamical bottleneck where the density of states has a minimum.

Figure 1.

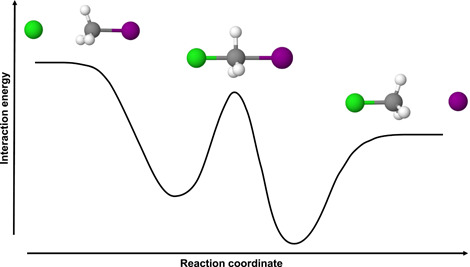
Double‐well potential of a typical gas phase ${\mathrm{S}}_{\mathrm{N}}2$ reaction (see reaction 1) [Color figure can be viewed at wileyonlinelibrary.com]

3. ION–MOLECULE KINETICS

For many years the research on gas phase nucleophilic substitution reactions focused on reaction kinetics and thermodynamics. Theoretically, a growing number of quantum chemical calculations have been performed and statistical modeling has been used to calculate rate coefficients. Experimentally, a range of techniques, such as ion flow tubes, ion cyclotron resonance mass spectrometry, high pressure mass spectrometry and, later, guided ion beam techniques were used to obtain kinetic data, in particular temperature‐ and collision‐energy‐dependent reaction rate coefficients, cross sections, and equilibrium constants. With these techniques, more detailed insight in the the reaction efficiencies, the energetics along the reaction coordinate, or the role of solvent molecules, in comparison with reactions in solution, has been obtained.

3.1. Theoretical modeling

Quantum chemical investigations of nucleophilic substitution reactions started in the mid 1970s. Early calculations at the self‐consistent field (SCF) level investigated possible different reactions pathways and calculated transition state energies, such as for the frontside and backside attack in the ${\mathrm{F}}^{-}+{\text{CH}}_3\mathrm{F}$ system (Schlegel et al., 1977). In further theoretical work different factors that influence barrier heights of ${\mathrm{S}}_{\mathrm{N}}2$ reactions were studied, in particular the ionization energy of the nucleophile and the electron affinity of the neutral molecule (Shaik & Pross, 1982), or the influence of substituents at the central carbon atom on the transition state energy (Wolfe et al., 1982). It was also calculated, in this case for the $C^{-}+{\text{CH}}_3\text{Cl}$ reaction, that the binding energies of the reaction complexes and the height of the barrier are strongly influenced by solvent effects (Chandrasekhar et al., 1984, 1985), which explains the strong suppression of ${\mathrm{S}}_{\mathrm{N}}2$ reactivity in solution phase compared to the gas phase.

Using post‐Hartree Fock methods the reaction profile of the ${\mathrm{H}}^{-}+{\text{CH}}_3\mathrm{F}$ reaction as well as the vibrational frequencies of the reaction complex at different stationary points was calculated by Zahradnik and coworkers (Havlas et al., 1988). Based on these quantum chemical calculations the group then performed detailed RRKM calculations to determine the absolute reaction rate coefficient for this reaction (Merkel et al., 1988). To achieve this they modeled the reaction as a three‐step process, capture into the entrance channel complex, passage of the transition state, and dissociation of the exit channel complex. They compared several quantum chemistry theories and basis sets and were able to reach good agreement with previous experimental results (Tanaka et al., 1976).

Shortly after, Vande Linde and Hase studied the symmetric ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\text{Cl}}^{-}+{\text{CH}}_3\text{Cl}$ in a series of articles (Vande Linde & Hase, 1989, 1990a, 1990b, 1990c). They were able to construct a global potential energy surface for this reaction (Vande Linde & Hase, 1990a) and used this to run classical trajectories to calculate the atomistic reaction dynamics and obtain absolute cross sections as a function of relative energy (see Figure 2). This allowed them to identify a direct reaction mechanism for this substitution reaction (Vande Linde & Hase, 1989). Furthermore, they found that this mechanism can be promoted by exciting several quanta of the C‐Cl stretch vibration in ${\text{CH}}_3\text{Cl}$, while exciting the ${\text{CH}}_3$ deformation did not lead to product formation (Vande Linde & Hase, 1989). In the final paragraph of their first article Vande Linde and Hase state: “It is hoped that the work presented here will lead to experimental investigations of a direct mechanism for ${\mathrm{X}}^{-}+{\text{CH}}_3\mathrm{Y}\to {\text{XCH}}_3+{\mathrm{Y}}^{-}$ nucleophilic substitution.” (Vande Linde & Hase, 1989). This in fact became true almost twenty years later, when a direct reaction mechanism was observed experimentally in the ${\text{Cl}}^{-}+{\text{CH}}_3\mathrm{I}$ reaction (Mikosch, Trippel, et al., 2008) (see Section 5).

Figure 2.

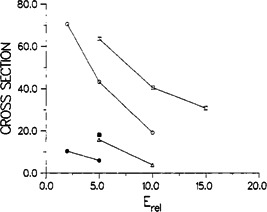
Absolute reactive cross section (${Å}^2$) as a function of the relative collision energy (kcal/mol) for the ${\text{Cl}}^{-}+{\text{CH}}_3\text{Cl}$ reaction. Open symbols are calculated for $T_{rot}=0$ K and full symbols for $T_{rot}=300$ K, triangles are for four quanta of excitation in the C‐Cl stretch vibration, circles for six quanta and squares for eight quanta. Reprinted with permission from Vande Linde and Hase (1989). Copyright (1989) American Chemical Society

In their next article, Vande Linde and Hase found non‐RRKM behavior for the above substitution reaction. Their calculated decomposition lifetimes of the ${\text{Cl}}^{-}\left({\text{CH}}_3\text{Cl}\right)$ complex showed a multiexponential decay. Further analysis revealed that vibrational coupling in the complex is weak, which prohibits the application of RRKM calculations since fast intramolecular vibrational energy redistribution (IVR) among all internal vibrational degrees of freedom is a fundamental assumption in RRKM theory. The application of trajectory simulations to nucleophilic substitution reactions and the discovery of non‐RRKM behavior stimulated the study of these reactions for many years. More of these simulations will be discussed in Section 5.1 below.

For the same reaction, ${\text{Cl}}^{-}+{\text{CH}}_3\text{Cl}$, the role of water as solvent molecules was calculated by Tucker and Truhlar both with respect to the reaction energetics and the expected rate coefficients (Tucker & Truhlar, 1990). The variational transition state theory calculations yielded a strong suppression of the reaction rate coefficient by several orders of magnitude when one or two water molecules are attached to the ${\text{Cl}}^{-}$ nucleophile. This trend follows a corresponding increase of the intermediate reaction barrier upon microsolvation. In a second publication they also investigated the kinetic isotope effect that occurs when hydrogen atoms are replaced by deuterium (Zhao et al., 1991).

Higher level quantum chemistry calculations have been carried out by Glukhovtsev et al. in a series of articles (Glukhovtsev et al., 1995; Glukhovtsev, Pross, & Radom, 1996; Glukhovtsev, Pross, Schlegel, et al., 1996). In their first article they studied the identity reactions of ${\mathrm{X}}^{-}$ with ${\text{CH}}_3\mathrm{X}$ for the four halides X = F, Cl, Br, and I. They obtained ${\mathrm{C}}_{3v}$ geometries for intermediate reaction complexes, the complexation energies, intermediate barrier heights, and charge distributions (Glukhovtsev et al., 1995). They then studied all nonidentity reactions ${\mathrm{X}}^{-}+{\text{CH}}_3\mathrm{Y}$ (X,Y = F, Cl, Br, I) at the same level of theory and analyzed the results using Marcus theory (Glukhovtsev, Pross, & Radom, 1996).

Further steps towards understanding chemical reactivity based on quantum chemical calculations have been presented by Bickelhaupt, who used density functional theory (DFT) and analyzed the Kohn‐Sham molecular orbitals to decompose the relevant energies of stationary states along the reaction coordinate (Bickelhaupt, 1999), which was also used for comparison with the energetics in solution. This study was later extended to a range of 64 ${\mathrm{S}}_{\mathrm{N}}2$ reactions, comparing several different DFT functionals (Swart et al., 2007).

3.2. Flow tube experiments on bimolecular rate coefficients

Experimental activity on the kinetics of substitution reactions continued to involve the use of the flow tube technique (Viggiano & Morris, 1996). Several improvements were developed that made more detailed experimental investigations possible: The addition of a reactant ion mass filter in the selected ion flow tube (SIFT) instrument allowed one to study only the ion of interest in the flow tube. The addition of a drift tube, where ions are slighly accelerated, allowed one to separate internal reactant temperature from average collision energy in the center of mass frame. And finally temperature‐variable setups yielded further control of the internal and translational energies of the reactants in ion‐molecule reactions.

Using a sensitive SIFT instrument, the identity ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\text{Cl}}^{-}+{\text{CH}}_3\text{Cl}$ was studied over a collision energy range of 0.04–2 eV (Barlow et al., 1988). With SIFT experiments also the role of solvents, which influence substitution reactions in the liquid phase significantly, moved into focus. Reactant ions were clustered to a selected number of chosen solvent molecules before they were brought to reaction in the flow or drift tube. Such micro‐solvation experiments were carried out for a range of ions and solvents. Reactions of ${\mathrm{F}}^{-}$ and ${\text{Cl}}^{-}$ attached to water, methanol, ethanol, aceton, formic acid, and acetic acid have been studied by Bohme and Raksit (1985). Experiments on the effect of water attached to ${\text{OH}}^{-}$ on reactions with methyl chloride were discussed by Hierl et al., who used flow tube and ion beam techniques to study reaction probabilities up to several electronvolt of translational energy (Hierl et al., 1988) and were also able to observe proton transfer in competition with ${\mathrm{S}}_{\mathrm{N}}2$ products. All these experiments showed an overall suppression of the reaction rate coefficients with increasing number of solvent molecules. This agrees with theoretical findings, as discussed in the previous section and the known lower reaction rate coefficients for substitution reactions in the liquid phase.

The development of temperature‐variable flow tubes allowed experiments to move beyond reaction kinetics at room temperature and provided insight into the temperature‐dependence of substitution kinetics. Using drift tube measurements over the temperature range of 200–560 K, Viggiano et al. showed that the ${\text{Cl}}^{-}+{\text{CH}}_3\text{Br}$ reaction rate coefficient is strongly dependent on the relative translational energy. At the same time it is insensitive to the internal temperature of the molecular reactant (Viggiano et al., 1992). This was clear experimental evidence that the main assumption of statistical theories, the fast randomization of energy in the reaction complex, is violated.

${\mathrm{S}}_{\mathrm{N}}2$ reaction kinetics have also been studied at ambient pressure using a kinetic ion mobility mass spectrometer developed by Giles and Grimsrud (1992). Using this instrument rate coefficients for the exothermic reactions of ${\text{Cl}}^{-}$ with methyl, ethyl, and n‐butyl bromide have been measured for temperatures of 35–$150^{\circ }$ C (Knighton et al., 1993). In case of the methyl chloride reactions, the authors observed collisional stabilization. By analysis of the measured rates, the energy of the submerged reaction barrier with respect to the energy of the reactant was extracted (Knighton et al., 1993).

With the CRESU (a French acronym for Cinétique de Réaction en Ecoulement Supersonique) technique, ion–molecule reactions can be studied under low‐temperature conditions. In the uniform expansion that forms after a precisely designed Laval nozzle constant high densities and temperatures are reached, which allows for the equilibration of all translational and internal degrees of freedom. The CRESU technique was employed by Le Garrec et al. (1997) to study the ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\text{Cl}}^{-}+{\text{CH}}_3\text{Br}$ from 180 K down to 23 K. Their results showed a strong increase of the rate coefficient with decreasing temperature (open circles in Figure 3). At 23 K the rate is only about a factor of two smaller than the capture rate, while a 30‐fold reduction is reached at 180 K. This trend extends up to 500 K when combining the CRESU data with previous rate coefficient measurements. Overall the rate decreases by a factor of 400 between 23 and 500 K. Quantum scattering calculations for different values of the total angular momentum have been performed and, after proper Boltzmann averaging, compared to the measurement, where a good agreement is found (see Figure 3). The strong decrease, not known in other ion–molecule reactions, is essentially attributed to the coupling of the intermolecular vibrational modes in the entrance channel with the density of states at the intermediate barrier for the reaction, which is just slightly submerged with respect to the energy of the reactants (Le Garrec et al., 1997).

Figure 3.

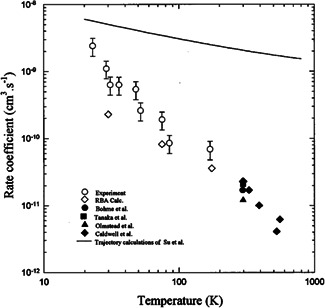
Open symbols: Measured and calculated absolute rate constant for the substitution reaction ${\text{Cl}}^{-}+{\text{CH}}_3\text{Br}$ (Le Garrec et al., 1997). Full symbols are data from Bohme and Raksit (1985), Caldwell et al. (1984), Olmstead and Brauman (1977), and Tanaka et al. (1976) shown for comparison. Solid line: Calculation from Su and Chesnavich (1982). Reprinted with permission from Le Garrec et al. (1997)

Significant effort has been put into understanding if ${\mathrm{S}}_{\mathrm{N}}2$ reactivity is enhanced if the anionic nucleophile carries a lone pair of electrons adjacent to the attacking atom, referred to as $\alpha$‐effect. Early studies indicated that this effect, which is important in solution phase, was not found in the gas phase when comparing the reactivity of ${\text{OH}}^{-}$ with ${\text{HOO}}^{-}$ (DePuy et al., 1983). However, more recently it could be shown that the $\alpha$‐effect is in fact an intrinsic property of gas phase ${\mathrm{S}}_{\mathrm{N}}2$ reactions (Garver et al., 2011; Thomsen et al., 2013).

Besides the predominantly studied substitution reactions with anionic nucleophiles, also cationic ${\mathrm{S}}_{\mathrm{N}}2$ reactions have been investigated. As an example, Kretschmer et al. (2012) present the formation of ${\text{CH}}_3{\text{NH}}_3^{+}$ following a Walden inversion in a collision of $\mathrm{M}{\left({\text{CH}}_3\right)}^{+}$ with ${\text{NH}}_3$, where M = Zn, Cd, or Hg. The measured reaction probabilites increased from about 2% for Cd up to about 20% for Hg, but remained far below the long‐range capture limit similar to what has been found for anionic ${\mathrm{S}}_{\mathrm{N}}2$ reactions.

3.3. Kinetic energy release measurements

A set of experiments on the kinetic energy release distribution of transient ${\mathrm{S}}_{\mathrm{N}}2$ complexes have been performed by Graul and Bowers (1991). In their first work ${\text{Cl}}^{-}\left({\text{CH}}_3\text{Br}\right)$ complexes were produced and mass‐selected. Then the unimolecular decay of these complexes was observed and the relative kinetic energy of the products was recorded. On the time‐scale of the experiment of tens of microseconds only the reactive product ion ${\text{Br}}^{-}$ was observed and not the decay back to reactant anion ${\text{Cl}}^{-}$. The measured kinetic energy release distribution for ${\text{Br}}^{-}+{\text{CH}}_3\text{Cl}$ shows an average energy release of $30\pm 10$ meV.

It was concluded that the produced metastable complexes carried between 1 and 2 eV of internal energy, more than the complex binding energy of about 0.5 eV, and decay with lifetimes below the observation time window of microseconds. With this input phase space theory (PST) calculations were performed to model the kinetic energy release following statistical randomization of the internal energy. The resulting PST distribution yielded more than twice the product kinetic energy than experimentally observed. This nonstatistical energy partitioning is clear evidence for the fact that this nucleophilic substitution reaction can not be correctly described by statistical models. Instead, the authors speculate that the excess energy may be stored in the C‐Cl stretch and/or the ${\text{CH}}_3$ umbrella vibration (Graul & Bowers, 1994).

In further work similar results have been found for the ${\text{Cl}}^{-}\left({\text{CH}}_3\mathrm{I}\right)$ and ${\text{Br}}^{-}\left({\text{CH}}_3\mathrm{I}\right)$ complexes for reactions towards I products, as well as for their deuterated variants (Graul & Bowers, 1994). The results were compared both with a statistical model and with a variant of that model where part of the energy was assumed to be locked‐up in vibrational excitation of the neutral reaction product ${\text{CH}}_3\text{Cl}$ or ${\text{CH}}_3\mathrm{I}$. Using that assumption the statistical model could be brought to agreement with the measured kinetic energy release distributions (Graul et al., 1998). Also larger reaction complexes, such as ${\text{Cl}}^{-}\left({\text{CH}}_3{\text{CH}}_2\mathrm{I}\right)$ or ${\mathrm{F}}^{-}\left({\mathrm{C}}_6{\mathrm{H}}_5{\text{OCH}}_3\right)$ were found to show qualitatively similar nonstatistical behavior, but with slightly smaller discrepancies between the measured distributions and the statistical model (Graul et al., 1998).

3.4. Ion cyclotron resonance measurements

The ion cyclotron resonance (ICR) technique has been continued to be used by Brauman and coworkers for a range of studies after their pioneering work (Olmstead & Brauman, 1977). Reactant ions were trapped in the ICR trap and exposed to a constant background gas density of the neutral reactant. The rate of disappearance of the reactant ion or the appearance of product ions can be measured, either by resonant excitation or by ion ejection. It has been tested that the reactant ions thermalize in the trap and that therefore reliable thermal rate coefficients are obtained. These measured rate coefficients were described by a step‐wise reaction model and involving statistical rate calculations for the individual steps: capture in the entrance channel complex, passage of the transition state to the exit channel complex, dissociation of the exit channel complex (see e.g., Chabinyc et al., 1998).

In later work, ICR studies of the identity ${\mathrm{S}}_{\mathrm{N}}2$ reactions of ${\mathrm{Y}}^{-}$ with ${\text{CH}}_2\text{CNY}$ or ${\mathrm{C}}_6{\mathrm{H}}_5{\text{CH}}_2\mathrm{Y}$ (Y = Cl and Br) have been performed (Wladkowski & Brauman, 1993). Thermal rate coefficients have been measured at a temperature estimated to be 350 K and binding energies of the reaction complexes have been determined from measured equilibrium constants. Using statistical theories the energetics of the potential energy surface have been determined and analyzed using Marcus theory (Wladkowski & Brauman, 1993). Gas phase ${\mathrm{S}}_{\mathrm{N}}2$ reactions of even larger neutral reactants have been studied by Craig et al. They investigated identity reactions of ${\text{Cl}}^{-}$ with $\text{Cl}{\left({\text{CH}}_2\right)}_n\mathrm{X}$, where the n‐alkyl chlorides are substituted, for example, with X = CN, Cl, or OH (Craig & Brauman, 1996, 1999).

Further work on identity reactions allowed Regan et al. to show that steric effects are less important for thermal ${\mathrm{S}}_{\mathrm{N}}2$ reactions in the gas phase than they are in solution. Also, it is shown that the strong increase of the ${\mathrm{S}}_{\mathrm{N}}2$ barrier height when moving from gas phase to solution phase is due to the strong interaction of the solvent molecules with the nucleophile and the leaving group (Regan et al., 2002).

Cationic reactions have also been investigated with the ICR technique, in particular by the Uggerud group. They studied, for example, reactions of different oxonium ions with ammonia observing a range of products (Bache‐Andreassen & Uggerud, 2000, 2003).

3.5. Guided ion beam studies of absolute cross sections

Higher collision energies than in heated flow or drift tube experiments are achieved with the guided ion beam technique (Armentrout, 2000). With this approach, absolute reaction cross sections have been measured by Ervin and coworkers for several nucleophilic substitution reactions. Given the higher collision energies that are accessible with this technique, up to many electronvolts, several endoergic reaction pathways could be studied as well. DeTuri et al. investigated the symmetric ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\text{Cl}}^{-}+{\text{CH}}_3\text{Cl}\to {\text{ClCH}}_3+{\text{Cl}}^{-}$ (DeTuri et al., 1997) by isotopic labeling. They found a threshold energy of 470 $\pm$ 160 meV for this reaction, in substantial disagreement with a previous determination of about 2 eV using a drift tube experiment (Barlow et al., 1988). The theoretically estimated barrier height at the tranistion state for the ${\mathrm{S}}_{\mathrm{N}}2$ backside attack amounts to only around 120 meV, which shows that additional dynamical constraints must be at work in this symmetric reaction.

In further guided ion beam‐experiments the exothermic ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\mathrm{F}}^{-}+{\text{CH}}_3\text{Cl}$ and its endothermic reverse reaction ${\text{Cl}}^{-}+{\text{CH}}_3\mathrm{F}$ have been studied (Angel & Ervin, 2001; Angel et al., 2002). The technique allowed for the measurement of absolute reaction cross sections over a dynamic range from more than $10^2{Å}^2$ down to $5\times 10^{-4}{Å}^2$ (see Figure 4). Several different product channels were studied besides nucleophilic substitution, including exoergic proton transfer reaction and dihalide (${\text{FCl}}^{-}$) formation channels.

Figure 4.

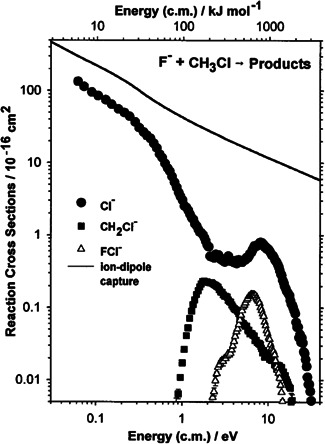
Measured reaction cross section for the ${\mathrm{F}}^{-}+{\text{CH}}_3\text{Cl}$ reaction as a function of collision energy in the center of mass frame. Reprinted with permission from Angel and Ervin (2001). Copyright (2001) American Chemical Society

The exothermic ${\mathrm{S}}_{\mathrm{N}}2$ reaction was found to be most efficient at low relative collision energies. Its cross section decreases rapidly in the energy range of 0.1 to 2 eV. This is attributed to more impulsive collisions at higher collision energy, where a reorientation of the neutral reactant to the incoming ion becomes less and less probable (Angel & Ervin, 2001). This explanation invokes a fast direct collision and is therefore different from the one given for the rate decrease observed at lower collision energies in the CRESU measurements of Le Garrec et al. (1997) discussed above. There it was attributed to the decreased probability for coupling of the vibrational states in the entrance channel with the density of states at the transition state.

For the endothermic ${\mathrm{S}}_{\mathrm{N}}2$ reaction an energy threshold is observed, which is determined to be about 1.9 eV. This value is larger than the calculated reaction endothermicity by about 0.5 eV and shows, similar to the symmetric ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\text{Cl}}^{-}+{\text{CH}}_3\text{Cl}$ that was discussed above, that dynamical constraints can suppress the reactivity in these reactions even above threshold. Similar results have been obtained for the endoergic reaction of ${\mathrm{I}}^{-}$ with ${\text{CH}}_3\text{Cl}$ and ${\text{CH}}_3\text{Br}$ (Angel & Ervin, 2004).

In a guided ion beam study of the ${\text{Cl}}^{-}+{\text{CH}}_3\text{Br}$ reaction not only absolute reaction cross sections, but also scattering angle‐dependent dynamical information was inferred (Angel & Ervin, 2003).

3.6. High pressure mass spectrometry and ternary rates in ion traps

High pressure mass spectrometry (HPMS) has become another powerful tool to study ion–molecule reactions, in particular their thermochemistry (Kebarle, 2000). McMahon and coworkers have used this to study a range of nucleophilic substitution reactions with particular focus on their equilibrium constants and the thermodynamics of their entrance channel wells and barrier heights. In C. Li et al. (1996) they studied the symmetric ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\text{Cl}}^{-}+{\text{CH}}_3\text{Cl}$ and the nonsymmetric reactions of ${\text{Cl}}^{-}$ with methyl‐, ethyl, iso‐propyl and t‐butyl bromide. Furthermore, they analyzed the three‐body association rate for the entrance channel complex ${\text{Cl}}^{-}\left({\text{CH}}_3\text{Cl}\right)$ of the symmetric ${\mathrm{S}}_{\mathrm{N}}2$ reaction and extracted its lifetime with respect to decay back to reactants (C. Li et al., 1996). Their value of about 12 ps agreed very well with trajectory simulations by Vande Linde and Hase on the same system (Vande Linde & Hase, 1990c).

In further work the HPMS technique was used to study the thermochemistry of reactions of ions that are micro‐solvated with several neutral solvent molecules (methanol, acetonitrile, acetone, and difluoroethane) (Bogdanov & McMahon, 2005) and of reactions with fluorine‐substituted neutrals, specifically trifluoromethyl halides (Bogdanov & McMahon, 2006). Both frontside and backside reaction complexes have been found, but it was shown that the ${\mathrm{S}}_{\mathrm{N}}2$ reaction with trifluoromethyl halides proceeds preferentially via backside attack and Walden inversion (Figure 5).

Figure 5.

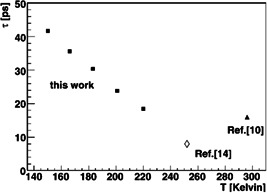
Lifetimes of the entrance channel complex ${\text{Cl}}^{-}\left({\text{CH}}_3\text{Cl}\right)$ of the corresponding symmetric ${\mathrm{S}}_{\mathrm{N}}2$ reaction, measured by high pressure mass spectrometry at room temperature (C. Li et al., 1996) (solid triangle) and as a function of temperature in a cryogenic radiofrequency ion trap (Mikosch, Otto, et al., 2008) (solid squares). The experimental values agree well with the trajectory simulation result (Vande Linde & Hase, 1990c) (open diamond). Reprinted with permission from Mikosch, Otto, et al. (2008). Copyright (2008) American Chemical Society

Complementary to the high pressure studies, reaction kinetics and three‐body collisions can also been studied in a low‐temperature radiofrequency ion trap (Wester, 2009). There, lower reactant gas densities and instead longer interaction times are available. In a study of the symmetric ${\mathrm{S}}_{\mathrm{N}}2$ reaction complex ${\text{Cl}}^{-}\left({\text{CH}}_3\text{Cl}\right)$ (Mikosch, Otto, et al., 2008), ternary collisions of ${\text{Cl}}^{-}$ with ${\text{CH}}_3\text{Cl}$ and different third bodies were investigated at temperatures between 150 and 220 K. The ternary rate coefficient has been determined and a much stronger inverse temperature dependence has been found than expected from a statistical model. From these data the lifetime of the transient ${\mathrm{S}}_{\mathrm{N}}2$ complex ${\text{Cl}}^{-}\left({\text{CH}}_3\text{Cl}\right)$ has been derived as a function of temperature. The lifetime increases significantly upon decreasing temperature, whereas at 220 K a good agreement is reached both with the HPMS lifetime discussed above (C. Li et al., 1996) and the trajectory calculation (Vande Linde & Hase, 1990c).

4. SPECTROSCOPY OF ${\mathrm{S}}_{\mathrm{N}}2$ REACTION COMPLEXES

Several spectroscopic approaches have attempted to shed light on the intermediate reaction complexes of nucleophilic substitution reactions. Negative ion photoelectron spectroscopy has been applied to several ${\mathrm{S}}_{\mathrm{N}}2$ reaction complexes by Cyr et al. They studied in particular the pre‐reaction complexes ${\mathrm{I}}^{-}\left({\text{CH}}_3\mathrm{I}\right)$ (Cyr et al., 1994, 1992, 1993). The photoelectron spectra revealed the red shift of the two photoelectron peaks of bare ${\mathrm{I}}^{-}$ due to the binding of ${\text{CH}}_3\mathrm{I}$ as well as a vibrational fine structure that could be assigned to a progression of the C‐I stretching vibration. Shortly after, zero‐electron kinetic energy spectroscopy could reveal several low‐frequency bands due to intermolecular vibrations in the pre‐reaction complex (Arnold et al., 1995). Recently the ${\mathrm{I}}^{-}\cdot {\text{ICF}}_3$ was studied using 2D photoelectron spectroscopy and compared to the earlier work. There the complex was shown to represent the frontside attack with ${\mathrm{I}}^{-}$ bound to the iodine atom of ${\text{CF}}_3$I (Mensa‐Bonsu et al., 2019).

Using infrared spectroscopy, Johnson and coworkers investigated the photo‐induced dissociation of the entrance and exit channel complexes of the ${\text{Cl}}^{-}+{\text{CH}}_3\text{Br}$ reaction following infrared CH stretch vibrational excitation (Ayotte et al., 1999). Using argon‐tagging predissociation spectroscopy, absorption was detected in the ${\text{Cl}}^{-}\left({\text{CH}}_3\text{Br}\right)$ complex, shifted to the blue with respect to the symmetric and asymmetric CH stretch excitations in bare ${\text{CH}}_3\text{Br}$ due to the interaction with the chlorine anion. Subsequently, product ${\text{Br}}^{-}$ formation was observed following this excitation for the entrance channel complex, which shows that the Walden transition state has been passed. In contrast, for the exit channel complex ${\text{Br}}^{-}\left({\text{CH}}_3\text{Cl}\right)$ no product formation was observed, because in this case the photon energy is insufficient to dissociate the complex. Shortly after, the dissociation of the entrance channel complex ${\text{Cl}}^{-}\left({\text{CH}}_3\text{Br}\right)$ into ${\text{CH}}_3\text{Cl}$ and ${\text{Br}}^{-}$ has also been detected using black‐body induced dissociation and using a continuous‐wave mid‐infrared ${\text{CO}}_2$ laser(Tonner & McMahon, 2000).

Femtosecond time‐resolved photoelectron spectroscopy has been used to access the dissociation of an ${\mathrm{S}}_{\mathrm{N}}2$ reaction complex in the time domain (Wester et al., 2003). The entrance channel complex ${\mathrm{I}}^{-}\left({\text{CH}}_3\mathrm{I}\right)$ has been prepared by photodissociation of the ${\mathrm{I}}_2^{-}$ bond in ${\mathrm{I}}_2^{-}\left({\text{CH}}_3\mathrm{I}\right)$ precursor anions with a femtosecond pump pulse. The time evolution of the ${\mathrm{I}}^{-}\left({\text{CH}}_3\mathrm{I}\right)$ complex has then been followed using a second femtosecond pulse that led to photodetachment. The resulting photoelectron kinetic energy spectra have been measured as a function of the pump–probe delay time. The observed decay back to to the ${\mathrm{I}}^{-}+{\text{CH}}_3\mathrm{I}$ reactants was found to occur with a bi‐exponential decay on two time scales, about 0.75 and 10 ps. The occurance of this bi‐exponential decay was attributed to nonstatistical vibrational energy redistribution in the complex (Wester et al., 2003).

5. ION–MOLECULE REACTION DYNAMICS

The following section describes the experimental and theoretical achievements that have been made towards understanding the reaction dynamics underlying nucleophilic substitution. Using energy‐ and angle‐differential reactive scattering experiments and elaborate direct dynamics and quasiclassical trajectory calculations, insight into reaction mechanisms, product energy partitioning, and dependence on initial rovibrational excitation has been obtained. Also quantum reactive scattering calculations are being performed, but they are mostly still restricted to reduced dimensions.

5.1. Trajectory simulations of substitution dynamics

Numerous chemical dynamics simulations have been carried out for substitution reactions using trajectory calculations. Several Pionieering studies were already discussed in Section 3.1 above, see also Hase (1994). With these simulations, reaction probabilities and opacity functions $P\left(b\right)$ are determined as a function of the classical impact parameters $b$, typically up to the maximum impact parameter given by Langevin or capture theory and as a function of collision energy. Integrating this function yields the energy‐dependent cross section and by thermal averaging the temperature‐dependent reaction rate coefficient. By closely inspecting the trajectories different reaction pathways and mechanisms can be investigated. Furthermore, scattering angle distributions and probability distributions for internal rovibrational or translational energies can be extracted in a straight‐forward manner. Quantum zero‐point vibrational energies can be introduced by adding initial internal energy to the molecular degrees of freedom and product rovibrational state analysis may be achieved by appropriate binning techniques.

Mostly, trajectory simulations make use of a potential energy surface (PES) to obtain the interatomic forces. However, for high‐dimensional scattering problems that involve six or more atoms, such as ${\mathrm{S}}_{\mathrm{N}}2$ reactions, full‐dimensional global potential energy surfaces are demanding to calculate. To avoid calculating a PES, direct dynamics calculations have been developed, in particular by Hase and coworkers (Lourderaj et al., 2014). Here, the potential energy gradients are calculated by solving the electronic structure problem on‐the‐fly, while integrating a trajectory. This makes the trajectory calculation computationally costly, but does not require prior knowledge of the PES and may also be used more easily for higher scattering energies. In addition, this method calculates the potential energy exactly at the required intermolecular geometries.

For the substitution reaction ${\text{Cl}}^{‐}+{\text{CH}}_3\text{Cl}$ both PES‐based (Mann & Hase, 1998) and direct dynamics (G. S. Li & Hase, 1999) trajectory simulations have been performed to gain more insight into this symmetric reaction. This study confirmed the backside attack mechanism, no frontside reactions were observed. Furthermore, it was found that the reaction proceeds via backward scattering in a rebound‐type mechanism, that is, the product ion velocity points in the same direction as the reactant ion velocity. Only a small fraction of the trajectories react via an indirect complex‐forming mechanism. This is discussed to occur, because the coupling of the translational collision energy to the internal degrees of freedom of the reaction complex is weak, which is clear evidence for nonstatistical reaction dynamics.

In the reaction ${\text{OH}}^{‐}+{\text{CH}}_3\mathrm{F}$ even more striking nonstatistical dynamics were discovered (Sun et al., 2002). Using direct dynamics trajectory calculations the chemical dynamics of this reaction have been investigated and it was found that the deep minimum in the exit region of the potential energy surface is only seldomly explored during the reaction. Most of the trajectories (about 90%) did not follow the internal reaction coordinate (IRC) pathway and avoided this minimum. This is in contrast to the underlying assumption of statistical models that a reaction proceeds by transitions from stationary state to stationary state with reaction rates for each step that only depend on the number or density of states at these configurations and the intermediate transition states. Sun et al. (2002) discussed their results in the context of IVR, which was found to be very inefficient in this reaction.

Further direct dynamics simulations have been carried out by Tachikawa on several substitution reactions (Tachikawa, 2006; Tachikawa & Igarashi, 1999, 2006), including reactions of singly hydrated anions, ${\mathrm{F}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$ and ${\text{OH}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$. This study supported the notion of a direct reaction and also found that most of the energy available to the products is partitioned into translational energy (Tachikawa & Igarashi, 1999). Despite the low number of computed trajectories also branching ratio for the different product channels of the micro‐hydrated reactions could be extracted (Tachikawa, 2006) and hydrated product ions were found to constitute only a minor channel in the reaction of ${\text{OH}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$ with ${\text{CH}}_3\text{Cl}$. ab initio molecular dynamics of the exothermic ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\text{Cl}}^{-}+{\text{CH}}_3\text{Br}$ have also been reported by Schettino and coworkers (Raugei et al., 1999) including the investigation of microsolvation effects (Raugei et al., 2001).

Stimulated by the advent of crossed‐beam reactive scattering experiments, the reactions of ${\text{Cl}}^{-},{\mathrm{F}}^{-},{\text{OH}}^{-}$, and ${\text{OH}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$ with ${\text{CH}}_3\mathrm{I}$ have been extensively studied by Hase and coworkers using direct dynamics simulations (Mikosch, Trippel, et al., 2008; Xie et al., 2015, 2013; Zhang & Hase, 2010; Zhang et al., 2009, 2013, 2010). In the next section these results are discussed together with the experimental findings. For the reaction ${\mathrm{F}}^{-}+{\text{CH}}_3\mathrm{I}$, where some deviation between experiment and theory was observed, thorough tests of the dependence of the results on the underlying electronic structure calculation were performed (Sun, Davda, et al., 2015; Sun, Xie, et al., 2015).

Within the last decade the development of full‐dimensional potential energy surfaces for ${\mathrm{S}}_{\mathrm{N}}2$ reactions has made great progress (Czakó et al., 2021). Czakó and coworkers developed global PESs for several substitution reactions including the ${\mathrm{F}}^{-}+{\text{CH}}_3\text{Cl}$ (Szabó et al., 2013) and ${\mathrm{F}}^{-}+{\text{CH}}_3\mathrm{I}$ reactions (Olasz et al., 2017). With a PES available, typically two orders of magnitude more trajectories can be calculated than possible with direct dynamics, more than 500,000 trajectories were calculated for the reaction ${\mathrm{F}}^{-}+{\text{CH}}_3\text{Cl}$ (Stei et al., 2016). Thus, the statistical significance of comparisons between experiment and theory has improved significantly, as shown in the good agreement with experimental differential scattering data for this reaction (Stei et al., 2016) (see Section 5.2).

With their accurate trajectory simulations for the ${\mathrm{F}}^{‐}+{\text{CH}}_3\text{Cl}$ reaction (Szabó et al., 2013), Czakó and coworkers discovered a novel and unexpected double‐inversion mechanism for nucleophilic substitution (Szabó & Czakó, 2015) and, in collaboration with experiment, realized the importance of the frontside attack for the reaction dynamics of ${\mathrm{S}}_{\mathrm{N}}2$ reactions (Stei et al., 2016; Szabó et al., 2017). Further results on mode‐specific ${\mathrm{S}}_{\mathrm{N}}2$ dynamics are discussed below together with the experimental results.

5.2. Mechanisms of substitution reactions by crossed‐beam scattering

Detailed insight into the dynamics of elementary reactions in the gas phase has been obtained from crossed‐beam scattering experiments. Such experiments have been pursued for decades on neutral‐neutral reactive collisions, such as the well‐known $\mathrm{F}+{\mathrm{H}}_2$ reaction (Herschbach, 1987; Lee et al., 1969; Neumark, Wodtke, Robinson, Hayden, & Lee, 1985; Neumark, Wodtke, Robinson, Hayden, Shobatake, et al., 1985). Using ion imaging detectors in crossed‐beam experiments a significant improvement in detection sensitivity could be made and at the same time fewer systematic errors affect the measured differential scattering cross section (Heck & Chandler, 1995; Kitsopoulos et al., 1993). With the advent of velocity map imaging (Eppink & Parker, 1997) a versatile electrode configuration with significantly enhanced ion velocity resolution became available and quickly spread to many laboratories around the world. The first attempt to use this for ion–molecule reaction studies were undertaken by Weishaar and coworkers for reactions of cobalt cations with propane and isobutane (Reichert et al., 2002a, 2002b).

In our group we have developed a crossed‐beam velocity map imaging spectrometer for ion–molecule reactions (Mikosch et al., 2006; Trippel et al., 2009; Wester, 2014), which we have employed for a number of cation‐ and anion‐reactions in the past 15 years (Carrascosa, Meyer, & Wester, 2017; Meyer & Wester, 2017). In the mean time ion–molecule crossed‐beam imaging spectrometers have also been developed by Farrar and coworkers (Pei & Farrar, 2012; Pei et al., 2015) and Tian and coworkers (Hu et al., 2018) and applied to several reactions of atomic cations. Another imaging setup for ion–molecule crossed‐beam studies has been presented by Gao and coworkers (Zhang et al., 2021).

A particular focus of our work has been on negative ion nucleophilic substitution reactions. Here, in an experiment on the ${\text{Cl}}^{-}+{\text{CH}}_3\mathrm{I}$ reaction, we were able to observe for the first time the direct rebound mechanism (Mikosch, Trippel, et al., 2008). Its signature is direct back‐scattering of the leaving anion ${\mathrm{I}}^{-}$ with respect to the direction of the incoming ${\text{CH}}_3\mathrm{I}$, with high translational energy close to the total available energy. Hence, little energy is deposited in internal degrees of freedom of the ${\text{CH}}_3\text{Cl}$ product (Xie et al., 2019). This reaction mechanism proceeds along a colinear reaction coordinate with ${\mathrm{C}}_{3v}$ symmetry and involves the inversion of the ${\text{CH}}_3$ group, as derived for bimolecular nucleophilic substitution (${\mathrm{S}}_{\mathrm{N}}2$) reactions by Ingold and coworkers in the 1930s (Cowdrey et al., 1937; Hughes & Ingold, 1935). In addition to the direct rebound mechanism, we observed an indirect complex‐mediated reaction mechanism. At high collision energy we discovered another indirect reaction mechanism. Based on direct dynamics simulations by Hase and coworkers, we could attribute this to a novel roundabout mechanism (Mikosch, Trippel, et al., 2008).

Overall, we have studied substitution reactions of ${\text{Cl}}^{-},{\mathrm{F}}^{-},{\text{OH}}^{-}$ and ${\text{CN}}^{-}$ nucleophiles with methyl iodide and methyl chloride reactants (Carrascosa et al., 2015; Mikosch et al., 2013; Otto et al., 2013; Otto, Brox, et al., 2012; Otto, Xie, et al., 2012; Stei et al., 2016). Striking differences have been observed for ${\mathrm{F}}^{-}$ and ${\text{OH}}^{-}$ nucleophiles. Their stronger interaction and the smaller volume of their electron density distribution compared to ${\text{Cl}}^{-}$ and ${\text{CN}}^{-}$ allows them to approach the neutral reactant much closer and form hydrogen‐bonded entrance channel complexes in addition to the more common reactant complexes with ${\mathrm{C}}_{3v}$ symmetry (Mikosch et al., 2013). This leads to an enhancement of indirect complex‐mediated reactive scattering as well as a forward‐scattering stripping mechanism, where the product ion moves roughly along the same direction as the incoming ${\text{CH}}_3\mathrm{I}$. A detailed summary of the different reaction mechanisms found is given in Xie et al. (2014).

Images of the differential cross section for the reaction of ${\mathrm{F}}^{-}$ with ${\text{CH}}_3\text{Cl}$ are shown in Figure 6 for two different collision energies (Stei et al., 2016). Two different features in the images are visible, a low product velocity distribution at the center of the image and a crescent‐shaped feature on the right side of the images. The first feature represents reactions occuring by an indirect complex‐mediated reaction mechanism, while the second feature is characteristic of the direct rebound mechanism.

Figure 6.

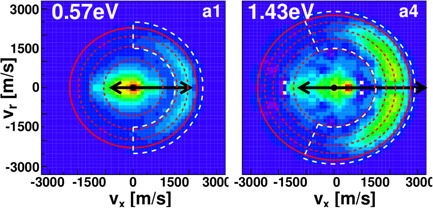
Differential scattering images for the ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\mathrm{F}}^{-}+{\text{CH}}_3\text{Cl}$ at two different collision energies. Reprinted with permission from Stei et al. (2016)​ [Color figure can be viewed at wileyonlinelibrary.com]

Similar to the guided‐ion‐beam experiments, the crossed‐beam experiments allow for larger collision energies up to several electronvolts. Moving to these higher energies, differential scattering cross sections for the endothermic reaction channels of the ${\mathrm{F}}^{-}+{\text{CH}}_3\mathrm{I}$ reaction, proton transfer to ${\text{CH}}_2{\mathrm{I}}^{-}$, dihalide ${\text{FI}}^{-}$ formation and also formation of ${\text{FHI}}^{-}$ could be studied (Carrascosa et al., 2016).

5.3. Influence of water molecules on the reaction dynamics

In further work, we investigated the reactive scattering of ${\text{OH}}^{-}$ anions attached to one or two water water molecules with ${\text{CH}}_3\mathrm{I}$ (Otto, Brox, et al., 2012). To prepare the anion clusters with only a small, well‐controlled amount of internal excitation, they were trapped in a radiofrequency octupole trap for about 20 ms before being brought to collision with the molecular beam of ${\text{CH}}_3\mathrm{I}$. The trap was cooled to about 100 K, which is sufficient to freeze out almost all vibrational excitation in the negative ions (Otto, Xie, et al., 2012).

For bare ${\text{OH}}^{-}$ anions reacting with ${\text{CH}}_3\mathrm{I}$ three different reaction mechanisms were observed in the differential scattering cross sections for 0.5–2 eV collision energy: indirect complex‐mediated dynamics, forward and sideways stripping, and direct rebound dynamics (Otto, Brox, et al., 2012). The differential scattering images then changed substantially when one or two water molecules bind to the ${\text{OH}}^{-}$ reactant. The forward scattered products are not observable when either one or two water molecules are attached. Instead, for the ${\text{OH}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$ cluster the back‐scattered ${\mathrm{I}}^{-}$ products become the most prominent reaction channel, which corresponds to the rebound mechanism. For two water molecules only isotropic scattering with low product velocities is observed.

The enhancement of the direct rebound mechanisms for one water attached to the ${\text{OH}}^{-}$ nucleophile was explained by structure calculations, which showed that the water molecule provides a steric guidance of the nucleophile towards the ${\text{CH}}_3$ group of methyl iodide in the reaction's entrance channel complex (Otto, Brox, et al., 2012). Detailed direct dynamics simulations by Xie et al. (2015) confirmed this and found good overall agreement with the experimental scattering data.

Micro‐hydration effects have recently also been studied in reactions ${\mathrm{F}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$ and ${\text{Cl}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$ reacting with ${\text{CH}}_3\mathrm{I}$ (Bastian, Michaelsen, Li, et al., 2020). The dominant product in these reactions is bare ${\mathrm{I}}^{-}$ and not the thermodynamically favored ${\mathrm{I}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$, in good agreement with trajectory simulations by Zhang and coworkers. Similar findings have been made earlier for microhydrated ${\text{OH}}^{-}$ reactions (Otto et al., 2013). Both ${\mathrm{I}}^{-}$ and ${\mathrm{I}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$ products form mostly via an indirect mechanism with isotropic and small product velocities. Compared to unsolvated reactions, the indirect fraction is significantly increased due to the water molecule. At 2.6 eV the scattering images for ${\mathrm{F}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$ also show the signature of the direct rebound mechanism (Bastian, Michaelsen, Li, et al., 2020).

In the microhydrated reaction of ${\text{Cl}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)$ very small product velocities were found to be fully suppressed, in contrast to other studied indirect reaction mechanisms (Bastian, Michaelsen, Li, et al., 2020; Bastian et al., 2021). A very similar feature was found in ligand exchance reaction pathway of singly hydrated halides ${\mathrm{F}}^{-}\left({\mathrm{H}}_2\mathrm{O}\right)+{\text{CH}}_3\mathrm{I}\to {\left[{\text{FCH}}_3\mathrm{I}\right]}^{-}+{\mathrm{H}}_2\mathrm{O}$ (Bastian, Michaelsen, Ončák, et al., 2020). This suppression could be explained by the fragmentation of a transient or product reaction complex, which occurs when the internal energy is large enough to initiate unimolecular dissociation before the complex can be detected (Bastian et al., 2021).

5.4. Controlling ${\mathrm{S}}_{\mathrm{N}}2$ reactions with initial vibrational excitation

In a set of experiments the influence of vibrational excitation of the CH‐stretching mode on the ${\mathrm{S}}_{\mathrm{N}}2$ reaction ${\mathrm{F}}^{-}+{\text{CH}}_3\mathrm{I}$ has been investigated (Michaelsen, Bastian, Ayasli, et al., 2020; Michaelsen, Bastian, Strübin, et al., 2020; Stei et al., 2018). Overall, CH stretching vibrations had been considered spectator modes that do not affect the reaction, when it occurs via backside attack by the direct rebound mechanism. This was supported by QCT calculations (Wang et al., 2016), while earlier quantum scattering calculations had predicted different cross sections for vibrationally excited reactants in the ${\text{Cl}}^{-}+{\text{CH}}_3\text{Br}$ reaction (Hennig & Schmatz, 2007). In experiments where the symmetric CH stretching vibration in ${\text{CH}}_3\mathrm{I}$ was excited in a few percent of the reactants right before the interaction with the anionic nucleophile occured, we were able to show that the excitation does not change the reactivity of this ${\mathrm{S}}_{\mathrm{N}}2$ reaction (Stei et al., 2018). Experimental proof that scattering indeed occured with excited reactants was provided by the strong influence of the vibrational excitation on the proton transfer reaction pathway, which leads to ${\text{CH}}_2{\mathrm{I}}^{-}$ formation and was measured together with the ${\mathrm{S}}_{\mathrm{N}}2$ product ${\mathrm{I}}^{-}$.

In further work on the ${\mathrm{F}}^{-}+{\text{CH}}_3\mathrm{I}$ reaction, which included different collision energies, we could identify that vibrational enhancement may indeed enhance ${\mathrm{S}}_{\mathrm{N}}2$ reactivity when occuring at a collision energy of 2.5 eV (Michaelsen, Bastian, Ayasli, et al., 2020). A similar trend has been found in QCT simulations (Olasz and Czakó, 2018). In contrast, the proton transfer reaction is strongly enhanced at low collision energies, and much less affected at high collision energies. For halide abstraction, which leads to the formation of ${\text{FI}}^{-}$ and ${\text{FHI}}^{-}$ products, the reactivity was found to be suppressed. The spectator mode behavior for ${\mathrm{S}}_{\mathrm{N}}2$ reactions and the enhancement of proton transfer rections is in agreement with the sudden vector projection (SVP) model (Guo & Jiang, 2014; Jiang & Guo, 2013), which provides an extension of the Polanyi rules (Polanyi, 1972) to polyatomic reactions.

Vibrational excitation not only influences the overall reactivity of different reaction pathways, it can also directly affect the reaction dynamics. This was found for the proton transfer reaction in ${\mathrm{F}}^{-}+{\text{CH}}_3\mathrm{I}$ collisions where indirect complex‐mediated dynamics dominate at low collision energies (0.7 eV), whereas a shift to a direct stripping mechanism is observed at high collision energies (2.3 eV) (Michaelsen, Bastian, Strübin, et al., 2020).

5.5. Quantum scattering calculations of substitution reactions

Full quantum scattering calculations of chemical reactions are necessary to properly account for zero‐point energies and include interference, resonance, and tunneling effects (Clary, 1998). However, they are computationally much more demanding than trajectory simulations. For many years only three‐atom reactions, such as F + ${\mathrm{H}}_2$ Qiu et al. (2006), were calculated in this way. For larger systems, reduced‐dimensionality quantum scattering calculations are being pursued.

Clary was the first to perform quantum scattering calculations for an ${\mathrm{S}}_{\mathrm{N}}2$ reaction (Le Garrec et al., 1997) (see Section 3.2). Later Schmatz and coworkers studied the identity and nonidentity ${\mathrm{S}}_{\mathrm{N}}2$ reactions of ${\text{Cl}}^{-}$ with ${\text{CH}}_3\text{Cl}$ and ${\text{CH}}_3\text{Br}$ by including up to 4 of 12 internal degrees of freedom in their time‐independent quantum scattering calculations (Hennig & Schmatz, 2004, 2005, 2007; Schmatz, 2004). In this way, vibrational state‐dependent reaction cross sections were obtained. By selecting different degrees of freedom for the quantum calculations, specifically rotational instead of vibrational degrees of freedom, differential scattering cross sections (Hennig & Schmatz, 2012) and the dependence of the cross section on the initial rotational angular momentum could be calculated (Hennig & Schmatz, 2016).

Recently, a six‐dimensional quantum scattering calculation has been achieved by Wang et al. (2016), who studied the ${\mathrm{F}}^{-}+{\text{CH}}_3\text{Cl}$ reaction based on the model of Palma and Clary (2000). These calculations supported the indirect mechanism at low and the direct mechanism at higher collision energies. They also analyzed the vibrational state‐dependence of the reaction cross section, as discussed in Section 5.4 above. Furthermore, time‐dependent wavepacket calculations have also been carried out, again in reduced dimensions, and the product internal energy has been computed, which were found to compare qualitatively well with experiment (Kowalewski et al., 2014).

6. SUMMARY AND OUTLOOK

Interest in gas phase nucleophilic substitution reactions has been driven by the ability to investigate the reactivity of this important class of reactions without the influence of solvent molecules (Bohme & Young, 1970). During the last 50 years, experimental and theoretical studies have provided a wealth of insight into their intrinsic dynamics. Reaction probabilities have been extracted from rate coefficient and cross section measurements by comparing measured data with capture cross sections that are determined purely by the long‐range interaction. Equilibrium constants yielded exothermicities and binding energies of reaction complexes. From these data the view of a reaction resulted that proceeds across a double‐well potential energy landscape with an intermediate, often submerged, reaction barrier (Olmstead & Brauman, 1977). Using this view, calculations based on statistical theories allowed for quantitative comparison with measured rate coefficients. The ability to add solvent molecules to the reactant ion one by one has been widely used to investigate how the reaction is influenced (Chabinyc et al., 1998). The statistical picture, however, was soon challenged by various experimental and theoretical evidence, such as reaction probabilities that do not change with vibrational excitation (Viggiano et al., 1992), product energy partitioning that does not couple to certain vibrational modes of a transient reaction complex (Graul & Bowers, 1994), or reactions that avoids trapping in its intermediate reaction complexes (Sun et al., 2002).

In the last 20 years the research focus has shifted to obtain a better and more quantitative understanding of the atomistic dynamics of nucleophilic substitution reactions. The advent of ion–molecule crossed‐beam reactive scattering experiments (Mikosch, Trippel, et al., 2008) and the improvement of trajectory simulations, most recently on accurate full‐dimensional potential energy surfaces (Czakó et al., 2021), has made this possible. Energy‐ and angle‐differential cross sections have been obtained, and remarkable agreement has been achieved between experiment and theory (Stei et al., 2016). A range of reaction mechanisms have been disentangled, including the direct rebound mechanism via backside attack, the complex‐mediated mechanism, the direct stripping mechanism, or the roundabout mechanism (Mikosch, Trippel, et al., 2008; Xie et al., 2014).

The question is what is ahead? ${\mathrm{S}}_{\mathrm{N}}2$ reactions have continued to surprise, for example, with the recent discovery of a novel double‐inversion mechanism (Szabó & Czakó, 2015). One of the most important questions for chemical reactions in general, what is the role of quantum mechanical dynamics, is nowhere near to being answered, despite the fact that zero‐point energy and tunneling through the intermediate barrier may impact the dynamics significantly. The study of isotope effects, using deuterated reactants, may shed some light on this. Also, precise comparison of differential cross sections from experiment and theory have shown some remaining deviations. Further precision crossed‐beam studies will be carried out to clarify if these deviations point to nonclassical dynamics. With better understanding comes the aim to control reaction outcomes of ${\mathrm{S}}_{\mathrm{N}}2$ reactions. Vibrational state‐selected reaction experiments have already shown that reaction cross sections can be influenced (Michaelsen, Bastian, Ayasli, et al., 2020). It will be interesting, and challenging, to extend this study to the lower lying vibrational modes of the ${\text{CH}}_3$ umbrella and to the C‐Y vibration.

A range of studies have already focused on the reaction dynamics of micro‐hydrated reactants. In applications, however, ${\mathrm{S}}_{\mathrm{N}}2$ reactions are not only used in water, but in a range of solvents. Comparing the influence of different solvents on the atomistic dynamics in micro‐solvation experiments is still in its infancy. Furthermore, when substituting the hydrogen atoms in reaction (1) by alkyl chains, different and in general even richer reaction dynamics become possible.

With two or more carbon centers, base‐induced elimination can occur and competes with nucleophilic substitution. A review of E2 reaction studies over the last fifty years would fill a second article. Research on the competition between these and ${\mathrm{S}}_{\mathrm{N}}2$ reactions, which lead to the same ionic product, started early using kinetic isotope effects or secondary reactions to distinguish the two pathways (Gronert et al., 1991; Wladkowski & Brauman, 1992). Later dianion reactants were employed for this purpose (Gronert, 2003). More recently, crossed‐beam imaging has allowed us to study the direct competition betwen ${\mathrm{S}}_{\mathrm{N}}2$ and E2 reactions (Carrascosa et al., 2018; Carrascosa, Meyer, Zhang, et al., 2017; Meyer et al., 2019). In the future this technique may also be applied to aromatic substitution (${\mathrm{S}}_{\mathrm{N}}\text{Ar}$) reactions (Sharma et al., 2020). Thus, gas phase studies can be expected to continue to improve our understanding of chemical reactions for many years to come.

Biography

Roland Wester studied physics at the Universities of Konstanz and Heidelberg. He received his PhD from the University of Heidelberg in 1999 for Coulomb explosion imaging experiments of molecular ions. He then worked for two years at the University of California in Berkeley on femtosecond spectroscopy. From 2003 to 2010 he carried out research on ultracold molecules and cold molecular ions at the University of Freiburg. Since 2010 he is full professor at the University of Innsbruck.

Wester R. Fifty years of nucleophilic substitution in the gas phase. Mass Spec Rev. 2022;41:627‐644. 10.1002/mas.21705