Bayesian dose regimen assessment in early phase oncology incorporating pharmacokinetics and pharmacodynamics

Abstract

Phase I dose‐finding trials in oncology seek to find the maximum tolerated dose of a drug under a specific schedule. Evaluating drug schedules aims at improving treatment safety while maintaining efficacy. However, while we can reasonably assume that toxicity increases with the dose for cytotoxic drugs, the relationship between toxicity and multiple schedules remains elusive. We proposed a Bayesian dose regimen assessment method (DRtox) using pharmacokinetics/pharmacodynamics (PK/PD) to estimate the maximum tolerated dose regimen (MTD‐regimen) at the end of the dose‐escalation stage of a trial. We modeled the binary toxicity via a PD endpoint and estimated the dose regimen toxicity relationship through the integration of a dose regimen PD model and a PD toxicity model. For the first model, we considered nonlinear mixed‐effects models, and for the second one, we proposed the following two Bayesian approaches: a logistic model and a hierarchical model. In an extensive simulation study, the DRtox outperformed traditional designs in terms of proportion of correctly selecting the MTD‐regimen. Moreover, the inclusion of PK/PD information helped provide more precise estimates for the entire dose regimen toxicity curve; therefore the DRtox may recommend alternative untested regimens for expansion cohorts. The DRtox was developed to be applied at the end of the dose‐escalation stage of an ongoing trial for patients with relapsed or refractory acute myeloid leukemia (NCT03594955) once all toxicity and PK/PD data are collected.

1. INTRODUCTION

Phase I dose‐finding clinical trials in oncology seek to find the maximum tolerated dose (MTD) to obtain reliable information regarding the safety profile of a drug or a combination of drugs, pharmacokinetics, and the mechanism of action (Crowley et al., ²⁰⁰⁵; Chevret, ²⁰⁰⁶). In this phase, the endpoint is defined as the dose‐limiting toxicity, which is mainly based on the National Cancer Institute (NCI) Common Toxicity Criteria for Adverse Events (CTCAE, ²⁰¹⁷). Usually, standard algorithm‐based or model‐based dose‐escalation methods (Storer, 1989; O'Quigley et al., ¹⁹⁹⁰) aim to find the MTD while considering the entire cycle dosing as a single administration. Most methods assume that toxicity increases with the dose; however, the estimation of the relationship between toxicity and multiple doses over a cycle remains elusive as we can observe nonlinear dose‐response profiles (Schmoor and Schumacher, 1992; Bullock et al., ²⁰¹⁷; Musuamba et al., ²⁰¹⁷). We assume that considering the complete cycle dosage could improve treatment safety while maintaining future potential efficacy.

To account for dosage repetition over the treatment cycle, some authors have considered either the dose‐schedule or the dose regimen relationship. The NCI defines “schedule” as “A step‐by‐step plan of the treatment that a patient is going to receive. A treatment schedule includes the type of treatment that will be given (such as chemotherapy or radiation therapy), how it will be given (such as by mouth or by infusion into a vein), and how often it will be given (such as once a day or once a week). It also includes the amount of time between courses of treatment and the total length of time of treatment” (https://www.cancer.gov/publications/dictionaries/cancer‐terms/def/treatment‐schedule). Moreover, the NCI defines “regimen” as “A treatment plan that specifies the dosage, the schedule, and the duration of treatment” (https://www.cancer.gov/publications/dictionaries/cancer‐terms/def/regimen). Following these definitions, we considered the dose regimen relationship, as it includes the dosage, the repetition scheme, and the duration.

For some molecules, it has been observed that, in the same patient, starting a dose regimen with a lower lead‐in dose and increasing the dose step‐by‐step before reaching the steady‐state dose can reduce the occurrence of acute toxicities (Chen et al., ²⁰¹⁹). However, a dose regimen starting with higher lead‐in doses can increase the efficacy.

Dose‐finding trials can aim to study different dose regimens with the same or different total cumulative dose to determinate the most appropriate regimen supported by pharmacokinetics/pharmacodynamics (PK/PD) profiles. Several methodological papers have attempted to address the issue of prospective dose and schedule finding methods. Braun et al. (2005), Braun et al. (2007), Liu and Braun (2009), and Zhang and Braun (2013) proposed considering the time‐to‐toxicity rather than the usual binary outcome to optimize dose and schedule, as the timing of administration. Wages et al. (2014) proposed considering dose‐schedule finding as a two‐dimensional problem and extended the partial‐order continual reassessment method developed for combination trials. Other authors, such as Li et al. (2008), Thall et al. (2013), and Guo et al. (2016), proposed dose‐schedule‐finding methods that jointly model toxicity and efficacy outcomes. Lyu et al. (2018) proposed a hybrid design that is partially algorithm‐based and partially model‐based for sequences of doses over multiple cycles when few doses are under study.

Only a few methods consider PK/PD data in the prospective dose‐allocation design. Ursino et al. (2017) compared multiple methods that enable the use of PK measures in sequential Bayesian adaptive dose‐finding designs, including a dose‐AUC‐toxicity model combining two models to recommend the dose. Günhan et al. (2020) proposed a Bayesian time‐to‐event pharmacokinetic adaptive model for multiple regimens using PK latent profiles to measure drug exposure. Our aim is to extend these propositions by modeling the dose regimen toxicity relationship using PK/PD.

2. MOTIVATION

This work was motivated by the ongoing first‐in‐human dose‐escalation study of SAR440234 (https://www.cancer.gov/publications/dictionaries/cancer-drug/def/798327) administered as a single agent to patients with relapsed or refractory acute myeloid leukemia, high‐risk myelodysplastic syndrome, or B‐cell acute lymphoblastic leukemia (NCT03594955 https://clinicaltrials.gov/ct2/show/NCT03594955). SAR440234 is a novel bispecific T‐cell engager antibody that activates and redirects cytotoxic T lymphocytes (CTLs) to enhance the CTL‐mediated elimination of CD123‐expressing tumor cells. CTL activation induces the release of inflammatory cytokines, which can potentially cause cytokine release syndrome (CRS). CRS is a systemic inflammatory response and among the most commonly observed toxicities of T‐cell engaging bispecific antibodies, such as blinatumomab, which is a bispecific anti‐CD19/CD3 antibody (Shimabukuro‐Vornhagen et al., ²⁰¹⁸). Several cytokines, such as IL6, IL10, and INFγ, are consistently found to be elevated in serum from patients with CRS. The association between the peak of cytokine and CRS has been evaluated by Teachey et al. (2016). It has been shown that repeating the dosing of the drug can decrease CRS, particularly when the first administration is divided into several steps progressively (Chen et al., ²⁰¹⁹). Therefore, intrapatient dose‐escalation with a dose regimen consisting of lower initial doses followed by a higher maintenance dose was implemented in this study to reduce the occurrence of CRS (Boissel et al., ²⁰¹⁸).

The aim of the trial was to find the MTD of SAR440234 using the 3+3 design as the dose‐escalation design. However, the 3+3 design and more general dose‐finding designs ignore part of the dose regimen information: these designs were not developed to account for multiple dose administrations in the model. Therefore, they map the entire dose regimen administered to the patient in a single dose‐level, that is, a single value. This mapping is defined prior to the trial onset and depends on the design chosen. This approach is inefficient for achieving the trial goal.

In this paper, we propose to model the binary toxicity endpoint (CRS) and the continuous PD response (cytokine profile) at the end of the trial, once all data have been collected, to characterize the dose regimen toxicity relationship. This dose regimen assessment method (DRtox) allows the determination of the maximum tolerated dose regimen (MTD‐regimen), as illustrated in Figure 1.

FIGURE 1.

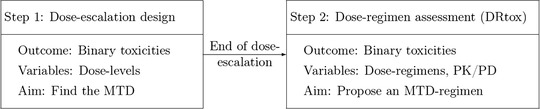
Trial scheme: the DRtox method is applied at the end of the dose‐escalation stage of a phase I trial

3. MODEL

Let $\mathcal{D}=\{d_1,\text{…},d_L\}$ be the set of doses that can be administered to patients, where $d_l<d_{l+1}$. Let $\mathcal{S}=\{{\mathit{S}}_{\mathbf{1}},\text{…},{\mathit{S}}_{\mathbf{K}}\}\subset \mathbb{S}$ be the panel of dose regimens to be studied in the trial. The dose regimen ${\mathit{S}}_{\mathbf{k}}\in \mathcal{S}$, where $k\in \{1,\text{…},K\}$, is defined as the sequence of J doses, ${\mathit{S}}_{\mathbf{k}}=(d_{k,1},d_{k,2},\text{…},d_{k,J})$, administered at times $\mathit{t}=(t_1,t_2,\text{…},t_J)$, where $d_{k,j}\in \mathcal{D}$ for $j\in \{1,\text{…},J\}$. To simplify the notations, we assumed that all dose regimens have the same number of drug administrations at the same times, but this assumption can be relaxed. Let S_{k, j} be the subregimen of S_k until the $j\text{th}$ administration, ${\mathit{S}}_{\mathbf{k},\mathbf{j}}=(d_{k,1},d_{k,2},\text{…},d_{k,j})$, for $j<J$. Let $n\in \mathbb{N}$ be the number of patients included in the trial. Let $Y_{i,j}$ be the binary toxicity response of patient i observed exactly after the $j\text{th}$ administration, and let $Y_i$ be his/her global toxicity response at the end of the administrations.

Let ${\stackrel{\sim }{\mathbf{s}}}_{\mathbf{i}}=(d_{i,1},d_{i,2},\text{…},d_{i,J})\in \mathcal{S}$ be the dose regimen planned for the $i\text{th}$ patient. We assume that the drug administration is stopped if toxicity occurs; thus let $j_i$ denote the last administration of patient i. We denote the actual regimen received by patient i as ${\mathit{s}}_{\mathbf{i}}=(d_{i,1},d_{i,2},\text{…},d_{i,j_i})\subset {\stackrel{\sim }{\mathbf{s}}}_{\mathbf{i}}$, where ${\mathit{s}}_{\mathbf{i}}={\stackrel{\sim }{\mathbf{s}}}_{\mathbf{i}}$ if no toxicity is observed. Let s_{i, j} be the subregimen until j of s_i , where $j\le j_i$.

The aim is to estimate the MTD‐regimen at the end of the trial, which is defined as the dose regimen with the toxicity probability closest to the target toxicity rate ${\delta }_T$, that is, the MTD‐regimen is the regimen ${\mathit{S}}_{{\mathbf{k}}^{★}}$, where $k^{★}={\mathrm{arg\; min}}_k|p_T({\mathit{S}}_{\mathbf{k}})-{\delta }_T|$ and $p_T({\mathit{S}}_{\mathbf{k}})$ is the toxicity probability of S_k .

We assume that a PD endpoint extracted from the continuous PD profile of a biomarker related to toxicity plays an intermediate role in the dose regimen toxicity relationship. We propose the DRtox approach in which the first model is built for the dose regimen and the PD endpoint, and the second model is built for the PD endpoint and the toxicity response. Therefore, integrating both models links the dose regimen to the toxicity response to find the MTD‐regimen. In the following section, the structure of the PK/PD models is described, two approaches between the PD endpoint and toxicity response are proposed, as well as a practical method for their integration.

3.1. Dose regimen PD response model

Let $C(t)$ be the continuous drug concentration and $E(t)$ be the continuous PD response related to toxicity measured at time t. We assume that $C(t)$ and $E(t)$ can be modeled using nonlinear mixed‐effects models as follows:

$$\left\{\begin{array}{c}C(t)=f^{(1)}\left({\mathbf{\theta }}_{\mathbf{i}}^{(\mathbf{1})},t\right)+g^{(1)}\left({\mathbf{\theta }}_{\mathbf{i}}^{(\mathbf{1})},t,{\mathbf{\xi }}_{\mathbf{1}}\right){\epsilon }^{(1)},\hfill \\ E(t)=f^{(2)}\left({\mathbf{\theta }}_{\mathbf{i}}^{(\mathbf{2})},t\right)+g^{(2)}\left({\mathbf{\theta }}_{\mathbf{i}}^{(\mathbf{2})},t,{\mathbf{\xi }}_{\mathbf{2}}\right){\epsilon }^{(2)},\hfill \end{array}\right.$$ (1)

where f ⁽¹⁾ and f ⁽²⁾ represent the structural models, which are usually solutions of differential equations based on biological knowledge. ${\mathbf{\theta }}_{\mathbf{i}}=({\mathbf{\theta }}_{\mathbf{i}}^{(\mathbf{1})},{\mathbf{\theta }}_{\mathbf{i}}^{(\mathbf{2})})$ represents the ith patient's specific parameter vector, where usually, ${\mathbf{\theta }}_{\mathbf{i}}=\mathit{\mu }{e}^{{\mathbf{\eta }}_{\mathbf{i}}}$, with μ denoting the fixed effects vector, and η_i denoting the random effects vector defined as ${\mathbf{\eta }}_{\mathbf{i}}\sim \mathcal{N}(\mathbf{0},\mathbf{\Omega })$, with Ω denoting the variance–covariance matrix.

g ⁽¹⁾ and g ⁽²⁾ represent the error models, which depend on the additional parameters ξ₁ and ξ₂ , and ε⁽¹⁾ and ε⁽²⁾ are standard Gaussian variables. The usual error models are the constant model where $g^{(l)}({\mathbf{\theta }}_{\mathbf{i}}^{(\mathbf{l})},t,{\xi }_l=a)=a$, the proportional model where $g^{(l)}({\mathbf{\theta }}_{\mathbf{i}}^{(\mathbf{l})},t,{\xi }_l=b)=b{f}^{(l)}({\mathbf{\theta }}_{\mathbf{i}}^{(\mathbf{l})},t)$ and combinations of the constant and proportional models.

3.2. PD endpoint toxicity model

$r({\mathbf{\theta }}_{\mathbf{i}},{\mathit{s}}_{\mathbf{i},\mathbf{j}})$ is defined as the function derived from the PK/PD models that returns the value of the PD endpoint (such as the peak of a biomarker) exactly after the administration of the dose regimen s_{i, j} with individual PK/PD parameters θ_i . Let $\mathit{R}({\mathbf{\theta }}_{\mathbf{i}},{\mathbf{s}}_{\mathbf{i},\mathbf{j}})=(r({\mathbf{\theta }}_{\mathbf{i}},s_{i,1}),\text{…},r({\mathbf{\theta }}_{\mathbf{i}},{\mathit{s}}_{\mathbf{i},\mathbf{j}}))$ be the function derived from the PK/PD models that returns the vector of all PD endpoints (such as all biomarker peaks) observed after the administration of the regimen s_{i, j} with individual PK/PD parameters θ_i . For patient i, we can simplify the notations considering $r_{i,j}=r({\mathbf{\theta }}_{\mathbf{i}},{\mathit{s}}_{\mathbf{i},\mathbf{j}})$, ${\mathit{R}}_{\mathbf{i},\mathbf{j}}=\mathit{R}({\mathbf{\theta }}_{\mathbf{i}},{\mathbf{s}}_{\mathbf{i},\mathbf{j}})$ and the vector of all PD endpoints ${\mathit{R}}_{\mathbf{i}}={\mathit{R}}_{\mathbf{i},{\mathbf{j}}_{\mathbf{i}}}$.

Then, let $r_i^M=\underset{l\in \{1,\text{…},j_i\}}{\max }(r_{i,l})$ be the summary PD endpoint (such as the highest peak) observed in patient i, which we assume is related to toxicity.

To define the prior distributions, let $({\overline{r}}_1^M,{\overline{r}}_2^M,\text{…}{\overline{r}}_K^M)$ denote the reference values of the summary endpoint of all dose regimens of the trial ( S₁ , …, S_k ); for example, we can consider population values ${\overline{r}}_k^M=\max \{r(\mathit{\mu },{\mathit{S}}_{\mathbf{k},\mathbf{1}}),\text{…},r(\mathit{\mu },{\mathit{S}}_{\mathbf{k}})\}$ with μ as the PK/PD vector of fixed effects.

In the following section, two statistical models establishing the relationship between the PD endpoint and the toxicity response are shown.

3.2.1. Logistic‐DRtox

We propose a Bayesian logistic model to link the global binary toxicity response of patient i receiving s_i to his summary PD endpoint related to toxicity as follows:

$$\mathrm{logit}\left\{\mathbb{P}\left(Y_i=1\right)\right\}={\beta }_0+{\beta }_1\log \left({\displaystyle \frac{r_i^M}{{\overline{r}}_{k_T}^M}}\right),$$ (2)

where ${\beta }_1>0$ to have the toxicity probability that increases with the value of the summary PD endpoint. We normalize the PD endpoint for prior elicitation using ${\overline{r}}_{k_T}^M$, which is the reference value of dose regimen ${\mathit{S}}_{{\mathbf{k}}_{\mathbf{T}}}$, which we initially guess to have a toxicity probability of ${\delta }_T$. In this model, we do not consider the longitudinal values of the biomarker as we assume that toxicity is not due to the cumulative effect of the biomarker profile. However, previous drug administrations are considered in the construction of the biomarker through the PK/PD model. Let ${\pi }_1\{({\beta }_0,{\beta }_1),r_i^M\}={\mathrm{logit}}^{-1}\left\{{\beta }_0+{\beta }_1\log \left(\frac{r_i^M}{{\overline{r}}_{k_T}^M}\right)\right\}$.

Regarding prior distributions, we consider a normal distribution for the intercept, ${\beta }_0\sim \mathcal{N}({\overline{\beta }}_0,{\sigma }_{{\beta }_0}^2)$ and a gamma distribution for the slope to ensure positivity, ${\beta }_1\sim \gamma ({\alpha }_1,\frac{{\alpha }_1}{{\overline{\beta }}_1})$, where α₁ is the shape parameter, ${\overline{\beta }}_0=\mathbb{E}[{\beta }_0]$, and ${\overline{\beta }}_1=\mathbb{E}[{\beta }_1]$. By construction, we have ${\overline{\beta }}_0=\mathrm{logit}({\delta }_T)$, obtained via Equation (2) with $r_i^M={\overline{r}}_{k_T}^M$. Then, let $(p_1,\text{…},p_K)$ be the initial guesses of the toxicity probabilities of regimens ( S₁ , …, S_K ), where $p_{k_T}={\delta }_T$. We can determine ${\overline{\beta }}_1$ using either only one regimen, which differs from the reference regimen ${\mathit{S}}_{{\mathbf{k}}_{\mathbf{T}}}$, as ${\pi }_1\{(\overline{{\beta }_0},\overline{{\beta }_1}),{\overline{r}}_k^M\}=p_k$, with $k\in \{1,\text{…},K\}$ and $k\ne k_T$, or multiple regimens, such as the neighbors of the reference regimen, as follows:

$${\overline{\beta }}_1=\underset{{\beta }_1}{\mathrm{arg\; min}}\sum _{k=k_T-1}^{k_T+1}{\left[p_k-{\pi }_1\left\{\left({\overline{\beta }}_0,{\beta }_1\right),{\overline{r}}_k^M\right\}\right]}^2.$$ (3)

3.2.2. Hierarchical‐DRtox

In this approach, we assume that patients experience toxicity if their PD response exceeds an unknown threshold specific to each patient. To consider interindividual variability in toxicity, we introduce a patient‐specific continuous latent variable, $Z_i$, which represents the toxicity threshold of the PD response. In contrast to the previous approach, we model toxicity after each administration using a modification of the hierarchical probit model (Berry et al., ²⁰¹⁰) as follows:

$$\left\{\begin{array}{c}{Y}_{i,j}=\left\{\begin{array}{c}0\text{if}{Z}_i>\log \left({\displaystyle \frac{r_{i,j}}{{\overline{r}}_{k_{50}}^M}}\right)\hfill \\ \\ 1\text{if}{Z}_i\le \log \left({\displaystyle \frac{r_{i,j}}{{\overline{r}}_{k_{50}}^M}}\right)\hfill \end{array}\right.\hfill \\ \\ Z_i\sim \mathcal{N}({\mu }_z,{\tau }_z^2),\hfill \end{array}\right.$$ (4)

where ${\overline{r}}_{k_{50}}^M$ is the reference value at the dose regimen ${\mathit{S}}_{{\mathbf{k}}_{\mathbf{50}}}$, which we initially guess to have a toxicity probability of 0.5. By adding the random effect, this Bayesian hierarchical model shares common features with the probit model, where ${\tau }_z^2$ represents the between‐subject variance and controls the extent of the borrowing across all patients.

If we consider a new patient i with a vector of biomarker endpoints R_i , we can predict his probability of toxicity by $\mathbb{P}(Y_i=1)=F_z\left\{\log \left(\frac{r_i^M}{{\overline{r}}_{k_{50}}^M}\right)\right\}$, where $F_z$ is the cumulative distribution function of $\mathcal{N}({\mu }_z,{\tau }_z^2)$. The details of the formula are shown in Web Appendix A. Let ${\pi }_2\{({\mu }_z,{\tau }_z^2),r_i^M\}=F_z\left\{\log \left(\frac{r_i^M}{{\overline{r}}_{k_{50}}^M}\right)\right\}$.

Regarding the prior distributions, we consider ${\mu }_z\sim \mathcal{N}(0,{\sigma }_{{\mu }_z}^2)$ and ${\tau }_z\sim \text{half-Cauchy}(0,{\sigma }_{{\tau }_z}^2)$. Regarding the half‐Cauchy distribution, we followed the recommendations by Gelman (2006), as we assumed that ${\tau }_z$ could be near 0. Web Appendix G shows how this model can be implemented.

3.3. Dose regimen toxicity model

The posterior toxicity probability of dose regimen S_k is estimated by integrating the PD endpoint toxicity model on all possible values of the PD endpoint. As this integral cannot usually be solved analytically, the posterior toxicity probability of regimen S_k is estimated via the drawing of a hypothetical set of M patients with M‐vector $(p_T{({\mathit{S}}_{\mathbf{k}})}^{(1)},\text{…},p_T{({\mathit{S}}_{\mathbf{k}})}^{(M)})$ as posterior toxicity probabilities. Then, the posterior toxicity probability of regimen S_k is estimated as the posterior mean $\widehat{p_T}({\mathit{S}}_{\mathbf{k}})=\frac{1}{M}{\sum }_{m=1}^M{p}_T{({\mathit{S}}_{\mathbf{k}})}^{(m)}$. This sample of the posterior toxicity probability requires the following three major steps:

• (1) Model fitting:
  • (a)First, the PK/PD models are fitted to obtain estimates of the population parameters comprising the fixed effects, $\widehat{\mathbf{\mu }}$, and the random effects variance–covariance matrix, $\widehat{\mathbf{\Omega }}$, under the Frequentist paradigm. The patients' individual PK/PD parameters, $({\widehat{\mathbf{\theta }}}_{\mathbf{1}},\text{…},{\widehat{\mathbf{\theta }}}_{\mathbf{n}})$, are also estimated.
  • (b)Based on the estimated PK/PD parameters, the PD biomarkers are predicted for each patient:
    • •For the logistic‐DRtox: the global biomarker peaks $({\widehat{r}}_1^M,\text{…},{\widehat{r}}_n^M)$ are predicted for each patient as ${\widehat{r}}_i^M=\max \{r({\widehat{\mathbf{\theta }}}_{\mathbf{i}},{\mathit{s}}_{\mathbf{i},\mathbf{1}}),\text{…},r({\widehat{\mathbf{\theta }}}_{\mathbf{i}},{\mathit{s}}_{\mathbf{i}})\}$ for $i\in \{1,\text{…},n\}$. The vector of toxicity responses and biomarker responses, $((Y_1,\text{…},Y_n),({\widehat{r}}_1^M,\text{…},{\widehat{r}}_n^M))$, constitutes the data of the trial.
    • •For the hierarchical‐DRtox: the biomarker peaks vectors $({\widehat{\mathbf{R}}}_{\mathbf{1}},\text{…},{\widehat{\mathbf{R}}}_{\mathbf{n}})$ are predicted for each patient as ${\widehat{\mathbf{R}}}_{\mathbf{i}}=\mathit{R}({\widehat{\mathbf{\theta }}}_{\mathbf{i}},{\mathbf{s}}_{\mathbf{i}})$ for $i\in \{1,\text{…},n\}$. The vector of toxicity responses and biomarker responses, $((Y_{1,1},\text{…},Y_{n,j_n}),({\widehat{\mathbf{R}}}_{\mathbf{1}},\text{…},{\widehat{\mathbf{R}}}_{\mathbf{n}}))$, constitutes the data of the trial.
  • (c)A vector of the parameters of the PD endpoint toxicity model of size m _iter is sampled from their posterior distribution:
    • •For the logistic‐DRtox, $(({\beta }_0^{(1)},{\beta }_1^{(1)}),\text{…},({\beta }_0^{(m_{\mathrm{iter}})},{\beta }_1^{(m_{\mathrm{iter}})}))$ is sampled.
    • •For the hierarchical‐DRtox, $(({\mu }_z^{(1)},{\tau }_z^{(1)}),\text{…},({\mu }_z^{(m_{\mathrm{iter}})},{\tau }_z^{(m_{\mathrm{iter}})}))$ is sampled.
• (2) Prediction of new patients for the sampling distribution of the PD endpoint:
  • (a)The individual PK/PD parameters of m _predict simulated patients, $({\mathbf{\theta }}^{(\mathbf{1})},\text{…},{\mathbf{\theta }}^{({\mathbf{m}}_{\mathrm{predict}})})$, are sampled from $\widehat{\mathbf{\mu }}$ and $\widehat{\mathbf{\Omega }}$ as ${\mathbf{\theta }}^{({\mathbf{m}}_{\mathbf{p}})}=\widehat{\mathbf{\mu }}{e}^{{\mathbf{\eta }}^{({\mathbf{m}}_{\mathbf{p}})}}$, with ${\mathbf{\eta }}^{({\mathbf{m}}_{\mathbf{p}})}\sim \mathcal{N}(\mathbf{0},\widehat{\mathbf{\Omega }})$ for $m_p\in \{1,\text{…},m_{\mathrm{predict}}\}$.
  • (b)The maximum biomarker endpoint of each simulated patient receiving regimen S_k is obtained as $r^{M^{(m_p)}}=\max (r({\mathbf{\theta }}^{({\mathbf{m}}_{\mathbf{p}})},{\mathit{S}}_{\mathbf{k},\mathbf{1}}),\text{…},r({\mathbf{\theta }}^{({\mathbf{m}}_{\mathbf{p}})},{\mathit{S}}_{\mathbf{k}}))$ for $m_p\in \{1,\text{…},m_{\mathrm{predict}}\}$.
• (3) Estimation of the posterior distribution of the probability of toxicity:
  • (a)The $m\text{th}$ iteration, $m=(m_i,m_p)\in \{1,\text{…},M\}$, where $M=m_{\mathrm{iter}}\ast m_{\mathrm{predict}}$, of the posterior probability of toxicity of dose regimen S_k , $p_T{({\mathit{S}}_{\mathbf{k}})}^{(m)}$, is obtained depending on the method chosen:

    • For the logistic‐DRtox, $p_T{({\mathit{S}}_{\mathbf{k}})}^{(m)}={\pi }_1\left\{\left({\beta }_0^{(m_i)},{\beta }_1^{(m_i)}\right),r^{M^{(m_p)}}\right\}$.

    • For the hierarchical‐DRtox, $p_T{({\mathit{S}}_{\mathbf{k}})}^{(m)}={\pi }_2\left\{\left({\mu }_z^{(m_i)},{\tau }_z^{(m_i)}\right),r^{M^{(m_p)}}\right\}$.

The DRtox approach allows us to estimate the toxicity probability of the panel of dose regimens $\mathcal{S}$ and predict the toxicity probability of each new regimen defined from the set of doses $\mathcal{D}$.

4. SIMULATION STUDY

4.1. Simulation settings

The performance of the DRtox was evaluated through a simulation study. We assumed that toxicity was related to a PD endpoint (the peak of cytokine in the context of our motivating example). Therefore, to simulate toxicity, we first needed to simulate the PK/PD profiles and simulate toxicity from the PD profile.

Regarding the PK/PD models, we were inspired by published models on blinatumomab, which is another bispecific T‐cell engager that binds to CD3 on T‐cells and to CD19 on tumor cells. Regarding the PK model, we considered a 1‐compartment infusion model (Zhu et al., ²⁰¹⁶) in which the parameters are the volume of distribution V and the clearance of elimination Cl and assumed 4 h of infusion. The model is defined in Web Appendix B. Regarding the PD aspect, the objective was to model cytokine mitigation in the case of intrapatient dose‐escalation. We simplified the model developed by Chen et al. (2019), which assumes that cytokine production is stimulated by the drug concentration but inhibited by cytokine exposure through the AUC. We defined the PD model as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\mathrm{d}E\left(t\right)}{\mathrm{d}t}}& =& {\displaystyle \frac{E_{\max }C{\left(t\right)}^H}{{E{C}_{50}}^H+C{\left(t\right)}^H}\left\{{\displaystyle 1-\frac{I_{\max }AU{C}_E\left(t\right)}{{\displaystyle \frac{I{C}_{50}}{K^{J-1}}+AU{C}_E\left(t\right)}}}\right\}}\hfill \\ & & -k_{\text{deg}}E\left(t\right),\hfill \end{array}$$ (5)

where $E(t)$ and $C(t)$ are the cytokine and drug concentration at time t, respectively, $AU{C}_E(t)$ is the cumulative cytokine exposure, and the parameters are defined in Table 1. Additional information concerning the PK/PD models is provided in Web Appendix B.

TABLE 1.

Definition and values of the PK/PD parameters used for the simulation study. Parameter estimates represent the fixed effects, and coefficients of variation (CV) are the square root of the diagonal of the variance–covariance matrix. They are inspired by the parameters estimated on blinatumomab (Zhu et al., ²⁰¹⁶; Chen et al., ²⁰¹⁹), with a modification of I_max to observe cytokine mitigation after several administrations

	Parameter	Estimate (% CV)	Unit	Description
PK model	Cl	1.36 (41.9)	L/h	Clearance
	V	3.4 (0)	L	Volume of distribution
	Emax	3.59 · 105 (14)	pg/mL/h	Maximum cytokine release rate
	EC50	1 · 104 (0)	ng/mL	Drug exposure for half‐maximum cytokine release rate
	H	0.92 (3)		Hill coefficient for cytokine release
PD model	Imax	0.995 (0)		Maximum inhibition of cytokine release
	IC50	1.82 · 104 (12)	pg/mL· h	Cytokine exposure for half‐maximum cytokine inhibition
	kdeg	0.18 (13)	h−1	Degradation rate for cytokine
	K	2.83 (36)		Priming factor for cytokine release

In both the PK and PD models, we considered a proportional error model with $b=0.1$. The values of the PK/PD parameters used for the simulations were inspired by the estimated parameters of blinatumomab (Zhu et al., ²⁰¹⁶; Chen et al., ²⁰¹⁹) and are displayed in Table 1.

To simplify and accelerate the PK/PD estimation during the simulations, we followed the traditional PK/PD modeling strategy for small sample size data by fixing some parameters. We considered the parameters EC₅₀, I_max, and IC₅₀ fixed and no random effects on V and H. In this work, we decided to simplify a previously validated PK/PD model that mimics the behavior we expect in our motivating trial: our aim was to show the performance of a global modeling approach including PK/PD estimation in a phase I toxicity model and not to propose a PK/PD model for the drug.

We used as the PD endpoint $r_{i,j}$ the peak of cytokine observed for patient i after the $j\text{th}$ administration, and for $r_i^M$ the highest peak of cytokine observed for patient i. Using the PK/PD models presented above and the parameters shown in Table 1, we were able to model the mitigation of cytokine release on repeating dosing, which was reflected by the decrease in the cytokine peak with repeating dosing. Hence, we were able to model that slowly increasing the dose reduces the cytokine peak compared to directly giving the steady‐state dose. For example, we compared the concentration and cytokine profiles of patients i and $i^{\prime }$ who received regimens s_i = (1, 5, 10, 25, 25, 25, 25) μg/kg and ${\mathit{s}}_{{\mathbf{i}}^{\prime }}=(25,25,25,25,25,25,25)$ μg/kg administered on days 1, 5, 9, 13, 17, 21, and 25 (Figure 2). From the fourth administration, the concentration profiles of patients i and $i^{\prime }$ are the same, but in the cytokine profile, the maximum peak of cytokine of patient $i^{\prime }$ is much higher than that of patient i, $r_{i^{\prime }}^M=r_{i^{\prime },1}>r_i^M=r_{i,4}$.

FIGURE 2.

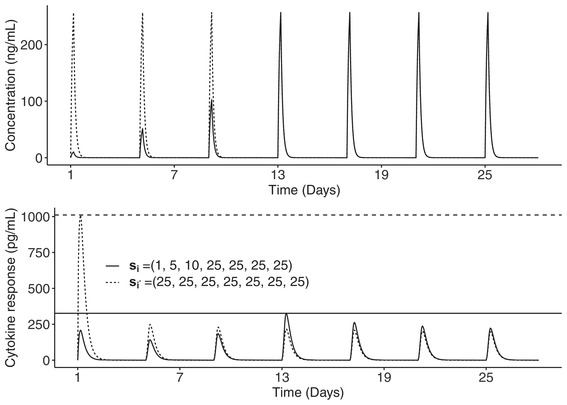
Concentration (up) and cytokine (down) profiles of two patients, one receiving a dose regimen with intrapatient escalation in solid line and the other receiving a dose regimen without intrapatient escalation in dashed line, administered on days 1, 5, 9, 13, 17, 21, and 25. Horizontal lines represent the maximum peak of cytokine observed after each dose regimen

To simulate toxicity from the cytokine profile, we defined a threshold ${\tau }_T$ on the cytokine response and assumed that toxicity occurred if this threshold was exceeded (Ursino et al., ²⁰¹⁷). To introduce between‐subject variability, we defined a log‐normally distributed measure of subject sensitivity, ${\alpha }_i$ for patient i, where ${\alpha }_i={\mathrm{e}}^{{\eta }_{{\alpha }_i}}$ and ${\eta }_{{\alpha }_i}\sim \mathcal{N}(0,{\omega }_{\alpha }^2)$. We assumed that patient i experienced toxicity at the $j\text{th}$ administration, $Y_{i,j}=1$, if ${\alpha }_i{r}_{i,j}\ge {\tau }_T$.

To compute the toxicity probability of regimen S_k , we used the Monte‐Carlo method by simulating $N=10,000$ cytokine profiles under S_k and computing

$${\displaystyle p_T({\mathit{S}}_{\mathbf{k}})=\frac{1}{N}\sum _{i=1}^N\left[1-\mathrm{\Phi }\left\{\frac{\log \left({\tau }_T\right)-\log \left(r_i^M\right)}{{\omega }_{\alpha }}\right\}\right],}$$ (6)

where Φ is the cumulative distribution function of the standard normal distribution.

We present the results of three toxicity scenarios by varying the dose regimens and the value of the threshold ${\tau }_T$ to explore different positions of the MTD‐regimen (with ${\omega }_{\alpha }=0.25$). Additional scenarios are presented in Web Appendix F. In each scenario, we considered six dose regimens, and each dose regimen included seven dose administrations on days 1, 5, 9, 13, 17, 21, and 25. The dose regimens chosen for each scenario and the dose regimen toxicity curves are displayed in Figure 3. Values of the dose regimens can be found in Web Appendix C. In Scenarios 1–3, the MTD‐regimen is situated at dose regimens S₄ , S₂ , and S₄ , respectively. Scenarios 1 and 2 are inspired from the motivating trial in which the dose regimens reach the steady‐state dose at approximately the same time, and have increasing steady‐state doses. However, Scenario 3 represents a case in which the objective is to reach the steady‐state dose, 40 μg/kg, as fast as possible to increase potential efficacy under toxicity constraints. The dose regimen toxicity relationship is similar to that in Scenario 1 but with less difference between the MTD‐regimen and its neighbors.

FIGURE 3.

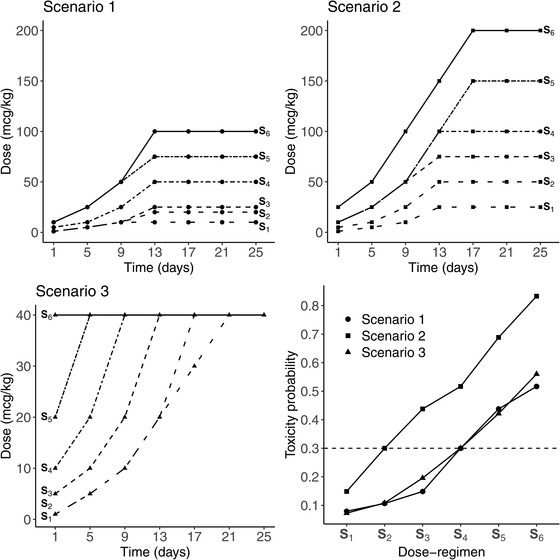
The first three subplots represent the panel of dose regimens from S₁ in spaced dashed line to S₆ in solid line, for the three main scenarios, where the type of points is specific to each scenario. In the last subplot in the lower right corner, the dose regimen toxicity relationship is represented for each scenario, where the MTD‐regimen is the dose regimen having the toxicity probability the closest to the target ${\delta }_T$, plotted in dashed line

For each scenario, 1000 trials were simulated, and ${\delta }_T=0.3$ was considered the toxicity target. Because we applied our methods once all patients from the trial were included, we evaluated the impact of two traditional dose‐escalation designs, that is, the 3+3 design and a modified continual reassessment method (CRM) initially proposed by O'Quigley et al. (1990). A flow diagram of the rules of the 3+3 design is provided in Web Appendix D. For the modified CRM, we considered a 2‐parameter logistic regression model with cohorts of a size of 3 and a total sample size of 30 patients (Cheung, 2011). Dose skipping was not allowed, and early stopping rules were not implemented. We based the skeleton of the CRM, that is, the prior guesses of the toxicity probabilities, on Scenario 1, that is, (0.06, 0.12, 0.20, 0.30, 0.40, 0.50). This skeleton was used in all simulations and scenarios.

When defining the prior distributions for our proposed models, we calibrated the model prior distributions based on the initial guesses of the toxicity probabilities (we used the same initial guesses for the CRM). To quantify the information provided by the prior distribution, we computed the approximate effective sample size (ESS), which was defined as the equivalent sample size embedded in the prior distribution of the model parameters (Yuan et al., ²⁰¹⁷). In practice, we approximated the ESS by matching the mean and variance of the toxicity probabilities computed from the prior distributions to those of a beta distribution. Then, the ESS was computed as the sum of the parameters of the beta distribution (Morita et al., ²⁰⁰⁸). More details of the ESS computation are shown in Web Appendix E. In our settings, for the logistic‐DRtox, we considered $k_T=4$, ${\sigma }_{{\beta }_0}=2$, and $\alpha =5$, leading to an approximate mean ESS of 1.6. For the hierarchical DRtox, we considered $k_{50}=6$, ${\sigma }_{\mu }=1$, and ${\sigma }_{\tau }=1$, leading to an approximate mean ESS of 1.8.

All simulations were performed in the R environment (R Core Team, ²⁰¹⁸), using Monolix software (Lixoft SAS, 2019) for the PK/PD estimation and Stan (Stan Development Team, 2019) for the Bayesian analysis.

4.2. Simulation results

4.2.1. Proportions of correct selection

We first evaluated the performance of the DRtox according to the proportions of correct selection (PCS) based on the proportions that each regimen is selected as the MTD‐regimen over the trials. We evaluated the impact of the dose regimens and the position of the MTD‐regimen in three toxicity scenarios, and the impact of the dose‐escalation design, that is, either the 3+3 design or the CRM. The PCS results of the three main scenarios and the mean sample size of each dose regimen across the trials due to the chosen dose‐escalation design are displayed in Table 2. The PCS of additional scenarios are displayed in Web Appendix F. As a practical rule, we could only recommend as the MTD‐regimen a dose regimen that was administered during the dose‐escalation phase of the trial.

TABLE 2.

Proportions that each dose regimen is being selected as the MTD‐regimen over the 1000 trials in the three toxicity scenarios and the two dose‐allocation designs, either the 3+3 design or the CRM. For each scenario, the PCS on the true MTD‐regimen are represented in bold. For each dose‐allocation design, the mean sample size of each dose regimen is displayed

		S1	S2	S3	S4	S5	S6
Scenario 1		0.08	0.11	0.15	0.3	0.44	0.52
3+3	Mean sample size	3.6	3.5	3.5	3	1.6	0.4
	Logistic‐DRtox	8.6	5.9	19	42.2	19.6	4.7
	Hierarchical‐DRtox	7.5	7.6	19.1	43.8	18.6	3.4
	3+3	13.9	16.1	32.2	27.6	8.6	1.6
CRM	Mean sample size	4.2	3.7	5.6	8.8	5.6	2.1
	Logistic‐DRtox	0	1.2	15.5	64.6	15.5	3.2
	Hierarchical‐DRtox	0	0.8	12.8	64.3	19.4	2.7
	Logistic CRM	0	1.4	15.1	50.4	27.1	6
Scenario 2		0.15	0.3	0.44	0.52	0.69	0.83
3+3	Mean sample size	4	3.6	1.8	0.5	0.1	0
	Logistic‐DRtox	27.2	42.5	24.7	5.2	0.4	0
	Hierarchical‐DRtox	29.3	41.2	24.3	4.8	0.4	0
	3+3	57.3	31	9.8	1.7	0.2	0
CRM	Mean sample size	8.7	11.1	7.5	2.3	0.3	0
	Logistic‐DRtox	14.8	65.9	17.4	1.7	0.2	0
	Hierarchical‐DRtox	12.3	66.2	18.9	2.6	0	0
	Logistic CRM	12.5	56	26.7	4.7	0.1	0
Scenario 3		0.07	0.11	0.2	0.3	0.42	0.56
3+3	Mean sample size	3.6	3.6	3.7	2.7	1.4	0.4
	Logistic‐DRtox	7.8	6.4	25.2	34.1	21.6	4.9
	Hierarchical‐DRtox	5.9	7.9	27.3	35.8	20.6	2.5
	3+3	13.1	24.4	29.5	24	7.7	1.3
CRM	Mean sample size	4	4	6.4	8	5.2	2.3
	Logistic‐DRtox	0.1	1.4	19.6	52	25.1	1.8
	Hierarchical‐DRtox	0.1	0.8	17.7	54.4	25.9	1.1
	Logistic CRM	0.1	2.3	20.3	44.5	26.4	6.4

In all scenarios, the PCS of the logistic‐DRtox and the hierarchical‐DRtox are very similar. Both methods outperform the dose‐escalation design implemented in most scenarios. After implementing the 3+3 design, our methods correctly select the MTD‐regimen in more than 10% more trials compared to the dose‐allocation design. After implementing the CRM design, both methods correctly select the MTD‐regimen in approximately 10% more trials compared to the CRM.

The results of Scenarios 1, 3, and 6 (presented in Web Appendix F) illustrate the effect of the variation in the dose regimen scheme with a similar dose regimen toxicity relationship. Compared to Scenario 1, the PCS of the logistic‐DRtox and hierarchical‐DRtox are decreased by approximately 10% in Scenario 3, while there is not much difference in the results between Scenarios 1 and 6. Therefore, the loss of performance in Scenario 3 is caused not only by the variation in the dose regimen scheme but also by the difference in the dose regimen toxicity relationship, as in Scenario 3 there is less difference in the toxicity probabilities between the MTD‐regimen and its neighbors.

However, the performance of the DRtox is heavily impacted by the dose‐escalation design implemented; after implementing the CRM design, the DRtox correctly selects the MTD‐regimen in more than 50% of the trials, but its PCS can decrease by 20% when applied after the 3+3 design. This loss of performance is due to the small sample size after implementing the 3+3 design and the higher proportion of patients allocated to suboptimal dose regimens.

Additional results on robustness (with various prior distributions and variability to simulate toxicity) are given in Web Appendix F.

4.2.2. Estimation of the toxicity probabilities

We also evaluated the performance of the DRtox based on the precision of the estimation of the toxicity probabilities of all dose regimens. We represented the distribution of the estimated toxicity probabilities, defined as the mean of the posterior distribution, over 1000 trials. The results of Scenario 3 obtained after implementing the CRM are presented in the lower part of Figure 4. The results of the other scenarios are displayed in Web Appendix F.

FIGURE 4.

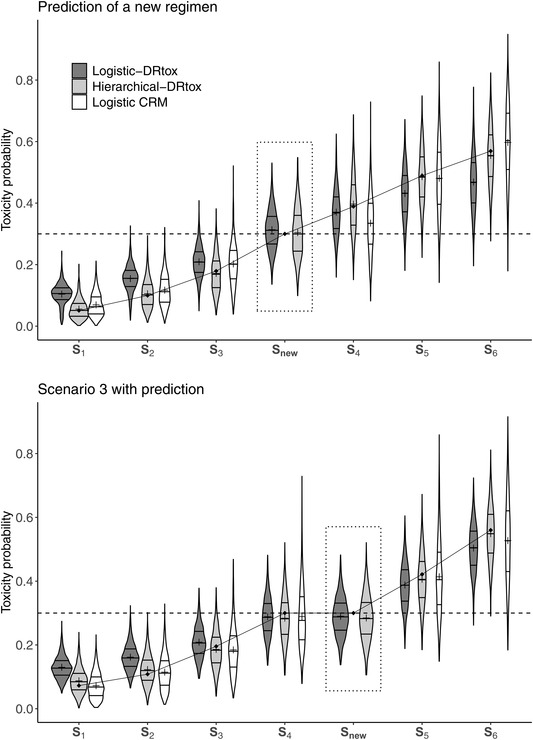
Violin plots of the estimated toxicity probabilities in an additional scenario in which the dose regimen panel missed the true MTD‐regimen and in Scenario 3 on 1000 trials implemented with the CRM including 30 patients. The predicted toxicity probability of a new regimen ${\mathit{S}}_{\mathrm{new}}$ is framed in dotted line. Horizontal lines on the density estimates represent the median and first and third quantiles of the distributions and the plus sign represents the mean. The dashed line represents the toxicity target and the solid line represents the true toxicity probabilities

In all scenarios, the toxicity probability of the MTD‐regimen is well estimated by the DRtox and the CRM. Both the hierarchical‐DRtox and the logistic‐DRtox seem to be better in estimating the toxicity probability at all dose regimens, even those far from the MTD‐regimen. This phenomenon could be due to the additional PK/PD information and the correct understanding of the toxicity mechanism. Using the CRM, the entire dose regimen toxicity curve is well estimated when the skeleton is close to the truth, as shown in Scenario 1 (Web Appendix F). However, in most cases, the toxicity estimation is precise around the MTD‐regimen, but not reliable for the other dose regimens. Regarding the dose regimens far from the MTD‐regimen, the hierarchical‐DRtox seems to estimate the toxicity probability with less bias but more variance than the logistic‐DRtox. In Web Appendix F, the distribution of the root mean square error (RMSE) of all methods is plotted; the RMSE is computed on all dose regimens or on the MTD‐regimen and its neighbors. Near the MTD‐regimen, the estimation of the logistic‐DRtox is better than that of the hierarchical‐DRtox; both models are better than the CRM. However, in the scenarios in which the MTD‐regimen is at extreme positions of the dose regimens panel (Scenarios 2 and 4 in Web Appendix F), the entire dose regimen toxicity relationship is better estimated with the hierarchical‐DRtox than the logistic‐DRtox.

4.2.3. Recommendation of a more suitable untested dose regimen

Finally, one of the strengths of the DRtox is that it models the entire relationship between the dose regimen and toxicity and can predict the toxicity probability of any new dose regimen. Notably, in this work, we assumed that the administration times were fixed to simplify the notations but regimens with different times of drug administration can also be considered. Therefore, at the end of the dose‐escalation stage of the trial, the DRtox can recommend dose regimens that were not tested in the trial to be investigated in expansion studies. For example, let us imagine a scenario in which the panel of dose regimens missed the true MTD‐regimen, as illustrated in the upper plot of Figure 4, where regimen S₃ = (5, 10, 25, 50, 50, 50, 50) μg/kg is underdosing and regimen S₄ = (10, 25, 50, 100, 150, 150, 150) μg/kg is overdosing.

The upper plot of Figure 4 illustrates the gap between the estimated toxicity probabilities of regimens S₃ and S₄ , suggesting that an alternative regimen could be found to have a toxicity probability closer to the target. At the end of the dose‐escalation stage of the trial, the DRtox can predict the toxicity probability of any new regimen, such as regimen S_new = (10, 25, 50, 100, 100, 100, 100) μg/kg, whereas the CRM is unable to perform predictions as the model is built on a skeleton based on the panel of dose regimens. In the upper plot of Figure 4, we can observe that both the hierarchical‐DRtox and the logistic‐DRtox predict that new regimen S_new has a toxicity probability closer to the target; therefore we can propose to evaluate the new regimen in expansion cohorts.

Another practical case is illustrated in Scenario 3 in which the objective was to administer the steady‐state dose of 40 μg/kg as soon as possible. As shown in the lower plot of Figure 4, the estimated MTD‐regimen is S₄ = (10, 20, 40, 40, 40, 40, 40) μg/kg, and the next regimen of the panel, S₅ = (20, 40, 40, 40, 40, 40, 40), is estimated to be too toxic. Nevertheless, one might wonder whether another regimen with an acceptable toxicity could be found in which the steady‐state dose is administered from the second administration. The DRtox predicts the toxicity probability of new regimen S_new = (10, 40, 40, 40, 40, 40, 40) to be approximately 0.3 as shown in the lower plot of Figure 4, and this new regimen can be compared in terms of efficacy to the estimated MTD‐regimen S₄ in subsequent stages of the trial. Therefore, at the end of the trial, the DRtox can evaluate alternative regimens that were not included in the panel for future studies.

5. DISCUSSION

In this work, we developed the DRtox approach to model the relationship between the dose regimen and toxicity by modeling a PD endpoint. We estimated the toxicity related to the PD endpoint in the context of an ongoing phase I trial in which the assumption of a monotonic increase in the dose regimen toxicity relationship did not hold. We found that when the process generating toxicity was reasonably understood and approximated, adding PK/PD information increased the PCS. This method allowed for a better estimation of the dose regimen toxicity curves, as this type of modeling enabled the sharing of more information across regimens. Moreover, the DRtox was able to evaluate additional regimens for expansion cohorts that were not present in the dose regimen panel but may have a predicted toxicity probability closer to the target. In practice, our methods should be applied at the end of the dose‐escalation phase of the motivating trial once all PK/PD and toxicity data are collected. Our model can address missing data as follows: (1) Regarding missing doses in the dose regimen and associated cytokine profiles, as we are using nonlinear PK/PD modeling, our method would take into account whether a patient misses one or more planned doses as the model considers the actual regimen received and not the planned regimen. (2) Regarding missing cytokine data, which is expected to be rare in this trial as the cytokine is carefully monitored by frequent sampling to detect its peak, individual cytokine peaks could be predicted from the population PK/PD model. However, it would be more common for PK/PD data to be below the limit of quantification, but these data are considered by the PK/PD model as censored data rather than missing data. (3) During the enrollment, and due to the sequential feature of the dose‐allocation design, patients with missing or with nonevaluable toxicity outcome are replaced. In this case, during the enrollment, new patients are treated at the same dose‐levels to account for the design requirements.

In the simulation study, we assumed that the dose regimens were ordered, but the DRtox can be applied when only partial ordering is known. As the DRtox is applied at the end of the trial, the choice of the dose‐escalation design may have a significant impact on the results. The performance achieved using a model‐based design, such as the CRM with 30 patients, is better than that achieved using an algorithm‐based design, such as the 3+3 design, which has the main disadvantage of treating most patients at subtherapeutic doses and having a small total sample size that cannot be fixed before the trial.

Regarding the logistic‐DRtox, since drug administration is stopped in the case of toxicity, the performance can be impacted by incomplete observations of the PD endpoint, even though it seemed to lightly impact our simulation study. In the case toxicities occur at the beginning of the administrations, resulting in a high number of incomplete PD observations, we propose the use of the predicted PD given by the PK/PD model under the complete regimen planned.

The hierarchical‐DRtox added a constraint, that is, toxicity must occur at the maximum of the PD response. Errors in the PK/PD estimation may lead to an undefined hierarchical model. In our simulation study, we observed this latter issue in less than 2% of the trials. In the real world, this issue could indicate that the proposed PK/PD model is incorrect, and that another model should be considered. However, in our simulation study, we decided to run other simulated datasets for all methods to replace the 2% of the trials having the issue defined above. One way to relax this constraint is to allow the patients' toxicity threshold to vary among administrations by adding a second latent variable, which could lead to complex models that are challenging to estimate.

In this work, we assumed that all dose regimens have the same repetition scheme and duration. However, the DRtox can address regimens with different schemes, administration modes, etc. The first part of the DRtox relies on PK/PD modeling, so an incorrect PK/PD model may have a negative impact on the full method. However, as usual in the PK/PD field, the aim of the modeling is to have a good fit/prediction of the patients' PK/PD profiles even with simplified models. Therefore, an approximated PK/PD model could still be applied without DRtox performance loss if the PD endpoint is well fitted.

In conclusion, we proposed a general approach for modeling toxicity through a PK/PD endpoint. In this work, we considered a specific PD endpoint in the context of an actual ongoing clinical trial, but various endpoints (such as the AUC or a combination of several toxicity biomarkers) could be used depending on the type of toxicity considered. Moreover, we developed the DRtox under the assumption that toxicity was linked to the maximum value of the PD biomarker, but other assumptions could be raised, such as assuming a cumulative effect. The usual dose‐finding designs were developed to determine the MTD in the first cycle of treatment after a single administration. However, with the increase in the number of targeted molecules, immuno‐oncology therapies, and combinations with alternative dose regimens, standard dose‐allocation designs fail to identify the dose regimen recommended for future studies. Incorporating PK/PD exposure data in early phase toxicity modeling through stronger collaboration between biostatisticians and pharmacometricians may lead to a better understanding of the entire dose regimen toxicity relationship and provide alternative dosage recommendation for the next phases of the clinical development.

Supporting information

Web Appendices, Tables, and Figures referenced in Sections 3 and 4 and the code are available with this paper at the Biometrics website on Wiley Online Library.

Gerard E, Zohar S, Thai H‐T, Lorenzato C, Riviere M‐K, Ursino M. Bayesian dose regimen assessment in early phase oncology incorporating pharmacokinetics and pharmacodynamics. Biometrics. 2022;78:300–312. 10.1111/biom.13433

DATA AVAILABILITY STATEMENT

Data sharing is not applicable to this article as no new data were created or analyzed in this paper.