Bayesian modeling of a bivariate toxicity outcome for early phase oncology trials evaluating dose regimens

Abstract

Most phase I trials in oncology aim to find the maximum tolerated dose (MTD) based on the occurrence of dose limiting toxicities (DLT). Evaluating the schedule of administration in addition to the dose may improve drug tolerance. Moreover, for some molecules, a bivariate toxicity endpoint may be more appropriate than a single endpoint. However, standard dose‐finding designs do not account for multiple dose regimens and bivariate toxicity endpoint within the same design. In this context, following a phase I motivating trial, we proposed modeling the first type of DLT, cytokine release syndrome, with the entire dose regimen using pharmacokinetics and pharmacodynamics (PK/PD), whereas the other DLT (DLT_o) was modeled with the cumulative dose. We developed three approaches to model the joint distribution of DLT, defining it as a bivariate binary outcome from the two toxicity types, under various assumptions about the correlation between toxicities: an independent model, a copula model and a conditional model. Our Bayesian approaches were developed to be applied at the end of the dose‐allocation stage of the trial, once all data, including PK/PD measurements, were available. The approaches were evaluated through an extensive simulation study that showed that they can improve the performance of selecting the true MTD‐regimen compared to the recommendation of the dose‐allocation method implemented. Our joint approaches can also predict the DLT probabilities of new dose regimens that were not tested in the study and could be investigated in further stages of the trial.

1. INTRODUCTION

Most phase I dose‐finding trials in oncology aim to determine the maximum tolerated dose (MTD), which is defined as the highest dose that does not exceed a predefined probability of dose‐limiting toxicity (DLT), in a prespecified observational window. The DLT is a binary outcome defined to summarize the patient's toxicity profile and is usually derived from toxicity classification in severity grades according to the National Cancer Institute (NCI) Common Toxicity Criteria for Adverse Events. ¹ For instance, a DLT may be defined as the occurrence of a grade 3 or higher toxicity observed in at least one organ. Algorithm‐based designs, such as the 3+3, ² or model‐based designs, such as the continual reassessment method (CRM), ³ are the most common adaptive approaches for recommending the MTD based on the occurrence of DLT. Evaluating the schedule of administration, in addition to the dose, is increasingly being investigated during this phase to improve drug tolerance. For example, lead‐in dose step‐up dosing is common in immunotherapy trials. ⁴ , ⁵ , ⁶ , ⁷ , ⁸ However, traditional designs reduce the entire dose regimen, defined by the NCI as “a treatment plan that specifies the dosage, the schedule, and the duration of treatment” ⁹ , to a single value.

While a binary toxicity outcome is convenient in the context of small sample size, various types of DLT might not be identified as equally important. ¹⁰ Several authors have proposed to define a continuous toxicity score to differentiate the types of toxicity ¹⁰ , ¹¹ , ¹² and to define multiple toxicity constraints on the toxicity types and grades to define the MTD. ¹³ , ¹⁴ , ¹⁵ , ¹⁶

Several methods have been developed to consider more complex schedules of administration. Dose‐finding designs have been proposed to evaluate the dose‐schedule combination in a two‐dimensional framework. ¹⁷ , ¹⁸ The toxicity outcome can also be modeled in a longitudinal setting where a dose regimen composed of multiple administrations of the same or various doses is evaluated. Legedza and Ibrahim ¹⁹ proposed modeling the repeated treatment administrations using the total amount of drug in the body based on pharmacokinetic principles. Other methods account for the cumulative effect of the dose regimens using a time to toxicity outcome and by modeling the total hazard of toxicity for the dose regimen as the sum of the hazard of each administration. ²⁰ , ²¹ , ²² , ²³ Another possibility, proposed by Fernandes et al, ²⁴ is to estimate the conditional probability of toxicity at each administration given that no toxicity was observed in the previous administrations. Ursino et al ²⁵ developed a model for the cumulative probability of toxicity by accounting for the first dose administered and the cumulative dose. Finally, to model the cumulative effect of multiple administrations, other authors have included pharmacokinetic and pharmacodynamic (PK/PD) modeling in the dose regimen recommendation. Günhan et al ²⁶ considered latent PK profiles to measure drug exposure in a Bayesian adaptive model, and Gerard et al proposed complete PK/PD modeling to assess the relationship between the dose regimen and a specific toxicity outcome.

Motivating trial

This work is based on an ongoing first‐in‐human dose‐escalation trial of SAR440234 ²⁷ administered as a single agent to patients with relapsed or refractory acute myeloid leukemia, high‐risk myelodysplastic syndrome or B‐cell acute lymphoblastic leukemia (NCT03594955 ²⁸ ). SAR440234 is a novel bispecific T‐cell engager antibody that activates and redirects cytotoxic T lymphocytes (CTLs) to enhance the CTL‐mediated elimination of CD123‐expressing tumor cells. Due to this mechanism of action, the main toxicity expected in this trial is the cytokine release syndrome (CRS), which is a systemic inflammatory response that has been associated with the peak of cytokine, considered as a pharmacodynamic endpoint. ²⁹ , ³⁰ Since repeated administrations of the drug can reduce the risk of CRS, ³¹ dose regimens with a fixed intrapatient dose‐escalation scheme are evaluated in this trial as already proposed for other similar molecules. ⁴ , ⁵ , ⁶ , ⁷ , ⁸ Namely, before administrating repeatedly the steady‐state dose, defined as the maximum dose the regimen should reach, patients are treated with lower initial increasing doses, defined as the lead‐in doses. This administration scheme attempts to decrease the peak of cytokine observed when the steady‐state dose is administered directly. The objective of the trial is to find the MTD of SAR440234, and a standard dose‐escalation procedure is implemented (3+3 design), in which each dose regimen is associated with a single dose‐level. ³²

Objective

To obtain a better estimate of the maximum tolerated dose regimen (MTD‐regimen), defined as the dose regimen having the probability of DLT closest to the toxicity target, at the end of the trial, a Bayesian dose regimen assessment method (DRtox) was firstly developed. ³³ The DRtox proposed to model the binary CRS incorporating pharmacokinetic and pharmacodynamic (PK/PD) modeling. Since the development of the DRtox, the investigators have gained knowledge about the potential occurrences of other important dose‐limiting toxicities (DLT_o) that should be considered when recommending the MTD‐regimen. Unlike the CRS, the PK/PD process generating the DLT_o might be unknown. ³⁴ Moreover, the CRS can be associated with several types of other toxicities. ³⁵ , ³⁶ , ³⁷ , ³⁸ Thus, a new modeling approach that accounts for the potential interactions between the CRS and the DLT_o and the multiple dose administrations was required. Since the CRS and DLT_o are clinically different and can be distinguished, we propose to model the DLT as a bivariate binary endpoint with the dose regimen, preserving the PK/PD approach for the CRS and adding a cumulative modeling approach for the DLT_o.

The objective of this paper is to model the probability of DLT as a bivariate binary endpoint (CRS and DLT_o) in the context of multiple dose administrations in order to determine the MTD‐regimen while preserving the modeling of the CRS with PK/PD. As PK/PD measures are usually analyzed by batch and may therefore not be available in real time after each cohort is treated, a complete sequential dose‐allocation approach incorporating PK/PD can be difficult to perform in practice. We then develop our modeling strategy to be performed at the end of the trial, that is, once all data have been collected.

2. MODEL

Let $𝒟=\{d_1,...,d_L\}$ be the set of doses that can be administered to patients and let $\mathcal{S}=\{{\mathit{S}}_{\mathbf{1}},...,{\mathit{S}}_{\mathit{K}}\}\subset 𝕊$ be the panel of K dose regimens to be studied in the trial. The dose regimen ${\mathit{S}}_{\mathit{k}}\in 𝒮$ is defined as a sequence of J doses, ${\mathit{S}}_{\mathit{k}}=(d_{k,1},d_{k,2},...,d_{k,J})$, administered at times $\mathit{t}=(t_1,t_2,...,t_J)$, where $d_{k,j}\in 𝒟$, $j\in \{1,...,J\}$ and $k\in \{1,...,K\}$. Let $n\in \mathbb{N}$ be the number of patients included in the trial. Let $Y_{i,j}^{(1)}$ be the binary CRS response and $Y_{i,j}^{(2)}$ be the binary DLT_o response (another DLT, different from the CRS) of patient i observed exactly after the j ^th administration. As we assume that both a CRS and a DLT_o can occur during the same administration, the binary DLT response $Y_{i,j}$ is defined as $Y_{i,j}=\max \left(Y_{i,j}^{(1)},Y_{i,j}^{(2)}\right)$. Let $Y_i$, $Y_i^{(1)}$, and $Y_i^{(2)}$ be the global DLT, CRS, and DLT_o responses of patient i at the end of the dose regimen, respectively. Let ${\tilde{\mathit{s}}}_{\mathit{i}}=(d_{i,1},d_{i,2},...,d_{i,J})\in \mathcal{S}$ be the dose regimen planned for the i ^th patient. As we assume that the administration of the drug is stopped if a DLT occurs (either a CRS or a DLT_o), let $j_i$ be the final administration of patient i. Let ${\mathit{s}}_{\mathit{i}}=(d_{i,1},d_{i,2},...,d_{i,j_i})\subset {\tilde{\mathit{s}}}_{\mathit{i}}$ be the actual dose regimen received by patient i; this implies that ${\mathit{s}}_{\mathit{i}}={\tilde{\mathit{s}}}_{\mathit{i}}$ if no DLT occurs. The aim is to estimate the MTD‐regimen at the end of the trial, and this is defined as the dose regimen with the probability of DLT closest to the target toxicity rate ${\delta }_T$. To define the prior distributions, let $({\pi }_1,...,{\pi }_K)$ be the initial guesses of the DLT probabilities of dose regimens $({\mathit{S}}_{\mathbf{1}},...,{\mathit{S}}_{\mathit{K}})$, where a selected probability, ${\pi }_{k_T}$, is equal to the target ${\delta }_T$.

The proposed modeling strategy is divided into three steps, as shown in Figure 1. In the first step, the CRS is modeled via PK/PD outcomes using the DRtox approach. ³³ In the second step, the DLT_o, using either a marginal or conditional definition, is modeled via the cumulative dose to account for the multiple dose administrations. Finally, in the third step, the DLT is modeled as a bivariate binary endpoint using both previous models under three approaches: the DRtox_indep assumes independence between the two types of toxicity, the DRtox_copula models the correlation between them via a copula model and the DRtox_cond accounts for the potential correlation between them via a conditional modeling. In the following sections, the three steps are detailed.

FIGURE 1.

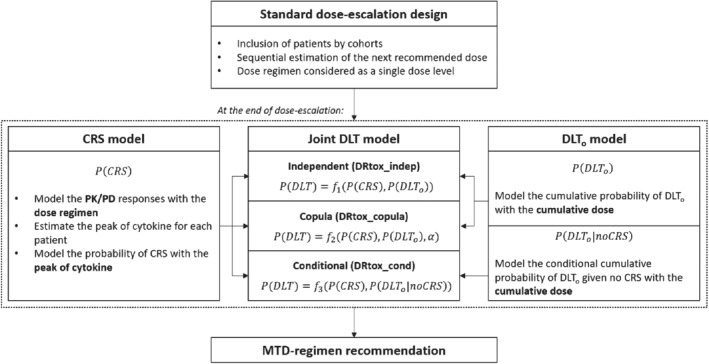
Illustration of the proposed modeling process of the bivariate toxicity endpoint at the end of the dose‐escalation phase of the trial

2.1. CRS modeling

As the CRS is assumed to be linked to the peak of cytokine, considered a PD endpoint, we propose to model the binary CRS using the logistic‐DRtox approach ³³ that incorporates PK/PD modeling. The logistic‐DRtox approach is performed in three steps:

1. The continuous concentration response (PK) and cytokine response (PD) are linked to the dose regimen using nonlinear mixed effects models. The peak of cytokine $r_i^M$ is predicted for each patient i according to the received dose regimen ${\mathit{s}}_{\mathit{i}}$.

2. The predicted peak of cytokine is used to model the binary CRS via the following Bayesian model:

   $$\text{logit}\left(\mathbb{P}\left(Y_i^{(1)}=1\right)\right)={\beta }_{0,1}+{\beta }_{1,1}\log \left(\frac{r_i^M}{{\bar{r}}_{k_T}^M}\right)$$ (1)

   where ${\beta }_{1,1}>0$ is required for the probability of CRS to increase with the peak of cytokine. We normalize the peak of cytokine for prior elicitation using ${\bar{r}}_{k_T}^M$, which is the population value of the peak of cytokine of dose regimen ${\mathit{S}}_{{\mathit{k}}_{\mathit{T}}}$ that we initially guess to have a DLT probability of ${\delta }_T$.

3. The posterior marginal CRS probability $p_k^{(1)}$ of dose regimen ${\mathit{S}}_{\mathit{k}}$ is estimated by a Monte‐Carlo method to integrate both the PK/PD estimated variability and the posterior distributions resulting from the Bayesian logistic model. A point estimate is obtained by the posterior mean.

Regarding prior distributions, we consider a normal distribution for the intercept, ${\beta }_{0,1}\sim 𝒩\left({\bar{\beta }}_{0,1},{\sigma }_{{\beta }_{0,1}}^2\right)$, and a gamma distribution for the slope to ensure positivity, ${\beta }_{1,1}\sim \gamma \left({\alpha }_1,\frac{{\alpha }_1}{{\bar{\beta }}_{1,1}}\right)$, where ${\alpha }_1$ is the shape parameter, ${\bar{\beta }}_{0,1}=𝔼[{\beta }_{0,1}]$ and ${\bar{\beta }}_{1,1}=𝔼[{\beta }_{1,1}]$. The values of ${\bar{\beta }}_{0,1}$ and ${\bar{\beta }}_{1,1}$ are elicited from the prior guesses of the probability of CRS. Additional details on prior elicitation can be found in Appendix A.

2.2. DLT_o modeling

To perform the joint DLT modeling, we model either the marginal probability of DLT_o (a DLT other than a CRS) or the conditional probability of DLT_o given that no CRS has occurred. Both approaches are based on the cumulative probability of DLT_o.

2.2.1. Marginal DLT_o modeling

Contrary to the CRS, we do not assume that the DLT_o is linked to a PD endpoint. To account for the multiple dose administrations that constitute the dose regimen, we model the cumulative probability of DLT_o ²⁵ for patient i at administration j, and this is defined as:

$$p_{i,j}^{{(2)}^{\text{cum}}}=\mathbb{P}\left(\exists !l\in \{1,...,j\}{Y}_{i,l}^{(2)}=1\right)=\sum _{l=1}^j\mathbb{P}\left(Y_{i,1}^{(2)}=0,Y_{i,2}^{(2)}=0,...,Y_{i,l-1}^{(2)}=0,Y_{i,l}^{(2)}=1\right).$$ (2)

The likelihood is computed as $\prod _{i=1}^n{\left(p_{i,j_i}^{{(2)}^{\text{cum}}}-p_{i,j_i-1}^{{(2)}^{\text{cum}}}\right)}^{y_i^{(2)}}{\left(1-p_{i,j_i}^{{(2)}^{\text{cum}}}\right)}^{1-y_i^{(2)}}$ from the following probabilities of experiencing a DLT_o and not experiencing a DLT_o at administration j:

$$\left\{\begin{array}{l}\mathbb{P}\left(Y_{i,1}^{(2)}=0,Y_{i,2}^{(2)}=0,...,Y_{i,j-1}^{(2)}=0,Y_{i,j}^{(2)}=1\right)=p_{i,j}^{{(2)}^{\text{cum}}}-p_{i,j-1}^{{(2)}^{\text{cum}}}\\ \mathbb{P}\left(Y_{i,1}^{(2)}=0,Y_{i,2}^{(2)}=0,...,Y_{i,j-1}^{(2)}=0,Y_{i,j}^{(2)}=0\right)=1-p_{i,j}^{{(2)}^{\text{cum}}}.\end{array}\right.$$

Since we model two types of toxicity but with a standard joint target toxicity, we have to deal with very small marginal probabilities of toxicity. Therefore, we propose to adapt the model proposed by Ursino et al ²⁵ for intrapatient dose‐escalation. As DLT_o is only one type of the bivariate DLT, the number of observed DLT_o is relatively small; thus we propose to reduce the number of parameters to two as follows:

$$\text{logit}\left(p_{i,j}^{{(2)}^{\text{cum}}}\right)={\beta }_{0,2}+\exp \left({\beta }_{1,2}\right)\log \left(\frac{1}{D_{k_T}}\sum _{l=1}^j{d}_{i,l}\right)$$ (3)

where $D_{k_T}=\sum _{l=1}^J{d}_{k_T,l}$ is the cumulative dose of the reference dose regimen, which we assume has a DLT probability of ${\delta }_T$. The posterior marginal probability of DLT_o of dose regimen ${\mathit{S}}_{\mathit{k}}$ is then defined as $p_k^{(2)}={\text{logit}}^{-1}\left({\beta }_{0,2}+\exp \left({\beta }_{1,2}\right)\log \left(\frac{1}{D_{k_T}}\sum _{l=1}^j{d}_{i,l}\right)\right)$. A point estimate is obtained by the mean of the posterior toxicity distribution.

Regarding prior distributions, we consider a normal distribution for the intercept ${\beta }_{0,2}\sim 𝒩\left({\bar{\beta }}_{0,2},{\sigma }_{{\beta }_{0,2}}^2\right)$ and the slope ${\beta }_{1,2}\sim 𝒩\left({\bar{\beta }}_{1,2},{\sigma }_{{\beta }_{1,2}}^2\right)$, ${\bar{\beta }}_{0,2}=𝔼\left[{\beta }_{0,2}\right]$ and ${\bar{\beta }}_{1,2}=𝔼\left[{\beta }_{1,2}\right]$. Values of ${\bar{\beta }}_{0,2}$ and ${\bar{\beta }}_{1,2}$ are elicited from the prior guesses of the probability of DLT_o. Additional details on prior elicitation can be found in Appendix A.

2.2.2. Conditional DLT_o modeling

The conditional DLT_o model is very similar to the marginal DLT_o model. We define the conditional cumulative probability of DLT_o, given that no CRS has occurred, as follows:

$$p_{i,j\star }^{{(2)}^{\text{cum}}}=\mathbb{P}\left(\exists !l\in \{1,...,j\}{Y}_{i,l}^{(2)}=1|Y_i^{(1)}=0\right).$$ (4)

The conditional cumulative model is applied on a subset of the population, that is, on the patients who do not experience a CRS. The likelihood is computed similarly to that of the marginal DLT_o model as $\prod _{i=1,Y_i^{(1)}=0}^n{\left(p_{i,j_i\star }^{{(2)}^{\text{cum}}}-p_{i,j_i-1\star }^{{(2)}^{\text{cum}}}\right)}^{y_i^{(2)}}{\left(1-p_{i,j_i\star }^{{(2)}^{\text{cum}}}\right)}^{1-y_i^{(2)}}$.

We consider the same model as the one proposed in Section 2.2.1, and it is defined as:

$$\text{logit}\left(p_{i,j\star }^{{(2)}^{\text{cum}}}\right)={\beta }_{0,2\star }+\exp \left({\beta }_{1,2\star }\right)\log \left(\frac{\sum _{l=1}^j{d}_{i,l}}{D_{k_T}}\right).$$ (5)

The posterior conditional probability of DLT_o given that no CRS has occurred of dose regimen ${\mathit{S}}_{\mathit{k}}$ is then defined as $p_{k\star }^{(2)}={\text{logit}}^{-1}\left({\beta }_{0,2\star }+\exp \left({\beta }_{1,2\star }\right)\log \left(\frac{\sum _{l=1}^J{d}_{k,l}}{D_{k_T}}\right)\right)$. A point estimate is obtained by the mean of the posterior toxicity distribution.

We consider the same prior distributions as those of the marginal model described in Section 2.2.1.

2.3. Joint DLT modeling

The final step is to model the probability of DLT from the joint probability of CRS and DLT_o. The probability of DLT of dose regimen ${\mathit{S}}_{\mathit{k}}$ is defined as:

$$p_k=\mathbb{P}\left(Y=1|{\mathit{S}}_{\mathit{k}}\right)=1-\mathbb{P}\left(Y=0|{\mathit{S}}_{\mathit{k}}\right)=1-\mathbb{P}\left(Y^{(1)}=0,Y^{(2)}=0|{\mathit{S}}_{\mathit{k}}\right).$$ (6)

Different assumptions can be used when modeling the joint probability of CRS and DLT_o. The easiest assumption is to consider that both toxicities are independent (conditionally on the dose regimen). However, we can also assume a correlation between the two toxicities; ³⁵ , ³⁶ , ³⁷ , ³⁸ for example, a patient experiencing one kind of toxicity may be more sensitive to the drug than others and therefore be at higher risk of experiencing other toxicities. We propose three approaches to compute the probability of DLT starting from the probabilities of CRS and DLT_o using a marginal or conditional formulation.

2.3.1. Independent model: DRtox_indep

The first assumption that can be raised is that $Y^{(1)}$ and $Y^{(2)}$ are independent (conditionally on the dose regimen ${\mathit{S}}_{\mathit{k}}$). In this case, the posterior distribution of DLT can be directly expressed from the posterior marginal probabilities of CRS and DLT_o defined in Sections 2.1 and 2.2.1 as follows:

$$p_k=1-\mathbb{P}\left(Y^{(1)}=0|{\mathit{S}}_{\mathit{k}}\right)\mathbb{P}\left(Y^{(2)}=0|{\mathit{S}}_{\mathit{k}}\right)=1-\left(1-p_k^{(1)}\right)\left(1-p_k^{(2)}\right).$$ (7)

The probability of DLT $p_k$ is then estimated as the mean of the posterior distribution.

2.3.2. Copula model: DRtox_copula

When dependence between both toxicities is assumed, the joint probability of DLT can be modeled via a copula distribution defined from the marginal distribution of each toxicity. In this case, the modeling process is performed in two steps. First, marginal models are developed for the CRS and the DLT_o, as shown in Sections 2.1 and 2.2.1. Then, the copula model is fitted on all patients from the resulting point estimates of the marginal probabilities of each toxicity of all dose regimens estimated from the two previous models.

We consider the popular class of Archimedeans copulas ³⁹ that have already been used in phase I trials when modeling both toxicity and efficacy ⁴⁰ , ⁴¹ , ⁴² or in combination trials of two agents. ⁴³ , ⁴⁴ The Archimedean copula has an explicit distribution defined from the marginal distributions of each variable and an association parameter as follows:

$$C_{\alpha }\left(p_k^{(1)},p_k^{(2)}\right)={\mathrm{\Phi }}_{\alpha }^{-1}\left({\mathrm{\Phi }}_{\alpha }\left(p_k^{(1)}\right)+{\mathrm{\Phi }}_{\alpha }\left(p_k^{(2)}\right)\right),$$ (8)

where ${\mathrm{\Phi }}_{\alpha }$ is a continuous, strictly decreasing and convex function and ${\mathrm{\Phi }}_{\alpha }^{-1}$ is its inverse.

Let $k_i$ be the level of the dose regimen administered to patient i. As we assume that both toxicities can be distinguished, we can define the binary bivariate model in terms of the four possible outcomes as follows ⁴⁵ :

$$\left\{\begin{array}{l}{p}_i^{11}=\mathbb{P}\left(Y_i^{(1)}=1,Y_i^{(2)}=1\right)=C_{\alpha }\left(p_{k_i}^{(1)},p_{k_i}^{(2)}\right)\\ p_i^{01}=\mathbb{P}\left(Y_i^{(1)}=0,Y_i^{(2)}=1\right)=p_{k_i}^{(2)}-C_{\alpha }\left(p_{k_i}^{(1)},p_{k_i}^{(2)}\right)\\ p_i^{10}=\mathbb{P}\left(Y_i^{(1)}=1,Y_i^{(2)}=0\right)=p_{k_i}^{(1)}-C_{\alpha }\left(p_{k_i}^{(1)},p_{k_i}^{(2)}\right)\\ p_i^{00}=\mathbb{P}\left(Y_i^{(1)}=0,Y_i^{(2)}=0\right)=1-p_{k_i}^{(1)}-p_{k_i}^{(2)}+C_{\alpha }\left(p_{k_i}^{(1)},p_{k_i}^{(2)}\right)\end{array}\right.$$ (9)

The log‐likelihood is then computed as:

$$\sum _{i=1}^n{y}_i^{(1)}{y}_i^{(2)}\log \left(p_i^{11}\right)+y_i^{(1)}\left(1-y_i^{(2)}\right)\log \left(p_i^{10}\right)+\left(1-y_i^{(1)}\right)y_i^{(2)}\log \left(p_i^{01}\right)+\left(1-y_i^{(1)}\right)\left(1-y_i^{(2)}\right)\log \left(p_i^{00}\right).$$ (10)

The toxicity probability of dose regimen ${\mathit{S}}_{\mathit{k}}$ is then defined as $p_k=p_k^{(1)}+p_k^{(1)}-C_{\alpha }\left(p_k^{(1)},p_k^{(2)}\right)$. We consider the Clayton distribution, which is defined as $C_{\alpha }\left(p_k^{(1)},p_k^{(2)}\right)={\left(\max \left({p_k^{(1)}}^{-\gamma }+{p_k^{(2)}}^{-\gamma }-1,0\right)\right)}^{-1/\gamma }$, where $\gamma$ is the association parameter. We assume a positive association between both toxicities and therefore consider a gamma distribution for the prior on $\gamma$. Another popular choice for the copula distribution is the Farlie‐Gumbel‐Morgenstern distribution (Web Appendix B.3 of Data S1). The probability of DLT $p_k$ is estimated as the mean of the posterior distribution.

2.3.3. Conditional model: DRtox_cond

In this approach, we assume an association between both toxicities and express the joint distribution of DLT using a conditional formulation. As we assume that the CRS has a tendency to occur at the beginning of the dose regimen while the DLT_o occurs at the end, we express the posterior distribution of DLT from the posterior marginal probability of CRS (Section 2.1) and the posterior conditional probability of DLT_o (Section 2.2.2) given that no CRS has occurred, as follows:

$$p_k=1-\mathbb{P}\left(Y^{(1)}=0|{\mathit{S}}_{\mathit{k}}\right)\mathbb{P}\left(Y^{(2)}=0|Y^{(1)}=0,{\mathit{S}}_{\mathit{k}}\right)=1-\left(1-p_k^{(1)}\right)\left(1-p_{k\star }^{(2)}\right).$$ (11)

The probability of DLT $p_k$ is then estimated as the mean of the posterior distribution.

3. SIMULATION STUDY

3.1. Simulation settings

We defined two sets of dose regimens based on the motivating trial, Set A and Set B, as shown in Table 1. Each set included six dose regimens, where each dose regimen was defined with intra‐patient dose‐escalation. Each dose regimen was defined as a sequence of seven doses administered at days $\left(t_1=1,t_2=5,t_3=9,t_4=13,t_5=17,t_6=21,t_7=25\right)$ where the dose was increased during the first four administrations to reach the steady‐state dose, that was repeated for the last three administrations. In both sets, we assumed that the six dose regimens were completely ordered in terms of toxicity as the doses administered in the dose regimens were increased when increasing the level of the dose regimen. Set A and Set B shared common dose regimens (${\mathit{S}}_{\mathbf{1}}$, ${\mathit{S}}_{\mathbf{5}}$ and ${\mathit{S}}_{\mathbf{6}}$), but Set B included an accelerated component since the middle dose regimens (from ${\mathit{S}}_{\mathbf{2}}$ to ${\mathit{S}}_{\mathbf{4}}$) reached higher steady‐state doses more quickly than in Set A. Simulations under another set of dose regimens (Set C) that differs from the motivating trial are available in the supporting information (Web Appendix C of Data S1). The dose regimen escalation in Set C was slower than in Set A and Set B because the higher the steady‐state dose is, the slower it is reached.

TABLE 1.

Dose regimens defined in Set A and Set B used in the simulation study (in $\mathrm{\mu }$g/kg) where each dose regimen ${\mathit{S}}_{\mathit{k}}$ is defined as the sequence of seven doses administered at days (t₁=1, t₂=5, t₃=9, t₄=13; t₅=17, t₆=21, t₇=25)

		$t_1$	$t_2$	$t_3$	$t_4$	$t_5$	$t_6$	$t_7$
Set A	${\mathit{S}}_{\mathbf{1}}$	1	5	10	20	20	20	20
	${\mathit{S}}_{\mathbf{2}}$	1	5	10	25	25	25	25
	${\mathit{S}}_{\mathbf{3}}$	1	5	10	30	30	30	30
	${\mathit{S}}_{\mathbf{4}}$	1	5	10	45	45	45	45
	${\mathit{S}}_{\mathbf{5}}$	5	10	25	75	75	75	75
	${\mathit{S}}_{\mathbf{6}}$	10	25	50	100	100	100	100
Set B	${\mathit{S}}_{\mathbf{1}}$	1	5	10	20	20	20	20
	${\mathit{S}}_{\mathbf{2}}$	1	5	10	30	30	30	30
	${\mathit{S}}_{\mathbf{3}}$	1	5	10	40	40	40	40
	${\mathit{S}}_{\mathbf{4}}$	1	5	10	50	50	50	50
	${\mathit{S}}_{\mathbf{5}}$	5	10	25	75	75	75	75
	${\mathit{S}}_{\mathbf{6}}$	10	25	50	100	100	100	100

Both toxicities, CRS and DLT_o, were simulated under different assumptions. The CRS was simulated from the cytokine PD profile as proposed by Gerard et al. ³³ The PK/PD models used for CRS simulation were inspired by the published models on blinatumomab, which is another bispecific T‐cell engager that binds to CD3 on T‐cells and to CD19 on tumor cells. ³¹ , ⁴⁶ To simulate the CRS from the cytokine profile, we defined a threshold ${\tau }_T$ for the cytokine response and assumed that a CRS occurred if this threshold was exceeded, that is, $Y_{i,j}^{(1)}=1$ if ${\alpha }_i{r}_{i,j}\ge {\tau }_T$, where ${\alpha }_i$ is a log‐normally distributed measure of subject sensitivity. The true probability of CRS, $p_T^{(1)}({\mathit{S}}_{\mathit{k}})$, of each dose regimen ${\mathit{S}}_{\mathit{k}}$ was computed using a Monte‐Carlo method. Additional details on the PK/PD simulation and estimation can be found in Appendix B.1.

To create an association between the CRS and the DLT_o, we simulated the DLT_o conditionally on the CRS status. For example, if a patient experiences a CRS, s/he may be more sensitive to the drug and, consequently, would have a higher probability of DLT_o than a patient without CRS. We therefore simulated the DLT_o from the conditional probability of DLT_o at each administration (1) given that no DLT_o had occurred in the previous administrations and (2) given that the patient would experience a CRS at some point. This conditional probability was inspired by the model proposed by Fernandes et al to account for the current and previous drug administrations as follows:

$$\text{logit}\left(\mathbb{P}\left(Y_{i,j}^{(2)}=1|\left(Y_{i,j-1}^{(2)}=0,...,Y_{i,1}^{(2)}=0\right);Y_i^{(1)}=1\right)\right)=a+b\log \left(d_{i,j}\right)+c\log \left(D_{i,j-1}+1\right),$$ (12)

where $d_{i,j}$ represents the dose given to patient i during the j ^th administration and $D_{i,j}=\sum _{l=1}^j{d}_{i,j}$ is the cumulative dose using the convention $D_{i,0}=0$. Let $\theta =\left(a,b,c\right)$ be the simulation parameters and $f_{\theta }\left(d_j,D_{j-1}\right)={\text{logit}}^{-1}\left(a+b\log \left(d_j\right)+c\log \left(D_{j-1}+1\right)\right)$ be the simulation model.

The conditional probability of DLT_o for patient i given that s/he would not experience CRS was defined from the previous model as follows:

$$\begin{array}{ll}\mathbb{P}\left(Y_{i,j}^{(2)}=1|\left(Y_{i,j-1}^{(2)}=0,...,Y_{i,1}^{(2)}=0\right);Y_i^{(1)}=0\right)& =\frac{1}{\lambda }\mathbb{P}\left(Y_{i,j}^{(2)}=1|\left(Y_{i,j-1}^{(2)}=0,...,Y_{i,1}^{(2)}=0\right);Y_i^{(1)}=1\right)\\ & =\frac{1}{\lambda }{f}_{\theta }\left(d_{i,j},D_{i,j-1}\right),\end{array}$$ (13)

where $\lambda$ represents the risk ratio of experiencing a DLT_o during administration j (given that no DLT_o was experienced before) for patients who would experience a CRS vs patients with no CRS. A value of $\lambda =1$ denotes independence between the CRS and the DLT_o, $\lambda >1$ represents positive association and $\lambda <1$ represents negative association.

The marginal probability of DLT_o was computed from the previous conditional probabilities and from the marginal probability of CRS as follows:

$$p_T^{(2)}({\mathit{S}}_{\mathit{k}})=1-\prod _{j=1}^J\left(1-f_{\theta }\left(d_{k,j},D_{k,j-1}\right)\right)p_T^{(1)}({\mathit{S}}_{\mathit{k}})-\prod _{j=1}^J\left(1-\frac{1}{\lambda }{f}_{\theta }\left(d_{k,j},D_{k,j-1}\right)\right)\left(1-p_T^{(1)}({\mathit{S}}_{\mathit{k}})\right).$$ (14)

Finally, the joint probability of DLT of dose regimen ${\mathit{S}}_{\mathit{k}}$ was computed as follows:

$$p_T({\mathit{S}}_{\mathit{k}})=1-\prod _{j=1}^J\left(1-\frac{1}{\lambda }{f}_{\theta }\left(d_{k,j},D_{k,j-1}\right)\right)\left(1-p_T^{(1)}({\mathit{S}}_{\mathit{k}})\right).$$ (15)

Details of the mathematical development are provided in Appendix B.2.

We studied six main dose regimen toxicity scenarios, which are represented in Figure 2. Each toxicity scenario was defined by the marginal probabilities of DLT, CRS, and DLT_o and the conditional probabilities of DLT_o given CRS and DLT_o given no CRS. The target probability of DLT was defined as ${\delta }_T=0.30$. Scenarios 1 to 5 were built on Set A of dose regimens while Scenario 6 was built on Set B. The six toxicity scenarios studied various distributions of the probabilities of DLT, CRS, and DLT_o and various associations between the CRS and the DLT_o. The latter association was measured for each scenario as the average risk ratio over the set of dose regimens of experiencing a DLT_o for patients who would experience a CRS versus those who would not experience a CRS. In Scenario 1, the true MTD‐regimen was ${\mathit{S}}_{\mathbf{4}}$, which had similar probabilities of CRS and DLT_o. The CRS and DLT_o were positively correlated with an average risk ratio of 1.85, meaning that, on average, a patient experiencing a CRS has 1.85 times greater risk of also experiencing a DLT_o than that of a patient not experiencing a CRS. In Scenario 2, the association between the CRS and the DLT_o was increased to an average risk ratio of 5.91. In Scenarios 3 and 4, the true MTD‐regimen remained ${\mathit{S}}_{\mathbf{4}}$, but the proportion of each type of toxicity varied with a higher probability of DLT_o and CRS in Scenarios 3 and 5, respectively. Finally, the MTD‐regimen changed to dose regimens ${\mathit{S}}_{\mathbf{6}}$ and ${\mathit{S}}_{\mathbf{2}}$ for Scenarios 5 and 6, respectively. Additional scenarios are available in the supporting information (Web Appendix A.3 of Data S1).

FIGURE 2.

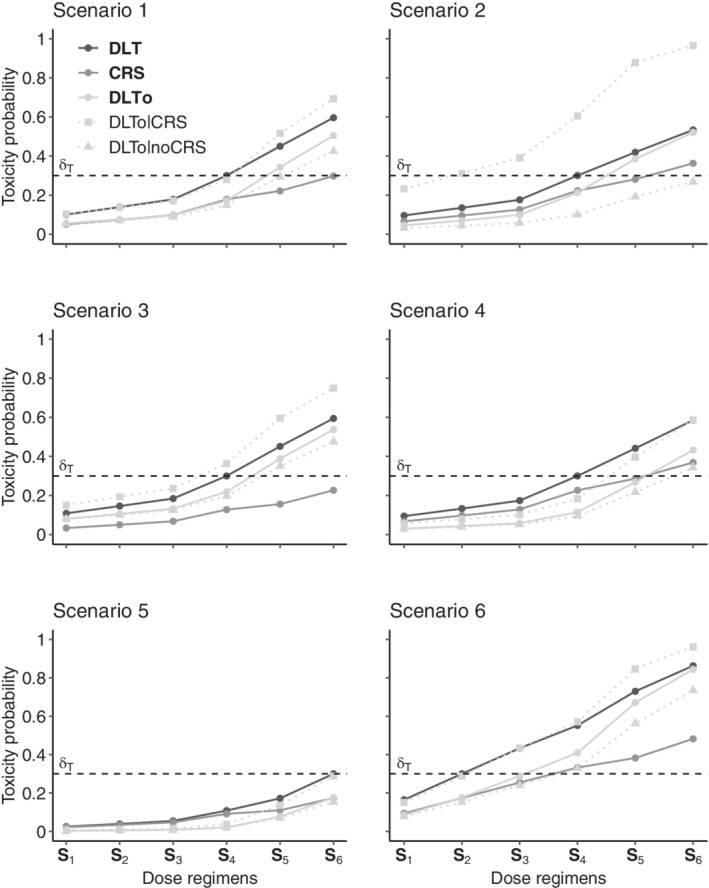
Definitions of the six toxicity scenarios in terms of the probabilities of dose limiting toxicity (DLT), cytokine release syndrome (CRS), and other DLT (DLT_o). For each scenario, the marginal probabilities of DLT, CRS, and DLT_o of each dose regimen are represented as solid lines, while the conditional probabilities of DLT_o given CRS and no CRS are represented as dotted lines. The target probability of DLT is represented by a dashed horizontal line

For each scenario, we first simulated 1000 trials with a modified CRM ³ using a two‐parameter logistic regression model based on a skeleton for the dose‐allocation rule. The skeleton, that reduced the dose regimen into a single dose level, was defined from the initial guesses of the probabilities of DLT that were set to (0.06, 0.12, 0.20, 0.30, 0.40, 0.50), leading to $k_T=4$ for the dose regimen of reference. The CRM sequentially included 30 patients with cohorts of size 3 and recommended a MTD‐regimen (simplified to a dose‐level) at the end of the dose‐escalation stage. We then computed our joint modeling approaches at the end of each simulated trial using all available information to recommend the MTD‐regimen.

Regarding the prior distributions, we evaluated the amount of information provided by the prior through the effective sample size (ESS) which represents the number of “hypothetical patients” used to define the prior distribution. ⁴⁷ For the CRS model, we considered ${\sigma }_{{\beta }_{0,1}}=2$ and $\alpha =5$, for the DLT_o model, we considered ${\sigma }_{{\beta }_{0,2}}=2$ and ${\sigma }_{{\beta }_{1,2}}=1$, and for the Clayton copula, we considered $\gamma \sim \gamma \left(1,1\right)$ leading to an approximated ESS of 2. Details on prior elicitation are provided in Appendix A and results with various ESS are provided in Web Appendix B.1 of Data S1.

All simulations were performed in the R environment ⁴⁸ using Monolix software ⁴⁹ for PK/PD estimation and Stan ⁵⁰ for Bayesian analysis.

3.2. Simulation results

We evaluated the performance of each of our three proposed joint approaches using the proportion of correct selection (PCS), the estimation of the dose‐toxicity curve and the ability of the methods to predict the toxicity probability of new dose regimens.

3.2.1. PCS of the MTD‐regimen

We compared the results of the DRtox_indep, DRtox_copula, and DRtox_cond with those of the logistic CRM. The performance of each method was evaluated with respect to the PCS, which is defined as the proportion over the 1000 trials for which the correct MTD‐regimen was selected. The proportions of selecting each dose regimen in all scenarios are shown in Table 2. The results of additional scenarios can be found in Web Appendix A.3 of Data S1.

TABLE 2.

Proportions of selecting each dose regimen ${\mathit{S}}_{\mathit{k}}$ as the MTD‐regimen over the 1000 trials in the six main toxicity scenarios. For each scenario, the marginal probabilities of dose limiting toxicity (DLT), cytokine release syndrome (CRS), and other DLT (DLT_o) are defined, and the association between the CRS and DLT_o is represented by the average risk ratio (RR). Results are presented for the three joint approaches (DRtox_indep, DRtox_copula, and DRtox_cond) and the continual reassessment method (CRM). The proportions of correct selection (PCS) of the MTD‐regimen are represented in bold

Scenario	Set	RR	Method		${\mathit{S}}_{\mathbf{1}}$	${\mathit{S}}_{\mathbf{2}}$	${\mathit{S}}_{\mathbf{3}}$	${\mathit{S}}_{\mathbf{4}}$	${\mathit{S}}_{\mathbf{5}}$	${\mathit{S}}_{\mathbf{6}}$
1	A	1.85		${\mathit{p}}_{\mathit{T}}$	0.10	0.14	0.18	0.30	0.45	0.60
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{1})}$	0.05	0.07	0.1	0.18	0.22	0.30
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{2})}$	0.06	0.08	0.1	0.17	0.34	0.50
			DRtox_indep		0	4	24	55	16	2
			DRtox_copula		0	2	20	55	20	3
			DRtox_cond		0	3	25	55	16	2
			Logistic CRM		0	4	22	46	22	5
2	A	5.91		${\mathit{p}}_{\mathit{T}}$	0.10	0.13	0.18	0.30	0.42	0.53
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{1})}$	0.07	0.10	0.13	0.22	0.28	0.36
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{2})}$	0.04	0.07	0.10	0.21	0.39	0.52
			DRtox_indep		0	4	27	48	16	3
			DRtox_copula		0	3	17	52	24	5
			DRtox_cond		0	3	23	52	18	4
			Logistic CRM		0	4	18	42	26	10
3	A	1.81		${\mathit{p}}_{\mathit{T}}$	0.11	0.15	0.18	0.30	0.45	0.59
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{1})}$	0.03	0.05	0.07	0.13	0.16	0.23
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{2})}$	0.08	0.11	0.13	0.22	0.39	0.54
			DRtox_indep		1	3	22	57	15	2
			DRtox_copula		1	2	16	58	20	2
			DRtox_cond		1	3	22	58	15	2
			Logistic CRM		1	5	22	48	19	5
4	A	1.90		${\mathit{p}}_{\mathit{T}}$	0.09	0.13	0.17	0.30	0.44	0.59
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{1})}$	0.07	0.10	0.13	0.23	0.29	0.37
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{2})}$	0.03	0.04	0.06	0.12	0.27	0.43
			DRtox_indep		0	3	24	56	14	2
			DRtox_copula		0	2	19	56	20	4
			DRtox_cond		0	3	24	55	15	2
			Logistic CRM		0	4	20	46	23	7
5	A	1.97		${\mathit{p}}_{\mathit{T}}$	0.03	0.04	0.05	0.11	0.17	0.30
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{1})}$	0.02	0.03	0.05	0.09	0.11	0.17
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{2})}$	0.00	0.01	0.01	0.02	0.08	0.18
			DRtox_indep		0	0	0	4	29	67
			DRtox_copula		0	0	0	3	20	77
			DRtox_cond		0	0	0	4	29	67
			Logistic CRM		0	0	0	2	21	77
6	B	1.70		${\mathit{p}}_{\mathit{T}}$	0.16	0.30	0.43	0.55	0.73	0.86
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{1})}$	0.09	0.17	0.25	0.33	0.38	0.48
				${\mathit{p}}_{\mathit{T}}^{(\mathbf{2})}$	0.08	0.18	0.29	0.41	0.67	0.84
			DRtox_indep		20	64	15	1	0	0
			DRtox_copula		14	63	21	2	0	0
			DRtox_cond		19	65	15	1	0	0
			Logistic CRM		17	56	24	3	0	0

In Scenarios 1 to 4, where the true MTD‐regimen is ${\mathit{S}}_{\mathbf{4}}$, the DRtox_indep, DRtox_copula, and DRtox_cond outperform the CRM by 10% in terms of the PCS. All three joint methods achieve very similar results and are robust to an unbalanced distribution of the probabilities of CRS and DLT_o, as illustrated in Scenarios 3 and 4. In Scenario 2, defined with a higher association between the CRS and the DLT_o, the DRtox_copula and DRtox_cond seem to perform better than the DRtox_indep as they account for the dependence between both toxicities. Indeed, in this scenario, more patients experience both toxicities (CRS and DLT_o) and therefore the DRtox_indep overestimates the probability of DLT. In Scenarios 1 to 4, the DRtox_copula has a higher proportion of trials in which the overdosing regimen ${\mathit{S}}_{\mathbf{5}}$ is recommended as the MTD‐regimen than the DRtox_indep and DRtox_cond, but this proportion is lower than or similar to that of the CRM.

In Scenario 5, where the true MTD‐regimen is ${\mathit{S}}_{\mathbf{6}}$, the CRM has higher PCS than those of the DRtox_indep and DRtox_cond but similar results to those of the DRtox_copula. In this scenario the MTD‐regimen is the last dose regimen of the panel; therefore fewer DLT, particularly fewer DLT_o, are observed. Indeed, on average, 5 DLT with 1.9 DLT_o occur per trial in Scenario 5, vs 7.7 DLT and 3.8 DLT_o in Scenario 1. In this scenario, the higher performance of the DRtox_copula and the CRM can be explained by their tendency to recommend higher dose regimens which was observed in Scenarios 1 to 4.

Scenario 6 was built on Set B which included an accelerated part for the first dose regimens to rapidly reach high steady‐state doses. In this scenario, where ${\mathit{S}}_{\mathbf{2}}$ is the true MTD‐regimen, all three joint models yield similar results and still outperform the CRM.

All three joint models still perform better than the CRM in cases of independence or negative association between the CRS and the DLT_o (Web Appendix A.3 of Data S1).

We evaluated the influence of the prior distribution by comparing the results obtained with a prior ESS of 0.2, 2, and 7, the results can be found in Web Appendix B.1 of Data S1. Increasing the prior ESS leads to better results when the prior guesses of DLT probabilities are close to the truth (Scenarios 1‐4 where ${\mathit{S}}_{\mathbf{4}}$ is the true MTD‐regimen), but also when the initial guesses of DLT probabilities underestimate the true DLT probabilities (Scenario 6 where ${\mathit{S}}_{\mathbf{2}}$ is the true MTD‐regimen). However, increasing the prior ESS leads to poorer results when the initial guesses of DLT probabilities overestimate the true DLT probabilities (Scenario 5 where ${\mathit{S}}_{\mathbf{6}}$ is the true MTD‐regimen). We also evaluated the impact of considering a gamma distribution for the DLT_o model and a log‐normal distribution for the CRS model, and observed only a limited impact (Web Appendix B.2 of Data S1). We also evaluated the effect of a noninformative distribution on the DRtox_copula parameter, that is, $\gamma (0.1,0.1)$. In this case, the results of the DRtox_copula are similar to the DRtox_indep (Web Appendix B.3 of Data S1). We also evaluated our methods after an empiric CRM and observed only limited impact on our proposed methods (Web Appendix B.4 of Data S1). Finally, we studied our methods on another set of dose regimens that is very different from the motivating trial to vary the timing of toxicity occurrences (Web Appendix C of Data S1). In this new set, our three joint models and the CRM have similar PCS so our three joint models do not improve the PCS but they can predict the probabilities of DLT of new dose regimens, and this will be developed in Section 3.2.3.

3.2.2. Estimation of the toxicity curves

Gerard et al ³³ showed that when only CRS occur, the DRtox leads to a better estimation of the entire dose regimen CRS relationship than the CRM. When enabling the occurrence of DLT_o, the probability of CRS is still well estimated with the DRtox. The joint probability of DLT is also well estimated around the MTD‐regimen for all three joint approaches and the CRM. Both the DRtox_indep and DRtox_copula estimate the marginal probability of DLT_o, while the DRtox_cond estimates the conditional probability of DLT_o given that no CRS has occurred. The latter conditional probability is well estimated by the DRtox_cond, while the marginal probability is underestimated by the DRtox_indep and DRtox_copula (and estimated to be similar to the previous conditional probability) in all six main scenarios. Indeed, estimating the marginal probability of DLT_o requires estimating the conditional probability of DLT_o given CRS. The latter probability can only be estimated when both toxicities occur at the same time as drug administration is stopped when a DLT (either a CRS or DLT_o) occurs. However, CRS tend to occur at the beginning of the dose regimen, mainly at the first and fourth administrations, while most DLT_o occur starting from the fourth administration. Thus, both toxicities rarely occur at the same time, and CRS occurrence may prevent future DLT_o from occurring. This topic will be further developed in the discussion. Figures that illustrate the estimation of the different toxicity probabilities can be found in the supporting information (Web Appendix A.2 of Data S1).

3.2.3. Prediction of new dose regimens

Our three proposed joint approaches and the CRM are able to recommend the MTD‐regimen in the panel of the trial. However, alternative dose regimens may increase the efficacy of the drug while maintaining an acceptable probability of toxicity. For example, dose regimens where a lower steady‐state dose is administered sooner or where a higher steady‐state dose is administered later could be of interest. As the DRtox_indep, DRtox_copula, and DRtox_cond model the relationship between the entire dose regimen and the probability of DLT, they can predict the probability of DLT of new dose regimens that were not administered in the trial. For example, in Scenario 1, ${\mathit{S}}_{\mathbf{4}}=(1,5,10,45,45,45,45)$ $\mathrm{\mu }$g/kg is selected for the MTD‐regimen in more than 50% of trials where the steady‐state dose of 45 $\mathrm{\mu }$g/kg is administered starting from the fourth administration. We are able to predict the probabilities of two new dose regimens. For dose regimen ${\mathit{S}}_{\mathbf{\text{new1}}}=(5,10,30,30,30,30,30)$ $\mathrm{\mu }$g/kg, having a true DLT probability of 0.27, the steady‐state dose is decreased to 30 $\mathrm{\mu }$g/kg but is administered earlier, from t₃. For dose regimen ${\mathit{S}}_{\mathbf{\text{new2}}}=(1,5,10,30,60,60,60)$ $\mathrm{\mu }$g/kg, having a true DLT probability of 0.31, the steady‐state dose is increased to 60 $\mathrm{\mu }$g/kg but is administered later, from t₅. The estimated probabilities of DLT of the six initial dose regimens of the trial and the predicted probabilities of DLT of ${\mathit{S}}_{\mathbf{\text{new1}}}$ and ${\mathit{S}}_{\mathbf{\text{new2}}}$ are displayed in Figure 3. All approaches yield good estimations of the DLT probability of ${\mathit{S}}_{\mathbf{4}}$, but only the DRtox_indep, DRtox_copula, and DRtox_cond can predict the DLT probabilities of ${\mathit{S}}_{\mathbf{\text{new1}}}$ and ${\mathit{S}}_{\mathbf{\text{new2}}}$ that are close to the target. The three joint approaches can therefore help the clinical team find alternative dose regimens that can be investigated for efficacy in further stages of the trial, for example, in an expansion cohort.

FIGURE 3.

Violin plots of the estimated probabilities of dose limiting toxicity (DLT) in Scenario 1 for the six dose regimens of the panel and two additional dose regimens (${\mathit{S}}_{\mathbf{new1}}$ and ${\mathit{S}}_{\mathbf{new2}}$), on 1000 trials with the three proposed joint approaches and the continual reassessment method (CRM). The predicted DLT probabilities of the new dose regimens are framed in dotted line. Horizontal lines on the density estimates represent the median and first and third quantiles of the distributions, and the plus sign represents the mean. The dashed line represents the toxicity target, and the solid line represents the true DLT probabilities

The DRtox_indep, DRtox_copula, and DRtox_cond have similar precision in predicting new dose regimens with DLT probabilities close to the target in case of various associations between the CRS and the DLT_o (Web Appendix A.3 of Data S1).

3.3. Example from a single simulated trial

We illustrate our proposed methods on one hypothetical trial inspired by the motivating example. The trial was simulated under Scenario 2 with the settings specified in Section 3.1: it was conducted using a modified logistic CRM where patients were included by cohorts of size 3 until a maximum of 30 patients included. The toxicity target was 0.30. The inclusion process and the timing of occurrence of each type of toxicity are represented in Figure 4. During the trial, 8 DLT were observed, with 4 CRS and 6 DLT_o. For example, at cohort 5, three patients were included at dose regimen ${\mathit{S}}_{\mathbf{4}}=\left(1,5,10,50,50,50,50\right)$ $\mathrm{\mu }$g/kg administered at days $\left(t_1=1,t_2=5,t_3=9,t_4=13,t_5=17,t_6=21,t_7=25\right)$. One of the three patient experienced a DLT, which was both a CRS and a DLT_o at administration $t_4$. As drug administration is stopped when a DLT occurs, this patient only received the dose regimen composed of the four initial doses: $\left(1,5,10,50\right)$ μg/kg. The CRM estimated (0.11, 0.15, 0.22, 0.30, 0.39, 0.47) for the posterior mean probabilities of DLT of ${\mathit{S}}_{\mathbf{1}}$ to ${\mathit{S}}_{\mathbf{6}}$, therefore ${\mathit{S}}_{\mathbf{4}}$ was estimated as the MTD‐regimen. We can apply our proposed methods at the end of the trial.

FIGURE 4.

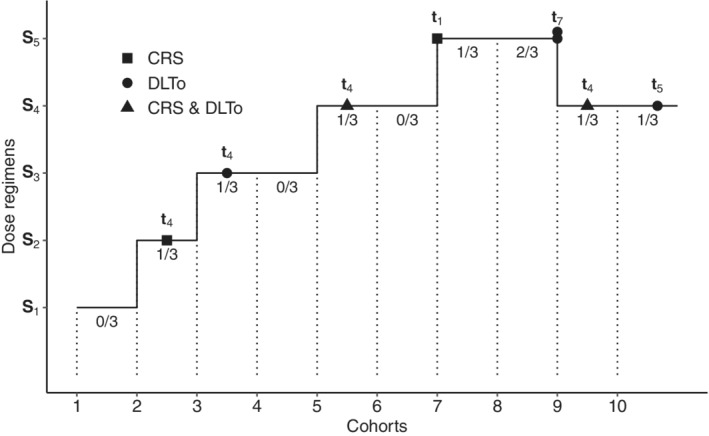
Inclusion process of the simulated trial under a modified continual reassessment method (CRM). The type of dose limiting toxicity (DLT) is specified by the type of point, and the administration of occurrence of each type of DLT is given. The global number of DLT observed in each cohort of three patients is provided under each horizontal bar

CRS model

1. The PK/PD models (Appendix B.1) are fitted to the sampled individual concentrations and cytokine responses. Population and individual PK/PD parameters as well as the individual maximum peak of cytokine are estimated (see Web Appendix A.1 of Data S1 for the fitted cytokine response on one patient).

2. The CRS model is then fitted, the estimated posterior means of ${\beta }_{0,1}$ and ${\beta }_{1,1}$ are $-$2.40 and 2.78, respectively.

3. The peak of cytokine at each dose regimen is simulated for 600 hypothetical patients from the population PK/PD parameters. The peak of cytokine can also be predicted for dose regimens that were not tested in the trial.

4. The posterior probabilities of CRS are estimated. The marginal probabilities of CRS are estimated by the mean of the posterior distributions: (0.05,0.07,0.09,0.17,0.22,0.28) for ${\mathit{S}}_{\mathbf{1}}$ to ${\mathit{S}}_{\mathbf{6}}$.

DLT_o model

1. The cumulative marginal (and conditional given no CRS) probabilities of DLT_o are modeled with the cumulative dose received. The estimated posterior means of ${\beta }_{0,2}$ $\left({\beta }_{0,2\star }\right)$ and ${\beta }_{1,2}$ $\left({\beta }_{1,2\star }\right)$ are −1.39 (−1.88) and 0.05 (0.31), respectively.

2. The marginal posterior probabilities of DLT_o (and conditional posterior probabilities of DLT_o given no CRS) are estimated. The marginal probabilities of DLT_o (and the conditional probabilities of DLT_o given no CRS) are estimated by the mean of the posterior distributions: (0.11 (0.06), 0.13 (0.08), 0.15 (0.09), 0.21 (0.15), 0.33 (0.28), 0.41 (0.39)) for ${\mathit{S}}_{\mathbf{1}}$ to ${\mathit{S}}_{\mathbf{6}}$.

DLT model

1. DRtox_indep: The posterior DLT probabilities are estimated from the marginal posterior probabilities of CRS and DLT_o. The marginal probabilities of DLT are estimated by the mean of the posterior distributions: (0.15, 0.19, 0.23, 0.34, 0.48, 0.58) for ${\mathit{S}}_{\mathbf{1}}$ to ${\mathit{S}}_{\mathbf{6}}$.

2. DRtox_copula: The DLT probabilities are modeled from the mean estimates of the marginal probabilities of CRS and DLT_o with the Clayton copula. The marginal probabilities of DLT are estimated by the mean of the posterior distributions: (0.13, 0.17, 0.20, 0.30, 0.43, 0.52) for ${\mathit{S}}_{\mathbf{1}}$ to ${\mathit{S}}_{\mathbf{6}}$.

3. DRtox_cond: The posterior DLT probabilities are estimated from the marginal posterior probabilities of CRS and the conditional posterior probabilities of DLT_o given no CRS. The marginal probabilities of DLT are estimated by the mean of the posterior distributions: (0.11, 0.14, 0.18, 0.29, 0.44, 0.56) for ${\mathit{S}}_{\mathbf{1}}$ to ${\mathit{S}}_{\mathbf{6}}$.

A figure of the posterior distributions can be found in Web Appendix A.1 of Data S1. The CRM and our three approaches lead to the same MTD‐regimen recommendation, that is ${\mathit{S}}_{\mathbf{4}}$. As two patients experienced both a CRS and a DLT_o, the DRtox_indep overestimates the probability of DLT of ${\mathit{S}}_{\mathbf{4}}$ while the DRtox_copula and DRtox_cond correctly estimate it because they account for the correlation between both toxicities. Moreover, as our methods model the relationship between the entire dose regimen and the probability of DLT, they can predict the probability of DLT of additional dose regimens that were not administered in the trial. For example, we can define the following additional dose regimen $(5,10,30,30,30,30,30)$ $\mathrm{\mu }$g/kg than may have a clinical relevance because it reaches a lower value of the steady‐state dose but earlier than ${\mathit{S}}_{\mathbf{4}}$. The DRtox_indep, DRtox_copula, and DRtox_cond predict 0.29, 0.26, and 0.24 for the probability of DLT of this new dose regimen, respectively. Therefore, at the end of the trial, our proposed methods support the recommendation of the CRM, and are able to propose an alternative dose regimen that could be evaluated in an expansion cohort.

4. DISCUSSION

The aim of this work was to model the probability of DLT defined from the occurrence of two types of toxicity (CRS and DLT_o) in multiple dose administrations, that is, when dose regimens were administered, assuming that the CRS and the DLT_o might be associated. We developed a modeling approach for the DLT_o in addition to the existing DRtox approach that provides the CRS modeling with PK/PD. We proposed three approaches to model the joint distribution of DLT using the independence assumption (DRtox_indep), a copula model (DRtox_copula), and a conditional formulation (DRtox_cond). Through an extensive simulation study, the three joint approaches were able to recommend the MTD‐regimen in a set of dose regimens and to predict the DLT probability of new dose regimens that could be investigated in later stages of the trial. These methods were developed to be used when the dose allocation process is finished and once all data are gathered, especially once PK/PD measurements have already been analyzed using a population PK/PD approach. However, our methods should not be applied if the trial is stopped very early in the inclusion process and when not enough data is gathered to guaranty a feasible and/or reliable estimation of the parameters.

In most cases, the PCS of the three proposed methods were higher than that of the CRM. When the interaction between the DLT_o and CRS was increased, the DRtox_copula and DRtox_cond gave better results as these two approaches account for the association between toxicities. When the MTD‐regimen was the last dose regimen of the set and therefore few DLT were expected, the CRM had better performance than our proposed methods. In this case, as very few DLT_o were observed, distinguishing between the different dose regimens was challenging for the cumulative DLT_o model built on the cumulative dose. A simpler model that does not account for repeated doses could be fit on the DLT_o to increase the PCS, but with such a model, prediction of new dose regimens would no longer be possible (Web Appendix A.4 of Data S1).

In addition to the potential gain in PCS compared to standard dose‐escalation methods, one important feature of our proposed methods is that they were able to propose alternative dose regimens that could have a better clinical benefit than the existing dose regimens, in terms of efficacy for example. Indeed, our joint approaches model the relationship between the entire dose regimen and the probability of DLT and can therefore predict the DLT probability of new dose regimens. This prediction was accurate in our simulation settings, but is dependent on the number of patients included and the number of DLTs observed, as well as on the confidence in the PK/PD estimates. These potential new dose regimens need to be discussed by the trial stakeholders to determine the most suitable ones to be included in the expansion cohorts.

One limitation of the DRtox_indep and DRtox_copula was that the marginal probability of DLT_o seemed to be underestimated (Web Appendix A.2 of Data S1). Indeed, from our motivating trial, CRS were expected to be observed at the beginning of the dose regimens, while DLT_o occurred at the end. Once a CRS was observed, the administration of the drug was stopped, so there was no possibility left to observe any DLT_o that might have occurred later in the planned drug administrations. This issue is different from censoring or competitive risks because the DLT_o could be observed at the same time as the CRS. However, as drug administration was stopped, the patient did not receive the remaining administrations of the entire dose regimen that may have caused a DLT_o. The DRtox_cond accounted for this issue as it modeled the conditional probability of DLT_o given that no CRS had occurred. A second limitation was associated with the use of copula models. Cunanan and Koopmeiners ⁵¹ showed that in the context of phase I/II trials, using a copula model instead of an independent model does not improve the performance in terms of correct dose selection, even in cases with highly correlated outcomes. They suggested adding a strong prior information on the correlation parameter of the copula models. In our case, we used an informative prior ($\gamma (1,1)$) and observed that when using a noninformative prior ($\gamma (0.1,0.1)$), the performance of the model could be decreased. We also observed that the DRtox_copula was more likely to recommend overdosing regimens than the DRtox_indep and DRtox_cond. Finally, as our modeling strategy requires multiple steps of modeling, it should only be considered when enough data is gathered. It should also be performed in close collaboration with pharmacometricians to be more confident about PK/PD models and estimates.

In conclusion, in this work we proposed to model a bivariate binary toxicity outcome in the context of an intrapatient dose‐escalation early phase trial in oncology. We accounted for all types of DLT while allowing the explicit modeling of the main type of toxicity expected (CRS) with PK/PD. Some dose‐finding methods have been proposed that include PK measures. ²⁶ , ⁵² However, as PK/PD measures are analyzed by batch (and therefore are not available in real time) and the PK/PD models are developed after several cohorts of patients, a full sequential dose‐allocation approach can be difficult to perform in practice. Our approaches were developed to be computed at the end of the trial, so using all trial information, including toxicities and PK/PD measures, is most practical. We have shown that even if the early phase trial is designed with a standard dose‐allocation method, modeling PK/PD and multiple dose administrations at the end of the trial can allow the study stakeholders to make decisions about future development using all available information within a single modeling process.

CONFLICT OF INTEREST

The authors declare no potential conflict of interests.

Supporting information

Data S1. Web Appendix A: Additional results Web Appendix B: Sensitivity analysis Web Appendix C: Alternative set of dose regimens

APPENDIX A. PRIOR ELICITATION

A.1.

The elicitation of prior distributions is based on the initial guesses of the probabilities of DLT$({\pi }_1,...,{\pi }_K)$ of dose regimens $(S_1,...,S_K)$. $S_{k_T}$ is the dose regimen of reference, where ${\pi }_{k_T}={\delta }_T$. We initially assume that the probabilities of CRS and DLT_o are independent and equal, meaning that ${\pi }_k=1-\left(1-{\pi }_k^{(1)}\right)\left(1-{\pi }_k^{(2)}\right)=1-{\left(1-{\pi }_k^{(1)}\right)}^2=1-{\left(1-{\pi }_k^{(2)}\right)}^2$, where ${\pi }_k^{(1)}$ and ${\pi }_k^{(2)}$ are the initial guesses of the probabilities of CRS and DLT_o, respectively. Therefore ${\pi }_k^{(1)}={\pi }_k^{(2)}=1-\sqrt{1-{\pi }_k}$.

For the CRS model, we consider ${\beta }_{0,1}\sim 𝒩({\bar{\beta }}_{0,1},{\sigma }_{{\beta }_{0,1}}^2)$ and ${\beta }_{1,1}\sim \gamma ({\alpha }_1,\frac{{\alpha }_1}{{\bar{\beta }}_{1,1}})$, where ${\bar{\beta }}_{0,1}=𝔼[{\beta }_{0,1}]$ and ${\bar{\beta }}_{1,1}=𝔼[{\beta }_{1,1}]$. By construction, we have ${\bar{\beta }}_{0,1}=\text{logit}\left(1-\sqrt{1-{\delta }_T}\right)$ with $r_i^M={\bar{r}}_{k_T}^M$. We can determine ${\bar{\beta }}_{1,1}$ using either only one dose regimen (differing from the reference dose regimen $S_{k_T}$), as follows:

$${\text{logit}}^{-1}\left({\bar{\beta }}_{0,1}+{\bar{\beta }}_{1,1}\log \left(\frac{{\bar{r}}_k^M}{{\bar{r}}_{k_T}^M}\right)\right)={\pi }_k^{(1)},$$ (A1)

where $k\in \{1,...,K\}$ and $k\ne k_T$, or multiple dose regimens, such as the neighbors of the reference dose regimen, as follows:

$${\bar{\beta }}_{1,1}=\underset{{\beta }_{1,1}}{\text{arg min}}\sum _{k=k_T-1}^{k_T+1}{\left({\pi }_k^{(1)}-{\text{logit}}^{-1}\left({\bar{\beta }}_{0,1}+{\bar{\beta }}_{1,1}\log \left(\frac{{\bar{r}}_k^M}{{\bar{r}}_{k_T}^M}\right)\right)\right)}^2.$$ (A2)

For the DLT_o model, we consider ${\beta }_{0,2}\sim 𝒩({\bar{\beta }}_{0,2},{\sigma }_{{\beta }_{0,2}}^2)$ and ${\beta }_{1,2}\sim 𝒩({\bar{\beta }}_{1,2},{\sigma }_{{\beta }_{1,2}}^2)$, where ${\bar{\beta }}_{0,2}=𝔼[{\beta }_{0,2}]$ and ${\bar{\beta }}_{1,2}=𝔼[{\beta }_{1,2}]$. By construction, we have ${\bar{\beta }}_{0,2}=\text{logit}\left(1-\sqrt{1-{\delta }_T}\right)$ with $\sum _{l=1}^J{d}_{i,l}=D_{k_T}$. We can determine ${\bar{\beta }}_{1,2}$ using either only one dose regimen (differing from the reference dose regimen ${\mathit{S}}_{{\mathit{k}}_{\mathit{T}}}$), as follows:

$${\text{logit}}^{-1}\left({\bar{\beta }}_{0,2}+\exp \left({\bar{\beta }}_{1,2}\right)\log \left(\frac{1}{D_{k_T}}\sum _{l=1}^J{d}_{k,l}\right)\right)={\pi }_k^{(2)},$$ (A3)

where $k\in \{1,...,K\}$ and $k\ne k_T$, or multiple dose regimens, such as the neighbors of the reference dose regimen, as follows:

$${\bar{\beta }}_{1,2}=\underset{{\beta }_{1,2}}{\text{arg min}}\sum _{k=k_T-1}^{k_T+1}{\left({\pi }_k^{(2)}-{\text{logit}}^{-1}\left({\bar{\beta }}_{0,2}+\exp \left({\beta }_{1,2}\right)\log \left(\frac{1}{D_{k_T}}\sum _{l=1}^J{d}_{k,l}\right)\right)\right)}^2.$$ (A4)

APPENDIX B. SIMULATION STUDY

B.1. PK/PD models

The PK/PD models were inspired by published models on blinatumomab. For the PK, we considered a 1‐compartment infusion model, ⁴⁶ where the drug concentration was defined as follows:

$$\begin{gathered} C(t)=\sum _{j=1}^J{\mathbb{1}}_{\{t-t_j>T_{in{f}_j}\}}\frac{d_{k,j}}{T_{in{f}_j}}\frac{1}{kV}\left(1-e^{-k{T}_{in{f}_j}}\right)e^{-k\left(t-t_j-T_{in{f}_j}\right)}+ \\ {\mathbb{1}}_{\{t-t_j\le T_{in{f}_j}\text{\&}t-t_j\ge 0\}}\frac{d_{k,j}}{T_{in{f}_j}}\frac{1}{kV}\{1-e^{-k\left(t-t_j\right)}\}, \end{gathered}$$ (B1)

where $T_{in{f}_j}$ is the duration of the infusion of the j ^th administration, V is the distribution volume, $Cl$ is the clearance of elimination, and k is the micro‐constant defined as $k=\frac{Cl}{V}$. We assumed that the delay between successive doses was greater than the infusion duration, meaning that $t_{j+1}-t_j>T_{in{f}_j}$ for $j\in \{1,...,J-1\}$.

For the PD, the objective was to model cytokine mitigation when intrapatient dose‐escalation was implemented. We simplified the model developed by Chen et al, ³¹ which assumes that cytokine production is stimulated by the drug concentration but inhibited by cytokine exposure through the AUC. We defined the cytokine response as follows:

$$\frac{\mathrm{d}E\left(t\right)}{\mathrm{d}t}=\frac{E_{\max }C{\left(t\right)}^H}{{{\text{EC}}_{50}}^H+C{\left(t\right)}^H}\left\{1-\frac{I_{\max }{\text{AUC}}_E\left(t\right)}{\frac{{\text{IC}}_{50}}{K^{J-1}}+{\text{AUC}}_E\left(t\right)}\right\}-k_{\mathrm{deg}}E\left(t\right)$$ (B2)

where ${\text{AUC}}_E\left(t\right)$ is the cumulative cytokine exposure.

For both the PK and PD models, we considered a proportional error model with a value of 0.1. The values of the PK/PD parameters used for the simulations were inspired by the estimated parameters of blinatumomab ³¹ , ⁴⁶ and are displayed in Table B1. For the estimation, we considered the parameters EC₅₀, I _max and IC${}_{\text{50}}$ fixed and no random effects on V and H. Estimation was performed with Monolix software (Lixoft SAS., 2019).

TABLE B1.

Definition and value of the pharmacokinetics and pharmacodynamics (PK/PD) parameters used for the simulation study. Parameter estimate represents the fixed effect, and the coefficient of variation (CV) is the square root of the diagonal of the variance‐covariance matrix. These values are inspired by the parameters estimated on blinatumomab, ³¹ , ⁴⁶ with a modification of I_max to observe cytokine mitigation after several administrations

	Parameter	Estimate (% CV)	Unit	Description
PK model	Cl	1.36 (41.9)	L/h	Clearance of elimination
	V	3.4 $(0)$	L	Volume of distribution
PD model	E${}_{\max }$	3.59 . 105 (14)	pg/mL/h	Maximum cytokine release rate
	EC50	1.104 (0)	ng/mL	Drug exposure for half‐maximum release
	H	0.92 $(3)$		Hill coefficient for cytokine release
	Imax	0.995 $(0)$		Maximum inhibition of cytokine release
	IC50	$1.82·10^4$ (12)	pg/mL$·$h	Cytokine exposure for half‐maximum inhibition
	kdeg	0.18 $(13)$	h−1	Degradation rate for cytokine
	K	2.83 $(36)$		Priming factor for cytokine release

B.2. Computation of toxicity probabilities

The true marginal probability of DLT was computed as follows:

$$\begin{array}{ll}{p}_T(S_k)& =1-\mathbb{P}\left(Y^{(1)}=0,Y^{(2)}=0\right)\\ & =1-\mathbb{P}\left(Y^{(1)}=0;Y_1^{(2)}=0,...,Y_J^{(2)}=0\right)\\ & =1-\mathbb{P}\left(Y_1^{(2)}=0,...,Y_J^{(2)}=0|Y^{(1)}=0\right)\mathbb{P}\left(Y^{(1)}=0\right)\\ & =1-\prod _{j=1}^J\mathbb{P}\left(Y_j^{(2)}=0|Y_{j-1}^{(2)}=0,...,Y_1^{(2)}=0;Y^{(1)}=0\right)\mathbb{P}\left(Y^{(1)}=0\right)\\ & =1-\prod _{j=1}^J\left(1-\mathbb{P}\left(Y_j^{(2)}=1|Y_{j-1}^{(2)}=0,...,Y_1^{(2)}=0;Y^{(1)}=0\right)\right)\left(1-\mathbb{P}\left(Y^{(1)}=1\right)\right)\\ & =1-\prod _{j=1}^J\left(1-\frac{1}{\lambda }{f}_{\theta }\left(d_{k,j},D_{k,j-1}\right)\right)\left(1-p_T^{(1)}(S_k)\right).\end{array}$$ (B3)

The true marginal probability of CRS was computed by simulations using a Monte‐Carlo method. The marginal probability of DLT_o was computed as follows:

$$\begin{array}{ll}{p}_T^{(2)}(S_k)& =1-\mathbb{P}\left(Y_1^{(2)}=0,...,Y_J^{(2)}=0\right)\\ & =1-\mathbb{P}\left(Y_1^{(2)}=0,...,Y_J^{(2)}=0|Y^{(1)}=1\right)p_T^{(1)}(S_k)-\mathbb{P}\left(Y_1^{(2)}=0,...,Y_J^{(2)}=0|Y^{(1)}=0\right)\left(1-p_T^{(1)}(S_k)\right)\\ & =1-\prod _{j=1}^J\mathbb{P}\left(Y_j^{(2)}=0|\left(Y_{j-1}^{(2)}=0,...,Y_1^{(2)}=0\right);Y_i^{(1)}=1\right)p_T^{(1)}(S_k)\\ & -\prod _{j=1}^J\mathbb{P}\left(Y_j^{(2)}=0|\left(Y_{j-1}^{(2)}=0,...,Y_1^{(2)}=0\right);Y_i^{(1)}=0\right)\left(1-p_T^{(1)}(S_k)\right)\\ & =1-\prod _{j=1}^J\left(1-f_{\theta }\left(d_{k,j},D_{k,j-1}\right)\right)p_T^{(1)}(S_k)-\prod _{j=1}^J\left(1-\frac{1}{\lambda }{f}_{\theta }\left(d_{k,j},D_{k,j-1}\right)\right)\left(1-p_T^{(1)}(S_k)\right).\end{array}$$ (B4)

Gerard E, Zohar S, Lorenzato C, Ursino M, Riviere M‐K. Bayesian modeling of a bivariate toxicity outcome for early phase oncology trials evaluating dose regimens. Statistics in Medicine. 2021;40:5096–5114. 10.1002/sim.9113