Impact of unequal cluster sizes for GEE analyses of stepped wedge cluster randomized trials with binary outcomes

Abstract

The stepped wedge (SW) design is a type of unidirectional crossover design where cluster units switch from control to intervention condition at different prespecified time points. While a convention in study planning is to assume the cluster‐period sizes are identical, SW cluster randomized trials (SW‐CRTs) involving repeated cross‐sectional designs frequently have unequal cluster‐period sizes, which can impact the efficiency of the treatment effect estimator. In this paper, we provide a comprehensive investigation of the efficiency impact of unequal cluster sizes for generalized estimating equation analyses of SW‐CRTs, with a focus on binary outcomes as in the Washington State Expedited Partner Therapy trial. Several major distinctions between our work and existing work include the following: (i) we consider multilevel correlation structures in marginal models with binary outcomes; (ii) we study the implications of both the between‐cluster and within‐cluster imbalances in sizes; and (iii) we provide a comparison between the independence working correlation versus the true working correlation and detail the consequences of ignoring correlation estimation in SW‐CRTs with unequal cluster sizes. We conclude that the working independence assumption can lead to substantial efficiency loss and a large sample size regardless of cluster‐period size variability in SW‐CRTs, and recommend accounting for correlations in the analysis. To improve study planning, we additionally provide a computationally efficient search algorithm to estimate the sample size in SW‐CRTs accounting for unequal cluster‐period sizes, and conclude by illustrating the proposed approach in the context of the Washington State study.

1. INTRODUCTION

Stepped wedge (SW) design is a type of unidirectional crossover design where units switch from control to intervention condition at different prespecified time points, or steps (Hussey & Hughes, 2007; Turner et al., 2017). This design has been increasingly adopted in cluster randomized trials (CRTs), where the unit of randomization is often a group of individuals such as hospitals or clinics. In a typical stepped wedge cluster randomized trial (SW‐CRT), the intervention is scheduled to implement in only a small fraction of the clusters at each step, which is often logistically more feasible compared to concurrently implementing the intervention within half of the clusters as in a parallel‐arm CRT. In addition, SW‐CRT allows all participating clusters to receive the intervention prior to the end of the study, and may facilitate recruitment when stakeholders perceive the intervention to be beneficial to the cluster population.

Methods for planning SW‐CRTs, especially those associated with sample size and power calculations, have been an active topic for statistical research over the past decades (Hemming et al., 2015; Hooper et al., 2016; Kasza et al., 2019; Li et al., 2018b; Li, 2020). However, a convention in deriving sample size formulae is to assume that the number of observations in each cluster‐period (referred to as the cluster‐period size) is the same both within and between clusters. This equal cluster‐period size assumption, while operationally convenient for study planning, is often questionable, especially in cross‐sectional designs where different individuals present for health care in each cluster during each period. For example, the Washington State Expedited Partner Therapy (EPT) trial rolled out a partner therapy intervention in 22 local health jurisdictions (LHJs) over four steps, where women attending sentinel clinics in each 6‐month time period were tested for chlamydia and Gonorrhea infection (Golden et al., 2015). Figure 1 presents a cluster‐by‐period diagram of this study, along with the cluster‐period sizes. While the average cluster‐period size is roughly 300, the actual cluster‐period sizes range from 17 to 1553 across $22\times 5=110$ cluster‐periods.

FIGURE 1.

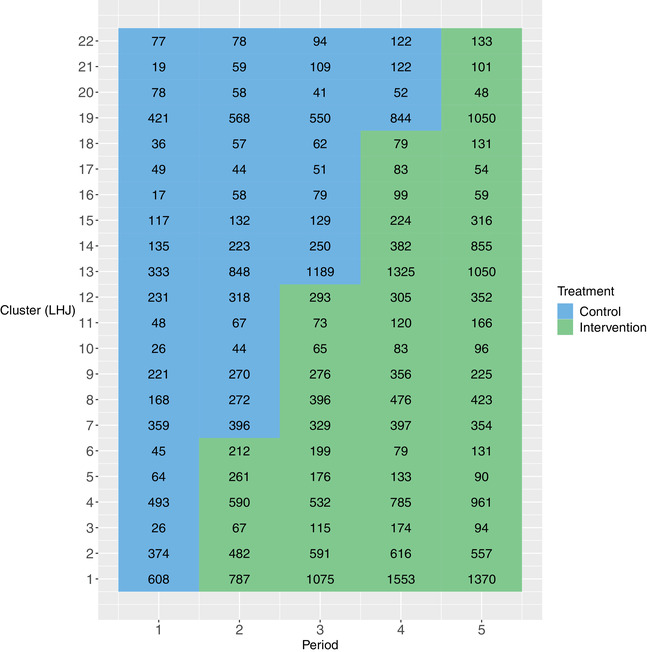
The cluster‐by‐period diagram for the Washington State Expedited Partner Therapy (EPT) trial. Local health jurisdictions (LHJs) are the clusters in this trial. Each cell represents a cluster‐period along with its cluster‐period size. The blue color and green color indicate the control and intervention condition, respectively

While the impact of unequal cluster sizes has been well studied for continuous, binary, and count outcomes in parallel CRTs (Candel & van Breukelen, 2010; Eldridge et al., 2006; Li & Tong, 2021a, 2021b; Liu & Colditz, 2018; Manatunga et al., 2001; van Breukelen et al., 2007), there are a limited number of studies investigating the impact of unequal cluster sizes in SW‐CRTs, all of which are restricted to continuous outcomes. For example, Kristunas et al. (2017) studied the impact of unequal cluster sizes in SW‐CRTs via simulations and found cluster size imbalances did not lead to notable loss in power. Martin et al. (2019) designed a series of simulations to study the relative efficiency (RE) of a linear mixed model treatment effect estimator under equal versus unequal cluster sizes. They concluded that the median RE is smaller in SW‐CRTs compared to parallel CRTs, while the variation of RE can be substantially larger in SW‐CRTs. Assuming a more general linear mixed model, Girling (2018) developed an analytical formula for RE in SW‐CRTs when the randomization is stratified by cluster size. Harrison et al. (2020) proposed analytical formulae as a function of the mean and variance of the cluster size based on the Hussey and Hughes (2007) linear mixed model for efficient sample size determination in SW‐CRTs. Matthews (2020) considered optimal SW‐CRTs that achieve the smallest variance of the treatment effect estimator under unequal cluster sizes. Despite these efforts, there is currently limited empirical evidence for the RE in SW‐CRTs with binary outcomes, whereas binary outcomes are of interest in the Washington State EPT trial, and are also fairly common according to the systematic review by Barker et al. (2016). Furthermore, the sample size formulae developed for continuous outcomes in SW‐CRTs can lead to inaccurate approximations when the outcomes are binary, even under equal cluster sizes (Zhou et al., 2020). Therefore, new sample size procedures that explicitly account for the mean–variance relationship of binary outcomes as well as unequal cluster sizes are needed.

Generalized linear mixed models (GLMMs) and marginal models represent two mainstream approaches for analyzing SW‐CRTs with binary outcomes. Because SW‐CRTs are often used in health care research to inform policy decisions, marginal models, which carry a population‐averaged interpretation, may be preferred (Drum et al., 1993; Preisser et al., 2003; Li et al., 2018b). Additional advantages of marginal models for analyzing SW‐CRTs were summarized in Li et al. (2021). In this paper, we aim to study the impact of unequal cluster sizes for marginal model analysis of SW‐CRTs such as the Washington State EPT study, with the purpose to inform study planning. Several major distinctions between our work and existing work on unequal cluster sizes for SW‐CRTs (Girling, 2018; Harrison et al., 2020; Kristunas et al., 2017; Martin et al., 2019) include the following: (i) we consider multilevel correlation structures in the context of binary outcomes arising from SW‐CRTs, including the nested exchangeable (NEX) and the exponential decay (ED) structure (Kasza et al., 2019; Li et al., 2021); while most previous efforts restrict to continuous outcomes with an overly simplified exchangeable correlation structure, the limitations of the exchangeable correlation structure for SW‐CRT applications have been pointed out by Taljaard et al. (2016) and Li et al. (2020); (ii) we study the implications of both the between‐cluster and within‐cluster imbalances in sizes, as opposed to previous efforts that exclusively focus on the between‐cluster variability; and (iii) we provide a comparison between the independence working correlation and the true working correlation and study the consequence of ignoring correlation estimation in SW‐CRTs with unequal cluster sizes. GEEs with independence working correlation structure has been studied, for example, in Wang et al. (2021) for designing SW‐CRTs, and in Thompson et al. (2020) for analyzing SW‐CRTs. Although the independence working assumption offers computational convenience and simplicity and is widely implemented in software, we will show that it can lead to dramatic efficiency loss in SW‐CRTs with unequal cluster sizes. Finally, we also introduce a computationally efficient Monte Carlo approach to estimate the sample size for SW‐CRTs with binary outcomes with unequal cluster sizes.

The outline of this paper is as follows. Section 2 reviews the individual‐level and cluster‐period‐level generalized estimating equations (GEEs) methods used to estimate treatment effect parameter in SW‐CRTs with binary outcomes. Section 3 defines the RE of unequal versus equal cluster‐period sizes for treatment effect estimation, and introduces a special result on RE under a three‐period SW design. Sections 4, 5, and 6 present our simulation design and results on RE in SW‐CRTs. We provide a Monte Carlo sample size method and demonstrate its application to our motivating trial in Section 7. Section 8 summarizes the key observations and discusses connections between this paper and the previous works.

2. MARGINAL MODELS FOR SW DESIGNS WITH BINARY OUTCOMES

2.1. Marginal model with individual‐level observations

We consider a cross‐sectional SW‐CRT with $I$ clusters and $J$ periods, where different sets of individuals are included in each period and their outcome measurements are taken at the end of that period. Let $y_{ijk}$ be the binary outcome of individual $k=1,\cdots ,n_{ij}$ from cluster $i=1,\cdots ,I$ during period $j=1,\text{…},J$. We assume a complete design so that outcomes are taken for all individuals in each period (Hemming et al., 2015). Let ${\mu }_{ijk}$ be the marginal mean outcome; the marginal model for an SW‐CRT was studied in Ford and Westgate (2020) and Li et al. (2018b) and relates the marginal mean to the period effect and treatment via the following generalized linear model:

$$g({\mu }_{ijk})={\beta }_j+X_{ij}\delta ,$$ (1)

where $g$ is a link function, ${\beta }_j$ is the $j$‐th time effect describing the secular trend, $X_{ij}$ is the treatment indicator that equals to 1 if cluster $i$ receives treatment during period $j$ and 0 otherwise, and $\delta$ denotes the treatment effect of interest. For example, if $g$ is chosen as the identity link, model (1) is a linear probability model and $\delta$ measures the time‐adjusted risk difference; if $g$ is chosen as the log link, model (1) is a log‐binomial model and $\exp (\delta )$ is interpreted as the time‐adjusted relative risk; and if $g$ is the canonical logit link, then model (1) is a logistic model and $\exp (\delta )$ is interpreted as the time‐adjusted odds ratio. In a marginal model, one only needs to specify the first two moments. For binary outcomes, we define the marginal variance function for each observation as ${\nu }_{ijk}={\mu }_{ijk}(1-{\mu }_{ijk})$. The within‐cluster correlation models are defined below.

Because outcomes in an SW‐CRT are correlated within each cluster, appropriate within‐cluster correlation structures are required to characterize their covariance. We consider two multilevel correlation structures developed for cross‐sectional SW‐CRTs: the NEX correlation structure (Li et al., 2018b) and the ED correlation structure (Kasza et al., 2019; Li et al., 2021). Both correlation structures distinguish between the within‐period and between‐period intraclass correlation coefficients (WP‐ICC and BP‐ICC) compared to the simple exchangeable correlation structure (Hussey & Hughes, 2007) and has been considered to be more realistic (Li et al., 2020; Taljaard et al., 2016). Under the NEX correlation structure, we define ${\alpha }_0$ as the WP‐ICC that measures the correlation between two outcomes from different individuals within the same cluster‐period, that is, $\text{corr}(y_{ijk},y_{ij{k}^{\prime }})={\alpha }_0$ for $k\ne k^{\prime }$. Further, we define the ${\alpha }_1$ as the BP‐ICC that measures the correlation between two outcomes from two different cluster‐periods, that is, $\text{corr}(y_{ijk},y_{i{j}^{\prime }{k}^{\prime }})={\alpha }_1$ for $j\ne j^{\prime }$, $k\ne k^{\prime }$. The cluster autocorrelation (CAC) can be represented by $\text{CAC}={\alpha }_1/{\alpha }_0$, which can be interpreted as the correlation between two population means from the same cluster at different times. Under the ED correlation structure, the WP‐ICC is still defined as ${\alpha }_0$, whereas the BP‐ICC is allowed to exponentially decay over time, that is, $\text{corr}(y_{ijk},y_{i{j}^{\prime }{k}^{\prime }})={\alpha }_0{\rho }^{|j-j^{\prime }|}$ for $j\ne j^{\prime }$, $k\ne k^{\prime }$ given the decay parameter $\rho \in [0,1]$. The CAC under the ED correlation structure is simply defined as $\text{CAC}=\rho$. In matrix notation, if we write ${\mathbf{Y}}_i={(y_{i11},y_{i12},\text{…},y_{iJ,n_{iJ}})}^T$ as the collection of outcomes in cluster $i$ ordered by period, the NEX correlation structure is given by

$$\text{corr}({\mathbf{Y}}_i)={\mathbf{R}}_i({\mathit{\alpha }}_{\mathrm{NEX}})=(1-{\alpha }_0){\mathbf{I}}_{n_i}+({\alpha }_0-{\alpha }_1){\oplus }_{j=1}^J{\mathbf{J}}_{n_{ij}}+{\alpha }_1{\mathbf{J}}_{n_i},$$

where ${\mathit{\alpha }}_{\mathrm{NEX}}={({\alpha }_0,{\alpha }_1)}^T$, ${\mathbf{I}}_s$ is the $s\times s$ identity matrix, ${\mathbf{J}}_s$ is the $s\times s$ matrix of ones, $n_i={\sum }_{j=1}^J{n}_{ij}$ is the $i$‐th cluster size, and “$\oplus$” is the block diagonal operator. With arbitrary cluster‐period sizes, there exists a closed‐form inverse of the NEX correlation matrix. We derive the explicit expression in Web Appendix A, which generalizes an earlier expression derived by Li et al. (2019) for $J=2$. On the other hand, the ED structure is given by

$$\text{corr}({\mathbf{Y}}_i)={\mathbf{R}}_i({\mathit{\alpha }}_{\mathrm{ED}})=(1-{\alpha }_0){\mathbf{I}}_{n_i}+{\alpha }_0\left\{{\mathbf{J}}_{n_i}*\mathbf{F}(\rho )\right\},$$

where ${\mathit{\alpha }}_{\mathrm{ED}}={({\alpha }_0,\rho )}^T$, $\mathbf{F}(\rho )$ is the $J\times J$ first‐order auto‐regressive (AR‐1) correlation matrix, “$*$” denotes the Khatri‐Rao product operator (Khatri & Rao, 1968) applied on each $n_{ij}\times n_{i{j}^{\prime }}$ block of ${\mathbf{J}}_{n_i}$ and each scalar element of $\mathbf{F}(\rho )$. Unlike the NEX structure, a closed‐form inverse of the ED correlation matrix is not available. Of note, the simple exchangeable correlation structure implied by the Hussey and Hughes (2007) model is obtained when ${\alpha }_1={\alpha }_0$ under the NEX structure or $\rho =1$ under the ED structure.

GEEs (Liang & Zeger, 1986) are often used to estimate the treatment effect parameter $\delta$ in marginal model (1). Defining ${\mathit{\mu }}_i={({\mu }_{i11},{\mu }_{i12},\text{…},{\mu }_{iJ,n_{iJ}})}^T$ as the collection of marginal means in cluster $i$ and mean model regression parameter $\mathit{\theta }={({\beta }_1,\text{…},{\beta }_J,\delta )}^T$, then the GEE with individual‐level observations is written as

$$\mathbf{U}(\mathit{\theta })=\sum _{i=1}^I{\mathbf{D}}_i^T{\stackrel{\sim }{\mathbf{M}}}_i^{-1}({\mathbf{Y}}_i-{\mathit{\mu }}_i(\mathit{\theta })),$$ (2)

where ${\mathbf{D}}_i=\partial {\mathit{\mu }}_i/\partial {\mathit{\theta }}^T$, ${\stackrel{\sim }{\mathbf{M}}}_i={\mathbf{A}}_i^{1/2}{\stackrel{\sim }{\mathbf{R}}}_i{\mathbf{A}}_i^{1/2}$ is the working variance, with ${\mathbf{A}}_i=\text{diag}\{{\nu }_{i11},{\nu }_{i12},\text{…},{\nu }_{iJ,n_{iJ}}\}$, and ${\stackrel{\sim }{\mathbf{R}}}_i$ as the working correlation model. When the working independence assumption is adopted and ${\stackrel{\sim }{\mathbf{R}}}_i={\mathbf{I}}_{n_i}$, the working correlation is misspecified when the truth is otherwise, either NEX or ED in the current study, but $\widehat{\delta }$ is still a consistent estimator of the treatment effect (Liang & Zeger, 1986). In this case, the large‐sample variance of $\widehat{\delta }$ can be obtained as the $(J+1,J+1)$‐th element of the sandwich variance matrix ${\mathbf{\Sigma }}_1^{-1}{\mathbf{\Sigma }}_0{\mathbf{\Sigma }}_1^{-1}$, where ${\mathbf{\Sigma }}_1^{-1}={({\sum }_{i=1}^I{\mathbf{D}}_i^T{\stackrel{\sim }{\mathbf{M}}}_i^{-1}{\mathbf{D}}_i)}^{-1}$ and ${\mathbf{\Sigma }}_0={\sum }_{i=1}^I{\mathbf{D}}_i^T{\stackrel{\sim }{\mathbf{M}}}_i^{-1}\text{cov}({\mathbf{Y}}_i){\stackrel{\sim }{\mathbf{M}}}_i^{-1}{\mathbf{D}}_i$. Alternatively, when ${\stackrel{\sim }{\mathbf{R}}}_i=\text{corr}({\mathbf{Y}}_i)\in \{{\mathbf{R}}_i({\mathit{\alpha }}_{\mathrm{NEX}}),{\mathbf{R}}_i({\mathit{\alpha }}_{\mathrm{ED}})\}$ and the correlation structure is correctly specified, ${\stackrel{\sim }{\mathbf{M}}}_i=\text{cov}({\mathbf{Y}}_i)$ and the large‐sample variance of $\widehat{\delta }$ can be obtained as the $(J+1,J+1)$‐th element of the model‐based variance matrix ${\mathbf{\Sigma }}_1^{-1}$. Details of the individual‐level GEE approaches that simultaneously estimate $\mathit{\theta }$ and ICC parameters were developed elsewhere (Preisser et al., 2008; Prentice, 1988; Li, 2020; Li et al., 2018b). The left column of Table 1 provides example matrix representations of different working correlation models, ${\stackrel{\sim }{\mathbf{R}}}_i$, for a hypothetical cluster with three periods.

TABLE 1.

Examples of the working correlation matrix for the individual‐level observations (left column) and the corresponding cluster‐period‐level working covariance matrix (right column) under the independence (IND), nested exchangeable (NEX), and exponential decay (ED) working assumptions. The illustration is based on a stepped wedge trial with $J=3$ periods and $(n_{i1},n_{i2},n_{i3})=(2,2,3)$ observations for cluster $i$ with ${\mathbf{Y}}_i={(y_{i11},y_{i12},y_{i21},y_{i22},y_{i31},y_{i32},y_{i33})}^T$

	${\stackrel{\sim }{\mathbf{R}}}_i=\text{corr}({\mathbf{Y}}_i)$	${\stackrel{\sim }{\mathbf{V}}}_i=\text{var}({\overline{\mathbf{Y}}}_i)$
IND	$\left(\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}\frac{{\nu }_{i1}}{2}& 0& 0\\ 0& \frac{{\nu }_{i2}}{2}& 0\\ 0& 0& \frac{{\nu }_{i3}}{3}\end{array}\right)$
NEX	$\left(\begin{array}{ccccccc}1& {\alpha }_0& {\alpha }_1& {\alpha }_1& {\alpha }_1& {\alpha }_1& {\alpha }_1\\ {\alpha }_0& 1& {\alpha }_1& {\alpha }_1& {\alpha }_1& {\alpha }_1& {\alpha }_1\\ {\alpha }_1& {\alpha }_1& 1& {\alpha }_0& {\alpha }_1& {\alpha }_1& {\alpha }_1\\ {\alpha }_1& {\alpha }_1& {\alpha }_0& 1& {\alpha }_1& {\alpha }_1& {\alpha }_1\\ {\alpha }_1& {\alpha }_1& {\alpha }_1& {\alpha }_1& 1& {\alpha }_0& {\alpha }_0\\ {\alpha }_1& {\alpha }_1& {\alpha }_1& {\alpha }_1& {\alpha }_0& 1& {\alpha }_0\\ {\alpha }_1& {\alpha }_1& {\alpha }_1& {\alpha }_1& {\alpha }_0& {\alpha }_0& 1\end{array}\right)$	$\left(\begin{array}{ccc}\frac{{\nu }_{i1}}{2}(1+{\alpha }_0)& \sqrt{{\nu }_{i1}{\nu }_{i2}}{\alpha }_1& \sqrt{{\nu }_{i1}{\nu }_{i3}}{\alpha }_1\\ \sqrt{{\nu }_{i1}{\nu }_{i2}}{\alpha }_1& \frac{{\nu }_{i2}}{2}(1+{\alpha }_0)& \sqrt{{\nu }_{i2}{\nu }_{i3}}{\alpha }_1\\ \sqrt{{\nu }_{i1}{\nu }_{i3}}{\alpha }_1& \sqrt{{\nu }_{i2}{\nu }_{i3}}{\alpha }_1& \frac{{\nu }_{i3}}{3}(1+2{\alpha }_0)\end{array}\right)$
ED	$\left(\begin{array}{ccccccc}1& {\alpha }_0& {\alpha }_0\rho & {\alpha }_0\rho & {\alpha }_0{\rho }^2& {\alpha }_0{\rho }^2& {\alpha }_0{\rho }^2\\ {\alpha }_0& 1& {\alpha }_0\rho & {\alpha }_0\rho & {\alpha }_0{\rho }^2& {\alpha }_0{\rho }^2& {\alpha }_0{\rho }^2\\ {\alpha }_0\rho & {\alpha }_0\rho & 1& {\alpha }_0& {\alpha }_0\rho & {\alpha }_0\rho & {\alpha }_0\rho \\ {\alpha }_0\rho & {\alpha }_0\rho & {\alpha }_0& 1& {\alpha }_0\rho & {\alpha }_0\rho & {\alpha }_0\rho \\ {\alpha }_0{\rho }^2& {\alpha }_0{\rho }^2& {\alpha }_0\rho & {\alpha }_0\rho & 1& {\alpha }_0& {\alpha }_0\\ {\alpha }_0{\rho }^2& {\alpha }_0{\rho }^2& {\alpha }_0\rho & {\alpha }_0\rho & {\alpha }_0& 1& {\alpha }_0\\ {\alpha }_0{\rho }^2& {\alpha }_0{\rho }^2& {\alpha }_0\rho & {\alpha }_0\rho & {\alpha }_0& {\alpha }_0& 1\end{array}\right)$	$\left(\begin{array}{ccc}\frac{{\nu }_{i1}}{2}(1+{\alpha }_0)& \sqrt{{\nu }_{i1}{\nu }_{i2}}{\alpha }_0\rho & \sqrt{{\nu }_{i1}{\nu }_{i3}}{\alpha }_0{\rho }^2\\ \sqrt{{\nu }_{i1}{\nu }_{i2}}{\alpha }_0\rho & \frac{{\nu }_{i2}}{2}(1+{\alpha }_0)& \sqrt{{\nu }_{i2}{\nu }_{i3}}{\alpha }_0\rho \\ \sqrt{{\nu }_{i1}{\nu }_{i3}}{\alpha }_0{\rho }^2& \sqrt{{\nu }_{i2}{\nu }_{i3}}{\alpha }_0\rho & \frac{{\nu }_{i3}}{3}(1+2{\alpha }_0)\end{array}\right)$

2.2. Marginal model with cluster‐period means

While the marginal model (1) provides a good basis for the design and analysis of SW‐CRTs with binary outcomes, the GEE procedure based on (2) may be computationally intensive as one needs to invert ${\stackrel{\sim }{\mathbf{M}}}_i$ and ${\stackrel{\sim }{\mathbf{R}}}_i$, which may have quite sizable dimensions as in Figure 1. To circumvent computationally challenges, Li et al. (2021) proposed a cluster‐period GEE approach. Specifically, we define the vector of cluster‐period means as

$${\overline{\mathbf{Y}}}_i={({\overline{Y}}_{ij},\text{…},{\overline{Y}}_{iJ})}^T={\left(\frac{1}{n_{i1}}\sum _{k=1}^{n_{i1}}{y}_{i1k},\text{…},\frac{1}{n_{iJ}}\sum _{k=1}^{n_{iJ}}{y}_{iJk}\right)}^T$$

and the marginal mean of ${\overline{\mathbf{Y}}}_i$ as ${\overline{\mathit{\mu }}}_i={({\mu }_{i1},\text{…},{\mu }_{iJ})}^T$. Then the individual‐level marginal mean model (1) can be equivalently represented by

$$g({\mu }_{ij})={\beta }_j+X_{ij}\delta ,$$ (3)

where ${\beta }_j$ and $\delta$ can preserve their original interpretations. The cluster‐period GEE is then represented as

$$\overline{\mathbf{U}}(\mathit{\theta })=\sum _{i=1}^I{\overline{\mathbf{D}}}_i^T{\stackrel{\sim }{\mathbf{V}}}_i^{-1}({\overline{\mathbf{Y}}}_i-{\overline{\mathit{\mu }}}_i),$$ (4)

where ${\overline{\mathbf{D}}}_i=\partial {\overline{\mathit{\mu }}}_i/\partial {\mathit{\theta }}^T$ and ${\stackrel{\sim }{\mathbf{V}}}_i$ is the working covariance matrix for the cluster‐period mean ${\overline{\mathbf{Y}}}_i$, which is only of dimension $J\times J$. In particular, the working variance ${\stackrel{\sim }{\mathbf{V}}}_i$ depends on the variance function, cluster‐period sizes as well as the working correlation structure. In parallel to Section 2.1, if ${\stackrel{\sim }{\mathbf{R}}}_i={\mathbf{I}}_{n_i}$ and the independence working assumption is adopted, then ${\stackrel{\sim }{\mathbf{V}}}_i=\text{diag}\{{\nu }_{i1}/n_{i1},\cdots ,{\nu }_{\mathrm{iJ}}/n_{\mathrm{iJ}}\}$, where ${\nu }_{ij}={\mu }_{ij}(1-{\mu }_{ij})$. Because the independence working correlation model is likely misspecified, the large‐sample variance of $\widehat{\delta }$ is obtained as the $(J+1,J+1)$‐th element of the sandwich variance matrix ${\overline{\mathbf{\Sigma }}}_1^{-1}{\overline{\mathbf{\Sigma }}}_0{\overline{\mathbf{\Sigma }}}_1^{-1}$, where ${\overline{\mathbf{\Sigma }}}_1^{-1}={({\sum }_{i=1}^I{\overline{\mathbf{D}}}_i^T{\stackrel{\sim }{\mathbf{V}}}_i^{-1}{\overline{\mathbf{D}}}_i)}^{-1}$ and ${\overline{\mathbf{\Sigma }}}_0={\sum }_{i=1}^I{\overline{\mathbf{D}}}_i^T{\stackrel{\sim }{\mathbf{V}}}_i^{-1}\text{cov}({\overline{\mathbf{Y}}}_i){\stackrel{\sim }{\mathbf{V}}}_i^{-1}{\overline{\mathbf{D}}}_i$. On the other hand, if the working correlation structure is the NEX or ED structure, the $j$‐th diagonal element of ${\stackrel{\sim }{\mathbf{V}}}_i$ is $\text{var}({\overline{Y}}_{ij})={\nu }_{ij}\{1+(n_{ij}-1){\alpha }_0\}/n_{ij}$. Furthermore, the $(j,j^{\prime })$‐th off‐diagonal element of ${\stackrel{\sim }{\mathbf{V}}}_i$ is $\text{cov}({\overline{Y}}_{ij},{\overline{Y}}_{i{j}^{\prime }})=\sqrt{{\nu }_{ij}{\nu }_{i{j}^{\prime }}}{\alpha }_1$ under the NEX correlation structure, and $\text{cov}({\overline{Y}}_{\mathrm{ij}},{\overline{Y}}_{i{j}^{\prime }})=\sqrt{{\nu }_{\mathrm{ij}}{\nu }_{i{j}^{\prime }}}{\alpha }_0{\rho }^{|j-j^{\prime }|}$ under the ED correlation structure. In these cases, if the working correlation model is also correctly specified, then the large‐sample variance of $\widehat{\delta }$ is obtained as the $(J+1,J+1)$‐th element of the model‐based variance matrix ${\overline{\mathbf{\Sigma }}}_1^{-1}$. In particular, the cluster‐period GEE approach for simultaneously estimating $\mathit{\theta }$ and ICCs based on cluster‐period means was developed in Li et al. (2021). The right column of Table 1 provides example matrix representations of different working variance models, ${\stackrel{\sim }{\mathbf{V}}}_i$, for a hypothetical cluster of three periods.

For numerically evaluating RE for marginal analyses of SW‐CRTs under unequal cluster sizes, we will make use of the following Theorem 2.1 established in Li et al. (2021).

Theorem 2.1

(Li et al., 2021) With the same choice of working correlation model ${\stackrel{\sim }{\mathbf{R}}}_i$ (independence, NEX, or ED) and compatible marginal mean models (1) and (3), the individual‐level GEE and the cluster‐period GEE have the same model‐based variance and the sandwich variance, even under unequal cluster‐period sizes. In other words, ${\overline{\mathbf{\Sigma }}}_0={\mathbf{\Sigma }}_0$, and ${\overline{\mathbf{\Sigma }}}_1={\mathbf{\Sigma }}_1$, regardless of the cluster‐period size distribution.

Theorem 2.1 shows that there is no loss of asymptotic efficiency by replacing the individual‐level GEE with the cluster‐period GEE under unequal cluster‐period sizes, and doing so simplifies the computation of RE for estimating $\delta$. For this reason, we will define RE in Section 3 based on the cluster‐period GEE. As will be seen in due course, the computation associated with the cluster‐period GEE is much faster given we only need to invert a $J\times J$ matrix ${\stackrel{\sim }{\mathbf{V}}}_i$ rather than the $({\sum }_{j=1}^J{n}_{ij})\times ({\sum }_{j=1}^J{n}_{ij})$ matrix ${\stackrel{\sim }{\mathbf{M}}}_i$. This insight also motivates the computationally efficient Monte Carlo sample size approach for SW‐CRTs with binary outcomes in Section 7.

3. RE OF UNEQUAL VERSUS EQUAL CLUSTER SIZES

We define RE as the relative variance of the treatment effect estimator based on the cluster‐period GEE under unequal versus equal cluster sizes. For equal cluster sizes, we only consider the scenarios where all cluster‐period sizes are equal. For unequal cluster size scenarios, we consider two types of cluster‐period size variability: (i) the cluster‐period sizes are the same within each cluster, but differ across clusters (between‐cluster imbalance) and (ii) the cluster‐period sizes are different both within each cluster and across clusters (between–within‐cluster imbalance). Let ${\mathbf{\Omega }}_{\text{equal}}$ denote a design with equal cluster sizes, and ${\mathbf{\Omega }}_{\text{unequal}}$ denote a design with unequal cluster‐period sizes. The RE of equal to unequal cluster sizes is written as

$$\text{RE}(\widehat{\delta })=\frac{\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{equal}})}{\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{unequal}})},$$ (5)

where the variance of $\widehat{\delta }$ can be the model‐based or sandwich variance, depending on the choice of the working correlation structure. With a continuous outcome and identity link function, the asymptotic variances of the treatment effect estimator based on GEE and linear mixed model coincide (Li et al., 2018b), and the analytical results on RE developed in Girling (2018) can be applied. However, binary outcomes have an explicit mean–variance relationship and therefore generally prohibit an analytical derivation of a scalar variance expression. Therefore, we will numerically study the trends and magnitude of RE under a variety of design configurations in Sections 4, 5, and 6.

While a simple analytical expression for RE is intractable with binary outcomes, we are able to obtain an interesting result on RE under the basic three‐period design, when the treatment effect is estimated under working independence assumption. We summarize the result in Theorem 3.1, with the detailed derivations in Web Appendix B.

Theorem 3.1

In an SW design with three time periods and hence two treatment sequences, the GEE estimator $\widehat{\delta }$ assuming working independence is equal to

$$\widehat{\delta }=\mathrm{logit}\left\{\frac{{\sum }_{i=1}^I{X}_{i2}{\overline{Y}}_{i2}}{{\sum }_{i=1}^I{X}_{i2}}\right\}-\mathrm{logit}\left\{\frac{{\sum }_{i=1}^I(1-X_{i2}){\overline{Y}}_{i2}}{{\sum }_{i=1}^I(1-X_{i2})}\right\}.$$ (6)

Further, if the true correlation structure is either NEX or ED, the sandwich variance of the cluster‐period GEE estimator $\widehat{\delta }$ assuming working independence is given in closed‐form by

$$\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{unequal}})=\frac{(b_1^{2}e-2b_1^{2}b{e}_1+b^2{e}_1){\alpha }_0+b_1{b}^2-b_1^{2}b}{{(b_{1}b-b_1^2)}^2},$$ (7)

where $b={\sum }_{i=1}^I{\nu }_{i2}{n}_{i2}$, $b_1={\sum }_{i=1}^I{X}_{i2}{\nu }_{i2}{n}_{i2}$, $e={\sum }_{i=1}^I{\nu }_{i2}{n}_{i2}(n_{i2}-1)$, $e_1={\sum }_{i=1}^I{X}_{i2}{\nu }_{i2}{n}_{i2}(n_{i2}-1)$, and ${\nu }_{ij}={\mu }_{ij}(1-{\mu }_{ij})$ is the variance function for binary outcomes. Further, estimator (6) represents a between‐cluster comparison at the second period; correspondingly, variance (7) does not involve the BP‐ICC, or any information from the first or third period.

Theorem 3.1 suggests that the treatment effect estimator (in log odds ratio) obtained from the independence GEE only depends on the cluster‐period mean of the outcome and the treatment indicators in the second (middle) period. In other words, the three‐period SW design contains the same amount of information as a parallel‐arm design (by only keeping the second period) under the independence working correlation. The variance of the treatment effect estimator obtained from the independence GEE thus only depends on WP‐ICC, the treatment indicator, cluster‐period sizes, and marginal variance of the outcome in the second period. This result is intuitive because all clusters receive the same intervention during the first and third periods and there is no effective information for a between‐cluster comparison, whereas the independence GEE heavily relies on between‐cluster comparisons. Furthermore, assuming equal cluster‐period sizes, we can obtain $\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{equal}})$ by setting $n_{i2}=n$ for all $i$ in (7). Because both $\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{unequal}})$ and $\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{equal}})$ depend on the correlation structure only through ${\alpha }_0$, the RE under the independence working assumption does not vary as a function of ${\alpha }_1$ (under the NEX structure) or $\rho$ (under the ED structure). This RE is also unaffected by any changes in cluster‐period sizes during the first and third periods. Collectively, these observations suggest that the RE under the independence working assumption is invariable to correlation decay or the magnitude of CAC in a three‐period design.

While Theorem 3.1 is simple and intuitive, it does not easily extend to cases where the working correlation structure is correctly specified as the NEX or ED structure, or where there are more than three periods. For instance, the main challenge in deriving more general forms of the variance of treatment effect estimator under working independence is due to the challenge of analytically inverting an unstructured $J\times J$ matrix for $J\ge 4$. In what follows, we will numerically evaluate the RE under a wide range of design configurations representing more general cases.

4. SIMULATION DESIGN

For binary outcomes, we investigate RE defined in (5) under standard and complete SW designs, where an equal number of clusters transition from control to intervention at each step. We consider two types of true correlation structures: NEX and ED, defined in Section 2. We study RE assuming a correctly specified working correlation structure as well as an incorrectly specified independence working correlation structure (IND). In the former case, $\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{unequal}})$ and $\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{equal}})$ are given by the model‐based variance, whereas in the latter case, $\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{unequal}})$ and $\text{var}(\widehat{\delta }|{\mathbf{\Omega }}_{\text{equal}})$ are given by the sandwich variance. Other design factors we consider include number of clusters $I$, number of periods $J$, and the degree and type of cluster size variability; other model factors we consider include the true mean model coefficients determining the baseline prevalence, secular trend and the treatment effect, as well as the true ICC parameters ${\mathit{\alpha }}_{\mathrm{NEX}}$ and ${\mathit{\alpha }}_{\mathrm{ED}}$ for the respective true correlation structures. For each parameter combination, we will simulate two designs: one with equal cluster sizes, ${\mathbf{\Omega }}_{\mathrm{equal}}$, and one with unequal cluster sizes, ${\mathbf{\Omega }}_{\mathrm{unequal}}$, and numerically compute RE. The distributions of RE are then summarized across 1000 simulation runs. Of note, there are a few cases where the maximum RE exceeds 1 especially when the number of clusters is small. This is closely related to the optimal SW design results obtained in Lawrie et al. (2015), Li et al. (2018a), and Matthews (2020), who suggested that an SW‐CRT could be made more efficient by allocating larger sample sizes to the first and last treatment sequences. To minimize confusion, we follow Martin et al. (2019) and present the median and interquartile range (IQR) of REs for each scenario. Source code to reproduce the simulation results is available as Supporting Information on the journal's web page.

We consider number of clusters, $I\in \{12,24,48,96\}$, with $I=24$ resembling the Washington State EPT trial. We consider $J\in \{3,5,13\}$ periods such that $I$ is divisible by the number of steps $J-1$. For example, when $I=24$ ad $J=13$, we assume $I/(J-1)=2$ randomly selected clusters switch from control to intervention during each post‐baseline period.

To simulate unequal cluster sizes, we first consider the simplified scenario with only between‐cluster imbalance, but homogeneous cluster‐period sizes within each cluster. To do so, we assume $n_{i1}=\cdots =n_{iJ}={\overline{n}}_i$ for each cluster $i$, and generate ${\overline{n}}_i\sim \text{Gamma}(\text{shape}={\text{CV}}^{-2},\text{rate}={\overline{n}}^{-1}{\text{CV}}^{-2})$, where $\overline{n}=\mathrm{E}({\overline{n}}_i)$ is the mean cluster‐period sizes and CV is the coefficient of variation. We focus on $\overline{n}=100$; results for $\overline{n}\in \{50,300\}$ are discussed in Section 5.5. The between‐cluster imbalance is measured by $\text{CV}\in \{0.25,0.5,0.75,1,1.25,1.5\}$; these values were also explored in Martin et al. (2019) and Harrison et al. (2020) for continuous outcomes under simpler correlation structures. For computational stability, we round each ${\overline{n}}_i$ to the nearest integer and set 5 as the lower bound. To ensure better comparability between the two designs, ${\mathbf{\Omega }}_{\text{unequal}}$ and ${\mathbf{\Omega }}_{\text{equal}}$, we scaled the simulated cluster‐period sizes proportionally such that the total number of observations across all cluster‐periods is around $IJ\overline{n}$. This procedure minimizes the difference in total sample size between ${\mathbf{\Omega }}_{\mathrm{equal}}$ and ${\mathbf{\Omega }}_{\mathrm{unequal}}$, which then guarantees the difference between the variance of estimated treatment effect under various designs is only attributable to the variability in cluster sizes rather than total sample size.

We further consider between‐within cluster imbalance by allowing the cluster‐period size to vary within each cluster. Conditional on the simulated mean cluster‐period sizes ${\overline{n}}_i$, we generate the actual cluster‐period sizes $(n_{i1},\text{…},n_{iJ})$ from a truncated multinomial distribution with total number of trials $J{\overline{n}}_i$ and a prespecified probability vector $(p_1,\text{…},p_J)$, where ${\sum }_{j=1}^J{p}_j=1$. The truncated multinomial distribution is used to ensure the smallest cluster‐period size is at least 2. The following four different specifications of $(p_1,\text{…},p_J)$ represent four different recruitment patterns that lead to unequal cluster‐period sizes:

• 1.Constant: $p_1=p_2=\cdots =p_J$. This pattern assumes the absence of any systematic variation of cluster‐period sizes for each cluster; any variation in cluster‐period sizes is only due to chance in balanced multinomial sampling;
• 2.Monotonically increasing: $p_1<p_2<\text{…}<p_J$. This pattern assumes that there is an increasing effort in recruitment leading to larger cluster‐period sizes at the later time periods. Specifically, we define a difference parameter $d$ such that $p_j=p_1+(j-1)\times d$ with $j=1,\text{…},J$. With the initial probability $p_1$ known, $d=2(1-J{p}_1)/\{J(J-1)\}$;
• 3.Monotonically decreasing: $p_1>p_2>\text{…}>p_J$. This pattern assumes a scenario where recruitment of patients become more challenging over time and the cluster‐period sizes on average decrease at the later time periods. Operationally, this is done by reversing the corresponding vector obtained under the monotonically increasing pattern;
• 4.Randomly permuted: $\text{perm}\{p_1<p_2<\text{…}<p_J\}$. A probability vector $(p_1,\text{…},p_J)$ that satisfies the monotonically increasing pattern is obtained. Then a random permutation of $(p_1,\text{…},p_J)$ is used to simulate cluster‐period sizes for each cluster. This pattern yields a more chaotic and nonmonotone within‐cluster imbalance.

When simulating the four patterns of between–within‐cluster imbalance, we specify $p_1=\{0.2,0.1,0.05\}$ for $J=\{3,5,13\}$, respectively. Besides cluster‐period sizes $n_{ij}$ in the case of unequal cluster sizes, no other data are simulated considering that ${\overline{\mathbf{\Sigma }}}_0$ and ${\overline{\mathbf{\Sigma }}}_1$ are computed using analytical calculations.

Finally, we choose several typical model parameters for our evaluation. We assume the logistic marginal mean model where the baseline prevalence $\exp ({\beta }_1)/\{1+\exp ({\beta }_1)\}=0.3$, and no true secular trend such that ${\beta }_1=\cdots ={\beta }_J$. Results with a smaller baseline prevalence 0.1, increasing or decreasing secular trend are presented in Section 5.6. We assume the intervention effect $\exp (\delta )=0.35$; results under a smaller nonnull intervention effects are compared with the previous $\delta =\log (0.35)$ in Section 5.6. For the true ICC parameters under the NEX or ED correlation structures, we consider the WP‐ICC ${\alpha }_0\le 0.2$, corresponding to the common range of reported ICCs in CRTs (Martin et al., 2016; Murray & Blitstein, 2003; Preisser et al., 2007). Under both correlation structures, we consider values of ${\alpha }_1$ or $\rho$ such that the BP‐ICC is positive and does not exceed the WP‐ICC ${\alpha }_0$ (or equivalently, $0<\text{CAC}\le 1$). Of note, there are natural restrictions of the range of plausible correlation parameters based on the marginal mean, and we have ensured that all combinations of ${\alpha }_0$, ${\alpha }_1$, or $\rho$ used in the scenarios do not violate those restrictions. The specific restrictions of correlation parameters are defined in Qaqish (2003) and reinterpreted under the NEX correlation structure as

$$\begin{array}{cc}& \max \left\{-\exp ({\beta }_j+X_{ij}\delta ),-\frac{1}{\exp ({\beta }_j+X_{ij}\delta )}\right\}\le {\alpha }_0\le 1,\forall i,j\hfill \end{array}$$ (8)

$$\begin{array}{cc}& \max \left\{-\exp \left(\frac{{\beta }_j+{\beta }_{j^{\prime }}}{2}+\frac{X_{ij}+X_{i{j}^{\prime }}}{2}\delta \right),-\exp \left(-\frac{{\beta }_j+{\beta }_{j^{\prime }}}{2}-\frac{X_{ij}+X_{i{j}^{\prime }}}{2}\delta \right)\right\}\le {\alpha }_1\hfill \\ & \le \min \left\{\exp \left(\frac{{\beta }_j-{\beta }_{j^{\prime }}}{2}+\frac{X_{ij}-X_{i{j}^{\prime }}}{2}\delta \right),\exp \left(-\frac{{\beta }_j-{\beta }_{j^{\prime }}}{2}-\frac{X_{ij}-X_{i{j}^{\prime }}}{2}\delta \right)\right\},\forall i,j\ne j^{\prime }.\hfill \end{array}$$ (9)

Because we specify ${\alpha }_0$ between 0 and 1, restriction (8) always holds and it is more critical to check (9). Furthermore, for the ED correlation structure, we modify restriction (9) by replacing ${\alpha }_1$ with ${\alpha }_0{\rho }^{|j-j^{\prime }|}$.

5. RESULTS WHEN THE TRUE CORRELATION STRUCTURE IS NEX

5.1. Cluster size variability

Figure 2 presents the median and IQR of RE as a function of CV with $I=12$ and 96 clusters and $J=5$ periods. The WP‐ICC, ${\alpha }_0$, is fixed at 0.05, and three values of $\text{CAC}\in \{0.02,0.5,1\}$ corresponding to the three values of BP‐ICC, ${\alpha }_1\in \{0.001,0.025,0.05\}$, are considered. We first focus on the between‐cluster imbalance as measured by the CV of the mean cluster‐period sizes ${\overline{n}}_i$, and assume no within‐cluster imbalance. When the working correlation structure is correctly specified as NEX, a larger CV leads to a small to moderate efficiency loss for estimating the treatment effect. For example, when $I=12$, the median RE is around 0.85 when $\text{CAC}=0.02$ and $\text{CV}=1$ in Figure 2(a). The IQR of RE increases as CV becomes larger, suggesting that the RE is more dispersed over repeated experiments with larger between‐cluster imbalance. Similar RE‐CV relationships are observed when the working correlation structure is IND; however, the efficiency loss in estimating the treatment effect is much more substantial. For example, when $I=12$, the median RE drops down to 0.63 when $\text{CAC}=0.02$ and $\text{CV}=1$ in Figure 2(c).

FIGURE 2.

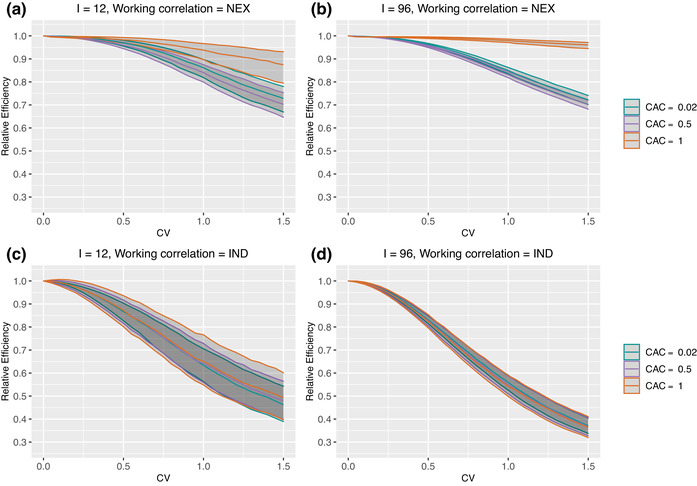
Median and IQR of relative efficiency when the true correlation model is NEX. Parameter specifications: number of clusters $I=12$ and 96, number of periods $J=5$, WP‐ICC is fixed at ${\alpha }_0=0.05$. No within‐cluster imbalance is introduced

In the presence of between‐cluster imbalance, the RE results are further impacted by the introduction of within‐cluster imbalance. Figure 3 presents the counterparts of Figure 2 under the within‐cluster imbalance pattern 4 (randomly permuted). Under the NEX working correlation structure, the RE further decreases and appears to be particularly sensitive to within‐cluster imbalance when $\text{CAC}=1$, that is, there is no correlation decay between periods. When ${\alpha }_1<{\alpha }_0$, the RE results are more robust to within‐cluster imbalance, with only a slightly lower median RE and slightly wider IQR at each CV compared to Figures 2(a) and 2(b). Under the IND working assumption, the RE, somewhat counterintuitively, increases after introducing the within‐cluster imbalance when $\text{CAC}=1$ given a fixed level of between‐cluster imbalance or CV. As the CAC deviates from 1 or ${\alpha }_1$ deviates from ${\alpha }_0$, the RE results become insensitive to within‐cluster imbalance. This sharp contrast between the behavior of RE under different working correlation models is further observed for other within‐cluster imbalance patterns (see Web Figures 1–3). Among the different within‐cluster imbalance patterns, pattern 1 (constant) corresponds to slightly larger RE compared to patterns 2–4, while any difference in RE across patterns 2–4 is negligible.

FIGURE 3.

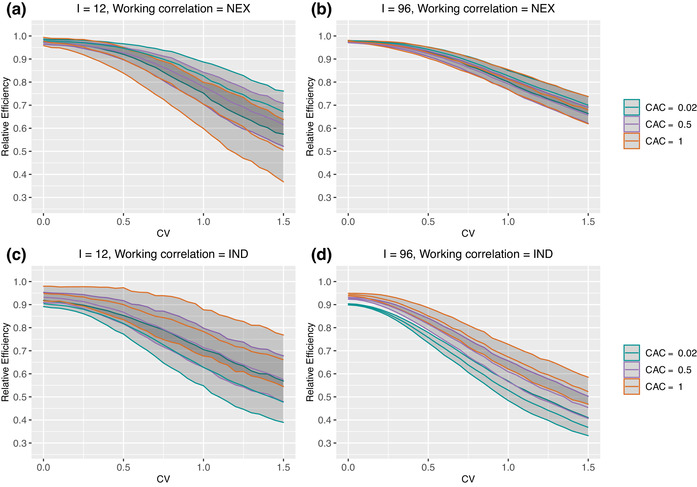
Median and IQR of relative efficiency when the true correlation model is NEX. Parameter specifications: number of clusters $I=12$ and 96, number of periods $J=5$, WP‐ICC is fixed at ${\alpha }_0=0.05$. Within‐cluster imbalance (pattern 4: randomly permuted) is introduced

5.2. ICCs

Figure 2 implies that the magnitude of ICCs can affect the median RE of the GEE analysis of SW trials due to unequal cluster sizes. To provide additional characterization of the RE–ICC relationship under the NEX working correlation structure, Figure 4 presents the median RE as a function of ${\alpha }_0\in \{0.01,0.05,0.1,0.2\}$ and $\text{CAC}\in [0,1]$, across $\text{CV}\in \{0.25,0.75,1.25\}$ but without within‐cluster imbalance. When the working correlation is correctly specified as NEX, the median RE increases with a larger WP‐ICC, when the CAC is small. However, when the BP‐ICC gets closer to the WP‐ICC or the CAC gets to 1, this relationship can be reversed. This is partly because the relationship between median RE and the CAC can be nonmonotone. For example, in Figure 4, the median RE increases monotonically with larger BP‐ICCs when the WP‐ICC is 0.01. However, when the CAC is at least 0.5, the median RE first sharply decreases and then gradually increases. Both Figures 2 and 4 suggest that the RE–CV relationship heavily depends on the difference between the WP‐ICC and the BP‐ICC, or the magnitude of CAC. When the CAC is equal to 1, namely, the true correlation model is simple exchangeable as implied by the classic Hussey and Hughes (2007) model, the efficiency loss due to unequal cluster sizes seems minimal. This agrees with the findings in Kristunas et al. (2017) and Martin et al. (2019), who restricted their investigations to the simple exchangeable correlation model. In general, however, the efficiency loss due to unequal cluster sizes becomes larger when CAC deviates from 1.

FIGURE 4.

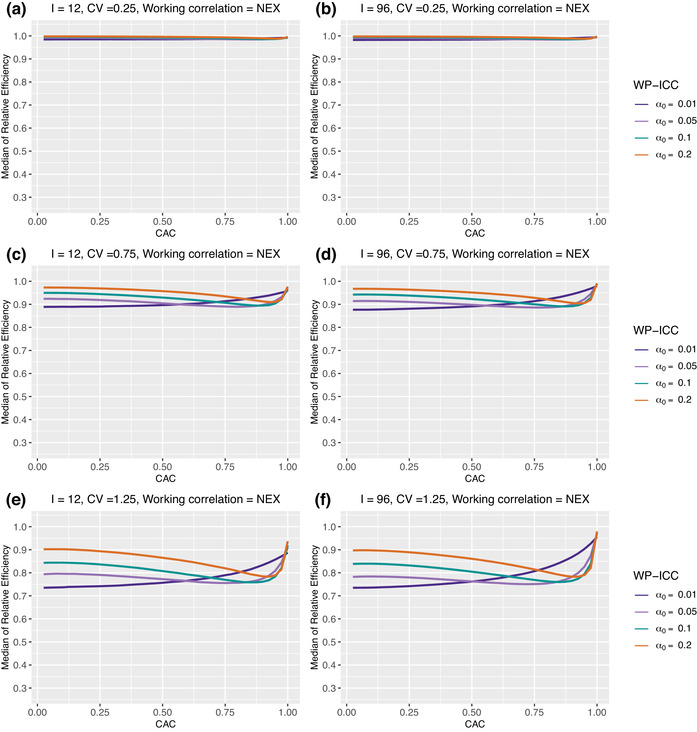
Median of relative efficiency when both the true correlation model and the working correlation model are NEX. Parameter specifications: number of clusters $I=12$ and 96, number of periods $J=5$, the degree of between‐cluster imbalance $\text{CV}\in \{0.25,0.75,1.25\}$. No within‐cluster imbalance is introduced

Web Figures 4–7 present the counterparts to Figure 4, with the introduction of the four within‐cluster imbalance patterns. As expected, the median RE becomes smaller when the cluster‐period sizes are different within each cluster. Of note, the median RE decreases most dramatically when $\text{CAC}=1$, suggesting that the simple exchangeable correlation model is most prone to efficiency loss as a result of within‐cluster imbalance, but is relatively robust to between‐cluster imbalance.

Figure 5 presents the counterpart of Figure 4 when the working correlation is IND. Different from the RE–ICC relationship under the NEX working correlation structure, the median RE monotonically decreases with a larger CAC under the IND working correlation structure. The median RE is also insensitive to CAC under the working independence assumption. This is not surprising, as in the special case of $J=3$ periods, Theorem 3.1 points out that the distribution of RE is independent of ${\alpha }_1$. However, the BP‐ICC, ${\alpha }_1$, plays a more prominent role in determining the RE in the presence of within‐cluster imbalance. For example, Web Figures 8–11 shows that, with different within‐cluster imbalance patterns, the median RE under the IND working structure becomes a mildly increasing function of the CAC, for fixed values of ${\alpha }_0$.

FIGURE 5.

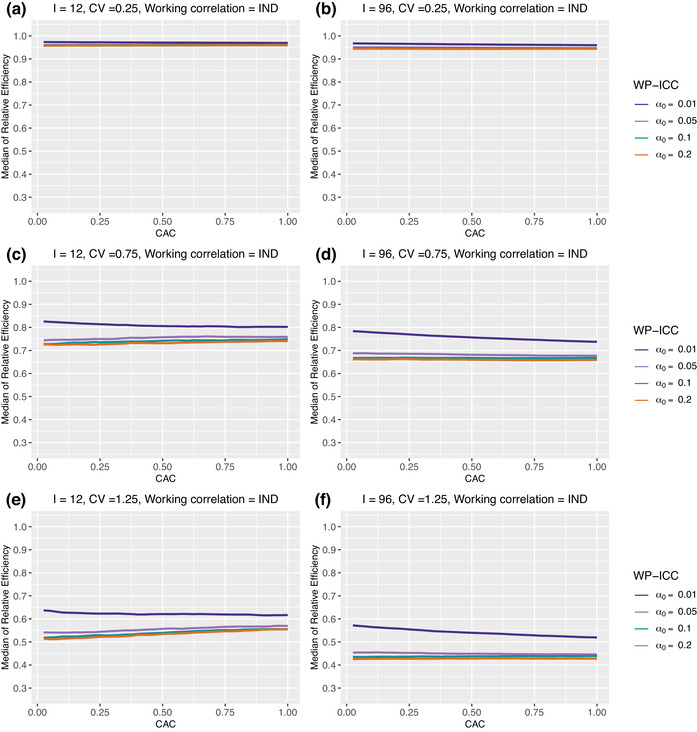
Median of relative efficiency when the true correlation model is NEX but the working correlation model is IND. Parameter specifications: number of clusters $I=12$ and 96, number of periods $J=5$, the degree of between‐cluster imbalance $\text{CV}\in \{0.25,0.75,1.25\}$. No within‐cluster imbalance is introduced

5.3. Number of clusters

Web Figure 12 presents the counterparts of Figure 2 but with $I=24$ and 48. When the working correlation structure is NEX, we observe a larger number of clusters $I$ leads to a more concentrated distribution of REs. When CAC is close to 1, or when the true correlation structure is nearly simple exchangeable, the median RE increases most notably when $I$ increases, indicating that a larger sample size effectively prevents efficiency loss due to between‐cluster imbalance in the absence of between‐period correlation decay. The change in median RE due to larger $I$, however, is almost negligible as CAC deviates from 1. The same pattern persists even after the introduction of within‐cluster imbalance. On the other hand, the impact of number of clusters on RE is completely different when the working correlation structure is IND. When $I$ increases from 12 to 96, even though the IQR of RE becomes smaller, the median RE decreases especially when CAC is large. This suggests that a larger SW trial is more susceptible to efficiency loss due to between‐cluster imbalance if it is analyzed by an independence GEE, and when the CAC is not negligible. The same pattern persists after introducing the within‐cluster imbalance, and we conclude that ignoring ICC estimation induces the greatest efficiency loss when both $I$ and CAC become large.

5.4. Number of periods

Table 2 summarizes the median and IQR of RE as a function of different number of periods $J$ and CV under two different working correlation specifications, with and without the within‐cluster imbalance, when there are $I=24$ clusters (mimicking the Washington State EPT study). For illustration, we choose ${\alpha }_0=0.05$ and $\text{CAC}=0.5$. We omitted the within‐cluster imbalance pattern 3 (monotonically decreasing), because the RE results are almost identical to those under pattern 2 (monotonically increasing). As long as the working correlation is NEX, the number of periods $J$ has negligible effect on the median and IQR of REs. The results are also not sensitive to within‐cluster imbalance. However, when the IND working correlation structure is considered, although the number of periods has minimum effect on RE with only between‐cluster imbalance, a trial with a longer duration can partially mitigate the efficiency loss in the presence of additional within‐cluster imbalance. The median and IQR of RE can increase substantially with a larger $J$ under any of the within‐cluster imbalance patterns, when there is already moderate to large between‐cluster imbalance. Web Tables 1 to 3 present the corresponding results with $I=12$, $48$, and 96 and the conclusions are identical.

TABLE 2.

Median and IQR (in parentheses) of relative efficiency when the true correlation model is NEX. Parameter specifications: number of clusters $I=24$, WP‐ICC ${\alpha }_0$ is 0.05, and the CAC is 0.5

Working	$J$	CV	No within‐cluster	Within‐cluster	Within‐cluster	Within‐cluster
correlation			imbalance	imbalance pattern 1	imbalance pattern 2	imbalance pattern 4
NEX	3	0.25	0.988 (0.985, 0.991)	0.986 (0.974, 0.996)	0.964 (0.953, 0.975)	0.963 (0.951, 0.975)
		0.75	0.901 (0.880, 0.919)	0.888 (0.833, 0.930)	0.864 (0.816, 0.905)	0.862 (0.815, 0.905)
		1.25	0.762 (0.724, 0.796)	0.726 (0.648, 0.796)	0.716 (0.640, 0.786)	0.703 (0.622, 0.779)
	5	0.25	0.988 (0.986, 0.991)	0.986 (0.977, 0.995)	0.958 (0.949, 0.966)	0.959 (0.949, 0.967)
		0.75	0.903 (0.882, 0.920)	0.888 (0.849, 0.923)	0.865 (0.824, 0.898)	0.864 (0.820, 0.905)
		1.25	0.765 (0.730, 0.798)	0.725 (0.659, 0.785)	0.705 (0.639, 0.765)	0.708 (0.647, 0.773)
	13	0.25	0.989 (0.986, 0.991)	0.985 (0.981, 0.988)	0.975 (0.971, 0.978)	0.977 (0.972, 0.980)
		0.75	0.905 (0.886, 0.922)	0.878 (0.851, 0.902)	0.868 (0.841, 0.889)	0.872 (0.847, 0.895)
		1.25	0.770 (0.735, 0.802)	0.703 (0.661, 0.744)	0.697 (0.653, 0.741)	0.696 (0.655, 0.741)
IND	3	0.25	0.955 (0.945, 0.964)	0.958 (0.942, 0.972)	0.878 (0.863, 0.892)	0.880 (0.865, 0.896)
		0.75	0.721 (0.673, 0.763)	0.767 (0.696, 0.831)	0.693 (0.629, 0.756)	0.700 (0.643, 0.756)
		1.25	0.501 (0.440, 0.560)	0.591 (0.508, 0.659)	0.532 (0.464, 0.611)	0.523 (0.453, 0.604)
	5	0.25	0.954 (0.937, 0.972)	0.971 (0.944, 0.994)	0.899 (0.878, 0.919)	0.903 (0.881, 0.928)
		0.75	0.722 (0.656, 0.776)	0.818 (0.751, 0.887)	0.760 (0.696, 0.816)	0.760 (0.689, 0.824)
		1.25	0.502 (0.430, 0.564)	0.639 (0.554, 0.725)	0.593 (0.513, 0.671)	0.593 (0.505, 0.681)
	13	0.25	0.953 (0.927, 0.978)	0.987 (0.973, 1.000)	0.975 (0.961, 0.988)	0.973 (0.957, 0.989)
		0.75	0.714 (0.641, 0.783)	0.909 (0.866, 0.945)	0.891 (0.847, 0.928)	0.891 (0.851, 0.928)
		1.25	0.492 (0.416, 0.573)	0.778 (0.714, 0.839)	0.770 (0.694, 0.832)	0.770 (0.700, 0.825)

5.5. Cluster‐period size

Web Figures 13 and 14 present the counterparts to Figure 4 but with the mean cluster‐period sizes $\overline{n}\in \{50,300\}$. As the mean cluster‐period size increases from 50 to 300, the median RE under the NEX working correlation model increase when the WP‐ICC is at least 0.05, and decreases when the WP‐ICC is 0.01. This pattern is mostly apparent when the degree of between‐cluster imbalance is large ($\text{CV}=1.25$), or there are a large number of clusters ($I=96$). When the within‐cluster imbalance patterns are introduced, we observed similar trends (see Web Figures 15 and 16). Web Figures 17 and 18 present the counterparts to Figure 5 with mean cluster‐period sizes $\overline{n}\in \{50,300\}$. Under the IND working correlation, the median RE simply decreases as the mean cluster‐period sizes increases, signaling additional efficiency loss under unequal cluster sizes with a larger total sample size. Findings remain the same when within‐cluster imbalance patterns are introduced, as in Web Figures 19 and 20.

5.6. Sensitivity to baseline prevalence, intervention effect, and secular trend

As a sensitivity analysis with limited scope, we also explored the impact of other model factors on the RE under the NEX and IND working correlation structures. We considered a smaller baseline prevalence ${\{1+\exp (-{\beta }_1)\}}^{-1}=0.1$, a smaller intervention effect OR, $\exp (\delta )=0.75$, and an increasing or decreasing secular trend. Specifically, we explore a gently increasing secular trend such that

$${\{1+\exp (-{\beta }_j)\}}^{-1}=\{1+0.2(j-1)/(J-1)\}\times {\{1+\exp (-{\beta }_1)\}}^{-1},j=1,\text{…},J,$$

as well as a gently decreasing secular trend such that

$${\{1+\exp (-{\beta }_j)\}}^{-1}=\{1-0.2(j-1)/(J-1)\}\times {\{1+\exp (-{\beta }_1)\}}^{-1},j=1,\text{…},J.$$

We did not consider a more dramatic secular trend as a recent reanalysis of the Washington State EPT trial suggests minimal secular trend (Li et al., 2021). Web Tables 4 to 11 each present the median and IQR of RE under a factorial combination of 2 levels of baseline prevalence $\times$ 2 levels of intervention effect $\times$ 3 different secular trends $\times$ 3 degrees of between‐cluster imbalance (36 cells in total), while holding the number of clusters constant. Relative to the factors described in the preceding texts, the impact of a smaller baseline prevalence, a smaller intervention effect, or nonconstant secular trend generally have negligible additional impact on the efficiency loss due to unequal cluster sizes, regardless of the specification of working correlation structures.

6. RESULTS WHEN THE TRUE CORRELATION STRUCTURE IS ED

In Web Appendix D, we present the results on RE when the underlying true correlation structure is ED, in parallel to results elaborated in Section 5. Under the ED correlation structure, we use $\rho$ to measure the degree of BP‐ICC decay, or CAC. Generally, we find that all the observed relationships between RE and key design and model factors are similar regardless of whether the true correlation structure is NEX or ED. For example, Web Figures 21 and 26 present highly similar RE–CV relationships to those in Figures 2 and 3. Surprisingly, while the exact value of the asymptotic variances can be quite different when the true correlation structure is NEX versus ED as studied in Kasza et al. (2019) under equal cluster sizes and with a continuous outcome, the impact of unequal cluster sizes measured by the median RE turns out to be highly similar across the two true correlation models in our evaluations with binary outcomes.

7. A MONTE CARLO PROCEDURE FOR SAMPLE SIZE CALCULATION

The RE of the treatment effect estimator has important implications for designing SW‐CRTs. In particular, our simulation procedure suggests a Monte Carlo power calculation procedure for SW‐CRTs with unequal cluster sizes and binary outcomes. Here we present this procedure as an extension to the sample size method developed in Li et al. (2018b), which assumes equal cluster‐period sizes.

Suppose we are interested in testing the null $H_0:\delta =0$ versus the alternative $H_1:\delta =\mathrm{\Delta }$ for some target effect size with odds ratio, $\exp (\mathrm{\Delta })$. Conditional on a specific design $\mathbf{\Omega }$, for a prescribed type I error rate ${\epsilon }_1$ and type II error rate ${\epsilon }_2$, the required number of clusters based on a $t$‐test to achieve $100(1-{\epsilon }_2)\%$ power satisfies the following generic inequality:

$$\begin{array}{c}\hfill I\ge \frac{{(t_{{\epsilon }_1/2,I-2}+t_{{\epsilon }_2,I-2})}^2{\sigma }^2(\mathbf{\Omega })}{{\mathrm{\Delta }}^2},\end{array}$$ (10)

where $t_{\epsilon ,I-2}$ is the $\epsilon$‐quantile of the $t$‐distribution with $I-2$ degree of freedom, and ${\sigma }^2(\mathbf{\Omega })=I\text{var}(\widehat{\delta }|\mathbf{\Omega })$ is the scaled variance of the intervention effect estimator. While other choices of the degrees of freedom are possible, we focus on the $I-2$ degrees of freedom because a number of previous simulation studies indicated adequate control of test size with a small number of clusters (Ford & Westgate, 2020; Li, 2020; Li et al., 2021). Given $\mathrm{\Delta }$, the required number of clusters $I$ is the smallest number such that (10) holds. Equivalently, (10) can be represented based on the minimum detectable effect size,

$$|\mathrm{\Delta }|\ge |t_{{\epsilon }_1/2,I-2}+t_{{\epsilon }_2,I-2}|\sqrt{\text{var}(\widehat{\delta }|\mathbf{\Omega })},$$

where $\text{var}(\widehat{\delta }|\mathbf{\Omega })$ is implicitly a function of $I$. Therefore, sample size determination boils down to the determination of ${\sigma }^2(\mathbf{\Omega })$ or $\text{var}(\widehat{\delta }|\mathbf{\Omega })$, which can be a complicated nonlinear function of design and model parameters. Because the scalar expression of $\text{var}(\widehat{\delta }|\mathbf{\Omega })$ is generally difficult to obtain with binary outcomes and unequal cluster sizes, we propose the following Monte Carlo approach to compute the required sample size for cross‐sectional SW‐CRTs:

• 1.Given an initial choice of number of clusters $I_0$, number of periods $J$ specify the treatment‐by‐period diagram with the desired number of treatment sequences, and number of clusters per sequence. For the cases that $J-1$ is not a divisor of $I_0$, (i.e., the clusters cannot be evenly distributed across the treatment sequences), one can decide a priori the steps with more clusters crossing over.
• 2.Given the model parameters including the baseline prevalence, anticipated secular trend, and intervention effect, obtain the prevalence of outcomes for each cluster (per sequence) during each period according to the marginal mean model, that is, ${\mu }_{ij}=g^{-1}({\beta }_j+X_{ij}\delta )$.
• 3.Specify the degree of between‐cluster imbalance and/or within‐cluster imbalance (e.g., following the strategies in Section 4), and simulate the cluster‐period sizes $n_{ij}$ for all $I\times J$ cluster‐periods such that the mean cluster‐period size equals to $\overline{n}$. Each simulation replicate corresponds to a possible design with unequal cluster sizes, ${\mathbf{\Omega }}_{\text{unequal}}$. Repeat this steps for $R$ times, and record each design as ${\mathbf{\Omega }}_{\text{unequal}}^{(r)}$ for $r=1,\text{…},R$.
• 4.Given the assumptions on the ICC parameters, and each simulated design ${\mathbf{\Omega }}_{\text{unequal}}^{(r)}$, numerically compute ${\sigma }^2({\mathbf{\Omega }}_{\text{unequal}}^{(r)})$. Based on Theorem 2.1, ${\sigma }^2({\mathbf{\Omega }}_{\text{unequal}}^{(r)})$ is the $(J+1,J+1)$‐th element of the sandwich variance matrix ${\overline{\mathbf{\Sigma }}}_1^{-1}{\overline{\mathbf{\Sigma }}}_0{\overline{\mathbf{\Sigma }}}_1^{-1}$ when independence working correlation structure is used, and is the $(J+1,J+1)$‐th element of the sandwich variance matrix of ${\overline{\mathbf{\Sigma }}}_1^{-1}$ when the correct NEX or ED working correlation structure is used.
• 5.Obtain the mean variance as ${\overline{\sigma }}^2=R^{-1}{\sum }_{r=1}^R{\sigma }^2({\mathbf{\Omega }}_{\text{unequal}}^{(r)})$ and plug it into the Equation (10). Check to see if $I_0$ satisfies the inequality. If so, then $I_0$ clusters already provides adequate power, and one can try to see whether a smaller $I_1<I_0$ satisfies the inequality and further reduce the sample size. If the inequality fails to hold with $I_0$, set $I_1=\lceil {(t_{{\epsilon }_1,I-2}+t_{{\epsilon }_2,I-2})}^2{\overline{\sigma }}^2{\mathrm{\Delta }}^{-2}\rceil$ and repeat the above steps. This iterative process is repeated until the smallest $I$ is identified to satisfy the inequality in Equation (10).

In principle, the above Monte Carlo procedure is iterative as the variance of treatment effect estimator depends on the current number of clusters, and one needs to search for the smallest number of clusters to provide adequate power. However, because the variance under a specific design ${\sigma }^2({\mathbf{\Omega }}_{\text{unequal}}^{(r)})$ is computed based on the cluster‐period mean model according to Theorem 2.1, we only need to invert $J\times J$ matrices and the computational burden can be dramatically reduced, as evidenced by the feasibility of our simulation study. Additionally, the computational efficiency of the sample size procedure also depends on appropriate choice of an initial value $I_0$. For example, one could first assume equal cluster sizes and use the existing sample size procedure in Li et al. (2018b) to obtain the required number of clusters $I_{\mathrm{equal}}$, and then set $I_0=I_{\mathrm{equal}}$ to reduce the iterations needed for convergence. We provide an illustrative sample size calculation using this approach below. Sample R code to obtain the sample size in the following illustrative example is provided in the Supporting Information in the journal website.

7.1. Application to the Washington State EPT trial

As shown in Figure 1, the Washington State EPT trial randomized 22 LHJs over four steps and five periods. This is a cross‐sectional design and the primary outcome was chlamydia test positivity among women tested in sentinel clinics (Golden et al., 2015). Based on the cluster‐period sizes, the CV of mean cluster‐period sizes within each cluster can be computed as 0.99, which is considerable even in the range of CV tried in the simulation analysis. Given the set of design and model parameters, we aim to compute the required number of clusters $I$ such that the trial has $80\%$ power. We assume the mean cluster‐period size is $\overline{n}=305$, as informed by Figure 1. In the absence of intervention, we assume the marginal prevalence of chlamydia positivity is approximately $7.6\%$ at baseline and no secular trend. This is concordant with the empirical reanalysis of the Washington State EPT study in Li et al. (2021), which suggested minimum secular trend for this outcome. To further illustrate potential differences due to assumptions on ICC, we consider the NEX and ED true correlation structures discussed in Table 1 as well as a simple exchangeable correlation model with equal WP‐ICC and BP‐ICC. For all three correlation structures, we assume the WP‐ICC, ${\alpha }_0=0.007$. Under the NEX and ED correlation structures, we assume ${\alpha }_1={\alpha }_0/2=0.0035$ and $\rho =0.7$. These values are informed by the analysis results in Li et al. (2021). Similar to Golden et al. (2015), assuming a 0.05 type I error rate and target effect size in OR of $\exp (\mathrm{\Delta })=0.7$, we estimate the required number of LHJs to achieve at least $80\%$ power. When the estimated $I$ is not divisible by 4, we try to have balanced an allocation as possible, but prioritize the first and last steps over the middle steps as suggested in Lawrie et al. (2015), Li et al. (2018a), and Matthews (2020) for efficiency considerations. To implement our sample size procedure, we choose the initial value $I_0$ using the equal cluster size method in Li et al. (2018b). We consider four levels of between‐cluster imbalance measured by $\text{CV}\in \{0,0.25,0.75,1.25\}$, as well as three levels of within‐cluster imbalance as introduced in our simulation design. The estimated sample size assuming a correctly specified working correlation and its counterpart assuming an independence working correlation (in parentheses) are presented in Table 3. Of note, the Monte Carlo procedure converged in seconds.

TABLE 3.

Estimated number of clusters for the Washington State Expedited Partner Therapy trial as a function of between‐cluster imbalance measured by coefficient of variation (CV) and three different patterns of within‐cluster imbalance, when the true correlation structure is exchangeable, nested exchangeable, or exponential decay. The first number in each cell is the sample size estimate under correctly specified correlation structure, while the number in the parenthesis corresponds to the sample size estimate assuming working independence

True correlation structure	CV	No within‐cluster	Within‐cluster	Within‐cluster
		imbalance	imbalance pattern 2	imbalance pattern 4
Simple exchangeable	0	11 (31)	11 (32)	11 (33)
	0.25	11 (33)	12 (33)	12 (33)
	0.75	12 (43)	13 (38)	13 (38)
	1.25	13 (64)	17 (48)	17 (48)
Nested exchangeable	0	18 (25)	19 (26)	19 (27)
	0.25	18 (26)	19 (27)	19 (27)
	0.75	20 (34)	21 (32)	21 (32)
	1.25	24 (50)	26 (42)	26 (42)
Exponential decay	0	17 (27)	18 (28)	18 (29)
	0.25	18 (28)	18 (29)	18 (29)
	0.75	19 (37)	21 (34)	21 (34)
	1.25	22 (54)	26 (43)	26 (43)

Under the correctly specified working correlation structure, the sample size estimates are reasonably insensitive to between‐cluster imbalance as long as the CV does not exceed 0.75. The patterns for within‐cluster imbalance also have negligible impact on the sample size. Among different working correlation structures, the exchangeable working structure corresponds to the smallest sample size, which is expected because Li et al. (2018b) showed that larger BP‐ICC generally increases study power. In contrast, if the independence working correlation is considered, the sample size estimates can be substantially larger than their counterparts obtained under the correct working correlation structure. This is especially true when the BP‐ICC equals to the WP‐ICC. In fact, even with equal cluster‐period sizes, the sample size obtained under the independence working correlation structure is at least three‐fold of that obtained under the correctly‐specified exchangeable working correlation structure. The sample size estimates under working independence also rapidly inflate with larger between‐cluster imbalance, and appear less robust to unequal cluster sizes compared to those obtained under the correct correlation model. In the presence of within‐cluster imbalance or when the BP‐ICC deviates from the WP‐ICC, the sample size estimates based on independence GEE become smaller. Overall, assuming a correct working correlation model, a maximum of 17 LHJs (corresponding to the most extreme imbalance scenario) are needed to ensure $80\%$ power under the working exchangeable structure. If the true correlation structure is NEX or ED, a maximum of 26 LHJs are needed. To conclude, modeling the correlation structure in this trial protects against dramatic efficiency loss due to unequal cluster sizes, and leads to much smaller sample sizes compared to assuming working independence.

7.2. Practical considerations

As we see above, designing SW‐CRTs often requires additional assumptions relative to designing parallel‐arm CRTs, and can be even more complex when the primary endpoint is binary. By incorporating new assumptions on cluster size variability compared to that of Li et al. (2018b). To facilitate practical implementation, we provide suggestions on assumptions for each step as follows. In Step 1, we require assumptions on number of periods (and number of clusters per treatment sequence if not a standard SW‐CRT). Such assumptions are generally prespecified given the context of the specific intervention and anticipated trial duration. Step 2 requires assumptions on the baseline prevalence, anticipated secular trend, and the target effect size. While the baseline prevalence and the target effect size are conventional input parameters in almost any other sample size methods with a binary outcome (and are arguably more available), the secular trend is more challenging to specify. However, we should recognize that the variance expression of the treatment effect estimator can depend on the secular trend for binary outcomes, and our procedure fittingly provides an approach for checking sensitivity of sample size to such secular trends. In practice, one could start with assuming no secular trend, as in our simulation study, and then investigate whether the required number of clusters changes under an increasing or decreasing secular trend, depending on domain knowledge. In Step 3, the mean and variability of cluster‐period sizes can also heavily depend on each specific trial and may be obtained from historical or routinely collected information from the pool of clusters to be recruited. As we demonstrate in our simulation study and application, the impact of between‐cluster size variability is usually not substantial with the correct working correlation model unless CV exceeds 0.75. Furthermore, the within‐cluster variability has a noticeable effect on the required sample size only when the between‐cluster variability is large (e.g., CV larger than 1) under the correct working correlation model. Such rules of thumb are also useful to assess the necessity of incorporating cluster size variability into sample size estimation. In Step 4, we require ICC and CAC parameters for the NEX or ED correlation models. When historical or routinely collected binary data are available, one may obtain ICC and CAC estimates by fitting the computationally efficient cluster‐period GEE of Li et al. (2021). Otherwise, empirical studies that report ICC and CAC estimates for a wide range of outcomes are particularly helpful. As an example, a recent study by Korevaar et al. (2021) calculated ICC and CAC from the CLustered OUtcome Dataset bank to inform the design of future SW‐CRTs, albeit for continuous outcomes. We encourage and expect more such studies to address unique challenges with binary outcomes. Step 5 of our procedure does not require additional assumptions, and only performs iterative calculations based on the provided design assumptions.

8. DISCUSSION

In this paper, we investigate the RE of the GEE treatment effect estimator under unequal versus equal cluster sizes in SW‐CRTs with binary outcomes. Because all prior studies assumed a linear mixed model with continuous outcomes, our results complement existing knowledge by exploring the properties and caveats for marginal analysis of SW‐CRTs with binary outcomes. We assume a cross‐sectional design as in the Washington State EPT study, and consider two popular multilevel correlation structures: the NEX and ED structures. Both correlation structures include the simple exchangeable structure (e.g., as implied by the Hussey & Hughes, 2007, model) as a special case, but are considered more realistic (Taljaard et al., 2016).

The main message of our simulation findings can be summarized as follows. First, the GEE analysis with the correct working correlation structure is much less prone to efficiency loss under between‐cluster imbalance compared to the independence GEE, whose RE sharply decreases with a larger degree of between‐cluster imbalance. Second, the RE of GEE analysis with the true working correlation structure critically depends on the magnitude of the WP‐ICC as well as the amount of BP‐ICC decay from WP‐ICC. In particular, when BP‐ICC equals WP‐ICC, the efficiency loss due to between‐cluster imbalance is minimal but can be larger when within‐cluster imbalance is introduced. However, the efficiency loss due to between‐cluster imbalance becomes more notable once BP‐ICC deviates from WP‐ICC. The statement in Kristunas et al. (2017) that “(between‐cluster) imbalance in cluster size was not found to have a notable effect on the power of SW‐CRTs” belies the dependence of RE on ICC as they assumed the random intercept linear mixed model Hussey and Hughes (2007), where BP‐ICC equals WP‐ICC. Third, the RE of the independence GEE estimator is particularly sensitive to values of WP‐ICC. Values of the BP‐ICC do not substantially affect the RE of the independence GEE, except with the introduction of within‐cluster imbalance. This finding is expected given our analytical result in Theorem 3.1 for three‐period designs. More intuitively, the independence GEE analysis heavily depends on between‐cluster comparisons (or “vertical analysis” as defined in Matthews and Forbes, 2017) instead of within‐cluster comparisons (or “horizontal analysis”), and therefore its variability is more dependent on the WP‐ICC than the BP‐ICC. Fourth, whereas a larger SW‐CRT with more clusters and larger mean cluster‐period sizes generally has a small effect on the RE of GEE analysis when the working correlation structure is correctly specified, a larger SW‐CRT is associated with greater efficiency loss due to between‐cluster imbalance for independence GEE. Finally, while the number of periods has minimum effect on the RE of the GEE analysis when the working correlation structure is correctly specified, the RE of the independence GEE estimator increases with a larger number of periods as long as there is within‐cluster imbalance. We checked to confirm that introducing within‐cluster imbalance in our simulation configuration can somewhat reduce the between‐cluster imbalance within each period (even though maintaining the overall between‐cluster imbalance on mean cluster‐period sizes), and therefore improves the stability of vertical analysis which is the dominating component of the independence GEE.

While we have mainly focused on the RE of GEE analysis under unequal versus equal cluster sizes, there remains interest in understanding the RE of GEE analysis under the true versus independence working correlation model in SW‐CRTs with binary outcomes. This is defined by

$${\text{RE}}_{\mathrm{w}}=\frac{\text{var}(\widehat{\delta }|{\stackrel{\sim }{\mathbf{R}}}_i=\text{corr}({\mathbf{Y}}_i))}{\text{var}(\widehat{\delta }|{\stackrel{\sim }{\mathbf{R}}}_i={\mathbf{I}}_{n_i})},$$

which is strictly below one unless all ICC parameters are zero. In the context of the Washington State EPT study, Table 3 implies that ${\text{RE}}_{\mathrm{w}}$ can substantially deviate from one even with a small WP‐ICC. To provide a more complete perspective, in Web Appendix E, we present ${\text{RE}}_{\mathrm{w}}$ as a function of ICC parameters under equal cluster‐period sizes. Evidently, ${\text{RE}}_{\mathrm{w}}$ is a monotonically decreasing function of both WP‐ICC and BP‐ICC, and the efficiency loss due to the incorrect working independence assumption becomes maximum when WP‐ICC equals BP‐ICC. These findings on ${\text{RE}}_{\mathrm{w}}$ reinterpret those of Mancl and Leroux (1996) and Wang and Carey (2003) in the context of SW‐CRTs, and confirm the notable efficiency loss under the independence GEE for estimating the regression coefficient of a covariate that varies within clusters. This is in contrast to parallel CRTs, where there can be no efficiency loss for independence GEE with equal cluster sizes (Li & Tong, 2021a, 2021b; Pan, 2001). From the efficiency perspective, our results favor the GEE analysis coupled with an appropriate working multilevel correlation structure in SW‐CRTs, possibly through the matrix‐adjusted estimating equations (MAEE) approach developed in Preisser et al. (2008) and Li et al. (2019, 2018b, 2021). The MAEE approach has been validated in previous simulations with SW‐CRTs, and is recently implemented in the geeCRT” R package. Relatedly, reporting ICC estimates is also recommended practice in SW‐CRTs per the CONSORT extension to SW‐CRTs (Hemming et al., 2018), as those values provide evidence for designing future trials with a similar endpoints.

To assist with sample size determination in SW‐CRTs with unequal cluster sizes, we further developed a Monte Carlo search algorithm in Section 7. This approach is computationally efficient since it only requires numerical inversion of $J\times J$ matrices regardless of the actual cluster‐period sizes (Theorem 2.1). Alternatively, for sample size calculation, Girling (2018) suggested two design effect expressions (DE)—one based on Taylor series expansion following van Breukelen et al. (2007) (expression given in Web Appendix F) and the other given by $(1+{\text{CV}}^2)$—due to between‐cluster imbalance in SW‐CRTs with continuous outcomes. With binary outcomes, we find in Web Appendix F that the inverse of Taylor series DE is more similar to the RE curves under the correct working correlation model, whereas ${(1+{\text{CV}}^2)}^{-1}$ is more similar to the RE curves under the independence working correlation model. However, these continuous outcome approximations are still imprecise, underscoring the utility of our Monte Carlo sample size algorithm for more accurate design calculations with binary outcomes.

There are a few limitations of our study. First, while our evaluations assumed that the independence working correlation structure is misspecified in SW‐CRTs, we have not investigated the efficiency implications when the exchangeable, NEX or ED correlation structure deviates from the underlying true correlation structure. Asymptotic efficiency evaluation under misspecified nonidentity correlation structure is generally challenging because the probability limits of the misspecified ICC estimators are not easy to identify analytically. Therefore, additional simulation studies are required to address this more complex question, possibly by summarizing the empirical variance of the GEE estimator under alternative data generating processes. Second, we have restricted consideration to cross‐sectional designs, as motivated by the Washington State EPT trial. On the other hand, unequal cluster sizes can also arise in closed‐cohort or open‐cohort SW‐CRTs. These alternative designs require slightly different formulations of the within‐cluster correlation structures due to repeated outcome measurements for the same subject (Kasza et al., 2020; Li et al., 2020, 2018b). It remains to be explored whether the current findings are generalizable to cohort SW‐CRTs. Third, our evaluation is based on GEE, whereas GLMM is an alternative approach for design and analysis of SW‐CRTs. We expect the RE due to unequal cluster sizes for GLMM behaves similarly to the RE of GEE under the correct correlation model specification, because maximum likelihood estimation of GLMM by default accounts for the within‐cluster correlations. A detailed investigation of GLMM is beyond the scope of this paper and merits future research. Finally, our simulation design parameters are not exhaustive. However, our comprehensive evaluation identified important factors that affect the efficiency patterns of the GEE estimators in cross‐sectional SW‐CRTs. We have also articulated the critical need to account for correlations in SW‐CRTs from an efficiency perspective, providing a rigorous justification for estimating and reporting ICCs, as recommended by the CONSORT extension to SW‐CRTs (Hemming et al., 2018).

CONFLICT OF INTEREST

The authors have declared no conflict of interest.

OPEN RESEARCH BADGES

This article has earned an Open Data badge for making publicly available the digitally‐shareable data necessary to reproduce the reported results. The data is available in the Supporting Information section.

This article has earned an open data badge “Reproducible Research” for making publicly available the code necessary to reproduce the reported results. The results reported in this article could fully be reproduced.

Supporting information

Supporting Information.

Supporting Information1.

Supporting Information2.

Tian, Z. , Preisser, J. S. , Esserman, D. , Turner, E. L. , Rathouz, P. J. , Li, F . Impact of unequal cluster sizes for GEE analyses of stepped wedge cluster randomized trials with binary outcomes. Biometrical Journal. 2022;64:419–439. 10.1002/bimj.202100112

DATA AVAILABILITY STATEMENT

The R code for the numerical studies in the paper is available in the supplementary materials. No statistical analysis of individual‐level data was involved because the primary focus of this paper is on study design. The cluster size information of the Washington State EPT study in Sections 1 and 7 were computed from data shared by Dr. James P. Hughes from the University of Washington.