PeacoQC: Peak‐based selection of high quality cytometry data

Abstract

In cytometry analysis, a large number of markers is measured for thousands or millions of cells, resulting in high‐dimensional datasets. During the measurement of these samples, erroneous events can occur such as clogs, speed changes, slow uptake of the sample etc., which can influence the downstream analysis and can even lead to false discoveries. As these issues can be difficult to detect manually, an automated approach is recommended. In order to filter these erroneous events out, we created a novel quality control algorithm, Peak Extraction And Cleaning Oriented Quality Control (PeacoQC), that allows for automated cleaning of cytometry data. The algorithm will determine density peaks per channel on which it will remove low quality events based on their position in the isolation tree and on their mean absolute deviation distance to these density peaks. To evaluate PeacoQC's cleaning capability, it was compared to three other existing quality control algorithms (flowAI, flowClean and flowCut) on a wide variety of datasets. In comparison to the other algorithms, PeacoQC was able to filter out all different types of anomalies in flow, mass and spectral cytometry data, while the other methods struggled with at least one type. In the quantitative comparison, PeacoQC obtained the highest median balanced accuracy and a similar running time compared to the other algorithms while having a better scalability for large files. To ensure that the parameters chosen in the PeacoQC algorithm are robust, the cleaning tool was run on 16 public datasets. After inspection, only one sample was found where the parameters should be further optimized. The other 15 datasets were analyzed correctly indicating a robust parameter choice. Overall, we present a fast and accurate quality control algorithm that outperforms existing tools and ensures high‐quality data that can be used for further downstream analysis. An R implementation is available.

1. INTRODUCTION

Flow cytometry is becoming a standard approach in daily clinical practice [1] and in large clinical studies where the underlying biological mechanisms of diseases are being investigated [2, 3]. Because of the technological advancements in these fields, more and more samples are being measured and for each sample, traditional flow cytometry can now measure up to 40 markers on millions of cells, whereas mass cytometry can measure more than 45 markers on thousands of cells [4, 5].

To ensure that the data measured for these samples is high quality and has little variation, standardization, calibration, and quality control guidelines have been set up [6, 7, 8]. However, even when using these procedures and taking care to have the instruments run in optimal conditions, technical issues can still occur. These can affect the quality of the cytometry data, influence the downstream analysis and lead to false discoveries [9].

Examples of technical issues are clogs during acquisition, resulting in abrupt signal changes for a short period of time, after which the signal typically returns to its original level, gradual signal intensity changes during the startup of the acquisition, and changes of the acquisition speed that can result in a signal shift that remains shifted [10]. Because of the wide variety in aberrations, it is not straightforward to find one universal cleaning or quality control approach that can identify and remove all of them.

Currently, there are four tools available to detect quality issues in cytometry data. With flowQ [11], figures can be generated to assert the quality of the samples visually, but it does not flag any anomalies itself. flowClean [12] will track changes in population frequency over time and flag problematic regions. Timepoints where the distribution of the populations are aberrant are detected by changepoint analysis and events during these timepoints get flagged by adding a new parameter to the fcs file. flowAI [9] works on three levels: it tests the stability of the flow rate by outlier detection analysis, the stability of the signal measurement by changepoint analysis of the medians, and the dynamic range by outlier detection. It automatically returns a cleaned file, or, if requested, adds a new parameter to the fcs file. The last algorithm, flowCut, will calculate summed density measures using the mean, median, several percentiles, skewness, and variation of the flow signal and will remove the erroneous measurements based on a density curve analysis [13].

One of the drawbacks of these algorithms is finding consistent parameter settings that are suitable for different datasets. Another disadvantage is that they were all developed for usage in flow cytometry analysis but not for mass cytometry. Due to the lower measurement speed, the different time unit and the presence of many zero values, alterations have to be made either in the implementation of the algorithms or in the data itself. A last limitation is the disadvantage of the changepoint analysis which only allows the selection of one consecutive part of the data. Therefore, flowAI and flowClean cannot select only a part in the middle of the file for removal, even when the signal returns to its original value afterwards. Additionally, the different approaches have not yet been extensively compared in the current literature.

In this work, we present a new tool, called Peak Extraction And Cleaning Oriented Quality Control (PeacoQC), that overcomes these limitations and that can handle flow cytometry (FCM) and mass cytometry data. To evaluate our tool, we quantitatively compare it to the three algorithms described above that can flag anomalies.

2. MATERIALS AND METHODS

2.1. Proposed method

An overview of the proposed method is found in Figure 1. As input, the algorithm needs a preprocessed (transformed and, if appropriate, compensated or unmixed) fcs file. Then it starts with identifying density peaks in the marker expressions and uses two steps to filter out the peaks that have aberrant values, based on their position in an isolation tree or based on their Mean Absolute Deviation (MAD) distance. This results in cleaned data that can be used for further analysis.

FIGURE 1.

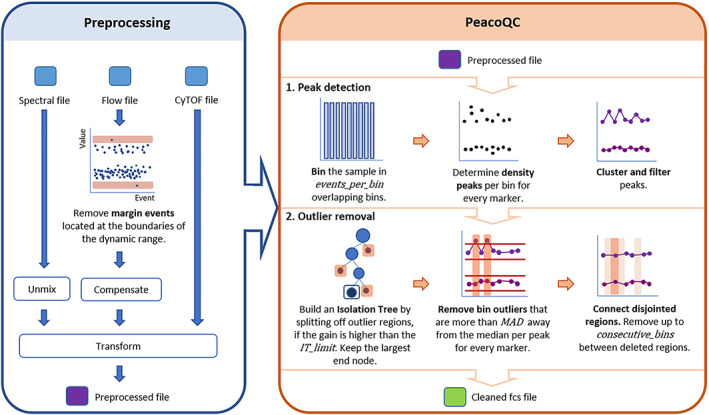
Schematic overview of the proposed method. The raw fcs files should first be preprocessed according to the suggested workflow in the blue box, which can include the removal of margins, compensation, and transformation. The method itself starts with a preprocessed fcs file. First, the sample is binned and density peaks are determined, clustered, and filtered per bin. The cleaning part of the method starts with the usage of an isolation tree, then it will remove peaks based on their MAD distance and it ends by connecting disjointed removed regions. The method returns a cleaned fcs file [Color figure can be viewed at wileyonlinelibrary.com]

2.1.1. Peak detection

Before the filtering steps, the measurements are split in overlapping bins over time where the second half of one bin will correspond to the first half of its consecutive bin. For each of these bins, density peaks are detected for every marker.

The number of events per bin are, by default, determined based on the datatype of the input. If the data consists of FCM data, the number of bins is determined by the number of measurements. The algorithm will look for a number of events per bin that falls between a default of 150 cells and a maximum that is determined by the total number of events and a default of maximum 500 bins, rounded up to a multiple of 500 events (Formula 1).

$$\text{EventsPerBin}=\left(\text{floor}\left(\text{MaxEvents}/500\right)\times 500\right)+500$$ (1)

where $\text{MaxEvents}=\left(\text{TotalEvents}/\text{MaxBins}\right)\times 2$ and floor rounds down to an integer.

When mass cytometry data is measured, the determination of the number of events per bin also takes into account the amount of zero values present. The maximum number of bins is not taken by default but is set to the number of nonzero values in the marker with the most zero values, divided by 150, which is in most cases less than the limit of 500. This is necessary to ensure enough nonzero values for a robust peak detection.

In each bin, peaks are determined per marker. A peak value is defined as a marker expression value that has a higher density than its previous and next expression value and that has a density value that is higher than 1/3th of the maximum density found in the given expression range. Peaks smaller than 1/3th of the maximum peak are considered as potential noise and are thus not required to be stable over time. Note that if mass cytometry data is given to the algorithm, the zero values are not taken into account while determining the peaks. To ensure stable peaks over the entire measurement, a peak selection step is performed where the medians of the peaks that are represented in at least a default of 10% of the bins are calculated. If a bin has multiple peaks, only those are kept that are closest to the determined medians.

At the end of the peak detection step, a matrix is built where the bins are represented in the rows and there is a column for each peak of each marker. This peak matrix is used in the following filtering steps.

Note that we recommend to apply the peak detection on a transformed and, when relevant, compensated or unmixed file, to improve the accuracy of the peak detection.

2.1.2. Filtering

A first filtering step is done by using an isolation tree, a method based on the anomaly detection method Isolation Forest which isolates every point in the data and classifies them as outliers if they are easily separable [14]. The implementation of the isolation tree used in the proposed algorithm is based on the IsolationForest package [15]. However, only one tree is used and no randomness is applied, as we are not concerned about overfitting issues or the generation of a model since the model only has to be used for this specific sample.

In this implementation, the tree is built by iteratively determining the marker and peak (i.e., a column in the peak matrix) that could produce the best split, grouping the bins (i.e., rows) with similar values. At the end of the iterative process, the largest node is kept and is considered to have similar peak values for every marker in every bin. This results in the removal of all bins that are not located in this one node from the peak matrix. Evaluating the quality of a split is done by Formula 2. Pseudocode for building the isolation tree is shown below. By grouping the bins by expression value rather than by time, we avoid the effect of changepoint detection methods where only one consecutive part of the data can be selected. Only applying splits with a minimal gain avoids unnecessary splits of similar values.

$$\text{CalculateGain}\left(X\right)={\max }_{\left(s\in X\right)}\left(\mathrm{sd}\left(X\right)-\left(\mathrm{sd}\left(\left\{y\mid y>s,y\in X\right\}\right)+\mathrm{sd}\left(\left\{y\mid y\le s,y\in X\right\}\right)\right)/2\right)$$ (2)

with $X$ all values in the column, computing the Gain as the maximum difference in standard deviation and the SplitValue as the s which maximizes this gain.

BuildIsolationTree(PeakMatrix, GainLimit = 0.6)


       MaxDepth = Log2(nrows (PeakMatrix))


       Root = node[ids=1:nrow(PeakMatrix),


              depth=0]


       IsolationTree.addChild(Root)


       NodesToSplit = list()


       NodesToSplit.add(Root)


       WHILE (any(NodesToSplit)){


           CurrentNode = NodesToSplit[1]


           CurrentMatrix = PeakMatrix[CurrentNode.ids, ]


           BestGain=0


           FOR (Column in CurrentMatrix){


             Gain, SplitValue = CalculateGain(CurrentMatrix[, Column])


             IF (Gain > BestGain){


                 BestColumn = Column


                 BestGain = Gain


                 BestSplit = SplitValue


         }



 }



 



 IF (BestGain > GainLimit) {


    ids_l = currentNode.ids[CurrentMatrix[,BestColumn] BestSplit]


    ids_g = currentNode.ids[CurrentMatrix[,BestColumn] > BestSplit]


    DaughterNode1 = node[ids = ids_l,


    depth = CurrentNode.depth+1]


    DaughterNode2 = node[ids = ids_g,


    depth = CurrentNode.depth+1]


    CurrentNode.addChild(DaughterNode1)


    CurrentNode.addChild(DaughterNode2)


    GainLimit = BestGain


    if(DaughterNode1.depth < MaxDepth)


       NodesToSplit.add(DaughterNode1, DaughterNode2)



 }



 NodesToSplit.remove(CurrentNode)



 }



 return IsolationTree

Note that the isolation tree can be sensitive to a low number of bins and is by default not used when less than a default of 150 bins were measured since it can remove too much of the data.

Since the isolation tree sometimes fails to find subtle changes in the peak ranges, a second filtering step is applied. In this filtering step, the noise is first removed by applying a smoothing spline to all peak ranges individually. Then, a bin is filtered out when its smoothed value is further than the default of six Median Absolute Deviations (MAD) away from the median of the entire smoothed peak range for any of the peaks.

$$\mathrm{MAD}\left(X\right)=\text{median}\left(\left|X_{\mathrm{i}}-\tilde{X}\right|\right)\text{with}{X}_{\mathrm{i}}\text{the individual values and}\tilde{X}\text{the median of}\mathrm{all}\text{values}$$

To avoid small regions being kept while the bins around them have been filtered out, any remaining regions of only five consecutive bins or less also get removed. This sometimes occurs when the algorithm is not stringent enough and a bin in a noisy region appears quite similar to the stable region in another part of the measurement (see Figure S3).

At the end of this process, cleaned data is returned where all the measurements from the bins that have been filtered out in the isolation tree or by the MAD detection method are removed.

2.1.3. Checks

Next to the filtering steps, PeacoQC checks if none of the markers have a monotonic increasing or decreasing signal since this can influence the further analysis of the data. This type of signal pattern can occur due to, for example, DAPI contamination when the cytometer is not properly cleaned between the measuring of different samples. If this pattern occurs, the algorithm will provide a warning, but will not filter out any cells based on this anomaly, as this issue is not specific to a limited region in the data.

A warning will also be given if more than 70% of the measurements are removed by the algorithm since this could indicate either a bad quality sample or a wrong parameter setting in the algorithm for this sample.

2.1.4. Parameter settings

In our experience, the default settings work in a wide range of datasets, as demonstrated in the results section. However, if the user would notice that the algorithm is more or less strict then required for their specific application, a number of parameters can be changed from their default value by the user to optimize the results. Three of these parameters indicate the strictness of the method, three influence the bin size and one specifies whether the data is mass cytometry data.

The gain limit of the isolation tree (IT_limit, default 0.6) indicates how strong outlier datapoints influence the standard deviation evaluated when building the tree, only making additional splits in the tree (and thus removing the outliers) if the decrease in standard deviation is sufficiently high. By lowering this limit, the algorithm will be more strict and outliers will be removed sooner.

The number of MADs allowed (MAD, default 6) is evaluated after the selection of the isolation tree to identify strong effects only present in individual channels, which might be missed in the high‐dimensional space. The lower the number of MADs allowed, the more strict the algorithm will be and more cells will be removed.

One of the strengths of our algorithm is that it can select disjointed regions for removal, for example in the case where two small blockages occur during the measurement. However, in some rare cases, this also results in small regions being kept, while the bins around them have been filtered out. In this case, the number of consecutive bins between regions of removed bins (consecutive_bins, default 5) can be increased in order to make the method more strict.

The number of measurements per bin is by default calculated based on the number of events of the entire sample. The minimal number of events per bin (min_cells, default 150) and the maximum number of bins (max_bins, default 500) can be chosen in this case. Increasing the minimal number of events per bin will improve the peak detection, as the density estimation will be more accurate, but having too few bins in total will make it more difficult to estimate whether a signal is stable. When the number of events per bin is high, removal of a single bin will also immediately have a big impact on the total number of cells remaining. The default values proposed present a good trade off in most cases we observed. Alternatively, the user can choose the exact number of events per bin. This can be relevant when there is an exceptionally high or low number of events. It should be kept in mind that increasing the number of bins will result in a longer computation time, and in all experiments reported in our results the number of bins is calculated by default.

As explained in the peak detection section, the zero events present in mass cytometry data can make the peak detection unstable. To indicate that the user is working with mass cytometry data, we recommend setting the remove_zeros parameter to TRUE.

2.1.5. Visualization of the result

At the end of the quality assessment, a figure is generated when, by default, more than 20% of the data is removed to allow for a visual assessment of the cleaning on all the markers of the data. When multiple samples are cleaned, a heatmap can also be made to quickly visualize how much each filter step removed for each sample and with which parameters the quality control has been done.

2.1.6. Availability

The proposed algorithm is implemented in the “PeacoQC” R package, available on github at www.github.com/saeyslab/PeacoQC and distributed by the BioConductor platform at https://doi.org/10.18129/B9.bioc.PeacoQC. As input, the user needs to provide a flowframe, a class of the flowCore package [16], and the markers on which the density peaks should be detected and cleaned. Optionally, the default parameters that were previously described can also be altered.

The evaluation pipelines that were used to generate the results for this manuscript are all coded in the R language and are available at www.github.com/saeyslab/PeacoQC_evaluation. Figures S4 and S5 are available here as well in high resolution.

Four different datasets were used for the generation of the results where PeacoQC is compared to three other algorithms. The first dataset is an inhouse dataset where three different types of anomalies were deliberately introduced during measurements on the flow cytometer using four mice spleen samples. The second dataset consists of one mass cytometry fcs file measured on human whole blood while the third dataset consists of a spectral cytometry file measured on mouse spleen. The mass cytometry file was provided by the GENYO institute. All donors signed an informed consent according to the ethical protocol of the Andalusian Biobank. The protocol of the project was approved by the Ethical Committee of Centro Granada (CEI‐Granada) according to the Helsinki declaration of 1975, as revised in 2013. The mouse spleen data was provided by the Center for Inflammation Research. Spleens were isolated from wild type C57Bl/6 J mice that were housed in SPF conditions. All experiments were performed in accordance with the ethical committee of the Faculty of Science of the VIB. The last dataset consists of 55 fcs files from the FlowCAP IV challenge [17] that were manually annotated by at least six different scientists. For each file, margin events were removed and data was compensated and transformed. A subset of 10,000 cells was then displayed for the following markers: FSC‐A, SSC‐A, IFNg, CD4, CD3, CD8. The figures were saved as svg files and the scientists were asked to manually gate multiple files. The events that were indicated as bad quality events and that should be removed could then be retrieved and linked back to the original data. The first three datasets are available at flowRepository ID FR‐FCM‐Z3YQ together with the svg files of the fourth dataset and an overview of which of the FlowCAP IV files were used. The FlowCAP IV files themselves can be accessed through flowRepository ID FR‐FCM‐ZZ99.

Additionally, we wanted to ensure that the default PeacoQC parameter choices are suitable for a wide range of datasets. To evaluate this, we selected all samples on flowRepository which fit the following criteria: the datasets had to be uploaded or updated in 2020, the data had to be published in Cytometry Part A and could not include data of other datasets, only samples that contained cells and were fully stained were selected and the samples could not be altered during their measurement since we expect a stable signal over time. The information of the selected datasets can be found back in Table S1. In total, we analyzed nine flow cytometry datasets, three mass cytometry datasets, and four spectral cytometry datasets.

Note that all the files used in this work were first put through a preprocessing pipeline that included the removal of margin events, compensation and transformation where necessary.

2.2. Comparison with other quality control algorithms

We compared PeacoQC to three other quality control algorithms: flowAI, flowClean and flowCut. The versions of the packages used in the comparison can be found in Table S2. The default settings were used for all the packages in all the experiments except for the runtime experiment where the parameters for generating a figure, report and fcs file were set to FALSE.

We used the in‐house data to highlight how the quality control algorithms handle some frequent recurring anomalies, as well as the mass cytometry and spectral cytometry examples. The annotated dataset from the FlowCAP IV challenge was used for a quantitative comparison. To quantify the evaluation, balanced accuracies were calculated for each method and each sample, as specified in Formula (3).

$$\begin{array}{l}\text{Balanced accuracy}:\left(\text{Sensitivity}+\text{Specificity}\right)/2\\ \text{Sensitivity}:\mathrm{TP}/\left(\mathrm{TP}+\mathrm{FN}\right);\text{Specificity}:\mathrm{TN}/\left(\mathrm{TN}+\mathrm{FP}\right)\end{array}$$ (3)

where TP, true positives; FP, false positives; TN, true negatives; FN, false negatives.

For every cell, a vote was taken to decide the true label: a cell was marked to be removed if the majority of the annotators labeled it as such. A true positive then corresponds to a measurement that is removed both by the algorithm and at least four scientists and a true negative corresponds to a measurement that is kept by both the majority of annotators and the algorithms. A false positive is a measurement that is removed by an algorithm but not in the manual annotation while a false negative is seen as a measurement that is kept by an algorithm but removed in the manual annotation. In the end, the balanced accuracy, sensitivity and specificity were calculated for the algorithms compared in this work.

For easier interpretation of these values, we also created a baseline by randomly removing the same amount of cells as was selected by the manual annotation for each file. This gives us a baseline value of the scores obtained by a method which works uncorrelated to the actual regions of interest (while still removing the correct amount of cells).

To evaluate algorithm running times, we artificially created a set of files ranging from 1000 to 3,000,000 cells, by concatenating file 010 of the flowCAPIV data five times and uniformly sampling the relevant number of cells. This approach ensures that the amount of quality issues to detect stays similar for all files in this evaluation. The duration that each quality control algorithm needed to clean the subsampled data was timed three times with the system.time function of the base R package and the average is reported.

All experiments described in this manuscript were run on a DELL Precision 5530 with a Intel(R) Core(TM) i9‐8950HK CPU processor and 32GB of installed RAM.

3. RESULTS

To illustrate the importance of quality control algorithms, we show an example where the anomaly influenced the clustering of a specific sample. Then, we show the robustness and precision of PeacoQC by comparing it to three other existing quality control algorithms: flowAI, flowCut, and flowClean. First, we compared the algorithms based on how they handle different types of anomalies on different types of data, and second, we compared their accuracy, precision and duration in a quantitative way on a bigger dataset.

3.1. Necessity of quality control algorithms

An often occurring issue is the signal increase during startup of the acquisition of the sample. To illustrate the impact of this aberration, we annotated a sample according to the time of acquisition (Figure 1). During the startup, the signal is not stable yet and is increasing over time for some channels, as indicated in red in Figure 2A. Independent of the time, a FlowSOM clustering [18] was computed on the sample, dividing the cells in small groups with similar marker expressions. These clusters were then visualized as nodes in a minimal spanning tree and colored by the time annotation, showing that the events that fall in the startup period are clustering together, resulting in fully red nodes (Figure 1B). We highlight two cluster subsets in Figure 2C where we only color the cells of group 1, indicated in the red box in Figure 2B, or group 2, indicated in the blue box. The cells contributing to group 1 were only measured during the startup phase of the acquisition, where the cells contributing to group 2 are spread during the entire measurement, as would be expected when the cells are in suspension. When this sample would be used for further analysis without any cleaning, wrong assumptions could be made, based on the clusters solely caused by a technical artifact.

FIGURE 2.

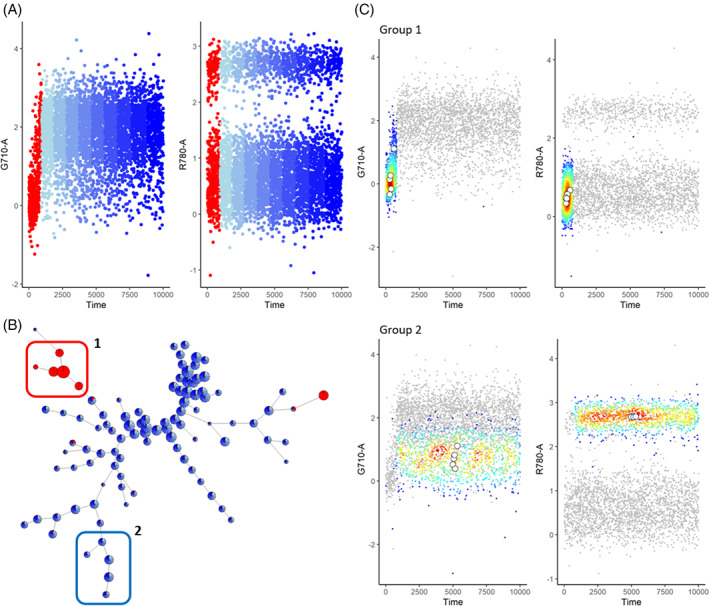
Clustering of uncleaned sample with start‐up aberration. (A) Scatterplots of channels G710‐a and R780‐a where the time parameter is divided into 10 equal‐sized parts. The first part, with the aberrant signal, is colored red while the other parts are colored in different shades of blue. (B) FlowSOM analysis of the sample with 100 clusters. The pies are colored with the same color scheme as in A. (C) Scatter‐density plots of channels G710‐a and R780‐a for groups 1 and 2 indicated in B. The colored dots correspond to the events falling in the group while the gray dots show a random sampling of all events. These plots were made for the compensated, transformed file 147 of the FlowCAPIV dataset where the margin events were removed [Color figure can be viewed at wileyonlinelibrary.com]

3.2. Different types of anomalies

We introduced three different types of anomalies on mouse cytometry data to mimic those that we encounter in real experiments: a permanent signal shift due to speed changes, a temporary shift in signal because of the slow uptake of a sample or a clog and the monotonic increasing or decreasing effect on a signal because of contaminations.

In two different samples, we introduced a speed change. The increase of the setting from low to medium to high in the first sample, caused no shifts in the signal medians (Figure 3A) which means that no data cleaning is necessary. However, flowClean and flowAI did remove a part of this sample that either corresponds to the first speed setting or the last two speeds settings together while flowCut and PeacoQC marked the file as clean.

FIGURE 3.

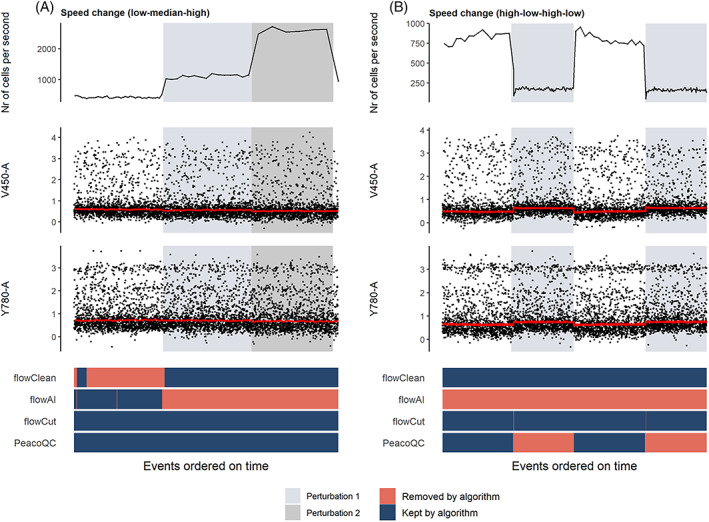
Cleaning of samples where speed changes were introduced. The top figure shows the flow rate of the sample and is followed by two scatterplots where the marker signals measured on channels V450‐a and Y780‐a are displayed. The red lines on these plots are the medians of the marker intensities determined in bins of 1000 events per bin. At the bottom, a heatmap is shown where the events are colored by whether they are removed by one of the four algorithms. (A) In this sample, two speed changes were introduced (from a low to a medium and a high setting) which do not seem to influence the signal intensities. (B) The speed setting was varied from high to low to high to low which did seem to introduce a permanent signal increase or decrease [Color figure can be viewed at wileyonlinelibrary.com]

In the second sample, when the speed setting was lowered, a drop in signal can be observed until the setting was changed again (Figure 3B). If this sample would not be cleaned, the downstream analysis could be influenced by these signal changes. The four methods all took different approaches when cleaning this sample. flowClean did not remove anything while flowAI almost deleted the entire sample. The other two algorithms only removed a part of the sample. Where flowCut filtered out the small transitional part of the data that corresponds to the change to a lower speed setting, PeacoQC removed the entire part where the signal is temporarily increased.

Another anomaly often observed is a temporary signal shift which shows a small signal drop in some but not all of the markers (Figure 4A). PeacoQC and flowClean both filtered out this part of the data while flowAI removed a much larger portion corresponding to the flow rate instability that occurred during the first part of the measurement (top graph). flowCut does not remove anything from this sample.

FIGURE 4.

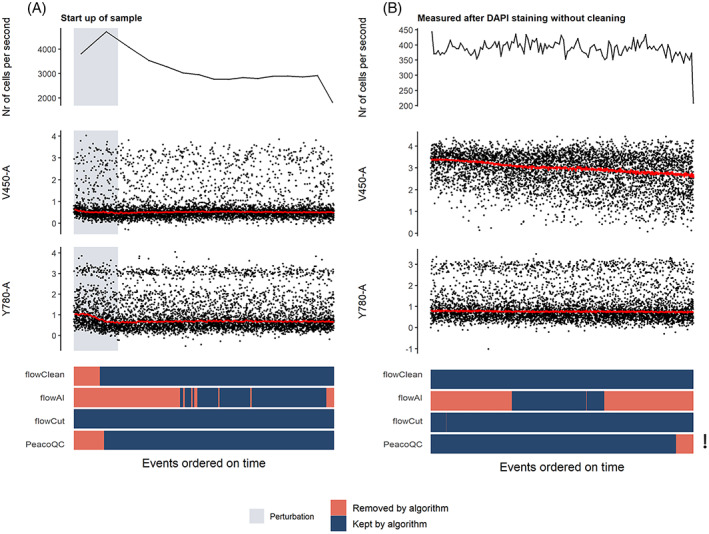
Cleaning of samples with temporary shift in signal or a monotonic decrease in signal. The top figure shows the flow rate of the sample and is followed by two scatterplots where the marker signals measured on channels V450‐a and Y780‐a are displayed. The red lines represent the medians of the marker intensities determined in bins of 1000 events per bin. At the bottom, a heatmap is shown where the events are colored whether they are removed by one of the four algorithms. The exclamation mark refers to the warning that PeacoQC gave due to the monotonic increasing or decreasing effect. (A) In this sample, the speed was set to the highest setting possible, resulting in an uptake of the sample with a lower amount of cells which influenced the signal intensity until a steady flow of events was reached. (B) A contamination was ensured in this sample by not cleaning the flow cell after measuring a DAPI stained sample. Due to the DAPI contamination into the measured sample, a monotonic increasing or decreasing effect was introduced in certain channels of the sample [Color figure can be viewed at wileyonlinelibrary.com]

To introduce a monotonic change in the marker signal, we acquired data directly after measuring a sample stained with DAPI without any cleaning procedures in between. This resulted in a contamination of the DAPI staining in the new sample resulting in a monotonic decrease, as displayed in Figure 4B. flowAI filtered out large parts of the data while flowClean and flowCut kept the entire sample. PeacoQC only removed a small part at the end of the data but gave a warning that one or more channels showed a monotonic increasing or decreasing trend.

3.3. Mass cytometry data and spectral flow cytometry data

We also tested the four quality control algorithms to clean a mass and a spectral cytometry file (Figure 5). Two of the four algorithms (flowClean and flowAI) gave errors and could not be run on the mass cytometry sample. On the other hand, flowCut and PeacoQC found an aberration at the end of the measurement, corresponding with the increase of the marker signal in certain channels, and removed it successfully. However, flowCut needed 1 min and 44 s to run while PeacoQC needed 14 s to analyze the sample with 409,222 events. For the spectral cytometry sample that consists out of 862,696 events, flowCut produced an error and flowClean was stopped after 2 h running time. While flowAI did run without errors, it marked part of the file to be removed based on the flow rate, and the other part based on the signal stability, resulting in all data being labeled as bad quality. PeacoQC correctly identified the signal change during startup and needed 20 s to run.

FIGURE 5.

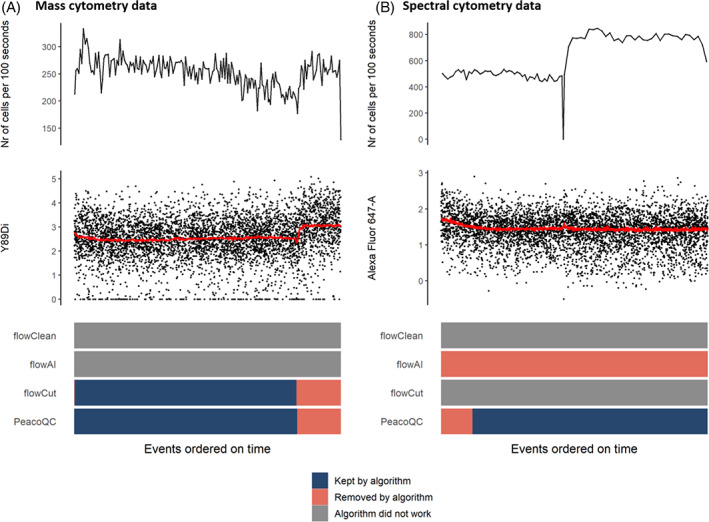
Cleaning mass cytometry and spectral cytometry sample. The top figures show the flow rate of the samples and are followed by a scatterplot where the marker signals measured on channels Y89Di (A) or Alexa Fluor 647 (B) are displayed. The red line on this plot indicates the medians of the marker intensities determined in bins of 1000 events per bin. At the bottom, a heatmap is displayed, showing for every algorithm which parts of the files were removed or kept, or whether the algorithm did not work at all [Color figure can be viewed at wileyonlinelibrary.com]

3.4. Quantitative analysis

To quantitatively compare the different algorithms, different scientists were asked to manually annotate a number of files and select the part they would remove from the data. Then, these annotations were compared to the outcome of the cleaning results of the different quality control algorithms and the balanced accuracy was calculated for each algorithm and each file. As baseline values, we determined the balanced accuracy for files where we randomly removed the same amount of cells as was selected by the manual annotation for each file (Random in Figure 6).

FIGURE 6.

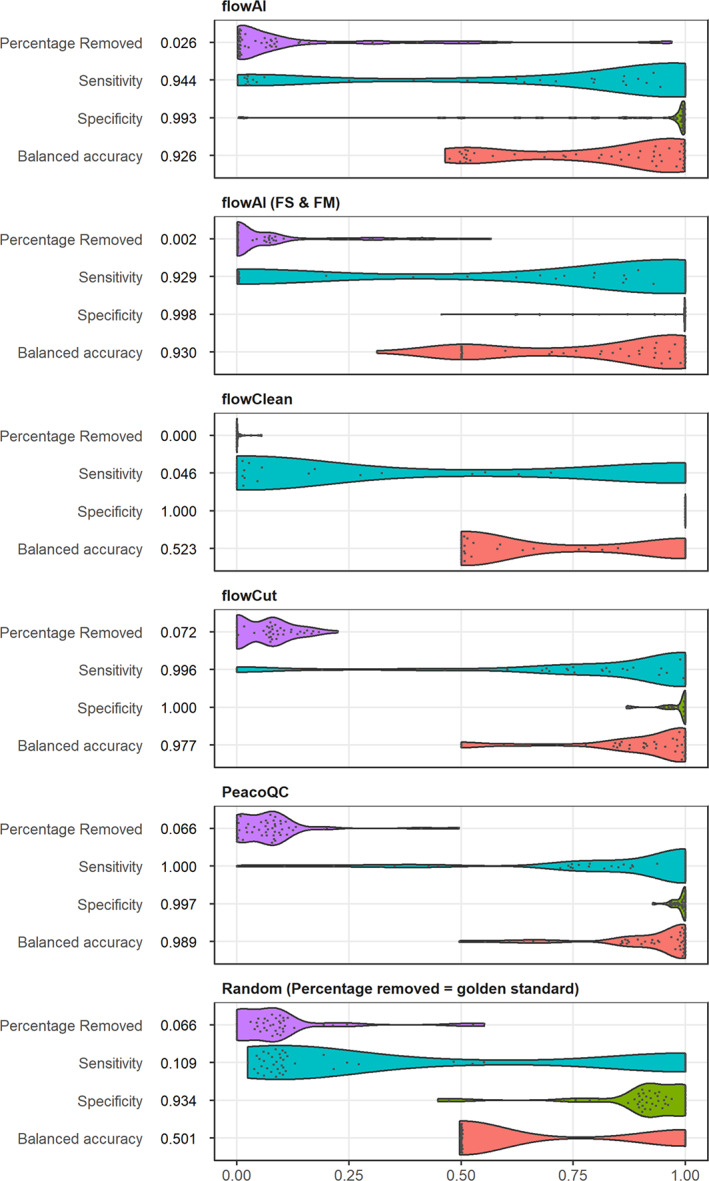
Overview of balanced accuracy and percentage removed of manual annotated dataset. Fifty five FlowCAPIV preprocessed files were manually annotated by a number of scientists based on six channels. The results were compared to the output of the different quality control algorithms that are presented in the first five plots. For each file, the sensitivity (blue), specificity (green), and balanced accuracy (red) were determined where a true positive is defined as an event that is removed by at least three scientists and the quality control algorithm. The percentage removed is displayed in purple. The last plot represents baseline values where the same amount of cells was removed from each file as were selected by the manual annotators, but randomly sampled from the file. The numbers displayed before each graph, refer to the median of the quantitative measure for that algorithm (FS & FM: for this comparison, a quality control analysis was done with the flowAI algorithm where the flow rate was not taken into account) [Color figure can be viewed at wileyonlinelibrary.com]

flowClean obtained a median balanced accuracy of 0.523, similar to the random baseline approach. Although it has the highest median specificity (1), its median sensitivity is low (0.046), due to the limited removal of events in all files.

flowAI can clean the data from three different aspects (flow rate, flow signal, and dynamic range) and while the default setting uses all three, it also offers the option to make a selection of which aspects to use. To accurately compare flowAI to the other algorithms, we compared all possible settings. The results of the full comparison are displayed in Figure S1 while the best result is shown in Figure 6 together with the default version. The result that obtained the highest balanced accuracy (0.930) occurs when the data were cleaned based on the flow signal and the dynamic range (FS & FM). It scores better than the full flowAI algorithm (0.926) which is due to the fact that some changes in the flow rate do not correspond to actual changes in the signal, and those were thus not filtered out by the manual annotators. Both versions of flowAI removed much less than the manual annotators (2.6% or 2% vs. 6.6%).

PeacoQC and flowCut are the highest scoring algorithms and do not have any significant differences on the quantitative measures (Figure S2). PeacoQC does obtain a higher median balanced accuracy (0.989 vs. 0.977) but they both remove approximately the same amount of events for every file as the annotators (6.6% and 7.2%). If we look at the sensitivity and specificity of the two algorithms, PeacoQC obtains a lower specificity (0.997 vs. 1) since it sometimes removed a small number of events that, according to the annotators, should not have been filtered out. However, it does obtain a higher median sensitivity (1 vs. 0.996) which indicates slightly better performance in removing the full anomaly from the sample.

To compare the different algorithms speed wise, one FCM file was concatenated until it obtained 3,000,000 events and a different subset of events were uniformly subsampled over time and supplied to the different quality control algorithms. The running time was then measured three times and the mean result is displayed in Figure 7. It should be noted that flowCut would not run on a file that only contained 1000 events and flowClean only started cleaning when more than 50,000 events were present in the file and needed much longer running times than the other algorithms. The time measurement even ran out when running flowClean on files that contained more than 1,000,000 events. For small files, flowCut is the fastest until the file reaches a limit of 1,000,000 events after which its running time starts to gradually increase over the running time of PeacoQC and the two flowAI versions. PeacoQC needs 1 or 2 s more than flowCut for small files, but the gradual increase for larger files in running time is much slower than the other quality control algorithms when the event number increases.

FIGURE 7.

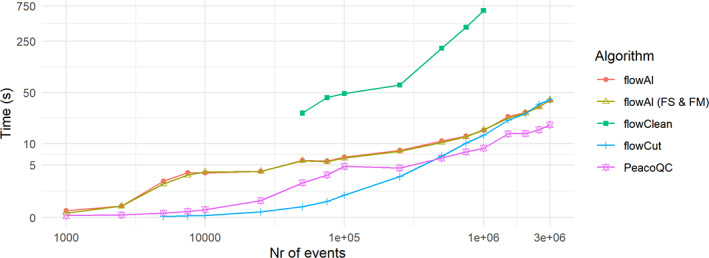
Running time analysis comparison of different quality control algorithms. The 010 file of the FlowCAPIV data was concatenated five times. From this data, a number of events were uniformly for peer review subsampled over time and used for quality control by the different quality control algorithms. The cleaning was done three times and timed by the system. Time function of the base R package. The mean of these results is displayed (FS & FM: for this comparison, a quality control analysis was done with the flowAI algorithm where the flow rate was not taken into account) [Color figure can be viewed at wileyonlinelibrary.com]

3.5. Robustness of parameter choices

To ensure that PeacoQC can run on different types of datasets generated in different experiments without tweaking its parameters, we ran the algorithm on the datasets described in Table S1. We compared its results with the flowAI algorithm (Figure 8). Both algorithms were run with their default parameters on the channels that had a description and on, if present, the scatter channels. Coinciding with previous results, PeacoQC could be run on all types of datasets while flowAI threw an error when trying to run mass cytometry datasets (Figure S4). For the flow cytometry datasets, PeacoQC and flowAI removed a similar amount of measurements (less than 10% difference) for 42 out of 49 samples. In three of these 42 samples, more than 10% was removed by both algorithms which could be validated after visual inspection. In the seven samples where a larger difference in percentage removal was obtained, flowAI removed more of the measurements than PeacoQC in six samples while PeacoQC removed more in one sample. Upon visual inspection, we noticed that flowAI removed many measurements based on its flow rate step, even when there was no impact on the signal stability. PeacoQC removed too much in a single instance (FR‐FCM‐Z2EY) where the file had less than 5000 cells, making the peaks unstable (Figure S5). When applying PeacoQC on such small samples, we recommend increasing the number of bins. flowAI also removed too much for 6 out of 10 spectral cytometry samples based on its flow signal while no anomalies were present while for one spectral dataset, flowAI and PeacoQC obtained similar results (Figure S6).

FIGURE 8.

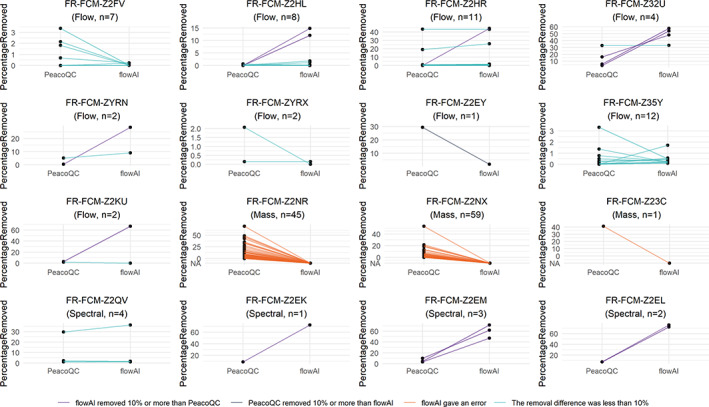
Comparison of PeacoQC and flowAI on flowRepository datasets. The PeacoQC and flowAI algorithms were both run with default parameters on 16 datasets that were uploaded or updated on flowRepository in 2020 and on samples that contained cells and where a stable signal was expected over time during the measurement. Each sample is represented as a line and the percentage of measurements removed is displayed on the y‐axis. If a value is NA, the algorithm failed to run the sample [Color figure can be viewed at wileyonlinelibrary.com]

4. DISCUSSION

We developed a new quality control algorithm for cytometry data and compared it to three other existing tools. In this work, we demonstrate that PeacoQC can accurately remove different types of anomalies that occur during the acquisition of samples. It does so by detecting stable density peaks during the sample measurement and filtering out the low quality events based on the usage of an isolation tree and MAD distances.

The default PeacoQC parameter settings are optimized in such a way that they work for most of the flow cytometry, mass cytometry and spectral cytometry datasets we tested. We confirmed this by running the algorithm on 16 different publicly available datasets that included flow, mass and spectral cytometry. Comparison with flowAI and visual inspection showed that the algorithm was successfully run on all 164 samples of all datasets, except for one case in which it removed too many measurements. This indicates that the chosen parameter settings are stable for all datasets and that not much tweaking needs to be done. However, if need be, the parameters can be adapted in an intuitive way. To determine if parameter alterations are required, we recommend trying the algorithm first on a subset of your dataset. By inspecting the resulting figures, the user can ensure the parameter settings are appropriate for the specific dataset, and then apply those settings to all files.

To evaluate our work, we compared PeacoQC with three existing quality control algorithms: flowAI, flowCut and flowClean.

First, a comparison was made on how the algorithms handle different types of anomalies often present in cytometry data, based on in‐house generated data. All algorithms divide the data into bins, but they assess the stability across the bins by different measures. flowClean uses population distributions, which is computationally expensive and not very sensitive to signal changes in only a subset of markers. The other algorithms check marker per marker to improve this sensitivity. Where flowAI uses median values and flowCut uses a combination of means, medians and several quantiles, PeacoQC determines the high density peaks to check the stability. We opted to use these peaks since we noticed that the stability of the medians and quantiles will vary more during the measurement depending on the expression distribution, bin size and measurement speed. Especially in cases where there is a bimodal distribution with about 50% positive and 50% negative cells, the median can have high variance. In some cases, artifacts could also influence only the background or only the positive peak, in which cases the median is too limited. While flowCut tries to resolve this by adding more quantiles, these still stay variable if they fall in the region between two peaks. We hypothesized that identifying the actual populations by peak detection would result in a more robust characterization of the data, which is confirmed in our evaluation: PeacoQC is indeed better in distinguishing the different types of anomalies while the other algorithms always struggle with at least one.

An additional limitation of applying flowAI with the default settings, is how this algorithm evaluates the flow rate independently from the signal stability. In some cases, this causes almost all data to be removed, when one half is removed based on one criterium and the other half on the other criterium. We consciously apply the different filtering steps in the PeacoQC algorithm sequentially to avoid this problem. The isolation tree allows for a disjointed filtering as well, in contrast to the signal stability check in flowAI which will look for a single stable region. This allows to remove small disturbances (e.g., during a blockage), while keeping both the measurements before and after the disturbance if they are sufficiently similar. However, this can result in a pattern where some small regions, located in the middle of a larger disturbance, seem similar to the good region. To avoid that these small regions are kept, we provided the consecutive bin parameter, ensuring that all the regions kept should contain a minimal amount of bins.

We also confirmed that PeacoQC performed well on mass cytometry data, where the other algorithms failed (flowClean and flowAI) or had a very slow running time (flowCut) and on spectral cytometry data where flowCut and flowClean failed. This ensures our algorithm is widely applicable.

Next, a more quantitative comparison was made. To overcome the hurdle of subjectivity when manually annotating the low quality regions, we set up a comparison where multiple scientists annotated the same data and where an event was only seen as a bad quality event when at least three scientists out of six or seven marked it to be removed. When comparing the different quality control algorithms to these results, PeacoQC obtained the highest median balanced accuracy meaning that it resembles the manual annotation the most. Overall, PeacoQC had similar running times to the other algorithms, but, thanks to a variable bin size dependent on file size, it was the fastest for larger files.

In summary, we propose a fast and accurate quality control algorithm that is able to filter out many anomalies that can occur during the measurement of flow and mass cytometry data, ensuring high‐quality data that can be further used in downstream analysis.

CONFLICT OF INTEREST

The authors declare they have no conflict of interest.

AUTHOR CONTRIBUTIONS

Annelies Emmaneel: Conceptualization (equal); data curation (equal); formal analysis (lead); investigation (lead); methodology (lead); software (lead); visualization (lead); writing – original draft (lead); writing – review and editing (equal). Katrien Quintelier: Investigation (supporting); methodology (supporting); validation (supporting); visualization (supporting); writing – review and editing (equal). Dorine Sichien: Data curation (equal); investigation (supporting); writing – review and editing (supporting). Paulina Rybakowska: Data curation (supporting); investigation (supporting); methodology (supporting); writing – review and editing (supporting). Concepción Marañón: Supervision (supporting). Marta E Alarcón‐Riquelme: Supervision (supporting). Gert Van Isterdael: Data curation (equal); investigation (supporting); supervision (equal); writing – review and editing (supporting). Sofie Van Gassen: Conceptualization (equal); investigation (supporting); methodology (supporting); supervision (equal); writing – review and editing (equal).

5.

PEER REVIEW

The peer review history for this article is available at https://publons.com/publon/10.1002/cyto.a.24501.

Supporting information

FIGURE S1: Overview of balanced accuracy and percentage removed of manual annotated dataset for different flowAI versions. Fifty five FlowCAPIV preprocessed files were manually annotated by a number of scientists based on six channels. The results were compared to the output of the different flowAI variations that are presented in the first eight plots. For each file, the sensitivity (blue), specificity (green), and balanced accuracy (red) were determined where a true positive is defined as an event that is removed by at least three scientists and the specific version of the flowAI method. The percentage removed is displayed in purple. The last plot represents baseline values where the same amount of cells was removed from each file as were selected by the manual annotators, but randomly sampled from the file. The numbers displayed before each graph, refer to the median of the quantitative measure for that algorithm (FS: Removal of events based on the flow signal, FM: removal based on the dynamic range, FR: removal based on the flow rate).

FIGURE S2: p Values of pairwise wilcox testing on quantitative measures of comparison quality control algorithms. Fifty five FlowCAPIV preprocessed files were manually annotated by a number of scientists based on six channels. These results were compared to the output of the different quality control algorithms displayed in the rows of the tables and the sensitivity, specificity, and balanced accuracy was calculated. For each quantitative measure, a pairwise wilcox test was computed between the different quality control algorithms of which the p value is displayed in the tables. As baseline values, the same amount of cells was removed from each file as were selected by the manual annotars, but randomly sampled from the file and the measures obtained from these results were also taken into account in the pairwise tests. The Benjamini‐Hochberg method was also applied to minimize the false discovery rate. The boxes are colored red when the p value is lower than 0.05. We expect there to be a significant difference between the balanced accuracy, sensitivity, and specificity of the different algorithms compared to the Random sampling but no significant difference when looking at the percentage removed since this should be similar (FS & FM: for this comparison, a quality control analysis was done with the flowAI algorithm where the flow rate was not taken into account).

FIGURE S3: Effect of consecutive_bins parameter (A = 0, B = 5, C = 10). If during a noisy period accidentally a few bins look close to the normal behavior during the rest of the file, they might not be filtered out. By defining the consecutive_bins parameter (default 5), good regions smaller or equal to this amount of bins surrounded by aberrant regions will still be filtered out. The extra filtering happening thanks to this step is indicated in the figure in a light pink shade and highlighted by a blue arrow.

FIGURE S4: PeacoQC and flowAI analysis on mass cytometry datasets. PeacoQC and flowAI were run with default settings on the selected mass cytometry datasets of Table S1. The top graphs show the flow rate of the samples and are followed by a scatterplot where variable marker signals are displayed. The red line on this plot indicates the medians of the marker intensities determined in bins of 1000 events per bin. At the bottom, a heatmap is displayed, showing for every algorithm which parts of the files were removed or kept, or whether the algorithm did not work at all. Note that not all channels that were used in the quality control algorithms.

FIGURE S5: PeacoQC and flowAI analysis on flow cytometry datasets. PeacoQC and flowAI were run with default settings on the selected flow cytometry datasets of Table S1. The top graphs show the flow rate of the samples and are followed by a scatterplot where variable marker signals are displayed. The red line on this plot indicates the medians of the marker intensities determined in bins of 1000 events per bin. At the bottom, a heatmap is displayed, showing for every algorithm which parts of the files were removed or kept, or whether the algorithm did not work at all. Note that not all channels that were used in the quality control algorithms.

FIGURE S6: PeacoQC and flowAI analysis on spectral cytometry datasets. PeacoQC and flowAI were run with default settings on the selected spectral cytometry datasets of Table S1. The top graphs show the flow rate of the samples and are followed by a scatterplot where variable marker signals are displayed. The red line on this plot indicates the medians of the marker intensities determined in bins of 1000 events per bin. At the bottom, a heatmap is displayed, showing for every algorithm which parts of the files were removed or kept, or whether the algorithm did not work at all. Note that not all channels that were used in the quality control algorithms.

TABLE S1: Overview of datasets uploaded or updated in 2020 on the flowRepository database. The reason for exclusion of a dataset from the experiment ran in this manuscript is listed in the last column. The datasets used in this manuscript were chosen based on following criteria: the datasets had to be uploaded or updated in 2020, the data had to be published in Cytometry Part A and could not include data of other datasets, only samples that contained cells and were fully stained were selected and the samples could not be altered during their measurement since we expect a stable signal over time.

TABLE S2: Overview of package versions used of the different quality control algorithms.

Appendix S1: Supporting information.

Emmaneel A, Quintelier K, Sichien D, Rybakowska P, Marañón C, Alarcón‐Riquelme ME, et al. PeacoQC: Peak‐based selection of high quality cytometry data. Cytometry. 2022;101:325–338. 10.1002/cyto.a.24501