Abstract
The increase in the expectations of artificial intelligence (AI) technology has led to machine learning technology being actively used in the medical field. Non-negative matrix factorization (NMF) is a machine learning technique used for image analysis, speech recognition, and language processing; recently, it is being applied to medical research. Precision medicine, wherein important information is extracted from large-scale medical data to provide optimal medical care for every individual, is considered important in medical policies globally, and the application of machine learning techniques to this end is being handled in several ways. NMF is also introduced differently because of the characteristics of its algorithms. In this review, the importance of NMF in the field of medicine, with a focus on the field of oncology, is described by explaining the mathematical science of NMF and the characteristics of the algorithm, providing examples of how NMF can be used to establish precision medicine, and presenting the challenges of NMF. Finally, the direction regarding the effective use of NMF in the field of oncology is also discussed.
Keywords: machine learning, NMF, omics analysis, single-cell analysis, meta-analysis
Introduction
In recent years, machine learning has gained considerable research interest with the advent of deep learning technology, and it is now widely recognized as a core technology in the field of artificial intelligence (AI) [1, 2]. Machine learning has a long history; it is believed that the concept was created by Arthur Samuel in 1959 and came to be used as an academic term [3]. Machine learning is currently used in a variety of fields, such as image recognition, natural language processing, data analysis and prediction, and is widely implemented in society [4–12]. The medical field is no exception, and machine learning technology is actively used in medical research, especially in medical image analysis [13–20]; further, there have been considerable research studies on the clinical applications [21–23]. Many medical papers that utilize machine learning technology have been published in recent years [24–28], and the technology is beginning to be introduced to omics analysis such as genome and epigenome [29–32]. Judging by recent developments, we expect machine learning technology to gain considerable importance in medical research in the future.
Non-negative matrix factorization (NMF) is a machine learning technique that analyzes matrices with zero or positive values. It has a wide range of applications and is used in various fields such as image analysis [33–35], speech recognition [36–38], astronomy [39–42], audio signal processing [43], and natural language processing [44–46]; recently, it has been applied to medical research [47–52]. In the real world, there is a large amount of data that is represented by non-negative values, e.g. power spectra, pixel values, and frequencies. In multivariate analysis, such as Principal Component Analysis (PCA) and Independent Component Analysis (ICA), the goal is to decompose the given data into multiple additive components; there are many scenarios where it is useful to extract components from non-negative data in the same manner. For example, if the power spectrum of an individual sound source can be successfully extracted from that of a multiplex sound, it can be used for noise removal and sound source separation; further, if face image data can be successfully decomposed into image data corresponding to facial parts such as the eyes and nose, it can be used for face recognition and face image synthesis. NMF has also been used in bioinformatics to cluster gene expression and identify the genes that are the most representative of the cluster [53, 54]. In addition, NMF has been used in the analysis of cancer mutations to identify common mutation patterns that occur in many cancers and probably have different causes [55]. NMF technology can also be used to identify sources of variation, such as cell type, disease subtype, population stratification, tissue composition, and tumor clonality [56].
In recent years, the importance of machine learning has been recognized in the medical field, and NMF technique has been actively applied in medical research. In this review, we focus on the recent status of the application of NMF technology in cancer research and its potential for the establishment of precision medicine.
History of NMF and its understanding in mathematical science
The concept of NMF has a long history in the field of chemometrics under the name ‘self-modeling curve resolution’ [57]. In this framework, the right matrix vector is not a discrete vector but a continuous curve. Early work on NMF was performed by Paatero and Tapper under the term positive matrix factorization [58, 59]. Later, in 1999, Lee and Seung investigated the properties of the algorithm and presented some simple and useful algorithms for two types of factorizations, which became more widely known as NMF [60].
Mathematically, we consider N non-negative data vectors 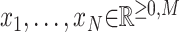 called observation vectors. Meanwhile,
called observation vectors. Meanwhile, 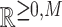 represents the set of all non-negative vectors of dimension M. The goal of NMF is to estimate the K basis vectors and weight coefficients that best explain all observation vectors assuming each vector is represented by an appropriately weighted sum of K basis vectors. Thus, NMF targets only quantities for which additivity holds. Additivity is assumed in scenarios where NMF is applied. In addition to the additivity assumption, another important assumption is that both the basis vectors and weight coefficients are non-negative. In other words, NMF can be approximated by
represents the set of all non-negative vectors of dimension M. The goal of NMF is to estimate the K basis vectors and weight coefficients that best explain all observation vectors assuming each vector is represented by an appropriately weighted sum of K basis vectors. Thus, NMF targets only quantities for which additivity holds. Additivity is assumed in scenarios where NMF is applied. In addition to the additivity assumption, another important assumption is that both the basis vectors and weight coefficients are non-negative. In other words, NMF can be approximated by
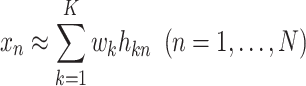 |
(1) |
where the observation vector 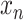 is a non-negative combination of the basis vector
is a non-negative combination of the basis vector 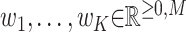 (a linear combination with a non-negative value for the coupling coefficient
(a linear combination with a non-negative value for the coupling coefficient 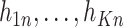 ).
).
If the matrices of observation vectors, basis vectors, and coupling coefficients 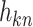 with k rows and n columns of element are
with k rows and n columns of element are 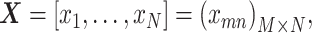
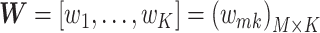 , and
, and 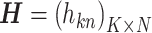 , respectively, equation (1) becomes
, respectively, equation (1) becomes
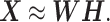 |
(2) |
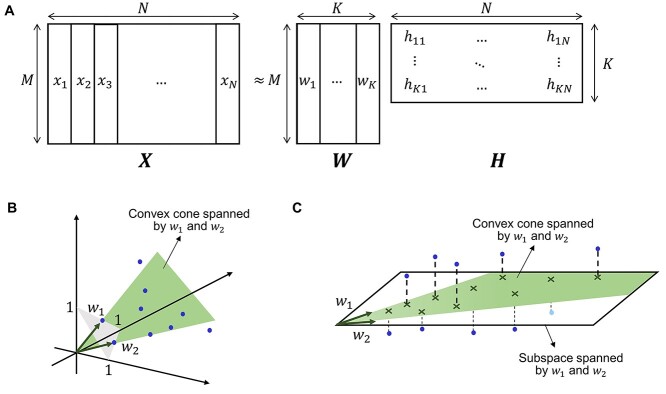
Thus, NMF can be viewed as a problem of decomposing the matrix of observation vectors into a product of two non-negative matrices (Figure 1A).
Figure 1.
Conceptual diagram of NMF. (A) If the matrix with the observation vectors is 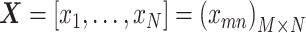 , the matrix with the basis vectors is
, the matrix with the basis vectors is 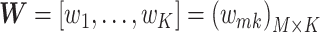 , and the matrix with the coupling coefficients
, and the matrix with the coupling coefficients 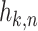 as elements in k rows and n columns is
as elements in k rows and n columns is 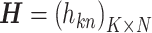 , then X ≈ WH. (B) Convex cone spanned by w1 and w2. (C) Convex cone and subspace spanned by w1 and w2.
, then X ≈ WH. (B) Convex cone spanned by w1 and w2. (C) Convex cone and subspace spanned by w1 and w2.
In NMF, the number of bases K is set smaller than the dimension M of the observation vector or the number of data N. For example, if K = M, we obtain a decomposition representation X = WH, if W = I (I is the unit matrix); however, this decomposition does not make sense. In addition, for K = N, we obtain a decomposition representation X = WH such that H = I; however, we cannot find any meaning from this decomposition either. K < min(M, N) corresponds to the fact that NMF attempts to approximate the observation matrix X with a matrix of lower rank; it is important to find the basis and coefficient matrices in this case. Geometrically, it can be interpreted that the principal component analysis (singular value decomposition) attempts to identify a subinterval to which the observed data belongs; NMF attempts to find a convex cone that fits the observed data well (Figure 1B and C) [61].
There are different types of NMFs that arise from using different cost functions to measure the divergence between X and WH and from regularizing the W and/or H matrices. Two simple divergence functions studied by Lee and Seung are the squared error (or Frobenius norm) and an extension of the Kullback–Leibler (KL) divergence to a positive matrix (the original KL divergence is defined on a probability distribution). Each divergence leads to a different NMF algorithm, which uses an iterative update rule to minimize the divergence. The factorization problem in the squared error version of NMF can be stated as follows:
Given a matrix X, find non-negative matrices W and H that minimize
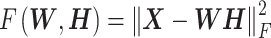 |
(3) |
In the NMF algorithm proposed by Lee and Seung, the initial values are set for W and H, and the update rules corresponding to the given loss function are alternately and repeatedly applied [60, 62]. This allows the loss function to be minimized under non-negative constraints, such as W ≥ 0 and H ≥ 0.
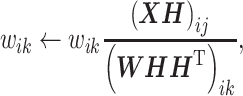 |
(4) |
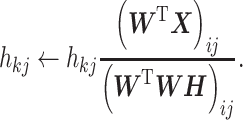 |
(5) |
Then, the update rule when KL divergence is adopted is
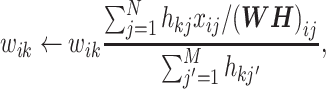 |
(6) |
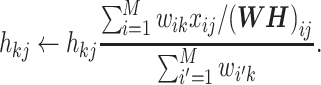 |
(7) |
These are called multiplicative algorithms; the estimated W and H elements are always non-negative if the elements of the observed data matrix X are non-negative. Lee and Seung proved that the loss function always decreases monotonically. Further, the multiplicative algorithm works in the case of missing values. In the iterative calculation process, the missing values can be supplemented naturally by replacing the missing parts with the expected values obtained from WH. Interested readers are encouraged to refer to older literature to gain a more detailed understanding of the mathematical properties of NMF [60, 63].
Currently, NMF is used in a wide range of fields and it is applied in various ways in the field of oncology. Table 1 summarizes various models based on NMF used in the field of oncology.
Table 1.
List of models based on NMF used in the field of oncology
| Model name | Cancer type | Type of data | Description | Year | Ref. |
|---|---|---|---|---|---|
| gNMF | NSCLC/CRC/MM | CNV | A genomic NMF algorithm, which is an unsupervised classification algorithm aimed at identifying the genomic subgroups of tumors. It is possible to define the genomic subclasses of disease and identify cell lines representing each genomic subtype using high-density SNP array data from patient tumors and established cell lines. The correlation of genomic classification with disease outcome showed that overall survival and the time to recurrence differed significantly among genomic subtypes. | 2010 | [131] |
| Convex-NMF | GBM | MRSI | A method for acquiring imaging and spectral information from brain tissue and applying convex NMF to extract tissue type-specific sources from these signals. Since convex-NMF is an unsupervised method and does not use prior information about the tumor region, it can identify tissue types one step further than the classical supervised methods that require labels, and it can minimize the negative effects of using mislabeled voxels. Further, convex-NMF relaxes the non-negativity constraint of the observed data, which allows for a natural representation of the MRSI signal. | 2012 | [132] |
| iNMF | CRC | mRNA | An iterative non-negative matrix factorization (iNMF) method based on a randomly selected set of probes was introduced and applied to stratify CRC samples into two main types and then into five subtypes in a two-step process. This iterative process makes it possible to detect hierarchical relationships between subtypes based on expression differences of various strengths. Because iNMF is based on a randomly selected set of probes, it has the advantage of being unbiased with respect to knowledge of genes and pathways. Subtype signatures consisting of probe sets with different expression levels can be easily applied to hierarchical clustering of independent CRC data sets in a two-step process, thereby assigning samples to each subtype. | 2012 | [133] |
| hNMF | GBM | MRSI | A hierarchical NMF method that allows the blind separation of the most important spectral sources in a short time TE 1H MRSI data. The algorithm comprises multiple levels of NMF, and only two tissue patterns are computed at each level. Further, hNMF can accurately estimate the three tissue patterns (normal, tumor, and necrosis) present in and around GBM tumors, which helps provide useful additional information for the diagnosis of GBM. | 2013 | [134] |
| SNMF | BRCA | IHC | An unsupervised sparse NMF-based approach for color unmixing. SNMF performed well in resolving the brown diaminobenzidine component from 36 IHC images and in accurately segmenting approximately 1400 nuclei and 500 lymphocytes from H&E images. | 2015 | [135] |
| intNMF | BRCA/GBM | mRNA/RPPA/ miRNA/ CNV | An integrated approach for disease subtyping based on NMF that uses multiple omics data to identify novel molecular subtypes of diseases that could influence therapeutic decisions. This method clusters multiple high-dimensional molecular data and uses multiple biological levels of information from the same person to perform a single comprehensive analysis. Since it does not assume any distributional form of the data, it is superior to other model-based clustering methods that need to assume a specific distributional form. | 2017 | [136] |
| RM-GNMF | CRC/GLI/AML/ALL | mRNA | An improved graph-regularized NMF algorithm to facilitate the display of geometric structures in data space. The combination of the l2,1 -norm NMF with spectral clustering and extensive experiments with three known data sets showed its usefulness in cancer gene clustering. | 2017 | [137] |
| NetNMF | BRCA | mRNA/miRNA | An NMF framework that integrates large pairwise datasets in a network-like manner to construct the modular network. The knowledge of prior interactions between molecules can be incorporated into the NetNMF framework in the form of network-based penalty terms to increase the likelihood that linked features in the network will be placed in the same module, which will help improve the accuracy of module discovery and the biological interpretability of the module. | 2018 | [138] |
| GMvNMF | PAAD/ESCA/ HNSC/ COAD | mRNA/CNV/DNA_ME | A new integrated model called multiview NMF (MvNMF) was proposed for the selection of common differentially expressed genes and multiview clustering. Then, a graph regularized MvNMF (GMvNMF) was constructed by applying graph regularization constraints to the objective function to encode the geometric information of the multiview genomic data. GMvNMF can not only obtain the potential shared feature structure and shared cluster group structure, but also capture the manifold structure of multiview data. | 2018 | [139] |
| CeModule | OV/UCEC | mRNA/miRNA/lncRNA | A model based on joint orthogonality NMF constructed to identify modules using matched lncRNA, miRNA, and mRNA expression profiles. The application of CeModule to two cancer datasets, including ovarian cancer and endometrial cancer of the uterus, showed that specific modules, which include lncRNA, miRNA, and mRNA, were significantly associated with and functionally enriched in cancer-related biological processes and pathways. | 2019 | [140] |
| nsNMF | GBM/BRCA/LUSC/PRAD | Somatic mutations data (WES) | A platform to apply non-smooth NMF and support vector machines to utilize the full range of sequence data, better aggregate genetic variation, and improve the power to predict disease type. Factor matrices derived from nsNMF were used to identify multiple genes and pathways significantly associated with each cancer type. | 2019 | [141] |
| DMAPred | BRCA/HCC/RCC/SCC/CRC/GBM/AML/LC/MM/ OV/PC/PRC/STO/URB | miRNA | An algorithm that can predict the likelihood of disease-related miRNA candidates based on NMF. This algorithm exploits the similarity and association between diseases and miRNAs, and it integrates local topological information of miRNA networks. Case studies of breast, prostate, and lung cancers have demonstrated DMAPred’s ability to discover miRNAs that may be associated with disease. | 2019 | [142] |
| pyCancerSig | BRCA/CRC | SNV/SV/MSI | A python package with a command line interface that integrates SNV, SV, and MSI profiles for sample profiling. Using NMF, the command to decipher the underlying process of cancer is also available. Evaluated using the TCGA breast and colorectal cancer cohorts, the integration of multiple mutation modes can help correctly identify cases with known clear mutational signatures and enhance signatures in cases where the signal is obscured by SNV-only profiles. | 2020 | [143] |
| LAceModule | BRCA/HCC | mRNA/miRNA/lncRNA | A framework for integrating Pearson correlation coefficients and dynamic correlation liquid association (LA) with multiview NMF. Experiments using breast and liver cancer datasets showed that LA is a useful indicator for detecting ceRNA pairs and modules; further, the identified ceRNA modules are involved in cell adhesion, cell migration, and cell-to-cell communication | 2020 | [144] |
| PathME | CRC/GB/LUSC/BRCA | mRNA/miRNA/CNV/ DNA_ME | A framework combining multimodal sparse denoising autoencoder and sparse NMF. It is possible to integrate multi-omics data effectively and interpretably at the pathway level while accommodating the high dimensionality of omics data. Patient-specific pathway score profiles derived from this model can reliably identify disease subgroups. | 2020 | [83] |
| SPOTlight | PC | scRNAseq/ST | A platform for decomposing spatial transcriptomics capture locations (spots) using NMF regression initialized with cell-type marker genes and subsequent non-negative least squares. With respect to human pancreatic cancer, patient sections can be segmented, and furthermore, the status of normal and tumor cells can be mapped in detail. In addition, training was performed using an external single-cell pancreatic tumor reference to illustrate clinically relevant tumor-specific immune cell status. | 2021 | [90] |
| CBP-JMF | BRCA | mRNA/miRNA/CNV | An algorithm based on the joint non-negative matrix tri-factorization framework. Significant overlap was found between genes extracted from CBPs and pathways of known subtypes when CBP-JMF was applied to identify CBPs in the four subtypes of breast cancer. | 2021 | [84] |
| NMFNA | PC | DNA_ME/CNV | An algorithm that introduces graph-regularized constraints into NMF to identify modules and characteristic genes from two types of data, DNA methylation, and CNV. Using Pearson correlation coefficients, three networks are constructed: methylation (ME), CNV, and ME-CNV. Next, modules can be effectively detected from these three networks by introducing the graph regularization constraint, which is a feature of NMFNA. Finally, gene ontology (GO) and pathway enrichment analysis are performed to detect characteristic genes by multimeasure scoring to gain a deeper understanding of the biological functions of the core modules. | 2021 | [145] |
| SOJNMF | LIC | mRNA/miRNA/DNA_ME | An algorithm that can analyze multidimensional omics data in an integrated manner. This method not only identifies the multidimensional molecular control modules, but also reduces the overlap rate of features among the multidimensional modules while ensuring the sparsity of the coefficient matrix after decomposition. | 2021 | [146] |
Abbreviations: NSCLC, non-small cell lung carcinoma; CRC, colorectal cancer; MM, malignant melanoma; CNV, copy number variation; GBM, glioblastoma multiforme; MRSI, magnetic resonance spectroscopic imaging; mRNA, messenger RNA expression; IHC, immunohistochemistry image data; BRCA, breast cancer; RPPA, reverse phase protein array; miRNA, microRNA expression; GLI, glioma; AML, acute myeloid leukemia; ALL, acute lymphoblastic leukemia; PAAD, pancreatic adenocarcinoma; ESCA, esophageal carcinoma data; HNSC, head and neck squamous cell carcinoma; COAD, colon adenocarcinoma; DNA_ME, DNA methylation; OV, ovarian cancer; UCEC, uterine corpus endometrial carcinoma; lncRNA, long non-coding RNA expression; LUSC, lung squamous cell carcinoma; PRAD, prostate adenocarcinoma; WES, whole exome sequencing; HCC, hepatocellular carcinoma; RCC, renal cell carcinoma; SCC, squamous cell carcinoma; LC, lung cancer; PC, pancreatic cancer; PRC, prostate cancer; STO, stomach cancer; URB, urinary bladder neoplasms; SNV, single nucleotide variation; SV, structural variation; MSI, microsatellite instability; scRNAseq, single-cell RNA sequencing; ST, spatial transcriptomics; and LIC, liver cancer.
Utilization of NMF in the field of oncology
Benefits of using NMF over other machine learning methods in cancer research
NMF is a type of matrix factorization technique; other matrix factorization techniques include PCA and ICA [60]. There are two primary advantages of using NMF over other machine learning methods for cancer research. First, an assumption of uncorrelation or independence of each component after decomposition is not necessary. In NMF, the components are decomposed to make them non-invalid after decomposition. Meanwhile in PCA, the components are decomposed to ensure that they are uncorrelated after decomposition and in ICA, they are decomposed to make them independent. The assumption of uncorrelatedness or independence of each component is not in line with the actual biomedical data such as transcriptome and epigenome, as genes are involved in multiple pathways and the gene expression is regulated by protein–protein interactions. Conversely, NMF uses matrix decomposition that does not assume uncorrelatedness or independence. Hence, it is possible to factorize the data according to its reality.
Second, interpretation of the NMF results is intuitive and easy. Unlike normal tissues, cancerous tissues have heterogeneous cell populations. Hence, the omics data obtained from cancerous tissues are the sum of values obtained from multiple cell types. In data decomposition using PCA and ICA, each component can take a negative value. This makes the interpretation of data difficult as its meaning in the real world is represented by positive values only. Interpretation of the biological meaning of latent features from NMF results is easy because each component takes a positive value.
Transcriptome analysis of gene expression profiles
Several reports on transcriptome analysis of the gene expression profiles using NMF in the field of oncology have been previously published. For example, Cho et al. identified six medulloblastoma subgroups by clustering gene expression microarray data comprising 194 primary medulloblastomas and 9 atypical teratoid/rhabdoid tumors for comparison using NMF [64]. Each subgroup had a unique combination of numerical and structural chromosomal aberrations that affected mRNA and miRNA expression. Genetically, it is characterized by an increased copy number of c-MYC, and transcriptionally, by the enrichment of the photoreceptor pathway and increased expression of miR-183-96-182. A previously unidentified molecular subgroup was associated with significantly lower event-free survival and overall survival.
Taylor et al. used iterative NMF on mRNA expression data from the Cancer Genome Atlas (TCGA) and 24 squamous cell carcinoma (SCC) cell lines to classify three disease segments of SCC [65]. The analysis of gene set enrichment and drug sensitivity identified an immune evasion subtype sensitive to nuclear factor-κB and mitogen-activated protein kinase (MAPK) inhibition, a replication stress-related subtype sensitive to ataxia telangiectasia inhibition, and a neuroendocrine-related subtype sensitive to phosphoinositide 3-kinase and fibroblast growth factor receptor inhibition. Further, each of these subtypes showed unique miRNA expression profiles. Focusing on the immune evasion subtype, the bioinformatics analysis of miRNA promoters revealed the enrichment of binding sites for the MAPK-driven transcription factor ETS1.
Barras et al. performed the unsupervised clustering of gene expression data from 218 patients with BRAF V600E mutation using NMF to identify subgroups based on gene expression and to analyze the characteristics of pathway activation [66]. The results strongly suggest a division into two groups (BM1 and BM2) that are independent of microsatellite instability status, PI3K mutation, gender, and sidedness. The pathway analysis showed that BM1 is characterized by the activation of the KRAS/AKT pathway, regulation of mTOR/4EBP, and EMT, while BM2 plays an important role in regulating the cell cycle. A proteomic analysis showed higher phosphorylation levels of AKT and 4EBP1 in BM1 and higher levels of CDK1 and lower levels of cyclin D1 in BM2.
Li et al. analyzed the mRNA expression data of 149 pancreatic ductal adenocarcinoma samples registered in TCGA by NMF and virtually isolated immune-related signals from a large amount of gene expression data [67]. The results showed that approximately 31% of the pancreatic ductal adenocarcinoma samples had higher immune cell infiltration, more active immune cell lysis activity, higher activation of the interferon pathway, higher tumor mutation burden, and less copy number alteration compared to other samples. This new molecular subtype, termed ‘Immune Class’, serves as an independent and favorable prognostic factor for the overall survival; PD-1 inhibitors may be effective against immune class.
Mutational signature analysis
Mutational signature analysis classifies the base substitution patterns of mutations and reveals its biological process and related background factors. It has proven to be an important component in somatic genome analysis, primarily for cancer [68, 69], and is expected to be applied as a biomarker in clinical practice [70, 71]. NMF has also been used for mutation signature analysis, and de novo signatures can be extracted by the NMF algorithm in MutationalPatterns [72], an R/Bioconductor package that includes all functions necessary to implement a mutation signature framework, in the R package SomaticSignatures [73], and in the Galaxy tool MutSpec [74]. MuSiCa, a web application built on top of the MutationalPatterns package, has also been developed to efficiently analyze mutation signatures in cancer samples through an easy-to-use web environment adapted for the entire research community [75].
Multiomics analysis
In recent years, the multimodal analysis of not only single omics data but also multiomics data has attracted considerable attention in the field of oncology [30, 76–81]; NMF has been reported to be useful for multiomics analysis. Wang et al. proposed ConMod, which compresses all networks into two feature matrices using a multiview NMF [82]. The multiview NMF does not depend on the number of input networks (types of omics data) because module detection is performed only with the feature matrix using the multiview NMF (Figure 2). Gene modules common to cancers were found when ConMod was applied to the co-expression networks of various cancers; most of these have functional significance such as ribosome biogenesis and immune response. In addition, the analysis of brain tissue-specific protein interaction networks revealed conserved modules related to nervous system development and mRNA processing.
Figure 2.
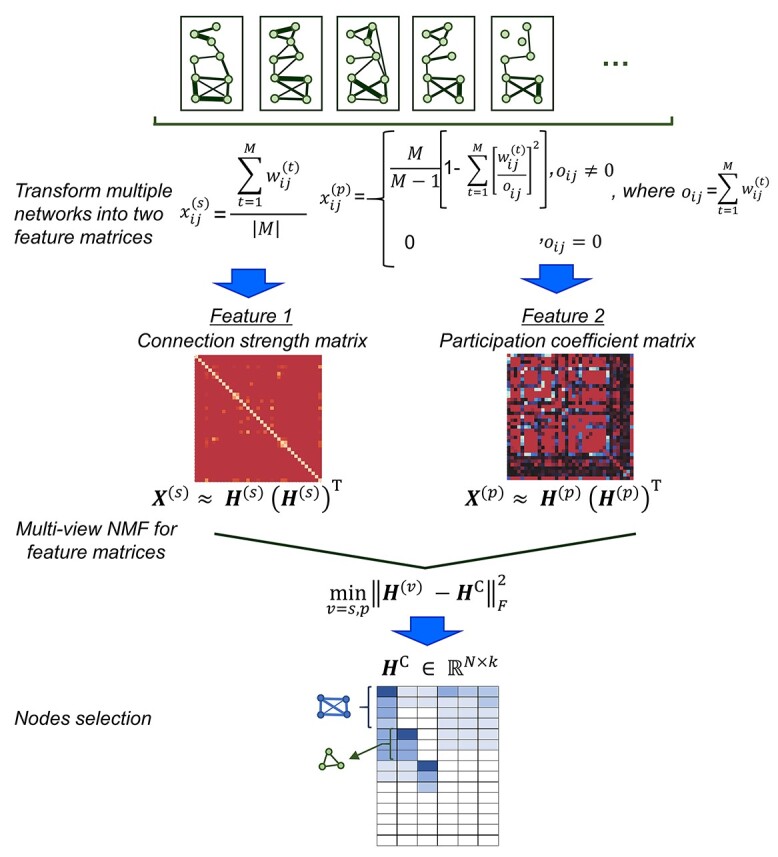
The ConMod approach modified from figure in Ref. 82. The ConMod includes three main steps: 1. transform multiple networks into two feature matrices, 2. factorize the two feature matrices jointly using multiview NMF to generate a consensus factor, and 3. select soft nodes from the consensus factor. Here, M, 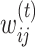 ,
, 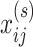 ,
, 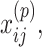 and
and 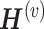 represent the number of layers, weights of the edges between nodes i and j in network layer t, connection strength of the edge between nodes i and j defined as the average weight of the entire network, participation coefficient of an edge, and low rank matrix representation close to the consensus matrix
represent the number of layers, weights of the edges between nodes i and j in network layer t, connection strength of the edge between nodes i and j defined as the average weight of the entire network, participation coefficient of an edge, and low rank matrix representation close to the consensus matrix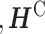 respectively.
respectively.
Lemsara et al. proposed PathMe, a framework that combines a multimodal sparse denoising autoencoder with sparse NMF to achieve robust patient clustering based on multiomics data [83]. The proposed model leverages pathway information to transform omics data dimensions into pathway- and patient-specific score profiles effectively (Figure 3). The authors applied the method to a clusters of patients in multiple cancer datasets and showed the possibility of obtaining biologically valid disease subtypes characterized by specific molecular features using four types of omics data: mRNA expression, miRNA expression, DNA methylation, and copy number variation. Further, post-hoc analyses using somatic mutations and clinical data provided support for and interpretation of the identified clusters.
Figure 3.
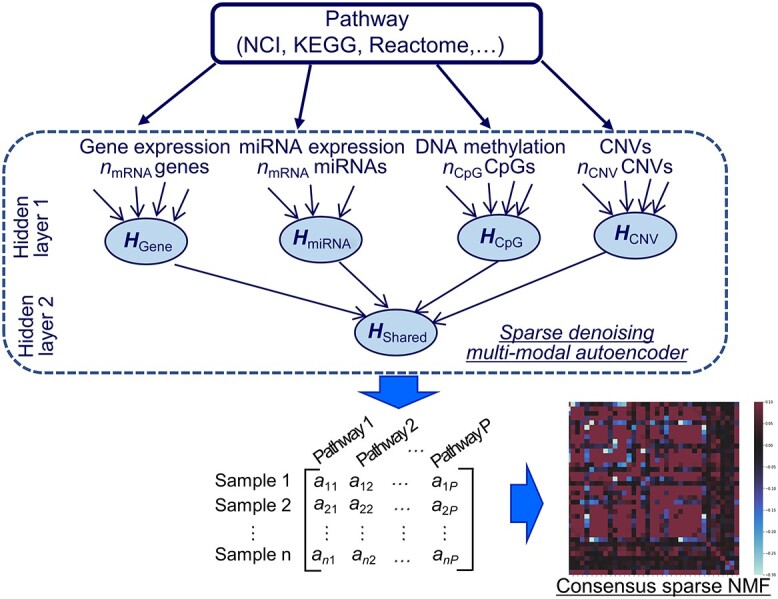
The PathMe approach modified from figure in Ref. 83. Multiomics features mapped to a particular pathway are summarized into pathway-level scores via a sparse denoising multimodal autoencoder architecture. Hidden layer 1 consists of up to 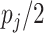 hidden units for each omics modality, where pj represents the number of features of omics type j. The hidden units of omics modality j are tightly connected to the input features of the same omics type; however, there are no connections from the input features of the other data modalities. Hidden layer 2 comprises one hidden unit that represents the overall score of the multiomics pathway. Consensus sparse NMF clustering can be applied in subsequent steps by concatenating the P multiomics pathway scores of each patient.
hidden units for each omics modality, where pj represents the number of features of omics type j. The hidden units of omics modality j are tightly connected to the input features of the same omics type; however, there are no connections from the input features of the other data modalities. Hidden layer 2 comprises one hidden unit that represents the overall score of the multiomics pathway. Consensus sparse NMF clustering can be applied in subsequent steps by concatenating the P multiomics pathway scores of each patient.
Wang et al. proposed CBP-JMF, a practical tool for inferring the complex biological process (CBP) underlying a group of samples as a disease subtype using a non-negative matrix tri-factorization framework [84]. Given P different multiomics datasets, they can be represented by multiple matrices 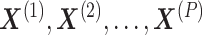 (Figure 4). In each matrix, the rows represent molecules such as genes, and the columns represent samples (e.g. patients); the values in the matrix are related to the meaning of the omics. Let
(Figure 4). In each matrix, the rows represent molecules such as genes, and the columns represent samples (e.g. patients); the values in the matrix are related to the meaning of the omics. Let 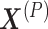 be a matrix of gene expression data, where
be a matrix of gene expression data, where 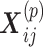 represents the expression value of the i-th row gene in the j-th sample. Each non-negative matrix
represents the expression value of the i-th row gene in the j-th sample. Each non-negative matrix 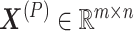 , p = 1, 2, …, P is factorized into three non-negative matrix factors based on matrix tri-factorization.
, p = 1, 2, …, P is factorized into three non-negative matrix factors based on matrix tri-factorization. 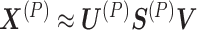 , where the molecular coefficient matrix (MCM)
, where the molecular coefficient matrix (MCM) 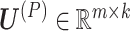 and the sample basis matrix (SBM)
and the sample basis matrix (SBM) 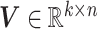 represent the pattern index matrices for k CBPs and k sample groups, respectively. The scale absorption matrix (SAM)
represent the pattern index matrices for k CBPs and k sample groups, respectively. The scale absorption matrix (SAM) 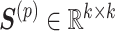 explores the relationship between the two pattern index matrices. Further, MCM shows the structural pattern between molecules (e.g. genes), SBM shows the structural pattern between samples, and SAM absorbs the difference in scale between MCM and SBM. Each column in the MCM infers a potential feature associated with CBP; its continuous values represent the relative contribution of each molecule in CBP. Each row of the SBM describes the relative contribution of the sample to the latent features. Sample groups can be detected by comparing the relative weights of each row of the SBM. As a practical application, CBP-JMF was applied to four subtypes of breast cancer to identify CBPs [84]. The results showed a significant overlap between the genes extracted from CBP and the pathways of the known subtypes.
explores the relationship between the two pattern index matrices. Further, MCM shows the structural pattern between molecules (e.g. genes), SBM shows the structural pattern between samples, and SAM absorbs the difference in scale between MCM and SBM. Each column in the MCM infers a potential feature associated with CBP; its continuous values represent the relative contribution of each molecule in CBP. Each row of the SBM describes the relative contribution of the sample to the latent features. Sample groups can be detected by comparing the relative weights of each row of the SBM. As a practical application, CBP-JMF was applied to four subtypes of breast cancer to identify CBPs [84]. The results showed a significant overlap between the genes extracted from CBP and the pathways of the known subtypes.
Figure 4.
The CBP-JMF approach modified from figure in ref. 84. 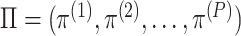 ; β and ω represent the importance of the Laplacian regularization of the graph and the weight constraint
; β and ω represent the importance of the Laplacian regularization of the graph and the weight constraint 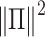 , respectively. V is divided into
, respectively. V is divided into 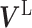 and
and 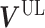 according to input data; L and UL mean ‘labeled’ and ‘unlabeled’ samples, respectively.
according to input data; L and UL mean ‘labeled’ and ‘unlabeled’ samples, respectively. 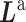 (
(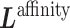 ) and
) and 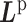 (
(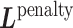 ) are Laplacian matrices of
) are Laplacian matrices of 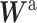 and
and 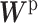 , respectively.
, respectively.
Single-cell sequencing analysis
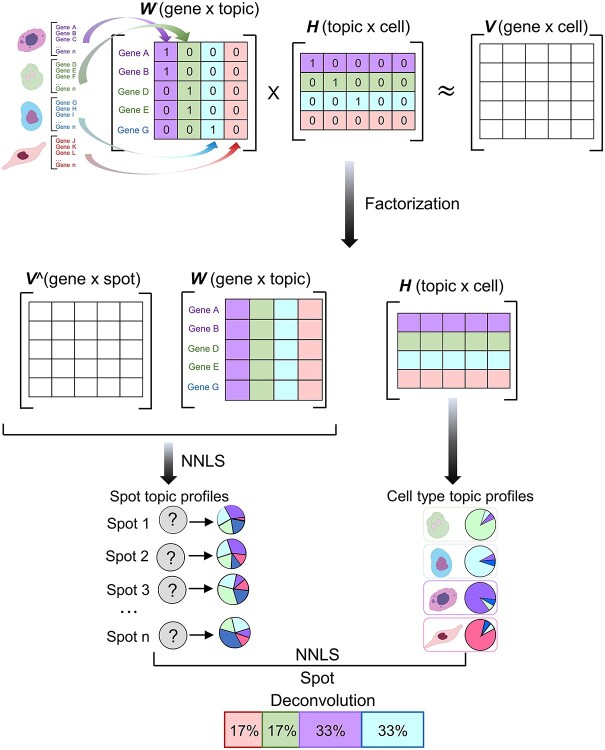
Single-cell analysis is an important analytical tool in cancer research because it overcomes the challenges of bulk analysis and provides insight into the complexity of cancer heterogeneity and lineage development at the cellular level [85–89]. Elosua-Bayes et al. developed SPOTlight, which is a computational tool that integrates spatial transcriptomics (ST) and single-cell RNA sequencing (scRNA-seq) data and leverages NMF to estimate the location of cell types and states in complex tissues (Figure 5) [90]. SPOTlight is built around a seeded NMF regression initialized using cell type marker genes and non-negative least squares, which then deconvolutes the ST capture locations (spots). Simulations with varying amounts and quality of references have been performed, and high prediction accuracy has been confirmed even with scRNA-seq reference datasets with shallow sequences or small sizes. The authors successfully segmented patient sections and finely mapped the status of normal and tumor cells using SPOTlight for the analysis of human pancreatic cancer. The authors trained on an external pancreatic cancer single-cell reference and schematized the localization of clinically relevant tumor-specific immune cells. Such visualization highlights the cooperative interactions of immune cells indigenous to the tumor, and it can provide additional insight into the specificity of the tumor microenvironment.
Figure 5.
SPOTlight approach modified from figure in Ref. 90. Initialize the basis and coefficient matrices, W and H, respectively, with prior information for the count matrix V of the scRNAseq data and the set of marker genes of the identified cell types. Assume that the number of topics k is equal to the number of cell types in the data set. The columns of W are initialized with the marker genes of the cell type associated with that topic; the rows of H are initialized with each cell’s membership in the associated topic. Next, matrix decomposition is performed from the gene distribution of each topic in W and the topic profile of each cell in H. W is used to map the ST data V^ by the non-negative least squares (NNLS) method to obtain H^. The H^ column represents the topic profile of each spot. Then, we aggregate all cells of the same cell type to obtain cell type-specific topic profiles from the H matrix obtained from the scRNAseq data. Finally, NNLS is used to find the combination of topics by cell type similar to the topic profile of each spot.
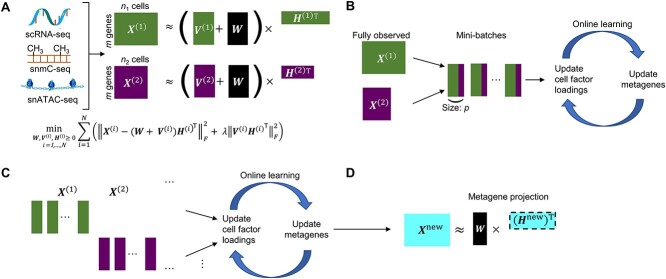
Gao et al. propose an algorithm called online integrative NMF (iNMF) for integrating large, diverse, and continuously arriving single-cell data sets [91]. This method is an extension of the NMF method, which is the core of the LIGER method already presented by the authors [92, 93]; it is developed as an online learning algorithm (Figure 6A). The authors envisioned using online iNMF to integrate single-cell data sets in three different patterns. In pattern 1, the algorithm simultaneously accesses mini-batches from all datasets and iteratively updates metagenes 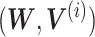 and cell factor loadings (
and cell factor loadings (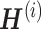 ) when the dataset is large and fully observed; each cell can be revisited through multiple learning epochs (Figure 6B). In pattern 2, the input data set is prepared sequentially, and the online algorithm uses each cell exactly once to update the metagenes; it does not revisit data that are already seen (Figure 6C). The advantage of pattern 2 is that it can improve the efficient factorization each time new data are prepared without requiring expensive recalculation. Pattern 3 allows us to project new data into the already learned potential space without using the new data to update the metagenes (Figure 6D). It allows for the efficient inclusion of new data without altering existing integration results, and it allows users to present their data to curated references. Single-cell analysis has so far focused on RNA-seq; however, it has recently been applied to epigenomic analysis such as ATAC-seq [94–96]. Single-cell level multiomics analysis methods are expected to become more important in the future. From this perspective, online iNMF is considered an important technology.
) when the dataset is large and fully observed; each cell can be revisited through multiple learning epochs (Figure 6B). In pattern 2, the input data set is prepared sequentially, and the online algorithm uses each cell exactly once to update the metagenes; it does not revisit data that are already seen (Figure 6C). The advantage of pattern 2 is that it can improve the efficient factorization each time new data are prepared without requiring expensive recalculation. Pattern 3 allows us to project new data into the already learned potential space without using the new data to update the metagenes (Figure 6D). It allows for the efficient inclusion of new data without altering existing integration results, and it allows users to present their data to curated references. Single-cell analysis has so far focused on RNA-seq; however, it has recently been applied to epigenomic analysis such as ATAC-seq [94–96]. Single-cell level multiomics analysis methods are expected to become more important in the future. From this perspective, online iNMF is considered an important technology.
Figure 6.
iNMF approach modified from figure in Ref. 91. (A) Conceptual diagram of iNMF: Input single-cell data are jointly decomposed into shared metagenes (W), dataset-specific metagenes (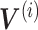 ), and corresponding ‘metagen expression levels’ or cell factor loadings (
), and corresponding ‘metagen expression levels’ or cell factor loadings (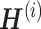 ). These metagenes and cell factor loadings quantitatively define the identity of the cell and how it changes in the biological environment. (B–D) Three different patterns of single-cell data integration with online learning. (B) Pattern 1: The single-cell data sets are large but well observed. Online iNMF processes data in random mini-batches, allowing for memory usage independent of the size of the data set. (C) Pattern 2: Datasets arrive sequentially, and the online iNMF processes the arriving datasets, using each cell only once to update the metagenes. The cell’s factor loadings on the newly arrived data set are calculated using the shared metagene (W) learned from the previously processed data set. The new dataset will not be used to update the metagene. (D) Pattern 3: Online iNMF is performed as in Pattern 1 or Pattern 2, and W and
). These metagenes and cell factor loadings quantitatively define the identity of the cell and how it changes in the biological environment. (B–D) Three different patterns of single-cell data integration with online learning. (B) Pattern 1: The single-cell data sets are large but well observed. Online iNMF processes data in random mini-batches, allowing for memory usage independent of the size of the data set. (C) Pattern 2: Datasets arrive sequentially, and the online iNMF processes the arriving datasets, using each cell only once to update the metagenes. The cell’s factor loadings on the newly arrived data set are calculated using the shared metagene (W) learned from the previously processed data set. The new dataset will not be used to update the metagene. (D) Pattern 3: Online iNMF is performed as in Pattern 1 or Pattern 2, and W and 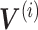 are learned. The cell’s factor loadings on the newly arrived data set are calculated using the shared metagene (W) learned from the previously processed data set.
are learned. The cell’s factor loadings on the newly arrived data set are calculated using the shared metagene (W) learned from the previously processed data set.
Meta-analysis
Meta-analytical methods of heterogeneous data are being utilized to uncover new medical and biological knowledge given the accumulation of vast amounts of omics data [97–100]. Most existing analysis methods show a high false positive rate in the detection of differentially expressed genes (DEGs) because each gene is analyzed independently [101–103]. Methods using NMF have been proposed as a solution to this problem.
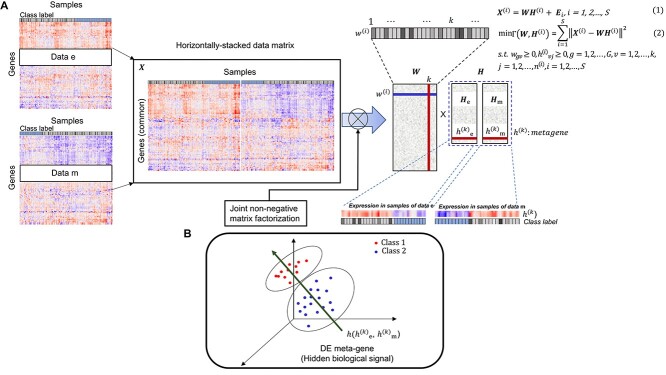
Wang et al. proposed a new meta-analysis method for DEG identification based on joint NMF (jNMFMA), which is a mathematical extension of the NMF method that decomposes multiple transcriptome data matrices into one common submatrix and multiple individual submatrices simultaneously as a joint version [102]. Given two or more transcriptome data 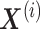 comprising the same genes, jNMFMA factors jointly into a common submatrix W (loading coefficient matrix (LCM)) for all data sets and an individual submatrix
comprising the same genes, jNMFMA factors jointly into a common submatrix W (loading coefficient matrix (LCM)) for all data sets and an individual submatrix 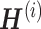 (metagen matrix (MGM)) for data set i (Figure 7A). We can form an overall metagene matrix
(metagen matrix (MGM)) for data set i (Figure 7A). We can form an overall metagene matrix 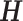 that comprises each row corresponding to metagenes representing the hidden biological signals behind the dataset by stacking all
that comprises each row corresponding to metagenes representing the hidden biological signals behind the dataset by stacking all 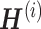 horizontally, as indicated in Figure 7B. Each row of W reflects the relationship between the metagenes and genes present in all data. As shown in Figure 7B,
horizontally, as indicated in Figure 7B. Each row of W reflects the relationship between the metagenes and genes present in all data. As shown in Figure 7B, 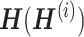 is used to identify differentially expressed (DE) metagenes associated with the phenotype of interest; DEG is identified as a gene associated with DE metagenes based on W. The authors adapted jNMFMA to three different datasets on lung cancer, performed meta-analysis, and compared its performance with five other methods reported so far. The results showed that jNMFMA had two unique features: removal of dependency structure and mitigation of data heterogeneity. Thus, we believe that the reliability and robustness of jNMFMA in detecting DEGs are improved.
is used to identify differentially expressed (DE) metagenes associated with the phenotype of interest; DEG is identified as a gene associated with DE metagenes based on W. The authors adapted jNMFMA to three different datasets on lung cancer, performed meta-analysis, and compared its performance with five other methods reported so far. The results showed that jNMFMA had two unique features: removal of dependency structure and mitigation of data heterogeneity. Thus, we believe that the reliability and robustness of jNMFMA in detecting DEGs are improved.
Figure 7.
Example of the application of NMF to cancer meta-analysis modified from figure in Ref. 102. (A) Suppose we have S datasets 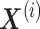 , i = 1, 2, …, S, and G common genes to be meta-analyzed. The i-th data set is denoted by
, i = 1, 2, …, S, and G common genes to be meta-analyzed. The i-th data set is denoted by 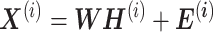 , where
, where 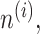 W,
W, 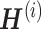 , and
, and 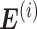 represent the number of samples in the data set, submatrix LCM of size G × k (k is an integer constant), submatrix MGM of size
represent the number of samples in the data set, submatrix LCM of size G × k (k is an integer constant), submatrix MGM of size 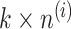 of dataset i, and error matrix of dataset i to accommodate data heterogeneity and noise, respectively. Since the objective function
of dataset i, and error matrix of dataset i to accommodate data heterogeneity and noise, respectively. Since the objective function  is not convex when W and H are combined, there is no standard algorithm for finding the immediate solution to equation (2). In practice, it is desirable to seek local minima in such optimization problems. Wang et al. develop a two-step multiplicative update algorithm for solving equation (2). (B) The DE metagenes associated with the target phenotype are identified by H(
is not convex when W and H are combined, there is no standard algorithm for finding the immediate solution to equation (2). In practice, it is desirable to seek local minima in such optimization problems. Wang et al. develop a two-step multiplicative update algorithm for solving equation (2). (B) The DE metagenes associated with the target phenotype are identified by H(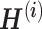 ), and DEGs are identified as genes associated with the DE metagenes based on W.
), and DEGs are identified as genes associated with the DE metagenes based on W.
The authors also performed a meta-analysis using jNMFMA on four datasets, three different transcriptome datasets, and a DNA methylation dataset with the aim of discovering cancer-related mDEGs dysregulated by DNA methylation. Consequently, NEK2 and TCF2 genes were identified as genes aberrantly expressed in lung cancer through epigenetic regulation [102]. In the future, it will be important to integrate and analyze the omics data of a large number of large cohorts in the field of oncology; we believe that it is important to use a method such as jNMFMA that can remove the dependent structure and mitigate the heterogeneity of data.
Discussion
We introduced the importance of NMF in gene expression, multiomics, single cell, and meta analyses, with a particular focus on the field of oncology. Since U.S. President Barack Obama announced the precision medicine initiative in his state of the union address in 2015, the promotion of precision medicine (i.e. personalized medicine) has become a key issue in the global health policy [104–106]. In the field of oncology, the term ‘precision oncology’ has been coined, and attempts have been started to administer optimal cancer drugs based on information about genetic mutations around the world [107–110]. The extraction of useful information from large-scale medical data is an essential task to promote medical care optimized for each individual, and machine learning techniques are expected to be introduced into the medical field in the future to help perform this task.
NMF retains various properties that can contribute to the developments in the field of precision oncology. The whole genome sequence contains an enormous amount of information (3 billion base pairs); however, only a limited amount of information is truly related to the disease. There is a need for a technology that extracts only important information while appropriately reducing dimensions; thus, the characteristics of NMF may be utilized in the future. Further, the multimodal analysis of data from various modalities is considered important in the medical field today. As discussed in this review, NMF supports multiomics analysis and is expected to be actively used for multimodal analysis in the future. A meta-analysis integrating multiple data is necessary when analyzing large-scale medical data; as indicated in this review, NMF is useful for the meta-analysis. Although not described in detail in this review due to space limitations, several publications have focused on the application of NMF to medical imaging analysis [111–116]. Further, NMF has been used for sound source separation; however, some problems related to the structure of the method have been reported. NMF is based on the following assumptions:
The observed spectrum (amplitude and power) at each time is represented by a weighted sum of the spectra (amplitude and power) of the constituent sounds (i.e. the spectrum is additive).
The amplitude ratio of the frequency components of each component is time-invariant, and only the power varies.
However, these assumptions are not valid when judged strictly [61]. This is because the conversion from the complex spectrum to the amplitude/power spectrum is non-linear and additivity does not hold, and further, the amplitude ratio of the frequency components of each component sound is invariant. To overcome this disadvantage and based on the advantage of NMF, ‘sparse signal decomposition’, and complex NMF has been developed as the new method [61].
The challenge of using NMF in cancer research, as with other matrix decomposition methods, is that loss of information due to data compression is inevitable. Therefore, it should not be used if the focus is on small changes in data components. Care must be taken when setting K, the number of bases, in NMF because the results depend on the number of latent features in the decomposition matrix i.e. K. K can be set heuristically based on domain knowledge, or a Bayesian statistical method can be devised to determine it by decomposition with multiple basis numbers [117]. As NMF extracts the common components in the data as latent features, it is also necessary to consider the effects of differences in the background and immune tissue, and tumor content in studies using cancer tissues.
There are cases where the use of NMF is not optimal depending on the nature of the data. Hence, there is a need for better understanding of the properties of NMF in the medical field before it can be widely used. In addition, the robustness of the results should be verified by conducting clinical trials, which is true not only for NMF but also for all medical research using machine learning.
Conclusions and future perspectives
NMF is a powerful tool for the promotion of precision medicine and is expected to be used in various ways in the field of oncology in the future. Currently, clinical applications of AI are advancing, and machine learning technology is recognized as an important tool for advancing medicine [21, 118–123]. In particular, the amount of data to be analyzed in the field of medicine, including whole genome analysis data, is becoming increasingly huge, and this trend is expected to become stronger in the future. Under the circumstances of the so-called ‘big data era’ [124–129], we believe that it is essential to properly introduce machine learning technology into the medical field [21, 32, 78, 130]. Considering the characteristics of NMF, it is not yet fully utilized in the medical field, and we hope that this method will be further utilized in the oncology field in the future. However, there are some cases in which it is not optimal to use NMF to analyze the data. Therefore, we need to proceed with the analysis using NMF after understanding the characteristics of the data and the NMF algorithm. We hope that this review will aid in this decision.
Key Points
NMF is a machine learning method that uses a dimensionality reduction method based on a low-rank approximation of the feature space. In addition to reducing the number of features, it ensures that the features are non-negative and generates additive models about, for example, the non-negativity of a physical quantity.
NMF has been used in various fields such as image analysis, speech recognition, and language processing, and has recently been applied in medical research.
NMF has been actively used in the field of oncology for gene expression analysis, mutational signature analysis, multi-omics analysis, single cell analysis, and meta-analysis. It is considered to be an approach that contributes to the realization of precision medicine.
As the use of NMF may not be optimal depending on the nature of the data, it is necessary to understanding the characteristics of NMF holistically is important to utilize it in the field of medicine.
Author Biographies
Ryuji Hamamoto is a Division Chief in the Division of Medical AI Research and Development, National Cancer Center Research Institute, a Professor in the Department of NCC Cancer Science, Graduate School of Medical and Dental Sciences, Tokyo Medical and Dental University, and a Team Leader of the Cancer Translational Research Team, RIKEN Center for Advanced Intelligence Project. His research interests include medical AI, omics analysis and bioinformatics.
Ken Takasawa is a Postdoctoral Researcher in the Cancer Translational Research Team, RIKEN Center for Advanced Intelligence Project, and an External Research Staff in the Medical AI Research and Development, National Cancer Center Research Institute. His research interests include medical applications of machine learning and bioinformatics.
Hidenori Machino is a Postdoctoral Researcher in the Cancer Translational Research Team, RIKEN Center for Advanced Intelligence Project, and an External Research Staff in the Medical AI Research and Development, National Cancer Center Research Institute. His research interests include gynecologic oncology and bioinformatics.
Kazuma Kobayashi is a Researcher in the Division of Medical AI Research and Development, National Cancer Center Research Institute and a Visiting Scientist in the Cancer Translational Research Team, RIKEN Center for Advanced Intelligence Project. His research interests include medical AI, radiation oncology and bioinformatics.
Satoshi Takahashi is Research Scientist in the Cancer Translational Research Team, RIKEN Center for Advanced Intelligence Project, and an External Research Staff of Medical AI Research and Development, National Cancer Center Research Institute. His research interests include brain tumors, medical AI and bioinformatics.
Amina Bolatkan is a Postdoctoral Researcher in the Cancer Translational Research Team, RIKEN Center for Advanced Intelligence Project, and an External Research Staff of Medical AI Research and Development, National Cancer Center Research Institute. Her research interests include medical AI, omics analysis and bioinformatics.
Norio Shinkai is a PhD candidate in the Department of NCC Cancer Science, Graduate School of Medical and Dental Sciences, Tokyo Medical and Dental University. His research interests include bioinformatics, omics analysis and machine learning applications in medicine.
Akira Sakai is a PhD candidate in the Department of NCC Cancer Science, Graduate School of Medical and Dental Sciences, Tokyo Medical and Dental University. His research interests include medical AI, machine learning and bioinformatics.
Rina Aoyama is a PhD candidate in the Department of Obstetrics and Gynecology, Showa University School of Medicine. Her research interests include obstetrics and gynecology, medical AI and bioinformatics.
Masayoshi Yamada is a Medical Staff in the Department of Endoscopy, National Cancer Center Hospital. His research interests include gastrointestinal endoscopy, medical AI and bioinformatics.
Ken Asada is a Research Scientist in the Cancer Translational Research Team, RIKEN Center for Advanced Intelligence Project, and an External Research Staff of Medical AI Research and Development, National Cancer Center Research Institute. His research interests include omics analysis, bioinformatics and medical AI.
Masaaki Komatsu is a Deputy Team Leader in the Cancer Translational Research Team, RIKEN Center for Advanced Intelligence Project, and an External Research Staff of Medical AI Research and Development, National Cancer Center Research Institute. His research interests include obstetrics and gynecology, medical AI and bioinformatics.
Koji Okamoto is a Division Chief in the Cancer Differentiation, National Cancer Center Research Institute. His research interests include oncology, single cell analysis and bioinformatics.
Hirokazu Kameoka is a Senior Distinguished Researcher at NTT Communication Science Laboratories. His research interests include machine learning and computer science.
Syuzo Kaneko is a Laboratory Head in the Division of Medical AI Research and Development, National Cancer Center Research Institute and a Visiting Scientist in the Cancer Translational Research Team, RIKEN Center for Advanced Intelligence Project. His research interests include epigenomics, bioinformatics and medical AI.
Contributor Information
Ryuji Hamamoto, National Cancer Center Research Institute.
Ken Takasawa, RIKEN Center for Advanced Intelligence Project.
Hidenori Machino, RIKEN Center for Advanced Intelligence Project.
Kazuma Kobayashi, National Cancer Center Research Institute.
Satoshi Takahashi, RIKEN Center for Advanced Intelligence Project.
Amina Bolatkan, RIKEN Center for Advanced Intelligence Project.
Norio Shinkai, Tokyo Medical and Dental University.
Akira Sakai, Tokyo Medical and Dental University.
Rina Aoyama, Showa University Graduate School of Medicine School of Medicine.
Masayoshi Yamada, National Cancer Center Hospital.
Ken Asada, RIKEN Center for Advanced Intelligence Project.
Masaaki Komatsu, RIKEN Center for Advanced Intelligence Project.
Koji Okamoto, National Cancer Center Research Institute.
Hirokazu Kameoka, NTT Communication Science Laboratories.
Syuzo Kaneko, National Cancer Center Research Institute.
Funding
This work was supported by MHLW ICT infrastructure establishment and implementation of artificial intelligence for clinical and medical research program, Grant Number (JP21AC5001) and RIKEN Center for the Advanced Intelligence Project.
References
- 1. Xu P. Review on studies of machine learning algorithms. J Phys Conf Ser 2019;1187:052103. [Google Scholar]
- 2. Jordan MI, Mitchell TM. Machine learning: trends, perspectives, and prospects. Science 2015;349:255–60. [DOI] [PubMed] [Google Scholar]
- 3. Samuel AL. Some studies in machine learning using the game of checkers. IBM J Res Dev 1959;3:210–29. [Google Scholar]
- 4. Rezapouraghdam H, Akhshik A, Ramkissoon H. Application of machine learning to predict visitors’ green behavior in marine protected areas: evidence from Cyprus. J Sustain Tour 2021;1–25. [Google Scholar]
- 5. Dey S, Singh AK, Wang X, et al. User interaction aware reinforcement learning for power and thermal efficiency of CPU-GPU mobile MPSoCs. In: 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE). Grenoble, France: IEEE 2020, pp. 1728–33.
- 6. Reyes-Campos J, Alor-Hernández G, Machorro-Cano I, et al. Discovery of resident behavior patterns using machine learning techniques and IoT paradigm. Mathematics 2021;9:219. [Google Scholar]
- 7. Ying W, Shou W, Wang J, et al. Automatic scaffolding workface assessment for activity analysis through machine learning. Appl Sci 2021;11:4143. [Google Scholar]
- 8. Lillstrang M, Harju M, del Campo G, et al. Implications of properties and quality of indoor sensor data for building machine learning applications: two case studies in smart campuses. Build Environ 2022;207:108529. [Google Scholar]
- 9. Sharif MS, Romo BA, Maltby H, et al. An effective hybrid approach based on machine learning techniques for auto-translation: Japanese to English. In: 2021 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT). Zallaq, Bahrain: IEEE, 2021, pp. 557–62.
- 10. Sharma N, Sharma R, Jindal N. Machine learning and deep learning applications-a vision. Global Transitions Proc 2021;2:24–8. [Google Scholar]
- 11. Iyer SS, Rajagopal S. Applications of machine learning in cyber security domain. In Handbook of Research on Machine and Deep Learning Applications for Cyber Security. Hershey, PA, USA: IGI Global, 2020; pp. 64–82. [Google Scholar]
- 12. Sharma R, Kamble SS, Gunasekaran A, et al. A systematic literature review on machine learning applications for sustainable agriculture supply chain performance. Comput Oper Res 2020;119:104926. [Google Scholar]
- 13. Jinnai S, Yamazaki N, Hirano Y, et al. The development of a skin cancer classification system for pigmented skin lesions using deep learning. Biomolecules 2020;10:1123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Kobayashi K, Hataya R, Kurose Y, et al. Decomposing normal and abnormal features of medical images for content-based image retrieval of glioma imaging. Med Image Anal 2021;74:102227. [DOI] [PubMed] [Google Scholar]
- 15. Komatsu M, Sakai A, Komatsu R, et al. Detection of cardiac structural abnormalities in fetal ultrasound videos using deep learning. Appl Sci 2021;11:371. [Google Scholar]
- 16. Yamada M, Saito Y, Imaoka H, et al. Development of a real-time endoscopic image diagnosis support system using deep learning technology in colonoscopy. Sci Rep 2019;9:14465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Giger ML. Machine learning in medical imaging. J Am Coll Radiol 2018;15:512–20. [DOI] [PubMed] [Google Scholar]
- 18. Rashidi HH, Tran NK, Betts EV, et al. Artificial intelligence and machine learning in pathology: the present landscape of supervised methods. Acad Pathol 2019;6:2374289519873088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Das K, Cockerell CJ, Patil A, et al. Machine learning and its application in skin cancer. Int J Environ Res Public Health 2021;18:13409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Math L, Fatima R. Adaptive machine learning classification for diabetic retinopathy. Multimed Tools Appl 2020;80:5173–86. [Google Scholar]
- 21. Hamamoto R, Suvarna K, Yamada M, et al. Application of artificial intelligence technology in oncology: towards the establishment of precision medicine. Cancers (Basel) 2020;12:3532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Bleijendaal H, Croon PM, Pool MDO, et al. Clinical applicability of artificial intelligence for patients with an inherited heart disease: a scoping review. Trends Cardiovasc Med 2022. https://pubmed.ncbi.nlm.nih.gov/35101643/. [DOI] [PubMed] [Google Scholar]
- 23. Gharavi SMH, Faghihimehr A. Clinical application of artificial intelligence in PET imaging of head and neck cancer. PET Clin 2022;17:65–76. [DOI] [PubMed] [Google Scholar]
- 24. Dozen A, Komatsu M, Sakai A, et al. Image segmentation of the ventricular septum in fetal cardiac ultrasound videos based on deep learning using time-series information. Biomolecules 2020;10:1526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Kobayashi K, Miyake M, Takahashi M, et al. Observing deep radiomics for the classification of glioma grades. Sci Rep 2021;11:10942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Shozu K, Komatsu M, Sakai A, et al. Model-agnostic method for thoracic wall segmentation in fetal ultrasound videos. Biomolecules 2020;10:1691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Yasutomi S, Arakaki T, Matsuoka R, et al. Shadow estimation for ultrasound images using auto-encoding structures and synthetic shadows. Appl Sci 2021;11:1127. [Google Scholar]
- 28. Capobianco E. High-dimensional role of AI and machine learning in cancer research. Br J Cancer 2022;126:523–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Albaradei S, Thafar M, Alsaedi A, et al. Machine learning and deep learning methods that use omics data for metastasis prediction. Comput Struct Biotechnol J 2021;19:5008–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Asada K, Kobayashi K, Joutard S, et al. Uncovering prognosis-related genes and pathways by multi-omics analysis in lung cancer. Biomolecules 2020;10:524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Kobayashi K, Bolatkan A, Shiina S, et al. Fully-connected neural networks with reduced parameterization for predicting histological types of lung cancer from somatic mutations. Biomolecules 2020;10:1249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Hamamoto R, Komatsu M, Takasawa K, et al. Epigenetics analysis and integrated analysis of multiomics data, including epigenetic data, using artificial intelligence in the era of precision medicine. Biomolecules 2020;10:62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Kumlu D, Erer I. Clutter removal in GPR images using non-negative matrix factorization. J Electromagn Waves Appl 2018;32:2055–66. [Google Scholar]
- 34. Yang Z, Zhang Y, Xiang Y, et al. Non-negative matrix factorization with dual constraints for image clustering. IEEE Trans Syst Man Cybern Syst 2020;50:2524–33. [Google Scholar]
- 35. Zhao Y, Wang H, Pei J. Deep non-negative matrix factorization architecture based on underlying basis images learning. IEEE Trans Pattern Anal Mach Intell 2021;43:1897–913. [DOI] [PubMed] [Google Scholar]
- 36. Bando Y, Mimura M, Itoyama K, et al. Statistical speech enhancement based on probabilistic integration of variational autoencoder and non-negative matrix factorization. In: 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Calgary, AB, Canada: IEEE, 2018, pp. 716–20.
- 37. Hou M, Li J, Lu G. A supervised non-negative matrix factorization model for speech emotion recognition. Speech Commun 2020;124:13–20. [Google Scholar]
- 38. Karan B, Sahu SS, Orozco-Arroyave JR, et al. Non-negative matrix factorization-based time-frequency feature extraction of voice signal for Parkinson’s disease prediction. Comput Speech Lang 2021;69:101216. [Google Scholar]
- 39. Ren B, Pueyo L, Zhu GB, et al. Non-negative matrix factorization: robust extraction of extended structures. Astrophys J 2018;852:104. [Google Scholar]
- 40. Blanton MR, Roweis S. K-corrections and filter transformations in the ultraviolet, optical, and near-infrared. Astron J 2007;133:734–54. [Google Scholar]
- 41. Berne O, Helens A, Pilleri P, et al. Non-negative matrix factorization pansharpening of hyperspectral data: an application to mid-infrared astronomy. In: 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing. Reykjavik, Iceland: IEEE, 2010, pp.1–4.
- 42. Ren B, Pueyo L, Chen C, et al. Using data imputation for signal separation in high-contrast imaging. Astrophys J 2020;892:74. [Google Scholar]
- 43. Kameoka H. Non-negative matrix factorization and its variants for audio signal processing. In Appl Matrix Tensor Variate Data Anal. Japan: Springer, 2016; pp. 23–50. [Google Scholar]
- 44. Arifin AZ, Sari YA, Ratnasari EK, et al. Emotion detection of tweets in Indonesian language using non-negative matrix factorization. Int J Intell Syst Appl 2014;6:54–61. [Google Scholar]
- 45. Lin C-Y, Kang L-W, Huang T-Y, et al. A novel non-negative matrix factorization technique for decomposition of Chinese characters with application to secret sharing. EURASIP J Adv Signal Process 2019;35:1–8. [Google Scholar]
- 46. Kysenko V, Rupp K, Marchenko O, et al. GPU-accelerated non-negative matrix factorization for text mining. Nat Lang Process Inf Syst 2012;7337:158–63. [Google Scholar]
- 47. Wu F, Cai J, Wen C, et al. Co-sparse non-negative matrix factorization. Front Neurosci 2021;15:804554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Li J, Wells J, Yang C, et al. A novel application of non-negative matrix factorization to the prediction of the health status of undocumented immigrants. Health Equity 2021;5:834–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Tang X, Cai L, Meng Y, et al. Indicator regularized non-negative matrix factorization method-based drug repurposing for COVID-19. Front Immunol 2020;11:603615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Kopriva I, Ju W, Zhang B, et al. Single-channel sparse non-negative blind source separation method for automatic 3-D delineation of lung tumor in PET images. IEEE J Biomed Health Inform 2017;21:1656–66. [DOI] [PubMed] [Google Scholar]
- 51. Chung Y, Lee H, the Alzheimer’s Disease Neuroimaging Initiative, et al. The Alzheimer's disease neuroimaging I. correlation between Alzheimer's disease and type 2 diabetes using non-negative matrix factorization. Sci Rep 2021;11:15265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Chen C, Zhou J, Yu H, et al. Identification of important risk factors for all-cause mortality of acquired long QT syndrome patients using random survival forests and non-negative matrix factorization. Heart Rhythm 2021;18:426–33. [DOI] [PubMed] [Google Scholar]
- 53. Taslaman L, Nilsson B. A framework for regularized non-negative matrix factorization, with application to the analysis of gene expression data. PLoS One 2012;7:e46331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Devarajan K. Nonnegative matrix factorization: an analytical and interpretive tool in computational biology. PLoS Comput Biol 2008;4:e1000029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Alexandrov LB, Nik-Zainal S, Wedge DC, et al. Deciphering signatures of mutational processes operative in human cancer. Cell Rep 2013;3:246–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Stein-O'Brien GL, Arora R, Culhane AC, et al. Enter the matrix: factorization uncovers knowledge from omics. Trends Genet 2018;34:790–805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Lawton WH, Sylvestre EA. Self modeling curve resolution. Dent Tech 1971;13:617. [Google Scholar]
- 58. Paatero P, Tapper U, Aalto P, et al. Matrix factorization methods for analysing diffusion battery data. J Aerosol Sci 1991;22:S273–6. [Google Scholar]
- 59. Paatero P, Tapper U. Positive matrix factorization: a non-negative factor model with optimal utilization of error estimates of data values. Environmetrics 1994;5:111–26. [Google Scholar]
- 60. Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature 1999;401:788–91. [DOI] [PubMed] [Google Scholar]
- 61. Kameoka H. Non-negative matrix factorization and its variants with applications to audio signal processing. J Jpn Stat Soc 2015;44:383–407. [Google Scholar]
- 62. Lee DD, Seung HS. Algorithms for non-negative matrix factorization. Adv Neural Inf Process Syst 2001;13:556–62. [Google Scholar]
- 63. Hoyer PO. Non-negative matrix factorization with sparseness constraints. J Mach Learn Res 2004;5:1457–69. [Google Scholar]
- 64. Cho YJ, Tsherniak A, Tamayo P, et al. Integrative genomic analysis of medulloblastoma identifies a molecular subgroup that drives poor clinical outcome. J Clin Oncol 2011;29:1424–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Taylor MA, Wappett M, Delpuech O, et al. Enhanced MAPK signaling drives ETS1-mediated induction of miR-29b leading to downregulation of TET1 and changes in epigenetic modifications in a subset of lung SCC. Oncogene 2016;35:4345–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Barras D, Missiaglia E, Wirapati P, et al. BRAF V600E mutant colorectal cancer subtypes based on gene expression. Clin Cancer Res 2017;23:104–15. [DOI] [PubMed] [Google Scholar]
- 67. Li R, He Y, Zhang H, et al. Identification and validation of immune molecular subtypes in pancreatic ductal adenocarcinoma: implications for prognosis and immunotherapy. Front Immunol 2021;12:690056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Alexandrov LB, Nik-Zainal S, Wedge DC, et al. Signatures of mutational processes in human cancer. Nature 2013;500:415–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Szuts D. A fresh look at somatic mutations in cancer. Science 2022;376:351–2. [DOI] [PubMed] [Google Scholar]
- 70. Langenbucher A, Bowen D, Sakhtemani R, et al. An extended APOBEC3A mutation signature in cancer. Nat Commun 2021;12:1602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. He Y, Shi M, Wu X, et al. Mutational signature analysis reveals widespread contribution of pyrrolizidine alkaloid exposure to human liver cancer. Hepatology 2021;74:264–80. [DOI] [PubMed] [Google Scholar]
- 72. Blokzijl F, Janssen R, van Boxtel R, et al. Mutational patterns: comprehensive genome-wide analysis of mutational processes. Genome Med 2018;10:33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Gehring JS, Fischer B, Lawrence M, et al. Somatic signatures: inferring mutational signatures from single-nucleotide variants. Bioinformatics 2015;31:3673–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Ardin M, Cahais V, Castells X, et al. MutSpec: a galaxy toolbox for streamlined analyses of somatic mutation spectra in human and mouse cancer genomes. BMC Bioinf 2016;17:170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Diaz-Gay M, Vila-Casadesus M, Franch-Exposito S, et al. Mutational signatures in cancer (MuSiCa): a web application to implement mutational signatures analysis in cancer samples. BMC Bioinf 2018;19:224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Takahashi S, Asada K, Takasawa K, et al. Predicting deep learning based multi-omics parallel integration survival subtypes in lung cancer using reverse phase protein array data. Biomolecules 2020;10:1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Takahashi S, Takahashi M, Tanaka S, et al. A new era of neuro-oncology research pioneered by multi-omics analysis and machine learning. Biomolecules 2021;11:565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Asada K, Kaneko S, Takasawa K, et al. Integrated analysis of whole genome and epigenome data using machine learning technology: toward the establishment of precision oncology. Front Oncol 2021;11:666937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Nicora G, Vitali F, Dagliati A, et al. Integrated multi-omics analyses in oncology: a review of machine learning methods and tools. Front Oncol 2020;10:1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Lindskrog SV, Prip F, Lamy P, et al. An integrated multi-omics analysis identifies prognostic molecular subtypes of non-muscle-invasive bladder cancer. Nat Commun 2021;12:2301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Taber A, Christensen E, Lamy P, et al. Molecular correlates of cisplatin-based chemotherapy response in muscle invasive bladder cancer by integrated multi-omics analysis. Nat Commun 2020;11:4858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Wang P, Gao L, Hu Y, et al. Feature related multi-view nonnegative matrix factorization for identifying conserved functional modules in multiple biological networks. BMC Bioinf 2018;19:394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Lemsara A, Ouadfel S, Frohlich H. PathME: pathway based multi-modal sparse autoencoders for clustering of patient-level multi-omics data. BMC Bioinf 2020;21:146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Wang B, Ma X, Xie M, et al. CBP-JMF: an improved joint matrix tri-factorization method for characterizing complex biological processes of diseases. Front Genet 2021;12:665416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Asada K, Takasawa K, Machino H, et al. Single-cell analysis using machine learning techniques and its application to medical research. Biomedicines 2021;9:1513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Tellez-Gabriel M, Ory B, Lamoureux F, et al. Tumour heterogeneity: the key advantages of single-cell analysis. Int J Mol Sci 2016;17:2142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Durante MA, Rodriguez DA, Kurtenbach S, et al. Single-cell analysis reveals new evolutionary complexity in uveal melanoma. Nat Commun 2020;11:496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Jackson HW, Fischer JR, Zanotelli VRT, et al. The single-cell pathology landscape of breast cancer. Nature 2020;578:615–20. [DOI] [PubMed] [Google Scholar]
- 89. Yuan H, Yan M, Zhang G, et al. CancerSEA: a cancer single-cell state atlas. Nucleic Acids Res 2019;47:D900–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90. Elosua-Bayes M, Nieto P, Mereu E, et al. SPOTlight: seeded NMF regression to deconvolute spatial transcriptomics spots with single-cell transcriptomes. Nucleic Acids Res 2021;49:e50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. Gao C, Liu J, Kriebel AR, et al. Iterative single-cell multi-omic integration using online learning. Nat Biotechnol 2021;39:1000–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Welch JD, Kozareva V, Ferreira A, et al. Single-cell multi-omic integration compares and contrasts features of brain cell identity. Cell 2019;177:1873–87.e17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Liu J, Gao C, Sodicoff J, et al. Jointly defining cell types from multiple single-cell datasets using LIGER. Nat Protoc 2020;15:3632–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. LaFave LM, Savage R, Buenrostro JD. Single-cell epigenomics reveals mechanisms of cancer progression. Ann Rev Cancer Biol 2022;6:167–85. [Google Scholar]
- 95. Lin Y, Wu TY, Wan S, et al. scJoint integrates atlas-scale single-cell RNA-seq and ATAC-seq data with transfer learning. Nat Biotechnol 2022;40:703–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Finkbeiner C, Ortuno-Lizaran I, Sridhar A, et al. Single-cell ATAC-seq of fetal human retina and stem-cell-derived retinal organoids shows changing chromatin landscapes during cell fate acquisition. Cell Rep 2022;38:110294. [DOI] [PubMed] [Google Scholar]
- 97. Field AP, Gillett R. How to do a meta-analysis. Br J Math Stat Psychol 2010;63:665–94. [DOI] [PubMed] [Google Scholar]
- 98. Trikalinos TA, Salanti G, Zintzaras E, et al. Meta-analysis methods. Adv Genet 2008;60:311–34. [DOI] [PubMed] [Google Scholar]
- 99. Gurevitch J, Koricheva J, Nakagawa S, et al. Meta-analysis and the science of research synthesis. Nature 2018;555:175–82. [DOI] [PubMed] [Google Scholar]
- 100. Efthimiou O. Practical guide to the meta-analysis of rare events. Evid Based Ment Health 2018;21:72–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Xia J, Fjell CD, Mayer ML, et al. INMEX--a web-based tool for integrative meta-analysis of expression data. Nucleic Acids Res 2013;41:W63–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102. Wang HQ, Zheng CH, Zhao XM. jNMFMA: a joint non-negative matrix factorization meta-analysis of transcriptomics data. Bioinformatics 2015;31:572–80. [DOI] [PubMed] [Google Scholar]
- 103. DerSimonian R, Laird N. Meta-analysis in clinical trials revisited. Contemp Clin Trials 2015;45:139–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Ashley EA. The precision medicine initiative: a new national effort. JAMA 2015;313:2119–20. [DOI] [PubMed] [Google Scholar]
- 105. Ashley EA. Towards precision medicine. Nat Rev Genet 2016;17:507–22. [DOI] [PubMed] [Google Scholar]
- 106. Saito M, Shiraishi K, Kunitoh H, et al. Gene aberrations for precision medicine against lung adenocarcinoma. Cancer Sci 2016;107:713–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107. Senft D, Leiserson MDM, Ruppin E, et al. Precision oncology: the road ahead. Trends Mol Med 2017;23:874–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108. Kumar-Sinha C, Chinnaiyan AM. Precision oncology in the age of integrative genomics. Nat Biotechnol 2018;36:46–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Shin SH, Bode AM, Dong Z. Addressing the challenges of applying precision oncology. NPJ Precis Oncol 2017;1:28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Singer J, Irmisch A, Ruscheweyh HJ, et al. Bioinformatics for precision oncology. Brief Bioinf 2019;20:778–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Aonishi T, Maruyama R, Ito T, et al. Imaging data analysis using non-negative matrix factorization. Neurosci Res 2021. https://pubmed.ncbi.nlm.nih.gov/34953961/. [DOI] [PubMed] [Google Scholar]
- 112. Xie Y, Zhao J, Zhang P. A multicompartment model for intratumor tissue-specific analysis of DCE-MRI using non-negative matrix factorization. Med Phys 2021;48:2400–11. [DOI] [PubMed] [Google Scholar]
- 113. Robert C, Patel R, Blostein N, et al. Analyses of microstructural variation in the human striatum using non-negative matrix factorization. Neuroimage 2022;246:118744. [DOI] [PubMed] [Google Scholar]
- 114. Sauwen N, Sima DM, Van Cauter S, et al. Hierarchical non-negative matrix factorization to characterize brain tumor heterogeneity using multi-parametric MRI. NMR Biomed 2015;28:1599–624. [DOI] [PubMed] [Google Scholar]
- 115. Sauwen N, Acou M, Sima DM, et al. Semi-automated brain tumor segmentation on multi-parametric MRI using regularized non-negative matrix factorization. BMC Med Imaging 2017;17:29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116. Deng J, Zeng W, Kong W, et al. Multi-constrained joint non-negative matrix factorization with application to imaging genomic study of lung metastasis in soft tissue sarcomas. IEEE Trans Biomed Eng 2020;67:2110–8. [DOI] [PubMed] [Google Scholar]
- 117. Cemgil AT. Bayesian inference for nonnegative matrix factorisation models. Comput Intell Neurosci 2009;2009:785152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118. Asada K, Komatsu M, Shimoyama R, et al. Application of artificial intelligence in COVID-19 diagnosis and therapeutics. J Pers Med 2021;11:886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119. Hamamoto R. Application of artificial intelligence for medical research. Biomolecules 2021;11:90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120. Komatsu M, Sakai A, Dozen A, et al. Towards clinical application of artificial intelligence in ultrasound imaging. Biomedicines 2021;9:720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121. Yamada M, Saito Y, Yamada S, et al. Detection of flat colorectal neoplasia by artificial intelligence: a systematic review. Best Pract Res Clin Gastroenterol 2021;52–53:101745. [DOI] [PubMed] [Google Scholar]
- 122. Kawaguchi RK, Takahashi M, Miyake M, et al. Assessing versatile machine learning models for glioma Radiogenomic studies across hospitals. Cancers (Basel) 2021;13:3611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123. Briganti G, Le Moine O. Artificial intelligence in medicine: today and tomorrow. Front Med (Lausanne) 2020;7:27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124. Manrai AK, Patel CJ, Ioannidis JPA. In the era of precision medicine and big data, who is normal? JAMA 2018;319:1981–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125. Yang J, Li Y, Liu Q, et al. Brief introduction of medical database and data mining technology in big data era. J Evid Based Med 2020;13:57–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126. Kinkorova J, Topolcan O. Biobanks in the era of big data: objectives, challenges, perspectives, and innovations for predictive, preventive, and personalised medicine. EPMA J 2020;11:333–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127. He Z, Tang X, Yang X, et al. Clinical trial generalizability assessment in the big data era: a review. Clin Transl Sci 2020;13:675–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128. Zhao L. Event prediction in the big data era. ACM Comput Surv 2022;54:1–37. [Google Scholar]
- 129. Lin JC, Fan CT, Liao CC, et al. Taiwan biobank: making cross-database convergence possible in the big data era. Gigascience 2018;7:1–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130. Weintraub WS, Fahed AC, Rumsfeld JS. Translational medicine in the era of big data and machine learning. Circ Res 2018;123:1202–4. [DOI] [PubMed] [Google Scholar]
- 131. Lu X, Zhang K, Van Sant C, et al. An algorithm for classifying tumors based on genomic aberrations and selecting representative tumor models. BMC Med Genomics 2010;3:23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132. Ortega-Martorell S, Lisboa PJ, Vellido A, et al. Convex non-negative matrix factorization for brain tumor delimitation from MRSI data. PLoS One 2012;7:e47824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133. Schlicker A, Beran G, Chresta CM, et al. Subtypes of primary colorectal tumors correlate with response to targeted treatment in colorectal cell lines. BMC Med Genomics 2012;5:66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134. Li Y, Sima DM, Cauter SV, et al. Hierarchical non-negative matrix factorization (hNMF): a tissue pattern differentiation method for glioblastoma multiforme diagnosis using MRSI. NMR Biomed 2013;26:307–19. [DOI] [PubMed] [Google Scholar]
- 135. Xu J, Xiang L, Wang G, et al. Sparse non-negative matrix factorization (SNMF) based color unmixing for breast histopathological image analysis. Comput Med Imaging Graph 2015;46(Pt 1):20–9. [DOI] [PubMed] [Google Scholar]
- 136. Chalise P, Fridley BL. Integrative clustering of multi-level 'omic data based on non-negative matrix factorization algorithm. PLoS One 2017;12:e0176278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137. Zhu R, Liu JX, Zhang YK, et al. A robust manifold graph regularized nonnegative matrix factorization algorithm for cancer gene clustering. Molecules 2017;22:2131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138. Chen J, Zhang S. Discovery of two-level modular organization from matched genomic data via joint matrix tri-factorization. Nucleic Acids Res 2018;46:5967–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139. Yu N, Gao YL, Liu JX, et al. Co-differential gene selection and clustering based on graph regularized multi-view NMF in cancer genomic data. Genes (Basel) 2018;9:586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140. Xiao Q, Luo J, Liang C, et al. CeModule: an integrative framework for discovering regulatory patterns from genomic data in cancer. BMC Bioinf 2019;20:67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141. Zeng Z, Vo AH, Mao C, et al. Cancer classification and pathway discovery using non-negative matrix factorization. J Biomed Inform 2019;96:103247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142. Xuan P, Zhang Y, Zhang T, et al. Predicting miRNA-disease associations by incorporating projections in low-dimensional space and local topological information. Genes (Basel) 2019;10:685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143. Thutkawkorapin J, Eisfeldt J, Tham E, et al. pyCancerSig: subclassifying human cancer with comprehensive single nucleotide, structural and microsatellite mutational signature deconstruction from whole genome sequencing. BMC Bioinf 2020;21:128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144. Wen X, Gao L, Hu Y. LAceModule: identification of competing endogenous RNA modules by integrating dynamic correlation. Front Genet 2020;11:235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145. Ding Q, Sun Y, Shang J, et al. NMFNA: a non-negative matrix factorization network analysis method for identifying modules and characteristic genes of pancreatic cancer. Front Genet 2021;12:678642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146. Wang Y, Guan T, Zhou G, et al. SOJNMF: identifying multidimensional molecular regulatory modules by sparse orthogonality-regularized joint non-negative matrix factorization algorithm. IEEE/ACM Trans Comput Biol Bioinf 2021;1. https://pubmed.ncbi.nlm.nih.gov/34546925/. [DOI] [PubMed] [Google Scholar]