Abstract
Interval-valued data have been commonly encountered in practice, and Symbolic Data Analysis provides a solution to the statistical treatment of these data. Regression analysis for interval-valued symbolic data is a topic that has been widely investigated in the literature of symbolic data analysis, and several models from different paradigms have been proposed. There are basic regression assumptions, and it is essential to validate them. This paper introduces an approach to check interval regression model adequacy based on residual analysis. Concepts of ordinary and standardized interval residual are presented, and graphical analysis of these residuals is also proposed. To show the usefulness of the proposed approach, an application for estimating school dropout in the scenario of Brazilian municipalities is performed. We observed some outliers from the interval residuals analysis, and interval robust regression models are more suitable for estimating school dropout.
Keywords: Symbolic data analysis, Educational data, Residual, Interval-valued symbolic data, Regression
Introduction
In many real experiences, data can have internal variation. These data can arise in two situations. First, the original data may be naturally collected as lists, intervals or histograms. For example, by recording air temperature changes in meteorological stations throughout the day, the result is not a single value but a range of values, i.e., an interval. Second, original data can be processed, and lists, intervals or histograms can be produced. With the advent of modern computer science, the ability to generate, store and collect massive size data sets is expected in the most varied scenarios. Often, the importance of analyze these massive data sets can require the use of specific methodologies. A example is to aggregate individual observations into groups of interests, especially when characteristics of groups are of higher interest to an analyst than those of individual observations. For example, data about scientific production for analyzing research groups and not individual researchers [23]. The result is not a single value as mean or median but can also be an interval for each variable. To represent data taking into account internal variability within each observation, variables have allowed assuming new forms.
Symbolic data analysis (SDA) provides a framework where the variability observed may effectively be considered in the data representation, and methods that take it into account. Symbolic data values can be intervals, histograms, distributions, lists of values, taxonomies, etc. This kind of data is called symbolic because it is not purely numerical to express the internal variation of each concept. Symbolic data can be induced from classical data, and this type of data allows to take into account more complete and complex information. SDA extends exploratory data analysis and data mining (regression, rule discovery, clustering, factor analysis, discriminant analysis, decision trees, neural networks, etc.) from standard data to symbolic data. An extensive coverage of symbolic data analysis methods can be found in Bock and Diday [7], Billard and Diday [4–6], Diday and Noirhomme-Fraiture [10], and Diday [9].
These symbolic variables can be obtained from classic variables to generate a symbolic data set. As an example, considering a data set with information on patients diagnosed with COVID-19 from different cities of a country. The classical variables include personal and demographics information, clinical characteristics, laboratory results, treatment options, and outcomes. Thus, the individual entities in the classical data set are patients and cities can aggregate these in order to obtain a new data set regarding different symbolic variables (histogram, bar chart of categories, interval) as presented in Fig. 1. In this example, the cities are new units, called classes [9], and the variability between patients inside their cities (classes) is described by symbolic variables expressing the variability of the patients inside each city.
Fig. 1.
Classic COVID data set describes a set of individuals by a set of standard variables (x). Symbolic COVID data set describes a set of cities by a set of symbolic variables ( )
Since interval-valued data are by far the most popular symbolic data type in the literature and the most commonly encountered one in practice, this paper focuses applied statistics for interval-valued data inherently symbolic or become symbolic data after processing. There are at least three reasons for inducing interval-valued symbolic data.
The variables take into account variability intrinsic to each unit.
Ensure the privacy of individuals: The original data contain information that explicitly classifies individuals. The generalization process by minimum and maximum values allows to ensure the confidentiality of the original data;
By using aggregated data, the number of individuals and the number of variables defined by the single value of each category are reduced. Moreover, the new data set can represent profiles.
In order to contribute to the practical and theoretical advances of statistical modelling for interval-valued symbolic data, this work introduces residual analysis with an application to interval-valued symbolic educational data. Key aspects of this approach are highlighted as follows:
In the theoretical context, this paper proposes a way for checking if a regression model for interval-valued symbolic data works well for the data at hand. Thus, new concepts of interval residual and graphical tools are presented. These can be applied to any interval regression model of the SDA literature. Regression diagnostic is an important task for evaluating models. Moreover, descriptive measures such as skewness and kurtosis for interval-valued data are introduced, and a box plot for interval-valued symbolic data is also proposed based on lower and upper bounds. The approach is evaluated based on different linear models regarding an application with education data.
In the practical context, a novel perspective of handling data in Brazilian educational data scenarios is presented to estimate school dropout in elementary education. Here, it provides a guide for selecting variables, performing regression analysis, checking the quality of the built models and evaluating the prediction ability of these models based on interval-valued symbolic data and can be applied to estimate an index of the educational domain. The use of interval-valued symbolic data allows solving dimension problems, reducing and preserving their information privacy. Moreover, this process can also be used in any data application domain regarding interval-valued symbolic data and regression approaches.
The rest of the paper is organized as follows: Sect. 2 discusses related works for interval regression analysis. Section 3 introduces residual analysis for interval-valued symbolic data. Section 4 relates the application with interval-valued symbolic educational data, and Sects. 5 and 6 show the potentiality of the proposed approach regarding different linear models of the SDA literature. Finally, Sect. 7 gives the concluding remarks.
Related works for interval linear regression analysis
Linear regression based on the least squares approach for interval-valued symbolic data has been attracting increasing interest among researchers.
The first work in the regression model for interval-valued symbolic data can be found in Billard and Diday [2] and Billard and Diday [3]. Lima Neto and De Carvalho [18] considered a representation for interval based on center and range of the interval. Also, they developed a regression model based on a new representation. Lima Neto and De Carvalho [19] proposed a constrained linear regression model on the center and range representation to ensure mathematical coherence between the predicted values of the lower and upper boundaries of the intervals. Fagundes et al. [11] presented a robust prediction method for interval-valued symbolic data based on the linear robust regression methodology.
Hao and Guo [13] presented constrained regression models for intervals based on ordinary least squares (OLS). Souza et al. [31] introduced the parametrized method, a linear regression model based on the lower-upper representation. Soares and Fagundes [30] proposed an interval quantile regression for interval-valued symbolic data represented by centers and ranges. Lima Neto and De Carvalho [20] introduced a robust based on the weighted least squares model. Reyes et al. [25] proposed a linear model to estimate systematic risk in capital asset pricing in which daily high and low prices on Microsoft and the S & P500 index are used to show the capabilities of this model.
Although there are different regression approaches for interval-valued symbolic data in the SDA literature, it is important to check whether the model works well for the data at hand. For this, diagnostic measures and graphical tools based on residuals can be used. In this context, Lima Neto et al. [17] proposed the first concept of residuals for interval-valued symbolic data as a unique continuous value and considered this concept for calculating diagnostic measures. This concept was used regarding a model that the authors also introduced. This model assumed the interval-valued symbolic response variable as a bivariate random vector having a bivariate Gaussian distribution. The residuals were used to make inferences about the response distribution, identify outliers, among other aspects.
In this work, a new concept of residuals for interval-valued symbolic data is introduced. This concept considers lower and upper boundaries of the residuals jointly, unlike definitions found in the literature [17, 32], which consider the interval residual based on statistical residuals for classical data. Our approach takes into account the variability intrinsic to each unit (class) to define the residuals (lower and upper boundaries). Thus, versions of these residuals are considered, and graphical tools are built in order to investigate the adequacy of regression models for the used data scenario. A descriptive analysis for interval residuals is performed. Box plot for interval residuals is also introduced and is considered for analyzing the interval residuals. This new residual concept can be applied to any regression model for interval-valued symbolic data of the SDA literature.
As already mentioned, this paper applies its theoretical contributions to educational data. In the framework of SDA applications for the educational scenario, Silva et al. [28] introduced a toolbox for symbolic polygonal data that was applied to data of the Brazilian Basic Education Assessment System (SAEB). The authors performed this application to estimate the mathematical proficiency of Brazilian students in the final year of elementary education using a symbolic regression model. Symbolic polygonal data are a new type of symbolic data that were introduced by Silva et al. [27].
Interval residual analysis
In the classic literature of regression models, the basic regression assumptions are: (i) the relationship between response and regressors to be approximately linear, (ii) error with zero mean and constant variance, (iii) errors are uncorrelated and (iv) errors follow approximately normal distribution. This paper presents methods useful for checking these assumptions based on interval residuals calculated from interval regression models.
Interval residual
Interval-valued symbolic data resulting from the aggregation process applied to large data sets are descriptions associated with individuals’ subsets. These descriptions are defined by a generalization tool, for example, [min, max]. However, overgeneralization can happen when individuals’ classes are described by a numerical variable generalized by an interval containing smaller and greater values. Problems with choosing [min, max] can arise when these extreme values are, in fact, outliers or when the set of individuals to generalize is composed of subsets of different distributions. Interval outliers’ definition is presented in ref [11].
Let be a data set of n objects each one described by an interval vector where with and . The objects are described by midpoint and range data of their intervals. Let be the interval-valued symbolic response variable with and .
Consider the matrix of interval-valued symbolic predictor variables, with , , and where with , . with , and and are zero and one vectors, respectively.
Regarding the vector and the matrix , the regression equation can be written as follows:
| 1 |
is a parameter vector, is a vector of error with and .
Let the residuals for center and range of interval-valued symbolic data given as:
Definition 1
The ordinary interval residual () is as:
| 2 |
Definition 2
A standardized version for can be defined as:
| 3 |
where
| 4 |
where and SDR is the standard deviation for interval residual . It follows according to the definition of standard deviation for interval-valued symbolic data presented in Bertrand and Goupil [1].
Residual analysis
Residual analysis is an essential step for identifying the effects of departures from assumptions of a regression model. The residual analysis for interval-valued symbolic data presented in this paper is based on residual analysis for classic data. Thus, to better understand this methodology’s use for interval-valued symbolic data, we exemplify two standard behaviors for interval residuals: when the assumptions of the linear model are satisfied and are not.
Situation when the assumptions of the interval linear model are satisfied
Initially, a Monte Carlo experiment was carried out using the interval regression model. The goal is to investigate the statistical properties of the proposed interval residuals in this paper. We generate a synthetic symbolic data set of size n = 30, according to the structure below, and Fig. 2 shows the scattering of the rectangles of these synthetic interval-valued symbolic data. Data were generated with the following configuration:
The midpoint predictor is generated from an uniform distribution in the interval [20,40].
The range predictor is generated from an uniform distribution in the interval [1,5].
The midpoint response , where (0,3).
The range response , where (0,3).
Fig. 2.

X versus Y in synthetic interval-valued symbolic data when assumptions of the interval linear model are satisfied
In the following, we consider 1,000 replications of the Monte Carlo simulation. In each replication, an interval linear regression model is fitted and the ordinary and standardized interval residuals given by Eqs. (2) and (3), respectively, are calculated. Tables 1 and 2 present descriptive statistics for both residuals. These measures are computed according to concepts described in Appendix A. We observe in these tables that the ordinary and standardized residuals have approximately zero interval mean and interval variances approximately 3 and 1, respectively. Moreover, both interval residuals have interval skewness close to zero and interval kurtosis close to 3.
Table 1.
Descriptive statistics for ordinary interval residual when assumptions of the interval linear model are satisfied
| Mean | Standard | Skewness | Kurtosis | |
|---|---|---|---|---|
| Deviation | ||||
| 1 | 0.0341 | 3.0689 | 0.0019 | |
| 2 | 0.0282 | 3.0725 | 0.0596 | 2.7851 |
| 3 | 0.0220 | 2.9739 | 0.0881 | 2.9647 |
| 4 | 0.0947 | 2.9635 | 0.0240 | 3.0810 |
| 5 | 0.0180 | 3.1218 | 0.0168 | 3.0486 |
| 6 | 0.0860 | 2.9301 | 0.0305 | 2.8569 |
| 7 | 0.0920 | 2.9714 | 0.0561 | 2.9522 |
| 8 | 0.0918 | 2.9425 | 0.0196 | 3.1115 |
| 9 | 0.0321 | 3.0088 | 0.0913 | 3.0211 |
| 10 | 0.0187 | 2.9318 | 0.0210 | 3.0215 |
| 11 | 0.1289 | 2.9941 | 0.0819 | 3.0499 |
| 12 | 0.1036 | 2.8692 | 0.0716 | 2.9559 |
| 13 | 0.1589 | 3.0396 | 0.0034 | 3.0836 |
| 14 | 0.0336 | 3.0434 | 0.0974 | 3.2109 |
| 15 | 0.0099 | 3.0438 | 0.0062 | 3.1218 |
| 16 | 0.0444 | 2.9754 | 0.1079 | 2.8265 |
| 17 | 0.0596 | 2.9915 | 0.0849 | 3.0955 |
| 18 | 0.0527 | 3.1402 | 0.0759 | 3.0201 |
| 19 | 0.0794 | 2.9478 | 0.0286 | 3.0871 |
| 20 | 0.0690 | 2.9998 | 0.1876 | 3.0799 |
| 21 | 0.0652 | 3.0617 | 0.0674 | 3.1612 |
| 22 | 0.0766 | 3.0687 | 0.0663 | 2.9854 |
| 23 | 0.0584 | 3.0893 | 0.0069 | 3.1285 |
| 24 | 0.1023 | 2.9639 | 0.0350 | 2.9402 |
| 25 | 0.0014 | 3.1457 | 0.1274 | 2.8466 |
| 26 | 0.0462 | 3.0207 | 0.0344 | 3.3147 |
| 27 | 0.0972 | 3.0024 | 0.0357 | 2.9513 |
| 28 | 0.1643 | 3.1306 | 0.0139 | 3.1070 |
| 29 | 0.1707 | 3.1497 | 0.0486 | 3.1865 |
| 30 | 0.0393 | 2.9797 | 0.0017 | 3.1857 |
Table 2.
Descriptive statistics for standardized interval residual when assumptions of the interval linear model are satisfied
| Mean | Standard | Skewness | Kurtosis | |
|---|---|---|---|---|
| Deviation | ||||
| 1 | 0.0124 | 1.0161 | 0.0267 | 2.8795 |
| 2 | 0.0046 | 1.0156 | 0.0179 | 2.6990 |
| 3 | 0.0077 | 0.9849 | 0.1149 | 2.8401 |
| 4 | 0.0326 | 0.9771 | 0.0126 | 2.7881 |
| 5 | 0.0008 | 1.0370 | 0.0326 | 2.8656 |
| 6 | 0.0187 | 0.9703 | 0.0103 | 2.7210 |
| 7 | 0.0333 | 0.9847 | 0.0104 | 2.8160 |
| 8 | 0.0317 | 0.9784 | 0.0284 | 2.9434 |
| 9 | 0.0160 | 0.9908 | 0.1096 | 2.8340 |
| 10 | 0.0050 | 0.9642 | 0.0058 | 2.7743 |
| 11 | 0.0421 | 0.9939 | 0.0379 | 2.9301 |
| 12 | 0.0348 | 0.9514 | 0.0711 | 2.8007 |
| 13 | 0.0520 | 1.0059 | 0.0118 | 2.9181 |
| 14 | 0.0134 | 1.0092 | 0.0437 | 3.0497 |
| 15 | 0.0083 | 1.0112 | 0.0045 | 2.8783 |
| 16 | 0.0114 | 0.9782 | 0.0711 | 2.6675 |
| 17 | 0.0252 | 0.9816 | 0.0418 | 2.7887 |
| 18 | 0.0199 | 1.0346 | 0.0231 | 2.8953 |
| 19 | 0.0340 | 0.9766 | 0.0259 | 2.9765 |
| 20 | 0.0205 | 0.9937 | 0.1300 | 2.8787 |
| 21 | 0.0231 | 1.0134 | 0.0587 | 2.9187 |
| 22 | 0.0218 | 1.0166 | 0.0155 | 2.9066 |
| 23 | 0.0187 | 1.0219 | 0.0128 | 2.9272 |
| 24 | 0.0318 | 0.9875 | 0.0889 | 2.8300 |
| 25 | 0.0024 | 1.0436 | 0.1061 | 2.7394 |
| 26 | 0.0162 | 0.9897 | 0.0292 | 2.9411 |
| 27 | 0.0254 | 0.9925 | 0.0088 | 2.7662 |
| 28 | 0.0508 | 1.0364 | 0.0223 | 2.7810 |
| 29 | 0.0496 | 1.0340 | 0.0455 | 2.8863 |
| 30 | 0.0112 | 0.9887 | 0.0454 | 3.0231 |
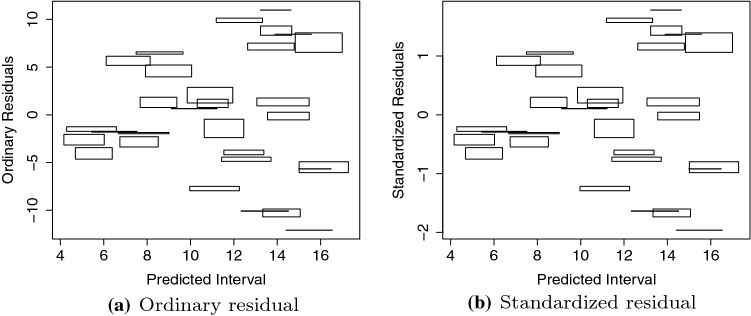
Figures 3 and 4 are developed with the interval.histogram.plot() function from the RSDA package [26] to generate histograms. We observe a good approximation of the normal distribution for interval residuals. Figure 5a and b suggest that the errors are homoscedastic and random for ordinary and standardized residuals, respectively. That is, the variance is constant and the assumption of linearity is satisfied in this scenario.
Fig. 3.
Histograms for ordinary interval residual when assumptions of the interval linear model are satisfied
Fig. 4.
Histograms for standardized interval residual when assumptions of the interval linear model are satisfied
Fig. 5.
Predicted interval versus interval residuals when assumptions of the interval linear model are satisfied
Situation when assumptions of the interval linear model are not satisfied
Here, we present two scenarios of interval synthetic data in which the assumptions of homoscedasticity and linearity are violated, respectively. In the first scenario (Fig. 6), data are generated with the configuration below. The idea is to show the behavior of the interval residuals when the homoscedasticity is violated. Figure 7a and b display an outward-opening funnel pattern, indicating that the error variance is not constant.
The midpoint predictor is generated from an uniform distribution in the interval [1,5].
The range predictor is generated from an uniform distribution in the interval [0.5,1].
The midpoint response , where (0,2).
The range response , where (0,1).
Fig. 6.

X versus Y in synthetic interval-valued symbolic data when assumptions of homoscedasticity are violated
Fig. 7.
Predicted interval versus interval residuals violating the assumption of homoscedasticity
The second scenario of interval-valued symbolic data is shown in Fig. 8. Here, we present an example in which the assumption of linearity for intervals is violated. The data scenario is generated with the configuration below. Figure 8 shows a nonlinear relationship between independent and dependent interval-valued symbolic variables, and Fig. 9a and b present the behavior of the interval residuals versus predicted intervals for this scenario violating the assumption of linearity.
The midpoint predictor is generated from an uniform distribution in the interval [− 6,6].
The range predictor is generated from an uniform distribution in the interval [1,3].
The midpoint response , where (0,2).
The range response , where (0,2).
Fig. 8.

X versus Y in synthetic interval-valued symbolic data when assumptions of linearity are violated
Fig. 9.
Predicted interval versus interval residuals violating the assumption of linearity
From Subsects. 3.2.1 and 3.2.2, we presented two situations of interval residual behaviors. In the first, Fig. 5 displays random and homogeneous behavior of the interval residuals around the horizontal axis satisfying the assumptions of adequacy of the regression models. In the second one, Figs. 7 and 9 show two scenarios where the assumptions of the linear interval model are violated: linearity and homoscedasticity, respectively. These experiments describe the importance of the residual analysis in the context of interval linear regression models.
Interval residual analysis with benchmark interval data sets
To evaluate the proposed methodology with real interval data, we performed the interval residual analysis with benchmark data sets in the SDA literature. The adequacy of the linear interval model was examined using the following databases:
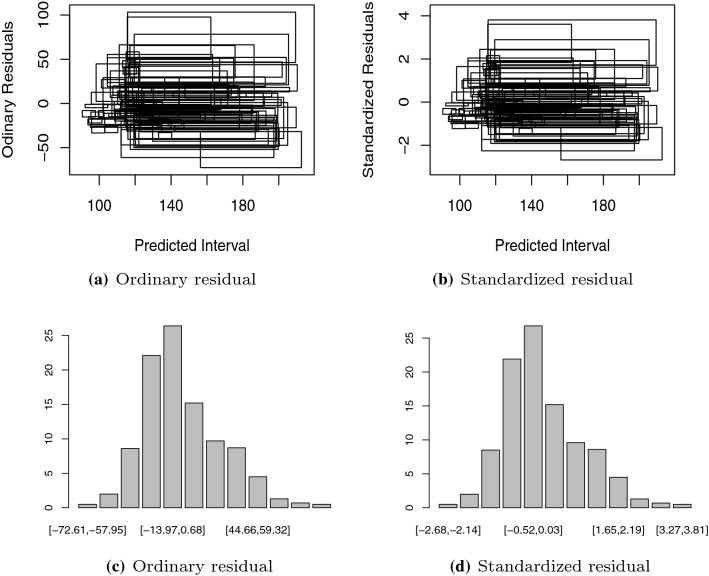
Soccer data set: it provides information about the professional football players of 20 teams in France. Each player is described by two independent variables: height and age and a dependent variable: weight. This data set was obtained through the iRegression package [21]. Figure 10a, b shows the scatter plot of the predicted intervals versus interval residuals. From this figure, we can observe that the interval residuals are randomly distributed around the zero mean. From Fig. 10c, d, we can observe that the interval residuals present an asymmetric behavior that violates the assumption of normality for errors.
Cardiology data set: it consists of 59 patients described by three interval variables. Two independent interval variables are systolic blood pressure and diastolic blood pressure, and the dependent variable is pulse rate. This data set is obtained through the iRegression package [21]. Figure 11a, b shows the scatter plot of the dependent variable versus interval residuals from the Cardiology data set. We can see in this example that there is no pattern in the distribution of rectangles. Moreover, we can infer through Fig. 11c, d that the errors follow an approximately normal distribution. For this data set, the assumptions considered in this paper are satisfied.
Airfares data set: it relates to quarterly average airfare and average weekly passengers in 2001 of the US Department of Transportation obtained through the PSDA package [29]. Two variables describe the data set. The dependent variable is the price; the independent variable is distance. The original data set is aggregated by departure city, resulting in 90 classes. Figure 12a, b shows a heteroscedastic behavior, and Fig. 12 c, d displays that there is slight asymmetry.
Fig. 10.
Soccer data set: Predicted interval versus interval residuals (a), (b) and histograms for residuals (c), (d)
Fig. 11.
Cardiology data set: Predicted interval versus interval residuals (a), (b) and histograms for residuals (c), (d)
Fig. 12.
Airfares data set: Predicted interval versus interval residuals (a, b) and histograms for residuals (c, d)
Interval educational data
The increase in resources, educational software, the use of the Internet in education, and the establishment of state data sets of student information have created large repositories of data [15]. Kriegel et al. [16] point out that manual analysis of large volumes of data is impracticable, and there is an increasing need for data mining techniques that are capable of discovering new knowledge in these complex and voluminous data. Therefore, discovering new knowledge can be exploited to improve the quality of decisions in education and teaching–learning methods.
However, exploiting this large mass of educational data is one of the significant challenges facing educational institutions. SDA provides tools that allow the processing and analyzing large volumes of educational data more efficiently than the original. Symbolic data can describe a group (class) of individual records of an extensive data set, and the original data set can be reduced to a smaller size. This data structure facilitates the use of the data set and generates new knowledge. Moreover, SDA promotes the confidentiality of information by increasing the granularity of the scenario in which the data are sensitive.
Educational indicators are essential tools for understanding educational systems [22]. They attribute statistical value to the quality of teaching. This allows knowing not only the performance of the students but also the socioeconomic context and the conditions in which the teaching–learning process takes place [8]. They are useful for monitoring educational systems and contributing to creating public policies to improve the quality of education and services offered to society by the school. The educational indicators used in this study are made available openly by the National Institute of Educational Studies and Research Anísio Teixeira (INEP) [14] for the year 2018. These indicators were organized in a single data set and referred to all Brazilian cities’ elementary schools. They are:
School dropout rate, the response variable (SDR).
Adequacy of teacher refers to the percentage of teachers’ adequacy to the discipline they teach in schools. There are five levels of suitability and therefore five variables (ATT1 to ATT5).
Students per class, average number of students per class in schools (SCL).
The complexity of schools’ management is related to the following characteristics: school size, shift number, quantity, and complexity of modalities offered (CMA).
Level-age distortion rate per school (DLA).
Percentage of teacher with higher education in schools (THE).
Average of the regularity of the teacher in school. For each teacher of the school, a score was assigned to the value: (a) of the total number of years that the teacher worked in the school in the last years; (b) the teacher’s performance in school in more recent years; and (c) the performance in consecutive years (RGT).
Teacher effort, This measure reveals aspects of the teacher’s work that contributes to the overload in the exercise of the profession. The indicator presents the percentage of teachers at six levels, and higher levels indicate more significant effort (TEF1 to TEF6).
Each indicator was integrated into a single data set, resulting in 17 variables and 128,366 school occurrences. The following subsection explains the transformation of the classic data set into interval-valued symbolic data.
Creation of the interval-valued symbolic educational data set
Before obtaining the data set for interval-valued symbolic data, we performed treatment for the original data set. The idea of this step was to deal with the missing data present in the original data set although this does not interfere with the data aggregation. The median measure was used to fill in missing data. The original data set was aggregated by city and, considering each variable, and the missing values are filled by the median of the values corresponding to the city. The highest overall occurrence of missing value at the base was the variable SCL, with 2,174. Table 3 displays a small part of the original data set.
Table 3.
Educational indicators described by classic data
| School | TEF1 | TEF2 | … | TEF6 | ATT1 | ATT2 | … | ATT5 | SCL | THE | CMA | RGT | DLA | SDR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 50.0 | 0.0 | … | 0.0 | 54.4 | 0 | … | 0 | 12.6 | 100 | 3 | 3.1 | 23.8 | 6.6 |
| 2 | 33.2 | 0.0 | … | 6.7 | 72.6 | 0 | … | 8.4 | 20.5 | 93.3 | 3 | 2.5 | 18.5 | 3.6 |
| 3 | 30.8 | 23.1 | … | 3.8 | 91 | 0 | … | 3.5 | 26.9 | 96.2 | 3 | 3.2 | 14.1 | 0 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 128,364 | 42.4 | 53.8 | … | 0.0 | 96.6 | 0 | … | 3.4 | 25.2 | 96.2 | 3 | 2.5 | 18.1 | 5.4 |
| 128,365 | 0.0 | 0.0 | … | 0.0 | 79.3 | 0 | … | 5 | 36.9 | 97.1 | 3 | 2,1 | 34.7 | 10.4 |
| 128,366 | 15.8 | 84.2 | … | 0.0 | 90.2 | 0 | … | 0 | 27.9 | 100 | 3 | 3.0 | 10 | 9.6 |
The next step was to identify the cities represented by a single school. In this case, the maximum and minimum values for each variable are identical. Thus, 80 cities are found, and we decided to exclude them from the study since these cities represent a minimum portion of the complete base records. Moreover, we kept only continuous variables in the study. After these steps, the aggregation process by city allowed to obtain 5,490 objects in which each instance represents a group of schools in a Brazilian city. We use the function classic_to_sym () from the RSDA package [26] which can be found in the R language [24]. The original data set has 128,366 school records, and the symbolic data set has 5,490 city records. Given a city is obtained minimum and maximum values for each variable. Table 4 shows a small part of the interval-valued symbolic data set. We can clearly observe the variability inside each city represented by the minimum and maximum values in the class.
Table 4.
Educational indicators described by interval-valued symbolic data
| City | TEF1 | . | TEF6 | ATT1 | . | ATT5 | SCL | THE | RGT | DLA | SDR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | [6.4, 100] | . | [0, 19.4] | [0, 91] | . | [0, 100] | [4, 26.9] | [0, 100] | [1.04, 5] | [0, 54.7] | [0, 7.1] |
| 2 | [0, 100] | . | [0, 11.8] | [41.2, 100] | . | [0, 33.3] | [10.3, 32.1] | [66.7, 100] | [2.08, 4.4] | [0, 35.1] | [0, 5] |
| 3 | [0, 100] | . | [0, 20] | [44.4, 100] | . | [0, 4.1] | [10.5, 22.2] | [95.7, 100] | [3.17, 4.31] | [2.5, 18.1] | [0, 0.4] |
| . | . | . | . | . | . | . | . | . | . | . | . |
| 5,488 | [0, 100] | . | [0, 11.1] | [0, 95.1] | . | [0, 58.3] | [10, 27.2] | [55.6, 100] | [1.32, 3.52] | [0, 54.4] | [0, 1.6] |
| 5,489 | [0, 100] | . | [0, 20] | [0, 70] | . | [0, 87.4] | [11, 28.7] | [22.2, 100] | [2.07, 3.08] | [0, 23.9] | [0, 1] |
| 5,490 | [0, 100] | . | [0, 15.4] | [0, 100] | . | [0, 100] | [1.8, 45.4] | [0, 100] | [1.14, 4.55] | [0, 100] | [0, 20] |
Exploratory analysis of interval-valued symbolic educational data
Table 5 shows descriptive measures such as mean, standard deviation, and coefficient of variation for all interval-valued symbolic variables of the interval-valued symbolic educational data set studied in this work. These measures are computed according to concepts described in Billard and Diday [2]. From the values in this table, we can see that the interval-valued symbolic variables have different behaviors. This table also presents that TEF6, ATT2, ATT4, and SDR variables have the highest values of coefficient of variation, all values greater than one.
Table 5.
Descriptive statistics of interval-valued symbolic variables in data set
| Variable | Mean | Standard |
|---|---|---|
| Deviation | ||
| TEF1 | 38.27 | 26.96 |
| TEF2 | 21.24 | 20.65 |
| TEF3 | 29.56 | 23.35 |
| TEF4 | 35.67 | 22.04 |
| TEF5 | 13.19 | 12.36 |
| TEF6 | 7.28 | 9.02 |
| SCL | 19.06 | 7.31 |
| THE | 71.27 | 27.11 |
| ATT1 | 51.63 | 25.74 |
| ATT2 | 2.56 | 6.11 |
| ATT3 | 33.94 | 24.12 |
| ATT4 | 9.18 | 13.63 |
| ATT5 | 29.17 | 27.38 |
| DLA | 19.78 | 16.29 |
| RGT | 3.04 | 0.78 |
| SDR | 3.75 | 6.73 |
In order to exhibit a summary of descriptive measures graphically, this work shows a new approach for building box plots for interval-valued symbolic data. The procedure is given as follows.
Fixed an interval-valued symbolic variable , let be a list of all lower and upper values of the variable such as .
Compute the the minimum, the maximum, the sample median, and the first and third quartiles of .
Obtain the box plot regarding the list of values .
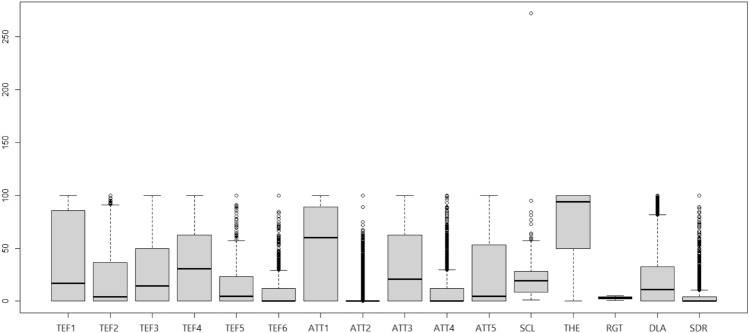
Figure 13 displays a box plot build from the bounds of interval-valued symbolic variables in the data set. Most of the variables have potential outliers, and two variables have a high interquartile range, such as TEF1 and ATT1. The variables ATT2 and RGT have an interquartile range close to zero. The response variable has a low interquartile range and many potential outliers.
Fig. 13.
Box plots for interval-valued symbolic variables
Selecting independent variables for estimating school dropout
Table 6 shows the linear correlations between all interval-valued symbolic variables present in the data set. The correlations are obtained using the measure proposed by Billard and Diday [5] method. Initially, we selected the independent variables (in bold) with the highest correlation values with the interval-valued symbolic response variable (SDR). They are: DLA and THE.
Table 6.
Correlations between the variables in the interval-valued symbolic data set
| TEF1 | ||||||||||||||||
| 0.41 | TEF2 | |||||||||||||||
| 0.26 | 0.38 | TEF3 | ||||||||||||||
| 0.03 | 0.14 | 0.20 | TEF4 | |||||||||||||
| 0.04 | 0.09 | 0.12 | 0.07 | TEF5 | ||||||||||||
| 0.07 | 0.17 | 0.20 | 0.12 | 0.29 | TEF6 | |||||||||||
| 0.61 | 0.41 | 0.33 | 0.13 | 0.06 | 0.09 | ATT1 | ||||||||||
| 0.15 | 0.16 | 0.16 | 0.05 | 0.18 | 0.15 | 0.13 | ATT2 | |||||||||
| 0.41 | 0.30 | 0.28 | 0.19 | 0.11 | 0.13 | 0.58 | 0.06 | ATT3 | ||||||||
| 0.27 | 0.31 | 0.28 | 0.18 | 0.17 | 0.20 | 0.29 | 0.20 | 0.21 | ATT4 | |||||||
| 0.59 | 0.51 | 0.45 | 0.15 | 0.11 | 0.18 | 0.69 | 0.16 | 0.32 | 0.28 | ATT5 | ||||||
| 0.58 | 0.51 | 0.45 | 0.15 | 0.10 | 0.16 | 0.70 | 0.15 | 0.33 | 0.28 | 0.96 | THE | |||||
| 0.02 | 0.19 | 0.11 | 0.04 | 0.08 | 0.16 | 0.08 | 0.11 | 0.01 | 0.09 | 0.01 | 0.01 | SCL | ||||
| 0.07 | 0.09 | 0.07 | 0.08 | 0.06 | 0.07 | 0.09 | 0.04 | 0.08 | 0.07 | 0.14 | 0.13 | 0.03 | RGT | |||
| 0.00 | 0.08 | 0.12 | 0.06 | 0.16 | 0.15 | 0.01 | 0.15 | 0.01 | 0.15 | 0.06 | 0.05 | 0.16 | 0.01 | CMA | ||
| 0.38 | 0.43 | 0.41 | 0.21 | 0.16 | 0.27 | 0.43 | 0.12 | 0.28 | 0.28 | 0.52 | 0.53 | 0.08 | 0.06 | 0.12 | DLA | |
| 0.34 | 0.39 | 0.36 | 0.19 | 0.12 | 0.21 | 0.34 | 0.11 | 0.27 | 0.27 | 0.44 | 0.45 | 0.08 | 0.10 | 0.11 | 0.58 | SDR |
Figure 14 shows the 3D scatter plot regarding SDR, THE, and DLA variables for center and range data. Moreover, this figure displays the corresponding 3D scatter plot interval-valued symbolic data. In the three plots, we can note outliers’ presence in the data set.
Fig. 14.
Dispersion of the variables selected by the correlation
In addition, Fig. 15 presents the graphical representation of the distribution of selected interval-valued symbolic variables through histograms. The histograms were developed with the interval.histogram.plot() function from the RSDA package [26]. In general, the variables have different behaviors with strong positive asymmetry. For example, in Fig. 15c, the response variable SDR has one of the highest kurtosis values, and its histogram reflects the highest peak of the histogram is to the first range of values. We can evaluate that the distribution of the intervals for the school dropout rate is more frequent to the lowest maximum and minimum values.
Fig. 15.
Histograms of interval-valued symbolic variables
Model adequacy checking for estimating interval school dropout
Four linear regression models for interval-valued data of the SDA literature are investigated in this application. They are: iLR [18], iRLR [11], iQR [12], and iETKKR [20]. These models have some common characteristics such as:
Two independent regressions are considered for the midpoint and range of the intervals, respectively.
The prediction of an interval is based on a linear combination regarding the fitted values for the midpoint and range of the intervals.
In this context, the coefficient vectors and of these interval regression models are estimated minimizing different criterion functions.
In the iLR model defined in Lima Neto and De Carvalho [18], the sum of squares of deviations is given by the sum of the midpoint square error plus the sum of the range square error, considering independent vectors of parameters to predict the midpoint and the range of the intervals. However, it is well known in the literature that a least squares model is sensitive to outliers.
In the iRLR model defined in Fagundes et al. [11], the fitting criterion for each regression is based on a class of robust estimators that minimizes a function of the residuals. The robust procedure replaces the sum of squared residuals of the least square method with some other function that is being less influenced by the unusual observations. The coefficients of the models are estimated by the iteratively reweighted least squares.
In the iQR method proposed in Fagundes et al. [12] each regression provides estimates based on -th quantile of the conditional distribution of the dependent variable, using for this, the minimization of the weighted absolute errors. It allows to model different quantities of the target variable. The advantages of quantile regression over least squares regression are its flexibility for modeling data with heterogeneous conditional distributions. We considered = 0.5 for this application.
In the iETKRR method defined in Lima Neto and De Carvalho [20], the parameter estimation is guided by the minimization of an objective function that penalizes the presence of outliers through the use of exponential-type kernel functions. This function is not defined in the original space but in a high-dimensional space through nonlinear mapping applied, respectively, on the midpoint and range response variables and its corresponding mean values.
Interval residual analysis for each model is performed to investigate possible problems in these models. This analysis involves descriptive statistics, scatter plot, and histograms for ordinary and standardized interval residuals. Table 7 presents the parameter estimates obtained from the interval regression models. Each model considers two regressions for the midpoint and range of the intervals, respectively.
Table 7.
Estimated models’ parameters
| Model | Parameter estimates | ||||||
|---|---|---|---|---|---|---|---|
| Midpoint | Range | ||||||
| Intercept | THE_c | DLA_c | Intercept | THE_r | DLA_r | ||
| iLR | 2.921 | 0.054 | 0.236 | 1.663 | 0.035 | 0.258 | |
| iRLR | 2.807 | 0.039 | 0.154 | 0.708 | 0.023 | 0.182 | |
| iQR | 2.536 | 0.035 | 0.145 | 0.639 | 0.019 | 0.175 | |
| iETKKR | 3.170 | 0.038 | 0.119 | 0.371 | 0.027 | 0.143 | |
Table 8 shows the descriptive statistics for ordinary and standardized interval residuals. As expected, both models’ standardized interval residuals have a mean close to zero and a standard deviation equal to 1. Regarding standard deviation, asymmetry, and kurtosis, the iLR and iQR models presented high values. This indicates that the interval errors for these models are highly skewed and distribution with shape leptokurtic. However, iRLR and iETKKR models presented that the errors are fairly symmetrical and distribution with fairly mesokurtic shape.
Table 8.
Descriptive statistics for interval residual
| Model | Mean | Standard | Skewness | Kurtosis |
|---|---|---|---|---|
| Deviation | ||||
| Ordinary | ||||
| iLR | 1.13×10 | 4.60 | 4.43 | 41.37 |
| iRLR | 3.41×10 | 1.62 | 0.13 | 2.33 |
| iQR | 8.99×10 | 4.78 | 5.30 | 51.01 |
| iETKKR | 8.14×10 | 1.42 | 0.19 | 2.81 |
| Standardized | ||||
| iLR | 2.46×10 | 1.00 | 4.43 | 41.37 |
| iRLR | 2.11×10 | 1.00 | 0.13 | 2.33 |
| iQR | 1.88×10 | 1.00 | 5.30 | 51.01 |
| iETKKR | 5.73×10 | 1.00 | 0.19 | 2.81 |
Figure 16 shows the histogram of interval residuals. The residual interval histograms from the fitted iLR and iQR models show a small positive skew, while iRLR and iETKKR are approximately symmetric. Figure 17 represents the scatter plots of the predicted versus interval residuals, from ordinary () and standardized () for models. The dark part means that the data have been randomly overlaid, considering the amount of records present in the data set.
Fig. 16.
Histograms for ordinary and standardized interval residuals
Fig. 17.
Scatter plots of the predicted intervals versus interval residuals
From these plots, we can extract some highlights:
There are interval outliers for fitted iLR and iQR (see Figs. 16a–d and 17a–d). The fitted iRLR and iETKKR do not present interval outliers (there are no interval outliers for iRLR (see Figs. 16 e–h and 17e–h).
For both fitted models, the interval residuals versus predict intervals plot present non-constant variance suggesting heteroscedasticity problem.
To finalize, we can say that the model diagnostic analysis was needed to assess a linear regression model’s appropriateness for interval-valued symbolic data. This study allowed to conclude that iRLR and iETKKR are appropriate models for estimating the school dropout rate regarding the interval-valued symbolic educational data set built in this work.
Model predictive power analysis
The predictive analysis is made to evaluate the performance of the model with new data. Test and training sets are randomly selected from the interval-valued educational symbolic data set. The training set corresponds to 75% of the original data set, and the test data set corresponds to 25%. The models’ accuracy prediction is measured by the mean magnitude of relative error (MMRE), as shown in Eq. 5. The estimated MMRE corresponds to the average of the metric found in a Monte Carlo simulation with 1000 replications and hold-out method, as in Algorithm 1. The MMRE is given as
| 5 |
Table 9 shows the mean and standard deviation values for the MMRE calculated from 1000 iterations. iETKKR has better performance than iRLR. We verified through the Student’s T-test, at 5% of significance level, for paired samples, the statistical difference between the iETKKR and iRLR. The test obtained p-value < 0.0001, and we can conclude that the iETKKR model is the best option for this application. The objective function found in iETKRR allows a combination of different hyper-parameter estimators on the center and on the range of the intervals, and thus, it provides more flexibility and robustness to treat different outliers types present in interval-valued symbolic data sets.
Table 9.
Average and standard deviation for MMRE of models
| Model | Mean | SD |
|---|---|---|
| iRLR | 0.5796 | 0.0083 |
| iETKKR | 0.5644 | 0.0074 |
Conclusions
Interval-valued data are a type of symbolic data widely considered in the Symbolic Data Analysis (SDA) literature. Our paper presented a way to check regression model adequacy for interval-valued symbolic data. In this context, we introduce concepts of ordinary and standardized interval residuals for regression models. In order to perform exploratory analysis for interval residuals, we present a way of building box plot and calculating descriptive measures such as skewness and kurtosis for interval-valued data. The residual analysis is based on plots and descriptive measures applied to interval residuals. Here, the use of interval for describing residuals allows to take into account the variability inherent to the residuals and consider measures and graphs defined for data type interval. Unlike of the approach presented in [17] that consider residuals as continuous values and the residual analysis is carried out investigating residuals for lower and upper bounds of the intervals separately. The framework proposed in this paper investigates residuals for lower and upper bounds of the intervals conjointly.
To show the usefulness of the proposed approach, an application for estimating school dropout in the scenario of Brazilian municipalities is performed. The data set was collected from the year 2018 provided by the National Institute of Educational Studies and Research Anísio Teixeira (INEP). It is known that SDA provides a way to handle a large data set according to the granularity of interest. Thus, the schools were aggregated by cities. The focus of the analysis was to predict school dropout in Brazilian cities. School dropout is one of the biggest challenges of student institutions, and research that addresses techniques to deal with this theme contributes to the literature.
From the application, four interval regression models for predicting school dropout are built regarding a subset of independent interval-valued symbolic variables. This subset is selected using a correlation measure of the SDA literature, and it was the best option to explain the school dropout rate. The models are evaluated based on residual analysis regarding descriptive measures and graphs. Least squares model is sensitive to outliers, and in this study, we identified that the iLM method had the worst results. The robust models were more suitable for modeling school dropout provided for the scenario studied since there are outliers in the interval data set. Between the robust models used to estimate school dropout, iETKKR presented more flexibility to treat interval-valued outliers. It is worth mentioning that the data set has interval outliers. Therefore, it needs to use models that are less sensitive to outliers for this educational scenario.
This research opens the way for the application of new approaches in the educational area. SDA provides formulations of data analysis, development of models, and evaluation of results that allow applications in different domains. Dealing with large masses of data is necessary for the educational area due to technological advances in storage, interaction, and content generation. SDA provides support on this issue. For example, it is possible to work on data groups such as classes, schools, and cities. Educational institutions and public initiatives can consider the factors related to school dropout presented and think of mechanisms to minimize this problem, such as helping professionals in their training and guaranteeing students’ access to school.
Acknowledgements
We are grateful to the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - (CAPES) and Conselho Nacional de Desenvolvimento Cientíco e Tecnológico (CNPq) for the funding of this research.
Appendix A concepts of empirical moments for interval-valued symbolic data
The k-th moment and descriptive measures for interval-valued symbolic data are based on a function of empirical density for the interval as found in Bock and Diday [2] and Billard and Diday [1].
Given a interval-valued symbolic variable Z measured by for each element of the random sample . For each denote an interval. An empirical distribution function of Z is a function of n uniform distributions. It is given by
| 6 |
According to Bertrand and Goupil [1], the empirical density function of Z based on Eq. (6) is defined as:
| 7 |
Definition 3
The k-th moment for an interval-valued symbolic variable Z is defined by:
where .
The first and second empirical moments for interval-valued symbolic data are given in Bertrand and Goupil [1], and they are defined by, respectively,
| 8 |
and
| 9 |
We develop the third and fourth empirical moments given, respectively, by
| 10 |
and
| 11 |
According to [1] and Eqs. (8) and (9), the empirical mean and empirical variance for interval-valued symbolic data are presented, respectively, as:
In this paper, the empirical skewness and empirical kurtosis for interval-valued symbolic are defined as follows.
Definition 4
The skewness for interval symbolic data can be defined by
| 12 |
Definition 5
The kurtosis for interval symbolic data can be defined by
| 13 |
Declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Rafaella L. S. do Nascimento, Email: rlsn@cin.ufpe.br
Roberta A. de A. Fagundes, Email: roberta.fagundes@upe.br
Renata M. C. R. de Souza, Email: rmcrs@cin.ufpe.br
Francisco José A. Cysneiros, Email: cysneiros@de.ufpe.br
References
- 1.Bertrand P, Goupil F (2000) Descriptive statistics for symbolic data. In: Analysis of symbolic data, pp. 106–124. Springer: Berlin
- 2.Billard L, Diday E (2000) Regression analysis for interval-valued data. In: Data analysis, classification, and related methods, pp. 369–374. Springer: Berlin
- 3.Billard L, Diday E (2002) Symbolic regression analysis. In: Classification, clustering, and data analysis, pp. 281–288. Springer: Berlin
- 4.Billard L, Diday E. Descriptive statistics for interval-valued observations in the presence of rules. Comput Stat. 2006;21(2):187–210. doi: 10.1007/s00180-006-0259-6. [DOI] [Google Scholar]
- 5.Billard L, Diday E. Symbolic data analysis: conceptual statistics and data mining. Chichester: Wiley; 2006. [Google Scholar]
- 6.Billard L, Diday E. Clustering methodology for symbolic data. London: Wiley; 2019. [Google Scholar]
- 7.Bock HH, Diday E. Analysis of symbolic data. Germany: Springer; 2000. [Google Scholar]
- 8.Brasil: Ministério da Educação. https://www.gov.br/mec/pt-br. Accessed Jul 12, 2020. (2020)
- 9.Diday E. Thinking by classes in data science: the symbolic data analysis paradigm. WIREs Comput Stat. 2016;8(5):172–205. doi: 10.1002/wics.1384. [DOI] [Google Scholar]
- 10.Diday E, Noirhomme-Fraiture M. Symbolic data analysis and the SODAS software. Chichester: Wiley; 2008. [Google Scholar]
- 11.Fagundes RAA, Souza RMCR, Cysneiros FJA. Robust regression with application to symbolic interval data. Eng Appl Artif Intell. 2013;26(1):564–573. doi: 10.1016/j.engappai.2012.05.004. [DOI] [Google Scholar]
- 12.Fagundes RAA, de Souza RMCR, Soares YMG (2016) Quantile regression of interval-valued data. In: 2016 23rd international conference on pattern recognition (ICPR), pp. 2586–2591
- 13.Hao P, Guo J. Constrained center and range joint model for interval-valued symbolic data regression. Comput Stat Data Anal. 2017;116:106–138. doi: 10.1016/j.csda.2017.06.005. [DOI] [Google Scholar]
- 14.INEP: Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. http://portalinep.gov.br/. Accessed Dec 14, 2020. (2020)
- 15.Koedinger K, Cunningham K, Skogsholm A, Leber B (2008) An open repository and analysis tools for fine-grained, longitudinal learner data. In: proceedings of the 1st international conference educational data mining, pp. 157–166. Montreal, Canada
- 16.Kriegel HP, Borgwardt KM, Kröger P, Pryakhin A, Schubert M, Zimek A. Future trends in data mining. Data Min Knowl Discov. 2007;15(1):87–97. doi: 10.1007/s10618-007-0067-9. [DOI] [Google Scholar]
- 17.Lima Neto EA, Cordeiro GM, De Carvalho FAT. Bivariate symbolic regression models for interval-valued variables. J Stat Comput Simul. 2011;81(11):1727–1744. doi: 10.1080/00949655.2010.500470. [DOI] [Google Scholar]
- 18.Lima Neto EA, De Carvalho FAT. Centre and range method for fitting a linear regression model to symbolic interval data. Comput Stat Data Anal. 2008;52(3):1500–1515. doi: 10.1016/j.csda.2007.04.014. [DOI] [Google Scholar]
- 19.Lima Neto EA, De Carvalho FAT. Constrained linear regression models for symbolic interval-valued variables. Comput Stat Data Anal. 2010;54(2):333–347. doi: 10.1016/j.csda.2009.08.010. [DOI] [Google Scholar]
- 20.Lima Neto EA, De Carvalho FAT. An exponential-type kernel robust regression model for interval-valued variables. Inf Sci. 2018;454:419–442. doi: 10.1016/j.ins.2018.05.008. [DOI] [Google Scholar]
- 21.Lima Neto EA, Souza Filho CA, Marinho P (2016) iRegression: regression methods for interval-valued variables. https://cran.r-project.org/package=iRegression. R package version 1.2.1
- 22.Nascimento RLS, Fagundes RAA, Maciel AMA (2019) Prediction of school efficiency rates through ensemble regression application. In: proceedings of the 19th international conference on advanced learning technologies (ICALT), pp. 194–198. IEEE, Maceió, Brazil. 10.1109/ICALT.2019.00050
- 23.Pimentel BA, Souza RMCR. A weighted multivariate fuzzy c-means method in interval-valued scientific production data. Expert Syst Appl. 2014;41(7):3223–3236. doi: 10.1016/j.eswa.2013.11.013. [DOI] [Google Scholar]
- 24.R Core Team (2020) A language and environment for statistical computing. R Foundation for statistical computing, Vienna, Austria. https://www.R-project.org/
- 25.Reyes DMA, Souza RMCR, Cysneiros FJA. Estimating risk in capital asset pricing for interval-valued data. Int J Bus Inf Syst. 2019;32(4):522–535. doi: 10.1504/IJBIS.2019.103795. [DOI] [Google Scholar]
- 26.Rodriguez O, Aguero C, Arce J (2020) RSDA: R to symbolic data analysis. R Foundation for statistical Ccomputing. R package version 3.0.4. https://CRAN.R-project.org/package=RSDA
- 27.Silva WJF, Souza RMCR, Cysneiros FJA. Polygonal data analysis: a new framework in symbolic data analysis. Knowl Based Syst. 2019;163:26–35. doi: 10.1016/j.knosys.2018.08.009. [DOI] [Google Scholar]
- 28.Silva WJF, Souza RMCR, Cysneiros FJA. psda: a tool for extracting knowledge from symbolic data with an application in brazilian educational data. Soft Comput. 2020 doi: 10.1007/s00500-020-05252-5. [DOI] [Google Scholar]
- 29.Silva WJF, Souza RMCR, Cysneiros FJA (2019) Symbolic polygonal data analysis. https://cran.r-project.org/package=psda. R package version 1.3.3
- 30.Soares YMG, Fagundes RAA. Interval quantile regression models based on swarm intelligence. Appl Soft Comput. 2018;72:474–485. doi: 10.1016/j.asoc.2018.04.061. [DOI] [Google Scholar]
- 31.Souza LC, Souza RMCR, Amaral GJ, Silva Filho TM. A parametrized approach for linear regression of interval data. Knowl Based Syst. 2017;131:149–159. doi: 10.1016/j.knosys.2017.06.012. [DOI] [Google Scholar]
- 32.Xu W (2010) Symbolic data analysis: interval-valued data regression. Ph.D. thesis, University of Georgia Athens, GA