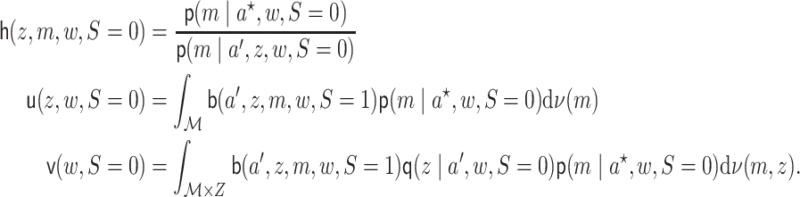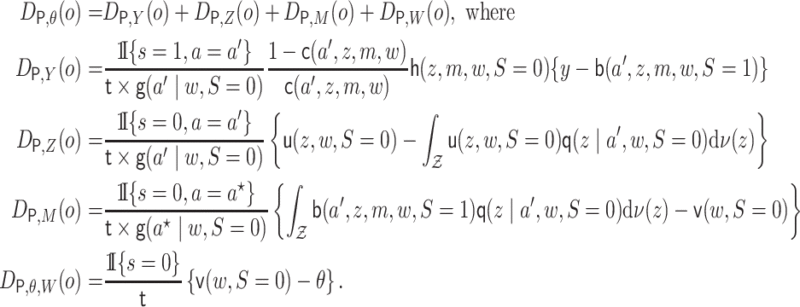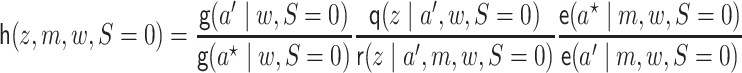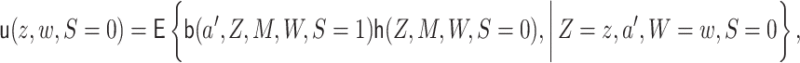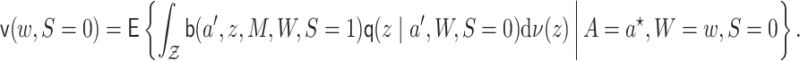Summary
The same intervention can produce different effects in different sites. Existing transport mediation estimators can estimate the extent to which such differences can be explained by differences in compositional factors and the mechanisms by which mediating or intermediate variables are produced; however, they are limited to consider a single, binary mediator. We propose novel nonparametric estimators of transported interventional (in)direct effects that consider multiple, high-dimensional mediators and a single, binary intermediate variable. They are multiply robust, efficient, asymptotically normal, and can incorporate data-adaptive estimation of nuisance parameters. They can be applied to understand differences in treatment effects across sites and/or to predict treatment effects in a target site based on outcome data in source sites.
Keywords: Interventional indirect effect, Non-parametric methods, Mediation, Stochastic indirect effect, Targeted learning
1. Introduction
The same intervention can produce different effects in different populations (e.g., Orr and others, 2003; Miller, 2015; Arnold and others, 2018). Different effects could arise from differences in (i) the distribution of compositional factors that modify aspects of the intervention’s effectiveness (e.g., gender, age), (ii) probability take-up or degree of adherence to the intervention, (iii) the mechanism by which important mediating or intermediate variables are produced, and/or (iv) the mechanism by which the outcome is produced in different populations, including different population- or site-level contextual variables that are predictive of the outcome (Pearl and Bareinboim, 2018). Transportability has been defined by Pearl and Bareinboim (2018) as the “license to transfer causal information learned in experimental studies to a different environment.” Previously, we proposed using the transport graphs of Pearl and Bareinboim (2018) coupled with a transport estimator that predicts effects “transported” to a target population as a tool for quantitatively examining the extent to which differences in effect estimates between sites could be explained by factors (i)–(iii) above (Rudolph and others, 2017; Rudolph and others, 2020). In this previous work, we developed an efficient and robust semi-parametric estimator of transported interventional (also called stochastic, see Rudolph and others, 2020) direct and indirect (what we refer to as (in)direct) effects in a target population. Although this previous estimator accounted for the presence of intermediate variables (those affected by treatment/exposure that could affect downstream mediator and outcome variables), it was limited in that it could only consider binary versions of a treatment/exposure variable, intermediate variable, and mediator variable and assumed that the distribution of the mediator was known (Rudolph and others, 2020). To our knowledge, it is currently the only available estimator for transporting (in)direct effects. However, many research questions involve continuous and/or multiple mediator variables. Thus, we address this methodologic gap by proposing novel nonparametric estimators of transported interventional (in)direct effects that allow for multiple, possibly high-dimensional mediators without constraints on their distributions.
To motivate this work, we consider an illustrative research question from the Moving to Opportunity study (MTO), a multi-site randomized controlled trial conducted by the US Department of Housing and Urban Development, where families living in high-rise public housing were randomized to receive a Section 8 housing voucher that they could use to move to a rental on the private market (Sanbonmatsu and others, 2011). Families were followed up at two subsequent time points with the final time point occurring 10–15 years after randomization. In this study, some unintended harmful effects on children’s mental health, substance use, and risk behavior outcomes were documented (Sanbonmatsu and others, 2011), and these overall effects were partially mediated by aspects of the peer and school environments (Rudolph and others, 2018b). However, these unintended harmful effects and their indirect effect components were not universal across sites (Rudolph and others, 2018a; Rudolph and others, 2020). To illustrate our proposed methods, we use the transportability framework and our novel estimators to shed light on possible reasons why the intervention had harmful effects in some sites, particularly in Chicago, but not in others. For example, if we take Chicago as the site we would like to transport to, then we borrow information from the remaining sites to learn the outcome model, we can predict the effect for Chicago, standardizing based on the covariates, intermediate and mediating variables.
Putting the above in more general terms: our approach to estimate transported interventional (in)direct effects involves (i) borrowing information from the source population about the conditional distribution of the outcome given the mediating variables, intermediate confounding variables, treatment, and covariates, and (ii) using data from the target population for the distributions of the mediating variables, intermediate confounding variables, treatment, and covariates to get estimates using the outcome model that are essentially standardized to the target population. The utility of borrowing or transporting information across sites applies more broadly than the above MTO example. It applies to questions that seek to: (i) understand differences in treatment, policy, or intervention effects across sites in multi-site trials or cohort studies, or to (ii) predict treatment effects in a target site based on outcome data in source sites. This article is organized as follows. In Section 2, we introduce notation, define the structural causal models we consider, and define and identify the transported interventional (in)direct effects. In Section 3, we describe the efficient influence function (EIF), including a reparameterization that allows for estimation with multiple and/or continuously distributed mediators, and derive the robustness properties of the EIF. In Section 4, we describe two efficient estimators for the transported interventional (in)direct effects, based on the EIF derived in Section 3: an estimator that solves the EIF in one step and a targeted minimum loss-based estimator (TMLE). In Section 5, we present results from a simulation study in which we demonstrate the consistency, efficiency, and robustness of the two estimators across various scenarios. In Section 6, we apply the two estimators to estimate the transported indirect effects of housing voucher receipt on subsequent behavioral problems as adolescents among girls in Chicago, operating through aspects of the school environment, borrowing information from the other MTO sites. Section 7 concludes the manuscript.
2. Notation and definition of (in)direct effects
Let 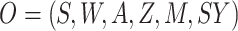 represent the
observed data, where
represent the
observed data, where 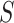 denotes a binary variable indicating
membership in the source population (
denotes a binary variable indicating
membership in the source population (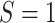 ) or target population
(
) or target population
(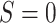 ),
), 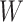 denotes a
vector of observed pretreatment covariates,
denotes a
vector of observed pretreatment covariates, 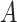 denotes a categorical
treatment variable,
denotes a categorical
treatment variable, 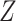 denotes an intermediate variable (a
mediator-outcome confounder affected by treatment),
denotes an intermediate variable (a
mediator-outcome confounder affected by treatment), 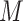 denotes a
multivariate mediator, and
denotes a
multivariate mediator, and 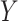 denotes a continuous or binary outcome. Let
denotes a continuous or binary outcome. Let
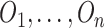 denote a sample of
denote a sample of
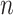 i.i.d. observations of
i.i.d. observations of
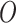 . Note that the outcome is only observed for
the source population/sites,
. Note that the outcome is only observed for
the source population/sites, 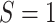 , but we are interested in estimating
effects for the target population/site,
, but we are interested in estimating
effects for the target population/site, 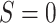 . We formalize the
definition of our counterfactual variables using the following nonparametric structural
equation model (NPSEM, Pearl, 2009) though equivalent
methods may be developed by taking the counterfactual variables as primitives (Rubin, 1974). Assume the data-generating process
satisfies:
. We formalize the
definition of our counterfactual variables using the following nonparametric structural
equation model (NPSEM, Pearl, 2009) though equivalent
methods may be developed by taking the counterfactual variables as primitives (Rubin, 1974). Assume the data-generating process
satisfies:
| (2.1) |
Here, 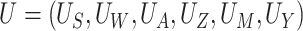 is a vector of
exogenous factors, and the functions
is a vector of
exogenous factors, and the functions 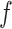 are assumed deterministic
but unknown. We use
are assumed deterministic
but unknown. We use 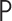 to denote the distribution of
to denote the distribution of
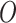 .
.
We let 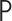 be an element of the nonparametric
statistical model defined as all continuous densities on
be an element of the nonparametric
statistical model defined as all continuous densities on 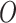 with
respect to some dominating measure
with
respect to some dominating measure 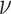 . Let
. Let
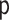 denote the corresponding
probability density function. We denote random variables with capital letters and
realizations of those variables with lowercase letters.
denote the corresponding
probability density function. We denote random variables with capital letters and
realizations of those variables with lowercase letters.
We define 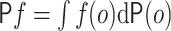 for a given function
for a given function 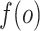 .
.
We use the following additional definitions. The function 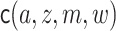 denotes
denotes
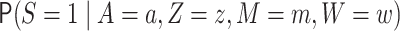 ,
,
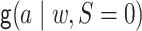 denotes
denotes
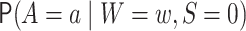 ,
,
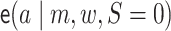 denotes
denotes
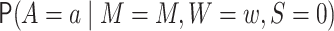 ,
,
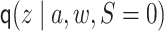 denotes the
density of
denotes the
density of 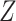 conditional on
conditional on 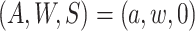 ,
, 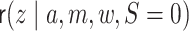 denotes the
density of
denotes the
density of 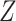 conditional on
conditional on 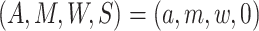 ,
, 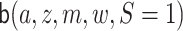 denotes
denotes
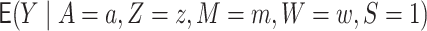 ,
and
,
and 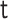 denotes
denotes 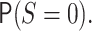
Let 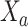 denote the counterfactual outcome
observed in a hypothetical world in which
denote the counterfactual outcome
observed in a hypothetical world in which 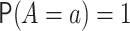 . For
example, we have
. For
example, we have 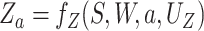 ,
,
 , and
, and
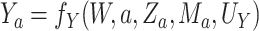 . Likewise, we let
. Likewise, we let
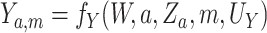 denote the value
of the outcome in a hypothetical world where
denote the value
of the outcome in a hypothetical world where 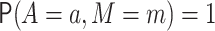 .
.
2.1. Transported interventional (in)direct effects
We define the total effect of 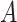 on
on
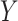 in the target population
in the target population
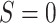 in terms of a contrast between two
user-given values
in terms of a contrast between two
user-given values 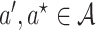 among
those for whom
among
those for whom 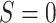 . The total effect can be decomposed
into the natural direct and indirect effects. However, natural direct and indirect effects
are not generally identified in the presence of a mediator-outcome confounder affected by
treatment (
. The total effect can be decomposed
into the natural direct and indirect effects. However, natural direct and indirect effects
are not generally identified in the presence of a mediator-outcome confounder affected by
treatment (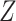 , using our notation above) (Avin and others, 2005; Tchetgen Tchetgen and VanderWeele, 2014). Direct and
indirect effects may be alternatively defined considering a stochastic intervention on the
mediator (Petersen and others,
2006; van der Laan and Petersen, 2008;
Zheng and van der Laan, 2012; VanderWeele and others, 2014; Rudolph and others, 2017).
, using our notation above) (Avin and others, 2005; Tchetgen Tchetgen and VanderWeele, 2014). Direct and
indirect effects may be alternatively defined considering a stochastic intervention on the
mediator (Petersen and others,
2006; van der Laan and Petersen, 2008;
Zheng and van der Laan, 2012; VanderWeele and others, 2014; Rudolph and others, 2017).
Let 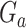 denote a random draw from the
conditional distribution of
denote a random draw from the
conditional distribution of 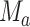 conditional on
conditional on
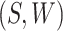 . The interventional indirect effect
(also called randomized interventional indirect effect) among those for whom
. The interventional indirect effect
(also called randomized interventional indirect effect) among those for whom
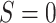 can be written:
can be written:
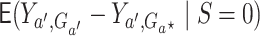 .
Generally speaking, this is the average effect of
.
Generally speaking, this is the average effect of 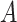 on
on
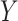 that operates through
that operates through
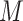 in the target population. Specifically,
it is the average difference in expected outcomes setting
in the target population. Specifically,
it is the average difference in expected outcomes setting 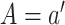 and stochastically drawing
and stochastically drawing
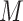 from the counterfactual joint
distribution of mediator values, conditional on
from the counterfactual joint
distribution of mediator values, conditional on 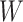 , in a hypothetical world
in which
, in a hypothetical world
in which 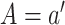 versus drawing from the
counterfactual joint distribution of mediator values, conditional on
versus drawing from the
counterfactual joint distribution of mediator values, conditional on
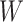 , in which
, in which 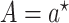 , in the target population. The
interventional direct effect among those for whom
, in the target population. The
interventional direct effect among those for whom 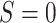 can
be similarly written:
can
be similarly written: 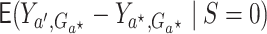 ,
and, generally speaking, is the average effect of
,
and, generally speaking, is the average effect of  on
on
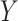 that does not operate through
that does not operate through
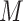 in the target population. Specifically,
it is the average difference in expected outcomes setting
in the target population. Specifically,
it is the average difference in expected outcomes setting 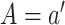 versus
versus 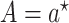 and stochastically drawing
and stochastically drawing 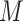 from the counterfactual joint
distribution of mediator values, conditional on
from the counterfactual joint
distribution of mediator values, conditional on 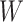 , in a hypothetical world
in which
, in a hypothetical world
in which 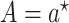 , in the target population.
, in the target population.
We focus on identification and estimation of  .
Contrasts of
.
Contrasts of 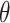 under the values of
under the values of
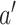 and
and 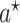 given in the above definitions correspond to the transported interventional (in)direct
effects.
given in the above definitions correspond to the transported interventional (in)direct
effects.
Under the assumptions
(1)
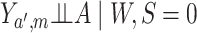 ,
,(2)
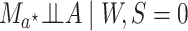 ,
,(3)
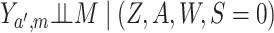 ,
,(4)
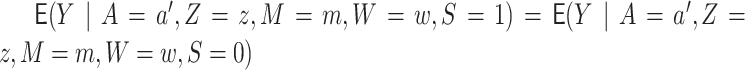 ,
and
,
and-
(5) positivity:
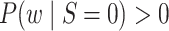 implies
implies 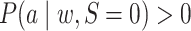 for
for 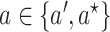
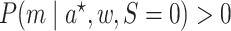 and
and 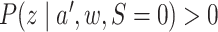 imply
imply
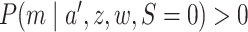
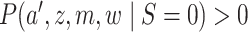 implies
implies 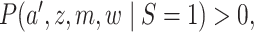
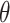 is identified and is equal to
is identified and is equal to
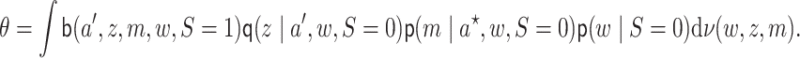 |
(2.2) |
(The identification proof is in the Supplementary materials available at Biostatistics online.)
Assumptions (1)–(3) are sequential randomization assumptions that involve the target
population only. Assumption (1) states that, conditional on  , there
is no unmeasured confounding of the relation between
, there
is no unmeasured confounding of the relation between 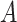 and
and
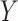 ; assumption (2) states that conditional
on
; assumption (2) states that conditional
on 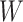 there is no unmeasured confounding of the
relation between
there is no unmeasured confounding of the
relation between 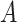 and
and 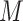 ; (3)
states that conditional on
; (3)
states that conditional on 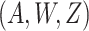 there is no unmeasured confounding
of the relation between
there is no unmeasured confounding
of the relation between 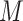 and
and 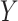 .
Assumption (4) is the transportability assumption and states that there is a common
outcome model across source and target populations. It is this last assumption (4) that
allows us to transport or borrow information on the outcome model from other sites. If an
alternative data source is available where
.
Assumption (4) is the transportability assumption and states that there is a common
outcome model across source and target populations. It is this last assumption (4) that
allows us to transport or borrow information on the outcome model from other sites. If an
alternative data source is available where 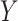 is observed among those
for whom
is observed among those
for whom 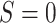 , then the null hypothesis of
equivalence between
, then the null hypothesis of
equivalence between 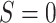 and
and 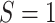 can
be tested nonparametrically (Luedtke and
others, 2019).
can
be tested nonparametrically (Luedtke and
others, 2019).
3. Efficient influence function for 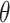
The efficient influence function (EIF) characterizes the asymptotic
behavior of all regular and efficient estimators (Bickel
and others, 1993; van der Vaart,
2002). In addition to being locally efficient, estimators constructed using the EIF
have advantages of multiple robustness, which means that some components of the data
distribution (i.e., nuisance parameters) can be inconsistently estimated while the estimator
remains consistent. The multiple robustness property also allows the use data-adaptive
machine learning algorithms in estimating nuisance parameters while retaining the ability to
compute correct standard errors and confidence intervals. This is due to fact that the
asymptotic analysis of the estimators yield second-order bias terms in differences of the
nuisance parameters, and therefore allow slow convergence rates (e.g.,
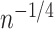 ) for estimating these nuisance
parameters.
) for estimating these nuisance
parameters.
Theorem 3.1 (Efficient influence function)
For fixed
,
define
(3.3) The efficient influence function for
in the nonparametric model
is equal to
(3.4)
This theorem makes two important contributions that advance the previous work deriving the
EIF for a similar 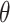 , but one that was limited in that it
(i) assumed that the distribution of
, but one that was limited in that it
(i) assumed that the distribution of 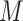 conditional on
conditional on
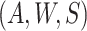 was known and (ii) could only
consider a single binary
was known and (ii) could only
consider a single binary 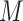 (Rudolph
and others, 2020). First, the EIF we derive does not assume that
that the distribution of
(Rudolph
and others, 2020). First, the EIF we derive does not assume that
that the distribution of 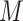 conditional on
conditional on 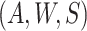 is
known, reflected in the
is
known, reflected in the 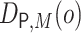 component of the EIF in
Equation 3.4, above.
component of the EIF in
Equation 3.4, above.
Second, we can overcome the challenge of estimating multivariate or continuous densities on
the mediator, 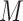 , and intermediate variable,
, and intermediate variable,
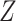 , as well as integrals with respect to these
densities, if either
, as well as integrals with respect to these
densities, if either 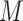 or
or 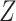 is
low-dimensional (though it can be multivariate) by using an alternative parameterization of
the densities that allows regression methods to be used in estimating the relevant
quantities. In the remainder of this work, we assume
is
low-dimensional (though it can be multivariate) by using an alternative parameterization of
the densities that allows regression methods to be used in estimating the relevant
quantities. In the remainder of this work, we assume 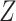 is
low-dimensional (e.g., binary, as in our MTO illustrative application), though similar
parameterizations may be achieved if
is
low-dimensional (e.g., binary, as in our MTO illustrative application), though similar
parameterizations may be achieved if 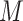 is low-dimensional.
is low-dimensional.
The EIF given in Theorem 3.1 may be represented in terms of the expressions given in Lemma 3.1 below, which does not depend on conditional densities or integrals on the mediating variables.
Lemma 3.1 (Alternative representation of the EIF for univariate
and multivariate
)
The functions
,
, and
may be parameterized:
(3.5)
(3.6)
(3.7)
In the remainder of the article, we denote 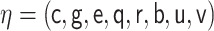 and
and 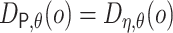 .
We let
.
We let 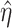 denote an estimator of
denote an estimator of
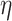 , and
, and 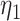 denotes the probability limit of
denotes the probability limit of 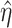 , which may be
different from the true value.
, which may be
different from the true value.
We derive the robustness properties of 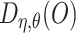 in the
Supplementary materials available at Biostatistics online; they are given
below in Lemma 3.2. The behavior of the term
in the
Supplementary materials available at Biostatistics online; they are given
below in Lemma 3.2. The behavior of the term 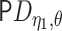 determines the
robustness properties of the EIF as an estimating equation. Theorem 1 in the Supplementary
materials available at Biostatistics online, together with the
Cauchy–Schwarz inequality shows that
determines the
robustness properties of the EIF as an estimating equation. Theorem 1 in the Supplementary
materials available at Biostatistics online, together with the
Cauchy–Schwarz inequality shows that 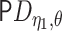 yields a term of
the order of:
yields a term of
the order of:
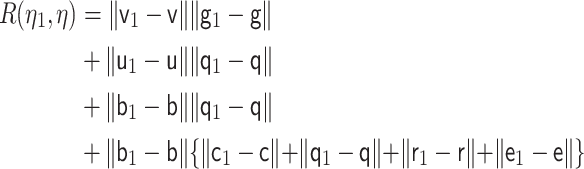 |
such that consistent estimation of 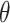 is
possible under consistent estimation of certain configurations of the parameters in
is
possible under consistent estimation of certain configurations of the parameters in
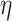 . The following lemma is a direct
consequence.
. The following lemma is a direct
consequence.
Lemma 3.2 (Multiple robustness of
)
Let
be such that one of the following conditions hold:
(1)
and either
or
or
, or
(2)
and either
or
or
.
Then
with
defined as in Theorem 3.1.
We note that the cases 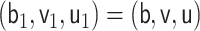 and
and 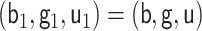 may be uninteresting if the re-parametrization in Lemma 3.1 is used to estimate the EIF,
because in that case, consistent estimation of
may be uninteresting if the re-parametrization in Lemma 3.1 is used to estimate the EIF,
because in that case, consistent estimation of 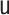 and
and
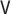 will generally require consistent
estimation of
will generally require consistent
estimation of 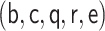 in addition to the outer conditional expectations in Equations (3.6) and (3.7).
in addition to the outer conditional expectations in Equations (3.6) and (3.7).
4. Estimators
We describe two efficient, robust estimators of 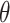 . In Section 4.1, we propose an estimator that solves the EIF
estimating equation in one step (Pfanzagl and Wefelmeyer,
1985) (which we refer to as a one-step estimator), and in Section 4.2, we propose a targeted minimum loss-based estimator
(TMLE, van der Laan and Rubin, 2006), which is a
substitution estimator that also solves the EIF estimating equation, but does it through
iterative de-biasing targeted updates to nuisance parameters. We provide the R code to
implement the proposed estimators, freely available at https://github.com/kararudolph/transport.
. In Section 4.1, we propose an estimator that solves the EIF
estimating equation in one step (Pfanzagl and Wefelmeyer,
1985) (which we refer to as a one-step estimator), and in Section 4.2, we propose a targeted minimum loss-based estimator
(TMLE, van der Laan and Rubin, 2006), which is a
substitution estimator that also solves the EIF estimating equation, but does it through
iterative de-biasing targeted updates to nuisance parameters. We provide the R code to
implement the proposed estimators, freely available at https://github.com/kararudolph/transport.
Let 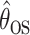 and
and
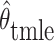 denote the
estimators defined below in Sections 4.1 and 4.2. Per the theorem below, the two estimators are
asymptotically normal and efficient.
denote the
estimators defined below in Sections 4.1 and 4.2. Per the theorem below, the two estimators are
asymptotically normal and efficient.
Theorem 4.1 (Asymptotic normality and efficiency)
Assume
(1) Positivity, described as identification assumption (1) in Section 2.1, and
(2) The class of functions
is Donsker for some
and such that
as
, and
(3) The second-order term
is
.
Then,
, and
where
is the nonparametric efficiency bound.
The proof of this theorem follows the general proof presented in Appendix 18 of van der Laan and Rose (2011). As a consequence, the
variance of the estimators that follow can be estimated as the sample variance of the EIF,
with 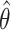 and the nuisance parameters
estimated as described above. This variance estimate may be used to construct Wald-type
confidence intervals.
and the nuisance parameters
estimated as described above. This variance estimate may be used to construct Wald-type
confidence intervals.
The Donsker condition of Theorem 4.1 may be avoided by using cross-fitting (Klaassen, 1987; Zheng and
van der Laan, 2011; Chernozhukov and
others, 2019) in the estimation procedure. Let 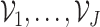 denote a
random partition of the index set
denote a
random partition of the index set 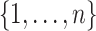 into
into
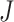 prediction sets of approximately the same
size. That is,
prediction sets of approximately the same
size. That is, 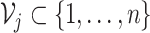 ;
;
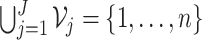 ;
and
;
and 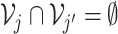 .
In addition, for each
.
In addition, for each 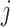 , the associated training sample is given by
, the associated training sample is given by
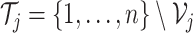 .
let
.
let 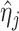 denote the estimator of
denote the estimator of
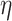 , obtained by training the corresponding
prediction algorithm using only data in the sample
, obtained by training the corresponding
prediction algorithm using only data in the sample 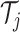 . Further, we let
. Further, we let
 denote the index of the validation set
which contains observation
denote the index of the validation set
which contains observation 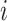 . The one-step and TMLE estimators may be
adapted to cross-fitting by substituting all occurrences of
. The one-step and TMLE estimators may be
adapted to cross-fitting by substituting all occurrences of 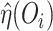 by
by 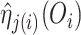 in the respective
algorithms.
in the respective
algorithms.
The third condition of Theorem 4.1 can be satisfied by many data-adaptive algorithms (e.g., lasso (Bickel and others, 2009), regression trees (Wager and Walther, 2015), neural networks (Chen and White, 1999), and highly adaptive lasso (HAL) (van der Laan, 2017)); we use HAL in the simulations that follow.
4.1. One-step estimator
The one-step estimate of 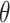 is given by the solution to the EIF
estimating equation:
is given by the solution to the EIF
estimating equation:
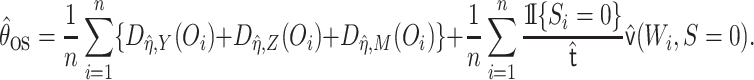 |
We first describe how to estimate 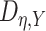 . The
regression
. The
regression 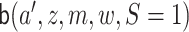 can be
estimated by fitting a regression of
can be
estimated by fitting a regression of 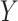 on
on
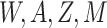 among observations with
among observations with
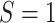 and then predicting values of
and then predicting values of
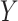 setting
setting 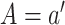 . The probability
. The probability
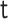 is estimated as the empirical
proportion of observations with
is estimated as the empirical
proportion of observations with 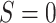 (i.e., in the target
population). The regression function
(i.e., in the target
population). The regression function 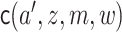 can be estimated
by fitting a regression of
can be estimated
by fitting a regression of 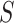 on
on 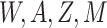 and predicting the probability that
and predicting the probability that 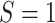 setting
setting
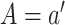 . The treatment mechanism
. The treatment mechanism
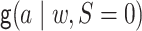 for
for
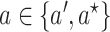 can be estimated
by fitting a regression of
can be estimated
by fitting a regression of 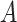 on
on 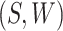 and predicting the probability that
and predicting the probability that 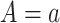 , setting
, setting
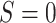 . For the motivating example, we
consider here in which assignment of
. For the motivating example, we
consider here in which assignment of 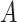 is randomized, these
can be estimated as the empirical probabilities that
is randomized, these
can be estimated as the empirical probabilities that 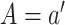 and
and 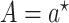 among those with
among those with
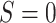 . Under the reparameterization in Lemma
3.1 and in our motivating example,
. Under the reparameterization in Lemma
3.1 and in our motivating example, 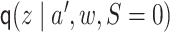 can be
estimated by fitting a regression of
can be
estimated by fitting a regression of 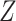 on
on
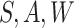 and predicting the probability that
and predicting the probability that
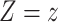 setting
setting 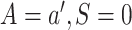 . Likewise,
. Likewise,
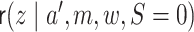 can be
estimated by fitting a regression of
can be
estimated by fitting a regression of 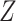 on
on
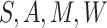 and predicting the probability that
and predicting the probability that
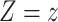 setting
setting 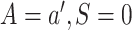 . The treatment
probabilities
. The treatment
probabilities 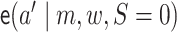 and
and
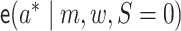 can be
estimated by fitting a regression of
can be
estimated by fitting a regression of 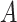 on
on
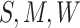 and predicting the probability that
and predicting the probability that
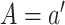 and
and 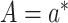 ,
respectively, setting
,
respectively, setting  .
.
We next describe how to estimate 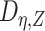 . For binary
. For binary
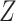 , the EIF simplifies to be
, the EIF simplifies to be
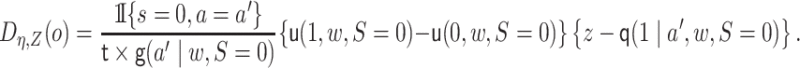 |
The parameters 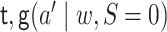 and
and 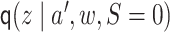 can be
estimated as described above. For each
can be
estimated as described above. For each 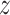 ,
,
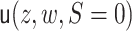 can be estimated by
regressing the quantity
can be estimated by
regressing the quantity 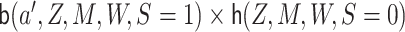 on
on 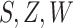 and getting predicted values, setting
and getting predicted values, setting
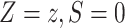 .
.
To estimate 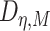 , we estimate
, we estimate
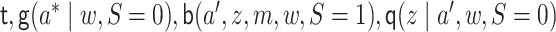 as described above. The function
as described above. The function 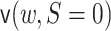 can be
estimated by marginalizing out
can be
estimated by marginalizing out 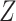 from
from
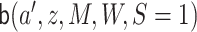 using
using
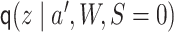 as
predicted probabilities for each
as
predicted probabilities for each 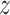 , and then regressing
the resulting quantity on
, and then regressing
the resulting quantity on 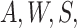 and predicting values setting
and predicting values setting
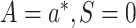 .
.
4.2. TML estimator
We now describe how to compute a related TML estimator. As an overview, this estimator
entails targeting 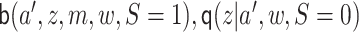 ,
and
,
and 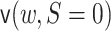 , which correspond to
solving terms 1, 2, and 3, respectively, in (3.4). Plugging in
, which correspond to
solving terms 1, 2, and 3, respectively, in (3.4). Plugging in 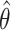 solves the
last term in (3.4).
solves the
last term in (3.4).
We assume 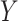 can be bounded in
can be bounded in
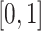 , as described previously (Gruber and van der Laan, 2010). Many of the steps are
identical to those for the one-step estimator, the differences are in the targeting of
, as described previously (Gruber and van der Laan, 2010). Many of the steps are
identical to those for the one-step estimator, the differences are in the targeting of
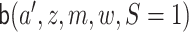 ,
,
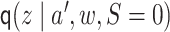 , and
, and
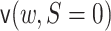 .
.
Let 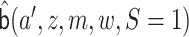 be
an initial estimate of
be
an initial estimate of 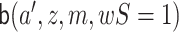 . We update
this initial estimate using covariate
. We update
this initial estimate using covariate
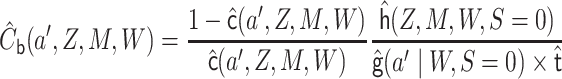 |
in a logistic regression of  with
with
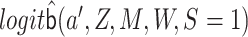 as an offset, among the subset for which
as an offset, among the subset for which  . Let
. Let
 denote the
maximum likelihood estimation (MLE) fitted coefficient associated with
denote the
maximum likelihood estimation (MLE) fitted coefficient associated with
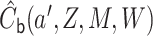 . The
targeted (i.e., updated) estimate is given by
. The
targeted (i.e., updated) estimate is given by
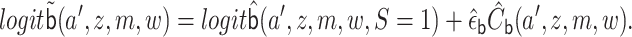 |
An alternative algorithm would use
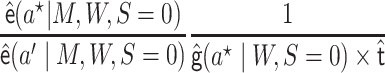 |
as weights of what would become a weighted logistic regression model with covariate
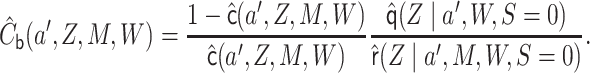 |
Next, let 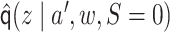 be
an initial estimate of
be
an initial estimate of 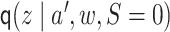 . We
update this initial estimate using covariate
. We
update this initial estimate using covariate
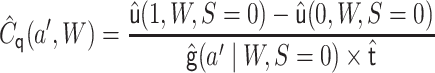 |
in a logistic regression of 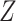 with
with
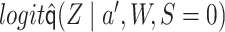 as an offset, among the subset for which
as an offset, among the subset for which 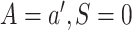 . Let
. Let
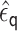 be the MLE fitted
coefficient associated with
be the MLE fitted
coefficient associated with 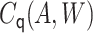 . The targeted estimate is
given by
. The targeted estimate is
given by
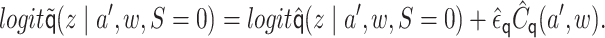 |
To potentially improve performance in finite samples, we can move
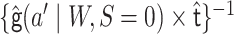 into the weights of a weighted logistic regression model, leaving
into the weights of a weighted logistic regression model, leaving
 as
as 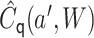 .
.
Replacing 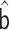 and
and
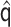 with
with
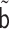 and
and
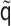 , the above steps can be
iterated until the score equation
, the above steps can be
iterated until the score equation 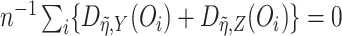 is solved up to a factor of
is solved up to a factor of 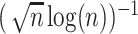 . This iterating
process and stopping criterion ensures that the efficient influence function is solved up
to
. This iterating
process and stopping criterion ensures that the efficient influence function is solved up
to 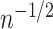 and mitigates risk of
overfitting.
and mitigates risk of
overfitting.
Next, we marginalize out 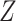 from
from 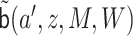 using
using
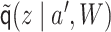 as
predicted probabilities for each
as
predicted probabilities for each 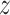 , and call the resulting
quantity
, and call the resulting
quantity 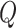 . This quantity is then regressed on
. This quantity is then regressed on
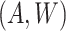 among units with
among units with
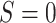 and
and 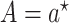 to obtain an estimator
to obtain an estimator
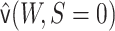 . This estimate is
updated using covariate
. This estimate is
updated using covariate
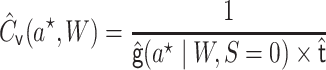 |
in a logistic regression of 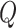 with
with
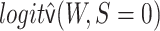 as an
offset, among the subset for which
as an
offset, among the subset for which 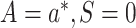 . Let
. Let
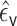 denote the MLE
fitted coefficient on
denote the MLE
fitted coefficient on 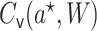 . The targeted
estimate is given by
. The targeted
estimate is given by
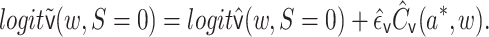 |
To potentially improve finite sample performance, 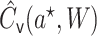 may be moved
into the weights of a weighted logistic regression model with intercept only. The
empirical mean of
may be moved
into the weights of a weighted logistic regression model with intercept only. The
empirical mean of 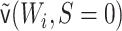 among those for
whom
among those for
whom 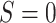 is the TMLE estimate. Its variance can
be estimated as the sample variance of the estimated EIF, given in (3.4).
is the TMLE estimate. Its variance can
be estimated as the sample variance of the estimated EIF, given in (3.4).
5. Simulation
We conducted a limited simulation study to examine and compare finite sample performance of these two estimators. We consider the data-generating mechanism (DGM) as follows. All variables are Bernoulli distributed with probabilities given by
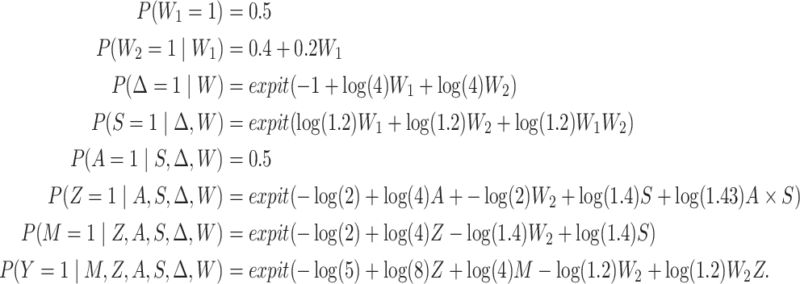 |
This DGM is formulated to align with features of the MTO study we use for the illustrative
example. For example, 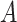 is randomly assigned and adheres to the
exclusion restriction (Angrist and others,
1996), aligned with its role as an instrumental variable. In addition, we consider
a modification of the observed data we have considered thus far:
is randomly assigned and adheres to the
exclusion restriction (Angrist and others,
1996), aligned with its role as an instrumental variable. In addition, we consider
a modification of the observed data we have considered thus far: 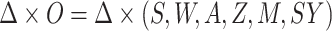 ,
where
,
where 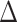 is an indicator of selection into the
survey sample. We assume the survey sampling weights are known or can be estimated as
is an indicator of selection into the
survey sample. We assume the survey sampling weights are known or can be estimated as
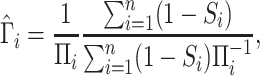 |
where 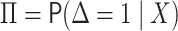 and
and
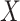 represents unobserved variables used in the
sampling design. Our previous identification result, which can alternatively be written as
represents unobserved variables used in the
sampling design. Our previous identification result, which can alternatively be written as
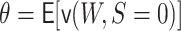 , then
becomes
, then
becomes
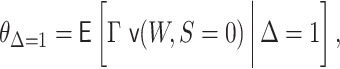 |
where we have added an index 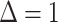 to emphasize that we are interested in parameters for the population from which the sample
was drawn.
to emphasize that we are interested in parameters for the population from which the sample
was drawn.
The EIF is modified to be 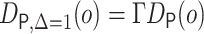 ,
and the estimators of the previous section can be applied by using the weights
,
and the estimators of the previous section can be applied by using the weights
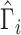 for each subject in the
sample.
for each subject in the
sample.
We consider estimator performance in terms of absolute bias, absolute bias scaled by
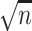 , influence curve-based standard
error relative to the Monte Carlo-based standard error, standard deviation of the estimator
relative to the efficiency bound scaled by
, influence curve-based standard
error relative to the Monte Carlo-based standard error, standard deviation of the estimator
relative to the efficiency bound scaled by 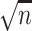 , mean squared
error relative to the efficiency bound scaled by
, mean squared
error relative to the efficiency bound scaled by 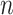 , and 95% confidence
interval (CI) coverage. We run 1000 simulations for sample sizes N = 1000
and N = 10 000. We also consider several model specifications. One in which
all nuisance parameters in
, and 95% confidence
interval (CI) coverage. We run 1000 simulations for sample sizes N = 1000
and N = 10 000. We also consider several model specifications. One in which
all nuisance parameters in 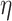 are correctly specified, others that
misspecify each nuisance parameter one at a time, another in which
are correctly specified, others that
misspecify each nuisance parameter one at a time, another in which 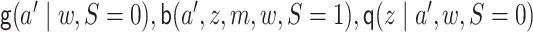 are correctly specified but the rest are not; and last, correctly specifying
are correctly specified but the rest are not; and last, correctly specifying
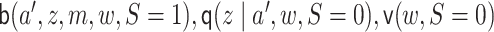 but incorrectly specifying the rest. Under correct specification scenarios, we use HAL
(Benkeser and van der Laan, 2016; van der Laan, 2017) to fit each nuisance parameter. For
incorrect specification, we use an intercept-only model.
but incorrectly specifying the rest. Under correct specification scenarios, we use HAL
(Benkeser and van der Laan, 2016; van der Laan, 2017) to fit each nuisance parameter. For
incorrect specification, we use an intercept-only model.
Table 1 shows simulation results for the transported
interventional direct effect, and Table 2 shows
simulation results for the transported interventional indirect effect comparing the one-step
and TML estimators under correct specification of all nuisance parameters and various
misspecifications. Given the robustness results in Lemma 3.2, we expect consistent estimates
for all specifications in Tables 1 and 2 except when 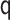 is misspecified.
We see this reflected in the results. We see that when the
is misspecified.
We see this reflected in the results. We see that when the 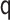 model is misspecified, bias is more than an order of magnitude greater than any other
specification for the transported interventional direct effect in Table 1, and also greater, though to a lesser extent for the transported
interventional indirect effect in Table 2. 95% CI
coverage using influence curve (IC)-based inference is close to 95% in the correctly
specified scenario but is poor when
model is misspecified, bias is more than an order of magnitude greater than any other
specification for the transported interventional direct effect in Table 1, and also greater, though to a lesser extent for the transported
interventional indirect effect in Table 2. 95% CI
coverage using influence curve (IC)-based inference is close to 95% in the correctly
specified scenario but is poor when 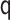 is misspecified
for the transported interventional direct effect (Table
1), which is not unexpected given the biased estimates in this scenario. Coverage
is less than 95% in other misspecified scenarios for both the transported direct and
indirect effects (e.g., 68% when the
is misspecified
for the transported interventional direct effect (Table
1), which is not unexpected given the biased estimates in this scenario. Coverage
is less than 95% in other misspecified scenarios for both the transported direct and
indirect effects (e.g., 68% when the 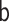 model is
misspecified for the transported interventional indirect effect, Table 2). This is not unexpected; the IC may not provide accurate
inference when the IC at the estimated distribution using misspecified models does not
converge to the IC at the true distribution. For robustness to extend to IC-based inference,
further targeting of the nuisance parameters would be necessary that would preserve
asymptotic linearity with a known influence curve at the cost of some efficiency (van der Laan, 2014; Benkeser and others, 2016). We note that under the smaller sample
size of N = 1000 we see some deterioration in performance, particularly for
the indirect effect, which is expected given that the true indirect effect is over five
times smaller than the direct effect.
model is
misspecified for the transported interventional indirect effect, Table 2). This is not unexpected; the IC may not provide accurate
inference when the IC at the estimated distribution using misspecified models does not
converge to the IC at the true distribution. For robustness to extend to IC-based inference,
further targeting of the nuisance parameters would be necessary that would preserve
asymptotic linearity with a known influence curve at the cost of some efficiency (van der Laan, 2014; Benkeser and others, 2016). We note that under the smaller sample
size of N = 1000 we see some deterioration in performance, particularly for
the indirect effect, which is expected given that the true indirect effect is over five
times smaller than the direct effect.
Table 1.
Simulation results for the transported interventional direct effect.
| Nuisance parameters misspecified | Estimator |
|
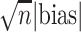
|
relse | relsd | relrmse | 95%CI Cov |
|---|---|---|---|---|---|---|---|
| Transported interventional direct effect | |||||||
| N = 10 000 | |||||||
| None | os | 0.0005 | 0.0490 | 1.0200 | 0.9489 | 0.9488 | 0.9570 |
| tmle | 0.0004 | 0.0415 | 1.0040 | 0.9610 | 0.9608 | 0.9530 | |
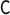
|
os | 0.0005 | 0.0519 | 1.0023 | 0.8226 | 0.8227 | 0.9570 |
| tmle | 0.0003 | 0.0312 | 0.9577 | 0.8579 | 0.8576 | 0.9460 | |
|
os | 0.0005 | 0.0480 | 1.0213 | 0.9481 | 0.9480 | 0.9580 |
| tmle | 0.0004 | 0.0408 | 1.0055 | 0.9600 | 0.9598 | 0.9520 | |
|
os | 0.0002 | 0.0156 | 1.0097 | 0.9431 | 0.9427 | 0.9520 |
| tmle | 0.0003 | 0.0301 | 0.9878 | 0.9602 | 0.9599 | 0.9460 | |
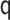
|
os | 0.0885 | 8.8488 | 0.7750 | 1.4727 | 5.2339 | 0.0250 |
| tmle | 0.0348 | 3.4814 | 1.0656 | 1.0154 | 2.2215 | 0.5580 | |
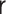
|
os | 0.0024 | 0.2382 | 1.0889 | 0.8724 | 0.8824 | 0.9640 |
| tmle | 0.0021 | 0.2134 | 1.0809 | 0.8788 | 0.8867 | 0.9640 | |

|
os | 0.0047 | 0.4739 | 1.0460 | 0.9615 | 0.9979 | 0.9470 |
| tmle | 0.0107 | 1.0661 | 0.9908 | 1.0007 | 1.1690 | 0.9070 | |
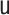
|
os | 0.0053 | 0.5285 | 0.9400 | 0.9405 | 0.9867 | 0.9230 |
| tmle | 0.0053 | 0.5262 | 0.9249 | 0.9530 | 0.9983 | 0.9150 | |
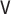
|
os | 0.0005 | 0.0499 | 1.0213 | 0.9476 | 0.9476 | 0.9570 |
| tmle | 0.0004 | 0.0421 | 1.0028 | 0.9621 | 0.9619 | 0.9520 | |
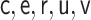
|
os | 0.0023 | 0.2293 | 0.8924 | 0.7159 | 0.7272 | 0.9140 |
| tmle | 0.0019 | 0.1889 | 0.8519 | 0.7465 | 0.7538 | 0.9020 | |
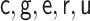
|
os | 0.0023 | 0.2321 | 0.8914 | 0.7165 | 0.7281 | 0.9140 |
| tmle | 0.0019 | 0.1904 | 0.8548 | 0.7438 | 0.7513 | 0.9030 | |
| N = 1000 | |||||||
| None | os | 0.0014 | 0.0454 | 1.0200 | 0.8925 | 0.8921 | 0.9591 |
| tmle | 0.0028 | 0.0880 | 0.9702 | 0.9309 | 0.9314 | 0.9414 | |

|
os | 0.0003 | 0.0104 | 1.0340 | 0.7691 | 0.7683 | 0.9600 |
| tmle | 0.0021 | 0.0648 | 0.9648 | 0.8190 | 0.8190 | 0.9460 | |

|
os | 0.0019 | 0.0617 | 1.0167 | 0.8958 | 0.8957 | 0.9520 |
| tmle | 0.0032 | 0.1009 | 0.9697 | 0.9317 | 0.9327 | 0.9424 | |
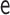
|
os | 0.0036 | 0.1134 | 1.0131 | 0.8855 | 0.8871 | 0.9520 |
| tmle | 0.0049 | 0.1550 | 0.9611 | 0.9252 | 0.9286 | 0.9440 | |
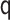
|
os | 0.0672 | 2.1252 | 0.7993 | 1.3098 | 1.7796 | 0.7560 |
| tmle | 0.0280 | 0.8862 | 1.0124 | 0.9771 | 1.0981 | 0.9300 | |
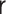
|
os | 0.0073 | 0.2303 | 1.1242 | 0.8149 | 0.8245 | 0.9620 |
| tmle | 0.0070 | 0.2202 | 1.0994 | 0.8315 | 0.8400 | 0.9620 | |
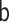
|
os | 0.0047 | 0.1499 | 1.0460 | 0.3041 | 0.3156 | 0.9470 |
| tmle | 0.0107 | 0.3371 | 0.9908 | 0.3164 | 0.3697 | 0.9070 | |
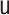
|
os | 0.0106 | 0.3362 | 0.9735 | 0.8614 | 0.8814 | 0.9420 |
| tmle | 0.0101 | 0.3186 | 0.9234 | 0.8993 | 0.9164 | 0.9180 | |
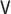
|
os | 0.0009 | 0.0295 | 1.0304 | 0.8827 | 0.8819 | 0.9589 |
| tmle | 0.0021 | 0.0668 | 0.9857 | 0.9152 | 0.9150 | 0.9498 | |
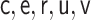
|
os | 0.0030 | 0.0949 | 0.9553 | 0.6643 | 0.6657 | 0.9315 |
| tmle | 0.0013 | 0.0424 | 0.9141 | 0.6898 | 0.6895 | 0.9224 | |
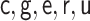
|
os | 0.0019 | 0.0591 | 0.9533 | 0.6663 | 0.6664 | 0.9291 |
| tmle | 0.0001 | 0.0034 | 0.9044 | 0.6981 | 0.6974 | 0.9222 | |
Table 2.
Simulation results for the transported interventional indirect effect.
| Nuisance parameters misspecified | Estimator |
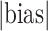
|
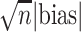
|
relse | relsd | relrmse | 95%CI Cov |
|---|---|---|---|---|---|---|---|
| Transported interventional indirect effect | |||||||
| N = 10 000 | |||||||
| None | os | 0.0000 | 0.0030 | 0.9966 | 0.9760 | 0.9755 | 0.9420 |
| tmle | 0.0001 | 0.0065 | 0.9895 | 0.9778 | 0.9774 | 0.9400 | |
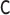
|
os | 0.0003 | 0.0272 | 0.9864 | 0.9445 | 0.9456 | 0.9410 |
| tmle | 0.0001 | 0.0147 | 0.9734 | 0.9530 | 0.9529 | 0.9370 | |
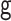
|
os | 0.0000 | 0.0004 | 0.9976 | 0.9749 | 0.9744 | 0.9430 |
| tmle | 0.0000 | 0.0044 | 0.9907 | 0.9768 | 0.9764 | 0.9430 | |
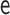
|
os | 0.0006 | 0.0632 | 0.9610 | 0.8917 | 0.9003 | 0.9390 |
| tmle | 0.0007 | 0.0668 | 0.9603 | 0.8887 | 0.8983 | 0.9380 | |
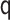
|
os | 0.0020 | 0.2035 | 0.9285 | 1.0709 | 1.1459 | 0.9070 |
| tmle | 0.0030 | 0.2951 | 0.8061 | 1.2396 | 1.3737 | 0.8410 | |
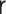
|
os | 0.0003 | 0.0324 | 1.0081 | 1.0034 | 1.0051 | 0.9500 |
| tmle | 0.0001 | 0.0075 | 1.0429 | 0.9652 | 0.9648 | 0.9590 | |
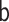
|
os | 0.0001 | 0.0067 | 0.4870 | 1.0879 | 1.0874 | 0.6850 |
| tmle | 0.0001 | 0.0099 | 0.4747 | 1.1763 | 1.1759 | 0.6700 | |
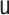
|
os | 0.0000 | 0.0020 | 0.9997 | 0.9714 | 0.9709 | 0.9440 |
| tmle | 0.0000 | 0.0009 | 0.9919 | 0.9744 | 0.9739 | 0.9440 | |
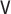
|
os | 0.0000 | 0.0026 | 1.0250 | 1.0114 | 1.0109 | 0.9550 |
| tmle | 0.0001 | 0.0058 | 1.0015 | 1.0259 | 1.0254 | 0.9480 | |
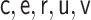
|
os | 0.0006 | 0.0618 | 0.9375 | 0.9834 | 0.9907 | 0.9400 |
| tmle | 0.0007 | 0.0696 | 0.9168 | 0.9947 | 1.0040 | 0.9310 | |

|
os | 0.0007 | 0.0676 | 0.9032 | 0.9399 | 0.9492 | 0.9150 |
| tmle | 0.0008 | 0.0767 | 0.8996 | 0.9387 | 0.9508 | 0.9150 | |
| N = 1000 | |||||||
| None | os | 0.0007 | 0.0229 | 0.9010 | 1.0200 | 1.0201 | 0.9041 |
| tmle | 0.0006 | 0.0200 | 0.8900 | 1.0209 | 1.0207 | 0.8988 | |
|
os | 0.0013 | 0.0407 | 0.8891 | 0.9901 | 0.9924 | 0.8900 |
| tmle | 0.0011 | 0.0337 | 0.8729 | 0.9970 | 0.9983 | 0.8880 | |
|
os | 0.0009 | 0.0293 | 0.9092 | 1.0185 | 1.0194 | 0.9072 |
| tmle | 0.0008 | 0.0242 | 0.8974 | 1.0193 | 1.0197 | 0.8992 | |
|
os | 0.0026 | 0.0818 | 0.9025 | 0.9447 | 0.9582 | 0.8992 |
| tmle | 0.0025 | 0.0797 | 0.8953 | 0.9415 | 0.9543 | 0.8976 | |
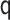
|
os | 0.0017 | 0.0541 | 0.8405 | 1.0920 | 1.0963 | 0.8700 |
| tmle | 0.0017 | 0.0525 | 0.7671 | 1.1978 | 1.2012 | 0.8440 | |
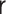
|
os | 0.0004 | 0.0120 | 0.8955 | 1.0476 | 1.0468 | 0.9080 |
| tmle | 0.0008 | 0.0263 | 0.9121 | 1.0109 | 1.0112 | 0.8980 | |
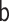
|
os | 0.0001 | 0.0021 | 0.4870 | 0.3440 | 0.3439 | 0.6850 |
| tmle | 0.0001 | 0.0031 | 0.4747 | 0.3720 | 0.3719 | 0.6700 | |
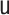
|
os | 0.0008 | 0.0264 | 0.8872 | 1.0328 | 1.0331 | 0.8900 |
| tmle | 0.0007 | 0.0215 | 0.8655 | 1.0424 | 1.0423 | 0.8800 | |
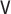
|
os | 0.0004 | 0.0114 | 0.9605 | 1.0274 | 1.0265 | 0.9247 |
| tmle | 0.0003 | 0.0086 | 0.9279 | 1.0450 | 1.0440 | 0.9110 | |
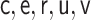
|
os | 0.0023 | 0.0733 | 0.8522 | 1.0237 | 1.0331 | 0.8973 |
| tmle | 0.0026 | 0.0831 | 0.8284 | 1.0286 | 1.0410 | 0.8881 | |
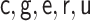
|
os | 0.0020 | 0.0618 | 0.8595 | 0.9285 | 0.9358 | 0.8741 |
| tmle | 0.0022 | 0.0708 | 0.8492 | 0.9229 | 0.9328 | 0.8741 | |
We also give simulation results in Table 3 comparing
performance of the transport one-step and TML estimators, assuming the outcome data are
unobserved for 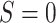 , and the nontransported versions of the
one-step and TML estimators developed previously (Díaz
and others, 2020). These nontransported estimators are
approximately 3 times more efficient than their transported counterparts (e.g., the
efficiency bound of the transported TMLE of the indirect effect is 3 times greater than the
efficiency bound of the nontransported TMLE of the indirect effect), reflecting the
advantage of observing the outcome data in the target population.
, and the nontransported versions of the
one-step and TML estimators developed previously (Díaz
and others, 2020). These nontransported estimators are
approximately 3 times more efficient than their transported counterparts (e.g., the
efficiency bound of the transported TMLE of the indirect effect is 3 times greater than the
efficiency bound of the nontransported TMLE of the indirect effect), reflecting the
advantage of observing the outcome data in the target population.
Table 3.
Simulation results comparing one-step (os) and TML (tmle) estimators for the transported interventional indirect and direct effects with those for the nontransported interventional indirect and direct effects.
| Effect type | Estimator |
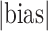
|
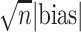
|
relse | relsd | relrmse | 95%CI Cov |
|---|---|---|---|---|---|---|---|
| N = 10 000 | |||||||
| Transported, indirect effect | os | 0.0000 | 0.0030 | 0.9966 | 0.9760 | 0.9755 | 0.9420 |
| Transported, indirect effect | tmle | 0.0001 | 0.0065 | 0.9895 | 0.9778 | 0.9774 | 0.9400 |
| Nontransported, indirect effect | os | 0.0000 | 0.0022 | 0.9413 | 1.1722 | 1.1717 | 0.9420 |
| Nontransported, indirect effect | tmle | 0.0000 | 0.0035 | 0.9412 | 1.1690 | 1.1685 | 0.9420 |
| Transported, direct effect | os | 0.0005 | 0.0490 | 1.0200 | 0.9489 | 0.9488 | 0.9570 |
| Transported, direct effect | tmle | 0.0004 | 0.0415 | 1.0040 | 0.9610 | 0.9608 | 0.9530 |
| Nontransported, direct effect | os | 0.0013 | 0.1344 | 1.0178 | 1.1003 | 1.1074 | 0.9620 |
| Nontransported, direct effect | tmle | 0.0014 | 0.1397 | 1.0150 | 1.1033 | 1.1110 | 0.9640 |
| N = 1000 | |||||||
| Transported, indirect effect | os | 0.0007 | 0.0229 | 0.9010 | 1.0200 | 1.0201 | 0.9041 |
| Transported, indirect effect | tmle | 0.0006 | 0.0200 | 0.8900 | 1.0209 | 1.0207 | 0.8988 |
| Nontransported, indirect effect | os | 0.0001 | 0.0045 | 0.9134 | 1.1626 | 1.1622 | 0.9340 |
| Nontransported, indirect effect | tmle | 0.0001 | 0.0042 | 0.9170 | 1.1495 | 1.1490 | 0.9300 |
| Transported, direct effect | os | 0.0014 | 0.0454 | 1.0200 | 0.8925 | 0.8921 | 0.9591 |
| Transported, direct effect | tmle | 0.0028 | 0.0880 | 0.9702 | 0.9309 | 0.9314 | 0.9414 |
| Nontransported, direct effect | os | 0.0025 | 0.0802 | 1.0212 | 1.0854 | 1.0876 | 0.9540 |
| Nontransported, direct effect | tmle | 0.0031 | 0.0968 | 1.0119 | 1.0949 | 1.0984 | 0.9540 |
6. Illustrative example
We apply the one-step and TML estimators proposed in Section 4 to estimate interventional indirect effects transported across MTO sites, as described in Section 1. Specifically, we are interested in the extent to which differences in: (i) the distribution of individual-level compositional factors between the sites, (ii) take-up of the intervention (i.e., using the housing voucher to move), and (iii) distribution of school environment mediating variables can explain the difference in the indirect effect estimates between MTO sites.
For this example, we consider the indirect effect of randomized receipt of a Section 8
housing voucher (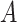 ) and subsequent use
(
) and subsequent use
(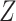 ) on behavioral problems
(
) on behavioral problems
(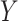 ) (Zill,
1990) through aspects of the school environment (
) (Zill,
1990) through aspects of the school environment (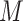 ), (i)
rank of the schools attended, (ii) whether ever attended a school in the top 50% of
rankings, (iii) number of schools attended, (iv) number of moves since baseline, (v) average
proportion of students receiving free or reduced lunch, (vi) ratio of students to teachers,
(vii) proportion of schools attended that were Title I, and (viii) whether or not the most
recent school attended was in the same district as the baseline school) among girls,
comparing the Los Angeles (LA) and New York City (NYC) sites (
), (i)
rank of the schools attended, (ii) whether ever attended a school in the top 50% of
rankings, (iii) number of schools attended, (iv) number of moves since baseline, (v) average
proportion of students receiving free or reduced lunch, (vi) ratio of students to teachers,
(vii) proportion of schools attended that were Title I, and (viii) whether or not the most
recent school attended was in the same district as the baseline school) among girls,
comparing the Los Angeles (LA) and New York City (NYC) sites (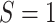 ,
N = 1000) to the Chicago site (
,
N = 1000) to the Chicago site (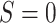 , N =
600) (rounded sample sizes per Census Bureau requirements). We do this in order to
illustrate our methods: the outcomes in Chicago were actually observed, so we can compared
the transported estimate with estimates obtained using Chicago outcome data. Variables
, N =
600) (rounded sample sizes per Census Bureau requirements). We do this in order to
illustrate our methods: the outcomes in Chicago were actually observed, so we can compared
the transported estimate with estimates obtained using Chicago outcome data. Variables
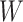 and
and 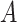 were
measured at baseline, when the children were 0–10 years old. Mediating variables were
measured during the interval between baseline and the final follow-up timepoint 10–15 years
later. The outcome was measured at the final follow-up timepoint. We account for a large
number of covariates at the child and family levels: child age, race/ethnicity, history of
behavioral problems, and gifted/talented status; parental education, marital status, whether
or not the parent was under 18 at the birth of the child, employment, receipt of other
public benefits, household size, feeling like the neighborhood was unsafe at night, feeling
very dissatisfied with the neighborhood, whether or not the family had previously moved more
than three times, wanting to move for better schools, whether or not the family had received
a Section 8 voucher before, and poverty level of the baseline neighborhood. For this
research question, randomization to receive a Section 8 housing voucher is an instrumental
variable that affects
were
measured at baseline, when the children were 0–10 years old. Mediating variables were
measured during the interval between baseline and the final follow-up timepoint 10–15 years
later. The outcome was measured at the final follow-up timepoint. We account for a large
number of covariates at the child and family levels: child age, race/ethnicity, history of
behavioral problems, and gifted/talented status; parental education, marital status, whether
or not the parent was under 18 at the birth of the child, employment, receipt of other
public benefits, household size, feeling like the neighborhood was unsafe at night, feeling
very dissatisfied with the neighborhood, whether or not the family had previously moved more
than three times, wanting to move for better schools, whether or not the family had received
a Section 8 voucher before, and poverty level of the baseline neighborhood. For this
research question, randomization to receive a Section 8 housing voucher is an instrumental
variable that affects 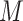 and
and 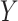 through
the intermediate variable of using the voucher to move out of public housing and into a
rental on the private market (
through
the intermediate variable of using the voucher to move out of public housing and into a
rental on the private market (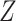 ). We use the MTO sampling weights as
described in Section 5. These weights account for
sampling of children within families, changing randomization ratios, and loss to follow-up
(Sanbonmatsu and others, 2011). We
use data-adaptive methods for fitting the nuisance parameters, using a cross-validated
ensemble of machine learning algorithms (Van der Laan
and others, 2007), that includes generalized linear models,
intercept-only models, and lasso (Tibshirani, 1996)
that included all first and second-order predictors. To estimate the observed,
nontransported interventional indirect effects, we use nontransported versions of the
one-step and TML estimators (Díaz and
others, 2020). Standard errors are estimated using the sample variance
of the influence curve.
). We use the MTO sampling weights as
described in Section 5. These weights account for
sampling of children within families, changing randomization ratios, and loss to follow-up
(Sanbonmatsu and others, 2011). We
use data-adaptive methods for fitting the nuisance parameters, using a cross-validated
ensemble of machine learning algorithms (Van der Laan
and others, 2007), that includes generalized linear models,
intercept-only models, and lasso (Tibshirani, 1996)
that included all first and second-order predictors. To estimate the observed,
nontransported interventional indirect effects, we use nontransported versions of the
one-step and TML estimators (Díaz and
others, 2020). Standard errors are estimated using the sample variance
of the influence curve.
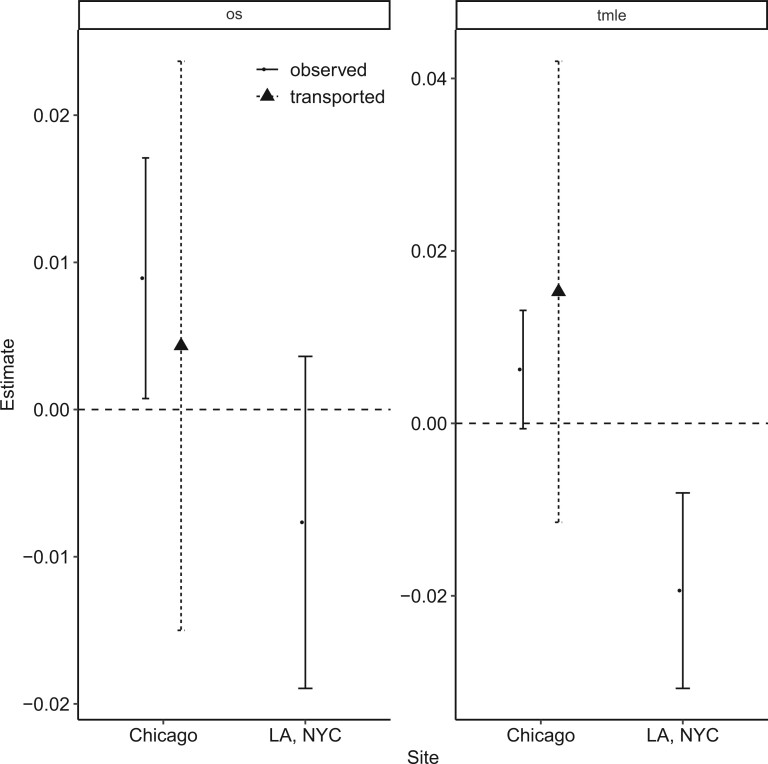
Figure 1 shows the transported and observed indirect
effect estimates and their 95% CIs. Looking at the observed estimates, the indirect pathway
from housing voucher receipt and use through the school environment to behavioral problems
is protective for girls in LA and NYC, resulting in a reduction in behavioral problems at
the final time point. However, the same pathway appears harmful for girls in Chicago,
resulting in an increase of behavioral problems. Comparing the transported interventional
indirect effect estimate (one-step estimator: 0.0043, 95% CI  0.0150 to
0.0237, risk difference scale; TMLE: 0.0153, 95% CI
0.0150 to
0.0237, risk difference scale; TMLE: 0.0153, 95% CI  0.0150 to
0.0420) to the observed estimate for girls in Chicago (one-step estimator: 0.0062, 95% CI
0.0027–0.0097; TMLE: 0.0089, 95% CI 0.0007–0.0171), we see that the two are similar even
though the outcome data from Chicago was not used in the transported estimates. Thus, by
taking the outcome model for LA and NYC and standardizing based on
0.0150 to
0.0420) to the observed estimate for girls in Chicago (one-step estimator: 0.0062, 95% CI
0.0027–0.0097; TMLE: 0.0089, 95% CI 0.0007–0.0171), we see that the two are similar even
though the outcome data from Chicago was not used in the transported estimates. Thus, by
taking the outcome model for LA and NYC and standardizing based on 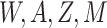 in Chicago, the predicted effect for Chicago is close to the observed. In contrast if they
were not close to each other, this would suggest that the identification assumptions were
not met.
in Chicago, the predicted effect for Chicago is close to the observed. In contrast if they
were not close to each other, this would suggest that the identification assumptions were
not met.
Figure 1.
Interventional indirect effects estimates of being randomized to the Section 8 voucher group on behavioral problems score in adolescence, 10–15 years later, mediated through features of the school environment, among girls. Estimates and 95% CIs for observed (nontransported) and transported predicted effects. All results were approved for release by the U.S. Census Bureau, authorization numbers CBDRB-FY20-ERD002-023 and CBDRB-FY20-ERD002-024.
In the context of MTO, identification assumption (iv) of a common outcome model (i.e., a
common relation of the voucher, moving, and mediators on behavioral problems among girls
across the MTO sites) is arguably the most tenuous. This assumption would not hold in the
presence of any contextual-level effects on the outcome model, such as the local economy,
housing market conditions, segregation, etc. In the presence of contextual-level effects on
the conditional outcome distribution, we would be extrapolating from the source population
to the target population using an inaccurate outcome model. Although we do not assume a
common relation of voucher and moving on the mediators among girls across sites, we do
assume that all 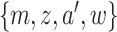 observed in the target
population are also observed in the source population.
observed in the target
population are also observed in the source population.
7. Conclusions
We proposed estimators for transported interventional direct and indirect effects under intermediate confounding and allowing for multiple, possibly related mediating variables arising from a true, unknown joint distribution. These estimators solve the efficient influence function; one that does so in one step and the other that is a substitution estimator that incorporates a series of targeting steps to optimize the bias-variance trade-off. We derived their multiple robustness properties and examined finite sample performance in a simulation study. Lastly, we applied our proposed estimators to better understand why a particular pathway from a housing intervention through changes in the school environment resulted in an unintended harmful effect on behavioral problems among girls in Chicago,when it led to improvements in behavioral problems among girls in other cities. However, in this illustrative example, the outcome data were, in fact, measured in the target population. Our proposed approach is arguably more useful in the scenario where outcome data are unobserved in the target population. An example of this could be a vaccine trial conducted in one or multiple countries where data consists of treatment (assignment to vaccine vs. placebo), intermediate variable (completion of treatment), mediators/surrogate outcomes (antibody titers), and long-term outcome (viral illness). One could use our proposed methods to predict the long-term effect of the same vaccine in a new target country where data on the treatment, intermediate variable, and mediators/surrogate outcomes have already been collected, but the long-term outcome has not yet had the opportunity to be observed.
8. Software
We provide the R code to implement the proposed estimators, freely available at https://github.com/kararudolph/transport.
Supplementary Material
Acknowledgments
This research was conducted as a part of the U.S. Census Bureau’s Evidence Building Project Series. The U.S. Census Bureau has not reviewed the article for accuracy or reliability and does not endorse its contents. Any conclusions expressed herein are those of the authors and do not necessarily represent the views of the U.S. Census Bureau. All results were approved for release by the U.S. Census Bureau, authorization numbers CBDRB-FY20-ERD002-023 and CBDRB-FY20-ERD002-024.
Conflict of Interest: None declared.
Contributor Information
Kara E Rudolph, Department of Epidemiology, Mailman School of Public Health, Columbia University; and Division of Biostatistics, Department of Population Health Sciences, Weill Cornell Medicine, New York, NY, USA.
Iván Díaz, Department of Epidemiology, Mailman School of Public Health, Columbia University; and Division of Biostatistics, Department of Population Health Sciences, Weill Cornell Medicine, New York, NY, USA.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
KER’s time was funded by the National Institute on Drug Abuse (R00DA042127).
References
- Angrist, J. D., Imbens, G. W. and Rubin, D. B. (1996). Identification of causal effects using instrumental variables. Journal of the American Statistical Association 91, 444–455. [Google Scholar]
- Arnold, B. F., Null, C., Luby, S. P. and Colford, J. M. (2018). Implications of wash benefits trials for water and sanitation—authors’ reply. The Lancet Global Health 6, e616–e617. [DOI] [PubMed] [Google Scholar]
- Avin, C., Shpitser, I. and Pearl, J. (2005). Identifiability of path-specific effects. In: Proceedings of the International Joint Conference on Artificial Intelligence. Morgan Kaufman, San Francisco, CA. MR2192340. pp. 357–363. [Google Scholar]
- Benkeser, D., Carone, M., van der Laan, M. J. and Gilbert, P. (2016). Doubly-robust nonparametric inference on the average treatment effect. Technical Report 356, U.C. Berkeley Division of Biostatistics Working Paper Series. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benkeser, D. and van der Laan, M. (2016). The highly adaptive lasso estimator. In: 2016 IEEE International Conference on Data Science and Advanced Analytics (DSAA). IEEE. pp. 689–696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bickel, P. J., Klaassen, C. A. J., Ritov, Y. and Wellner, J. A. (1993). Efficient and Adaptive Estimation for Semiparametric Models. Baltimore, MD: Johns Hopkins University Press. [Google Scholar]
- Bickel, P. J., Ritov, Y., Tsybakov, A. B. (2009). Simultaneous analysis of Lasso and Dantzig selector. The Annals of Statistics 37, 1705–1732. [Google Scholar]
- Chen, X. and White, H. (1999). Improved rates and asymptotic normality for nonparametric neural network estimators. IEEE Transactions on Information Theory 45, 682–691. [Google Scholar]
- Chernozhukov, V., Chetverikov, D., Demirer, M., Duflo, E., Hansen, C. Newey, W., Robins, J. (2019). Double machine learning for treatment and causal parameters. Econometrics Journal 21, C1–C68. [Google Scholar]
- Díaz, I., Hejazi, N. S., Rudolph, K. E. and van der Laan, M. J. (2020). Non-parametric efficient causal mediation with intermediate confounders. Biometrika, In Press. DOI: 10.1093/biomet/asaa085. [DOI] [Google Scholar]
- Gruber, S. and van der Laan, M. J. (2010). A targeted maximum likelihood estimator of a causal effect on a bounded continuous outcome. The International Journal of Biostatistics 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klaassen, C. A. J. (1987). Consistent estimation of the influence function of locally asymptotically linear estimators. The Annals of Statistics 15, 1548–1562. [Google Scholar]
- Luedtke, A., Carone, M. and van der Laan, M. J. (2019). An omnibus non-parametric test of equality in distribution for unknown functions. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 81, 75–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller, T. R. (2015). Projected outcomes of nurse-family partnership home visitation during 1996–2013, USA. Prevention Science 16, 765–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr, L., Feins, J., Jacob, R., Beecroft, E., Sanbonmatsu, L., Katz, L. F., Liebman, J. B. and Kling, J. R. (2003). Moving to Opportunity: Interim Impacts Evaluation. Washington DC: US Department of Housing and Urban Development, Office of Policy Development and Research. [Google Scholar]
- Pearl, J. (2009). Myth, Confusion, and Science in Causal Analysis. Technical Report R-348, Cognitive Systems Laboratory, Computer Science Department University of California, Los Angeles, Los Angeles, CA. [Google Scholar]
- Pearl, J. and Bareinboim, E. (2018). Transportability across studies: a formal approach. Technical Report R-372, Cognitive Systems Laboratory, Dept. Computer Science, University of California, Los Angeles. [Google Scholar]
- Petersen, M. L., Sinisi, S. E. and van der Laan, M. J. (2006). Estimation of direct causal effects. Epidemiology 17, 276–284. [DOI] [PubMed] [Google Scholar]
- Pfanzagl, J. and Wefelmeyer, W. (1985). Contributions to a general asymptotic statistical theory. Statistics & Risk Modeling 3, 379–388. [Google Scholar]
- Rubin, D. B. (1974). Estimating causal effects of treatments in randomized & nonrandomized studies. Journal of Educational Psychology 66, 688–701. [Google Scholar]
- Rudolph, K. E., Levy, J., Schmidt, N. M., Stuart, E. A. and Ahern, J. (2020). Using transportability to understand differences in mediation mechanisms across trial sites: applying a novel estimation approach to a large-scale housing voucher experiment. Epidemiology 31, 523–533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudolph, K. E., Levy, J. and van der Laan, M. J. (2020). Transporting stochastic direct and indirect effects to new populations. Biometrics, In Press. doi.org/10.1111/biom.13274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudolph, K. E., Schmidt, N. M., Glymour, M. M., Crowder, R., Galin, J., Ahern, J. and Osypuk, T. L. (2018a). Composition or context: using transportability to understand drivers of site differences in a large-scale housing experiment. Epidemiology (Cambridge, MA) 29, 199–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudolph, K. E., Sofrygin, O., Schmidt, N. M., Crowder, R., Glymour, M. M., Ahern, J. and Osypuk, T. L. (2018b). Mediation of neighborhood effects on adolescent substance use by the school and peer environments. Epidemiology 29, 590–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudolph, K. E., Sofrygin, O., Zheng, W. and Van Der Laan, M. J. (2017). Robust and flexible estimation of stochastic mediation effects: a proposed method and example in a randomized trial setting. Epidemiologic Methods 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanbonmatsu, L., Katz, L. F., Ludwig, J., Gennetian, L. A., Duncan, G. J., Kessler, R. C., Adam, E. K., McDade, T. and Lindau, S. T. (2011). Moving to opportunity for fair housing demonstration program: final impacts evaluation. Washington, DC: US Department of Housing and Urban Development, Office of Policy Development and Research. [Google Scholar]
- Tchetgen Tchetgen, E. J. and VanderWeele, T. J. (2014). On identification of natural direct effects when a confounder of the mediator is directly affected by exposure. Epidemiology (Cambridge, MA) 25, 282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological) 58, 267–288. [Google Scholar]
- van der Laan, M. (2017). A generally efficient targeted minimum loss based estimator based on the highly adaptive lasso. The International Journal of Biostatistics 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Laan, M. J. (2014). Targeted estimation of nuisance parameters to obtain valid statistical inference. The International Journal of Biostatistics 10, 29–57. [DOI] [PubMed] [Google Scholar]
- van der Laan, M. J. and Petersen, M. L. (2008). Direct effect models. The International Journal of Biostatistics 4. [DOI] [PubMed] [Google Scholar]
- van der Laan, M. J., Polley, E. C. and Hubbard, A. E. (2007). Super learner. Statistical Applications in Genetics and Molecular Biology 6. [DOI] [PubMed] [Google Scholar]
- van der Laan, M. J. and Rose, S. (2011). Targeted Learning: Causal Inference for Observational and Experimental Data. New York, NY: Springer. [Google Scholar]
- van der Laan, M. J. and Rubin, D. (2006). Targeted maximum likelihood learning. The International Journal of Biostatistics 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Vaart, A. (2002). Semiparameric statistics. Lectures on Probability Theory and Statistics. Ecole d/Ete de Probabilities de Saint-Flour XXIX-1999. Lecture Notes in Math. 1781, 331-457. New York, NY: Springer. MR1385671. [Google Scholar]
- VanderWeele, T. J., Vansteelandt, S. and Robins, J. M. (2014). Effect decomposition in the presence of an exposure-induced mediator-outcome confounder. Epidemiology (Cambridge, MA) 25, 300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wager, S. and Walther, G. (2015). Adaptive concentration of regression trees, with application to random forests. arXiv preprint arXiv:1503.06388. [Google Scholar]
- Zheng, W. and van der Laan, M. J. (2011). Cross-validated targeted minimum-loss-based estimation. In: Targeted Learning. Editors: van der Laan, MJ and Rose, S.. New York, NY: Springer, pp. 459–474. [Google Scholar]
- Zheng, W. and van der Laan, M. J. (2012). Targeted maximum likelihood estimation of natural direct effects. The International Journal of Biostatistics 8, 1–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zill, N. (1990). Behavior Problems Index Based on Parent Report. Washington DC: Child Trends. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.