Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Jun 30;11(7):2504–2512. doi: 10.1021/acssynbio.2c00270

Massively Parallel DNA Computing Based on Domino DNA Strand Displacement Logic Gates

Xin Chen †, Xinyu Liu †, Fang Wang †, Sirui Li †, Congzhou Chen ‡,*, Xiaoli Qiang †,*, Xiaolong Shi †,*
PMCID: PMC9295701  PMID: 35771957

Abstract

graphic file with name sb2c00270_0006.jpg

DNA computing has gained considerable attention due to the characteristics of high-density information storage and high parallel computing for solving computational problems. Building addressable logic gates with biomolecules is the basis for establishing biological computers. In the current calculation model, the multiinput AND operation often needs to be realized through a multilevel cascade between logic gates. Through experiments, it was found that the multilevel cascade causes signal leakage and affects the stability of the system. Using DNA strand displacement technology, we constructed a domino-like multiinput AND gate computing system instead of a cascade of operations, realizing multiinput AND computing on one logic gate and abandoning the traditional multilevel cascade of operations. Fluorescence experiments demonstrated that our methods significantly reduce system construction costs and improve the stability and robustness of the system. Finally, we proved stability and robustness of the domino AND gate by simulating the tic-tac-toe process with a massively parallel computing strategy.

Keywords: DNA computing, DNA strand displacement, tic-tac-toe, domino multi-input AND gate

1. Introduction

DNA computing has gained considerable attention due to the characteristics of high-density information storage and high parallel computing for solving computational problems.1 The predictability of Watson–Crick base complementary pairing is convenient for the construction of nanodevices. Tools studied by molecular biologists, such as restriction enzyme digestion, ligation, sequencing, amplification, and fluorescent labeling, facilitate the construction of molecular circuits. DNA can be used as biocomputer units,2 nanostructure materials,3−5 biosensors,6 and nanorobots.7 In digital integrated circuit research, logic gates are the basis for calculations and logical operations. Building addressable logic gates with biomolecules is essential for establishing biological computers. Many researchers have designed logic gates using DNA molecules as carriers. From the perspective of the logic system composition and the main implementation path, logic systems are divided into the following three categories: (1) constructed with the participation of light, electricity, and chemical signals; (2) constructed with deoxyribozymes; (3) constructed based on DNA strand displacement (DSD).

Cations can regulate the binding and release of ligands. Li et al.8 used K+ and Pb2+ as input, and G-quadruplex DNA as the logic drive, by measuring the enzyme activity as the output to construct a logic gate. Bi et al.9 constructed a logic gate system based on a supramolecular circular structure using Pb2+ and Mg2+ as the input and nanogold color rendering as the output. Such logic gates that use chemical and optical signals as the input or output are inconvenient for the cascading because of the material inconsistency between the input and output, thus, preventing the construction of large-scale molecular circuits.

Deoxyribozymes with phosphodiesterase activity can accurately identify the substrate, efficiently catalyze specific chemical reactions, and cause changes in the structure of the substrate.10−12 The DNA-cleaving deoxyribozyme technology13,14 greatly reduces the synthesis cost and improves the reaction efficiency, as RNA-cleaving deoxyribozymes must be embedded in RNA sequences. However, experimental conditions of logic circuits involving enzymes are complicated, the cost is high, and the system stability is difficult to guarantee.

DSD is the process of replacing a single strand in a complementary double-helical chain with a partially complementary toehold, which is driven by the free energy of the hybridization.15 This technology is simple and has the advantages of programmability, spontaneity, high sensitivity, accurate recognition, and large-scale cascade circuit construction. Seelig et al.16 proposed this technology first. Frezza et al.17 fixed logic gates on streptavidin-binding beads to maintain physical isolation between logic gates. Zhang et al.18 used circular DNA as a logic drive and single-stranded DNA as input and output signals, and logic calculation results were represented via fluorescent signals and gold nanoparticle assembly. Li et al.19 used circular DNA to construct a three-input “majority-logic” gate. Zhang et al.20 developed a programmable allosteric DNA regulation strategy and established the fan-in and fan-out logic gates and multilayer DNA cascade networks. With the development of DSD, complex applications are implemented. Examples include solving the square root calculator of a 4-bit binary input,21 handwriting recognition,22 signal amplifier,23−26 oscillator,27−29 decision-making machine,30−32 neural networks,33,34 disease detection,35 and 0–1 integer programming problem.36

Although DSD technology has shown great potential in the construction of large-scale molecular networks, a multilevel cascade increases the complexity of the circuit and causes leakage between the logic gates. Inspired by redundant error correction methods in electrical engineering, Wang et al.37 used the DNA chain energy by involving logical redundancy. Qian21 reduced leakage by setting a small number of “threshold gates” to consume some chains in advance and let the remaining chains participate in downstream reactions. Some researchers utilized the physical separation to avoid the occurrence of wrong reactions and thereby reduced leakage.38−40 However, these abovementioned methods either involved more control gates or increased the complexity of the experiment. In this paper, we reduced the DSD leakage with a domino gate by following the strategy of tuning DNA sequences using their melting temperature. Furthermore, we verified the scalability of this strategy on the tic-tac-toe network.

Tic-tac-toe is a simple yet interesting logic function that has been realized in molecular computing. Stojanovic and Stefanovic used a DNA logic gate based on DNA enzymes to construct a MAYA-I molecular robot. The MAYA-I molecular robot is based on two restrictions as follows: “robots take the lead and occupy the center” and “the player can only go to positions 1 and 4 in the first step.”31 Later, they removed the second restriction in the MAYA-II molecular robot.41 MAYA series robots use molecular circuits containing RNA-cleaving deoxyribozymes; they have disadvantages of complex experiments, high synthesis costs, and a low reaction efficiency. Petersen and colleagues42 drew “×” and “○” patterns on DNA square origami and applied the strand displacement reaction to DNA origami. The application achieves the assembly of square origami through strand displacement to form a corresponding chessboard array. However, it takes a long time to establish the model through this method, and the entire chess process takes approximately 8 days. Liu et al.43 constructed a bidirectional inhibitor in which when one pathway is active, other pathways are inhibited. The time-ordered inhibitor can verify the tic-tac-toe results. Unfortunately, the entire chess process was not simulated; only the result of the known chess play on the chessboard was verified.

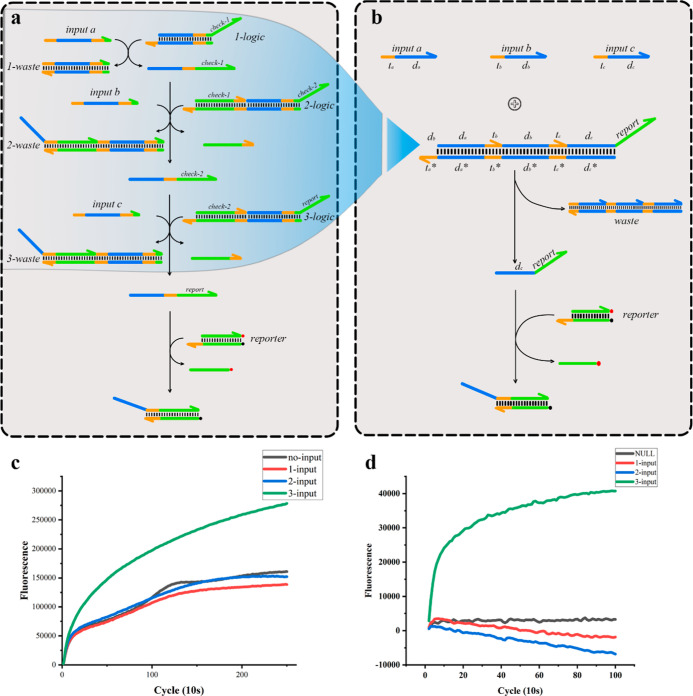
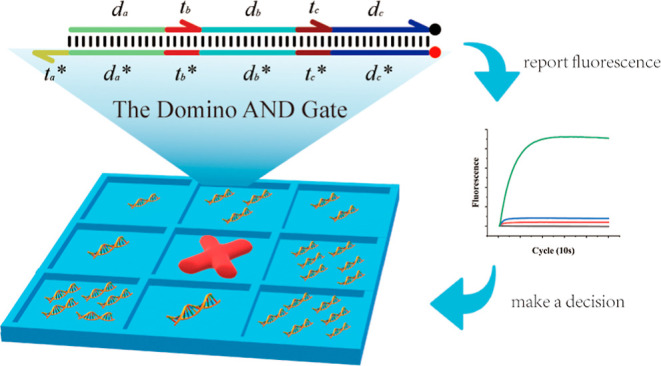
Here, we constructed a multiinput AND gate computing system similar to dominoes based on DSD (Figure 1b). The system implements multiple inputs of AND calculations on a logic gate, abandons the traditional multilevel cascade method, reduces DSD reaction leakages (Figure 1d), and improves the stability and robustness of the system. We used the domino AND gate system to construct massively parallel molecular circuits, simulate the chess process, and implement the tic-tac-toe approach, realizing chess in the true sense.

Figure 1.

Figure 1

Open in a new tab

Comparison between the domino multiinput AND computational system and traditional multilevel cascaded AND computational system. (a) Three-inputs AND gate calculation system implemented in a multilevel cascade method. There are three logic gates for calculation and one fluorescent report gate to output results in the system. (b) Domino three-input operating system. The system consists of inputs, AND logic gates, and reports of output results. The AND operation of the three inputs is implemented on a logic gate. (c) When there is no input, one input, two inputs, or three inputs, the multistage cascade and calculation systems output the fluorescence result. The results show that the crosstalk between cascaded logic gates is extensive. When three input signals are not used, the output signal is 50%; when three signals are used as the input, it is 60%. (d) Fluorescence output result of the domino and computing system. When all the input signals are not included, the fluorescence value is only about 10% of the total input fluorescence signal.

2. Results and Discussion

2.1. Construction of the Domino Logic Gate

In a calculation model that uses DNA molecules as a calculation unit, the AND operation under multiple inputs is often realized through a multilevel cascade between logic gates (Figure 1a). The AND operation under the three inputs was performed through logic gates 1-logic, 2-logic, and 3-logic, and the reporter gate produced the fluorescence result. The multilevel cascade of logic gates increases the complexity of the reaction system, and the mutual influence between the logic gates and the multilevel cascade causes leakage and failure of the logic system. Here, we tested a multilevel cascaded three-input AND gate computing system. When there was no input signal, the fluorescence value increased over time. The total value of the fluorescence response of one or two signal inputs was approximately 50% of the total signal (Figure 1c). A four-input operating system was constructed to explore the impact of the increase in cascades on the system. A larger number of cascades lead to more significant leakage problems. The total value of the fluorescence response for the input of the three signals was approximately 95% of the value when all four signals were present (Figure S1). Experimental results showed that the multilevel cascade of logic systems was not conducive to constructing multiinput and computing systems.

To improve the low response efficiency of the multilevel cascade system, we built a domino AND gate computing system (Figure 1b). The system comprised input signals, domino logic gates, and report gates. When the input chain input a(tada) existed, the chain input a(tada) would combine with the exposed toehold domain ta* to replace the da of the logic gate chain datb. The tb of the strand datb would break free because of the longer da being in a free state, so that the toehold domain tb* would be exposed. At this time, the input chain input b(tbdb) was combined with the toehold domain tb*, and the mechanism was the same as when the input chain input a(tada) was used as the input. Finally, the toehold domain tc* was exposed. When the input chain input C(tcdc) was used as the input, the substituted chain dc-report reacted with the reporter gate, modified by a fluorescent group and a quenching group, and finally, the substituted chain report emitted a fluorescent signal (Figure S2).

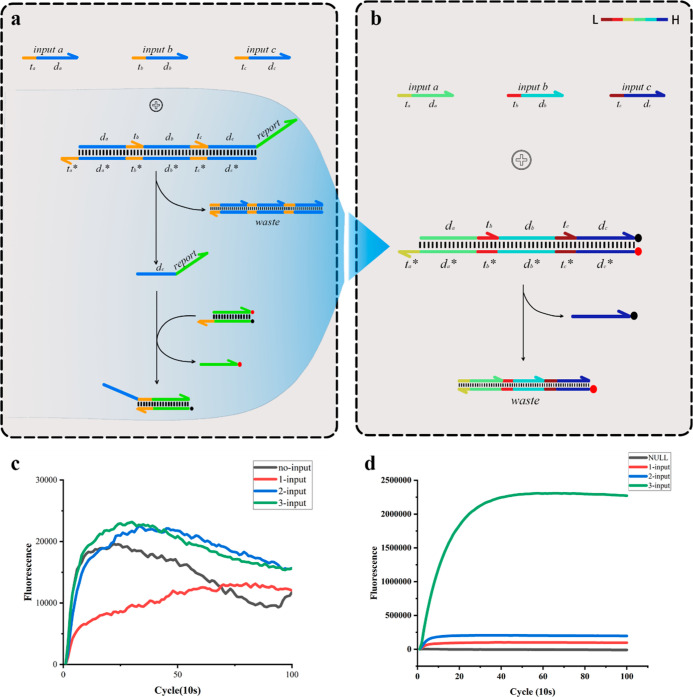
Although we initially tested the domino AND gate computing system, the logic system normally reported the fluorescence results. When we constructed multiple dominoes and gates with different sequences, the system reported fluorescence signal confusion, and the logic gate designed based on the dominoes did not respond as expected. When all three input signals were present, the system did not produce any fluorescence signals (Figure 2c). This phenomenon reflected the sequence design of the logic gates. After repeatedly studying the principle of dominoes, we imitated the increase in the potential energy observed with dominoes, and the sequence order was readjusted according to the melting temperature. Logic gates were arranged according to the sequence of the replacement sequence toehold field according to the gradually decreasing melting temperature, and the sequence of the information domain was arranged according to the increasing melting temperature (Figure 2b). After repeated experiments, the redesigned logic gate could correctly calculate the result according to the AND operation logic (Figure 2d).

Figure 2.

Figure 2

Open in a new tab

Optimization of the domino multiinput AND computational system. (a) Initial construction of the domino multiinput AND computational system. (c) Incorrect fluorescence signal reporting in multiple sets of domino AND gate computing systems with different sequences. (b) Domino multiinput AND computational system redesigned according to melting temperature. The color bar in the upper right corner indicates the melting temperature from low to high. Logic gates are arranged according to the sequence of the replacement toehold field according to the gradually decreasing melting temperature, and the sequence of the information domain is arranged according to the increasing melting temperature. (d) Correct fluorescence results are reported by the domino multiinput calculation system redesigned according to melting temperature.

The traditional way is using multiple separate and small gate complexes, and the cascade between logic gates are connected through the output single-strand DNA of the previous level. When implementing such a cascade, single strand input and output DNA of all separated gates exist in the solution at the same time, which will eventually cause an unexpected leak. One evidence is that leakage will be significantly reduced while the experiment is performed in separate tubes. Besides, leakage also increases exponentially with the increasing cascade layers. Leakage in cascades over three levels is unbearable. In addition, many free single strands also bring great challenges to coding separate gates because single strands without logical relationships should be, theoretically, orthogonal. Unsuitable DNA sequence coding can also lead to leaks. In this manuscript, the realization of the domino AND gate mode is driven by a long single chain and the toehold domain on the single chain. The reaction system is simple, and the crosstalk between the logic gates is small.

Moreover, domino and computing systems have higher coding efficiencies. Both use 14 bases to represent the information domain and 5 bases as toeholds. The conventional system requires 380 bases to achieve the three conditions and operations, and the domino and computing systems only required 222 bases, which had a lower redundancy. An increase in coding efficiency is bound to decrease economic costs. Taking the three-input AND gate computing system as an example, the cost of the domino AND gate computing system was only 58.4% of that of the traditional computing system. As the condition number increased, the cost advantage of domino logic gates became more evident. The results showed that the domino AND gate computing system had a high response efficiency and a low leakage rate. With the three-input AND operation, the fluorescence response of one or two signal inputs was only approximately 10%, which was more robust. We also tried to construct a four-inputs AND gate and found that the domino strategy could be implemented in a four-input logic gate, and the domino logic strategy had a certain degree of scalability.

2.2. Stability Analysis of Domino AND Gates

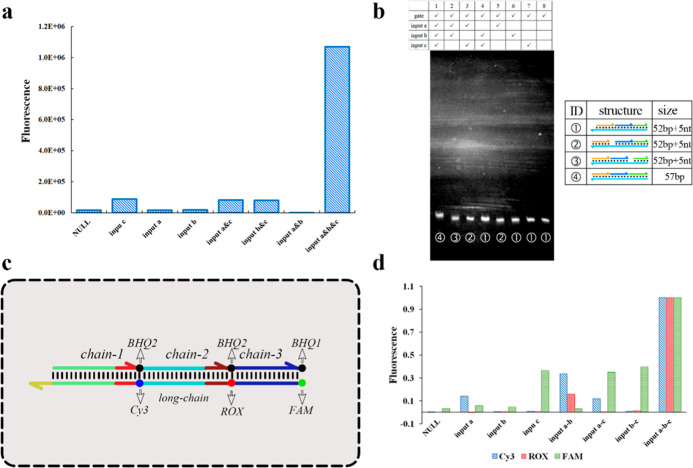
The AND gate computing system implemented by the multilevel cascade is driven by the input single chain and the single chain replaced by the previous level. The numerous free single chains increase the uncertainty and confusion of the system and cause certain difficulties in sequence design. The domino AND gate computing system is driven by a long chain of logic gates, and the toehold domain on the long chain promotes the reaction. The replaced single chain no longer participates in the reaction. The sequential substitution of domino logic gates is crucial for the stable operation of the system. To verify the robustness and stability of domino logic gates, the logic gates were tested by entering different input combinations. The logic gate separated the quencher and fluorophore only when all inputs were present, and the fluorescence signal value increased. When input c was present, the logic gate leaked slightly, corresponding to about 8% of the total response when all inputs were present, which is acceptable. Analysis of each input combination via polyacrylamide gel electrophoresis confirmed our results with clear target bands. The stability of the domino logic gate was proved.

To further explore the replacement efficiency of the first two steps on the logic gate and the replacement principle of the logic gate, we selected Cy3, ROX, and FAM to modify the long chain. The short chain at the corresponding position was modified with a quenching group (Figure 3c). According to the synthesis process, Cy3 adopted the modification of embedding the DNA backbone, ROX adopted the modification at the extended base T, and FAM modified the 5′ of the long chain. We also performed tests using different input combinations. The results showed a corresponding increase in the corresponding fluorescence signal (Figure 3d).

Figure 3.

Figure 3

Open in a new tab

Stability analysis of domino AND gates. (a) Difference in the fluorescence response for different input combinations of a three-input logical AND gate. The x-axis represents the difference between the final and initial fluorescence values. The reaction time is 1000 s. (b) Polyacrylamide gel electrophoresis results for various input combinations of three-input logic AND gates. Above are the components of each lane. (c) Fluorescent modification scheme to explore the logic of the reaction principle of dominoes and gates. Clockwise from 3′, each short 3′ end of the single chain is modified at BHQ2, BHQ2, and BHQ1. The long-chain 5′ end is modified with FAM, and the intermediate section is modified with ROX and Cy3. (d) Fluorescence signal response differences for various input combinations of a three-input logical AND gate. The x-axis represents the difference between the fluorescence value for the 1500 s reaction time and the initial fluorescence value.

In addition, the next input promoted the replacement of the previous input reaction according to the domino sequence. For example, the Cy3 fluorescence signal intensity of inputs a&b was approximately double that of input a/a&c. The ROX fluorescence signal intensity of input a&b&c was about 3 times higher than that of a&b (indicating 30–50% output on the current intermediate state and 100% on the final state). This is a good complement to the speculation on the replacement principle of domino logic gates. In each step of the domino sequence, the output strand is not displaced from the gate like the traditional DSD. The intermediate output strand contains a toehold domain of the next input and displaces it until the next input strand is present.

2.3. Implementation of the Tic-Tac-Toe Principle

Under the premise that the robot takes the center (position 5) first, and the player can only move to no. 1 or no. 4 position on the chessboard as the first step, Stojanovic et al. used high-cost RNA-cleaving deoxyribozymes to form a logic system based on multiple three-input AND–AND–NOT gates, enabling the MAYA-I robot to play a tic-tac-toe game. MAYA-I lists the tic-tac-toe game tree that can execute the no-loss strategy and convert the all-AND logic system into a logic system composed of yes gates and an AND–AND–NOT gate through a series of equivalent substitutions. We used domino AND gates to construct enzyme-free molecular circuits and directly implement the tic-tac-toe all-and-gate principle tree that executed the no-loss strategy (Figures S3 and S4).

We used 8 single DNA strands of 19 bases to simulate a piece, of which 5 bases were the toehold domain, and 14 bases were the information domain. Each time the player moved to a chessboard position, he added the corresponding numbered DNA strand to each tube. The piece could not be played at the positions that had previously been used. No DNA strands were added to the test tubes corresponding to the numbered positions on the chessboard where the player and the robot played. The corresponding test tube exhibited fluorescence, which was the response of the robot. This process was repeated until the end of the game. To reduce cross-talk in the logic system, we directly modified the fluorescent and quenching groups in the report gate on the domino AND gate, which had calculation and report functions (Figure 2b). The analysis of the tic-tac-toe application tree revealed that because of the rule that limited the player to position 1 or 4 in the first step, each game path contained one of these positions. Besides, when it was the player’s turn for the third time, he/she must have moved to position 6 or 9 on the chessboard. Therefore, to reduce the construction cost, we used positions 1 or 4 as the last step to replace all logic gates, and we could only modify the quenching group at the 3′ end of the information domains of positions 1 and 4. The fluorophore was modified at the 5′ end of the complementary strand. We used NUPACK to generate eight sequences and calculated the melting temperature of the toehold and information domains of each sequence. We found that most of the toehold domain melting temperatures were approximately −20 °C, and most of the information domain melting temperatures were approximately 46–50 °C. To satisfy the strategy of domino logic gates, the sequence of the toehold field was arranged according to the gradually decreasing melting temperature, and the sequence of the information field was arranged according to the increasing melting temperature. We took positions 6 or 9 as the first field to replace the three- or four-input domino logic gates. The melting temperature of a toehold of positions 6 or 9 was the highest among the eight candidate sequences of the toehold domain, and that of the information domain was the lowest among the eight candidate sequences of the information domain. Finally, position 1 or 4 was replaced. Therefore, the melting temperature of the toehold of positions 1 or 4 was the lowest among the eight candidate sequences of the toehold domain, and that of the information domain was the lowest among the eight candidate sequences of the information domain. The design and melting temperatures of all sequences are shown in Table S2.

We tested all the logic gates in the tac-tic-toe setting individually (Figure S5). Among the three-input domino AND gates, we found that the difference in the fluorescence signal of domino logic gates containing positions 4 and 9 was generally higher than that of domino logic gates containing positions 1 and 6. In other words, the replacement efficiencies of positions 4 and 9 were higher than those of positions 1 and 6. Domino logic gates containing positions 4 and 9 strictly complied with the three-level gradient change, and the gradient of the information field was different. However, the temperature gradient between the first and second levels of the logic gates containing positions 1 and 6 was relatively small. This result proved the correctness of the dominoes logic gate strategy once again.

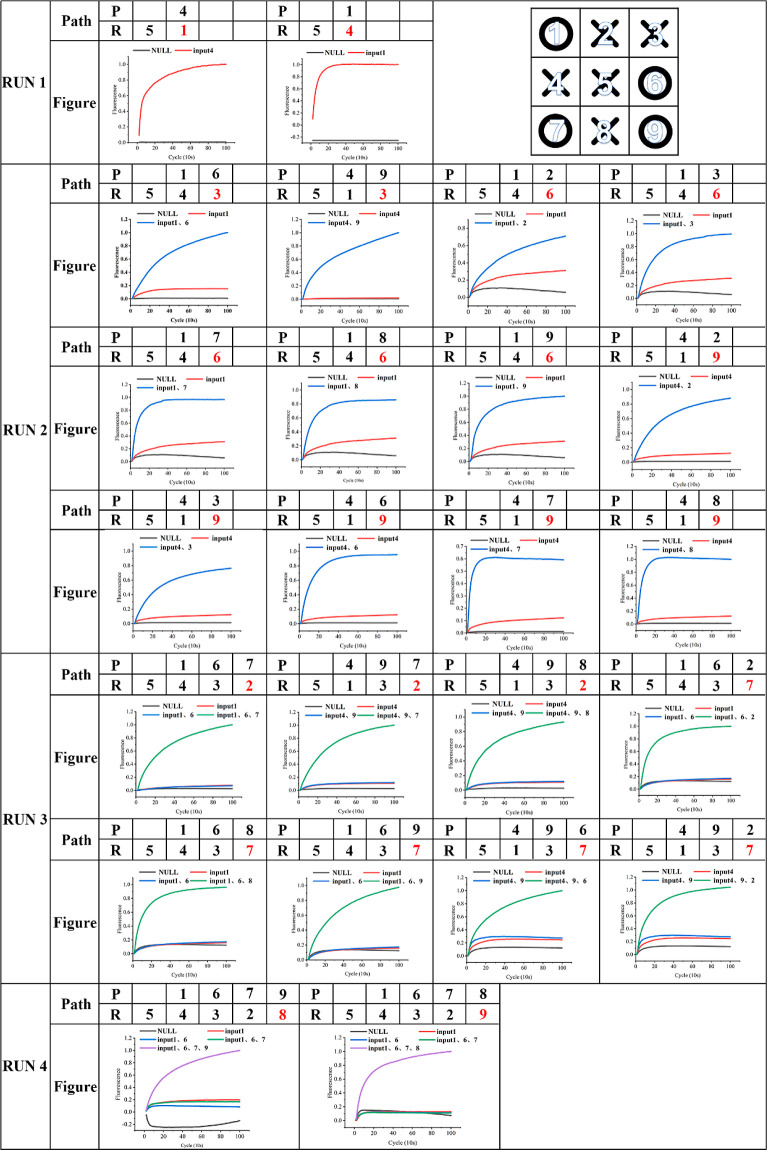
We implemented the tic-tac-toe game with eight test tubes, and the corresponding logic gate in each test tube was used to report the chess-response position of the robot (Figure S4). There were five domino AND gates among the test tubes on board position 7 under three inputs, and the reaction path was complicated, but the output fluorescent signals were all correct. The above phenomenon showed that domino AND gates had a strong parallelism, cross-talk between logic gates was small, and the system was stable and robust. However, owing to the design, there was a difference in the reaction efficiency between the domino logic gates containing positions 4 and 9 and those containing positions 1 and 6. In drawing the discounted statistical diagram of the fluorescence curve, the domino logic gates containing positions 4 and 9 and those containing positions 1 and 6 were normalized.

We simulated all game paths (Figure 3), and the robots based on the domino AND gate computing system responded correctly. Compared with MAYA, the domino AND gate has advantages in both experimental conditions and reaction efficiency. (1) MAYA requires Mg2+ activation, and the domino AND gate can directly start the game via an input chain at room temperature. (2) MAYA is constructed based on RNA-cleaving deoxyribozymes, the synthesis cost is higher, and experimental processes are more complex. The logic gate of MAYA requires at least two steps to report a fluorescence signal as follows: the first step is where the input chain causes structural changes; the second step is where RNA-cleaving deoxyribozymes cleave the substrate with a specific structure. However, the domino AND gate only requires input strands to complete the reaction. (3) MAYA-I reports the fluorescent intensity every 15 min. When the fluorescence increment >70,000 units, this indicates an adequate reaction. The required time is >45 min. The domino AND gate reaction achieves an adequate reaction in around 15 to 20 min, and the reaction rate is faster than that of MAYA (Figure 4).

Figure 4.

Figure 4

Open in a new tab

Implementation of the tic-tac-toe principle. According to MAYA-I strategy, there are a total of 19 game paths. All paths are implemented here with 24 parallel domino AND gates. The robot first takes the center (position 5) as run 0. In the figure, the numbering of checkerboard spots is shown in the upper right corner. “Path” is the chess path of the confrontation between the two sides. “R” is the position of the robot playing chess, and “P” is the position of the player playing chess. The robot takes the path taken by the player as the input, reacts to changes in the fluorescence curve of the domino and the computing system, and the result is the position marked in red. “Figure” is the fluorescence curve of the domino AND computing system, which is the calculation basis.

3. Conclusions

We constructed a multiinput AND calculation system similar to dominoes and designed the melting temperature of the toehold and information domains according to the replacement sequence. The sequence melting temperature of the toehold domain was arranged in a progressively increasing replacement order. The sequence design of the information domain was precisely the opposite of the toehold domain design. Strategies to adjust sequences according to melting temperature lay the foundation for the large-scale construction of logic gates. Domino AND gates implement multiinput AND operations in one logic gate, abandoning the traditional multilogic gate multilevel cascading approach and reducing the cross-talk between logic gates and the leakage impact caused by cascading. The robustness and stability of the system are enhanced, the coding efficiency of the logic gate is improved, and the construction cost is reduced. The structure of the domino multiinput AND gate can simplify many molecular circuits of DNA computation to a certain extent and provide reliability and stability to DNA circuits. The multiple-input-one-output feature of the domino multiinput AND gate operation system can realize complex molecular logic by constructing complex molecular circuits involving domino AND gates and provide new possibilities for detecting multifeatured diseases in medicine.

We used domino and gates to build large-scale enzyme-free molecular circuits to simulate the actual chess process and implement the tic-tac-toe principle. We inherited the advantages of the MAYA series of robots, including no-loss strategies, and modified the logic circuits that initially involved enzymes to increase the robot’s reaction speed and reduce the construction cost. In the future, we will create a DNA computer that can play chess by combining microfluidic and fluorescence detection technologies.

4. Materials and Methods

4.1. DNA Oligonucleotides

All DNA oligonucleotides were purchased from Sangon Biotech Co. Ltd. (Shanghai, China). Unmodified DNA strands were purified via polyacrylamide gel electrophoresis and dissolved in (1×) tris-acetate-ethylenediaminetetraacetic acid buffer containing 12.5 mM Mg2+ to a final concentration of 100 μM. Modified DNA strands were purified using high-performance liquid chromatography and dissolved in sterilized ddH2O (Sangon Biotech Co., Ltd, China).

4.2. DNA Sequence Design

The sequences of all the strands used in the experiment are listed in Table S1. Initially, all sequences were designed and the melting temperature of each DNA sequence was measured using Nucleic Acid Package (NUPACK; Table S2). Finally, the sequence was adjusted according to the domino logic gate strategy.

4.3. Logic Gate Assembly

The configuration concentration of the corresponding logic gate was calculated according to the final concentration of the reaction system at 500 nM, and the corresponding single strands were added in equal proportions according to the configuration concentration. The DNA oligonucleotide concentration was measured using a NanoPhotometer (Implen, BRD). All samples were annealed in a polymerase chain reaction thermal cycler (Thermo Fisher Scientific Inc., USA). The temperature was set at 90 °C for 5 min initially, decreased to 48 °C at a rate of −2 °C/min, and finally decreased to 20 °C at a rate of −1.5 °C/min.

4.4. Fluorescence Detection

The fluorescence kinetic detection of all logic gates was completed using QuantStudio 3 (Thermo Fisher Scientific Inc., USA). First, we let the machine temperature drop to 4 °C, quickly put the sample in, and raised the temperature to 23 °C at a rate of 1.6 °C/s to start fluorescence signal detection. Fluorescence was detected once per cycle for 10 s per cycle.

4.5. Polyacrylamide Gel Electrophoresis

The DNA solutions were analyzed in an 8% native polyacrylamide gel in 1× TBE buffer after running for 70 min at a constant power of 60 W using electrophoresis apparatus: DYCZ-20B (LIUYI BIOTECHNOLOGY CO., LTD., China). Gels were stained with GelRed, which was purchased from Sangon Biotech Co., Ltd. (Shanghai, China), and scanned with a scanner (ProteinSimple, USA).

Acknowledgments

This work was supported by the National Key R&D Program of China (grant 2019YFA0706401) and the National Natural Science Foundation of China under grants 62172302, 62172114, and 62072129.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acssynbio.2c00270.

  • Real-time fluorescence data from Figures 1c,d, 2c,d, and 3a,d (XLSX)

  • Real-time fluorescence data for the individual logic gate (XLSX)

  • Real-time fluorescence data for tic-tac-toe (XLSX)

  • DNA sequence design, sequence design used in tic-tac-toe games, melt profile of the sequence used in the tic-tac-toe game, fluorescence reporter results, three-condition domino AND gate replacement process, game tree for tic-tac-toe, implementation strategy of the tic-tac-toe game, and fluorescence detection results of tic-tac-toe game (PDF)

Author Contributions

X.C., C.C, X.Q., and X.S. designed the DNA strand displacement reaction network and DNA sequences and wrote the paper. X.C., X.L, F.W., and S.L. performed biological experiments. All authors participated in discussing the design and revising the paper and approved the manuscript.

The authors declare no competing financial interest.

Supplementary Material

sb2c00270_si_001.xlsx (356.6KB, xlsx)
sb2c00270_si_002.xlsx (269.1KB, xlsx)
sb2c00270_si_003.xlsx (287.9KB, xlsx)
sb2c00270_si_004.pdf (1.5MB, pdf)

References

  1. Ruben A. J.; Landweber L. F. The past, present and future of molecular computing. Nat. Rev. Mol. Cell Biol. 2000, 1, 69–72. 10.1038/35036086. [DOI] [PubMed] [Google Scholar]
  2. Xu J.; Qiang X.; Zhang K.; Zhang C.; Yang J. A DNA computing model for the graph vertex coloring problem based on a probe graph. Engineering 2018, 4, 61–77. 10.1016/j.eng.2018.02.011. [DOI] [Google Scholar]
  3. Chen C.; Xu J.; Shi X. Multiform DNA origami arrays using minimal logic control. Nanoscale 2020, 12, 15066–15071. 10.1039/d0nr00783h. [DOI] [PubMed] [Google Scholar]
  4. Shi X.; Wu X.; Song T.; Li X. Construction of DNA nanotubes with controllable diameters and patterns using hierarchical DNA sub-tiles. Nanoscale 2016, 8, 14785–14792. 10.1039/c6nr02695h. [DOI] [PubMed] [Google Scholar]
  5. Chen C.; Xu J.; Ruan L.; Zhao H.; Li X.; Shi X. DNA origami frame filled with two types of single-stranded tiles. Nanoscale 2022, 14, 5340–5346. 10.1039/d1nr05583f. [DOI] [PubMed] [Google Scholar]
  6. Chen C.; Lin T.; Ma M.; Shi X.; Li X. Programmable and scalable assembly of a flexible hexagonal DNA origami. Nanotechnology 2021, 33, 105606. 10.1088/1361-6528/ac2768. [DOI] [PubMed] [Google Scholar]
  7. Chao J.; Wang J.; Wang F.; Ouyang X.; Kopperger E.; Liu H.; Li Q.; Shi J.; Wang L.; Hu J.; Wang L.; Huang W.; Simmel F. C.; Fan C. Solving mazes with single-molecule DNA navigators. Nat. Mater. 2019, 18, 273–279. 10.1038/s41563-018-0205-3. [DOI] [PubMed] [Google Scholar]
  8. Li T.; Wang E.; Dong S. Potassium–Lead-Switched G-Quadruplexes: A New Class of DNA Logic Gates. J. Am. Chem. Soc. 2009, 131, 15082–15083. 10.1021/ja9051075. [DOI] [PubMed] [Google Scholar]
  9. Bi S.; Yan Y.; Hao S.; Zhang S. Colorimetric Logic Gates Based on Supramolecular DNAzyme Structures. Angew. Chem., Int. Ed. 2010, 49, 4438–4442. 10.1002/anie.201000840. [DOI] [PubMed] [Google Scholar]
  10. Stojanovic M. N.; Mitchell T. E.; Stefanovic D. Deoxyribozyme-based logic gates. J. Am. Chem. Soc. 2002, 124, 3555–3561. 10.1021/ja016756v. [DOI] [PubMed] [Google Scholar]
  11. Stojanović M. N.; Stefanović D. Deoxyribozyme-based half-adder. J. Am. Chem. Soc. 2003, 125, 6673–6676. 10.1021/ja0296632. [DOI] [PubMed] [Google Scholar]
  12. Lederman H.; Macdonald J.; Stefanovic D.; Stojanovic M. N. Deoxyribozyme-based three-input logic gates and construction of a molecular full adder. Biochemistry 2006, 45, 1194–1199. 10.1021/bi051871u. [DOI] [PubMed] [Google Scholar]
  13. Carmi N.; Shultz L. A.; Breaker R. R. In vitro selection of self-cleaving DNAs. Chem. Biol. 1996, 3, 1039–1046. 10.1016/s1074-5521(96)90170-2. [DOI] [PubMed] [Google Scholar]
  14. Chen X.; Wang Y.; Liu Q.; Zhang Z.; Fan C.; He L. Construction of Molecular Logic Gates with a DNA-Cleaving Deoxyribozyme. Angew. Chem. 2006, 118, 1791–1794. 10.1002/ange.200502511. [DOI] [PubMed] [Google Scholar]
  15. Yurke B.; Turberfield A. J.; Mills A. P.; Simmel F. C.; Neumann J. L. A DNA-fuelled molecular machine made of DNA. Nature 2000, 406, 605–608. 10.1038/35020524. [DOI] [PubMed] [Google Scholar]
  16. Seelig G.; Soloveichik D.; Zhang D. Y.; Winfree E. Enzyme-free nucleic acid logic circuits. science 2006, 314, 1585–1588. 10.1126/science.1132493. [DOI] [PubMed] [Google Scholar]
  17. Frezza B. M.; Cockroft S. L.; Ghadiri M. R. Modular multi-level circuits from immobilized DNA-based logic gates. J. Am. Chem. Soc. 2007, 129, 14875–14879. 10.1021/ja0710149. [DOI] [PubMed] [Google Scholar]
  18. Zhang C.; Yang J.; Xu J. Circular DNA logic gates with strand displacement. Langmuir 2010, 26, 1416–1419. 10.1021/la903137f. [DOI] [PubMed] [Google Scholar]
  19. Li W.; Yang Y.; Yan H.; Liu Y. Three-input majority logic gate and multiple input logic circuit based on DNA strand displacement. Nano Lett. 2013, 13, 2980–2988. 10.1021/nl4016107. [DOI] [PubMed] [Google Scholar]
  20. Zhang C.; Ma X.; Zheng X.; Ke Y.; Chen K.; Liu D.; Lu Z.; Yang J.; Yan H. Programmable allosteric DNA regulations for molecular networks and nanomachines. Sci. Adv. 2022, 8, eabl4589 10.1126/sciadv.abl4589. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Qian L.; Winfree E. Scaling up digital circuit computation with DNA strand displacement cascades. Science 2011, 332, 1196–1201. 10.1126/science.1200520. [DOI] [PubMed] [Google Scholar]
  22. Cherry K. M.; Qian L. Scaling up molecular pattern recognition with DNA-based winner-take-all neural networks. Nature 2018, 559, 370–376. 10.1038/s41586-018-0289-6. [DOI] [PubMed] [Google Scholar]
  23. Zhao L.; Zhou H.; Sun T.; Liu W.; He H.; Ning B.; Li S.; Peng Y.; Han D.; Zhao Z.; Cui J.; Gao Z. Complete antigen-bridged DNA strand displacement amplification immuno-PCR assay for ultrasensitive detection of salbutamol. Sci. Total Environ. 2020, 748, 142330. 10.1016/j.scitotenv.2020.142330. [DOI] [PubMed] [Google Scholar]
  24. Figg C. A.; Winegar P. H.; Hayes O. G.; Mirkin C. A. Controlling the DNA hybridization chain reaction. J. Am. Chem. Soc. 2020, 142, 8596–8601. 10.1021/jacs.0c02892. [DOI] [PubMed] [Google Scholar]
  25. Chang X.; Zhang C.; Lv C.; Sun Y.; Zhang M.; Zhao Y.; Yang L.; Han D.; Tan W. Construction of a multiple-aptamer-based DNA logic device on live cell membranes via associative toehold activation for accurate cancer cell identification. J. Am. Chem. Soc. 2019, 141, 12738–12743. 10.1021/jacs.9b05470. [DOI] [PubMed] [Google Scholar]
  26. Dirks R. M.; Pierce N. A. Triggered amplification by hybridization chain reaction. Proc. Natl. Acad. Sci. U.S.A. 2004, 101, 15275–15278. 10.1073/pnas.0407024101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Srinivas N.; Parkin J.; Seelig G.; Winfree E.; Soloveichik D. Enzyme-free nucleic acid dynamical systems. Science 2017, 358, eaal2052 10.1126/science.aal2052. [DOI] [PubMed] [Google Scholar]
  28. Lakin M. R.; Youssef S.; Cardelli L.; Phillips A. Abstractions for DNA circuit design. J. R. Soc., Interface 2012, 9, 470–486. 10.1098/rsif.2011.0343. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Franco E.; Friedrichs E.; Kim J.; Jungmann R.; Murray R.; Winfree E.; Simmel F. C. Timing molecular motion and production with a synthetic transcriptional clock. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, E784–E793. 10.1073/pnas.1100060108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Pei R.; Matamoros E.; Liu M.; Stefanovic D.; Stojanovic M. N. Training a molecular automaton to play a game. Nat. Nanotechnol. 2010, 5, 773–777. 10.1038/nnano.2010.194. [DOI] [PubMed] [Google Scholar]
  31. Stojanovic M. N.; Stefanovic D. A deoxyribozyme-based molecular automaton. Nat. Biotechnol. 2003, 21, 1069–1074. 10.1038/nbt862. [DOI] [PubMed] [Google Scholar]
  32. Chen Y. J.; Dalchau N.; Srinivas N.; Phillips A.; Cardelli L.; Soloveichik D.; Seelig G. Programmable chemical controllers made from DNA. Nat. Nanotechnol. 2013, 8, 755–762. 10.1038/nnano.2013.189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Qian L.; Winfree E.; Bruck J. Neural network computation with DNA strand displacement cascades. Nature 2011, 475, 368–372. 10.1038/nature10262. [DOI] [PubMed] [Google Scholar]
  34. Genot A. J.; Fujii T.; Rondelez Y. Scaling down DNA circuits with competitive neural networks. J. R. Soc., Interface 2013, 10, 20130212. 10.1098/rsif.2013.0212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Lopez R.; Wang R.; Seelig G. A molecular multi-gene classifier for disease diagnostics. Nat. Chem. 2018, 10, 746–754. 10.1038/s41557-018-0056-1. [DOI] [PubMed] [Google Scholar]
  36. Tang Z.; Yin Z.; Wang L.; Cui J.; Yang J.; Wang R. Solving 0-1 Integer Programming Problem Based on DNA Strand Displacement Reaction Network. ACS Synth. Biol. 2021, 10, 2318–2330. 10.1021/acssynbio.1c00244. [DOI] [PubMed] [Google Scholar]
  37. Wang B.; Thachuk C.; Ellington A. D.; Winfree E.; Soloveichik D. Effective design principles for leakless strand displacement systems. Proc. Natl. Acad. Sci. U.S.A. 2018, 115, E12182–E12191. 10.1073/pnas.1806859115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Chatterjee G.; Dalchau N.; Muscat R. A.; Phillips A.; Seelig G. A spatially localized architecture for fast and modular DNA computing. Nat. Nanotechnol. 2017, 12, 920. 10.1038/nnano.2017.127. [DOI] [PubMed] [Google Scholar]
  39. Mullor Ruiz I.; Arbona J.-M.; Lad A.; Mendoza O.; Aimé J.-P.; Elezgaray J. Connecting localized DNA strand displacement reactions. Nanoscale 2015, 7, 12970–12978. 10.1039/c5nr02434j. [DOI] [PubMed] [Google Scholar]
  40. Liu L.; Hong F.; Liu H.; Zhou X.; Jiang S.; Šulc P.; Jiang J.-H.; Yan H. A localized DNA finite-state machine with temporal resolution. Sci. Adv. 2022, 8, eabm9530 10.1126/sciadv.abm9530. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Macdonald J.; Li Y.; Sutovic M.; Lederman H.; Pendri K.; Lu W.; Andrews B. L.; Stefanovic D.; Stojanovic M. N. Medium scale integration of molecular logic gates in an automaton. Nano Lett. 2006, 6, 2598–2603. 10.1021/nl0620684. [DOI] [PubMed] [Google Scholar]
  42. Petersen P.; Tikhomirov G.; Qian L. Information-based autonomous reconfiguration in systems of interacting DNA nanostructures. Nat. Commun. 2018, 9, 5362. 10.1038/s41467-018-07805-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Liu C.; Liu Y.; Zhu E.; Zhang Q.; Wei X.; Wang B. Cross-Inhibitor: a time-sensitive molecular circuit based on DNA strand displacement. Nucleic Acids Res. 2020, 48, 10691–10701. 10.1093/nar/gkaa835. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

sb2c00270_si_001.xlsx (356.6KB, xlsx)
sb2c00270_si_002.xlsx (269.1KB, xlsx)
sb2c00270_si_003.xlsx (287.9KB, xlsx)
sb2c00270_si_004.pdf (1.5MB, pdf)

Articles from ACS Synthetic Biology are provided here courtesy of American Chemical Society

RESOURCES