Pruning recurrent neural networks replicates adolescent changes in working memory and reinforcement learning

Significance

Adolescence is a period during which there are important changes in behavior and the structure of the brain. In this manuscript, we use theoretical modeling to show how improvements in working memory and reinforcement learning that occur during adolescence can be explained by the reduction in synaptic connectivity in prefrontal cortex that occurs during a similar period. We train recurrent neural networks to solve working memory and reinforcement learning tasks and show that when we prune connectivity in these networks, they perform the tasks better. The improvement in task performance, however, can come at the cost of flexibility as the pruned networks are not able to learn some new tasks as well.

Abstract

Adolescent development is characterized by an improvement in multiple cognitive processes. While performance on cognitive operations improves during this period, the ability to learn new skills quickly, for example, a new language, decreases. During this time, there is substantial pruning of excitatory synapses in cortex and specifically in prefrontal cortex. We have trained a series of recurrent neural networks to solve a working memory task and a reinforcement learning (RL) task. Performance on both of these tasks is known to improve during adolescence. After training, we pruned the networks by removing weak synapses. Pruning was done incrementally, and the networks were retrained during pruning. We found that pruned networks trained on the working memory task were more resistant to distraction. The pruned RL networks were able to produce more accurate value estimates and also make optimal choices more consistently. Both results are consistent with developmental improvements on these tasks. Pruned networks, however, learned some, but not all, new problems more slowly. Thus, improvements in task performance can come at the cost of flexibility. Our results show that overproduction and subsequent pruning of synapses is a computationally advantageous approach to building a competent brain.

In both artificial and biological neural networks, cognitive operations are defined by patterns of synaptic connectivity in the network (1–4). During development, neurons across multiple cortical and subcortical systems first establish an abundance of synaptic contacts with downstream areas (5–7). Following this period, weak synapses are pruned through activity-dependent mechanisms (8–11). This process happens early in development for some systems, including retinal–geniculate synapses (5) and climbing fiber to Purkinje cell synapses in the cerebellum (12). However, in human prefrontal cortex, substantial pruning takes place beginning in late childhood and continuing into adulthood (13–15). The number of excitatory synapses in prefrontal cortex peaks between the ages of 5 and 10. After this it decreases exponentially. Estimates suggest that up to 40% of excitatory synapses are pruned in prefrontal cortex, between the ages of 10 and 30 (13). Studies also suggest that most of the pruning occurs on recurrent layer III connections within prefrontal cortex, as opposed to inputs from other areas (16). During this time the number of neurons remains relatively constant, having reached adult levels by about 6 mo of age (14). Similar changes in the number of prefrontal synapses during development have also been seen in monkeys (17–20) and rats (21).

Cognition and learning also change during adolescence (22–26). For example, there are consistent and systematic changes in performance on reinforcement learning (RL) tasks, in which participants have to learn from feedback to choose rewarding options and avoid punishing options (27–30). These studies often characterize performance using two variables, learning rate and decision noise (31). Learning rate is the rate at which subjects learn to select the better option, and decision noise characterizes the asymptotic level of performance. Decision noise, therefore, reflects the consistency with which subjects select the better option, after their performance has stabilized. When decision noise is high, subjects tend to sample multiple options, even late in learning. Studies most consistently report that decision noise decreases during adolescence (27), although some studies also suggest that learning rate increases (32). Similar developmental changes have also been seen in rodents (33). Although performance on well-defined bandit RL problems improves during adolescence, children are better at learning problems requiring exploration (34–37). Additionally, children can often learn new skills more quickly than adults, including languages, and this ability decreases during adolescence (9, 38). Some forms of exploration, for example, directed exploration, which requires an estimate of what is unknown, improve during adolescence (39).

Working memory performance and the ability to avoid distraction also improve during adolescence (40–44). Improvements in working memory may also underlie improvements in goal-directed behavior (45). Developmental improvements in working memory performance have also been seen in primates (46). Comparison of single-cell neurophysiology responses between pubertal and adult monkeys shows that neural responses reflecting remembered items were stronger in adults and less sensitive to distraction during delay periods (46).

Pruning of weak synapses was early recognized as an important technique to improve performance in artificial neural networks (47–50). Large artificial networks with many hidden units and connections can solve complex problems. However, these large networks generalize poorly beyond their training examples and rely on massive computational resources. Several techniques have been introduced to reduce network complexity by shrinking connection weights (51), as well as pruning or eliminating weights (47, 48), and these approaches have been shown to improve generalization performance. Pruning techniques, therefore, optimize the trade-off between network complexity and generalization.

Our goal in the present study was to understand how developmental pruning can account for changes in performance on working memory and RL tasks. To examine this, we trained two sets of recurrent neural networks. One set of networks was trained to carry out a delayed match to sample (DMS) task (46, 52, 53). The DMS task requires subjects to remember items over a delay, and therefore, it tests working memory. The second network was trained to carry out a two-armed bandit RL task (54–56). After the networks were trained, we incrementally pruned networks by removing weak connections. During pruning we continued to train the networks. We also trained a set of unpruned networks in parallel, such that they saw the same number of training examples. We then compared the performance of the pruned networks to the unpruned networks. We found that pruning led to changes in network dynamics that improved performance on both tasks. In the DMS task, the pruned network was less susceptible to distractors, and this improved performance was related to a strengthening of the attractor basin. In the RL task, the pruned network produced more accurate value estimates in the presence of noise. We also found corresponding changes in the dynamics that accounted for these improvements. The pruned networks, however, learned some new tasks and new choice options more slowly than the unpruned networks. Therefore, the increased performance on the tasks for which the networks were trained came at the cost of decreased flexibility.

Results

DMS.

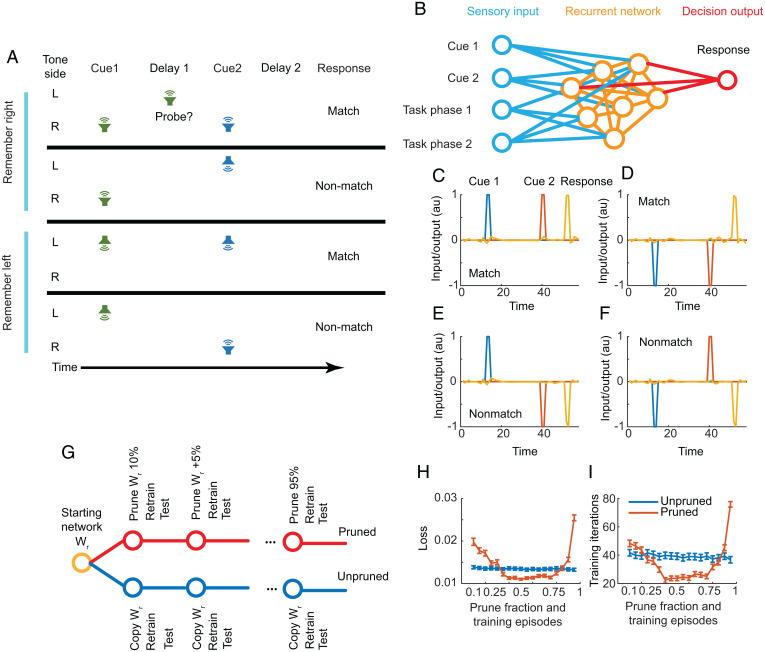
We fit recurrent neural networks to two cognitive tasks, performance on which is known to improve during adolescence: a DMS task that engages working memory (52) and a two-armed bandit RL task (54). DMS tasks come in many forms. Here we trained networks on a task inspired by a left/right auditory spatial match to sample task. In the task, a cue is presented either on the left or the right of the network agent (Fig. 1). Following a delay period during which the network has to remember the location of the first cue, a second cue is presented either on the left or the right. If the two cues are on the same side (i.e., if the sign of the input matches), it is a match trial and the network should give a match response. If the two cues are on opposite sides, it is a nonmatch trial, and the network should give a nonmatch response. There are four possible conditions identified by the side of the first and second cues. After training, a fully connected recurrent neural network (Fig. 1B) does well at the task (Fig. 1 C–F). Following cues presented on the same side, the network produces a match response (Fig. 1 C and D), and following cues presented on opposite sides the network produces a nonmatch response (Fig. 1 E and F).

Fig. 1.

DMS task and recurrent network. (A) In the DMS task, a cue is presented on either the left or right of a subject. After the cue, there is a delay, during which distractors might be presented. Following the delay a second cue is presented, after which there is another delay. After the second delay, a cue is given for the subject to respond. If the two cues were on the same side, a match response should be given. If the two cues were on opposite sides, a nonmatch response should be given. In some simulations, probes were delivered during the delay interval. (B) The network has four inputs and one output. Between the input and output is a recurrent layer. Cue 1 (+1 = left, −1 = right) is presented on the first input. Cue 2 is presented on the second input. The third and fourth inputs indicate the start of the trial (1, 1), the cue and delay periods (0, 0), and the response period (0, 1). Note that inputs and outputs were fully connected to the recurrent layer and never pruned. Only a subset are shown for clarity. All pruning was done in the recurrent layer. (C and D) When cue 1 and cue 2 are on the same side, the network produces a match response [$y\left(k\right)=1$]. (E and F) When cue 1 and cue 2 are on opposite sides, the network produces a nonmatch response [$y\left(k\right)=-1$]. (G) Training sequence for pruned and unpruned networks. Networks were first trained on the task, leading to a starting network. Then, this starting weight matrix was pruned (10%), or for the unpruned network copied forward, and retrained. We then pruned an additional 5% of the weights and retrained the network. In parallel, we also retrained the unpruned networks. As we introduced new training examples each time that had different noise realizations, both pruned and unpruned networks could be retrained. Thus, at each level of pruning, there was a pruned and unpruned network that had seen the same number of training examples and started from the same weight matrix. (H) Average final training loss for pruned and unpruned networks. Note that the x axis indicates prune fraction, but for unpruned networks, this indicates the number of equivalent training episodes since these networks were not pruned. (I) Number of CG training iterations when retraining pruned and unpruned networks.

We examined the effect of synaptic pruning on task performance and recurrent dynamics. To examine the effect of pruning, we first trained a large ensemble (400) of fully connected networks on the task. Each of these original 400 networks was then used to generate a sequence of pruned and unpruned networks (Fig. 1G). For the networks trained with pruning, we first pruned 10% of the weakest recurrent connections (after the initial training), either positive or negative, and then retrained the networks on a new set of training examples. Each new set of training examples, which was fixed for a training episode, was five trials of each condition, with additive noise. The noise was frozen for a training episode (see Methods for further details). We then pruned an additional 5% of the weakest connections and retrained on a new set of examples. We continued this iteratively until we had pruned 95% of the connections. For the unpruned networks, we did not prune the connectivity matrix. However, we introduced a new set of training examples and retrained to criterion. We repeated this, in parallel with the pruned networks, such that each unpruned network saw the same number of training examples as a corresponding pruned network. We found that with small amounts of pruning, the pruned networks tended to have higher final loss (Fig. 1H) and required more training iterations to converge (Fig. 1I). Over an intermediate range of pruning values, however, the pruned networks had lower final training loss and required a smaller number of training iterations. At the highest pruning levels, the pruned networks again had high loss and converged slowly. The unpruned networks had consistent training loss and iterations across the multiple training episodes. When we examined the appended series of training iterations (SI Appendix, Fig. S1), it could be seen that pruning led to a large training loss on the first iteration, which quickly decreased.

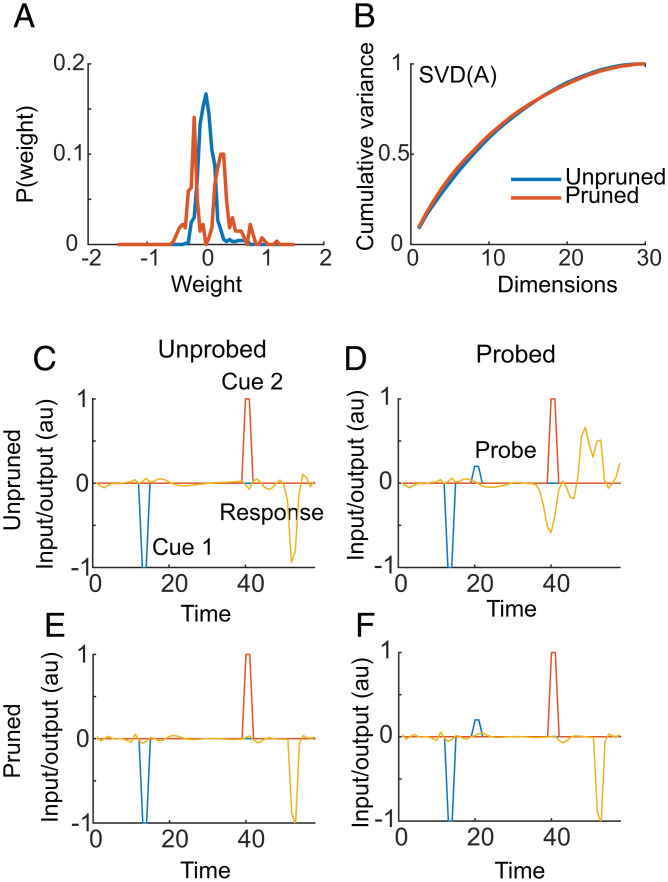
We next examined the performance of an example pruned (70%) and unpruned (trained for the same number of examples) network. The pruned network had a larger proportion of strong connections than the unpruned network (Fig. 2A). This is consistent with a biological process known as homeostatic synaptic scaling, which maintains the total input to single cells (57). To begin examining the effect of pruning on the neural dynamics we carried out singular value decomposition on the recurrent connectivity matrix, A, and found that the scaling of the singular values was similar between the pruned and unpruned networks (Fig. 2B). Thus, we had not reduced the rank of the recurrent dynamics, which suggests that all of the recurrent units were participating in the task after pruning.

Fig. 2.

Weight distribution and factorization of recurrent weight matrix, A. (A) Distribution of weights in the example pruned and unpruned network. (B) Normalized, cumulative spectrum of singular values of the recurrent matrix, A, for the pruned and unpruned network. The matrix A was factored as A = USV, and the singular values were sorted in S from largest to smallest. The plot shows the cumulative sum of the singular values, divided by the total sum of the singular values. (C–F) Example performance of pruned (70%) and unpruned network on example probed and unprobed trials. (C) Performance of unpruned network for condition 4 without a probe. The network generates the correct response. (D) Performance of same unpruned network following a probe. In this case the network gives the incorrect answer. (E) Performance of pruned network without probe. The network produces the correct output. (F) Same network as in E in a probe trial. The pruned network produces the correct output.

To compare the performance of the example pruned and unpruned networks we examined the ability of the networks to avoid distraction. Distraction was provided by delivering a probe cue during the delay period between cue 1 and cue 2. Probe cues were always delivered on the side opposite of the first cue. Therefore, if the network output was the same on probe and nonprobe trials, it was resistant to the distractor. Note that neither network was trained to ignore the probes. Thus, if the network could not ignore the probe cue, it would give the wrong answer. Both the pruned and unpruned networks gave the correct answer in unprobed trials (Fig. 2 C and E). In this example probe trial, however, the unpruned network provided the wrong response (Fig. 2D). The pruned network, however, was insensitive to the same probe cue (Fig. 2F).

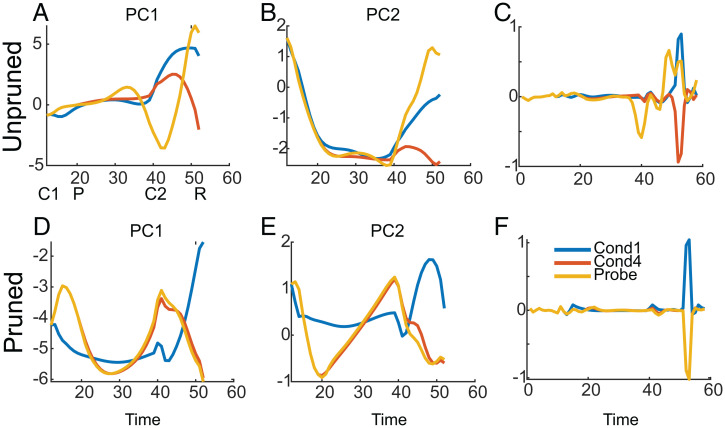
We explored the latent dynamics of the example networks to see the effects of the probe stimuli and the pruning (Fig. 3). For each network we calculated the principal components (PCs) of the activity in the recurrent layer and examined the time evolution of the activity in the first two PCs for probed and unprobed trials. When we examined activity in the first two PCs we found that the probe, delivered at time 20, drove the activity off the corresponding trajectory for the unprobed, condition 4 trial (Fig. 3 A and B). The activity diverged slowly over several time steps. However, later in the trial, after cue 2 was delivered, the activity was far off the trajectory of the unprobed trial, which led to the network producing an incorrect output at the response time (Fig. 3C). In the pruned network, however, the probed and unprobed trials had similar trajectories (Fig. 3 D and E), at least in the first two PC dimensions, and only diverged slightly later in the trial in PC2 (Fig. 3E). Thus, the network produced the correct output at the response time (Fig. 3F).

Fig. 3.

Low-dimensional representation of recurrent dynamics in pruned and unpruned networks. Same networks as shown in Fig. 2. (A) Evolution of activity over time in the first PC for trials of condition 1 (i.e., left/left, match), condition 4 (i.e., right/left, nonmatch), and a probe trial in which the condition 4 trial was probed during the delay (i.e., right/left probe/left). Note that condition 1 would correspond to the correct response if the network was responding to the probe instead of the first cue in condition 4. The perturbed and unperturbed trajectories for condition 4 diverge around time point 30. The symbols below the x axis indicate the times at which the first cue (C1), probe (P), second cue (C2), and response (R) occurred. These times were the same across all conditions. (B) Projection of the same trial on the second PC. (C) Network output, $y\left(k\right)$, in each trial. Note that the network produces the wrong response in the probe trial. (D–F) Data from the pruned network. (D) Evolution of activity projected on the first PC over time for the same conditions shown in A. Note that the trajectories diverge less and only late in the trial. (E) Projection of activity on the second PC. Note that in this dimension, there is also little divergence in the activity. (F) In this example the network gives the correct output.

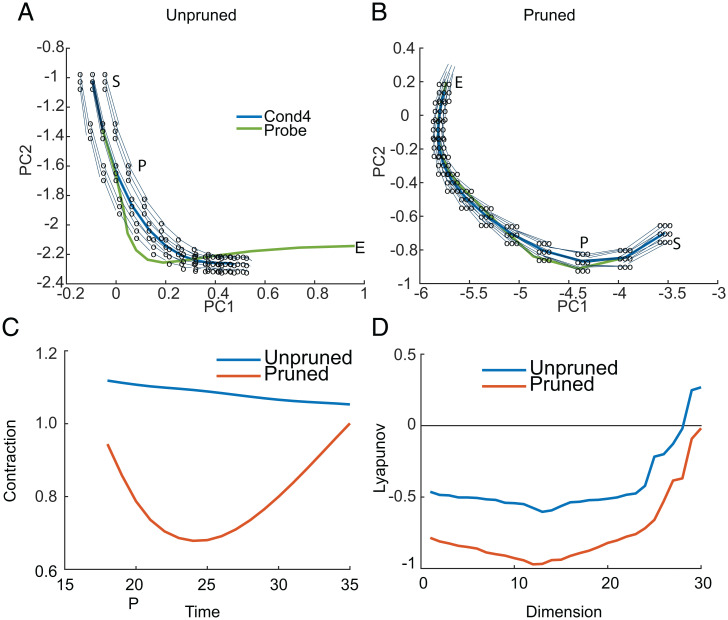
We next examined the network dynamics in two-dimensional (2D) PC space and overlaid the network’s vector field. The vector field shows how the network evolves from different points in phase space over one time step. We examined the vector field centered on the unprobed trajectory (condition 4) for the unpruned network (Fig. 4A) and the pruned network (Fig. 4B). The probe stimulus perturbs the network from the unprobed trajectory. If the vector field of the network is organized such that it pushes a perturbed trajectory back to the unperturbed trajectory, the network will be resistant to the probe and give the correct answer (46). Note that we only illustrate the 2D vector field that projects into low-dimensional PC space. The full vector field can diverge more or less in dimensions that we do not plot. We can see, however, that the vector field for the pruned network pushes the perturbed trajectories back to the unperturbed trajectories more effectively than the vector field for the unpruned network (Fig. 4 A and B). This is represented by the convergence of the perturbed points (i.e., open circles) in the pruned network, back to the unperturbed trajectory (i.e., end points of vectors from open circles). Thus, when a probe stimulus perturbs the network off the unperturbed trajectory, the network relaxes back to the unperturbed trajectory, in the pruned network (Fig. 4B) but not in the unpruned network (Fig. 4A). In the unpruned network the perturbed trajectories tend to diverge from the unperturbed trajectory, and the probe trajectory also diverges (Fig. 4A).

Fig. 4.

Evolution of activity in first two PCs with vector field overlay. (A) Evolution of activity for condition 4 and the probed condition 4 in the unpruned network. S indicates the start of the time window over which the plot is being shown, which starts two time steps before the probe (P) is given. The vector field around the probe trajectory is also shown. The network activity was perturbed from the mean trajectory in a grid around the mean, indicated by the open circles, and the network update equation was applied to the perturbed activity. The perturbations were carried out by displacing activity off the mean trajectory on the 2D PC plane by a fixed amount. The displaced trajectories were then projected back to the full dimensional space, and the network updates were calculated. These updates were then projected back to the 2D PC space for illustration. The light blue line connects the perturbed point to the subsequent position of the network after one iteration. Note that when lines are parallel to the trajectory, perturbed activity does not return to the unperturbed trajectory. (B) Same as A for the pruned network. Note that the open circles are the same displacement in both coordinate systems in A and B. (C) The contraction metric characterizes the expansion or contraction of the perturbed points after one iteration. First, the average Euclidean distance of the points after one iteration of the network is calculated. This is the spread of the vectors at their end. This was then normalized by the initial spread (which was constant) to calculate the fraction of expansion or contraction. These values are consistent with the LEs calculated over the delay interval. (D) The spectrum of LEs for the pruned and unpruned example networks.

To characterize this, we calculated the ratio of the spread of the end points (circles in Fig. 4 A and B) to the spread of the probed points after one iteration of the network (Fig. 4C). When this ratio < 1, the spread of the points after one iteration of the network is smaller than the spread when they are perturbed. This characterizes the extent to which the network collapses perturbed trajectories back to the unperturbed trajectory, by comparing the volume of perturbed trajectories before and after one time step of the network. We found that throughout the delay period, this fraction was smaller, and consistently less than 1, in the pruned network. It was greater than 1 throughout the delay in the unpruned network. Thus, when the network was pushed off the mean trajectory by a distractor, it tended to return to a point closer to the unperturbed trajectory in one iteration for the pruned network. In the unpruned network, however, the probed trajectory tended to diverge from the unprobed trajectory.

We further formalized this by calculating the spectrum of Lyapunov exponents (LEs) around the unperturbed trajectory averaged over the delay period (Fig. 4D). The LEs characterize the extent to which two nearby points diverge or converge over time, as the network is iterated. Values greater than 0 indicate that the network will diverge in that dimension over time, if perturbed. Values less than 0 indicate that the network will converge over time. The maximal LE characterizes the overall resistance of the network to perturbations. Thus, the LE characterizes the contraction (values < 0) or expansion (values > 0) over time of perturbed trajectories, and larger positive or negative values indicate networks in which the expansion or contraction occurs more rapidly. The maximal LE in this example was −0.02 for the pruned network and 0.27 for the unpruned network. Therefore, activity tended to diverge following a perturbation for the unpruned network but converge for the pruned network. This convergence is why the pruned network is resistant to distraction.

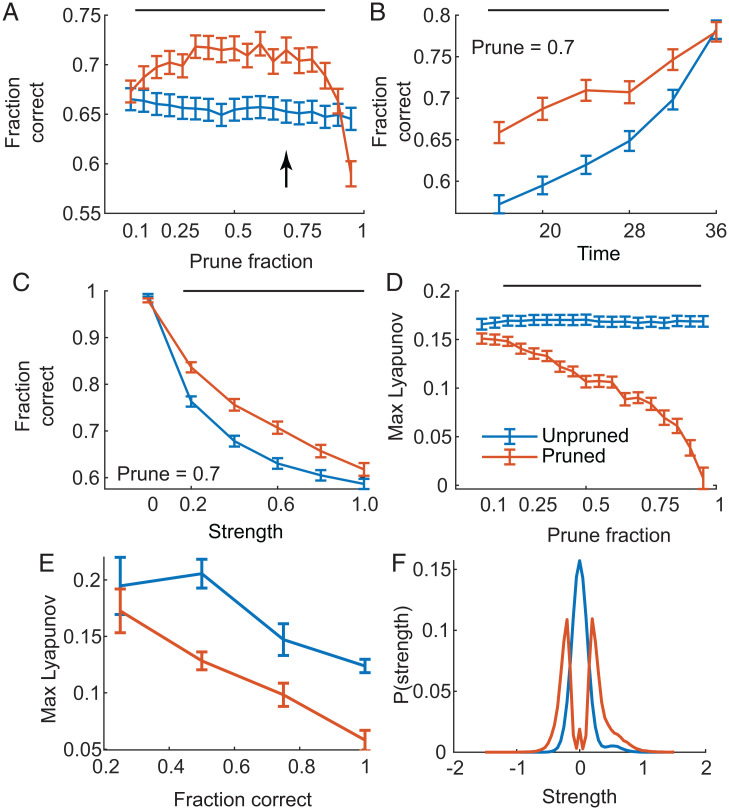
We characterized the performance and dynamics for our population of trained pruned and unpruned networks (Fig. 5). We found that networks pruned to intermediate values were more resistant to distractors of different strength, delivered throughout the delay period, than unpruned networks (Fig. 5A). The difference in performance was most pronounced early in the delay (Fig. 5B) and was minimal near the end of the delay, when pruned and unpruned networks were more resistant to distractors. In the absence of probe cues (probe strength 0), the networks were almost perfect (Fig. 5C). Performance, however, degraded slowly with increasing distractor strength (Fig. 5C) but was consistently higher for pruned networks. Pruned networks had lower maximum LEs, and the LE decreased with increased pruning (Fig. 5D). Unpruned networks had higher LEs, despite being continuously trained in parallel with the pruned networks (Fig. 5D). We also found that the networks that performed on average best when probed also had lower LEs for both pruned and unpruned networks (Fig. 5E). The LE was negatively correlated with performance for both the unpruned [r(400) = −0.299, P < 0.001] and pruned [r(400) = −0.318, P < 0.001] networks. The distribution of connection strengths, at 70% pruning, averaged across networks, showed fewer small and more large connections in the pruned than the unpruned networks (Fig. 5F).

Fig. 5.

Performance of population of pruned and unpruned networks with probes of different strengths and times relative to cue 1. Positive outputs during response time were counted as match responses, and negative outputs were counted as nonmatch responses. Error bars are SEM (n = 400). Data in B, C, E, and F are for a prune fraction of 0.7, indicated in A by the arrow. Bars at the top of A–D indicate the range over which the pruned and unpruned networks differ statistically (P < 0.01). (A) Performance of pruned and unpruned networks as a function of pruning, in probe trials. A correct response corresponds to ignoring the probe. Values are averaged over probes delivered at all time points, all strengths (greater than 0, which is no probe), and all trial conditions. Note the unpruned networks were not pruned, but they were trained to criterion in parallel with the pruned networks. (B) Average fraction of correct responses for pruned and unpruned networks when probes were delivered at different times during the delay. Values shown are for a prune fraction of 0.7 and averaged across probe strength, excluding a strength of 0 (i.e., when no probe was delivered). Note the time period examined with probes is the delay interval, and the first cue was delivered at time points 13 and 14, just before the illustrated data. (C) Average fraction of correct responses as a function of strength of probe. Values shown are averaged across all times at which probes were delivered for networks with a prune fraction of 0.7. A strength of 0 indicates no probe. (D) Maximal LE for pruned and unpruned networks. (E) Average LE of networks that were correct across all probe trials, across conditions, the number of times indicated on the x axis. Note that networks usually failed by not producing the correct response, when probed, for one or more of the conditions, so performance fell into the corresponding bins. Data shown are for a prune fraction of 0.7. (F) Average distribution of weights for networks pruned to 0.7. Note the small bump near zero for the pruned networks is for small weight values that fall into the middle bin.

In a final analysis, we trained pruned (70%) and unpruned networks and examined the rate at which they were able to learn the DMS task. To examine task learning of pruned and unpruned networks we randomly initialized networks, pruned 70% of the weakest connections, and then trained them on the DMS task. We compared these networks to randomly initialized unpruned networks. We found that the unpruned networks learned more quickly than the pruned networks (SI Appendix, Fig. S2A). The average performance of the pruned network became similar to the unpruned network after about 20 training iterations. We also compared this to retraining pruned (70%) and unpruned networks with a new pair of cues, after they had previously been trained on the original task. When we examined learning to do DMS with a new set of cues, we found that the pruned network was overall more efficient, similar to the results on the original cues (SI Appendix, Fig. S2B). Thus, the recurrent dynamics of the pruned network could be reused to learn DMS for new cues that the network had not seen previously, and unpruned networks can initially learn more quickly than pruned networks, but the pruned networks learned new cues more effectively, if not more quickly.

RL.

We next trained a series of networks to carry out an RL task. RL is often thought to be a dopamine-dependent process, with dopamine driving plasticity on frontal-striatal synapses during learning (58). However, recurrent neural networks can be trained to solve bandit tasks and may better reflect the neural processes that drive learning in these tasks, under some conditions (55, 56). After training, the weights of the network can be fixed, and the network can make correct choices, essentially matching performance of biological agents, by storing information about past outcomes in patterns of recurrent activity. We trained a population of networks on a two-state RL problem. Specifically, they were trained to select a fixation point when it was presented (SI Appendix, Fig. S3) and to learn to select one of two targets in each block of trials, depending on which target was most frequently rewarded. To match the noisy choice behavior of young subjects, networks were trained to match noisy value functions (Methods). We followed the same procedure of incrementally pruning and retraining the RL network that was used to train the DMS network and also training, in parallel, unpruned networks. Thus, we initially trained 100 networks to carry out the RL task. We then used the original set of 100 networks to generate a series of pruned and unpruned networks. At each stage, we pruned a fraction of connections in the pruned networks and retrained the networks with a new set of training examples. For the unpruned networks, we copied the unpruned weight matrix forward but retrained them on an equivalent set of training examples.

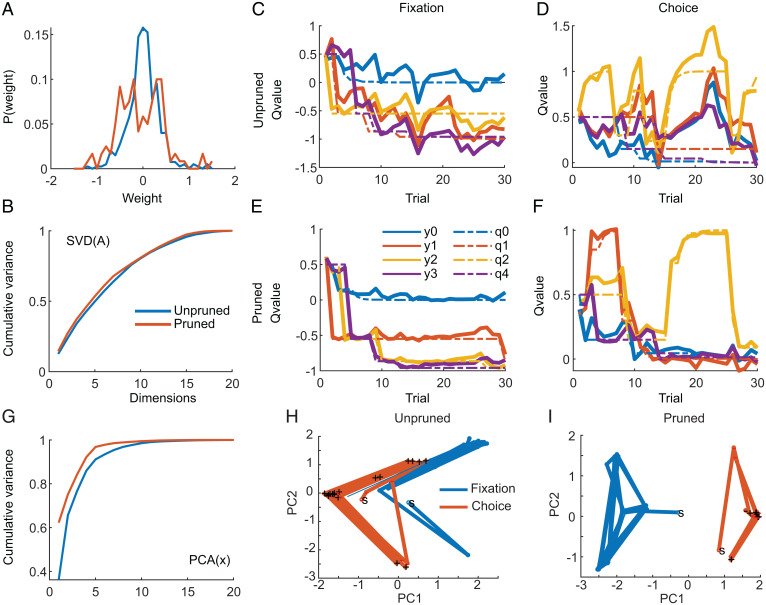
When we examined the performance of an example pruned and unpruned network we found that the pruned RL network had more large weights (in absolute value) than the unpruned network (Fig. 6A). SVD on the recurrent A matrix showed that it was full rank, and the spectrum of singular values was similar between the pruned and the unpruned networks (Fig. 6B). We also found that the unpruned network produced noisier results (higher Q-value error) during selection of both the fixation point (Fig. 6C) and the best choice option (Fig. 6D). The pruned network, on the other hand, produced results that matched the values predicted by the Q-learning algorithm well (Fig. 6 E and F). To explore the network features that led to the improved performance of the pruned network, we again examined activity in a low-dimensional PC space. The dynamics of both networks were relatively low dimensional and lower dimensional for the pruned than the unpruned network (Fig. 6G).

Fig. 6.

Weight distributions and example performance. (A) Distribution of weights in unpruned and pruned (70%) network. Note the distribution does not reach 0 at weights of 0 in this plot because of a binning effect. (B) Scaling of singular values extracted from the A matrix for trained unpruned and pruned network. (C–F) Example performance of unpruned and pruned networks on fixation and choice periods from RL task. (C) Network predictions and optimal Q values for an example block of trials for unpruned network, during fixation phase. y values indicate network output, and q values indicate Q values estimated with model. The four lines (0 to 3) indicate the choice options. (D) Same as C for choice phase. (E) Example network output and Q values for fixation period for pruned network. (F) Same as E for choice phase. (G) Fraction of variance explained by PCs extracted from the latent dynamics, x(k). (H) Example sequence of points in PC space for fixation and choice periods for unpruned network. Note the point clouds for the two epochs are not well separated. S indicates first trial, and plus indicates a rewarded choice. (I) Same as H for pruned network.

When we examined the data plotted in the first two PCs, we found that the recurrent activity patterns, which represent action values, during the fixation and choice periods were separated in state space. They were separated more, however, for the pruned network than the unpruned network (Fig. 6 H and I). When we calculated the Mahalanobis distances (59), in the full 20-dimensional latent space, between the value clouds for the two states, we found that the distances were larger for the pruned than the unpruned network (average values pruned = 39,261, unpruned = 5,200). Thus, there was more separation in the recurrent activity representations for the two states for the pruned network. We also characterized the LEs across the whole trial and found that they were consistently smaller in the pruned networks (−0.020) than the unpruned networks (0.031).

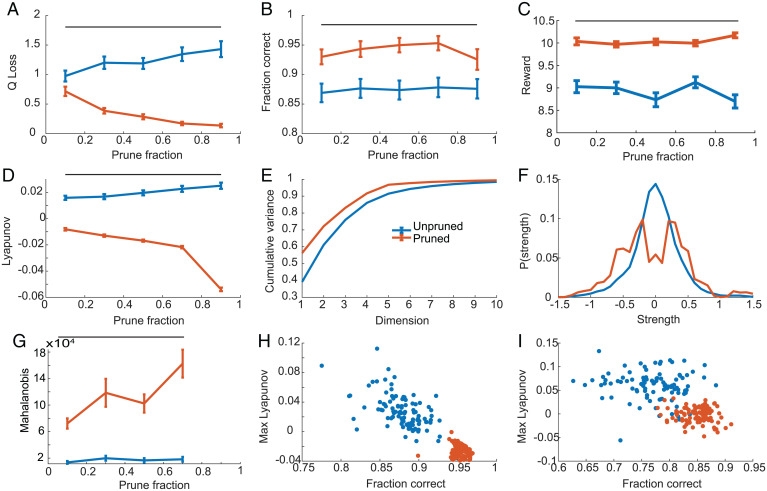
When we compared performance of a population of pruned and unpruned networks for a range of pruning values, we found that pruned networks outperformed unpruned networks, by better approximating Q values, when pruning fractions were greater than about 0.3 (Fig. 7A). Correspondingly, pruned networks also more frequently chose the same option as the Q-learning algorithm, which we defined as correct decisions (Fig. 7B), and obtained more total rewards per block (Fig. 7C). Similar to the DMS networks, pruned RL networks had lower LEs (Fig. 7D). For the pruned RL networks the LEs were negative on average. The pruned RL networks also had lower dimensional latent dynamics (Fig. 7E) and a larger fraction of higher strength connections (Fig. 7F). The separation of latent activity related to values for the two states was also larger for pruned than unpruned networks (Fig. 7G). When we examined the relation between LE and the fraction of decisions that were consistent with the Q-learning algorithm, we found that pooled across both pruned and unpruned networks, there was a significant correlation between fraction correct (i.e., consistency between network and Q-learning algorithm) and the LE at low [r(100) = −0.158, P = 0.025), medium [Fig. 7H; r(100) = −0.873, P < 0.001], and high [Fig. 7I; r(100) = −0.593, P < 0.001] training noise levels. Thus, lower LEs, mostly in the pruned networks, lead to better performance. Overall, performance mostly increased with additional pruning for the RL network, up to 90%. For the DMS network, performance began to decrease at about 85% pruning. This difference may relate to the underlying complexity of the task.

Fig. 7.

Performance and accuracy for population of pruned and unpruned RL networks. Bars at the top of A–D and G indicate values for which pruned and unpruned networks differ significantly. A–G are shown for intermediate noise level (0.1). Error bars are SEM, n = 100. (A) Q-value prediction accuracy on new blocks of data. Note that this is not the training loss, because when networks were trained, the target function had added noise. This is the accuracy with which the network predicts the underlying, noise-free Q values. (B) Accuracy (fraction correct) with which networks predict the same choice as the Q algorithm on new blocks of data. (C) Average reward collected per block for pruned and unpruned networks. (D) Average maximum LE for pruned and unpruned networks. (E) Cumulative variance explained for pruned and unpruned networks at a prune fraction of 70%. (F) Distribution of connection strength for pruned and unpruned networks, averaged across all networks. Note that values at 0 are for small nonzero values that fall into the central bin. (G) Mahalanobis distance between centroids for recurrent activity for fixation vs. choice periods. (H) Scatterplot of fraction correct vs. maximal LE, across pruned and unpruned networks, trained at a noise level of 0.1. Fraction correct refers to consistency with Q-learning algorithm shown in B. (I) Same as H for noise level of 1.

In a final analysis we trained both pruned (70%) and corresponding unpruned networks to learn to select between a new option, which the network had not previously seen (choice 3; SI Appendix, Fig. S3), and one of the options with which the network was previously familiar (SI Appendix, Fig. S4). In this case both networks were first trained to select between options 1 and 2. After this, the pruned and unpruned networks were retrained to select between options 1 and 3. Although there was some advantage for the pruned network over the first training iteration, the unpruned network quickly surpassed the performance of the pruned network. With extensive training the pruned network approached the performance of the unpruned network, which suggests that the pruned network had enough residual capacity to learn this task. However, the unpruned network learned more quickly.

Discussion

We have examined the effect of synaptic pruning in recurrent neural network models of working memory and RL. The networks were able to capture many features of behavior that change during development. Specifically, in the delayed DMS task, the pruned networks were more resistant to distractors. When we examined the local dynamics, we found that the distractor resistance followed from a smaller LE around the unperturbed trajectory in the pruned network. Thus, when a distractor perturbed the pruned network, it returned to the unperturbed trajectory, whereas the unpruned network did not. We used an incremental training and pruning approach. When we directly trained a network, after randomly initializing the weights and then pruning 70% of them, we found that the network learned more slowly than the unpruned network. However, when we first trained networks on the DMS task, with and without pruning, the pruned network learned with lower loss to do DMS with new cues.

When we examined the performance of a network trained to perform a two-armed bandit RL task, we also found that pruning improved performance. Pruned networks trained in the presence of noise were able to more accurately approximate optimal Q values than unpruned networks. Pruning has long been used as an approach in the feed-forward neural network literature, to improve generalization performance (47, 48), and pruning can be computationally optimized (60). The RL results follow from improved generalization performance. Every block of trials in a two-armed bandit RL task is unique because choice outcomes are stochastic. Additionally, there was noise in the Q values we used for training as this noise approximates noisier learning in children. Therefore, the network has to learn to generalize. Although the pruned network was better able to perform the RL task on which it was trained, it learned to select a novel option more slowly than the unpruned network. Thus, pruned networks are better at the tasks for which they have been trained, but they learn some new tasks slowly. It is not clear why the pruned DMS network learned a new option more effectively, which was not the case for the pruned RL network. These differences may be due to whether learned weights in the pruned network can generalize better to new options within a task.

The brain, at least at a thalamocortical level, produces an overabundance of synapses during development (7). The reasons for this are unclear. It may be a constraint of developmental processes, which are able to guide axons to their target structures but not able to establish precise connections (61). It is unlikely that the precise wiring of the brain, even in systems like the early visual system where adult plasticity is only minimally important, could be specified by genetics (9). In general, the brain relies on learning during development to establish adult behavior and corresponding neural connectivity (62). Development uses a mechanism by which axons are steered toward their target structures, and then synapses are overproduced. The synapses are then pruned through activity-dependent mechanisms in which weak synapses are eliminated (5, 8). These mechanisms have been most thoroughly investigated in a few model systems, including the retinogeniculate pathway, thalamocortical synapses in barrel cortex, and climbing fibers in the cerebellum (8, 9).

In addition to these model systems, it is also known that substantial pruning of excitatory synapses happens throughout cortex, including in prefrontal cortex (13, 14). Studies in human postmortem tissue, monkeys (17, 19, 20), and rats (21) have consistently shown substantial pruning. Across these studies, synapses appear to peak before puberty (13). They then decline exponentially and continue to decline with age. The timing of pruning differs from the timing of cell elimination. Specifically, the number of neurons in prefrontal cortex, which is highest at birth, drops to adult levels by about 6 mo of age (14). Thus, in cortical systems that support cognition, there is substantial synaptic pruning, specific to excitatory synapses on both excitatory and inhibitory neurons, during adolescent development.

Pruning was developed in machine learning to improve the generalization and computational efficiency of artificial neural networks (47, 48, 63). Large networks can learn complex problems. However, they generalize to new data poorly, especially when training data are limited. This is often referred to as the bias/variance trade-off (64). Large networks can approximate complex functions with minimal bias. However, they produce highly variable fits when they are trained on different datasets that represent variations on the same learning problem. Simpler networks produce biased fits to complex functions as they may smooth over the complexity. However, they produce less variable fits when trained on different datasets and therefore generalize better to new data. Pruning reduces the complexity of a large neural network, and therefore, pruning can be used to optimize the trade-off between bias and variance, for a given learning problem. Early (47) and more recent work (65) on pruning was also intended to reduce the memory requirements and computational demands of large networks. One important point is that it is not clear whether the pruning used in the present work directly produces networks that are better at the task or whether pruning facilitates training to higher levels of performance. Additionally, regularization techniques in machine learning, like pruning, improve performance in the presence of limited training data. With very large training datasets, regularization is less important. Other regularization approaches, for example, weight shrinkage (66), in which weights are shrunk toward zero on each training iteration, or adding noise to connection weights during training (67), could also lead to improved performance. However, these approaches are less related to known developmental processes.

Consistent with the earlier work in artificial intelligence and aside from possible developmental constraints, we have shown that there can be computational advantages to overproducing synapses and then pruning them incrementally while tasks are learned, in artificial neural networks. The DMS network was able to learn more efficiently before pruning. When we pruned a DMS network before training, it learned more slowly than the unpruned network. However, trained pruned DMS networks were able to learn new cues as fast, and more effectively, than unpruned DMS networks. Additionally, when we explored the ability of the pruned and unpruned RL networks to learn to select a novel option, to which the networks had not been previously exposed, the pruned network learned more slowly. Thus, consistent with developmental processes, unpruned networks are able to learn some new tasks or problems more quickly than pruned networks.

The rate-based recurrent network is simplified and lacks biological features. Simplified, formal models have provided insight into neural population coding (68, 69) and RL (31, 70). Connectionist models, particularly as extended in deep networks, provide a powerful description of tuning functions in sensory cortex (71, 72). Therefore, the basic computational principles captured by our model can provide a reasonable description of the effects of neural pruning in cortex. One feature of biological pruning not captured by our model, which should be explored in the future, is that only excitatory synapses are pruned. Studying the effects of pruning in spiking neural networks that learn arbitrary cognitive tasks and that have excitatory and inhibitory units will be challenging. There are methods to map between rate models and spiking models (73), and there has been progress in training spiking networks (74). Therefore, future work may allow a more detailed exploration of the effects of pruning in more realistic networks.

Our network makes several predictions that can be explored in neurophysiology recordings. First, as already shown in previous neurophysiology data, pruned networks should be more resistant to distractors in working memory tasks (46). Second, the resistance to distractors follows from steeper or larger attractor basins and correspondingly less positive or negative Lyapunov coefficients in the model networks. Thus, when activity is perturbed, it should relax back to the unperturbed trajectory more effectively in a pruned (i.e., adult) network. It should be possible to estimate statistics that capture the size and steepness of attractor basins with large-scale neural recordings that are becoming more prevalent (75). Finally, we also found that the dimensionality of neural activity was lower in pruned networks in the RL task. Although dimensionality has been estimated in many neural systems (76, 77), future work could compare dimensionality across developmental time points.

During the period over which synapses are pruned in cortical areas that support cognition, there is also improvement in several behavioral processes (25). Two processes that improve are working memory (40) and RL (22, 27–29, 32). In working memory tasks, both the span and resistance to distraction improve with development (40, 41). Similar improvements have been seen in monkeys (46). Furthermore, in monkeys, physiology recordings have shown that resistance to distraction is reflected in neural activity in prefrontal cortex. In young animals, distractors affected neural activity during a memory interval. However, in adult animals, distractor effects quickly dissipated. These results are consistent with the dynamic analysis we carried out on our network. The pruned network was more resistant to perturbation during the delay interval. By several related measures, when the pruned network was perturbed by a distractor, the trajectory relaxed back to the unperturbed trajectory. The unpruned network, on the other hand, frequently diverged after perturbation, and this led to the network sometimes providing the wrong answer. The robustness of the pruned network, reflected in a deeper basin of attraction and more stable dynamics, is similar to results we have seen when similar networks were trained on RL tasks, and the evolution over learning was examined (55).

Performance on RL tasks also improves during adolescence (22). Some studies report improvements in learning rates (32). However, the most consistent result is a decrease in decision noise, such that older subjects more frequently choose the most rewarded options (27). We found that pruned networks outperformed unpruned networks, having lower decision noise, when both were trained in the presence of noise. The pruned networks produced more accurate approximations to the optimal Q values and more consistently picked the same options as the Q algorithm. Thus, pruning affected decision noise, consistent with most studies (27). The networks were trained to reproduce a specific learning rate, and therefore, it is not straightforward to assess effects of pruning on learning rates. When we examined the latent space, we found that the state-dependent value functions were better separated in the pruned network than in the unpruned network. The result in the pruned network is consistent with analysis of neural data from prefrontal cortex in monkeys, which showed that when new pairs of options were learned, they were represented in different subspaces in prefrontal cortex (76). Qualitatively, there appeared to be more interference or cross-talk between value representations in the unpruned network than the pruned network. Therefore, outcomes tended to affect value updates across multiple options. This is also reminiscent of results following lesions of orbitofrontal cortex or ventrolateral prefrontal cortex in moneys, which lead to problems with credit assignment (78, 79).

Pruning appears to be a closely regulated process, such that insufficient pruning or overpruning can lead to disorders (80, 81). For example, it has been suggested that excessive synapses and insufficient pruning may underlie deficits in autism (82). In the opposite direction, it has been suggested that excessive pruning may underlie deficits in schizophrenia (83–87), and subsequent genetic and molecular work supports this hypothesis (88–90). We found that pruning led to a strengthening of the attractor basin. Thus, pruned networks are less distractable, which also implies that they may be harder to move out of certain attractor basins into which they have settled. While this can be useful when the pruned network functions on the task for which it has been trained, it can be less useful when the pruned and trained network is producing pathological output. This may apply to psychiatric disorders. For example, in depression, brain networks that underlie motivational processes (91) do not appropriately motivate behavior. In addiction, motivational processes are highly active but motivate harmful behavior. Both depression and addiction can be resistant to therapy, which is an effort to modify the input–output mappings of a patient’s brain. Consistent with this, we found that pruned networks can be more difficult to train on new tasks. Ultimately, unpruning an overpruned network, and restoring plasticity, may be a highly effective therapeutic approach. Unpruning a network can lead to a weakening of pathological attractors, and restoring plasticity can allow retraining the network such that it no longer produces pathological output.

Recent work with both ketamine and psilocybin, both of which may be treatments for depression (92–95), suggests that these drugs may lead to production of new spines (96–98). Similar results may also follow from other therapeutic techniques like electroconvulsive therapy or deep brain stimulation. These techniques may lead to therapeutic effects via an increase in spines and synapses. This increase in spines may flatten the attractor landscape of the brain and allow plasticity. Both effects can lead to eliminating pathological attractors. This may be why these therapies can open a therapeutic window. It is also the case that early interventions for mental health issues, when the brain is more plastic, can be more effective than interventions targeted at the adult, after pruning has taken place. Although this remains highly speculative, our simulation results at least provide a theoretical framework for approaching these issues (99). The theory suggests that an overpruned network can effectively become stuck in a deep basin of attraction, and the best way out is to increase synapses in the network, making the network more amenable to learning new solutions.

Methods

We trained a series of rate-based, recurrent neural networks to solve two cognitive tasks. The first set of networks was trained to solve a DMS working memory task (52). The second set of networks was trained to solve a two-armed bandit RL task (54). We trained networks of various sizes, N. As these are low-dimensional problems, small networks (n = 10) could solve the tasks well. However, we present results using n = 30 for the DMS task and n = 20 for the RL task. Results at n = 30 were more consistent at the population level for the DMS task.

The recurrent dynamics of our network are given by Eqs. 1–3. The network was simulated as a nonlinear iterative map. The variable $u\left(k\right)$ represents inputs to the network at time k; $x\left(k\right)$ represents the latent dynamics, or activity in the recurrent layer, at time k; and $y\left(k\right)$ is the output of the network. For consistency with tasks used in experimental work, k indexes ∼50-ms time bins.

$$x\left(k+1\right)=Af\left(x\left(k\right)\right)+Bu\left(k\right),$$ [1]

$$f\left(x\right)=\text{tanh}(x),$$ [2]

$$y\left(k\right)=Cx(k).$$ [3]

All networks were trained using the scaled conjugate gradient algorithm and back propagation through time (100, 101). The CG algorithm iteratively minimizes the loss using second-order information. One CG iteration is composed of weight updates over a full set of conjugate vectors, where the number of vectors is given by the dimensionality of the weight vector, W, for the network. The first update vector is given by the gradient calculated with back-propagation. Subsequent conjugate vectors are computed recursively, and step size for weight updates is calculated from the second-order approximation.

We trained matrices A, B, and C using a quadratic loss function on the output given by

$$L\left(W\right)={\displaystyle {\sum }_{k=1}^K{(y\left(k\right)-\widehat{y}\left(k\right))}^2}.$$ [4]

The variable W indicates the vector of all weights formed by vectorizing and concatenating matrices A, B, and C. The inputs and outputs were specific to each task. For additional details on network training, see SI Appendix, SI Methods.

LE.

We estimated a maximal LE for each network (102). The LE characterizes the rate at which trajectories, in the undriven network, diverge or converge in the latent space. Specifically, if we consider two nearby points in latent space, $x_1(k)$ and $x_2(k)$, the distance between these points at time k is given by ${\delta }_k=\Vert x_1(k)-x_2(k)\Vert$. After n iterations of the network, the distance between the subsequent points on each trajectory is given by ${\delta }_{k+n}=\Vert x_1(k+n)-x_2(k+n)\Vert$. The LE is then defined by ${\delta }_{k+n}=e^{\lambda n}{\delta }_k$.

For characterizing our networks we calculated (a local estimate of) the maximal LE by first calculating

$$Z={\left({\displaystyle {\prod }_{k=1:K}J(k)}\right)}^T\left({\displaystyle {\prod }_{k=1:K}J(k)}\right)$$ [5]

and then calculated the eigen-decomposition of $Z$. The maximal LE is the log of the absolute value of the largest eigenvalue of Z divided by the number of time steps K. This is defined as $\lambda =\log \left({\text{argmax}}_i\left(\left|{\upsilon }_i\right|\right)\right)/(2*K)$ where the values of ${\upsilon }_i$ are the eigenvalues of Z. The matrices $J(k)$ are the Jacobians of the network update equation, $F(x)=Af\left(x\right)$, evaluated at each time step k.

Data Availability

Code has been deposited in GitHub (https://github.com/baverbeck/Pruning-RNNs.git).