Low-dimensional Manifold Constrained Disentanglement Network for Metal Artifact Reduction

Abstract

Deep neural network based methods have achieved promising results for CT metal artifact reduction (MAR), most of which use many synthesized paired images for supervised learning. As synthesized metal artifacts in CT images may not accurately reflect the clinical counterparts, an artifact disentanglement network (ADN) was proposed with unpaired clinical images directly, producing promising results on clinical datasets. However, as the discriminator can only judge if large regions semantically look artifact-free or artifact-affected, it is difficult for ADN to recover small structural details of artifact-affected CT images based on adversarial losses only without sufficient constraints. To overcome the illposedness of this problem, here we propose a low-dimensional manifold (LDM) constrained disentanglement network (DN), leveraging the image characteristics that the patch manifold of CT images is generally low-dimensional. Specifically, we design an LDM-DN learning algorithm to empower the disentanglement network through optimizing the synergistic loss functions used in ADN while constraining the recovered images to be on a low-dimensional patch manifold. Moreover, learning from both paired and unpaired data, an efficient hybrid optimization scheme is proposed to further improve the MAR performance on clinical datasets. Extensive experiments demonstrate that the proposed LDM-DN approach can consistently improve the MAR performance in paired and/or unpaired learning settings, outperforming competing methods on synthesized and clinical datasets.

I. Introduction

Metal objects in a patient, such as dental fillings, artificial hips, spine implants, and surgical clips, will significantly degrade the quality of computed tomography (CT) images. The main reason for such metal artifacts is that the metal objects in the field of view strongly attenuate x-rays or even completely block them so that reconstructed images from the compromised/incomplete data are corrupted in various ways, which usually show as bright or dark streaks. As a result, the metal artifacts significantly affect medical image analysis and subsequent clinical treatment. Particularly, the metal artifacts degrade the counters of the tumor and organs at risk, raising great challenges in optimizing a radio-therapeutic plan [1], [2].

Over the past decades, extensive research efforts [3] have been devoted to CT metal artifact reduction (MAR), leading to various MAR methods. Traditionally, MAR methods mainly focus on the correction of projection data with psychical [4] and other prior knowledge [5], [6]. Particularly, the popular linear [5] and normalized [6] interpolation methods consider a metal trace in the sinogram as a data-missing region, and fill in this region with interpolated data. Then, artifact-reduced image can be reconstructed from the refined projection data using a reconstruction algorithm, such as filtered back-projection (FBP). However, the projection domain methods tend to produce secondary artifacts as it is difficult for the estimated projection values to perfectly match the ground truth. In practice, original projection data and the corresponding reconstruction algorithm are not publicly accessible. To apply the projection based methods in the absence of original sinogram data, researchers such as the authors of [7] proposed a post-processing scheme that generates the sinogram through forward projection of a CT image first and then applies the projection based method on the reprojected sinogram. However, the re-projection and reconstruction may introduce extra errors.

To overcome the limitations of the projection domain methods, researchers are dedicated to reduce metal artifacts in the image domain [8]–[12] or dual-domain [13]–[15]. Particularly, with deep learning techniques [16], data-driven methods have recently made great progress in the area of MAR. However, most existing deep learning based methods are fully-supervised, requiring a large number of paired training images, i.e., each artifact-affected image is associated with the co-registered artifact-free image. In clinical scenarios, it is infeasible to acquire a large number of such paired images. Therefore, the prerequisite for training these methods is to simulate artifact-affected images by inserting metal objects into artifact-free images so that paired images are obtained. However, simulated images cannot reflect all real conditions due to the complex physical mechanism of metal artifacts and many technical factors of the imaging system, degrading the performance of the fully-supervised models. To avoid synthesized data, the recently proposed ADN [17] only uses clinical unpaired artifact-affected and artifact-free CT images to train a disentanglement network for minimized adversarial losses, giving promising results on clinical datasets, outperforming the fully-supervised methods trained with the synthesized data. However, without strong supervision, the proposed ADN method is not perfect, and often fails to preserve structural details due to the insufficient constraints imposed by the discriminators.

In this study, we improve the MAR performance on clinical datasets from two aspects. First, we formulate the MAR problem as the artifact disentanglement while at the same time leveraging the low-dimensional manifold of image patches to help recover structural details. Specifically, we train a disentanglement network with ADN losses and simultaneously constrain a reconstructed artifact-free image to have a low-dimensional patch manifold. The idea is inspired by the low-dimensional manifold model (LDMM) [18] for image processing and CT image reconstruction [19]. However, how to apply the iterative LDMM algorithm to train the disentanglement network is not trivial. To this end, we carefully design an LDM-DN algorithm for simultaneously optimizing objective functions of the disentanglement network and the LDM constraint. Second, we improve the MAR performance of the LDM-DN on the real dataset by integrating both unpaired and paired supervision. Particularly, the unpaired supervision is the same as that used in ADN where unpaired images come from artifact-free and artifact-affected groups, and the paired supervision relies on synthesized paired images to train the model in a pixel-to-pixel manner. Although the synthesized data cannot perfectly simulate the clinical scenarios, they still provide helpful information for recovering artifact-free images from artifact-affected ones. Finally, we design a hybrid training scheme to combine both the unpaired and paired supervision for further improving MAR performance on clinical datasets.

The rest of this paper is organized as follows. In the next section, we review the related work. In Section III, we describe the proposed method, including the problem formulation, the construction of a patch set, the computation of a manifold dimensionality, the corresponding optimization algorithm, and the hybrid training scheme. In Section IV, we evaluate the proposed LDM-DN algorithm for MAR on synthesized and clinical datasets. Extensive experiments show that our proposed method consistently improve the performance of both the state-of-the-art ADN methods and the paired learning methods. Finally, we conclude the paper in Section V.

II. Related work

A. Metal Artifact Reduction

CT metal artifact reduction methods can be classified into three categories, including projection domain methods, image domain methods and dual domain methods.

Projection based methods correct projections for MAR. Some methods of this type [20]–[22] directly correct corrupted data by modeling the underlying physical process, such as beam hardening and scattering. However, the results with these methods are not satisfactory when high atoma number metals are presented. Thus, a more sophisticated way is to treat metal-affected data within the metal traces as unreliable and replace them with the surrogates estimated by reliable ones. Linear interpolation (LI) [5] is a basic and simple method for estimating metal corrupted data. The LI method is prone to generate new artifacts and distort structures due to mismatched values between the linearly interpolated data and the unaffected data. To address this problem, the prior information is employed to generate a more accurate surrogate in various ways [6], [7], [23]. Among these methods, the state-of-the-art normalized MAR (NMAR) method [6] is widely used due to its simplicity and accuracy. NMAR introduces a prior image of tissue classification for normalizing the projection data before the LI is operated. With the normalized projection data, the data mismatch caused by LI can be effectively reduced for better results than that of the generic LI method. However, the performance of NMAR largely depends on accurate tissue classification. In practice, the tissue classification is not always accurate so that NMAR also tends to produce secondary artifacts. Recently, deep neural networks [24]–[26] were applied for projection correction and achieved promising results. However, such learning based methods require a large number of paired projection data.

The image domain methods directly reduce metal artifacts by post-processing CT images. Conventionally, some image processing techniques were leveraged to estimate and remove streak artifacts in artifact-affected images. For example, [8] identified the streaking artifacts by thresholding the difference image between the original image and its specific low-passed version. However, these hand-crafted methods are limited in applications and performance due to the associated assumptions on metal artifacts. As the data-driven approach has a learning ability to identify various metal artifacts from complex background images, deep learning models for MAR are more advantageous than the traditional methods. The first work demonstrating the effectiveness of the deep learning method for MAR was proposed by Gjesteby et al. [27]. The authors designed an encoder-decoder network to remove remaining metal artifacts in images corrected using NMAR [6], showing a potential of deep learning for MAR. Also, RL-ARCNN [10] was designed for MAR, which uses a convolutional neural network via residual learning, achieving better results than the plain CNN [28]. cGANMAR [11] regards MAR as an image-to-image transformation, and adapts the Pix2pix [29] model to improve the MAR performance. DestreakNet [12] takes an NMAR-corrected image and a map of image details as the inputs to a dual-stream network, effectively improving the MAR results.

To benefit from both projection and image domains, various dual domain methods were also proposed. In the CNN-MAR method [13], the CNN first takes the original image and corrected images by BHC [4] and LI [5] as the inputs and then produces a CNN output image, which is used to generate a prior image. Then, the projection data of the prior image is used to correct the original projection data for the final reconstruction with FBP. DuDoNet [14] and its variant [15] introduce an end-to-end dual domain network to simultaneously correct a sinogram and the corresponding CT images.

All above deep learning methods for MAR require a large number of synthesized paired project datasets and/or CT images for training. A recent study [17] has shown that the models [11], [13] trained on the synthesized data cannot generalize well on the clinical datasets. Then, ADN was designed and tested on clinical unpaired data, achieving promising results. However, without a strong supervision, ADN can hardly recover structural details in challenging cases.

In this study, we introduce a novel image prior, i.e., low-dimensional manifold, and different levels of supervision to train an enhanced disentangle network for an improved MAR performance on clinical images. Our proposed LDM constrained disentanglement framework with synergistic supervision has a potential to empower image domain and dual domain based methods.

B. Low-dimensional manifold

The patch set of natural images has been proved coming from a low-dimensional manifold [30]–[33]. Based on this low dimensionality of the patch manifold, LDMM first computes the dimension of the patch manifold based on the differential geometry and then uses the dimension to regularize an image recovery problem, including image inpainting, super-resolution, and denoising. Based on LDMM, LDMNet [34] proposes to regularize the combination of input data and output features within a low-dimensional manifold in the context of the classification task, showing a competitive performance over popular regularizers such as low-rank and DropOut. Recently, Cong et al. [19] proposed to use LDMM in regularizing the CT image reconstruction, demonstrating that the LDMM has a strong ability to recover detailed structures in CT images. Abdullah et al. [35] leveraged LDMM to reconstruct magnetic resonance images from sparse k-space measurements by constraining the dimension of the patch manifold and obtained an improved performance. Zeng et al. [36] extended the LDMM from image patches to surface patches in the point cloud for 3D point cloud denoising. Zhu et al. [37] leveraged LDMM for hyperspectral image reconstruction, based on the observation that the spatial–spectral blocks of hyperspectral images are close to a collection of low dimensional manifolds. Inspired by the recent results with LDMM, here we propose an LDM constrained disentanglement network with both paired and unpaired supervision for improving the MAR performance on clinical datasets.

III. Method

A. Problem formulation

Let us first introduce the generic neural network based MAR method in the image domain. In the supervised learning mode, we assume that the paired data ${\left\{x_i^a,x_i^{gt}\right\}}_{i=1}^N$ are available, where each artifact-affected image $x_i^a$ has a corresponding artifact-free image $x_i^{gt}$ as the ground truth, and N is the number of paired images. Then, the deep neural network for metal artifact reduction can be trained on this dataset by minimizing the following loss function:

$${\mathcal{L}}_{sup}(\theta )=\frac{1}{N}\sum _{i=1}^N\ell \left(g\left(x_i^a;\theta \right),x_i^{gt}\right)$$ (1)

where ℓ denotes a loss function, such as the L1-distance function, and $g\left(x_i^a;\theta \right)$ represents the predicted artifact-free image of the artifact-affected imaged $x_i^a$ by the neural network function g with a parameter vector θ to be optimized. In practice, a large number of paired data are synthesized for training the model, as the clinical datasets only contain unpaired images.

To improve the MAR performance on clinical datasets, ADN adapts the generative adversarial learning based disentanglement network for MAR, only requiring the unpaired dataset, $\left\{x_i^a;y_j\right\}$, i = 1,·⋯ , N₁, j = 1,·⋯ , N₂, where y_j represents an artifact-free image that is not paired with $x_i^a$, and N₁ and N₂ denote the number of artifact-affected and artifact-free images respectively. The ADN [17] model consists of several encoders and decoders, which are trained with several loss functions, including two adversarial losses, a reconstruction loss, a cycle-consistent loss, and an artifact-consistent loss. For simplicity, we denote the ADN loss functions as

$${\mathcal{L}}_{adn}(\theta )=\frac{1}{N_1{N}_2}\sum _{i=1}^{N_1}\sum _{j=1}^{N_2}{\ell }_{adn}\left(f\left(\left[x_i^a,y_j\right],\theta \right),\left[y_j,x_i^a\right]\right)$$ (2)

where l_adn is the combination of all losses of ADN, f(·) represents a general function of all ADN modules during training and has multiple inputs and outputs, and here θ denotes the parameters of all modules in ADN. Specifically, the losses of ADN include two adversarial losses that respectively remove and add metal artifacts, a reconstruction loss to preserve the original contents and avoid fake regions/tissues, the artifact consistency loss to enforce the removed and synthesized metal artifacts to be consistent, and the self-reduction loss to constrain that the clean images can be recovered from the synthesized artifact-affected images. During training, all loss functions are optimized simultaneously. Without the paired supervision, the ADN can hardly recover the detailed structures accurately.

In this work, we introduce a general image property known as LDM to improve the MAR performance.

As analyzed in the previous studies [18], [19], we reasonably assume that a patch set of artifact-free images samples a low-dimensional manifold. Then, we formulate the MAR problem as follows:

$$\underset{\theta ,\mathcal{M}}{\text{min}}\mathcal{L}(\theta )+\lambda \mathit{\text{dim}}(\mathcal{M}(P(\theta ))$$ (3)

where P(θ) denotes the patch set of artifact-free and/or artifact-corrected images and is determined by the network parameters θ, $\mathcal{M}$ is a smooth manifold isometrically embedded in the patch space, $\mathcal{L}(\theta )$ can be any network loss functions, such as ${\mathcal{L}}_{sup}$ for paired learning or ${\mathcal{L}}_{adn}$ for unpaired learning, and λ is a balance hyperparameter. Instead of optimizing the pixel values of an individual image in the traditional image processing method [18], here we aim to optimize network parameters by constraining the predicted patch set P(θ) to have a low-dimensional manifold for all training images.

To solve the above optimization problem, we need to specify the construction of a patch set, the computation of a manifold dimensionality, and the learning algorithm for simultaneously optimizing the network loss functions and the dimensionality of a patch manifold. In the following sections, we will describe each of these components.

B. Construction and manifold dimensionality of a patch set

In this work, we adapt the state-of-the-art disentangle network in our proposed LDM-based optimization framework under different levels of supervision. For such a disentanglement network, we leverage its two branches to construct a patch set. As shown in Fig. 1, one is the artifact-correction branch that maps an artifact-affected image x^a to an artifact-corrected image $\widehat{x}$, and the other is an artifact-free branch that maps an artifact-free image y to itself $\widehat{y}$. Considering the spatial correspondence between the input/output image and its convolutional feature maps, we concatenate each image patch and its feature vectors to represent the patch. Specifically, some papers [38], [39] have demonstrated that each feature vector in the learned convolutional feature maps corresponds to a fine-gained image patch. Therefore, the high-level feature vectors of the encoder can be used to enhance the representation ability of pixel values, which has been empirically demonstrated effective in Section IV-C2. For the artifact-correction branch, we take patches from the artifact-corrected images, denoted as $\left\{P_i\left(\widehat{x},z_x^t\right)\right\}$, where $z_x^t$ denotes the transformed version of the original latent code in ADN using a convolutional layer. This transformation aims to compress the feature channels so the the dimension of feature vector is equal to that of the patch vector, please see Section IV-B for the specific values. Similarly, for the artifact-free branch, we take patches from the original images, denoted as $\left\{P_j\left(y,z_y^t\right)\right\}$, where $z_y^t$ denotes the transformed latent code of z_y. As we assume that the patch set of the images without artifacts samples a low-dimensional manifold, the final patch set is the concatenation of these two patch sets, i.e., $P\left(\widehat{x},z_x^t\right)\cup P\left(y,z_y^t\right)$. Since the patches are determined by the network parameters θ and input images, hereafter we simply denote the patch set constructed from all possible unpaired images as $P(\theta )=\left\{P\left(\widehat{x},z_x^t\right)\cup P\left(y,z_y^t\right)\right\}$.

Fig. 1.

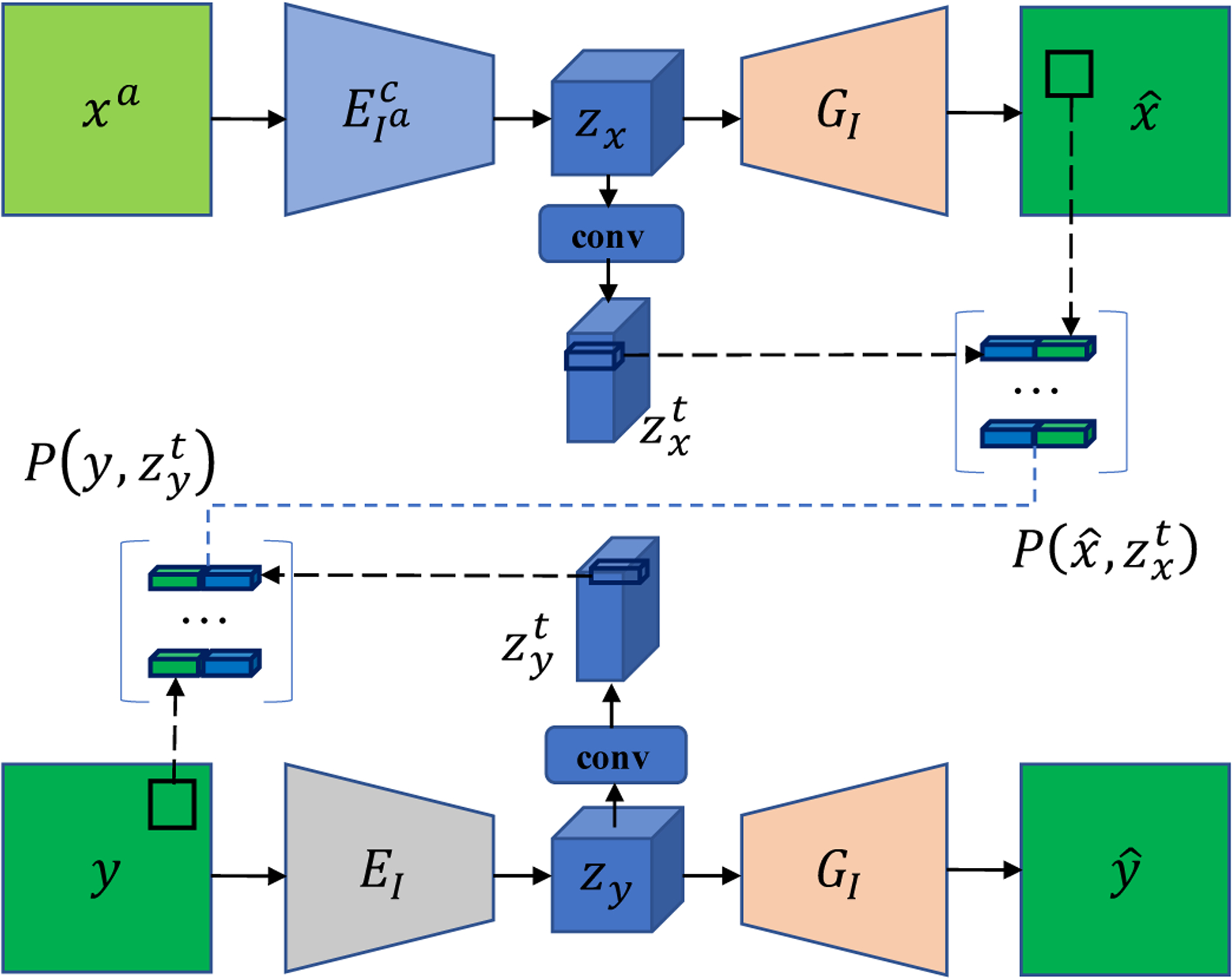
Diagram of patch set construction. The top branch is the artifact-correction branch and the bottom branch is the artifact-free branch. Note that the whole ADN model contains four branches, and here only two branches are shown for illustrating patch construction as the artifact-affected images in the other branches are not constrained to have an LDM. Please refer to [17] for details of the whole ADN model.

In our implementation, the input image size is H × W and the step size is s for down-sampling the encoder features, then the patch size is s × s, the dimension of $z_x^t$ or $z_y^t$ is $s^2\times \frac{H}{s}\times \frac{W}{s}$, and each patch vector P_j(θ) ∈ R^d, d = 2s². The effect of this design for patch set construction is shown in Sub-section IV-C2.

We adopt the method of LDMM [18] to compute the dimensionality $dim(\mathcal{M})$ of a patch manifold $\mathcal{M}$ as expressed in the following theorem.

Theorem 1. Let $\mathcal{M}$ be a smooth submanifold isometrically embedded in R^d. For any patch $P_j(\theta )\in \mathcal{M}$,

$$dim(\mathcal{M})=\sum _{i=1}^d\Vert {\nabla }_{\mathcal{M}}{\alpha }_i{\left(P_j(\theta )\right)\Vert }^2$$ (4)

where α_i(·) is the coordinate function, i.e., ${\alpha }_i\left(P_j(\theta )\right)=P_j^i(\theta )$, $P_j^i(\theta )$ is the i^th element in the patch vector P_j(θ), and ${\nabla }_{\mathcal{M}}{\alpha }_i\left(P_j(\theta )\right)$ denotes the gradient of the function α_i on $\mathcal{M}$. More details on the definition of α_i on $\mathcal{M}$ can be found in [18]. In our implementation, the patch is parameterized by the network parameter vector θ.

C. Optimization

According to the construction of a patch set and the definition of a patch manifold dimensionality, we can reformulate Eq. (3) as

$$\begin{gathered} \underset{\theta ,\mathcal{M}}{\text{min}}\mathcal{L}(\theta )+\sum _{i=1}^d{\Vert {\nabla }_{\mathcal{M}}{\alpha }_i\Vert }_{L^2(\mathcal{M})}^2, \\ s.t.P(\theta )\subset \mathcal{M}. \end{gathered}$$ (5)

where

$${\Vert {\nabla }_{\mathcal{M}}{\alpha }_i\Vert }_{L^2(\mathcal{M})}={\left({\int }_{\mathcal{M}}{\Vert {\nabla }_{\mathcal{M}}{\alpha }_i(p)\Vert }^{2}dp\right)}^{1/2}$$ (6)

where Eq. (6) is the continuous version of Eq. (4), and $p\in \mathcal{M}$ is a patch vector and equivalent to P_j(θ). To solve this problem, we design an iterative algorithm, named LDM-DN, for optimizing the LDM constrained disentanglement network. The LDM-DN is based on the algorithm for image processing introduced in [18]. However, the original LDMM [18] is to applied to process a single image while LDM-DN is to optimize the parameters of neural networks using all training images.

Specifically, given (θ^k, ${\mathcal{M}}^k$) at step k satisfying $P_{{\theta }^k}^k\subset {\mathcal{M}}^k$, step k + 1 consists of the following sub-steps:

• Update θ^k+1 and ${\alpha }^{k+1}=\left({\alpha }_1^{k+1},\cdots ,{\alpha }_d^{k+1}\right)$ as the minimizers of the following objective with the fixed manifold ${\mathcal{M}}^k$:

  $$\begin{gathered} \underset{\theta ,\alpha }{\text{min}}\mathcal{L}(\theta )+\sum _{i=1}^d{\Vert {\nabla }_{\mathcal{M}}{\alpha }_i\Vert }_{L^2(M)}^2, \\ s.t.\hspace{1em}{\alpha }_i\left(P_j\left({\theta }^k\right)\right)=P_j^i(\theta ) \end{gathered}$$ (7)
• Update ${\mathcal{M}}^{k+1}$:

  $${\mathcal{M}}^{k+1}=\left\{\left({\alpha }_1^{k+1}(p),\cdots ,{\alpha }_d^{k+1}(p)\right):p\in {\mathcal{M}}^k\right\}$$ (8)

• Repeat above two sub-steps until convergence.

It is noted that if the iteration converges to a fixed point, α^k+1 will be very close to the coordinate functions, and ${\mathcal{M}}^{k+1}$ and ${\mathcal{M}}^k$ will be very close to each other.

Eq. (7) is a constrained linear optimization problem, which can be solved using the alternating direction method of multipliers. Thus, we reduce the above optimization algorithm to the following iterative procedure:

• Update ${\alpha }_i^{k+1}$, i = 1, ⋯ , d, with a fixed P(θ^k),

  $${\alpha }_i^{k+1}=\text{arg}\underset{{\alpha }_i}{\text{min}}\sum _{i=1}^d{\Vert {\nabla }_{\mathcal{M}}{\alpha }_i\Vert }_{L^2\left({\mathcal{M}}^k\right)}^2+\mu {\Vert \alpha \left(P\left({\theta }^k\right)\right)-P\left({\theta }^k\right)+d^k\Vert }_F^2.$$ (9)

  where α(P(θ^k)) = [α_i(P_j(θ^k))]^m×d and $P\left({\theta }^k\right)={\left[P_j^i\left({\theta }^k\right)\right]}^{m\times d}$ are matrices, and m is the number of patch vectors.
• Update θ^k+1,

  $${\theta }^{k+1}=\text{arg}\underset{\theta }{\text{min}}\mathcal{L}(\theta )+\mu {\Vert {\alpha }^{k+1}\left(P\left({\theta }^k\right)\right)-P(\theta )+d^k\Vert }_F^2$$ (10)
• Update d^k+1,

  $$d^{k+1}=d^k+{\alpha }^{k+1}\left(P\left({\theta }^k\right)\right)-P\left({\theta }^{k+1}\right)$$ (11)

  where d^k is the dual variable.

Using the standard variational approach, the solutions to the objective function (9) can be obtained by solving the following PDE:

$$\begin{gathered} -{\Delta }_{\mathcal{M}}u(p)+\mu \sum _q\delta (p-q)(u(q)-v(q))=0,\hspace{1em}p\in \mathcal{M} \\ \frac{\partial u}{\partial n}(p)=0,\hspace{1em}p\in \partial \mathcal{M}. \end{gathered}$$ (12)

where $\partial \mathcal{M}$ is the boundary of $\mathcal{M}$, and n is the out normal of $\partial \mathcal{M}$. Note that here variables p and q mean the patche vectors that are determined by the network parameter vector θ, which is not explicitly denoted for simplicity.

Eq. (12) can be solved with the point integral method. For solving the Laplace-Beltrami equation, the key is the following integral approximation:

$$\begin{gathered} {\int }_{\mathcal{M}}{\Delta }_{\mathcal{M}}u(q){\overline{R}}_t(p,q)dq\approx -\frac{1}{t}{\int }_{\mathcal{M}}(u(p)-u(q))R_t(p,q)dq \\ +2{\int }_{\partial \mathcal{M}}\frac{\partial u(q)}{\partial n}{\overline{R}}_t(p,q)d{\tau }_q, \end{gathered}$$ (13)

where t > 0 is a hyper parameter and

$$R_t(p,q)=C_{t}R\left(\frac{|p-q{|}^2}{4t}\right).$$ (14)

R : R⁺ → R⁺ is a positive C² function which is integrable over [0, +∞), and C_T is a normalizing factor

$$\overline{R}(r)={\int }_r^{+\infty }R(s)ds,\mathit{\text{ and}}\hspace{1em}{\overline{R}}_t(p,q)=C_t\overline{R}\left(\frac{|p-q{|}^2}{4t}\right)$$ (15)

We usually set R(r) = e^−r, then ${\overline{R}}_t(p,q)=R_t(p,q)=C_t\mathit{\text{exp}}\left(\frac{|p-q{|}^2}{4t}\right)$ is Gaussian.

Based on the above integral approximation, we approximate the original Laplace-Beltrami equation as:

$${\int }_M(u(p-u(q))R_t(p,q)dq+\mu t\sum _{q\in \omega }{\overline{R}}_t(p,q)(u(q)-v(q))=0$$ (16)

This integral equation is easy to discretize over a point cloud.

To simplify the notation, we denote the patch set $P\left({\theta }^k\right)={\left\{p_i\right\}}_{i=1}^m$, where m is the number of patches. We assume that the patch set samples the submanifold $\mathcal{M}$ and is uniformly distributed. Then, the integral equation can be written as

$$\frac{\left|\mathcal{M}\right|}{m}\sum _{j=1}^m{R}_t\left(p_i,p_j\right)\left(u_i-u_j\right)+\mu t\sum _{j=1}^m{\overline{R}}_t\left(p_i,p_j\right)\left(u_j-v_j\right)=0$$ (17)

where v_j = v(p_j), and $|\mathcal{M}|$ is the volume of the manifold $\mathcal{M}$.

We rewrite Eq. (17) in the matrix form:

$$(L+\overline{\mu }W)u=\overline{\mu }Wv.$$ (18)

where v = (v₁, ⋯ , v_m), $\overline{\mu }=\frac{\mu tm}{|\mathcal{M}|}$, and L is an m×m matrix,

$$L=D-W$$ (19)

W = (w_ij), i, j = 1, ⋯ , m is the weight matrix, D = diag(d_i) with $d_i={\sum }_{j=1}^m{w}_{ij}$, and

$$w_{ij}=R_t\left(p_i,p_j\right),\hspace{1em}{p}_i,p_j\in P\left({\theta }^k\right),\hspace{1em}i,j=1,\cdots ,m.$$ (20)

Then, the solutions to the objective function (9) can be obtained by solving u in Eq. (18).

More specifically, the final LDM-DN learning algorithm is described in Algorithm 1, where we assume that the patch set of all images samples a low-dimensional manifold. However, it is impractical to optimize the LDM problem when the number of patches is very large. To this end, we randomly select a batch of images to construct the patch set, and then estimate the coordinate functions U, update the network parameters θ and dual variables d in each iteration. Thus, in our implementation the number of iterations in training the network is the same as that in the LDM optimization. While practically updating the dual variables d in the original LDMM algorithm [18], the values of d usually increase as the number of iterations increases. As the number of iterations is usually very large, the loss value of the LDM term in Step 6 of Algorithm 1 will become increasingly large, leading to an instability. To overcome this problem, the dual variables are normalized in Step 7 of Algorithm 1. The LDM involved parameters μ = 0.5 and d⁰ = 0 were set to the same values as those used in [18].

D. Combination of paired and unpaired learning

ADN only requires unpaired clinical images for training so that the performance degradation of a supervised learning model can be avoided when it is first trained on the synthesized dataset and then transferred to a clinical application. However, the GAN loss based weak supervision is not enough for recovering full image details. On the other hand, although the synthesized data may not perfectly simulate real scenarios, it does provide helpful information via strong supervision. To benefit from both the strongly and weakly supervised learning, here we design a hybrid training scheme. During training, both unpaired clinical images and paired synthetic images are selected to construct a mini-batch, where the number of unpaired images is the same as that of paired images. Specifically, the unpaired images are used to train all modules and the paired images are naturally used to train the artifact-correction branch, where artifact-free and artifact-corrected images are constrained by the LDM, as shown in Fig. 2. Therefore, the loss function of the combination learning strategy is:

$$\underset{\theta ,\mathcal{M}}{\text{min}}{\mathcal{L}}_{adn}(\theta )+{\mathcal{L}}_{sup}(\theta )+\mathit{\text{dim}}(\mathcal{M}(P(\theta )),$$ (21)

where we simply set each loss term having the same contribution to the total loss, and all terms are simultaneously used to optimize the network parameters.

Fig. 2.

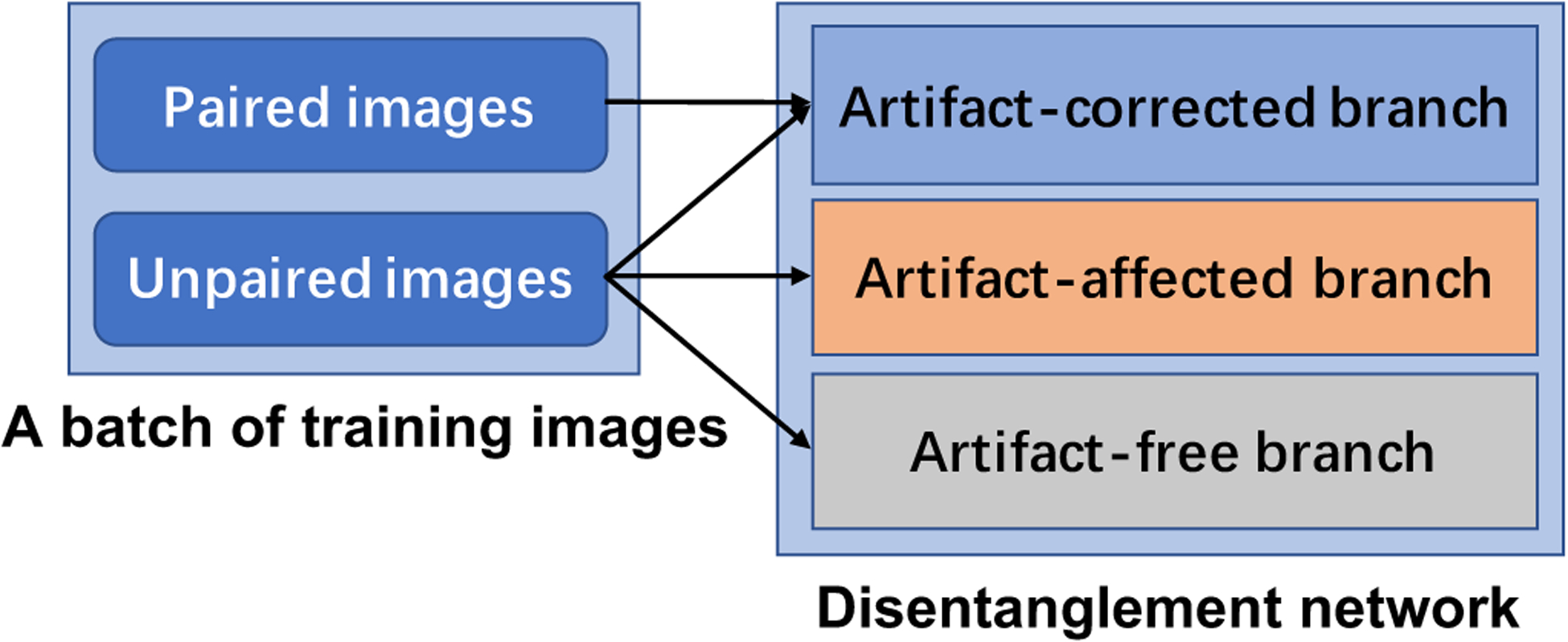
Combination of paired and unpaired learning.

IV. Experimental design and results

A. Datasets

In our experiments we evaluated the proposed method on one synthesized dataset from DeepLesion [40] and one clinical dataset from Spineweb¹, which are the same as those used in ADN [17]. It is worth to mention that the proposed and all competing methods in this paper only focus on 2D slices.

For the synthesized dataset, 4,118 artifact-free CT images were randomly selected from DeepLesion. Then, the paired images with and without metal artifacts were synthesized using the method introduced in CNNMAR [13]. Finally, 3,918 pairs of images were used for training and 200 pairs for testing. For a fair comparison, the images used for training and testing, and all pre-processing processes are the same as those used in the paper of ADN [17].

For the clinical dataset, 6,170 images with metal artifacts and 21,190 images without metal artifacts are selected for training, and additional 100 images with metal artifacts were selected for evaluation. The criteria for selecting these images are the same as that in the ADN study. Specifically, if an image contains pixels with Hounsfield Unit (HU) values greater than 2,500 HU and the number of these pixels is larger than 400, then it is grouped into the artifact-affected class. The images with the largest HU values less than 2,000 are grouped into the artifact-free class. Furthermore, to study the effectiveness of combining both paired and unpaired supervision, we randomly selected 6,170 images from the artifact-free group. Then, we extracted 6,170 metal objects from the images in the artifact-affected group, and used CatSim [41] to simulate the paired images by inserting each extracted metal shape into a selected artifact-free image. Finally, 6,170 synthesized paired images were obtained.

B. Implementation details

We implemented different network architecture variants for different learning paradigms, as shown in Fig. 3. For unpaired learning, we use the same architecture as ADN [17] as shown in Fig. 3 (a), and the architectures of all other learning paradigms are the variants of ADN. In Fig. 3 (b), to construct the patch set for the LDM constraint, we add two convolutional layers on the top of the encoders in the artifact-corrected and artifact-free branches respectively, as described in Sub-section III-B. For paired learning only, we simply use the encoder-decoder in the artifact-correction branch as shown in Fig. 3 (c). In combination of paired learning and the LDM constraint, we keep two encoder-decoder branches as shown in Fig. 3 (d).

Fig. 3.

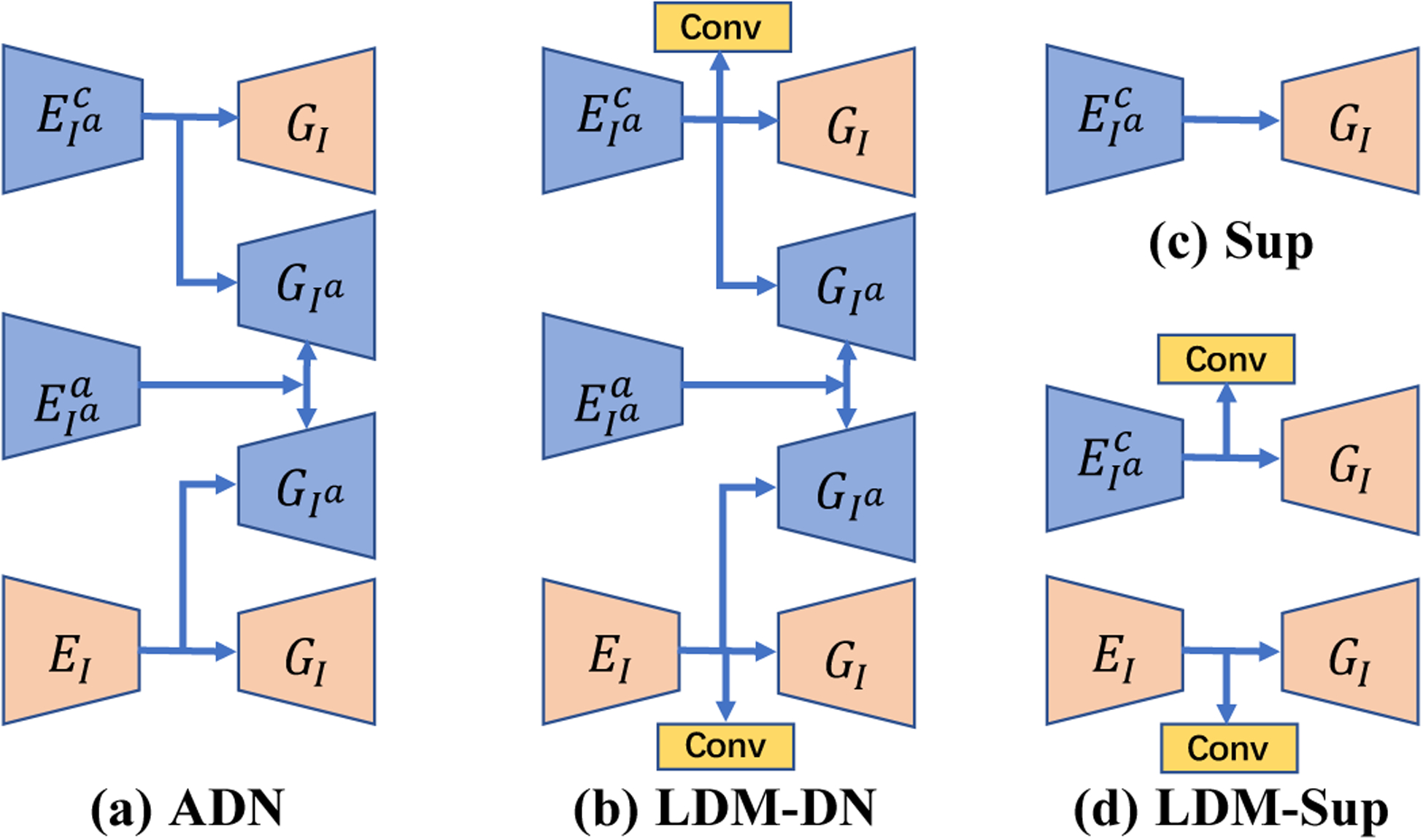
Network architectures of different learning paradigms. $E_{I^a}^c$, $E_{I^a}^a$ denote the encoders that respectively extract content and artifact features from artifact-affected images. E_I is the encoder that extracts content features from the artifact-free images. G_I and $G_{I^a}$ represent the decoders that output the artifact-free/artifact-corrected and artifact-affected images respectively. The combinations of $E_{I^a}^c\to G_I$, $E_{I^a}^a\to G_{I^a}$ or $E_I\to G_{I^a}$, and E_I → G_I construct artifact-corrected, artifact-affected, and artifact-free branches respectively. Conv denotes a convolutional layer. Note that in sub-figures (a) and (b) $E_I\to G_{I^a}$ is further followed by $E_{I^a}^c\to G_I$ to remove the added metal artifacts with the self-reduction loss [17].

In Fig. 1 and Fig. 3 (b) and (d), the extra convolutional layers are used to compress the channels of the latent code. Specifically, the input image size is 1 × 256 × 256, the down-sampling rate is 8, the matrix of Z_x is of 512 × 64 × 64, the matrix of $Z_x^t$ is of 64 × 64 × 64, the patch size is 8 × 8, and the dimension of the point in the patch set is 128. Note that these values are automatically computed according to the descriptions in Section III-B.

We implemented the proposed method in PyTorch. To be fair, we keep all hyper parameters the same as those in ADN [17]. In Algorithm 1, we set the batch size bs = 1 due to the limited GPU memory and we empirically set λ = 1 to balance the LDM and ADN loss terms.

C. Results on synthesized dataset

To quantitatively evaluate different methods, we used the popular peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) metrics in our experiments.

1). Reimplementation of ADN:

To simulate the unpaired learning, the synthesized paired images were divided into two groups, and then the artifact-affected images were selected from one group and the artifact-free images from the other group. In [17], the ratio of numbers of images in these two groups was simply set to 1:1. However, in clinical scenarios, the number of artifact-affected images is much smaller than the number of artifact-free images. Therefore, we evaluated the effect of the ratio on the MAR performance in the unpaired learning setting. In Table I, ADN-0.85, ADN-0.50 and AND-0.15 signify various ratios of artifact-affected images to all images. Table I shows that there is little difference among the models trained with different ratios between artifact-affected and artifact-free images. As a representative ratio between the artifact-affected and artifact-free images in the clinical conditions, the ADN-0.15 serves as the baseline in all following experiments, which is denoted as ADN* for simplicity. We found that our reproduced results of ADN* are slightly better than the reported results in the original paper as shown in Table III. To be fair, we use the better reproduced results for comparison.

TABLE I.

Results of the models trained with different ratios of numbers of images in the artifact-free and artifact-affected groups.

	ADN-0.85	ADN-0.50	ADN-0.15
PSNR	34.1	34.0	34.0
SSIM	92.8	92.8	92.9

TABLE III.

Comparison results on DeepLesion.

	Paired leaning					Unpaired learning
	CNNMAR [13]	UNet [42]	cGANMAR [11]	Sup	LDM-Sup	CycleGAN [43]	DIP [44]	MUNT [45]	DRIT [46]	ADN [17]	ADN*	LDM-DN
PSNR	32.5	34.8	34.1	37.6	38.0	30.8	26.4	14.9	25.6	33.6	34.0	35.0
SSIM	91.4	93.1	93.4	96.1	96.3	72.9	75.9	7.5	79.7	92.4	92.9	94.2

2). Ablation study on the patch set construction:

To study the effectiveness of the approach for constructing the patch set introduced in Sub-section III-B, here we evaluated some alternative variants. For the full setting, we use the pixel values concatenated with its convolutional features to represent this patch, and then the patch set is constructed with the patches from both artifact-corrected and artifact-free branches as shown in Fig. 1. Based on this full setting, we evaluated other three variants. First, we only use the pixel values to represent the patch, and the patch set only consists of the patches from the artifact-correction branch, denoted as LDM-basic. Second, we use the pixel values with its convolutional features to represent this patch, and the patch set only consists of the patches from the artifact-correction branch, denoted as LDM-fea. Third, we only use the pixel values to represent the patch, and the patch set consists of the patches from both artifact-corrected and artifact-free branches, denoted as LDM-high. Table II presents the results of different variants. Specifically, the basic variant LDM-basic can improve the performance of the baseline method ADN*. Then, LDM-fea can further improve the performance, demonstrating the effectiveness of extra latent features for enhancing the patch representation. In contrast, LDM-high that incorporates the artifact-free image patches without enhanced patch representation even harmed the performance compared with that of LDM-basic. However, the full setting that incorporates the patches from artifact-free branch with enhanced patch representation can further improve the performance of LDM-fea. We attribute these results to that the effectiveness of LDM depends on the measurement of patch similarity according to Eq. (20), which is further determined by the representing features of patches. When using the pixel values with limited ability to represent patches, it is hard to accurately measure the similarity especially for the patches from different unpaired images. In this case, the errors may be introduced in estimating the dimension of patch manifold, leading to degraded results. On the contrary, incorporating the artifact-free patches represented by augmented features can help estimate the dimension of manifold, leading to the improved results.

TABLE II.

Results of the ablation study.

	ADN*	LDM-basic	LDM-fea	LDM-high	Full setting
PSNR	34.0	34.1	34.3	34.0	35.0
SSIM	92.9	93.3	93.4	93.0	94.2

3). Comparative results:

On the synthesized dataset, we evaluated the quantitative and qualitative performance of our proposed method as well as the compared methods. Table III gives the comparison results of the proposed method with the competing methods in the paired and unpaired learning settings. In Table III, ADN* is our improved ADN, see Section IV-C1 for details. The results show that the proposed LDM-DN method outperformed ADN in terms of both PSNR and SSIM metrics in the unpaired learning setting. For the paired learning part in Table III, Sup corresponds to the network architecture in Fig. 3 (c), which was trained with the paired data. It is noted that this encoder-decoder architecture contains the skip connections between the encoder and the decoder, which is the same as ADN. LDM-Sup adds the LDM constraints to the Sup during the paired training, corresponding to the architecture in Fig. 3 (d). Although the paired images have accurate pixel-to-pixel supervision, the LDM based learning algorithm can further improve the performance. These results demonstrate that our proposed LDM-DN algorithm explicitly incorporates the LDM prior and consistently improves the existing models in the paired and unpaired learning settings. Clearly, other ways exist to enforce the LDM constraint and could be used or synergistically incorporated into this framework for even better MAR results.

We also visually compared the results as shown in Fig 4. The visual impressions are consistent with the numerical results. In the unpaired learning setting, although ADN can remove a majority of metal artifacts, the local details were not well preserved. By comparing the results of ADN* and LDM-DN, an evident improvement was made on these details. Compared with the unpaired learning (Sup vs. ADN*), the ideal paired learning gave better results on the synthesized test dataset. In this case, our proposed LDM-DN learning algorithm obtained further improvements, where the boundaries of structures are sharper visually (LDM-Sup vs. Sup). In addition, we also inspected the difference of CT values between the predicted and the ground-truth images for each method, showing that the predicted pixels values of the proposed methods LDM-Sup and LDM-DN are closer to the ground-truth. Fig. 5 shows that LDM-DN consistently works better than the state-of-the-art unpaired learning method ADN for processing different levels of metal artifacts. On the other hand, the proposed LDM constraint is only required in the off-line training process. When the trained networks are used for inference, LDM-ADN and LDM-AND-Sup take the same amount of time as ADN and AND-Sup, because all of them use the same encoder and decoder, i.e., $E_{I^a}^c\to G_I$ in Fig. 3, to process testing images without extra computation burden. All above results demonstrate the effectiveness of the proposed LDM-DN algorithm.

Fig. 4.

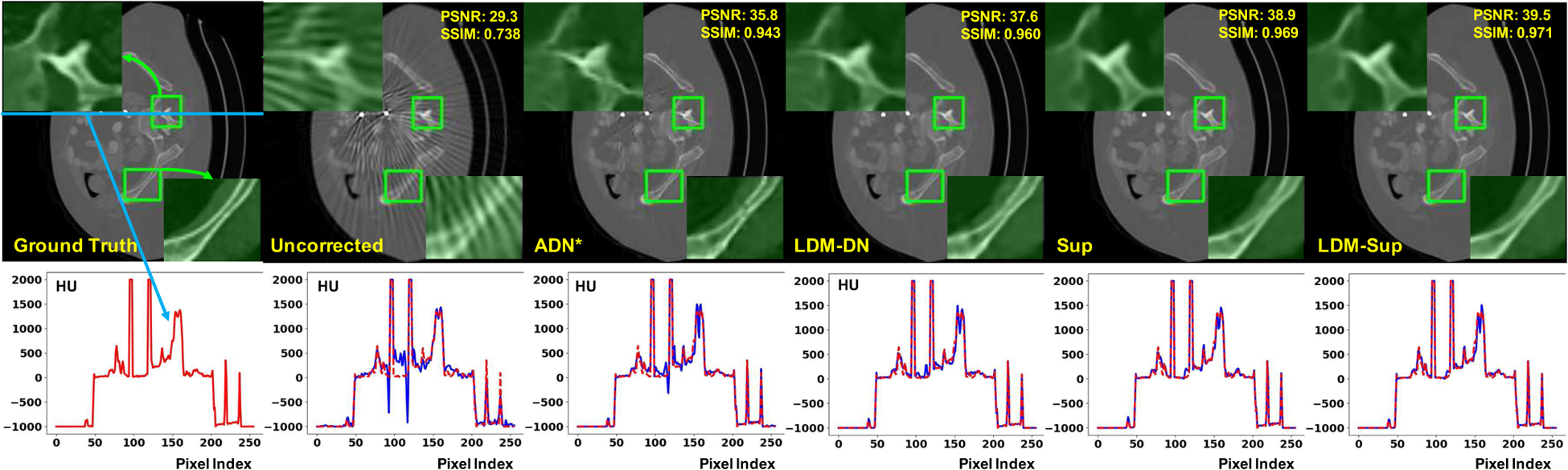
Visual comparison of our methods with both paired and unpaired learning methods. The metal objects are inserted back by thresholding. The first row gives the numerical evaluation of the sample image and presents two ROI regions for comparison. The second row inspects the detailed difference of image values from the ground-truth (red line) and the predicted/raw images.

Fig. 5.

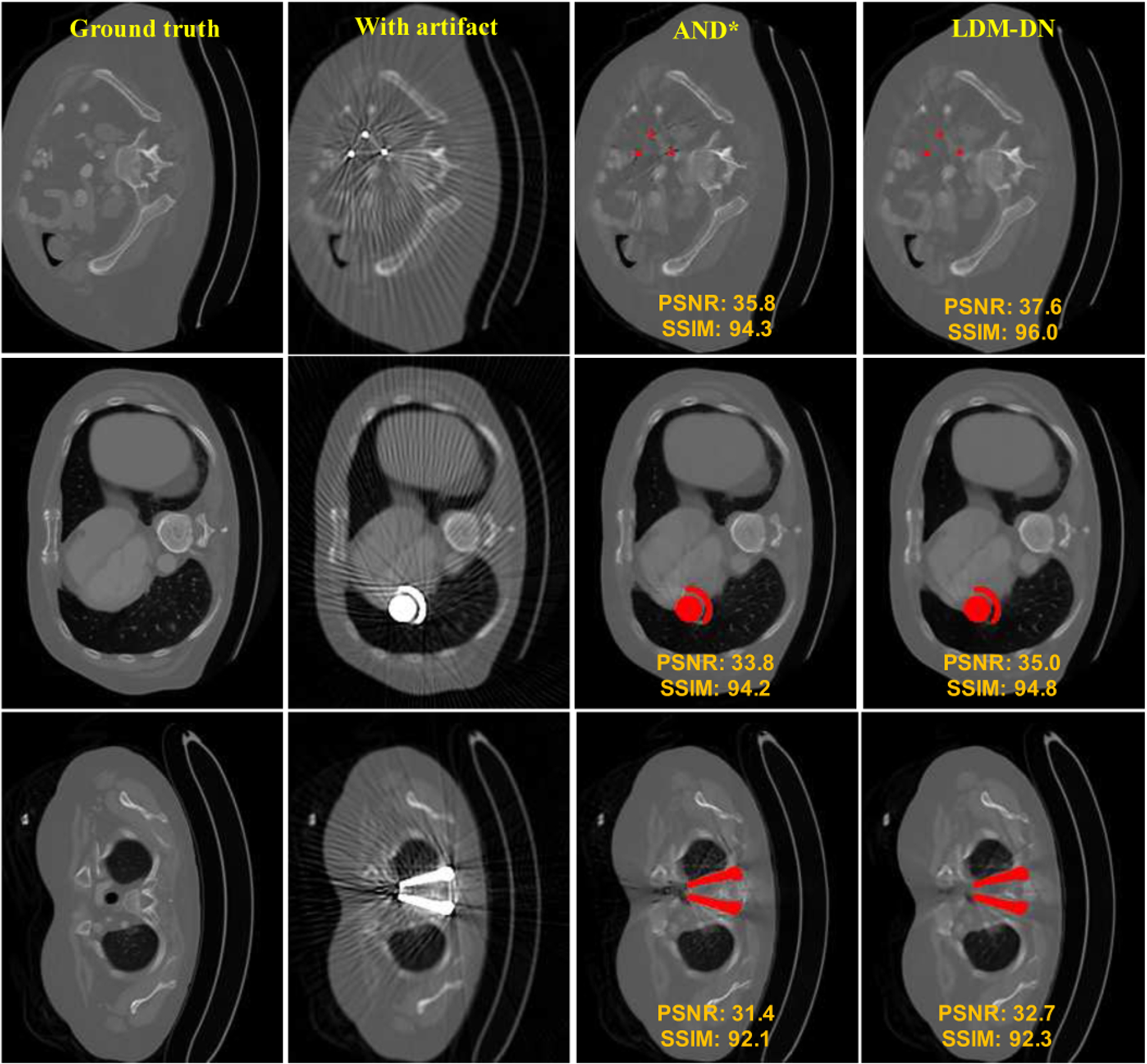
More visual comparison between LDM-DN and ADN. The region of metal objects are covered with red masks.

D. Results on clinical dataset

In this subsection, we evaluated the proposed networks on the clinical dataset. As there are no ground truth images for evaluating the performance of the models, here we can only show the visual results of three examples in Fig. 6. The qualitative results were compared in two aspects. First, the artifact-affected regions should be recovered as much as possible. Second, the structures that are not affected by metal artifacts should be preserved as much as possible. In Fig. 6, red and blue boxes are used to emphasize the artifact-affected regions, and the green boxes are to emphasize the artifact-free structures. We see the superiority of the proposed LDM-DN algorithm in preserving artifact-free contents (the green boxes for LDM-DN vs. ADN* especially in the first and third cases) and recovering artifact-affected regions (the blue and red boxes for LDM-DN vs. ADN* especically in the second and third cases). We also evaluated the performance of the model trained with synthesized images on the same dataset in a supervised learning manner. As analyzed in Section IV-C, the results of paired learning are better than those unpaired learning counterparts on the synthesized dataset. However, the results in Fig. 6 indicate that the performance of Sup is definitely worse than that of the unpaired learning model for the clinical dataset, as the synthesized data does not reflect the real conditions. This is consistent with the observation in [17]. However, although the performance of Sup is degraded, it still shows some merits over the unpaired learning methods, such as some structures are sharper (green boxes of Sup vs. ADN* and LDM-DN) and some regions are better (the blue boxes for Sup vs. ADN* and LDM-DN in the second case). Combining ADN and Sup leads to an over-correction, where some structures are overly brighter (the green boxes for AND-Sup vs. others) and some regions are overly dark (the blue boxes for ADN-Sup vs. others). We attribute these results to that Sup tends to keep and sharpen the edges and simultaneously ADN is enforcing the structures to look real by enlarging the ‘black holes’ especially when the artifact-affected regions are relative large. Here we propose to combine all merits of unpaired learning, paired learning and LDM through a hybrid learning scheme. As the results of LDM-DN-Sup shown in Fig. 6, it can inherit all good points as analyzed above. Particularly, compared with ADN-Sup, LDM in LDM-DN-Sup constrains that the structurally similar patches, especially the adjacent patches, to be coherent without dramatic changes to become too dark or too bright, so that the ‘black holes’ generated by ADN-Sup can be avoided. The above results on the clinical dataset demonstrate the effectiveness of LDM and the superiority of the hybrid training scheme.

Fig. 6.

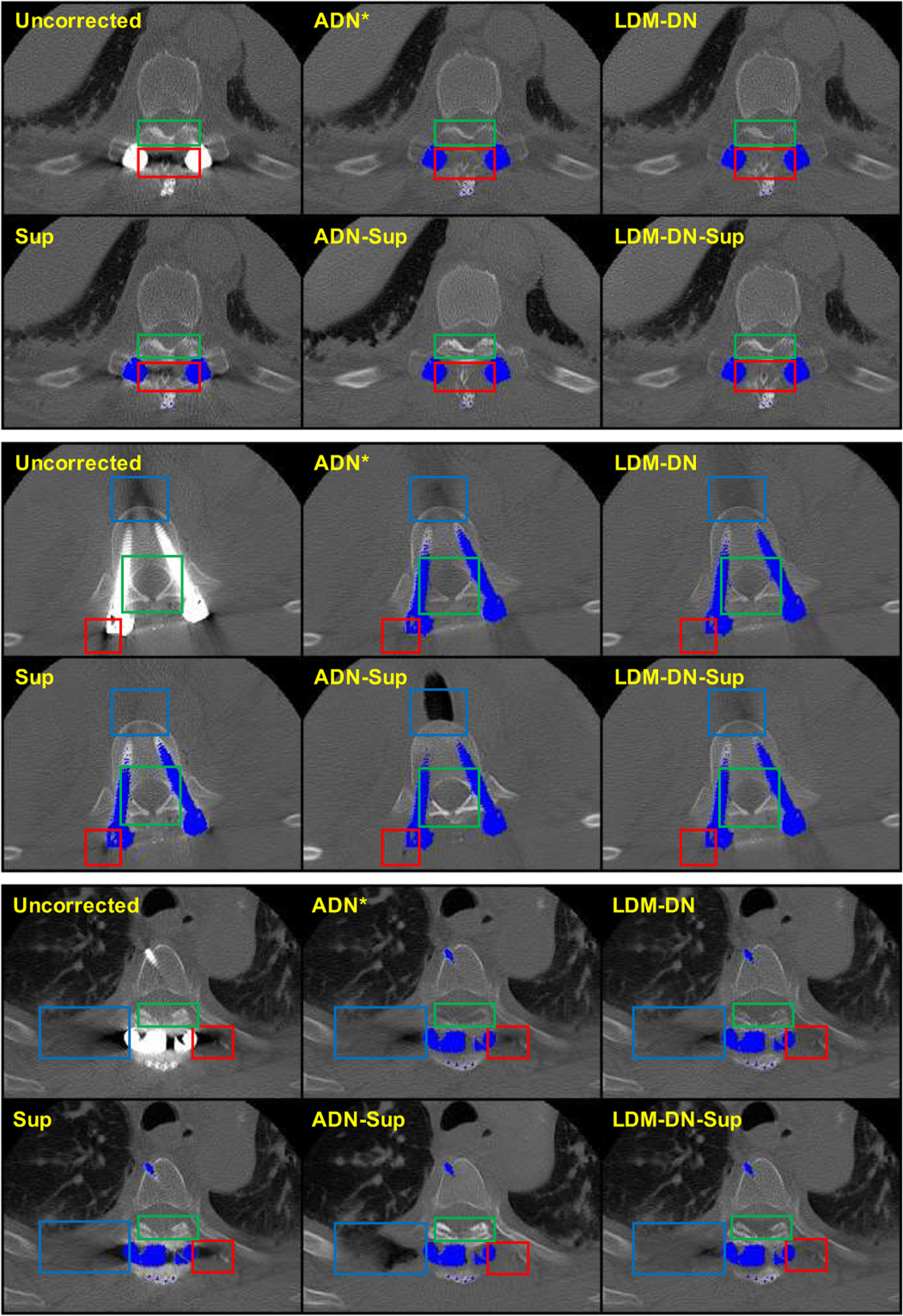
Clinical results from different variants. The region of metal objects are covered with blue masks. Three sample images are selected for comparison. For each sample, different boxes focus on different regions and the detailed comparison results are described in the Sub-section IV-D.

V. Discussion and Conclusion

In this study, we used the CT images under a large HU window for training and testing, which is consistent with the settings in [17]. However, in a recent study [47] we found that if the metal artifact reduction network is trained with images under a large window, it is difficult to produce good results when images are analyzed in a small window. Furthermore, we proposed a multi-window network in [47] to solve this problem. This multi-window network can be incorporated into the LDM-DN framework to improve the MAR performance in multi-window settings. On the other hand, most MAR methods were evaluated with not only image quality metrics but also visual inspection. These quantitative metrics are useful to evaluate and compare the effectiveness among different MAR methods, such as for radiation therapy and proton therapy planning [48], in which HU accuracy and structural fidelity are clinically important. Nevertheless, not all textural information can be fully reflected, and PSNR and SSIM are not strongly correlated to diagnostic performance. Therefore, the effectiveness of various MAR methods should be studied further in an application-specific fashion.

We have proposed an LDM constrained disentanglement network for MAR. Specifically, we have designed a LDM-DN learning algorithm to simultaneously optimize the ADN losses of the deep neural networks and constrain the recovered images to have a low-dimensional patch manifold representation. The LDM-DN algorithm can effectively help preserve and recover structural details in CT images. Finally, we have designed a hybrid optimization scheme to combine strongly- and weakly-supervised learning via our LDM-DN optimization algorithm for integrating paired synthetic data and unpaired clinical data. The experimental results on synthesized and clinical datasets have clearly demonstrated the superiority of the proposed method over the competing methods. At this stage, neither the ADN method nor our proposed method LDM-DN could be perfect but we need to keep improving CT metal artifact reduction results step by step. LDM-DN serves as such a step has a clear potential to boost the performance of various CT MAR methods.