Performance of the StaphGold ELISA test in determining subclinical Staphylococcus aureus infections in dairy cows using a Gaussian mixture model

Abstract

Background

A novel ELISA test has been developed to detect antigen‐specific IgG in early and late lactation cows in New Zealand.

Objectives

This study was to evaluate the discriminatory ability of the ELISA based on the detection of S. aureus‐specific IgG as a screening test.

Methods

The ELISA was used for the composite milk samples taken during routine herd testing in 2018–2019 milking season in New Zealand. In the absence of a gold standard test, the diagnostic specificity and sensitivity was estimated using a Gaussian mixture model.

Results

The ELISA test had a high accuracy (AUC = 0.98) to detect antigen‐specific IgG in early and late lactation cows with high somatic cell count due to either subsequent to or contemporaneous with the S. aureus invasion. Using an S/P ratio = 0.3 as the cut‐off value, the ELISA test has sensitivity of 0.9 and specificity of 0.95, while the sensitivity increased to 0.94 at a cost of a decreased specificity of 0.9 at a lower cut‐off value 0.26.

Conclusions

The integration of the ELISA test as a screening tool into specific control programs may be useful to reduce the spread of S. aureus infections, to aid with treatment decisions, and to establish a correct milking order.

A novel ELISA based on S. aureus‐specific IgG was thus developed and evaluated using composite milk samples taken during routine herd testing in 2018 – 2019 milking season in New Zealand. In the absence of a gold standard test, the transformed ELISA sample / positive ratio was modelled using a Gaussian mixture model. This analysis found that the ELISA had a high diagnostic accuracy for detecting antigen‐specific IgG in early and late lactation cows with high somatic cell count due to either subsequent to or contemporaneous with the presence of S. aureus. This ELISA has the potential to be a screening tool for helping farmers make a prompt and effective management decisions and thereby reduce S. aureus infection in their herds.

1. INTRODUCTION

Infections of the mammary gland with Staphylococcus aureus are a common problem in dairy herds worldwide (Levison et al., 2016; Liu et al., 2017; Taponen et al., 2017). In many countries S. aureus is the main cause of subclinical mastitis, high somatic cell counts (SCC) and reduced milk production and quality (Hoekstra et al., 2020). The infection cycle is maintained by chronically infected animals which represent the main reservoir of S. aureus in herds and the main source of infection for other cows (Rainard et al., 2018). Control of S. aureus is limited by the ineffectiveness of therapeutic approaches, especially in lactating cows (Barkema et al., 2006). Another issue limiting control of S. aureus is the difficulty of identifying all infected cattle, as if infected cattle are missed they can continue to spread infection within the herd (Rainard et al., 2018).

Diagnosis of persistent or subclinical infections with S. aureus can be performed using tests that are based on direct pathogen detection in milk such as bacterial culture or PCR. Bacterial culture of milk has a low sensitivity due to S. aureus having an intermittent or cyclical pattern of shedding of (Sears et al., 1990). Thus, to reach a sensitivity of 94%–99%, two or three consecutive samples are required, which significantly increases the cost of diagnosis (Godden et al., 2002). PCR testing for S. aureus has a higher test sensitivity than bacterial culture (Mahmmod et al., 2013), but its sensitivity is still affected by the shedding pattern of S. aureus. In addition, using PCR requires appreciable investment in equipment and is generally more costly per sample than bacteriology. Thus, Rainard et al. (2018) identified the development of an alternative fast, cost‐efficient and accurate tools for early detection of S. aureus as a high research priority.

A potential alternative test to bacterial culture and PCR is testing for antibodies. In contrast to direct pathogen detection tests, antibody tests are less affected by irregular shedding as antibodies persist even if bacteria are not present in the milk (Fabres‐Klein et al., 2014). Additionally, antibody ELISA tests are rapid and relatively cheap (Fabres‐Klein et al., 2014). The first commercial ELISA for S. aureus IgG antibody detection in milk (the Pro‐Staph antibody ELISA test) became available in the early 1990s (Poutrel & Sarradin, 1992), but had a variable performance. Grove and Jones (1992) reported a sensitivity of 0.9 and a specificity of 0.97 calculated based on 20 chronically infected and 77 uninfected cows. When a more rigorous case definition was formulated, that was, an animal was defined as S. aureus infected if bacteria growth was found in two of three consecutive milk samples, both sensitivity and specificity dropped dramatically to 0.69 and 0.61, respectively (Hicks et al., 1994). The product was later withdrawn from the market. More recently, Leitner et al. (2000) showed that there was a strong association between chronic S. aureus mammary gland infection and the resulting specific IgG response in milk which indicated that a specific S. aureus IgG ELISA could be a suitable diagnostic test for S. aureus infection.

The aim of this study was therefore to evaluate the discriminatory ability of a novel ELISA based on the detection of S. aureus‐specific IgG (StaphGold™ ELISA) as a screening test for detecting S. aureus in subclinical and chronic mastitis cases using milk samples collected from individual cows at herd tests. The aim of the analysis was to estimate the diagnostic specificity (DSp) and sensitivity (DSe) of the ELISA test and to estimate the effect of cut‐off value used for the Elisa on DSp and DSe

2. MATERIALS AND METHODS

2.1. Study design and samples

The study was carried out using composite milk samples (pooled samples from all four quarters) from 13 commercial dairy herds in the North Island, New Zealand. Samples from 11 herds (899 individual cows) were collected at the beginning of the 2018–2019 milking season. In addition, at the end of the milking season, a further 1029 samples were collected from seven herds (of which five had been sampled at the beginning of the season). All tested samples were from cows considered by the farmer to have high somatic cell counts. Test samples (composite milk samples) were collected during routine herd testing and bronopol preservative added at the time of collection. Approximately 1 ml of a subsample was stored frozen at –20^оC in deep‐well plates until assay.

2.2. ELISA assay

The ELISA test was conducted according to the KORU StaphGold ELISA protocol (Koru Diagnostics Ltd, New Zealand). Test reagents that were included in the kit were used throughout the experiments. Samples were allowed to thaw out at 4°C to enable separation of fat from milk by gravity. A subsample of 100 μl was then removed from underneath the fat layer and diluted in 900 μl of sample diluent using a 96‐well plate format. Plates and reagents were allowed to warm up to room temperature before the addition of thoroughly mixed 1:10 diluted test and re‐constituted three positive and three negative control samples, followed by incubation at 37°C for 1 h. Plates were then washed 3× in PBS‐Tween 20 and 3x in PBS using an automated plate washer (ELx405 Select; BioTek Instruments USA). Plates were then incubated at 37°C for 1 h after the addition of a 1:100 dilution of conjugate, rewashed as above and then developed for 15 min using Tetramethylbenzididne (B) as a substrate. Plates were then read with an automated plate reader (SPECTRAmax PLUS; Molecular Devices, USA) at A450 and A650 nm and data were expressed as OD (450–650 nm). Each plate was tested against a set of acceptance criteria [mean OD values of negative control samples (NC) < 0.2; mean OD values for positive control (PC) samples > 0.5; ratio of PC/NC > 4, sample diluent < 0.03]. The mean values for NC and PC were used to calculate a Sample/Positive (S/P) ratio as follows:

$$S/Pratio=\frac{SampleA\left(450-650\right)-MeanNC}{MeanPC-MeanNC}\times 100$$

2.3. Statistical analysis

A finite mixture model, often referred to as a latent class model, was applied to this dataset as the true infection status of the sampled cows was unobserved. The results of the novel ELISA contained negative values, which precluded the use of many continuous distributions which have supports [0, +∞). While Gaussian mixture model can be adopted in this study since this type of models (1) allows negative values and (2) has been previously used successfully in analysing veterinary diagnostic test outcome data due to its interpretability in the context of the biological science (Giles et al., 2018; Jones et al., 2009). A histogram of the ELISA S/P ratio of all data points was then plotted to examine its distribution. To obtain a mixture of two unimodal symmetrical distributions as an approximation of a Gaussian mixture, the original ELISA S/P ratio ($y$) was transformed to its natural log (abbreviated to ‘log’ throughout the text) scale ($x$), that is, $x=\log (y+c),$ where $c$ is a constant that ensures that all input values for the above function were > 0. To decide the ‘best’ value $c$ in the log transformation, a list of values was set (from 0.1 to 0.5 by 0.05 increment) for $c$, and an expectation–maximisation (EM) algorithm was applied to fit a Gaussian mixture model to the transformed ELISA S/P ratio ($x$) as described by Thompson et al. (1998). The log‐likelihood was then computed on the original ELISA S/P ratio ($y$) using the change of variable technique. If $X_i$ is the underlying random variable of the transformed ELISA S/P ratio for a cow and $Y_i$ is the underlying random variable of the original ELISA S/P ratio, then $Y_i=e^{X_i}-c$. Therefore, the probability density function for $Y_i$ (or likelihood function if viewed as a function of $c)$ given the original ELISA S/P ratio $y_i$ is:

$$f_{Y\left(y_i\right)}=f_X\left(\log \left(y_i+c\right)\right)\left|\frac{1}{y_i+c}\right|,$$

where $f_X()$ is the probability density function of $X$, in this case the Gaussian mixture model. The log‐likelihood of the original ELISA S/P ratio is then the natural logarithm of the joint probability density evaluated at data vector $y$ and regarded as a function of $c$. The EM algorithm was implemented in R and provided in the Supplementary Material 1. To assess whether the transformed ELISA S/P ratio approximated Gaussian mixture model sufficiently, the histogram of the transformed data was compared with the distribution of the same data with the model‐based estimates.

After the log transformation, the transformed S/P ratio for the ith animal was denoted as $X_i$. Conditional on the unobserved true S. aureus infection status $S_i$ (the latent class), the conditional distribution of $X_i$ was modelled using a normal distribution. Precisely, the latent class ‘infection’ means the elevated somatic cell count due to the presence and persistence of S. aureus sufficiently long to produce a detectable antigen specific IgG. $S_i$ was a Bernoulli random variable with the parameter $p_i\equiv Pr(S_i=1)$, namely, the probability of an animal being infected with S. aureus. Therefore, we have:

$$S_i\sim \mathrm{Bern}\left(p_i\right),$$

$$X_i|S_i=1\sim N\left({\mu }_2,{\sigma }_2^2\right),$$

$$X_i|S_i=0\sim N\left({\mu }_1,{\sigma }_1^2\right),$$

where the subscripts ‘2’ and ‘1’ indicate the S. aureus‐infected and non‐infected subgroups, respectively. In this study, the constraint that ${\mu }_2>{\mu }_1$ (i.e. mean S/P ratio was higher in infected animals than non‐infected ones) was placed to ensure that the model was identifiable (Choi et al., 2006).

If a random sample is obtained, then $p_i=p$ (the overall prevalence). As there were multiple herds enrolled in the study, then $p_i=p_{j(i)},$ where j is the herd for animal i. This creates a random effect distribution for $p_j$ which can be modelled using a logit‐normal distribution (Yang et al., 2017) such that $\mathrm{Logit}(p_{j(i)})\sim N({\beta }_0,{\sigma }_{herd}^2)$. This random effect treats the same herd tested at the different time points as two separate units, as the time gap between the two herd tests was sufficient for the prevalence of a herd to change. This also applied to repeated measures on individual cows (i.e. if one cow had been tested twice) – they did not necessarily have the same infection status on each occasion. This led to 18 independent ‘herds’.

The proposed analytical model was then fit to the transformed ELISA S/P ratio. Due to the involvement of the random effect, the parameter estimation process was much more complex than a Gaussian mixture model on a random sample. We hence implemented the model using JAGS (Plummer, 2003) which has a built‐in Markov chain Monte Carlo (MCMC) simulation, which, in practice, reduces the complexity of the parameter estimation process for a user, as one neither needs to find out the full conditional distributions mathematically nor implements the algorithm manually. Diffuse prior distributions such as ${\mu }_1\sim N(-0.5,100)$, ${\mu }_2\sim N(0.5,100)$, $1/{\sigma }_k^2\sim \mathrm{\Gamma }(0.01,0.01)$ for $k=1,2$, $\mathrm{Sigmoid}({\beta }_0)\sim \mathrm{Beta}(5,5)$ and ${\sigma }_{herd}\sim \mathrm{U}(0,1)$ were used for the model parameters. Note, instead of placing a prior directly on ${\beta }_0$, a prior distribution was induced for the parameter by specifying a prior distribution for $\mathrm{Sigmoid}({\beta }_0)$ – the median herd prevalence (Yang et al., 2019).

Three MCMC chains of 20,000 iterations were used, after discarding 5000 iterations. Chain convergence was assessed using trace plots and Gelman and Rubin's convergence diagnostic (Gelman & Rubin, 1992). Data were re‐analysed with different prior distributions for all the parameters and the choice of priors was confirmed to have a minimal effect on results. The JAGS code is available in the Supplementary Material 2.

2.4. Predictive inference

According to a pre‐defined cut‐off point $d$, a cow is rated as positive if its ELISA S/P ratio > $d$, otherwise, the cow is considered negative. Thus, the Dse and DSp of the ELISA test were computed using the cumulative distribution function of the conditional distribution of the ELISA S/P ratio. Since a log transformation was applied to the ELISA S/P ratio, the computation was performed at log scale such that:

$$\mathrm{Ds}{\mathrm{e}}_{ELISA}\left[\log \left(d+c\right)\right]=1-F_2\left[\log \left(d+c\right)\right],$$

$$\mathrm{DS}{\mathrm{p}}_{ELISA}\left[\log \left(d+c\right)\right]=F_1\left[\log \left(d+c\right)\right],$$

where $F_k$()$,k=1,2$ is the cumulative distribution function for the transformed ELISA S/P ratio conditional on the S. aureus infection status of a cow. The set of sensitivity and 1‐specificity values were plotted to construct a receiver operating characteristic (ROC) curve. The area under the ROC curve (AUC) was then computed to quantify the quality of the ELISA test (Choi et al., 2006):

$$\mathrm{AUC}=\mathrm{\Phi }\left(\frac{{\mu }_2-{\mu }_1}{\sqrt{{\sigma }_2^2+{\sigma }_1^2}}\right),$$

where Φ is the cumulative distribution function of a standard normal random variable.

3. RESULTS

After excluding one cow with a missing ELISA test outcome, 1927 data points were retained for statistical analysis With the EM algorithm, the best value for $c$ was determined as 0.1. Figure 1 shows the histogram of the transformed ELISA S/P ratios as well as the density curve based on the model‐based estimates, confirming the data were properly transformed to meet the Gaussian mixture assumption. The ROC curve is shown in Figure 2.

FIGURE 1.

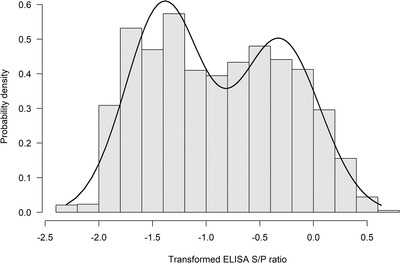
The transformed S/P ratios of KORU StaphGold ELISA for antibodies to S. aureus in milk sample collected from New Zealand dairy herds. A close approximation of a mixture of two normal distributions

FIGURE 2.

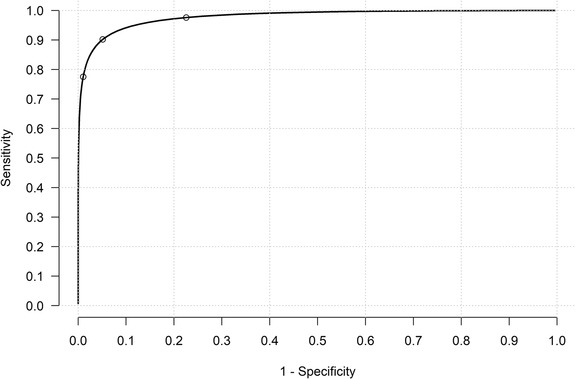
Model‐based receiver operating characteristic curve for results of KORU StaphGold ELISA for antibodies to S. aureus in milk sample collected from New Zealand dairy herds. The circles display the different cut‐off values at 0.2, 0.3 and 0.4 for the ELISA

The posterior distributions of the parameters using the proposed analytical model are summarised in Table 1. According to this analysis, the ELISA test had high diagnostic accuracy (AUC = 0.98) to detect antigen‐specific IgG in cows with high somatic cell count due to either subsequent to or contemporaneous with the presence of S. aureus. The sensitivities and specificities of the ELISA were computed at different cut‐off values from 0.1 to 0.5 by 0.01 increments. For cut‐offs in the range of 0.26–0.30, the ELISA test had high Dse and DSp (both > 0.9). If an S/P ratio of 0.3 was used as the cut‐off value, the Dse and DSp of the ELISA were 0.902 [95% probability interval (PI): 0.869–0.931] and 0.949 (95% PI: 0.925–0.968), respectively. Table 2 provides a more detailed analysis of the choices of candidate cut‐off values in the range of 0.2–0.45.

TABLE 1.

The posterior distributions of the parameters of the Gaussian mixture model summarised using posterior means, 95% probability intervals (PI) and standard deviations (SD) along with time‐series Monte Carlo standard error (MC error)

		95% Probability interval
Parameter	Mean	Lower limit	Upper limit	SD	MC error
${\mu }_1$	–1.449	–1.485	–1.412	0.0184	0.0003
${\mu }_2$	–0.381	–0.427	–0.336	0.0233	0.0004
${\sigma }_1$	0.325	0.302	0.350	0.0123	0.0002
${\sigma }_2$	0.413	0.385	0.444	0.0152	0.0002
${\beta }_0$	0.173	‐0.284	0.631	0.2331	0.0071
$\mathrm{Sigmoid}({\beta }_0)$	0.543	0.430	0.653	0.0571	0.0017
${\sigma }_{herd}$	0.949	0.835	0.998	0.0445	0.0004

${\mu }_k$ for $k=1,2$, mean of the transformed ELISA S/P ratio in non‐infected or infected group.

${\sigma }_k$ for $k=1,2$, standard deviation of the transformed ELISA S/P ratio in non‐infected or infected group.

${\beta }_0$, mean of the logit‐normal random effect.

${\sigma }_{herd}$, standard deviation of the logit‐normal random effect.

TABLE 2.

Model‐based estimates of the diagnostic sensitivities and specificities of KORU StaphGold ELISA given a range of cut‐off values

		95% Probability interval			95% Probability interval
Cut‐offs	Sensitivity	Lower limit	Upper limit	Specificity	Lower limit	Upper limit
0.2	0.976	0.962	0.987	0.774	0.728	0.819
0.21	0.972	0.955	0.984	0.803	0.759	0.845
0.22	0.966	0.948	0.981	0.829	0.787	0.869
0.23	0.960	0.940	0.976	0.852	0.812	0.889
0.24	0.954	0.932	0.972	0.872	0.834	0.907
0.25	0.947	0.923	0.967	0.890	0.854	0.922
0.26	0.939	0.913	0.961	0.905	0.872	0.934
0.27	0.931	0.903	0.954	0.918	0.888	0.945
0.28	0.922	0.892	0.947	0.930	0.902	0.954
0.29	0.912	0.881	0.940	0.940	0.914	0.962
0.3	0.902	0.869	0.931	0.949	0.925	0.968
0.31	0.891	0.856	0.923	0.956	0.935	0.974
0.32	0.880	0.844	0.913	0.963	0.943	0.978
0.33	0.869	0.830	0.903	0.968	0.950	0.982
0.34	0.856	0.817	0.893	0.973	0.957	0.985
0.35	0.844	0.803	0.882	0.977	0.962	0.988
0.36	0.831	0.789	0.870	0.980	0.967	0.990
0.37	0.817	0.774	0.858	0.983	0.972	0.992
0.38	0.804	0.759	0.845	0.986	0.975	0.993
0.39	0.790	0.745	0.832	0.988	0.978	0.994
0.4	0.775	0.729	0.819	0.990	0.981	0.995
0.41	0.761	0.714	0.805	0.991	0.984	0.996
0.42	0.746	0.699	0.791	0.992	0.986	0.997
0.43	0.731	0.683	0.777	0.994	0.988	0.997
0.44	0.716	0.668	0.762	0.994	0.989	0.998
0.45	0.701	0.653	0.748	0.995	0.991	0.998

Figure 3 presents the model predicted distribution of the untransformed ELISA S/P ratio in both S. aureus‐infected and non‐infected subgroups. From this figure it is clear, although very unlikely, that non‐infected cows can have a high S/P ratio.

FIGURE 3.

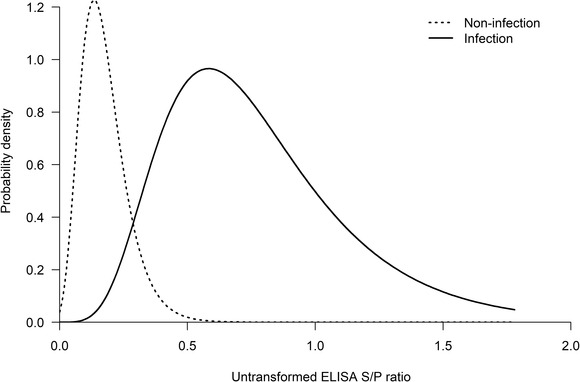
Predicted distribution of the untransformed KORU StaphGold ELISA S/P ratios in both S. aureus‐infected and non‐infected subgroups

4. DISCUSSION

This study evaluated the diagnostic performance of a novel ELISA test (StaphGold) for detecting S. aureus‐specific IgG in composite milk samples taken during herd testing. The ELISA test had a high accuracy (AUC = 0.98) for detecting antigen‐specific IgG due to the presence and persistence of S. aureus in cows causing elevated somatic cell counts. Using an S/P ratio = 0.3 as the cut‐off value, the ELISA test correctly classified approximately 90% of such cows and 95% of cows that do not belong to the latent membership, respectively. However, we have also presented Dse and DSp for cut‐off values between 0.2 and 0.45. This means that rather than the cut‐off value being an intrinsic property of a diagnostic test, the choice of cut‐off can be based on the testing rationale and the epidemiological situation in the targeted population (Greiner et al., 2000). For example, in a high prevalence herd where infected animals make a significant contribution to disease transmission, false‐negative animals are particularly undesirable. In that context, lower cut‐off values that maximise diagnostic sensitivity will be more ‘optimal’. In contrast, if infection is rare and the cost of a false positive high, choosing a higher cut‐off value will be more ‘optimal’. Thus providing the data for a range of S/P means that the cut‐off value can be individualised to meet the requirements for each test population

The test population included only early and late lactation cattle. These are crucial screening times as cows that are identified as S. aureus positive in early lactation are likely to have had an infection at drying‐off, thus the infection has persisted during the dry period even if the animals have been treated with antibiotics. The use of antibody tests at this time is supported by Fox and Adams (2000) who found that antibody titres remained elevated in cows in which the S. aureus infection persisted during the dry period, whereas, when intramammary infections were cured during the dry period, only a short transient increase was seen in antibody titres during the periparturient period which then quickly declined below threshold levels. The implementation of a screening test for cows with an elevated SCC before dry‐off may allow the user to make aid with informed treatment decisions.

In the long term, control programs can only be successful when adequate treatment decisions are integrated into a wider control program that includes use of dry cow antibiotics, milking hygiene and culling of cows that are not responsive to treatment (Sartori et al., 2018). However, any control program relies heavily on an accurate, high throughput, easy‐to‐use and affordable S. aureus identification procedure. Such demands may be met by utilising existing sampling procedures and integrating such tests into routine milk testing regimes such as those offered by herd testing or milk recording companies. The ELISA evaluated in this study would seem to fit that demand as it is designed for high throughput use with composite milk samples. It remains to be seen how the test performs in problem herds where basic reproduction number (R ₀) is high, and recent infections can be expected. In such a herd, ELISA test results may be a mixture of three distributions (non‐infected, recently infected, persistently infected). Such a distribution mixture has to our knowledge not been studied in veterinary diagnostic science. Previous latent class analyses have assumed two latent classes (infected vs. non‐infected) regardless of whether a continuous or categorised ELISA outcome was used (Arif et al., 2018; Giles et al., 2018). Further research is required to investigate the use of this ELISA in that circumstance.

From a technical point of view, the analytical model used in this study is very similar to the latent class models with discrete diagnostic outcomes summarised by Johnson et al. (2019). Models based on both continuous and discrete outcomes are used to study the latent infection pattern within an animal population using the observed test outcomes. Although many studies have evaluated the performances of ELISA tests by first dichotomising the original serology scores based on cut‐off values (Haley et al., 2011; Nielsen et al., 2015), the statistical model that uses the continuous test outcomes is also well‐established (Choi et al., 2006; Steinhauser et al., 2016). Compared to latent class analysis with dichotomised test outcomes, using methods with continuous test outcomes avoids the tedious process of applying the same model to different datasets to identify specificity and sensitivity for a range of cut‐off values. If continuous data are used, once the model parameters are estimated, all of the relevant specificities and sensitivities can be calculated as part of a single analysis. In addition, the use of the continuous outcome allows sensitivity and specificity to be estimate with only a single test, which is not possible if a dichotomous test outcome is used (Branscum et al., 2005). Nevertheless, it would be useful to assess this ELISA further by comparing results to other tests for S. aureus as this will refine our definition of the latent class. With the aid of bacteriological methods, the refined latent class could be the presence of S. aureus for a sufficient long period to produce a detectable systematic immune response and to contribute shedding though not fully detectable due to the irregular shedding pattern.

5. CONCLUSIONS

Early diagnosis of subclinical or persistent S. aureus infection in dairy herds with a comparatively rapid, cost‐effective and accurate methods is a critical part of any control strategy. A novel ELISA based on S. aureus‐specific IgG was thus developed and evaluated using composite milk samples taken during routine herd testing. This analysis found that the ELISA had a high diagnostic accuracy (AUC = 0.98) to detect antigen‐specific IgG in cows with high somatic cell count due to either subsequent to or contemporaneous with the presence of S. aureus, with both sensitivity and specificity > 0.9 at the cut‐off range from 0.26 (sensitivity = 0.94, specificity = 0.91) to 0.3 (sensitivity = 0.9, specificity = 0.95). This ELISA has the potential to be a screening tool for helping farmers make a prompt and effective management decisions and thereby reduce S. aureus infection in their herds.

CONFLICT OF INTEREST

The authors declare that they have no conflict of interest.

ETHICS STATEMENT

The authors confirm that the ethical policies of the journal, as noted on the journal's author guidelines page, have been adhered to. No ethical approval was required as no animal experiments were used for this study. Milk samples were obtained as part of a routine herd testing program to which farmers subscribed.

AUTHOR CONTRIBUTIONS

Modelling and data analysis: DAY. Writing—original draft preparation: DAY. Writing—review and editing: RAL. All authors have read and agreed to the published version of the manuscript.

Supporting information

Supporting Information

Yang, D. A. , & Laven, R. A. (2022). Performance of the StaphGold ELISA test in determining subclinical Staphylococcus aureus infections in dairy cows using a Gaussian mixture model. Veterinary Medicine and Science, 8, 1632–1639. 10.1002/vms3.785

DATA AVAILABILITY STATEMENT

Data are available from the corresponding author upon reasonable request.