In‐Situ Electronegativity and the Bridging of Chemical Bonding Concepts

Abstract

One challenge in chemistry is the plethora of often disparate models for rationalizing the electronic structure of molecules. Chemical concepts abound, but their connections are often frail. This work describes a quantum‐mechanical framework that enables a combination of ideas from three approaches common for the analysis of chemical bonds: energy decomposition analysis (EDA), quantum chemical topology, and molecular orbital (MO) theory. The glue to our theory is the electron energy density, interpretable as one part electrons and one part electronegativity. We present a three‐dimensional analysis of the electron energy density and use it to redefine what constitutes an atom in a molecule. Definitions of atomic partial charge and electronegativity follow in a way that connects these concepts to the total energy of a molecule. The formation of polar bonds is predicted to cause inversion of electronegativity, and a new perspective of bonding in diborane and guanine−cytosine base‐pairing is presented. The electronegativity of atoms inside molecules is shown to be predictive of pK _a.

The orbital and the density, hand in hand: Three perspectives for conceptualizing chemical bonding are connected here within one framework: experimental quantum chemistry. A new definition for atoms inside molecules leads to quantification of atomic energy, partial charge, and in‐situ electronegativity. Predictions follow, of pK _a, of electronegativity inversions in polar bonds, and of hydrogen stabilization‐driven electron‐deficient bonding in diborane.

Introduction

The purpose of this work is to demonstrate a complementarity of perspectives for analyzing electronic structure or chemical bonding. One aim is to practically combine the predictive utility of molecular orbital (MO) theory[ ¹ , ² ] with successful descriptive topological analyses of electron density, such as the quantum theory of atoms in molecules (QTAIM). ^[3] We do so by building upon an energy decomposition analysis (EDA) that we call experimental quantum chemistry (EQC).[ ⁴ , ⁵ ] Through a series of examples, we will gradually show how this combination of perspectives – MO, quantum chemical topology and EDA – enables the definition of energies, partial charges, and electronegativity of atoms inside molecules. Several connections of these theories and concepts are known,[ ⁶ , ⁷ , ⁸ , ⁹ ] but not between all. Here we attempt to close some of these gaps and build explicit connections within one framework.

Electronegativity and atomic charge are cornerstone concepts for rationalizing trends in charge transfer, bond polarity, bond strength, reactivity, and various chemical properties.[ ¹⁰ , ¹¹ , ¹² , ¹³ ] Electronegativity enables to predict where electrons may migrate upon formation of bonds, that is, bond polarity. Atomic charge, on the other hand, quantifies such charge distributions, or polarities, post facto. Concepts of formal charge and oxidation number are similarly essential parts of the grammar of chemical language. ^[14] There exists a plethora of methods that can derive partial charges from, for example, orbitals,[ ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ ] electron densities,[ ³ , ¹⁹ , ²⁰ ] electrostatic potentials,[ ²¹ , ²² ] and experimental data.[ ²³ , ²⁴ , ²⁵ ] Oxidation states can also be estimated by various theoretical and experimental means.[ ²⁶ , ²⁷ ]

Electronegativity can similarly be defined and quantified in many ways (e. g., refs. [28]–[39]). Agreeing on a definition of electronegativity has at times been a contentious issue in chemistry. For example, depending on whom you ask, electronegativity might relate to properties of atoms in molecules, or of isolated atoms. ^[10] Whereas there exists many scales of atomic electronegativity, few methods are readily available for quantifying the notion for atoms inside of molecules and materials. Some have approached this problem by defining or relating electronegativity to the radii of atoms in different ways.[ ⁴⁰ , ⁴¹ ] Others have relied on topological analyses of electron densities,[ ⁴² , ⁴³ , ⁴⁴ ] or various thermochemical and spectroscopical data.[ ⁴⁵ , ⁴⁶ ] Electronegativities of bonded atoms have also been evaluated from orbital analyses[ ⁴⁷ , ⁴⁸ ] and using various correction schemes to existing electronegativity scales.[ ⁴⁹ , ⁵⁰ ] Some approaches rely on electronegativity being defined as the chemical potential, as suggested by Iczkowski and Margrave. ^[34] The latter definition agree with the postulate of Sanderson, which states that all bonded atoms should share the same electronegativity,[ ³⁵ , ⁵¹ , ⁵² ] with some claimed exceptions.[ ⁵³ , ⁵⁴ , ⁵⁵ ]

Electronegativity as an average electron binding energy

Following previous work, ^[38] we attribute the electronegativity concept to an average electron binding energy, $\bar{\chi }$ . This definition is related to that of Allen ^[56] and has allowed for the construction of a ground state (T→0 K) scale of electronegativity from averages of ionization potentials. ^[38] The change in the average electron binding energy, $\Delta \bar{\chi }$ , calculated over bond formation processes has been shown to be a potent indicator for covalent and ionic character in diatomic molecules. ^[5] Computation of $\Delta \bar{\chi }$ has also brought insight into the variability of electronegativity as a function of pressure.[ ⁵⁷ , ⁵⁸ ] One expression for the average energy of electrons at a point r in a molecule is:

$${\displaystyle \bar{\chi }\left(\mathbf{r}\right)=-\frac{1}{\rho \left(\mathbf{r}\right)}\left({\tau }_L\left(\mathbf{r}\right)+\upsilon \left(\mathbf{r}\right)\rho \left(\mathbf{r}\right)+2\int \frac{P\left(\mathbf{r},{\mathbf{r}}_2\right)}{\left|\mathbf{r}-{\mathbf{r}}_2\right|}\mathrm{d}{\mathbf{r}}_2\right)}$$ (1)

This form reflects our goal of providing a spatially resolved mapping inside molecules. In Equation (1), ${\tau }_L\left(\mathbf{r}\right)$ is the local kinetic energy, expressed in terms of the Laplacian of the one‐electron reduced density matrix. The kinetic energy density is not uniquely defined ^[59] but a justification for the form we use can be found in work by Bader. ^[60] $\rho \left(\mathbf{r}\right)$ is the electron density, $\upsilon \left(\mathbf{r}\right)$ is the external potential, and $P(\mathbf{r},{\mathbf{r}}_2)$ is the diagonal of the two‐electron reduced density matrix.[ ⁵ , ⁶¹ ] One way to approximate $\bar{\chi }\left(\mathbf{r}\right)$ with methods such as Hartree–Fock or density functional theory (DFT), is as an average energy of all occupied molecular orbitals,

$${\displaystyle \bar{\chi }\left(\mathbf{r}\right)\approx -\frac{{\sum }_i{ϵ}_i{\rho }_i\left(\mathbf{r}\right)}{\rho \left(\mathbf{r}\right)}}$$ (2)

where ${ϵ}_i$ and ${\rho }_i\left(\mathbf{r}\right)$ are the eigenvalue and the electron density associated to the $i$ ^th occupied orbital, respectively, and $\rho \left(\mathbf{r}\right)$ is the total electron density. In this work, we will (fully realizing the inherent approximations) estimate $\bar{\chi }\left(\mathbf{r}\right)$ within a Kohn–Sham (KS) DFT formalism, where ${\rho }_i\left(\mathbf{r}\right)$ in Equation (2) is the electron density associated to the $i$ ^th occupied KS orbital. Note that the sign convention used for $\bar{\chi }$ , in Equations (1) and (2) vary in some past work[ ⁴ , ⁵ ] depending on if $\bar{\chi }$ is defined from energy levels relative to vacuum, which is negative for most bound systems, or, as in this work, as an average binding energy, which is positive by definition. Positive values of $\bar{\chi }$ connect more naturally to the notion of conventional electronegativity. The terms average electron binding energy and average orbital energy are used interchangeably in what follows, where the latter approximates the former.

We stress that Equation (2) is not presented for the first time here. $\bar{\chi }\left(\mathbf{r}\right)$ has been extensively studied with single reference methods, following Equation (2), at the surfaces of molecules by Politzer and co‐workers under a different name, the average local ionization energy$.$ ^[62] $\bar{\chi }\left(\mathbf{r}\right)$ has also been calculated by using multi‐reference calculations, following Equation (1), by Ryabinkin and Staroverov for a few atoms and molecules, who refer to it as the average local electron energy. ^[61] The topology of $\bar{\chi }\left(\mathbf{r}\right)$ on molecular surfaces (usually defined as 0.001 e⋅bohr⁻³ contours) has been successfully correlated to molecular reactivity and properties like Hammett constants, ^[63] electrophilic reactive sites, ^[64] and, importantly, electronegativity.[ ¹³ , ⁶² ] The focus of this work is different. The distribution of $\bar{\chi }\left(\mathbf{r}\right)$ is needed here for a topological partitioning of the space within molecules.

Electronegativity is one component of the electron energy density

Our focus on $\bar{\chi }\left(\mathbf{r}\right)$ is primarily motivated by an EDA that relates the average electron binding energy (or electronegativity) of Equation (1) to the total energy E of a system as:[ ⁴ , ⁵ ]

$${\displaystyle E=-\int \rho \left(\mathbf{r}\right)\bar{\chi }\left(\mathbf{r}\right)d\mathbf{r}-E_{ee}+V_{NN},}$$ (3)

where E _ee is the electron–electron repulsion energy and V _NN is the nuclear–nuclear repulsion energy. The V _NN and E _ee terms are both electrostatic in nature, and their changes often largely cancel each other in chemical transformations. The negative sign in front of the E _ee term accounts for the double‐counting of electron–electron interactions in the average electron binding energy $\bar{\chi }$ . Our preferred unit of measure for $\bar{\chi }\left(\mathbf{r}\right)$ , eV e⁻¹, allows for an interpretation of the spatially resolved average electron binding energy as a local potential.

We refer to Equation (3) as an EQC[ ⁴ , ⁵ ] energy decomposition, as it is possible to interchangeably evaluate each of its terms using quantum mechanical calculations as well as to approximate them (especially in a relative sense, over a transformation) from a combination of experimental measurements.[ ⁴ , ⁵ , ³⁸ ] Whereas we will demonstrate energy partitioning using the EQC‐EDA in a few examples, our focus is to use the framework itself to formalize a connection between the total energy and topologically defined atoms, energies, electronegativity and atomic charge. Utility of the individual energy terms of the EQC‐EDA for distinguishing bonds and predicting chemical properties is exemplified in several previous work.[ ⁴ , ⁵ , ³⁸ , ⁵⁷ , ⁵⁸ , ⁶⁵ , ⁶⁶ , ⁶⁷ ]

Ours is but one kind of EDA. There exists many other methods, each with its respective advantages (see, e. g., refs. [68]–[73]). EDA methods typically work by describing bonding in terms of a molecular wavefunction that in a first step is decomposed into a set of non‐interacting fragment reference states. The interaction of such reference states, often defined to take place at fixed molecular geometries, that is, where ΔV _NN would equal zero, subsequently allows for the quantification of energy terms interpretable as, for example, Pauli repulsion, electrostatics, dispersion interactions, and charge transfer. Our approach is different in that it is aimed at analyzing energies of processes that are, at least in principle, observable. For example, in this work we choose to study the physical processes of atomization of molecules as well as the dissociation of molecular complexes. Our choice of such physical reference states admittedly has various pros and cons, and motivations for our choice is discussed elsewhere.[ ⁴ , ⁵ , ⁸ , ⁶⁷ ]

The first term of Equation (3) is essential for our analysis. This term corresponds to an electron energy density, which we denote by$\mathrm{X}\left(\mathbf{r}\right)$ , that is,

$${\displaystyle \mathrm{X}\left(\mathbf{r}\right)=\rho \left(\mathbf{r}\right)\bar{\chi }\left(\mathbf{r}\right).}$$ (4)

Because $\mathrm{X}\left(\mathbf{r}\right)$ is an energy density, it takes units such as eV Å⁻³, which corresponds to pressure, where 1.0 eV Å⁻³=160.2 GPa. Note that this energy density is not the same as the chemical pressure successfully used by Fredricksson and co‐workers to study crystal structures, ^[74] neither is it the same as the quantum pressure described by Bader. ^[75]

The $\mathrm{X}\left(\mathbf{r}\right)$ density is instead a union of sorts between two disparate paradigms in chemical bonding analysis: on one hand, the quantum theory of atoms in molecules (QTAIM), ^[3] which is based on the topological analysis of the electron density, $\rho \left(\mathbf{r}\right)$ , and on the other hand, MO theory. The connection with MO theory comes about because ‐$\bar{\chi }\left(\mathbf{r}\right)$ can be interpreted as the energy of the average occupied MO in a point r [Eq. (2)]. The change in the average electron binding energy, $\Delta \bar{\chi }$ , calculated over a chemical transformation, can therefore be approximately equated to the average orbital stabilization or destabilization (Figure 1). ^[4]

Figure 1.

Valence MO diagram showing the formation of CO from ground‐state carbon and oxygen atoms. Energy levels are not to scale. σ bonding/antibonding interactions are shown in blue, π symmetry interactions are in red. The negative of the average valence electron binding energy $\bar{\chi }$ is shown in green. The electronegativity of CO, ${\bar{\chi }}_{\mathrm{C}\mathrm{O}}$ , is larger than for the constituent atoms.

The combination of Equation (3) and (4) is also important as it makes explicit the relationship between: 1) electronegativity, which we will quantify for atoms inside molecules, 2) the electron density, which can be integrated to attain atomic partial charges, and 3) the changing total energy, which ultimately governs most chemical reactions. Before we move on to describe these connections further, we shall familiarize ourselves with$\rho \left(\mathbf{r}\right),\bar{\chi }$ , $\bar{\chi }\left(\mathbf{r}\right)$ and $\mathrm{X}\left(\mathbf{r}\right)$ by means of an example.

An example: Carbon monoxide

CO is interesting for a number of reasons and has been extensively studied computationally.[ ² , ⁷⁶ , ⁷⁷ , ⁷⁸ ] The molecule stands out mainly because of its small dipole moment, whose direction is contrary to what is expected from electronegativity arguments, and its large bond energy, which is higher than that of N₂. We will not solve the subjective conundrum of CO, but repeatedly return to the molecule as an example, to offer a complementary perspective.

Figure 1 shows an example of a MO diagram for CO. In order to explain the low dipole moment of CO using a MO diagram, it is necessary to correctly estimate the degree of mixing between valence 2s and 2p levels of carbon and oxygen.[ ² , ⁷⁶ ] The highest occupied MO then becomes strongly polarized towards carbon, counteracting the opposite polarization of all lower lying orbitals. We refer to Frenking et al. for an insightful commentary on the influence of individual valence orbitals and the topology of the electron distribution on the dipole moment of CO. ^[78] In a MO diagram, − $\bar{\chi }$ represents the average energy of all occupied orbitals.

An example of how $\bar{\chi }$ is calculated and related to $\mathrm{X}$ can be found in the Supporting Information. In short, the total electron energy X is nothing but $\bar{\chi }$ multiplied by the number of electrons n attributable to a given species, that is, $\mathrm{X}=n\bar{\chi }$ . What about the three‐dimensional representations of these quantities?

Some chemical consequences of both $\bar{\chi }\left(\mathbf{r}\right)$ and $\mathrm{X}\left(\mathbf{r}\right)$ appear clear at the onset: we expect it to be more difficult to expel electrons from regions of larger average electron binding energies (larger values of $\bar{\chi }\left(\mathbf{r}\right)$ correspond to a larger electronegativity). The values of $\mathrm{X}\left(\mathbf{r}\right)$ are directly connected to the total energy via the EQC‐EDA shown as Equation (3), and we may expect increases in its value in regions attributed to favorable interactions, such as near covalent bonds and nuclei.

Figure 2 shows $\rho \left(\mathbf{r}\right)$ , $\bar{\chi }\left(\mathbf{r}\right)$ and their product $\mathrm{X}\left(\mathbf{r}\right)$ in two ways. In Figure 2A–C we look in one dimension, along the bond axis of the molecule. In Figure 2D–F, we instead look in two dimensions, across the plane of the molecule. For the electron density shown in Figure 2A and D, the nuclear positions coincide with familiar sharp cusps in $\rho \left(\mathbf{r}\right)$ , which decays exponentially with distance from the molecule.

Figure 2.

One‐dimensional plots and two‐dimensional contour maps of A), D) $\rho \left(\mathbf{r}\right)$ , B), E) $\bar{\chi }\left(\mathbf{r}\right)$ and C), F) $\mathrm{X}\left(\mathbf{r}\right)$ along the bond axis of CO. Note that the scales in A–C and D–F are different; the values shown in D–F are not multiplied by 10 ^x .

In contrast, for the electronegativity, nuclear coordinates reside on plateaus, from which the function $\bar{\chi }\left(\mathbf{r}\right)$ decays to non‐zero values at longer distances.

The behavior of $\bar{\chi }\left(\mathbf{r}\right)$ in molecules can be understood intuitively (and approximately) from Equation (2), as a consequence of multiple orbitals with different energies contributing to the same point in space. It is, for example, not only the O 1s orbital that contributes to the value of $\bar{\chi }\left(\mathbf{r}\right)$ near the oxygen's core (at x $\approx$ 1.1 Å in Figures 2A), but the valence O 2 s and 2p as well. Further out from the nucleus, the contribution of core orbitals is negligible, and the value of $\bar{\chi }\left(\mathbf{r}\right)$ gradually converges to that of the most diffuse valence orbital(s). For a more in‐depth discussion on the spatial variation of $\bar{\chi }\left(\mathbf{r}\right)$ and its sensitivity to the level of theory we refer to the work by Politzer and co‐workers ^[79] and Ryabinkin and Staroverov. ^[61] For now, note the different spatial variation of $\bar{\chi }\left(\mathbf{r}\right)$ near the carbon and oxygen atoms in CO: the larger values of $\bar{\chi }\left(\mathbf{r}\right)$ are found near the oxygen nucleus, signifying a larger electronegativity in this region. However, the distribution of $\bar{\chi }\left(\mathbf{r}\right)$ surrounding the carbon nucleus is clearly broader. So, what electronegativity can be attributed to each atom?

A definition for atoms inside molecules

To attribute properties such as electronegativity and charge to atoms in molecules, a method for partitioning is required. In this work, we choose to partition space through a topological analysis of the electron energy density $\mathrm{X}\left(\mathbf{r}\right)$ , exemplified for CO in Figure 2C and F.

The method we use is adapted from the QTAIM approach of Bader, ^[3] in which space is partitioned into so‐called atomic basins, ${\Omega }_{\mathrm{A}}$ . Atomic basins are here defined as regions of space where all trajectories of the gradient of the electron energy density, $\nabla \mathrm{X}\left(\mathbf{r}\right)$ , terminate at the same local maximum ($\nabla \mathrm{X}\left(\mathbf{r}\right)=0$ ) in space. The boundary condition of each basin in a multi‐atomic system is given by the equation $\nabla \mathrm{X}\left(\mathbf{r}\right)·\mathbf{n}\left(\mathbf{r}\right)=0$ for each point at the dividing surface, where $\mathbf{n}\left(\mathbf{r}\right)$ is the unit vector normal to the surface at r . ^[3] The QTAIM approach to partitioning molecular space has been adapted to analyze several other kinds of densities in the past and is generally applied within the field of quantum chemical topology. ^[80] For example, Francisco, Pendás and Blanco rely on QTAIM basins in their interacting quantum atoms energy decomposition analysis. ^[6] The latter method is similar in spirit to our own, in that it combines a topological analysis with an EDA. Tognetti et al.[ ⁸¹ , ⁸² ] and Tachibana ^[83] have discussed the decomposition of total energies within related frameworks. In the latter method, regions in molecules are, however, defined from the topology of the kinetic energy density. ^[83] The topology of the electron localization function of Becke and Edgecombe ^[84] is one of several other examples that can used to dissect molecular space.[ ⁸⁵ , ⁸⁶ ] Nakai has proposed another EDA method that partition the total energy into atomic energies, but using a Mulliken analysis. ^[87]

Figure 3 shows computed atomic electron energy basins of CO. Figure S1 in the Supporting Information shows corresponding basins obtained with a conventional QTAIM analysis.

Figure 3.

Atomic basins of CO (carbon=gray; oxygen=red) calculated from a topological analysis of the electron energy density $\mathrm{X}\left(\mathbf{r}\right)$ . Insert on the right shows gradient vectors in a plane bisecting the bond axis.

Our justification for using the $\mathrm{X}\left(\mathbf{r}\right)$ energy density for the topological partitioning instead of $\bar{\chi }\left(\mathbf{r}\right)$ or $\rho \left(\mathbf{r}\right)$ is both conceptual and practical: the nature of the spatial variation of $\bar{\chi }\left(\mathbf{r}\right)$ , with plateaus near nuclei (cf. Figure 2B), does not permit for a straightforward partition into atomic basins using gradient vectors. As $\bar{\chi }\left(\mathbf{r}\right)$ gradually converges to the value of the most diffuse valence orbital at long distances, the field cannot be uniquely integrated to a value for open‐ended basins. In contrast, the $\mathrm{X}\left(\mathbf{r}\right)$ energy density shares common features with the electron density and is amenable to atomic partitioning. The spatial distribution of $\mathrm{X}\left(\mathbf{r}\right)$ resembles the electron density in that it is concentrated at nuclei while decaying to zero at long distances. The electron energy attributable to each atom can be calculated as the integral of $\mathrm{X}\left(\mathbf{r}\right)$ over the atomic basins ${\Omega }_{\mathrm{A}}$ :

$${\displaystyle {\mathrm{X}}_{\mathrm{A}}={\int }_{{\Omega }_{\mathrm{A}}}\mathrm{X}\left(\mathbf{r}\right)\mathrm{d}\mathbf{r}.}$$ (5)

Partitioning $\mathrm{X}\left(\mathbf{r}\right)$ according to Equation (5) can be equated to decomposing the total electron energy into atomic contributions. From a MO perspective, $\mathrm{X}$ is a sum of orbital energies of occupied levels (counted with a reversed sign) distributed into topologically defined atoms,

$${\displaystyle \mathrm{X}={\sum }_{\mathrm{A}}{\mathrm{X}}_{\mathrm{A}}.}$$ (6)

Relating atoms in molecules to the total energy

By combining Equations (3)–(6), we can now write:

$${\displaystyle E=-{\sum }_{\mathrm{A}}{\mathrm{X}}_{\mathrm{A}}+V_{\mathrm{N}\mathrm{N}}-E_{\mathrm{e}\mathrm{e}}.}$$ (7)

Equation (7) is a development of the EQC‐EDA expressed as Equation (3) and partitions the total electron energy $\mathrm{X}$ into atomic contributions. Tables 1 and S1 show results from this analysis when applied to CO.

Table 1.

EQC‐EDA for the formation of CO from ground state atoms.^[a]

C (3P0)+O (3P2)→CO (1∑+)
$\Delta {\mathrm{X}}_{\mathrm{C}}$	−0.55
$\Delta {\mathrm{X}}_{\mathrm{O}}$	30.50
$\Delta (V_{\mathrm{N}\mathrm{N}}-E_{\mathrm{e}\mathrm{e}})$	18.35
$\Delta E$	−11.60[b]

[a] Energies in eV are derived from a LC‐BLYP/ATZ2P wavefunction. [b] Calculated from Equation (7) as: ΔE=$-\Delta X+\Delta (V_{\mathrm{N}\mathrm{N}}-E_{\mathrm{e}\mathrm{e}})$ , where $\Delta \mathrm{X}=\Delta {\mathrm{X}}_{\mathrm{C}}+\Delta {\mathrm{X}}_{\mathrm{O}}.$

From Table 1, we can understand the bond energy of CO (ΔE=11.60 eV) in part as a consequence of a small carbon destabilization ($\Delta {\mathrm{X}}_{\mathrm{C}}$ =−0.55 eV) and large oxygen stabilization ($\Delta {\mathrm{X}}_{\mathrm{O}}=$ 30.50 eV). The formation of the CO bond is at the same time resisted by the Δ(V _NN−E _ee) term, which quantifies the degree to which changes to nuclear and electron repulsions differ upon bond formation. The reason why the E _ee energy is negative is due to the double count of these contributions in $\bar{\chi }$ (or $\mathrm{X}$ ). ^[4] A more detailed partitioning of the energy of CO using the EQC‐EDA can be found in ref. [5].

We remind that the partitioning scheme used in this instance is not unique, and that any number of other methods might be useful for dividing $\mathrm{X}$ into atomic contributions. The electron energy basins ${\Omega }_{\mathrm{A}}$ are but one way of defining, or identifying, atoms in molecules. In what comes next, we will use these same basins to quantify the notions of atomic charges and electronegativity inside molecules. As we do so, we will use the terms atom and basin interchangeably.

Results and Discussion

Atomic charges

With atomic electron energy basins ${\Omega }_{\mathrm{A}}$ in hand, we can compute the number of electrons $n_{\mathrm{A}}$ attributable to each constituent atom of a molecule as,

$${\displaystyle n_{\mathrm{A}}={\int }_{{\Omega }_{\mathrm{A}}}\rho \left(\mathbf{r}\right)d\mathbf{r},}$$ (8)

and evaluate the corresponding atomic charges $q_{\mathrm{A}}$ as,

$${\displaystyle q_{\mathrm{A}}=Z_{\mathrm{A}}-n_{\mathrm{A}},}$$ (9)

where Z _A is the nuclear charge of atom A. Calculated atomic charges and comparison with established methods for a selection of molecules are shown in Table 2. Additional examples, testing and details of our numerical methods can be found in the Supporting Information. One advantage of our method is that it appears rather insensitive to the level of theory, including the size of the basis set (Table S3). The robustness is near identical to a conventional QTAIM analysis, that is, when basins are defined from the topology of the electron density, in our testset of molecules. However, what is clear from the charges shown in Tables 2 and S2 is that the electron energy basins ${\Omega }_{\mathrm{A}}$ are sometimes rather different compared to their QTAIM analogues.

Table 2.

Atomic charges, q _A, obtained from topological analysis of the electron energy density $\mathrm{X}\left(\mathbf{r}\right)$ and from other methods.^[a] Atoms in question are underlined in the leftmost column.

Molecule	q A	QTAIM	Mulliken[b]	Hirshfeld
CO	0.79	1.20	0.30	0.10
LiF	0.83	0.92	0.71	0.61
HF	0.80	0.75	0.64	0.23
H 2O	0.65	0.60	0.22	0.17
NH 3	0.42	0.37	0.01	0.12
CH 4	0.07	−0.01	−0.15	0.05
BH 3	−0.30	−0.59	−0.12	−0.05
B 2H6	0.90	1.73	0.69	0.04
B2 H 6 [c]	−0.27	−0.56	−0.16	−0.04
B2 H 6 [d]	−0.37	−0.61	−0.37	0.03
CF	0.66	0.70	0.21	0.00
NO	0.43	0.45	0.18	0.02
CH3OH	0.27	0.59	0.72	−0.08
CH3 OH	−1.15	−1.15	−0.50	−0.25
CH3OH	0.64	0.59	0.16	0.17
CH 3OH	0.08	−0.01	−0.13	0.05
CH3F	0.39	0.64	0.96	−0.05
CH3 F	−0.65	−0.68	−0.56	−0.13
CH 3F	0.09	0.01	−0.13	0.06

[a] Computed from wavefunctions obtained at the LC‐BLYP/ATZ2P level of theory. [b] Mulliken charges are known to depend strongly on the basis set, ^[20] but are shown here as they represent the simplest MO‐based method for charge partitioning. [c] Terminal hydrogen. [d] Bridging hydrogen.

Returning to our example, we see in Table 2 that the carbon atom in CO is predicted to bear a positive charge of +0.8. The value is intermediate between a more ionic value of +1.2 predicted by QTAIM, and lower charge of +0.3, predicted using a Mulliken‐type partitioning. We gleam here a general feature of our analysis: it often conveys a less polar picture of chemical bonding compared to QTAIM, and one that we think is often in fair agreement with expectations arising from conventional atomic electronegativity arguments, with chemical intuition. Some charges, for example, in CF and NO, agree closely with those derived from a QTAIM analysis, whereas others, for example, in HF and H₂O, compute as more polar with our method compared to any other. The carbon atom in methane is predicted to be partially reduced and hold a charge of −0.3. This predicted C−H bond polarity is not obvious and opposite to the results of several other partitioning methods. However, positive charges on H in hydrocarbons are in accord with a slightly larger electronegativity of C compared to H. ^[38]

Can we understand the reasons behind these polarities, and do they make sense? To find out, we turn next to quantifying atomic electronegativities in these molecules.

Electronegativities of atoms inside of molecules

In our framework, atomic electronegativities ${\bar{\chi }}_{\mathrm{A}}$ are defined as,

$${\displaystyle {\bar{\chi }}_{\mathrm{A}}=\frac{{\int }_{{\Omega }_{\mathrm{A}}}\mathrm{X}\left(\mathbf{r}\right)\mathrm{d}\mathbf{r}}{{\int }_{{\Omega }_{\mathrm{A}}}\rho \left(\mathbf{r}\right)\mathrm{d}\mathbf{r}}=\frac{{\mathrm{X}}_{\mathrm{A}}}{n_{\mathrm{A}}},}$$ (10)

where $n_{\mathrm{A}}$ , the number of electrons attributed to an atom A, is obtained through Equation (8), and where ${\mathrm{X}}_{\mathrm{A}}$ , the electron energy associated with each atom, is obtained through Equation (5). Note that this definition is different from what would result following integration of Equation (2), that is, $\int \bar{\chi }\left(\mathbf{r}\right)\mathrm{d}\mathbf{r}$ , because the latter integral is divergent.[ ⁶¹ , ⁷⁹ ]

We need to recognize that the ${\bar{\chi }}_{\mathrm{A}}$ values we compute in Equation (10) are average electron energies of all electrons in a basin. Such full potential averages are large and often become dominated by core electrons. Including all electrons is not a problem when calculating relative changes in ${\bar{\chi }}_{\mathrm{A}}$ over transformations. Such ${\Delta \bar{\chi }}_{\mathrm{A}}$ values tend to be governed by changes to the valence levels and be on the order of a few eV e⁻¹.[ ⁴ , ⁵ ]

In‐situ electronegativity

To reconcile our ${\bar{\chi }}_{\mathrm{A}}$ values with conventional notions of electronegativity, we do the following. First, we calculate ${\Delta \bar{\chi }}_{\mathrm{A}}$ for the reversed atomization of the molecule (e. g., C (³P₀)+O (³P₂)→CO (¹∑⁺)). In other words, we calculate ${\Delta \bar{\chi }}_{\mathrm{A}}$ by subtracting ${\bar{\chi }}_{\mathrm{A}}$ calculated for atom A in vacuum from the value of ${\bar{\chi }}_{\mathrm{A}}$ calculated for the electron energy basin A in a molecule. Second, we offset each such ${\Delta \bar{\chi }}_{\mathrm{A}}$ value by a conventional reference scale of atomic electronegativity. ^[38] Our final electronegativities of atoms in molecules, ${\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ , which we refer to as in‐situ electronegativities, are given as:

$${\displaystyle {\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}={\bar{\chi }}_{\mathrm{A}}^0+{\Delta \bar{\chi }}_{\mathrm{A}},}$$ (11)

where ${\bar{\chi }}_{\mathrm{A}}^0$ corresponds to an established scale of electronegativity, defined as the average binding energy of the valence electrons as T→0 K. ^[38] This “valence‐normalization” approach is inspired by past work where it was successfully used to derive electronegativities for atoms under conditions of high pressure. ^[57] Table 3 shows conventional atomic electronegativity ${\bar{\chi }}_{\mathrm{A}}^0$ for isolated atoms and in situ electronegativity ${\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ for a selection of atoms in molecules. Complementary data of ${\Delta \bar{\chi }}_{\mathrm{A}}$ , ${\mathrm{X}}_{\mathrm{A}}$ and ${\bar{\chi }}_{\mathrm{A}}$ are reported in Tables S4 and S5.

Table 3.

Electronegativity for isolated atoms, ${\bar{\chi }}_{\mathrm{A}}^0$ ^[a] and for atoms in molecules, ${\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ .^[b]

Molecule	${\bar{\chi }}_{\mathrm{A}}^0$	${\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$
CO	13.9	29.5
CO	18.6	9.0
LiF	5.4	18.5
LiF	23.3	4.9
HF	23.3	10.3
HF	13.6	22.7
H2 O	18.6	−0.2[d]
H 2O	13.6	20.2
NH3	16.9	0.0
NH 3	13.6	18.1
CH4	13.9	10.3
CH 4	13.6	15.9
BH3	11.4	27.6
BH 3	13.6	14.5
B 2H6	11.4	28.0
B2 H 6 [c]	13.6	14.4
B2 H 6 [d]	13.6	17.4
N 2	16.9	19.4
CF	13.9	25.7
CF	23.3	15.3
NO	16.9	25.9
NO	18.6	14.3
CH3OH	13.9	19.7
CH3 OH	18.6	1.3
CH3OH	13.6	20.0
CH 3OH	13.6	17.8
CH3F	13.9	22.3
CH3 F	23.3	11.7
CH 3F	13.6	17.0

[a] Data for ${\bar{\chi }}_{\mathrm{A}}^0$ are from ref. [38]. [b] ${\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ was evaluated by using Equation (11) at the LC‐BLYP/ATZ2P level of theory. Because the 1s energy of the isolated H atom is inaccurately predicted with most DFT methods, we used the experimental ionization potential, 13.598 eV, obtained from the National Institute of Standard and Technology to compute ${\Delta \bar{\chi }}_{\mathrm{A}}$ when H was involved. This empirical adjustment makes the in‐situ electronegativity of H less method dependent and does not affect trends or conclusions of this work. Values are provided in eV e⁻¹. [c] Terminal hydrogen. [d] Bridging hydrogen. [d] Negative value for O in H₂O is likely a computational artifact (see Section 1.5 in the Supporting Information).

Apparent from Table 3 is that our method predicts atoms to take distinctly different electronegativities in molecules compared to in isolation. Noteworthily, a reversal of electronegativity occurs in all our heteroatomic‐examples: least electronegative atoms before bond formation become most electronegative atoms after bond formation, and vice versa. The magnitude of the inversion varies between bonds. For example, in CO the electronegativity of oxygen is predicted to decrease by 9.6 eV e⁻¹, while that of carbon is predicted to increase by 15.6 eV e⁻¹.

Reversals of electronegativity can be explained in different ways by the concurrent charge transfer between the atoms (Table 2). For example, it is well known that there exists a qualitative connection between sizes of atoms and electronegativity. ^[58] The addition of negative charge density, or partial reduction, causes an atom to expand. A more diffuse electron density is less bound to the nucleus, resulting in lowered electronegativity. Conversely, removal of electron density, or partial oxidation, shrinks an atom. ^[88] Similar arguments can be couched in familiar terms of nuclear screening, in which positively charged ions bind electrons stronger than anions. In a MO description, valence levels move up in energy with the addition of electrons on a fragment orbital. What is clear is that as the oxygen in our CO example becomes partially negatively charged, the in situ electronegativity of O decreases to reflect its chemical reduction. The arguments we make touch on a well‐known idea in chemistry, that of electronegativity equalization. ^[51]

Sanderson posited that the values of electronegativity of atoms in molecules should equal the mean of the values for the isolated atoms. Support for Sanderson's idea was later provided by Parr and co‐workers, who defined electronegativity to equal the chemical potential, in turn a singular value across a system in equilibrium. ^[35] Alternative viewpoints have been voiced by several, for example by Allen, ^[10] Reed ^[53] and Szentpály. ^[89] This disjoint between conceptual frameworks is a natural consequence of different definitions of electronegativity. We will address electronegativity equalization in the EQC framework in depth in future work, and in particular detail its relationship to the chemical potential that is so fruitfully used within conceptual DFT. ^[90]

As a quick analysis of Table 3 shows, our method, which is rooted in the EDA described by Equation (7), clearly does not permit for a strict adherence to electronegativity equalization in the traditional sense. Maybe most telling is an example such as N₂. In a homopolar molecule there is per definition no difference in electronegativity between the constituent atoms of the molecule for reasons of symmetry. At the same time, the electronegativities for the bonded atoms are notably different from those of the isolated nitrogen atoms (and we do not need partitioning methods to know this). The reason is simple: because electrons are more bound in N₂ than they are in isolated N atoms, the electronegativity of the nitrogen atom in the two different environments is not equal. The value for ${\bar{\chi }}_{\mathrm{N}}$ in N₂ can be approximated from the average eigenvalue of the occupied MOs of N₂ [viz. Eq. (2)]. For heteropolar bonds, the situation becomes more complicated, and we do need a partitioning scheme (such as the topological one used herein) to draw conclusions regarding the individual atoms and their chemical interactions.

In polar diatomics, like LiF and HF, the in‐situ difference in electronegativity between atoms is predicted to be large (>12 eV e⁻¹, Table 3). In some cases, the computed difference between bonded atoms is substantial (e. g., CO: 20.5 eV e⁻¹ and H₂O: 20.4 eV e⁻¹). In contrast, for less polar molecules such as CH₄ the electronegativity difference between bonded atoms is considerably smaller (5.6 eV e⁻¹ in CH₄, see Table S4 for more examples).

Whereas a relationship between charge and electronegativity can be discerned in Tables 2 and 3, it is not linear, or a general rule. We can, for example, compare the predicted charges and electronegativities in CO and CH₃OH with the values computed for CF and CH₃F. In the first example, the in situ electronegativity and charge of O go together and are noticeably lower in CH₃OH compared to in CO. In contrast, the atomic charge on F is nearly identical in CF and CH₃F even as the in‐situ electronegativity of F is predicted to be considerably larger in CF. In other words, changes in bond polarity are not always reflected in the in‐situ electronegativity of the constituent atoms. This seemingly conceptual disjoint is not necessarily a surprise. A tentative explanation is provided by Equation (4), which highlights how the electron density $\rho \left(\mathbf{r}\right)$ and electronegativity $\bar{\chi }\left(\mathbf{r}\right)$ may go hand in hand yet relate differently to the underlying electronic structure of a given system.

Electron‐deficient bonding

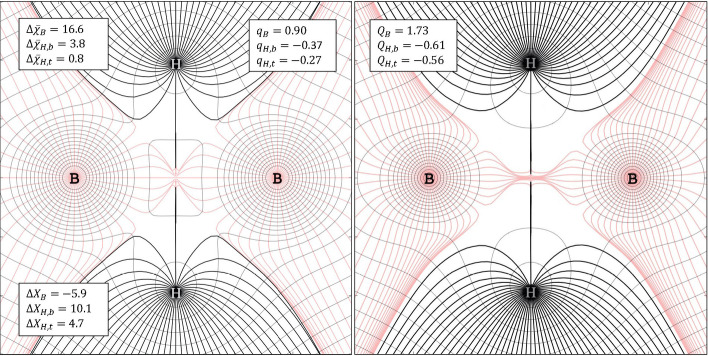
Diborane, B₂H₆, is a classic example of electron‐deficient three‐center two‐electron bonding,[ ⁹¹ , ⁹² ] and maybe the most noteworthy outlier in our set of molecules. We will use it as an example to demonstrate the complementarity of our MO, EDA and topology‐based framework for analysis. In the formation of B₂H₆, changes in atomic charge and electronegativity go in opposite directions compared to what may be expected (Tables 2 and 3). Bridging H atoms in B₂H₆ are more electronegative compared to atoms in isolation and in BH₃, even as they attain a negative charge in diborane.

Figure 4 visualizes the topological atoms of B₂H₆ derived from both $\mathrm{X}\left(\mathbf{r}\right)$ and $\rho \left(\mathbf{r}\right).$ The sharing of electrons, that is, the covalent nature of the B−H−B interaction, is apparent from overall stabilization of valence levels ($\Delta {\bar{\chi }}_{\mathrm{H},\mathrm{b}}>0$ ) and a rather weak (−0.37) hydridic character of the bridging H atoms. Together, atomic charge and in‐situ electronegativity points to hydrogen stabilization ($\Delta {\mathrm{X}}_{\mathrm{H},\mathrm{b}}>0$ ) as the main driving force for the formation of these electron deficient bonds.

Figure 4.

Atoms inside B₂H₆ defined from a topological analysis of the electron energy density $\mathrm{X}\left(\mathbf{r}\right)$ (left) and the electron density $\rho \left(\mathbf{r}\right)$ (right). Gradient lines of $\mathrm{X}\left(\mathbf{r}\right)$ and $\rho \left(\mathbf{r}\right)$ are shown in a plane bisecting the bridging hydrogen. Atomic charges derived from $\mathrm{X}\left(\mathbf{r}\right)$ ($q$ ) portray a less hydridic nature of the bridging H atoms compared to QTAIM charges (Q). b and t refer to the bridging and terminal hydrogen atoms, respectively. Values for $\Delta \bar{\chi }$ and $\Delta X$ are computed relative isolated ground‐state atoms and quantify orbital and electron stabilization due to interactions between B and H.

Relating in situ electronegativity of hydrogen to pK _a

The concept of atomic charges has a well‐known use in chemistry, and so we expect our definition from Equation (9) to be useful. In what follows, we explore instead the utility of in‐situ electronegativity of hydrogens for predicting Brønsted acidity, pK _a. Our focus on this central chemical scale is in part inspired by Politzer and co‐workers, who have demonstrated a correlation between the pK _a of some hydrocarbons with the value of the average local ionization energy, that is, $\bar{\chi }\left(\mathbf{r}\right)$ , at certain points on electron density isosurfaces. ^[93] The importance of accurate prediction of pK _a in chemistry cannot be understated, and many other computational methods have been devised for this purpose (see, e. g., refs. [94]–[101], and references therein).

Figure 5 shows a surprisingly strong linear relationship between in‐situ electronegativities of various bonded hydrogens computed in vacuum and experimentally determined pK _a in aqueous solution. The comparison we make spans a wide range of diverse molecules: from very weak bases, such as hydrocarbons (pK _a∼50), to very strong acids, such as sulfuric and nitric acid (pK _a=−1.4 and −3, respectively). The potential utility of the linear relationship in Figure 5 is tantalizing for it suggests we can predict pK _a of hydrogen atoms inside of a wide range of molecules.

Figure 5.

The in‐situ electronegativity, ${\bar{\chi }}_{\mathrm{H}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ , of hydrogen atoms in molecules shows a linear correlation with aqueous pK _a across a wide range of compounds (see also Table S6). The linear relationship reads as pK _a=−7.526 ${\bar{\chi }}_{\mathrm{H}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ +167.78. HCl, the one outlier is noted as a single red cross in the figure and is omitted from the linear fit. Chloride and halide ions in general present both high net charge and stability in aqueous solution. These aspects can produce unusual trends between the electronegativity of hydrochloric acid and the pK _a.[ ¹⁰⁴ , ¹⁰⁵ ] Alternatively, the outlier may be explained by the significantly disordered first solvation shell surrounding chloride anions in aqueous solution. ^[106]

Whereas the linear relationship in Figure 5 highlights an intrinsic connection between ${\bar{\chi }}_{\mathrm{H}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ and pK _a in radically different molecules, the shown relationship in aqueous solutions is arguably best suited for relatively rough estimations. Increasingly accurate predictions of acidity, in varying chemical environments, can instead be reached when families of more similar compounds are considered.

Figure 6 exemplifies our approach on four complex carboxylic acids 1–4, whose pK _a values have been determined in 50 wt% ethanol−water solution at room temperature. ^[102] One of the compounds (4) has two different pK _a values reported in the literature, 6.6 ^[103] and 6.9, ^[102] but which one is more accurate? To find out, we can perform a linear regression between ${\bar{\chi }}_{\mathrm{H}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ and pK _a for compounds 1–3 and predict value of 7.0 for the pK _a of 4.

Figure 6.

The in‐situ electronegativity ${\bar{\chi }}_{\mathrm{H}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ of acidic hydrogens in 4‐cyanobicyclo[2,2,2]oct‐2‐ene‐1‐carboxylic acid (1), 4‐trifluoromethylbicyclo [2,2,2]oct‐2‐ene‐1‐carboxylic acid (2), 4‐trifluoromethylbicyclo[2,2,2]octane‐1‐carboxylic acid (3) and 4‐methylbicyclo[2,2,2]octane‐1‐carboxylic acid (4) can be used to predict the experimentally uncertain pK _a of 4 in ethanol/water solution 50 % w/w (○). Experimental data for 4 are indicated as a red square ^[102] (pK _a=6.9) and a blue triangle ^[103] (pK _a=6.6). The linear regression of compounds 1–3 is: pK _a=−2.9024 ${\bar{\chi }}_{\mathrm{H}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ +68.109.

We have discussed how atomic charge and electronegativity often, but not always (see B₂H₆), go hand in hand, as expected. However, the large coefficient of determination r ² of 0.979 in Figure 5 is not reproduced if atomic charges are used instead of ${\bar{\chi }}_{\mathrm{H}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ . Neither our own definition of atomic charge (q _A, r ²=0.859) nor QTAIM (r ²=0.887) appears as suitable for predicting pK _a (Table S6 and Figure S2). We note here a possible practical distinction between estimates of atomic charge and in‐situ electronegativity. Atomic charges convey information related to electrostatics and can hence be expected to be useful indicators of electrophilicity or nucleophilicity. In‐situ electronegativities, on the other hand, may prove more suitable to quantify properties and notions related to covalent bonding, such as acid–base equilibria (pK _a) and possibly, as we shall see next, donor–acceptor interactions.

A biological example: The guanine–cytosine base pair

As a final example of our methodology for topological analysis of $\mathrm{X}\left(\mathbf{r}\right)$ , we show in Figure 7 the electron energy basins of the guanine–cytosine base pair. Associated computed charges and electronegativities are shown for selected atoms (data for all atoms is shown in Table S7). For each selected atom in Figure 7 we also indicate, within parenthesis, the corresponding charge and electronegativity inside isolated guanine or cytosine molecules. The analogous QTAIM partitioning, that is, based on $\rho \left(\mathbf{r}\right)$ , for the guanine–cytosine complex is shown in Figure S3 for comparison.

Figure 7.

Atoms inside the guanine‐cytosine (G‐C) base pair defined from a topological analysis of the electron energy density $\mathrm{X}\left(\mathbf{r}\right)$ [eV ⋅ Å ⁻³]. Contour lines are derived from the gradient of $\mathrm{X}\left(\mathbf{r}\right)$ . Atoms are color coded as: oxygen=red, nitrogen=blue, carbon=gray, hydrogen=black. In‐situ atomic electronegativities ${\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ and partial charges q _A are shown for selected atoms. Corresponding values for the separated (G and C) molecules are given in parentheses.

Figure 7 helps to highlight and explain several factors important for structure and reactivity. As a consequence of taking part in polar bonds, the electronegativities of most oxygen and nitrogen atoms are lowered relative to their atomic references provided in ref. [38]. As expected, these atoms are also partially reduced. We stress again that the differences in the electronegativities of atoms in molecules and in isolation can be drastic: in guanine and cytosine, oxygen and nitrogen atoms are reduced by more than one electron each and are predicted to have electronegativities on par with isolated alkali metal atoms! However, these atoms do not exist in isolation, and the electronegativity and charge of surrounding atoms – carbon and hydrogen – are significantly increased due to partial oxidation. Overall, electrons are stabilized in these compounds relative to the isolated atoms: $\Delta \mathrm{X}$ for the formation of guanine and cytosine from isolated atoms are 141.6 and 93.6 eV, respectively.

Using ${\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ , we can identify H−N3 as the most acidic proton in the gas phase for the isolated guanine molecule, in agreement with other theoretical and experimental studies. ^[107] The correct identification of H−N3 as the most acidic proton in vacuum does not appear possible using atomic charge estimates (Table S7).

Further subtleties of the electronic structure of guanine and cytosine become apparent when comparing atomic charges and electronegativities of atoms before and after base‐pair formation. Upon complexation, charges and electronegativities reproduce the expected donor–acceptor interaction characteristic of the base pair. The hydrogen atoms directly involved in hydrogen bonds become more electronegative and take values comparable to the hydroxylic hydrogen in methanol (cf. Table 3). In a similar fashion to CH₃F mentioned earlier, the two carbonyl oxygen atoms in the complex show largely the same charge but differ noticeably in electronegativity (by about 1 eV e⁻¹). The amine nitrogen atoms behave similarly and are more distinguished by their in situ electronegativity ${\bar{\chi }}_{\mathrm{N}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ than by their atomic partial charge, q _N.

Carbon is arguably the most flexible atom in chemistry, and the degree to which the nature of this atom can be different is clearly reflected in a large range of possible values of ${\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$ (compare also compounds in Tables 3, S5, and S7). As expected, a drastically varying chemical environment matters: a carbon atom adjacent to a carbonyl oxygen (e. g., C6) is attributed both a higher positive charge and a higher electronegativity. Base pair formation also affects the carbon atoms in an understandable manner: atoms nearer to formed H‐bonds, such as C6 and C7, are perturbed more compared to those further away, such as C3.

The carbonyl oxygen atom of cytosine (O2) is unique in this example in that the atom upon complexation exhibits an increase in electronegativity even as it is further reduced. The fact that individual atomic charges need not necessarily follow changes in in‐situ electronegativity points to the important role of the surrounding chemical environment. For the carbonyl oxygen atom of cytosine, the combined effect of a changing electronic structure – most notably due to the formation of a hydrogen bond – suffices to override our expectations. It appears that there are circumstances, in addition to diborane, which allow atoms to be reduced while also causing electrons attributable to them to be more strongly bound.

Conclusions

This work is an attempt to bring together ideas from three major ways in which chemical bonding is typically represented and analyzed: MO theory, quantum chemical topology, and EDA. Central to our approach is the partitioning of the electron energy density, $\mathrm{X}\left(\mathbf{r}\right)$ , which itself is a product of two other functions: 1) the electron density $\rho \left(\mathbf{r}\right)$ , which is the linchpin of conventional topological QTAIM analysis, and 2) the spatially resolved average electron binding energy, $\bar{\chi }\left(\mathbf{r}\right)$ . The latter distribution can be approximated from an average energy of occupied molecular orbitals, creating a strong conceptual link to MO theory. All these densities are explicitly related to the total energy of a system through an energy partitioning, or EDA, written as Equation (3). Our framework makes two perspectives possible. The electron density $\rho \left(\mathbf{r}\right)$ can either be viewed as the weight by which the average electron binding (or orbital) energy $\bar{\chi }\left(\mathbf{r}\right)$ is distributed in a material. Conversely, $\bar{\chi }\left(\mathbf{r}\right)$ , which can be conceptually connected to the idea of electronegativity, may be viewed as a potential that distributes the electron density.

In‐situ electronegativities are presented as atomic measures of the average electron binding energy inside molecules and come together with complementary partial charges. The atomic charges represent an effective compromise between approaches relying on the analysis of the electron density, such as QTAIM (or Bader) charges, and charges derived from wavefunctions or orbitals, such as the Mulliken population analysis. Our electron energy‐derived partial charges, here denoted as q _A, are relatively insensitive to computational parameters such as basis sets and appear in good agreement with chemical expectations of bond polarity.

Several expectations rooted in conventional electronegativity arguments are upheld. Atomic charges and in‐situ electronegativity largely follow each other, with some notable exceptions. For example, the formation of electron‐deficient diborane bonds is predicted to both cause chemical reduction and enhance electronegativity in bridging hydrogens. The formation of most heteropolar bonds is predicted to result in inversions of electronegativities, causing the most electronegative atom before bond formation to become the least electronegative atom afterwards. The latter prediction is at odds with ideas based on electronegativity equalization. In our framework, atoms of the same type in molecules are distinguishable entities with markedly different properties. One clear use of in‐situ electronegativities is as predictors of pK _a.

In summary, we have outlined a chemical theory and method for analyzing electronic structure that can be applied in a straightforward way to general challenges in chemical sciences. We shall extend the methodology to condensed matter in a separate paper.

Abbreviations

${\mathrm{X}}_{\mathrm{A}}$

The total electron energy of atom A, equal to ${\int }_{{\Omega }_{\mathrm{A}}}\rho \left(\mathbf{r}\right)\bar{\chi }\left(\mathbf{r}\right)\mathrm{d}\mathbf{r}$ .

${\bar{\chi }}_{\mathrm{A}}$

The electronegativity, or average electron binding energy, including core electrons, computed either for an atom in isolation or for an atom in a molecule.

${\bar{\chi }}_{\mathrm{A}}^0$

Tabulated average valence electron binding energies, or conventional electronegativities of an isolated atom (see ref. [38]).

${\Delta \bar{\chi }}_{\mathrm{A}}$

The difference in electronegativity between atom $A$ in a molecule and in isolation. For example, in CO ${\Delta \bar{\chi }}_{\mathrm{C}}$ equals ${\bar{\chi }}_{\mathrm{C}}$ in CO minus ${\bar{\chi }}_{\mathrm{C}}$ computed for the ground‐state carbon atom in vacuum.

${\bar{\chi }}_{\mathrm{A}}^{\mathrm{v}\mathrm{a}\mathrm{l}}$

Valence‐normalized in‐situ electronegativity of an atom A in a molecule, defined as ${\bar{\chi }}_{\mathrm{A}}^0+{\Delta \bar{\chi }}_{\mathrm{A}}$ .

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Supporting Information

S. Racioppi, M. Rahm, Chem. Eur. J. 2021, 27, 18156.