Using fractional polynomials and restricted cubic splines to model non‐proportional hazards or time‐varying covariate effects in the Cox regression model

Abstract

The Cox proportional hazards model is used extensively in clinical and epidemiological research. A key assumption of this model is that of proportional hazards. A variable satisfies the proportional hazards assumption if the effect of that variable on the hazard function is constant over time. When the proportional hazards assumption is violated for a given variable, a common approach is to modify the model so that the regression coefficient associated with the given variable is assumed to be a linear function of time (or of log‐time), rather than being constant or fixed. However, this is an unnecessarily restrictive assumption. We describe two different methods to allow a regression coefficient, and thus the hazard ratio, in a Cox model to vary as a flexible function of time. These methods use either fractional polynomials or restricted cubic splines to model the log‐hazard ratio as a function of time. We illustrate the utility of these methods using data on 12 705 patients who presented to a hospital emergency department with a primary diagnosis of heart failure. We used a Cox model to assess the association between elevated cardiac troponin at presentation and the hazard of death after adjustment for an extensive set of covariates. SAS code for implementing the restricted cubic spline approach is provided, while an existing Stata function allows for the use of fractional polynomials.

1. INTRODUCTION

The use of the Cox proportional hazards models is ubiquitous in modern medical and epidemiological research. ¹ This model regresses the hazard of the occurrence of the outcome on a set of covariates: $\log (h(t))=\log \left(h_0(t)\right)+\mathbf{\beta X}$, where $h(t)$ denotes the hazard function at time t, $h_0(t)$ denotes the baseline hazard function for a subject whose covariates are equal to zero, $\mathbf{X}$ denotes a vector of covariates, and $\mathbf{\beta }$ denotes a vector of regression coefficients. The model can also be written in multiplicative form as: $h(t)=h_0(t)e^{\mathbf{\beta X}}$. A key assumption of the model is the proportional hazards assumption, which states that the hazard ratio associated with any specific difference in any value of any covariate is constant over time.

Analysts should assess whether model covariates satisfy the proportional hazards assumption. In a review of papers published in the cancer literature in an earlier period and whose findings may not pertain to current statistical practice, Altman et al ² found that only 5% of papers assessed whether the assumptions of the Cox model were satisfied. Ngari et al ³ examined the quality of survival analyses in studies of tuberculosis outcomes published between 2010 and 2020. Of the 67 studies that reported using a Cox proportional hazards model, 32 (48%) stated that the proportional hazards assumption had been tested, while only 2 (3%) reported the results of such a test. Kuitunen et al ⁴ reviewed the assessment of non‐proportionality in studies published between 1987 and 2019 (with the large majority published since 2000) reporting on research in total joint arthroplasty. Out of 318 included studies, 127 (40%) reported assessing the proportional hazards assumption. Thus, even in more recent eras, fewer than half of studies reported assessing the proportional hazards assumption. When a covariate is found to not satisfy the proportional hazards assumption one option is to explicitly model the non‐proportionality. This can be achieved by incorporating a time‐varying covariate effect (ie, allowing the regression coefficient for that variable to be a function of time). A common way to achieve this is by assuming that the regression coefficient is a linear function of time (or of the logarithm of time). However, this may not be a realistic assumption in all settings. Instead, in some settings, the log‐hazard ratio may have a nonlinear relationship with time. A nonlinear relationship could arise in settings where a variable exerts an initially strong effect that is then dampened quickly, so that the effect of the varies decays exponentially. In studies comparing a surgical intervention with medical care, there may be an initially elevated hazard of mortality immediately after surgery (eg, due to the risk of surgical complications in the peri‐operative period, etc.). However, the initial large hazard ratio for surgery may decrease rapidly as the patient heals from the surgery and exits the peri‐operative period. From that point onwards, one could expect that, for patients who survive the peri‐operative period, the hazard of mortality may be lower in those who underwent surgery compared to those receiving only medical care. Quantin et al ⁵ found a non‐monotone relationship between cancer stage and mortality in patients with colon cancer. Similarly, Tsang et al ⁶ found that the hazard ratio for all‐cause mortality comparing those with heart failure and adult congenital heart disease to those with heart failure without adult congenital heart disease displayed a U‐shaped relationship with time.

Methods to allow for modeling of time‐varying effects in the Cox model have been described by many different authors. Cox suggested that the time‐varying covariates could be incorporated by considering interactions between covariates and functions of time. ¹ Hess ⁷ described using cubic splines to model covariates as a function of time. Similarly, Gray ⁸ used splines to allow covariate effects to vary as a function of time. Abrahamowicz et al ⁹ used regression splines to model the hazard ratio as a function of time and developed tests of non‐proportionality and of no association. Note that the test of non‐proportionality that they developed does not assume that the hazard ratio is a linear function of time under the alternate hypothesis. Kooperberg et al ¹⁰ developed hazard regression models that use linear splines and tensor products to model the logarithm of the hazard function. These models contain proportional hazards models as a subclass, and thus allow for assessing the proportional hazards assumption. Hastie and Tibshirani ¹¹ developed varying‐coefficient models in which coefficients are allowed to vary as smooth functions of other variables. Grambsch and Therneau ¹² describe how, in a Cox model, the regression coefficient as a function of time can be visualized by using a smoothed plot of the standardized Schoenfeld residuals. Buchholz and Sauerbrei ¹³ reviewed different methods for assessing whether coefficients in a Cox model vary over time, and how they do so if non‐proportionality is present. Similarly, Andersen et al ¹⁴ briefly reviewed different methods that can be used to explicitly account for non‐proportionality of a given effect.

In this tutorial article, we describe two flexible methods to account for non‐proportionality in a covariate. We consider the use of fractional polynomials (FPs) and restricted cubic splines to model time‐varying covariate effects, thereby explicitly incorporating non‐proportional effects into the fitted Cox model. This article is structured as follows. In Section 2, we describe two (among many) existing methods to flexibly model non‐proportionality. In Sections 3 and 4, we provide a case study illustrating the application of these methods. Finally, in Section 5, we summarize our findings and place them in the context of the existing literature.

2. DESCRIPTION OF THREE (AMONG MANY) EXISTING STATISTICAL METHODS TO ACCOUNT FOR NON‐PROPORTIONALITY

In this section, we describe three (out of many) existing statistical methods that account for non‐proportionality by modeling the regression coefficient as a function of time. The proportional hazards assumption can be relaxed by modifying the Cox model as follows: $\log (h(t))=\log \left(h_0(t)\right)+\mathbf{\beta }(t)\mathbf{X}$, so that the regression coefficients are a function of time. We describe three different methods to account for non‐proportionality: (i) modeling the regression coefficient as a linear function of time; (ii) using FPs; (iii) using restricted cubic splines (RCS). In the description that follows, we relax the proportionality assumption for a single variable. We assume the following model: $\log (h(t))=\log \left(h_0(t)\right)+\beta (t)X+\mathbf{\alpha Z}$, where X denotes a single variable for which we want to relax the proportional hazards assumption, while $\mathbf{Z}$ denotes a vector of variables for which the proportional hazards assumption is assumed to hold. In Section 2.4, we describe how these methods can be extended to allow for non‐proportionality for multiple variables.

2.1. The regression coefficient is a linear function of time

A common method in the medical literature to account for non‐proportionality is to allow the regression coefficient to vary as a linear function of time. ¹⁵ The proportional hazards model is modified to: $\log (h(t))=\log \left(h_0(t)\right)+\left({\beta }_1+{\beta }_{2}t\right)X+\mathbf{\alpha Z}$. The hazard ratio at time t comparing two subjects who differ by one unit in the variable X (and have identical values of $\mathbf{Z}$) is $\exp \left({\beta }_1+{\beta }_{2}t\right)$.

2.2. The regression coefficient is modeled as a function of time using FPs

FP is a method to allow for nonlinear transformation of a strictly positive continuous variable by considering a number of pre‐specified polynomial transformations of that variable. ¹⁶ Royston and Sauerbrei proposed two classes of FP transformations: FP1 transformations and FP2 transformations. Given a continuous strictly positive variable x, the FP1 transformations are defined as $x^{p_1}$, while the FP2 transformations are defined as $x^{p_1}+x^{p_2}$. The exponents p ₁ and p ₂ are taken from the set S = (−2, −1, −0.5, 0, 0.5, 1, 2, 3), with the convention that $x^0=\log (x)$ (ie, the transformation associated with p ₁ = 0 or p ₂ = 0 is the logarithmic transformation). Furthermore, for p ₁ = p ₂ = p, the associated FP2 transformation is defined by $x^p+x^p\log (x)$. Thus, there are 8 FP1 transformations and 36 FP2 transformations, for a total of 44 FP transformations. We use the notation FP1(p ₁) and FP2(p ₁, p ₂) to denote a given FP1 or FP2 transformation, respectively.

One fits 44 different regression models, 1 for each of the 44 FP transformations. When considering an FP1 transformation, the following model is fit: $\log (h(t))=\log \left(h_0(t)\right)+{\beta }_{1}X+{\beta }_2{t}^{p_1}X+\mathbf{\alpha Z}$. When considering an FP2 transformation, the following model is fit: $\log (h(t))=\log \left(h_0(t)\right)+{\beta }_{1}X+\left({\beta }_2{t}^{p_1}+{\beta }_3{t}^{p_2}\right)X+\mathbf{\alpha Z}$, for $p_1\ne p_2$ and $\log (h(t))=\log \left(h_0(t)\right)+{\beta }_{1}X+\left({\beta }_2{t}^p+{\beta }_3{t}^p\log (t)\right)X+\mathbf{\alpha Z}$, for $p_1=p_2=p$. Royston and Sauerbrei ¹⁶ described an FP transformation selection procedure based on a sequence of likelihood ratio tests to determine which FP transformation to use. When used to model time‐varying covariates, the FP1 transformations are restricted to modeling the covariate as a monotone function of time, while the FP2 transformations allow for the covariate to be a non‐monotone function of time.

2.3. The regression coefficient is modeled as a function of time using restricted cubic splines

In this paragraph, we define restricted cubic splines in the context of a generic continuous variable. Cubic splines are a method to represent nonlinear relationships using a set of cubic polynomials, each over a different domain, to represent a continuous variable. ¹⁷ Cubic splines require the analyst to specify a set of knots, which are specific values of the continuous variable X. In practice, three, four, or five knots are often used. When three knots are selected, the recommended locations of the knots are the 10th, 50th, and 90th percentiles of the continuous variable. When four knots are used, the recommended locations are the 5th, 35th, 65th, and 95th percentiles of the continuous variable, while when five knots are used the locations are often selected as the 5th, 27.5th, 50th, 72.5th, and 95th percentiles (we refer to these as Harrell's suggested knot locations, to distinguish them from those described below). ¹⁷ A separate cubic polynomial is fit in each of the intervals defined by the knots (with k knots there are k + 1 intervals). The cubic polynomials are fit such that the cubic polynomials meet smoothly at each of the k knots (eg, the polynomial in the first interval and the polynomial in the second interval meet smoothly at the first knot). Cubic splines can behave poorly in the tails (ie, before the first knot and after the last knot). ¹⁷ Restricted cubic splines address this limitation by constraining the function to be linear in the tails. Given a continuous variable X and k knots $t_1,t_2,\dots ,t_k$, the restricted cubic spline function for X is $f(X)={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_{k-1}{X}_{k-1}$, where $X_1=X$ and for $j=1,\dots ,k-2,X_{j+1}={\left(X-t_j\right)}_{+}^3-{\left(X-t_{k-1}\right)}_{+}^3\left(t_k-t_j\right)/\left(t_k-t_{k-1}\right)+{\left(X-t_k\right)}_{+}^3\left(t_{k-1}-t_j\right)/\left(t_k-t_{k-1}\right),$ where ${(u)}_{+}=\left\{\begin{array}{l}u,u>0\\ 0,u\le 0\end{array}\right.$ _. ¹⁷

The definition and location of knots in the previous paragraph was in the context of a generic continuous variable. When using RCS to model the effect of covariate on time, time is the variable whose relationship with the regression coefficient is being modeled. As such, the knots are defined at specific event times. When using RCS to model a time‐varying covariate effect, the analyst must select the number and location of the knots. There is limited guidance on selecting the number of knots. The number of knots selected should be influenced by the sample size or by the number of observed outcome events. Hess ⁷ suggested that three to five knots is usually adequate and that the knots be placed at quantiles of the observed follow‐up times (ie, considering both the censoring and event times). When using four knots, he suggested using the 5th, 25th, 75th, and 95th percentiles of observed follow‐up times, which differs slightly from the percentiles suggested by Harrell above in the context of a generic continuous covariate (Harrell suggested equidistant percentiles). In contrast to this, Abrahamowicz et al ⁹ suggested choosing the knots so that there are an approximately equal number of outcome events within each interval (their suggestion was in the context of using regression splines, rather than RCS).

2.4. Extensions to modeling the time‐varying effect of multiple covariates

The methods described in Sections 2.1 to 2.3 permit for modeling the effect of one covariate as a function of time. Wynant and Abrahamowicz ¹⁸ found that it was important to account for the possible time‐dependent effect of all covariates when estimating the time‐dependent effect of a main exposure of interest. Similarly, Buchholz and Sauerbrei ¹³ state that “spurious time‐varying effects may also be introduced by mismodeling other parts of the multivariable model.” Thus, it is important to be able to relax the proportional hazards assumption for multiple covariates simultaneously. The RCS approach can be easily extended to use RCS to model the relationship between each regression coefficient and time. Using RCS to model time‐dependent effects for all covariates can result in a very complex model. Wynant and Abrahamowicz ¹⁸ described a backwards selection approach that can result in a more parsimonious model. One begins by fitting the full model in which time‐varying effects are incorporated for all the covariates. Then, for each covariate, the full model is compared to the model in which only that covariate is assumed to have a time‐invariant effect and all the other covariates are allowed to have time‐varying effects. A likelihood ratio test is used to produce a P‐value testing the null hypothesis that the given covariate has a time‐invariant effect. This process is done sequentially for all covariates and the model is modified so that the covariate with the largest P‐value (assuming it is >0.05) is assumed to be time‐invariant. This process is then repeated until all the obtained P‐values are ≤0.05. When using FP, Sauerbrei et al ¹⁹ described an algorithm to (i) select covariates; (ii) select appropriate transformations for continuous covariates; (iii) select appropriate functions to model time‐varying covariate effects. It is important to note that the both the selection algorithm described by Wynant and Abrahamowicz and by Sauerbrei et al allow for selection of both nonlinear effects (continuous covariates having a nonlinear relationship with the log‐hazard function) and time‐dependent effects (the log‐hazard ratio varying as a function of time).

2.5. Statistical software for implementing these methods

The methods described above can be implemented in any statistical software package that permits the inclusion of time‐varying covariate effects in the Cox regression model. In SAS, the methods can be implemented using the PHREG procedure. A SAS macro for modeling time‐varying covariate effects using restricted cubic splines is available from the authors (contact: jiming.fang@ices.on.ca). A Stata function (stmfpt) has been developed by Patrick Royston (https://mfp.imbi.uni‐freiburg.de/software) to fit Cox models in which FPs are used to model time‐varying covariate effects. This function uses FP1 transformations to allow the log‐hazard ratio to be a monotone function of time and FP2 transformations to allow the log‐hazard ratio to be a non‐monotone function of time. In the selection algorithm, the default FP1 transformation is the FP(0) transformation, in which the log‐hazard ratio is a function of the logarithm of time.

In PROC PHREG in SAS, the ZPH option in the PROC PHREG statement allows for assessing the validity of the proportional hazards assumption using weighted Schoenfeld residuals. This includes both a graphical assessment as well as a formal statistical test of non‐proportionality. The formal test is based on testing for a nonzero slope when fitting a univariate regression model in which the weighted Schoenfeld residuals are regressed on one of four transformations of event times (the identity transformation, the logarithmic transformation, the complement of the Kaplan‐Meier transformation, and the rank transformation). ²⁰ Similarly, the cox.zph function in the survival package for R tests the proportional hazards assumption for a fitted Cox regression model. ¹²

3. CASE STUDY: METHODS

We used data from a previously published study examining the effect of elevated cardiac troponin in patients with acute heart failure syndromes. ²¹ Cardiac troponins are heart muscle‐specific proteins that are released during myocyte injury and may indicate the presence of underlying ischemic heart disease. The presence of elevated cardiac troponin in acute decompensated heart failure indicates heightened risk for adverse outcomes. ²² However, the leakage of troponin during cardiac events is most marked early after injury and diminishes over time. We used data on 12 705 patients aged ≥18 years who presented to a hospital emergency department (ED) in Ontario, Canada with a primary diagnosis of heart failure. Patients presented to hospital between April 1999 and March 2001 and between April 2004 and March 2007. Mortality following ED presentation was determined through linkage with the provincial death registry. Subjects were followed for up to 2 years and subjects were censored after 2 years if death had not yet occurred, as in the original study. ²¹ Of the 12 705 patients, 4495 (35.4%) died within 2 years of ED presentation, with the remaining 64.6% of patients being censored at 2 years.

We fit a Cox regression model in which the hazard of death was regressed on a binary variable denoting elevated troponin in addition to the following variables: age, sex, transport by emergency medical services, systolic blood pressure, heart rate, oxygen saturation, serum creatinine, serum potassium, use of metolazone, myocardial infarction, previous heart failure, coronary artery bypass graft surgery, percutaneous coronary intervention, diabetes mellitus, hypertension, active and metastatic cancer, unstable angina, stroke, functional disability, cardiopulmonary respiratory failure and shock, pneumonia, chronic pulmonary obstructive disease, protein calorie malnutrition, dementia, trauma, major psychiatric disorders, peripheral vascular disease, chronic liver disease, chronic atherosclerotic disease, valvular disease, and time period of ED presentation (1999‐2001 vs 2004‐2007). As our focus was on modeling time‐varying covariate effects, we made the simplifying assumption that each continuous variable was linearly related to the log‐hazard of death in all regression models.

The proportional hazards assumption for the elevated troponin variable was rejected using a Kolmogorov‐Smirnov supremum‐type test on 1000 resamplings of the cumulative sums of martingale residuals (P < 0.0001). ²³ We then applied the methods described in Section 2 to model the time‐varying hazard ratio for elevated troponin. We estimated the elevated troponin hazard ratio at days 0 to 730 (ie, 2 years).

While our focus was on estimating the time‐varying effect of elevated troponin on the hazard of mortality, we allowed the effect of each of the other covariates to vary as a function of time. The same method was used to model the time‐varying effect of each covariate as was used for elevated troponin.

When using RCS to model the time‐varying effect of elevated troponin we used three knots. The location of the knots was selected so that there was an approximately equal number of outcome events within each of the four intervals (we thus followed Abrahamowicz's suggested location of knots when using regression splines in a similar context). Note that using Hess's suggestion to determine the knot locations based on the percentiles of survival time would not work well in our setting as 65% of the subjects were censored at 2 years, and thus had survival times of 730 days.

FPs require that all values of the variable under consideration (in this case, time) be strictly positive. Thus, when using FPs, subjects who had a survival time of 0 (ie, who died on the day of ED presentation) had their survival time changed to 0.5 (ie, they were recorded as having died a half‐day after ED presentation). The Stata function stmfpt was used to select the FP transformations. This function requires that time is divided up into intervals. We used intervals of length 5 days. Once the final model had been selected we refit the final model using PROC PHREG in SAS, which does not require that the time scale be divided into intervals.

Ninety‐five percent confidence intervals for each day‐specific hazard ratio (from day 0.5 to day 730, in increments of 1 day) were computed using model‐based standard errors.

For comparative purposes, we examined two other methods for modeling the time‐varying effect of elevated troponin. First, we allowed the log‐hazard ratio to vary as a linear function of time. To mirror what was done above, the log‐hazard ratio for each covariate was allowed to vary as a linear function of time. Second, we partitioned the time axis into four intervals of equal length: date of ED presentation to 6 months, 6 to 12 months, 12 to 18 months, and 18 to 24 months. We then fit a model in which the log‐hazard ratio was constant within each of these four time intervals. This “piecewise proportional hazards model” was proposed by Moreau et al ²⁴ as a test of the proportional hazards assumption. Quantin et al ⁵ compared the use of the piecewise proportional hazards model with that of an approach that used regression splines for modeling time‐varying effects. To reflect what was done above, we forced the log‐hazard ratio for each of the model covariates to be constant within each of these intervals, but allowed the log‐hazard ratios to vary across intervals.

We also examined the sensitivity of the RCS results to the number of knots and the method for selecting the location of the knots. We considered three different methods for selecting the location of the knots: (i) the knots were selected so that there were an equal number of deaths within each interval; (ii) the knots were placed so that adjacent knots were equidistant (ie, so that $t_{j+1}-t_j=d,j=1,\dots ,k-1$); (iii) using the percentiles of observed times of death for those subjects who died. When using percentile‐based locations for the knots, we used Harrell's suggested percentiles. We did not use Hess's suggestion to place knots at specified percentiles of the observed survival times due to the large percentage of subjects who were censored (65%) and who thus had survival times of 730 days. We also conducted analyses with 3, 4, and 5 knots, for a total of 9 analyses (3 methods for selecting the locations of the knots × 3 different numbers of knots).

4. CASE STUDY: RESULTS

The time‐invariant troponin hazard ratio from a Cox model that assumed a proportional hazards effect for elevated troponin was 1.47 (95% confidence interval: 1.35‐1.59). Thus, over the course of follow‐up time, an elevated troponin at ED presentation was associated with a 47% increase in the instantaneous hazard of death.

The time‐varying hazard ratio for elevated troponin for each of the three methods (linear relationship, RCS, FP) are reported in Figure 1, both without the associated 95% confidence intervals (left panel) and with the associated 95% confidence intervals (right panel). When using the FP method, the selected FP transformation was the FP1(0) transformation. Thus, the regression coefficient for elevated troponin varied as a function of the logarithm of time. The FP analysis indicated that initially the hazard ratio for elevated troponin was very high (hazard ratio = 3.5) and that it then decreased rapidly, until about 6 months, after which the rate of decrease was substantially attenuated. The RCS analysis indicated that the hazard ratio for elevated troponin followed an approximately J‐shaped relationship. The hazard ratio was initially high (2.0), decreased to a nadir around 10 months, and then increased gradually from that time onwards. In contrast to these two analyses, the analysis that assumed that the log‐hazard ratio was a linear function of time indicated that the initial hazard ratio was modest (1.76) and then decreased over time.

FIGURE 1.

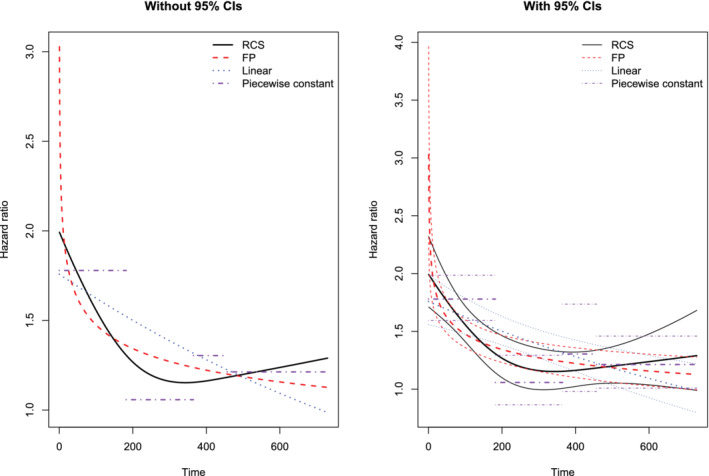
Comparison of different time‐varying hazard ratios

The deviance (−2 log‐likelihood), Akaike's information criterion (AIC), and Bayesian information criterion (BIC) for each of the models are reported in Table 1. AIC = deviance + p, while BIC = deviance + p × log(d), where p is the number of model parameters and d is the number of deaths that were observed to occur. ²⁵ Given the large number of model parameters (range: 35‐140) and the large number of deaths that occurred (4495), BIC may be overly conservative, and we will focus on the AIC in comparing the different models. The AIC ranged from a high of 80 972.439 (model with piecewise constant hazard ratio) to a low of 80 821.062 (the model using FPs to model the time‐varying covariate effects). While the deviance was lower for the RCS model than for the FP model, the larger number of model parameters (105 vs 46) resulted in a greater penalty for the former model. Consequently, the use of AIC favored the FP model over the RCS model. It should be noted that while the selected FP model used 46 degrees of freedom, a selection algorithm had been used and it is not clear what the effect of such a selection algorithm would be on AIC. Note that the model degrees of freedom for the FP model (46) reflects the degrees of freedom of final selected model. This does not reflect the fact that at each step of the selection algorithm, 44 transformations were considered for each time‐dependent effect. A reviewer suggested that for each selected variable, one could add one degree of freedom for the choice between an FP1 and an FP2 transformation and an additional degree of freedom for the choice of specific transformation within either the FP1 or FP2 families of transformations. Subsequent research is necessary to determine how best to inflate the apparent degrees of freedom to account for the selection process.

TABLE 1.

Measures of model fit for different regression models

Model	Model df	Deviance	AIC	BIC
Constant hazard ratio	35	80 892.525	80 962.525	81 186.900
Log‐hazard ratio a linear function of time	70	80 766.060	80 906.060	81 354.811
Restricted cubic splines to model log‐hazard ratio	105	80 664.393	80 874.393	81 547.519
Fractional polynomials to model log‐hazard ratio	46	80 729.062	80 821.062	81 115.955
Piecewise constant hazard ratio	140	80 692.439	80 972.439	81 869.940

The time‐varying hazard ratios from the nine analyses that varied the number of knots for the RCS and how the locations of the knots were selected are reported in Figure 2. Neither the number of knots nor how the locations of the knots were selected had a meaningful effect on the qualitative interpretation of the pattern of change in the hazard ratio for troponin over time. The AIC statistics for the nine different RCS models are reported in Table 2. For a given method of selecting the locations of the knots, AIC decreased with a decreasing number of knots. AIC was lowest with 3 knots chosen so that there was an equal number of deaths per interval (however, the AIC for the model with 3 knots chosen using equidistant percentiles of event time was very similar). The two curves (5 knots chosen for an equal number of events in each interval and 5 knots chosen using equidistant percentiles of event times) that were most different from the other seven curves were from models that had relatively little support compared to the models with 3 or 4 knots.

FIGURE 2.

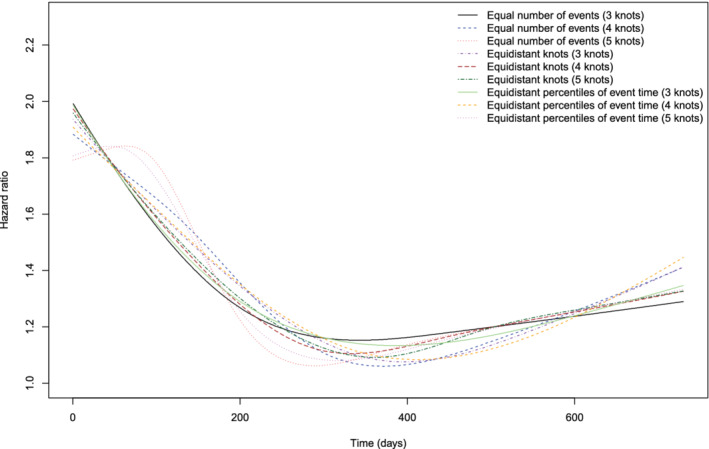
Comparison of different methods for selecting knots for RCS

TABLE 2.

AIC statistics for the nine different RCS models

	Method to select location of knots
Number of knots	Equal number of deaths per interval	Equidistant knots	Equidistant percentiles
3	80 874.393	80 886.104	80 875.787
4	80 906.441	80 921.564	80 905.902
5	80 923.246	80 955.543	80 917.574

When we fit the model that assumed a piecewise constant hazard ratio for elevated troponin, the estimated hazard ratios were 1.78 (95% CI: 1.59‐1.99) over 0 to 6 months, 1.06 (95% CI: 0.87‐1.29) over 6 to 12 months, 1.30 (95% CI: 0.98‐1.74) over 12 to 18 months, and 1.21 (95% CI: 1.01‐1.46) over 18 to 24 months. These estimated hazard ratios display a pattern that is similar to the relationship identified using RCS above.

We used the Kolmogorov‐Smirnov supremum‐type test on 1000 resamplings of the cumulative sums of martingale residuals to assess the validity of the proportional hazards assumption for all model covariates. In addition to elevated troponin, 11 variables were identified for which the proportional hazards assumption was violated: systolic blood pressure (P < 0.0001), transport to hospital by emergency medical services (EMS) (P < 0.0001), heart rate (P < 0.0001), pneumonia (P < 0.0001), male sex (P = 0.0070), oxygen saturation (P < 0.0001), myocardial infarction (P = 0.0200), cardiopulmonary respiratory failure and shock (P = 0.0060), renal failure (P = 0.0020), dementia (P = 0.0450), and metastatic cancer (P = 0.0160).

The FP selection algorithm identified nine covariates (apart from elevated troponin) that displayed a time‐varying covariate effect: systolic blood pressure, transport to hospital by EMS, heart rate, history of pneumonia, male sex, history of heart failure, history of psychiatric disorder, history of hypertension, and oxygen saturation. Transport to hospital by EMS used the FP(−0.5, 3) transformation, while history of hypertension used the FP(−2) transformation. The other seven covariates used a FP(0) transformation. Note that the FP selection algorithm uses the FP(0) transformation as the default time‐varying FP1 transformation (ie, that the log‐hazard ratio is a logarithmic function of time). The selected function relating the log‐hazard ratio to time for each covariate is reported in Table 3. The relationship between time and the time‐varying hazard ratio for these nine covariates are displayed in Figure 3. Estimates of the time‐varying hazard ratio obtained using both FPs and restricted cubic splines are illustrated in this figure.

TABLE 3.

Function describing the log‐hazard ratio as a function of time for the variables identified as having non‐proportional effects using the FP selection algorithm

Variable	Log‐hazard ratio as a function of time
Elevated troponin	0.949 − 0.122log(t)
Transport by EMS	−0.072 − 1.350t −0.5 − 0.000000001t 3
Systolic blood pressure	−0.025 + 0.002log(t)
Heart rate	0.014 − 0.003log(t)
Pneumonia	0.576 − 0.095log(t)
Heart failure	−0.121 + 0.058log(t)
Male sex	−0.229 + 0.063log(t)
Psychiatric disorder	−0.225 + 0.113log(t)
Hypertension	−0.151 − 0.297t −2
Oxygen saturation	−0.026 + 0.004log(t)

FIGURE 3.

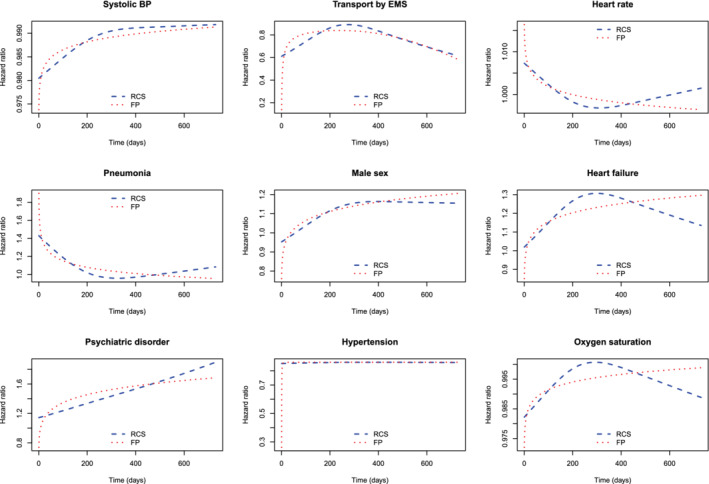
Time‐varying hazard ratios for other covariates

Note that there were five variables that were identified as violating the proportional hazards assumption using the supremum‐type test that were not identified as such using the FP selection algorithm (myocardial infarction, cardiopulmonary respiratory failure and shock, renal failure, dementia, and metastatic cancer). Similarly, there were three variables that were identified as having time‐varying effects using the FP selection algorithm that were not identified as such using the supremum‐type test (history of heart failure, history of psychiatric disorder, and history of hypertension). This difference likely reflects the fact that different methods for testing the proportional hazards assumption have different statistical power. ²⁶

The confidence intervals reported above were constructed using normal‐theory methods based on model‐based estimates of SEs. We conducted a secondary set of analyses to examine the degree to which these model‐based confidence intervals reflected the variation induced by the selection process. For computational reasons, we used a simplified model in which only the effect of elevated troponin was allowed to vary as a function of time. The remaining covariates were assumed to have time‐invariant effects. For both the RCS approach and FP approach, we used bootstrap‐based methods to estimate the SEs of the estimated log‐hazard ratios at each time. For the FP approach, we drew 200 bootstrap samples and applied the FP selection algorithm in each bootstrap and then estimate the log‐hazard ratio at each time (day 1 to day 730) in each bootstrap sample. Then, at each day (day 1 to day 730), we computed the SD of the estimated log‐hazard ratio across the 200 bootstrap samples and used this as an estimate of the standard error of the estimated log‐hazard ratio obtained in the original sample. Confidence intervals were then constructed using normal‐theory methods. For the RCS method, the identical approach was used. We also examined a second bootstrap approach for the RCS method. In this second approach, we drew 2000 bootstrap samples and computed bootstrap percentile‐intervals using the 2.5th and 97.5th percentiles of the estimated hazard ratio across the 2000 bootstrap samples. Results are reported in Figure 4. The left panel has results for the RCS method while the right panel has results for the FP approach. In each panel, confidence intervals constructed using bootstrap methods are compared with conventional model‐based standard errors.

FIGURE 4.

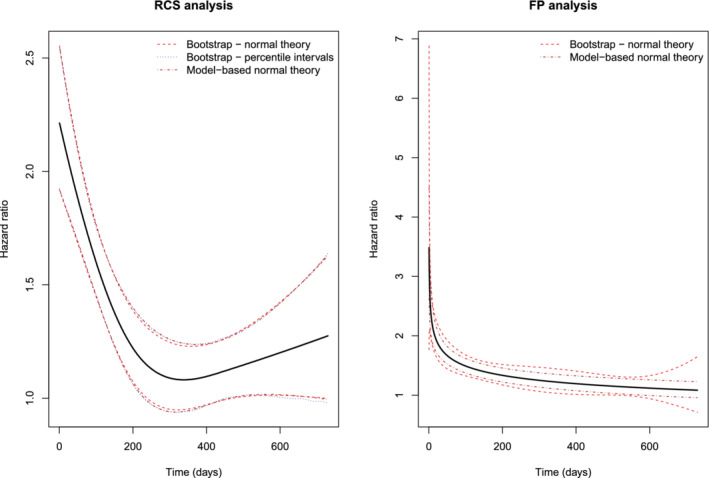
Comparison of model‐based and bootstrap confidence intervals

For the RCS analysis, there was very good agreement between the three different sets of confidence intervals. When comparing the model‐based normal‐theory confidence intervals with the normal‐theory bootstrap confidence intervals, the minimum and maximum differences in the widths of the confidence intervals across the 731 times were −0.022 and 0.028, respectively. When comparing the model‐based normal‐theory confidence intervals with the bootstrap percentile confidence intervals, the minimum and maximum differences in the widths of the intervals were −0.022 and 0.018, respectively. When comparing the normal‐theory bootstrap confidence intervals with the bootstrap percentile intervals, the minimum and maximum differences in the widths of the intervals were −0.033 and 0.031, respectively. For the FP analysis, the minimum and maximum differences in the widths of the confidence intervals were 0.052 and 3.252, while the median difference was 0.139 (25th and 75th percentiles: 0.094 and 0.167). The greatest differences in the widths occurred at the extremes of time. Thus, there is some evidence that, in this specific setting, the model‐based standard errors for the selected FP model do not adequately reflect the true sampling variability that is induced by the FP selection algorithm.

5. DISCUSSION

We described two methods, the first based on FPs and the second based on RCS, to model hazard ratios as a smooth nonlinear function of time.

There are advantages and disadvantages to each method. A limitation of the RCS method is that it requires selecting both the number of knots and the location of the knots. In our application, we found that the estimated time‐specific hazard ratios were relatively insensitive to these choices. However, this may not be so in all applications (however, it has been suggested that, as long as the location of knots are chosen sensibly, the location of knots will have a minimal impact on the subsequent analysis ¹⁷ ). In contrast to this, the FP method provides a structured procedure for choosing between the 44 different FP1 and FP2 transformations. An advantage to the FP method is that the available transformations include the logarithmic transformation, which was found to work well in our application. A drawback to the FP method is that it is substantially more computationally demanding. Fitting the model that used RCS to model time‐varying effects for all covariates required approximately 3 hours and 40 minutes (using SAS), while the FP selection algorithm required approximately 268 hours (using Stata) on the same computing environment.

In our application, the estimated hazard ratios from the FP approach are more clinically plausible than are those from the RCS analysis. It is more likely that elevated troponins exert an initial strong effect which then declines over time. This pattern of initial risk escalation with elevated troponin has multiple potential mechanisms, including acute cardiac injury or ischemia, inflammatory cytokine release, and other early effects. ²⁷ From a clinical perspective, there is no rationale for the troponin hazard ratio to decline to a nadir at 10 months and then to subsequently increase over time. Indeed, in the context of non‐ST‐elevation myocardial infarction, another condition characterized by acute cardiac injury and troponin release, an early acceleration of mortality was demonstrated in a merged analysis of 14 trials from the thrombolysis in myocardial infarction (TIMI) investigators. ²⁸

The methods described in the current study are not novel. When using FPs to model time‐varying covariate effects, our approach was based on that described by Sauerbrei et al ¹⁹ and described above. Similarly, Hess described methods to use RCS to model time‐varying covariate effects in the Cox model. Abrahamowicz et al ⁹ used regression splines (which differ from RCS) to model the hazard ratio as a flexible function of time. There is an approach to addressing non‐proportionality that we did not consider. An alternative approach is to stratify on the variable that violated the proportional hazards assumption. ¹⁵ In doing so, one is allowing the baseline hazard to vary across strata defined by levels of this variable. However, in doing so, one is no longer able to estimate the effect of that covariate on the hazard function. When the variable in question is the primary variable or exposure of interest, this option is not possible as one can no longer make inferences about this variable.

In the current study, we have focused on methods to model the non‐proportional effects of covariates as smooth functions of time. We have not examined issues around simultaneously relaxing the assumption that a continuous covariate is linearly related to the log‐hazard of the outcome. Abrahamowicz and MacKenzie ²⁹ described methods based on regression splines to relax both the proportional hazards assumption and the assumption that covariates are linearly related to the log‐hazard function. Both Abrahamowicz and MacKenzie ²⁹ and Wynant and Abrahamowicz ¹⁸ demonstrated that estimation of nonlinear effects and time‐dependent effects are dependent on one another and that mismodeling of one aspect can lead to biased estimation of the other aspect. Similarly, as noted above, Sauerbrei et al ¹⁹ describe how FPs can be used to identify nonlinear transformations of continuous covariates and allow for non‐proportional hazards.

In the current study we have focused on time‐invariant covariates. Kooperberg and Clarkson ³⁰ extended the hazard regression model, earlier developed by Kooperberg, to allow for the inclusion of time‐dependent covariates. Heinzl et al ³¹ described methods to use cubic spline functions to allow the hazard ratio for time‐dependent covariates to vary as a function of time. Wang et al ³² described a method based on B‐splines to model time‐varying effects of time‐dependent covariates.

If one ignores the violation of the proportional hazards assumption and fits a model in which the effect of a covariate is assumed to be constant over time, the resultant hazard ratio can be interpreted as the weighted average of the time‐specific hazard ratios, where the weights reflect the distribution of event times (not survival times). ³³ In our case study, the naïve adjusted hazard ratio for elevated troponin when we assumed a time‐constant hazard ratio was 1.47. The weighted average of the time‐specific hazard ratios obtained using the FP and RCS approaches were both equal to 1.44. We suspect that when the proportional hazards assumption is violated and as the duration of follow‐up increases, reporting a time‐averaged hazard ratio may be of less utility than reporting time‐specific hazard ratios.

In the case study, we considered an alternative approach which involved partitioning time into distinct intervals and allowing the hazard ratio to be constant within each interval. There are several limitations to this approach. First, it involves categorizing time, which is an inherently continuous variable. In general, the categorization of continuous variables has been criticized because of the inherent loss of information. ¹⁷ , ³⁴ Second, the resultant hazard ratio is a step function of time. From a biological perspective step functions often lacks plausibility. In our context, it is unlikely that the hazard ratio changes discretely at a given point in time and is then constant over the next duration of time. Third, the choice of number of time intervals and their duration is somewhat subjective. We suspect that the estimated hazard ratios using this approach are more affected by the choice of the number of intervals and their duration than the estimated hazard ratios obtained from an RCS analysis are affected the number and location of the knots. Quantin et al ⁵ noted that the use of the piecewise proportional hazard model can result in “jumpy” estimates that may be clinically implausible and that the results may depend on the number of time intervals and how they are constructed.

When including continuous variables as predictors in regression models (eg, age), analysts are increasingly encouraged to not categorize the variable and also to not assume a linear relationship between the continuous predictor and the outcome. ¹⁶ , ¹⁷ , ³⁴ Categorization entails an implicit loss of information and imposes an assumption that the underlying relationship involves a step function, which is often clinical implausible. Similarly, imposing an assumption of linearity is often unnecessarily restrictive. Consequently, authors are increasing using flexible methods such as RCS and FPs to allow for nonlinear association between predictors and outcomes. The methods that we have summarized in this article allow authors to extent these flexible modeling methods to time‐varying covariate effects, not just the effect of covariates on the outcome.

In conclusion, we have described two flexible methods to relax the proportional hazards assumption for a variable in a Cox regression model. Both methods allow the estimated regression coefficient, and thus the hazard ratio, to vary smoothly as a function of time. These methods permit a more detailed examination of the effect of a covariate on the hazard function over time than more simplistic methods such as assuming that the log‐hazard ratio is a linear function of time.

Austin PC, Fang J, Lee DS. Using fractional polynomials and restricted cubic splines to model non‐proportional hazards or time‐varying covariate effects in the Cox regression model. Statistics in Medicine. 2022;41(3):612–624. doi: 10.1002/sim.9259

DATA AVAILABILITY STATEMENT

The datasets used for this study were held securely in a linked, de‐identified form and were linked using unique encoded identifiers and analyzed at ICES. While data sharing agreements prohibit ICES from making the data set publicly available, access may be granted to those who meet pre‐specified criteria for confidential access, available at www.ices.on.ca/DAS.