Abstract
Biological behaviour‐driven self‐organized patterns have recently been confirmed to play a key role in ecosystem functioning. Here, we develop a theoretical phase‐separation model to describe spatiotemporal self‐similar dynamics, which is a consequence of behaviour‐driven trophic interactions in short‐time scales. Our framework integrates scale‐dependent feedback and density‐dependent movement into grazing ecosystems. This model derives six types of selective foraging behaviours that trigger pattern formation for top‐down grazing ecosystems, and one of which is consistent with existing foraging theories. Self‐organized patterns nucleate under moderate grazing intensity and are destroyed by overgrazing, which suggests ecosystem degradation. Theoretical results qualitatively agree with observed grazing ecosystems that display spatial heterogeneities under variable grazing intensity. Our findings potentially provide new insights into self‐organized patterns as an indicator of ecosystem transitions under a stressful environment.
Keywords: herbivores‐grazing systems, movement behaviour, phase separation, scaling law, self‐organization
Biological behavior‐driven self‐organized patterns have recently been confirmed to play a key role in ecosystem functioning. Here we develop a theoretical phase‐separation model describing spatiotemporal self‐similar dynamics, which is a consequence of behavior‐driven trophic interactions in short‐time scales. Our findings potentially provide new insights into self‐organized patterns as an indicator of ecosystem transitions under a stressful environment.

INTRODUCTION
Impressive self‐organized spatial patterns are ubiquitous in ecosystems of different scales, from the network of bacteria colonization to the labyrinthic coral reef (Mistr & Bercovici, 2003; Tsimring et al., 1995). According to Turing principle (also called scale‐dependent feedbacks), the spatial patterns are generally considered to result from the local facilitation and competition at large scales (Klausmeier, 1999; Rietkerk & van de Koppel, 2008). Along with spatial pattern formation, the emergent properties from the self‐organization processes determine the ecosystem functioning at ecosystem levels like primary or secondary production, resilience, stability, as well as the indicator of ecosystem collapse (Bonachela et al., 2015; Guttal & Jayaprakash, 2007; Rietkerk et al., 2004). The present prevailing ecological self‐organization theoretical framework is based on Turing principle, which well describes the formation of persistent patterns. Turing‐type models couple the processes of dispersal, growth and mortality, so that they describe non‐equilibrium patterns based on a demographic process (Liu et al., 2016; Meinhardt et al., 2009). Vegetation patterns of arid ecosystems tardily arise from the scale‐dependent feedbacks between plant and soil water within decades or even centuries (Rietkerk et al., 2002). Different from scale‐dependent feedbacks, motility‐induced phase separation (MIPS) that is driven by density‐dependent movement behaviours can rapidly produce arrested or transient spatial patterns in the timescale of days or years (Table 1, Liu et al., 2016).
TABLE 1.
Joining the theoretical and experimental ecologists' perspectives on terms and interpretations of spatial‐temporal dynamics
| Term | Interpretation | Mathematical expression | |
|---|---|---|---|
| Thermodynamic phase separation | Two distinct phases generate from a single homogeneous mixture, driven by an associated reduction in free energy of the system. A classic example is that when water and oil are mixed together, they spontaneously separate to form a water phase and an oil phase. The mobility of the phase‐separating components is similar. |
is the volume fraction or mass fraction of one component in binary mixtures systems. |
|
| Motility‐induced phase separation | The mobility of self‐propelled organism/particle is featured with density‐dependent movement. Self‐propelled individuals tend to accumulate where they move more slowly, whereas dissipate from over‐dense areas. This positive feedback makes the system separate into dense and dilute phases. | Equation (2) and Equation (5) | |
| Spinodal instability | In phase‐separation principle, one homogeneous mix phase spontaneously separates into two distinct phases with infinitesimal disturbance. | is the free‐energy function of the systems. | |
| Velocity‐induced drift flux | Drift is the slow movement of an object toward something, and the drift velocity is the average‐velocity of an object during drift. Drift flux is defined as the volumetric flux of either component relative to a surface moving at drift velocity. |
|
|
| Biased random walk | Non‐Brownian diffusion, a random walk that is biased in certain directions, leading to a net drift on average of particles in one specific direction. A random walk can be based on three circumstances: 1) a higher probability of moving to certain directions under uniform moving step lengths; 2) suppose the probabilities of moving to all directions remain equal, but nonuniform moving step lengths; 3) nonuniform moving directions and moving step lengths. | Codling et al., 2010 | |
| Coarsening/Ostwald ripening | A phenomenon originally observed in solid solutions or liquid sols that describes the change of an inhomogeneous structure over time: the growth of large clusters at the expense of smaller ones (Movie S1). | , where is patch size or spatial wavelength, is the exponent of scaling law, and is the classic Lifshitz–Slyozov law. | |
| Hyperuniform structure | In d‐dimensional Euclidean space, a hyperuniform structure is characterized by an anomalous suppression of large‐scale density fluctuations relative to those in typical disordered systems. Thus, the hyperuniform structure is more uniformly distributed than Poisson spatial distribution in large spatial scales. | , and . |
Phase‐separation patterning is ubiquitous in polymers, cells, organs, organisms, ecosystems and even astronomical systems (Alberti, 2017; Brangwynne et al., 2015; Tremaine, 2003). Unlike the traditional thermodynamic phase separation that is driven by enthalpy and entropy in equilibrium systems, MIPS has been proved to be driven by active motility in non‐equilibrium systems (Table 1; Cates & Tailleur, 2015; Dong & Granick, 2021). In ecosystems, MIPS has been theoretically and experimentally confirmed to perform in a single trophic level (Liu et al., 2013; de Paoli et al., 2017). The density‐dependent movement broadly appears in many ecosystems like bacteria, elegans, ants, birds and elk (Demir et al., 2020; Liu et al., 2016). Thus, phase separation has the potential to become a novel theoretical framework of behaviour‐driven ecological self‐organization. Phase separation can bridge individual plasticity and the collective actions of individuals, and can be used to study the interaction between the evolution of biological behaviours and ecological pattern formation. Phase separation can function in short term, which makes it a powerful tool to infer or identify ecological processes from ecosystem‐level scales. Besides that, rapidly emerging transient patterns can affect ecosystem functioning more quickly than persistent patterns do (de Paoli et al., 2017; Zhao et al., 2021). Therefore, massive efforts should be urgently devoted to developing theories that integrate biological behaviour and ecological processes.
Spatial vegetation patterns are widely present in grazing ecosystems (Figure 1). Grazing ecosystems provide humans with huge amounts of edible protein, but excessive anthropogenic grazing activities increase ecosystem vulnerability (Steinfeld et al., 2006). Spatial vegetation patterns are closely linked with the forage quality and are sensitive to degradation under stressful environments (Mueller et al., 2014; Steinfeld et al., 2006). Thus, understanding the grazing‐induced pattern formation of vegetation is obligatory for rangeland management and ecological conservation, and tackles ‘the central problem in ecology’ (Levin, 1992). Hitherto, the interpretation of spatial vegetation patterns in grazing ecosystems has largely depended on a bottom‐up or top‐down viewpoint. From the bottom‐up perspective, herbivores affect plant mortality and then indirectly influence regular vegetation patterns in Turing‐type models or power‐law vegetation patterns of Mediterranean arid ecosystems (HilleRisLambers et al., 2001; Kéfi et al., 2007; Siero, 2018). Herbivores grazing and the disturbance to nutrient input lead to the formation of the shifting mosaics of the grazing lawn in African savanna grasslands (Cromsigt & Olff, 2008). However, few studies explicitly consider the role of herbivores’ behaviour in shaping spatial vegetation patterns.
FIGURE 1.
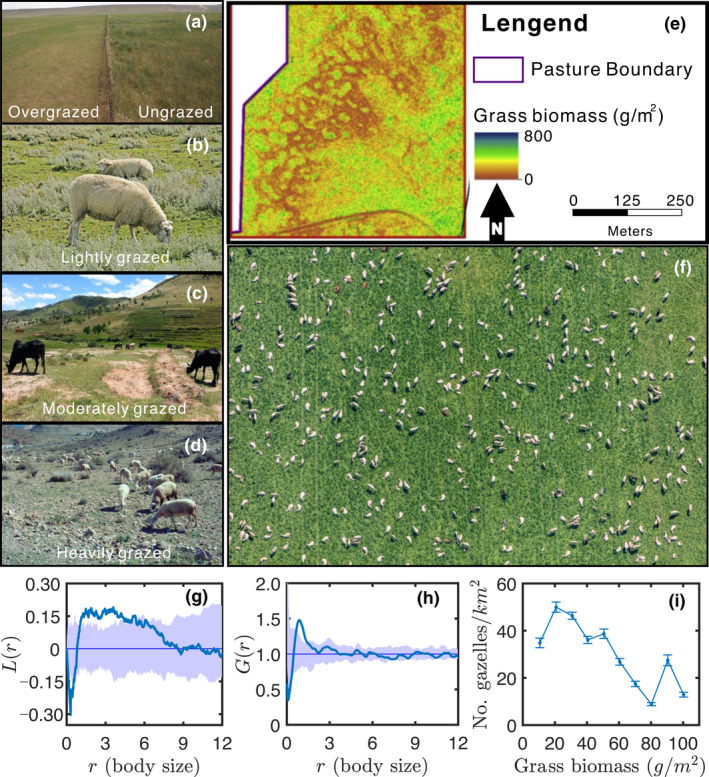
Patterns of some grazing ecosystems. (a) Overgrazed and 30 years grazing‐excluded grassland in inner Mongolia, China [reprinted with permission from Hobley et al. (2018)]. (b) Lightly grazed salt marsh in north Germany. Photo credit: Leser Nicolas. (c) Moderately grazed grassland in Madagascar. Photo credit: Maria S. Vorontsova. (d) Heavily grazed dryland in southeast Spain [reprinted with permission from Mueller et al. (2014)]. (e) The spatial pattern of grass biomass after grazing in the Zumwalt Prairie, northeast Oregon [reprinted with permission from Jansen et al. (2019)]. (f) The spatial pattern of sheep on Ölling, Bayern, Germany [Image credit: Klaus Leidorf]. (g) and (h) Ripley's L function and pair correlation function for the point pattern of sheep in (f), and is Euclidean distance. The lighter blue shaded areas represent 95% simulation envelopes to distinguish from complete spatial randomness. Details of images analyses are in the Supporting Information. (i) Densities (mean ± SD) of adult Thomson's gazelles in relation to grass biomass over 16 censuses during 1995–1996 in Serengeti. This figure was modified from Fryxell et al. (2004)
Ample evidence shows that ungulate herbivores and herbivorous birds have selective foraging behavior that they prefer short and low‐biomass plants because of their high energy and rich nutrients (Menard et al., 2002; Person et al., 2003; Van der Heide et al., 2012; Wilmshurst et al., 1995, 1999). From the top‐down perspective, this selective foraging behavior and the optimal foraging of herbivores are considered as the potential mechanisms by which herbivores create spatial vegetation patterns in short term (Mouissie et al., 2008). By considering food/energy intake and digestive limitations, existing lattice cell models of foraging set the purpose of herbivore movement as maximizing food/energy intake. These models have been parameterized against Serengeti wildebeest, and well explained the spatial heterogeneity of the herbivores and vegetation (Fryxell et al., 2004, 2005; Holdo et al., 2009). In top‐down grazing ecosystems, selective foraging behaviours drive distinct vegetation landscapes under different grazing intensities, and overgrazing leads to a uniform state of degradation (Person et al., 2003; Van der Heide et al., 2012; Weerman et al., 2011). However, identifying the selective foraging behaviour of herbivores as a necessary condition for inducing spatial heterogeneity of vegetation in top‐down grazing ecosystems has yet to be theoretically proved.
Here, we derive the bivariant coupled partial differential equations (PDEs) based on herbivore‐behavioural movement and the interaction between herbivores and resources. The theoretical analysis of our MIPS model shows that six types of selective foraging behaviours can generate spatial patterns in grazing ecosystems. Our results suggest that besides the scale‐dependent feedback, the previously observed vegetation patterns are also attributed to phase separation. Self‐similar coarsening is also considered as a hallmark to distinguish phase separation in ecosystems. We find that spatial pattern transits from labyrinths to isolated spots to homogeneous states when the ecosystem experiences overgrazing, and self‐organized patterns can indicate ecological degeneration. Our findings provide new insights into the spatial self‐organization of grazing ecosystems induced by the behaviour of consumers.
METHODS
The theoretical model of grazing behaviour
We build a theoretical model based on the framework of resource‐dependent movement instead of pure Brownian‐like motion. The original idea is motivated by the pioneering works of Focardi et al., (1996) and Liu et al., (2013). In both of them, experimental evidence showed organisms (adult female fallow deer, Dama dama L., and blue mussel, Mytilus edulis) displaying aimless foraging behaviour with a first‐order biased random walk (Table 1). Following these findings, we assume that herbivores do unconventional random walks to graze. In general, an herbivore could adjust its movement speed according to the local resource concentration and the local herbivore density , where is a spatial location and is time. Then, the herbivore movement in space can be described as diffusivity of Brownian‐like particles (Berg, 1983; Einstein, 1905): . Here, is the turning rate of herbivore trajectories during foraging, and is the spatial dimensionality.
If depends on both herbivore density and resource concentration in a biased random walk, it leads to a local‐drift flux which also depends on herbivore density and resource concentration (Table 1; Schnitzer, 1993; Tailleur & Cates, 2008), i.e.:
| (1) |
where is the spatial gradient operator. Note that when is independent of herbivore density or resource concentration (i.e., is a positive constant), Equation (1) degenerates into the classic Fick's law in classic population models (Murray, 2002). In this sense, Equation (1) distinguishes from the previous reaction‐diffusion models and is the core of MIPS systems (Cates & Tailleur, 2015).
However, no experimental data shows that the speed of herbivores is simultaneously regulated by herbivore density and resource concentration. Hence, we assume the movement speed of an herbivore only depends on because existing field evidence implies that , experimentally confirmed to be inversely proportional to forage quality, regulates the movement speed of ungulate herbivores (Focardi et al., 1996; Fryxell et al., 2004; Wilmshurst et al., 1999). These density‐dependent movements suggest that the speed of an individual has a parabolic relationship with local density (Liu et al., 2016), so is also assumed to be a quadratic polynomial here:
| (2) |
where and are real coefficients, and is the movement speed of an herbivore when there is no resource. Note that we only assume a polynomial function here, and none of the monotonous properties are presupposed. Higher‐order polynomials like a cubic or quartic function can also be assumed, and the order of the polynomial does not qualitatively change the condition of pattern formation. It is worth mentioning that non‐polynomial functional form of density‐dependent movement can also cause MIPS for sorted patterned ground (Li et al., 2021).
Substituting into Equation (1) and introducing a high‐order correction term:
| (3) |
where is a positive coefficient. This high‐order correction term indicates that the movement speed of an herbivore may also depend on a small local region around it because an herbivore cannot be infinitely small in the real world (Tailleur & Cates, 2008), and also mathematically eliminates the possibility of explosive solutions. Besides that, since the timescale of herbivore movement is much shorter than that of the birth/death process of herbivores, demographic process of herbivores in short term is excluded from consideration here. With the general conservation dynamics , we obtain the dynamics equation for herbivores density as:
| (4a) |
where is a positive coefficient.
For resource (e.g. plants), we consider logistic growth, herbivore grazing and classic random dispersion:
| (4b) |
where is the intrinsic growth rate of the plants, is the environmental carrying capacity for plants, is the feeding rate of herbivores and is the diffusivity of plants. Equations (4a and 4b) form the model of a movement‐behavior‐driven grazing ecosystem. The loss of resource mainly depends on herbivores, which suggests this model being a top‐down consumer‐resource system.
With scaling , , , , , , , , , we obtain the dimensionless form of Equations (4a and 4b) as follows:
| (5) |
Here and are dimensionless resource concentration (e.g., plant density) and herbivore density, respectively. Parameter , related to environmental factors like precipitation or nutrition, is the growth rate of resource, and parameters and are behaviour coefficients of the dimensionless movement speed of an herbivore :
| (6) |
Equation (5) is our MIPS model. In this study, the theoretical analysis of Equation (5) is limited to linear stability analysis (see the Supporting Information). The nonlinear properties of Equation (5), not relevant to the main results of this study, are left for future work. The numerical implementation of Equation (5) is described in the Supporting Information.
Spatial characteristic scales
The patch size of spatial patterns, , is defined as a distance at which the variable (e.g. resource concentration) is no longer autocorrelated, and is used to check if the temporal evolution of spatial patterns experiences coarsening (Table 1). Lifshitz–Slyozov (LS) law, describes the patch size of the spatial pattern growing with a scaling‐law of , is a standard procedure to check the coarsening behaviour (Lifshitz & Slyozov, 1961). Structural factor analysis is used to identify if our model is featured with spatiotemporal self‐similar dynamics. The density fluctuation of spatial patterns is adopted to measure aggregation or dispersion degree of the spatial distribution of systems. The details of these methods and the image analysis of Figure 1f are described in the Supporting Information.
RESULTS
Diverse selective foraging behaviours causing pattern formation
Herbivores have been found to have selective foraging behaviours in both the wild and fenced environments. The movement speed of herbivores varies significantly during foraging: the herbivores speed off to seek for short and low‐biomass plants when they meet tall and high‐biomass plants and slow down to graze short and low‐biomass plants (Figure 2a). The theoretical analysis of Equation (5) shows that this resource‐dependent foraging behaviour of herbivores is essential to the natural emergence of spatial heterogeneity in top‐down grazing ecosystems (Equation (S11), e.g. Figure 2b). This foraging behaviour yields a variation of net diffusion from negative to positive with the increase of local plant density (Figure 2c), and the mass of the system could spontaneously transport from low density to high density. The positive feedback, short and low‐biomass plants attract more herbivores and grazing of herbivores produces short and low‐biomass plant, consequently forms between grazing and palatability (Bakker et al., 1984). This positive feedback leads to herbivores assembling in areas of lower plant density and dispersing from areas of higher plant density (Figure 2c).
FIGURE 2.
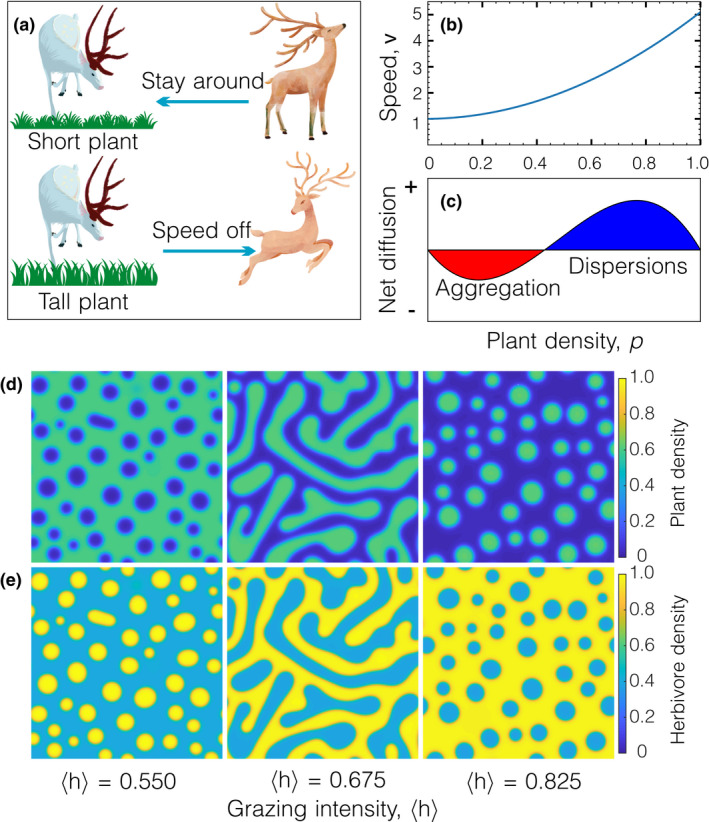
The density‐dependent movement of herbivores leads to diverse spatial patterns of vegetation. (a) Selective foraging behaviour of herbivores. Herbivores prefer short and low‐biomass plants and stay around while they dislike tall and high‐biomass plants and speed off. (b) An example of herbivore movement speed depending on plant density with and . (c) Schematic representation of the feedback in phase separation. Low plant density induces the aggregation of herbivores while high plant density triggers the dispersion of herbivores. (d) and (e) The transient spatial patterns under different stocking rates with , , and . is the spatial average of herbivore density corresponding to the stocking rate
Further analysis of Equation (S11) shows that the two behavioural parameters, and , are constrained by six different conditions (Table S1). This means that the six types of resource‐dependent movement behaviours can lead to pattern formation (Figure 3). The of Types I to III and V are monotonically increasing functions that consist with the idea of selective foraging behaviour. However, these types of suggest that herbivores most strongly cling to locations with no plants, and this situation is inconsistent with ungulate herbivores, such as Gazella thomsoni thomsoni in Serengeti (Figure 1i). The of Type VI is a function that increases first and then decreases, but it is inconsistent with the idea of selective foraging behaviour of ungulate herbivores. The of Type IV implies that herbivores prefer low plant density rather than no plants. This result consists with the idea of selective foraging behaviour as well as the current foraging theories of grazing ecosystems (Fryxell et al., 2004). Our framework suggests that resource‐dependent foraging behaviour of herbivores could exclusively shape spatial heterogeneity of grazing ecosystems. Although individuals may have variable selective foraging behaviours in a population, numerical simulations of our model manifest that the ability to shape spatial heterogeneity relies on the personalities at the population level rather than the personality at the individual level of herbivores (Figure S1).
FIGURE 3.
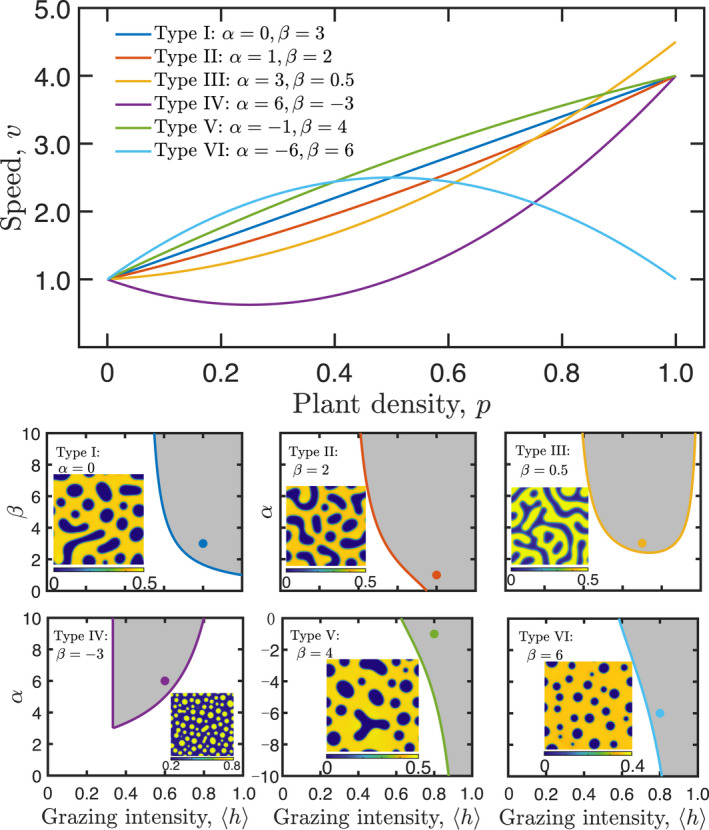
Six types of selective foraging behaviours leading to pattern formation derived from the model. Top: specific examples of six types of selective foraging behaviours. See the Supporting Information for the constraints of behaviour coefficients and (Table S1). Bottom: the phase diagram of grazing intensity and behaviour coefficients for six types of selective foraging behaviours in the model (Equation (S12) in the Supporting Information). Shaded areas are spinodal zones where infinitesimal perturbation to the initial uniform condition of herbivores or vegetation can cause pattern formation. In every image, the spatial pattern is a transient vegetation pattern with , and the parameters of the spatial pattern are associated with the dot
Phase separation in grazing ecosystems
Figure 1i shows that there are two distinct phases in the grazing ecosystem of Gazella thomsoni thomsoni in Serengeti. One phase is featured with many Thomson's gazelles and low grass biomass, and the other one is featured with few Thomson's gazelles and high grass biomass. The model‐generated spatial patterns capture this characteristic of the grazing ecosystem that the spatial patterns of herbivores are antiphase to that of plants (Figure 2d,e). Livestock rarely needs to actively form herds to cope with predators and long‐distance migrations. The sheep present spatial aggregation in the spatial scale of about 1~2 body size and form a labyrinth pattern in a commercial pasture (Figure 1f‐h), which is probably due to selective foraging behaviour (see the Supporting Information). Our model also generate a labyrinth pattern of herbivores (Figure 2e). Besides that, increasing grazing intensity (, spatial average of ) or decreasing growth rate of plants () both sequentially create transient spatial patterns from gaps, labyrinths/strips to spots (Figure S2). These shapes are also common in traditional Turing‐type models, which makes it necessary to further clarify the difference between our phase‐separation model and traditional Turing‐type models.
The most intuitive and important hallmark of a phase‐separation process is the coarsening of spatial patterns (Movie S1). Spatial vegetation patterns start with fine‐grain then change over time toward a coarse‐grain structure as adjacent patches merge to form larger patches, and this coarsening‐like phenomenon has been reported in both grassland and salt marsh grazing ecosystems. Berg et al., (1997) showed that sheep grazing leads to small patches of tall F. rubra merging into bigger patches in the salt marsh, and both Bakker et al., (1984) and Dumont et al., (2012) showed similar phenomenon caused by sheep/cattle grazing in the grassland. We infer that the coarsening‐like phenomenon of vegetation patterns in grazing ecosystems is possibly attributed to Ostwald ripening in the phase‐separation theory (Table 1). Our model slightly deviates the standard exponent of of LS law in the thermodynamic phase separation, but it holds a robust scaling law or which is still a hallmark of patterns manifesting phase separation (Figure 4b,d). However, the patch size of Turing‐type instability usually grows with a sigma‐type curve, which shows no such type of scaling law. Our model is a non‐conservative system, and the pattern is not arrested at a fixed patch size and continues coarsening with time (Figure S3). This feature is also similar to the thermodynamic phase separation featured with the conservative dynamics. This coarsening behaviour of patterns has been observed in natural grazing ecosystems while unfortunately none of these studies recorded enough data to check the scaling law of pattern coarsening.
FIGURE 4.
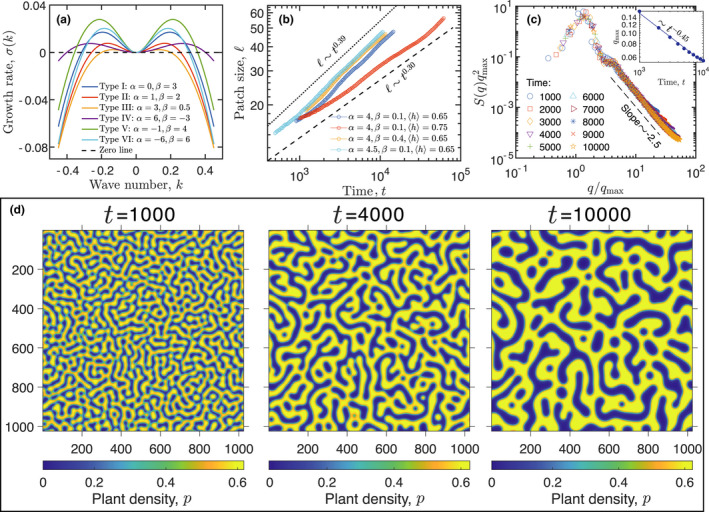
The occurrence of phase separation in Equation (5). (a) The growth rates of six types of selective foraging behaviour corresponding to Figure 3. (See the Supporting Information for details of ). (b) The scaling law of coarsening dynamics of patch size based on numerical analysis of the vegetation patterns in the model. is the spatial average of herbivore density. (c) The vegetation patterns, corresponding to the dotted blue line as shown in (b), show spatiotemporal self‐similarity through structure factor analysis. (d) The coarsening vegetation patterns of the dotted blue line in (b)
The other two hallmarks of a phase‐separation system are the zero point of growth rate (, where is wave number, see the Supporting Information) and spatiotemporal self‐similar dynamics. A phase‐separation system requires (Figure 4a), whereas the Turing‐type instability requires . The rescaled dynamic structural factors collapse to a master line and its tail satisfies a scaling law (Equation (S31) and Equation (S32)), suggesting the temporal and spatial scaling property of the emergent length scale in our MIPS model (Figure 4c). This property indicates that our model is featured with the dynamics of spatiotemporal self‐similarity, which is similar to the thermodynamic phase separation, whereas the traditional Turing‐type models only have spatial self‐similarity.
Pattern transition and the implications
An important phenomenon that moderate grazing intensity causes prominent spatial vegetation patterns has been observed in many commercial pastures. Berg et al., (1997) set up experimental treatments with 0, 1.5, 3, 4.5 and 10 sheep/ha with an initially uniform vegetative state in the salt marsh. During the three years of the experiment, spatial vegetation patterns only occurred under moderate treatments (1.5–4.5 sheep/ha) with the most remarkable spatial patterns under the treatment of 3 sheep/ha. The first regime shift, featured with a transition from a homogenous vegetative state to a spatially patterned vegetative state, occurred from 0 to 1.5 sheep/ha. The second regime shift, in contrast to the first one, appeared from 4.5 to 10 sheep/ha. Cid and Brizuela (1998) experimentally confirmed that moderate cattle grazing always caused spatial heterogeneity of vegetation with a single species Festuca arundinacea Schreb. Jansen et al., (2019) used LiDAR to quantify the high spatial resolution aboveground plant biomass of 23 commercial pastures in grassland (Figure 1e). Their experimental evidence demonstrated that the spatial heterogeneity of vegetation and stocking rate present quadratic function relation, and striking spatial vegetation patterns appeared under moderate stocking rates. Our MIPS model provide a theoretical explanation for these field experiments and observations.
The grazing intensity () and selective foraging behaviour coefficient () are used as key factors to understand grazing ecosystems. Equation (5) has three distinct regimes in the ‐plane space: unstable two‐phase zone, metastable zone with one or two phases, and stable zone with one phase (Figure 5a). Spatial patterns under variable grazing intensity with fixed selective foraging behaviour coefficient () are shown in Figure 5. No spatial patterns form under nearly ungrazed condition (‘1’ in Figure 5a,c1). Spatial patterns may appear with grazing intensity increases from nearly ungrazed to lightly grazed condition (‘2’ in Figure 5a,c2) and are almost inevitable under moderately grazed condition (‘3’ in Figure 5a,c3). Spatial patterns may disappear when grazing intensity increases from moderately grazed to heavily grazed condition (‘4’ in Figure 5a,c4), and will completely disappear under overgrazed condition (‘5’ in Figure 5a,c5). Under the moderate grazing intensity, any spatially slight disturbances of plants or herbivores lead to pattern formation (the light blue region in Figure 5a). The unstable two‐phase zone corresponding to moderate grazing intensity indicates that our model is capable of capturing the important phenomenon in top‐down grazing ecosystems.
FIGURE 5.
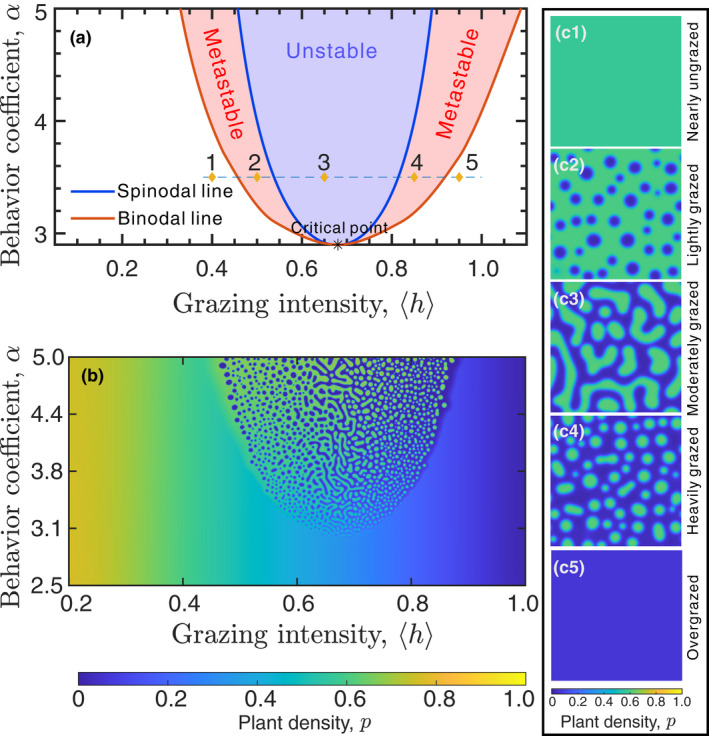
The phase diagram of our phase‐separation model. (a) The phase diagram with , and is obtained by Equation (S12) in the Supporting Information. This system mainly undergoes the first‐order phase transition between spatially homogeneous state and patterned state, and shows the continuous phase transition close to the critical point. The characters ‘1’–‘5’ are corresponding to Figures c1‐c5. The spinodal line and binodal line separate the phase diagram into three zones: the interior of the spinodal line is the unstable zone (light blue region) where infinitesimal perturbation to the initial uniform condition of herbivores or vegetation can cause phase separation; the portion between the spinodal line and the binodal line is the metastable zone (light red region) where large enough perturbation to the initial uniform condition of herbivores or vegetation can trigger phase separation; the portion beyond the binodal line is the stable zone (white region) where any initial states of herbivores and vegetation turn into near‐homogeneous states without the occurrence of phase separation. (b) The numerical simulation of spinodal instability shows decent consistency with the theoretical analysis of spinodal instability (Table 1). (c1)‐(c5) The transient spatial patterns that locate at the five different zones described in panel (a) with
The phase‐separation patterns generated by our model can indicate regime shifts of top‐down grazing ecosystems. Identifying the regime shift of an ecosystem by the shape of the spatial patterns has long been dependent on Turing principle (Rietkerk et al., 2004). Different from Turing‐type self‐organization, phase‐separation systems display two isolated metastable regimes (the light red region in Figure 5a), where the formation of spatial patterns strongly depends on the intensity and scale of the disturbance to the system and the former states of the system. This implies that the ecosystem can experience hysteresis under variable environmental stress. No patterns form under the one‐phase regime, and the spatial state of vegetation either is a healthy state or experiences degradation (the white region in Figure 5a).
DISCUSSION
Our MIPS model provides new insights into grazing ecology and foraging theory. Previous studies considered selective foraging behaviour of herbivores as an important disturbance that enhances pre‐existing vegetation patterns (Adler et al., 2001; Parsons & Dumont, 2003). Our work shows that herbivores can dominate heterogeneous landscape of grazing ecosystems through resource‐dependent foraging behaviour. In previous foraging models, selective foraging behaviour of herbivores is simultaneously driven by Brownian‐like random walk and the assumption of maximizing the food/energy intake (Farnsworth & Beecham, 1999; Pyke et al., 1977). In our model, herbivores do not need to choose a direction pointing to a location with the most food/energy intake, while selective foraging behaviour only requires that herbivores adjust their speeds based on local resource concentration. Previous experiments found the spatial scale of the initial disturbance and grazing intensity jointly dominate the spatial heterogeneity of vegetation in a savanna grazing ecosystem (Cromsigt & Olff, 2008). The existence of a metastable zone of our MIPS model may interpret this experimental result. Previous interpretation attributes the vegetation patch coarsening phenomenon to the proactive promotion of herbivores through certain animal wisdom (Dumont et al., 2000). Our study suggests that selective foraging behaviour of herbivores, rather than some wise behaviours, can exclusively cause coarsening of spatial vegetation patterns.
Our study highlights behaviour‐driven self‐organization in the top‐down consumer‐resource ecosystems. Previous studies of biological behaviour‐driven self‐organization focus on a single trophic level. For instance, mussels form regular patterns within a day through density‐dependent movement, and these patterns effectively reduce the mortality of mussels dislodged by waves (de Paoli et al., 2017); the stem inclination of sunflowers shift mediated by light signals to increase oil yield when sunflowers are planted at a high density (López Pereira et al., 2017); social insects conduct cooperative transport through the dynamic signal communication‐driven processes (Gelblum et al., 2015). Our work provides a theoretical foundation for behaviour‐driven phase‐separation patterns in two trophic levels. Although a system with passive movement (directional or random dispersal) can also generate similar spatial patterns, it still belongs to Turing instability paradigm with birth/death process (Anderson et al., 2012). Our MIPS model explains transient pattern formation that is driven by active consumer‐behavioural movement within the lifetime of consumers. We conclude that selective foraging behaviour is a key mechanism for understanding the observed patterns in grazing ecosystems and underlying processes.
Our model advances the current understandings regarding the ecosystem functioning of the ecological self‐organization mechanisms. The emergent properties that are accompanied by spatial self‐organized processes are critical to the maintenance of ecosystems and the realization of corresponding ecological functioning (Levin, 2005). Turing‐type self‐organization has been verified to enhance primary or secondary production in bottom‐up ecosystems. For example, plants of dryland zones could concentrate limited water recourse to maximize their biomass through the formation of Turing‐type patterns (Yizhaq et al., 2005). Although phase separation has induced cognitive revolution of cell functions, little is known about the ecological functioning of phase separation (Alberti & Dormann, 2019; Liu et al., 2016). Our results theoretically show that phase‐separation patterning could enhance primary production through increasing carrying capacity (Figure S4 and S5a), which agrees with the existing perspective that spatial heterogeneity could increase carrying capacity (Zhang et al., 2017). Our model also shows that phase separation may optimize foraging conditions for herbivores. With the occurrence of phase separation, herbivores establish spatial vegetation patterns with a hyperuniform structure (Table 1, Figure S5b, Torquato, 2018). This hyperuniform landscape minimizes the averaged distance from spatial points in the landscape to the nearest palatable plant areas. Thus, herbivores arrive at the palatable plant areas at the least cost within this landscape. Our finding is consistent with the ecosystem functioning of the Turing‐type hexagonal dryland termite mounds (Pringle et al., 2010). Hence, optimal foraging may be an outcome of the spatial self‐organization driven by phase separation in the top‐down consumer‐resource ecosystems.
Our work suggests that scale‐dependent feedback can be coupled with phase‐separation systems for spatial self‐organization. The traditional view considers scale‐dependent feedback and phase separation as two distinct principles that function separately in ecology (Liu et al., 2016). However, recent studies demonstrate that the Turing‐type system is an active phase‐separation system with a conservation law (Bergmann et al., 2018; Halatek & Frey, 2018). In Turing‐type systems, the scale‐dependent feedback contains short‐distance positive feedback and long‐distance negative feedback (Rietkerk & van de Koppel, 2008). The activators have positive feedback on the production of activators and inhibitors in a short distance; because the inhibitors have a faster diffusion rate, the inhibitors have negative feedback on the production of the activators at a long distance. In the model here, the scale‐dependent feedback includes short‐distance negative feedback and long‐distance positive feedback. Under the induction of activators, inhibitors with a conserved number actively and quickly accumulate to areas featured with a low density of activators, causing negative feedback to the production of activators in a short distance. Due to the limited number of inhibitors, the activators that are far away from the inhibitors’ aggregation area can generate positive feedback through self‐activation. Therefore, density‐dependent movement can induce phase separation directly or indirectly by triggering scale‐dependent feedback. Our model, characterized by two trophic levels and hybrid mechanisms, implies that the phase‐separation system may be a general framework for the studies of behaviour‐driven self‐organization in ecology.
Going beyond the ecology scope here, our model shows that the grazing ecosystem can be considered as an ‘active matter’ system. The constituent elements of active‐matter systems consume energy from the surrounding environment and make active‐matter systems out‐of‐equilibrium. Previous studies focused on the interactions between the constituent elements, such as birds in a flock (Bechinger et al., 2016). These studies did not consider energy sources, so the moving elements implicitly consume energy and form collective behaviour. The model here explicitly treats plants and herbivores as energy sources and moving objects, respectively. Herbivores are individually self‐propelled by the consumption of plants, and tend to accumulate where they slow down. The spatial heterogeneity of the landscape appears as a feature of the self‐assembly of this macro active matter system. Moreover, the directionality of biological movement has been widely modelled according to the idea of chemotaxis (or phototaxis, thermotaxis, etc.). For instance, a thermotaxis‐diffusion equation described the pattern formation of honeybees induced by thermoregulation‐driven movement (Watmough & Camazine, 1995). Our MIPS model has a similar structure of nonlinear diffusion coefficients with the chemotaxis models (Keller & Segel, 1970). This point implies that the movement behaviour of herbivores could be featured with ‘forage‐quality‐taxis’, which has been considered to be driven by optimal foraging in existing foraging theory (Farnsworth & Beecham, 1999).
Although some control experiments and field observations qualitatively confirm our results, our model needs more rigorously quantitative tests in at least three aspects: (1) whether the movement speed of herbivores depends on local resource concentration; (2) whether the direction of movement of an herbivore is random during grazing and (3) whether the coarsening of vegetation patches has a scaling law. The former two points are the basic assumptions of our model, and the latter point is one character of a phase‐separation system. These behaviours can be validated with reasonable experimental design in the future, such as monitoring grazing ecosystems with different grazing intensities. Although a thermodynamic phase‐separation system stabilizes with coarsening process, whether our MIPS model has similar properties is still unknown because the free energy of a non‐equilibrium system is currently difficult to obtain theoretically. It is interesting and necessary to verify whether the coarsening of the grazing ecosystem has a special ecological functioning from an experimental point of view.
The nonlinear interactions between biological behaviour and the environment could produce patterns at the ecosystem level, for instance, ecological engineers shape habitats. The patterns profoundly affect the intra‐ and inter‐species relationships in ecosystems and change the relative intensity of facilitation and competition. Variation in environmental conditions (e.g. climate change) could induce changes in biological behaviour, leading to transition in ecological patterns and subsequent modifications of the ‘flow field’ of matter and energy in ecosystems. Although biological behaviours could arouse huge uncertainties in ecological evolution, they usually affect ecosystems in the short term. This feature determines that the modelling of behaviour‐driven self‐organization has more application prospects.
CONFLICT OF INTERESTS
The authors declare that they have no competing interests.
AUTHOR CONTRIBUTIONS
Q.X.L. designed the research. Z.G. did the theoretical and numerical analysis. Z.G. and Q.X.L.wrote the paper.
PEER REVIEW
The peer review history for this article is available at https://publons.com/publon/10.1111/ele.13928.
Supporting information
Supplementary Material
Video S1
ACKNOWLEDGEMENTS
We thank Johan v.d. Koppel and Nigel Goldfeld for fruitful discussions, reviewer John Fryxell for suggestions, in particular for selective foraging behaviour of ungulate herbivores in existing foraging theories, Tjisse van der Heide and one anonymous reviewer for constructive comments. This work was supported by the project ‘Coping with deltas in transition’ within the Program of Strategic Scientific Alliances between China and The Netherlands (PSA), financed by the Chinese Ministry of Science and Technology (2016YFE0133700), and the National Natural Science Foundation of China (32061143014 and 41676084).
Ge, Z. & Liu, Q.‐X. (2022) Foraging behaviours lead to spatiotemporal self‐similar dynamics in grazing ecosystems. Ecology Letters, 25, 378–390. Available from: 10.1111/ele.13928
DATA AVAILABILITY STATEMENT
No new data are presented. The code to reproduce the results of this study is available on the publicly available repository GitHub, https://github.com/liufengyinxue/Herbivore_plant.
REFERENCES
- Adler, P. , Raff, D. & Lauenroth, W. (2001) The effect of grazing on the spatial heterogeneity of vegetation. Oecologia, 128, 465–479. [DOI] [PubMed] [Google Scholar]
- Alberti, S. (2017) Phase separation in biology. Current Biology, 27, R1097–R1102. [DOI] [PubMed] [Google Scholar]
- Alberti, S. & Dormann, D. (2019) Liquid‐liquid phase separation in disease. Annual Review of Genetics, 53, 171–194. [DOI] [PubMed] [Google Scholar]
- Anderson, K.E. , Hilker, F.M. & Nisbet, R.M. (2012) Directional biases and resource‐dependence in dispersal generate spatial patterning in a consumer‐producer model: spatial patterns caused by directional dispersal. Ecology Letters, 15, 209–217. [DOI] [PubMed] [Google Scholar]
- Bakker, J.P. , Leeuw, J. & Wieren, S.E. (1984) Micro‐patterns in grassland vegetation created and sustained by sheep‐grazing. Vegetatio, 55, 153–161. [Google Scholar]
- Bechinger, C. , Di Leonardo, R. , Löwen, H. , Reichhardt, C. , Volpe, G. & Volpe, G. (2016) Active particles in complex and crowded environments. Reviews of Modern Physics, 88, 045006. [Google Scholar]
- Berg, G. , Esselink, P. , Groeneweg, M. & Kiehl, K. (1997) Micropatterns in Festuca rubra‐dominated salt‐marsh vegetation induced by sheep grazing. Plant Ecology, 132, 1–14. [Google Scholar]
- Berg, H. (1983) Random walks in biology. Princeton University Press. [Google Scholar]
- Bergmann, F. , Rapp, L. & Zimmermann, W. (2018) Active phase separation: a universal approach. Physical Review E, 98, 020603. [DOI] [PubMed] [Google Scholar]
- Bonachela, J.A. , Pringle, R.M. , Sheffer, E. , Coverdale, T.C. , Guyton, J.A. , Caylor, K.K. et al. (2015) Termite mounds can increase the robustness of dryland ecosystems to climatic change. Science, 347, 651–655. [DOI] [PubMed] [Google Scholar]
- Brangwynne, C.P. , Tompa, P. & Pappu, R.V. (2015) Polymer physics of intracellular phase transitions. Nature Physics, 11, 899–904. [Google Scholar]
- Cates, M.E. & Tailleur, J. (2015) Motility‐induced phase separation. Annual Review of Condensed Matter Physics, 6, 219–244. [Google Scholar]
- Cid, M.S. & Brizuela, M.A. (1998) Heterogeneity in tall fescue pastures created and sustained by cattle grazing. Rangeland Ecology & Management, 51, 644–649. [Google Scholar]
- Codling, E.A. , Bearon, R.N. & Thorn, G.J. (2010) Diffusion about the mean drift location in a biased random walk. Ecology, 91, 3106–3113. [DOI] [PubMed] [Google Scholar]
- Cromsigt, J.P.G.M. & Olff, H. (2008) Dynamics of grazing lawn formation: an experimental test of the role of scale‐dependent processes. Oikos, 117, 1444–1452. [Google Scholar]
- de Paoli, H. , van der Heide, T. , van den Berg, A. , Silliman, B.R. , Herman, P.M.J. & van de Koppel, J. (2017) Behavioral self‐organization underlies the resilience of a coastal ecosystem. Proceedings of the National Academy of Sciences of the United States of America, 114, 8035–8040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demir, E. , Yaman, Y.I. , Basaran, M. & Kocabas, A. (2020) Dynamics of pattern formation and emergence of swarming in caenorhabditis elegans. eLife, 9, e52781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong, R.‐Y. & Granick, S. (2021) Reincarnations of the phase separation problem. Nature Communications, 12, 911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumont, B. , Maillard, J.F. & Petit, M. (2000) The effect of the spatial distribution of plant species within the sward on the searching success of sheep when grazing. Grass and Forage Science, 55, 138–145. [Google Scholar]
- Dumont, B. , Rossignol, N. , Loucougaray, G. , Carrère, P. , Chadoeuf, J. , Fleurance, G. et al. (2012) When does grazing generate stable vegetation patterns in temperate pastures? Agriculture, Ecosystems and Environment, 153, 50–56. [Google Scholar]
- Einstein, A. (1905) Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Annalen der Physik, 322, 549–560. [Google Scholar]
- Farnsworth, K.D. & Beecham, J.A. (1999) How do grazers achieve their distribution? A continuum of models from random diffusion to the ideal free distribution using biased random walks. American Naturalist, 153, 509–526. [DOI] [PubMed] [Google Scholar]
- Focardi, S. , Marcellini, P. & Montanaro, P. (1996) Do ungulates exhibit a food density threshold? A field study of optimal foraging and movement patterns. Journal of Animal Ecology, 65, 606. [Google Scholar]
- Fryxell, J.M. , Wilmshurst, J.F. & Sinclair, A.R.E. (2004) Predictive models of movement by Serengeti grazers. Ecology, 85, 2429–2435. [Google Scholar]
- Fryxell, J.M. , Wilmshurst, J.F. , Sinclair, A.R.E. , Haydon, D.T. , Holt, R.D. & Abrams, P.A. (2005) Landscape scale, heterogeneity, and the viability of Serengeti grazers: landscape scale, heterogeneity and Serengeti grazers. Ecology Letters, 8, 328–335. [Google Scholar]
- Gelblum, A. , Pinkoviezky, I. , Fonio, E. , Ghosh, A. , Gov, N. & Feinerman, O. (2015) Ant groups optimally amplify the effect of transiently informed individuals. Nature Communications, 6, 7729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guttal, V. & Jayaprakash, C. (2007) Self‐organization and productivity in semi‐arid ecosystems: implications of seasonality in rainfall. Journal of Theoretical Biology, 248, 490–500. [DOI] [PubMed] [Google Scholar]
- Halatek, J. & Frey, E. (2018) Rethinking pattern formation in reaction–diffusion systems. Nature Physics, 14, 507–514. [Google Scholar]
- HilleRisLambers, R. , Rietkerk, M. , van den Bosch, F. , Prins, H.H.T. & de Kroon, H. (2001) Vegetation pattern formation in semi‐arid grazing systems. Ecology, 82, 50–61. [Google Scholar]
- Hobley, E. , Garcia‐Franco, N. , Hübner, R. & Wiesmeier, M. (2018) Reviewing our options: managing water‐limited soils for conservation and restoration. Land Degradation and Development, 29, 1041–1053. [Google Scholar]
- Holdo, R.M. , Holt, R.D. & Fryxell, J.M. (2009) Opposing rainfall and plant nutritional gradients best explain the wildebeest migration in the Serengeti. American Naturalist, 173, 431–445. [DOI] [PubMed] [Google Scholar]
- Jansen, B.V.S. , Kolden, C.A. , Greaves, H.E. & Eitel, J.U.H. (2019) Lidar provides novel insights into the effect of pixel size and grazing intensity on measures of spatial heterogeneity in a native bunchgrass ecosystem. Remote Sensing of Environment, 235, 111432. [Google Scholar]
- Kéfi, S. , Rietkerk, M. , Alados, C.L. , Pueyo, Y. , Papanastasis, V.P. , ElAich, A. et al. (2007) Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature, 449, 213–217. [DOI] [PubMed] [Google Scholar]
- Keller, E.F. & Segel, L.A. (1970) Initiation of slime mold aggregation viewed as an instability. Journal of Theoretical Biology, 26, 399–415. [DOI] [PubMed] [Google Scholar]
- Klausmeier, C.A. (1999) Regular and irregular patterns in semiarid vegetation. Science, 284, 1826–1828. [DOI] [PubMed] [Google Scholar]
- Levin, S.A. (1992) The problem of pattern and scale in ecology: the Robert H. MacArthur award lecture.Ecology, 73, 1943–1967. [Google Scholar]
- Levin, S.A. (2005) Self‐organization and the emergence of complexity in ecological systems. BioScience, 55, 1075. [Google Scholar]
- Li, A. , Matsuoka, N. , Niu, F. , Chen, J. , Ge, Z. , Hu, W. et al. (2021) Ice needles weave patterns of stones in freezing landscapes. Proceedings of the National Academy of Sciences of the United States of America, 118, e2110670118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lifshitz, I.M. & Slyozov, V. (1961) The kinetics of precipitation from supersaturated solid solutions. Journal of Physics and Chemistry of Solids, 19, 35–50. [Google Scholar]
- Liu, Q.‐X. , Doelman, A. , Rottschafer, V. , de Jager, M. , Herman, P.M.J. , Rietkerk, M. et al. (2013) Phase separation explains a new class of self‐organized spatial patterns in ecological systems. Proceedings of the National Academy of Sciences of the United States of America, 110, 11905–11910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, Q.‐X. , Rietkerk, M. , Herman, P.M.J. , Piersma, T. , Fryxell, J.M. & van de Koppel, J. (2016) Phase separation driven by density‐dependent movement: A novel mechanism for ecological patterns. Physics of Life Reviews, 19, 107–121. [DOI] [PubMed] [Google Scholar]
- López Pereira, M. , Sadras, V.O. , Batista, W. , Casal, J.J. & Hall, A.J. (2017) Light‐mediated self‐organization of sunflower stands increases oil yield in the field. Proceedings of the National Academy of Sciences of the United States of America, 114, 7975–7980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinhardt, H. (2009) The algorithmic beauty of sea shells. The virtual laboratory, 4th edition. Berlin, London: Springer. [Google Scholar]
- Menard, C. , Duncan, P. , Fleurance, G. , Georges, J.‐Y. & Lila, M. (2002) Comparative foraging and nutrition of horses and cattle in European wetlands. Journal of Applied Ecology, 39, 120–133. [Google Scholar]
- Mistr, S. & Bercovici, D. (2003) A theoretical model of pattern formation in coral reefs. Ecosystems, 6, 0061–0074. [Google Scholar]
- Mouissie, A.M. , Apol, M.E.F. , Heil, G.W. & van Diggelen, R. (2008) Creation and preservation of vegetation patterns by grazing. Ecological Modelling, 218, 60–72. [Google Scholar]
- Mueller, E.N. , Wainwright, J. , Parsons, A.J. & Turnbull, L. s (Ed.s) (2014) Patterns of land degradation in Drylands. Dordrecht, Netherlands: Springer. [Google Scholar]
- Murray, J.D. (2002) Mathematical biology: an introduction. Interdisciplinary Applied Mathematics, 3rd edition. New York: Springer. [Google Scholar]
- Parsons, A.J. & Dumont, B. (2003) Spatial heterogeneity and grazing processes. Animal Research, 52, 161–179. [Google Scholar]
- Person, B.T. , Herzog, M.P. , Ruess, R.W. , Sedinger, J.S. , Anthony, R.M. & Babcock, C.A. (2003) Feedback dynamics of grazing lawns: coupling vegetation change with animal growth. Oecologia, 135, 583–592. [DOI] [PubMed] [Google Scholar]
- Pringle, R.M. , Doak, D.F. , Brody, A.K. , Jocqué, R. & Palmer, T.M. (2010) Spatial pattern enhances ecosystem functioning in an African savanna. PLoS Biology, 8, e1000377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pyke, G.H. , Pulliam, H.R. & Charnov, E.L. (1977) Optimal foraging: a selective review of theory and tests. The Quarterly Review of Biology, 52, 137–154. [Google Scholar]
- Rietkerk, M. , Boerlijst, M. , van Langevelde, F. , HilleRisLambers, R. , de Koppel, J. , Kumar, L. et al. (2002) Self‐organization of vegetation in arid ecosystems. American Naturalist, 160, 524–530. [DOI] [PubMed] [Google Scholar]
- Rietkerk, M. , Dekker, S.C. , de Ruiter, P.C. & van de Koppel, J. (2004) Self‐organized patchiness and catastrophic shifts in ecosystems. Science, 305, 1926–1929. [DOI] [PubMed] [Google Scholar]
- Rietkerk, M. & van de Koppel, J. (2008) Regular pattern formation in real ecosystems. Trends in Ecology and Evolution, 23, 169–175. [DOI] [PubMed] [Google Scholar]
- Schnitzer, M.J. (1993) Theory of continuum random walks and application to chemotaxis. Physical Review E, 48, 2553–2568. [DOI] [PubMed] [Google Scholar]
- Siero, E. (2018) Nonlocal grazing in patterned ecosystems. Journal of Theoretical Biology, 436, 64–71. [DOI] [PubMed] [Google Scholar]
- Steinfeld, H. , Gerber, P. , Wassenaar, T.D. , Castel, V. , Rosales, M. , Rosales, M. et al. (2006) Livestock’s long shadow: environmental issues and options. Food and Agriculture Org. [Google Scholar]
- Tailleur, J. & Cates, M.E. (2008) Statistical mechanics of interacting run‐and‐tumble bacteria. Physical Review Letters, 100, 218103. [DOI] [PubMed] [Google Scholar]
- Torquato, S. (2018) Hyperuniform states of matter. Physics Reports, 745, 1–95. [Google Scholar]
- Tremaine, S. (2003) On the origin of irregular structure in Saturn’s rings. Astronomical Journal, 125, 894. [Google Scholar]
- Tsimring, L. , Levine, H. , Aranson, I. , Ben‐Jacob, E. , Cohen, I. , Shochet, O. et al. (1995) Aggregation patterns in stressed bacteria. Physical Review Letters, 75, 1859–1862. [DOI] [PubMed] [Google Scholar]
- van der Heide, T. , Eklöf, J.S. , van Nes, E.H. , van der Zee, E.M. , Donadi, S. , Weerman, E.J. et al. (2012) Ecosystem engineering by seagrasses interacts with grazing to shape an intertidal landscape. PLoS One, 7, e42060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watmough, J. & Camazine, S. (1995) Self‐organized thermoregulation of honeybee clusters. Journal of Theoretical Biology, 176, 391–402. [Google Scholar]
- Weerman, E.J. , Herman, P.M.J. & Van de Koppel, J. (2011) Top‐down control inhibits spatial self‐organization of a patterned landscape. Ecology, 92, 487–495. [DOI] [PubMed] [Google Scholar]
- Wilmshurst, J.F. , Fryxell, J.M. & Colucci, P.E. (1999) What constrains daily intake in Thomson’s gazelles? Ecology, 80, 2338–2347. [Google Scholar]
- Wilmshurst, J.F. , Fryxell, J.M. & Hudsonb, R.J. (1995) Forage quality and patch choice by wapiti (Cervus elaphus). Behavioral Ecology, 6, 209–217. [Google Scholar]
- Yizhaq, H. , Gilad, E. & Meron, E. (2005) Banded vegetation: biological productivity and resilience. Physica A: Statistical Mechanics and Its Applications, 356, 139–144. [Google Scholar]
- Zhang, B.O. , Kula, A. , Mack, K.M.L. , Zhai, L.U. , Ryce, A.L. , Ni, W.‐M. et al. (2017) Carrying capacity in a heterogeneous environment with habitat connectivity. Ecology Letters, 20, 1118–1128. [DOI] [PubMed] [Google Scholar]
- Zhao, L.‐X. , Zhang, K. , Siteur, K. , Li, X.‐Z. , Liu, Q.‐X. & van de Koppel, J. (2021) Fairy circles reveal the resilience of self‐organized salt marshes. Science Advances, 7, eabe1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Video S1
Data Availability Statement
No new data are presented. The code to reproduce the results of this study is available on the publicly available repository GitHub, https://github.com/liufengyinxue/Herbivore_plant.


