Abstract
Of profound astrobiological interest, Enceladus appears to have a global saline subsurface ocean, indicating water-rock reaction at present or in the past, an important mechanism in the moon’s potential habitability. Here, we investigate how salinity and the partition of heat production between the silicate core and the ice shell affect ocean dynamics and the associated heat transport—a key factor determining equilibrium ice shell geometry. Assuming steady-state conditions, we show that the meridional overturning circulation of the ocean, driven by heat and salt exchange with the poleward-thinning ice shell, has opposing signs at very low and very high salinities. Regardless of these differing circulations, heat and fresh water converge toward the equator, where the ice is thick, acting to homogenize thickness variations. Among scenarios explored here, the pronounced ice thickness variations observed on Enceladus are most consistent with heating that is predominantly in the ice shell and a salinity of intermediate range.
The ice shell geometry on Enceladus may tell us about its ocean salinity.
INTRODUCTION
Since the Cassini and Galileo missions, Enceladus (a satellite of Saturn) and Europa (a satellite of Jupiter) have been revealed to have high astrobiological potential, satisfying all three necessary conditions for life: (i) the presence of liquid water (1, 2), (ii) a source of energy (3, 4), and (iii) a suitable mix of chemical elements (1, 5–10). In particular, the geyser-like sprays ejected from the fissures over Enceladus’ south pole (11–13) provide a unique opportunity to understand the chemistry and dynamics of Enceladus’ interior without landing on and drilling through a typically 20-km-thick ice shell (14–18). Within the geyser samples collected by Cassini, CO2 and methane (5), sodium salt (1), hydrogen (7), and macromolecular organic compounds (8) have been found. These data a chemically active environment that could sustain life (9, 10). However, to infer the chemical environment of the subsurface ocean from plume samples, one needs to better understand ocean circulation. This governs the transport of chemical tracers and sets the pathways and time scales over which particles or potential biosignatures react with the ocean before being detected. Understanding this ocean circulation, and how it depends on salinity, is the main goal of the present study.
Ocean circulation on Enceladus is driven by heat and salinity fluxes from the core (3) and the ice shell (4, 19, 20), as well as mechanical forcing, such as tides and libration (21, 22). The partition of heat production between the ice and the core has a direct control over ocean dynamics. Moreover, ocean salinity plays a key role because it determines whether density decreases or increases with temperature (see Fig. 1C) (23). For example, if the ocean is very fresh, then heat released by hydrothermal vents will not trigger penetrative convection from below (24). Furthermore, the global scale circulation of a salty ocean could be completely different from that of a fresh ocean, as has been explored in Earth’s ocean and terrestrial exoplanets (25, 26).
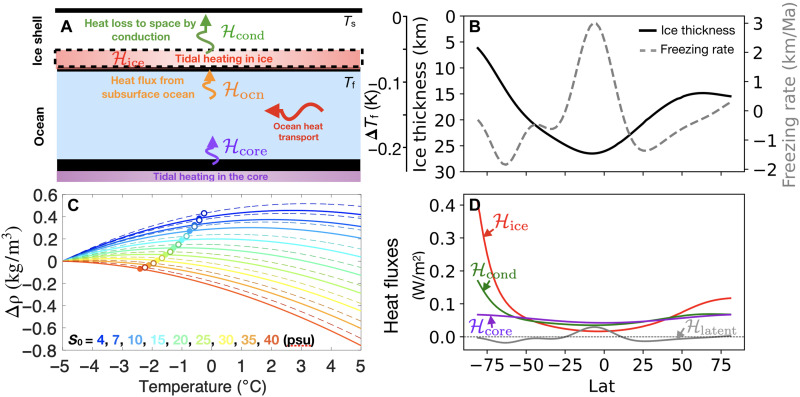
Fig. 1. Considered heat sources/sinks and salinity/temperature forcings in our Enceladus experiments.
(A) Primary heat sources and heat fluxes, including heating due to tidal dissipation in the ice ℋice and the silicate core ℋcore, the heat flux from the ocean to the ice ℋocn, and the conductive heat loss to space ℋcond. Ocean heat transport is shown by the horizontal arrow. (B) Observed ice shell thickness of Enceladus (18) (black solid curve, left y axis). The suppression of the freezing point of water by these thickness variations, relative to that at zero pressure, is indicated by the outer left y axis. The gray dashed curve shows the freezing (positive) and melting (negative) rate required to maintain a steady state based on an upside-down shallow ice flow model (y axis on the right). (C) Density of water varies with temperature near the freezing point (marked by circles) for different assumed salinities. Moving from cold to warm colors denotes increasing salinity. The solid (dashed) curves are computed assuming the pressure under the 26.5 km (5.6 km) of ice at the equator (south pole). (D) Typical magnitudes and profiles of ℋice, ℋcore, ℋcond, and ℋlatent. More details can be found in the “Boundary conditions” section.
Despite its importance, the heat partition is poorly constrained because of our limited understanding of the rheology of both the ice shell and the silicate core. Hydrogen and nanometer-sized silica particles have been detected on Enceladus, providing clear geochemical evidence for active seafloor venting (6, 7). However, whether this submarine hydrothermalism, powered by tidal dissipation (3), is the dominant heat source preventing the ocean from freezing remains inconclusive because of our limited understanding of the core’s rheology (3, 27). Another potential heat source is tidal dissipation within the ice shell itself. While poleward-thinning ice geometry on top of the ocean is qualitatively consistent with heating primarily occurring in the ice shell (18), present dynamical models of ice are unable to reproduce enough heat to maintain such a thin ice shell (4, 28). Attempts to account for higher heat generation through use of more advanced models of ice rheology have thus far not been successful (4, 19, 28–32).
An additional complication is that the salinity of Enceladus’ ocean remains uncertain. Calculations of thermochemical equilibria over a range of hydrothermal and freezing conditions for chondritic compositions suggest a salinity ranging between 2 and 20 psu (g/kg), with a high likelihood of it being below 10 psu (33–35). However, at least 17 psu is required to keep the liquid-gas interface of the south polar geysers convectively active enough to ensure that they do not freeze up (36). Sodium-enriched samples taken from south pole sprays by Cassini have a salinity of 5 to 20 psu. This can be considered a lower bound because the interaction of cold water vapor sprays with their environment is likely to lower the salinity of droplets through condensation (1). This is also uncertain, however, because fractional crystallization and disequilibrium chemistry may partition components in such a way that geyser particles are not directly representative of the underlying ocean (37). Furthermore, if particles originate from a hydrothermal vent, then composition can also deviate far from that of the overall ocean (3, 35). In a separate line of argument, the size of silica nanoparticles carried along in the sprays suggests a salinity <40 psu, but this inference is sensitive to assumptions about ocean pH and the dynamics of hydrothermal vents (6).
Given the uncertainties associated with the ocean salinity and heat partition, it is crucial to consider different possible scenarios. Once we understand how ocean circulation and heat transport vary with these variables, we may be able to put further constraints on them, because ocean heat transport can shape the ice shell on a geological time scale and the observed ice geometry should not be far from equilibrium.
Drivers of ocean circulation on Enceladus
Data provided by Cassini have enabled reconstructions to be made of Enceladus’ ice thickness variations (14–18). The solid curve in Fig. 1B shows the zonal-mean ice thickness deduced by Hemingway and Mittal (18), where a notable poleward thinning trend can be seen. The ice shell over the south pole is only 6 km thick, one-fifth that of the equatorial ice shell. These ice thickness variations have two effects. First, thick equatorial ice creates high pressure, depressing the local freezing point and leading to a roughly 0.1-K depression of the temperature just beneath the ice compared to the poles, assuming that the interface is at the melting temperature (solid curve in Fig. 1B).
Second, thickness variations will drive ice to flow from thick-ice regions to thin-ice regions on million-year time scales (38–41). To compensate the smoothing effect of the ice flow, ice must form in low latitudes and melt in high latitudes. Assuming an ice rheology, we can calculate ice flow speeds using an upside-down shallow ice model (details are given in the “Boundary conditions” section). In this way, we can infer the freezing/melting rate needed to maintain the observed ice geometry, as shown by the dashed curve in Fig. 1B. Over time, this freezing and melting will lead to a meridional salinity gradient through brine rejection and freshwater input that, in steady state (assumed), must be balanced by salinity transport in the ocean.
The combined effect of these temperature and salinity forcings associated with the ice topography is to make equatorial waters saltier and colder than polar waters. This equator-to-pole temperature and salinity contrast, denoted as Δθ and ΔS, jointly affects the equator-to-pole (defined here as equator minus pole) density contrast Δρ through
| (1) |
where ρ0 is the reference density of water and αT and βS are the thermal expansion and haline contraction coefficient, respectively. In a salty ocean, where water volume contracts when it is cold (αT > 0), we expect the ocean to sink at the cold low latitudes, because the water is dense there (see Fig. 2B). In contrast, in a fresh ocean (αT < 0), the opposite is possible because of seawater’s anomalous expansion upon cooling (see Fig. 2A). In addition, the salinity anomalies induced by freezing/melting increasingly diminish as the assumed ocean salinity approaches zero. Thus, the global overturning circulation in very salty and very fresh oceans can be expected to be of opposite sign. However, irrespective of which direction the ocean circulates, heat will be converged toward the equator, because of the mixing between cold equatorial water and warm polar water induced by the circulation. Limited by the efficiency of conductive heat loss through the thick equatorial ice, the equatorward heat convergence cannot be arbitrarily strong. As a result, scenarios with various salinities and core-shell heat partitions can potentially be discriminated for they would manifest different heat transport efficiencies and affect the heat budget of the ice.
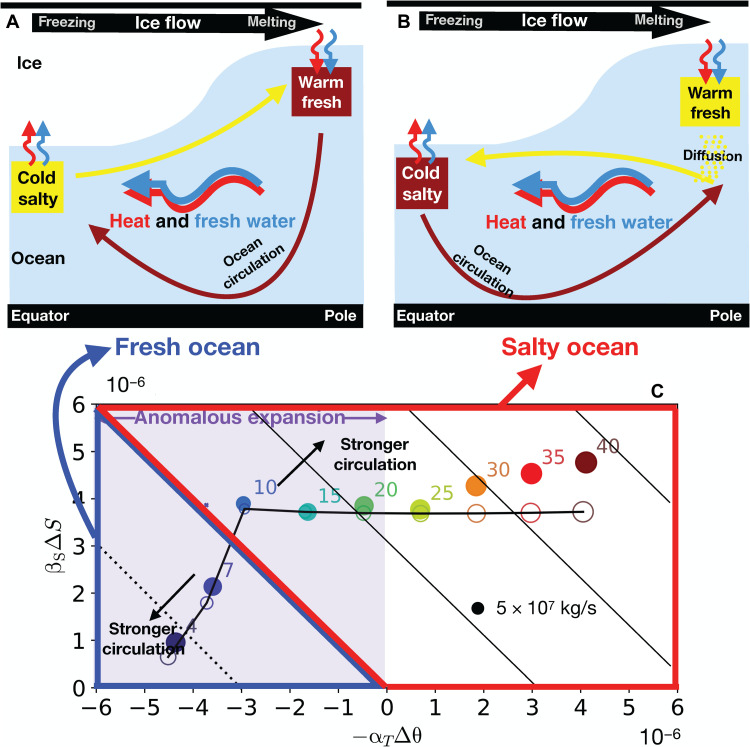
Fig. 2. Different ocean circulations in salty and fresh ocean.
At the top, we show schematics of ocean circulation and associated transports of heat (red wiggly arrows) and fresh water (blue wiggly arrows) for (A) a fresh ocean (αT < 0) and (B) a salty ocean (αT > 0). Dark brown (yellow) arrows denote sinking (rising) of dense (buoyant) water. (C) Regime diagram demonstrating the influence of temperature and salinity anomalies on the equator-to-pole density difference assuming different salinities (marked on the shoulder of each circle), and how the ocean’s overturning circulation responds in general circulation model (GCM) simulations (filled circles) and our conceptual model (empty circles; see the “Exploring mechanisms with a conceptual model” section). Horizontal and vertical axes are the density difference associated with temperature and salinity anomalies, −αTΔθ and βSΔS. Both ΔS and −Δθ are positive in our setup; they are computed by taking the difference between the maximum and minimum within the northern hemisphere. The sign of the coordinates reflects the sign of αT and βS. In the high/low S0 experiments, the signs of −αTΔθ and βSΔS are the same/opposite. The size of each circle represents the amplitude of the overturning circulation (the peak Ψ occurs in the northern hemisphere). The 45° tilted black lines are isolines of the equator-to-pole density difference Δρ. Solid (dotted) lines denote dense water near the equator (poles).
To study the possible ocean circulations and heat transports on Enceladus in this way, we set up a zonally averaged ocean circulation model to sweep across a range of mean salinities (S0 = 4, 7, 10, 15, 20, 25, 30, 35, and 40 psu) and core-shell heat partitions (0 to 100%, 100 to 0%, and 20 to 80%). Our model has its ocean covered by an ice shell that resembles that of the present-day Enceladus (solid curve in Fig. 1B) (18), which is assumed to be sustained against the ice flow by a prescribed freezing/melting q (gray dashed curve in Fig. 1B), regardless of the ice shell’s heat budget. By prescribing q, we guarantee the ice shell to be in mass balance and, furthermore, cut off the positive feedback loop between the ocean heat transport and the ice freezing/melting rates, thus preventing the simulated circulation from seeking a completely new state. When heat production by the silicate core is assumed to be nonzero, an upward heat flux at the bottom is prescribed. Guided by models of tidal heating described in the “Boundary conditions” section, this is assumed to be slightly polar-amplified (see purple curve in Fig. 1D). By design, the globally integrated heat budget is guaranteed to be in balance.
At the water-ice interface, a downward salinity flux S0q is imposed to represent the brine rejection and freshwater production associated with freezing/melting. Meanwhile, the ocean temperature there is restored toward the local freezing point. Thus, the ocean will deposit heat to the ice when its temperature is slightly higher than the freezing point and vice versa. In order for the heat budget of the ice to close, this ocean-ice heat exchange ℋocn, together with the tidal heat produced in the ice ℋice (red curve in Fig. 1D) and the latent heat released ℋlatent (ℋlatent = ρLfq, where ρ and Lf are the density and fusion energy of ice, see the gray curve in Fig. 1D), should balance the conductive heat loss through the ice shell ℋcond (green curve in Fig. 1D). Because the freezing/melting rate is not allowed to respond to the simulated ocean-ice heat exchange, the aforementioned heat budget is not necessarily in balance, and the extent to which it is not informs us of the plausibility of the assumed salinity and heat partition.
Before going on to describe our results, we emphasize that we have adopted a zonally averaged modeling framework so that we can readily explore parameter space while integrating out to an equilibrium state, which takes about 10,000 modeled years. This necessarily implies that our ocean model is highly parameterized—as are the models of tidal heating and ice flows that are used to provide the forcing at the boundaries that drive it—and so have many unavoidable uncertainties. In particular, as described in detail in the “Parameterization of subgridscale processes” section and just as in terrestrial ocean models, processes such as convection, diapycnal mixing, and baroclinic instability are parameterized guided by our knowledge of the mechanisms that underlie them.
RESULTS
Patterns of ocean circulation, temperature, and salinity
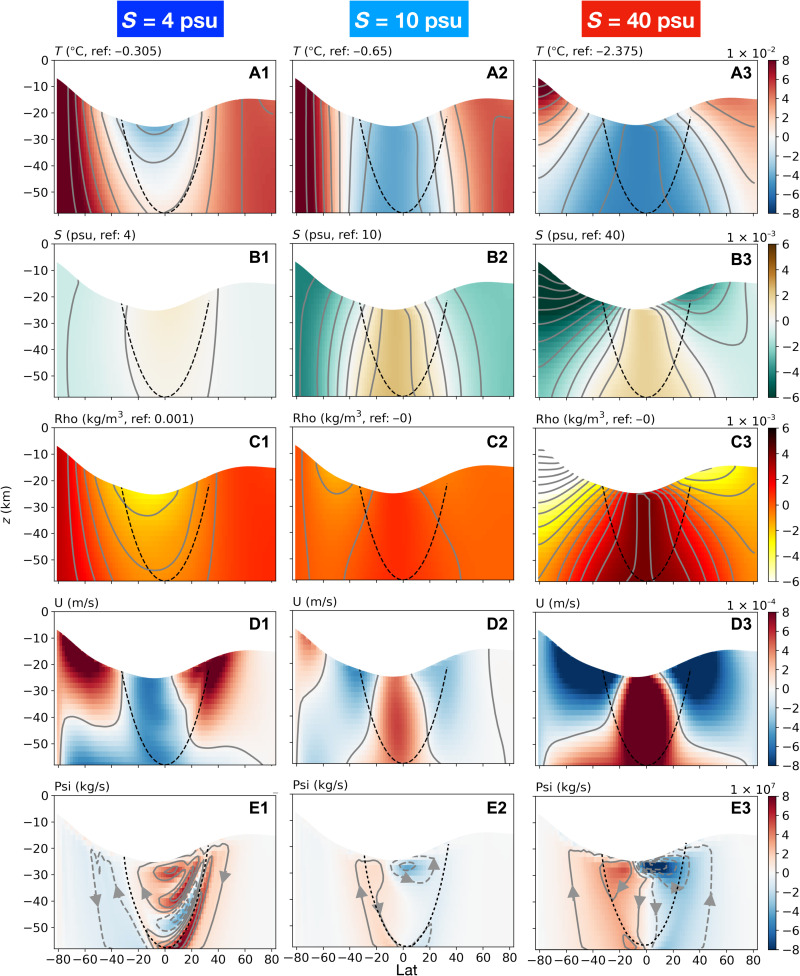
Because of the relatively low freezing point (Fig. 1C) and elevated freezing rate (Fig. 1B) of low latitudes, water just under the ice is colder and saltier than near the poles, regardless of the mean salinity. This pole-to-equator temperature and salinity contrast leads to variations in density, which, in turn, drive ocean circulation. In Fig. 3 (C and E), we present the density anomaly, ρ0( − αTθ′ + βSS′), and the meridional overturning streamfunction . Here, θ′ and S′ (plotted in Fig. 3, A and B) are the deviation in potential temperature and salinity from the reference, V is the meridional current, ρ0 is the water density, a is the radius of the moon, D is the ocean depth, ϕ denotes latitude, and z points upward.
Fig. 3. Ocean circulation and thermodynamic state from GCM simulations assuming various ocean salinities.
Moving from top to bottom, we present temperature T (A), salinity S (B), density anomaly Δρ (C), zonal flow speed U (D), and meridional overturning streamfunction Ψ (E) with arrows indicating the sense of flow. The left column presents results for a low-salinity ocean (S0 = 4 psu), the right column for high-salinity ocean (S0 = 40 psu), and the middle column for an ocean with intermediate salinity (S0 = 10 psu). The reference temperature and salinity (marked at the top of each plot) are subtracted from T and S to better reveal spatial patterns. Positive U indicates flow to the east, and positive Ψ indicates a clockwise overturning circulation. Black dashed lines mark the position of the tangent cylinder, an imaginary cylinder that is parallel to the rotation vector and touches the core.
Because, depending on the mean salinity, the density gradient induced by temperature variations can either enhance or diminish that induced by salinity, the overturning circulation can sink either over the poles or over the equator. When S0 is greater than 22 psu, water expands with increasing temperature (αT > 0, see reddish curves in Fig. 1C, 2 MPa pressure assumed). As a result, the cold and salty water under the thick equatorial ice shell is denser than polar waters, as shown in Fig. 3C3 and sketched in Fig. 2B using the dark brown color. Equatorial waters therefore sink, as shown in Fig. 3E3 (indicated in Fig. 2B using the dark brown arrow), constrained by the direction of the rotation vector (marked by the thin dashed curves).
However, when S0 is below 22 psu, the thermal expansion coefficient changes sign (αT < 0, as shown by the bluish curves in Fig. 1C). This so-called anomalous expansion of water results in the temperature-induced density difference and the salinity-induced density difference partially canceling one another, giving rise to two possibilities. If the salinity factor dominates, then the overturning circulation becomes one of sinking at the equator, as show in Fig. 3D2 and sketched in Fig. 2B using a dark brown arrow. However, if the temperature factor dominates, then the overturning circulation flips direction with sinking over the poles (Fig. 3D1, and Fig. 2A) because water is denser there (Fig. 3C1). The switch in overturning circulation with salinity can also occur in models of Earth’s ocean (25, 26), although Earth’s ocean is forced mostly by wind stress.
The transition from polar to equatorial sinking is governed by the density difference between the poles and the equator. Taking the north pole as a reference, the temperature-related density anomaly at the equator can be written as −αTΔθ, and the salinity-related density anomaly as βSΔS, where Δθ and ΔS are the potential temperature and salinity anomaly at the equator relative to the north pole. Figure 2C presents the strength of the overturning circulation from all nine experiments in (−αTΔθ, βSΔS) space: The size of the circles are proportional to Ψ. The 45° tilted line denotes perfect cancelation between the saline and temperature-driven overturning circulations: It passes near 10 psu, explaining why the 10-psu experiment has the weakest circulation compared to all others. On moving away from this line in either direction, the strength of the overturning circulation increases but is of opposite sign, as represented schematically in Fig. 2 (A and B).
The overturning circulation shapes the tracer distributions and the zonal currents. Downwelling regions (low latitudes for a salty ocean and high latitudes for a fresh ocean) advect density, temperature, and salinity anomalies, set at the ocean-ice interface, into the interior ocean. Note the bending of the temperature and salinity contours equatorward (poleward) when downwelling occurs at the poles (equator), as shown in Fig. 3. This results in meridional density gradients that are in a generalized thermal wind balance with zonal currents in which all components of the Coriolis force are included (Fig. 3D).
Thus far, we have assumed zero heat flux from the bottom. With all the required heating generated in the silicate core (core-heating), a salty ocean will become more convectively unstable, whereas a fresh ocean will become more stably stratified because of the negative thermal expansion coefficient (see fig. S1C), which pertains before the maximum density point (typically several degrees above freezing) is reached. As a result, the overturning circulation strengthens (weakens) in a salty (fresh) ocean. The temperature/salinity profiles and even the circulation patterns remain qualitatively similar to the shell-heating scenarios, especially for the salty scenarios, because the heating-induced bottom-to-top temperature difference is typically only a few tens of milliKelvin when convection is active, much smaller than the equator-to-pole temperature difference induced by the freezing point variations due to ice topography (Fig. 3) that is order 0.1 K—see Fig. 1 (B and C). The vertical temperature gradient induced by the bottom heating is much larger in a fresh ocean because of the suppression of convection by anomalous expansion. The strengthening of vertical temperature gradient largely enhances the ocean heat transport (OHT), although the circulation is weakened slightly.
It is important to note that the ocean circulation that we have obtained here penetrates throughout the entire depth of the ocean, much deeper than suggested by Lobo et al. (42) based on a more idealized ocean model. This is despite the fact that the forcing amplitude assumed in (42) is a full three orders of magnitude larger. Our circulation is deep because, in the absence of strong viscosity, the circulation in the ocean interior aligns with the direction of the rotation axis (see Fig. 3E), a consequence of the Taylor-Proudman theorem. Only adjacent to the ice shell and the seafloor can currents flow normal to the sides of tangent cylinder [see (41) for a discussion of the importance of the tangent cylinder]. Moreover, in all the shell-heating scenarios, the downwelling regions are convectively unstable, allowing dense water formed near the surface to sink all the way to the bottom.
This is rather different from the physical picture presented by Lobo et al. (42), who describe an ocean that is strongly stratified and whose circulation is confined near the ice shell. These differences likely stem from the values adopted for the eddy diffusivity representing baroclinic instability, κGM, and diapycnal diffusivity associated with convective mixing, κconv: Lobo et al. (42) assume a very large value of κGM = 1000 m2/s based on observations of Earth’s ocean, and a rather small κconv = 0.01 m2/s for the convective regions over the poles. This dominance of lateral baroclinic instability over vertical convection gives rise to very strong stratification that, in turn, confines the vertical extent of the circulation. Instead, here, we estimate an eddy diffusivity appropriate to Enceladus to be of order 0.3 m2/s based on energetic arguments (43) (see the “Parameterization of subgridscale processes” section for a derivation) and a convective mixing rate to be order 1 m2/s based on the scaling laws governing convection in a rapidly rotating system (44). In this parameter setting, the stratification is weak and almost half of the ocean is convecting because of loss of buoyancy through interaction with the ice.
Ocean heat transport and the heat budget of the ice shell
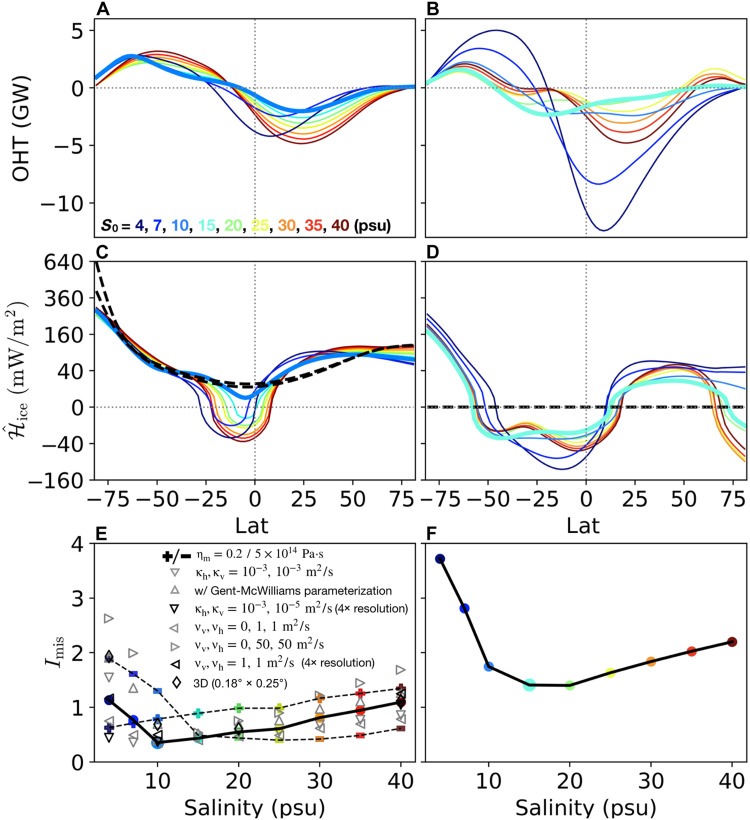
We have seen that the freezing point depression of water due to pressure results in the polar oceans being warmer than the tropical ocean just beneath the ice, because the ice is thin at the poles relative to the equator. One might expect, then, that OHT would be directed equatorward—from warm to cold—irrespective of the sense of the ocean’s overturning circulation. The amplitude of OHT, which is proportional to the overturning strength multiplied by a temperature contrast, (45), will depend on the strength of the circulation, which, in turn, depends on ocean salinity and the heat partition between the core and the ice shell. As can be clearly seen in Fig. 4 (A and B), heat is indeed converged toward the equator in all scenarios. However, because of the cancelation between temperature- and salinity-driven circulation, the heat convergence in an ocean with an intermediate salinity is a small fraction of that in the end-member cases. If there is no tidal heating produced in the ice shell, then such an equatorward OHT will inevitably melt the ice shell over the equator because the conductive heat loss is smaller there because of the relatively thick ice shell. In addition, ice will be transported poleward, from thick to thin, accelerating the flattening of the ice shell. Therefore, to sustain the observed ice geometry (18), a polar-amplified tidal heating in the ice that has a meridional gradient strong enough to compensate equatorward OHT is necessary.
Fig. 4. Meridional heat transport and heat budget.
Left column shows the shell-heating scenario and the right column shows the core-heating scenario. The top panels (A and B) show the vertically integrated meridional OHT for various assumed S0. Positive values denote northward heat transport. The middle panels (C and D) show the inferred tidal heating (solid curves), in comparison with the heating predicted by a tide model ℋice (dashed curves). As a measure of uncertainties in the tide model, two pα values, −2 and −1, are used to compute ℋice. The black dashed curves in (D) coincide with the zero line, because ℋice = 0 when all heating is in the core. The bottom panels (E and F) show the mismatch index Imis, defined in Eq. 3. Filled colored dots connected by a thick solid line correspond to the default setup (horizontal/vertical diffusivity κh= κv = 0.005 m2/s, horizontal/vertical viscosity νh = νv = 10 m2/s, 100% heat produced in the ice, and melting-point ice viscosity ηm = 1014 Pa·s). Other symbols represent sensitivity tests to ice viscosity, mixing coefficients, and model resolution. The Imix of the low and high ηm experiments are multiplied by a factor of 0.3 and 2, respectively, so that all plots make use of the same scale.
To quantify the impact of OHT on ice geometry, we compute the heat flux transmitted from the ocean to the ice ℋocn and diagnose how much tidal heating is required in the ice shell to close the ice’s heat budget
| (2) |
The inferred from our various ocean circulations is shown by the solid curves in Fig. 4 (C and D) for the shell-heating and core-heating scenarios, respectively. If all is consistent, then this inferred ice dissipation rate should be close to the estimate given by a tidal dissipation model ℋice (details of the model can be found in the “Model of tidal dissipation in the ice shell” section), which is shown in the same figure using black dashed curves. The tidal dissipation model, of course, is also subject to substantial uncertainties because of our limited understanding of the ice rheology, but it should be positive definite. However, for many assumed salinities (very fresh and very salty), the implied tidal heating is actually large and negative, indicating that these scenarios are incompatible with the observed ice geometry and therefore less likely.
We measure the mismatch between and ℋice by the following index
| (3) |
where the over-bar represents a global area-weighted average and the max function in the denominator helps avoid the singularity when ℋice → 0. We show the shell-heating and core-heating mismatch indices Imis as a function of the ocean salinity in Fig. 4 (E and F) using filled dots.
The dependence of Imis on ocean salinity in the shell-heating scenarios
Although OHT is always equatorward, those ocean solutions with a strong overturning circulation (e.g., S0 = 4,40 psu) focus large amounts of heat into low latitudes, resulting in a heat budget discrepancy of almost 80 mW/m2 (see Fig. 4C), twice the global-mean heat production rate; if used to melt ice, then a rate of 7.5 km/Ma would result. Near the equator, even becomes significantly negative, conflicting with the need for tidal dissipation to be positive definite. This is reflected in the relatively large values of Imis evident in Fig. 4E. The heat budget improves significantly at intermediate salinities, and the best match is achieved in the S0 = 10 psu scenario. This corresponds to the near-cancelation of the temperature- and salinity-induced density anomalies (see Fig. 2C).
Note that the increase in the mismatch is steeper on the fresh side of 10 psu than the salty side (Fig. 4E). This is related to the different energetics of ocean circulation in a very fresh ocean close to the freezing point (where αT < 0) and a salty ocean (where αT > 0). As pointed out by Zeng and Jansen (24), if the buoyancy gain at the equator is deeper in the water column than the buoyancy loss at the poles, then ocean circulation can always be energized because dense polar water higher up the water column is transported to depth. However, in a salty ocean, the opposite is true and equatorial dense water cannot be drawn upward to the polar ice shell without invoking diffusive processes (46). This difference can be seen in Fig. 3E. The overturning circulation in the fresh ocean (Fig. 3E1) can directly connect the water-ice interface at the pole to equatorial regions; in contrast, in a salty ocean (Fig. 3E3), the circulation weakens moving poleward and almost completely vanishes in the freshwater lens formed under the polar ice shell. Strong stratification develops in the diffusive layer (Fig. 3C3) that sustains an upward buoyancy flux without strong circulation, as indicated in the schematic diagram Fig. 2B.
Dependence on the core-shell heat partition
Because, in realistic scenarios, the bottom-to-top temperature difference induced by core heating is far smaller than the equator-to-pole temperature difference induced by the freezing point variations, the circulation patterns and temperature/salinity profiles of the core-heating solutions remain broadly the same as those in which shell-heating dominates (see Fig. 3 and fig. S1). As a result, the OHT and are qualitatively similar too, as can be seen in Fig. 4 (B and D). What is different, however, is that the core-heating cases have, by construction, zero heat production in the ice shell and so equatorward OHT and polar-amplified conductive heat loss can no longer be effectively compensated by polar-amplified dissipation in the ice shell. Over the thin polar ice, heat lost to the space is much more efficient than elsewhere and, furthermore, OHT is equatorward. Thus, polar ice will accumulate over time in the absence of local heating within it (black dashed curve in Fig. 4D). The mismatch indices for the core-heating scenarios are higher overall as shown by Fig. 4F. More detailed discussions of the bottom heating solutions can be found in section S1.1.
Sensitivity tests
To explore sensitivity to parameter choices, we carried out many sets of experiments changing the assumed ice rheology, mixing rates in the ocean and model resolution. By default, the melting point ice viscosity ηm is set to 1014 Pa·s, an intermediate value between an estimated lower bound of 1013 Pa·s and an upper bound of 1015 Pa·s (38). In the ice rheology sensitivity test, we examined ηm = 2 × 1013 Pa·s and ηm = 5 × 1014 Pa·s. A lower (higher) ice viscosity induces stronger (weaker) ice flows, which require a greater (smaller) balancing freezing/melting rate; this, in turn, enhances (suppresses) the salinity flux imposed upon the ocean, giving rise to larger (weaker) salinity gradients. Compensating the density anomaly implied by this salinity gradient thus requires a more (less) negative αT and lower S0. As shown by the plus signs in Fig. 4E, the best matching S0 is indeed reduced from 10 to 4 psu (the full solution is summarized in fig. S2) with ηm = 2 × 1013 Pa·s and increased from 10 psu to 15 to 30 psu (the full solution is summarized in fig. S3) with ηm = 5 × 1014 Pa·s. Because of the stronger latent heating, the overall matching significantly deteriorates in experiments with lower ice viscosity. Note that in the ηm = 2 × 1013 Pa·s sensitivity test, a factor of 0.3 premultiplies Imis so that the same scale can be used in all plots.
The dissipation rate within the ocean driven by libration/tidal motions is also under debate (21, 47, 48) leading to a wide range of possible diapycnal diffusivities. Assuming a dissipation rate given by Rekier et al. (21), we estimate a vertical diffusivity for Enceladus to be around 5 × 10−3 m2/s (see the “Parameterization of subgridscale processes” section), which is orders of magnitude greater than the molecular diffusivity. To place this in context, Zeng and Jansen (24) suggest that the vertical diffusivity can reach 3 × 10−3 m2/s. This is the diffusivity assumed in our default experiment for both the vertical and horizontal directions. To explore solution sensitivity, we carried out experiments with different horizontal/vertical explicit diffusivity κh, κv, and horizontal/vertical viscosity νh, νv. We also explored sensitivity to the parameterization of baroclinic instability by varying the eddy diffusivity used in the Gent and McWilliams (GM) scheme (49). The resulting Imis in these sensitivity experiments are plotted on Fig. 4E using triangular markers. Just as in the control (solid line with filled dots), Imis first decreases and then increases as the ocean salinity is changed, and a minimum is achieved near 10 psu. Among all the sensitivity tests, those with lower diffusivities/viscosities result in a weaker OHT (see panel E of figs. S4, S5, S8, and S9) and better matching of the heat budget. However, in the least diffusive experiments (κh = 10−3, κv = 10−5 m2/s), the heat budget matching over the polar regions deteriorates because of the strong temperature gradient developed under the ice shell, as indicated by the downward black triangles in Fig. 4E. More detailed discussions of these sensitivity tests can be found in the Supplementary Materials (section S1.3).
Sensitivity to model resolution and three-dimensional (3D) representation of dynamics has also been explored. In Fig. 4E, the black leftward triangles show results for the low viscosity sensitivity test repeated using 4× resolution. The general trend of Imis against salinity remain unchanged but the matching deteriorates for the fresh ocean scenario because of strong heat transport (see fig. S10). Also shown are results from 3D simulations (black diamonds). These experiments are continued on from an equilibrated 2D solution and have a horizontal resolution of 0.18° by 0.25°, and a vertical resolution of 500 m. A Smagorinsky viscosity parameterization (νsmag = 4) is used in place of high explicit viscosity to allow improved treatment of the dynamics. The Imis again achieves a minimum at intermediate salinities. Vertical and horizontal sections through the solution are presented in figs. S10 and S11. We note that even at this resolution, we are barely able to resolve eddy dynamics. More detailed analysis and exploration of 3D dynamics requires much higher resolution than we can afford here.
Last, we note that there is heat transported across the equator into the southern hemisphere in all our experiments. Depending on the model setup, the amplitude ranges from a few to tens of gigawatts (GW), which is a significant fraction of the 35GW of heating being generated by the tide. If this southward heat transport pattern were to also exist when the ocean is fully coupled to the ice, then it will provide a mechanism to induce hemispheric symmetry breaking of the ice thickness, in addition to the ice-rheology feedback proposed by Kang and Flierl (50).
Exploring mechanisms with a conceptual model
The numerical solutions presented above suggest that if Enceladus’ ocean is of intermediate salinity with canceling salinity- and temperature-driven overturning circulations, then equatorial convergence of heat is minimized, allowing a thick equatorial ice shell to be maintained. This is much less likely in very fresh or very salty oceans. Here, we use a conceptual model that is similar to that of Stommel (51) to highlight the physical processes that control the circulation strength and explore a wider range of parameter space that can be applied to other icy moons.
We represent the overall density contrast using the equator minus north pole density difference Δρ. The temperature-related density anomaly is −αTΔθ, and salinity-related one is βSΔS, where Δθ and ΔS are the potential temperature and salinity anomaly at the equator relative to the north pole. We expect the circulation-induced mass exchange between the equatorial and polar regions, denoted by ψ, to vary proportionally with Δρ (Eq. 1). For simplicity, we assume a linear form
| (4) |
where the constant A (units: kg/s) maps the density contrast on to the vigor of the overturning circulation, βS ≈ 8 × 10−4/psu for all S0, but αT depends sensitively on S0, as given by the Gibbs Seawater Toolbox (23). A positive ψ corresponds to a circulation that sinks at the equator and vice versa.
The temperature contrast Δθ is determined by the pressure-induced freezing point shift from the north pole to the equator
| (5) |
where b0 = −7.61 × 10−4 K/dbar, ρi = 917 kg/m3 is the ice density, g = 0.113 m/s2 is the surface gravity of Enceladus, and ΔH = 11 km is the difference in ice thickness between the equator and the north pole.
The lateral salinity flux is given by the product of ψ and a salinity contrast ΔS and balances the salinity flux due to freezing and melting yielding [see a detailed derivation by Marshall and Radko (52)]
| (6) |
Here, Δq, the difference in the freezing rate between low and high latitudes, is chosen to be 2 km/Ma based on Fig. 1B, ψbase is the circulation due to the imperfect cancelation between temperature- and salinity-induced buoyancy forcing, a = 250 km is the radius of Enceladus, H0 = 20.8 km is the mean thickness of the ice shell, and S0 is the mean salinity. The fact that ψ and ΔS appear as a product indicates that the salinity gradient will weaken as the overturning circulation strengthens for fixed salinity forcing.
Combining Eqs. 4, 5, and 6, we can solve for ΔS and ψ. The only tunable parameter here is A, which controls the strength of the overturning circulation and can be adjusted to fit that obtained in our ocean model. With A = 1013 kg/s and ψbase = 2 × 107 kg/s (based on Fig. 3E2), we obtain the solutions shown by the open circles in Fig. 2C (the size of the circle reflect the amplitude of ∣ψ∣ + ψbase). The conceptual model solution broadly captures the behavior of the numerical simulations (filled circles), including the strengthening of the overturning circulation and the weakening of salinity gradient away from the transition zone separating the fresh and salty oceans.
When S0 < 22 psu, −αTΔθ and βSΔS take on opposite signs, and depending on which one has a greater absolute value, the circulation ψ can be in either direction. Each possibility corresponds to one solution. The solution in the fresh ocean regime matches the numerical model results. The solution in the salty ocean regime (marked by a cross mark in Fig. 2) requires an extraordinarily strong salinity gradient to dominate the αTΔθ term. This is only possible when the mixing is extremely weak because the freezing/melting rate is fixed, and that is somewhat implausible in real world.
What is the all-important heat flux implied by our conceptual model? Analogously to Eq. 6, the meridional heat transport can be written
| (7) |
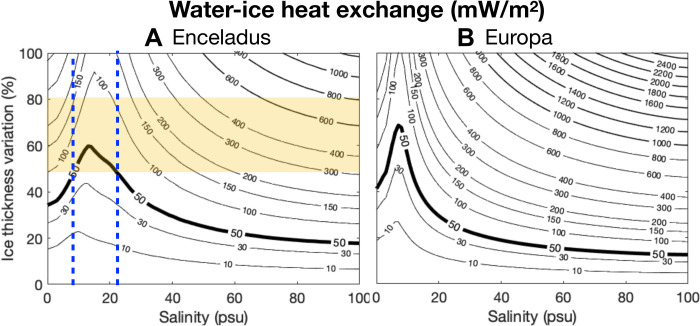
This is shown as a function of salinity and equator-to-pole thickness variations in Fig. 5A. Recall that the water-ice heat exchange must be smaller than the heat conduction rate of 50 mW/m2 to maintain observed thickness variations of the Enceladus ice shell. The likely parameter regime is shaded yellow (14–18). We see that a salinity between roughly 7 and 22 psu (marked by two vertical blue dashed lines) is required to maintain ice thickness variations as large as are seen on Enceladus.
Fig. 5. The water-ice heat exchange in equatorial regions.
(A) Enceladus and (B) for Europa. Equation 7 is used to estimate the heat exchange rates for various salinities and equator-to-pole percentage ice thickness variations (equatorial minus polar ice thickness divided by the mean). Two-degree poleward-thinning structure is assumed and physical parameters are defined in Table 1. Parameter regimes that are consistent with observations are shaded in yellow: The ice shell of Enceladus is thought to have large thickness variations (14–18). The 50 mW/m2 contour is highlighted by a thicker curve; heat exchange rates that exceed this are considered unphysical as the equatorial ice sheet of both Enceladus and Europa only allow ∼40 mW/m2 or so of heat flux to conduct through. Our simplified model suggests that salinities on Enceladus and ice thickness variations for Europa lie in the region enclosed by the blue dashed lines. The most plausible ice-thickness variations and salinity on Enceladus thus lie in the yellow areas between the blue dashed lines.
DISCUSSION
In conclusion, from knowledge of the geometry of the ice shell on Enceladus, we have deduced likely patterns of (i) salinity gradients associated with freezing and melting and (ii) under-ice temperature gradients due to the depression of the freezing point of water due to pressure. We have considered the resulting ocean circulation driven by these boundary conditions, along with the effect of putative heat fluxes emanating from the seafloor if tidal dissipation in the core is significant. We find that the ocean circulation strongly depends on its assumed salinity. If the ocean is fresh, then sinking occurs at the poles driven by the meridional temperature gradient (Fig. 3, first column); if the ocean is salty, then sinking occurs at the equator driven by the salinity gradient (Fig. 3, third column). In both cases, heat is converged toward the equator as the warm polar water is mixed with the cold equatorial water.
In the absence of polar-amplified ice dissipation to counterbalance equatorward heat transport, the polar (equatorial) ice shell will inevitably freeze (melt), because the conductive heat loss through the ice shell also tends to cool polar regions. This, together with the tendency of ice to flow from regions where it is thick to thin, will flatten ice geometry in the core-heating scenarios. Ocean salinity and the heat partition between the core and the ice shell affect ocean circulation and thereby the heat budget, which should be close to balanced—this provides us an opportunity to infer these properties using the relatively well-constrained ice shell geometry. It is found that scenarios without plenty of heat production in the shell cannot prevent the equatorial ice shell from being thinned by the equatorward heat convergence and the ice flow. Even when all heat is assumed to be produced in the ice shell, equatorward heat convergence in a very salty or very fresh ocean is implausibly strong to maintain a balanced heat budget. Instead, if heat production is assumed to occur primarily in the ice shell and salinity assumed to have an intermediate value (our calculations suggest between 7 and 30 psu), then temperature- and salinity-driven overturning circulations largely cancel one another and equatorward heat transport diminishes. If these conditions are met, then polar-amplified dissipation in the ice shell can sustain a broadly balanced heat budget.
As discussed in the introduction, such salinity ranges are consistent with those inferred from chemical equilibrium models of the interaction between the rocky core and the ocean (33–35).
Our study has focused on Enceladus, but it may also have implications for other icy moons. For example, Europa perhaps has a salinity in excess of 50 psu, as suggested by the strong magnetic induction field measured by the Galileo mission (53)—see the studies by Zolotov and Shock (54), Khurana et al. (55), and Vance et al. (56) for discussions of possible ocean compositions together with uncertainties. With a higher ocean salinity, 10 times stronger gravity and a slower rotation rate, we expect the circulation coefficient A for Europa to be considerably higher than the value that we have found here for Enceladus. That said, even if we adopt the lower Enceladus value of A, the implied OHT convergence beneath the ice shell of Europa near the equator still exceeds the conductive heat loss rate there, if the ice thickness variation exceeds 20% of the mean thickness (assuming that ocean salinity is greater than 50 psu; see Fig. 5B). Thus, our simple model leads us to believe that Europa may have a rather flat ice sheet, in line with the observation (57, 58). Moreover, no fissures that mimic the “tiger stripes” of Enceladus have been found on Europa. For icy moons with thicker ice shells, such as Dione, Titan, Ganymede, and Callisto, the high pressure under the ice shell would remove any anomalous expansion unless the ocean is very fresh, for high pressure suppresses hydrogen bond formation, which is the key for anomalous expansion. This would make it unlikely for temperature- and salinity-driven overturning circulations to cancel one another. Furthermore, ice flow becomes more efficient because, if all else is the same, it is proportional to the ice thickness cubed (see Eq. 24). Our conceptual model indeed indicates that icy ocean worlds with thick ice shells are likely to have small spatial shell thickness variations. This is consistent with shell thickness reconstructions based on gravity and shape measurements (56, 59–61). With improved measurements of gravity, topography, and induced magnetic fields for icy moons made possible by future space missions (e.g., Europa Clipper), our conceptual model could provide a useful framework to interpret them.
Last, it should be noted that, given the simplifications made in our study, our quantitative results are far from conclusive. Instead of trying to put a solid constraint on the salinity of Enceladus’ ocean, our purpose is to provide a broad physical picture of ocean circulation and heat transport on icy satellites forced by ice thickness variations and how these patterns depend on salinity. Further studies are needed to better understand and represent eddies, convection, and boundary layer turbulence on icy moons and their impact on heat/tracer transport.
MATERIALS AND METHODS
An overview of the general circulation model
Our simulations are carried out using the Massachusetts Institute of Technology Ocean General Circulation Model [MITgcm (62, 63)] configured for application to icy moons. Our purpose is to (i) simulate the large-scale circulation and tracer transport driven by under-ice salinity gradients induced by patterns of freezing and melting, under-ice temperature gradients due to the pressure dependence of the freezing point of water, and bottom heat fluxes associated with tidal dissipation in the core; (ii) diagnose the water-ice heat exchange rate; and (iii) examine whether this heat exchange is consistent with the heat budget of the ice sheet, comprising heat loss due to conduction, tidal heating in the ice sheet, and heating due to latent heat release on freezing, as presented graphically in Fig. 1.
In our calculations, the ice shell freezing/melting rate is derived from a model of ice flow (described below), based on observational inferences of ice shell thickness, prescribed, and held constant: It is not allowed to respond to the heat/salinity exchange with the ocean underneath. To enable us to integrate our ocean model out to equilibrium on a 10,000-year time scales and to explore a wide range of parameters, we use a zonally symmetric configuration at relatively coarse resolution and parameterize the diapycnal mixing, convection, and baroclinic instability of small-scale turbulent processes that cannot be resolved. Each experiment is initialized from rest and a constant salinity distribution. The initial potential temperature at each latitude is set to be equal to the freezing point at the water-ice interface. The simulations are then launched for 10,000 years. By the end of 10,000 years of integration, thermal equilibrium has been reached.
The model integrates the nonhydrostatic primitive equations for an incompressible fluid in height coordinates, including a full treatment of the Coriolis force in a deep fluid, as described in (62, 63). These terms are typically neglected when simulating Earth’s ocean because the ratio between the fluid depth and horizontal scale is small. Instead, Enceladus’ aspect ratio is order 40 km/252 km ∼ 0.16 and so not negligibly small. The size of each grid cell shrinks with depth because of spherical geometry and is accounted for by switching on the “deepAtmosphere” option of MITgcm. Because the depth of Enceladus’ ocean is comparable to its radius, the variation of gravity with depth is significant. The vertical profile of gravity in the ocean and ice shell is given by, assuming a bulk density of ρout = 1000 kg/m3
| (8) |
In the above equation, G = 6.67 × 10−11 N/m2/kg2 is the gravitational constant and M = 1.08 × 1020 kg and a = 252 km are the mass and radius of Enceladus.
Because it takes several tens of thousands of years for our solutions to reach equilibrium, we use a moderate resolution of 2° (8.7 km) and run the model in a 2D, zonal-average configuration while retaining full treatment of Coriolis terms. By doing so, the zonal variations are omitted (the effects of 3D dynamics are to be explored in future studies). In the vertical direction, the 60-km ocean-ice layer is separated into 30 layers, each of which is 2 km deep. The ocean is encased by an ice shell with meridionally varying thickness using MITgcm’s “shelf-ice” and ice “boundary layer” module (64). We set the ice thickness H using the zonal average of the thickness map given by Hemingway and Mittal (18), as shown by a solid curve in Fig. 1B, and assume hydrostacy (i.e., ice is floating freely on the water). We use partial cells to better represent the ice topography: Water is allowed to occupy a fraction of the height of a whole cell with an increment of 10%.
Parameterization of subgrid-scale processes
Key processes that are not explicitly resolved in our model are diapycnal mixing, convection, and baroclinic instability. Here, we review the parameterizations and mixing schemes used in our model to represent them. Sensitivity tests of our solutions when mixing parameters are varied about reference values are presented in the Supplementary Materials.
Vertical mixing of tracers and momentum
To account for the mixing of momentum, heat, and salinity by unresolved turbulence, in our reference calculation, we set the explicit horizontal/vertical diffusivity to 0.005 m2/s. This is roughly three orders of magnitude greater than molecular diffusivity but broadly consistent with dissipation rates suggested by Rekier et al. (21) for Enceladus, where both libration and tidal forcing are taken into account. According to (21), the tidal dissipation in the ocean is mostly induced by libration implying a global dissipation rate E of order 1 MW, but with considerable uncertainty. As reviewed by Wunsch and Ferrari (65), this suggests a vertical diffusivity given by
| (9) |
where Γ ∼ 0.2 is the efficiency at which dissipation of kinetic energy is available for production of potential energy. Here, ε = E/V is the dissipation rate per volume, V ≈ 4π(a − H0 − D/2)2D is the total volume of the ocean (H0 and D are the mean thickness of the ice layer and ocean layer, and a is the moon’s radius), and ρ0 ∼ 1000 kg/m3 is the density of water. N2 = g(∂ ln ρ/∂z) ∼ g(Δρ/ρ0)/D is the Brunt-Vaisala frequency, where g is the gravity constant. Δρ/ρ0 can be estimated from αTΔTf, where αT is the thermal expansion coefficient near the freezing point and ΔTf is the freezing point difference between the underside of the equatorial and the north polar ice shell. Here, we take ∣αT∣ ∼ 1 × 10−5/K (corresponding to S0 = 27 and S0 = 17 psu) and ∣ΔTf ∼ 0.07∣K (a measure of the overall vertical temperature gradients in our default set of experiments). Substituting into Eq. 9 yields κv ∼ 0.005 m2/s, which we choose as our default horizontal and vertical diffusivity. The diffusivity for temperature and salinity are set to be the same, so that double diffusive effects are excluded. Uncertainties stem from both E and N2 and show considerable spatial variability in our experients—see the discussion in (21). One might expect N2 to be smaller (κ larger) in cases where temperature- and salinity-induced density gradients cancel one another and vice versa; the former scenario seems to be more plausible, a main conclusion of our study. It is for this reason that we set our default diffusivities to the above high values in all our reference experiments and explore the impact of lower diffusivities as sensitivity tests.
The horizontal and vertical viscosity νh, νv are set to 10 m2/s. This value is the minimum needed to control grid-scale noise. In addition, to damp numerical noise induced by our use of stair-like ice topography, we use a biharmonic hyperviscosity of 109 m4/s and a biharmonic hyperdiffusivity of 5 × 107 m4/s.
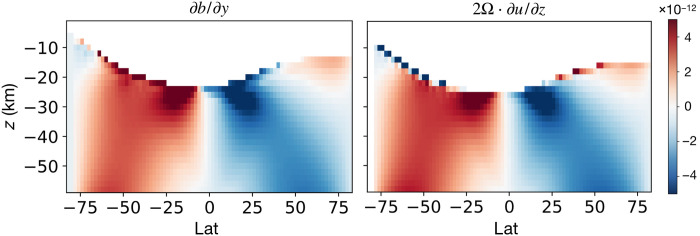
Despite use of these viscous and smoothing terms, the dominant balance in the momentum equation is between the Coriolis force and the pressure gradient force, and so zonal currents on the large scale remain in thermal wind balance, especially in the interior of the ocean. As shown by Fig. 6, the two-term balance in the thermal wind equation, 2Ω · ∇ U = ∂b/a∂ϕ (see legend), are almost identical. Because thermal wind balance is a consequence of geostrophic and hydrostatic balance and the latter is always a good approximation on the large scale, geostrophic balance is indeed well satisfied.
Fig. 6. Thermal wind balance in the control simulation.
Panels shows the two terms in the thermal wind balance, 2Ω · ∇ U and ∂b/a∂ϕ, respectively. Here Ω is the rotation rate of the moon, tU is the zonal flow speed, b = − g(ρ − ρ0)/ρ0 is buoyancy, a is the moon’s radius, and ϕ is latitude.
Convection
Because of the coarse resolution of our model, convection cannot be resolved and must be parameterized. In regions that are convectively unstable, we set the diffusivity to a much larger value, 1 m2/s, to represent the vertical mixing associated with convective overturns. Similar approaches are widely used to parameterize convection in coarse resolution ocean models [see, e.g., Klinger and Marshall (66)] and belong to a family of convective adjustment schemes. This value is obtained on the basis of the equilibrium top-to-bottom temperature gradient in a high-resolution Enceladus simulation carried out by the listed authors at MIT, where we assume a salty ocean (40 psu) and enforce ∼50 mW/m2 of heat from the bottom. Scaling arguments lead to similar results. According to Jones and Marshall (44), the velocity in a rotation-dominated regime scales with , where B is the buoyancy flux and f is the Coriolis coefficient. Using the fact that convective plumes/rolls should occupy the whole ocean depth D, a diffusivity can be estimated by multiplying the length scale and velocity scale together
| (10) |
Here, we have chosen B to be 10−13 m3/s2, which corresponds to the buoyancy flux produced by a 50 mW/m2 bottom heat flux, or the buoyancy flux induced by a 1-km/Ma freezing rate, in an ocean with 40-psu salinity. This is two orders of magnitude lower than assumed by Lobo et al. (42).
Our results are not found to be sensitive to the choice of κconv provided the associated diffusive time scale D2/νconv ≈ 0.5 years is much shorter than the advective time scale Mhalf/Ψ ≈ 2000 years (Mhalf is half of the total mass of the ocean and Ψ is the maximum meridional streamfunction in kg/s). It should be emphasized that, as noted above, away from boundary layers our solutions are close to geostrophic, hydrostatic, and thermal wind balance and are not convectively unstable. However, convective heating from the bottom and/or salinization of water at the top can and do lead to convective instability that are mixed away diffusively.
Baroclinic instability
The large-scale currents set up in our model are in thermal wind balance with horizontal density gradients induced by under-ice temperature and salinity gradients. There is thus a store of available potential energy that will be tapped by baroclinic instability, a process that is not resolved in our model because of its zonally symmetric configuration. In the default setup, we ignore the extra mixing induced by baroclinic eddies, which may lead to an underestimate of the ocean heat transport. In one of our sensitivity test, we try to test the baroclinic eddies’ potential impact by turning on the GM scheme (49, 68), which is a widely used approach to parameterize the associated eddy-induced circulation and mixing of tracers along isopycnal surfaces in modeling Earth’s ocean. The key parameter that characterize the efficiency of the along-isopycnal mixing is the GM diffusivity κGM. To allow the along-isopycnal mixing rate to vary with the local stratification and isentrope slope, we adopt the κGM formula by Visbeck et al. (43). The relevant parameters are listed in Table 1.
Table 1. Model parameters used in our study.
| Symbol | Name | Definition/value |
| Enceladus parameters | ||
| a | Radius | 252 km |
| δ | Obliquity | 27° |
| H | Global mean ice thickness | 20.8 km: (18) |
| D | Global mean ocean depth | 39.2 km: (18) |
| Ω | Rotation rate | 5.307 × 10−5 s−1 |
| g 0 | Surface gravity | 0.113 m/s2 |
| Mean surface temperature | 59 K | |
| Europa parameters | ||
| a | Radius | 1561 km |
| δ | Obliquity | 3.1° |
| H | Global mean ice thickness | 15 km: (53) |
| D | Global mean ocean depth | 85 km: (53) |
| Ω | Rotation rate | 2.05 × 10−5 s−1 |
| g 0 | Surface gravity | 1.315 m/s2 |
| Mean surface temperature | 110 K | |
| Physical constants | ||
| L f | Fusion energy of ice | 334,000 J/kg |
| Cp | Heat capacity of water | 4000 J/kg per Kelvin |
| Tf(S, P) | Freezing point | Eq. 14 |
| ρi | Density of ice | 917 kg/m3 |
| ρw | Density of the ocean | Eq. 12 |
| α, β | Thermal expansion and saline contraction coeff. | Using Gibbs Seawater Toolbox: (23) |
| κ0 | Conductivity coeff. of ice | 651 W/m: (74) |
| p α | Ice dissipation amplification factor | −2 to −1 |
| ηm | Ice viscosity at freezing point | 1014 Ps·s |
| Default parameters in the ocean model | ||
| νh, νv | Horizontal/vertical viscosity | 10 m2/s |
| Biharmonic hyperviscosity | 109 m4/s | |
| κh, κv | Horizontal/vertical diffusivity | 0.005 m2/s |
| (γT, γS, γM) | Water-ice exchange coeff. for T, S, and momentum | (10−5, 10−5, 10−3) m/s |
| g | Gravity in the ocean | Eq. 8 |
| P 0 | Reference pressure | ρig0H = 2.16 × 106 Pa |
| θ0 | Reference potential temperature | Tf(S0, P0) |
| ρw0 | Reference density of ocean | Eq. 13 |
| ℋcond | Conductive heat loss through ice | Eq. 15, Fig. 7 |
| ℋice | Tidal heating produced in the ice | Eq. 26, Fig. 7 |
| ℋcore | Bottom heat flux powered by the core | Eq. 16, Fig. 7 |
| A | Surface albedo | 0.81 |
| T s | Surface temperature profile | Fig. 7 |
A rough estimate of the magnitude of κGM can be obtained by applying the Visbeck formula
| (11) |
where is proportional to the Eady growth rate, lGM is the width of the baroclinic zone, α = 0.015 is a universal constant, f is the Coriolis parameter, and Ri = N2/Uz is the Richardson number. We estimate lGM to be around 3 km using the Rhine’s scale , where U is the zonal flow speed and β is the meridional gradient of the Coriolis parameter.
To obtain an estimate for the diffusivity induced by baroclinic eddies, we substitute N2 ∼ 10−11 s−2, f ∼ 10−4 s−1, U ∼ 10−3 m, and β ∼ 10−10 s−1m−1 in Eq. 11 and find κGM ∼0.3 m2/s. It is notable that this is two to three orders of magnitude smaller than the value used for Earth’s ocean and those adopted by Lobo et al. (42).
Equation of state and the freezing point of water
To make the dynamics as transparent as possible, we adopt a linear equation of state to determine how density depends on temperature, salinity, and pressure. The dependence of potential density ρ on potential temperature θ and salinity S is determined as follows
| (12) |
| (13) |
Here, ρ0, θ0, and S0 are the reference potential density, potential temperature, and salinity. αT and βS, the thermal expansion coefficient and the haline contraction coefficient, are set to the first derivative of density with respect to potential temperature and salinity at the reference point using the Gibbs Seawater Toolbox (23). We carried out two test experiments (one with S0 = 10 psu and the other with S0 = 20 psu) using the full “MDJWF” equation of state (68) and obtained almost identical results. To explore a wide range of background salinity, S0 is prescribed to values between 4 and 40 psu. θ0 is set to be the freezing temperature at S0 and P0 = 2.2 × 106 Pa (this is the pressure under a 20.8-km-thick ice sheet on Enceladus).
The freezing point of water Tf is assumed to depend on local pressure P and salinity S as follows
| (14) |
where a0 = −0.0575 K/psu, b0 = −7.61 × 10−4 K/dbar, and c0 = 0.0901°C. The pressure P can be calculated using hydrostatic balance P = ρigH (ρi = 917 kg/m3 is the density of the ice and H is the ice thickness).
Boundary conditions
Our ocean model is forced by heat and salinity fluxes from the ice shell at the top and heat fluxes coming from below.
Diffusion of heat through the ice
Heat loss to space by conduction through the ice ℋcond is represented using a 1D vertical heat conduction model
| (15) |
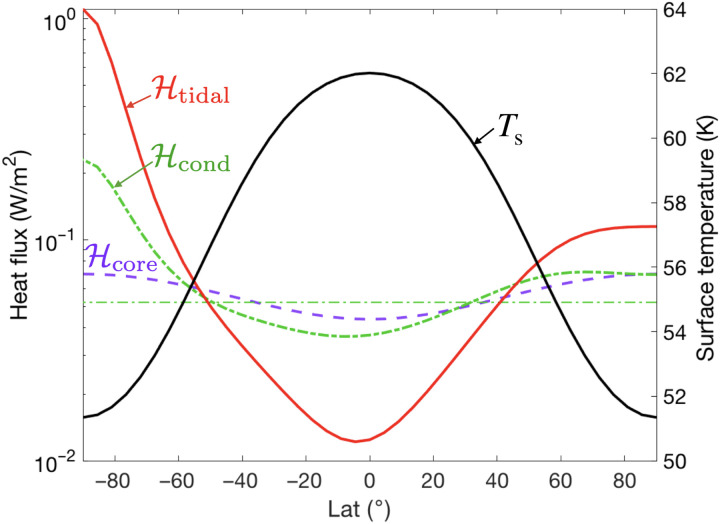
where H is the thickness of ice (solid curve in Fig. 1B), the surface temperature is Ts, and the ice temperature at the water-ice interface is the local freezing point Tf (Eq. 14). We approximate the surface temperature Ts using radiative equilibrium based on the incoming solar radiation and obliquity (δ = 27°) assuming an albedo of 0.81. The Ts profile is shown by the black solid curve in Fig. 7. Typical heat losses averaged over the globe are ℋcond = 50 mW/m2, broadly consistent with observations (16).
Fig. 7. Meridional profiles of heat fluxes and surface temperature.
Heat fluxes are plotted using colored curves, with a scale on the left. Conductive heat loss ℋcond (Eq. 15) is shown by a thick green dash-dotted line that, in the global average, is balanced by heat generation in the silicate core ℋcore (purple dashed line, Eq. 16) and ℋice (red solid line, Eq. 26). All heat fluxes are normalized to have the same global mean value of ℋcond. The surface temperature Ts (black solid line, axis on the right) is set to be in radiative equilibrium with the solar radiation and is warmer at the equator.
Tidal heating in the core
Conductive heat loss is primarily balanced by tidal dissipation in the ice shell ℋice and the core ℋcore (dissipation in the ocean plays a negligible role) (21, 48, 69, 70). For each assumed heat partition between the shell and the core, we use the same meridional heating profiles for ℋcore and ℋice (see below). According to Beuthe (4) and Choblet et al. (3), the core dissipation ℋcore peaks at the two poles. We obtain the meridional heat profile using equation 60 in the study by Beuthe (4)
| (16) |
where ϕ denotes latitude and is the global mean heat flux from the bottom. Because the global surface area shrinks going downward because of the spherical geometry, a factor of (a − H)2(a − H − D)2 (H is ice thickness, D is ocean depth) needs to be considered when computing . The expression within the bracket is normalized for the globe, adjusted to take account of the fact that our model only covers 84°S-84°N. Using the above formula, the bottom heat flux is twice as strong over the poles than equator, as can be seen in Fig. 1D. We note that the heating profile here is highly idealized and does not have the localized heating stripes seen in the study by Choblet et al. (3) that arise from the interaction between the porous core and the fluid in the gaps.
Ice-ocean fluxes
The interaction between ocean and ice is simulated using MITgcm’s shelf-ice package (64, 71). We turn on the boundary layer option to avoid possible numerical instabilities induced by an ocean layer that is too thin. The code is modified to account for a gravitational acceleration that is very different from that on Earth, the temperature dependence of heat conductivity, and the meridional variation of tidal heating generated inside the ice shell and the ice surface temperature. In the description that follows, we begin by introducing the shelf-ice parameterization in a fully coupled ocean-ice system and then make simplifications that fit our goal here.
The heat budget involves three terms: the heat transmitted upward by ocean ℋocn, the heat loss through the ice shell due to heat conduction ℋcond (Eq. 15), and the tidal heating generated inside the ice shell ℋice (Eq. 26). As elucidated by Holland and Jenkins (71) and Losch (64), the continuity of heat flux and salt flux through the boundary layer gives
| (17) |
| (18) |
where Tocn−top and Socn−top denote the temperature and salinity in the top grid of the ocean, Sb denotes the salinity in the boundary layer, and q denotes the freezing rate in kg/m2/s. Cp = 4000 J/kg per Kelvin is the heat capacity of the ocean, and Lf = 334,000 J/kg is the latent heat of fusion of ice.
ℋocn and ℱocn in Eq.17 can be written as
| (19) |
| (20) |
where γT = γS = 10−5 m/s are the exchange coefficients for temperature and salinity and Tb denotes the temperature in the boundary layer. The terms associated with q are the heat/salinity change induced by the deviation of Tocn − top, Socn−top from that in the boundary layer, where melting and freezing occur. Tb = Tf(Sb, P), the freezing temperature at pressure P and salinity Sb (see Eq. 14).
In a fully coupled system, we would solve Sb and q from Eqs. 17 to 20. When freezing occurs (q > 0), the salinity flux ρw0γS(Socn−top − Sb) is negative (downward). This leads to a positive tendency of salinity at the top of the model ocean, together with changes of temperature, thus
| (21) |
| (22) |
where δz = 2 km is the thickness of the boundary layer at the ocean-ice interface.
It should be noted that the top ocean grid is close to, but not exactly at, the freezing point. Our imaginary boundary layer, however, is at the freezing point. When the ice is melting, the boundary layer will be fresher than the top ocean grid to support a freshwater flux into the ocean. Having a relatively low salinity in the boundary layer means that the temperature there will be slightly higher given the dependence of freezing point on salinity (Eq. 14). This, in turn, allows heat to be transmitted into the ocean, without requiring the ocean temperature to be below freezing.
If we allow the freezing/melting of ice and the ocean circulation to feedback onto one another, the positive feedback between them renders it difficult to find consistent solutions. We therefore cut off this feedback loop by setting the freezing rate, q, to that which is required to sustain the prescribed ice sheet geometry (details can be found in the next subsection where the ice flow model is described), while allowing a heating term to balance the heat budget (Eq. 17). The amplitude of this heat imbalance can then be used to discriminate between different steady-state solutions (Eq. 2). This also simplifies the calculation of the T/S tendencies of the uppermost ocean grid. The S tendency can be directly calculated from Eq. 21, and the T tendency is approximated by
| (23) |
replacing the boundary layer freezing temperature Tb = Tf(Sb, P) in Eq. 22 with Tf,ocn−top = Tf(Socn−top, P), the freezing temperature determined by the uppermost ocean grid salinity and pressure. The difference between Sb and Socn−top can be estimated from ℱocn/(ρ0γS) = qSocn−top/(ρ0γS), guided by Eqs. 20 and 21, given that ∣q∣ ≲ 10−7 kg/m2 per second is orders of magnitude smaller than ρ0γS = 0.01 kg/m2/s. Even in the saltiest scenario, we consider here, ∣Sb − Socn−top∣ does not exceed 0.0004 psu, and the associated freezing point change is lower than 10−5 K. Readers interested in the formulation of a freely evolving ice-water system are referred to the method section of Losch (64). In addition to the above conditions on temperature and salinity, the tangential velocity is relaxed back to zero at a rate of γM = 10−3m/s at the upper and lower boundaries.
Ice flow model
We prescribe q using the divergence of the ice flow, assuming that the ice sheet geometry is in equilibrium. We use an upside-down land ice sheet model following Ashkenazy et al. (40). The ice flows down its thickness gradient, driven by the pressure gradient induced by the spatial variation of the ice top surface, somewhat like a second-order diffusive process. At the top, the speed of the ice flow is negligible because the upper part of the shell is so cold and hence rigid; at the bottom, the vertical shear of the ice flow speed vanishes, as required by the assumption of zero tangential stress there. This is the opposite to that assumed in the land ice sheet model. In rough outline, we calculate the ice flow using the expression below obtained through repeated vertical integration of the force balance equation (the primary balance is between the vertical flow shear and the pressure gradient force), using the aforementioned boundary conditions to arrive at the following formula for ice transport Q
| (24) |
Here, ϕ denotes latitude, a = 252 km, and g = 0.113 m/s2 are the radius and surface gravity of Enceladus, Ts and Tf are the temperature at the ice surface and the water-ice interface (equal to local freezing point; Eq. 14), and ρi = 917 kg/m3 and ρ0 are the ice density and the reference water density (Eq. 12). Ea = 59.4 kJ/mol is the activation energy for diffusion creep, Rg = 8.31 J/K/mol is the gas constant, and ηmelt is the ice viscosity at the freezing point. The latter has considerable uncertainty (1013 to 1015 Pa·s) (38), but we choose to set ηmelt = 1014 Pa·s.
In steady state, the freezing rate q must equal the divergence of the ice transport thus
| (25) |
As shown by the dashed curve in Fig. 1B, ice melts in high latitudes and forms in low latitudes at a rate of a few kilometers every million years. A more detailed description of the ice flow model can be found in the studies by Kang and Flierl (50) and Ashkenazy et al. (40). Freezing and melting lead to changes in local salinity and thereby a buoyancy flux. At S0 = 30 psu, the salinity-associated buoyancy flux is approximately gqβSS0 ≈ 10−13 m2/s3, which is three to six orders of magnitude smaller than the buoyancy flux used by Lobo et al. (42).
Model of tidal dissipation in the ice shell
Enceladus’ ice shell is periodically deformed by tidal forcing and the resulting strains in the ice sheet produce heat. We follow Beuthe (4) to calculate the implied dissipation rate. Instead of repeating the whole derivation here, we only briefly summarize the procedure and present the final result. Unless otherwise stated, parameters are the same as assumed by Kang and Flierl (50).
Tidal dissipation consists of three components (4): a membrane mode due to the extension/compression and tangential shearing of the ice membrane, a mixed mode due to vertical shifting, and a bending mode induced by the vertical variation of compression/stretching. Following Beuthe (4), we first assume the ice sheet to be completely flat. By solving the force balance equation, we obtain the auxiliary stress function F, which represents the horizontal displacements, and the vertical displacement w. The dissipation rate (where x ={mem, mix, bend}) can then be written as a quadratic form of F and w. In the calculation, the ice properties are derived assuming a globally uniform surface temperature of 60 K and a melting viscosity of 5 × 1013 Pa·s.
Ice thickness variations are accounted for by multiplying the membrane mode dissipation , by a factor that depends on ice thickness. This makes sense because this is the only mode that is amplified in thin ice regions [see the study by Beuthe (4)]. This results in the expression
| (26) |
where H is the prescribed thickness of the ice shell as a function of latitude and H0 is the global mean of H. Because thin ice regions deform more easily and produce more heat, pα is negative. Because more heat is produced in the ice shell, the overall ice temperature rises, which, in turn, further increases the mobility of the ice and leads to more heat production (the rheology feedback).
Using reasonable parameters for Enceladus, ℋice turns out to be at least an order of magnitude smaller than the heat loss rate ℋcond. This is a universal flaw of present tidal dissipation models and could be due to use of an oversimplified Maxwell rheology (19, 74). We therefore scale up ℋice by a constant factor to obtain the desired magnitude. The tidal heating profile corresponding to pα = −1.5 is the red solid curve plotted in Fig. 7. In Fig. 4 (C and D), we show the tidal heating profile for pα = −1 and pα = −2.The distribution of ℋice is insensitive to the assumed ice viscosity, but the amplitude (before rescaling) could vary by a lot as indicated by previous studies (73).
Acknowledgments
This work was carried out in the Department of Earth, Atmospheric and Planetary Science (EAPS) in MIT. We thank M. Beuthe and M. Jansen for advice and discussions and very helpful reviews by J. Buffo and a further anonymous reviewer.
Funding: W.K. and T.M. acknowledge support as a Lorenz and Crosby Fellow supported by endowed funds in EAPS. S.B., J.-M.C., and J.M. acknowledge part support from NASA Astrobiology Grant 80NSSC19K1427 Exploring Ocean Worlds.
Author contributions: W.K.: Conceptualization, formal analysis, investigation, methodology, software, validation, visualization, writing—original draft, and writing—review and editing. T.M.: Writing—original draft and writing—review and editing. S.B.: Software, visualization, and validation. J.-M.C.: Methodology and software. J.M.: Writing—review and editing.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials.
Supplementary Materials
This PDF file includes:
Exploring the sensitivity of ocean model solutions to parameters
Section S1
Figs. S1 to S11
References
REFERENCES AND NOTES
- 1.Postberg F., Kempf S., Schmidt J., Brilliantov N., Beinsen A., Abel B., Buck U., Srama R., Sodium salts in E-ring ice grains from an ocean below the surface of Enceladus. Nature 459, 1098–1101 (2009). [DOI] [PubMed] [Google Scholar]
- 2.Thomas P. C., Tajeddine R., Tiscareno M. S., Burns J. A., Joseph J., Loredo T. J., Helfenstein P., Porco C., Enceladus’s measured physical libration requires a global subsurface ocean. Icarus 264, 37–47 (2016). [Google Scholar]
- 3.Choblet G., Tobie G., Sotin C., Běhounková M., Čadek O., Postberg F., Souček O., Powering prolonged hydrothermal activity inside Enceladus. Nat. Astron. 1, 841–847 (2017). [Google Scholar]
- 4.Beuthe M., Enceladus’s crust as a non-uniform thin shell: II tidal dissipation. Icarus 332, 66–91 (2019). [Google Scholar]
- 5.Waite J. H. Jr., Combi M. R., Ip W.-H., Cravens T. E., McNutt R. L. Jr., Kasprzak W., Yelle R., Luhmann J., Niemann H., Gell D., Magee B., Fletcher G., Lunine J., Tseng W.-L., Cassini ion and neutral mass spectrometer: Enceladus plume composition and structure. Science 311, 1419–1422 (2006). [DOI] [PubMed] [Google Scholar]
- 6.Hsu H.-W., Postberg F., Sekine Y., Shibuya T., Kempf S., Horányi M., Juhász A., Altobelli N., Suzuki K., Masaki Y., Kuwatani T., Tachibana S., Sirono S.-I., Moragas-Klostermeyer G., Srama R., Ongoing hydrothermal activities within Enceladus. Nature 519, 207–210 (2015). [DOI] [PubMed] [Google Scholar]
- 7.Waite J. H., Glein C. R., Perryman R. S., Teolis B. D., Magee B. A., Miller G., Grimes J., Perry M. E., Miller K. E., Bouquet A., Lunine J. I., Brockwell T., Bolton S. J., Cassini finds molecular hydrogen in the Enceladus plume: Evidence for hydrothermal processes. Science 356, 155–159 (2017). [DOI] [PubMed] [Google Scholar]
- 8.Postberg F., Khawaja N., Abel B., Choblet G., Glein C. R., Gudipati M. S., Henderson B. L., Hsu H.-W., Kempf S., Klenner F., Moragas-Klostermeyer G., Magee B., Nölle L., Perry M., Reviol R., Schmidt J., Srama R., Stolz F., Tobie G., Trieloff M., Waite J. H., Macromolecular organic compounds from the depths of Enceladus. Nature 558, 564–568 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Taubner R.-S., Pappenreiter P., Zwicker J., Smrzka D., Pruckner C., Kolar P., Bernacchi S., Seifert A. H., Krajete A., Bach W., Peckmann J., Paulik C., Firneis M. G., Schleper C., Rittmann S. K.-M. R., Biological methane production under putative Enceladus-like conditions. Nat. Commun. 9, 748 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Glein C. R., Waite J. H., The carbonate geochemistry of Enceladus’ ocean. Geophys. Res. Lett. 47, e2019GL085885 (2020). [Google Scholar]
- 11.Hansen C. J., Esposito L., Stewart A. I. F., Colwell J., Hendrix A., Pryor W., Shemansky D., West R., Enceladus’ water vapor plume. Science 311, 1422–1425 (2006). [DOI] [PubMed] [Google Scholar]
- 12.Howett C. J. A., Spencer J. R., Pearl J., Segura M., High heat flow from Enceladus’ south polar region measured using 10–600 cm–1Cassini/CIRS data. J. Geophys. Res. Atmos. 116, 10.1029/2010JE003718 (2011). [Google Scholar]
- 13.J. R. Spencer, C. J. A. Howett, A. Verbiscer, T. A. Hurford, M. Segura and D. C. Spencer, European Planetary Science Congress 8, EPSC2013 (2013).
- 14.Iess L., Stevenson D. J., Parisi M., Hemingway D., Jacobson R. A., Lunine J. I., Nimmo F., Armstrong J. W., Asmar S. W., Ducci M., Tortora P., The gravity field and interior structure of Enceladus. Science 344, 78–80 (2014). [DOI] [PubMed] [Google Scholar]
- 15.Beuthe M., Rivoldini A., Trinh A., Geophys. Res. Lett. 43, 10,088–10,096 (2016). [Google Scholar]
- 16.Tajeddine R., Soderlund K. M., Thomas P. C., Helfenstein P., Hedman M. M., Burns J. A., Schenk P. M., True polar wander of Enceladus from topographic data. Icarus 295, 46–60 (2017). [Google Scholar]
- 17.Čadek O., Souček O., Běhounková M., Choblet G., Tobie G., Hron J., Long-term stability of Enceladus’ uneven ice shell. Icarus 319, 476–484 (2019). [Google Scholar]
- 18.Hemingway D. J., Mittal T., Enceladus’s ice shell structure as a window on internal heat production. Icarus 332, 111–131 (2019). [Google Scholar]
- 19.McCarthy C., Cooper R. F., Tidal dissipation in creeping ice and the thermal evolution of Europa. Earth & Planet. Sci. Lett., 185–194 (2016). [Google Scholar]
- 20.Tobie G., Mocquet A., Sotin C., Tidal dissipation within large icy satellites: Applications to Europa and Titan. Icarus 177, 534–549 (2005). [Google Scholar]
- 21.Rekier J., Trinh A., Triana S. A., Dehant V., Internal energy dissipation in Enceladus’s subsurface ocean from tides and libration and the role of inertial waves. J. Geophys. Res. 124, 2198–2212 (2019). [Google Scholar]
- 22.Soderlund K. M., Kalousová K., Buffo J. J., Glein C. R., Goodman J. C., Mitri G., Patterson G., Postberg F., Rovira-Navarro M., Rüeckriemen T., Saur J., Schmidt B. E., Sotin C., Spohn T., Tobie G., Van Hoolst T., Vance S. D., Vermeersen B., Ice-ocean exchange processes in the Jovian and Saturnian satellite. Space Sci. Rev. 216, 80 (2020). [Google Scholar]
- 23.McDougall T. J., Barker P. M., SCOR/IAPSO WG 127, 1 (2011). [Google Scholar]
- 24.Zeng Y., Jansen M. F., Ocean circulation on Enceladus with a high- versus low-salinity ocean. Planet. Sci. J. 2, 151 (2021). [Google Scholar]
- 25.Cullum J., Stevens D. P., Joshi M. M., Importance of ocean salinity for climate and habitability. Proc. Natl. Acad. Sci. U. S. A. 113, 4278–4283 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cael B., Ferrari R., The ocean’s saltiness and its overturning. Geophys. Res. Lett. 44, 1886–1891 (2017). [Google Scholar]
- 27.Travis B. J., Schubert G., Keeping Enceladus warm. Icarus 250, 32–42 (2015). [Google Scholar]
- 28.Souček O., Běhounkova M., Čadek O., Hron J., Tobie G., Choblet G., Tidal dissipation in Enceladus’ uneven, fractured ice shell. Icarus 328, 218–231 (2019). [Google Scholar]
- 29.Robuchon G., Choblet G., Tobie G., Čadek O., Sotin C., Grasset O., Coupling of thermal evolution and despinning of early lapetus. Icarus 207, 959–971 (2010). [Google Scholar]
- 30.Shoji D., Hussmann H., Kurita K., Sohl F., Ice rheology and tidal heating of Enceladus. Icarus 226, 10–19 (2013). [Google Scholar]
- 31.Běhounková M., Tobie G., Choblet G., Čadek O., Impact of tidal heating on the onset of convection in Enceladus’s ice shell. Icarus 226, 898–904 (2013). [Google Scholar]
- 32.Gevorgyan Y., Boué G., Ragazzo C., Ruiz L. S., Correia A. C., Andrade rheology in time-domain. Application to Enceladus’ dissipation of energy due to forced libration. Icarus 343, 113610 (2019). [Google Scholar]
- 33.Zolotov M. Y., An oceanic composition on early and today’s Enceladus. Geophys. Res. Lett. 34, 10.1029/2007GL031234 (2007). [Google Scholar]
- 34.M. Y. Zolotov, F. Postberg, LPI p. 2496 (2014).
- 35.C. R. Glein, F. Postberg, S. D. Vance, Enceladus and the Icy Moons of Saturn (University of Arizona Press, 2018) 39. [Google Scholar]
- 36.Ingersoll A. P., Nakajima M., Controlled boiling on Enceladus. 2. Model of the liquid-filled cracks. Icarus 272, 319–326 (2016). [Google Scholar]
- 37.Fox-Powell M. G., Cousins C. R., Partitioning of crystalline and amorphous phases during freezing of simulated enceladus ocean fluids. JGR: Planets 126, e2020JE006628 (2021). [Google Scholar]
- 38.Tobie G., Choblet G., Sotin C., Tidally heated convection: Constraints on Europa’s ice shell thickness. J. Geophys. Res. 108, 219 (2003). [Google Scholar]
- 39.A. C. Barr, A. P. Showman, Europa (Univ. Arizona Press, 2009), pp. 405–430. [Google Scholar]
- 40.Ashkenazy Y., Sayag R., Tziperman E., Dynamics of the global meridional ice flow of Europa’s icy shell. Nat. Astron. 2, 43–49 (2018). [Google Scholar]
- 41.Bire S., Kang W., Ramadhan A., Campin J.-M., Marshall J., Exploring ocean circulation on icy moons heated from below. JGR: Planets 127, e2021JE007025 (2022). [Google Scholar]
- 42.Lobo A. H., Thompson A. F., Vance S. D., Tharimena S., A pole-to-equator ocean turning circulation on Enceladus. Nat. Geosci., 185–189 (2021). [Google Scholar]
- 43.Visbeck M., Marshall J., Haine T., Spall M., Specification of eddy transfer coefficients in coarse-resolution ocean circulation models*. J. Phys. Oceanogr. 27, 381–402 (1997). [Google Scholar]
- 44.Jones H., Marshall J., Convection with rotation in a neutral ocean: A study of open-ocean deep convection. J. Phys. Oceanogr. 23, 1009–1039 (1993). [Google Scholar]
- 45.Czaja A., Marshall J., The partitioning of poleward heat transport between the atmosphere and ocean. J. Atmos. Sci. 63, 1498–1511 (2006). [Google Scholar]
- 46.Jeffreys H., On fluid motions produced by differences of temperature and humidity. Quart. J. Roy. Meteor. Soc. 51, 347–356 (1925). [Google Scholar]
- 47.Chen E. M. A., Nimmo F., Glatzmaier G. A., Tidal heating in icy satellite oceans. Icarus 229, 11–30 (2014). [Google Scholar]
- 48.Hay H. C. F. C., Matsuyama I., Nonlinear tidal dissipation in the subsurface oceans of Enceladus and other icy satellites. Icarus 319, 68–85 (2019). [Google Scholar]
- 49.Gent P. R., Mcwilliams J. C., Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr. 20, 150–155 (1990). [Google Scholar]
- 50.Kang W., Flierl G., Spontaneous formation of geysers at only one pole on Enceladus’s ice shell. Proc. Natl. Acad. Sci. U.S.A. 117, 14764–14768 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Stommel H., Thermohaline convection with two stable regimes of flow. Tellus 13, 224–230 (1961). [Google Scholar]
- 52.Marshall J., Radko T., Residual-mean solutions for the Antarctic Circumpolar Current and its associated overturning circulation. J. Phys. Oceanogr. 33, 2341–2354 (2003). [Google Scholar]
- 53.Hand K., Chyba C., Empirical constraints on the salinity of the europan ocean and implications for a thin ice shell. Icarus 189, 424–438 (2007). [Google Scholar]
- 54.Zolotov M. Y., Shock E. L., Composition and stability of salts on the surface of Europa and their oceanic origin. J. Geophys. Res. Planets 106, 32815–32827 (2001). [Google Scholar]
- 55.K. K. Khurana, M. G. Kivelson, K. P. Hand, C. T. Russell, in Electromagnetic Induction from Europa’s Ocean and the Deep Interior, R. T. Pappalardo, W. B. Mc Kinnon, K. Khurana, Eds. (Europa, University of Arizona Press, 2009), pp. 572–586. [Google Scholar]
- 56.Vance S. D., Styczinski M. J., Bills B. G., Cochrane C. J., Soderlund K. M., Gómez-Pérez N., Paty C., Magnetic induction responses of Jupiter’s ocean moons including effects from adiabatic convection. Journal of Geophysical Research: Planets 126, e2020JE006418 (2021). [Google Scholar]
- 57.Howell S. M., The likely thickness of Europa’s icy shell. Planet. Sci. 2, 129 (2021). [Google Scholar]
- 58.Nimmo F., Thomas P., Pappalardo R., Moore W., The global shape of Europa: Constraints on lateral shell thickness variations. Icarus 191, 183–192 (2007). [Google Scholar]
- 59.Zannoni M., Hemingway D., Casajus L. G., Tortora P., The gravity field and interior structure of Dione. Icarus 345, 113713 (2020). [Google Scholar]
- 60.Durante D., Hemingway D. J., Racioppa P., Iess L., Stevenson D. J., Titan’s gravity field and interior structure after Cassini. Icarus 326, 123–132 (2019). [Google Scholar]
- 61.Nimmo F., Bills B. G., Shell thickness variations and the long-wavelength topography of Titan. Icarus 208, 896–904 (2010). [Google Scholar]
- 62.MITgcm-group, MITgcm User Manual, Online documentation (MIT/EAPS, 2010); http://mitgcm.org/public/r2_manual/latest/online_documents/manual.html.
- 63.Marshall J., Adcroft A., Hill C., Perelman L., Heisey C., A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys. Res. 102, 5753–5766 (1997). [Google Scholar]
- 64.Losch M., Modeling ice shelf cavities in a z-coordinate ocean general circulation model. J. Geophys. Res. 113, 2007JC004368 (2008). [Google Scholar]
- 65.Wunsch C., Ferrari R., Vertical mixing, energy, and the general circulation of the oceans. Ann. Rev. Fluid Mech. 36, 281–314 (2004). [Google Scholar]
- 66.Klinger B. A., Marshall J., Send U., Representation of convective plumes by vertical adjustment. J. Geophys. Res. Oceans 101, 18175–18182 (1996). [Google Scholar]
- 67.Redi M. H., Oceanic isopycnal mixing by coordinate rotation. J. Phys. Oceanogr. 12, 1154–1158 (1982). [Google Scholar]
- 68.McDougall T. J., Jackett D. R., Wright D. G., Feistel R., Accurate and computationally efficient algorithms for potential temperature and density of seawater. J. Atmos. Oceanic Tech. 20, 730–741 (2003). [Google Scholar]
- 69.Chen E. M. A., Nimmo F., Obliquity tides do not significantly heat Enceladus. Icarus 214, 779–781 (2011). [Google Scholar]
- 70.Beuthe M., Crustal control of dissipative ocean tides in Enceladus and other icy moons. Icarus 280, 278–299 (2016). [Google Scholar]
- 71.Holland D. M., Jenkins A., Modeling thermodynamic ice–ocean interactions at the base of an ice shelf. J. Phys. Oceanogr. 29, 1787–1800 (1999). [Google Scholar]
- 72.Renaud J. P., Henning W. G., Increased tidal dissipation using advanced rheological models: implications for io and tidally active exoplanets. ApJ 857, 98 (2018). [Google Scholar]
- 73.Beuthe M., Enceladus’s crust as a non-uniform thin shell: I tidal deformations. Icarus 302, 145–174 (2018). [Google Scholar]
- 74.V. F. Petrenko, R. W. Whitworth, Physics of Ice (OUP Oxford, 1999). [Google Scholar]
- 75.Smagorinsky J., General circulation experiments with the primitive equations. Mon. Weath. Rev. 91, 99–164 (1963). [Google Scholar]
- 76.Soderlund K. M., Ocean dynamics of outer solar system satellites. Geophys. Res. Lett. 46, 8700–8710 (2019). [Google Scholar]
- 77.Ashkenazy Y., Tziperman E., Dynamic Europa ocean shows transient Taylor columns and convection driven by ice melting and salinity. Nat. Commun. 12, 6376 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Exploring the sensitivity of ocean model solutions to parameters
Section S1
Figs. S1 to S11
References