Population pharmacokinetics of clonazepam in saliva and plasma: Steps towards noninvasive pharmacokinetic studies in vulnerable populations

Abstract

Aim

Traditional studies focusing on the relationship between pharmacokinetics (PK) and pharmacodynamics necessitate blood draws, which are too invasive for children or other vulnerable populations. A potential solution is to use noninvasive sampling matrices, such as saliva. The aim of this study was to develop a population PK model describing the relationship between plasma and saliva clonazepam kinetics and assess whether the model can be used to determine trough plasma concentrations based on saliva samples.

Methods

Twenty healthy subjects, aged 18‐30, were recruited and administered 0.5 or 1 mg of clonazepam solution. Paired plasma and saliva samples were obtained until 48 hours post‐dose. A population pharmacokinetic model was developed describing the PK of clonazepam in plasma and the relationship between plasma and saliva concentrations. Bayesian maximum a posteriori optimization was applied to estimate the predictive accuracy of the model.

Results

A two‐compartment distribution model best characterized clonazepam plasma kinetics with a mixture component on the absorption rate constants. Oral administration of the clonazepam solution caused contamination of the saliva compartment during the first 4 hours post‐dose, after which the concentrations were driven by the plasma concentrations. Simulations demonstrated that the lower and upper limits of agreements between true and predicted plasma concentrations were −28% to 36% with one saliva sample. Increasing the number of saliva samples improved these limits to −18% to 17%.

Conclusion

The developed model described the salivary and plasma kinetics of clonazepam, and could predict steady‐state trough plasma concentrations based on saliva concentrations with acceptable accuracy.

What is already known about this subject

• Traditional studies focusing on pharmacokinetics (PK) necessitate multiple blood draws.

• Noninvasive PK sampling, using saliva, could significantly reduce the burden in paediatric clinical trials.

• Studies investigating salivary PK generally do not employ nonlinear pharmacokinetic modelling techniques.

What this study adds

• Plasma and salivary kinetics of clonazepam can be adequately described with a nonlinear mixed effects model.

• Applying this model in the context of noninvasive clinical trials or therapeutic drug monitoring is possible and yields acceptable prediction errors.

• This study represents a step towards completely noninvasive clinical trials in vulnerable populations.

1. INTRODUCTION

Traditional studies focusing on pharmacokinetics (PK) in plasma necessitate multiple blood samples and therefore may become too invasive for a paediatric population. However, the determination of pharmacokinetic‐pharmacodynamic (PKPD) relationships between a drug and an endpoint is an important method for evaluation of drug effects and dose optimization. A possible solution is to determine drug concentrations in sampling matrices that can be collected in a noninvasive manner, such as saliva. Salivary kinetics have been determined in a wide range of compounds, and applications in the field of therapeutic drug monitoring (TDM) have been explored. ¹ , ² , ³ However, analyses have been mainly performed by calculating the plasma concentrations based on a constant ratio over time with the saliva concentrations. Nonlinear mixed effects models have potential advantages, such as accounting for a changing ratio over time and different sources of variability, in the evaluation of the population kinetics in plasma and saliva. This approach could potentially also be used for the prediction of plasma concentrations when only saliva concentrations are available.

This study is conducted in preparation of a clinical trial researching the therapeutic effects of clonazepam on patients with ARID1B‐related intellectual disability (ID) ⁴ , ⁵ Clonazepam is a GABA‐A positive allosteric modulator used to treat a range of clinical conditions, such as epilepsy, panic disorder, depression and bipolar disease. ⁶ , ⁷ Although clonazepam has been prescribed less often in recent years, ⁸ the drug is a candidate for rediscovery in other conditions, and preclinical evidence shows possible efficacy of clonazepam on behavioural and cognitive symptoms in ARID1B‐related ID. ⁵ A clinical trial in patients is a logical next step. However, conducting clinical trials in a (paediatric) intellectually disabled population is challenging, as trial designs must be unobtrusive to motivate as many patients as possible to participate. ⁹ , ¹⁰ Inclusion of noninvasive pharmacokinetic assessments may help in this respect. A preparatory study with a dense blood and saliva sampling design in competent adults will allow for the identification of the saliva:plasma relationship of the compound and subsequently allow for a noninvasive clinical trial with ARID1B‐related ID patients.

Therefore, the aims of this study were to study the population kinetics of clonazepam, to determine the relationship between salivary and plasma clonazepam concentrations, and to investigate the performance of a population PK model describing this relationship to predict trough plasma concentrations based on saliva samples in patients treated with clonazepam in the context of clinical trials or TDM.

2. MATERIALS AND METHODS

2.1. Location and ethics

This study was conducted in at the Centre for Human Drug Research in Leiden, the Netherlands from June 2020 until July 2020. Ethical approval was obtained from the Beoordeling Ethiek Biomedisch Onderzoek Foundation Review Board (Assen, the Netherlands) prior to initiation of the study. The study was conducted in compliance with the Dutch Act on Medical Research Involving Human Subjects and Good Clinical Practice. Informed consent was obtained prior to study‐mandated procedures.

2.2. Study design and sample collection

This was an open‐label, single‐dose study in 20 healthy subjects aged 18‐30. Exclusion criteria were history of disease or use of medications that might interfere with saliva production, such as opiates and anticholinergics. Subjects were asked to refrain from alcohol and caffeine use for 24 hours prior to drug administration until the end of the study, and from any nutrients with Cytochrome P450 (CYP)‐modulating activity for 3 days prior to drug administration. Subjects were administered a single dose of 0.5 mg (n = 10) or 1.0 mg (n = 10) clonazepam solution (Rivotril) dissolved in lemonade, after which paired plasma and saliva samples were taken at 0.5, 1, 2, 4, 6, 8, 24 and 48 hours post dose. Subjects thoroughly rinsed their mouths with water 10 minutes prior to saliva sampling. Saliva samples were obtained using the SalivaBio Infant Swab (Salimetrics, Carlsbad, CA, USA) according to the manufacturer's instructions.

2.3. Bioanalytical assay

Clonazepam (1 mg/mL; Duchefa Farma, Haarlem, the Netherlands), clonazepam‐d4 (0.1 mg/mL; LGC Standards, Luckenwalde, Germany), methanol and acetonitril (Merck BV, Darmstadt, Germany) were obtained. Assay validation was performed in accordance with European Medicines Agency (EMA) guidelines. ¹¹ From the clonazepam solution, standards were prepared in saliva at concentrations of 0.1, 0.5, 2.5, 5, 10 and 20 μg/L. The internal standard clonazepam‐d4 was diluted with methanol to a final concentration of 30 μg/L. The lower limit of quantification (LOQ), low, medium and high reference samples were prepared in saliva with concentrations of respectively 0.1, 1, 5 and 15 μg/L. For the measurement of the plasma samples Recipe ClinChek calibrators were used, as well as controls with a linear range of 2‐72.3 μg/L and the LLQ, LOW, MED and HIGH samples with a concentration of resp. 2, 5.25, 14.8 and 48.1 μg/L.

Sample preparation of saliva samples was performed by diluting each aliquot of 20 μL of saliva with 20 μL of internal standard solution in Eppendorf cups, which were vortexed for 1 minute and centrifuged at 13000 rpm for 5 minute. The extract was transferred in vials. For plasma samples, each aliquot of 50 μL of plasma was diluted with 50 μL of internal standard solution and 150 μL of acetonitrile in Eppendorf cups. The Eppendorf cups were vortexed for 1 minute and centrifuged at 13000 rpm for 5 minute. The extract was transferred in a vial with 150 μL of water.

Analysis was performed via liquid chromatography‐mass spectrometry (LC‐MS). Extracts (2 μL) were injected onto a Thermo Scientific Hypersil GOLD C18 column (Thermo Fisher, Waltham, MA, USA), with methanolic mobile phase gradient elution. Clonazepam was detected with a Thermo Scientific TSQ Quantiva triple quadrupole mass spectrometer (Thermo Fisher, Waltham, MA, USA) with positive ionization. Ions monitored in the selected reaction monitoring mode were m/z 316‐270 for clonazepam (at 2.97 minutes) and m/z 320‐274 for clonazepam‐d4 (at 2.96 minutes).

2.4. Pharmacokinetic modelling

A population PK analysis was performed with a sequential nonlinear mixed effects modelling approach, to prevent structural model misspecifications driven by the saliva data, using NONMEM (version 7.3). ¹² Structural plasma model selection was performed by fitting both one‐ and two‐compartment models to the plasma concentrations over time. An allometric scaling component (normalized around 70 kg) was included on clearance and intercompartmental clearance, with an exponent of 0.75, and on all volume of distribution parameters, with an exponent of 1, to account for weight‐based influences. As only oral data was available, no bioavailability component could be estimated, but variability on the relative bioavailability (F _plasma) was explored. Interindividual variability following a lognormal distribution with variance ω ² on population parameters was selected by a forward inclusion procedure (P < .01) and the residual error structure was introduced as proportional and checked for appropriateness with goodness‐of‐fit figures.

The empirical Bayes estimates of the developed plasma model were implemented on an individual level in the modelling dataset for the development of the saliva model. ¹³ The saliva concentrations over time were used as the dependent variable during model development. Model structure selection was driven by exploratory figures of the data and contained a constant plasma:saliva ratio, a nonlinear plasma:saliva ratio and a first‐order elimination component to account for the contamination in the saliva compartment immediately after dosing. Interindividual variability following a lognormal distribution was selected following the same procedure as for the plasma model.

Improvements in model fit were judged on a decrease in objective function value (OFV) of 6.64 (P < .01) after inclusion of one parameter, the relative standard errors (RSE) of parameters and shrinkage, and evaluation of goodness‐of‐fit figures.

After the saliva model was developed, both models were integrated and estimated simultaneously to obtain the full covariance matrix, judge the numerical stability and assess the model performance via a prediction‐corrected visual predictive check (pcVPC) and the individual model fit over time in both matrices. A pcVPC was preferred as this enables the assessment of the model fit on all the combined data, considering two dose levels were used. ¹⁴

2.5. Simulations

R version 4.0.2 ¹⁵ and the mrgsolve package ¹⁶ were used to simulate the predictive capability of saliva concentrations in the context of clinical trials. A simulation cohort (n = 2000) with a uniform distribution of age between 6 and 30 years and corresponding weights (10th‐90th centiles ¹⁷ ) was prepared, and twice‐daily administration of 0.015 mg/kg (maximum 0.5 mg per dose) was simulated for each subject taking into account interindividual and residual variability. As interindividual variability on the relative bioavailability (F _plasma) of clonazepam might be lower in the healthy population on which the model was built, this parameter was increased to a coefficient of variation of 50% to allow for the simulation of a wider range of trough concentrations and therefore provide a more conservative simulation. Simulated saliva and plasma samples were obtained at 5, 6, 8, 10 and 11.5 hours post‐dose to simulate as closely as possible a future clinical trial with a twice‐daily dosing regimen. The accuracy of predicting the trough concentration (C _trough) in plasma after dose 1 (based on samples obtained after dose 1) and at steady state (based on samples obtained during steady state) that could be obtained by using one to five saliva samples was assessed using Bayesian maximum a posteriori (MAP) optimization and traditional linear regression. An additional scenario (no samples) without saliva sampling was simulated to establish baseline predictive capability of the model based on population parameters and the weight of a subject, but without any sampling information.

2.6. Bayesian maximum a posteriori optimization

The simulated saliva concentrations of each simulated individual were used as input for the Bayesian MAP estimation. ¹⁸ During this process, the most likely F _plasma was estimated for each individual within the constraints provided by the residual and between‐subject variability in the population PK model, based on the individual saliva samples and covariates. ¹⁹ From the individual Bayes estimates, the corresponding plasma C _trough after dose 1 (based on samples obtained after dose 1) and at steady state (after 240 hours of twice‐daily dosing, based on samples obtained after dose 20) was calculated. As the true simulated Bayes estimates and accompanying C _trough were known for an individual, the predicted C _trough was compared with the true plasma C _trough to evaluate the predictive performance of this approach. Predictive performance was quantified for each sampling scenario using the root mean squared prediction error (RMSPE), which is a predictive error expressed in the original units (μg/L). Additionally, the average bias and limits of agreement (LOA) of the predictions, expressed as percentages, were calculated according to the methods of Bland and Altman. ²⁰ As additional internal validation of the fitted model, Bayesian MAP was performed to predict individual plasma concentrations of the subjects included in the study. Here, saliva observation at 6, 8, 24 and 48 hours post‐dose was used as input to predict plasma concentrations on the respective time points. Predicted concentrations were compared to observed concentrations and bias, RMSPE and LOA were calculated.

2.7. Linear regression

Traditionally, plasma:saliva relationships are calculated as a constant ratio or linear regression formula. To compare these traditional methods with Bayesian optimization, a linear relationship between the two matrices was estimated via a linear mixed model based on the plasma and saliva samples obtained during the study. In the model, saliva concentration was considered as a fixed effect and subject as a random intercept. The derived equation was used to predict plasma concentrations in the simulation cohort after dose 1 based on a single saliva trough sample obtained either at 11.5 hours post‐dose after dose 1 or at 11.5 hours post‐dose at steady state.

2.8. Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY, and are permanently archived in the Concise Guide to PHARMACOLOGY 2021/22. ²¹

3. RESULTS

Of the 20 subjects included in the study, nine were male, and the average age was 22 years. Other baseline characteristics are displayed in Table 1. Of the 160 saliva samples taken during the study, 154 provided enough volume for analysis. All 160 plasma samples were collected successfully and none of the post‐dose saliva or plasma concentrations were below the LOQ. The concentration‐time profiles of clonazepam in plasma and saliva are displayed in Figure 1. Plasma concentrations showed variability in C _max and t _max, with some subjects immediately reaching C _max at the first sample (30 minutes) after dosing. Salivary concentrations were high and could not be correlated with plasma concentrations directly post‐dose, which indicates that clonazepam contamination was present in the saliva. However, the salivary concentration decreased exponentially and appeared correlated with plasma concentrations after 4 hours post‐dose.

TABLE 1.

Baseline characteristics

Parameter	All subjects (n = 20)
Age (years)	22.4 (2.8)
Sex (% male)	45%
Ethnicity (% Caucasian)	100%
Weight (kg)	67.8 (8.3)
Height (cm)	175.1 (7.3)
BMI (kg/m2)	22.2 (2.4)

Data is presented as mean (SD), unless otherwise specified.

FIGURE 1.

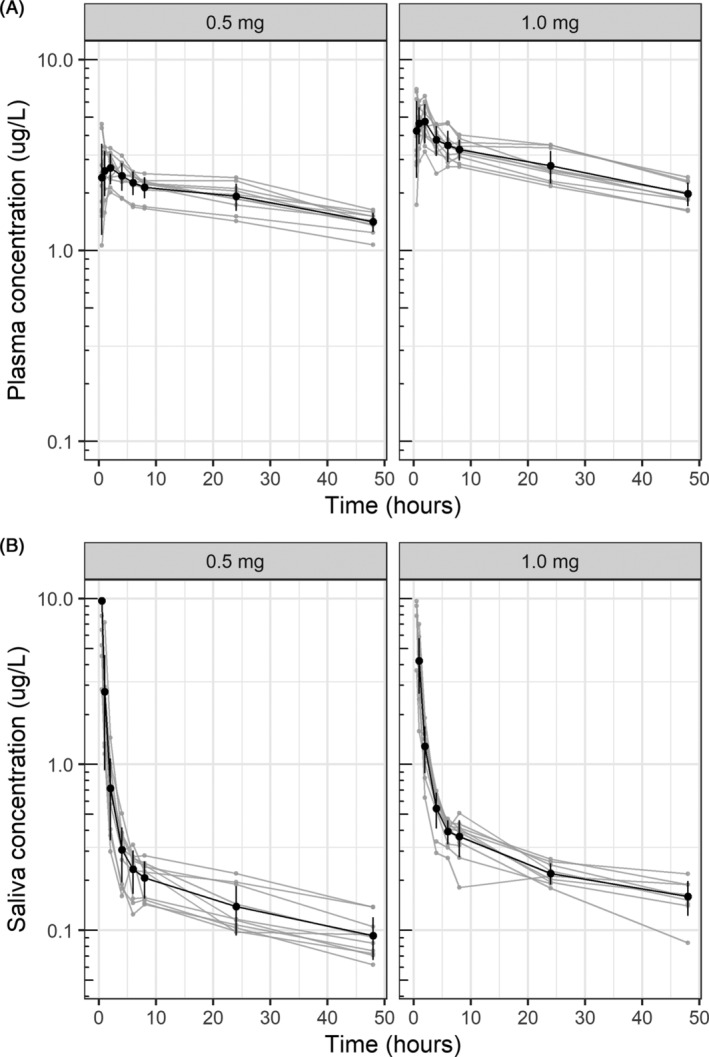
Individual and mean (SD) concentration‐time profiles of clonazepam in plasma and saliva. (A) Plasma concentration over time for the 0.5 mg dose group (left panel) and the 1.0 mg dose group (right panel). (B) Saliva concentration over time for the 0.5 mg dose group (left panel) and the 1.0 mg dose group (right panel). Individual concentration‐time profiles are displayed as light‐grey lines. The bold lines and dots represent the mean (±SD) concentration on each time point. Each grey dot represents a single observation. Each grey line represents a single subject

3.1. Population model

Structural plasma model development resulted in a two‐compartment model which showed an improved fit as compared to a one‐compartment model (ΔOFV = −17.34). Interindividual variability was identified on, in order of inclusion, absorption rate constant (k _a), relative bioavailability (F _plasma) and intercompartmental clearance. However, the interindividual variability (ω ²) on k _a was high, with a value of 0.66, and showed a binominal distribution. This was corrected for by inclusion of a mixture component, in which a fast absorption population and a slow absorption population were identified, where the fast absorption population had a fixed k _a of 100/h. This resulted in a significant improvement in model fit and reduced ω ² to 0.16, with 75% of subjects in the slow absorption group. Changing the fixed k _a to 10/h or 250/h did not change the model fit. No covariates for the subgroups were identified. All parameters were estimated with low RSEs and no changes were made to the proportional residual error structure.

To account for the saliva contamination, a saliva contamination compartment was added, in which a fraction of the full dose (F _saliva) remained in this compartment. The volume of this compartment was fixed to 1 mL and is represented by the following differential equation:

$$\mathsf{\text{dContamination}}/\mathsf{d}\mathsf{t}=-{\mathsf{k}}_{\mathsf{el}}\times \mathsf{\text{Contamination}}$$ (1)

Data exploration on data >4 hours post‐dose, after which contamination was no contributing factor anymore, showed a nonlinear relationship between the saliva:plasma ratio over the explored concentration range in which a steady‐state ratio was reached for the higher concentrations (Supporting Information Figure S1). The estimation of a saturable function on the saliva:plasma ratio improved the model fit significantly compared to a constant saliva:plasma ratio (ΔOFV = −16.65). As such, the saliva:plasma ratio and saliva concentrations were represented in the model as follows:

$$\mathsf{\text{saliva}}:\mathsf{\text{plasma ratio}}={\mathsf{\text{ratio}}}_{\mathsf{MAX}}\times {\mathsf{C}}_{\mathsf{\text{PLASMA}}}/\left({\mathsf{C}}_{\mathsf{\text{PLASMA}}}+{\mathsf{\text{ratio}}}_{\mathsf{KM}}\right)$$ (2)

$${\mathsf{C}}_{\mathsf{\text{SALIVA}}}=\left(\mathsf{\text{Contamination}}/\mathsf{0.001}\right)+{\mathsf{C}}_{\mathsf{\text{PLASMA}}}\times \mathsf{\text{saliva}}:\mathsf{\text{plasma ratio}}$$ (3)

where 0.001 is the volume of the saliva compartment in litres. Equation 3 therefore accounts for the level of contamination in the initial phase after dosing and for the nonlinear saliva:plasma ratio observed in the data.

Interindividual variability was only identified on the contamination part of the model (F _saliva, k _el‐saliva) and not on the saliva:plasma ratio. Inclusion of interindividual variability on the Ratio_MAX and Ratio_KM resulted in increased RSE without a change in the residual error.

The final parameter estimates are displayed in Table 2 and goodness‐of‐fit plots are displayed in Supporting Information Figure S2 . Parameters were estimated with sufficient parameter precision and moderate interindividual variability and residual error. The plasma residual error was lower than saliva concentrations, indicating that a higher degree of unexplained variability was present in the saliva concentrations over time. The pcVPC show that the model was able to capture the median trend of the data and the level of variability in both matrices correctly. Additionally, internal validation trough Bayesian MAP, predicting individual plasma concentrations at 6, 8, 24 and 48 hours post‐dose based on the respective saliva observations of included subjects, revealed a mean bias of 0.2%, LOA of −27% and 27%, and an RMSPE of 0.4 μg/L.

TABLE 2.

Parameter estimates of the population pharmacokinetic plasma and saliva model

	Parameter	Estimate (shrinkage %)	SE	RSE (%)
Plasma kinetics	θ k a ‐ slow group (h−1)	1.106	0.14	12.8
	θ Prob. slow group	0.75	0.10	13.0
	θ V D central (L)	109.5	11.5	10.4
	θ clearance (L h−1)	2.98	0.16	5.5
	θ V D peripheral (L)	130.6	12.9	9.9
	θ Q (L h−1)	61.37	11.2	18.3
Saliva kinetics	θ F saliva (% 1000−1)	0.033	0.005	14.5
	θ K el saliva (h−1)	1.95	0.12	6.0
	θ RatioMAX	0.195	0.031	16.0
	θ RatioKM (μg/L)	2.581	0.74	28.5
IIV	ω 2 k a ‐ slow group	0.16 [2.24%]	0.065	40.8
	ω 2 Q	0.25 [0.33%]	0.12	45.7
	ω 2 F plasma	0.026 [3.98%]	0.008	28.9
	ω 2 F saliva	0.28 [5.30%]	0.12	42.7
	ω 2 K el saliva	0.056 [17.2%]	0.025	44.2
Residual error	σ 2 proportional plasma	0.0058 [15.9%]	0.0009	14.9
	σ 2 proportional saliva	0.057 [16.5%]	0.009	15.4

Note: ω ² and σ ² are the variances of interindividual variability and residual variability, respectively.

TVCL = θ clearance × (WGT/70)^0.75, TVVC = θ V _D centrasl × (WGT/70)¹, TVVP = θV _D peripheral × (WGT/70)¹, TVQ = θ Q × (WGT/70)^0.75, TVRatio = Ratio_MAX × C _PLASMA/(C _PLASMA + Ratio_KM).

Abbreviations: IIV, interindividual variability; RSE, relative standard error; SE. standard error.

3.2. Simulations

The concentration‐time profiles of the simulation cohort are displayed in Figure 2A. On average, subjects achieved a median plasma C _trough of 2.1 μg/L after dose 1 and 13.7 μg/L at steady state. First, the C _trough after dose 1 and at steady state was predicted based on the population PK model parameters and weight of the subject only, which results in a single prediction for each weight, without taking into account any interindividual variability (equivalent to using no samples for the estimation). This scenario leads to an RMSPE of 1.39 μg/L after dose 1 and 8.8 μg/L at steady state, and an average proportional bias of −2.7% and −2.4% (95% limits of agreement (LOA) − 92% to 87%), respectively (Table 3), meaning that there was a high level of uncertainty in the predicted individual plasma concentration. In the case of one saliva sample, the RMSPE was 3.6 μg/L at steady state, the proportional bias was 4.0% and the limits of agreement were reduced to −28% to 36% (Figure 2B). There was a correlation between true and predicted C _trough in this scenario (R = 0.93, P < .001). Increasing the number of saliva samples improved the accuracy of the prediction, as can be seen by the reduction in the RMSPE and narrowing of the LOAs (Table 3). For the simulation scenario with five saliva samples, RMSPE was 2.3 μg/L, with a proportional bias of −0.3% and LOA of −18% to 17%. For all scenarios applying Bayesian optimization, the true and predicted C _trough values were correlated, with correlation coefficients >0.93 (P < .001; Supporting Information Figures S3 and S4 ). There was an eightfold difference in RMSPE between scenarios estimating C _trough after dose 1 compared to scenarios at steady state, which can be explained by the increased concentration after multiple dosing. The proportional bias and LOAs were comparable for the estimation after dose 1 and at steady state.

FIGURE 2.

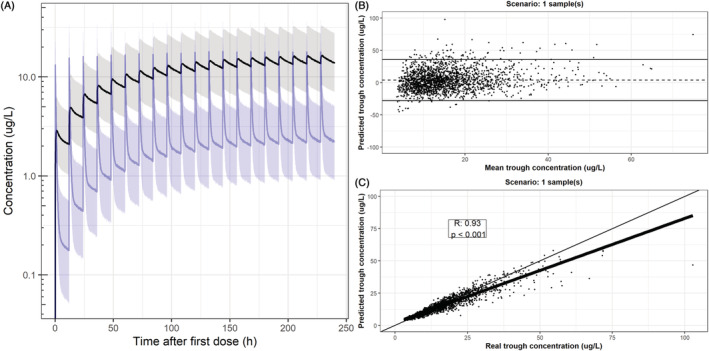
Population prediction (80% prediction interval) in simulation cohort and visualization of predictive capability based on one saliva sample at steady state. (A) Median population prediction (solid lines) and 80% prediction interval of the simulation cohort (n = 2000) in plasma (black) and saliva (blue). (B) Proportional bias in the prediction (dotted line) and proportional limits of agreement (solid lines) of predicted C _trough during steady state after Bayesian optimization based on a single saliva sample 11.5 h post‐dose (during steady state). The x axis displays the mean of the predicted and real C _trough and the y axis displays the proportional difference between the predicted and real C _trough. (C) Pearson correlation between true and predicted plasma C _trough of the scenario displayed in B. The bold black line represents the regression line, the thin black line represents the line of unity and each dot represents a simulated subject. For proportional bias plots and linear correlations of all scenarios, please refer to Supporting Information Figures S3 and S4

TABLE 3.

Simulation of predictive capability of using a saliva sample to determine the plasma trough concentration while varying the number of saliva samples used for the analysis

Scenario	C trough after first dose Median: 2.1 μg/L				C trough steady state Median: 13.7 μg/L
	RMSPE (μg/L)	Bias (%)	LLOA (%)	ULOA (%)	RMSPE (μg/L)	Bias (%)	LLOA (%)	ULOA (%)
No samples, population model	1.39	−2.7	−93	87	8.8	−2.4	−92	87
One sample, linear regression a	0.57	−9.5	−54	35	4.4	5.2	−40	51
One sample, Bayesian a	0.57	3.7	−28	36	3.6	4.0	−28	36
Two samples, Bayesian b	0.44	−0.2	−25	25	2.8	0.1	−25	25
Three samples, Bayesian c	0.40	−0.4	−21	21	2.5	−0.2	−21	21
Four samples, Bayesian d	0.39	−0.7	−20	19	2.5	−0.4	−20	19
Five samples, Bayesian e	0.37	−0.6	−18	17	2.3	−0.3	−18	17

Abbreviations: LLOA, lower limit of agreement (−2SD); RMSPE, root mean squared prediction error; ULOA, upper limit of agreement (+2SD).

^a Sample at 11.5 h post‐dose.

^b Samples at 5 h and 11.5 h post‐dose.

^c Samples at 5 h, 8 h, and 11.5 h post‐dose.

^d Samples at 5 h, 6 h, 8 h, and 10 h post‐dose.

^e Samples at 5 h, 6 h, 8 h, 10 h, and 11.5 h post‐dose.

3.3. Linear regression

The predictive performance of traditional (mixed effects) linear regression was assessed to determine the added value of Bayesian optimization methods. Because of the evident contamination in saliva during the first 4 hours after dosing, the correlation between saliva and plasma concentrations was not calculated during this time window. The estimated linear regression equation for the relationship between plasma and salivary concentrations during this time window was C _PLASMA = C _SALIVA × 5.42 + 1.20 (marginal R ² = 0.68). Plasma concentrations predicted with the linear regression formula based on the 11.5 hours post‐dose saliva trough sample at steady state were correlated with the true plasma concentration (R = 0.91, P < .001), but led to a larger RMSPE (4.4 μg/L) compared to Bayesian MAP, with a proportional bias of 4.4% (LOA −41% to 50%; Supporting Information Figure S3‐4E ).

4. DISCUSSION

During this study, the PK of saliva and plasma concentrations of clonazepam were characterized by a nonlinear mixed effects model. Furthermore, the potential use of salivary concentrations for prediction of plasma pharmacokinetics was studied. The developed model was able to predict trough concentrations at steady state with an RMSPE as low as 2.3 μg/L (median concentration of 13.7 μg/L), with a 95% proportional limit of agreement of −18% to 17%. The model can therefore be used in a future noninvasive study investigating the effects of clonazepam on children with ARID1B‐related ID and can be employed in the case of salivary TDM of clonazepam. Additionally, the methodology described in this study can be used to develop and evaluate similar models incorporating both saliva and plasma concentrations to allow for noninvasive pharmacokinetic sampling in future clinical trials in paediatric or other vulnerable populations.

We found high concentrations of clonazepam in saliva samples taken during the first 4 hours after administration of the oral solution. This indicates significant contamination in the initial saliva samples by clonazepam residue, a finding that has been reported in the past. ²² This contamination could have been avoided by using regular tablets. However, as this study was performed in preparation for a study in children, the current droplet formulation was chosen. This finding precluded the use of rate constants in which there was a slow increase in salivary concentrations driven by plasma pharmacokinetics because the time points earlier than 4 hours post‐dose did not contain any information about the transfer rate from the plasma compartment to the saliva compartment. However, the inclusion of an exponential elimination of the contaminated saliva in combination with a saliva:plasma ratio in the model led to a good model fit and adequate predictive performance. A consequence of this finding is that saliva samples taken during the first 4 hours do not provide any information regarding the plasma concentrations during that time, and that the current model is precluded for use with this particular formulation. However, considering the long half‐life and the fact clonazepam therapy is guided via trough concentrations, this has little impact. The estimated model parameters regarding plasma kinetics were comparable to the population model developed by dos Santos et al. ²³ Distribution from the water compartment of the body, part of which is saliva, towards the lipophilic compartment may be an alternative or additional explanation of the high saliva concentrations during the first 4 hours. A study setup with continuous intravenous infusion of clonazepam could have allowed for a more precise description of the saliva‐plasma relationship at a certain concentration and identify whether this is the case. However, the current results indicate the saliva:plasma ratio is dynamic over time and the use of a single ratio might result in a worse predictive capability.

Predictive performance was assessed through simulation in a fictional cohort aged 6‐30. Simulated salivary samples were obtained that included the residual error component of the model, and the most likely relative bioavailability and the corresponding C _trough were predicted via Bayesian MAP optimization. There are several advantages to using Bayesian methodologies for this purpose. First, the prediction error, represented by the RMSPE, was lower compared to the prediction error based on linear modelling. Additionally, one can use information obtained from multiple samples to estimate the most likely C _trough, reducing the prediction error in the process. We found that with the current model predictive performance increases by obtaining additional samples up to five samples. It is possible that more saliva samples would increase the performance even more. However, obtaining more than five samples in future paediatric PK studies would not be in line with the noninvasive approach taken here. Third, the method allows for convenience sampling at time points that are logistically feasible, as long as the chosen time points are obtained on time points after 4 hours post‐dose. Samples up to that point do not have a valid saliva:plasma correlation.  Fourth, the optimization process takes residual variability into account, and the prediction shrinks towards the population mean in the case of high residual variability. This prevents outlier saliva observations being extrapolated to extreme predicted plasma concentrations on which dose adaptions are made. Finally, estimates cannot be outside the constraints provided by the population model, as opposed to linear regression methods that have no such limits. The relevance of several of these advantages are confirmed in our simulations of the predictive capability of Bayesian MAP versus linear regression equations. The predictive capability of the linear regression equation was adequate but inferior to Bayesian MAP based on multiple samples. The simulations confirm that saliva sampling is eminently feasible for monitoring of clonazepam trough concentrations in the context of TDM and for the estimation of individual PK trajectories in the context of clinical trials, although in practice a balance must be found between the burden of a single venipuncture and multiple saliva samples spread over a day. However, this balance is dependent on the particular population and the number of saliva samples. Correlations between real and predicted C _trough were found, although these showed a slight underprediction at higher concentrations, which can be explained by shrinkage to the population mean during the Bayesian optimization process.

In this study, a saliva:plasma ratio was described which was not constant over time, even after accounting for the initial levels of contamination. The apparent decrease in the ratio driven by decreasing plasma concentrations is a phenomenon that has been reported before, ²⁴ , ²⁵ , ²⁶ but the underlying mechanism causing this relationship is unclear. The current study focuses on total plasma concentrations. Additional data on the measured free plasma concentrations could have been advantageous as it is hypothesized that saliva concentration is highly dependent on the free plasma concentration. As an alternative to using the free plasma concentrations, we have included individual albumin concentrations as covariates during model building. However, no correlation was identified. We hypothesize that the observed relationship may be caused by competitive protein binding of clonazepam metabolites, a mechanism previously observed for prednisone. ²⁷ Nevertheless, it remains an important finding in the context of TDM, as this invalidates the use of ‘traditional’ linear regression equations that do not take this variable saliva:plasma ratio into account. This may be one of the reasons that Bayesian optimization outperformed linear regression in our simulations, even in the scenario with a single saliva sample.

This study has several limitations. First, the population PK model for plasma and saliva was developed using observations after a single administration of clonazepam. Application of the model for the purpose of TDM or clinical trials will usually occur when subjects have reached steady state, and in that case it is assumed that the saliva:plasma ratio observed here can be extrapolated to these higher concentrations. As this is the first study systematically exploring the relationship between saliva and plasma concentrations of clonazepam, this assumption cannot be verified at this time, but it can be confirmed in future studies by obtaining paired saliva and plasma samples from subjects who have reached steady state. Furthermore, some subjects had reached plasma C _MAX at the first sampling time point in this study. Inclusion of earlier samples may have led to a different description of the absorption profile.

Using this model in a future paediatric clinical trial is reliant on several other assumptions as well. First, it is assumed that plasma kinetics in children adhere to the allometric scaling employed in this study, which is subject to recurrent discussion. ²⁸ , ²⁹ However, several studies indicate that this approach is reasonably accurate. ³⁰ The second assumption is that the saliva:plasma ratio in children is comparable to the ratio in the young adults included in this study. For example, saliva production may vary in children, especially in infants and when children are in a stimulated state. ³¹ Furthermore, the proportion of saliva that is discharged from the parotid and submandibular glands may vary and impact the saliva:plasma ratio. Little comparative research has been performed on this subject, but Michael et al report highly similar saliva:plasma ratios in children and adults for voriconazole, and a systematic review regarding saliva:plasma ratios in infants showed comparability for several compounds. ³ , ³² Although these assumptions may cause additional variability and less precise results in paediatric patients, we expect that the prediction error remains small enough to adequately identify a PKPD relationship based on saliva samples. Furthermore, saliva samples will aid in the identification of ultrafast metabolizers and subjects that do not adhere to the treatment regimen. The currently developed model can already be applied in adults, where saliva‐based TDM could be preferable over plasma‐based TDM. However, the simulations performed here assume a perfect time registration, something which is usually not possible in the clinic or in a home‐setting. In addition, it is possible that patients would not adhere to instructions regarding food and water intake, or rinse their mouth as thoroughly as was performed during the current study. These factors are assumed to affect equilibrium kinetics and therefore the true performance of clonazepam saliva TDM should be assessed in a future study. A mechanistic (quantitative systems pharmacology) model which would include all physiological components of saliva production could be developed in the future and may result in even better predictions compared to the current empirical model. In addition, studies should focus on external validation of the developed model, as the current simulations assume correct model specification, and determine whether the underlying assumptions in the paediatric populations described above are valid in general and in the case of clonazepam. If confirmed, we believe this methodology could be implemented in the future to aid clinical trial conduct in paediatrics and apply precision‐dosing in paediatric populations.

5. CONCLUSION

The developed population pharmacokinetic model describes the salivary and plasma kinetics of clonazepam well and simulations show that plasma C _trough can be predicted from saliva concentrations through Bayesian MAP optimization.

COMPETING INTERESTS

Nothing to declare.

AUTHOR CONTRIBUTIONS

M.K. conducted the study, analysed the data and wrote the manuscript. K.B supported the pharmacometric analysis and reviewed the manuscript. A.E. supervised the bio‐analysis and reviewed the manuscript. R.Z., G.S. and A.C. conceptualized and supervised the study and reviewed the manuscript. M.vE. performed the pharmacometric analysis and co‐wrote the manuscript.

FINANCIAL DISCLOSURE

The author(s) received no specific funding for this work.

TRIAL REGISTRATION

NL8792 (NTR, Dutch trial registry).

ETHICS AND PATIENT CONSENT

Ethical approval was obtained from the Beoordeling Ethiek Biomedisch Onderzoek Foundation Review Board (Assen, the Netherlands) prior to initiation of the study. The study was conducted in compliance with the Dutch Act on Medical Research Involving Human Subjects and Good Clinical Practice. Informed consent was obtained prior to study‐mandated procedures.

Supporting information

Supporting Information Figure S1 Nonlinear saliva: plasma ratio

Supporting Information Figure S2 Goodness‐of‐fit plots

Supporting Information Figure S3 Relative bias, limits of agreement and correlation of predictions in different scenarios after dose 1

Supporting Information Figure S4 Relative bias, limits of agreement and correlation of predictions in different scenarios at steady state

Kruizinga MD, Zuiker RGJA, Bergmann KR, et al. Population pharmacokinetics of clonazepam in saliva and plasma: Steps towards noninvasive pharmacokinetic studies in vulnerable populations. Br J Clin Pharmacol. 2022;88(5):2236-2245. doi: 10.1111/bcp.15152

DATA AVAILABILITY STATEMENT

All data presented in this manuscript is available from the corresponding author upon reasonable request.