Abstract
Radial stem growth dynamics at seasonal resolution are essential to understand how forests respond to climate change. We studied daily radial growth of 160 individuals of seven temperate tree species at 47 sites across Switzerland over 8 years. Growth of all species peaked in the early part of the growth season and commenced shortly before the summer solstice, but with species‐specific seasonal patterns. Day length set a window of opportunity for radial growth. Within this window, the probability of daily growth was constrained particularly by air and soil moisture, resulting in intermittent growth to occur only on 29 to 77 days (30% to 80%) within the growth period. The number of days with growth largely determined annual growth, whereas the growth period length contributed less. We call for accounting for these non‐linear intra‐annual and species‐specific growth dynamics in tree and forest models to reduce uncertainties in predictions under climate change.
Keywords: dendrometer, intra‐annual growth, phenology, seasonality, soil water potential, tree growth, TreeNet, vapour pressure deficit
We analysed daily radial stem growth dynamics of 160 individuals of seven temperate tree species at 47 sites in Switzerland measured over 8 years with automatic dendrometers. We found that trees grow only on very few days within the growth season to achieve their annual growth, and most of the growth days occurred before the summer solstice. The annual growth was strongly related to the number of days with growth, whereas the beginning, ending and length of the growth period have much less predictive power.

INTRODUCTION
Wood formation is the primary biological process by which carbon is allocated in woody plants. Temperate forests sequester around 400 Tg C per year and act as an important terrestrial C sink (Pan et al., 2011). However, this sink role becomes uncertain in the future due to unknown effects of climate change on stem growth (Pugh et al., 2018). Annual stem growth variation across years and sites is influenced by underlying seasonal growth responses (Forrest & Miller‐Rushing, 2010; Sellier & Ségura, 2020; Steppe et al., 2015) and possible legacy effects (Ogle et al., 2015; Zweifel et al., 2020; Zweifel & Sterck, 2018). Multiple studies have described a sigmoidal curve to model annual radial growth, being fastest at the beginning and slowest at the end of the growth period (Cruz‐García et al., 2019; Deslauriers et al., 2003; van der Maaten et al., 2018). On shorter time scales, however, cambial activity is non‐linear (Peltier & Ogle, 2020; Zweifel et al., 2021b) and highly discontinuous. This intermittent growth can result from unfavourable environmental conditions including droughts and tree water deficits (Cabon et al., 2020b; Peters et al., 2020; Zweifel et al., 2016), internal tree processes related to phenology or resource allocation (Devine & Harrington, 2009), or involve responses to competition (Drew & Downes, 2018) or pathogens (Schuldt et al., 2017). However, such intra‐annual variations are not well understood, because analyses of fine‐resolution intra‐annual stem growth dynamics across species, sites and years are scarce (Forrest & Miller‐Rushing, 2010).
Components of radial stem growth
Radial growth involves the production of new xylem and phloem cells by the cambium and the expansion of these cells (‘growth in size’) followed by cell wall formation or maturation (‘growth in biomass’; Cuny et al., 2015; Lehnebach et al., 2021; Rathgeber et al., 2016). The expansion of cells leads to irreversible increase in stem diameter and is considered ‘radial growth’ in this study. In temperate forests, cambial activity of trees is seasonally variable due to annual fluctuations in key environmental variables, such as temperature, water availability and day length (Cabon et al., 2020b; Delpierre et al., 2016a; Huang et al., 2020). As such, the following characteristics of radial growth dynamics can be distinguished: (i) the stem growth phenology (beginning, ending and length of the growth period), and (ii) stem growth activity within the growth period (growth rate and number of days with growth) (Figure S1). Stem phenology varies among species, sites and time (Cuny et al., 2012; Delpierre et al., 2016b; Michelot et al., 2012) and might reflect genetic differences, but also plastic responses to environmental heterogeneity (Forrest & Miller‐Rushing, 2010). Some dendrochronological studies have found a positive relation between radial growth and start or length of growth period (Rossi et al., 2013), while others have not (Gričar et al., 2019). This makes it hard to predict how forest productivity will respond to future phenological shifts resulting from ongoing climate change (Delpierre et al., 2016b; Richardson et al., 2010).
Environmental forcing of stem growth
Recent studies provide evidence that cambial activity is directly constrained by limiting environmental conditions, especially over short time periods, although CO2 assimilation can still be substantial (Fatichi et al., 2019; Körner, 2003; Zweifel et al., 2021b). Thus, plant cells only expand when cell turgor pressure exceeds a threshold (Lockhart, 1965), which is determined by temperature and water potential (Cabon et al., 2020a; Hsiao & Acevedo, 1974; Peters et al., 2020). Therefore, tree water relations driven by atmospheric and soil moisture are a keystone in explaining the cambial activity of a tree (Cabon et al., 2020b; Passioura, 1982; Peters et al., 2020). Furthermore, increasing temperatures in spring may promote cell production (Körner & Paulsen, 2004; Rossi et al., 2007), but high temperatures can limit metabolic activity and reduce cambial activity later during the growth period (Parent et al., 2010; Ruehr et al., 2015). Physiological processes of cell expansion and elongation, as well as their relation to environmental conditions have been studied intensively (Rathgeber et al., 2016). Still, it is not yet possible to clearly explain inter‐annual variability of tree growth with environmental conditions, despite a huge amount of available dendrochronological data (Peltier & Ogle, 2020). This might be due to different growth limiting factors depending on site conditions and species, but also likely because growth dynamics and responses to environmental conditions may change throughout the year and differ across years. Thus, understanding intra‐annual growth patterns and climate sensitivities is key to understand inter‐annual growth variability (Dietrich et al., 2019; Zweifel et al., 2021b). There are a few regional studies accounting for intra‐annual variations of radial growth and related environmental drivers, but which are focused on single species and/or single sites and cover short time periods (e.g. Skomarkova et al., 2006; Vieira et al., 2013). A comprehensive study in Austria including four species at four sites over four years was rather focused on modelling stem radius changes while also including stem water relations (Vospernik et al., 2020). Thus, we are still lacking a systematic assessment of intra‐annual radial growth dynamics comparing species across sites with varying environmental conditions and over multiple years. Thus, a detailed examination of intra‐annual growth dynamics is crucial to understand radial growth variation across species, sites and years, which is integral to predict forest productivity now, and in the future (Huang et al., 2020).
The key questions of this work address the shape of intra‐annual growth patterns in relation to species and environmental conditions and their importance for annual growth. Specifically, we address the following questions:
To what extent do species differ in their growth characteristics (beginning, ending and length of growth period, daily growth rate and number of growth days)?
How do these intra‐annual growth characteristics determine the inter‐annual variability in radial growth?
Which environmental conditions determine the probability of daily growth?
To answer these questions, we used a unique dataset of daily atmospheric and edaphic measurements as well as stem dendrometer readings from the extensive TreeNet monitoring network covering 47 sites across a large climatic gradient in Switzerland.
MATERIALS AND METHODS
Study sites and species
The 47 study sites of the network TreeNet (Zweifel et al., 2021a) represent a strong climate gradient within Switzerland (Figure S2), with mean annual temperature (MAT) ranging from 4.5 to 12.1°C and mean annual precipitation (MAP) from 600 to 1580 mm (Table S1, Figure S3). The species studied include three evergreen, coniferous species (Picea abies (L.) H. Karst, Pinus sylvestris L., Abies alba Mill.) and four deciduous, broadleaved species: one of them has a diffuse‐porous wood anatomy (Fagus sylvatica L.), while the other three have ring‐porous wood (Fraxinus excelsior L., Quercus petraea Liebl., Quercus pubescens Willd.). The species partially differ in ecological niches and drought tolerances (Etzold et al., 2019; Lévesque et al., 2013; Walthert & Meier, 2017; Zang et al., 2014) with P. sylvestris and Q. pubescens occurring at the driest sites, and A. alba located at the moistest sites (Figures S3 and S4). In each of the 47 sites, two or more individuals of one to four species were studied. The total number of trees per species (across all sites) ranged from seven to 55 (Table S1). Timeseries of tree, atmosphere and soil measurements cover the years from 2011 until 2018, with at least 2 and up to 8 years of measurements (mean 6 years), including around 342’000 daily measurement points.
Environmental conditions
Meteorological data were obtained either from weather stations from nearby MeteoSwiss stations (www.meteoswiss.admin.ch, mean distance: 8 km, max: 15 km) or were recorded at the site (www.treenet.info, www.lwf.ch, www.empa.ch/web/s503/nabel), and aggregated to daily values. Hourly precipitation data were derived from the CombiPrecip model by MeteoSwiss, in which rain‐gauge measurements and radar estimates are combined and interpolated at a 1‐km2 grid. Air temperature (Temp, °C) and relative humidity (RelH, %) were measured at 2 m height within the forest stands, and global radiation (RAD, W m−2) was measured above the canopy or at a nearby open site, all at a 10‐min resolution. In case of missing data, gaps were filled with data derived from the nearest MeteoSwiss station, which were corrected according to established linear regressions for periods with available data of both datasets. Vapour pressure deficit (VPD, kPa) was calculated from Temp and RelH according to Jones (1992) with the R package ‘plantecophys’ (Duursma, 2015). Soil water potential (SWP, MPS‐2/MPS‐6 sensors, Decagon Devices) was measured at 10–20 cm soil depth at each site and corrected for soil temperature (Walthert & Schleppi, 2018). For each site, the day length (hours of daylight between sunrise and sunset) was obtained as a function of latitude with the R package ‘insol’ (Corripio, 2019).
Dendrometer measurements and extraction of growth fraction
Stem radius changes were derived from point dendrometers (ZN11‐T‐IP and ZN11‐T‐WP, Natkon), mounted perpendicular to the stem in a slope‐parallel orientation, 1.3 m above the ground (Zweifel et al., 2016). Trees equipped with dendrometers were mature, dominant trees. Details about the installation of sensors in the field, data acquisition and processing, as well as extraction of the growth component and associated uncertainties are described in Zweifel et al. (2021a). Briefly, the growth component from the stem radius changes was extracted based on the ‘zero growth’ concept (Zweifel et al., 2021a; Zweifel et al., 2016). Hereby, the accumulated growth (GRO) appears as stepped line, which increases in periods when the stem radius exceeds a former maximum.
Definition of stem growth characteristics
The growth period is here defined as the period when 5% to 95% of the annual growth happens (Knüsel et al., 2021). The first and last 5% of the growth period were excluded to avoid outliers influencing the timing of the growth period. Start and end of the growth period (GROstart, GROend) represent the Day of Year (DOY), where 5% and 95% of the annual growth were reached, respectively. Growth period length (GROlength) is the number of days between GROstart and GROend. Furthermore, we calculated the daily growth rate of a tree (µm day−1) and the number of days with growth (daily growth rate >0, N daysgrowth) within the growth period (Figure S1). Stem growth characteristics were calculated for each year separately. Beyond this, the climatic vegetation period per site was defined as the period of the year when the conditions were sufficient for plants to grow. Here we used the part of the year where the daily average temperature exceeded a threshold of +5°C for six consecutive days (MeteoSwiss, 2013).
Statistical methods
All figures were produced and statistical models run with the R statistical software (R Core Team, 2021). Average values refer to the median with a 25%–75% interquartile range (IQR). Differences in growth characteristics among species were tested with a Kruskal–Wallis and post hoc Dunn test.
Variance components of species, site and year levels of the stem growth characteristics were analysed by mixed effect models, using the function lmer of the R package ‘lme4’ (Bates et al., 2012), with year nested in site nested in species as random effects, to account for temporal and spatial variability, as well as species identity. The significance of the random effect was tested by the function ranova of the R package ‘lmerTest’ (Kuznetsova et al., 2017). In order to approximate the spatial variability of growth characteristics with site environmental conditions, we calculated generalised additive models (GAM), using the R package ‘mgvc’ (Wood, 2012) with site averages of growth phenology and activity as response variables as well as site MAT, MAP and elevation as predictors.
Variability in annual radial growth was analysed with species‐specific linear mixed effects models (LMM) using the function lme of the R package ‘nlme’ (Pinheiro et al., 2015) with annual growth as response variable, and tree nested in site as random intercepts. The response variable was logarithmically transformed to achieve normality, fixed effects were scaled (i.e. mean = 0 and SD = 1). An initial pool of variables, including stem growth phenology (GROstart, GROend, GROlength) and growth activity (median daily growth rate, N daysgrowth) was used. For stem growth phenology, we included also squared terms since their relationship to annual growth was observed to be non‐linear. From this pool of variables, all possible model combinations were calculated and ranked according to the AIC, using the dredge function of the R package ‘MuMin’ (Bartoń, 2016). The best model was visually checked for heterogeneity of variance and normality of residuals, and the conditional and marginal R 2 were calculated (Nakagawa & Schielzeth, 2013).
In order to assess the explanatory power of environmental variables for the probability of growth, species‐specific generalised linear mixed effects models (GLMM) with growth/no growth as binary response variable (link = ‘logit’) and year nested in tree nested in site as random effects were calculated. The time period considered in this analysis covered April to end of September since during this time period growth potentially occurred over all species and all sites. Temp, RelH, Precip, VPD, RAD, SWP and day length were included as fixed effects, as well as the interactions of all variables with day length, and the interaction of VPD and SWP. Fixed effects were scaled. We tested for collinearity in the model with the variance inflation factor (vif). In case of collinearity (vif > 4), we checked which of the two collinear variables had the higher correlation with the response variable and kept this variable in the model. We started with the full model including all variables and interactions, and removed those variables step‐wise, for which the AIC was reduced the most, until no reduction in the AIC was obtained anymore. We checked the model assumptions with binned plots, plotting the average residual versus the average fitted value for each bin (Gelman & Hill, 2007), with the binnedplot function of the R package ‘arm’ (Gelman et al., 2020).
RESULTS
Seasonality of radial growth activity
The intra‐annual course of radial growth showed a distinct seasonality with species‐specific patterns (Figure 1). In general, the highest growth rates occurred in May and June, for the ring‐porous species (i.e. F. excelsior and oaks) already in April (Figure 2a). A sharp decline in growth activity happened shortly before the summer solstice (21st of June) for all species, except A. alba, which continued to have daily growth rates >5 µm day−1 until September (Figure 1). Growth rates of F. sylvatica, P. abies and P. sylvestris, and to a lesser extent A. alba showed a distinct peak in June. The increase in the growth rate between GROstart until peak growth of conifers and F. sylvatica was linearly related to day length (median R 2 = 0.85, ranging from 0.59 for A. alba to 0.96 for F. sylvatica, p < 0.001). Growth of the ring‐porous species exhibited two peaks, one already in April, the second one in June, and growth rates were less related to day length (F. excelsior: adj. R 2 = 0.45, p < 0.001, Q. petraea, adj. R 2 = 0.06, p < 0.05, Q. pubescens: n.s.). These species started growth earliest (mid‐April) and showed also the earliest cessation of growth, finishing 80% of their annual growth already before end of June (Figures S5 and S6). GROstart differed especially between conifers and the ring‐porous deciduous species with conifers starting about one month later than the deciduous species (Figure 3a). Conifers ceased growth also later than the broadleaved species, but the variability was large. GROlength was not significantly different among species.
FIGURE 1.
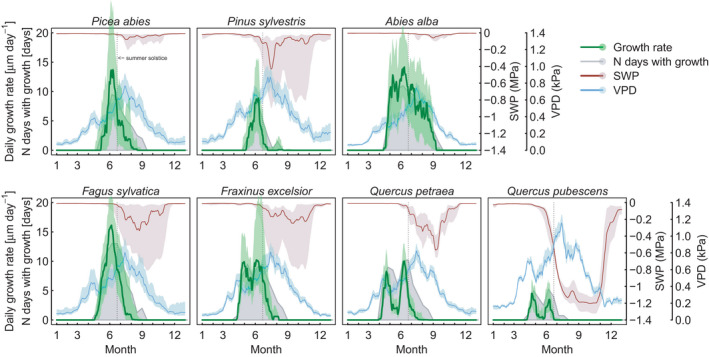
The intra‐annual course of growth activity of seven tree species: 14‐days running mean of median growth rates (green) with the 25%–75% interquartile range (light green area), and the number of days with growth (growth frequency) within a 14‐day window as grey area. 14‐days running mean of median soil water potential (SWP) is indicated in red (+/− 25% IQR), and of median vapour pressure deficit (VPD) in turquoise (+/− 25% IQR) respectively. The 21st of June (summer solstice) is indicated by the dotted vertical line
FIGURE 2.
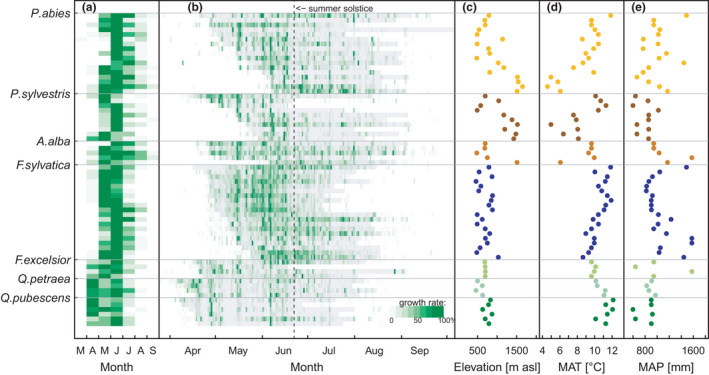
Monthly and daily growth rates of seven tree species at 47 sites in Switzerland covering the years 2012 till 2018. (a) Median monthly growth rates in % per species and site. (b) Median daily growth rates in % per species and site. Grey areas indicate the median growth period per species and site. Growth values in (a) and (b) are scaled per row (site × species) so that each row has mean = 50% and SD = 1. All trees and years per site and species were averaged. (c) Elevation per site, (d) Mean annual temperature (MAT) per site and (e) Mean annual precipitation (MAP) per site. Colours in (c–e) indicate different species. Sites are ordered according to GROstart
FIGURE 3.
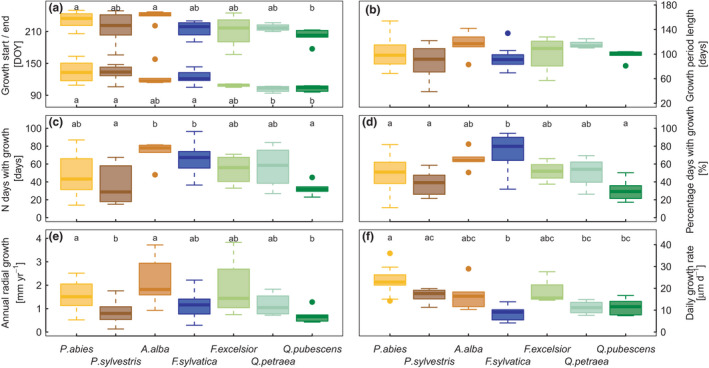
Species‐specific characteristics of growth (median with 25%–75% IQR in boxes). (a) Start and end of growth period, (b) Growth period length, (c) Number of days with growth, (d) Percentage of days with growth in relation to growth period length, (e) Annual growth, (f) Daily growth rate. Letters give significant differences between species, tested by Kruskal–Wallis and post hoc Dunn test. Colours indicate different species. See also Table S2
Intermittent occurrence of growth
Growth occurred from April to September (Figure 2a,b), and GROlength spanned 89 to 117 days on average (Figure 3b), while the (climatically derived) vegetation period was around 250 days. Within the growth period, growth was intermittent and showed frequent switching between days with and without growth (Figure 2b). Thus, actual growth occurred on average on 29 (P. sylvestris) to 77 (A. alba) days, with values in between for the other species (Figure 3c). From GROstart till GROend, F. sylvatica grew on 80% of the days and A. alba on 64% of the days, respectively, while the other species grew only on half of the days or even less (Figure 3d). In general, the longer the growth period lasted the more days with growth occurred (LMM on site, and site and year level, p < 0.001).
Variation in stem growth phenology and activity across species, sites and years
For all growth characteristics, except daily growth rate, variation among sites was higher than among species (Table 1). Temporal variation among years was lowest for GROstart, but it was highest for GROend and GROlength. The spatial variability of GROstart and GROend, could be best approximated by MAT, that is, the warmer the site, the earlier trees started and ended growing (Figures S7). GROlength depended more on GROend than on GROstart (standardised coefficients of LME with GROstart and GROend as fixed effects: GROstart: −20 ± 0.36, p < 0.001, GROend: 33 ± 0.35, p < 0.001), but GROlength was neither related to MAP, MAT nor elevation (Table 1). Spatial variability of N daysgrowth was best explained by MAP, that is trees at sites with higher precipitation grew more often than trees at sites with lower precipitation. The largest part of the variance in the growth rate appeared not among sites, but among species. When trees showed growth, they grew on average 17 µm day−1 with F. sylvatica having the lowest daily growth rate (9.4 µm day−1, IQR: 6.0 −10.2 µm day−1) and P. abies having the highest (24.1 µm day−1, IQR: 20.4 −27.5 µm day−1; Figure 3f; note that these rates differ from the ones shown in Figure 1 as here also days without growth are included). Beyond the species identity, growth rate was negatively related to MAT, that is the cooler the conditions for growth, the higher the growth rate (Figure S7).
TABLE 1.
(a) Variance components of the species, site and year level within stem growth phenology and activity, given in standard deviation and percent of variation, derived from mixed effect models with GROstart, GROend, GROlength, daily growth rate or N daysgrowth as dependent variable, and year, site and species as nested random effects. (b) Approximation of the spatial variability of growth phenology and activity was tested by GAM of median values of the respective variables per site against mean annual precipitation (MAP), mean annual temperature (MAT) and elevation. Given is the sign of the relationship, dAIC of the model against the lowest AIC of all models, the adjusted R 2 of the model and the p‐value
| (a) Variance partitioning of growth phenology and activity | (b) Approximation of spatial variability of growth phenology and activity | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Random factor | Std. Dev | % | p‐value | Explaining variable | Sign | dAIC | Adj. R 2 | p‐value | |
| GROstart | Species | 11.5 | 25.5 | *** | MAP | 45 | — | n.s. | |
| Site | 12.2 | 27.1 | *** | MAT | − | 0 | 0.64 | *** | |
| Year | 9.1 | 20.2 | *** | Elevation | + | 16 | 0.49 | *** | |
| Residual | 12.1 | 27.0 | |||||||
| GROend | Species | 7.0 | 10.2 | n.s. | MAP | + | 9 | 0.18 | * |
| Site | 12.5 | 18.2 | *** | MAT | − | 0 | 0.33 | ** | |
| Year | 18.4 | 26.7 | *** | Elevation | 14 | — | n.s. | ||
| Residual | 30.8 | 44.8 | |||||||
| GROlength | Species | 4.5 | 6.5 | n.s. | MAP | 0 | — | n.s. | |
| Site | 14.7 | 21.4 | *** | MAT | 1 | — | n.s. | ||
| Year | 15.8 | 23.0 | *** | Elevation | 0 | — | n.s. | ||
| Residual | 33.5 | 49.0 | |||||||
| Daily growth rate | Species | 4.5 | 22.5 | *** | MAP | 17 | — | n.s. | |
| Site | 4.0 | 19.8 | *** | MAT | − | 0 | 0.33 | *** | |
| Year | 2.6 | 12.8 | n.s. | Elevation | + | 8 | 0.22 | * | |
| Residual | 9.0 | 44.9 | |||||||
| N daysgrowth | Species | 11.7 | 22.1 | *** | MAP | + | 0 | 0.28 | ** |
| Site | 15.3 | 28.9 | *** | MAT | 14 | — | n.s. | ||
| Year | 11.8 | 22.3 | n.s. | Elevation | 12 | — | n.s. | ||
| Residual | 26.8 | 26.8 | |||||||
Significance is given as ***p < 0.001, **p < 0.01, p < 0.05, ‘n.s.’ not significant. See also Figure S7.
Predictors of annual stem growth
Trees grew on average 1.2 mm year−1 (IQR: 0.9–1.5 mm year−1), with A. alba (1.8 mm year−1) and P. abies (1.5 mm year−1) exhibiting the highest increment, and P. sylvestris (0.8 mm year−1) and Q. pubescens (0.7 mm year−1) the lowest (Figure 3e). A. alba had the largest variability of annual increments among sites (see IQR in Figure 3e). The inter‐annual variation in annual growth within species and sites was on average 0.4 mm year−1, with the largest variability for F. sylvatica (median: 0.6 mm year−1, max:1.4 mm year−1) and P. abies (median: 0.6 mm year−1, max: 2.1 mm year−1). Annual growth was non‐linearly related to stem phenology with a bell‐shaped optimum, whereas it was positively related to N daysgrowth (Figure 4). Thus, phenology hardly contributed to explain the inter‐annual variation in annual growth, whereas growth activity, particularly N daysgrowth, turned out to be the most important predictor in the LMM, explaining 65% to 88% of the inter‐annual variation (Table S3, Figure S8).
FIGURE 4.
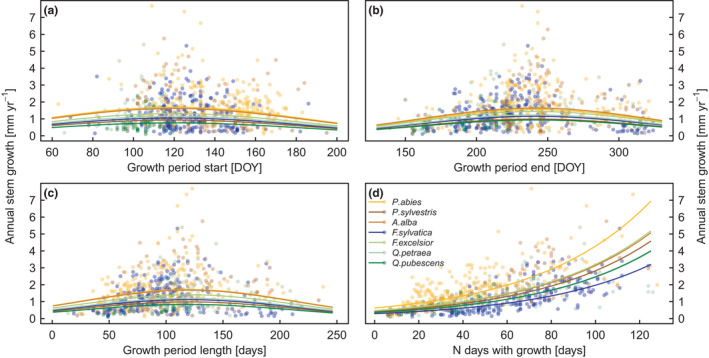
Linear mixed effects models of annual stem growth against growth characteristics, with tree nested in site nested in species as random effects. Annual stem growth in relation to (a) growth period start (GROstart), (b) growth period end (GROend), (c) growth period length (GROlength) and (d) number of days with growth (N daysgrowth). Lines indicate the fit per species
Environmental drivers of daily stem growth
Generalised mixed effect models (GLMM) showed that the occurrence of daily growth was closely related to day length for all species (Figure 5a,d). Furthermore, the probability of growth for the conifers increased at low VPD and in addition at high SWP for P. sylvestris, and at high temperature for P. abies and A. alba. For the deciduous species, the probability for growth increased at high SWP, followed by low VPD, and for F. excelsior by low temperature. All other available meteorological variables had much less predictive power. For the ring‐porous species, interactions of SWP and day length were negative, meaning that the impact of SWP on growth increased with decreasing day length, whereas the effect of VPD was the opposite. The probability of growth could be predicted with day length and meteorological conditions in 45% of the cases by GLMM, ranging from 28% (A. alba) to 60% (Q. pubescens). Selection of the wettest years per site, based on mean SWP during April to September, showed that decrease in SWP was delayed by 47 days (ranging from 11 to 61 days) in wet years compared to average, while peak growth was delayed by only 3 days (−1 to 27 days, Figure S9). However, in wet years, higher growth rates were maintained after the summer solstice.
FIGURE 5.
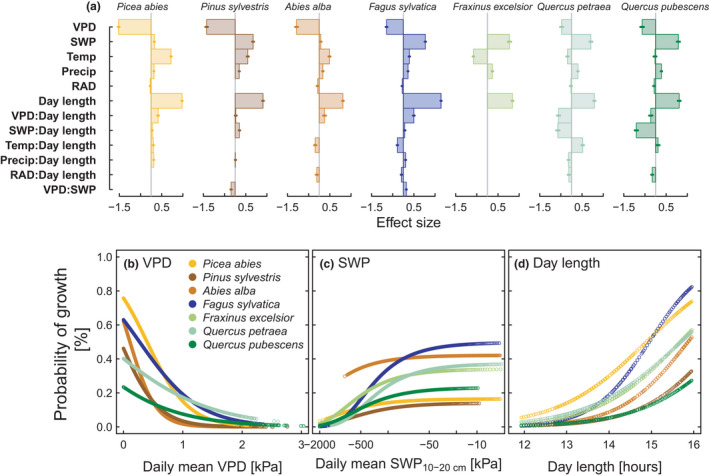
Probability of growth in relation to environmental variables. (a) Effect sizes of fixed effects derived from GLMM in Table S4 with growth/no growth as binary response variable and year nested in tree nested in site as random effects. (b–d) Probability of growth derived from GLMM in relation to (b) VPD, (c) SWP and (d) Day length. Different colours indicate different species
DISCUSSION
Eight years of daily radial growth data revealed a strong seasonality of radial growth for all species with distinct species‐specific characteristics. In general, growth rates increased after growth initiation in spring, with peak growth in early summer (April–June), and a mostly sharp decrease shortly before summer solstice and the onset of summer dryness. Two important aspects have to be considered when discussing inter‐ and intra‐annual radial growth patterns, namely the number of growth days and the growth rate. The intra‐annual pattern of both was closely related to day length, and the probability of growth was largely constrained by a high VPD and a low SWP. All species showed a highly intermittent growth pattern, and annual growth was achieved with 29 to 77 days with growth only, depending on species. The number of days with growth explained much of the inter‐annual variability of radial growth, whereas phenology contributed less.
Species‐specific intra‐annual patterns of stem growth
Intra‐annual growth dynamics varied among species, sites and year, but the distribution of variation differed across growth characteristics. GROstart showed the strongest relation to the sites’ temperature gradient. The higher MAT was, the earlier trees started to grow, which is in line with earlier findings (Cuny et al., 2019; Rossi et al., 2007). The growth period also ended earlier at warmer sites, but the relationship was weaker than for GROstart. Variability among years for GROend was highest, indicating that GROend was triggered by other—temporally variable—factors. The close relationship of the probability of growth to moisture conditions, especially later in the year (Figure 5, Table S4) might indicate that GROend is more constrained by water deficits than temperature. Additionally, GROend might also be influenced by how much growth already had been achieved before (Zani et al., 2021).
The major part of the variation in growth rate was due to species identity, with the largest differences between conifers and ring‐porous deciduous species, potentially due to differences in wood density. Ring‐porous species showed two peaks of high growth activity with a drop in between. Similar patterns had been observed for shoot growth of oak species (Bobinac et al., 2012) and might be determined genetically. The first growth peak is probably related to the production of larger earlywood vessels to allow fast xylem water transport early in the season (Copini et al., 2019; Pérez‐de‐Lis et al., 2016), the second peak to latewood production. Other species started to grow later and showed only one pronounced peak in June. F. sylvatica had the shortest GROlength and the smallest daily growth rate, but the highest percentage of N daysgrowth. This means that this species used a comparably short time window for growth, but within this window thresholds for growth limitation (e.g. VPD and SWP) were larger compared to other species (Figure 5). This was probably due to the thin bark and quick growth resumption after dry periods, enabling growth on a low, but constant level. In contrast, P. abies had on average the highest daily growth rates, but grew only half of the days of its growth period. P. sylvestris started to grow later than most of the other species (Figure 3a), but with higher growth rates compared to the rest of the year, reaching half of its annual increment in much shorter time than all other species (Figures S5 and S6). These results indicate that the intra‐annual radial growth patterns of different species emerge from very different patterns in growth phenology, growth frequency and daily growth rate responses to environmental conditions, but also that the divergence in wood and bark anatomy can partly explain such species differences. Taking into account the fact that each species has different growth dynamics can also help to understand species‐specific sensitivities to meteorological events, especially in terms of the timing of extreme events.
Variation in annual stem growth is related more to stem growth activity than to stem phenology
Our results highlight that only a small fraction of the growth period (30% to 80%) and the vegetation period (12% to 30%) was actually used for annual growth. Days with growth were also not homogenously distributed, but occurred mainly during the first part of the growth period (April/May–June), explaining the stronger impact of spring compared to summer droughts on tree growth (Bose et al., 2021; Martin‐Benito et al., 2018). Although, discontinuity and irregularity of stem growth processes have been discussed since long (Kozlowski & Pallardy, 1996), general assumptions in annual tree growth models (Fatichi et al., 2019; Peltier & Ogle, 2020) or yield studies (Drew & Downes, 2018) often imply linear growth responses to environmental conditions. However, days with growth appeared quite irregularly and could on average only be predicted by environmental conditions in 45% of cases (27% to 68%, Table S4), confirming the non‐linearity of growth processes not only on an annual scale (Wilmking et al., 2020), but also on shorter time‐scales (Peltier & Ogle, 2020). This means, that average meteorological conditions during the entire year, the growth period, or even monthly values might not be the best predictor for annual growth variability particularly at smaller geographical scales. This is, however, still being implemented in many tree growth models (Wilmking et al., 2020). although this may hide contrasting responses to the meteorology on shorter time‐scales that in turn might affect growth differently (Forrest & Miller‐Rushing, 2010).
Growth activity, that is N daysgrowth and daily growth rate, explained most of the inter‐annual variability in radial growth independent of species, whereas stem phenology hardly contributed (Figure 4, Table S3). Hereby, the relationship between N daysgrowth and annual growth was not linear, but logarithmic (Figures S8). In essence, this indicates that it is not simply an additive effect that makes N daysgrowth important. In times of high N daysgrowth, the growth rate was highest, contributing to the non‐linearity between annual growth and N daysgrowth. Recent studies found weekly growth rates to significantly influence tree ring width (Cuny et al., 2012; Ren et al., 2019), and weak or no correlation between GROlength and annual growth (Kolar et al., 2016; Liu et al., 2013). However, other studies found the growth onset (Lupi et al., 2010), or duration (Michelot et al., 2012) being significantly related to annual growth, but these studies could not consider growth frequency due to coarser measurement techniques. N daysgrowth and GROlength were indeed positively correlated. But GROlength showed a non‐linear relationship to annual growth with a bell‐shaped optimum, while N daysgrowth was clearly positively related (Figure 4). This leads to the conclusion that a prolongation of the growth period does not necessarily lead to higher annual growth or carbon sequestration as often expected in CO2 mitigation strategies. This is particularly true at a lower elevation where a longer growth period could aggravate drought severity due to earlier soil water depletion caused by increased water uptake by trees due to earlier evapotranspiration (Meier et al., 2021). Especially an earlier GROstart in spring when growth conditions are favourable is thought to have the potential to enhance annual growth. Our results, however, showed that GROstart was quite constant among years, that GROstart did not contribute much to the variability in annual growth, and that the relationship to annual growth was—as for GROlength—non‐linear with low annual growth at early GROstart. We conclude that what happens within the growth period is more important to explain annual growth than knowing the conditions that influence the start and end of growth. Noteworthy, the temporally relatively consistent GROstart contrasts with the known earlier start of leaf phenology with increasing spring temperatures (Vitasse et al., 2018). This raises the question, unanswered here, of what this decoupling of leaf versus stem phenology actually means for the long‐term growth performance of trees.
What drives the probability of daily growth?
Since N daysgrowth is essential for annual growth, it is of interest what are the conditions that make a day a growth day. Growth activity was closely related to day length and the progression of the phenological cycle. In general, growth decreased sharply around the summer solstice, mostly regardless of moisture conditions in the air and soil (Figure S9), confirming observations of growth patterns in four coniferous species in the Northern Hemisphere (Rossi et al., 2006). Thus, 80% of the annual growth was already completed before end of June for the broadleaves, and before end of July for the conifers in most of the years. Growth of F. sylvatica reacted most sensitively to the day length, being also the most sensitive species to photoperiod for budburst (Vitasse & Basler, 2013). The photoperiod is suggested to act as a growth constraint or a signal after which the growth activity tends to decrease, thus allowing plants to safely complete secondary cell wall lignification and investment in other structures (e.g. fruits, buds) and reserves before winter (Duchesne et al., 2012; Körner et al., 2016; Larysch et al., 2021).
Within this seasonal window of growth opportunity mainly moisture conditions in soil and air limited the probability of growth, confirming an analysis on an hourly resolution for the same trees (Zweifel et al., 2021b). Our results are also in line with studies showing that cambial activity is limited by low water potential during summer (Cabon et al., 2020a; Peters et al., 2020) and the importance of increasing VPD for declining forest growth (Babst et al., 2019; Grossiord et al., 2020; Sanginés de Cárcer et al., 2018; Trotsiuk et al., 2021). The probability of growth was mainly limited by VPD for conifers, and by SWP for broadleaves, probably due to different hydraulic strategies of gymnosperms and angiosperms (Choat et al., 2012; Flo et al., 2021; Johnson et al., 2012), an assumption that could be of interest for future research. In addition, the probability of growth of P. abies and P. sylvestris was enhanced at higher temperatures, likely due to the higher elevation (>1000 m a.s.l.) sites (seven per species) included, at which temperature is the main limiting factor for growth (Körner & Paulsen, 2004). Our results highlight that there is not much delay between the main growth season and the seasonal drying of the topsoil at many lowland sites in Switzerland, and climate change could advance soil drought to potentially the best season for radial growth (April–June).
To conclude, different tree species showed very distinctive intra‐annual stem growth patterns, which were largely driven by plant functional types and site environments. For all species, the annual day length pattern seems to set a window of opportunity for radial growth, particularly before the summer solstice. Within that window, the water availability in air and soil is decisive for the probability of growth, and the temporal fluctuations in those conditions cause highly intermittent growth patterns. The resulting number of days with growth are more important for annual growth than stem phenology. Overall, we call for accounting intra‐annual and species‐specific responses to climate in tree and forest models to reduce the uncertainty of forest productivity predictions under ongoing global warming.
AUTHOR CONTRIBUTIONS
Conceptualisation: Roman Zweifel, Frank Sterck, Sophia Etzold. Methodology: Roman Zweifel, Frank Sterck, Nina Buchmann, Werner Eugster, Sabine Braun, Arthur Gessler, Kasia Ziemińska, Sophia Etzold. Investigation: Roman Zweifel, Sabine Braun, Lorenz Walthert. Data analyses: Sophia Etzold, Roman Zweifel, Kasia Ziemińska, Frank Sterck, Lorenz Walthert, Richard L. Peters, Yann Vitasse. Visualisation: Sophia Etzold, Roman Zweifel, Richard L. Peters, Ansgar Kahmen, Yann Vitasse, Kasia Ziemińska. Writing – original draft: Sophia Etzold, Roman Zweifel, Frank Sterck, Arun K. Bose, Sabine Braun, Nina Buchmann, Werner Eugster, Arthur Gessler, Ansgar Kahmen, Richard L. Peters, Yann Vitasse, Lorenz Walthert, Kasia Ziemińska.
PEER REVIEW
The peer review history for this article is available at https://publons.com/publon/10.1111/ele.13933.
Supporting information
Supplementary Material
ACKNOWLEDGEMENTS
We acknowledge the technical support from the Swiss Long‐term Forest Ecosystem Research Programme LWF and thank Nicolas De Girardi, Roger Köchli and Käthi Liechti for their field work within the TreeNet network. Furthermore, we acknowledge the work of our TreeNet data scientists Matthias Häni, Micah Wilhelm and Volodymyr Trotsiuk. Meteorological data were provided by the National Air Pollution Monitoring Network NABEL, MeteoSwiss and the Swiss Long‐term Forest Ecosystem Research programme LWF (www.lwf.ch), which is part of the UNECE Co‐operative Programme on Assessment and Monitoring of Air Pollution Effects on Forests ICP Forests (www.icp‐forests.net). Funding: ICOS Switzerland (SNF projects 20FI21_148992 and 20FI20_173691) and Federal Office for the Environment FOEN (grants: 18.0031.PJ/E2C9DDCC1, 00.25992A/E3D4E3424 and 00.25992A/08B6EC6C3). Open access funding provided by ETH‐Bereich Forschungsanstalten. Open Access Funding provided by Lib4RI Library for the Research Institutes within the ETH Domain Eawag Empa PSI and WSL.
Etzold, S. , Sterck, F. , Bose, A.K. , Braun, S. , Buchmann, N. , Eugster, W. , et al. (2022) Number of growth days and not length of the growth period determines radial stem growth of temperate trees. Ecology Letters, 25, 427–439. Available from: 10.1111/ele.13933
DATA AVAILABILITY STATEMENT
All the data supporting the results can be archived at https://doi.org/10.5061/dryad.hdr7sqvjv.
REFERENCES
- Babst, F. , Bouriaud, O. , Poulter, B. , Trouet, V. , Girardin, M.P. & Frank, D.C. (2019) Twentieth century redistribution in climatic drivers of global tree growth. Science Advances, 5. eaat4313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartoń, K. (2016) MuMIn: multi‐model inference. R package version 1.15.6.
- Bates, D. , Maechler, M. & Bolker, B. (2012). lme4: linear mixed effects models using S4 classes. R package version 0.999999‐0.
- Bobinac, M. , Batos, B. , Miljikovic, D. & Radulovic, S. (2012) Polycyclism and phenological variability in the common oak (Quercus robur L.). Archives of Biological Sciences Belgrade, 64, 97–105. [Google Scholar]
- Bose, A.K. , Scherrer, D. , Camarero, J.J. , Ziche, D. , Babst, F. , Bigler, C. et al. (2021) Climate sensitivity and drought seasonality determine post‐drought growth recovery of Quercus petraea and Quercus robur in Europe. Science of the Total Environment, 784. [DOI] [PubMed] [Google Scholar]
- Cabon, A. , Fernández‐de‐Uña, L. , Gea‐Izquierdo, G. , Meinzer, F.C. , Woodruff, D.R. , Martínez‐Vilalta, J. et al. (2020a) Water potential control of turgor‐driven tracheid enlargement in Scots pine at its xeric distribution edge. New Phytologist, 225, 209–221. [DOI] [PubMed] [Google Scholar]
- Cabon, A. , Peters, R.L. , Fonti, P. , Martínez‐Vilalta, J. & De Cáceres, M. (2020b) Temperature and water potential co‐limit stem cambial activity along a steep elevational gradient. New Phytologist, 226, 1325–1340. [DOI] [PubMed] [Google Scholar]
- Choat, B. , Jansen, S. , Brodribb, T.J. , Cochard, H. , Delzon, S. , Bhaskar, R. et al. (2012) Global convergence in the vulnerability of forests to drought. Nature, 491, 752–755. [DOI] [PubMed] [Google Scholar]
- Copini, P. , Vergeldt, F.J. , Fonti, P. , Sass‐Klaassen, U. , den Ouden, J. , Sterck, F. et al. (2019) Magnetic resonance imaging suggests functional role of previous year vessels and fibres in ring‐porous sap flow resumption. Tree Physiology, 39, 1009–1018. [DOI] [PubMed] [Google Scholar]
- Corripio, J.G. (2019) insol—solar radiation. R package to compute insolation on complex terrain. https://meteoexploration.com/R/insol/insol.pdf
- Cruz‐García, R. , Balzano, A. , Čufar, K. , Scharnweber, T. , Smiljanić, M. & Wilmking, M. (2019) Combining dendrometer series and xylogenesis imagery—DevX, a simple visualization tool to explore plant secondary growth phenology. Frontiers in Forests and Global Change, 2. [Google Scholar]
- Cuny, H.E. , Fonti, P. , Rathgeber, C.B.K. , Von Arx, G. , Peters, R.L. & Frank, D.C. (2019) Couplings in cell differentiation kinetics mitigate air temperature influence on conifer wood anatomy. Plant, Cell & Environment, 42, 1222–1232. [DOI] [PubMed] [Google Scholar]
- Cuny, H.E. , Rathgeber, C.B.K. , Frank, D. , Fonti, P. , Mäkinen, H. , Prislan, P. et al. (2015) Woody biomass production lags stem‐girth increase by over one month in coniferous forests. Nature Plants, 1, 15160. [DOI] [PubMed] [Google Scholar]
- Cuny, H.E. , Rathgeber, C.B.K. , Lebourgeois, F. , Fortin, M. & Fournier, M. (2012) Life strategies in intra‐annual dynamics of wood formation: example of three conifer species in a temperate forest in north‐east France. Tree Physiology, 32, 612–625. [DOI] [PubMed] [Google Scholar]
- Delpierre, N. , Berveiller, D. , Granda, E. & Dufrêne, E. (2016a) Wood phenology, not carbon input, controls the interannual variability of wood growth in a temperate oak forest. New Phytologist, 210, 459–470. [DOI] [PubMed] [Google Scholar]
- Delpierre, N. , Vitasse, Y. , Chuine, I. , Guillemot, J. , Bazot, S. , Rutishauser, T. et al. (2016b) Temperate and boreal forest tree phenology: from organ‐scale processes to terrestrial ecosystem models. Annals of Forest Science, 73, 5–25. [Google Scholar]
- Deslauriers, A. , Morin, H. & Begin, Y. (2003) Cellular phenology of annual ring formation of Abies balsamea in the Quebec boreal forest (Canada). Canadian Journal of Forest Research, 33, 190–200. [Google Scholar]
- Devine, W.D. & Harrington, C.A. (2009) Relationships among foliar phenology, radial growth rate, and xylem density in a young Douglas‐Fir plantation. Wood and Fiber Science, 41, 300–312. [Google Scholar]
- Dietrich, L. , Delzon, S. , Hoch, G. & Kahmen, A. (2019) No role for xylem embolism or carbohydrate shortage in temperate trees during the severe 2015 drought. Journal of Ecology, 107, 334–349. [Google Scholar]
- Drew, D.M. & Downes, G.M. (2018) Growth at the microscale: long term thinning effects on patterns and timing of intra‐annual stem increment in radiata pine. Forest Ecosystems, 5. [Google Scholar]
- Duchesne, L. , Houle, D. & D’Orangeville, L. (2012) Influence of climate on seasonal patterns of stem increment of balsam fir in a boreal forest of Québec, Canada. Agricultural and Forest Meteorology, 162–163, 108–114. [Google Scholar]
- Duursma, R.A. (2015) Plantecophys—an R package for analysing and modelling leaf gas exchange data. PLoS One, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Etzold, S. , Ziemińska, K. , Rohner, B. , Bottero, A. , Bose, A.K. , Ruehr, N.K. et al. (2019) One century of forest monitoring data in Switzerland reveals species‐ and site‐specific trends of climate‐induced tree mortality. Frontiers in Plant Science, 10, 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fatichi, S. , Pappas, C. , Zscheischler, J. & Leuzinger, S. (2019) Modelling carbon sources and sinks in terrestrial vegetation. New Phytologist, 221, 652–668. [DOI] [PubMed] [Google Scholar]
- Flo, V. , Martinez‐Vilalta, J. , Mencuccini, M. , Granda, V. , Anderegg, W.R.L. & Poyatos, R. (2021) Climate and functional traits jointly mediate tree water‐use strategies. New Phytologist, 231, 617–630. [DOI] [PubMed] [Google Scholar]
- Forrest, J. & Miller‐Rushing, A.J. (2010) Toward a synthetic understanding of the role of phenology in ecology and evolution. Philosophical Transactions of the Royal Society B: Biological Sciences, 365, 3101–3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman, A. & Hill, J. (2007) Data analysis using regression and multilevel/hierarchical models. New York, Cambridge: Cambridge University Press. [Google Scholar]
- Gelman, A. , Su, Y.‐S. , Yajima, M. , Hill, J. , Pittau, M.G. , Kerman, J. et al. (2020). arm—data analysis using regression and multilevel/hierarchical models. https://cran.r‐project.org/web/packages/arm/arm.pdf
- Gričar, J. , Vedenik, A. , Skoberne, G. , Hafner, P. & Prislan, P. (2019) Timeline of leaf and cambial phenology in relation to development of initial conduits in xylem and phloem in three coexisting sub‐Mediterranean deciduous tree species. Forests, 11, 1104. [Google Scholar]
- Grossiord, C. , Buckley, T.N. , Cernusak, L.A. , Novick, K.A. , Poulter, B. , Siegwolf, R.T.W. et al. (2020) Plant responses to rising vapor pressure deficit. New Phytologist, 226, 1550–1566. [DOI] [PubMed] [Google Scholar]
- Hsiao, T.C. & Acevedo, E. (1974) Plant responses to water deficits, water‐use efficiency, and drought resistance. Agricultural Meteorology, 14, 59–84. [Google Scholar]
- Huang, J.‐G. , Ma, Q. , Rossi, S. , Biondi, F. , Deslauriers, A. , Fonti, P. et al. (2020) Photoperiod and temperature as dominant environmental drivers triggering secondary growth resumption in Northern Hemisphere conifers. Proceedings of the National Academy of Sciences of the United States of America, 117, 20645–20652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, D.M. , McCulloh, K.A. , Woodruff, D.R. & Meinzer, F.C. (2012) Hydraulic safety margins and embolism reversal in stems and leaves: why are conifers and angiosperms so different? Plant Science, 195, 48–53. [DOI] [PubMed] [Google Scholar]
- Jones, H.G. (1992) Plants and microclimate: a quantitative approach to environmental plant physiology, 2nd edition. Cambridge: Cambridge University Press. [Google Scholar]
- Knüsel, S. , Peters, R.L. , Haeni, M. , Wilhelm, M. & Zweifel, R. (2021) Processing and extraction of seasonal tree physiological parameters from stem radius time series. Forests, 12, 765. [Google Scholar]
- Kolar, T. , Giagli, K. , Miroslav, T. , Bednarova, E. , Vavrcik, H. & Rybnicek, M. (2016) Response of the leaf phenology and tree‐ring width of European beech to climate variability. Silva Fennica, 50. [Google Scholar]
- Körner, C. (2003) Carbon limitation in trees. Journal of Ecology, 91, 4–17. [Google Scholar]
- Körner, C. , Basler, D. , Hoch, G. , Kollas, C. , Lenz, A. , Randin, C.F. et al. (2016) Where, why and how? Explaining the low temperature range limits of temperate tree species. Journal of Ecology, 104, 1076–1088. [Google Scholar]
- Körner, C. & Paulsen, J. (2004) A world‐wide study of high altitude treeline temperatures. Journal of Biogeography, 31, 713–732. [Google Scholar]
- Kozlowski, T. & Pallardy, S. (1996) Growth control in woody plants, 1st edition. Academic Press. [Google Scholar]
- Kuznetsova, A. , Brockhoff, P.B. & Christensen, R.H.B. (2017) lmerTest package: tests in linear mixed effects models. Journal of Statistical Software, 82, 1–26. [Google Scholar]
- Larysch, E. , Stangler, D.F. , Nazari, M. , Seifert, T. & Kahle, H.‐P. (2021) Xylem phenology and growth response of European beech, silver fir and scots pine along an elevational gradient during the extreme drought year 2018. Forests, 12, 75. [Google Scholar]
- Lehnebach, R. , Campioli, M. , Gričar, J. , Prislan, P. , Mariën, B. , Beeckman, H. et al. (2021) High‐resolution X‐ray computed tomography: a new workflow for the analysis of xylogenesis and intra‐seasonal wood biomass production. Frontiers in Plant Science, 12, 1495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lévesque, M. , Saurer, M. , Siegwolf, R. , Eilmann, B. , Brang, P. , Bugmann, H. et al. (2013) Drought response of five conifer species under contrasting water availability suggests high vulnerability of Norway spruce and European larch. Global Change Biology, 19, 3184–3199. [DOI] [PubMed] [Google Scholar]
- Liu, B. , Li, Y. , Eckstein, D. , Zhu, L. , Dawadi, B. & Liang, E. (2013) Has an extending growing season any effect on the radial growth of Smith fir at the timberline on the southeastern Tibetan Plateau? Trees, 27, 441–446. [Google Scholar]
- Lockhart, J.A. (1965) An analysis of irreversible plant cell elongation. Journal of Theoretical Biology, 8, 264–275. [DOI] [PubMed] [Google Scholar]
- Lupi, C. , Morin, H. , Deslauriers, A. & Rossi, S. (2010) Xylem phenology and wood production: resolving the chicken‐or‐egg dilemma. Plant, Cell and Environment, 33, 1721–1730. [DOI] [PubMed] [Google Scholar]
- Martin‐Benito, D. , Pederson, N. , Köse, N. , Doğan, M. , Bugmann, H. , Mosulishvili, M. et al. (2018) Pervasive effects of drought on tree growth across a wide climatic gradient in the temperate forests of the Caucasus. Global Ecology and Biogeography, 27, 1314–1325. [Google Scholar]
- Meier, M. , Vitasse, Y. , Bugmann, H. & Bigler, C. (2021) Phenological shifts induced by climate change amplify drought for broad‐leaved trees at low elevations in Switzerland. Agricultural & Forest Meteorology, 307, 108485. [Google Scholar]
- MeteoSwiss . (2013). Klimaszenarien Schweiz—eine regionale Übersicht, Fachbericht MeteoSchweiz. p. 36.
- Michelot, A. , Simard, S. , Rathgeber, C. , Dufrene, E. & Damesin, C. (2012) Comparing the intra‐annual wood formation of three European species (Fagus sylvatica, Quercus petraea and Pinus sylvestris) as related to leaf phenology and non‐structural carbohydrate dynamics. Tree Physiology, 32, 1033–1045. [DOI] [PubMed] [Google Scholar]
- Nakagawa, S. & Schielzeth, H. (2013) A general and simple method for obtaining R2 from generalized linear mixed‐effects models. Methods in Ecology and Evolution, 4, 133–142. [Google Scholar]
- Ogle, K. , Barber, J.J. , Barron‐Gafford, G.A. , Bentley, L.P. , Young, J.M. , Huxman, T.E. et al. (2015) Quantifying ecological memory in plant and ecosystem processes. Ecology Letters, 18, 221–235. [DOI] [PubMed] [Google Scholar]
- Pan, Y. , Birdsey, R.A. , Fang, J. , Houghton, R. , Kauppi, P.E. , Kurz, W.A. et al. (2011) A large and persistent carbon sink in the world’s forests. Science, 333(6045), 988–993. [DOI] [PubMed] [Google Scholar]
- Parent, B. , Turc, O. , Gibon, Y. , Stitt, M. & Tardieu, F. (2010) Modelling temperature‐compensated physiological rates, based on the co‐ordination of responses to temperature of developmental processes. Journal of Experimental Botany, 61, 2057–2069. [DOI] [PubMed] [Google Scholar]
- Passioura, J.B. (1982) Water in the soil‐plant‐atmosphere continuum. In: Lange, O.L. , Nobel, P.S. , Osmond, C.B. & Ziegler, H. (Eds.), Physiological plant ecology II. Encyclopedia of plant physiology (new series). Berlin, Heidelberg: Springer, pp. 5–33. [Google Scholar]
- Peltier, D.M.P. & Ogle, K. (2020) Tree growth sensitivity to climate is temporally variable. Ecology Letters, 23, 1561–1572. [DOI] [PubMed] [Google Scholar]
- Pérez‐de‐Lis, G. , Rossi, S. , Vázquez Ruiz, R. , Rozas, V. & García González, I. (2016) Do changes in spring phenology affect earlywood vessels? Perspective from the xylogenesis monitoring of two sympatric ring‐porous oaks. New Phytologist, 209, 521–530. [DOI] [PubMed] [Google Scholar]
- Peters, R.L. , Steppe, K. , Cuny, H.E. , De Pauw, D.J.W. , Frank, D.C. , Schaub, M. et al. (2020) Turgor—a limiting factor for radial growth in mature conifers along an elevational gradient. New Phytologist, 229, 213–229. [DOI] [PubMed] [Google Scholar]
- Pinheiro, J. , Bates, D. , DebRoy, S. , Sarkar, D. & R Core Team . (2015) nlme: linear and nonlinear mixed effects models. R package version 3.1‐122.
- Pugh, T.A.M. , Lindeskog, M. , Smith, B. , Poulter, B. , Arneth, A. , Haverdh, V. et al. (2018) Role of forest regrowth in global carbon sink dynamics. Proceedings of the National Academy of Sciences of the United States of America, 116, 4382–4387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team . (2021) R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R‐project.org/ [Google Scholar]
- Rathgeber, C. , Cuny, H.E. & Fonti, P. (2016) Biological basis of tree‐ring formation: a crash course. Frontiers in Plant Science, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren, P. , Ziaco, E. , Rossi, S. , Biondi, F. , Prislan, P. & Liang, E. (2019) Growth rate rather than growing season length determines wood biomass in dry environments. Agricultural and Forest Meteorology, 271, 46–53. 10.1016/j.agrformet.2019.02.031 [DOI] [Google Scholar]
- Richardson, A.D. , Andy Black, T. , Ciais, P. , Delbart, N. , Friedl, M.A. , Gobron, N. et al. (2010) Influence of spring and autumn phenological transitions on forest ecosystem productivity. Philosophical Transactions of the Royal Society B: Biological Sciences, 365, 3227–3246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossi, S. , Anfodillo, T. , Čufar, K. , Cuny, H.E. , Deslauriers, A. , Fonti, P. et al. (2013) A meta‐analysis of cambium phenology and growth: linear and non‐linear patterns in conifers of the northern hemisphere. Annals of Botany, 112, 1911–1920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossi, S. , Deslauriers, A. , Anfodillo, T. & Carraro, V. (2007) Evidence of threshold temperatures for xylogenesis in conifers at high altitudes. Oecologia, 152, 1–12. [DOI] [PubMed] [Google Scholar]
- Rossi, S. , Deslauriers, A. , Anfodillo, T. , Morin, H. , Saracino, A. , Motta, R. et al. (2006) Conifers in cold environments synchronize maximum growth rate of tree‐ring formation with day length. New Phytologist, 170, 301–310. [DOI] [PubMed] [Google Scholar]
- Ruehr, N.K. , Gast, A. , Weber, C. , Daub, B. & Arneth, A. (2015) Water availability as dominant control of heat stress responses in two contrasting tree species. Tree Physiology, tpv102. [DOI] [PubMed] [Google Scholar]
- Sanginés de Cárcer, P. , Vitasse, Y. , Penuelas, J. , Jassey, V.E. , Buttler, A. & Signarbieux, C. (2018) Vapor–pressure deficit and extreme climatic variables limit tree growth. Global Change Biology, 24, 1108–1122. [DOI] [PubMed] [Google Scholar]
- Schuldt, A. , Hönig, L. , Li, Y. , Fichtner, A. , Härdtle, W. , Oheimb, G. et al. (2017) Herbivore and pathogen effects on tree growth are additive, but mediated by tree diversity and plant traits. Ecology and Evolution, 7, 7462–7474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sellier, D. & Ségura, R. (2020) Radial growth anisotropy and temporality in fast‐growing temperate conifers. Annals in Forest Science, 77, 85. [Google Scholar]
- Skomarkova, M.V. , Vaganov, E.A. , Mund, M. , Knohl, A. , Linke, P. , Boerner, A. et al. (2006) Inter‐annual and seasonal variability of radial growth, wood density and carbon isotope ratios in tree rings of beech (Fagus sylvatica) growing in Germany and Italy. Trees, 20, 571–586. [Google Scholar]
- Steppe, K. , Sterck, F. & Deslauriers, A. (2015) Diel growth dynamics in tree stems: linking anatomy and ecophysiology. Trends in Plant Science, 20, 335–343. [DOI] [PubMed] [Google Scholar]
- Trotsiuk, V. , Babst, F. , Grossiord, C. , Gessler, A. , Forrester, D.I. , Buchmann, N. et al. (2021) Tree growth in Switzerland is increasingly constrained by rising evaporative demand. Journal of Ecology, 109, 2981–2990. [Google Scholar]
- van der Maaten, E. , Pape, J. , van der Maaten‐Theunissen, M. , Scharnweber, T. , Smiljanić, M. , Cruz‐García, R. et al. (2018) Distinct growth phenology butsimilar daily stem dynamics in three co‐occurring broadleaved tree species. Tree Physiology, 38, 1820–1828. [DOI] [PubMed] [Google Scholar]
- Vieira, J. , Rossi, S. , Campelo, F. , Freitas, H. & Nabais, C. (2013) Seasonal and daily cycles of stem radial variation of Pinus pinaster in a drought‐prone environment. Agricultural & Forest Meteorology, 180, 173–181. [Google Scholar]
- Vitasse, Y. & Basler, D. (2013) What role for photoperiod in the bud burst phenology of European beech. European Journal of Forest Research, 132, 1–8. [Google Scholar]
- Vitasse, Y. , Signarbieux, C. & Fu, Y.H. (2018) Global warming leads to more uniform spring phenology across elevations. Proceedings of the National Academy of Sciences of the United States of America, 115, 1004–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vospernik, S. , Nothdurft, A. & Mehtätalo, L. (2020) Seasonal, medium‐term and daily patterns of tree diameter growth in response to climate. Forestry: An International Journal of Forest Research, 93, 133–149. [Google Scholar]
- Walthert, L. & Meier, E.S. (2017) Tree species distribution in temperate forests is more influenced by soil than by climate. Ecology and Evolution, 9473–9484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walthert, L. & Schleppi, P. (2018) Equations to compensate for the temperature effect on readings from dielectric Decagon MPS‐2 and MPS‐6 water potential sensors in soils. Journal of Plant Nutrition and Soil Science, 181, 749–759. [Google Scholar]
- Wilmking, M. , Maaten‐Theunissen, M. , Maaten, E. , Scharnweber, T. , Buras, A. , Biermann, C. et al. (2020) Global assessment of relationships between climate and tree growth. Global Change Biology, 26, 3212–3220. [DOI] [PubMed] [Google Scholar]
- Wood, S. (2012). mgcv: mixed GAM computation vehicle with GCV/AIC/REML smoothness estimation. R package version 1.8‐91.8‐9.
- Zang, C. , Hartl‐Meier, C. , Dittmar, C. , Rothe, A. & Menzel, A. (2014) Patterns of drought tolerance in major European temperate forest trees: climatic drivers and levels of variability. Global Change Biology, 20, 3767–3779. [DOI] [PubMed] [Google Scholar]
- Zani, D. , Crowther, T.W. , Mo, L. , Renner, S.S. & Zohner, C.M. (2021) Increased growing‐season productivity drives earlier autumn leaf senescence in temperate trees. Science, 370, 1066–1071. [DOI] [PubMed] [Google Scholar]
- Zweifel, R. , Etzold, S. , Basler, D. , Bischoff, R. , Braun, S. , Buchmann, N. et al. (2021a) TreeNet—the biological drought and growth indicator network. Frontiers in Forests and Global Change, 4. [Google Scholar]
- Zweifel, R. , Etzold, S. , Sterck, F. , Gessler, A. , Anfodillo, T. , Mencuccini, M. et al. (2020) Determinants of legacy effects in pine trees—implications from an irrigation‐stop experiment. New Phytologist, 227, 1081–1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zweifel, R. , Haeni, M. , Buchmann, N. & Eugster, W. (2016) Are trees able to grow in periods of stem shrinkage? New Phytologist, 211, 839–849. [DOI] [PubMed] [Google Scholar]
- Zweifel, R. & Sterck, F. (2018) A conceptual tree model explaining legacy effects on stem growth. Frontiers in Forests and Global Change, 1, 9. [Google Scholar]
- Zweifel, R. , Sterck, F. , Braun, S. , Buchmann, N. , Eugster, W. , Gessler, A. et al. (2021b) Why trees grow in the dark. New Phytologist, 231, 2174–2185. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Data Availability Statement
All the data supporting the results can be archived at https://doi.org/10.5061/dryad.hdr7sqvjv.


