Effect of the Axially Inserted Solid Rod on the Flow Field Characteristics and Separation Performance of a Hydrocyclone

Abstract

In this paper, the experimental validation and numerical simulation were used to investigate the effect of the inserted solid rod on the separation process of the hydrocyclone. The simulation results are analyzed in terms of the pressure drop, air core, velocity component, turbulence intensity, and separation performance when the air core is completely inhibited or not. The results indicate that the solid rod with the smaller size cannot completely inhibit the air core, but it can still affect the separation process. The variable diameter inserted solid rod (d_vr) could inhibit the air core and ensure a larger effective separation space, which could improve the separation performance of the hydrocyclone. Specifically, the d_vr could improve energy conversion ability, tangential velocity, and separation sharpness and decrease axial velocity and turbulence intensity. Therefore, inhibiting the air core is conducive to the separation process of hydrocyclone, and the variable diameter inserted solid rod has better inhibited effect.

1. Introduction

In 1891, Bretney¹ invented the hydrocyclone and applied the patent for it. The conventional hydrocyclone has a simple structure consisting of cylindrical and conical sections, including one inlet and two outlets (overflow and underflow outlets). The suspension enters the hydrocyclone with a certain velocity and pressure from the inlet. Due to the difference of force acting on particles, the coarse particles would move toward the wall and remove from the underflow outlet, and the fine particles would move inward and discharge from the overflow outlet. A hydrocyclone has the advantages of simple structure, large processing capacity, convenient maintenance, small occupation area, and serial and parallel utilization. It has been widely used in coal mining, mineral processing, petrochemical engineering, and other traditional fields. With the miniaturization of equipment, the application of hydrocyclones in biomedicine,² cell culture,³ and sewage treatment⁴ is gradually increasing. Although the structure of a hydrocyclone is simple, its flow field is complicated. The influencing factors of hydrocyclone performance can be divided into three parts: structural parameters, operating parameters, and feed parameters. Furthermore, the structural parameters mainly include the diameter, wall thickness, and length of the vortex finder, the inlet configuration, the form of underflow, the height of the cylindrical section, and the angle and shape of the conical section. Operating parameters include the inlet velocity and the feed pressure. Feed parameters include feed density and concentration, the feed volume fraction, and feed particle size distribution.

The hydrocyclone is a complex system composed of the gas phase (air core), liquid phase, and solid phase (particles). The air core is located at the axis line of equipment and runs through the overflow and underflow outlets. When the suspension enters the hydrocyclone at a certain velocity and pressure, the linear flow becomes a high-speed tangential motion, resulting in a lower pressure in the central region of the cyclone, and then the air enters from the underflow outlet to form the air core. The air core is not a steady cylinder but a spiral of periodic oscillation. Since there are no particles in the air core, it does not directly participate in the separation process. However, due to the instability of the air core, it directly affects the flow field of the hydrocyclone, and then indirectly participates in the separation process. Therefore, scholars have carried out related research works on the air core of the hydrocyclone. Wang et al.⁵ found that the air core can form only when the underflow outlet is connected to the atmosphere. Lim et al.⁶ presented the transient development of the air core structure in the hydrocyclone and indicated that the air core is a highly unsteady structure that interacts strongly with the surrounding turbulent liquid. In terms of the vortex finder and underflow outlet, research shows that the characteristic of the air core is affected by the ratio of the vortex finder diameter to the underflow diameter (D_o/D_u).⁷ Ghodrat et al.⁸ indicated that the air core might be suppressed by a small underflow diameter and high feed solid concentration. Wang and co-workers^9,10 demonstrated that once the diameter of the vortex finder exceeds a critical value, the air core diameter would be larger than that of the underflow, and then the separation performance would deteriorate rapidly. Li et al.¹¹ changed the outwall of the vortex finder to a hexagon and found that the air core diameter near the vortex finder is decreased. Wang and Wu¹² introduced a membrane overflow pipe and indicated that it could eliminate the turbulence surrounding the overflow outlet. In addition, the air core is affected by the inlet configuration. Zhang et al.¹³ pointed out that the air core diameter increases with the decrease of the inlet curvature radius. In terms of the operating parameters, Xu et al.¹⁴ studied the effect of outside atmospheric pressure on the air core and found that the shape and average diameter of the air core in the hydrocyclone are more changeable on the plain than on the plateau. At present, there are two different views on the effect of the air core on the separation process. Some scholars think that the air core occupies a separation space. The smaller the air core diameter is, the more effective the separation space in the hydrocyclone.¹⁵ Others hold the opinion that the air core would be beneficial to separation. Because the tangential velocity of the air core edge is higher than that of water, it helps improve the velocity of water combined with particles near the interface.¹⁶ Therefore, scholars have researched the influence of the presence or absence of the air core on the separation process.

Two methods can inhibit the air core: water-sealing and inserting a solid rod. Luo et al.¹⁷ used water to seal the underflow outlet and indicated that the tangential velocity in the water-sealed hydrocyclone increases. At present, the most adopted method of inhibiting the air core is to insert a solid rod to replace it. Lee and Williams¹⁸ demonstrated that the separation efficiency decreased when inserting the solid rod. However, Chu et al.¹⁶ indicated that the velocity and turbulence near the vortex finder would decrease, and the separation performance would increase after inserting the solid rod. In addition, they explained that the lower separation efficiency obtained by Lee and Williams¹⁸ is because the “body support” of the solid rod destroys the flow field. Sripriya et al.¹⁹ also obtained the same conclusion as Chu et al.,¹⁶ and he pointed out that if the diameter of the solid rod increases, the insertion height can decrease appropriately. Evans et al.²⁰ indicated that the insertion of a solid rod could reduce pressure consumption. Vakamalla et al.²¹ indicated that the air core elimination by placing a rod in the center decreases the turbulent levels drastically. In addition, the difference in liquid–solid density will also affect the effectiveness of the air core suppression on the improvement of separation performance. The improvement is obvious when the relative density of liquid–solid is close.¹⁹ Li et al.²² indicated that the inserted solid rod is conducive to decreasing the short-circuit flow, increasing the pressure drop, and increasing tangential velocity. The inserted rods discussed above are all solid. However, Lin and Wu²³ inserted a tubular ceramic membrane to offset the air core and change the turbulence structure for enhancing separation efficiency. Most of the inserted solid rod is vertical and connects the overflow and underflow outlets. However, Gupta et al.²⁴ pointed out that a horizontal inserted solid rod at the middle of the conical section is beneficial to eliminate the air core and decrease the pressure drop. With the comparison of the above literature, we can reach a consensus that inhibiting the air core is beneficial to improve the separation performance of the hydrocyclone. However, the inserted solid rods studied above are regular cylinders (constant diameter), while the air core diameter is not constant in the axial direction. Furthermore, most of the research focuses on the inhibition of the air core by inserting the solid rod and ignores the effect of the rod on the separation process when the air core is not completely inhibited. Therefore, we designed four types of inserted solid rods: inserted solid rod connecting two outlets, overflow outlet fixed inserted solid rod, underflow outlet fixed inserted solid rod, and variable diameter inserted solid rod. The effect of the diameter, fixed position, and inserted length of the solid rod on the separation performance is systematically analyzed in this paper. More importantly, the effect of the inserted solid rod on the separation process when the air core is not completely inhibited was studied.

The research methods of hydrocyclones can be summarized into three categories: theoretical method, experimental test, and numerical simulation. The theoretical method includes summarizing empirical formulas and establishing a unified model, which is difficult for hydrocyclone research. The experimental test includes the study of flow field characteristics and separation efficiency. Nowadays, the flow field test can be tested by the laser doppler velocity test technology (LDV)¹⁷ and particle image velocimetry test technology (PIV).²⁴ The LDV test can only measure one point in the flow field in one operation, and the obtained flow field distribution is actually a data set of spatial points measured at different times. However, the PIV is a non-interference test that uses high-speed cameras to capture the tracer particles irradiated by laser on the measuring surface of the flow field to obtain flow field information. With the development of computer technology and numerical software, CFD has been increasingly used in research works. The experimental test needs to build an equipment platform, and it has high requirements on the site, equipment, and operators. Furthermore, the experimental data is greatly affected by the environment and testers. While numerical simulation has gotten rid of many limitations, it not only has a broader scope of research but can also obtain relatively detailed and accurate data. Reynolds stress model (RSM)²⁵ and large eddy simulation (LES)²⁶ are widely used in calculating the turbulent flow field in hydrocyclones. The predicted accuracy of the LES model on the flow field is closely related to the minimum grid size, and it needs more compute resources. However, the RSM does not have high requirements on the grid and can obtain more accurate flow field information. The air core in the flow field is predicted by the volume of fluid (VOF) model, which detects the proportion of gas in each grid to present the interface between the liquid and gas phases. As for separation efficiency, the methods that simulate the multiphase flow can divide into the Euler–Euler method and the Euler–Lagrange method. The mixture model belongs to the Euler–Euler method, and it fully considers the collision and shear stress between particles and has a good prediction of particle separation performance.²⁷ The DPM method belongs to the Euler–Lagrange method, and it can predict the trajectory of the particles and suit the dilute system. Furthermore, the CFD-DEM coupling method has gradually been applied to the study of hydrocyclone.²⁸ The method fully considers the interaction between particles and fluid and can simulate the true separation process, but it also requires considerable computing resources.

In this paper, the effect of different types of the inserted solid rod on the separation performance of the hydrocyclone is studied by using experimental validation and numerical simulation. The variables of the inserted solid rod include the diameter, fixed position, and inserted length. The formation of the air core, energy consumption, velocity component, turbulence intensity, separation performance, etc., are comparatively analyzed when the air core is completely inhibited or not.

2. Mathematical Model

2.1. Model Description

The geometrical parameters of the hydrocyclone are shown in Figure 1. The cyclone with a nominal diameter of 50 mm and the vortex finder wall thickness of 9.5 mm was designed as the base hydrocyclone, as shown in Figure 1a. The origin of the three-dimensional Cartesian coordinates is located at the center of the section z = 0. The variables of the inserted solid rod are the diameter, fixed position, and inserted length. In Figure 1b, the diameter of the inserted solid rod is represented by d_r. Based on the air core diameter of the base hydrocyclone, the inserted solid rods with diameters of d_r = 1, 3, and 5 mm were selected to study. The inserted solid rod with a diameter of d_r = 5 mm is smaller than the air core diameter in the base hydrocyclone. Therefore, the inhibited effect when the inserted solid rod diameter is smaller than the air core diameter is studied. In Figure 1c, the inserted solid rod was fixed to the overflow outlet, and the inserted length of l_o = 65, 130, and 195 mm were selected to study. Likewise, in Figure 1d, the inserted solid rod was fixed to the underflow outlet. The inserted lengths of l_u = 65, 130, and 195 mm were selected to study. Meanwhile, the values of d_r and l_o, l_u in Figure 1 are 5 and 195 mm, respectively. In Figure 1e, the diameter of the inserted solid rod is variable (d_vr). The diameter of the solid rod in the overflow pipe is 10 mm, and the rest is 6 mm.

Figure 1.

Structural parameters (a–e) and grid discretization model (f) of the hydrocyclone.

The separation process of the hydrocyclone involves a gas–liquid–solid three-phase system. Therefore, the numerical simulation was divided into two steps, as reported by Wang et al.¹⁰ First, the RSM model was used to simulate the turbulent flow, and the VOF model was used to predict the air core. Then, the stable flow field calculated by the first step was used as the initial flow field at the second step. The mixture model was introduced to predict the motion of particles. In this model, in order to calculate the drift velocity between the water and air, the bubble size is set to 1 × 10^–5 m.^29,30 Furthermore, it has to point out that the above calculation methods have been verified to accurately predict the flow field characteristics and separation performance of the hydrocyclone.^13,22,27,28

For the incompressible fluid, the governing equations of continuity and Reynolds-averaged Navier–Stokes can be expressed as

1

2

where the Reynolds stress term −ρu_i^’u_j is a new unknown term for the turbulent fluctuation value, which has been modeled to the close momentum equation (eq 2).

The extract transport equations for the transport of the Reynolds stresses −ρu_i^’u_j can be written as

3

where ρ, u_i, u_i^’, and x_i are liquid density, velocity, velocity fluctuation, and positional length, respectively. D_T, ij is the turbulent diffusion term, D_L, ij is the molecular diffusion term, P_ij is the stress production term, G_ij is the buoyancy production term, φ_ij is the pressure strain term, ε_ij is the dissipation term, and F_ij is the production by system rotation term.

The tracking of the interface between the water and air is achieved by solving the control equation of the VOF model.

4

where a_q is the volume fraction of the qth phase and v_q→ is the velocity vector of the qth phase.

Only one momentum equation is solved in the whole domain, and the resulting velocity field is shared. The momentum equation, which depends on the volume fraction of a fluid phase, is given by

5

where the density ρ and viscosity μ are derived from the values of component phases in each control cell by the volume fraction averaged method.

As for the mixture model, the solid phase is treated as continuous and can be interpenetrating. The continuity equation of the model is

6

The momentum equation for the mixture can be obtained by summing the individual momentum equations for all phases. It can be expressed as:

7

where n is the number of phases, F⃗ is a body force, and μ_m is the viscosity of the mixture.

2.2. Simulation Conditions

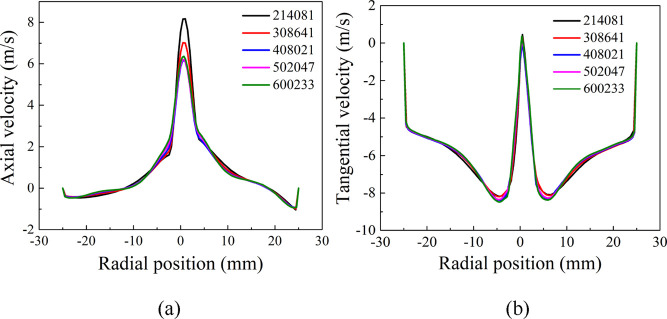
The grid discretization is one of the most critical steps in the pretreatment of the numerical simulation. The appropriate grid type and number can make the calculation more efficient. In this paper, the hexahedral grid was determined to discretize the computational domain. The node number of the hexahedral mesh is less than that of the tetrahedral grid under the same grid number. Also, the quality of the hexahedral mesh is higher than that of the tetrahedral mesh. Therefore, the structural mesh could accurately predict the separation process in less time. This paper conducted grid independence verification to eliminate the effect of grid numbers on calculation results. The computational domain was discretized by different grid numbers. The grid number of the five mesh models are 214,081, 308,641, 408,021, 502,047, and 600,233, respectively. The predicted results of the axial velocity and tangential velocity at z = 0 mm on the y = 0 plane under different grid numbers are shown in Figure 2. It can be observed that when the grid number exceeds 408,021, the tangential and axial velocity seems stable. Therefore, considering the calculation time and accuracy, we selected the grid number 4.0 × 10⁵ to discretize the computational domain, as shown in Figure 1f.

Figure 2.

Axial velocity (a) and tangential velocity (b) at z = 0 mm on the y = 0 plane under different grid numbers.

Water with a density of 998.2 kg·m^–3 and a viscosity of 1.003 × 10^–3 Pa·s is the liquid phase. Quartz particles with a density of 2650 kg·m^–3 are the solid phase. The inlet is set as “velocity-inlet”, and the water and particles have the same velocity of 6 m·s^–1. The turbulent intensity and hydraulic diameter of the inlet are 4.068% and 9.60 mm, respectively. The overflow outlet and underflow outlet are set as “pressure-outlet.” The backflow volume fraction of the two outlets is set as 1. It means that only air can go back into the flow field through the two outlets. The wall is set as “stationary wall,” and the shear condition is set as “no slip”. The standard wall function was used as the near-wall treatment method. The calculation result is considered to be convergent when the residual is less than 1 × 10^–5.

2.3. Experimental Setup

It is essential to validate the simulated accuracy of the selected numerical models before carrying out the numerical calculation. In our work, The PIV field test system was used to validate the RSM model and VOF model. The mixture model was validated by comparing the separation efficiency of both the experimental and numerical results. The experimental apparatus and PIV test system are shown in Figure 3. The PIV system consists of PIV equipment manufactured by Dantec Dynamics A/S and the Dynamics Studio V3.0 image processing system. The laser emitter is a Nd:YAG double-pulse laser; the output laser wavelength is 532 nm; and the repetition frequency is 1–15 Hz. The Ruston impeller was used to keep the uniformity of the fluid–solid mixing system. The pump provides the power of the suspension transportation process, and the adjustable value controls the inlet flow rate of the cyclone. A transparent plexiglass square tank is installed on the outside of the cyclone to reduce the light scattering of the hydrocyclone surface. The position of the tracer particles on the measuring surface can be captured by the high-speed camera. Then, the PIV post-processing system will analyze the captured pictures at different times. Finally, the flow field information, including the flow velocity, can be obtained. The solid volume fraction is 5%, and the diameter and the proportion of particles are shown in Table 1. The range of the particles is 0.5 to 40 μm, and the particles are divided into 11 parts. When the separation process is stable, the suspension of inlet and underflow are collected synchronously. The particle distribution of the selected samples is analyzed by the Mastersizer 2000 laser diffraction particle size analyzer. Therefore, we can obtain the recovery ratio of different particles to the underflow.

Figure 3.

Experimental setup: 1-mixing tank; 2-valve; 3-pump; 4-rotor flow meter; 5-piezometer; 6-hydrocyclone; 7-plexiglass tank; 8-high-speed camera; 9-laser generator; 10-high-performance computer.

Table 1. Particle Size Distribution and Volume Fraction of Quartz in the Feed.

sequence number	size interval/μm	mean size/μm	yield/%	volume fraction/%
1	–40 + 35	37.5	4.14	0.2070
2	–35 + 30	32.5	4.92	0.2460
3	–30 + 25	27.5	11.41	0.5705
4	–25 + 20	22.5	6.03	0.3015
5	–20 + 15	17.5	11.75	0.5875
6	–15 + 10	12.5	19.63	0.9815
7	–10 + 5	7.5	17.65	0.8825
8	–5 + 3	4.0	10.62	0.5310
9	–3 + 2	2.5	6.23	0.3115
10	–2 + 1	1.5	5.82	0.2910
11	–1	0.5	1.80	0.0900
total			100	5

2.4. Model Validation

Figure 4 indicates the axial and radial velocity extracted from the z = 18 mm line on the y = 0 mm section of the steady flow field. Due to the air core, only half of the velocity component can be captured and displayed in this experiment. Figure 4a shows the axial velocities of the simulated and experimental results, and the researched results of Cui²⁹ are added and compared. The axial velocity is zero on the inner wall, decreases along the radial direction, and then increases to the maximum value until it reaches the air core. Compared with the experimental results, the numerical results are in good agreement with it. At the same time, the experimental and numerical results are consistent with the findings of Cui. Also, the changing trend and values of the radial velocity in both the experimental and simulated results are similar, as shown in Figure 4b. It indicated that the turbulence and multiphase models used in this paper could accurately predict the gas–liquid flow with higher turbulence.

Figure 4.

Comparison of the distribution of axial velocity (a) and radial velocity (b) at z = 18 mm.

Figure 5 shows the separation efficiency of the simulated and experimental results. The separation efficiency shown on the Y-axis represents the recovery rate of different particles to the underflow. The larger the particle diameter, the higher the proportion of entering the underflow. When the particle diameter is smaller than 5 μm, the separation efficiency of the experimental test is higher than that of the numerical simulation. This phenomenon might be caused by the underflow entrainment effect during the experimental test. Furthermore, the maximum error of the mixture model on the separation efficiency is only 4.46%, which is acceptable. As the particle size increases, numerical simulation greatly predicts the separation process. Therefore, the multiphase model used in this paper could accurately predict the separation performance of the hydrocyclone.

Figure 5.

Comparison of the simulated and experimental partition curves.

3. Results and Discussion

3.1. Flow Field Characteristics

The inserted solid rod would affect the formation and development of the air core and further affect the flow pattern and separation performance. Therefore, first, it is necessary to analyze the effect of the inserted solid rod on the flow field in terms of the pressure drop, air core, velocity distribution, and turbulence intensity.

3.1.1. Pressure Drop

When the hydrocyclone runs, the pressure energy would be converted into kinetic energy, accompanied by energy dissipation. The pressure drop (Δp) is defined as the difference between the static pressure at the inlet and overflow outlets, representing the energy consumption in the separation process, as shown in eq 8. In order to illustrate the energy conversion efficiency, Misiulia³⁰ proposed a dynamic efficiency factor (ζ) to evaluate the ability of pressure energy to transform into kinetic energy of a flow field. It is defined as the ratio of the pressure drop to the kinetic energy of the flow field, as shown in eq 9. It can be seen that the smaller the dynamic efficiency factor, the higher the energy conversion efficiency (lower dissipation of energy). The pressure drop and dynamic efficiency factor of hydrocyclone with different inserted solid rods are shown in Table 2.

8

9

where p_i is the static pressure at the inlet, p_o is the static pressure at the overflow, ρ is the liquid density, and u_t – max is the maximum value of the tangential velocity in the flow field.

Table 2. Pressure Drop and Dynamic Efficiency Factor of Hydrocyclone with Different Inserted Solid Rods.

	value	pressure drop (Pa)	Ut-max (m/s)	dynamic efficiency factor ζ
base_H	dr = 0	100030.70	9.14	2.402
dr	5	106787.85	10.14	2.081
	3	104530.21	9.66	2.244
	1	104439.32	9.55	2.294
lo	195	106245.72	10.34	1.991
	130	106081.32	10.17	2.055
	65	104838.69	9.76	2.205
lu	195	106806.14	10.40	1.979
	130	106213.57	10.16	2.062
	65	105271.44	9.93	2.139
dvr		102549.50	10.39	1.903

As shown in Table 2, the base hydrocyclone has the lowest pressure drop (about 1 atm). When l_u = 195 mm, the hydrocyclone has the highest pressure drop, and it increases by 6.77% compared with that of the base hydrocyclone. The pressure drop increases as the diameter of the inserted solid rod increases, which is consistent with the findings of Li et al.²² When the inserted solid rod is fixed at the overflow and underflow outlets, the pressure drop increases as the inserted length increases. In other words, when the air core is not completely inhibited, the bigger the volume of the inserted solid rod in the hydrocyclone, the higher the pressure drop. That might be because the inserted solid rod increases the resistance during the formation and development of the air core. However, when the inserted solid rod d_vr completely inhibits the air core, the pressure drop decreases compared to that when the air core was not completely inhibited. Compared to the base hydrocyclone, the pressure drop of the hydrocyclone without the air core increased by 2.52%. This may be caused by the friction between the liquid and the solid rod. However, the energy conversion ability is significantly improved when the air core is completely inhibited. The specific analysis is as follows.

In terms of the maximum tangential velocity, the base hydrocyclone has the smallest value: 9.14 m·s^–1. The U_t-max increases with the increase of the inserted solid rod diameter and length. Compared with the U_t-max of the base hydrocyclone, when the parameters of the inserted solid rod are d_r = 5 mm, l_o = 195 mm, l_u = 195 mm, and d_vr, the U_t-max increased by 10.94, 13.13, 13.79, and 13.68%, respectively. As for the dynamic efficiency factor, the base hydrocyclone has the largest value. It means that the energy dissipation of the base hydrocyclone is bigger, and it has a lower energy conversion ability. With the inserted solid rod diameter and length increase, the ζ decreases, meaning the lower energy dissipation. Especially, when the inserted solid rod parameter is d_vr, the hydrocyclone has the smallest ζ. This demonstrates that the hydrocyclone with an inserted solid rod (d_vr) has a higher energy conversion ability because the air core was completely inhibited. Therefore, inhibiting the air core can avoid the dissipation of energy due to its unstable oscillation, significantly improving the energy conversion ability of the hydrocyclone, even though there is a slight increase in pressure drop.

3.1.2. Air Core

Figure 6 shows the spatial distribution of air volume fraction in the base hydrocyclone over time. Red represents the air phase, and blue represents the liquid phase. The hydrocyclone was initially filled with air; then, the liquid phase enters through the inlet and moves tangentially along the inner wall and gradually discharges the gas in the cavity. The air core initially formed at 0.4 s and gradually stabilized at 0.7 s. It should be pointed out that the air core is not a regular stationary cylinder but a spiral of periodic oscillation, as shown in the figure when t = 0.7–1.5 s. Obviously, the air core diameter in the overflow pipe is larger than that of the rest of the parts. In order to investigate the effect of the inserted solid rod on the air core, the shape of the air core in the steady flow field of the hydrocyclone with different inserted solid rods is shown in Figure 7.

Figure 6.

Formation process of the air core in the base hydrocyclone (t is the simulation time).

Figure 7.

Shape of air core of hydrocyclone with different types of inserted solid rod.

In Figure 7, the air core in the hydrocyclone would still form when the inserted solid rods cannot completely replace the air core. However, when the inserted solid rod parameter is d_vr, although the parameters of the variable diameter inserted solid rod do not reach the actual diameter of the air core in base hydrocyclone, the rod can inhibit the generation of the air core. In addition, the air core would appear discontinuous when d_r = 5 mm and the insertion length can reach the cylindrical section. This might be caused by the interaction between the surface of the solid rod and the surface of the air core because the air core diameter is smaller in this part. As for the influence of d_r on the air core, it can be found that as the inserted solid rod diameter increases, the air core diameter in the overflow pipe decreases.

In order to quantitively compare the effect of the inserted solid rod on the air core diameter, the change of the air core diameter along the axial line is shown in Figure 8. In general, the air core diameter increases along the axial direction and suddenly increases at the bottom of the overflow. The changing trend is consistent with that shown in Figures 6 and 7. In the conical section of the hydrocyclone (z<0 mm), the inserted solid rod can effectively reduce the air core diameter except for d_r = 5 mm. When d_r = 5 mm, the diameter might be at a critical point of inhibition, resulting in a poor inhibition effect on the air core in the conical section. In the cylindrical section (0 ≤ z<36 mm), the air core diameter of the base hydrocyclone changes dramatically. The periodic fluctuation of the air core is not conducive to the separation process. When l_o = 195 mm and l_u = 195 mm, the air core appears discontinuous due to the interaction between the boundary of the air core and the solid rod surface. This is represented by the sudden drop of the curve in Figure 8b,c. However, the air core diameter under the other structural forms of the inserted solid rod has small changes, and the air core is stable. In the overflow section (z ≥ 36 mm), the air core diameter of the base hydrocyclone is the largest, and the inserted solid rod can restrain the air core. Furthermore, when the inserted solid rod is d_vr, the air core is completely replaced, and there is no air core in the hydrocyclone. Therefore, considering that the air core diameter in the overflow is much larger than that of the other parts, the variable diameter inserted solid rod is more conducive to inhibiting the air core and maximizing the separation region. In addition, the smaller diameter of the inserted solid rod could still reduce the air core diameter though it cannot completely replace the air core.

Figure 8.

Effect of the inserted solid rod on the air core diameter in hydrocyclone: (a) diameter of the inserted solid rod, (b) overflow insertion length, and (c) underflow insertion length.

3.1.3. Axial Velocity

Figure 9 shows the effect of the inserted solid rod on the spatial distribution of axial velocity and the locus of zero vertical velocity (LZVV). The black curve in the figure is the LZVV, which is formed by connecting the points where the axial velocity is zero in the stable flow field. The LZVV divided the flow field into two parts: the internal and external flows. The axial velocity of the internal flow field is positive, and the fluid flows into the overflow outlet. The axial velocity of the external flow field is negative, and the fluid flows into the underflow outlet. It can be seen that the upward axial velocity at the bottom of the overflow pipe is greater than elsewhere. When the air core is not completely replaced, the axial velocity at the bottom of the overflow pipe increases as the diameter and length of the inserted solid rod increases. However, when the inserted solid rod is d_vr, the axial velocity at the bottom of the overflow pipe decrease obviously compared with that of the base hydrocyclone. It might be because when the air core is not completely replaced, the air flows along the solid rod, causing an increase in axial velocity. When the air core is completely replaced, the liquid is no longer accelerated by the air core, resulting in the decrease of the axial velocity. Researchers have found that the lower axial velocity at the bottom of the overflow pipe is conducive to decreasing the misplacement of coarse particles into overflow.^16,20 Therefore, the inserted solid rod (d_vr) is beneficial to improve the separation sharpness of the hydrocyclone. The finding is consistent with the improvement of the separation sharpness when the hydrocyclone with a variable diameter solid rod in Section 3.2. In terms of the LZVV, relevant studies have shown that the LZVV is related to the particle cut size and separation sharpness of the hydrocyclone, and a cylindrical LZVV in the separation region is more conducive to the separation process.^22,27 It can be seen from Figure 9 that the LZVV changes when the inserted solid rod is d_r = 5, l_o = 195/130, l_u = 195/130, and d_vr. In other words, it can be summarized as follows: the shape of the LZVV would be changed when d_r ≥ 5 mm and the solid rod reaches the separation region. Furthermore, it is obvious that the LZVV in the separation region is relatively more cylindrical and stable when the inserted solid rod is d_vr.

Figure 9.

Effect of the inserted solid rod on axial velocity and the LZVV.

3.1.4. Tangential Velocity

Tangential velocity is the velocity component with the largest relative value and the greatest influence on the separation process in hydrocyclone. The tangential velocity is directly affected by the inlet velocity. In general, the higher the inlet velocity, the higher the tangential velocity. Tangential velocity is also related to the separation of solid particles and can affect the radial motion of particles. The particles in the flow field are mainly affected by the centrifugal force (F_c), centripetal buoyancy force (F_B), and fluid medium resistance of particles (F_D). The above three forces can be expressed as follows:

10

11

12

where ρ_s is the particle density, u_t is the tangential velocity, ρ is the fluid density, ξ is the resistance coefficient, A is the projected area of the particle in the radial direction, and v is the relative velocity between the particles and fluid.

Thus, the radial settlement motion equation of spherical particles in the centrifugal force field can be obtained by Newton’s second law:

13

When the particles move at a constant velocity in the radial direction (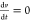), the relationship between the radial motion and tangential velocity of particles can be expressed as follows:

14

It can be seen from eq 14 that the radial velocity of particles is positively correlated with tangential velocity. The effect of the inserted solid rod on the tangential velocity is shown in Figure 10. When the air core is not completely replaced, the inserted solid rod mainly affects the tangential velocity of the flow field in the cylindrical region. Therefore, only the tangential velocity of this region is shown in Figure 10. It can be observed that the tangential velocity near the air core increases significantly after inserting the solid rod. Furthermore, the tangential velocity near the air core increases obviously when the diameter and length of the inserted solid rod increase. In particular, when the inserted solid rod is d_vr, the tangential velocity shows the periodic change. In order to quantitatively compare the influence of the inserted solid rod on the tangential velocity, the tangential velocities at z = 18 mm on the y = 0 mm plane were extracted, as shown in Figure 11. It can be seen that the tangential velocity increases gradually along the radial direction and reaches the maximum value at the surface of the air core. Meanwhile, the tangential velocity is not strictly axisymmetric because there is only one inlet. As shown in the red curve box shown in Figure 11, the tangential velocity of the base hydrocyclone is the smallest and increases gradually with the increase of the inserted solid rod diameter. When d_r = 5 mm, the tangential velocity is largest, followed by that of d_vr. In terms of the effect of the insertion length, the tangential velocity increases with the insertion length longer. Furthermore, the tangential velocity when l_u = 195 mm is larger than that when l_o = 195 mm. The result of the qualitative analysis is consistent with the conclusion of the cloud image. Therefore, the inserted solid rod can increase the tangential velocity of the separation region and change the radial distribution of particles in the hydrocyclone. Generally speaking, a higher tangential velocity is conducive to improving separation efficiency. However, it does not mean that the separation performance of the hydrocyclone can be improved by increasing tangential velocity blindly. Because excessive tangential velocity may lead to increased energy consumption of the flow field, reduced residence time of particles, severe turbulence, and deterioration of separation performance.

Figure 10.

Effect of the inserted solid rod on the spatial distribution of the tangential velocity.

Figure 11.

Comparison of tangential velocity under different inserted solid rods (z = 18 mm on the x–z plane).

3.1.5. Turbulence Intensity

The turbulence intensity, also often referred to as turbulence level, is defined as follows:

15

where u^’ is the root-mean-square of the turbulent velocity fluctuations and U is the mean velocity.

u^’ can be computed as follows:

16

U can be computed from the three mean velocity components U_x, U_y, and U_z as follows:

17

The effect of the inserted solid rod on the turbulence intensity of the flow field in the hydrocyclone is shown in Figure 12. The base hydrocyclone shows that the turbulence intensity near the air core at the bottom of the overflow pipe is larger and gradually decreases along the radial direction. When the inserted solid rod diameter is 5 mm and the insertion length is longer than 130 mm, the turbulence intensity in the flow field is relatively homogeneous. Whereas, when the inserted solid rod diameter is less than 5 mm and the insertion length is 65 mm, the turbulence intensity is larger than that of the base hydrocyclone. This might be because the inserted solid rod as a moving carrier promotes the flow of the air core, making the surrounding flow field more unstable and turbulent. In addition, it can be observed that the region of high turbulence intensity moves with the end of the inserted solid rod. Studies showed that the turbulence intensity affects the separation performance of the hydrocyclone because it directly determines the number of misplaced particles in the overflow and underflow products.³¹ Therefore, the greater turbulence intensity at the bottom of the overflow pipe may increase the chance of particles misplacement, causing coarse particles to flow into overflow. So, the larger diameter and longer length of the inserted solid rod are conducive to promoting the separation performance of the hydrocyclone. Especially, when the inserted solid rod is d_vr, the overall turbulence intensity is lower, indicating that the flow field is more stable and beneficial to the separation process.

Figure 12.

Effect of the inserted solid rod on the spatial distribution of the turbulence intensity.

3.2. Separation Performance

Separation efficiency is one of the most widely used parameters to evaluate the separation performance of the hydrocyclone. It is obtained by calculating the recovery rate of different diameter particles in the underflow. The proportion of given particles in the underflow or overflow can be calculated by analyzing the efficiency curve. The effect of the inserted solid rod on the separation efficiency of the hydrocyclone is shown in Figure 13a–c. In order to quantitatively compare the influence of inserted solid rod on the separation performance, the particle cut-size (d₅₀) and separation sharpness (H_35/65) were calculated. The particle cut size is defined as the particle diameter corresponding to 50% of the underflow recovery rate. The smaller particle cut-size means that the hydrocyclone can separate smaller particles. In Figure 13, the values of particle cut-size of each efficiency curve are marked. H_35/65 is used to characterize the separation sharpness or separation accuracy of the hydrocyclone. Separation sharpness is expressed by the sharpness index, and the calculation equation is eq 18.

18

Where d₃₅ and d₆₅ represent the particle diameter corresponding to the underflow recovery rates of 35 and 65% obtained from the efficiency curves, respectively. Ideally, the larger sharpness index is better because it means precise classification. The sharpness indexes of the different inserted solid rods are marked on the figure of efficiency curves. In order to clearly compare the effect of the inserted solid rod on the particle cut-size, Figure 13d is drawn.

Figure 13.

Effect of the inserted solid rod on the separation efficiency (a–c) and the sharpness index (d).

When the particle diameter is larger than 22.5 μm, the particles would be almost completely discharged from the underflow. Therefore, in order to clearly show the difference between the partition curves, Figure 13a–c only shows that the underflow recovery rate with the particle diameter is smaller than 22.5 μm. In Figure 13a, The base hydrocyclone has the largest particle cut-size of 8.44 μm. The particle cut-size decreases with the increase of the inserted solid rod diameter. When the inserted rod is d_vr, the particle cut-size has the smallest value of 7.52 μm, which is 10.90% lower than that of the base hydrocyclone. In Figure 13b,c, the particle cut-size decreases as the inserted solid rod length increases, but the decrease is small. In terms of the separation sharpness, research data indicate that the inserted solid rod has little effect on the separation sharpness, and the separation sharpness decreases slightly when the air core is completely inhibited. Figure 13d can intuitively compare the effect of the inserted solid rod on the particle cut-size, and it can be seen that the hydrocyclone with inserted solid rod could be used to classify the relative fine particles. When the inserted solid rod is d_vr, the air core is completely inhibited, and the hydrocyclone has the minimal particle cut-size. That is because the internal flow field of the hydrocyclone is no longer influenced by the periodically oscillating air core, the flow field is more stable, the energy conversion ability of the hydrocyclone is higher, and the misplacement of particles is effectively inhibited. Therefore, the inserted solid rod is conducive to improving the separation performance of the hydrocyclone, especially when the air core is completely inhibited.

4. Conclusions

The effects of the inserted solid rod on the separation process of the hydrocyclone are numerically studied. The pressure drop, air core form, velocity component, turbulence intensity, and separation performance are analyzed when the air core is completely replaced or not. The major findings from this work can be summarized as follows:

• (1)The inserted solid rod improves both the pressure drop and the tangential velocity, leading to the improvement of the energy utilization efficiency. In particular, the hydrocyclone with a variable diameter inserted solid rod has a higher energy utilization efficiency because the air core is completely replaced.
• (2)When d_r ≤ 5 mm, no matter what the inserted solid rod length is, it cannot inhibit the generation of the air core. However, when the inserted solid rod is d_vr, even if the inserted solid rod diameter is not bigger than the air core diameter, it can also inhibit the air core. Therefore, an appropriate inserted solid rod diameter can inhibit the air core generation without reaching the air core diameter.
• (3)The inserted solid rod greatly affects the velocity of the flow field near the air core. Especially, when the air core is not completely replaced, the larger the inserted solid rod diameter and the longer the insertion length, the more obvious the increase of tangential velocity and axial velocity. When the air core is completely replaced, the axial velocity decreases while the tangential velocity increases.
• (4)For the turbulence intensity, the inserted solid rod can reduce the turbulence of the flow field. The smaller turbulence intensity would be obtained when the inserted solid rod has a larger diameter and longer length. When the inserted solid rod is d_vr, the turbulence intensity of the flow field is smaller and more stable, which is beneficial to the separation process.
• (5)The inserted solid rod has an effect on the separation performance of the hydrocyclone, regardless of whether the air core is completely inhibited or not. The inserted solid rod can effectively reduce the particle cut-size. Especially, when the inserted solid rod is d_vr, the particle cut-size is decreased by 10.90% compared to the base hydrocyclone.

The authors declare no competing financial interest.