Abstract
In patch foraging tasks, animals must decide whether to remain with a depleting resource or to leave it in search of a potentially better source of reward. In such tasks, animals consistently follow the general predictions of optimal foraging theory (the marginal value theorem; MVT): to leave a patch when the reward rate in the current patch depletes to the average reward rate across patches. Prior studies implicate an important role for the anterior cingulate cortex (ACC) in foraging decisions based on MVT: within single trials, ACC activity increases immediately preceding foraging decisions, and across trials, these dynamics are modulated as the value of staying in the patch depletes to the average reward rate. Here, we test whether these activity patterns reflect dynamic encoding of decision-variables and whether these signals are directly involved in decision-making. We developed a leaky accumulator model based on the MVT that generates estimates of decision variables within and across trials, and tested model predictions against ACC activity recorded from male rats performing a patch foraging task. Model predicted changes in MVT decision variables closely matched rat ACC activity. Next, we pharmacologically inactivated ACC in male rats to test the contribution of these signals to decision-making. ACC inactivation had a profound effect on rats' foraging decisions and response times (RTs) yet rats still followed the MVT decision rule. These findings indicate that the ACC encodes foraging-related variables for reasons unrelated to patch-leaving decisions.
SIGNIFICANCE STATEMENT The ability to make adaptive patch-foraging decisions, to remain with a depleting resource or search for better alternatives, is critical to animal well-being. Previous studies have found that anterior cingulate cortex (ACC) activity is modulated at different points in the foraging decision process, raising questions about whether the ACC guides ongoing decisions or serves a more general purpose of regulating cognitive control. To investigate the function of the ACC in foraging, the present study developed a dynamic model of behavior and neural activity, and tested model predictions using recordings and inactivation of ACC. Findings revealed that ACC continuously signals decision variables but that these signals are more likely used to monitor and regulate ongoing processes than to guide foraging decisions.
Keywords: anterior cingulate cortex, decision-making, electrophysiology, foraging, marginal value theorem, rats
Introduction
Animals frequently encounter patch-foraging decisions; that is, decisions about whether to persist in harvesting a depleting resource within a patch, or to leave the patch, incurring a cost of time and effort, in search of a potentially better resource. The ability to make adaptive foraging decisions, choosing the appropriate time to leave a patch to maximize rewards or resources over time, is a critical skill. The mathematically optimal behavior in patch foraging tasks, described by the marginal value theorem (MVT; Charnov, 1976), is to leave a patch when the local reward rate (the reward rate offered by the current patch) depletes below the level of the global reward rate (the average reward rate across all patches visited in the environment). Although animals sometimes deviate quantitatively from the predictions of this theory (Nonacs, 2001; Wikenheiser et al., 2013; Kane et al., 2019), behavior is generally qualitatively consistent with the idea that decisions are based on maximizing overall rewards by comparing estimates of the local reward rate with estimates of the global reward rate (Hayden et al., 2011; Constantino and Daw, 2015; Hayden, 2018).
Previous research into the neural mechanisms of foraging decisions has focused on the role of the anterior cingulate cortex (ACC). The ACC exhibits foraging decision-related changes in neural activity: on average, ACC activity is greater when the current offer of reward is close to the average of alternative options in foraging tasks (e.g., when reward has depleted to the level of the global reward rate; Hayden et al., 2011; Kolling et al., 2012; Shenhav et al., 2014). Furthermore, single unit recordings in foraging tasks have revealed that ACC neurons exhibit transient increases in activity around the time of foraging decisions, and that ACC activity is modulated by task variables after decisions (Hayden et al., 2011; Blanchard and Hayden, 2014). Whether these foraging-related signals in ACC reflect a role for this region in guiding patch-leaving decisions (e.g., by encoding value signals that are used directly in the MVT value comparison process or by updating action selection policies for future trials) has been heavily debated (Rushworth et al., 2011; Ebitz and Hayden, 2016; Kolling et al., 2016; Shenhav et al., 2016a). Foraging decision-related signals observed in the ACC could be important for several functions unrelated to guiding decisions to stay in versus leave a patch, such as monitoring of task performance (Shenhav et al., 2014, 2016b; Li et al., 2019). Furthermore, foraging value signals may be particularly important for regulating response vigor (Niv et al., 2007; Yoon et al., 2018).
In the present study, we investigated whether within trial dynamics of ACC (e.g., transient increases around the time of foraging decisions) reflected continuous encoding of foraging decision variables and whether these dynamics guided foraging decisions. We developed an evidence accumulation model of foraging decision-making, similar to Davidson and El Hady (2019), to (1) compare changes in ACC activity to moment-by-moment changes in MVT-derived decision variables, such as the local reward rate, global reward rate, and choice difficulty; and (2) examine which components of the foraging decision process were affected by ACC inactivation. We report two key findings. First, changes in ACC activity within and across trials closely matched moment-by-moment changes in MVT-derived decision variables. Second, although ACC inactivation increased harvesting of rewards from patches, rats retained sensitivity to foraging-related information (i.e., rats still followed the MVT decision rule) and model-based analyses revealed that increased harvesting was associated with changes to nondecision components of the decision process (components not related to deliberation to stay in vs leave the patch).
Materials and Methods
Animals
Adult, male Long–Evans rats (Charles River; n = 22) were used. Rats were housed on a reverse 12/12 h light/dark cycle (lights off at 8 A.M.). All testing was conducted during the dark period. Throughout behavioral testing, rats were food restricted to maintain a weight of 85–90% ad libitum feeding weight and were given ad libitum access to water. All procedures were approved by the Rutgers University Institutional Animal Care and Use Committee.
Foraging task
The task was implemented using Med Associates operant conditioning chambers. Animals were trained and tested as previously described (Kane et al., 2017, 2019). Rats were first trained to lever press for 10% sucrose water on a fixed ratio (FR1) reinforcement schedule. Once exhibiting 100+ lever presses in a 1-h session, rats were trained on a sudden patch depletion paradigm: the lever stopped yielding reward after 4–12 lever presses, and rats learned to nose poke to reset the lever. Next, rats were tested on the full foraging task.
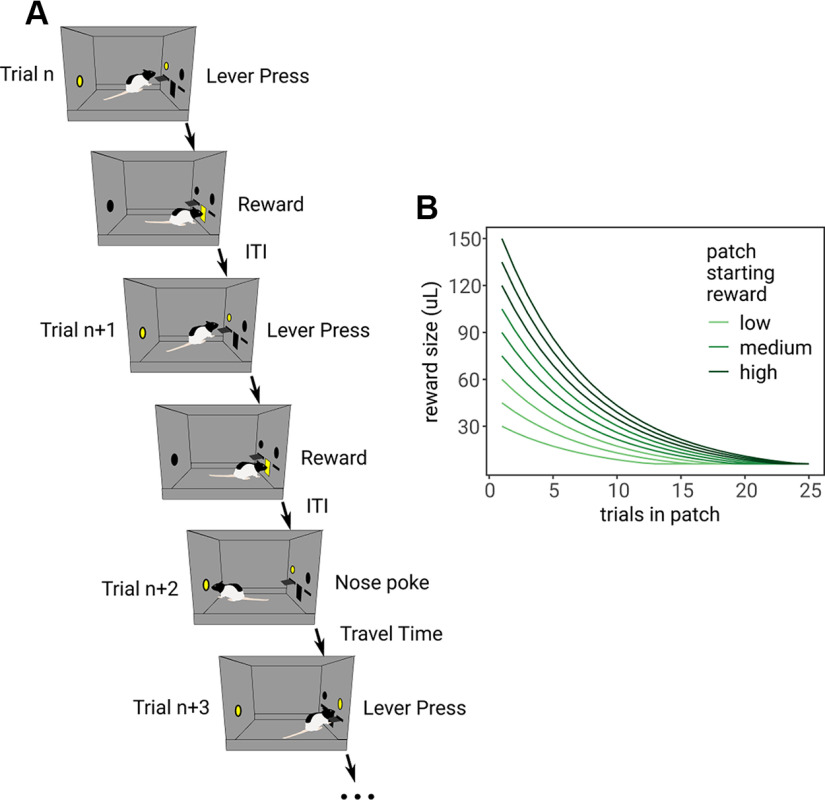
A diagram of the foraging task is shown in Figure 1A. On a series of trials, rats had to repeatedly decide to lever press to harvest reward from the patch or to nose poke to travel to a new, full patch, incurring the cost of a time delay. At the start of each trial, a cue light above the lever and inside the nose poke turned on, indicating rats could now make a decision. The time from cues turning on until rats pressed a lever or used the nose poke was recorded as the decision time (DT). A decision to harvest from the patch (lever press) yielded reward (10% sucrose water) as soon as the rat entered the reward magazine. The next trial began after a 7-s intertrial interval (ITI). With each consecutive harvest, rats received a smaller (exponentially diminished) volume of reward to simulate depletion from the patch. A nose poke to leave the patch caused the lever to retract for a delay of 10-s simulating the time to travel to a new patch. After the delay, the other lever extended, and rats could harvest from that now replenished patch. Replenished patches started with varying amounts of reward, depleting via the same exponential decay function (e.g., if the rat received 90 µl on one trial, they would receive 80 µl on the next trial regardless of the patch starting reward; Fig. 1B). Rats were trained until they exhibited stable behavior, no change in the mean number of trials spent in patches, across at least 3 d before testing sessions.
Figure 1.
Diagram of the foraging task. A, On trial n, the rat chose to press the lever to harvest from the patch, then received reward in the reward magazine in the center of the chamber. After an ITI (7 s), the rat chose to press the same lever on trial n + 1 to harvest a smaller volume of reward. On trial n + 2, the rat chose to nose poke in the back of the chamber, initiating a “travel time” delay (10 s), after which, the rat could continue to harvest in a replenished patch by pressing the lever on the other side of the chamber (trial n + 3). B, Reward depletion curves for each of the nine patch starting reward volumes. Colors indicate whether the patch was a subjective low, medium, or high reward patch, for consistency with further analyses.
Leaky competing accumulator (LCA) model
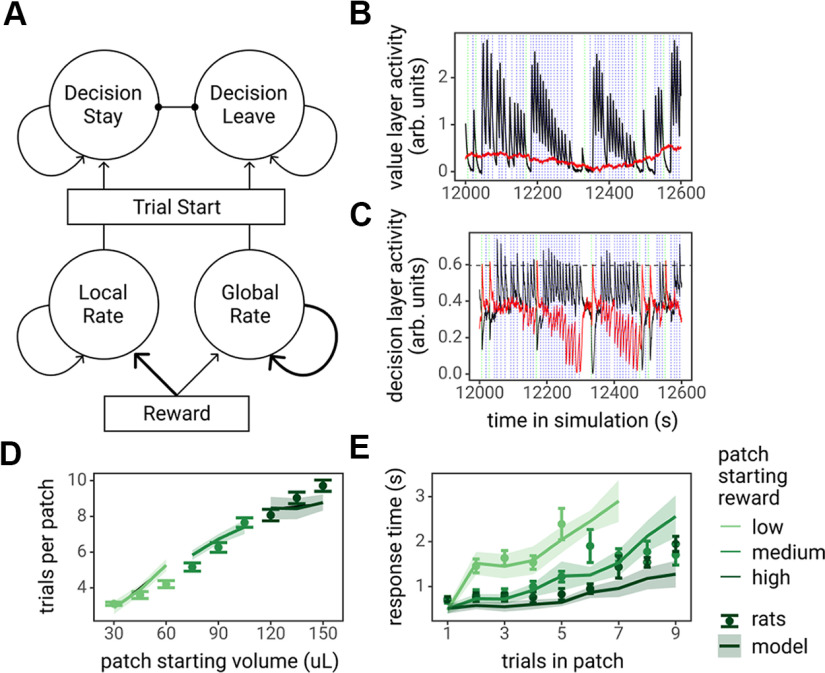
The model of the foraging task had two layers. The first layer, termed the value layer, consisted of two leaky accumulator units: one encoded the value of staying in the patch as the local reward rate and the other encoded the value of leaving the patch as the global reward rate. Importantly, these units were not in competition with one another (no mutual inhibition between them). The second layer, termed the decision layer, was a two-unit LCA layer (Usher and McClelland, 2001). The two units in this layer accumulated input from the value of staying and value of leaving units in the value layer, respectively. Additionally, there was mutual inhibition between these units. Decisions to stay versus leave the patch on each trial were made when the activity of one of the decision units crossed a predefined threshold.
The value layer estimated the local reward rate, , and the global reward rate unit, , by integrating reward input, , at different timescales: integrated rewards quickly but decayed quickly, and integrated rewards slowly but decayed slowly. The change in and over time were:
where indicates the weight between units and and . for all simulations. , , , and were all free parameters (the noise terms for both value layer units had the same variance).
The and units in the value layer units were inputs to respective units in the decision layer, and . During the decision period, between the start of the trial and the execution of the lever press or nose poke, decision layer units integrated input from the value layer. The activity of the decision units was:
where during the decision period and otherwise, is the weight between the value layer units and their respective decision layer unit (), is the weight of the recurrent connections in the decision layer (), and represents the competition between the decision units (), and . A sigmoidal activation function was used to normalize the activity of the decision units, instead of the ReLU function often used with LCA models (Usher and McClelland, 2001):
A decision to stay versus leave was made when the activity of one of the decision units, or , crossed a threshold , where . Response times (RTs) were recorded as the time from the start of a trial until threshold crossing, plus some non-DT. Rats' RTs were highly variable, with many very short (<0.1 s) responses, as well as very long responses (>5 s). To accommodate this variability, the non-DT was drawn from a long-tailed Weibull distribution, characterized by a mean and coefficient of variation . Thus, the accumulation to bound process consisted of nine free parameters: , , , , , , , , and .
Following decisions to stay in the patch, an additional delay (0.4 s) was added to the model to simulate the time it took rats to enter the reward port after a lever press. To model slow delivery of reward (sucrose water) from a syringe pump and the extra time rats spend consuming the reward, reward input was switched from an off state () to an on state () for double the duration that the syringe pump was turned on. As in the rat foraging task, the model experienced a 7-s ITI starting at the beginning of reward delivery, after which, the next trial began. Following decisions to leave the patch, the model experienced a 10-s travel time delay with no input, after which, the next trial began. The model was simulated at time steps of 0.1 s (10 steps/s).
LCA model fitting procedure
The model was fit to rats' choices and RTs. As there was no closed-form solution for the likelihood of choices and RTs given a set of parameters, we devised a method to approximate the likelihood of choices and RTs as a function of the number of trials spent in patches and the patch starting reward volume. This method is outlined below:
For a given set of parameters, simulate a session of the foraging task and record choices and RTs. For each simulation, we ran the equivalent of a 6-h simulation to generate a large sample of simulated trials. Because the global reward rate was initialized to a value of zero, the first 1 h of the simulated choices and RTs were discarded to allow the model sufficient time to “learn” the global reward rate through experience.
- Measure the likelihood of choices to stay versus leave as a function of the patch starting reward and the number of trials spent in the patch. Simulated choices were fit with a logistic regression model using the glm function in R. The probability of observed choices as a function of the simulated choices was calculated using the coefficients from this logistic regression (i.e., using the predict function):
- Measure the likelihood of RTs as a function of the choice (stay vs leave), patch starting reward, and number of trials spent in the patch. Simulated RTs were fit with a linear regression model using the lm function in R. Coefficients from this regression model were used to predict the observed (i.e., rats') RTs. The probability of an observed RT was assumed to be normally distributed, where the mean was equal to the predicted RT and the variance was the residual variance from the regression model:
- Calculate negative log likelihood of the joint likelihood of choices and RTs:
We found that this method produced a better fit to rat behavior than other approaches to fit parameters to simulated RT distributions, such as minimizing χ2 between simulated and observed RT distributions often used with diffusion models of decision-making (Ratcliff and Tuerlinckx, 2002). The maximum likelihood estimate (i.e., the parameters that minimized the negative log likelihood) was found using a genetic algorithm (the GA package in R; Scrucca, 2013).
Electrophysiology
Before behavioral training, 11 rats underwent surgery to implant electrode arrays consisting of 32, 50-µm diameter single stainless-steel wires or 8 tetrodes, each consisting of four, 25-µm diameter stainless steel wires. Wires were connected to a 32-channel Omnetics connector, serving as the interface between microwires and the headstage. First, two 0–80 machine screws were inserted into the skull over the posterior parietal cortex (approximately −4 mm AP, ±3 mm ML from bregma). A ground wire (125 µm stainless steel with insulation removed from 3 mm of the tip of the wire) was fixed to one of the skull screws. Next, a 4 × 2 mm craniometry was made above the anterior cingulate (Cg1), from +4 to 0 mm anterior-posterior from bregma and 0 to ±2 mm medial-lateral from bregma. Arrays (∼2 × 1 mm) were centered at approximately +2 mm anterior-posterior and positioned such that the most medial wires were just lateral to the sagittal sinus (centered at ∼0.6 mm ML), then lowered slowly (0.1 mm/min) down to 1.25 mm below brain surface. Once arrays were in their final position, craniotomies were filled with kwik-cast (WPI; https://www.wpiinc.com/kwik-cast-kwik-cast-sealant), then arrays were cemented to the skull using metabond (Parkell; http://www.parkell.com/c-b-metabond_3). Additional Jet Denture Repair Acrylic (Lang; https://www.langdental.com/products-Jet-Denture-Repair-Package-44) was applied over the entire surface of exposed skull and over the metabond to provide further stability to the headcap, to secure the 32-channel Omnetics connector to the skull, and this dental acrylic was shaped to provide a protective barrier in front of the microwire array and connector. After the dental cement dried, sutures were placed at the front and back of the incision as needed, and rats were returned to their home cage to recover. Rats were given meloxicam (1 mg/kg, s.c.) at the start of the surgery for analgesia and again once every 24 h for 3 d after surgery. Rats were left to recover for one week before beginning testing.
After recovery, rats were trained 5 d/week for three to six weeks on the foraging task before recordings. One recording session was taken per rat. Before the recording session, a 32-channel digitizing headstage (Plexon) was plugged into the Omnetics connector on the rats' head. From the headstage, signals were passed via a flexible cable, through a commutator, then to a Plexon Omniplex recording system. Wideband signals were sampled at 40,000 Hz. Further processing was performed in Plexon Offline Sorter software. The wideband signal for each channel was first bandpass filtered between 600 and 6000 Hz, and spikes were detected using a threshold of five times the median absolute deviation of the signal. Spike waveforms, from 1 ms before threshold crossing to 2 ms after threshold crossing, were extracted and clusters were manually identified using a combination of principal components (PCs), waveform energy, and waveform amplitude. Only clusters that exhibited consistent firing throughout the entire session were included for analysis. Clusters were characterized as single units if <2% of spikes within the cluster exhibited an interspike interval of <2 ms, and the cluster had an L-ratio (Schmitzer-Torbert et al., 2005) of <0.1. All other clusters were characterized as multi-units. Altogether, this resulted in a total of 42 single-units and 106 multi-units. All units were combined for all further analyses unless otherwise noted.
After the completion of recordings, small electrolytic lesions were made by passing current (25 µA for 15 s) through wires at the front and back of the array. Twenty-four hours later, rats were perfused with 4% paraformaldehyde (PFA) and their brains were extracted. Brains were postfixed in 4% PFA for 24 h, then cryoprotected in 30% sucrose in phosphate buffered saline for 72 h. Finally, brains were flash frozen and sectioned into 40-µm sections on a cryostat. Electrode locations were confirmed by locating lesions.
Pharmacological inactivation of ACC
Before behavioral training,11 rats underwent surgery to implant a bilateral cannula targeting the ACC (Cg1). Similar to electrode array implant surgeries, two 0–80 machine screws were inserted into the skull above the posterior parietal cortex. Next, a large craniotomy was drilled, spanning the ACC bilaterally (from approximately −1 to +1 mm ML and +1 to +3 mm AP from bregma). The bilateral cannula (PlasticsOne) was positioned to target Cg1 at ±0.5 ML and +2 mm AP from bregma. The cannula was lowered slowly (0.1 mm/min) to a depth of 0.75 mm below the brain surface. The implant was secured to the skull using metabond, and the Jet Denture acrylic was used to further secure the implant to the skull and skull screws, and it was shaped to create a protective barrier in front of the cannula. Following completion of the surgery, sutures were applied as needed to secure the front and back of the incision and was then placed in its home cage to recover. Rats followed the same analgesia protocol and postoperative recovery as with electrode array implants.
After full recovery, rats were trained 5 d/week for four weeks on the foraging task before testing. On test days, 15 min before the start of the session, rats underwent a microinjection of either a cocktail of the GABA agonists baclofen and muscimol (Bac-Mus; 1 and 0.1 mm, respectively; 0.5 µl/side), or artificial CSF (aCSF; 0.5 µl/side) as a control. A bilateral injector (33 G, PlasticsOne) that protruded 0.5 mm below the bottom of the cannula (to a depth of 1.25 mm) was inserted through the cannula, and Bac-Mus or aCSF was injected at a rate of 100 nl/min. The injector was left in place for 2 min after completion of the injection to allow the drug cocktail to diffuse into the tissue and to avoid backflow of the drug cocktail up the cannula track. The injector was then removed, and rats were placed in the operant chamber awaiting testing. The day before the first injection, rats underwent one sham injection to acclimate to the procedure. Rats were tested with Bac-Mus and aCSF for one session with each drug, counterbalanced (four rats received aCSF followed by Bac-Mus, four vice versa). Rats were given one recovery day, in which they were tested without an injection, between the two testing sessions.
Experimental design and statistical analysis
Rat foraging behavior
All statistical analyses and computational modeling were conducted in R (R Core Team, 2020). Mixed effects (ME) models were fit using the lme4 package (Bates et al., 2015), and significance tests for linear ME models were performed using the lmerTest package (Kuznetsova et al., 2017). Unless otherwise specified, all continuous predictors in ME models were z-scored.
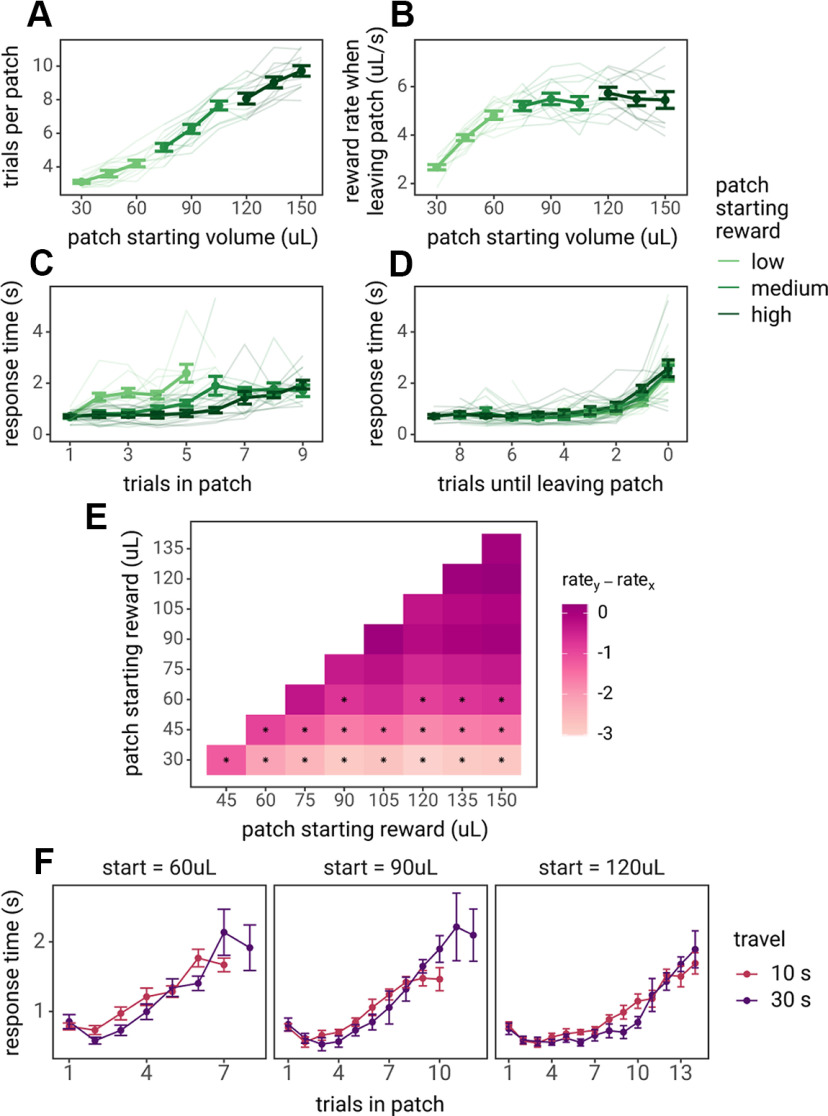
To investigate the behavioral performance of rats that participated in the ACC recording experiment, we analyzed rats' foraging decisions (the number of trials spent in each patch) and RTs (the time from the start of the trial until the lever press or nose poke) during the final three training sessions before the recording session. Examination of their training data allowed us to pool behavior across multiple sessions. In this experiment, two main hypotheses were tested: (1) that rats would spend more trials in patches that offered greater rewards (a standard prediction of the MVT); and (2) as patches depleted, RTs to decide to stay versus leave would increase (reflecting greater decision difficulty). The first hypothesis was tested using a linear ME model of the number of trials spent in each patch, with a fixed effect of the starting reward volume of the patch and random intercept for each rat (lme4 syntax: ). To test whether rats adopted the same reward rate leaving threshold across patches, a ME model of the reward rate at the time rats left patches, with a fixed effect of the patch starting volume and random intercept for each rat. In this model, to directly compare the leaving threshold at each of the nine patch starting reward volumes, patch starting reward was treated as a categorical variable (dummy coded) and we conducted pairwise comparisons of the reward rate when rats left the patch across all patch starting reward volumes.
The second hypothesis, that RTs would increase as patches depleted, was initially tested using a linear ME model of the log of RTs with fixed effects of the patch starting reward volume, the number of trials spent in the patch, and the starting reward × trials in patch interaction, and a random intercept for each rat (). The log of RTs was used as the raw RTs were positively skewed. However, if rats exhibit longer RTs as patches deplete, then it is likely that they will exhibit longer RTs, on average, in patches that start with smaller rewards because a greater proportion of trials spent in these patches will be at lower reward volumes. To better examine whether there were differences in RTs across patches, another linear ME model was used to examine the effect of the number of trials remaining in the patch and patch starting reward on the log of RTs (). An exponential function of was used, as it proved to be a better fit to data than a linear function (Fig. 2D). In this model, if the RTs around the trial at which rats chose to leave the patch were similar across different patch types, there would be no main effect of .
Figure 2.
Rat behavior in the patch foraging task. In all panels, points, dark lines, and error bars represent the mean and SE across rats, and lighter lines represent behavior of each individual rat. A, The number of trials spent in each patch as a function of the starting reward volume of the patch. B, The reward rate (reward volume/trial time) rats received on the trial before rats chose to nose poke to leave the patch. C, The median RTs for each rat over the course of trials in the patch, split by patches that started with low (30–60 μl), medium (75–105 μl), or high (120–150 μl) starting reward volumes. D, The median RTs for each rat as rats became closer to leaving patches; 0 trials remaining in the patch indicated the trial in which they nose poked to leave the patch, 1 trial remaining is the last lever press to stay in the patch, 2 is the second to last lever press before leaving the patch, etc. E, Pairwise t tests across the patch leaving threshold (the local reward rate when rats decided to leave the patch), for all patch types. Colors indicate the difference in the reward rate threshold at which rats decided to leave the patches (i.e., y-axis leaving threshold – x-axis leaving threshold). Asterisks indicate statistically significant comparisons (pairwise χ2 tests with Holm–Bonferroni correction). F, Median RTs of rats from the travel time experiment by Kane et al. (2019). Rats visited patches that started with 60, 90, or 120 μl within sessions and experienced travel time delays of 10 or 30 s in separate sessions.
As it was not possible to test the hypothesis that RTs are influenced by foraging decision variables and not only tied to the magnitude of reward in the novel experiments conducted here, we tested this hypothesis by conducting new analyses on data initially reported in Kane et al. (2019). In this experiment, rats were tested in the same foraging task described above, but in two conditions: a 10- and a 30-s travel time delay between patches. A ME model was used to test the effect of the starting reward in the patch, the number of trials in the patch, and travel time on the log of RTs (). Trials in the patch and travel time were treated as random effects, including any additional random effects led to a singular fit of the model and did not alter any of the reported statistical effects. As reward magnitude is entirely dependent on the patch starting reward and the number of trials in the patch, a significant effect of travel time on RTs would indicate that RTs are not entirely tied to the reward magnitude, but are influenced by foraging decision variables (e.g., the change in the global reward rate which is caused by a change in the travel time).
Leaky accumulator model predictions
To examine whether the LCA model with 13 parameters overfit behavioral data, that parameters were optimized to capture noise in the data and, thus, would not generalize to new data, cross validation analysis was performed. Behavioral data for each rat was separated into three “splits.” The LCA model was fit to data in which one of the splits was omitted, and the likelihood of the model on the left-out data was calculated. This process was repeated such that each split served as the left-out data. The sum of the likelihoods on the three left-out splits was compared with the likelihood of the model fit to all the data from each rat using a paired t test.
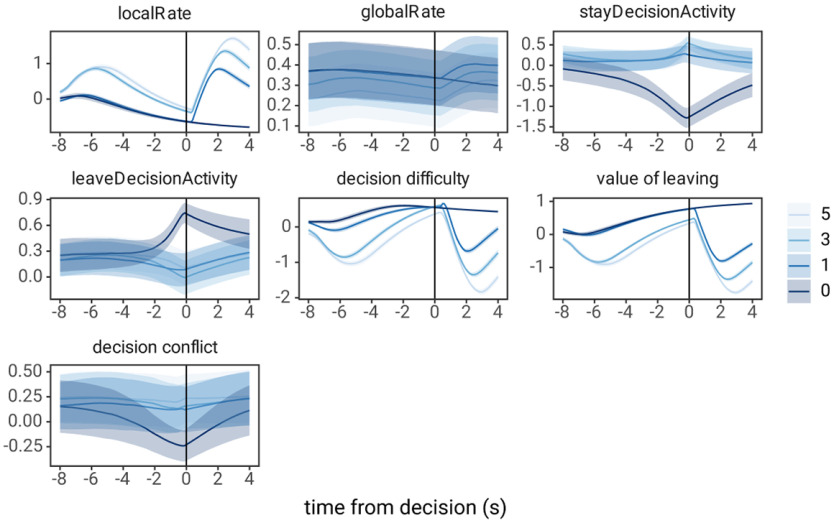
Simulated behavioral data and the time course of activity of each of the LCA units were obtained via simulations as described above. To generate peri-event time histograms (PETHs) of LCA unit activity around the time of decisions, first, the time of decisions was obtained from the simulated behavioral data and the activity of each LCA unit was extracted for eight simulated seconds (80 time steps) before the decision and 4 s (40 time steps) after. PETHs were created for three additional foraging decision variables, the relative value of leaving the patch, decision difficulty, and decision conflict. The relative value of leaving the patch was the moment-by-moment difference between the local and global reward rate units: ; decision difficulty or the similarity in the value of staying versus leaving was defined as: ; and decision conflict was the product of the activity of the decision units: ; decision difficulty or the similarity in the value of staying versus leaving was defined as: ; and decision conflict was the product of the activity of the decision units: . Each of these variables were first normalized (z-scored), then PETHs were created the same as for the four LCA model units.
Analysis of ACC activity
First, generalized linear models (GLMs) were used to examine whether ACC neurons were responsive in specific trial epochs and whether such responses varied between patches on the right versus the left lever. Spike counts for each unit were calculated in 100-ms nonoverlapping bins through the entire session. Spike counts were regressed using GLMs with a quasi-Poisson link function (Poisson regression with overdispersion parameter) against three trial events: the start of the trial (when cue lights turn on), the decision, and reward delivery (. Fifteen regressors were used for each trial event (15 time bins spanning 0.5 s before the event and 1 s after the event). As these events were sometimes overlapping, to distinguish responses to a particular event, four total models were fit: a model containing all regressors (15 regressors/event × three events = 45 regressors), and three additional models in which one of the events had been removed. If, for example, a unit was responsive to decision events, removing the decision event regressors would lead to a significantly worse model fit. Units were considered responsive to an event if the full model produced a significantly better fit than the model that omitted regressors for a particular event, as determined by the likelihood ratio between the models. P-values were determined using a permutation test: the null distribution of likelihood ratios was determined by conducting this analysis on shuffled data (using randomly generated event times), and p-values were corrected for multiple comparisons (across 148 units) using Holm–Bonferroni correction.
To test whether ACC neurons exhibited side-selective responses to these task epochs, a similar GLM approach was used. In addition to event-specific regressors, interaction terms between events and left versus right side were included (SpikeCounts ∼ startEpoch + decisionEvent + rewardEvent + startEvent : PatchSide + decisionEvent PatchSide + rewardEvent:PatchSide). Again, four total models were fit: the full model and three additional models in which one of the interaction terms was omitted. A unit was considered responsive to a trial event in a side-selective manner if the full model provided a better fit than a model omitting only one of the event × side interaction terms as determined by the likelihood ratio test. P-values were calculated using the same permutation test procedure described above.
To analyze the correlation between average ACC activity and foraging decisions and RTs, first, the firing rate of each unit was calculated for each trial. A linear ME model was used to test the effect of trials until leaving, the number of trials the rat spent in the patch before choosing to leave (e.g., trials until leaving = 0 is the trial in which the rat chose to leave and trials until leaving = 1 is the last decision to stay before choosing to leave on the next trial), and starting patch reward, with random effects for all parameters for each unit:
A second linear ME model was used to test the effect of the log of RTs, with random intercepts and slopes for each unit:
To examine (1) at what point in the decision process ACC activity was influenced by foraging decisions and RTs and (2) which units encoded these two variables over the course of the entire trial, PETHs were created for each unit, from 8 s before the lever press to stay in the patch to 4 s after the lever press, in time bins of 0.1 s (120 total time points). Next, three GLMs with a quasi-Poisson link function (Poisson regression with an overdispersion parameter) were fit to the spike counts in each bin of the PETH for each unit. The first model included an intercept, effect of trials until leaving, and effect of the log of RTs for each time point (a total of 360 parameters). Coefficients of the effect of trials until leaving and effect of log of RTs were used to determine the strength of encoding of these variables at that specific point within the trial. To determine whether these variables significantly contributed to the variance in each unit's activity, separate GLMs that excluded either the effect of trials until leaving or the effect of log of RTs were fit to each unit, and likelihood ratio tests were conducted between the full model and the models excluding one of these variables. If the full model provided a better fit to a specific unit's PETH, assessed via likelihood ratio test against a model with one predictor removed, that would indicate significant encoding of the variable excluded from the reduced model. Based on this analysis, units were characterized as encoding the number of trials until leaving, the log of RTs, or both.
Finally, the dynamics of ACC activity within trials and the modulation of these dynamics were compared with moment-by-moment changes in decision variables derived from the LCA model. Cross-correlations between PETHs of LCA model activity and PETHs of neural activity were computed, with a maximum time lag of ±1 s in 0.1-s shifts. To test for statistical significance, correlation coefficients were compared with “shuffled” neural activity data. Shuffled PETHs were created using random event times instead the time of the decision, this method was chosen to preserve any autocorrelation present in neural activity. Cross-correlations were conducted on 10,000 shuffled PETHs. For each cross-correlation, only the strongest correlation coefficient was used (i.e., using the lag that exhibited the greatest correlation coefficient). P-values were calculated as the probability that the correlation coefficient from real neural data is greater than the correlation coefficient using shuffled data.
First, LCA derived variables were compared with an average PETH, constructed by taking the PETH for each unit described above, normalizing the activity of each unit, taking the z-score of activity across all bins for that unit, and taking the average normalized activity within each bin across units. Next, to examine the diversity in encoding across units, two approaches were taken. (1) The average, normalized PETH was calculated for each unit on a subset of trials leading up to the decision to leave the patch (5, 3, 1, or 0 trials until leaving the patch). For each unit, these four PETHs were concatenated into a vector with 480 features (120 timepoints for each of the four PETHs), and PC analysis (PCA) was performed on these 480 features across all 148 units to extract the dimensions that capture the most variance across all units at each time point for each of these four trials until leaving the patch. PCs, representing the dimensions which captured the most variance across units on these trials, were compared with LCA model units. (2) LCA derived variables were directly compared with PETHs of each individual unit. For the PCA and individual unit correlations, p-values were further corrected for multiple comparisons (148 PCs or units).
Pharmacological inactivation of ACC
Foraging behavior in the inactivation experiment was analyzed in a similar manner as described above. Linear ME models were used to test the effect of ACC inactivation (aCSF injection vs Bac-Mus injection) on the number of trials spent in the patch (lme4 syntax: TrialsInPatch ∼ PatchStartingReward * Inactivation + (PatchStartingReward * Inactivation|Rat)) and RTs (lme4 syntax: logRT ∼ exp(TrialsUnitLeaving) * PatchStartingReward * Inactivation + (exp(TrialsUnitLeaving) * PatchStartingReward * Inactivation|Rat)). An additional ME model was used to test the relative value of leaving the patch (the difference in the global and local reward rate) at the time that rats chose to leave the patch, termed the . This analysis was designed to measure whether ACC inactivation caused rats to overharvest to a greater degree than observed in control sessions. was calculated as follows:
The value of leaving across the three patch types was tested as a function of the patch starting reward and drug treatment (ACC inactivation vs control; lme4 syntax: valueAtLeaving ∼ PatchStartingReward * Treatment + (PatchStartingReward * Treatment|Rat)).
To further examine the effect of ACC inactivation on foraging behavior, the optimal number of trials in each patch, according to MVT, was calculated for each rat in control and inactivation sessions. The relative value of leaving (, as described above) was calculated for all trials. For each rat, we found the average relative value of leaving across trials in the patch for each patch starting reward that rats encountered. The optimal time to leave the patch was the first trial in which the average relative value of leaving for that trial was >0.
Finally, the LCA model was fit to each drug treatment as described above. Paired t tests were run on each of the 13 parameters, and Holm–Bonferroni-corrected p-values (Holm, 1979) are reported.
Results
Rats spend more time in patches that offer greater rewards
Rats (n = 11) were trained to perform a patch foraging task in which they randomly encountered patches with starting rewards that ranged from 30 to 150 µl (Fig. 1B). This wide range in reward offered by different patches tested whether rats followed a central prediction of MVT: when offered greater levels of reward, rats should harvest for more trials until these patches deplete to the leaving threshold (the global reward rate or average reward rate across all patches). To test this prediction, rat behavior during their final three training sessions was analyzed. Rats participated in 553–1162 trials, visiting 99–202 patches each. As in a previous study (Kane et al., 2017), rats harvested for more trials in patches that started with greater rewards (main effect of patch starting reward: β = 2.294, SE = 0.079, F(1,11.332) = 837.14, p < 0.001; Fig. 2A). Among patches that started with greater rewards (75–150 µl), there was no difference in the reward rate at which rats chose to leave patches. However, rats left patches that started with smaller rewards (30–60 µl) at a lower reward rate than patches that started with greater rewards (Fig. 2B; pairwise χ2 tests presented in Fig. 2E). As predicted by MVT, rats adopted a constant reward rate threshold at which to leave patches when in patches that yielded larger rewards, but contrary to MVT, they exhibited a bias to harvest reward beyond this threshold in patches that yielded smaller amounts of reward.
Rats' RTs increase as patches deplete
As the reward rate within the patch depleted to the level of the global reward rate across patches, rats may have experienced increased difficulty to decide to stay versus leave, which would be reflected in increased RTs. As rats spent more time in patches, their RTs increased (main effect of trials in patch: β = 0.512, SE = 0.056, F(1,9.791) = 85.203, p < 0.001; Fig. 2C). Furthermore, their RTs were, on average, greater in lower rewarding patches (β = −0.398, SE = 0.046, F(1,9.830) = 75.67, p < 0.001). Slower average RTs in lower starting reward patches is likely because of a greater proportion of trials spent with lower reward volumes, as lower starting reward patches start out in a depleted state, there are few to no trials in which rats should exhibit faster RTs to stay in the patch. To test this hypothesis, RTs were also analyzed as a function of the number of trials remaining in the patch. If rats experienced reduced decision difficulty in patches that started with smaller rewards, then RTs should have been faster as rats approached the point to leave these patches. Across all patch types, rats' RTs increased as they approached the point at which they left patches (main effect of trials remaining in the patch: β = 0.555, SE = 0.058, F(1,10.751) = 92.662, p < 0.001; Fig. 2D), but there was no difference in the average RTs (main effect of patch starting reward: β = 0.691, SE = 0.118, F(1,9.963) = 0.002, p = 0.968) or in the rate at which RTs increased among different patch types (trials remaining × patch starting reward interaction: β = 0.010, SE = 0.018, F(1,9.663) = 0.290, p = 0.602; Fig. 2D). Despite leaving smaller starting reward patches at a lower threshold than higher starting reward patches, rats exhibited similar RTs in these patches as they became closer to leaving, suggesting that they experienced the same decision difficulty when deciding to leave patches that started with greater rewards. Alternatively, this increase in RT as patches depleted could be interpreted as an increased need to override the default response of staying in the patch to choose to leave or a reduction in motivation or response vigor in anticipation of smaller rewards.
To test whether reduction in response vigor in anticipation of smaller rewards can fully explain rats' increase in RTs as patches deplete, additional analysis were conducted on rat foraging task data previously reported (Kane et al., 2019). In this experiment, rats visited three patch types that started with 60, 90, or 120 µl of reward. In separate sessions, rats experienced either a 10- or 30-s travel time delay between patches. If rats' RTs are tied to reward magnitudes and not influenced by decision difficulty or increased need for cognitive control, then there should be no effect of the travel time on RTs. If rats' RT increase as patches deplete because of increasing decision difficulty, then longer travel times should result in faster RTs earlier in the patch. Consistent with the hypothesis that rats increase in RTs is driven by decision difficulty, RTs were faster when the travel time was longer, given the same reward magnitude (main effect of travel time: β = 0.364, SE = 0.154, F(1,664) = 5.589, p = 0.018; Fig. 2F).
An LCA model of rat foraging behavior
Evidence accumulation models have proven successful in describing not only perceptual decisions requiring moment-to-moment sampling of sensory information, but also value-based decisions (Polanía et al., 2014; Tajima et al., 2016; Pisauro et al., 2017; Frömer et al., 2019; Lin et al., 2020; Peters and D'Esposito, 2020; Callaway et al., 2021). Recent theoretical work has applied the evidence accumulation framework to foraging decisions (Davidson and El Hady, 2019). To describe rats' foraging decisions as a function of their moment-by-moment estimate of the local versus global reward rates, we developed an evidence accumulation model that implemented the MVT decision rule, to leave a patch when the local reward rate in the current patch depletes to the level of the global reward rate, using leaky accumulators. The model consisted of two layers, the value and decision layer. The value layer units estimated the local and global reward rate by integrating rewards at different timescales: the local reward rate unit integrated rewards quickly but decayed quickly, whereas the global reward rate unit integrated rewards slowly but decayed slowly. These units were not in competition with one another, there was no reciprocal inhibition between them. The decision layer was an LCA (Usher and McClelland, 2001) that implemented an accumulation to bound process. At the start of the trial, decision layer units integrated the activity of the value layer units until one of the decision units crossed a threshold, at which point, the model chose the corresponding option (Fig. 3A). A demonstration of the activity of the value layer and decision layer units during a simulation is shown in Figure 3B,C. The model was fit to rats' choices and RTs (see Materials and Methods for details, fit parameter estimates in Table 1). This LCA model, fit to rat behavioral data, captured important features of rats' behavior: the model predicted spending more trials in patches that yielded larger rewards and predicted longer RTs as patches depleted, with longer RTs for patches that started with smaller rewards (Fig. 3D,E).
Figure 3.
The leaky accumulator model of the foraging task. A, Diagram of the model, consisting of two layers of leaky accumulators. The bottom layer, the value layer (“local rate” and “global rate” units), estimated the local reward rate and global reward rate by integrating over rewards on different timescales. The top layer, the decision layer, was an LCA model that made decisions to stay versus leave via an accumulation to bound process at the start of the trial, with input from the local and global rate units. B, C, Example activity of the value layer and decision layer units during a 600-s sample of a model simulation. The solid black lines represent the local reward rate and decision stay unit activity, and the solid red lines represent the global reward rate and decision leave unit activity. The dotted blue and green vertical lines indicate the start of a trial in which the model decided to stay in the patch or to leave the patch, respectively. The horizontal dashed line in C represents the decision threshold. D, E, The leaky accumulator model-predicted number of trials spent in each patch type (D) and predicted RTs as by the number of trials spent in patches (E) plotted against observed rat behavior. Points and error bars represent the mean ± SE across rats, lines and ribbon represents the mean ± SE of model-predicted behavior for each rat.
Table 1.
Parameter estimates for LCA fits to animal behavior during recording sessions
| Parameter | 1st quartile | Median | 3rd quartile |
|---|---|---|---|
| 0.008 | 0.01 | 0.012 | |
| 0.753 | 0.766 | 0.775 | |
| 0.994 | 0.995 | 0.996 | |
| 0.025 | 0.026 | 0.029 | |
| 1.181 | 1.443 | 1.913 | |
| 0.675 | 0.707 | 0.743 | |
| −1.497 | −1.147 | −0.814 | |
| 0.023 | 0.026 | 0.03 | |
| 0.61 | 0.648 | 0.665 | |
| 4.997 | 5.15 | 5.274 | |
| −0.1 | −0.05 | 0.048 | |
| 2.44 | 2.895 | 3.225 | |
| 1.635 | 1.777 | 1.999 |
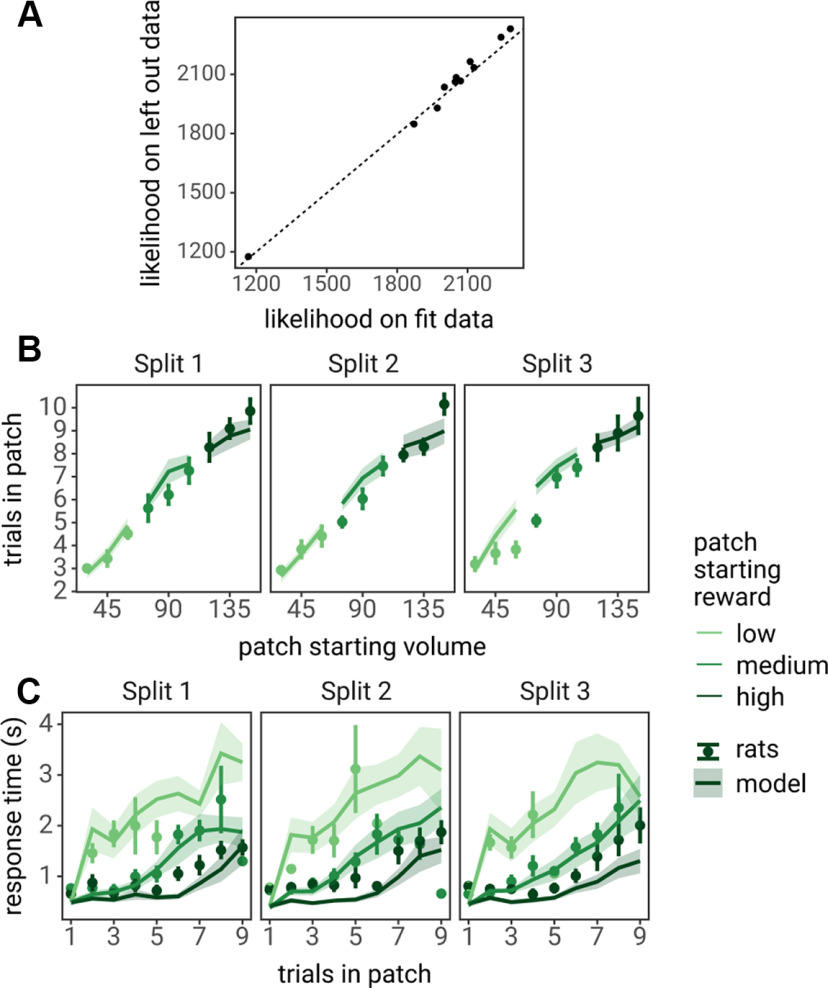
To ensure that this model would accurately predict foraging behavior, that it was not overfit or overly flexible as to explain noise in the dataset used to estimate model parameters, a cross-validation analysis was performed. Rat behavioral data were separated into three “splits.” The LCA model was fit to behavioral data in which one of the splits was omitted and the likelihood of the model was calculated on the left-out split. This process was repeated such that each split served as the omitted data. The likelihood of the model on the omitted splits was not significantly different from the likelihood of the model when fit to all behavioral data (t(10) = 1.790, p = 0.104; Fig. 4).
Figure 4.
Cross-validation analysis of the LCA model. A, The likelihood of the LCA model fit to all data (x-axis) compared with the likelihood of the model on left-out samples (parameters fit to two thirds of the data, likelihood calculated on the left-out third; y-axis). Each point represents individual rats; the dashed line represents the identity line (y = x). B, C, LCA predicted behavior (lines and ribbon) plotted against the left-out splits (points and error bars). Number of trials spent in patches is shown in B and RTs as a function of the number of trials spent in patches is shown in C. Points and lines indicate the mean across rats, error bars and ribbon indicate the SEM across rats.
The LCA model was then used to generate predictions regarding ACC activity in the foraging task. As the model estimates important MVT decision variables, the local and global reward rates, on a moment-by-moment basis, the activity of LCA model units was used to calculate specific decision variables that the ACC has been hypothesized to encode. Three particular hypotheses were tested: (1) ACC encodes the relative value of leaving a patch as the difference between the global reward rate and local reward rate (Kolling et al., 2012); (2) ACC encodes decision difficulty, quantified as the similarity in the value of staying and the value of leaving a patch (Shenhav et al., 2014); and (3) ACC encodes the conflict between choosing to stay versus choosing to leave a patch, defined as the product of the decision units (Botvinick et al., 2001). The relative value of leaving the patch and decision difficulty hypotheses are equivalent while the rat is in the patch; however, they differ during the travel time. PETHs of the activity of each model unit, as well as the relative value of leaving the patch, decision difficulty, and decision conflict, were created from simulation data by averaging the value of these variables over trials, locked to the time of the decision (time of execution of the lever press or nose poke in the simulation; Fig. 5). These PETHs were later compared with recorded ACC activity.
Figure 5.
PETHs of LCA model unit activity in the foraging task. Each panel represents the PETH of activity of LCA model units (localRate, globalRate, stayDecisionActivity, leaveDecisionActivity) or hypotheses for ACC activity measured from LCA model units (decision difficulty, value of leaving, and decision conflict) during a simulation of the foraging task. For each PETH, time = 0 represents the time of the lever press to harvest reward or nose poke to leave the patch, and colors represent the number of trials until leaving the patch.
ACC activity correlates with foraging decisions and RTs
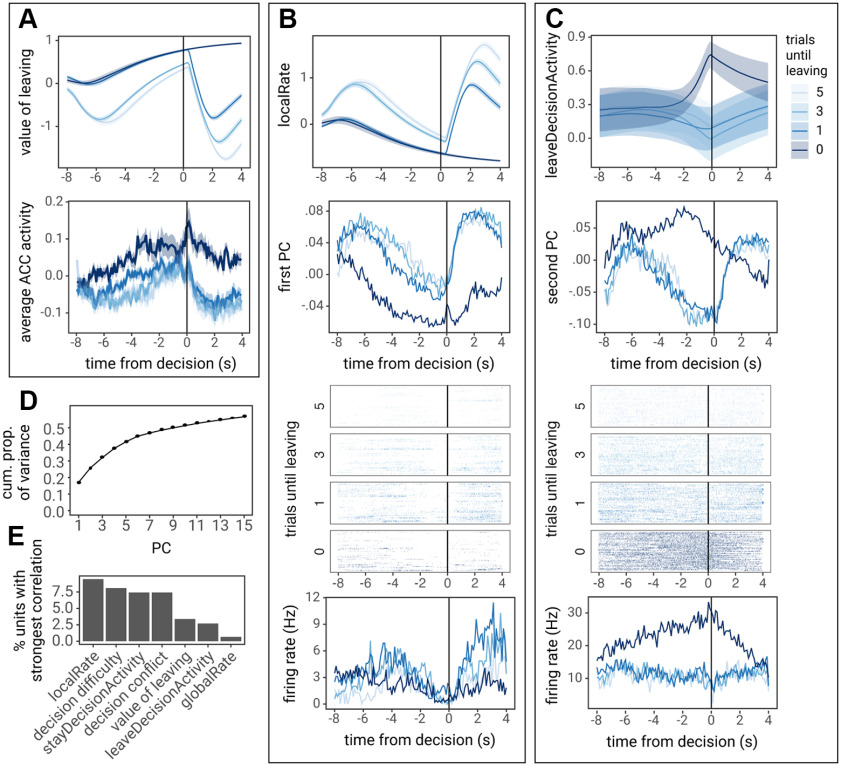
First, we examined whether ACC neurons (n = 148; Fig. 6A; Extended Data Fig. 6-1) were responsive to different task events: cue lights turning on at the start of the trial, execution of decisions (lever press or nose poke) and reward delivery. ACC activity was regressed against the time period surrounding each trial event (0.5 s before to 1 s after). A large proportion of units were responsive to trial events (41% to trial start, 52% to decisions, and 68% to rewards). We also tested whether ACC responses were side-selective, whether ACC neurons responded differently to events in patches on the right lever versus the left lever; 10% of units exhibited significantly different responses around the time of decisions based on the side, but only 3% of units exhibited side selectivity to rewards (which were always delivered in the center of the box) and <1% exhibited side selectivity to cue lights turning on (example units in Fig. 6D). Responsivity of ACC neurons in these different epochs, as well as side selectivity in responses of a subset of ACC neurons is consistent with prior investigations (Strait et al., 2016).
Figure 6.
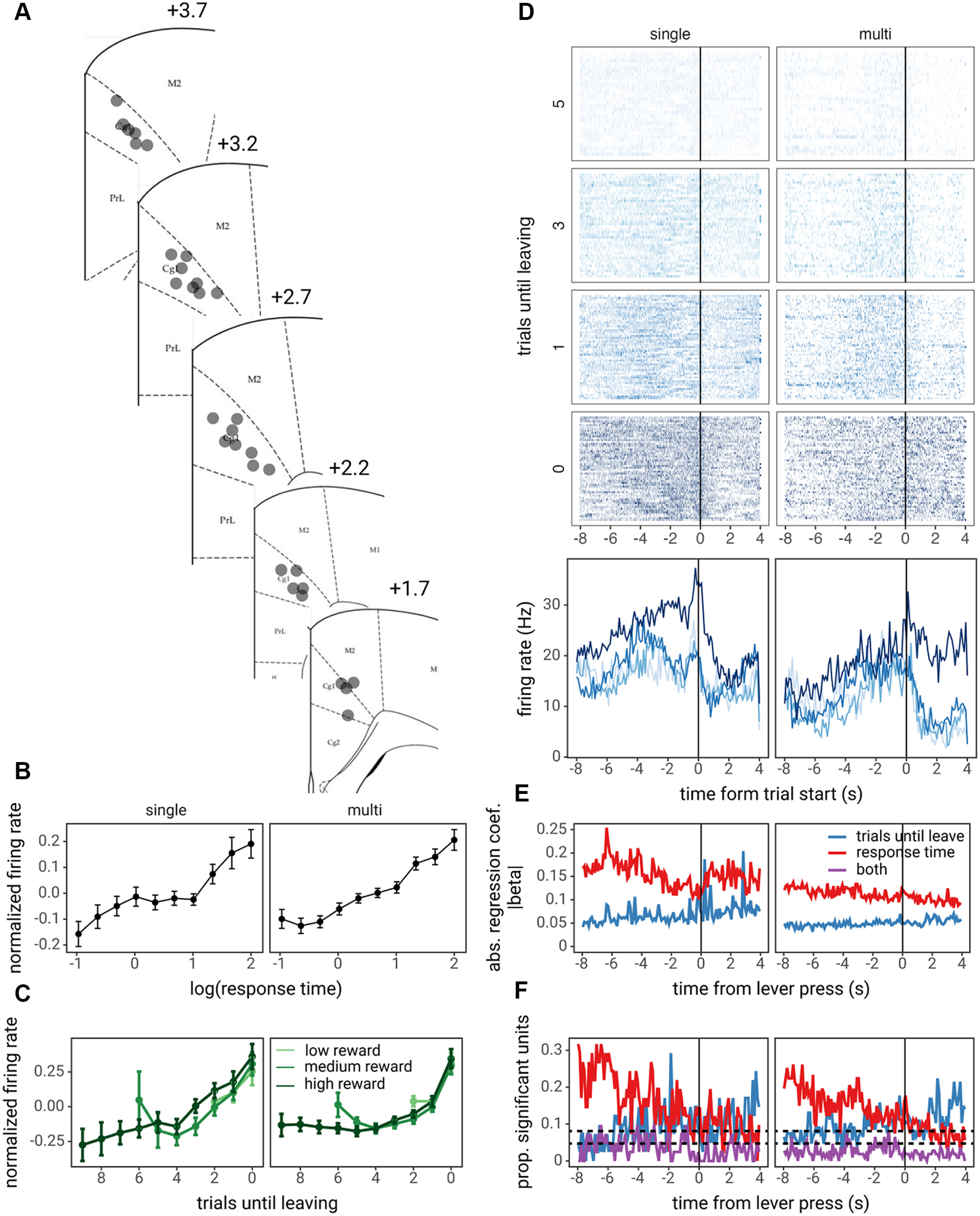
ACC activity correlates with foraging decisions and RTs. A, Diagram of recording locations within the Cg1 region; labels indicate distance from bregma. Example unit traces and isolation are shown in Extended Data Figure 6-1. B, C, Average ACC activity over the course of entire trials, normalized and averaged across units, as a function of the log of RTs (B) and trials until leaving the patch and the patch starting reward (C). Points and lines represent the mean normalized (z-scored) activity across units and error bars represent the SE across units. D, Trial-by-trial raster plot (top) and trial-averaged PETH (bottom) locked to the time of decisions for one example single unit and one example multi-unit. E, The average absolute effect of trials until leaving and RTs at each time point within a trial, locked to the time of the lever press to stay in the patch. F, The proportion of units with significant effects of trials until leaving, RTs or both (p < 0.05, z-test on regression coefficient), at each time point within the trial. The horizontal dashed lines represent the median and 95% confidence interval of the expected proportion of false positives given α = 0.05.
Example recording trace and unit isolation. A, An example trace of a bandpass filtered signal (300–3000 Hz) of a single channel for the duration of one trial. The solid black line indicates the start of the trial, and the dashed black line indicates the time of the lever press. The colored portion of the trace indicates spikes assigned to one of two units on this channel. B, The waveforms of the units in A. Download Figure 6-1, TIF file (3.7MB, tif) .
Next, we examined whether changes in ACC activity correlated with rats' foraging decisions and RTs. Average ACC activity over the course of trials (the number of spikes during trial/time of trial, averaged across units) increased as rats became closer to leaving a patch (main effect of trials until leave or the number of times the rat chose to stay before choosing to leave that particular patch: = 0.287, SE = 0.061, F(1,147) = 22.028, p < 0.001). Similar to the relationship between trials until leaving the patch and RTs, average ACC activity as rats became closer to leaving a patch was not influenced by the patch starting reward (main effect of patch starting reward: = 0.008, SE = 0.043, F(1,138) = 0.032, p = 0.858). Also, the rate at which ACC activity increased as rats became closer to leaving a patch did not depend on the patch starting reward (patch starting reward × trials until leave interaction: = 0.013, SE = 0.019, F(1,145) = 0.509, p = 0.477; Fig. 6C). Accordingly, average ACC activity over the course of trials increased linearly with RTs (main effect of RTs: = 0.175, SE = 0.038, F(1,148) = 20.883, p < 0.001; Fig. 6B). No differences were noted between single- and multi-units (Fig. 6B,C).
To investigate the effect of rats' foraging decisions and RTs on ACC activity in more detail, PETHs of activity around the time of the lever press to stay in the patch were created for each unit, and a series of GLMs was used to examine (1) at which point in the decision process ACC encoded the number of trials until leaving the patch versus the RT on a given trial, and (2) which units significantly encoded either variable over the entire course of the trial (see Materials and Methods for full details). Encoding of the number of trials until leaving the patch was weakest during the time period before decisions and grew stronger after decisions (through the reward and ITI periods), evidenced by increasing average regression coefficients and an increase in the number of units with a statistically significant regression coefficient for the number of trials until leaving (with p < 0.05, z-test; Fig. 6E,F). At the same time, encoding of RTs was strongest preceding decisions, with the strongest regression coefficients occurring during a window of ∼6–2 s preceding the decision, and a greater number of units encoding RTs preceding the decision versus after the decision (Fig. 6E,F). Lastly, we found that a large number of units (69 of 148) encoded both RTs and trials until leaving, excluding one of these variables resulted in a worse model fit according to likelihood ratio tests (p < 0.05 with Holm–Bonferroni correction for multiple comparisons across 148 units), with additional units encoding either RTs only (36/148) or trials until leaving only (6/148). Again, no differences in encoding were observed between single- and multi-units (Fig. 6E,F).
ACC activity continuously tracks decision variables
To examine potential causes for encoding of RTs before the decision and encoding of decisions later in the trial, PETHs of recorded ACC activity were compared with decision variables derived from the LCA model. First, we discovered that average normalized ACC activity, the average PETH across neurons, split by the number of trials until leaving the patch, closely tracked the value of leaving or the difference between the value of staying in the patch versus leaving the patch ( - ; Fig. 7A). Importantly, both the value of leaving the patch and average normalized ACC activity (1) increased leading up to decisions; (2) was inhibited during reward delivery following a decision to stay in the patch (5, 3, or 1 trial until leaving); and (3) maintained elevated activity following decisions to leave (0 trials until leaving). A cross-correlation analysis revealed a strong quantitative correlation between average ACC activity and the value of leaving (r = 0.797, p < 0.001, tested against shuffled data; Fig. 7A). As many LCA variables are highly correlated with one another, there were also strong correlations among average ACC activity and additional LCA variables (Table 2). This finding indicates that the dynamics of ACC activity within and across trials are consistent with the hypothesis that ACC activity is related to LCA-derived decision variables, such as the value of leaving the patch.
Figure 7.
ACC activity correlates with leaky accumulator model decision variables. A, The value of leaving (globalRate – localRate; top) plotted next to average, normalized PETH across ACC units for 5, 3, 1, or 0 trials until leaving the patch (bottom). B, C, PCA was performed across the PETH for all units on these trials. The first nine PCs are presented in Extended Data Figure 7-1. B, The localRate unit activity from the model (top), next to the first PC of ACC activity (second panel), and an example unit that with a strong loading for the first PC (trial-by-trial raster in the third panel and trial-averaged PETH in the bottom panel). C, leaveDecisionActivity from the model (top), next to the second PC of ACC activity (second panel), and an example unit with a strong loading for the second PC (trial-by-trial raster in the third panel and trial-averaged PETH in the bottom panel). PETHs are locked to the time of decisions (the lever press or nose poke). PETHs of leaky accumulator model decision variables were created from simulations using parameters fit to each rat, lines and ribbon represent the average across these simulations. D, Cumulative proportion of variance explained by each PC. E, The proportion of individual units that correlated with each model variable. As many units exhibited significant correlations with multiple model variables, units were assigned to the variable with which they exhibited the strongest correlation.
Table 2.
Correlation between PETH of average ACC activity and LCA model variables
| LCA variable | R-value | P-value |
|---|---|---|
| −0.798 | <0.001 | |
| 0.268 | 0.008 | |
| −0.715 | <0.001 | |
| 0.492 | <0.001 | |
| decision difficulty | 0.767 | <0.001 |
| value of leaving | 0.797 | <0.001 |
| decision conflict | −0.678 | <0.001 |
R-values represent the strongest absolute correlation coefficient observed across all lags tested; p-values are calculated by comparing correlation coefficients against the correlation coefficient observed using shuffled data.
PCs of ACC unit activity. A, The first nine PCs across all individual units for 5, 3, 1, and 0 trials until leaving the patch. B, Correlations among the first 15 PCs and seven leaky accumulator model variables. Color indicates the strength of the correlation, asterisks denote statistically significant correlations (permutation test). Download Figure 7-1, TIF file (4.7MB, tif) .
To better understand the heterogeneity in the modulation of ACC firing across different units, we created PETHs for each unit (both single- and multi-units) at 5, 3, 1, and 0 trials until leaving the patch, and compared unit activity to LCA variables. To determine whether there are components of neural activity across units that correlate with LCA variables, PCA was performed on PETHs for each unit (including 120 time points × four trials = 480 features and 148 units or observations). Next, the PCs, the dimensions which explained the most variance in ACC activity (Extended Data Fig. 7-1A), were compared with decision variables derived from the LCA model using cross-correlation analyses. The first two PCs explained 25% of variance across ACC units, and it required 10 PCs to explain >50% of the variance (Fig. 7D). A total of five out of 148 PCs were significantly correlated with at least one LCA model variable: PC1 correlated most strongly with (r = 0.872, p < 0.001), PC2 and PC6 with (r = −0.656 and −0.715, p = 0.027 and 0.004, respectively), and PC3 and PC4 with decision difficulty (r = −0.562 and 0.664, p = 0.045 and 0.001, respectively; see Extended Data Fig. 7-1B for complete cross-correlation results).
Individual ACC units also exhibited correlations with a diverse set of LCA model variables. Overall, 39% of ACC units correlated with at least one LCA model variable. Units were characterized by the LCA variable with which it exhibited the strongest correlation (the greatest absolute correlation coefficient). ACC units most strongly correlated with a diverse set of LCA model variables, with the greatest proportion of units correlating with (9.5%), followed by decision difficulty (8.1%) and (7.4%; Fig. 7E). These findings suggest that the ACC signals multiple decision variables such as reward rates and decision accumulators.
ACC inactivation does not alter the foraging decision process
Continuous encoding of decision variables in ACC could play a central role in decision-making, such as participating in the value comparison process for ongoing decisions, or indicate a more general role such as monitoring ongoing performance for the purpose of allocating cognitive control or regulating response vigor. To test the contribution of the ACC to foraging decisions, ACC was pharmacologically inactivated via microinjection of a cocktail of the GABA receptor agonists Bac-Mus immediately before testing rats in the foraging task (Fig. 8A). In this experiment, rats were tested on a simplified version of the foraging task, with only three starting patch reward volumes (60, 90, and 120 µl). Compared with control sessions in which rats were injected with aCSF as a control, ACC inactivation caused rats to stay in patches for more trials (main effect of aCSF versus Bac-Mus: = 2.397, SE = 0.227, F(1,870) = 111.913, p < 0.001; Fig. 8B), and increased RTs as rats came closer to leaving the patch (main effect of aCSF vs Bac-Mus: = 0.669, SE = 0.054, F(1,7876) = 149.849, p < 0.001; Fig. 8C). However, despite ACC inactivation, rats still stayed longer in patches that started with greater rewards (main effect of patch starting reward: = 1.635, SE = 0.144, F(1,869) = 202.462, p < 0.001; no patch starting reward × treatment interaction; = 0.056, SE = 0.226, F(1,869) = 0.062, p = 0.803), and rats still exhibited longer RTs as they became closer to leaving the patch (main effect of trials until leaving: = 0.287, SE = 0.022, F(1,7876) = 277.213, p < 0.001; no trials until leaving × treatment interaction; = 0.043, SE = 0.032, F(1,7877) = 1.876, p = 0.171).
Figure 8.
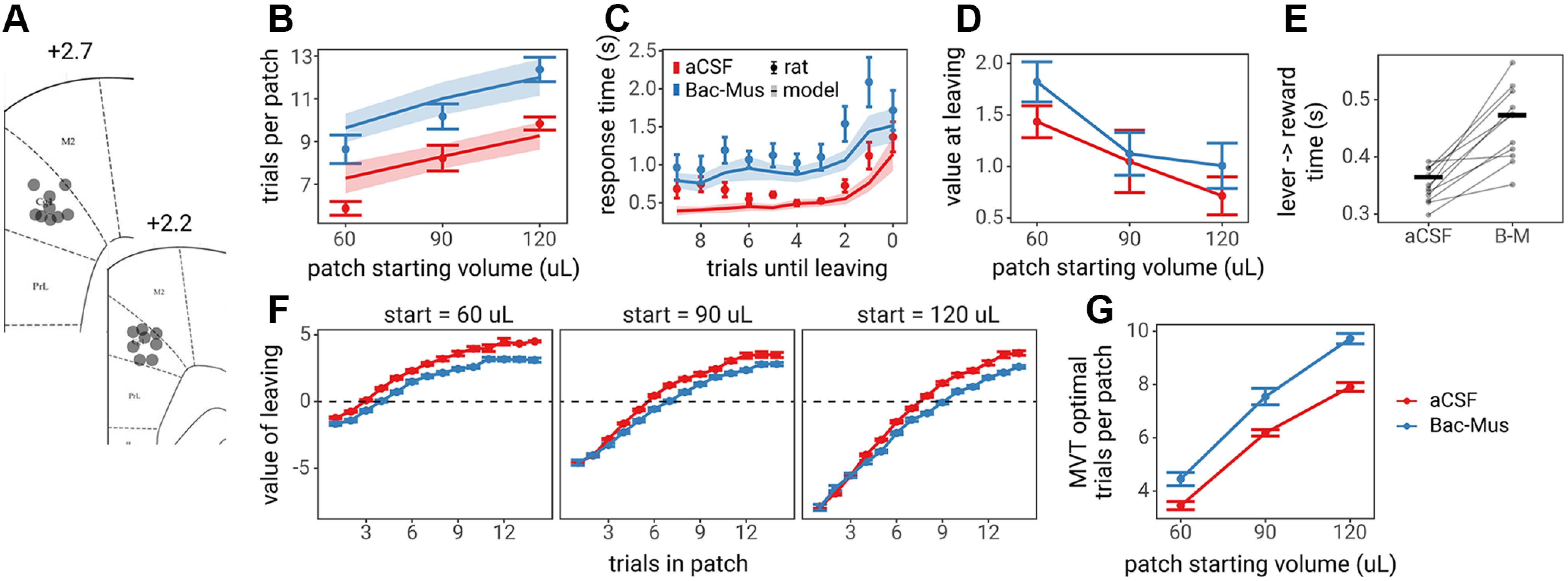
Effects of Inactivation of ACC on foraging behavior. A, Diagram of cannula locations in Cg1. B, The number of trials spent in each of the three patch types. C, RTs as rats became closer to leaving patches, where 0 trials until leaving is the nose poke to leave the patch, 1 is the last lever press in the patch, and so on. D, The value of leaving (global reward rate – local reward rate) the rat experienced on the last trial in which they harvested reward from the patch (trials until leaving = 1). In B–D, points and error bars represent the mean and SE across rats, whereas lines and ribbons represent mean and SE across leaky accumulator model predictions for each rat. E, The handling time or time from lever press to entering the reward magazine. Transparent points and lines represent individual rat behavior, and the horizontal bar shows the mean across rats for each condition. F, The value of leaving (global reward rate – local reward rate) over the course of trials in the patch for each of the three patch starting reward volumes. Points and error bars represent the mean and SE across rats. The horizontal dashed line represents the optimal time to leave patches (global rate – local rate = 0), according to MVT. G, Extrapolating from F, the optimal time to leave patches in the aCSF and Bac-Mus conditions, according to MVT.
That rats stay longer in patches and exhibit longer RTs because of ACC inactivation does not necessarily imply that the ACC is directly involved in comparing the value of staying versus leaving a patch. MVT predicts that foraging decisions are based on estimates of reward rate, not reward value, and animals that exhibit longer RTs experience lower reward rates. Thus, staying longer in patches could be a compensatory mechanism for lower reward rates experienced as a consequence of longer RTs. The relative value of leaving, the difference between the global and local reward rate, over the course of trials in patches was lower during sessions in which rats were injected with Bac-Mus compared with aCSF (Fig. 8F). Furthermore, there was little to no difference in the value of leaving on the last decision to stay in patches between Bac-Mus and aCSF sessions (main effect of Bac-Mus vs aCSF: = 0.245, SE = 0.128, F(1,887) = 3.690, p = 0.055; Fig. 8D). We also examined the optimal number of trials to spend in each patch, according to MVT, in aCSF versus Bac-Mus sessions. Given the observed RTs in each condition, MVT predicts that rats should spend one to two additional trials in each patch during Bac-Mus sessions (Fig. 8G). Finally, to determine whether ACC inactivation may have caused rats to move slower, we examined the time it took rats to move from the lever to the reward magazine, a period of time that reflects only movement as no decision needs to be made. Rats were slower to move from the lever to the reward port during Bac-Mus sessions compared with aCSF sessions (t(10) = 5.649, p < 0.001, paired t test; Fig. 8E). These findings did not provide evidence for the hypothesis that the ACC plays an important role in comparing the value of staying versus leaving. Rather, they supported the notion that ACC inactivation may have slowed RTs unrelated to decision deliberation (or value comparison), causing rats to stay longer in patches to compensate for lower reward rates.
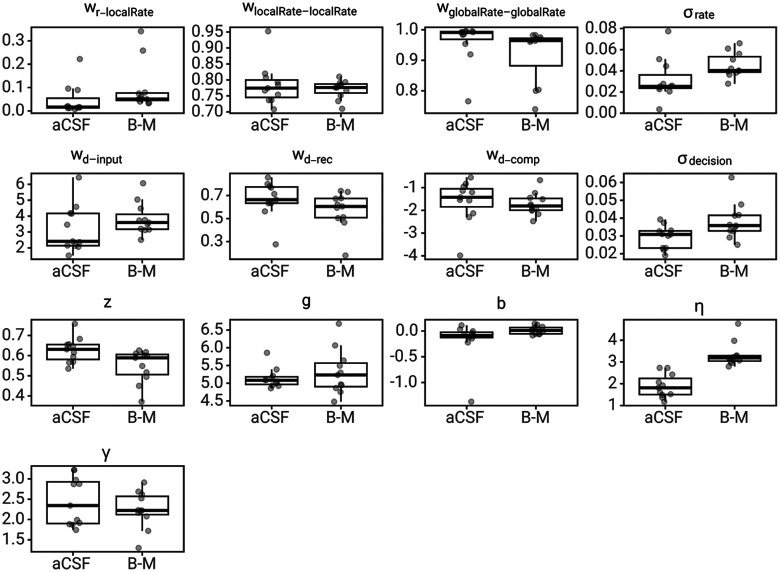
To better understand how ACC inactivation altered the foraging decision process to produce slower RTs without altering the relative patch leaving threshold (the value of leaving at the time that rats chose to leave the patch), the LCA model was fit to rat behavior on aCSF and Bac-Mus sessions. Changes in LCA parameters across sessions were tested using paired t tests with Holm–Bonferroni correction for multiple comparisons (across 13 parameters). Model predictions for aCSF and Bac-Mus sessions and all parameter estimates are shown in Figure 9. Only one parameter, the non-DT, , was significantly different across sessions (results for all parameters in Table 3). This finding corroborated the hypothesis that during ACC inactivations, rats stayed in patches longer to compensate for lower reward rates because of slower movement and slower RTs. Furthermore, this finding did not provide evidence that behavioral changes because of ACC inactivation were related to altered encoding of the value of staying versus leaving, nor to changes in the accumulation to bound decision process.
Figure 9.
LCA model parameters fit to aCSF and Bac-Mus (B-M) sessions. The box represents the first and third quartile, whiskers represent 1.5 times the interquartile range, with all individuals plotted transparently.
Table 3.
Pairwise t tests on LCA model parameters fit to aCSF sessions versus parameters fit to Bac-Mus sessions
| Parameter | t value | df | P-value |
|---|---|---|---|
| −1.468 | 10 | 1 | |
| 0.636 | 10 | 1 | |
| 1.186 | 10 | 1 | |
| −2.102 | 10 | 0.618 | |
| −1.221 | 10 | 1 | |
| 1.398 | 10 | 1 | |
| 0.362 | 10 | 1 | |
| −2.421 | 10 | 0.396 | |
| 2.492 | 10 | 0.383 | |
| −1.047 | 10 | 1 | |
| −1.726 | 10 | 1 | |
| −9.287 | 10 | < 0.001 | |
| 0.709 | 10 | 1 |
Discussion
Previous studies showed that ACC activity is modulated during foraging decisions (Hayden et al., 2011; Kolling et al., 2012, 2014; Blanchard and Hayden, 2014; Shenhav et al., 2014, 2016b), but what this modulation of ACC activity represents, or how the ACC contributes to foraging decisions, is not fully understood. In the present study, we found that rat ACC neurons separately correlate with both foraging decisions and RTs. Using an LCA model that estimates MVT-derived decision variables within and across trials, we found that individual ACC neurons encode lower-level task variables such as the reward rate and decision accumulators, and that as a population, the average ACC activity reflects decision difficulty as indexed by the similarity in the value of staying in the patch versus leaving. Finally, inactivation of ACC neurons altered foraging behavior, but this change was best explained not by changes to the decision process, but by altering non-DT, a latent variable meant to represent the time for nondecisional sensory processing and motor execution, which may include motivation or response vigor.
The findings that ACC neurons continuously signal important foraging decision variables, but that the ACC is not necessary to follow the MVT decision rule, may provide important information about its function. Despite encoding value signals that could be used for decisions, results from the ACC inactivation experiment indicate that the ACC is not necessary for comparing the values of options for the decision at hand in the task we employed. The lack of involvement of ACC in the primary decision strategy is consistent with a recent study that performed optogenetic silencing of ACC in mice performing a foraging-style task (Vertechi et al., 2020). In this study, mice chose to stay versus leave a patch for which the probability of receiving a reward was reduced with every decision to stay, and decisions to stay versus leave were equally guided by failures to receive reward despite ACC inactivation. These findings, together with the results of the present experiment, support a more general role for the ACC. One possibility is that the ACC regulates cognitive control, a function long associated with the ACC (Botvinick et al., 2001), and a role that ACC has been previously hypothesized to perform in foraging tasks (Blanchard and Hayden, 2014; Shenhav et al., 2014, 2016b). Another, closely related interpretation of the effect of ACC inactivation on non-DTs is that the ACC may play a role in setting response vigor, or the speed at which animals choose to perform a task, rather than a specific role in discrete patch leaving decisions. These two hypothetical functions parallel to one another, in that both sorts of decisions should, for essentially the same reasons, be governed by the long-run average reward acting as the opportunity cost of time. Thus, both interpretations are consistent with a general role for ACC in optimizing performance. In particular, models of how animals should rationally govern response vigor, trading off energetic costs of speedy actions versus the opportunity costs of delay, predict that vigor should increase in more rewarding environments (Niv et al., 2007). Human participants have been shown to modulate their response vigor in response to changes in the foraging environment in an information foraging task (Yoon et al., 2018). Thus, although the ACC may not contribute to setting the patch leaving threshold, it may serve to optimize performance by setting response vigor based on the estimated patch-leaving threshold.
Alternatively, it is possible that the ACC plays a critical role in the value comparison process of foraging decisions, but only in settings (unlike the current one) that require updating of one's internal model (e.g., a change in the possible patch types that animals may encounter). Previous studies found that perturbation of ACC activity affects animals' ability to perform task or strategy switching or to update internal models of the environment (Kennerley et al., 2006; Tervo et al., 2014; Sarafyazd and Jazayeri, 2019; Akam et al., 2021). In foraging tasks, even if there is some uncertainty about the exact reward to be received in future patches (e.g., if there are multiple patch types), animals have learned the average expected future reward. Thus, an animal can learn the appropriate time to leave different patch types without updating internal models of the environment.
The present findings also contribute to a growing body of literature that indicates that rodents can serve as a model to understand the function of the ACC and the behavioral consequences of ACC dysfunction. Although the degree of homology between rodent and primate cingulate cortex is still not entirely clear (Seamans et al., 2008; Heilbronner and Hayden, 2016; Heilbronner et al., 2016; van Heukelum et al., 2020), multiple recent reports indicate that rodent ACC exhibits similar signals to human and nonhuman primate ACC. In this study, rat ACC activity correlates closely with decision difficulty in a foraging task, similar to foraging-related ACC activity that has been reported in humans and nonhuman primates (Hayden et al., 2011; Shenhav et al., 2014, 2016b). Rodent ACC neurons also exhibit other signals that have long been associated with human ACC, including the feedback-related negativity (Warren et al., 2015), error monitoring (Narayanan et al., 2013), and increased activity during response competition (Bryden et al., 2018). Additionally, a recent lesion study found that the ACC is necessary to resolve response competition (Brockett et al., 2020). Together, these studies indicate that the use of rodent models, and the advanced tools for recording and perturbing neural activity in rodent models, promise to advance knowledge of ACC function.
Footnotes
This work was supported by National Institutes of Health Grants F31MH109286 (to G.A.K.), K99DA045765 (to M.H.J.), R01MH124849 (to A.S.), and R01MH092868 (to G.A.-J.). We thank Jeremy Autore for assistance with computational modeling and the Shenhav Lab at Brown University for valuable discussions on this work.
The authors declare no competing financial interests.
References
- Akam T, Rodrigues-Vaz I, Marcelo I, Zhang X, Pereira M, Oliveira RF, Dayan P, Costa RM (2021) The anterior cingulate cortex predicts future states to mediate model-based action selection. Neuron 109:149–163.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates D, Mächler M, Bolker BM, Walker SC (2015) Fitting linear mixed-effects models using lme4. J Stat Soft 67:1–48. 10.18637/jss.v067.i01 [DOI] [Google Scholar]
- Blanchard TC, Hayden BY (2014) Neurons in dorsal anterior cingulate cortex signal postdecisional variables in a foraging task. J Neurosci 34:646–655. 10.1523/JNEUROSCI.3151-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick MM, Braver TS, Barch DM, Carter CS, Cohen JD (2001) Conflict monitoring and cognitive control. Psychol Rev 108:624–652. 10.1037/0033-295x.108.3.624 [DOI] [PubMed] [Google Scholar]
- Brockett AT, Tennyson SS, deBettencourt CA, Gaye F, Roesch MR (2020) Anterior cingulate cortex is necessary for adaptation of action plans. Proc Natl Acad Sci U S A 117:6196–6204. 10.1073/pnas.1919303117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryden DW, Brockett AT, Blume E, Heatley K, Zhao A, Roesch MR (2018) Single neurons in anterior cingulate cortex signal the need to change action during performance of a stop-change task that induces response competition. Cereb Cortex 29:1020–1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callaway F, Rangel A, Griffiths TL (2021) Fixation patterns in simple choice reflect optimal information sampling. PLoS Comput Biol 17:e1008863. 10.1371/journal.pcbi.1008863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charnov EL (1976) Optimal foraging, the marginal value theorem. Theor Popul Biol 9:129–136. 10.1016/0040-5809(76)90040-x [DOI] [PubMed] [Google Scholar]
- Constantino SM, Daw ND (2015) Learning the opportunity cost of time in a patch-foraging task. Cogn Affect Behav Neurosci 15:837–853. 10.3758/s13415-015-0350-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidson JD, El Hady A (2019) Foraging as an evidence accumulation process. PLoS Comput Biol 15:e1007060. 10.1371/journal.pcbi.1007060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebitz RB, Hayden BY (2016) Dorsal anterior cingulate: a Rorschach test for cognitive neuroscience. Nat Neurosci 19:1278–1279. 10.1038/nn.4387 [DOI] [PubMed] [Google Scholar]
- Frömer R, Dean Wolf CK, Shenhav A (2019) Goal congruency dominates reward value in accounting for behavioral and neural correlates of value-based decision-making. Nat Commun 10:4926. 10.1038/s41467-019-12931-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayden BY (2018) Economic choice: the foraging perspective. Curr Opin Behav Sci 24:1–6. 10.1016/j.cobeha.2017.12.002 [DOI] [Google Scholar]
- Hayden BY, Pearson JM, Platt ML (2011) Neuronal basis of sequential foraging decisions in a patchy environment. Nat Neurosci 14:933–939. 10.1038/nn.2856 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heilbronner SR, Hayden BY (2016) Dorsal anterior cingulate cortex: a bottom-up view. Annu Rev Neurosci 39:149–170. 10.1146/annurev-neuro-070815-013952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heilbronner SR, Rodriguez-Romaguera J, Quirk GJ, Groenewegen HJ, Haber SN (2016) Circuit-based corticostriatal homologies between rat and primate. Biol Psychiatry 80:509–521. 10.1016/j.biopsych.2016.05.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm S (1979) A simple sequentially rejective multiple test procedure. Scand J Stat 6:65–70. [Google Scholar]
- Kane GA, Vazey EM, Wilson RC, Shenhav A, Daw ND, Aston-Jones G, Cohen JD (2017) Increased locus coeruleus tonic activity causes disengagement from a patch-foraging task. Cogn Affect Behav Neurosci 17:1073–1083. 10.3758/s13415-017-0531-y [DOI] [PubMed] [Google Scholar]
- Kane GA, Bornstein AM, Shenhav A, Wilson RC, Daw ND, Cohen JD (2019) Rats exhibit similar biases in foraging and intertemporal choice tasks. Elife 8:e48429. 10.7554/eLife.48429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennerley SW, Walton ME, Behrens TEJ, Buckley MJ, Rushworth MFS (2006) Optimal decision making and the anterior cingulate cortex. Nat Neurosci 9:940–947. 10.1038/nn1724 [DOI] [PubMed] [Google Scholar]
- Kolling N, Behrens TEJ, Mars RB, Rushworth MFS (2012) Neural mechanisms of foraging. Science 336:95–98. 10.1126/science.1216930 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolling N, Wittmann M, Rushworth MFS (2014) Multiple neural mechanisms of decision making and their competition under changing risk pressure. Neuron 81:1190–1202. 10.1016/j.neuron.2014.01.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolling N, Wittmann MK, Behrens TEJ, Boorman ED, Mars RB, Rushworth MFS (2016) Value, search, persistence and model updating in anterior cingulate cortex. Nat Neurosci 19:1280–1285. 10.1038/nn.4382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuznetsova A, Brockhoff PB, Christensen RHB (2017) lmerTest package: tests in linear mixed effects models. J Stat Soft 82:1–26. 10.18637/jss.v082.i13 [DOI] [Google Scholar]
- Li YS, Nassar MR, Kable JW, Gold JI (2019) Individual neurons in the cingulate cortex encode action monitoring, not selection, during adaptive decision-making. J Neurosci 39:6668–6683. 10.1523/JNEUROSCI.0159-19.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Z, Nie C, Zhang Y, Chen Y, Yang T (2020) Evidence accumulation for value computation in the prefrontal cortex during decision making. Proc Natl Acad Sci U S A 117:30728–30737. 10.1073/pnas.2019077117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan NS, Cavanagh JF, Frank MJ, Laubach M (2013) Common medial frontal mechanisms of adaptive control in humans and rodents. Nat Neurosci 16:1888–1895. 10.1038/nn.3549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niv Y, Daw ND, Joel D, Dayan P (2007) Tonic dopamine: opportunity costs and the control of response vigor. Psychopharmacology (Berl) 191:507–520. 10.1007/s00213-006-0502-4 [DOI] [PubMed] [Google Scholar]
- Nonacs P (2001) State dependent behavior and the marginal value theorem. Behav Ecol 12:71–83. 10.1093/oxfordjournals.beheco.a000381 [DOI] [Google Scholar]
- Peters J, D'Esposito M (2020) The drift diffusion model as the choice rule in inter-temporal and risky choice: a case study in medial orbitofrontal cortex lesion patients and controls. PLoS Comput Biol 16:e1007615. 10.1371/journal.pcbi.1007615 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pisauro MA, Fouragnan E, Retzler C, Philiastides MG (2017) Neural correlates of evidence accumulation during value-based decisions revealed via simultaneous EEG-fMRI. Nat Commun 8:15808. 10.1038/ncomms15808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polanía R, Krajbich I, Grueschow M, Ruff CC (2014) Neural oscillations and synchronization differentially support evidence accumulation in perceptual and value-based decision making. Neuron 82:709–720. 10.1016/j.neuron.2014.03.014 [DOI] [PubMed] [Google Scholar]
- R Core Team (2020) R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. Available at http://www.r-project.org/. [Google Scholar]
- Ratcliff R, Tuerlinckx F (2002) Estimating parameters of the diffusion model: approaches to dealing with contaminant reaction times and parameter variability. Psychon Bull Rev 9:438–481. 10.3758/bf03196302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rushworth MFS, Noonan MP, Boorman ED, Walton ME, Behrens TE (2011) Frontal cortex and reward-guided learning and decision-making. Neuron 70:1054–1069. 10.1016/j.neuron.2011.05.014 [DOI] [PubMed] [Google Scholar]
- Sarafyazd M, Jazayeri M (2019) Hierarchical reasoning by neural circuits in the frontal cortex. Science 364:eaav8911. 10.1126/science.aav8911 [DOI] [PubMed] [Google Scholar]
- Schmitzer-Torbert N, Jackson J, Henze D, Harris K, Redish AD (2005) Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience 131:1–11. 10.1016/j.neuroscience.2004.09.066 [DOI] [PubMed] [Google Scholar]
- Scrucca L (2013) GA: a package for genetic algorithms in R. J Stat Soft 53:1–37. 10.18637/jss.v053.i04 [DOI] [Google Scholar]
- Seamans JK, Lapish CC, Durstewitz D (2008) Comparing the prefrontal cortex of rats and primates: insights from electrophysiology. Neurotox Res 14:249–262. 10.1007/BF03033814 [DOI] [PubMed] [Google Scholar]
- Shenhav A, Straccia MA, Cohen JD, Botvinick MM (2014) Anterior cingulate engagement in a foraging context reflects choice difficulty, not foraging value. Nat Neurosci 17:1249–1254. 10.1038/nn.3771 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shenhav A, Cohen JD, Botvinick MM (2016a) Dorsal anterior cingulate cortex and the value of control. Nat Neurosci 19:1286–1291. 10.1038/nn.4384 [DOI] [PubMed] [Google Scholar]
- Shenhav A, Straccia MA, Botvinick MM, Cohen JD (2016b) Dorsal anterior cingulate and ventromedial prefrontal cortex have inverse roles in both foraging and economic choice. Cogn Affect Behav Neurosci 16:1127–1139. 10.3758/s13415-016-0458-8 [DOI] [PubMed] [Google Scholar]
- Strait CE, Sleezer BJ, Blanchard TC, Azab H, Castagno MD, Hayden BY (2016) Neuronal selectivity for spatial positions of offers and choices in five reward regions. J Neurophysiol 115:1098–1111. 10.1152/jn.00325.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima S, Drugowitsch J, Pouget A (2016) Optimal policy for value-based decision-making. Nat Commun 7:12400. 10.1038/ncomms12400 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tervo DGR, Proskurin M, Manakov M, Kabra M, Vollmer A, Branson K, Karpova AY (2014) Behavioral variability through stochastic choice and its gating by anterior cingulate cortex. Cell 159:21–32. 10.1016/j.cell.2014.08.037 [DOI] [PubMed] [Google Scholar]
- Usher M, McClelland JL (2001) The time course of perceptual choice: the leaky, competing accumulator model. Psychol Rev 108:550–592. 10.1037/0033-295x.108.3.550 [DOI] [PubMed] [Google Scholar]
- van Heukelum S, Mars RB, Guthrie M, Buitelaar JK, Beckmann CF, Tiesinga PHE, Vogt BA, Glennon JC, Havenith MN (2020) Where is cingulate cortex? A cross-species view. Trends Neurosci 43:285–299. 10.1016/j.tins.2020.03.007 [DOI] [PubMed] [Google Scholar]
- Vertechi P, Lottem E, Sarra D, Godinho B, Treves I, Quendera T, Oude Lohuis MN, Mainen ZF (2020) Inference-based decisions in a hidden state foraging task: differential contributions of prefrontal cortical areas. Neuron 106:166–176.e6. 10.1016/j.neuron.2020.01.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren CM, Hyman JM, Seamans JK, Holroyd CB (2015) Feedback-related negativity observed in rodent anterior cingulate cortex. J Physiol Paris 109:87–94. 10.1016/j.jphysparis.2014.08.008 [DOI] [PubMed] [Google Scholar]
- Wikenheiser AM, Stephens DW, Redish a. D (2013) Subjective costs drive overly patient foraging strategies in rats on an intertemporal foraging task. Proc Natl Acad Sci U S A 110:8308–8313. 10.1073/pnas.1220738110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoon T, Geary RB, Ahmed AA, Shadmehr R (2018) Control of movement vigor and decision making during foraging. Proc Natl Acad Sci U S A 115:E10476–E10485. 10.1073/pnas.1812979115 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Example recording trace and unit isolation. A, An example trace of a bandpass filtered signal (300–3000 Hz) of a single channel for the duration of one trial. The solid black line indicates the start of the trial, and the dashed black line indicates the time of the lever press. The colored portion of the trace indicates spikes assigned to one of two units on this channel. B, The waveforms of the units in A. Download Figure 6-1, TIF file (3.7MB, tif) .
PCs of ACC unit activity. A, The first nine PCs across all individual units for 5, 3, 1, and 0 trials until leaving the patch. B, Correlations among the first 15 PCs and seven leaky accumulator model variables. Color indicates the strength of the correlation, asterisks denote statistically significant correlations (permutation test). Download Figure 7-1, TIF file (4.7MB, tif) .