Abstract
Understanding the laser-nanomaterials interaction including nanomaterial fragmentation has important implications in nanoparticle manufacturing, energy, and biomedical sciences. So far, three mechanisms of laser-induced fragmentation have been recognized including non-thermal processes and thermomechanical force under femtosecond pulses, and the phase transitions under nanosecond pulses. Here we show that single picosecond (ps) laser pulse stimulation leads to anomalous fragmentation of gold nanoparticles that deviates from these three mechanisms. The ps laser fragmentation was weakly dependent on particle size, and it resulted in a bimodal size distribution. Importantly, ps laser stimulation fragmented particles below the whole particle melting point and below the threshold for non-thermal mechanism. We propose a framework based on near-field enhancement and nanoparticle surface melting to account for the ps laser-induced fragmentation observed here. This study reveals a new form of surface ablation that occurs under picosecond laser stimulation at low fluence.
Keywords: Plasmonic nanoparticle, Picosecond laser, Fragmentation, Laser manufacturing
Graphical Abstract
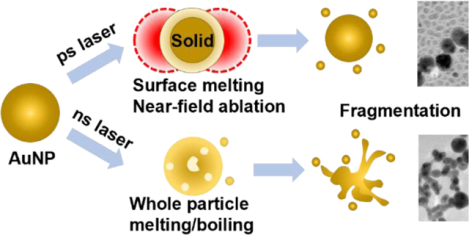
INTRODUCTION:
The interaction between light and nanomaterials leads to many interesting phenomena, such as near-field enhancement1, surface-enhanced Raman scattering2, and photothermal effects3. These phenomena have been harnessed for a variety of applications. For example, near-field enhancement can be used for optical trapping of molecules4, while surface-enhanced Raman scattering and photothermal effects have found applications in imaging5–6, sensing7–10 and actuation of biological activities11–12. However, nanoparticles subjected to pulsed laser irradiation may also undergo laser-induced fragmentation, in which the original nanoparticles are fragmented into smaller particles13. The previously noted applications often rely on maintaining the plasmonic nanomaterial’s structural integrity during laser irradiation, as any alterations to nanoparticle morphology may adversely affect functionality14–15. Moreover, laser-induced fragmentation has been used as an alternative form of green manufacturing for difficult-to-synthesize nanomaterials16–21, an application that also requires accurate control of the structural integrity of plasmonic nanostructures under laser irradiation. It is therefore critical to understand what conditions lead to laser-induced fragmentation and how fragmentation mechanisms change when the laser condition varies.
Three major categories of mechanisms have been proposed for laser-induced nanoparticle fragmentation: i) phase transition (PT) mechanisms, ii) a thermomechanical mechanism and iii) non-thermal processes. First, according to PT mechanisms, the strong heating effect of laser causes the nanoparticle to undergo phase transitions. The fragmentation can be driven by the material phase change when the particle reaches the melting point, known as the heating-melting-evaporation route22. The material can also be heated to the boiling point within a short period which leads to a more violent fragmentation, known as phase explosion22–24. Second, in the thermomechanical mechanism, the thermomechanical force plays an important role when heating happens much faster than the mechanical relaxation time (~3 ps for a AuNP with a diameter of 10 nm), a condition known as mechanical confinement25–26. The particle may fragment when the thermomechanical force exceeds the physical strength of the material without a necessary phase transition27. Finally, the non-thermal processes are related to the excitation of electrons, including near-field ablation and Coulomb instability (CI). The strong near-field enhancement that occurs during femtosecond (fs) laser irradiation induces nanoparticle fragmentation without melting the material18, 28–30. For CI, the laser irradiation ionizes the nanoparticles and causes them to fragment when the Coulombic repulsion forces within the particles exceed the surface tension of the nanoparticle. Since the melted nanoparticles have a smaller surface tension than solid ones31–32, CI tends to fragment molten particles rather than solid particles23. So far, most research has relied on these mechanisms to rationalize nanoparticle fragmentation33–34.
Although mechanisms based on non-thermal and thermomechanical processes have proven useful in interpreting fragmentation under fs pulse laser irradiation29, 32, 35, and PT is thought to be the principal mechanism of fragmentation under nanosecond (ns) laser irradiation32, 36, the mechanism of fragmentation under the intermediate duration of picosecond (ps) pulse laser irradiation is unclear 22, 33, 37. The complication of ps laser fragmentation comes from the nature of the laser-plasmonic nanoparticle interaction. The energy transfer from electrons to phonons requires a time period characterized by electron-phonon coupling time, which is on the order of ps for gold38. A previous study has identified that non-thermal effects such as ionization and near-field effect are dominant during fragmentation by short laser pulses (< 3 ps), while thermal effects such as phase transitions mainly contribute to fragmentation by long laser pulses (ns laser)32. ps laser heating falls within a transition zone between being dominated by non-thermal effects and dominated by thermal effects, therefore both thermal and non-thermal effects can be significant for ps laser stimulation23, 37, 39. These overlapping factors may both contribute to nanoparticle fragmentation, complicating the mechanistic description of ps laser-induced nanoparticle fragmentation. For example, it was recently reported that although ps laser-induced fragmentation of 54 nm gold nanoparticles was found to be an ultrafast single-step reaction near the gold particle boiling point, it remained unclear whether the fragmentation was due to PT, CI, or a thermomechanical mechanism 33. Additionally, previous work has indicated that ps-laser induced fragmentation may occur by both CI and PT mechanisms depending on the laser fluence23, while other work has suggested that both CI and near-field ablation may be possible under ps pulse laser irradiation. Although several mechanisms have been considered for ps laser-induced fragmentation, our understanding of nanoparticle fragmentation under this regime is still limited.
Here, we report that stimulation with a single 28 ps laser pulse leads to anomalous gold nanoparticle (AuNP) fragmentation at temperatures below the melting transition and below the threshold for CI. We compared the ps laser-induced fragmentation to that by ns laser pulse stimulation and found that the laser fluence threshold for fragmentation under ps laser pulse stimulation was about 1–2 orders of magnitude lower than that of AuNPs subjected to ns laser pulse stimulation. Importantly, the fluence threshold for ps laser pulse fragmentation shows a weak dependence on the particle size and it emits smaller nanoparticles with distinct size distributions, in contrast to the strong size-dependence and formation of continuous extrusions by AuNPs fragmented by ns pulsed laser stimulation. Next, by analyzing the temperature changes and particle instability, we determined that fragmentation of AuNPs by ps laser pulse stimulation occurred when the whole AuNPs were still in the solid phase and that the fluence level was much lower than that needed to induce fragmentation by Coulomb instability. Analysis of the thermomechanical stress suggests that it only fragments melted particles based on molecular dynamics (MD) simulation. To account for the ps laser-induced fragmentation observed here, we proposed a framework based on near-field enhancement and nanoparticle surface melting. Under this framework, part of the incident light was deposited as thermal energy and partially melts the surface of gold. The other part of the light energy was focused on the nanoparticle surface and induces a strong near-field. Combining these thermal and non-thermal mechanisms, this work reveals a new form of surface ablation that leads to nanoparticle fragmentation by a single ps laser at a low laser fluence.
METHODS
Nanoparticle synthesis
All chemicals were purchased from Sigma-Aldrich unless otherwise indicated. 15 nm AuNPs was synthesized with the Frens’ method following the previous report40. All glassware was soaked in aqua regia for 30 mins and rinsed with the Millipore water before using. 98 mL Millipore water and 1 mL HAuCl4 (25 mM) were added to 250 mL Erlenmeyer flask and brought to a boil, following the rapid addition of 1 mL trisodium citrate (112.2 mM). The solution was heated for 10 minutes and cooled down to the room temperature. Particles were concentrated with centrifugation (10 krcf, 30 minutes), and stored in 4°C environment until experiment.
30, 45, 100 nm AuNPs were synthesized with the seed-growth method with 15 nm AuNPs as seeds41–42. Briefly, 15 nm AuNP (2.23 nM), HAuCl4 (25 mM) and trisodium citrate (15 mM) solution was mixed and brought to the volume of 100 mL with Millipore water. Under rigorous mixing, hydroquinone (25 mM) solution was added into the vortex swiftly. The solution was stirred for half an hour under the high-speed stirring and then changed to low-speed stirring overnight. The volume of each solution is dependent on NP sizes and can be found in previously published paper 42. Particles will be concentrated by centrifugation and stored in 4°C environment until experiment. The centrifugation speed and time were dependent on particle sizes.
5 nm AuNPs was synthesized following a previously reported procedure43. The reduction solution was prepared by mixing 16 mL water, 4 mL trisodium citrate (1% w/v), 1 mL tannic acid (1% w/v) and 1 mL potassium carbonate (3.26 mg/mL). The reaction is started by injecting reduction solution to 80 mL HAuCl4 solution (312.5 μM). The reaction was kept under 60 °C for half hour and then brought to 90 °C for 10 minutes.
All nanoparticles were cooled to room temperature. The sizes of AuNPs were characterized with a transmission electron microscope (TEM) and dynamic light scattering (DLS, Malvern Nano ZS). To characterize the AuNP sample with TEM, AuNP solution (10 μL) was dropped on the TEM grid and air-dried. The TEM imaging was taken in JOEL-2100 (100 keV). Imaging analyses were conducted in ImageJ software.
Laser beam size measurements
The ns pulsed laser is generated from a Quantel Q-smart 450 Nd:YGA laser. The ps pulsed laser is generated from EKSPLA PL 2230 Nd:YGA laser. The laser beam sizes are calibrated with blade-edge method following a previous report44. We first fixed a razor blade on a translation stage in front of the laser beam. Next, the laser energy was monitored while a blade edge is gradually blocking the laser beam. The curve shows the relation between the blade position and laser power used to calibrate the gaussian beam size using the relation below.
| (1) |
| (2) |
where β−1 is radius where laser intensity drops to 1/e of the maximum intensity in the center of the beam. And is the diameter where intensity drops to 1/e2 of the maximum intensity.
Laser-induced nanoparticle fragmentation
Before the laser-induced fragmentation experiment, all AuNP are diluted to the OD=0.3 at 532 nm. Then AuNP solution is added to a 96 well-plate (115 μL/well). We irradiated samples well by well with increasing laser fluence. The pulse energy was monitored simultaneously with a beam splitter which can reflect a portion of the beam. The transmission and reflection were measured by an energy meter, and the linear relation between transmission and reflection was calculated in Excel. Reported fluences were the fluence measured at the surface of the sample and corresponded to the peak fluence of the Gaussian energy distributions. Note that the well diameter in the 96 well plate (7 mm) is smaller than the ps laser diameter (8.2 mm), so the entire sample is irradiated during the ps pulse. However, the ns laser diameter (5.4 mm) is smaller than the well diameter (7 mm), so only 60% of the sample loaded in the plate was exposed to laser during the ns pulse. Additionally, the 115 μL samples loaded in wells have a depth of about 3 mm. Due to absorbance (Beer-Lambert law) the fluence at the bottom of the sample is about 81% of that at the sample surface. After exposing to single laser pulse, samples (110 μL/well) were transferred to 384 well plate. We used a plate reader (BioTek Synergy 2) to measure the extinction spectrum from 400 nm to 800 nm.
Data processing and extinction analysis
The extinction spectrum for different laser fluences was organized in Excel. The data was then processed with MATLAB 2019a. The extinction spectrum is a function for both wavelength (λ, from 400–800 nm) and laser fluence (F), as shown in Eq. 3. Here, A is extinction spectrum.
| (3) |
The extinction spectrum of AuNP after laser was treated as a vector [A]. The extinction ratio, as a matrix [R], was calculated by Eq. 1. For each laser frequency, we can obtain a matrix [R].
| (4) |
We then normalized the extinction ratio by scaling between 0 to ±1 with Eq. 4 where F = 0 indicates the control sample without laser irradiation, and F = Fq, refers to the sample with the largest ratio change among all laser fluences.
| (5) |
The threshold fluence was defined as where the normalized extinction ratio starts to increase. We used a piecewise fitting model to fit the data and found the optimized breaking point which indicates the threshold fluence45.
Mie theory calculation
The extinction of AuNP before and after fragmentation under ps laser was calculated by Mie theory with MNPBEM MATLAB toolbox 46. We assume the gold density is constant for particles with different sizes and there are only two discrete sizes of particles according to TEM images. The average diameters (dNP) of nanoparticles were obtained from TEM imaging analysis. The collective extinction spectrum of AuNP sample (Cext_mix) can be calculated by eq. 6–10.
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
where Cext is the extinction cross section, p is distribution of particles with different sizes. fd is the size distribution of particles before laser treatment, can be simplified as a gaussian distribution. N is the number of fragments that the ablated surface layer forms. pf is probability of particle fragmentation. d is particle diameter, Lliq is the melted layer thickness (3% to 5% of dNP) Subscripts “NP”, “small” and “large” indicates the particle without size changing, small daughter particle, and large daughter particles, respectively.
Electric field distribution using MNPBEM.
We calculated the near-field enhancement of different sizes of particles under the 532 nm laser. The laser was considered as a plane wave. The calculation was conducted in MNPBEM MATLAB toolbox. The parameters of materials were set the same as the Mie theory calculation. The strength of electric field of incident light was calculated by eq. 11.
| (11) |
where I is the light intensity, c is the speed of light, and ε0 is permeability of free space.
Two-temperature heat transfer model
In this paper, the shortest pulse we used was ps laser which should be sufficiently long to neglect electron relaxation process (in several femtoseconds). Therefore, the parabolic two-step heat conduction model (P2T) is sufficient for our estimation of the temperature evolution47. TTM describes that the electron subsystem in the AuNP obtains energy from laser, and then transfer energy to lattice.
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
where the Qv is volumetric heat source, Cabs is absorption cross section computed from Mie theory, F is laser fluence in mJ/cm2. The laser is treated as a gaussian pulse in the simulation. The total pulse duration was set as 6σ of the gaussian function. And the peak of the pulse occurs at μ. For ps laser (FWHM=28 ps), the μ is 35.67 ps. For ns laser (FWHM = 6 ns), the μ is 7.64 ns. Subscript letters “e”, “l” and “m” refer to electron, lattice and medium. K is thermal conductivity, C is specific heat and G is thermal coupling factor. The heat trasfer between water and nanoparticle has a finite interfacial thermal conductance, h. The value and expression of thermal properties are listed in table S1.
For ns laser heating, due to the relatively long laser duation, we neglected the electron-phonon interaction and only consider heat transfer by phonons. Therefore, tradiational one temperature model (OTM, heat conduction equation) and TTM leads to the same result.
The size dependent melting point for gold nanosphere is calculated through the Gibbs-Thomson relation:
| (17) |
where Lm is the latent heat of gold during melting, Tm is the size dependent melting point, Tm* is the melting point of the bulk gold, σsl is the interface tension between the solid and liquid gold, κ is the mean curvature, ρs is the solid gold density (19300 kg m−3). Δc is the difference between the specific heat of solid and liquid gold (34 J kg−1 K−1)48.
Molecular dynamics simulation
The process of gold nanoparticle fragmentation induced by ps laser irradiation was numerically investigated using the LAMMPS molecular dynamics package49–50. Single AuNPs with diameters of 5 and 15 nm were immersed in a cubic water box with side dimension of 10 and 20 nm, respectively. The system was initially equilibrated to ambient temperature (300K) and pressure (1atm) under NPT ensemble. Laser heating was then simulated by applying a uniform heating power to the AuNP atoms in order to rapidly heat the AuNP, followed by a final time period during which the system was allowed to return back to ambient conditions. The periodic boundary condition (PBC) was applied along every direction for all the simulations. For solvation, the TIP3P water model was adopted with the interaction energy computed as follows51,
| (18) |
| (19) |
| (20) |
| (21) |
The Ustretch and Ubend compute the bonded interaction for bond stretching between neighbor atoms and angle bending between neighbor bonds, respectively. The nonbonded interaction composed of two terms. First, the van der Waals interaction, ULJ, which was described by 12–6 Lennard-Jones (LJ) potential. Second, the Uelectrostatic accounts for the Columbic interaction between charged atoms. The parameters are listed in Table S1.
For the interaction among gold atoms, the embedded atom method (EAM) was adopted using the parameters developed by Grochola et al.52. The total energy of each atom was computed as follows,
| (22) |
where Fα is the embedding energy which is a function of the atomic electron density ρβ, φαβ is the pair potential interaction with α and β denoting each pair of atom type. Since we only have one metal atom, Au, in the system, α and β would be identical here.
Models for the thermionic emission and the Coulomb instability
When electrons exceed the critical energy state, they can be ejected from gold atoms and leave the atom with positive charges, known as electron ejection. The multiphoton stimulation and photoelectronic effect can be neglect for ps and ns laser heating23. Therefore, the thermionic emission is the only mechanism for electron ejection in our model. The number of ejected electrons from single particle was calculated by equation:
| (23) |
where nε is electrons that ejected per atom and α is the total number of single AuNP. nε can be calculated by following equation:
| (24) |
where EDOS is electron density of states function, εc is critical energy state (10.23 eV). f is Fermi-Dirac distribution:
| (25) |
where E is energy level (in eV), μ(Te) is chemical potential, and Te is electron temperature.
α can be calculated by following equation:
| (26) |
We assumed the AuNP is spherical and VNP is volume of the AuNP. afcc is the basic length of the unit cell in fcc crystal, 4.08 Å for gold.
Lastly, we calculated Coulomb instability using Rayleigh instability and metal fission model. The Rayleigh instability factor X was calculated by following equation:
| (27) |
where Ne is total number of free electrons in gold. We assume every atom contributes one electron, thus, Ne = α. rws is Wigner-Seitz radius, σ is surface tension of gold, and e is elementary charge. The parameters used in this paper are listed in Table S1.
RESULTS AND DISCUSSION
Picosecond laser pulse induced fragmentation is weakly dependent on the nanoparticle size and occurs at laser fluence 1–2 orders of magnitude lower than that of nanosecond laser.
We first developed a simple but sensitive method to monitor nanoparticle fragmentation by extinction spectral analysis and validated the method with electron microscopy. The extinction spectrum changes of AuNP colloidal solution after laser originated from nanoparticle fragmentation, and increases with higher laser fluence (Figure 1A, steps 1&2). A 2D ratio map was used to find the extinction ratio that is sensitive to the fragmentation (Figure 1A, step 3). For instance, for 15 nm AuNP under ps laser (532 nm, full width half maximum (FWHM) = 28 ps), the fluence dependence of two representative extinction ratios is shown in Figure 1A (step 4, 500/525 nm, and 550/570 nm). The TEM images support the extinction analysis that fragmentation under ps laser occurs around 1 mJ/cm2 (Figure 1B). On the other hand, fragmentation under ns laser requires much higher fluence (532 nm, 300–400 mJ/cm2, FWHM = 6 ns, Figure 1C), as confirmed by TEM imaging. Importantly, instead of forming small spherical fragments under ps laser, ns laser-induced fragmentation forms continuous extrusions that attach onto original particles. A previous study demonstrated that particle fragmentation under ns laser can be a single-step process where the whole particle is fragmented into uniform daughter particle only when the laser fluence is sufficiently large (2000 mJ/cm2, peak power > 1.6 × 1012 W/m2)53. The fragmentation threshold for ns laser fragmentation in our experiments has a peak power lower than the whole particle fragmentation threshold. Therefore, large particles along with continuous extrusions are expected in our ns pulse laser experiments. These results confirm that extinction analysis is a feasible method to monitor nanoparticle fragmentation under pulsed lasers.
Figure 1. Fragmentation threshold fluences for gold nanosphere (AuNP) by laser irradiation.
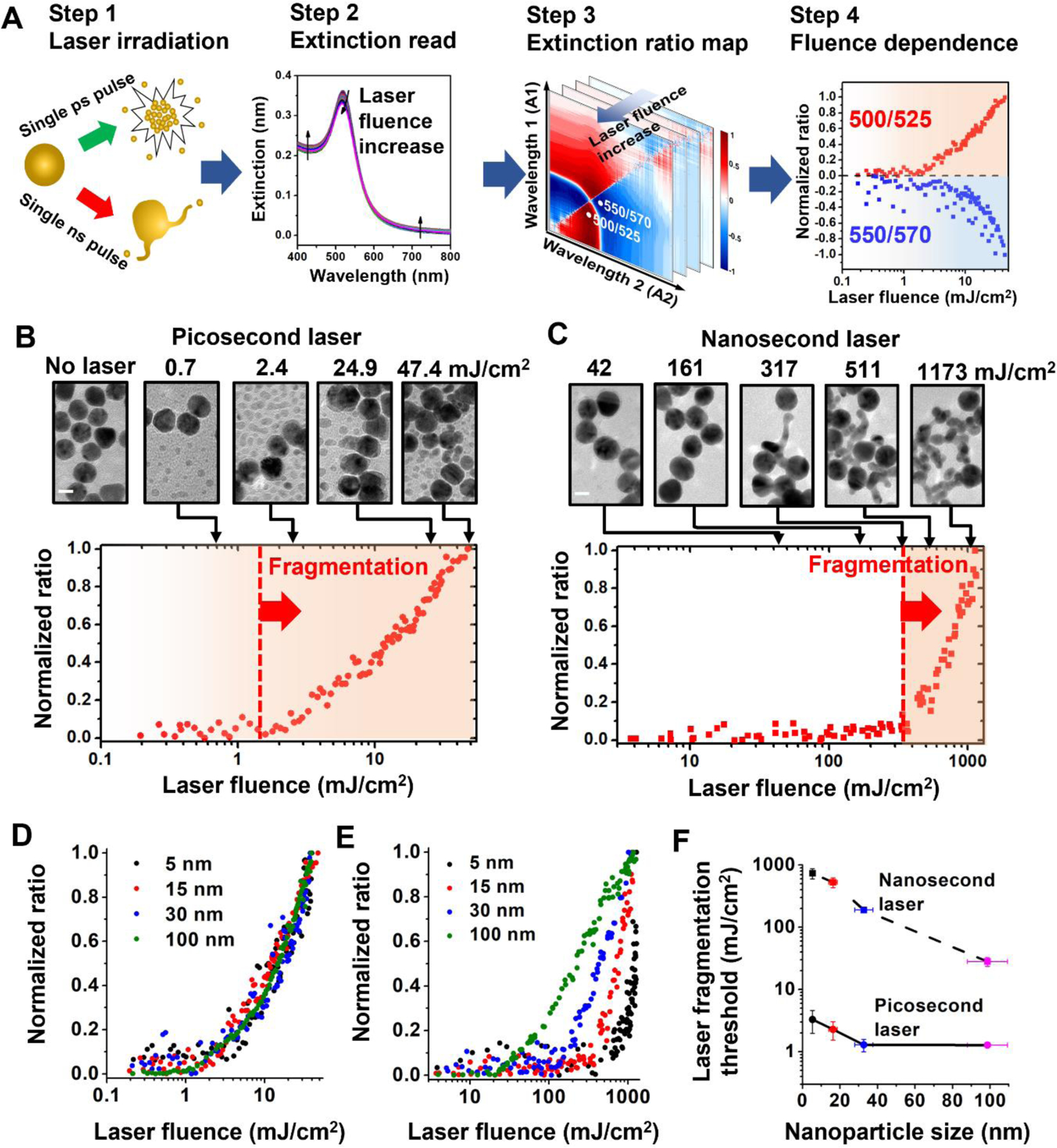
(A) Experimental and analysis procedure for fragmentation of AuNPs. (B-C) Extinction analysis and TEM images for fragmentation of AuNPs (diameter = 15 nm) by picosecond laser (B, Full width half maximum, FWHM = 28 ps) and nanosecond laser (C, FWHM = 6 ns). For picosecond laser, the normalized ratio at 500/525 nm shows increases when fluence is large than 1 mJ/cm2. For nanosecond laser, the ratio (450/500 nm) increase occurs when laser fluence is higher than 300 mJ/cm2 as the fragmentation threshold. TEM images support extinction analysis for fragmentation. (D-E) Extinction analysis for different particle sizes under picosecond laser (D) and nanosecond laser (E). (F) Threshold fluences of fragmentation under picosecond and nanosecond laser for different particle sizes. Note that the reported laser fluences are the peak fluence of the Gaussian energy distributions at the surface of irradiated sample wells.
Next, we examined nanoparticle fragmentation under ps and ns laser for a broad range of AuNP particle sizes (5 nm to 100 nm). We compared the fluence dependence for extinction ratios with different particle sizes (Figure 1D–E and S2). We found that for ps laser-induced fragmentation the laser fluence threshold occurred in the range of 1–2 mJ/cm2 for all particle sizes (Figure 1D and 1F), indicating that the threshold for ps laser induced-fragmentation was weakly dependent on particle size. In contrast, the threshold fluence of fragmentation for ns laser exhibits a clear dependence on the particle size (Figures 1E and 1F), a 30-fold decrease from 600 mJ/cm2 for 5 nm AuNPs to 20 mJ/cm2 for 100 nm AuNPs. Finally, the thresholds for fragmentation observed for ps laser irradiation (1–2 mJ/cm2) were approximately 1–2 orders of magnitude lower than those observed for ns laser irradiation (20–600 mJ/cm2, Figure 1F).
Picosecond laser excitation generates a bimodal nanoparticle size distribution that is dependent on original particle size.
To investigate the morphology of fragmentated nanoparticles under ps laser pulse, TEM images were analyzed to obtain the histograms for the size distribution of the AuNPs with different nominal sizes (5 nm, 15 nm, and 100 nm for Figure 2A–C) before and after exposure to single ps laser pulse. After laser irradiation, small fragments were detached from original particles. These newly generated daughter particles are mostly spherical but much smaller than parent particles.
Figure 2. Bimodal size distribution for fragmentation under picosecond laser.
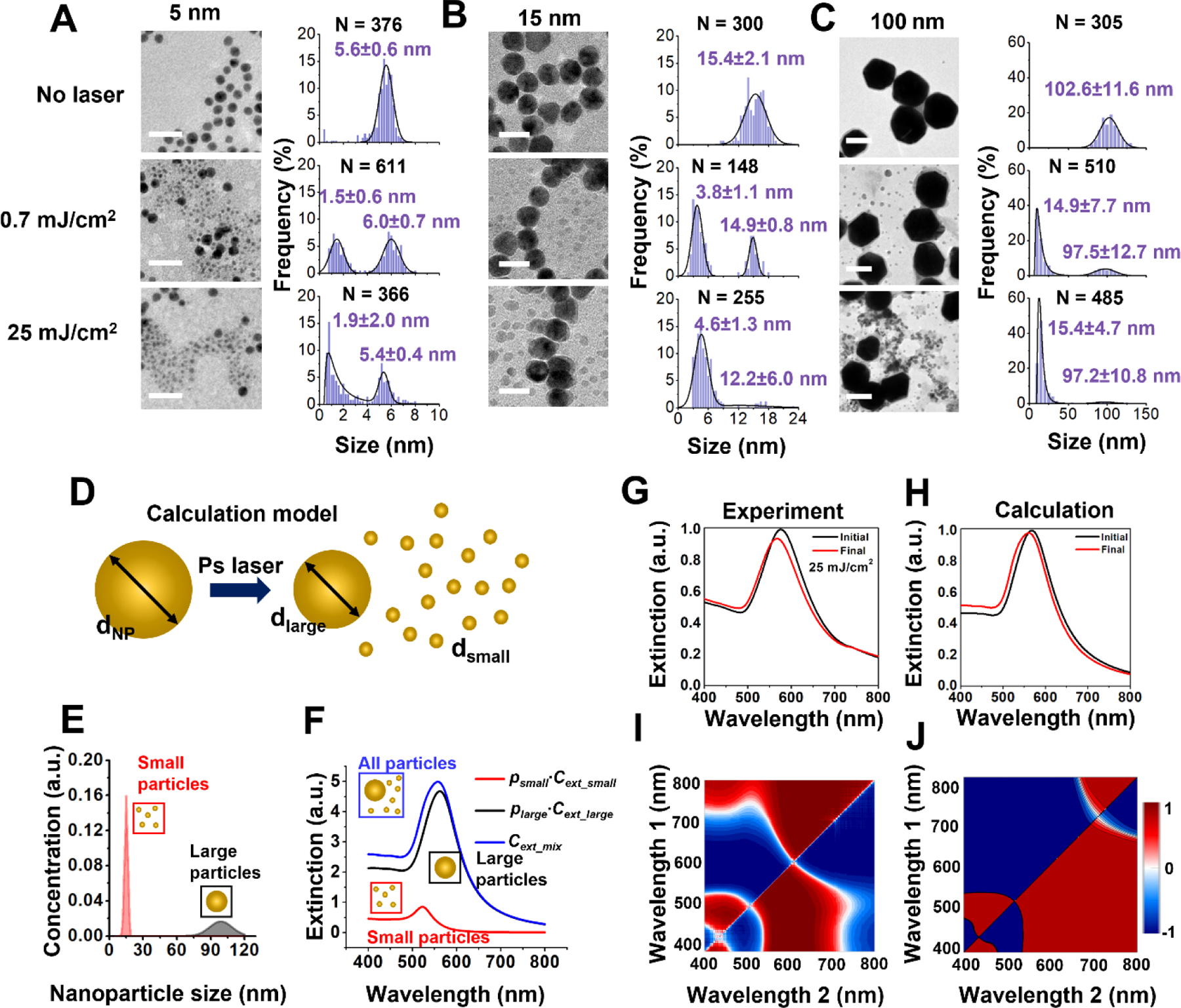
TEM images and particle size distribution before and after picosecond laser irradiation for (A) 5 nm, (B) 15 nm and (C) 100 nm AuNPs. Scale bars are 20 nm for TEM images in (A) and (B) and 100 nm for TEM images in (C). Small particles with a relatively uniform size form after picosecond laser pulse irradiation. Higher laser energy (0.7 mJ/cm2 to 25 mJ/cm2) increases the number of small particle formation. The solid curve is a fit to a distribution function (normal or lognormal) with the corresponding mean and standard deviation. The value of N denotes the number of particles analyzed to generate the histogram. (D) Schematic for modeling extinction spectrum change induced by AuNP size reduction. The initial particle (dNP) will fragment into a large daughter particle (dlarge) and many small daughter particles (dsmall) (E) The size distribution of 100 nm AuNPs after laser treatment when 1% of particles are fragmented. (F) Contributions of small particles (psmall∙Cext_small) and large particles(plarge∙Cext_large) to collective extinction (Cext_mix). p is the number percentage of the corresponding population. (G-H) Experimental and predicted extinction spectra before and after laser fragmentation. (I-J) The extinction ratio maps from experiment and Mie theory calculation. The blue and red color correspond to the decrease and increase of the absorption ratio at the wavelength set relative to the original sample. The experimental and computed extinction ratio maps show qualitative similarity, demonstrating that we could recover the spectral changes resulting from the nanoparticle fragmentation under ps laser.
The population of daughter particles increases with laser fluence, and the size of daughter particles increases with the original particle size. For instance, after ps laser irradiation, the diameters of daughter fragments are around 2 nm, 5 nm, and 15 nm for AuNPs with original sizes of 5 nm, 15 nm, and 100 nm, respectively. We calculated the extinction spectra based on the size analysis of TEM images for 100 nm AuNPs (average dNP = 99 nm), under the assumption that the change of total volume of AuNPs induced by fragmentation is negligible (Figure 2D). After laser treatment, a portion of particles fragmented to generate a bimodal size distribution which had sizes around 10 nm (average dsmall) and 90 nm (average dlarge) (Figure 2E). Because the concentration of 10 nm AuNPs is much higher than that of 90 nm AuNPs (Figure 2E), the contribution of 10 nm AuNPs to the collective extinction is evident and causes a blue shift of the extinction peak. (Figure 2F–H). The calculated extinction spectra of AuNPs before and after laser treatment are comparable with experimental data (Figure 2G–J), and the 2D ratio map for extinction shows similar trend between experiment and calculation (Figure 2I–J). Therefore, we were able to recover the spectral changes resulting from the nanoparticle fragmentation under ps laser.
Picosecond laser pulse fragments nanoparticles below whole particle melting point and Coulomb instability.
Next, we compared ps and ns laser-induced fragmentation against known mechanisms of nanoparticle fragmentation, including Coulomb instability (CI) and phase transition (PT). The temperature evolution of a AuNP with a diameter of 15 nm was calculated by a two-temperature heat transfer model (TTM) under both ps and ns laser irradiation, at their respective laser fluence thresholds for fragmentation of 2.3 mJ/cm2 (ps laser) and 527 mJ/cm2 (ns laser) (Figure 3A–B & S5). Because the ns laser has a duration (6 ns) that is much longer than electron-phonon coupling time (few ps), electrons are in equilibrium with the phonons so that the electron temperature (Te) calculation can be neglected23, 47. Under ns laser irradiation, the model predicts that the gold lattice temperature exceeds the boiling point at its peak, suggesting that ns laser induced fragmentation is likely due to the PT mechanism. Although the electrons in gold are heated up to a very high temperature (~3000 K) during ps laser irradiation, the gold lattice temperature is predicted to be well below the melting point, eliminating the possibility for the PT mechanism. To investigate whether CI contributes to nanoparticle fragmentation, the Rayleigh stability factor (X) was used to estimate the balance between the Coulomb force and the surface tension (Figure S5). The particle is unstable due to CI when the X factor is larger than 0.3 54. For instance, the X factor of AuNPs with a diameter of 45 nm exceeds 0.3 when the fluence of the ps laser is between 17 and 18 mJ/cm2 (Figure S5C), indicating the fluence threshold for CI. For AuNP with a diameter of 15 nm, to reach the CI threshold, the fluence of the ps laser would need to be 10 times larger than the fragmentation threshold. Therefore, the ps induced particle fragmentation cannot be explained by the CI mechanism.
Figure 3. Mechanism of laser-induced fragmentation under picosecond (ps) and nanosecond (ns) laser.
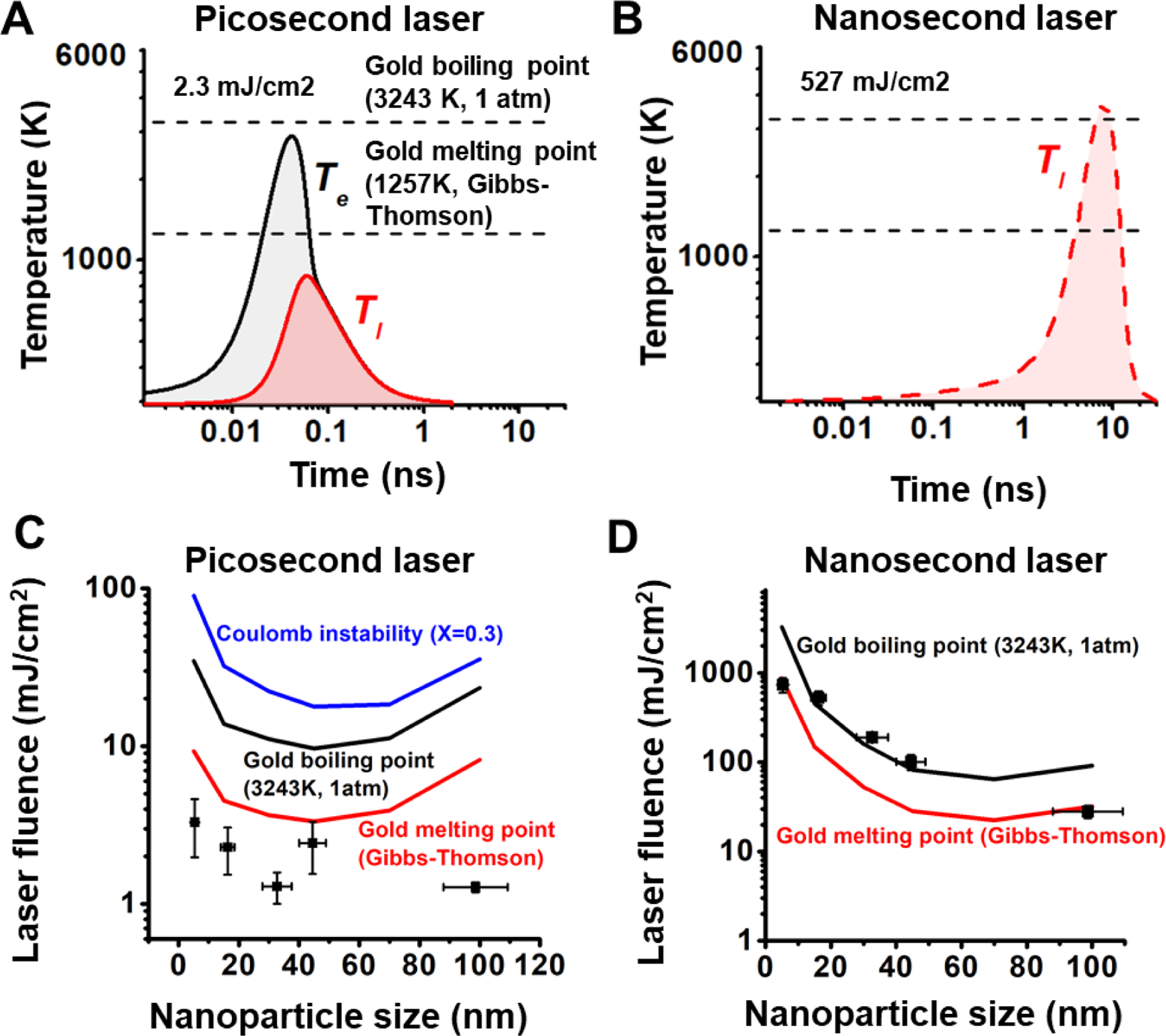
(A-B) Temperature evolution for 15 nm AuNP under ps (A) and ns (B) laser at fragmentation threshold fluences. Gold melting point and boiling point are marked with dashed line in the plot. (C-D) Comparison of the particle fragmentation threshold with gold melting and boiling point, and Coulomb instability for ps laser (C) and ns laser (D). The fluence of Coulomb instability achieves when Rayleigh instability factor (X) reaches to 0.3.
We further examined the fragmentation across a range of nanoparticle sizes. Varying nanoparticle size affects the plasmonic heating process in two ways. First, the absorption cross section is strongly dependent on particle size, causing different levels of heat generation for different particle sizes. Second, the heat dissipation from AuNP to water is dependent on the surface-to-volume ratio of the particle10. Small particles have larger surface-to-volume ratio which makes the heat transfer more efficient than for larger particles. The temperature of a AuNP reflects the balance between these two factors. For instance, the 45 nm AuNPs achieve the highest particle temperature under ps laser heating, while the 70 nm AuNPs have the highest NP temperature under ns laser heating (Figure S6). This demonstrates that the duration of laser irradiation can have a significant effect on the nanoparticle heat transfer, allowing different thermophysical processes to occur for different sized particles.
Next, we systematically examined the threshold fluences for different particle sizes (Figure 3C–D). Interestingly, the threshold fluence for fragmentation under the ps laser is below the melting point for all particle sizes (5~100 nm). Since both PT and CI explains fragmentation of AuNPs above the melting point, these two mechanisms cannot be responsible for the ps laser-induced fragmentation. On the other hand, the threshold fluence for fragmentation under ns laser shows a similar trend as the gold boiling point55. Therefore, we conclude that the PT mechanism is the dominant mechanism for fragmentation of AuNPs under ns laser heating. We also tested the effect of sodium dodecyl sulfate (SDS) on the particle fragmentation. We compared the fragmentation behavior of 15 nm AuNPs in pure water with that in the SDS solution at a concentration of 90 mM, which is higher than its critical micelle concentration (8.9 mM) (Figure S7). A previous study demonstrated that the negative charge of SDS micelles is able to stabilize holes formed upon ionization, resulting in an increase in the ionization yield56. If the fragmentation is induced by thermionic emission under the CI mechanism, the fragmentation should be enhanced by the addition of SDS. However, our results show that the addition of SDS hindered the fragmentation under ps laser, suggesting that the fragmentation under ps laser does not originate from laser ionization.
Lastly, we studied the contribution of thermomechanical force to the ps laser fragmentation using molecular dynamics (MD) simulation57. AuNPs with diameter of 5 nm and 15 nm can be fragmented when the laser intensity was higher than 40 and 20 mJ/cm2, respectively (Figure S8A–B). The fragmentation cases show the maximum gold temperature above the boiling point (Figure S8C–D). The nanoparticle heating leads to thermal expansion and a high mechanical stress within the nanoparticle (Figure S8E–G). The thermomechanical force causes movement of atoms and leads to a disordered lattice structure. In order to release the thermomechanical force, some unstable atoms are ejected from the particle, behaving as the fragmentation. The MD simulation demonstrated the thermomechanical force plays an important role in the phase explosion induced fragmentation. However, it is worth noting that our MD study demonstrates that particle fragmentation occurs only above the boiling point which does not agree with our experimental observations. Therefore, the thermomechanical stress was not sufficient to explain the anomalous fragmentation observed in ps laser experiments.
Comparison with previous work.
We summarized previous reported experimental conditions for ps laser induced plasmonic nanoparticle fragmentation in Table S2. Most studies reported plasmonic nanoparticles can be fragmented by lasers with fluences in the range of 10~30 mJ/cm2, which brought the particle temperature above the boiling point and suggested a phase explosion mechanism. The ps induced AuNP fragmentation at solid state in this study has threshold fluences lower than most published data, which indicates a mechanism that has not been reported.
Differences in the heating dynamics of nanosecond and picosecond laser excitation.
The laser pulse duration can have a significant effect on the plasmonic heating of nanoparticles. A detailed discussion of the timescales involved in laser heating of nanoparticles and how they relate to pulse duration can be found in the review by Baffou and Quidant58. Briefly, plasmonic heating consists of three basic processes: light absorption, nanoparticle heating, and heat dissipation from the nanoparticle into the surrounding medium. Whether these processes are effectively sequential or overlapping is largely dependent on the laser pulse duration. The duration of a ns pulse is long enough that the three plasmonic heating processes tend to be overlapping, so the particle can dissipate a significant portion of heat into the solvent during the laser pulse. In contrast, the duration the ps pulse is closer in scale to the electron-phonon coupling time (~2 ps) and the amount of heat dissipated during the laser pulse tends to be much more limited as compared to a ns pulse. Additionally, the electron and lattice temperatures remain out of equilibrium for duration of a ps pulse, which is why a two-temperature heat transfer model is required to accurately model the ps laser heating during the pulse duration. As a result, the AuNP temperature dynamics resulting from ps pulse heating are quite different from those of ns pulse heating (Figure 3A–B).
As noted in the previous section, past studies suggest that ps laser irradiation tends to fragment plasmonic particles by a PT mechanism at a lower range of fluences (10~30 mJ/cm2, Table S2) than what we observed for ns laser fragmentation (20–600 mJ/cm2, Figure 1F). In part, the differences in heat dissipation between ns and ps pulse irradiation can account for the lowered threshold for fragmentation by ps laser due to a PT mechanism. Regardless, as we previously discussed, the lattice temperature remains below the whole particle melting point during ps laser irradiation at the fragmentation threshold fluence (Figure 3A,C), and the Rayleigh stability is well below the threshold necessary for fragmentation by CI (Figure 3C). Therefore, neither PT nor CI mechanisms can fully explain the ps laser induced fragmentation we observed at low laser fluence (~1–3 mJ/cm2, Figure 1B,F).
Proposed mechanism of combined near-field enhancement and surface melting.
Near-field ablation is another mechanism responsible for nanostructure fragmentation. The near-field ablation is related to field enhanced diffusion that a strong electric field in the vicinity of nanostructure surface can enhance the surface atom diffusion and causes material deformation/emission59–61. The alteration of surface atoms by the near-field does not necessarily require an obvious heating59 or material phase transition28. For example, Plech et al. demonstrated that AuNPs can be fragmented by near-field ablation without particle melting under fs laser irradiation28. In this case, the solid surface layers were ablated from the nanoparticle at a near-field threshold strength of 9.3 ~ 12.3 V/nm 28.
Another important factor that contributes to the change of particle morphology is particle surface melting47. Importantly, surface melting of gold nanostructures can be observed at a much lower temperature than the melting point of bulk gold. For instance, Inasawa et al. demonstrated that AuNPs can be reshaped and fragmented under 355 nm ps62. Under those conditions the laser energy was insufficient to melt the whole particle, suggesting that the observed change in morphology was induced by surface melting. Petrova et al. observed obvious shape transitions of gold nanorods under oven heating of less than an hour at 423K (~32% of the melting point of bulk gold)63. Similarly, Plech et al. demonstrated the surface melting of AuNPs supported on a surface occurs at 377 K (30% of the melting point of bulk gold)64. Based on these observations, we reasoned that the surface of AuNPs becomes molten while the core of the particle remains still solid during ps laser heating (Figure 3).
Considering that both near-field enhancement and surface melting may occur under ps laser heating, we propose a fragmentation mechanism that combines these two phenomena to explain small particle ejection from the surface AuNPs during low fluence ps laser heating. Briefly, the surface temperature of the AuNP exceeds the surface melting point while the core of the particle is still solid during the ps laser. The molten surface layer has a weak surface tension which leads to a reduced threshold of electrostatic instability for the particle. Meanwhile, the near-field enhancement leads to a strong electric field in the vicinity of the particle. Combining these two effects, the molten material can be ejected from the surface by electrostatic force and forms small fragments around the large particle (Figure 4A).
Figure 4. Electric field enhancement and surface melting of gold nanoparticles (AuNPs).
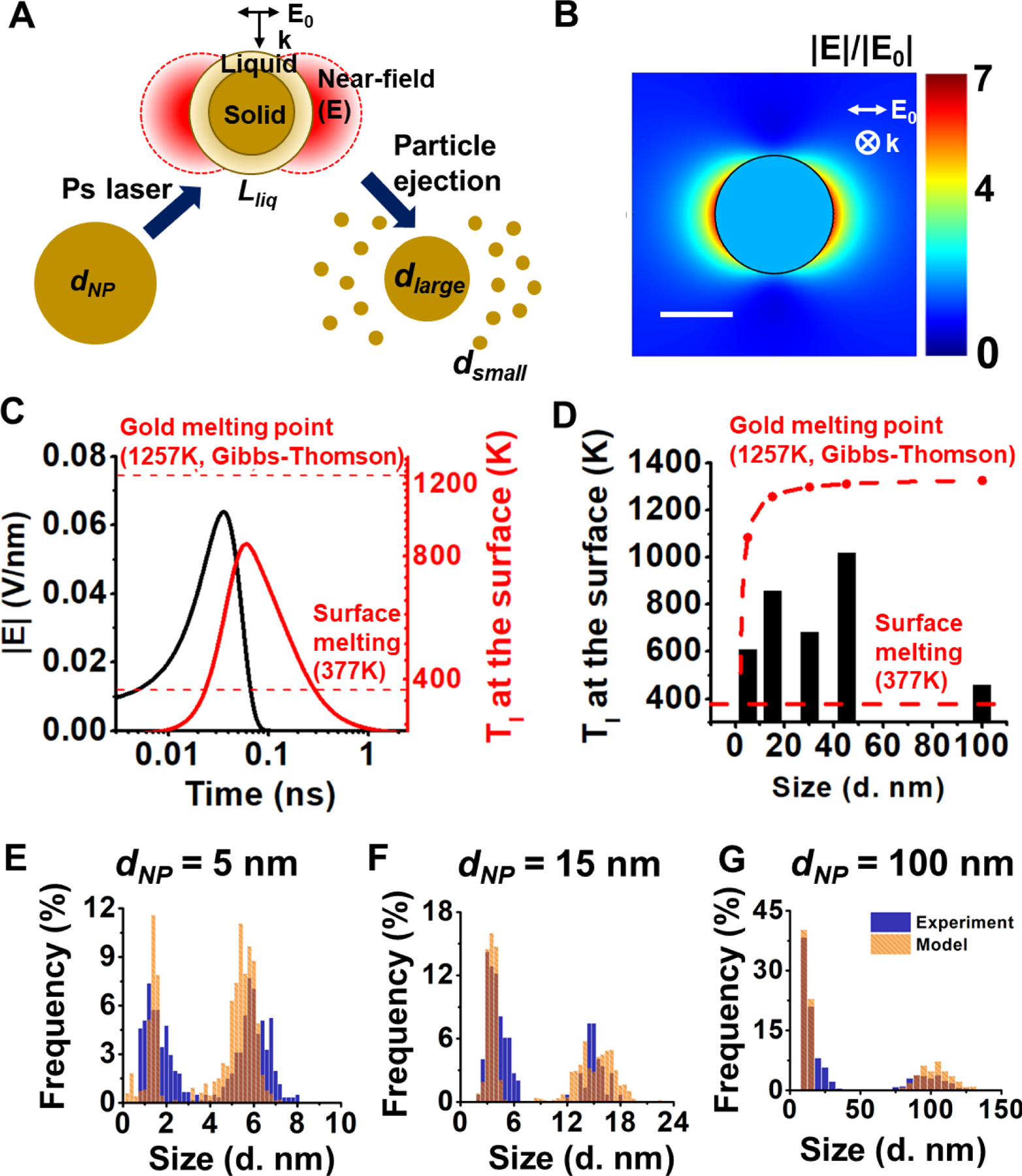
(A) Schematic of proposed mechanism for fragmentation under ps laser. The strong enhanced electric field combing with surface partial melting leads to a layer of material ejection (Lliq) and particle fragmentation. The final product is composed of particles with two different sizes (dsmall and dlarge). (B) The enhancement of electric field around a AuNP with the diameter of 15 nm. Scale bare is 10 nm. (C) The electric filed strength (|E|) and gold lattice temperature (Tl) at the surface of the 15 nm AuNP when expose to the fragmentation threshold fluence (2.3 mJ/cm2). The reported surface partial melting point of gold (377 K) and the whole particle melting point (1257 K for 15 nm AuNP) are marked by red dash lines. (D) The maximum gold lattice temperature at the surface of particles with different sizes at their fragmentation threshold fluences. For comparison, the surface melting temperature and particle melting temperature are shown. (E-G) The fitting for the distribution of particles after laser treatment for 5 nm (E), 15 nm (F), 100 nm (G) AuNPs by starting with the experimentally determined size distributions before laser irradiation and assuming 6~10% surface melting.
To investigate this hypothesis, we first calculated the electric field enhancement around the nanoparticle. The electric field can be enhanced by 6~7 fold compared with the electric field of the incident light which translates to an electric field with the strength of 0.04~0.08 V/nm (15 nm AuNP as an example, Fig. 4B–C). Next, we calculated the gold lattice temperature (Tl) at the surface under the ps laser fragmentation threshold (Figure 4C). For instance, the maximum lattice temperature for 15 nm AuNP at the particle surface is 855 K, which is well above the surface melting point (377K) but lower than the whole particle melting point (1257 K, calculated from Gibbs-Thomson equation) and the bulk gold melting point (1337K). This can lead to a gold nanoparticle with a molten surface and a solid core. This surface melting of gold nanoparticles can occur for all sizes of nanoparticles at their fragmentation threshold (Figure 4D). The surface tension of molten gold (<1.15 N/m)65 is much smaller than that of solid gold (8.78 N/m)66. The instability factor of electrostatic instability of a spherical droplet in an electric field can be expressed as R|E|2/σ, where R is the radius, E is the electric field and σ is the surface tension of the droplet67. By considering a constant particle radius during heating, the instability factor increases by 274 to 372 times when considering the enhanced electric field and surface melting. It is worth noting that although the instability model of liquid droplet was derived from micrometer sized droplets, the surface tension has been demonstrated valid and significant for the stability of metal nanostructures68–70. Furthermore, we estimated the size of fragmented particles by assuming a layer of molten material ejected from the surface (Table S3). The molten layer thickness is around 6% to 10% of the original particle diameter at the surface melting temperature64. By starting with the size distribution before fragmentation and then assuming the complete removal of the thin molten layer and formation of small particles from the ablated layer, we were able to accurately fit the bimodal particle size distribution that occurs after laser irradiation (Figure 4 E–G). In this fitting, we assumed that the original particles were perfectly spherical with sizes corresponding to the distribution before fragmentation at the given nominal diameter and that the diameter of daughter particles formed from the ablated surface layer could be estimated by dividing the volume corresponding to the surface layer (6–10 % of original particle diameter) uniformly into equal-sized spherical fragments. The remaining core particle after surface ablation was also assumed to be perfectly spherical with a diameter given by the difference of the parent particle diameter and the thickness of the molten surface layer. We found that when a 5 nm AuNP fragments, about 4 small daughter particles will be ejected from the molten layer. For 100 nm AuNP, there will be on the order of 100 or more small daughter particles with the average size of 12 nm when fragmentation happens, as well as a remaining core of 90 nm. The particle size estimation based on surface melting model agrees with our experimental observation (Table S3). Therefore, the enhanced electric field could eject materials from the melted particle surface, leading to the observed fragmentation below the whole particle melting.
We have summarized how this proposed mechanism relates to other fragmentation mechanisms in Figure 5. Under femtosecond laser irradiation, the particle can be fragmented in the solid-state by a mechanism known as near-field ablation28. As the laser fluence increases, particles can be fragmented by Coulomb instability (fission) which requires the particle to be molten71. For the picosecond laser, particles can be fragmented with a low-energy laser that does not cause the whole particle to melt. Instead, the molten surface layer of particles can be ejected by the enhanced near-field during laser excitation: the model proposed in our work. If the laser energy is high enough to melt the whole particle, the fragmentation can be by Coulomb instability or thermomechanical force, depending on the particle size35. For laser energy high enough to induce particle boiling, the violent phase transition is the dominant force for particle fragmentation under all laser durations23, 36.
Figure 5.
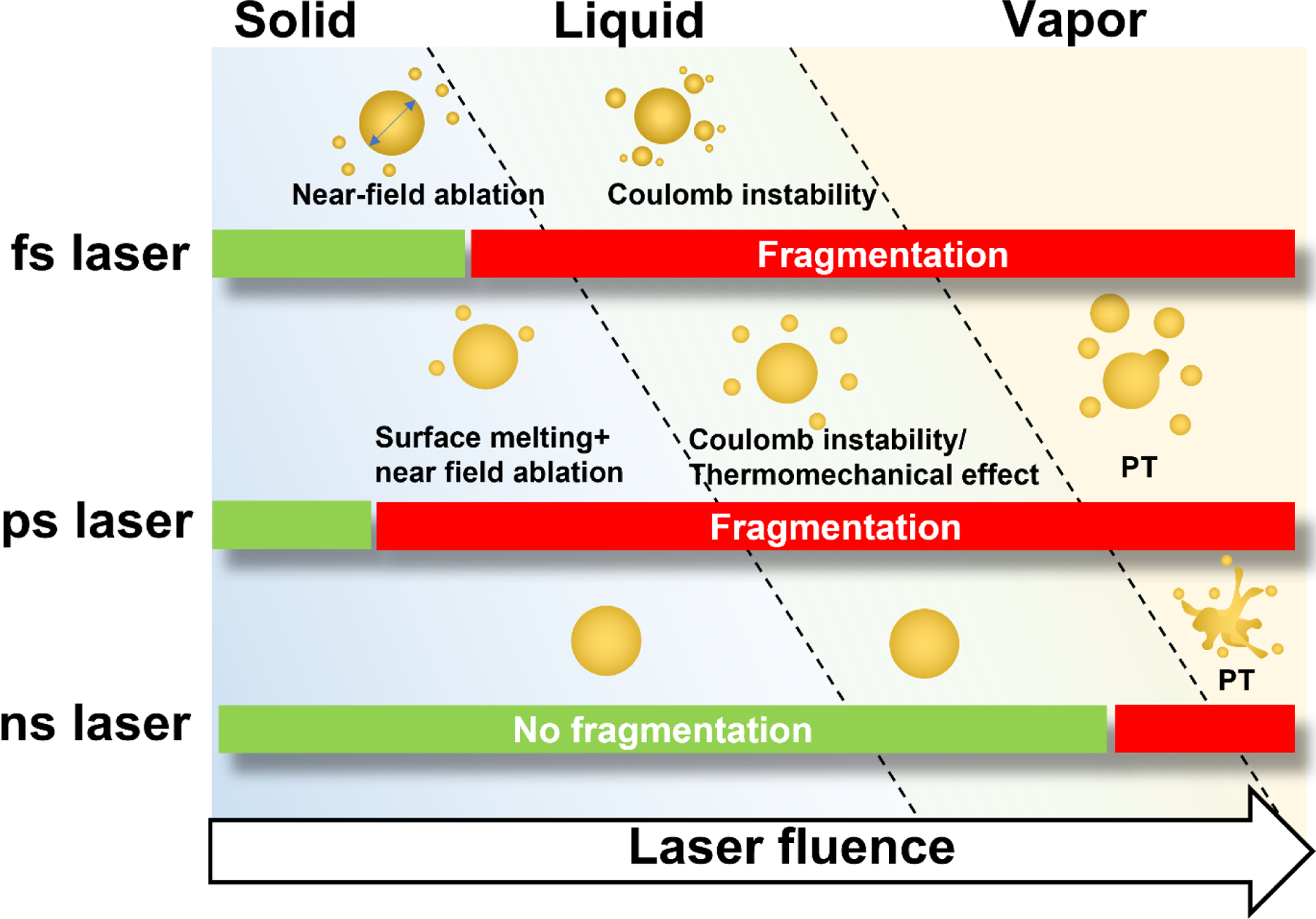
Proposed schemes for laser-induced fragmentation under picosecond and known mechanisms for other laser pulse-induced fragmentation.
It is worth further clarifying how our proposed model differs from Coulomb instability invoked by previous studies. Coulomb instability was mainly observed under fs laser due to the multiphoton ionization of the nanoparticles32, 71. Although not theoretically required, Coulomb instability practically requires the particle to be molten before fragmentation for electrostatic forces to overcome the surface tension23. The requirements for multiphoton ionization and particle melting are in conflict because the time ranges of ionization and melting are very different. In other words, when melting happens (in ps range), ionization of the particle has already ended (in fs range). To resolve this contradiction, the negative charges emitted by the particle should have a lifetime that is longer than the melting and fission processes. In order to observe dual-core formation, multiple pulses need to be applied to the sample. In contrast, our model does not require the particle to be ionized by the laser. Instead, the particle may be uncharged, and instability arises from an applied electric field that creates polarization and electrostatic stress across the particle surface67. Because our laser duration is beyond 10s of ps, our model allows the simultaneous existence of both surface melting and the enhanced electrostatic near-field. The near-field and melting can interact with each other which leads to small particle ejection. Therefore, our model allows for fragmentation within a single laser pulse exposure. It’s also worth noting that surface melting is another key distinction between the mechanism we propose, and the near-field ablation observed for fs laser pulse stimulation. In near-field ablation, solid surface atoms are ejected by the enhanced near-field without any melting, which is why the threshold field strength (9.3 ~ 12.3 V/nm) is much higher than what we estimated for ps laser heating (0.04~0.08 V/nm for 15 nm AuNP).
The effect of interfacial heat transfer.
The heat transfer process at the interface of nanostructures is still an emerging area with many unknowns. The interface thermal resistance used in this study is obtained from previous measurement72. However, the interface heat transfer can be a function of temperature, interface curvature, solvent type, synthesis method, and nanoparticle morphology73–75. The variation of interface heat transfer can significantly affect the gold temperature, especially for ns laser 76. Also, the phase change in water was not considered in the current model. Water can be heated and evaporated on the surface of the nanoparticle upon laser irradiation, generating what is known as a plasmonic vapor bubble. The vapor bubble formation will modulate the resonance condition of a AuNP and alter the heat transfer. The nanobubble forms when the water temperature reaches the spinodal temperature, which is 85% of the critical temperature of water 77. The water temperature of ns laser fragmentation is beyond the nanobubble threshold while that of ps laser fragmentation is below this point. The formation of vapor bubble may hinder the heat transfer from gold to water and leads to heat accumulation in the particle during nanosecond laser. The real gold temperature may be higher than our estimation which means PT mechanism may contribute more to the ns laser fragmentation. For ps laser, we measured the nanobubble generation of 100 nm AuNPs with a pump-probe optical setup42, the vapor nanobubble generation probability at the fragmentation threshold (1.3 mJ/cm2) is less than 1% (Figure. S9). Therefore, no vapor bubble formation is expected during the ps laser fragmentation.
In our experiment, we utilized citrate coated gold nanoparticle to conduct the laser fragmentation experiment. Some studies demonstrated that the citrate molecules can play an important role in the particle shape evolution during laser irradiation78. Using bare AuNPs to study the laser-induced fragmentation can exclude the effect of surface ligands33. So far, it is still not clear how the surface ligands affect the laser-nanomaterial interaction as well as the heat transfer process. It is possible that the citrate coating alters the interfacial thermal resistance and cause a temperature difference in gold than the model prediction76.
CONCLUSIONS
In this study, we investigated the fragmentation of AuNPs under ps and ns laser with experiments and numerical simulations. The behaviors of fragmentation induced by ps and ns laser show large differences including the threshold fluence (1–2 orders of magnitude lower for ps) and morphology change (discrete particles versus extrusions). Whereas the ns laser induced fragmentation can be explained by the PT mechanism, neither PT nor CI mechanisms can fully explain the ps laser induced fragmentation which occurs while the whole AuNPs are still in the solid state (Figure 5). Although the molecular dynamic simulations suggested that the mechanical stress may play a significant role in ps laser-induced fragmentation under high laser intensity, it could not explain ps laser-induced fragmentation below the AuNP melting point. Lastly, we provided a framework based on near-field enhancement and nanoparticle surface melting to account for the ps laser-induced fragmentation under low laser intensity. This study reveals a previously unknown regime of nanoparticle fragmentation.
Supplementary Material
ACKNOWLEDGMENT:
Funding:
Research reported in this publication was partially supported by National Institute of General Medical Sciences of the National Institutes of Health under award number R35GM133653, and by the National Science Foundation under Grant No. 1631910. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.
Footnotes
Supporting Information. Supporting information contains following content: Figure S1. Laser beam profile measurement. Figure S2. Extinction analysis for different particle sizes. Figure S3. Material properties for two temperature model. Figure S4. Temperature evolution for 15 nm AuNP under the ns laser in figure 3A. Figure S5. Parameters for the Rayleigh instability model. Figure S6. Volumetric heating factor and the maximum temperature of gold lattice. Figure S7. Influence of sodium dodecyl sulfate (SDS) on picosecond laser fragmentation. Figure S8. Molecular dynamics simulation for fragmentation of AuNP. Figure S9. The probability of vapor nanobubble generation measured by an optical pump-probe setup. Table S1. Parameters in TTM model and MD simulation. Table S2. Previous reported laser fluence of ps laser fragmentation for plasmonic nanoparticles. Table S3. Estimation of particle sizes after a layer of molten material is ejected from the surface and form one daughter particles. The following files are available free of charge. References of supporting information are also included in the main paper.
Supporting information (PDF)
Competing Interests. The authors declare no competing interests.
REFERENCES
- 1.Lalisse A; Tessier G; Plain J; Baffou G, Quantifying the Efficiency of Plasmonic Materials for Near-Field Enhancement and Photothermal Conversion. J. Phys. Chem. C 2015, 119 (45), 25518–25528. [Google Scholar]
- 2.Langer J; Jimenez de Aberasturi D; Aizpurua J; Alvarez-Puebla RA; Auguié B; Baumberg JJ; Bazan GC; Bell SEJ; Boisen A; Brolo AG, et al. , Present and Future of Surface-Enhanced Raman Scattering. ACS Nano 2020, 14 (1), 28–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Moustaoui H; Saber J; Djeddi I; Liu Q; Diallo AT; Spadavecchia J; Lamy de la Chapelle M; Djaker N, Shape and Size Effect on Photothermal Heat Elevation of Gold Nanoparticles: Absorption Coefficient Experimental Measurement of Spherical and Urchin-Shaped Gold Nanoparticles. J. Phys. Chem. C 2019, 123 (28), 17548–17554. [Google Scholar]
- 4.Grigorenko AN; Roberts NW; Dickinson MR; Zhang Y, Nanometric Optical Tweezers Based on Nanostructured Substrates. Nat. Photonics 2008, 2 (6), 365–370. [Google Scholar]
- 5.Adhikari S; Spaeth P; Kar A; Baaske MD; Khatua S; Orrit M, Photothermal Microscopy: Imaging the Optical Absorption of Single Nanoparticles and Single Molecules. ACS Nano 2020, 14 (12), 16414–16445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ando J; Fujita K; Smith NI; Kawata S, Dynamic SERS Imaging of Cellular Transport Pathways with Endocytosed Gold Nanoparticles. Nano Lett. 2011, 11 (12), 5344–5348. [DOI] [PubMed] [Google Scholar]
- 7.Yeh Y-T; Gulino K; Zhang Y; Sabestien A; Chou T-W; Zhou B; Lin Z; Albert I; Lu H; Swaminathan V, et al. , A Rapid and Label-Free Platform for Virus Capture and Identification from Clinical Samples. Proceedings of the National Academy of Sciences 2020, 117 (2), 895–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Huang J-A; Mousavi MZ; Giovannini G; Zhao Y; Hubarevich A; Soler MA; Rocchia W; Garoli D; De Angelis F, Multiplexed Discrimination of Single Amino Acid Residues in Polypeptides in a Single SERS Hot Spot. Angew. Chem. Int. Ed 2020, 59 (28), 11423–11431. [DOI] [PubMed] [Google Scholar]
- 9.Ye H; Liu Y; Zhan L; Liu Y; Qin Z, Signal Amplification and Quantification on Lateral Flow Assays by Laser Excitation of Plasmonic Nanomaterials. Theranostics 2020, 10 (10), 4359–4373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen Y-S; Zhao Y; Yoon SJ; Gambhir SS; Emelianov S, Miniature Gold Nanorods for Photoacoustic Molecular Imaging in the Second near-Infrared Optical Window. Nat. Nanotechnol 2019, 14 (5), 465–472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kang P; Li X; Liu Y; Shiers SI; Xiong H; Giannotta M; Dejana E; Price TJ; Randrianalisoa J; Nielsen SO, et al. , Transient Photoinactivation of Cell Membrane Protein Activity without Genetic Modification by Molecular Hyperthermia. ACS Nano 2019, 13 (11), 12487–12499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alghazali KM; Hamzah RN; Nima ZA; Steiner R; Dhar M; Anderson DE; Hayar A; Griffin RJ; Biris AS, Plasmonic Nanofactors as Switchable Devices to Promote or Inhibit Neuronal Activity and Function. Nanomaterials 2019, 9 (7), 1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tarasenko NV; Butsen AV; Nevar EA, Laser-Induced Modification of Metal Nanoparticles Formed by Laser Ablation Technique in Liquids. Appl. Surf. Sci 2005, 247 (1), 418–422. [Google Scholar]
- 14.Yoon SJ; Murthy A; Johnston KP; Sokolov KV; Emelianov SY, Thermal Stability of Biodegradable Plasmonic Nanoclusters in Photoacoustic Imaging. Opt. Express 2012, 20 (28), 29479–29487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen Y-S; Frey W; Kim S; Homan K; Kruizinga P; Sokolov K; Emelianov S, Enhanced Thermal Stability of Silica-Coated Gold Nanorods for Photoacoustic Imaging and Image-Guided Therapy. Opt. Express 2010, 18 (9), 8867–8878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Besner S; Kabashin AV; Winnik FM; Meunier M, Ultrafast Laser Based “Green” Synthesis of Non-toxic Nanoparticles in Aqueous Solutions. Appl. Phys. A 2008, 93 (4), 955–959. [Google Scholar]
- 17.Popov AA; Tselikov G; Dumas N; Berard C; Metwally K; Jones N; Al-Kattan A; Larrat B; Braguer D; Mensah S, et al. , Laser- Synthesized Tin Nanoparticles as Promising Plasmonic Alternative for Biomedical Applications. Sci. Rep 2019, 9 (1), 1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li Z-Z; Wang L; Fan H; Yu Y-H; Chen Q-D; Juodkazis S; Sun H-B, O-Fib: Far-Field-Induced near-Field Breakdown for Direct Nanowriting in an Atmospheric Environment. Light: Sci. Appl 2020, 9 (1), 41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Violi IL; Gargiulo J; von Bilderling C; Cortés E; Stefani FD, Light-Induced Polarization-Directed Growth of Optically Printed Gold Nanoparticles. Nano Lett. 2016, 16 (10), 6529–6533. [DOI] [PubMed] [Google Scholar]
- 20.Liu D; Li C; Zhou F; Zhang T; Zhang H; Li X; Duan G; Cai W; Li Y, Rapid Synthesis of Monodisperse Au Nanospheres through a Laser Irradiation -Induced Shape Conversion, Self-Assembly and Their Electromagnetic Coupling SERS Enhancement. Sci. Rep 2015, 5 (1), 7686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.González-Rubio G; Díaz-Núñez P; Rivera A; Prada A; Tardajos G; González-Izquierdo J; Bañares L; Llombart P; Macdowell LG; Alcolea Palafox M, et al. , Femtosecond Laser Reshaping Yields Gold Nanorods with Ultranarrow Surface Plasmon Resonances. Science 2017, 358 (6363), 640–644. [DOI] [PubMed] [Google Scholar]
- 22.Inasawa S; Sugiyama M; Yamaguchi Y, Bimodal Size Distribution of Gold Nanoparticles under Picosecond Laser Pulses. J. Phys. Chem. B 2005, 109 (19), 9404–9410. [DOI] [PubMed] [Google Scholar]
- 23.Werner D; Hashimoto S, Improved Working Model for Interpreting the Excitation Wavelength- and Fluence-Dependent Response in Pulsed Laser-Induced Size Reduction of Aqueous Gold Nanoparticles. J. Phys. Chem. C 2011, 115, 5063–5072. [Google Scholar]
- 24.Werner D; Hashimoto S; Uwada T, Remarkable Photothermal Effect of Interband Excitation on Nanosecond Laser-Induced Reshaping and Size Reduction of Pseudospherical Gold Nanoparticles in Aqueous Solution. Langmuir 2010, 26 (12), 9956–63. [DOI] [PubMed] [Google Scholar]
- 25.Spellauge M; Winter J; Rapp S; McDonnell C; Sotier F; Schmidt M; Huber HP, Influence of Stress Confinement, Particle Shielding and Re-Deposition on the Ultrashort Pulse Laser Ablation of Metals Revealed by Ultrafast Time-Resolved Experiments. Appl. Surf. Sci 2021, 545, 148930. [Google Scholar]
- 26.Ihm Y; Cho DH; Sung D; Nam D; Jung C; Sato T; Kim S; Park J; Kim S; Gallagher-Jones M, et al. , Direct Observation of Picosecond Melting and Disintegration of Metallic Nanoparticles. Nat Commun 2019, 10 (1), 2411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Perez D; Lewis LJ, Ablation of Solids under Femtosecond Laser Pulses. Phys. Rev. Lett 2002, 89 (25), 255504. [DOI] [PubMed] [Google Scholar]
- 28.Plech A; Kotaidis V; Lorenc M; Boneberg J, Femtosecond Laser Near-Field Ablation from Gold Nanoparticles. Nat. Phys 2005, 2, 44. [Google Scholar]
- 29.Plech A; Leiderer P; Boneberg J, Femtosecond Laser Near Field Ablation. Laser Photonics Rev. 2009, 3 (5), 435–451. [Google Scholar]
- 30.Plech A; Ibrahimkutty S; Reich S; Newby G, Thermal Dynamics of Pulsed-Laser Excited Gold Nanorods in Suspension. Nanoscale 2017, 9 (44), 17284–17292. [DOI] [PubMed] [Google Scholar]
- 31.Werner D; Furube A; Okamoto T; Hashimoto S, Femtosecond Laser-Induced Size Reduction of Aqueous Gold Nanoparticles: In Situ and Pump−Probe Spectroscopy Investigations Revealing Coulomb Explosion. J. Phys. Chem. C 2011, 115 (17), 8503–8512. [Google Scholar]
- 32.Voss JM; Olshin PK; Charbonnier R; Drabbels M; Lorenz UJ, In Situ Observation of Coulomb Fission of Individual Plasmonic Nanoparticles. ACS Nano 2019, 13 (11), 12445–12451. [DOI] [PubMed] [Google Scholar]
- 33.Ziefuss AR; Reich S; Reichenberger S; Levantino M; Plech A, In Situ Structural Kinetics of Picosecond Laser-Induced Heating and Fragmentation of Colloidal Gold Spheres. Phys. Chem. Chem. Phys 2020, 22, 4993–5001. [DOI] [PubMed] [Google Scholar]
- 34.Hashimoto S; Werner D; Uwada T, Studies on the Interaction of Pulsed Lasers with Plasmonic Gold Nanoparticles toward Light Manipulation, Heat Management, and Nanofabrication. Journal of Photochemistry and Photobiology C: Photochemistry Reviews 2012, 13 (1), 28–54. [Google Scholar]
- 35.Delfour L; Itina TE, Mechanisms of Ultrashort Laser-Induced Fragmentation of Metal Nanoparticles in Liquids: Numerical Insights. J. Phys. Chem. C 2015, 119 (24), 13893–13900. [Google Scholar]
- 36.Fales AM; Vogt WC; Pfefer TJ; Ilev IK, Quantitative Evaluation of Nanosecond Pulsed Laser-Induced Photomodification of Plasmonic Gold Nanoparticles. Sci. Rep 2017, 7 (1), 15704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Giammanco F; Giorgetti E; Marsili P; Giusti A, Experimental and Theoretical Analysis of Photofragmentation of Au Nanoparticles by Picosecond Laser Radiation. J. Phys. Chem 2010, 114, 3354–3363. [Google Scholar]
- 38.Lee JB; Kang K; Lee SH, Comparison of Theoretical Models of Electron-Phonon Coupling in Thin Gold Films Irradiated by Femtosecond Pulse Lasers. Mater. Trans 2011, advpub, 1101311287–1101311287. [Google Scholar]
- 39.Jeon J-W; Yoon S; Choi HW; Kim J; Farson D; Cho S-H, The Effect of Laser Pulse Widths on Laser—Ag Nanoparticle Interaction: Femto- to Nanosecond Lasers. Applied Sciences 2018, 8 (1), 112. [Google Scholar]
- 40.Frens G, Controlled Nucleation for the Regulation of the Particle Size in Monodisperse Gold Suspensions. Nature Physical Science 1973, 241 (105), 20–22. [Google Scholar]
- 41.Perrault SD; Chan WCW, Synthesis and Surface Modification of Highly Monodispersed, Spherical Gold Nanoparticles of 50−200 Nm. J. Am. Chem. Soc 2009, 131 (47), 17042–17043. [DOI] [PubMed] [Google Scholar]
- 42.Liu Y; Ye H; Huynh H; Kang P; Xie C; Kahn JS; Qin Z, Single-Particle Counting Based on Digital Plasmonic Nanobubble Detection for Rapid and Ultrasensitive Diagnostics. medRxiv 2021, 2021.02.18.21252027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ohta S; Glancy D; Chan WCW, DNA-Controlled Dynamic Colloidal Nanoparticle Systems for Mediating Cellular Interaction. Science 2016, 351 (6275), 841–845. [DOI] [PubMed] [Google Scholar]
- 44.de Araújo MA; Silva R; de Lima E; Pereira DP; de Oliveira PC, Measurement of Gaussian Laser Beam Radius Using the Knife-Edge Technique: Improvement on Data Analysis. Appl. Opt 2009, 48 (2), 393–396. [DOI] [PubMed] [Google Scholar]
- 45.D’Errico J Slm - Shape Language Modeling (Https://Www.Mathworks.Com/Matlabcentral/Fileexchange/24443-Slm-Shape-Language-Modeling), Matlab Central File Exchange. Retrieved February 23, 2021.
- 46.Hohenester U; Trügler A, Mnpbem – a Matlab Toolbox for the Simulation of Plasmonic Nanoparticles. Computer Physics Communications 2012, 183 (2), 370–381. [Google Scholar]
- 47.Chen JK; Beraun JE; Tham CL, Investigation of Thermal Response Caused by Pulse Laser Heating. Numer. Heat Transfer, Part A 2003, 44 (7), 705–722. [Google Scholar]
- 48.Font F; Myers TG, Spherically Symmetric Nanoparticle Melting with a Variable Phase Change Temperature. J. Nanopart. Res 2013, 15, 2086–2099. [Google Scholar]
- 49.Plimpton S, Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys 1995, 117 (1), 1–19. [Google Scholar]
- 50.Lammps Molecular Dynamics Simulator. http://lammps.sandia.gov.
- 51.Price DJ; III CLB, A Modified Tip3p Water Potential for Simulation with Ewald Summation. The Journal of Chemical Physics 2004, 121 (20), 10096–10103. [DOI] [PubMed] [Google Scholar]
- 52.Grochola G; Russo SP; Snook IK, On Fitting a Gold Embedded Atom Method Potential Using the Force Matching Method. J. Chem. Phys 2005, 123 (20), 204719. [DOI] [PubMed] [Google Scholar]
- 53.Ziefuß AR; Reichenberger S; Rehbock C; Chakraborty I; Gharib M; Parak WJ; Barcikowski S, Laser Fragmentation of Colloidal Gold Nanoparticles with High-Intensity Nanosecond Pulses Is Driven by a Single-Step Fragmentation Mechanism with a Defined Educt Particle-Size Threshold. J. Phys. Chem. C 2018, 122 (38), 22125–22136. [Google Scholar]
- 54.Muto H; Miyajima K; Mafuné F, Mechanism of Laser-Induced Size Reduction of Gold Nanoparticles as Studied by Single and Double Laser Pulse Excitation. J. Phys. Chem. C 2008, (15), 5810–5815. [Google Scholar]
- 55.Inasawa S; Sugiyama M; Noda S; Yamaguchi Y, Spectroscopic Study of Laser-Induced Phase Transition of Gold Nanoparticles on Nanosecond Time Scales and Longer. J Phys Chem B 2006, 110 (7), 3114–9. [DOI] [PubMed] [Google Scholar]
- 56.Shoji M; Miyajima K; Mafuné F, Ionization of Gold Nanoparticles in Solution by Pulse Laser Excitation as Studied by Mass Spectrometric Detection of Gold Cluster Ions. J. Phys. Chem. C 2008, 112 (6), 1929–1932. [Google Scholar]
- 57.Karim MR; Li X; Kang P; Randrianalisoa J; Ranathunga D; Nielsen S; Qin Z; Qian D, Ultrafast Pulsed Laser Induced Nanocrystal Transformation in Colloidal Plasmonic Vesicles. Adv. Opt. Mater 2018, 6 (21), 1800726. [Google Scholar]
- 58.Baffou G; Quidant R, Thermo-Plasmonics: Using Metallic Nanostructures as Nano-Sources of Heat. Laser Photonics Rev.2013, 7 (2), 171–187. [Google Scholar]
- 59.Mayer TM; Houston JE; Franklin GE; Erchak AA; Michalske TA, Electric Field Induced Surface Modification of Au. J. Appl. Phys 1999, 85 (12), 8170–8177. [Google Scholar]
- 60.Olsen M; Hummelgård M; Olin H, Surface Modifications by Field Induced Diffusion. PLoS One 2012, 7 (1), e30106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Mamin HJ; Guethner PH; Rugar D, Atomic Emission from a Gold Scanning-Tunneling-Microscope Tip. Phys. Rev. Lett 1990, 65 (19), 2418–2421. [DOI] [PubMed] [Google Scholar]
- 62.Inasawa S; Sugiyama M; Yamaguchi Y, Laser-Induced Shape Transformation of Gold Nanoparticles Below the Melting Point: The Effect of Surface Melting. J. Phys. Chem. B 2005, 109 (8), 3104–3111. [DOI] [PubMed] [Google Scholar]
- 63.Petrova H; Perez Juste J; Pastoriza-Santos I; Hartland GV; Liz-Marzán LM; Mulvaney P, On the Temperature Stability of Gold Nanorods: Comparison between Thermal and Ultrafast Laser-Induced Heating. Phys. Chem. Chem. Phys 2006, 8, 814. [DOI] [PubMed] [Google Scholar]
- 64.Plech A; Cerna R; Kotaidis V; Hudert F; Bartels A; Dekorsy T, A Surface Phase Transition of Supported Gold Nanoparticles. Nano Lett. 2007, 7 (4), 1026–1031. [DOI] [PubMed] [Google Scholar]
- 65.Egry I; Lohoefer G; Jacobs G, Surface Tension of Liquid Metals: Results from Measurements on Ground and in Space. Phys. Rev. Lett 1995, 75 (22), 4043–4046. [DOI] [PubMed] [Google Scholar]
- 66.Nanda KK; Maisels A; Kruis FE, Surface Tension and Sintering of Free Gold Nanoparticles. J. Phys. Chem. C 2008, 112 (35), 13488–13491. [Google Scholar]
- 67.Grigor’ev AI; Shiryaeva SO, Criterion of Instability of a Charged Drop in an Electrostatic Suspension. Surf. Engin. Appl. Electrochem 2015, 51 (3), 246–252. [Google Scholar]
- 68.Luna MMD; Gupta M, Effects of Surface Tension and Viscosity on Gold and Silver Sputtered onto Liquid Substrates. Appl. Phys. Lett 2018, 112 (20), 201605. [Google Scholar]
- 69.Novo C; Mulvaney P, Charge-Induced Rayleigh Instabilities in Small Gold Rods. Nano Lett. 2007, 7 (2), 520–524. [DOI] [PubMed] [Google Scholar]
- 70.Gill SPA, Controlling the Rayleigh Instability of Nanowires. Appl. Phys. Lett 2013, 102 (14), 143108. [Google Scholar]
- 71.Bongiovanni G; Olshin PK; Yan C; Voss JM; Drabbels M; Lorenz UJ, The Fragmentation Mechanism of Gold Nanoparticles in Water under Femtosecond Laser Irradiation. Nanoscale Adv. 2021, 3 (18), 5277–5283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Plech A; Kotaidis V; Grésillon S; Dahmen C; von Plessen G, Laser-Induced Heating and Melting of Gold Nanoparticles Studied by Time-Resolved X-Ray Scattering. Phys. Rev. B: Condens. Matter Mater. Phys 2004, 70, 195423. [Google Scholar]
- 73.Alosious S; Kannam SK; Sathian SP; Todd BD, Prediction of Kapitza Resistance at Fluid-Solid Interfaces. J. Chem. Phys 2019, 151 (19), 194502. [DOI] [PubMed] [Google Scholar]
- 74.Merabia S; Shenogin S; Joly L; Keblinski P; Barrat J-L, Heat Transfer from Nanoparticles: A Corresponding State Analysis. Proc. Natl. Acad. Sci. U. S. A 2009, 106 (36), 15113–15118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Neidhart SM; Gezelter JD, Thermal Transport Is Influenced by Nanoparticle Morphology: A Molecular Dynamics Study. J. Phys. Chem. C 2018, 122 (2), 1430–1436. [Google Scholar]
- 76.Kang P; Xie C; Fall O; Randrianalisoa J; Qin Z, Computational Investigation of Protein Photoinactivation by Molecular Hyperthermia. Journal of Biomechanical Engineering 2020, 143 (3). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Siems A; Weber SAL; Boneberg J; Plech A, Thermodynamics of Nanosecond Nanobubble Formation at Laser-Excited Metal Nanoparticles. New J. Phys 2011, 13, 043018. [Google Scholar]
- 78.Tsuji T; Yahata T; Yasutomo M; Igawa K; Tsuji M; Ishikawa Y; Koshizaki N, Preparation and Investigation of the Formation Mechanism of Submicron-Sized Spherical Particles of Gold Using Laser Ablation and Laser Irradiation in Liquids. PCCP 2013, 15 (9), 3099–3107. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


