Heteropolymetallic Architectures as Snapshots of Transmetallation Processes at Different Degrees of Transfer

Abstract

Novel heteropolymetallic architectures have been built by integrating Pd, Au and Ag systems. The dinuclear [(CNC)(PPh₃)Pd‐^G11M(PPh₃)](ClO₄) (^G11M=Au (3), Ag (4); CNC=2,6‐diphenylpyridinate) and trinuclear [{(CNC)(PPh₃)Pd}₂ ^G11M](ClO₄) (^G11M=Au (6), Ag (5)) complexes have been accessed or isolated. Structural and DFT characterization unveil striking interactions of one of the aryl groups of the CNC ligand(s) with the ^G11M center, suggesting these complexes constitute models of transmetallation processes. Further analyses allow to qualitatively order the degree of transfer, proving that Au promotes the highest one and also that Pd systems favor higher degrees than Pt. Consistently, Energy Decomposition Analysis calculations show that the interaction energies follow the order Pd−Au > Pt−Au > Pd−Ag > Pt−Ag. All these results offer potentially useful ideas for the design of bimetallic catalytic systems.

Frustrated R‐transfer processes: The catalytic use of bimetallic couples acting in a cooperative way affords novel and efficient chemical transformations. The presence of M−M’ interactions is a key feature in these processes. We describe here a complete series of complexes containing ^G10M−^G11M bonds (^G10M=Pd, Pt; ^G11M=Ag, Au) that can be considered as snapshots of transmetallation processes. All together they compose a sort of short movie that allows to rank the progression of such processes depending on of the metals involved.

Introduction

Palladium catalyzed cross coupling reactions have become a very powerful tool for the synthesis of added value chemicals. ^[1] Methodologies have been continuously developed and today a high level of excellence has been achieved. However, there is still much room for improvement. For instance, in the last decade, the combined use of two transition metal systems for cooperative catalysis has emerged as a strategy affording novel and more efficient chemical transformations. ^[2]

In this context, chemical species containing metal‐metal bonds have attracted considerable attention over the years because of their unique electronic structures. More specifically, the combination of an electron‐donating metal (M) with an electron‐accepting metal (M’) is especially interesting. Along with the potential to activate some chemical bonds in small molecules shown by classical Lewis acid‐base adducts, these M−M’ systems provide additional features, as is the presence of d orbitals for further interactions. The judicious selection of metals allows to fine‐tune the degree of polarization of the system, whereas the choice of ligands can be further used for designing systems favoring bond‐forming and bond‐breaking processes more specifically. ^[3]

Thus, the combined use of a metal species, typically a closed‐shell group‐11 or group‐12 metal system, together with a conventional palladium catalyst, have afforded remarkable results in the outcome of certain chemical reactions.[ ^2a , ⁴ ] These systems typically operate through combined cycles that connect through an intersecting step: the transmetallation. Accordingly, obtaining fundamental information on every aspect of this crosslinking step is of crucial importance for the design of efficient catalytic systems.

Several studies point to the formation of dative Pd−M interactions as a key feature in transmetallation processes. For example, Chen and coworkers showed that the formation of Pd−M (M=Cu, Ag, Au) species decreases the energetic barrier on the transmetallation step in Sonogashira reactions. ^[5] Besides, Lledós and Khusnutdinova found that subtle changes in Pd−Cu distances have a large effect in the efficiency of the Sonogashira coupling, the shorter the better. ^[6] Similar results were described by Espinet and coworkers in Pd arylation processes by Au aryls, ^[7] by Zhang and coworkers in the cross coupling reaction of iodobenzene facilitated by Pd−Au species, ^[8] and by Hashmi and coworkers in several Pd−Au transmetallation scenarios. ^[9] On the other hand, Takita, Uchiyama and coworkers used Pd−Cu catalysts in cross coupling reactions for C−C bonds on highly sterically hindered structures by taking advantage of the lowered activation energy for the transmetallation process due to the presence of the intermetallic interactions. ^[10]

Scheme 1 shows a broad‐ranging picture of a transmetallation, including five different degrees of transfer (A to E). During the last years, we have been interested in the construction of heteropolynuclear architectures showing dative metal‐metal bonds. ^[11] Taking advantage of the chemical inertia of platinum complexes, we have prepared rare Pt−Au and Pt−Ag species that can be interpreted as arrested intermediates of transmetallation reactions. ^[12] We have now turned our attention to more labile palladium systems, and asked ourselves if we would be able to assemble and isolate Pd−Ag and Pd−Au complexes. In the context of palladium promoted R‐transfer processes and bimetallic catalysis, we have focused in determining the degree of transmetallation achieved as a function of the Group‐11 metal system, and in monitoring the concomitant dynamic processes. Furthermore, we have compared these results with those found for our previously reported Pt−M analogues, ^[12] thus obtaining a broader picture of some of the factors governing the transmetallation process.

Scheme 1.

Transmetallation process in a ^G10M−^G11M heterometallic system, showing five different degrees of transfer (A to E).

Results and Discussion

Preparation of the starting materials [Pd(CNC‐H)Cl(PPh₃)] (1) and [Pd(CNC)(PPh₃)] (2)

Taking advantage of our know‐how, we have chosen a pincer CNC ligand for the design the donor palladium fragment. Preparation of the Pd starting material required a different methodology than that leading to the analogous Pt complex. Whereas the latter is obtained through the [Pt(CNC)(dmso)] intermediate, ^[13] the palladium counterpart was accessible through the reaction of [Pd(CNC−H)(μ‐Cl)]₂ with PPh₃ and subsequent deprotonation with potassium bis(trimethylsilyl)amide (Scheme 2).

Scheme 2.

Synthetic pathways leading to complexes 1 and 2.

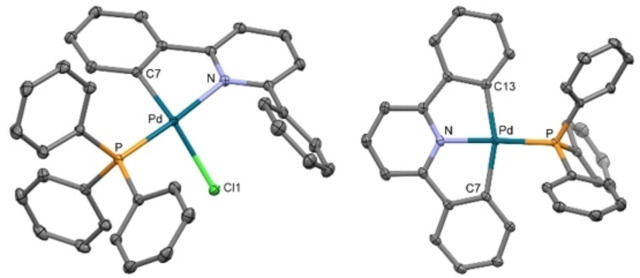
Complexes [Pd(CNC−H)Cl(PPh₃)] (1) and [Pd(CNC)(PPh₃)] (2) show ¹H and ³¹P NMR spectra according to the expected ones. Their crystal structures have been further determined by X‐ray diffraction (Figure 1). In both cases, the phosphane is located trans to the N atom of the CNC ligand. The Pd environment in 1 is distorted from an ideal square planar disposition, as highlighted by the bent C−Pd−Cl angle (153.8(1)°). This distortion is caused by the steric requirements of the PPh₃ and the Ph substituent of the bidentate ligand, as previously observed in related complexes. ^[14] Conversely the Pd environment of 2 is planar and shows similar geometric parameters as those of its Pt counterpart. ^[13] Interesting data in the context of this work are the Pd−C_ipso distances and Pd−C_ipso−C_para angles in 2 (average, 2.0788(14) Å and 167.4(1)°, respectively)

Figure 1.

(left) Crystal structure of the complex 1. Relevant distances (Å) and angles (°): Pd−C(7) 2.0007(19), Pd−N 2.1034(17), Pd−P 2.2497(5), Pd−Cl(1) 2.4182(5); C(7)−Pd−N 80.99(7), C(7)−Pd−P 97.47(6), N−Pd−P 173.90(5), C(7)−Pd−Cl(1) 153.80(6), N−Pd−Cl(1) 96.04(5), P−Pd−Cl(1) 87.932(18). (right) Crystal structure of the complex 2. Relevant distances (Å) and angles (°): Pd−N, 2.0109(12), Pd−C(13), 2.0788(14), Pd−C(7) 2.0787(14), Pd−P 2.2250(4); N−Pd−C(13) 80.58(5), N−Pd−C(7) 80.73(5), C(13)−Pd−C(7) 160.74(6), N−Pd−P 175.57(4), C(13)−Pd−P 101.87(4), C(7)−Pd−P 97.09(4).

Choice of the acidic metal fragment

Following our approach, we chose Group‐11 metals with a d¹⁰ configuration (^G11M=Ag, Au) as the acceptor metallic fragment. Two common fragments potentially usable as cocatalysts in the context of bimetallic catalysis can be envisaged: naked ^G11M⁺ and [^G11M(PPh₃)]⁺. In the case of naked ^G11M⁺, trinuclear [Pd−^G11M−Pd)]⁺ species are obtained (see below). Since in solution one should expect a generic [^G11M−L] fragment acting as acceptor, in the case of naked ^G11M⁺ and the resulting trinuclear [Pd−(^G11M−Pd)]⁺ we consider the [^G11M−Pd]⁺ fragment as the acceptor. Consequently, the donor‐acceptor interactions in which the ligand transfer will be scrutinized will push us to target [Pd‐(^G11M−Pd)]⁺ and [Pd−(^G11M−PPh₃)]⁺ derivatives as models.

Preparation of heterodinuclear [(CNC)(PPh₃)Pd−M(PPh₃)](ClO₄) (M=Au (3), Ag (4)) complexes

Firstly, we will describe the preparation of the [Pd−(^G11M‐PPh₃)]⁺ complexes (Scheme 3). The Pd−Au one has been successfully synthesized by reacting equimolecular amounts of 2, [AuCl(PPh₃)] and silver perchlorate in tetrahydrofuran at −60 °C. Thus, the dinuclear adduct [(CNC)(PPh₃)Pd−Au(PPh₃)](ClO₄) (3) was obtained pure, as a yellow solid in 90 % yield. The silver counterpart, [(CNC)(PPh₃)Pd−Ag(PPh₃)](ClO₄) (4), has been accessed by a similar procedure but using [Ag(OClO₃)(PPh₃)] as silver source. Interestingly, complex 4 presents a labile behavior in solution, as it undergoes phosphane exchange processes. Thus, the obtained solid results not a pure compound, and will be labelled 4*.

Scheme 3.

Synthetic pathways leading to heterodinuclear complexes 3 and 4.

The molecular structure of 3 has been determined by XRD, but no crystals of 4 could be achieved. Complementarily, the geometries of both adducts were optimized by DFT calculations (3‐DFT, 4‐DFT, see Computational details, Supporting Information). Figure 2‐left shows a drawing of the complex cation of 3. The structure confirms the existence of a Pd−Au bond (Pd−Au distance: 2.7422(3) Å). This is remarkable, as the number of Pd(II)−Au complexes structurally characterized is very small, and typically present bridging ligands between the metals and longer intermetallic distances. ^[15] The only shorter Pd−Au distance reported to date (2.6174(9) Å) belongs to an electron deficient polynuclear complex. ^[16] Nevertheless, the most striking feature of our structure is the presence of a very short Au−C(7) distance (2.119(3) Å), which indicates a strong interaction linking the C_ipso of one of the phenylene rings of the CNC ligand and the Au center. Consequently, the Pd−C_ipso distances are mutually different (Pd−C(7), 2.393(3); Pd−C(13), 2.031(3) Å). Furthermore, the phenylene ring that interacts with the Au center clearly deviates from the main plane formed by the rest of the CNC ligand and the square planar environment of the Pd atom (dihedral angle 37.8(1)°). All these geometrical parameters are indicative of a frustrated R transfer process between the two metal centers that cannot progress further given the nature of the CNC ligand.

Figure 2.

(left) Crystal structure of the cation complex of 3. Relevant distances (Å) and angles (°): Pd−Au, 2.7422(3); Pd−C(13) 2.031(3); Pd−C(7), 2.393(3); Au−C(7), 2.119(3); C(7)−Pd−Au, 48.16(7); P(2)−Au−Pd, 127.87(2). (right) DFT optimized structure 4‐DFT. Relevant distances (Å) and angles (°): Pd−Ag, 2.75; Pd−C’ 2.07; Pd−C, 2.21; Ag−C, 2.22; C−Pd−Ag, 51.7; P−Ag−Pd, 126.3.

Figure 2‐right shows a drawing of the DFT optimized structure of the complex cation of 4. The structure (4‐DFT) is qualitatively similar to that of 3, with very short Ag−Pd (2.75 Å) and Ag−C (2.22 Å) distances serving as a probe of the interaction of the silver center with one of the Pd−C_ipso axis, and dissimilar Pd−C distances (2.21 and 2.07 Å).

Comparison of the structures 3, 4‐DFT, and those of the analogous platinum complexes ^[12] is of particular interest. Firstly, a more pronounced deformation of the Pd−CNC moiety in 3 with regard to that of 4‐DFT is prominent. In parallel, comparison of each ^G10M−Au and ^G10M−Ag pair also reveals that the Pd systems experience more marked deformations than the Pt analogs. Thus, the progression of the frustrated R transfer process is greater for the former. Figure 3 visually shows this difference in the geometrical parameters of 3 and its Pt counterpart (Figures S48–S53, Supporting Information, show similar comparisons for other structures). This question will be addressed later on in this paper.

Figure 3.

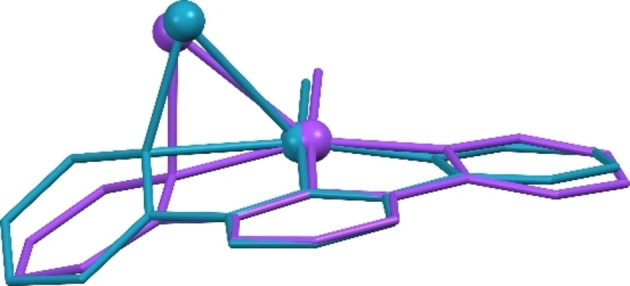
Overlay of the cores of the X ray structures of 3 (green) and its Pt analog (purple).

The ³¹P NMR spectra of 3 in CD₂Cl₂ show a two‐signal pattern at all recorded temperatures (Figure S20, Supporting Information), consistent with the formation of a heterodinuclear complex. The ¹H NMR spectrum at RT (Figure S18, Supporting Information) suggests a strong C−Au interaction, as it shows a pattern fully consistent with its XRD structure. Indeed, the hydrogen atoms of the CNC ligand give rise to eleven inequivalent signals, a feature that is maintained up to 313 K. This contrasts to the ¹H NMR spectrum of the Pt counterpart, where a dynamic exchange process with a coalescence temperature of about 203 K is observed. ^[13] The latter has been explained by the operation of a metronome‐like dynamic process, consisting of the ^G11M−L fragment bouncing along the C−Pt−C axis, thus implying Au−C bond forming and breaking processes. An analogous process is to be expected for 3, but the experiments suggest that it must be slow in the NMR timescale and in the studied temperature range, differently to that observed for the Pt−Au complex. Further insights obtained from the DFT calculations are discussed below.

The ³¹P NMR spectrum of 4* (Figure S29, Supporting Information) in CD₂Cl₂ at RT shows one signal and some broad features distorting the baseline. However, at 173 K a more complex pattern is observed, mainly consisting of a sharp singlet at 43.5 ppm and two doublets with a pattern typical of a P−Ag system at 18.6 ppm, which corresponds to complex 4. Besides, additional signals are found supporting the presence of 2, 5 and [Ag(PPh₃)₂]⁺ in minor quantities, and therefore revealing the existence of the equilibrium depicted in Scheme 3. The ¹H NMR spectrum of 4* (Figure S28, Supporting Information) at RT shows a collection of broad signals with poor resolution, a consequence of both the equilibrium of species described and also the fast dynamics of some of them. Among these, a broad singlet is observed isolated from the rest, at 6.10 ppm, which we assign to the aromatic C_ortho‐H protons in 4. At 173 K the signals become sharper, and the decoalescence of the latter into two broad doublets at 5.98 and 5.22 ppm becomes evident. This feature is due to the deceleration of a metronome‐like intramolecular dynamics in 4, a peculiar type of dynamics recently described by us in some related systems. ^[13]

Preparation of heterotrinuclear [{(CNC)(PPh₃)Pd}₂M](ClO₄) (M=Ag (5), Au (6)) complexes

Following our masterplan, [Pd−(^G11M−Pd)]⁺ complexes have been synthesized (Scheme 4). Access to the trinuclear Pd−Au−Pd, [{(CNC)(PPh₃)Pd}₂Au](ClO₄) (6), can be achieved by mixing in THF at 203 K [AuCl(tht)], silver perchlorate, and subsequently adding 2.0 equiv. of 2. Filtration and additional workup afforded a yellow solid which corresponds to a mixture of compounds (6*). Differently, the trinuclear [{(CNC)(PPh₃)Pd}₂Ag](ClO₄) (5) can be purely prepared and isolated in a 72 % yield by reaction of 2 with 0.5 equiv. of AgClO₄ in acetone at RT.

Scheme 4.

Synthetic pathways leading to heterotrinuclear complexes 5 and 6.

The ¹H NMR spectrum of 6* in CD₂Cl₂ at RT indicates it is a mixture of the trinuclear 6 and minor quantities of the dinuclear 3, which entails the formation of other species during the course of the reaction. The proportions seem to be dependent on the reaction time and on the temperature evolution of the mixtures. Nevertheless, careful workup has afforded crystalline materials of 6 suitable for structural characterization.

The molecular structures of 6 and 5 have been determined by XRD. Views of their complex cations are shown in Figure 4. Both can be first described as the result of two Pd(CNC)(PPh₃) units “sandwiching” one group‐11 metal center. They present a virtual C₂ symmetry, so our discussion will focus on one of the [Pd]⋅⋅⋅[(^G11M−Pd)]⁺ donor‐acceptor interactions. In the case of 6, very short Pd−Au and Au−C_ipso bonds are evident, with average distances of 2.7429(4) and 2.103(5) Å, respectively. These values support the existence of intermetallic bonds and of strong interactions between one of the Pd−C_ipso bonds of each Pd−CNC system with the Au center. Consequently, two pairs of dissimilar Pd‐C_ipso distances are also found in the structure (2.459(5) Å, av. for Pd(1)−C(7) and Pd(2)−C(42); 2.025(5) Å, av. for Pd(1)−C(13) and Pd(2)−C(48)). Besides, complex 5 present short Pd−Ag bonds, with average distances of 2.9008(2) Å. The silver center is interacting with one of the C_ipso of each CNC ligand, with av. distances of 2.225(2) Å (Ag−C(7) and Ag−C(42)). Thus, two pairs of dissimilar Pd−C_ipso distances are found, with average values of 2.154(2) (Pd(1)−C(7) and Pd(2)−C(42)) and 2.072(2) Å (Pd(1)−C(13) and Pd(2)−C(48)). Interestingly, the difference between these is smaller in 5 compared to 6, suggesting that the interaction is markedly stronger in the Pd−Au−Pd complex. In both structures the interacting phenylene rings deviate from the coplanarity with the rest of the CNC ligands and the Pd square environments. This deviation is more pronounced for the Au complex 6 (av. dihedral angle 45.6(1)°) than for the Ag complex 5 (av. dihedral angle 21.4(1)°). Again, all these parameters reveal the initial steps of a frustrated transfer process of the aromatic ring between the metals.

Figure 4.

above) Crystal structure of the cation complex of 6. Relevant distances (Å) and angles (°): Pd(1)−Au, 2.7366(4); Pd(1)−C(13), 2.020(5); Pd(1)−C(7), 2.498(5); Au−C(7), 2.098(5); C(7)−Pd(1)−Au, 46.98(11); Pd(1)−Au−Pd(2), 128.659(13). below) Crystal structure of the cation complex of 5. Relevant distances (Å) and angles (°): Pd(1)‐Ag, 2.8597(2); Pd(1)−C(13), 2.072(2); Pd(1)−C(7), 2.143(2); Ag−C(7), 2.239(2); C(7)−Pd(1)−Ag, 50.73(6); Pd(1)−Ag−Pd(2), 132.774(8).

Complementarily, the structures of the trimetallic complexes have been optimized by DFT methods. The obtained geometries (6‐DFT and 5‐DFT) show excellent agreements with the experimentally determined ones (Table S2, Supporting Information).

Comparison of the structures 6 and 5 with those of their platinum analogs ^[12] is again interesting. Visual inspection of each separate pair (^G10M−Au−^G10M and ^G10M−Ag−^G10M) unveils more marked deformations of the ^G10M(CNC) moieties in the Au counterparts, and points to stronger interactions for the Pd species as previously stated for the heterodinuclear systems (Figures S52 and S53, Supporting Information).

The set of crystals obtained for 6 have allowed to study its NMR behavior as a pure compound, and also to perform a careful comparison with that of its silver counterpart 5. Both complexes show interesting differences. Whereas the ³¹P NMR spectra at RT show one singlet in both cases, at 40.3 (6) and 42.5 (5) ppm, at 193 K two singlets of different relative intensities are found for 5 (Figures S36, S46, and S37, Supporting Information). The ¹H NMR spectra also show distinct features. The gold complex 6 (Figure S44, Supporting Information) presents signals consistent with the inequivalence of the two halves of each CNC ligand, a pattern that remains uniform down to 193 K. Conversely, the silver complex 5 (Figure 5) shows at room temperature the equivalence of the four phenylene rings (red asterisks in Figure 5 mark the signals corresponding to the four equivalent H2, see Chart 1 in Supporting Information for the atom numbering scheme). However, at 173 K the signals suffer a double splitting, giving rise to two independent sets with different intensities (green and blue asterisks mark two H2 signals from different sets, the other two are in the 5.9‐7 ppm region and cannot be unambiguously assigned). This pattern can be explained by considering the concurrence of two events related to the operation of a metronome‐like dynamics. Indeed, the simultaneous operation of such dynamics on the two sides of the Pd−^G11M−Pd system is a degenerate process causing signal equivalence and simplification of the spectra, as it is observed in the RT spectrum of 5. The coalescence temperature is about 213 K. However, the operation of this process only on one side shall generate a necessary intermediate presenting a slightly different spectroscopic dataset (Figure S61, Supporting Information). This hypothesis suggests that in the case of 5 such intermediate must be close in energy to the ground state minimum, and therefore in the slow exchange temperature two different species shall be observed. Oppositely for 6, a higher barrier would prevent detecting the analogous intermediate. Consistently, the activation energy for the interconversion process should also be smaller for 5, which would explain the low temperature of coalescence observed (213 K), whilst the coalescence temperature has not been achieved for 6. DFT calculations are in good agreement with these hypotheses (see below).

Figure 5.

VT ¹H NMR spectra (CD₂Cl₂) of complex 5.

Structural analysis of complexes ^G10M−^G11M

With all the structural information in our hands, additional geometrical analysis focusing on the ^G10M⋅⋅⋅R⋅⋅⋅^G11M unit affords deeper insight. The intermetallic transfer process can be analyzed by looking at several geometric descriptors. A selection of them is shown in Supporting Information (Table S3). For example, the ^G10M−C_ipso−C_para (α ₁) and ^G11M−C_ipso−C_para (α ₂) angles (Table 1, Figure 6) can be used to describe the deformation of the interacting phenylene ring with respect to the ideal planar disposition of the CNC ligand and thus the degree of the incipient transmetallation of this ring. In the limit situation, in which ^G11M establishes no interaction with the aromatic ring (A in Scheme 1), the value of ^G10M−C−C angle (α ₁) should approach 180°. Indeed, the corresponding angles α ₁ in the starting material 2 and in its Pt counterpart, where no R transfer has started yet, are 167.4(1)° and 168.1(2)° ^[13] respectively. The deviation from the ideal value (180°) arises from the restraint imposed by the pincer nature of the CNC ligand. On the other hand, a situation in which the transfer to a ^G11M center completes would render ^G11M−C−C angles of 180° (E in Scheme 1). Both situations define the boundaries of the R transfer process and are marked as purple stars in Figure 6.

Table 1.

^G10M−C_ipso−C_para (α ₁) and ^G11M−C_ipso−C_para (α ₂) angles (°) in the compounds under scrutiny. Data collected from XRD (cursive) and DFT calculations).

Angle	G11M	Pd systems		Pt systems
		Pd G11M	Pd2 G11M	Pt G11M	Pt2 G11M
G10M−C−C (α1)	Au	140.7(2) 138.3	133.2(4) 134.7	160.5(2) 152.8	152.9(2) 156.6
	Ag	– 157.7	161.6(2) 160.9	– 163.0	162.1(2) 164.0
G11M−C−C (α2)	Au	143.1(2) 147.0	152.7(4) 152.4	120.1(2) 128.5	128.2(2) 123.3
	Ag	– 123.2	111.5(2) 118.6	– 115.7	108.5(2) 111.9

Figure 6.

Different degrees of transfer achieved in the ^G10M−^G11M−P and ^G10M−^G11M−^G10M systems under scrutiny (Square=Pt; Dot=Pd; Red=Ag. Yellow=Au; Stars: reference compounds). Descriptors: ^G10M−C_ipso−C_para and ^G11M−C_ipso−C_para angles (°) obtained from the DFT calculations (Table 1).

Comparatively, the Au systems give rise to the most distorted scenarios and thus to the highest degree of transfer (yellow marks, Figure 6) with regard to the Ag ones (red marks). Besides, the Pd ones (dot marks) are more prone to attain higher degrees of transfer than the Pt ones (square marks). Thus, the ^G10M−C_ipso−C_para angles in the PdAu and Pd₂Au derivatives are 138.3° and 134.7°, respectively (152.8° and 156.6° in the PtAu and Pt₂Au counterparts). Oppositely, the ^G10M−C_ipso−C_para angles in the PdAg and Pd₂Ag complexes are 157.7° and 160.9° respectively (163.0° and 164.0° in the Pt analogues).

The values of the ^G10M−C_ipso and ^G11M−C_ipso distances can also be used as descriptors of the progression of the frustrated transmetallation process. Longer ^G10M−C_ipso distances are always paired with shorter ^G11M−C_ipso distances, and vice versa (see Table S3 and Figure S55, Supporting Information). The shorter ^G11M−C_ipso (and thus the longer ^G10M−C_ipso) the higher degree of transfer, as it is observed for the Pd−Au complexes.

Computational analysis

Further understanding of this process has been obtained from DFT calculations (see Computational Details, Supporting Information). The interaction energies of the ^G10M donor and ^G11M acceptor fragments have been computed by Energy Decomposition Analysis (EDA) for the corresponding [^G10M−(^G11M−PPh₃)]⁺ and [^G10M−(^G11M−^G10M)]⁺ adducts (^G10M=Pd, Pt; ^G11M=Ag, Au; see Table 2, and Figure S56 and Table S4 in Supporting Information). Illuminating trends can be inferred from these data. Firstly, the ^G10M−Au interactions are markedly stronger that the ^G10M−Ag, which aligns with the observed lability of the silver systems. Secondly, the Pd−^G11M interactions are stronger than the Pt−^G11M (exception: the ^G10M₂Ag pair), which agrees with the different rates and behavior observed in the dynamics of the [^G10M−(Au−PPh₃)]⁺ systems. Thirdly, stronger interactions are found in the trinuclear than in the dinuclear adducts. The computed Wiberg indexes and their related bond distances point in coherent directions (Figures S57 and S58, Supporting Information).

Table 2.

Interaction energies E _int (EDA)^[a] and activation energies E _act for the metronome‐like dynamics calculated at the DFT/BP86‐D3 level (kcal/mol).

	G11M	Pd systems		Pt systems
		Pd G11M	Pd2 G11M	Pt G11M	Pt2 G11M
E int (EDA)[a]	Au	−108.0	−112.6	−92.6	−98.9
	Ag	−83.2	−85.6	−80.6	−88.0
E (act,metr) [b]	Au	14.2	14.5	–	–
	Ag	11.7	11.4	–	–

[a] See Figure S56 and Table S4 in Supporting Information for description of the fragments and full EDA analysis. [b] Estimated from the calculated energy profiles (Figures S60 and S62, Supporting Information).

Furthermore, we have carefully explored the mechanism of the metronome‐like dynamics in all these systems with DFT calculations (Figures S59–S62, Supporting Information). In good agreement with the exposed hypotheses explaining the NMR behavior of these Pd heteropolynuclear complexes, the optimized transition state for the above process is characterized by larger activation barriers (Table 2) for the Pd−Au systems (14.2 kcal/mol for 3 and 14.5 for 6) than for the Pd−Ag ones (11.7 kcal/mol for 4 and 11.4 for 5). This explains why only the latter ones reach fast exchange temperatures at RT and show coalescence temperatures around 203–213 K. Besides, for the trinuclear complexes 6 and 5 additional conformational isomers have been found. Qualitative data suggest that only in the case of the Ag system this isomer will be present in a sufficient concentration as to be observed by NMR at low temperatures, which happens to be the case.

Finally, QTAIM analysis has been performed for the four Pd complexes under scrutiny (Figures S63–S66, Tables S5 and S6 Supporting Information). Interestingly, ^G11M−Pd bond paths have been found only for the Au complexes, which again highlight stronger Pd⋅⋅⋅Au interactions with regard to the Pd⋅⋅⋅Ag ones. Moreover, the data extracted from this analysis at the Pd−C_A, Pd−C_B, Au−C_A and Ag−C_A bond critical points also support a more marked weakening of the Pd−C bonds upon interaction with the Au centers.

Conclusion

The Pd−Au and Pd−Ag systems described herein have allowed us to observe and scrutinize their concomitant ^G10M−R−^G11M interactions, and compare them to previous Pt−Au and Pt−Ag species. ^[12] These complexes constitute excellent models to study the initial stages of transmetallation process. Their structures can be regarded as arrested intermediates or snapshots for ligand transfer processes, which, given the nature of the CNC ligand, cannot progress further. Several geometrical descriptors related with the ^G10M−R−^G11M fragment have been used to evaluate the progression of the frustrated transmetallation.

This analysis led to the conclusion that Au promotes the highest degree of transfer from the ^G10M−CNC systems. Also, the Pd systems are more prone to the transfer than the Pt counterparts. DFT calculations provide a deeper insight and show that the interaction energies between the metal fragments follow the order Pd−Au > Pt−Au > Pd−Ag > Pt−Ag. Moreover, NMR studies and DFT modelization of the dynamic processes in solution are consistent with this ranking, showing that the energetic barrier of the related metronome‐like motion, which is dependent on the strength of the ^G11M−C_ipso interactions, is maximum for the Pd−Au complexes and minimum for the Pt−Ag ones.

These results furnish useful ideas that will be of interest and application in the field of bimetallic catalysis, an emerging and rapidly evolving field in chemical science.

Experimental Section

X‐ray structure determinations: Crystal data and other details of the structure analyses are presented in the Supporting Information. Deposition Number(s) 2113354 (for 1), 2113355 (for 2), 2113356 (for 3), 2113357 (for 5), 2113358 (for 6) contain(s) the supplementary crystallographic data for this paper. These data are provided free of charge by the joint Cambridge Crystallographic Data Centre and Fachinformationszentrum Karlsruhe Access Structures service.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Supporting Information

D. Campillo, D. Escudero, M. Baya, A. Martín, Chem. Eur. J. 2022, 28, e202104538.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.