Identification of rare cell populations in autofluorescence lifetime image data

Abstract

Drug‐resistant cells and anti‐inflammatory immune cells within tumor masses contribute to tumor aggression, invasion, and worse patient outcomes. These cells can be a small proportion (<10%) of the total cell population of the tumor. Due to their small quantity, the identification of rare cells is challenging with traditional assays. Single cell analysis of autofluorescence images provides a live‐cell assay to quantify cellular heterogeneity. Fluorescence intensities and lifetimes of the metabolic coenzymes reduced nicotinamide adenine dinucleotide and oxidized flavin adenine dinucleotide allow quantification of cellular metabolism and provide features for classification of cells with different metabolic phenotypes. In this study, Gaussian distribution modeling and machine learning classification algorithms are used for the identification of rare cells within simulated autofluorescence lifetime image data of a large tumor comprised of tumor cells and T cells. A Random Forest machine learning algorithm achieved an overall accuracy of 95% for the identification of cell type from the simulated optical metabolic imaging data of a heterogeneous tumor of 20,000 cells consisting of 70% drug responsive breast cancer cells, 5% drug resistant breast cancer cells, 20% quiescent T cells and 5% activated T cells. High resolution imaging methods combined with single‐cell quantitative analyses allows identification and quantification of rare populations of cells within heterogeneous cultures

1. INTRODUCTION

Tumors are a diverse microsystem that includes immune cells, stromal cells, and the extracellular matrix (ECM). Targeted anti‐cancer therapies use drugs to target specific genes and proteins that are involved in the proliferation and survival pathways of cancer cells [1]. While these interventions have improved clinical outcomes for many cancer patients, innate and acquired drug resistance due to intra‐tumor heterogeneity remain clinical challenges. Pro‐tumorigenic and anti‐tumorigenic immune cells also contribute to tumor heterogeneity. T cells, identified by the expression of CD3, have diverse cytotoxic and immune modulating activities upon activation [2, 3]. Currently, tumor heterogeneity is quantified and studied by methods such as flow cytometry, single cell sequencing, and single‐cell mapping of epigenetic markers [4]. However, these methods require a large number of cells, use cell‐destructive protocols, and typically depend on antibody or exogenous labelling which prevents temporal analysis of the same cells, analysis of dynamic events, evaluation of spatial relationships, and in vivo measurements. Therefore, new methods that can identify distinct subpopulations of rare cells within complex 3D tissues and tumors with non‐destructive protocols are needed for studies of tumor heterogeneity and drug response.

Optical metabolic imaging (OMI) detects the fluorescence intensity and lifetime of the endogenous fluorophores reduced nicotinamide adenine (phosphate) dinucleotide (NAD[P]H) and flavin adenine dinucleotide (FAD). The metabolic coenzymes NADH and FAD are primary electron carriers that participate in metabolic reactions including glycolysis and oxidative phosphorylation. The fluorescence lifetime is the time a fluorophore remains in the excited state and is on the order of hundreds of picoseconds to nanoseconds in duration. NAD(P)H and FAD have two‐component fluorescence decays, due to the difference in lifetime between free and protein‐bound configurations [5, 6]. NAD(P)H τ₁ (short lifetime) corresponds to the NAD(P)H free in solution, while NAD(P)H τ₂ (long lifetime) corresponds to the NAD(P)H that is protein‐bound [5]. On the other hand, FAD τ₁ corresponds to the protein‐bound FAD, while FAD τ₂ corresponds to the free FAD [6]. The short fluorescence lifetimes of both protein‐bound FAD and free NADH are a result of dynamic quenching by the adenine moiety [5, 7]. The mean fluorescence lifetime (τ_m) can be calculated from the weighted average of the short and long lifetime components through the equation τ_m = α₁τ₁ + α₂τ₂, where α₁ and α₂ are the fractional contributions of the short and long lifetimes, respectively. These OMI features are useful biomarkers for the identification of cancer from non‐cancerous tissue and anti‐cancer drug response due to metabolic adaptations of cancer cells [8, 9, 10, 11, 12, 13]. Additionally, due to the increased metabolic demands of activated T cells compared with quiescent T cells, OMI features allow classification of T cell activation with high accuracy [14, 15].

Single‐cell segmentation and analysis of fluorescence microscopy images provide a unique method to detect and quantify cellular heterogeneity. Prior work has demonstrated that Gaussian mixed models and machine learning classification can be used to identify cell populations within datasets of OMI data that is segmented and analyzed at a single‐cell level [8, 10, 14, 16, 17, 18, 19]. A Gaussian mixture model (GMM) is a composite density model that is the sum of individual Gaussian density functions. Subpopulation analysis (SPA) by GMM identifies the best fitting population density representation of the data. Previously, SPA of cell OMI data has been used to identify and quantify subpopulations of triple negative breast cancer cells from HER2+ breast cancer cells and non‐responding cancer cells from drug‐responsive cells within drug‐treated breast and pancreas organoids [8, 17]. Logistic regression and random forest classification of T cells from OMI features achieved identification of activated T cells from quiescent T cells with 97–99% accuracy and CD4+ from CD8+ T cells with 97% accuracy [14]. While the SPA method and machine learning classification are robust for analysis and identification of subpopulations within OMI datasets, these subpopulation analysis methods have not been evaluated for the identification of rare cells that comprise <10% of the total cell population.

In this study, we used simulated OMI datasets to evaluate SPA and machine learning classification methods to identify rare cells (<10% of the total population) within autofluorescence images. Simulated datasets were comprised of mixtures of drug responsive cancer cells, drug resistant cancer cells, quiescent T cells, and activated T cells. SPA successfully identified two populations for varying combinations and proportions of cells but is limited to the analysis of a single OMI feature. Machine learning classification uses the full set of OMI features and can be used to evaluate complex, multi‐population datasets consisting of drug‐responsive breast cancer cells, drug‐resistant breast cancer cells, quiescent T cells, and activated T cells. OMI combined with these computational analyses provides a label‐free, non‐destructive method to identify rare subpopulations of cells within complex tissues.

2. METHODS

2.1. Simulated OMI datasets

OMI data for cell populations of trastuzumab‐responsive breast cancer cells (BT474), trastuzumab‐resistant breast cancer cells (HR6), quiescent T cells, and activated T cells were generated in MATLAB from published mean and standard deviation values (Table  s1 ) of OMI data [14, 17]. The cancer data came from NAD(P)H and FAD fluorescence lifetime images of control group BT474 and HR6 organoids imaged 48 h after organoid generation [17]. The T cell data is from NAD(P)H and FAD fluorescence lifetime images of bulk CD3+ T cells that were extracted from peripheral human whole blood using negative selection methods and cultured in the presence or absence of the activating antibodies anti‐CD2/CD3/CD28 [14]. To simulate OMI single cell datasets, arrays of random‐floating‐point numbers were drawn from normal distributions with the specific means and standard deviations of T cells and cancer cells (Table  s1 ). Histograms were used to visually represent the different population groups: drug responsive and drug resistant cancer cells, activated and quiescent T cells and mixtures of the four different populations, with proportions ranging from 1% to 10% for drug‐resistant cancer cells and T cells.

2.2. Subpopulation analysis

Subpopulation analysis (SPA) was performed by fitting the histograms of the simulated datasets to a Gaussian mixture distribution model (GMModel) with 1, 2, 3, and 4 components through the fitgmdist function in MATLAB. The fitgmdist() function returns a Gaussian mixture distribution model with k components (input variable) fitted to the input dataset. Model fit parameters including the Akaike Information Criteria (AIC), population means, population standard deviations, and proportions were recorded. The lowest AIC signified the most representative model [20].

2.2.1. Unnormalized simulations

SPA was used to identify the number of populations and population proportions of simulated datasets of 10,000 cells. The combinations of cells included the following pairs with the main population listed first, followed by the smaller population: Drug Responsive Cells & T Cells, Drug Resistant Cells & T cells, Quiescent & Activated T cells, Drug Responsive Cells & Drug Resistant Cells, Drug Responsive Cells & Quiescent T cells, and Drug Responsive Cells & Activated T cells. The analysis was performed for both cases in which the subpopulation is 5% and 1% of the total population.

2.2.2. Normalized simulations

SPA was used to identify the number of populations and population proportions of datasets of 100,000 cells, with a normalized mean (large population mean = 1). Experimental replicates were evaluated for large population standard deviations of 0.1, 0.2, 0.3, and 1. The mean and standard deviation of the smaller population were varied and 3D plots allow visualization of the number of components identified by the model as a function of the smaller population's statistical metrics. Normalized simulations were repeated for subpopulations of 5% and 1% of the total population.

2.3. UMAP

The Uniform Manifold Approximation and Projection (UMAP) algorithm was used as a data‐dimension reduction technique to visualize the multivariate separation of cell populations [21]. Similar analyses can be performed with principal component analysis (PCA) or t‐Distributed Stochastic Neighbor Embedding (tSNE), but UMAP was chosen for its fast and efficient performance as well as the preservation of the global structure of the data. Within the simulated OMI datasets, each row represented a single cell and each column the simulated OMI feature value for that cell. The OMI features vary across different scales (0–1 for optical redox ratio, 100–3000 ps for fluorescence lifetimes, and 0–100% for lifetime component weights), so each feature was converted into z‐scores (number of standard deviations from the mean) for comparability and all seven features (redox ratio, NAD(P)H τ₁, FAD τ₁, NAD(P)H τ₂, FAD τ₂, NAD(P)H α₁, and FAD α₁) were used. The UMAP dimensions were obtained using the UMAP library in Python. UMAP was performed on simulated OMI datasets of a random population of cells consisting of drug resistant and responsive cancer cells and quiescent and activated T cells and for two blind populations as shown in Table S2.

2.4. Machine learning

Machine learning was used to identify small subpopulations of cells within simulated OMI multivariate datasets of multiple cell groups. WEKA is a free software that provides a collection of machine learning algorithms. The same random simulated cell population (15,877 cells: 37.8% drug responsive BC, 31.4% drug resistant BC, 20.4% quiescent T cells, and 10.3% activated T cells) that was visualized with UMAP was analyzed via various machine learning algorithms to determine which model provides the highest classification accuracy. Classification was performed using the seven OMI fluorescence features simulated for each cell: redox ratio, NAD(P)H τ₁, FAD τ₁, NAD(P)H τ₂, FAD τ₂, NAD(P)H α₁, and FAD α_1. The data was split into train and test groups using 10‐fold cross validation and a 66% percentage split. Random Forest, Logistic Classifier, and Multilayer Perceptron models were tested. The Random Forest algorithm had the highest accuracy and was used for the additional multivariant classification experiments.

In order to robustly train a classification model without bias to a single larger population, a dataset with 5000 cells of each of the 4 populations was created. Each dataset included 7 OMI fluorescence features simulated for each cell: redox ratio, NAD(P)H τ₁, FAD τ₁, NAD(P)H τ₂, FAD τ₂, NAD(P)H α₁, and FAD α_1. All seven features were used for the classification models. All datasets were created manually in Python. The simulated dataset with 20,000 cells was separated into train and test groups with either a 90%/10% or 70%/30% split between the train and test data. A random forest classification algorithm was trained on the training dataset using 10‐fold cross‐validation. The number of iterations, or trees in the random forest, was set to 100 (WEKA). Then, the model was evaluated against the test dataset, which was unseen during the model training. The trained model was not exposed to the test dataset during training and any predictions made on the test dataset are indicative of the performance of the model in general. We created two models, one that was trained with 70% of the full data and tested on 30% of the data, and the other was trained with 90% of the full data and tested on 10% of full data. The 70% Train/30% Test model was applied on completely unseen simulated OMI datasets with T cell subpopulations that comprise 10%, 5%, and 1% of the full dataset, as well as a mixed population of 70% drug responsive cancer cells, 5% drug resistant cancer cells, 20% quiescent T cells, and 5% activated T cells. In addition, since all previous experiments used simulated data, the model was evaluated on a published dataset [14] of fluorescence lifetime images of quiescent and activated T cells. This dataset consists of 47.5% quiescent T cells (n = 331) and 52.4% (n = 365) activated T cells and was used to test the Random Forest classification model (Table S2). Data was provided by AJ Walsh and MC Skala. The methods for T cell isolation, activation, fluorescence lifetime imaging, and analysis are provided in full detail in Walsh et al. [14].

Finally, in order to see which features were most significant to the classification accuracy of the model, feature selection was performed in WEKA by both correlation and information gain techniques. The attribute evaluator in WEKA is a technique by which each attribute in the dataset is evaluated in the context of the output variable (e.g., the class). The correlation attribute evaluator evaluates the worth of an attribute by measuring the correlation (Pearson's) between it and the class. It calculates the correlation between each attribute and the output variable and selects only the attributes that have a positive correlation or negative correlation (close to −1 or 1). The information gain‐based feature selection process calculates the information gain or entropy for each attribute and the output variable. Values vary from 0 (no information) to 1 (maximum information).

2.5. Code availability

The custom Matlab and Python scripts for the generation and analysis of simulated OMI data is available in this GitHub repository.

3. RESULTS

3.1. Histogram analysis

First, simulated datasets of 100,000 drug responsive cancer cells with a 10% subpopulation of either drug resistant cancer cells or T cells were visualized with histograms of the OMI features (Figure 1). A dataset size of 100,000 cells was selected to be comparable with traditional flow cytometry assays. The subpopulation of T cells is separated from the drug responsive cancer cells for NAD(P)H α₁, the fraction of free NAD(P)H (Figure 1A). However, there is overlap of the NAD(P)H α₁ histograms of drug responsive cancer cells and drug resistant cancer cells (Figure 1B). Neither the T cells nor drug resistant cancer cells were distinguishable from the main population of drug responsive cancer cells within the optical redox ratio (intensity of NAD(P)H/intensity of FAD) histograms (Figure 1C–D).

FIGURE 1.

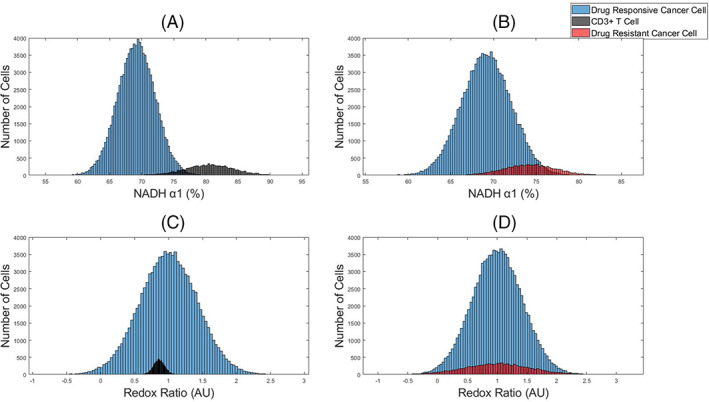
Representative histograms of OMI features to identify subpopulations within simulated OMI datasets of tumors. NAD(P)H α₁ (A–B) and optical redox ratio (C–D) data of a main population of drug responsive cancer cells (blue) and a subpopulation of either T cells (black) or drug resistant cancer cells (red). The main population consists of 100,000 cells and the subpopulation is 10,000 cells, 10% of the total population [Color figure can be viewed at wileyonlinelibrary.com]

3.2. Subpopulation analysis by mixed Gaussian models

SPA via mixed Gaussian models was performed on simulated OMI datasets of 100,000 cells to evaluate the performance of this method to identify a smaller subset of a population within a larger population of cells (Figure 2). T cell populations were simulated for CD3⁺ (all T cells), quiescent CD3⁺, and activated CD3⁺. When the subpopulation of cells is 5% of the total population, subpopulation analysis of OMI data by GMM correctly identifies 2 populations for all of the simulated datasets for a subset of the OMI features. All OMI features except for the optical redox ratio and NAD(P)H τ₁ allow identification of T cells and T cell subsets from drug responsive and resistant cancer cell populations (Figure 2A Rows 1–4).While SPA analysis of a rare drug resistant population within a drug responsive tumor correctly yielded two populations for three of the variables, NAD(P)H τ₂, FAD τ₂, and FAD τ₁, the proportion or mean error exceeded 5%, and SPA by the additional OMI features failed to identify 2 populations (Figure 2A, Row 5). Likewise, SPA with four of the features, FAD a₁, the optical redox ratio, NAD(P)H τ₁, and NAD(P)H τ₂, yielded two populations for the comparison of activated T cells from quiescent T cells. However, of these OMI features, only the FAD α₁, fraction of bound FAD, analysis identified the correct population proportions.

FIGURE 2.

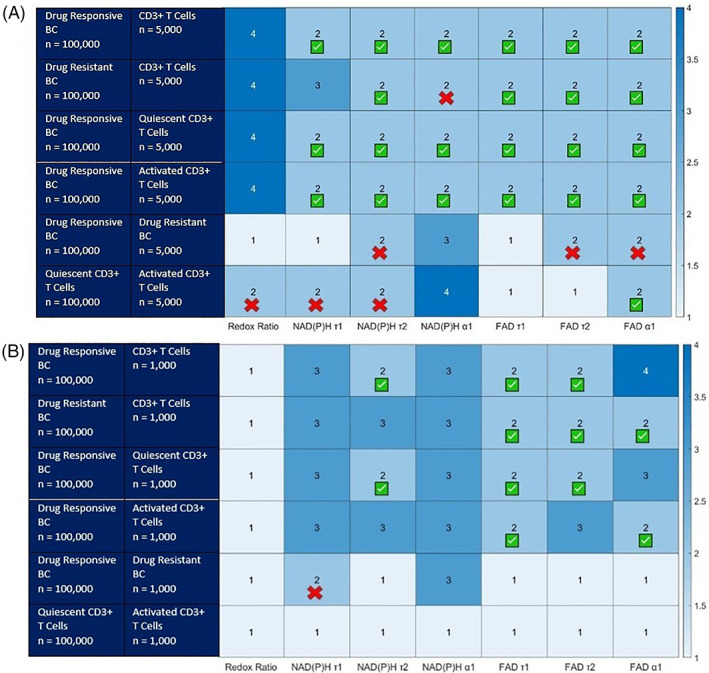
Number of distinct cell populations identified using Gaussian mixed models within simulated OMI datasets of varying combinations of drug resistant cancer cells, drug responsive cancer cells, and T cells. [A] (top) the smaller population is 5% of the total population, 100,000 total simulated cells. [B] (bottom) the smaller population is 1% of the total population, 100,000 total simulated cells. The red Xs identify models where the proportion error exceeds 5% (false positive). These population and features cannot be counted as successful. The green check indicates the proportion, mean, and standard deviation of each population is identified correctly (less than 5% error. BC = breast cancer [Color figure can be viewed at wileyonlinelibrary.com]

When the subpopulation of cells is 1% of the total population, the SPA method is less successful at correctly identifying two populations of cells (Figure 2B). Analysis with FAD τ₁, the lifetime of bound FAD, was the most successful for identifying two populations for the four datasets consisting of T cells, quiescent T cells, or activated T cells and drug‐responsive or drug‐resistant cancer cells. SPA by GMM of each OMI feature identified a single population within the dataset of quiescent and activated T cells. SPA analysis of NAD(P)H τ₁, the lifetime of free NAD(P)H, identified two populations for the combination of drug resistant cells and drug responsive cancer cells. However, the proportion and mean of the identified subpopulation were 20% instead of 1%, and 500 ns versus 460 ns, respectively.

The performance of SPA with Gaussian models depends on the statistical metrics of the OMI features of the two populations. To understand this relationship and identify for what mean and standard deviation values a rare cell population must have to be identified by SPA, OMI datasets were generated with a main population of mean of 1 and standard deviation of 0.1 and a subpopulation with a mean varied from 0 to 3 and a standard deviation varied from 0 to 0.5. 3D plots of the mean and standard deviation values versus the number of components identified by SPA in which the subpopulation is 5% or 1% of the total population (n = 100,000 cells, mean = 1, sd = 0.1) allow visualization of the means and standard deviations that will yield multivariate populations via SPA. For the normalized analysis in which the subpopulation is 5% of the total population, two populations are identified for all mean values except those in the range of 0.63 to 1.33 and standard deviation values less than 0.27 (Figure 3A). Additionally, there is a very small portion in which the population overlaps, and the model only identifies one population. This occurs in the range of mean values from 0.89 to 1.11 and when the standard deviation of the subpopulation is 0.9–0.99.

FIGURE 3.

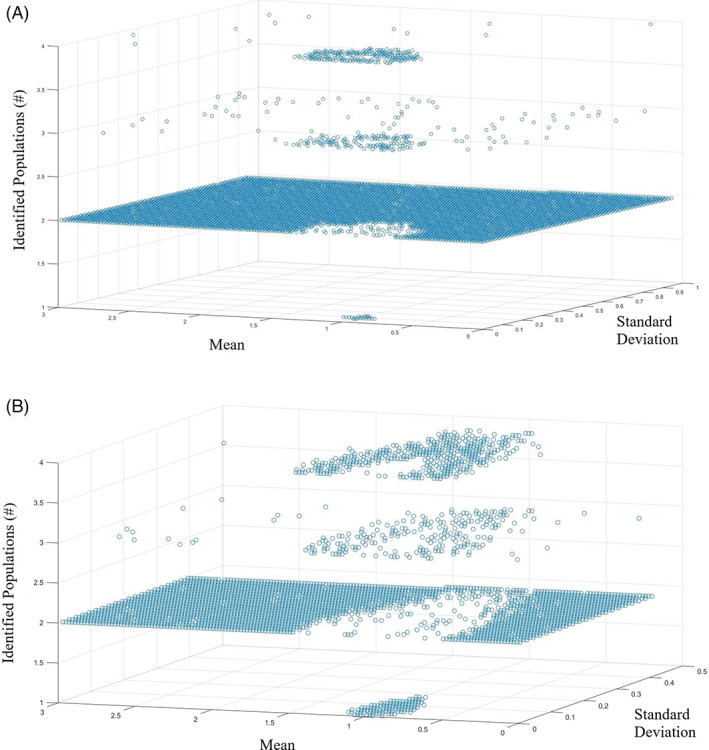
Normalized mean and standard deviation values in which the model identifies two separate populations. [A] (top) shows the case where the subpopulation is 5% of the total population. [B] (bottom) shows the case where the subpopulation is 1% of the total population [Color figure can be viewed at wileyonlinelibrary.com]

For the population in which the subpopulation is 1% of the total population, similar patterns are observed. However, two populations are identified for all mean values except those with a mean value in the range of 0.5–1.49 and standard deviation values less than 0.5 (Figure 3B). For this case, the values in which the population overlaps, and the model only identifies one population is for mean values from 0.81 to 1.10 and all standard deviation values, 0–0.17. Similar results were obtained for simulations with a main population with increased standard deviations (0.2, 0.3, and 1; Figure  s1 ). Increasing the standard deviation of the main population reduces the range of mean and standard derivation values of the subpopulation for which SPA correctly identifies two populations.

3.3. Identification of multiple subpopulations within OMI data using multiple variables

UMAP was used as a data dimension reduction technique to visualize clustering of the different cell populations from differences in autofluorescence lifetime features (Figure S2 and S3). UMAP visualization of a simulated OMI dataset consisting of 6000 drug responsive cancer cells, 5000 drug resistant cancer cells, 3234 quiescent T cells, and 1643 activated T cells shows the greatest separation between cancer cells and T cells (Figure S2). A 20,000 cells were selected as a representative OMI dataset because this is a reasonable number of cells to extract from a single experiment with 5–10 images per group for a 2–4 group experiment with 500–1000 cells/image (20× or 40× objective). Pair plots of the OMI data show clustering of the different features for the four cell populations (Figure S2). While pair‐wise analysis of some OMI features including provide separation of the four groups (Figure S2), the greatest separations are achieved with the UMAP visualization that uses all OMI features.

Machine learning was performed to identify cell populations within simulated OMI datasets of drug responsive cancer cells, drug resistant cancer cells, quiescent T cells, and activated T cells. A dataset (Original, Table S2) with 20,000 cells with equal portions of each population was randomized, and two different train/test datasets were created from the data, 90% train/10% test and 70% Train/30%Test. Random forest, logistic classifier, and multilayer perceptron algorithms were compared for performance to classify cells into the four cell populations. Of these models, the random‐forest algorithm achieved the best classification accuracy (Figure S4), 92.4% for the 30% test data (Figure 4[II]) and 92.1% accuracy for the 10% test data (Figure S5[II]).

FIGURE 4.

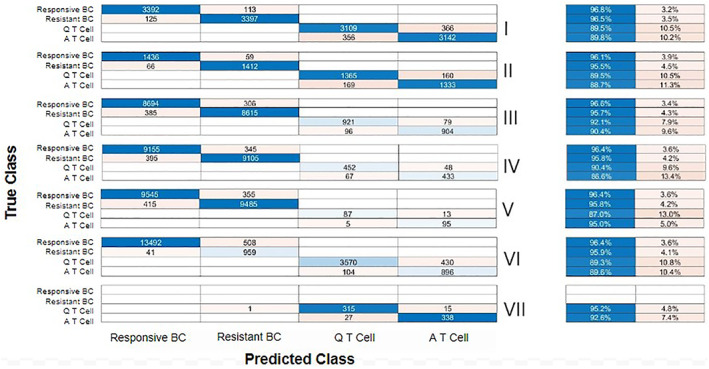
Confusion matrices show the number of correctly and incorrectly identified cells and tables show the percent accuracy (left, blue) and error (right, orange) for each cell population (cell population details provided in Table S2). The top graph (I) shows the random Forest Model's performance for the train data, (II) shows the test data, (III) shows a blind 4 cell population with 45% responsive cancer cells, 45% resistant cancer cells, 5% quiescent T cells, and 5% activated T cells, (IV) shows a blind 4 cell population with 47.5% responsive cancer cells, 47.5% resistant cancer cells, 2.5% quiescent T cells, and 2.5% activated T cells, (V) shows a blind 4 cell population with 49.5% responsive cancer cells, 49.5% resistant cancer cells, 0.5% quiescent T cells and 0.5% activated T cells, (VI) shows a blind 4 cell population with 70% responsive cancer cells, 5% resistant cancer cells, 20% quiescent T cells, and 5% activated T cells, and (VII) shows the experimental T cell dataset with 47.5% quiescent T cells, and 52.4% activated T cells. BC = breast cancer, Q = quiescent, and a = activated [Color figure can be viewed at wileyonlinelibrary.com]

The random forest model trained with 70% of the Original dataset was then used to determine the classification performance for four unseen datasets of unequal cell populations (Table S2). The pretrained random forest model classified cell type for three datasets with equal proportions of drug resistant and drug responsive cancer cells and equal proportions of quiescent and activated T cells for a combined total of 10%, 5%, and 1% of the total population, with overall classification accuracies of 95.67% (III), 92.73% (IV), and 96.06% (V), respectively (Figure 4). Additionally, the cell type was predicted for a model tumor dataset with 70% drug responsive cancer cells, 5% drug resistant cancer cells, 25% quiescent T cells, and 5% activated T cells. An overall classification accuracy of 94.59% (VI) was determined for the pre‐trained random forest model evaluated on the unseen simulated tumor data set (Figure 4). The pre‐trained random forest model had an overall accuracy of 93.82% (VII) for the real T cell imaging data.

For each dataset, the random forest model identified the drug responsive cancer cells with an accuracy above 96%. The most misclassified cells are activated T cells which are misclassified as quiescent T cells with a 13% misclassification in the blind 4 cell population with 95% Responsive and Resistant Cancer cells and 5% Quiescent and Activated T cells (IV). Table 1 shows how accurate the technique was in identifying the percent of cells in every population. At the population level, the random forest classifier identified the population proportions within 3% of the true value and was within 1% for populations smaller than 5%.

TABLE 1.

Actual population percentages and model predictions T = true, P = predicted

	I		II		III		IV		V		VI		VII
	T (%)	P (%)	T (%)	P (%)	T (%)	P (%)	T (%)	P (%)	T (%)	P (%)	T (%)	P (%)	T (%)	P (%)
Responsive BC	25	25.1	25	25.0	45	45.4	47.5	47.8	49.5	49.8	70	67.7	0	0
Resistant BC	25	25.1	25	24.5	45	44.6	47.5	47.3	49.5	49.2	5	7.36	0	0.1
Quiescent T cell	25	24.8	25	25.6	5	5.01	2.5	2.60	0.5	0.46	20	18.4	47.5	49.1
Activated T cell	25	25.1	25	24.9	5	4.92	2.5	2.41	0.5	0.54	5	6.63	52.4	50.7

Feature analysis was used to determine which features are contributing to the classification results. The redox ratio had the lowest ranking in three different training and testing datasets for both the Correlation Attribute and Information Gain Evaluators methods (Table 2). For the correlation attribute evaluator, FAD τ₁, the lifetime of bound FAD, shows the best correlation followed closely by FAD α₁, the fraction of bound FAD. Similar results were found for the information gain evaluator, but FAD α₁ had superior performance with NAD(P)H τ₁, the lifetime of free NAD(P)H, and FAD τ₁ also showing high contributions.

TABLE 2.

Feature ranking of seven different features

	Redox ratio	NAD(P)H τ1	NAD(P)H τ2	NAD(P)H α1	FAD τ1	FAD τ2	FAD α1
Correlation attribute evaluator
Full dataset	0.109	0.472	0.462	0.45	0.563	0.466	0.527
70% Test set	0.108	0.472	0.472	0.45	0.564	0.466	0.526
90% Test set	0.109	0.471	0.462	0.451	0.563	0.466	0.527
Information Gain Evaluator
Full dataset	0.6012	1.1393	0.91	0.968	1.0984	0.8809	1.224
70% Test set	0.6033	1.1441	0.9089	0.969	1.0986	0.88	1.221
90% Test set	0.604	1.143	0.908	0.971	1.1	0.882	1.222

Since the redox ratio achieved the lowest ranking for both evaluators, it was removed from all datasets and the random forest algorithm was rerun to generate classification models. The models achieved an overall accuracy of 91.4% and 91.5% for the 30% and 10% test data, respectively. While these percentages were very close to those gathered from the data with all features included, they were slightly lower which indicates that removing the redox ratio from the datasets does not improve the classification accuracy of the model.

4. DISCUSSION

Tumor heterogeneity remains challenging to detect and quantify with existing biomolecular tools. Fluorescence microscopy of the endogenous fluorophores NAD(P)H and FAD provides a label‐free method to evaluate cell metabolism and quantify multiple imaging features. Cell segmentation of NAD(P)H and FAD images allows single cell analysis of populations of cells. The functions of many different cells including drug response in cancer and activation of immune cells are dependent on cellular metabolism. Cancer cells frequently exhibit increased aerobic glycolysis to support growth and proliferation [22], and metabolic differences have been observed between drug resistant and drug responsive cancers [10]. Immune cells require high rates of metabolism once activated to support anti‐cancer activities [23, 24]. T cells in particular switch from oxidative metabolism of quiescent cells to glycolysis and glutaminolysis when activated [24]. OMI detects metabolic differences and can evaluate heterogeneity within cell populations [14, 16, 17, 18].

Using simulated fluorescence microscopy datasets of seven fluorescence intensity and lifetime features for four different cell populations including drug responsive and drug resistant cancer cells, and quiescent and activated T cells (Table  s1 ), we evaluated two quantitative methods, SPA and machine learning classification, to identify small populations of T cells and drug‐resistance cancer cells within a larger tumor mass. Histograms allowed visualization of different cell populations by OMI features (Figure 1). While it was possible to visualize two distinct populations with histogram analysis, this method is limited because it only allows for combinations of two populations and only one feature. The subpopulation analysis via mixed Gaussian models (Figures 2 and 3) allows identification of multiple modes or populations of data within histograms. The unnormalized SPA (Figure 2) revealed that FAD τ₁, the lifetime of bound FAD, is the best performing OMI feature for the identification of rare subpopulations of T cells and drug resistant cancer cells within larger drug responsive tumors. FAD τ₁ was also consistently weighted high in the classification feature analysis (Table 2). SPA revealed that the correct number of components may be identified but with high error for the proportions or means, demonstrating a potential error of this approach. To evaluate what the typical properties of a subpopulation must look like to be able to be successfully identified by the model, we simulated datasets with normalized mean and standard deviation values (Figure 3). As expected, two populations are identified when the mean population values are sufficiently separated and the standard deviations are low, relative to the mean values.

To overcome the single variable and two‐population limitations of SPA, we used data dimensionality reduction for data visualization and machine learning methods for cell classification and subpopulation identification. Whereas the histogram analysis of the Drug Responsive Cancer Cells and all CD3+ T cells populations failed to show clear separation between the cells (Figure 1A), accounting for all the OMI features via UMAP allowed clear visualization of clustering between the four populations of cells (Figures S2B and S3A), highlighting the importance of using multivariant analysis methods for analysis of OMI data.

Machine learning classification achieved accuracies >96% for the identification of drug responsive cancer cells and drug resistant cancer cells in a population of 20,000 cells equally divided into four populations and using 70% for training and 30% for testing. Consistent results were achieved whether 30% or 10% of the data was used to test, suggesting the model is not overly fit to the training data since there is not an increase in misclassification error as the population sizes are reduced (Figure S5). The responsive cancer cells were the most accurately classified population in every dataset, with accuracy above 96%. The T cell populations were the least correctly identified, with accuracies above 88%. These results of accuracies above 80% are comparable with other machine learning identification of immune cell populations from microscopy data [14, 15, 25].

When identifying rare events, it is important to consider the false positive rate as a high false positive rate coupled with a low incidence of true positives can lead to a substantial number of false positives (base rate fallacy). The false positive rates for the groups of the test dataset are 1.47% for responsive breast cancer cells, 1.3% for resistant breast cancer cells, 3.6% for quiescent T cells, and 3.6% for activated T cells (Figure 4). Despite these false positive rates exceeding the 0.5% population percentage of the T cell groups in dataset V, the number of false positives is not a majority of the identified cells, 5/92 (5.4%) for quiescent T cells and 13/108 (12.2%) for activated T cells. However, false positives dominate in dataset VI where 35% of resistant cancer cells and 32% of activated T cells are falsely positive. Models that will be used to identify rare cell populations should be evaluated for false positive rates and tested to characterize the probability of false positive events.

Given that FLIM data is highly dependent on the microenvironment and in order to better evaluate the classification methods, the results were tested on real experimental data. An imaging dataset of quiescent and activated T cells was evaluated by the simulation data‐trained random forest model, and 93.8% of the cells were accurately classified (Figure 4VII) demonstrating that the model is applicable to real experimental data. However, when the same algorithm was tested with drug responsive and resistant head and neck cancer cells, the model correctly identified the cells as cancer, but was unable to label the resistant cells correctly. This shows that the model that was built for breast cancer cells is not transferable to other experiments and needs to be remade for the new dataset. Different microscopes, cell types, and experimental conditions may alter the data sufficiently to require training of new classification models. The minimum number of datapoints to generate robust models depends on the statistical parameters of the data, number of groups to differentiate, and size of the feature set. As shown here, simulated data can be included for model training to boost dataset sizes, provided that the simulated data mimics the parameters of the real data.

The feature analysis results showed more dependence of the classification models on FAD lifetime features than NAD(P)H lifetime features or the redox ratio. The redox ratio was the lowest ranking feature, but removing it did not improve the results. The reason for the low ranking of the redox ratio may be due to the dependence of the fluorescence intensity measurements on laser power, detector gain and experimental conditions that may not have been the same between the breast cancer cell study and the T cell study from which the mean and standard deviation measurements were derived. The importance of the FAD lifetime parameters for classification, particularly the fraction of bound FAD (FAD α₁) and the lifetime of bound FAD (τ₁) suggest differences in mitochondrial metabolism or oxidative phosphorylation among the four cell groups [26, 27]. Abnormal metabolism is a hallmark of cancer and differences in glycolysis and oxidative phosphorylation are well documented between quiescent and activated T cells [22, 24, 28].

The results demonstrate that SPA and classification algorithms based on autofluorescence imaging features can be used to identify rare cell subpopulations within heterogeneous mixtures of cells. Future work could potentially combine the use of Convolutional Neural Networks (CNNs), Transfer Learning (TL), and data augmentation techniques to classify the datasets and the corresponding images from experimental work. Leveraging these computational methods with existing technologies to identify and track rare populations of cells will enable time‐course studies of cancer stem cells, immune cells, and drug‐resistant cells to elucidate cell behaviors and allow testing of novel therapeutics.

AUTHOR CONTRIBUTIONS

Elizabeth N. Cardona: conceptualization (equal); formal analysis (equal); investigation (lead); methodology (lead); project administration (supporting); software (lead); validation (lead); visualization (supporting); writing original draft (lead); writing review & editing (equal). Alex J. Walsh: conceptualization (equal); formal analysis (equal); funding acquisition (lead); investigation (supporting); methodology (supporting); project administration (lead); resources (lead); software (supporting); supervision (lead); writing review & editing (supporting).

CONFLICT OF INTEREST

The authors have no conflicts of interest to disclose.

PEER REVIEW

The peer review history for this article is available at https://publons.com/publon/10.1002/cyto.a.24534.

Supporting information

table s1 Experimental mean and standard deviation values for seven features

Table S2: Machine learning train/test datasets cell count

Figure S1: Normalized SPA for increasing sigmas

Figure S2: UMAP 2D visualization of four distinct cell populations

Figure S3: UMAP 2D feature combination images

Figure S4: Confusion matrices for algorithm down selection

Figure S5: Confusion matrices for 90% train/10% test group.

Cardona EN, Walsh AJ. Identification of rare cell populations in autofluorescence lifetime image data. Cytometry. 2022;101:497–506. 10.1002/cyto.a.24534

DATA AVAILABILITY STATEMENT

The custom Matlab and Python scripts for the generation and analysis of simulated OMI data are available in this GitHub repository (https://github.com/walshlab/Subpopulation-analysis).