Abstract
An Azospirillum brasilense Sp7 strain containing a plasmid-borne translational cytN-gusA fusion was grown in a continuous culture to quantitatively evaluate the influence of extracellular signals (such as O2) on expression of the cytNOQP operon. The dissolved oxygen concentration was shifted at regular time intervals before the steady state was reached. The measured β-glucuronidase activity was used to monitor cytN gene expression. However, as the β-glucuronidase activity in the experimental setup not only depended on altered transcription of the hybrid gene when the signal was varied but was also influenced by cellular accumulation, degradation, and dilution of the hybrid fusion protein, a mathematical method was developed to describe the intrinsic properties of the dynamic bioprocess. After identification and validation of the mathematical model, the apparent specific rate of expression of the fusion, which was independent of the experimental setup, could be deduced from the model and used to quantify gene expression regulated by extracellular environmental signals. In principle, this approach can be generalized to assess the effects of external signals on bacterial gene expression.
Gene fusions containing reporter genes are widely used to monitor and quantify the effects of external signals on bacterial gene expression (11, 14). However, complications may arise if the external signals, such as the levels of O2 and other substrates utilized by the bacteria, cannot be kept constant during the test (7). Since O2 level is a very important external signal regulating expression of certain genes, a reliable method is needed to study the influence of O2 on bacterial gene expression.
The use of a continuous culture in an O2-stat to test the influence of O2 on expression of a gene represents a major improvement in such studies (5, 12, 23, 24). In a continuous culture the O2 concentration can be adjusted easily; thus, the effects of fluctuating cell densities and respiratory rates on O2 concentrations can be compensated for. When the effects of constitutive O2 shifts on gene expression are studied, measurements in a continuous fermentation are usually taken after establishment of a steady state (5, 12). Such experiments require extended fermentation times and therefore might involve a high risk of biological instability problems.
An experimental setup in which measurements could be taken after the O2 shift occurs and before a steady state is reached would significantly enhance analysis. It should be noted that in such a setup the absolute expression level not only is dependent on altered transcription of the hybrid gene when the signal is varied but also is influenced by the cellular accumulation, degradation, and dilution rate of the hybrid fusion protein. (It should also be noted that even in a steady state, the absolute value for fusion protein activity depends on the implemented dilution rate and therefore is not completely independent of the experimental setup.) Therefore, a reliable method which is independent of the experimental parameters to describe the influence of O2 on expression of genes can facilitate interpretation of the experimental data.
In this study, a method was developed to determine the mere influence of O2 on expression of target genes. A general dynamic model was used to describe cell growth and fusion protein expression in a continuous culture in which the dissolved oxygen (DO2) concentration was shifted at regular time intervals before the steady state was reached. The apparent specific rate of expression of the gene fusion, which was intrinsically independent of the experimental parameters, was defined and deduced from a validated mathematical model. The model was used to study induction of cytN gene expression by O2 in Azospirillum brasilense Sp7 based on the activities of a cytN-gusA fusion. The A. brasilense cytNOQP operon, encoding a cytochrome cbb3 terminal oxidase, has been shown to be involved in microaerobic growth and respiration (16). Model-based data analysis indicated that the optimal DO2 level for expression of the cytNOQP genes is in the microaerobic range, which is consistent with a previous study (16).
MATERIALS AND METHODS
Plasmids, bacterial strains, and growth conditions.
The strains and plasmids used in this study are listed in Table 1. Luria-Bertani medium was used for Escherichia coli, while MMAB medium (29) was used for Azospirillum strains. When required, ampicillin (100 μg/ml) or tetracycline (10 μg/ml) was added to the medium.
TABLE 1.
Plasmids and bacterial strains used in this study
| Plasmid or strain | Relevant characteristic(s) | Reference or source |
|---|---|---|
| pFAJ1171 | pUC18 derivative containing the promoterless gusA gene from pBI101.3 on a 2-kb BamHI-EcoRI fragment | 25 |
| pFAJ870 | pFAJ1171 derivative containing a 517-bp fragment from the cytN gene of A. brasilense Sp7 | This study |
| pFAJ873 | pLAFR3 derivative containing a 2.6-kb PstI-EcoRI fragment from pFAJ870 | This study |
| pLAFR3 | Broad-host-range vector, Tcr | 21 |
| Azospirillum brasilense Sp7 | Wild type (= ATCC 29145) | 22 |
| Escherichia coli DH5α | hsdR17 endA1 thi-1 gyrA96 relA1 recA1 supE44 ΔlacU169 (Φ80lacZ ΔM15) | Gibco-BRL |
To construct the translational cytN-gusA fusion used in this study, a 517-bp upstream region of the cytN gene was PCR amplified and inserted into the PstI-XbaI sites of plasmid pFAJ1171 (25) to generate plasmid pFAJ870. After verification by DNA sequence analysis, a 2.6-kb PstI-EcoRI fragment from pFAJ870, containing the cytN upstream region fused to the promoterless gusA reporter gene, was cloned into the corresponding sites of plasmid pLAFR3 (21), yielding pFAJ873, which contained 427 bp of the cytN upstream region and the sequences encoding the first 29 amino acids of CytN fused to the GusA coding sequence. This plasmid was mobilized from E. coli DH5α to A. brasilense Sp7 by triparental conjugation.
Continuous fermentation was performed in a 2-liter O2-stat fermentor as previously described (16) by using MMAB medium (29). The concentration of DO2 was controlled by varying the air flow into the fermentor on the basis of the measured DO2 value. Gaseous nitrogen was sparged into the fermentor at a flow rate of 1.27 liters/min at low DO2 levels (0 to 15% DO2).
Analytical procedures.
Quantitative β-glucuronidase activity was measured as previously described (26); this activity was expressed in Miller units (17) but was calculated per hour instead of per minute. Cell growth was monitored by measuring the optical density at 578 nm (OD578) with a Perkin-Elmer Lambda 2 UV spectrum spectrophotometer. The l-malate concentration in the culture broth was determined with a test kit from Boehringer (Mannheim, Germany). All data in this paper are averages based on at least two replicates.
Fermentation strategy.
The bacteria were first cultivated in a batch fermentation. At the end of the exponential growth phase, continuous fermentation started. Consecutive small DO2 concentration shifts were made before a new steady state was reached. The profiles of DO2 concentrations during fermentation are shown in Fig. 1A, 2A, and 3A. Samples were taken about each 1.5 h (just before a DO2 concentration shift) and used to determine the β-glucuronidase activity and cell density. To monitor strain stability and purity, samples were collected at the end of the fermentation period and spread on indicator plates containing bromo-4-chloro-3-indolyl-β-glucuronide (X-Gluc) (11). During the continuous fermentation, the carbon source (malate) was designed to be the limiting factor.
FIG. 1.
Identification of the mathematical model. (A) Profile of on-line-measured values for DO2 concentration (DO2) (solid line) and dilution rate (D) (dashed and dotted dot line). (B to D) ○, experimental data; solid line, simulation results obtained with the full model; dashed line, simulation results obtained with the simplified model. EFT, elapsed fermentation time; GUS, β-glucuronidase.
FIG. 2.
Validation of the mathematical model. The symbols and abbreviations are the same as those described in the legend to Fig. 1.
FIG. 3.
Further validation of the mathematical model with a different DO2 profile. The symbols and abbreviations are the same as those described in the legend to Fig. 1.
Analysis of the fermentation data.
Changes in the β-glucuronidase activity of a hybrid gene reporter in the presence of a changing external signal indicate that the external signal is the transcriptional activation signal. However, in the experimental setup described above, not only alterations in transcriptional activation of the plasmid encoding the cytN-gusA fusion induced by the DO2 concentration shifts but also accumulation and turnover of the fusion protein can account for the β-glucuronidase activity measured. Therefore, only the specific rate of expression of the fusion protein, which is independent of the experimental design, can reflect the influence of O2 on expression of the target gene. In order to derive the specific rate of expression of the fusion protein from the β-glucuronidase activity measured, the following general dynamic mathematical model based on mass balances was applied (28):
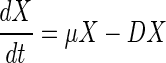 |
1 |
 |
2 |
 |
3 |
where X is the concentration of biomass (grams of cells per liter), S is the concentration of the carbon source (grams of malate per liter), Sin is the concentration of the carbon source in the feed flow (grams of malate per liter), P is the concentration of the fusion protein (grams of protein per liter), D is the dilution rate (per hour), μ is the specific growth rate of cells (per hour), ς is the specific rate of consumption of the carbon source (grams of malate per gram of cells per hour), π is the specific rate of expression of the fusion protein (grams of protein per gram of cells per hour), and k is the in vivo rate of degradation of the fusion protein (per hour).
According to the definition of β-glucuronidase activity (17), the β-glucuronidase activity value is assumed to be proportional to the amount of fusion protein per cell:
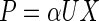 |
4 |
where U is the β-glucuronidase activity (Miller units [enzyme activity per gram of cells per hour]) and α is a proportionality constant (grams of protein per gram of cells per Miller unit).
By combining equation 4 with equations 1 and 3, the following equation can be deduced:
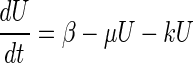 |
5 |
where β is π/α (Miller units per hour), the apparent specific rate of expression of the fusion protein, and reflects the direct influence of the external signal on transcriptional activation of the hybrid gene fusion.
The three specific reaction rates can be correlated with equation 6:
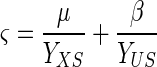 |
6 |
where YXS (grams of cells per gram of malate) and YUS (Miller units per gram of cells) are two positive constant yield coefficients.
To complete the model, the following kinetic expressions are proposed. A double Haldane model is used to describe the specific growth rate of cells as a function of two substrates, malate and O2 (1). The apparent specific rate of expression of the fusion protein is described as a function of the carbon substrate (malate) concentration with a Monod model (18) and as a function of DO2 concentration with a Haldane-like model in which background expression of the fusion protein is introduced since constitutive background expression of the fusion protein has been observed under anaerobic conditions (data not shown). Although it is generally known that E. coli β-glucuronidase is a very stable enzyme in cell extracts and in cells (10, 11), no value for in vivo decay of any β-glucuronidase protein in A. brasilense has been described so far. However, the dependence of degradation of the fusion protein on DO2 concentration has also been observed in experiments carried out in test tubes (data not shown). The rate of degradation of the fusion protein can be expressed as a function of DO2 concentration in the frame of the Monod model (18). Therefore, the following equations are proposed:
 |
7 |
 |
8 |
 |
9 |
where DO2 is the concentration of dissolved oxygen (percent); KMXS and KIXS are the saturation constant and inhibition constant of malate for cell growth (grams of malate per liter), respectively; KMXG and KIXG are the saturation constant and inhibition constant of DO2 for cell growth (percent), respectively; KMPS is the saturation constant of malate for fusion protein expression (grams of malate per liter); KMPG and KIPG are the saturation constant and inhibition constant of DO2 for fusion protein expression (percent), respectively; KBPG is the constant for background expression of the fusion protein (percent); Kk is the saturation constant of DO2 for decay of the fusion protein (percent); μmax is the maximal growth rate of cells (per hour); βmax is the maximal apparent rate of expression of the fusion protein (Miller units per hour); and kmax is the maximal rate of degradation of the fusion protein (per hour).
In order to assess the influence of DO2 on the specific level of expression of the cytN-gusA fusion, the measured experimental values were fed into the model to identify the appropriate parameters. Once the values are identified, the complete model (parameters and model structure) can be used to predict the behavior of the hybrid fusion protein as a function of the external variables.
Simulation and parameter identification for the model described above were performed by using Matlab 5.3 (The MathWorks, Inc., Natick, Mass.) on a Linux platform.
RESULTS
Parameter identification.
A. brasilense Sp7 containing plasmid pFAJ873 was cultivated in a fermentor for 13 h. Subsequently, continuous fermentation was started by maintaining the dilution rate at 0.15 h−1. The DO2 concentrations were shifted before a steady state was reached at regular intervals (about 1.5 h). The profile of DO2 concentration is shown in Fig. 1A. The parameters in the mathematical model were identified by minimizing the following cost function (J):
 |
10 |
where i is the sampling time; j is the components X, S, and U; n (n = 3 in this case) and m are the number of components and the sampling time, respectively; Ys,ij is the data set for the simulation results; Ye,ij is the data set for the experimental results; Ỹe,j is the average value for the components; and ςsj is the standard deviation of the experimental data. In order to diminish the effects of the different physical quantities of the measurements, the relative errors, (Ys,ij − Ye,ij)/Ỹe,j, are taken into account in cost function J.
The identification results are shown in Figure 1B to D, while the values for the identified parameters are summarized in Table 2. The estimated initial (zero-time) values were as follows: S = 5.2087 g of malate per liter; X = 0.0554 OD578 unit; and U = 41.9123 Miller units. The carbon source concentration in the feed flow (Sin) was 5.0075 g of malate per liter. Because cell density rather than dry weight of cells was used to monitor cell growth, the yield coefficient YXS as defined in equation 6 was expressed in OD578 units per gram of malate instead of grams of cells per gram of malate. The agreement between the simulation results and the experimental data is remarkable.
TABLE 2.
Summary of the parameters used in the general mathematical model
| Parameter | Units | Description | Value |
|---|---|---|---|
| μmax | Per hour | Maximal growth rate of cells | 0.2785 h−1 |
| βmax | Miller units per hour | Maximal rate of expression of fusion protein | 1.0387 × 104 Miller units/h |
| kmax | Per hour | Maximal rate of degradation of fusion protein | 0.1270 h−1 |
| KMXS | Grams of malate per liter | Saturation constant of malate for cell growth | 1.58 × 10−2 g of malate/liter |
| KIXS | Grams of malate per liter | Inhibition constant of malate for cell growth | 7.805 × 103 g of malate/liter |
| KMXG | Percent | Saturation constant of DO2 for cell growth | 0.1533% |
| KIXG | Percent | Inhibition constant of DO2 for cell growth | 6.1583 × 103% |
| KMPS | Grams of malate per liter | Saturation constant of malate for fusion protein expression | 5.7782 × 10−4 g of malate/liter |
| KBPG | Percent | Background expression constant of fusion protein | 0.0056% |
| KMPG | Percent | Saturation constant of DO2 for fusion protein expression | 7.6233% |
| KIPG | Percent | Inhibition constant of DO2 for fusion protein expression | 0.6527% |
| Kk | Percent | Saturation constant of DO2 for degradation of fusion protein | 0.4781% |
| YXS | OD578 units per gram of malate | Yield coefficient for biomass on carbon substrate | 0.3282 OD578 unit/g of malate |
| YUS | Miller units per gram of malate | Yield coefficient for GUS activity on carbon substratea | 2.7181 × 104 Miller units/g of malate |
GUS, β-glucuronidase.
Validation of the mathematical model.
To validate the model structure and parameters, an experimental test set was generated by performing a continuous fermentation similar to the one used for parameter identification but with a slightly different DO2 profile (Fig. 2A) and different initial values. The continuous fermentation started at 10 h with a dilution rate of 0.1125 h−1. The following initial values for validation were chosen from the first experimental measurements: S = 4.8388 g of malate per liter; X = 0.097 OD578 unit; and U = 25.5267 Miller units. For the carbon source concentrations in the feed flow, the following experimentally measured value was used: Sin = 4.989 g of malate per liter. Both the simulation results, as obtained by applying the model and parameters identified above, and the experimental data are shown in Fig. 2. The good agreement between the simulated and experimental results indicates the applicability of the model when comparable experimental conditions (such as DO2 profile) are used.
In order to further validate the applicable range of the model, a continuous fermentation with a totally different DO2 profile (Fig. 3A) was performed. The DO2 concentration was kept at 10% during the batch fermentation, and it was subsequently shifted from low to high values during the continuous fermentation. The continuous fermentation started at 12 h with a dilution rate of 0.1193 h−1. The following initial values used for validation were based on the first experimental measurements: S = 5.3812 g of malate per liter; X = 0.038 OD578 unit; and U = 126.84 Miller units. For the carbon source concentration in the feed flow, the following measured value was used: Sin = 5.308 g of malate per liter. The simulation results and the experimental data are shown in Fig. 3. The agreement between the simulated and experimental results corroborates the generality of the model.
Influence of O2 on the rate of expression of the target genes.
As indicated in Fig. 4A and B, the rate of expression of the cytN-gusA fusion is very dependent on the DO2 concentration, and the maximal values occur under microaerobic conditions (a DO2 concentration of 2.23% results in maximal expression).
FIG. 4.
(A) Apparent specific rate of expression of fusion protein as a function of the concentrations of the substrates malate and DO2. (B) Cross section of panel A at a constant malate concentration of 1 g/liter. (C) Specific rate of degradation of fusion protein as a function of DO2 concentration.
As shown by the values for KMXG and KIXG in Table 2, the model predicts that O2 is not a limiting factor for cell growth under the conditions tested. In view of the highly efficient microaerobic metabolism of Azospirillum (30), such behavior is not unexpected. The minor effect of carbon substrate concentration on the apparent specific rate of expression is also predicted by the model, implying that the cytNOQP operon is not subject to catabolic repression by malate. Furthermore, the specific rate of degradation of the fusion protein as a function of the DO2 concentration is shown in Fig. 4C. The maximal specific rate of degradation of the fusion protein is 0.1270 h−1, corresponding to a half-life of 5.46 h. The native CytN protein is a transmembrane protein (16), but its GusA fusion counterpart lacks any potential transmembrane region and should therefore be cytoplasmically located. The cytoplasmic GusA fusion appears to be a stable protein in A. brasilense.
Towards a simplified model.
When the general model structure represented by equations 1, 2, 5, and 6 to 9 is examined and the large range of orders of magnitude for the 14 parameters summarized in Table 2 is considered, a legitimate question is whether a similar high-quality fit of the experimental data can be obtained with a simplified model that includes fewer parameters. In order to mathematically investigate this possibility, a thorough sensitivity analysis was performed.
The dilution rate and the DO2 concentration were defined as system inputs u1 and u2, respectively, and the biomass concentration, the malate concentration, and the β-glucuronidase activity were defined as system outputs y1, y2, and y3, respectively. The parameters were denoted pj with j ranging from 1 to 14.
A 3 × 14 sensitivity matrix containing the sensitivity functions (∂yi/∂pj)(t) was then computed. These sensitivity functions represent the sensitivity of each output (yi) to (small) variations in each model parameter (pj). More details on sensitivity function-related procedures have been described by Bernaerts et al. (3).
Based on the sensitivity functions and the experimental data, the kinetic expressions (equations 7 to 9) of the general model described above could be substantially simplified as follows:
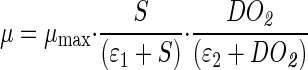 |
11 |
 |
12 |
 |
13 |
Meanwhile, the correlation among the three specific reaction rates can be simplified as equation 14:
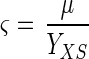 |
14 |
The number of model parameters has been reduced to six. The parameters and constants in the simplified kinetic expressions (equations 11 to 13) are summarized in Table 3.
TABLE 3.
Summary of the parameters used in the simplified mathematical model
| Parameter | Units | Description | Value |
|---|---|---|---|
| μmax | Per hour | Maximal growth rate of cells | 0.2785 h−1 |
| βmax | Miller units per hour | Maximal rate of expression of fusion protein | 1.0387 × 104 Miller units/h |
| kmax | Per hour | Maximal rate of degradation of fusion protein | 0.1270 h−1 |
| KMPG | Percent | Saturation constant of DO2 for fusion protein expression | 7.6233% |
| KIPG | Percent | Inhibition constant of DO2 for fusion protein expression | 0.6527% |
| YXS | OD578 units per gram of malate | Yield coefficient for biomass on carbon substrate | 0.3282 OD578 unit/g of malate |
| ɛ1 | Constant | 10−2 | |
| ɛ2 | Constant | 10−6 |
As Table 3 and equations 11 to 14 show, most of the saturation constants are replaced by ɛ1 or ɛ2. The former is the same order of magnitude as the residual substrate concentration (i.e., 10−2) and results in a 50% reduction in the specific growth rate when the malate concentration is low. The latter is a very small number (e.g., 10−6) and results in a switch from the maximum specific rate when substrate or DO2 is present to a rate of zero when both substrates are absent. Furthermore, the inhibition constants (i.e., KIXS and KIXG) that have been omitted can be considered replaced by an infinitely large (positive) number corresponding to a noninhibition situation. Note, however, that from a mechanistic point of view, it cannot be claimed that growth of A. brasilense is not inhibited by high substrate or DO2 concentrations. We merely concluded that an inhibition effect cannot be inferred from the available experimental data. Also, the yield coefficient YUS is assumed to be infinitely large to reflect the negligible contribution of product formation to the substrate consumption rate.
Figure 1 (identification) and Fig. 2 and 3 (validation) illustrate that the descriptive quality of this simplified model is as good as the descriptive quality of the original 14-parameter model. Note that there was apparently no need to reoptimize the six parameters in the simplified model (Tables 2 and 3).
Detailed exploration of the significance of model parameters in the general model, as well as in the simplified model, is the subject of ongoing research. Thus, optimal experiments (complemented with parameter uncertainty analysis) will be designed to check whether the model features present in the general model but omitted in the simplified model (e.g., inhibition of the specific growth rate at high substrate or DO2 concentrations, the presence of background gene expression in the absence of DO2) are truly needed.
DISCUSSION
Use of a dynamic mathematical model allows reliable quantitative interpretation of gene expression measurements as a function of varying environmental conditions without a requirement for a steady state. The parameters of the model are determined by using experimental data. When validated, the model can be used to predict in silico the effects of external signals on expression of the gene studied under nonexperimentally tested conditions. The use of mathematical models based on differential equations to describe and predict the behavior of cellular processes is becoming widespread (4, 6, 8, 9, 13, 20, 27). According to previous studies with E. coli, a steady state can be achieved within 5 reactor residence times (12, 23, 24), which equals 33 h at a dilution rate of 0.15 h−1. A total fermentation time of 297 h (12 days) would be needed to test nine different DO2 levels. The overall experimental time can be decreased to only 15 h when the DO2 level is varied each 1.5 h and a mathematical model is used to analyze the results; this yields more detailed information about the effects of external signals on expression of the genes.
In this study, a mathematical model was used to predict the specific pattern of expression of an A. brasilense cytN-gusA fusion as a function of DO2 concentration. The role of the cytNOQP-encoded oxidase during microaerobic respiration and the presence of an FNR-binding consensus sequence in the upstream region of the A. brasilense cytN gene (16) point towards microaerobic regulation of the operon by an FNR-like protein. The simulated behavior of the A. brasilense hybrid cytN-gusA fusion, showing clear upregulation under microaerobic conditions, was therefore in good agreement with results obtained previously for the A. brasilense cytochrome cbb3 oxidase. Moreover, it is noteworthy that the DO2 concentration that resulted in maximal specific expression of the cytN-gusA fusion was approximately the same as the DO2 concentration reported by Zhulin et al. (30) and coincided with generation of a maximal proton motive force. Furthermore, an expression pattern similar to the one obtained in this study has been reported for the CytN-like protein of Rhodobacter sphaeroides (19).
The model assumes that the shift in expression of the target gene occurs as soon as the DO2 shift occurs. However, we cannot exclude the possibility that there may be a lag between signal transduction and fusion protein synthesis (for example, the delay between maximal mRNA synthesis and maximal protein synthesis). Usually, such a delay in prokaryotes is minimal (15). If a longer response time is expected (2), it is advisable to adapt the time intervals for measurements accordingly. Thus, the effects caused by the transition are similar for different DO2 levels, and the results are comparable.
On the basis of a careful sensitivity analysis, a simplified model (with fewer parameters) was deduced in this case study, and this model had predictive values similar to those of the full model. The key feature of both the full model and the simplified model is mathematical description of fusion protein biosynthesis and degradation during bacterial growth. Given the high predictive value of these models, it is sensible to assume that they can form a basis for evaluating the effects of other external environmental signals, such as nitrogen source or other substrates which can be utilized by bacteria, on expression of target genes by using suitable fusions with the appropriate reporter genes. In view of fermentation technology, when optimization of heterologous gene expression is desired, such studies might allow workers to determine the environmental conditions that result in maximal gene expression.
ACKNOWLEDGMENTS
J.S. is a recipient of a predoctoral fellowship from the Research Council, Katholieke Universiteit Leuven. I.S. is a research assistant with the Fund for Scientific Research Flanders. K.B. is a research assistant with the Institute for the Promotion of Innovation by Science and Technology in Flanders, Belgium.
This work was supported in part by grants (to J.V.) from the Flemish Government (GOA) and the Fund of Scientific Research-Flanders, project OT/99/24 of the Research Council of Katholieke Universiteit Leuven and the Belgian Program on Interuniversity Poles of Attraction, initiated by the Belgian State Prime Minister's Office for Science, Technology and Culture.
REFERENCES
- 1.Andrews J F. A mathematical model for the continuous culture of microorganisms utilizing inhibiting substrates. Biotechnol Bioeng. 1968;10:707–723. [Google Scholar]
- 2.Baumann B, Snozzi M, Zehnder A J B, van der Meer J R. Dynamics of denitrification activity of Paracoccus denitrificans in continuous culture during aerobic-anaerobic changes. J Bacteriol. 1996;178:4367–4374. doi: 10.1128/jb.178.15.4367-4374.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bernaerts K, Versyck K J, Van Impe J F. On the design of optimal dynamic experiments for parameter estimation of a Ratkowsky-type growth kinetics at suboptimal temperatures. Int J Food Microbiol. 2000;54:27–38. doi: 10.1016/s0168-1605(99)00140-3. [DOI] [PubMed] [Google Scholar]
- 4.Cain S J, Chau P C. Transition probability cell cycle model with product formation. Biotechnol Bioeng. 1998;58:387–394. [PubMed] [Google Scholar]
- 5.Chao G, Shen J, Tseng C P, Park S-J, Gunsalus R P. Aerobic regulation of isocitrate dehydrogenase gene (icd) expression in Escherichia coli by the arcA and fnr gene products. J Bacteriol. 1997;179:4299–4304. doi: 10.1128/jb.179.13.4299-4304.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen T, He H L, Church G M. Modeling gene expression with differential equations. In: Altman R B, editor. The Pacific Symposium of Biocomputing ‘99. Hawaii: World Scientific; 1999. pp. 29–40. [PubMed] [Google Scholar]
- 7.Cotter P A, Gunsalus R P. Contribution of the fnr and arcA gene products in coordinate regulation of cytochrome o and d oxidase (cyoABCDE and cydAB) genes in Escherichia coli. FEMS Microbiol Lett. 1992;91:31–36. doi: 10.1016/0378-1097(92)90558-6. [DOI] [PubMed] [Google Scholar]
- 8.Goldbeter A. A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase. Proc Natl Acad Sci USA. 1991;88:9107–9111. doi: 10.1073/pnas.88.20.9107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Goldbeter A, Dupont G, Berridge M J. Minimal model for signal-induced Ca2+ oscillations and for their frequency encoding through protein phosphorylation. Proc Natl Acad Sci USA. 1990;87:1461–1465. doi: 10.1073/pnas.87.4.1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jefferson R A, Burgess S M, Hirsh D. β-Glucuronidase from Escherichia coli as a gene-fusion marker. Proc Natl Acad Sci USA. 1986;83:8447–8451. doi: 10.1073/pnas.83.22.8447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jefferson R A, Kavanagh T A, Bevan M W. GUS fusions: β-glucuronidase as a sensitive and versatile gene fusion marker in higher plants. EMBO J. 1987;6:3901–3907. doi: 10.1002/j.1460-2075.1987.tb02730.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kasimoglu E, Park S-J, Malek J, Tseng C P, Gunsalus R P. Transcriptional regulation of the proton-translocating ATPase (atpIBEFHAGDC) operon of Escherichia coli: control by cell growth. J Bacteriol. 1996;178:5563–5567. doi: 10.1128/jb.178.19.5563-5567.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Koh B-T, Tan R B H, Yap M G S. Genetically structured mathematical modeling of trp attenuator mechanism. Biotechnol Bioeng. 1998;58:502–509. doi: 10.1002/(sici)1097-0290(19980605)58:5<502::aid-bit6>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- 14.Lambrecht M, Vande Broek A, Vanderleyden J. The use of GUS reporter system to study molecular aspects of interactions between bacteria and plants. In: Jansson J, editor. Tracking genetically engineering microorganisms: method development from microcosms to the field. Georgetown, Tex: RG Landes Bioscience; 1999. pp. 87–97. [Google Scholar]
- 15.Lodish H, Baltimore D, Berk A, Zipursky S L, Matsudaira P, Darnell J. Molecular cell biology. New York, N.Y: Scientific American Books, Inc.; 1995. pp. 406–407. [Google Scholar]
- 16.Marchal K, Sun J, Keijers V, Haaker H, Vanderleyden J. A cytochrome cbb3 (cytochrome c) terminal oxidase in Azospirillum brasilense Sp7 supports microaerobic growth. J Bacteriol. 1998;180:5689–5696. doi: 10.1128/jb.180.21.5689-5696.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Miller J H. Experiments in molecular genetics. Cold Spring Harbor, N.Y: Cold Spring Harbor Laboratory; 1972. pp. 354–358. [Google Scholar]
- 18.Monod J. Recherches sur la croissance des cultures bactériennes. Paris, France: Hermann; 1942. [Google Scholar]
- 19.Mouncey N J, Kaplan S. Oxygen regulation of the ccoN gene encoding a component of the cbb3 oxidase in Rhodobacter sphaeroides 2.4.1T: involvement of the FnrL protein. J Bacteriol. 1998;180:2228–2231. doi: 10.1128/jb.180.8.2228-2231.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Novak B, Tyson J J. Modeling the control of DNA replication in fission yeast. Proc Natl Acad Sci USA. 1997;94:9147–9152. doi: 10.1073/pnas.94.17.9147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Staskawicz B, Dahlbeck D, Keen N, Napoli C. Molecular characterization of cloned avirulence genes from race 0 and race 1 of Pseudomonas syringae pv. glycinea. J Bacteriol. 1987;169:5789–5794. doi: 10.1128/jb.169.12.5789-5794.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tarrand J J, Krieg N R, Döbereiner J. A taxonomic study of the Spirillum lipoferum group, with description of a new genus, Azospirillum gen. nov., and two species, Azospirillum lipoferum (Beijerinck) comb. nov. and Azospirillum brasilense sp. nov. Can J Microbiol. 1978;24:967–980. doi: 10.1139/m78-160. [DOI] [PubMed] [Google Scholar]
- 23.Tseng C-P, Albrecht J, Gunsalus R P. Effect of microaerophilic cell growth conditions on expression of the aerobic (cyoABCDE and cydAB) and anaerobic (narGHJI, frdABCD, and dmsABC) respiratory pathway genes in Escherichia coli. J Bacteriol. 1996;178:1094–1098. doi: 10.1128/jb.178.4.1094-1098.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Tseng C-P, Hansen A K, Cotter P, Gunsalus R P. Effect of cell growth rate on expression of the anaerobic respiratory pathway operons frdABCD, dmsABC, and narGJJI of Escherichia coli. J Bacteriol. 1994;176:6599–6605. doi: 10.1128/jb.176.21.6599-6605.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vande Broek A. Histochemical and genetic analysis of the A. brasilense-plant root association. Ph.D. thesis. Heverlee, Belgium: Katholieke Universiteit Leuven; 1994. [Google Scholar]
- 26.Vande Broek A, Michiels J, de Faria S M, Milcamps A, Vanderleyden J. Transcription of the Azospirillum brasilense nifH gene is positively regulated by NifA and NtrA and is negatively controlled by the cellular nitrogen status. Mol Gen Genet. 1992;232:592–600. doi: 10.1007/BF00280007. [DOI] [PubMed] [Google Scholar]
- 27.Van Dien A J, Keasling J D. A dynamic model of the Escherichia coli phosphate-starvation response. J Theor Biol. 1998;190:37–49. doi: 10.1006/jtbi.1997.0524. [DOI] [PubMed] [Google Scholar]
- 28.Van Impe J F, Bastin G. Optimal adaptive control of fed-batch fermentation processes. Control Eng Practice. 1995;3:939–954. [Google Scholar]
- 29.Vanstockem M, Michiels K, Vanderleyden J, Van Gool A. Transposon mutagenesis of Azospirillum brasilense and Azospirillum lipoferum: physical analysis of Tn5 and Tn5-mob insertion mutants. Appl Environ Microbiol. 1987;53:410–415. doi: 10.1128/aem.53.2.410-415.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhulin I B, Bespalov V A, Johnson M S, Taylor B L. Oxygen taxis and proton motive force in Azospirillum brasilense. J Bacteriol. 1996;178:5199–5204. doi: 10.1128/jb.178.17.5199-5204.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]






