Abstract
The influence of metabolism on signaling, epigenetic markers, and transcription is highly complex yet important for understanding cancer physiology. Despite the development of high-resolution multi-omics technologies, it is difficult to infer metabolic activity from these indirect measurements. Fortunately, genome-scale metabolic models and constraint-based modeling provide a systems biology framework to investigate the metabolic states and define the genotype-phenotype associations by integrations of multi-omics data. Constraint-Based Reconstruction and Analysis (COBRA) methods are used to build and simulate metabolic networks using mathematical representations of biochemical reactions, gene-protein reaction associations, and physiological and biochemical constraints. These methods have led to advancements in metabolic reconstruction, network analysis, perturbation studies as well as prediction of metabolic state. Most computational tools for performing these analyses are written for MATLAB, a proprietary software. In order to increase accessibility and handle more complex datasets and models, community efforts have started to develop similar open-source tools in Python. To date there is a comprehensive set of tools in Python to perform various flux analyses and visualizations; however, there are still missing algorithms in some key areas. This review summarizes the availability of Python software for several components of COBRA methods and their applications in cancer metabolism. These tools are evolving rapidly and should offer a readily accessible, versatile way to model the intricacies of cancer metabolism for identifying cancer-specific metabolic features that constitute potential drug targets.
Keywords: cancer, metabolism, constraint-based modeling, genome-scale metabolic models, systems biology, omics, python, single-cell analysis
Introduction
Cancer involves a complex set of dysregulations in multiple biomolecular layers including metabolism. Metabolic changes in cancer result from and lead to profound changes in the behavior of cancer cells and their surrounding environment. Although extensively studied, these metabolic changes are difficult to accurately measure and model in an unbiased manner due to the need to consider a heterogeneous tumor environment encompassing different cell types, many difficult-to-measure metabolites, and lack of standardization of models (1). While recent years have yielded a wealth of methods to measure and analyze biological systems at multiple omics layers (genomic (2, 3), epigenomic (4), proteomic (5–8), and metabolomic (9–11), often extending to single-cell resolution (12), metabolic systems are difficult to systematically assess because gene expression or protein levels may not directly translate into metabolic activity (1).
Genome-scale metabolic models (GEMs) can provide a compelling approach towards understanding cellular metabolism. GEMs are curated computational descriptions of entire cellular metabolic networks. Derived from genome annotations and experimental data, GEMs are composed of mass-balanced metabolic reactions and gene-protein associations that map the relationship of genes to proteins involved in each reaction ( Figure 1 ). The accumulation of high-throughput data has contributed to the reconstruction of GEMs for hundreds of organisms, from microbes and model organisms to animals and humans (13). Whole-organism GEMs can further be reduced into context-specific and cell type-specific models for analyzing specific tissue phenotypic states performing different cellular functions. Metabolic flux analyses of GEMs have led to various model-guided applications, such as hypothesis generation, strain design, drug target discovery, multicellular interactions modeling, and disease etiology (14–16). With the rapidly increasing availability of high-resolution multi-omics datasets, there is an increasing need for tools to interpret data using a mathematical framework that also integrates existing vast and complex biological knowledge. In particular, dysregulated metabolic systems in cancer interact heavily with the surrounding environment, and metabolic flux analysis may prove especially beneficial to modeling these systems.
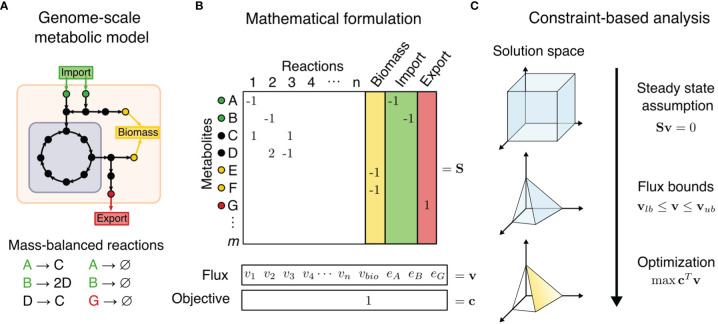
Figure 1.
Constraint-based metabolic modeling. (A) A genome-scale metabolic model is a compartmentalized network of mass-balanced reactions that convert products to reactants, and boundary pseudo-reactions that import or export metabolites. Biological objectives, such as biomass production, require activity through a subset of internal reactions. (B) The metabolic model is converted into a stoichiometric matrix (S) of size m × n, with rows representing m metabolites and columns n reactions. Reaction flux through all internal reaction (vi ) and exchange reactions (ei ) is represented by vector v of length n. Objective function Z = c T v is formulated as a linear combination of desired fluxes, weighted by vector c. (C) At steady state, the rate of production and consumption of a metabolite must be zero, which is described by the system of equations Sv = 0. There are many solutions to this system of equations, but the solution space can be constrained by imposing flux bounds (v lb ≤ v ≤ v ub ) and optimization such as maximization of objective function.
Compared to omics analysis, cancer metabolism may be more accurately modeled by combination of GEMs and a family of methods called Constraint-Based Reconstruction and Analysis (COBRA). COBRA methods perform systems-level analyses on metabolic networks to uncover how genetic and environmental factors affect phenotype on a biomolecular basis. COBRA framework utilizes a stoichiometric matrix that transcribes mass-balanced metabolic reactions of a cellular system, including the system’s uptake and secretion rates, into a matrix that represents the change in levels of reactants and products for each reaction ( Figure 1 ). While there are many allowable states of reaction fluxes through a metabolic network, COBRA reduces this solution space of feasible flux distributions by adding constraints. Some basic constraints are mass conservation (stoichiometry of reaction and products in a reaction), steady-state assumption (input and output fluxes are balanced), and reaction flux bounds (inequalities of upper and lower bounds). Additional constraints can be determined by metabolite and enzyme levels, thermodynamics directionality, enzyme capacities, spatial compartmentalization, and genome regulatory mechanisms (15, 17). This induces a space of feasible fluxes which fulfill the used balance equations and constraints, often called the “flux cone”. Constraint-based analysis methods then aim to find biologically relevant flux distributions within the flux cone.
COBRA methods for metabolic network analysis are now incorporated into many software packages across several programming languages like MATLAB and Python (15). Of these, MATLAB packages such as COBRA Toolbox, Raven Toolbox, and CellNetAnalyzer have been the leading standard platforms that integrate with many existing COBRA methods (18–20). However, the reliance on MATLAB, a proprietary and closed-source software, reduces the accessibility of metabolic flux analysis, especially for teaching and reproducibility purposes. Recent open-source community efforts have promoted the development of a similar ecosystem of COBRA software in Python, starting with the development of COBRApy (21) under the openCOBRA Project (22) and PySCeS CBMPy (23). As an open-source language, Python opens COBRA methods to greater possibilities by enabling deployment on machines without a proprietary license, which is especially convenient for cloud computing. Due to Python being widely adopted for data science and computation, it provides state-of-the-art scientific tools for accessing databases, integrating various data modalities, and interfacing with computational tools like parallel computing, machine learning, visualizations, and web applications.
This review will summarize the set of packages currently available in Python for various COBRA methods. We identify the advantages and shortcomings of the Python ecosystem to guide users’ decisions on their choice of a software platform and inspire future research ideas. We focus on the application of COBRA methods to cancer metabolism. Finally, we will explore the future directions of COBRA methods development and their importance in cancer modeling.
COBRA Methods in Python
To make COBRA open-source and accessible, multiple Python packages have been developed by the scientific community to perform the different analyses within COBRA. Here we describe the major components of COBRA and list their associated packages ( Figure 2 ; Table 1 ), and assess their strengths and weaknesses ( Table 2 ). First, we start with the core package COBRApy, which handles the details of metabolic models and basic simulations. We then describe methods for determining metabolic flux, such as flux balance analysis, flux variability analysis, and in silico perturbation. Next, we summarize various methods for adding biological constraints like multi-omics and biophysics. In addition, we review methods for unbiased pathway analysis and sampling methods. We also summarize the development of COBRA methods for models at the single-cell and population level. Finally, we touch upon packages for visualization and interactive web applications.
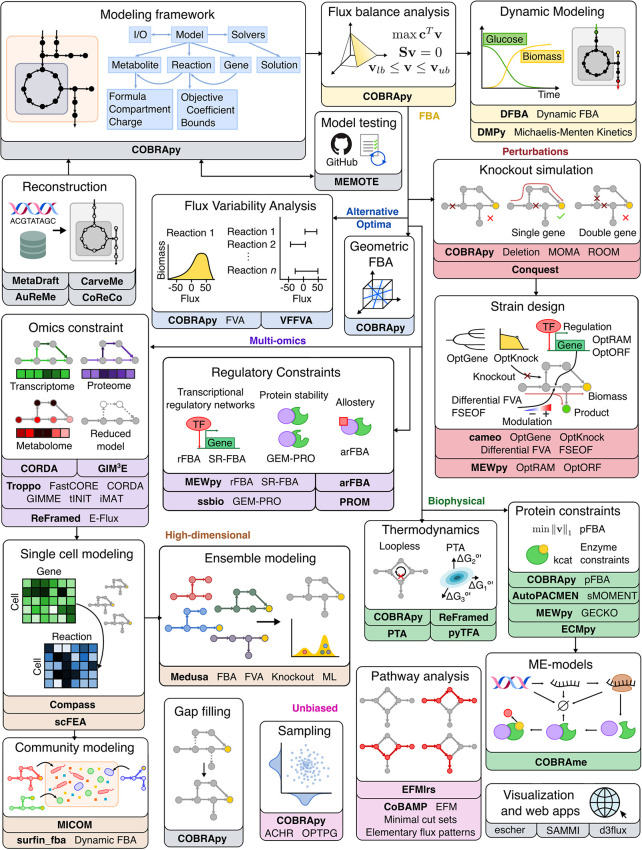
Figure 2.
Overview of Python software for major components of COBRA methods. Constraint-based metabolic modeling first requires loading a metabolic model into software that handles the various parts of the modeling framework (grey), such as metabolites, reactions, genes, stoichiometric matrix, and flux solutions. New metabolic models can be reconstructed from genome sequences and database, quality-checked by model testing software, made consistent using gap-filling tools, and visualized using web-based packages. Using the metabolic model, FBA (yellow) finds an optimal flux distribution that follows stoichiometry under steady state and can further be extended to dynamic systems. Since there are alternative optima (blue) to FBA, FVA and geometric FBA can be used to characterize the solution space. We can perturb (red) the system to predict the effect of knockouts and use such predictions to design an optimal system (‘strain’). To improve FBA predictions, we can add biophysical (green) constraints based on thermodynamics, proteins, and macromolecular expression. Metabolic modeling can be further enhanced by integration of multi-omics (purple) data, such as extracting reduced models based on omics data and adding regulatory constraints. Using omics data, metabolic modeling can become high-dimensional (brown), through single cell modeling and community modeling. Multiple metabolic models can be reduced into ensemble objects. In contrast to FBA, unbiased (pink) approaches do not require an objective function. These include methods for sampling flux distributions and pathway analyses. Names of software packages are in bold.
Table 1.
Python tools for constraint-based modeling.
Methods and their associated software packages as illustrated in Figure 2 , organized by their general function. Weblinks to each software’s official website and documentation are provided if available. Each software is assessed for availability of documentation (Doc.) or any form of demonstrative examples.
Table 2.
Pros and cons of COBRA methods.
| Category | Method/Tool | Pros | Cons |
|---|---|---|---|
| Reconstruction | AuReMe | - Support for eukaryotes model - Good traceability - Automatic integration of experimental data |
- Some manual refinement assistance - Not FBA-ready |
| CarveMe | - GEMs ready for FBA - Fast - Customizable for large number of genomes |
- No manual refinement assistance - Some support for eukaryotes model |
|
| MetaDraft | -Support for eukaryotes model - Fast |
- No manual refinement assistance - Not FBA-ready |
|
| CoReCo | - Support for eukaryotes model - GEMs nearly ready for FBA - Simultaneous reconstruction for multiple species (parallelizable) |
- Requires KEGG license - No manual refinement assistance |
|
| FBA | FBA | - Does not require kinetic parameters | - Requires objective function - Requires reaction bounds (especially exchange flux) |
| Dynamic modeling | Dynamic FBA (SOA and DAE) | - Couples pseudo-steady states to dynamical systems - Does not require kinetic parameters |
- SOA requires small steps and thus more computation |
| DMPy | - Infers missing kinetic parameters using thermodynamics constraints | - Requires >80% of kinetic parameters for accuracy | |
| Alternative optima | Geometric FBA | - Gives single representative solution – Reproducible typical solution (avoids randomly picking one solution from flux cone) | - Weak correlation with protein levels (without omics constraint) |
| FVA/VFFVA | - Determines min and max flux for a reaction would achieve optimal objective state - (VFFVA) Increased speed and reduced memory usage |
- Varies one reaction at a time | |
| Sampling | - Estimates probability distribution of feasible fluxes - Can be unbiased (not using an objective function) |
- Computationally intensive | |
| Omics constraints | E-flux | - Constraints reaction bounds only - No discretization of data |
- May over-constrain model based on noisy data - Poor growth rate prediction |
| GIMME | - LP problem (fast) - Ensures operability of required metabolic function - Predicts growth rate, uptake/secretion rates, essential genes, and oncogenes |
- Discretizes data - Models have high fractions of blocked reactions, moderate resolution power, poor robustness to missing data/noise |
|
| GIM3E | - Ensures operability of required metabolic function - Integrates metabolomics data |
- Discretizes data - MILP problem (slow) |
|
| (t)INIT | - Ensures operability of required metabolic functions - (INIT) predicts oncogenes and tumor suppressor genes, consistent model, good resolution power, robust to noise/missing data |
- MILP problem (slow) - (INIT) Poor predictions of growth rate, uptake/secretion rates, and essential genes |
|
| iMAT | - No objective required - Consistent model, good resolution power, robust to noise/missing data - Predicts oncogenes |
- Discretizes data - MILP problem (slow) - Weak predictions of growth rate, uptake/secretion rates, and essential genes |
|
| FASTCORE | - LP problem (fast) - Obtains minimal consistent model - Predicts oncogenes and loss of function mutations - Moderately consistent model, good resolution power, robust to noise |
- Requires specification of core reactions - Poor predictions of growth rate, uptake/secretion rates, and essential genes |
|
| CORDA | - LP problem (fast) - Non-parsimonious pruning - Predicts oncogenes and loss of function mutations |
- Requires specification of core reactions - Weak predictions of growth rate and essential genes - Poor predictions of uptake/secretion rates |
|
| Regulatory constraints | rFBA | - Predicts flux over time intervals - Models transcriptional regulation |
- Uses boolean TRN - Stepwise calculation of metabolic and regulatory states - Chooses only one solution per time interval |
| SR-FBA | - Combined calculation using metabolic and regulatory constraints - Models transcriptional regulation |
- Uses boolean TRN - Calculates flux for one time step (steady-state) - Does not account for metabolic transitions and feedback loops |
|
| PROM | - Uses continuous TRN - Models transcriptional regulation |
- Requires TF-target gene relationships | |
| GEM-PRO | - Models protein instability | - Requires protein structures | |
| arFBA | - Models allosteric regulation | - Requires regulation matrix defining effector-reaction relationship - Small-scale applications |
|
| Thermodynamics | ll-FBA | - Does not require metabolite concentrations or free energies | - MILP problem (slow) |
| CycleFreeFlux | - Post-process using LP problem (fast) - Can be applied to any flux distribution including sampled solutions - Does not require metabolite concentrations or free energies |
- Biased towards solutions with small total flux and those with same direction as their overlapping internal cycles | |
| TFA, TVA | - Explicitly models thermodynamics | - Requires metabolite concentrations and free energies - Over-approximates uncertainty |
|
| PTA | - Explicitly models thermodynamics for optimization and sampling - Models uncertainty of free energies and metabolite concentrations |
- Requires metabolite concentrations and free energies - Computationally intensive |
|
| Protein constraints | pFBA | - Predicts growth rate, uptake/secretion rates, and essential genes | - Assumes that flux distribution with smallest magnitude minimizes protein costs |
| Enzymatic constraints (GECKO, sMOMENT, ECMpy) |
- Model proteome limitation at enzyme resolution - (sMOMENT) Automates enzyme database query - (ECMpy) Automates enzyme parameters calibration - (ECMpy) Does not increase model size |
- Requires experimentally measured enzyme turnover numbers - (GECKO) Increases model size - (sMOMENT) Moderately increases model size - (ECMpy) Manually obtains protein subunit composition data |
|
| ME-modeling | COBRAme | - Modeling proteome composition improves predictive accuracy - Framework for building ME-models for new organisms |
- Large model size and complexity - No standardized SBML format for ME-models - Only applied to bacteria so far |
| Ensemble modeling | Medusa | - Compresses multiple models into compact ensemble objects - Reduces memory usage of storing ensembles - Interfaces with machine learning |
- No standardized SBML format for ensemble objects |
| Single cell modeling | Compass | - Genome-scale modeling - Maximizes agreement with gene expression - Handles sparsity by sharing information across neighbors - Uses multiple objective functions |
- Map gene expression to reaction expression using boolean relationships (GPR) |
| scFEA | - Minimizes flux imbalance of all cells to simulate exchange of metabolites - Less stringent flux balance and steady-state assumption - Uses neural net to model nonlinear relationship between gene expression and reaction rates |
- Not easily scalable due to large memory usage - Applied to small-scale models |
|
| Community modeling | MICOM | - Models exchanges and interactions between communities and environment - Automates building community models from a model database - Predicts replication rates in human gut microbiome |
- Assumes trade-offs between individual and community growth rate (gut microbiome specific) - Metabolic models may not be accurate (labratory vs. gut conditions, species differences) |
| Dynamic FBA (surfin_fba) | - Reduces optimizations problems (and parameter space) required for dynamic FBA for communities | - Non-biological approach to choosing between non-unique optima | |
| Pathway Analysis | EFM | - Unbiased characterization of models (no objective function required) - (EFMlrs) Pre- and post-process models for EFM calculations |
- (EFMlrs) EFM calculation performed by other tools not included in program - EFM calculations are memory intensive and not scalable |
Some method comparisons extracted from literature for reconstruction (87, 88), dynamic modeling (89), omics constraints (90, 91), and regulatory constraints (92). Growth rate, uptake/secretion rates, and cancer essential gene prediction performances from Jamialahmadi et al. are based on human metabolic models and available only for GIMME, INIT, iMAT, FASTCORE, CORDA, and pFBA (91).
Modeling Framework
COBRA for Python (COBRApy) uses an object-oriented programming approach to represent models, metabolites, reactions, and genes as class objects with accessible attributes. Using this design, COBRApy recapitulates functions for standard metabolic flux analyses of its MATLAB counterpart while being extendible and accessible. First, it has the capabilities to read and write models in various formats such as MAT-file (for storing MATLAB variables), JSON, YAML, and Systems Biology Markup Language (SBML) (93), the current community-accepted standard for computational systems biology. SBML incorporates the Flux Balance Constraints (FBC) version 2 package (94), which supports constraint-based modeling by encoding objective functions, flux bounds, model components, and gene-protein associations, whose usage will be discussed below. COBRApy can also load SBML models from web databases such as BiGG and BioModels (95, 96). The quality of such metabolic models can be assessed using a Python test suite called MEMOTE that integrates version control of models via GitHub and checks for correct annotation, model components, and stoichiometry (24). To use these models for various optimization problems, COBRApy interfaces with either commercial or open-source solvers that implement linear programming algorithms. We will detail additional built-in or integrated functionalities for various COBRA methods ( Figure 2 ).
Flux Balance Analysis
The most common COBRA method is flux balance analysis (FBA), which assumes the system is at steady state, follows mass-balance described in the stoichiometric matrix, and restricts reaction fluxes by bounds. Furthermore, FBA searches for sets of steady-state reaction fluxes that maximize or minimize an objective function representing a biological function, such as using biomass production objective to model cellular growth (29). The objective function is an artificial reaction formulated by linear combinations of reactions that would contribute to the desired biological function. For example, the biomass production can be represented by the consumption of biomass precursors in different proportions. Components of the biomass production may include amino acids, lipids, nucleotides, carbohydrates, cofactors, and other molecules based stoichiometrically on the macromolecular composition of a cell measured as weight fractions under specific experimental conditions, typically during exponential growth. Although the biomass equation is the de facto choice for the objective function and macromolecular compositions are more similar across related species, certain components such as fatty acids are sensitive to environmental and genetic conditions (97). Therefore, caution is required when choosing an appropriate objective function that reflects the system’s experimental condition. Sensitivity analysis of FBA could be performed using different objectives (or ensemble of objectives) accounting for the natural variation in biomass equation across different conditions (97). Assessment of bias introduced by the objective function would require experimental validation of growth dynamics or knockout simulations discussed below. Under the above mathematical constraints, FBA is an optimization problem involving a system of equations that can be solved by linear programming, as initially proposed in 1984 (98). Functions for FBA and customization of objective functions are included in COBRApy. With these basic constraints, FBA is the foundation from which many forms of COBRA methods evolved.
Dynamic Metabolic Modeling
Although FBA assumes that a system is unchanging at steady state, these pseudo-steady states can be coupled to a dynamical system with changing environmental variables using dynamic FBA (DFBA) (99). There are several approaches to DFBA: 1) dynamical optimization approach (DOA) that uses ordinary differential equations (ODEs) to describe an optimization problem of entire time profiles of metabolites, 2) statistic optimization approach (SOA) that divides the time period into time intervals to perform instantaneous optimization (LP) per time interval with flux rate-of-change constraints, 3) direct approach (DA) that resolves the LP of the right-hand side of ODEs, and 4) reformulation of the ODEs as differential-algebraic equation (DAE) system (30, 89, 99). The fourth approach via DAE is implemented in Python package dfba (31), while the second approach via SOA can be implemented using COBRApy and SciPy. Alternatively, a very different approach to dynamical metabolic modeling was proposed by DMPy, which translates a GEM into a dynamic reaction equation model using Michaelis-Menten approximations and infers missing kinetic constants using Bayesian parameter estimation with thermodynamics constraints (32). However, this method requires extensive measurements of reaction rates to accurately parameterize a large-scale model. All these constraint-based methods for dynamical metabolic modeling enable the utilization of high-throughput and longitudinal data to interrogate changes in metabolism.
Alternative Optimal Solutions
Flux distributions, even under an optimal objective, are usually not unique as many alternative fluxes can yield a maximum biomass production. The most representative solution can be found using geometric FBA in COBRApy, which looks for a unique flux distribution that is central to the entire solution space (33). To better characterize all alternative optima that satisfy the constraints of FBA, flux variability analysis (FVA) finds the range of alternative fluxes for a reaction that maintains optimization of the objective function within a margin of error (34). The search for alternate optimal solutions is time-intensive, but COBRApy has addressed this problem in FVA by implementing parallel computing. For example, Very Fast Flux Variability Analysis (VFFVA) is available in Python and its implementation of FVA is much faster and more memory-efficient than its analog in MATLAB, fastFVA (35).
System Perturbations, In Silico Knockout, and Strain Design
Quantitative flux predictions are useful to experimentalists because of their potential to explain or even predict the effect of environmental and genetic changes. For investigating the relationship between the external environment and the modeled system, COBRApy provides tools for specifying the growth medium and exchange rates of a model. Instead of extracellular conditions, intracellular changes such as genetic mutations and gene modulation can be interrogated as well. To identify essential genes and reactions for biological functions, FBA is performed with gene knockout simulations to assess the effects of the knockouts on objective functions (36). Similar to COBRA Toolbox, COBRApy includes functions for knocking out single or double genes and reactions by restricting the flux through associated reactions. Another algorithm for assessing the effect of a perturbation is minimization of metabolic adjustment (MOMA), which determines the post-perturbation flux vector that is closest to a reference flux vector (e.g., FBA solution before change) (37). Currently, COBRApy implementation of MOMA is the only one that does not require a commercial quadratic programming solver but instead uses OSQP, which is an open-source solver (100). Another method, called Regulatory-on-off minimization (ROOM), finds the new flux distribution with minimal reaction changes compared to a reference state (38). Available in COBRApy, these methods characterize the effects of gene deletion relative to a wild-type reference. Adding to flux-based determination of essentiality, a new metabolite essentiality analysis combining graph-based and flux-based analysis was proposed by Conquests (Crossroad in metabOlic Networks from Stoichiometric and Topologic Studies) (39).
The iterative testing of gene or reaction deletions was initially developed for in silico strain design, which determines optimal genetic changes that would maximize production of desired metabolites. Straight maximization of only the desired reaction is problematic, since it ignores the drainage of cellular resources needed for cellular growth. Therefore, strain design methods couple product yields with cellular objectives to optimize for fast-growing cells that have high productivity. Such metabolic engineering tools are available in a COBRApy-derived package called cameo (41). It provides efficient, parallelized implementations of standard in silico strain design methods for predicting gene knockout strategies (OptGene [evolutionary algorithm] (40), OptKnock [linear programming] (42) and for predicting gene expression modulation targets (Differential FVA, Flux Scanning based on Enforced Objective Flux [FSEOF] (43). Instead of modulating genes, there are algorithms that optimize at the regulatory level by changing transcription factors, such as OptRAM (44) and OptORF (46) in MEWpy (Metabolic Engineering Workbench in python) (45). These simulation tools for strain design and in silico knockouts/perturbations can be easily adapted to study metabolism in the context of physiology and disease, especially cancer. For example, we will later discuss studies that use in silico knockout to screen for cancer drug targets. Other studies integrated genetic variants by simulating knock out of enzymes with loss of function mutations (101–103).
Integrating Multi-Omics Data With GEMs
Integration of omics data into metabolic models is now critical to standard analysis of GEMs to improve flux predictions and interpret multi-omics data. Prior to applying constraints, gene-level data must first be processed to reflect reaction-level data. This involves calculating a reaction expression matrix that evaluates gene-protein-associations (GPR, nested logic rules representing gene essentiality and redundancy). For example, we take the minimum expression of required subunits, but take the sum of isozyme expression. This calculation can be performed in Python packages like CORDA (Cost Optimization Reaction Dependency Assessment) (49) and MEWpy (45). Marín de Mas et al. further improved GPR evaluation in their Python implementation of stoichiometric GPR (S-GPR) that considers the stoichiometry of protein subunits (104).
The resulting reaction expression levels are used subsequently to extract a context-specific metabolic model of active reactions from the whole-organism GEM to reflect a phenotypic state specific to cell type and condition, such as disease state or nutrient level. The simplest transcriptome constraints can be applied by setting associated expression levels as the reaction upper bound, as demonstrated in E-flux and other studies (47, 105, 106). Instead of constraining all genes, PRIME is method that adjusts reaction upper bounds of phenotype-associated genes that are correlated with phenotypic data such as growth rate (90). Additional methods for extraction of context-specific models from transcriptome, metabolome, and proteome have been reviewed previously and can be summarized into three main families of approaches (107): 1) GIMME-like (GIMME (53), GIM3E (50), tINIT (54)), which aims to maximize the correspondence of flux phenotype to data while maintaining required metabolic functions; 2) iMAT-like (iMAT (55), INIT (108), Lee-12 (109), which only maximizes similarity of flux phenotype to data; and 3) MBA-like (MBA (110), mCADRE (111), FASTCORE (51), FASTCORMICS (112), CORDA (49), which removes non-core reactions while ensuring consistency of the model. Currently, integration of these methods with COBRApy is still in development within the DRIVEN project (113). Fortunately, some of these reconstruction methods have been reimplemented in other Python packages ( Table 1 ). For example, ReFramed implemented E-flux (48), CORDA and GIM3E have standalone Python packages, and Troppo implemented FASTCORE, CORDA, GIMME, tINIT, and iMAT (52). Nonetheless, the Python ecosystem has shortcomings in reconstruction methods, such as the unavailability of some methods (INIT, MBA, mCADRE, FASTCORMICS, and PRIME), and the lack of documentation and usage examples for the Troppo package.
Reconstruction methods could result in incomplete and infeasible networks, partly due to errors in experimental data and curated knowledge, and partly due to parsimonious approaches when pruning reactions. To make reconstructed models feasible, one can use the gap-filling functionality in COBRApy to infer missing pathways using mixed-integer linear program (MILP). However, due to stochasticity and existence of alternative optima, GEM reconstruction and gap-filling of the same network can give rise to multiple GEMs that could yield different flux predictions. To account for the uncertainty in network structure, ensemble modeling compresses such a set of alternative models into an ensemble object to reduce redundancy while capturing variation. Ensemble modeling can be performed through Medusa, a Python package for generating ensembles, performing ensemble simulations, and coupling ensembles with machine learning (ML) (72).
Despite reconstruction of context-specific GEMs, GEMs are still flawed in flux prediction due to their inability to account for cellular mechanisms that regulate metabolic activity. A recent review has outlined the major methods for integrating regulatory mechanisms into metabolic models as the following: transcriptional regulatory networks (TRNs), post-translational modifications, epigenetics, protein–protein interactions and protein stability, allostery, and signaling networks (92). Several methods using TRNs have been translated from MATLAB to Python ( Table 1 ), including boolean TRN methods like regulatory FBA (rFBA) (56) and steady-state regulatory FBA (SR-FBA) (57) available via MEWpy, and a continuous TRN method called probabilistic regulation of metabolism (PROM) (58, 114). Other regulatory mechanisms are also available: 1) GEM-PRO (59) integrates protein structure information, and 2) arFBA (61) integrates allosteric interactions respectively. However, methods for integrating post-translational modifications, epigenetics, and signaling networks are not yet available in Python. Future development is needed to account for the complex cellular regulatory activity.
Extraction of context-specific GEMs requires a reference GEM that is often manually curated. To automate the laborious process of GEM reconstruction, several tools were developed to reconstruct microbial GEMs from genome sequences (87). Several examples of Python-based software are AuReMe (25), CarveMe (26), MetaDraft (27), and CoReCo (28). Among these, Mendoza et al. (87) reviewed the first three and found them all to generate GEMs that have high reaction sets similarity to manually curated models, but only CarveMe generates GEMs ready-to-use for FBA ( Table 2 ). A more recent tool called gapseq (88) was shown to outperform CarveMe, but it is written in shell-script and R.
Biophysical Constraints
To ensure that reaction directionalities in computational results agree with biological findings, COBRA methods include addition of thermodynamic constraints via removal of thermodynamically infeasible pathways or calculations of Gibbs free energy. The vastness of solution space can also be attributed to thermodynamically infeasible loops where metabolites are cycled infinitely. COBRApy includes two implementations for removing such loops: one method ll-FBA (add_loopless) utilizes mixed-integer linear programming (62), and another faster method CycleFreeFlux (loopless_solution) uses postprocessing of solutions (63). Additionally, there are other Python packages that interface with COBRApy to implement thermodynamics analysis. For example, probabilistic thermodynamics analysis (PTA) models use joint probability distributions of free energies and concentrations for stream optimization and sampling flux analysis (64). Earlier methods such as thermodynamic flux analysis (TFA) and thermodynamic variability analysis (TVA) (65) were implemented in ReFramed (48). Another Python package for thermodynamic-based flux analysis (pyTFA) couples thermodynamics feasibility into FBA calculations (66). Thermodynamics constraints ensure physiological flux predictions and help to reduce the solution space.
Another theme of biophysical constraints involves modeling the proteome limitation of a cell due to molecular crowding in a cell. A simple method within this theme is parsimonious FBA (pFBA), which assumes that minimizing overall total flux approximately finds efficient pathways that minimizes the total enzyme mass (67). Available in COBRApy, pFBA first determines the maximum value of the objective function, then adds it as a model constraint and solves for the flux distribution with the smallest magnitude, minimizing protein costs (67). However, this assumption may not always hold for all conditions and complex cellular networks. Another way to limit proteins is to add constraints based on enzyme parameters such as turnover number (kcat) and molecular weight. These protein allocation constraints are applied by Python package MEWpy using a method called GECKO (Genome-scale model enhancement with Enzymatic Constraints accounting for Kinetic and Omics data), which adds many pseudo-metabolites and pseudo-reactions to represent enzymes (68). Another package for protein allocation constraints is AutoPACMEN (Automatic integration of Protein Allocation Constraints in MEtabolic Networks) (69). AutoPACMEN can automate database query and creation of models using sMOMENT (short metabolic modeling with enzyme kinetics), which introduces only one pseudo-reaction and pseudo-metabolite. Further improving upon these methods, ECMpy adds enzyme constraints without increasing model size (70). Studies have shown that adding protein constraints improves the accuracy of flux predictions by explaining suboptimal overflow metabolism and metabolic switches (69, 70). Instead of high-level protein constraints, the machinery cost of protein expression can be explicitly modeled using genome-scale models of metabolism and macromolecular expression (ME-models). ME-models extend GEMs by computing optimal composition of macromolecules like proteins, nucleotides, and cofactors, to model the entire process from transcription and translation, to complex formation and metabolic reaction. Software for building and simulating ME-models is currently only available in Python via COBRAme (71) and was extended to dynamic systems via dynamicME (115). All packages for protein constraints mentioned above are compatible with COBRApy.
Unbiased Characterization of Solution Space
There are unbiased methods for analyzing distribution of steady-state flux through a metabolic model. One set of unbiased methods performs network-based pathway analysis without knowledge of traditional pathway annotations: elementary flux mode (EFM) analysis finds the minimum reaction sets (i.e., pathways) that can maintain steady state. Different variations of EFM have been implemented in Python. For example, EFMlrs is a Python package that performs EFM enumeration via lexicographic reverse search, an implementation that significantly improves performance and memory usage (79). In addition, CoBAMP is another package that has implemented EFM (80), minimal cut sets (82), and elementary flux patterns (81, 116). Extreme pathway (ExPa) analysis is another method for identifying reaction sets but it is not currently available in Python (83).
Another set of unbiased methods is Markov chain Monte Carlo (MCMC) sampling methods, which can characterize the solution space by estimating the probability distribution of feasible fluxes. This could be performed with or without constraining by an objective function. Currently, COBRApy integrated MCMC methods such as artificial centering hit-and-run (ACHR) (77) and optimized general parallel (OPTPG) (78) samplers, but not coordinate hit-and-run with round (CHRR) (117) that was found to be the best performing (118).
Single-Cell Metabolic Modeling
Our ability to interrogate the heterogeneity of cell populations has grown rapidly due to advances in single-cell technologies that can measure the transcriptome, proteome, epigenome, and even metabolome at the single-cell level (2–7, 11, 12, 119–126). While single cell multi-omics data can be analyzed by pathway enrichment, clustering, and correlation methods (16, 122, 123), recent studies have developed algorithms in Python to calculate metabolic flux from single-cell transcriptome (119, 127). Zhang et al. demonstrated the usage of CORDA for the reconstruction of cell type-specific metabolic models from murine single-cell transcriptome and their subsequent FBA simulations of NAD+ biosynthesis using COBRApy (128). Instead of optimizing for a specified objective function, Compass is an FBA-based method that scores the ability of cell transcriptome to maintain high flux through each reaction (73). Rather than using linear programming to solve for flux distribution, scFEA first reconstructs a metabolic model into a directed factor graph, then trains a deep neural network to learn metabolic flux distributions by minimizing flux imbalance across all cells and maximizing correspondence with gene expression (74). Due to drop-outs in single-cell RNA-seq, these algorithms took different approaches to handle the sparsity of expression data: 1) Zhang et al. calculated mean expression profiles per tissue and cell ontology class, 2) Compass allows information sharing between cells that are similar in transcriptional space, and 3) scFEA trains the model on all cells and removes metabolic modules only if they are entirely composed of significantly unexpressed genes. These methods allow metabolic flux interpretation of single-cell transcriptome at the single-cell resolution; however, not all flux estimation methods account for the interaction of cells via uptake and secretion of metabolites into the environment.
Multicellular Metabolic Modeling
To account for metabolic interactions, multicellular modeling was devised to model interplay between multiple metabolic networks coming from different species or tissues, with applications from microbiology to human physiology (129). Community modeling of the human gut microbiome reveals community-level function and cross-feeding interactions, as demonstrated by Python package MICOM (75). Community models are further extended using dynamic FBA of microbial communities, which can be efficiently calculated using Python package called surfin_fba that reduces the number of optimization timesteps when modeling communities (76). Early attempts to model human cell populations were explored using MATLAB, beginning with popFBA that simulated clones of cancer cells with identical stoichiometry and capacity constraints while allowing extracellular fluxes (130). PopFBA searched for combinations of individual metabolic flux distributions that would maximize a population object, e.g., total biomass, to explore metabolic heterogeneity and cooperation between single cells. However, this method gives many possible solutions and ignores the differences in metabolic requirements, functions, and proliferation rates of heterogeneous populations. To address both issues, single-cell FBA (scFBA) in MATLAB optimizes individual objective functions within a multi-scale model constrained by single-cell transcriptome and bulk extracellular fluxes to reduce the solution space (131). Overall, the added complexity of multicellular modeling can improve our interpretation of omics data and provide insights into cell-cell interactions important to many biological systems.
Visualization and Web Application
While algorithm development for COBRA is important, the utility of COBRA methods also depends on the usability and dissemination of scientific results. Python libraries have enabled the development of more interactive, user-friendly applications for analysis and visualization of metabolic networks. For example, Escher is a web application for visualizing metabolic models and also a Python package with interactive widgets for Jupyter Notebooks that can visualize COBRApy models (84). Escher has been integrated into other Python COBRA packages such as cameo to visualize flux analysis results. Additional interactive visualization packages include SAMMI for semi-automated visualization and d3flux for d3.js based plots (85, 86). Due to open-source nature of Python packages, future COBRA web applications can be deployed for public use without licensing limitations.
Genome-Scale Modeling of Cancer Metabolism With COBRA Tools
Cancer cells undergo metabolic reprogramming to promote proliferation and invasion, and in turn alter the nutrient-levels and cell types within the tumor microenvironment (TME). We here summarize these metabolic changes and provide the rationale for using COBRA methods to analyze cancer metabolism and TME. Indeed, COBRA methods have been utilized for various applications in cancer research in the past decades. We describe how the analyses begin with building cancer-specific metabolic models, from which one can infer metabolic dysregulation through pathway and network analyses. Next, we showed how these models were used for quantitative prediction of cancer metabolic activity and drug targets. Finally, we highlight the frontiers of modeling the TME using multicellular or single-cell COBRA methods.
Metabolism of Cancer and the Tumor Microenvironment
The dramatic functional and environmental changes that occur during cancer formation and progression are accompanied by accordingly dramatic metabolic reprogramming in cancer cells ( Figure 3 ). These changes canonically include the Warburg effect (132, 133), the switch from predominantly mitochondrial oxidative phosphorylation to aerobic glycolysis, potentially done to increase biomass production critical to maintain high proliferation (133); this leads to increased glucose uptake and lactate secretion by cancer cells. Increased energy and biomass production in cancer cells is also associated with increased uptake and synthesis of amino acids (134), fatty acids (135), and nucleotides (136). The TME is also quite distinct from normal physiology as it espouses a different set of spatial structures, nutrient/metabolite compositions, and cellular heterogeneities, and thus the metabolism of cancer cells is further perturbed just as the cancer cells metabolically influence the TME in turn (137). In the TME, tumor cells also inhibit immune cells by outcompeting them for critical nutrients with finite supply, such as glucose and amino acids, thereby limiting immune anti-tumor activity. The manifold metabolic changes that occur in cancer pose a challenging question to faithfully model. However, overcoming this challenge to establish an accurate model of this complicated metabolic reprogramming may prove useful for identifying potential targets, such as cell-cell metabolic interactions between tumor and immune cells, for cancer therapy.
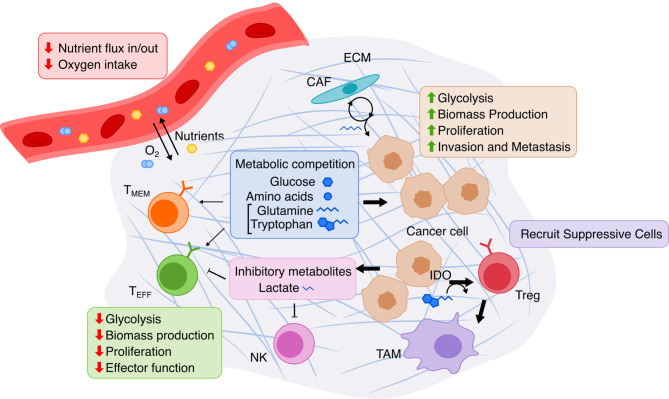
Figure 3.
Overview of metabolic interactions within the tumor microenvironment. The TME is composed of cancer cells, immune cells, and stromal cells embedded in extracellular matrix (ECM). Limited nutrients and oxygen lead to metabolic competition between cancer and various lymphocytes, especially hampering anti-tumor activity of effector T cells (TEFF). Cancer cells adapts via upregulating nutrient transport and altering cancer-associated fibroblasts (CAF) to replenish metabolites. T cell immunity is further suppressed by cancer cells’ release of lactate produced by glycolysis and by recruitment of immune-suppressive cells due to Indoleamine 2,3-dioxygenase (IDO) activity. TMEM, memory T cell; NK, natural killer cell; Treg, regulatory T cell; TAM, tumor-associated macrophage.
COBRA methods offer a way to computationally achieve this goal, such as inferring metabolic state via FBA which requires an objective function. While designing an objective function for tissue-specific eukaryotic cells is usually challenging, cancer cells can be reasonably modeled by biomass objective function, because cancer is mainly characterized by cellular growth (138). This makes flux predictions better suited for modeling cancer than healthy tissues, which do not actively proliferate. To simulate flux through cancer GEMs, studies have used objective functions representing growth as consumption of biomass precursors (139), or individual required metabolic tasks such as energy and redox, internal conversions, substrate utilization, biosynthesis, and biomass growth (54, 108). Some studies found gene-essentiality predictions from GEMs to be robust to definition of biomass composition (139) and capable of predicting growth kinetics in small-scale model (140), suggesting that the biomass equation is not significantly biased. However, another small-scale model claimed that elemental mode flux predictions using lactate objective is better than biomass objective at predicting experimental fluxes (141). These differences emphasize the importance of experimental validation to look for bias and sensitivity analysis to see if our biological insights are heavily affected by objective function definition and other system assumptions. Furthermore, the assumption that cancer cells optimize for cell growth may not always hold as tumors adapt, especially under selective pressure from therapies and immune system to adopt a quiescent state (138). Even if a proper objective is used, there are many optimal FBA solutions, and some may not be biologically viable due to inaccurate reaction bounds, violation of steady-state assumption, regulatory processes, and other limitations to our biological knowledge. Despite these limitations, past cancer applications of COBRA methods strived to improve our understanding of the disease and identify drug targets via comparative analysis, network analyses, quantitative flux simulations, and TME modeling. These studies have been reviewed multiple times (13, 14, 138, 142–144), and we have compiled the collection of these studies in Table 3 and summarized their applications below ( Figure 4 ).
Table 3.
List of cancer metabolic modeling studies.
| Ref. | Cancer | Purpose | Method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Drug design Predict drug targets Explore Cancer biology Explain Warburg effect Patient classification | Integration | Model | Analysis | Constraints | Objective | ||||||||
| (145) | Breast | x | x | Lee-12 | HMR 1 | FBA, Comparative, Topological | Transcriptome, Fluxomic | Data Correlation | |||||
| (146) | Colorectal | x | x | tINIT | Human1 | TFA, TFVA, pTFVA | Thermodynamic, Transcriptome, Biomass | Biomass | |||||
| (147) | Eye | x | x | iMAT | Recon 2 | Gap filling, FBA, FVA, Knockout | Transcriptome | Biomass, Tasks | |||||
| (148) | Head and Neck | x | x | Upper bound | Recon 2 | FBA, Sampling, Knockout | Thermodynamics, Enzyme kinetics, Transcriptome, Metabolome | ATP, NADPH | |||||
| (149) | Liver | x | x | iMAT-like | Recon 1 | Comparative, FBA, Sampling | Transcriptome | Data Similarity | |||||
| (150) | Multiple | x | x | tINIT | HMR 2 | Comparative, Knockout | Transcriptome | Tasks | |||||
| (151) | Multiple | x | x | tINIT | HMR 2 | FBA, Knockout | Transcriptome | Biomass, Tasks | |||||
| (140) | Generic | x | x | Small-scale | FBA, DFBA, FVA, Knockout, Sampling | Biomass | |||||||
| (152) | Kidney | x | x | tINIT | iCancer-Core | FBA, Knockout | Transcriptome | Biomass | |||||
| (153) | Brain | x | tINIT | HMR 2 | Comparative, FBA, Knockout | Transcriptome | Biomass, Tasks | ||||||
| (105) | Breast, Lung, Multiple | x | Upper bound | HMR 1 | FBA, Sampling, Knockout | Transcriptome | Biomass | ||||||
| (139) | Generic | x | MBA | Recon 1 | FBA, Knockout | Transcriptome | Biomass | ||||||
| (154) | Kidney | x | MBA | Recon 1 | FBA, Knockout | Transcriptome | Biomass | ||||||
| (54) | Liver | x | tINIT | HMR 2 | Comparative, FBA, Knockout | Proteome | Biomass, Tasks | ||||||
| (155) | Liver | x | tINIT | HMR 2 | FBA, Knockout, Topological | Transcriptome | Biomass, Tasks | ||||||
| (156) | Multiple | x | iMAT | Recon 1 | FBA, ML, Topological | Transcriptome | Data Similarity | ||||||
| (102) | Multiple | x | GIMME | Recon 2 | FBA, Sampling, Knockout | Mutations, Transcriptome | Biomass | ||||||
| (157) | Prostate | x | tINIT | iCancer-Core | FBA, Knockout, Sampling | Transcriptome, Proteome | Biomass, Tasks | ||||||
| (158) | Breast, Kidney, Liver, Prostate | x | x | KEGG | Network Propagation, Knockout, ML | Transcriptome | |||||||
| (159) | Colorectal | x | x | tINIT | HMR 2 | Comparative | Transcriptome | ||||||
| (160) | Multiple | x | x | Recon 2 | Regulatory, Topological, ML | Transcriptome, Metabolome | |||||||
| (111) | Multiple | x | x | mCADRE | Recon 1 | Comparative | Transcriptome | Tasks, Biomass | |||||
| (103) | Multiple, Brain, Lung, Breast, Leukemia, Prostate | x | x | tINIT | Recon 3D | Comparative, Knockout, ML | Mutations, Protein Structures | Biomass | |||||
| (161) | Prostate | x | x | iMAT | Recon 2 | FBA, FVA | Transcriptome | Data Similarity | |||||
| (162) | Kidney, Prostate | x | INIT | HMR 1 | Knockout | Proteome, Fluxomic | Biomass | ||||||
| (108) | Multiple | x | INIT | HMR 1 | Comparative | Proteome | |||||||
| (163) | Multiple | x | Topological | ||||||||||
| (164) | Generic | x | x | C2M2N | FBA | Biosynthesis, Biomass | |||||||
| (165) | Breast, Colorectal | x | x | Recon 2 | FVA, ML | Metabolome | Metabolite Change | ||||||
| (166) | Liver | x | x | tINIT | HMR 2 | Comparative | Transcriptome, Proteome | Biomass, Tasks | |||||
| (167) | Brain | x | GIMME, MADE | iMS570 | pFBA, Sampling | Transcriptome | Biomass | ||||||
| (168) | Breast | x | E-Flux | Recon2 | FBA | Proteome | Biomass | ||||||
| (169) | Colorectal | x | Recon 2.2 | Comparative | Transcriptome | ||||||||
| (170) | Colorectal | x | CORDA | Recon 2.2 | FBA, FVA, Topological | Proteome | Biomass, ATP | ||||||
| (130) | Generic | x | HMRcore | popFBA, Sampling | Loopless | Biomass | |||||||
| (171) | Kidney | x | Recon 1 | pFBA | Flux measurements | Biomass | |||||||
| (172) | Kidney | x | INIT | HMR 1 | Comparative | Proteome | |||||||
| (173) | Liver | x | tINIT | HMR 2 | Comparative, Gap filling, Regulatory, FBA | Transcriptome, Metabolome | Biomass | ||||||
| (174) | Lung | x | 13C flux analysis | Flux measurements, Labeling measurements | |||||||||
| (141) | Lung | x | Central Carbon, Recon 2 | Elementary modes, Structural fluxes, pFBA | Protein efficiency | Biomass, Biosynthesis | |||||||
| (131) | Lung, Breast | x | E-Flux | HMRcore | scFBA | scRNA-seq, metabolomics | Biomass | ||||||
| (175) | Lung, Prostate | x | E-Flux | Recon 1 | FVA | Transcriptome | Biomass | ||||||
| (176) | Multiple | x | tINIT | HMR 2 | Comparative | Transcriptome | |||||||
| (104) | Prostate | x | IMAT, GIMME, Gonçalves, MADE | HMR 2 | FBA | Transcriptome | Data Similarity | ||||||
| (177) | Generic | x | Recon 1 | FBA, FVA, Sampling | Protein efficiency, Enzyme kinetics | Biomass | |||||||
| (178) | Generic | x | ATP | FBA | Protein efficiency | ATP | |||||||
| (179) | Generic | x | ATP, BiGG | FBA | Protein efficiency | ATP, Nutrient cost | |||||||
| (180) | Liver | x | MADE | Recon 2 | Comparative | Transcriptome | Data Similarity | ||||||
| (106) | Liver | x | Upper bound | Recon 3D | FBA, FVA | Transcriptome, Nutrient availability | Biomass | ||||||
| (181) | Liver | x | Bounds | Recon 2 | FBA | Protein efficiency, Transcriptome | ATP | ||||||
| (182) | Multiple | x | E-Flux | Recon 1 | FBA | Transcriptome | Biomass | ||||||
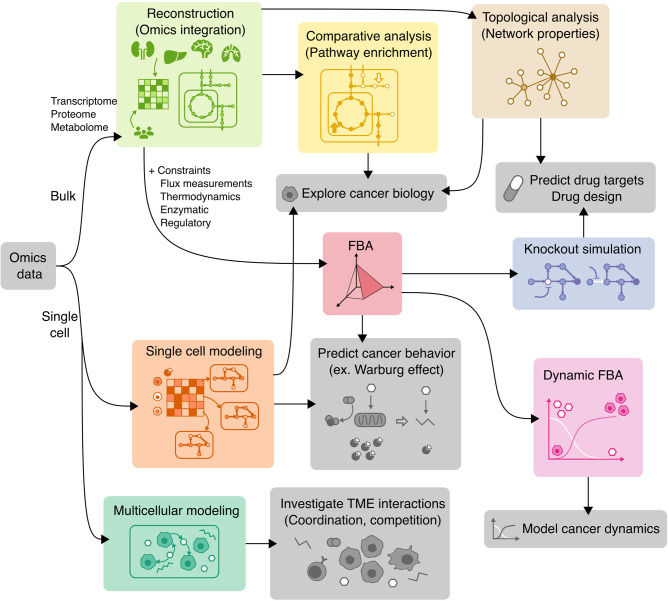
Figure 4.
Applications of COBRA methods to cancer research. Workflow diagram of using various COBRA methods (colored) in combination to achieve different objectives (grey).
Reconstruction of Cancer Metabolic Models
To date, numerous efforts have iteratively improved reconstruction of the human metabolic network within the Recon series (Recon 1, 2, 3D) (103, 183, 184), the Human Metabolic Reaction (HMR) series (HMR 1 and 2) (185, 186), and their derived unified model Human1 (187) ( Table 4 ). From these generic human GEMs, cancer-specific metabolic models were generated by integrating multi-omics data to reduce the number of reactions to reflect cancer-specific activity. To extract multiple healthy and cancerous tissue-specific GEMs, studies utilized protein levels from Human Protein Atlas along with INIT algorithm (108) or CORDA algorithm (170). Other studies constructed cancer GEMs using transcriptomic data from 1) cancer cell lines in combination with different integration algorithms such as MBA (139), tINIT (150), a likelihood-based method (156), PRIME (90), and FASTCORMICS (112), or 2) transcriptomic data from tissue samples in combination with mCADRE algorithm (111). While transcriptome measurements can capture more genes, its data is noisy and does not correlate well with protein levels (190). In contrast, proteomic data more directly corresponds to enzymatic activity, but was previously limited by antibody or spectrometry methods that are low-throughput and less quantitative. Emerging evidence shows that newly developed quantitative proteome may better explain genetic disease and metabolism (191), emphasizing the advantage of using proteome evidence for metabolic model reconstruction. However, accuracy of proteome-based reconstructions is still limited due to various regulatory mechanisms such as protein modifications that have yet to be integrated into cancer metabolic models.
Table 4.
Human metabolic generic models and cancer models.
This table describes various human reconstructions that are used as the starting reference models in various cancer applications listed in Table 3 . The most updated online links to these models may be different than previously described in their original manuscripts.
In the past decade, many more cancer-specific models have been reconstructed for liver (106, 149, 155, 166, 173, 181), kidney (152, 154, 162, 172, 172), breast (103, 105, 131, 145, 168), prostate (103, 104, 157, 161, 162, 175), brain (103, 153, 167), colorectal (159, 170, 192), head and neck (148), eye (147), and lung (103, 105, 131, 175) cancer to generate cancer-specific hypotheses. To compare these various methods for reconstruction of cancer metabolic models, a study benchmarked their predictive performance and consistency (91), with relevant findings summarized in Table 2 . In pursuit of personalized medicine to find optimal treatment based on patient’ genetic factors, researchers have also built personalized cancer GEMs from patient sample data to identify metabolic features that are commonly-shared or patient-specific (54). Furthermore, patient genetic variants were integrated in the Recon3D model with protein structures to look for cancer mutation hotspots in glioblastoma patients (103). Nam et al. modeled loss of function mutations via knockouts and analyzed potential gain of function mutations by adding promiscuous reactions predicted by chemoinformatics (102). Overall, these various reconstructions of cancer metabolic models aim to capture the heterogeneity of cancer.
Pathway and Network Analyses of Cancer GEM
To find metabolic differences between cancer and healthy cell types and between patients, these reconstructed metabolic networks are analyzed for enrichment of biological features, generating biologically relevant hypotheses that can guide mechanistic interpretation, biomarker discovery, and drug development. Comparative analysis involves statistical testing for the enrichment of reactions, genes, and metabolites to identify differentially activated pathways. Comparing networks of healthy and cancer cell types using hypergeometric test identified enrichment of not only well-known drug targets (polyamines, isoprenoid biosynthesis, prostaglandins and leukotrienes), but also new drug targets explained by protection against oxidative stress and methylglyoxal toxicity (108). Another study that used Wilcoxon rank sum test to compare tumor and normal metabolic models also found enrichment of leukotriene synthesis in addition to other tumor supporting pathways such as folate metabolism, eicosanoid metabolism, fatty acid synthesis, and nucleotide metabolism (111). Of note, these pathways were not statistically significant from pathway analysis of gene expression data alone, emphasizing the importance of systems-level network analysis to extract biological signal. In addition, the presence and absence of active genes, metabolites, and reactions can be characterized by clustering to validate similarity of related cell types (108), and calculating Hamming distance or pairwise comparisons to find the most different cancer GEMs (150). Comparing cancer-specific GEMs can reveal cancer types with more severe metabolic dysfunction. For example, clear cell renal cell carcinoma (ccRCC) GEM showed loss of redundant genes in key metabolic pathways (162, 172), suggesting that ccRCC might be more responsive to metabolic anticancer drugs due to reduced capacity to evade drug inhibition via alterative enzymes and pathways.
While the presence of pathways is indicative of activity, analyzing the pattern of how these pathways connect could provide additional insights. For this purpose, topological analysis is a network-based analysis that characterizes metabolic models based on network properties that describes the degree and patterns of connection between metabolites, genes, and reactions. The same models from Agren et al. (108) were converted to enzyme-enzyme networks and re-analyzed using topological analysis, which revealed that most approved cancer drugs do not correlate with centrality (measure of importance) of individual enzymes, but do belong to a specific cluster in a cancer enzyme-centric networks (163). Furthermore, the analysis found that certain network motifs, such as feed-forward loop, are enriched in cancer networks compared to healthy cell type. Utilized in several other cancer studies ( Table 3 ), topological analyses reveal insights about cancer based on the structure of cancer-specific metabolic networks without using flux simulations. Topological analyses emphasize the importance of system-oriented cancer drug design to find therapy that change the entire metabolic state instead of a single drug target that can be easily compensated by alternative pathways.
Quantitative Prediction of Cancer Behavior
To better understand metabolic reprogramming within cancer cells, cancer-specific metabolic models were used to simulate flux distributions to illustrate their metabolic state. Initial efforts built generic small-scale cancer models that only included the major pathways in cancer such as ATP and biomass production (140, 178) to demonstrate the usefulness of standard COBRA methods as such FBA, FVA, and in silico knockouts (140). Performing dynamical FBA on such model was able to predict the growth rates of HeLa cells, validating the use of biomass objective with FBA for cancer predictions (140). While constraints on glucose uptake and solvent capacity initially predicted the Warburg effect (178), later implementations of protein constraints in these small-scale (179) and genome-scale (177) cancer models explained the Warburg effect as a result of maximizing enzyme efficiency. Another protein efficiency constraint, flux minimization with FBA, predicted the Warburg effect in liver-specific GEMs and agreed with metabolic profiling of Mir122a knockout mice (181). Another cancer metabolic adaptation that bypass mutation of enzymes from the TCA cycle was recapitulated by adding upper flux bounds during flux simulations (154). In addition to these methods for modeling intracellular constraints, it is also important to account for cell-extrinsic factors imposed by the tumor microenvironment. Approaches to impose nutrient constraints include constraining exchange reaction bounds by experimentally measured flux (145, 162), transporter expression (105), concentration and membrane potential-dependent free energy calculations (148), and concentration gradient over time (106). These quantitative predictions of cancer metabolic reprogramming further demonstrate the applicability of COBRA methods to model cancer metabolic programs.
In Silico Drug Discovery
Furthermore, quantitative flux predictions can guide drug therapy design by simulating the effect of enzyme inhibition on cellular metabolic function in both cancer and healthy GEMs to maximize therapeutic effect while minimizing toxicity. In silico knockouts are performed by constraining one or more reactions’ flux to zero, setting an objective function that represents growth or other metabolic tasks, and finally performing FBA to calculate the change in maximum objective. One approach aims to find drug targets based on gene essentiality–knock out of enzymes that inhibit cancer growth. In silico gene knockout simulations of genome-scale cancer model identified drug targets and combination drug strategies (double gene knockout) that could reduce cancer growth (139). These candidates include known drugs and are validated via shRNA gene silencing data and cancer somatic mutations. Another study found that gene essentiality by FBA using biomass objective is better than chance but has limited accuracy depending on cancer type, especially after adding exchange flux constraints (162). A second approach based on metabolite essentiality screens for antimetabolites (metabolite analogs), which would compete with endogenous metabolites to inhibit their associated enzymes. By simulating in silico knockout of all enzymes acting on each metabolite, studies have identified antimetabolite drug candidates that could selectively disable critical metabolic task in cancer cell line-specific GEMs (150) and personalized hepatocellular carcinoma (HCC) patient GEMs (54). Out of 101 antimetabolite candidates, many were already used (22%) or proposed as anticancer drug targets (60%), and some targets were shown to be highly patient-specific, supporting the use of flux predictions of cancer GEMs for both general and personalized drug discovery (54). Many more studies applying in silico knockouts are listed in Table 3 . While using FBA for in silico drug design is well established, the predictions maybe inaccurate due to bias introduced by the choice of objective function and reaction bounds, such as those for cell-specific exchange fluxes that are not always experimentally determined (91, 162). Furthermore, simulations based on cell line measurements and culturing conditions cannot faithfully reflect multi-cellular tissues and physiological environments in vivo.
Multicellular and Single-Cell Modeling of TME
To analyze cell-heterogeneous systems like the TME, it is important to investigate metabolic programs within a multi-scale population model and at the single-cell level. To model interactions between multiple cells, multicellular modeling accounts for metabolite exchange between single cells within the environment. This was attempted by popFBA (130), which simulated a spatial model of identical cancer cells that adapted heterogeneously and cooperatively to maximize growth of the entire tumor mass. To account for tumor heterogeneity, a population model can be constrained by single-cell RNA-seq (scRNA-seq) data containing different tissue subpopulations in the scFBA method (131). When applied to lung adenocarcinoma and breast cancer cells, scFBA reveals metabolically defined subpopulations, some of which have coordinated metabolic fluxes (e.g., uptake or secretion of opposite sets of metabolites) suggesting potential cell-cell metabolic interactions. Other methods, such as scFEA or Compass, calculates cell-wise metabolic flux from scRNA-seq data to interpret cellular metabolic activity. Compass revealed metabolic states associated with functional states of T helper 17 (Th17) cells, in particular an increase in arginine and polyamine metabolism that resulted in a regulatory T cell (Treg)-like, dysfunctional cell state (73). The other single-cell method, scFEA, applied to patient-derived pancreatic cancer cells with metabolic perturbations (gene knockout, hypoxia), predicted flux variation that correlates with measured metabolomics. These methods could be applied to infer metabolic states of tumor and immune cells from existing scRNA-seq datasets of tumor samples. In future studies, algorithms for microbial community-modeling can be repurposed to investigate the interactions of cancer and immune cells in the TME (MICOM) and model the dynamics of immunosurveillance and tumor resistance (surfin_fba).
Discussion
COBRA methods have proved useful for systems-level inference of metabolic activity under a mathematical framework built upon biomolecular knowledge. The accessibility and algorithms of COBRA methods have been improved with the development of open-source COBRA Python packages. We have identified Python packages available to handle the major areas of COBRA methods: FBA, FVA, gene knockout, strain design, omics integration, regulatory constraints, reconstruction, gap filling, ensemble modeling, thermodynamics, enzymatic constraints, EFM, sampling, single-cell modeling, multicellular modeling, and visualization. However, the Python COBRA ecosystem is currently missing some methods for constraining models by regulatory mechanisms and reconstruction of context-specific GEMs. However, these gaps are only due to limitations of time and effort, not limitations of the Python programming language. In fact, many features involving complex models, parallelization, and efficient memory management are available in Python instead of MATLAB. For example, ME-models, a set of multi-scale problems describing multiple biological processes across different space and time scales such as transcription, translation, and protein interactions, are handled by Python packages only for now. Integration of protein structure into the Recon3D human GEM was facilitated by Python packages ssbio and GEM-PRO (103). GEMs interface with machine learning in Medusa and scFEA. Likewise, upcoming COBRA packages will likely integrate with existing Python tools for statistical learning and analysis of single-cell multi-omics data. As models and omics datasets increase in complexity, COBRA methods will thrive in the open-source Python environment. While we improve our modeling techniques, it is also important to validate flux predictions using experimental techniques such as metabolomics profile and label tracing experiments. To interpret isotope tracing data, 13C-Metabolic Flux Analysis was developed to infer intracellular fluxes. While 13C-MFA allows direct measurement of metabolic flux, the method is limited to small-scale models (central metabolism) and requires more expertise than the typical omics measurements for constraining COBRA methods. Python packages for modeling label tracing data are available via FluxPyt and mfapy (193, 194). While these experimental techniques are outside the scope of this review, they have been reviewed previously for bulk, single-cell, and cancer applications (119, 195, 196). Another alternative computational metabolic modeling approach is parametric kinetic modeling, which mathematically describes enzyme activity involving regulatory mechanisms (17). While this paradigm may offer accurate prediction of perturbation outcomes, systems emergent properties (e.g., switches, oscillations, bistability), and non-steady state concentrations, scaling kinetic models to genome-scale metabolic models is a challenge due to the requirement for intracellular concentrations, kinetic parameters, and rate laws. DMPy attempts to overcome the challenge by incorporating thermodynamics constraints to infer missing kinetic parameters. Hybrid approaches combining kinetic modeling with constraints-based models may bring kinetic modeling closer to genome-scale.
Applications of GEMs and COBRA methods to cancer research have improved our understanding of how molecular mechanisms translate to cancer phenotype, aiding interpretation of multi-omics data and guiding drug designs that target cell metabolism at the systems-level. Metabolic models of cancer have evolved from small-scale models of essential pathways to genome-scale cancer-specific models, and they are now expanding to the realm of single-cell modeling. The computational resources required for numerous single-cell reconstructions and optimizations can be costly. Single-cell methods reduce complexity by pooling of reactions and similar cells and could benefit from ensemble modeling techniques that reduce a large number of models into ensemble objects. As demonstrated by bulk-level modeling, future single-cell modeling can improve prediction accuracy by incorporating constraints determined by multi-omics, thermodynamics, protein crowding and kinetics, genotype, and regulatory mechanisms. Furthermore, single-cell methods that estimate the metabolic flux of individual cells can be improved by integration of spatial information and inter-cell metabolic exchange to model crosstalk between cancer, immune, and stromal cells within the TME. By understanding the cancer-immune metabolic competition, we can design drugs that disrupt pathophysiologic interactions to enhance antitumor immune response and prevent evasion of immunosurveillance.
Author Contributions
RN conceived the review, wrote the manuscript, and created visualizations. JL wrote the manuscript and created visualizations. YS and JH supervised and edited the manuscript. PB and CD edited the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the Andy Hill Cancer Research Endowment Fund (JH) and the Parker Institute for Cancer Immunotherapy (JH). YS is a Damon Runyon Quantitative Biology Fellow supported by the Damon Runyon Cancer Research Foundation (DRQ-13-22). YS was additionally supported by the Mahan Fellowship at the Herbold Computational Biology Program of Fred Hutch Cancer Research Center and the Translational Data Science Integrated Research Center New Collaboration Award at Fred Hutch Cancer Research Center and in part through a pilot fund from the NIH/NCI Cancer Center Support Grant P30 CA015704. PB acknowledges the support of 5U01AG061359-02 and 5U01AG061359-03 from NIA and 5R01HD091527-06 from NICHD. JL was funded by the Brotman Baty Institute Catalytic Collaborations Trainee Grant program.
Conflict of Interest
JH is a board member of PACT Pharma and Isoplexis and receives support from Gilead, Regeneron and Merck.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Herbert Sauro for comments on initial draft for Computation Systems Biology class at University of Washington.
References
- 1. Kumar A, Misra BB. Challenges and Opportunities in Cancer Metabolomics. Proteomics (2019) 19:1900042. doi: 10.1002/pmic.201900042 [DOI] [PubMed] [Google Scholar]
- 2. Chen C, Xing D, Tan L, Li H, Zhou G, Huang L, et al. Single-Cell Whole-Genome Analyses by Linear Amplification via Transposon Insertion (LIANTI). Science (2017) 356:189–94. doi: 10.1126/science.aak9787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Macosko EZ, Basu A, Satija R, Nemesh J, Shekhar K, Goldman M, et al. Highly Parallel Genome-Wide Expression Profiling of Individual Cells Using Nanoliter Droplets. Cell (2015) 161:1202–14. doi: 10.1016/j.cell.2015.05.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Shema E, Bernstein BE, Buenrostro JD. Single-Cell and Single-Molecule Epigenomics to Uncover Genome Regulation at Unprecedented Resolution. Nat Genet (2019) 51:19–25. doi: 10.1038/s41588-018-0290-x [DOI] [PubMed] [Google Scholar]
- 5. Bendall SC, Simonds EF, Qiu P, Amir ED, Krutzik PO, Finck R, et al. Single-Cell Mass Cytometry of Differential Immune and Drug Responses Across a Human Hematopoietic Continuum. Science (2011) 332:687–96. doi: 10.1126/science.1198704 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Ma C, Fan R, Ahmad H, Shi Q, Comin-Anduix B, Chodon T, et al. A Clinical Microchip for Evaluation of Single Immune Cells Reveals High Functional Heterogeneity in Phenotypically Similar T Cells. Nat Med (2011) 17:738–43. doi: 10.1038/nm.2375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Shi Q, Qin L, Wei W, Geng F, Fan R, Shik Shin Y, et al. Single-Cell Proteomic Chip for Profiling Intracellular Signaling Pathways in Single Tumor Cells. Proc Natl Acad Sci (2012) 109:419–24. doi: 10.1073/pnas.1110865109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Stoeckius M, Hafemeister C, Stephenson W, Houck-Loomis B, Chattopadhyay PK, Swerdlow H, et al. Simultaneous Epitope and Transcriptome Measurement in Single Cells. Nat Methods (2017) 14:865–8. doi: 10.1038/nmeth.4380 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Xue M, Wei W, Su Y, Kim J, Shin YS, Mai WX, et al. Chemical Methods for the Simultaneous Quantitation of Metabolites and Proteins From Single Cells. J Am Chem Soc (2015) 137:4066–9. doi: 10.1021/jacs.5b00944 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Xue M, Wei W, Su Y, Johnson D, Heath JR. Supramolecular Probes for Assessing Glutamine Uptake Enable Semi-Quantitative Metabolic Models in Single Cells. J Am Chem Soc (2016) 138:3085–93. doi: 10.1021/jacs.5b12187 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Du J, Su Y, Qian C, Yuan D, Miao K, Lee D, et al. Raman-Guided Subcellular Pharmaco-Metabolomics for Metastatic Melanoma Cells. Nat Commun (2020) 11:4830. doi: 10.1038/s41467-020-18376-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Chappell L, Russell AJC, Voet T. Single-Cell (Multi)omics Technologies. Annu Rev Genomics Hum Genet (2018) 19:15–41. doi: 10.1146/annurev-genom-091416-035324 [DOI] [PubMed] [Google Scholar]
- 13. Gu C, Kim GB, Kim WJ, Kim HU, Lee SY. Current Status and Applications of Genome-Scale Metabolic Models. Genome Biol (2019) 20:121. doi: 10.1186/s13059-019-1730-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Chowdhury S, Fong SS. Leveraging Genome-Scale Metabolic Models for Human Health Applications. Curr Opin Biotechnol (2020) 66:267–76. doi: 10.1016/j.copbio.2020.08.017 [DOI] [PubMed] [Google Scholar]
- 15. Lewis NE, Nagarajan H, Palsson BO. Constraining the Metabolic Genotype–Phenotype Relationship Using a Phylogeny of In Silico Methods. Nat Rev Microbiol (2012) 10:291–305. doi: 10.1038/nrmicro2737 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Lee JW, Su Y, Baloni P, Chen D, Pavlovitch-Bedzyk AJ, Yuan D, et al. Integrated Analysis of Plasma and Single Immune Cells Uncovers Metabolic Changes in Individuals With COVID-19. Nat Biotechnol (2022), 40:110–120. doi: 10.1038/s41587-021-01020-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Yasemi M, Jolicoeur M. Modelling Cell Metabolism: A Review on Constraint-Based Steady-State and Kinetic Approaches. Processes (2021) 9:322. doi: 10.3390/pr9020322 [DOI] [Google Scholar]
- 18. Heirendt L, Arreckx S, Pfau T, Mendoza SN, Richelle A, Heinken A, et al. Creation and Analysis of Biochemical Constraint-Based Models Using the COBRA Toolbox V.3.0. Nat Protoc (2019) 14:639–702. doi: 10.1038/s41596-018-0098-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Agren R, Liu L, Shoaie S, Vongsangnak W, Nookaew I, Nielsen J. The RAVEN Toolbox and Its Use for Generating a Genome-Scale Metabolic Model for Penicillium Chrysogenum. PLOS Comput Biol (2013) 9:e1002980. doi: 10.1371/journal.pcbi.1002980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. von Kamp A, Thiele S, Hädicke O, Klamt S. Use of CellNetAnalyzer in Biotechnology and Metabolic Engineering. J Biotechnol (2017) 261:221–8. doi: 10.1016/j.jbiotec.2017.05.001 [DOI] [PubMed] [Google Scholar]
- 21. Ebrahim A, Lerman JA, Palsson BO, Hyduke DR. COBRApy: COnstraints-Based Reconstruction and Analysis for Python. BMC Syst Biol (2013) 7:74. doi: 10.1186/1752-0509-7-74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. The openCOBRA Project . SourceForge . Available at: https://sourceforge.net/projects/opencobra/ (Accessed December 14, 2021).
- 23. Olivier B, Gottstein W, Molenaar D, Teusink B. CBMPy Release 0.8.2. Zenodo; (2021). doi: 10.5281/ZENODO.5546608 [DOI] [Google Scholar]
- 24. Lieven C, Beber ME, Olivier BG, Bergmann FT, Ataman M, Babaei P, et al. MEMOTE for Standardized Genome-Scale Metabolic Model Testing. Nat Biotechnol (2020) 38:272–6. doi: 10.1038/s41587-020-0446-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Aite M, Chevallier M, Frioux C, Trottier C, Got J, Cortés MP, et al. Traceability, Reproducibility and Wiki-Exploration for “À-La-Carte” Reconstructions of Genome-Scale Metabolic Models. PLOS Comput Biol (2018) 14:e1006146. doi: 10.1371/journal.pcbi.1006146 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Machado D, Andrejev S, Tramontano M, Patil KR. Fast Automated Reconstruction of Genome-Scale Metabolic Models for Microbial Species and Communities. Nucleic Acids Res (2018) 46:7542–53. doi: 10.1093/nar/gky537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Hanemaaijer M, Olivier BG, Röling WFM, Bruggeman FJ, Teusink B. Model-Based Quantification of Metabolic Interactions From Dynamic Microbial-Community Data. PLOS One (2017) 12:e0173183. doi: 10.1371/journal.pone.0173183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Pitkänen E, Jouhten P, Hou J, Syed MF, Blomberg P, Kludas J, et al. Comparative Genome-Scale Reconstruction of Gapless Metabolic Networks for Present and Ancestral Species. PLOS Comput Biol (2014) 10:e1003465. doi: 10.1371/journal.pcbi.1003465 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Orth JD, Thiele I, Palsson BØ. What Is Flux Balance Analysis? Nat Biotechnol (2010) 28:245–8. doi: 10.1038/nbt.1614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Harwood SM, Höffner K, Barton PI. Efficient Solution of Ordinary Differential Equations With a Parametric Lexicographic Linear Program Embedded. Numer Math (2016) 133:623–53. doi: 10.1007/s00211-015-0760-3 [DOI] [Google Scholar]
- 31. Tourigny DS, Muriel JC, Beber ME. Dfba: Software for Efficient Simulation of Dynamic Flux-Balance Analysis Models in Python. J Open Source Softw (2020) 5:2342. doi: 10.21105/joss.02342 [DOI] [Google Scholar]
- 32. Smith RW, van Rosmalen RP, Martins dos Santos VAP, Fleck C. DMPy: A Python Package for Automated Mathematical Model Construction of Large-Scale Metabolic Systems. BMC Syst Biol (2018) 12:72. doi: 10.1186/s12918-018-0584-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Smallbone K, Simeonidis E. Flux Balance Analysis: A Geometric Perspective. J Theor Biol (2009) 258:311–5. doi: 10.1016/j.jtbi.2009.01.027 [DOI] [PubMed] [Google Scholar]
- 34. Mahadevan R, Schilling CH. The Effects of Alternate Optimal Solutions in Constraint-Based Genome-Scale Metabolic Models. Metab Eng (2003) 5:264–76. doi: 10.1016/j.ymben.2003.09.002 [DOI] [PubMed] [Google Scholar]
- 35. Guebila MB. VFFVA: Dynamic Load Balancing Enables Large-Scale Flux Variability Analysis. BMC Bioinf (2020) 21:424. doi: 10.1186/s12859-020-03711-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Edwards JS, Palsson BO. The Escherichia Coli MG1655 In Silico Metabolic Genotype: Its Definition, Characteristics, and Capabilities. Proc Natl Acad Sci (2000) 97:5528–33. doi: 10.1073/pnas.97.10.5528 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Segrè D, Vitkup D, Church GM. Analysis of Optimality in Natural and Perturbed Metabolic Networks. Proc Natl Acad Sci (2002) 99:15112–7. doi: 10.1073/pnas.232349399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Shlomi T, Berkman O, Ruppin E. Regulatory on/Off Minimization of Metabolic Flux Changes After Genetic Perturbations. Proc Natl Acad Sci (2005) 102:7695–700. doi: 10.1073/pnas.0406346102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Laniau J, Frioux C, Nicolas J, Baroukh C, Cortes M-P, Got J, et al. Combining Graph and Flux-Based Structures to Decipher Phenotypic Essential Metabolites Within Metabolic Networks. PeerJ (2017) 5:e3860. doi: 10.7717/peerj.3860 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Patil KR, Rocha I, Förster J, Nielsen J. Evolutionary Programming as a Platform for in Silico Metabolic Engineering. BMC Bioinf (2005) 6:308. doi: 10.1186/1471-2105-6-308 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Cardoso JGR, Jensen K, Lieven C, Lærke Hansen AS, Galkina S, Beber M, et al. Cameo: A Python Library for Computer Aided Metabolic Engineering and Optimization of Cell Factories. ACS Synth Biol (2018) 7:1163–6. doi: 10.1021/acssynbio.7b00423 [DOI] [PubMed] [Google Scholar]
- 42. Burgard AP, Pharkya P, Maranas CD. Optknock: A Bilevel Programming Framework for Identifying Gene Knockout Strategies for Microbial Strain Optimization. Biotechnol Bioeng (2003) 84:647–57. doi: 10.1002/bit.10803 [DOI] [PubMed] [Google Scholar]
- 43. Choi HS, Lee SY, Kim TY, Woo HM. In Silico Identification of Gene Amplification Targets for Improvement of Lycopene Production. Appl Environ Microbiol (2010) 76:3097–105. doi: 10.1128/AEM.00115-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Shen F, Sun R, Yao J, Li J, Liu Q, Price ND, et al. OptRAM: In Silico Strain Design via Integrative Regulatory-Metabolic Network Modeling. PLOS Comput Biol (2019) 15:e1006835. doi: 10.1371/journal.pcbi.1006835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Pereira V, Cruz F, Rocha M. MEWpy: A Computational Strain Optimization Workbench in Python. Bioinformatics (2021) 37:2494–6. doi: 10.1093/bioinformatics/btab013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Kim J, Reed JL. OptORF: Optimal Metabolic and Regulatory Perturbations for Metabolic Engineering of Microbial Strains. BMC Syst Biol (2010) 4:53. doi: 10.1186/1752-0509-4-53 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Colijn C, Brandes A, Zucker J, Lun DS, Weiner B, Farhat MR, et al. Interpreting Expression Data With Metabolic Flux Models: Predicting Mycobacterium Tuberculosis Mycolic Acid Production. PLOS Comput Biol (2009) 5:e1000489. doi: 10.1371/journal.pcbi.1000489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Machado D. ReFramed: Metabolic Modeling Package (2021). Available at: https://github.com/cdanielmachado/reframed (Accessed February 22, 2022).
- 49. Schultz A, Qutub AA. Reconstruction of Tissue-Specific Metabolic Networks Using CORDA. PLOS Comput Biol (2016) 12:e1004808. doi: 10.1371/journal.pcbi.1004808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Schmidt BJ, Ebrahim A, Metz TO, Adkins JN, Palsson BØ, Hyduke DR. GIM3E: Condition-Specific Models of Cellular Metabolism Developed From Metabolomics and Expression Data. Bioinformatics (2013) 29:2900–8. doi: 10.1093/bioinformatics/btt493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Vlassis N, Pacheco MP, Sauter T. Fast Reconstruction of Compact Context-Specific Metabolic Network Models. PLOS Comput Biol (2014) 10:e1003424. doi: 10.1371/journal.pcbi.1003424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Ferreira J, Vieira V, Gomes J, Correia S, Rocha M. “Troppo - A Python Framework for the Reconstruction of Context-Specific Metabolic Models.,”. In: Fdez-Riverola F, Rocha M, Mohamad MS, Zaki N, Castellanos-Garzón JA, editors. Practical Applications of Computational Biology and Bioinformatics, 13th International Conference. Advances in Intelligent Systems and Computing. Cham: Springer International Publishing; (2020). p. 146–53. doi: 10.1007/978-3-030-23873-5_18 [DOI] [Google Scholar]
- 53. Becker SA, Palsson BO. Context-Specific Metabolic Networks Are Consistent With Experiments. PLOS Comput Biol (2008) 4:e1000082. doi: 10.1371/journal.pcbi.1000082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Agren R, Mardinoglu A, Asplund A, Kampf C, Uhlen M, Nielsen J. Identification of Anticancer Drugs for Hepatocellular Carcinoma Through Personalized Genome-Scale Metabolic Modeling. Mol Syst Biol (2014) 10:721. doi: 10.1002/msb.145122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Shlomi T, Cabili MN, Herrgård MJ, Palsson BØ, Ruppin E. Network-Based Prediction of Human Tissue-Specific Metabolism. Nat Biotechnol (2008) 26:1003–10. doi: 10.1038/nbt.1487 [DOI] [PubMed] [Google Scholar]
- 56. Covert MW, Palsson BØ. Transcriptional Regulation in Constraints-Based Metabolic Models of Escherichia Coli. J Biol Chem (2002) 277:28058–64. doi: 10.1074/jbc.M201691200 [DOI] [PubMed] [Google Scholar]
- 57. Shlomi T, Eisenberg Y, Sharan R, Ruppin E. A Genome-Scale Computational Study of the Interplay Between Transcriptional Regulation and Metabolism. Mol Syst Biol (2007) 3:101. doi: 10.1038/msb4100141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. jseidel5 . Python Implementation of Probabilistic Regulation of Metabolism (PROM) (2020). Available at: https://github.com/jseidel5/Python-Probabilistic-Regulation-of-Metabolism (Accessed February 22, 2022).
- 59. Brunk E, Mih N, Monk J, Zhang Z, O’Brien EJ, Bliven SE, et al. Systems Biology of the Structural Proteome. BMC Syst Biol (2016) 10:26. doi: 10.1186/s12918-016-0271-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Mih N, Brunk E, Chen K, Catoiu E, Sastry A, Kavvas E, et al. Ssbio: A Python Framework for Structural Systems Biology. Bioinformatics (2018) 34:2155–7. doi: 10.1093/bioinformatics/bty077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Machado D, Herrgård MJ, Rocha I. Modeling the Contribution of Allosteric Regulation for Flux Control in the Central Carbon Metabolism of E. Coli(2015) (Accessed February 9, 2022). [DOI] [PMC free article] [PubMed]
- 62. Schellenberger J, Lewis NE, Palsson BØ. Elimination of Thermodynamically Infeasible Loops in Steady-State Metabolic Models. Biophys J (2011) 100:544–53. doi: 10.1016/j.bpj.2010.12.3707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Desouki AA, Jarre F, Gelius-Dietrich G, Lercher MJ. CycleFreeFlux: Efficient Removal of Thermodynamically Infeasible Loops From Flux Distributions. Bioinformatics (2015) 31:2159–65. doi: 10.1093/bioinformatics/btv096 [DOI] [PubMed] [Google Scholar]
- 64. Gollub MG, Kaltenbach H-M, Stelling J. Probabilistic Thermodynamic Analysis of Metabolic Networks. Bioinforma Oxf Engl (2021) 37:2938–2945, btab194. doi: 10.1093/bioinformatics/btab194 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Henry CS, Broadbelt LJ, Hatzimanikatis V. Thermodynamics-Based Metabolic Flux Analysis. Biophys J (2007) 92:1792–805. doi: 10.1529/biophysj.106.093138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Salvy P, Fengos G, Ataman M, Pathier T, Soh KC, Hatzimanikatis V. pyTFA and matTFA: A Python Package and a Matlab Toolbox for Thermodynamics-Based Flux Analysis. Bioinforma Oxf Engl (2019) 35:167–9. doi: 10.1093/bioinformatics/bty499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Lewis NE, Hixson KK, Conrad TM, Lerman JA, Charusanti P, Polpitiya AD, et al. Omic Data From Evolved E. Coli Are Consistent With Computed Optimal Growth From Genome-Scale Models. Mol Syst Biol (2010) 6:390. doi: 10.1038/msb.2010.47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Sánchez BJ, Zhang C, Nilsson A, Lahtvee P, Kerkhoven EJ, Nielsen J. Improving the Phenotype Predictions of a Yeast Genome-Scale Metabolic Model by Incorporating Enzymatic Constraints. Mol Syst Biol (2017) 13:935. doi: 10.15252/msb.20167411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Bekiaris PS, Klamt S. Automatic Construction of Metabolic Models With Enzyme Constraints. BMC Bioinf (2020) 21:19. doi: 10.1186/s12859-019-3329-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Mao Z, Zhao X, Yang X, Zhang P, Du J, Yuan Q, et al. ECMpy, a Simplified Workflow for Constructing Enzymatic Constrained Metabolic Network Model. Biomolecules (2022) 12:65. doi: 10.3390/biom12010065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Lloyd CJ, Ebrahim A, Yang L, King ZA, Catoiu E, O’Brien EJ, et al. COBRAme: A Computational Framework for Genome-Scale Models of Metabolism and Gene Expression. PLOS Comput Biol (2018) 14:e1006302. doi: 10.1371/journal.pcbi.1006302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Medlock GL, Moutinho TJ, Papin JA. Medusa: Software to Build and Analyze Ensembles of Genome-Scale Metabolic Network Reconstructions. PLOS Comput Biol (2020) 16:e1007847. doi: 10.1371/journal.pcbi.1007847 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Wagner A, Wang C, Fessler J, DeTomaso D, Avila-Pacheco J, Kaminski J, et al. Metabolic Modeling of Single Th17 Cells Reveals Regulators of Autoimmunity. Cell (2021) 184:4168–85.e21. doi: 10.1016/j.cell.2021.05.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Alghamdi N, Chang W, Dang P, Lu X, Wan C, Gampala S, et al. A Graph Neural Network Model to Estimate Cell-Wise Metabolic Flux Using Single-Cell RNA-Seq Data. Genome Res (2021) 31:1867–84. doi: 10.1101/gr.271205.120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Diener C, Gibbons SM, Resendis-Antonio O. MICOM: Metagenome-Scale Modeling To Infer Metabolic Interactions in the Gut Microbiota. mSystems (2020) 5:e00606–19. doi: 10.1128/mSystems.00606-19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Brunner JD, Chia N. Minimizing the Number of Optimizations for Efficient Community Dynamic Flux Balance Analysis. PLOS Comput Biol (2020) 16:e1007786. doi: 10.1371/journal.pcbi.1007786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Kaufman DE, Smith RL. Direction Choice for Accelerated Convergence in Hit-And-Run Sampling(1998) (Accessed May 19, 2022).
- 78. Megchelenbrink W, Huynen M, Marchiori E. Optgpsampler: An Improved Tool for Uniformly Sampling the Solution-Space of Genome-Scale Metabolic Networks. PLOS ONE (2014) 9:e86587. doi: 10.1371/journal.pone.0086587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Buchner BA, Zanghellini J. EFMlrs: A Python Package for Elementary Flux Mode Enumeration via Lexicographic Reverse Search. BMC Bioinf (2021) 22:547. doi: 10.1186/s12859-021-04417-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Schuster S, Hilgetag C. On Elementary Flux Modes in Biochemical Reaction Systems at Steady State. J Biol Syst (1994) 02:165–82. doi: 10.1142/S0218339094000131 [DOI] [Google Scholar]
- 81. Vieira V, Rocha M. CoBAMP: A Python Framework for Metabolic Pathway Analysis in Constraint-Based Models. Bioinformatics (2019) 35:5361–2. doi: 10.1093/bioinformatics/btz598 [DOI] [PubMed] [Google Scholar]
- 82. Klamt S, Gilles ED. Minimal Cut Sets in Biochemical Reaction Networks. Bioinformatics (2004) 20:226–34. doi: 10.1093/bioinformatics/btg395 [DOI] [PubMed] [Google Scholar]
- 83. Schilling CH, Letscher D, Palsson BØ. Theory for the Systemic Definition of Metabolic Pathways and Their Use in Interpreting Metabolic Function From a Pathway-Oriented Perspective. J Theor Biol (2000) 203:229–48. doi: 10.1006/jtbi.2000.1073 [DOI] [PubMed] [Google Scholar]
- 84. King ZA, Dräger A, Ebrahim A, Sonnenschein N, Lewis NE, Palsson BO. Escher: A Web Application for Building, Sharing, and Embedding Data-Rich Visualizations of Biological Pathways. PLOS Comput Biol (2015) 11:e1004321. doi: 10.1371/journal.pcbi.1004321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Schultz A, Akbani R. SAMMI: A Semi-Automated Tool for the Visualization of Metabolic Networks. Bioinformatics (2020) 36:2616–7. doi: 10.1093/bioinformatics/btz927 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. John PS. D3flux (2021). Available at: https://github.com/pstjohn/d3flux (Accessed December 14, 2021).
- 87. Mendoza SN, Olivier BG, Molenaar D, Teusink B. A Systematic Assessment of Current Genome-Scale Metabolic Reconstruction Tools. Genome Biol (2019) 20:158. doi: 10.1186/s13059-019-1769-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Zimmermann J, Kaleta C, Waschina S. Gapseq: Informed Prediction of Bacterial Metabolic Pathways and Reconstruction of Accurate Metabolic Models. Genome Biol (2021) 22:81. doi: 10.1186/s13059-021-02295-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Höffner K, Harwood SM, Barton PI. A Reliable Simulator for Dynamic Flux Balance Analysis. Biotechnol Bioeng (2013) 110:792–802. doi: 10.1002/bit.24748 [DOI] [PubMed] [Google Scholar]
- 90. Yizhak K, Gaude E, Le Dévédec S, Waldman YY, Stein GY, van de Water B, et al. Phenotype-Based Cell-Specific Metabolic Modeling Reveals Metabolic Liabilities of Cancer. eLife (2014) 3:e03641. doi: 10.7554/eLife.03641 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. Jamialahmadi O, Hashemi-Najafabadi S, Motamedian E, Romeo S, Bagheri F. A Benchmark-Driven Approach to Reconstruct Metabolic Networks for Studying Cancer Metabolism. PLOS Comput Biol (2019) 15:e1006936. doi: 10.1371/journal.pcbi.1006936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Chung CH, Lin D-W, Eames A, Chandrasekaran S. Next-Generation Genome-Scale Metabolic Modeling Through Integration of Regulatory Mechanisms. Metabolites (2021) 11:606. doi: 10.3390/metabo11090606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Hucka M, Finney A, Bornstein BJ, Keating SM, Shapiro BE, Matthews J, et al. Evolving a Lingua Franca and Associated Software Infrastructure for Computational Systems Biology: The Systems Biology Markup Language (SBML) Project. Syst Biol (2004) 1:41–53. doi: 10.1049/sb:20045008 [DOI] [PubMed] [Google Scholar]
- 94. Olivier BG, Bergmann FT. SBML Level 3 Package: Flux Balance Constraints Version 2. J Integr Bioinforma (2018) 15:20170082. doi: 10.1515/jib-2017-0082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. King ZA, Lu J, Dräger A, Miller P, Federowicz S, Lerman JA, et al. BiGG Models: A Platform for Integrating, Standardizing and Sharing Genome-Scale Models. Nucleic Acids Res (2016) 44:D515–22. doi: 10.1093/nar/gkv1049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Li C, Donizelli M, Rodriguez N, Dharuri H, Endler L, Chelliah V, et al. BioModels Database: An Enhanced, Curated and Annotated Resource for Published Quantitative Kinetic Models. BMC Syst Biol (2010) 4:92. doi: 10.1186/1752-0509-4-92 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97. Choi Y-M, Choi D-H, Lee YQ, Koduru L, Lewis NE, Lakshmanan M, et al. Mitigating Biomass Composition Uncertainties in Flux Balance Analysis Using Ensemble Representations. bioRxiv (2022), 652040. doi: 10.1101/652040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98. Watson MR. Metabolic Maps for the Apple II. Biochem Soc Trans (1984) 12:1093–4. doi: 10.1042/bst0121093 [DOI] [Google Scholar]
- 99. Mahadevan R, Edwards JS, Doyle FJ. Dynamic Flux Balance Analysis of Diauxic Growth in Escherichia Coli. Biophys J (2002) 83:1331–40. doi: 10.1016/S0006-3495(02)73903-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100. Stellato B, Banjac G, Goulart P, Bemporad A, Boyd S. OSQP: An Operator Splitting Solver for Quadratic Programs. Math Program Comput (2020) 12:637–72. doi: 10.1007/s12532-020-00179-2 [DOI] [Google Scholar]
- 101. Cardoso JGR, Andersen MR, Herrgård MJ, Sonnenschein N. Analysis of Genetic Variation and Potential Applications in Genome-Scale Metabolic Modeling(2015) (Accessed February 9, 2022). [DOI] [PMC free article] [PubMed]
- 102. Nam H, Campodonico M, Bordbar A, Hyduke DR, Kim S, Zielinski DC, et al. A Systems Approach to Predict Oncometabolites via Context-Specific Genome-Scale Metabolic Networks. PLOS Comput Biol (2014) 10:e1003837. doi: 10.1371/journal.pcbi.1003837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Brunk E, Sahoo S, Zielinski DC, Altunkaya A, Dräger A, Mih N, et al. Recon3D Enables a Three-Dimensional View of Gene Variation in Human Metabolism. Nat Biotechnol (2018) 36:272–81. doi: 10.1038/nbt.4072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Marín de Mas I, Torrents L, Bedia C, Nielsen LK, Cascante M, Tauler R. Stoichiometric Gene-to-Reaction Associations Enhance Model-Driven Analysis Performance: Metabolic Response to Chronic Exposure to Aldrin in Prostate Cancer. BMC Genomics (2019) 20:652. doi: 10.1186/s12864-019-5979-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105. Raškevičius V, Mikalayeva V, Antanavičiūtė I, Ceslevičienė I, Skeberdis VA, Kairys V, et al. Genome Scale Metabolic Models as Tools for Drug Design and Personalized Medicine. PLOS ONE (2018) 13:e0190636. doi: 10.1371/journal.pone.0190636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106. Weglarz-Tomczak E, Mondeel TDGA, Piebes DGE, Westerhoff HV. Simultaneous Integration of Gene Expression and Nutrient Availability for Studying the Metabolism of Hepatocellular Carcinoma Cell Lines. Biomolecules (2021) 11:490. doi: 10.3390/biom11040490 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107. Robaina Estévez S, Nikoloski Z. Generalized Framework for Context-Specific Metabolic Model Extraction Methods. Front Plant Sci (2014) 5:491. doi: 10.3389/fpls.2014.00491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108. Agren R, Bordel S, Mardinoglu A, Pornputtapong N, Nookaew I, Nielsen J. Reconstruction of Genome-Scale Active Metabolic Networks for 69 Human Cell Types and 16 Cancer Types Using INIT. PLOS Comput Biol (2012) 8:e1002518. doi: 10.1371/journal.pcbi.1002518 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Lee D, Smallbone K, Dunn WB, Murabito E, Winder CL, Kell DB, et al. Improving Metabolic Flux Predictions Using Absolute Gene Expression Data. BMC Syst Biol (2012) 6:73. doi: 10.1186/1752-0509-6-73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Jerby L, Shlomi T, Ruppin E. Computational Reconstruction of Tissue-Specific Metabolic Models: Application to Human Liver Metabolism. Mol Syst Biol (2010) 6:401. doi: 10.1038/msb.2010.56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Wang Y, Eddy JA, Price ND. Reconstruction of Genome-Scale Metabolic Models for 126 Human Tissues Using mCADRE. BMC Syst Biol (2012) 6:153. doi: 10.1186/1752-0509-6-153 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112. Pacheco MP, John E, Kaoma T, Heinäniemi M, Nicot N, Vallar L, et al. Integrated Metabolic Modelling Reveals Cell-Type Specific Epigenetic Control Points of the Macrophage Metabolic Network. BMC Genomics (2015) 16:809. doi: 10.1186/s12864-015-1984-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113. Cardoso J, Redestig H, Galkina S, Sonnenschein N. Driven (2021). openCOBRA. Available at: https://github.com/opencobra/driven (Accessed February 9, 2022). [Google Scholar]
- 114. Chandrasekaran S, Price ND. Probabilistic Integrative Modeling of Genome-Scale Metabolic and Regulatory Networks in Escherichia Coli and Mycobacterium Tuberculosis . Proc Natl Acad Sci (2010) 107:17845–50. doi: 10.1073/pnas.1005139107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115. Yang L, Ebrahim A, Lloyd CJ, Saunders MA, Palsson BO. DynamicME: Dynamic Simulation and Refinement of Integrated Models of Metabolism and Protein Expression. BMC Syst Biol (2019) 13:2. doi: 10.1186/s12918-018-0675-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116. Kaleta C, de Figueiredo LF, Schuster S. Can the Whole be Less Than the Sum of its Parts? Pathway Analysis in Genome-Scale Metabolic Networks Using Elementary Flux Patterns. Genome Res (2009) 19:1872–83. doi: 10.1101/gr.090639.108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117. Haraldsdóttir HS, Cousins B, Thiele I, Fleming RMT, Vempala S. CHRR: Coordinate Hit-and-Run With Rounding for Uniform Sampling of Constraint-Based Models. Bioinformatics (2017) 33:1741–3. doi: 10.1093/bioinformatics/btx052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118. Fallahi S, Skaug HJ, Alendal G. A Comparison of Monte Carlo Sampling Methods for Metabolic Network Models. PLOS ONE (2020) 15:e0235393. doi: 10.1371/journal.pone.0235393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119. Artyomov MN, Van den Bossche J. Immunometabolism in the Single-Cell Era. Cell Metab (2020) 32:710–25. doi: 10.1016/j.cmet.2020.09.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120. Su Y, Wei W, Robert L, Xue M, Tsoi J, Garcia-Diaz A, et al. Single-Cell Analysis Resolves the Cell State Transition and Signaling Dynamics Associated With Melanoma Drug-Induced Resistance. Proc Natl Acad Sci (2017) 114:13679–84. doi: 10.1073/pnas.1712064115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121. Su Y, Ko ME, Cheng H, Zhu R, Xue M, Wang J, et al. Multi-Omic Single-Cell Snapshots Reveal Multiple Independent Trajectories to Drug Tolerance in a Melanoma Cell Line. Nat Commun (2020) 11:2345. doi: 10.1038/s41467-020-15956-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122. Su Y, Chen D, Yuan D, Lausted C, Choi J, Dai CL, et al. Multi-Omics Resolves a Sharp Disease-State Shift Between Mild and Moderate COVID-19. Cell (2020) 183:1479–95.e20. doi: 10.1016/j.cell.2020.10.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123. Su Y, Yuan D, Chen DG, Ng RH, Wang K, Choi J, et al. Multiple Early Factors Anticipate Post-Acute COVID-19 Sequelae. Cell (2022) 185:881–95.e20. doi: 10.1016/j.cell.2022.01.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124. Wei W, Shin YS, Xue M, Matsutani T, Masui K, Yang H, et al. Single-Cell Phosphoproteomics Resolves Adaptive Signaling Dynamics and Informs Targeted Combination Therapy in Glioblastoma. Cancer Cell (2016) 29:563–73. doi: 10.1016/j.ccell.2016.03.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125. Su Y, Shi Q, Wei W. Single Cell Proteomics in Biomedicine: High-Dimensional Data Acquisition, Visualization, and Analysis. Proteomics (2017) 17:1600267. doi: 10.1002/pmic.201600267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126. Heath JR, Ribas A, Mischel PS. Single-Cell Analysis Tools for Drug Discovery and Development. Nat Rev Drug Discov (2016) 15:204–16. doi: 10.1038/nrd.2015.16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127. Hrovatin K, Fischer DS, Theis FJ. Toward Modeling Metabolic State From Single-Cell Transcriptomics. Mol Metab (2022) 57:101396. doi: 10.1016/j.molmet.2021.101396 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128. Zhang Y, Kim MS, Nguyen E, Taylor DM. Modeling Metabolic Variation With Single-Cell Expression Data. bioRxiv [Preprint] (2020). doi: 10.1101/2020.01.28.923680 [DOI] [Google Scholar]
- 129. Martins Conde P do R, Sauter T, Pfau T. Constraint Based Modeling Going Multicellular. Front Mol Biosci (2016) 3:3. doi: 10.3389/fmolb.2016.00003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130. Damiani C, Di Filippo M, Pescini D, Maspero D, Colombo R, Mauri G. popFBA: Tackling Intratumour Heterogeneity With Flux Balance Analysis. Bioinforma Oxf Engl (2017) 33:i311–8. doi: 10.1093/bioinformatics/btx251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131. Damiani C, Maspero D, Filippo MD, Colombo R, Pescini D, Graudenzi A, et al. Integration of Single-Cell RNA-Seq Data Into Population Models to Characterize Cancer Metabolism. PLOS ONE Comput Biol (2019) 15:e1006733. doi: 10.1371/journal.pcbi.1006733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132. Warburg O, Wind F, Negelein E. The Metabolism Of Tumors In The Body. J Gen Physiol (1927) 8:519–30. doi: 10.1085/jgp.8.6.519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133. Heiden MGV, Cantley LC, Thompson CB. Understanding the Warburg Effect: The Metabolic Requirements of Cell Proliferation. Science (2009) 324:1029–1033. doi: 10.1126/science.1160809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134. Dolfi SC, Chan LL-Y, Qiu J, Tedeschi PM, Bertino JR, Hirshfield KM, et al. The Metabolic Demands of Cancer Cells are Coupled to Their Size and Protein Synthesis Rates. Cancer Metab (2013) 1:20. doi: 10.1186/2049-3002-1-20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135. Koundouros N, Poulogiannis G. Reprogramming of Fatty Acid Metabolism in Cancer. Br J Cancer (2020) 122:4–22. doi: 10.1038/s41416-019-0650-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136. Villa E, Ali ES, Sahu U, Ben-Sahra I. Cancer Cells Tune the Signaling Pathways to Empower De Novo Synthesis of Nucleotides. Cancers (2019) 11:688. doi: 10.3390/cancers11050688 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137. Anderson KG, Stromnes IM, Greenberg PD. Obstacles Posed by the Tumor Microenvironment to T Cell Activity: A Case for Synergistic Therapies. Cancer Cell (2017) 31:311–25. doi: 10.1016/j.ccell.2017.02.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138. Nilsson A, Nielsen J. Genome Scale Metabolic Modeling of Cancer. Metab Eng (2017) 43:103–12. doi: 10.1016/j.ymben.2016.10.022 [DOI] [PubMed] [Google Scholar]
- 139. Folger O, Jerby L, Frezza C, Gottlieb E, Ruppin E, Shlomi T. Predicting Selective Drug Targets in Cancer Through Metabolic Networks. Mol Syst Biol (2011) 7:501. doi: 10.1038/msb.2011.35 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140. Resendis-Antonio O, Checa A, Encarnación S. Modeling Core Metabolism in Cancer Cells: Surveying the Topology Underlying the Warburg Effect. PLOS One (2010) 5:e12383. doi: 10.1371/journal.pone.0012383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141. Schwartz J-M, Barber M, Soons Z. Metabolic Flux Prediction in Cancer Cells With Altered Substrate Uptake. Biochem Soc Trans (2015) 43:1177–81. doi: 10.1042/BST20150149 [DOI] [PubMed] [Google Scholar]
- 142. Frades I, Foguet C, Cascante M, Araúzo-Bravo MJ. Genome Scale Modeling to Study the Metabolic Competition Between Cells in the Tumor Microenvironment. Cancers (2021) 13:4609. doi: 10.3390/cancers13184609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143. Lewis N, Abdel-Haleem A. The Evolution of Genome-Scale Models of Cancer Metabolism. Front Physiol (2013) 4:237. doi: 10.3389/fphys.2013.00237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144. Bordbar A, Palsson BO. Using the Reconstructed Genome-Scale Human Metabolic Network to Study Physiology and Pathology. J Intern Med (2012) 271:131–41. doi: 10.1111/j.1365-2796.2011.02494.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145. Granata I, Troiano E, Sangiovanni M, Guarracino MR. Integration of Transcriptomic Data in a Genome-Scale Metabolic Model to Investigate the Link Between Obesity and Breast Cancer. BMC Bioinf (2019) 20:162. doi: 10.1186/s12859-019-2685-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146. Herrmann HA, Rusz M, Baier D, Jakupec MA, Keppler BK, Berger W, et al. Thermodynamic Genome-Scale Metabolic Modeling of Metallodrug Resistance in Colorectal Cancer. Cancers (2021) 13:4130. doi: 10.3390/cancers13164130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147. Sahoo S, Ravi Kumar RK, Nicolay B, Mohite O, Sivaraman K, Khetan V, et al. Metabolite Systems Profiling Identifies Exploitable Weaknesses in Retinoblastoma. FEBS Lett (2019) 593:23–41. doi: 10.1002/1873-3468.13294 [DOI] [PubMed] [Google Scholar]
- 148. Lewis JE, Costantini F, Mims J, Chen X, Furdui CM, Boothman DA, et al. Genome-Scale Modeling of NADPH-Driven β-Lapachone Sensitization in Head and Neck Squamous Cell Carcinoma. Antioxid Redox Signal (2018) 29:937–52. doi: 10.1089/ars.2017.7048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149. Goldstein I, Yizhak K, Madar S, Goldfinger N, Ruppin E, Rotter V. P53 Promotes the Expression of Gluconeogenesis-Related Genes and Enhances Hepatic Glucose Production. Cancer Metab (2013) 1:1–6. doi: 10.1186/2049-3002-1-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150. Ghaffari P, Mardinoglu A, Asplund A, Shoaie S, Kampf C, Uhlen M, et al. Identifying Anti-Growth Factors for Human Cancer Cell Lines Through Genome-Scale Metabolic Modeling. Sci Rep (2015) 5:8183. doi: 10.1038/srep08183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151. Uhlen M, Zhang C, Lee S, Sjöstedt E, Fagerberg L, Bidkhori G, et al. A Pathology Atlas of the Human Cancer Transcriptome. Science (2017) 357:eaan2507. doi: 10.1126/science.aan2507 [DOI] [PubMed] [Google Scholar]
- 152. Li X, Kim W, Juszczak K, Arif M, Sato Y, Kume H, et al. Stratification of Patients With Clear Cell Renal Cell Carcinoma to Facilitate Drug Repositioning. iScience (2021) 24:102722. doi: 10.1016/j.isci.2021.102722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153. Larsson I, Uhlén M, Zhang C, Mardinoglu A. Genome-Scale Metabolic Modeling of Glioblastoma Reveals Promising Targets for Drug Development(2020) (Accessed March 17, 2022). [DOI] [PMC free article] [PubMed]
- 154. Frezza C, Zheng L, Folger O, Rajagopalan KN, MacKenzie ED, Jerby L, et al. Haem Oxygenase is Synthetically Lethal With the Tumour Suppressor Fumarate Hydratase. Nature (2011) 477:225–8. doi: 10.1038/nature10363 [DOI] [PubMed] [Google Scholar]
- 155. Bidkhori G, Benfeitas R, Elmas E, Kararoudi MN, Arif M, Uhlen M, et al. Metabolic Network-Based Identification and Prioritization of Anticancer Targets Based on Expression Data in Hepatocellular Carcinoma. Front Physiol (2018) 9:916. doi: 10.3389/fphys.2018.00916 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156. Li L, Zhou X, Ching W-K, Wang P. Predicting Enzyme Targets for Cancer Drugs by Profiling Human Metabolic Reactions in NCI-60 Cell Lines. BMC Bioinf (2010) 11:501. doi: 10.1186/1471-2105-11-501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157. Turanli B, Zhang C, Kim W, Benfeitas R, Uhlen M, Arga KY, et al. Discovery of Therapeutic Agents for Prostate Cancer Using Genome-Scale Metabolic Modeling and Drug Repositioning. eBioMedicine (2019) 42:386–96. doi: 10.1016/j.ebiom.2019.03.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158. Çubuk C, Hidalgo MR, Amadoz A, Rian K, Salavert F, Pujana MA, et al. Differential Metabolic Activity and Discovery of Therapeutic Targets Using Summarized Metabolic Pathway Models. NPJ Syst Biol Appl (2019) 5:1–11. doi: 10.1038/s41540-019-0087-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159. Zhang C, Aldrees M, Arif M, Li X, Mardinoglu A, Aziz MA. Elucidating the Reprograming of Colorectal Cancer Metabolism Using Genome-Scale Metabolic Modeling(2019) (Accessed February 6, 2022). [DOI] [PMC free article] [PubMed]
- 160. Ortmayr K, Dubuis S, Zampieri M. Metabolic Profiling of Cancer Cells Reveals Genome-Wide Crosstalk Between Transcriptional Regulators and Metabolism. Nat Commun (2019) 10:1841. doi: 10.1038/s41467-019-09695-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161. Marín de Mas I, Aguilar E, Zodda E, Balcells C, Marin S, Dallmann G, et al. Model-Driven Discovery of Long-Chain Fatty Acid Metabolic Reprogramming in Heterogeneous Prostate Cancer Cells. PLOS Comput Biol (2018) 14:e1005914. doi: 10.1371/journal.pcbi.1005914 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162. Gatto F, Miess H, Schulze A, Nielsen J. Flux Balance Analysis Predicts Essential Genes in Clear Cell Renal Cell Carcinoma Metabolism. Sci Rep (2015) 5:10738. doi: 10.1038/srep10738 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163. Asgari Y, Salehzadeh-Yazdi A, Schreiber F, Masoudi-Nejad A. Controllability in Cancer Metabolic Networks According to Drug Targets as Driver Nodes. PLOS ONE (2013) 8:e79397. doi: 10.1371/journal.pone.0079397 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164. Mazat J-P, Ransac S. The Fate of Glutamine in Human Metabolism. The Interplay With Glucose in Proliferating Cells. Metabolites (2019) 9:81. doi: 10.3390/metabo9050081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165. Cakmak A, Celik MH. Personalized Metabolic Analysis of Diseases. IEEE/ACM Trans Comput Biol Bioinform (2021) 18:1014–25. doi: 10.1109/TCBB.2020.3008196 [DOI] [PubMed] [Google Scholar]
- 166. Björnson E, Mukhopadhyay B, Asplund A, Pristovsek N, Cinar R, Romeo S, et al. Stratification of Hepatocellular Carcinoma Patients Based on Acetate Utilization. Cell Rep (2015) 13:2014–26. doi: 10.1016/j.celrep.2015.10.045 [DOI] [PubMed] [Google Scholar]
- 167. Özcan E, Çakır T. Reconstructed Metabolic Network Models Predict Flux-Level Metabolic Reprogramming in Glioblastoma. Front Neurosci (2016) 10:156. doi: 10.3389/fnins.2016.00156 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168. Gámez-Pozo A, Trilla-Fuertes L, Berges-Soria J, Selevsek N, López-Vacas R, Díaz-Almirón M, et al. Functional Proteomics Outlines the Complexity of Breast Cancer Molecular Subtypes. Sci Rep (2017) 7:10100. doi: 10.1038/s41598-017-10493-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169. Fuhr L, El-Athman R, Scrima R, Cela O, Carbone A, Knoop H, et al. The Circadian Clock Regulates Metabolic Phenotype Rewiring Via HKDC1 and Modulates Tumor Progression and Drug Response in Colorectal Cancer. EBioMedicine (2018) 33:105–21. doi: 10.1016/j.ebiom.2018.07.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170. Wang F-S, Wu W-H, Hsiu W-S, Liu Y-J, Chuang K-W. Genome-Scale Metabolic Modeling With Protein Expressions of Normal and Cancerous Colorectal Tissues for Oncogene Inference. Metabolites (2020) 10:16. doi: 10.3390/metabo10010016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171. Fan J, Ye J, Kamphorst JJ, Shlomi T, Thompson CB, Rabinowitz JD. Quantitative Flux Analysis Reveals Folate-Dependent NADPH Production. Nature (2014) 510:298–302. doi: 10.1038/nature13236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172. Gatto F, Nookaew I, Nielsen J. Chromosome 3p Loss of Heterozygosity is Associated With a Unique Metabolic Network in Clear Cell Renal Carcinoma. Proc Natl Acad Sci (2014) 111:E866–75. doi: 10.1073/pnas.1319196111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173. Hur W, Ryu JY, Kim HU, Hong SW, Lee EB, Lee SY, et al. Systems Approach to Characterize the Metabolism of Liver Cancer Stem Cells Expressing CD133. Sci Rep (2017) 7:45557. doi: 10.1038/srep45557 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174. Faubert B, Li KY, Cai L, Hensley CT, Kim J, Zacharias LG, et al. Lactate Metabolism in Human Lung Tumors. Cell (2017) 171:358–71.e9. doi: 10.1016/j.cell.2017.09.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175. Asgari Y, Khosravi P, Zabihinpour Z, Habibi M. Exploring Candidate Biomarkers for Lung and Prostate Cancers Using Gene Expression and Flux Variability Analysis. Integr Biol (2018) 10:113–20. doi: 10.1039/c7ib00135e [DOI] [PubMed] [Google Scholar]
- 176. Gatto F, Ferreira R, Nielsen J. Pan-Cancer Analysis of the Metabolic Reaction Network. Metab Eng (2020) 57:51–62. doi: 10.1016/j.ymben.2019.09.006 [DOI] [PubMed] [Google Scholar]
- 177. Shlomi T, Benyamini T, Gottlieb E, Sharan R, Ruppin E. Genome-Scale Metabolic Modeling Elucidates the Role of Proliferative Adaptation in Causing the Warburg Effect. PLOS Comput Biol (2011) 7:e1002018. doi: 10.1371/journal.pcbi.1002018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 178. Vazquez A, Liu J, Zhou Y, Oltvai ZN. Catabolic Efficiency of Aerobic Glycolysis: The Warburg Effect Revisited. BMC Syst Biol (2010) 4:58. doi: 10.1186/1752-0509-4-58 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179. Vazquez A, Oltvai ZN. Molecular Crowding Defines a Common Origin for the Warburg Effect in Proliferating Cells and the Lactate Threshold in Muscle Physiology. PLOS ONE (2011) 6:e19538. doi: 10.1371/journal.pone.0019538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180. Steenbergen R, Oti M, ter Horst R, Tat W, Neufeldt C, Belovodskiy A, et al. Establishing Normal Metabolism and Differentiation in Hepatocellular Carcinoma Cells by Culturing in Adult Human Serum. Sci Rep (2018) 8:11685. doi: 10.1038/s41598-018-29763-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181. Wu H-Q, Cheng M-L, Lai J-M, Wu H-H, Chen M-C, Liu W-H, et al. Flux Balance Analysis Predicts Warburg-Like Effects of Mouse Hepatocyte Deficient in miR-122a. PLOS Comput Biol (2017) 13:e1005618. doi: 10.1371/journal.pcbi.1005618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182. Asgari Y, Zabihinpour Z, Salehzadeh-Yazdi A, Schreiber F, Masoudi-Nejad A. Alterations in Cancer Cell Metabolism: The Warburg Effect and Metabolic Adaptation. Genomics (2015) 105:275–81. doi: 10.1016/j.ygeno.2015.03.001 [DOI] [PubMed] [Google Scholar]
- 183. Duarte NC, Becker SA, Jamshidi N, Thiele I, Mo ML, Vo TD, et al. Global Reconstruction of the Human Metabolic Network Based on Genomic and Bibliomic Data. Proc Natl Acad Sci (2007) 104:1777–82. doi: 10.1073/pnas.0610772104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184. Thiele I, Swainston N, Fleming RMT, Hoppe A, Sahoo S, Aurich MK, et al. A Community-Driven Global Reconstruction of Human Metabolism. Nat Biotechnol (2013) 31:419–25. doi: 10.1038/nbt.2488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185. Mardinoglu A, Agren R, Kampf C, Asplund A, Nookaew I, Jacobson P, et al. Integration of Clinical Data With a Genome-Scale Metabolic Model of the Human Adipocyte. Mol Syst Biol (2013) 9:649. doi: 10.1038/msb.2013.5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186. Mardinoglu A, Agren R, Kampf C, Asplund A, Uhlen M, Nielsen J. Genome-Scale Metabolic Modelling of Hepatocytes Reveals Serine Deficiency in Patients With non-Alcoholic Fatty Liver Disease. Nat Commun (2014) 5:3083. doi: 10.1038/ncomms4083 [DOI] [PubMed] [Google Scholar]
- 187. Robinson JL, Kocabaş P, Wang H, Cholley P-E, Cook D, Nilsson A, et al. An Atlas of Human Metabolism. Sci Signal (2020) 13:eaaz1482. doi: 10.1126/scisignal.aaz1482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188. Di Filippo M, Colombo R, Damiani C, Pescini D, Gaglio D, Vanoni M, et al. Zooming-In on Cancer Metabolic Rewiring With Tissue Specific Constraint-Based Models. Comput Biol Chem (2016) 62:60–9. doi: 10.1016/j.compbiolchem.2016.03.002 [DOI] [PubMed] [Google Scholar]
- 189. Sertbaş M, Ülgen K, Çakır T. Systematic Analysis of Transcription-Level Effects of Neurodegenerative Diseases on Human Brain Metabolism by a Newly Reconstructed Brain-Specific Metabolic Network. FEBS Open Bio (2014) 4:542–53. doi: 10.1016/j.fob.2014.05.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190. Liu Y, Beyer A, Aebersold R. On the Dependency of Cellular Protein Levels on mRNA Abundance. Cell (2016) 165:535–50. doi: 10.1016/j.cell.2016.03.014 [DOI] [PubMed] [Google Scholar]
- 191. Jiang L, Wang M, Lin S, Jian R, Li X, Chan J, et al. A Quantitative Proteome Map of the Human Body. Cell (2020) 183:269–83.e19. doi: 10.1016/j.cell.2020.08.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192. Herrmann HA, Dyson BC, Vass L, Johnson GN, Schwartz J-M. Flux Sampling Is a Powerful Tool to Study Metabolism Under Changing Environmental Conditions. NPJ Syst Biol Appl (2019) 5:1–8. doi: 10.1038/s41540-019-0109-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193. Desai TS, Srivastava S. FluxPyt: A Python-Based Free and Open-Source Software for 13C-Metabolic Flux Analyses. PeerJ (2018) 6:e4716. doi: 10.7717/peerj.4716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194. Matsuda F, Maeda K, Taniguchi T, Kondo Y, Yatabe F, Okahashi N, et al. Mfapy: An Open-Source Python Package for 13C-Based Metabolic Flux Analysis. Metab Eng Commun (2021) 13:e00177. doi: 10.1016/j.mec.2021.e00177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195. Antoniewicz MR. A Guide to 13C Metabolic Flux Analysis for the Cancer Biologist. Exp Mol Med (2018) 50:1–13. doi: 10.1038/s12276-018-0060-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196. Lagziel S, Lee WD, Shlomi T. Studying Metabolic Flux Adaptations in Cancer Through Integrated Experimental-Computational Approaches. BMC Biol (2019) 17:51. doi: 10.1186/s12915-019-0669-x [DOI] [PMC free article] [PubMed] [Google Scholar]