Abstract
Recent technological advances have enabled the generation of large amounts of data consisting of RNA sequences and their functional activity. Here, we propose a method for extracting secondary structure features that affect the functional activity of RNA from sequence–activity data. Given pairs of RNA sequences and their corresponding bioactivity values, our method calculates position-specific structural features of the input RNA sequences, considering every possible secondary structure of each RNA. A Ridge regression model is trained using the structural features as feature vectors and the bioactivity values as response variables. Optimized model parameters indicate how secondary structure features affect bioactivity. We used our method to extract intramolecular structural features of bacterial translation initiation sites and self-cleaving ribozymes, and the intermolecular features between rRNAs and Shine–Dalgarno sequences and between U1 RNAs and splicing sites. We not only identified known structural features but also revealed more detailed insights into structure–activity relationships than previously reported. Importantly, the datasets we analyzed here were obtained from different experimental systems and differed in size, sequence length and similarity, and number of RNA molecules involved, demonstrating that our method is applicable to various types of data consisting of RNA sequences and bioactivity values.
INTRODUCTION
Intra- and intermolecular RNA secondary structures can have various roles, including as sensors of specific molecules (1), sequence-specific binding sites (2) and autocatalytic enzymes (3), and are involved in various biological processes, including transcriptional termination (4), splicing (5), translation initiation (6), plasmid maintenance (7) and responses to cellular conditions (8). To both understand the molecular mechanisms of these biological processes and artificially control them, it is important to accurately understand the roles of RNA secondary structures. Recent substantial advances in DNA sequencing and synthesis technologies have enabled the creation of datasets consisting of RNA sequences and their activities. For example, Cambray et al. examined data on 244 000 mRNA sequences (around translation start sites) and their corresponding protein expression levels in E. coli (9). Wong et al. measured the splicing activity for all possible 9-mer sequences around GU/GC donor sites in humans (10). Kobori et al. measured self-cleavage activity of >10 000 twister ribozyme mutants (11). However, there is no general method for extracting secondary structure features that affect the activity of targeted biological processes from such datasets. Currently, combinations of secondary structure prediction algorithms and tailormade statistical analyses are used for the analysis of such data.
RNA secondary structures are expected to behave stochastically inside cells. In situations where the stochastic behavior affects biological activity, it is necessary to consider fluctuations in RNA secondary structure. Indeed, we have shown that secondary structural features inferred by taking into account all possible secondary structures are the most accurate predictors of protein abundance in Escherichia coli (12). It has also been shown that the accuracy of RNA secondary structure prediction can be improved by considering a probabilistic distribution of RNA secondary structures (13,14).
In this study, we propose a method for extracting relevant structural features from datasets consisting of RNA sequences and their activity values, which was implemented as the software QRNAstruct (https://github.com/gterai/QRNAstruct). Given pairs of RNA sequences and their corresponding bioactivity values, our method first calculates position-specific structural features of the input RNA sequences while considering the stochastic fluctuation of RNA secondary structures. Then, a Ridge regression model is trained using the structural features and bioactivity data values as training data. Optimized model parameters allow us to determine the structural features that increase or reduce bioactivity. Ridge regression serves a crucial function because it deals well with correlations among the position-specific features. It should also be mentioned that the secondary structures of RNA are not included in the input but implicitly considered as a probability distribution.
Various types of tools for the analysis of RNA secondary structures have been proposed, including secondary structure prediction (13,15), alignment of secondary structures (16), homology search considering secondary structures (17,18), and RNA gene discovery (19). However, no specialized method for analyzing the relationship between RNA sequences and bioactivity values has yet been reported.
Here, we first describe an overview of our method and then present the results of its application to the analysis of bacterial translation initiation sites, self-cleaving ribozymes, rRNA–Shine–Dalgarno (SD) sequence interactions, and U1 RNA–donor site interactions. We show that our method successfully extracted detailed structural features affecting the activity of targeted biological processes. Then, we discuss possible extensions of our method that should be examined and implemented in the future.
MATERIALS AND METHODS
In our method, the parameters of a regression model for bioactivity values are optimized using training data, and the optimized parameters represent how secondary structure features affect bioactivity. The regression model is defined as follows:
 |
(1) |
where t(x) is the predicted bioactivity value of an RNA sequence x (or a pair of interacting RNA sequences, in which case x is substituted with two RNA sequences, x, y), ϕ is a secondary structure formed by x, and  is a vector of parameters to be optimized. P(ϕ|x) is the probability of the structure ϕ, and it represents the stochastic behavior of the RNA secondary structures formed by x. In this study, we used the conditional log-linear model developed by Do et al. (the CONTRAfold model) (13) as P(ϕ|x). We used the CONTRAfold model because in our previous study, it showed higher accuracy than did the widely used Turner model in predicting translation efficiency in prokaryotes (12).
is a vector of parameters to be optimized. P(ϕ|x) is the probability of the structure ϕ, and it represents the stochastic behavior of the RNA secondary structures formed by x. In this study, we used the conditional log-linear model developed by Do et al. (the CONTRAfold model) (13) as P(ϕ|x). We used the CONTRAfold model because in our previous study, it showed higher accuracy than did the widely used Turner model in predicting translation efficiency in prokaryotes (12).
In Equation (1),  is a function that evaluates the effect of the structure ϕ on bioactivity. We defined the function f(ϕ, x) as follows.
is a function that evaluates the effect of the structure ϕ on bioactivity. We defined the function f(ϕ, x) as follows.
 |
(2) |
where 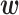 is a vector of parameters to be optimized and
is a vector of parameters to be optimized and 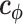 is a vector of indicator functions, each of which takes a value of 1 or 0. Each parameter
is a vector of indicator functions, each of which takes a value of 1 or 0. Each parameter  represents the contribution of a certain position belonging to a specific structural component such as a hairpin, bulge, or internal loop. The indicator function
represents the contribution of a certain position belonging to a specific structural component such as a hairpin, bulge, or internal loop. The indicator function 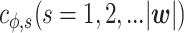 is 1 if the position belongs to the structural component in the structure ϕ or 0 otherwise. For example, when
is 1 if the position belongs to the structural component in the structure ϕ or 0 otherwise. For example, when 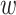 s represents the contribution of position i in a bulge loop, cϕ, s is 1 if a base in position i is in a bulge loop in structure ϕ or 0 otherwise.
s represents the contribution of position i in a bulge loop, cϕ, s is 1 if a base in position i is in a bulge loop in structure ϕ or 0 otherwise.
By inserting Equation (2) into Equation (1), we can obtain the following representation.
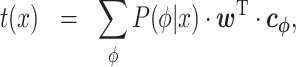 |
(3) |
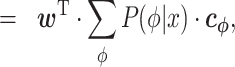 |
(4) |
 |
(5) |
We can employ any linear regression algorithm to optimize  using
using 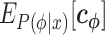 , the vector expectation of
, the vector expectation of  , as a feature vector and t(x) as the response value. In this study, we use Ridge regression (20) to optimize
, as a feature vector and t(x) as the response value. In this study, we use Ridge regression (20) to optimize 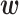 because
because 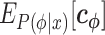 contains correlated values, as described below. When regression analyses are conducted, the presence of feature variables that are highly related to each other can cause instability in the analytical calculations, exhibiting a phenomenon called multicollinearity. Ridge regression is appropriate for constructing a regression model when multicollinearity is present (20). It optimizes
contains correlated values, as described below. When regression analyses are conducted, the presence of feature variables that are highly related to each other can cause instability in the analytical calculations, exhibiting a phenomenon called multicollinearity. Ridge regression is appropriate for constructing a regression model when multicollinearity is present (20). It optimizes  by minimizing the following loss function.
by minimizing the following loss function.
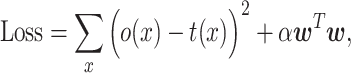 |
(6) |
where o(x) is an observed bioactivity value and α is the so-called regularization parameter, which controls the relative importance of the first (objective) term versus the second (regularization) term in Equation (6). The use of a positive alpha value reduces overfitting by penalizing 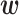 as it becomes too large.
as it becomes too large.
We normalize the observed bioactivity values from 0 to 1 as follows.
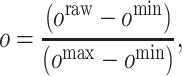 |
(7) |
where oraw is the raw (unnormalized) activity value and omin and omax are the minimum and maximum raw values in the training data, respectively. Before conducting regression analyses, o is further normalized by subtracting the mean value of o from it.
Definition of model parameters
Let x(i) be the ith base in RNA sequence x. For an intramolecular RNA secondary structure formed by x affecting bioactivity, we used the six types of parameters described below.
 : contribution of x(i) in the left side of a base pair
: contribution of x(i) in the left side of a base pair : contribution of x(i) in the right side of a base pair
: contribution of x(i) in the right side of a base pair : contribution of x(i) in a hairpin loop
: contribution of x(i) in a hairpin loop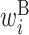 : contribution of x(i) in a bulge loop
: contribution of x(i) in a bulge loop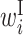 : contribution of x(i) in an internal loop
: contribution of x(i) in an internal loop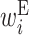 : contribution of x(i) in an external loop
: contribution of x(i) in an external loop
Figure 1A shows an example RNA secondary structure formed by a single molecule. There are six base pairs in this structure, where x(2), x(3), x(5), x(6), x(8) and x(9) are bases on the left side of base pairs and x(14), x(15), x(16), x(17), x(19) and x(20) are bases on the right side of base pairs. Additionally, x(10), x(11), x(12) and x(13) are contained in a hairpin loop, x(7) is contained in a bulge loop, and x(4) and x(18) are contained in an internal loop. Lastly, x(1), x(21), and x(22) are contained in an external loop. In this case, the effect of the secondary structure on bioactivity is calculated as  . In this study, we defined an external loop as a single-stranded region that is not included in a hairpin, bulge, or internal loop. (We also treated multi-loops as a kind of external loop in this study.) We used different sets of parameters for RNA secondary structures between two short RNA sequences affecting bioactivity. We denote the two RNA sequences as x and y and the i-th bases in RNA x and y as x(i) and y(i), respectively. In this case, we used the four types of parameters described below:
. In this study, we defined an external loop as a single-stranded region that is not included in a hairpin, bulge, or internal loop. (We also treated multi-loops as a kind of external loop in this study.) We used different sets of parameters for RNA secondary structures between two short RNA sequences affecting bioactivity. We denote the two RNA sequences as x and y and the i-th bases in RNA x and y as x(i) and y(i), respectively. In this case, we used the four types of parameters described below:
Figure 1.

Examples of RNA secondary structures. RNA secondary structures formed by (A) a single RNA sequence and (B) two short RNA sequences are shown. Circles represent bases, while their numbers and colors indicate the base position and the type of loop to which a base belongs, respectively. Black lines represent base pairings.
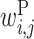 : contribution of a base pair between x(i) and y(j)
: contribution of a base pair between x(i) and y(j) : contribution of s(i) in a bulge loop (s ∈ {x, y})
: contribution of s(i) in a bulge loop (s ∈ {x, y})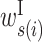 : contribution of s(i) in an internal loop (s ∈ {x, y})
: contribution of s(i) in an internal loop (s ∈ {x, y}) : contribution of s(i) in an external loop (s ∈ {x, y})
: contribution of s(i) in an external loop (s ∈ {x, y})
Figure 1B shows an example RNA secondary structure between x and y. There are five base pairs in this structure. In this case, the effect of the secondary structure on bioactivity is calculated as 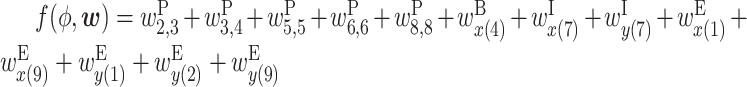 . We assume that the formation of intra-molecular base pairs can be ignored when two RNA sequences are short. This assumption is appropriate when an RNA is part of a protein–RNA complex, and hence intramolecular structural bendability is spatially restricted.
. We assume that the formation of intra-molecular base pairs can be ignored when two RNA sequences are short. This assumption is appropriate when an RNA is part of a protein–RNA complex, and hence intramolecular structural bendability is spatially restricted.
Calculation of feature vectors and correlations between feature values
In the analysis of single RNA sequences, a feature vector consisting of the expectation of cϕ, s corresponding to  ,
, 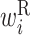 ,
,  ,
, 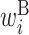 ,
, 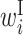 and
and  , can be calculated using the CapR algorithm (21). We modified the CONTRAfold program (13) such that it calculates these expectations according to the CapR algorithm and used it to identify feature vectors. As an example, we calculated the mean of the expectations of cϕ, s for each column of the alignment of purine riboswitch (RF00167) in the Rfam database (22), and observed that the profiles of mean expectations are in good agreement with the annotation of the consensus secondary structure in the database, as shown in Supplementary Figure S1. In rendering this figure, the mean expectations for the alignment columns with more than 50% gaps were excluded.
, can be calculated using the CapR algorithm (21). We modified the CONTRAfold program (13) such that it calculates these expectations according to the CapR algorithm and used it to identify feature vectors. As an example, we calculated the mean of the expectations of cϕ, s for each column of the alignment of purine riboswitch (RF00167) in the Rfam database (22), and observed that the profiles of mean expectations are in good agreement with the annotation of the consensus secondary structure in the database, as shown in Supplementary Figure S1. In rendering this figure, the mean expectations for the alignment columns with more than 50% gaps were excluded.
In the analysis of two RNA sequences, we developed an algorithm for calculating a feature vector corresponding to 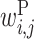 ,
,  ,
, 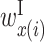 ,
,  ,
, 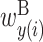 ,
,  and
and  . The algorithm uses the score parameters developed by (13) to evaluate the feature vector, assuming that two input RNA sequences have no intra-molecular base pairs. We describe the algorithm in the Supplementary Methods.
. The algorithm uses the score parameters developed by (13) to evaluate the feature vector, assuming that two input RNA sequences have no intra-molecular base pairs. We describe the algorithm in the Supplementary Methods.
It is important to note that the expected values of the above parameters are not independent, and hence some values in the feature vector are correlated. For example, as consecutive base pairs are energetically stable, neighboring bases tend to belong to base pairs at the same time. A hairpin loop usually has a length of at least 3 nt. Thus, if a particular base is in a hairpin loop, neighboring bases are also more likely to be in the hairpin loop. Therefore, the expectations of cϕ, s corresponding to the same type of parameters tend to be correlated among the neighboring positions. In addition, the sum of expectations of cϕ, s involving a particular position is 1. For example, at position k, the sum of expectations of cϕ, s corresponding to 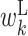 ,
,  ,
, 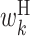 ,
,  ,
,  and
and 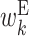 is 1. This imposes anticorrelation on the expected values of cϕ, s at a particular position. Thus, values in the feature vector exhibit position-wise correlation and type-wise anticorrelation.
is 1. This imposes anticorrelation on the expected values of cϕ, s at a particular position. Thus, values in the feature vector exhibit position-wise correlation and type-wise anticorrelation.
Our vector representation of the RNA secondary structure for a single RNA is conceptually similar to that used in the forgi (https://github.com/ViennaRNA/forgi) which is a Python library focused on secondary structure elements. While the forgi uses the vector representation obtained from a single secondary structure (such as the MFE structure), our method uses the vector representation that takes into account the distribution of all possible secondary structures.
Software and flowchart of our method
Our method has been implemented as the program QRNAstruct, which is available at the aforementioned URL. Figure 2 shows the flowchart of QRNAstruct from input to output data. The user inputs RNA sequences and their activity values. In Step 1, the position-specific features (i.e. 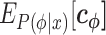 in Equation 5) for each RNA sequence are calculated and integrated with the activity value data to create a single series of tabular data. The user can retrieve these tabular data and use them for various analyses. In Step 2, Ridge regression is used to calculate the weights of the position-specific features. The optimized weights are output as textual data and a visually pleasing heatmap. Step 1 can be time consuming if the amount of data is large, so Step 2 can be conducted independently based on the results already created in Step 1. For more information, see the software tutorial.
in Equation 5) for each RNA sequence are calculated and integrated with the activity value data to create a single series of tabular data. The user can retrieve these tabular data and use them for various analyses. In Step 2, Ridge regression is used to calculate the weights of the position-specific features. The optimized weights are output as textual data and a visually pleasing heatmap. Step 1 can be time consuming if the amount of data is large, so Step 2 can be conducted independently based on the results already created in Step 1. For more information, see the software tutorial.
Figure 2.

Flowchart of our method.
Computational environment
We used an Intel Xeon W-2195 2.30 GHZ CPU with 18 cores to measure the running times of our calculation.
RESULTS
We applied our method to datasets on bacterial translation initiation sites, twister ribozyme mutants, rRNA–SD interactions, and U1 RNA–donor site interactions. Table 1 summarizes the training data used in this study. The number of data points differs by a factor of >100 between the training data for translation initiation sites and those for GC donor sites. RNA sequences in the training data for translation initiation sites were highly variable, whereas those of twister ribozyme mutants were highly similar. For donor site data, mean bioactivity values are very low. This is because most of the RNA sequences in the donor site data have no splicing activity. All the datasets listed in Table 1 are available from GitHub (https://github.com/gterai/QRNAstruct). Supplementary Figure S2 shows the distribution of activity values for each dataset.
Table 1.
Summary of the training data
| Dataset | Number of data points | Sequence length (nt) | Sequence identitya (%) | Activityb | Reference | Running time | Regularization parameter αc |
|---|---|---|---|---|---|---|---|
| Translation initiation | 242 269 | 120 | 47.3 | 0.49 | (9) | 54 min 23.6 s | 104 |
| Twister ribozymes | 5778 | 57 | 93.3 | 0.30 | (11) | 8.6 s | 103 |
| Shine–Dalgarno | 3070 | 20 | 77.9 | 0.29 | (30) | 3.4 s | 103 |
| GU donor sites | 16 216 | 15 | 65.0 | 0.04 | (10) | 12.0 s | 104 |
| GC donor sites | 972 | 15 | 65.1 | 0.04 | (10) | 1.0 s | 104 |
a Mean pairwise identities between RNA sequences. b Mean bioactivity values normalized from 0 to 1. c α values used for obtaining results shown in the main text.
As the most time-consuming step of our method is calculating the feature vectors, we measured its calculation time for each dataset (Table 1). For large datasets, such as the translation initiation dataset, calculation of the feature vectors required approximately 1 hour using 18 CPUs (36 threads).
Secondary structural features near translation initiation sites
It is known that RNA secondary structures near the start codon have a significant effect on translation initiation in E. coli (6,12,23,24). RNA secondary structures near the start codon inhibit protein expression, probably by blocking the approach of ribosomes. Cambray et al. evaluated the protein expression levels of 244 000 synthetic sequences in E. coli (9). We applied our method to this dataset to investigate the relationship between secondary structural features near the start codon and protein expression levels. We used 90-nt regions downstream of start codons and 30-nt regions upstream as the training data. The expression system used by Cambray et al. contains an upstream ORF that is stably translated by ribosomes and hence inhibits the formation of secondary structures beyond the 30-nt upstream regions. Indeed, Cambray et al. used up to 30-nt upstream regions to investigate secondary structural features in their own analysis (9). Therefore, the use of 30-nt regions is appropriate for the investigation of secondary structural features in this dataset. (However, we also show results using longer upstream and downstream regions; see below).
Figure 3A shows the optimized parameters of  using the training data. The columns of this matrix are the positions of the translation initiation sites relative to the start codon (where the first base of the start codon is 0). The rows indicate the types of parameters (i.e.
using the training data. The columns of this matrix are the positions of the translation initiation sites relative to the start codon (where the first base of the start codon is 0). The rows indicate the types of parameters (i.e. 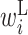 ,
,  ,
, 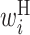 ,
, 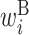 ,
,  ,
,  ). Here, we used α = 104, and the effect of using different α values is discussed in the last part of this section.
). Here, we used α = 104, and the effect of using different α values is discussed in the last part of this section.
Figure 3.
Secondary structural features of bacterial translation initiation sites. (A) Optimized parameter values for bacterial translation initiation sites. Columns represent the relative position from the start codon. Rows represent the type of parameter: L,  ; R,
; R, 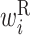 ; H,
; H, 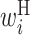 ; B,
; B, 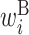 ; I,
; I, 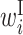 ; E,
; E,  . The sequence pattern in the training data is shown above the heatmap, where N represents any base. The Shine–Dalgarno (SD) sequence and start codon are indicated by the green and red boxes, respectively. (B–D) The secondary structures discussed in the main text. The green and red bases represent the SD sequence and start codon, respectively. (B) An internal loop containing an SD sequence and start codon. (C) Hairpin structure around a start codon. (D) Partial secondary structure in which the bases from +4 to +18 are in the left side of base pairs.
. The sequence pattern in the training data is shown above the heatmap, where N represents any base. The Shine–Dalgarno (SD) sequence and start codon are indicated by the green and red boxes, respectively. (B–D) The secondary structures discussed in the main text. The green and red bases represent the SD sequence and start codon, respectively. (B) An internal loop containing an SD sequence and start codon. (C) Hairpin structure around a start codon. (D) Partial secondary structure in which the bases from +4 to +18 are in the left side of base pairs.
The  value of the region from −12 to +18 is higher, which indicates that the protein expression level is higher when bases in this region are within an external loop. This region overlaps with the SD sequence motif that is complimentary with the 3′ end of ribosomal RNA (rRNA) and is important for translation initiation. The length of this region is about 30 nt, which corresponds well with the length of the region occupied by ribosomes in ribosome profile experiments (25). The
value of the region from −12 to +18 is higher, which indicates that the protein expression level is higher when bases in this region are within an external loop. This region overlaps with the SD sequence motif that is complimentary with the 3′ end of ribosomal RNA (rRNA) and is important for translation initiation. The length of this region is about 30 nt, which corresponds well with the length of the region occupied by ribosomes in ribosome profile experiments (25). The 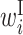 value in the same region also tends to be high, which suggests that a large internal loop structure containing a SD sequence and start codon, such as the structure in Figure 3B, does not significantly lower the protein expression level.
value in the same region also tends to be high, which suggests that a large internal loop structure containing a SD sequence and start codon, such as the structure in Figure 3B, does not significantly lower the protein expression level.
The 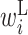 value in the region from −11 to −7 is low. This region overlaps with the SD sequence. Therefore, when the SD sequence is on the left side of the base pair, the protein expression level is reduced. Additionally, the
value in the region from −11 to −7 is low. This region overlaps with the SD sequence. Therefore, when the SD sequence is on the left side of the base pair, the protein expression level is reduced. Additionally, the 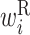 values in the region from +4 to +10 are low. Therefore, a hairpin loop structure, such as the one shown in Figure 3C, lowers the expression level significantly.
values in the region from +4 to +10 are low. Therefore, a hairpin loop structure, such as the one shown in Figure 3C, lowers the expression level significantly.
The 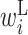 values in the region from +4 to +18 are low. Therefore, when this region forms a base pair with the downstream region, the expression level is reduced (Figure 3D). In the region downstream from +30 and beyond, the parameters have relatively small absolute values. This indicates that the RNA secondary structure in this region does not affect the protein expression level.
values in the region from +4 to +18 are low. Therefore, when this region forms a base pair with the downstream region, the expression level is reduced (Figure 3D). In the region downstream from +30 and beyond, the parameters have relatively small absolute values. This indicates that the RNA secondary structure in this region does not affect the protein expression level.
Next, we investigated the results obtained by Lasso (26), another widely used linear regression algorithm (Supplementary Figure S3). As expected, the obtained parameter values were sparse, but they were also difficult to interpret. It is possible that complex correlations between the position-specific features prevent the Lasso algorithm from extracting interpretable parameters.
We also investigated the effect of using longer upstream and downstream regions on optimized parameter values. For this purpose, we included 150-nt regions downstream of start codons and 90-nt regions upstream as the training data. Supplementary Figure S4 shows a comparison of the optimized parameters with α = 104 using the longer RNA sequences (240 nt) and those with the original length (120 nt). Overall, the results were quite similar. Parameter values corresponding to all the RNA secondary structures discussed above were found even when we used the longer RNA sequences. However, we observed an additional hairpin structure in the region from −40 to −3 only when the longer RNA sequences were used. The hairpin structure may have been falsely detected because, as described above, RNA secondary structures overlapping with >30-nt upstream regions are continuously disrupted in the expression system of Cambray et al. (9).
Finally, to investigate the impact of biases in datasets, we applied our method to three types of datasets consisting of 5% of the translation initiation dataset. The first dataset consists of RNA sequences with the top 2.5% and bottom 2.5% of activity. The second consists of the top 1.0% and bottom 4.0% of activity. The third consists of the top 4.0% and bottom 1.0% of activity. Interestingly, the results (with α = 103) were similar to those obtained using the whole dataset (with α = 104), regardless of the bias in the distribution of activities (Supplementary Figure S5). These results suggest that our method is robust against biases in datasets and can be used for RNAs classified into two classes such as active/inactive.
Secondary structural features of twister ribozyme mutants
The twister ribozyme is a type of ribozyme with self-cleavage catalytic activity. Figure 4A shows the experimentally determined secondary structure of the twister ribozyme. This ribozyme has two characteristic pseudoknot structures (indicated by arrows in Figure 4A). These pseudoknots play an important role in the activity of this ribozyme (27).
Figure 4.
Secondary structural features of twister ribozyme mutants. (A–D) RNA secondary structure of a wild-type twister ribozyme and three mutants. Circles represent bases. Black lines represent base pairs. Colored circles indicate regions forming pseudoknots. Pairs in regions shown in the same color interact with each other and form pseudoknots. Arrowheads indicate cleavage sites of the ribozyme. The numbers associated with bases indicate the base positions. (A) RNA secondary structure of a wild-type twister ribozyme experimentally determined by Liu et al. (27). Double and dotted lines represent trans Watson–Crick and cis-Hoogsteen:sugar edge base pairs, respectively. Arrows indicate pairs of regions forming a pseudoknot structure. (B–D) The predicted RNA secondary structure of three mutants. Mutated bases are shown in red letters. Values in parentheses are the self-cleavage activities normalized from 0 to 1. The shaded areas shown in the dashed boxes indicate the locations of a change in RNA secondary structure of the mutants compared with the wild-type twister ribozyme. (E) Optimized parameter values for twister ribozyme mutants. Each column represents a base position. Each row represents a different type of parameter: L, 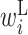 ; R,
; R, 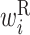 ; H,
; H,  ; B,
; B,  ; I,
; I,  ; E,
; E,  . The RNA sequence of the wild-type twister ribozyme is shown above the heatmap. Boxes above the heatmap indicate regions forming pseudoknots. The base changes in the three mutants are indicated above the wild-type RNA sequence.
. The RNA sequence of the wild-type twister ribozyme is shown above the heatmap. Boxes above the heatmap indicate regions forming pseudoknots. The base changes in the three mutants are indicated above the wild-type RNA sequence.
Kobori et al. measured the self-cleavage activity for 10,296 different mutants of the twister ribozyme (11). All of these mutants are either single or double mutants of the wild type. We used these data to extract secondary structural features that affect self-cleavage activity. The authors have already shown in detail the effect of mutations in the regions forming base pairs of the pseudoknots (colored circles in Figure 4A). Thus, we tried to extract new insights on secondary structural features using data from 5,778 mutants that had base mutations in regions other than the pseudoknots.
Figure 4E shows the optimized parameter values with α = 103; the values for 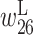 and
and  are particularly low. Thus, the activity of the ribozyme is greatly reduced when the bases at positions 26 and 33 are on the left and right sides of the base pair, respectively. We extracted two mutants, mutants B and C, from the training data in which positions 26 and 33 are predicted to form a base pair. Figure 4B and C show their predicted RNA secondary structure. In these two mutants, the upper part of the secondary structures has changed, which probably inhibits the formation of the pseudoknots, resulting in a decrease in self-cleavage activity.
are particularly low. Thus, the activity of the ribozyme is greatly reduced when the bases at positions 26 and 33 are on the left and right sides of the base pair, respectively. We extracted two mutants, mutants B and C, from the training data in which positions 26 and 33 are predicted to form a base pair. Figure 4B and C show their predicted RNA secondary structure. In these two mutants, the upper part of the secondary structures has changed, which probably inhibits the formation of the pseudoknots, resulting in a decrease in self-cleavage activity.
Another set of prominent features in the optimized parameters is the high values of  and
and 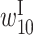 , indicating that self-cleavage activity is high when the bases at positions 9 and 10 belong to an internal loop. Positions 9 and 10 are located next to the cleavage site. When these bases are single stranded, cleavage may be likely to occur. Conversely, when these bases are double stranded, self-cleavage may be less likely to occur. Figure 4D shows an example of a mutant, mutant D, in which the bases at positions 9 and 10 are predicted to be double stranded. The normalized self-cleavage activity of mutant D was low, possibly because the base changes at positions 9 and 10 result in stable base pairing around the cleavage site and inhibit self-cleaving. The changes in RNA secondary structure shown in Figure 4B–D and their effects on self-cleavage activity were reasonable but were not reported by Kobori et al. (11). The predicted RNA secondary structures shown in Figure 4B–D were obtained using the CONTRAfold program (13) with the optional argument ‘–gamma 1.’
, indicating that self-cleavage activity is high when the bases at positions 9 and 10 belong to an internal loop. Positions 9 and 10 are located next to the cleavage site. When these bases are single stranded, cleavage may be likely to occur. Conversely, when these bases are double stranded, self-cleavage may be less likely to occur. Figure 4D shows an example of a mutant, mutant D, in which the bases at positions 9 and 10 are predicted to be double stranded. The normalized self-cleavage activity of mutant D was low, possibly because the base changes at positions 9 and 10 result in stable base pairing around the cleavage site and inhibit self-cleaving. The changes in RNA secondary structure shown in Figure 4B–D and their effects on self-cleavage activity were reasonable but were not reported by Kobori et al. (11). The predicted RNA secondary structures shown in Figure 4B–D were obtained using the CONTRAfold program (13) with the optional argument ‘–gamma 1.’
Interactions between rRNAs and Shine–Dalgarno sequences
In addition to the intramolecular RNA secondary structures around the translation initiation site, the intermolecular structures between the 3′ end of the rRNA and the SD sequences immediately upstream of the initiation codon are known to play important roles in translation initiation (28,29). In general, the stronger this interaction is, the higher the protein expression level will be.
We extracted secondary structural features of rRNA–SD interactions from data obtained by Bonde et al. (30). They comprehensively measured the effect on protein expression of all possible base changes in six defined positions in the region upstream of the start codon. The sequence pattern they investigated was 5′-UUAAAGNNNNNNAAUACUAG-3′, where N represents any base. They ultimately determined the expression level for 3070 types of upstream sequences out of 46 = 4096 possible sequence variants in their experimental design. We applied the proposed method to the 3070 sequences and their protein expression levels in order to determine which secondary structural features affect protein expression levels.
Figure 5 shows the optimized values of  with α = 103, arranged in three matrices; the i and j components of matrix P are the values of
with α = 103, arranged in three matrices; the i and j components of matrix P are the values of  . Matrix X shows the values of
. Matrix X shows the values of  ,
, 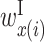 , and
, and  , and matrix Y shows the values of
, and matrix Y shows the values of  ,
, 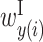 and
and  , where x and y represent the rRNA and upstream sequences, respectively. Each row of matrices X and P represents a single rRNA position, and each column of matrices Y and P represents the relative position in the region upstream of the start codon.
, where x and y represent the rRNA and upstream sequences, respectively. Each row of matrices X and P represents a single rRNA position, and each column of matrices Y and P represents the relative position in the region upstream of the start codon.
Figure 5.

Optimized parameter values for the interaction between rRNAs and Shine–Dalgarno sequences. Matrix P shows 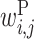 values. The rows and columns of this matrix correspond to the rRNA positions and the upstream region positions relative to the start codon, respectively. The letters associated with the row and column of matrix P are the rRNA and upstream sequence patterns, respectively, where N represents any base. Matrix X shows the values of
values. The rows and columns of this matrix correspond to the rRNA positions and the upstream region positions relative to the start codon, respectively. The letters associated with the row and column of matrix P are the rRNA and upstream sequence patterns, respectively, where N represents any base. Matrix X shows the values of  ,
,  and
and 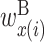 , and matrix Y shows the values of
, and matrix Y shows the values of  ,
, 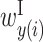 and
and  , where x and y represent the rRNA and upstream sequences, respectively. Each row of matrix X represents the position of a base in a rRNA sequence, and each column of matrix Y represents the relative position of a base in the sequence upstream of the start codon.
, where x and y represent the rRNA and upstream sequences, respectively. Each row of matrix X represents the position of a base in a rRNA sequence, and each column of matrix Y represents the relative position of a base in the sequence upstream of the start codon.
The large 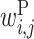 values clustered around the center of matrix P indicate that base pairs between the middle parts of rRNA and upstream sequences increase protein expression. Bases 2 to 7 of rRNA sequences (UCCUCC) are complementary with the typical SD sequence (AGGAGG). It has been reported that the position of the SD sequence is not strictly fixed but allows for some deviation (31). This is reflected in our value of
values clustered around the center of matrix P indicate that base pairs between the middle parts of rRNA and upstream sequences increase protein expression. Bases 2 to 7 of rRNA sequences (UCCUCC) are complementary with the typical SD sequence (AGGAGG). It has been reported that the position of the SD sequence is not strictly fixed but allows for some deviation (31). This is reflected in our value of 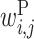 ; the positive
; the positive 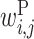 values scattered around the center of the matrix indicate that there are multiple possible locations inside the upstream region where rRNA (UCCUCC) interacts and promotes protein expression.
values scattered around the center of the matrix indicate that there are multiple possible locations inside the upstream region where rRNA (UCCUCC) interacts and promotes protein expression.
There is a strong trend in the parameters of external bases (wE). The values of  ,
,  and
and  are very low. This means that rRNA bases 4 to 6 are especially important and that the protein expression level is greatly reduced if even one of the three bases is within an external loop.
are very low. This means that rRNA bases 4 to 6 are especially important and that the protein expression level is greatly reduced if even one of the three bases is within an external loop.
Interactions between U1 RNAs and 5′ splice sites
The interaction between U1 RNAs and 5′ splice sites in pre-mRNAs is essential for mRNA splicing in eukaryotes. The 5′ splice (i.e. donor) sites are most often GU, but there are a few variants, including GC donor sites. Wong et al. comprehensively measured the splicing activity for all seven possible bases surrounding the 5′ splice site (10). Specifically, they measured the splicing activity for the sequence pattern 5′-AUANNNGUNNNNUUA-3′, which contains the canonical GU donor site, and 5′-AUANNNGCNNNNUUA-3′, which contains the non-canonical GC donor site (N represents any base in both patterns). As both patterns contain seven N bases, they measured the splicing activity for 74 = 16 384 different sequences (including about 1% of sequences for which the efficiency could not be measured). We used these data to analyze the secondary structural features of U1 RNA–donor site interactions.
Figure 6A shows 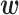 values optimized using the GU splice site data with α = 104, arranged in three matrices. The rows of matrices P and X represent the U1 RNA positions. The columns of matrices P and Y represent the donor site positions. In matrix P, one diagonal line with high
values optimized using the GU splice site data with α = 104, arranged in three matrices. The rows of matrices P and X represent the U1 RNA positions. The columns of matrices P and Y represent the donor site positions. In matrix P, one diagonal line with high  values can be seen, which corresponds to the nine consecutive base pairs shown in Figure 6C. The closer the position of a base pair is to the GU donor site, the greater its
values can be seen, which corresponds to the nine consecutive base pairs shown in Figure 6C. The closer the position of a base pair is to the GU donor site, the greater its  value is. Thus, our method detected the expected trend in which base pairs closer in position to the GU splice sites are more important.
value is. Thus, our method detected the expected trend in which base pairs closer in position to the GU splice sites are more important.
Figure 6.
Optimized parameter values for interactions between U1 RNAs and donor sites. (A and B) Parameter values for GU and GC donor sites, respectively. Matrix P shows 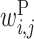 values; the rows and columns of this matrix correspond to the U1 RNA and donor site positions, respectively. The letters associated with the rows and columns of matrix P are the U1 RNA and donor site sequence patterns, respectively, where N represents any base. Matrix X shows the values of
values; the rows and columns of this matrix correspond to the U1 RNA and donor site positions, respectively. The letters associated with the rows and columns of matrix P are the U1 RNA and donor site sequence patterns, respectively, where N represents any base. Matrix X shows the values of  ,
, 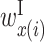 and
and  , and matrix Y shows the values of
, and matrix Y shows the values of  ,
,  and
and  , where x and y represent U1 RNA and donor site sequences, respectively. Each row of matrix X represents a U1 RNA base position, and each column of matrix Y represents a donor site position. (C, D) RNA secondary structures between U1 RNAs and donor sites predicted to have splicing activity. Donor sites (GU or GC) are indicated by black circles. Arrowheads indicate possible cleavage sites. (C) One RNA secondary structure between U1 RNA and GU donor site sequences associated with high splicing activity. (D) One secondary structure between U1 RNA and GC donor site sequences, in which the cleavage site is likely to be located two bases upstream of the GC site. (E) Another secondary structure between U1 RNA and GC donor site sequences.
, where x and y represent U1 RNA and donor site sequences, respectively. Each row of matrix X represents a U1 RNA base position, and each column of matrix Y represents a donor site position. (C, D) RNA secondary structures between U1 RNAs and donor sites predicted to have splicing activity. Donor sites (GU or GC) are indicated by black circles. Arrowheads indicate possible cleavage sites. (C) One RNA secondary structure between U1 RNA and GU donor site sequences associated with high splicing activity. (D) One secondary structure between U1 RNA and GC donor site sequences, in which the cleavage site is likely to be located two bases upstream of the GC site. (E) Another secondary structure between U1 RNA and GC donor site sequences.
In the GC donor site data, only about 1% of the sequences had splice activity. Therefore, we used 162 sequences from among those with the top 1% of splice activity values and 162 × 5 sequences randomly selected without replacement from the remaining sequences as the training data, in consideration of the relative number of positive and negative data points. Figure 6B shows optimized 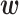 values for the GC splice site data with α = 104. In matrix P, two diagonal lines are visible, although the right diagonal line is not particularly obvious. The presence of these two lines suggests that there are two types of RNA secondary structures that promote splicing activity. Indeed, we found that the two secondary structures shown in Figure 6D and E, which corresponded to the left and right diagonal lines, respectively, showed high splicing activity in the training data. The structure shown in Figure 6D indicates a two-base upstream shift of the donor site may occur, and the GU site, which is immediately upstream of the GC site and complementary with the CA in the middle of U1 RNA, may function as a donor site. In Figure 6E, the C in the GC donor site belongs to an internal loop but can still function as a splice site.
values for the GC splice site data with α = 104. In matrix P, two diagonal lines are visible, although the right diagonal line is not particularly obvious. The presence of these two lines suggests that there are two types of RNA secondary structures that promote splicing activity. Indeed, we found that the two secondary structures shown in Figure 6D and E, which corresponded to the left and right diagonal lines, respectively, showed high splicing activity in the training data. The structure shown in Figure 6D indicates a two-base upstream shift of the donor site may occur, and the GU site, which is immediately upstream of the GC site and complementary with the CA in the middle of U1 RNA, may function as a donor site. In Figure 6E, the C in the GC donor site belongs to an internal loop but can still function as a splice site.
The effect of the regularization parameter α
Supplementary Figures S6– S10 show optimized values of  obtained with various α values (from 0 to 106) for the translation initiation, twister ribozyme, SD, GU donor sites, and GC donor sites datasets, respectively. As expected, the smaller α was, the larger the absolute values of the optimized parameters became. When α ≤ 1, optimized parameters were more dispersed and less interpretable. On the other hand, use of α ≥ 104 tended to give similar and interpretable results. However, in the translation initiation dataset, the secondary structure shown in Figure 3D could not be obtained when α = 106 (Supplementary Figure S6). In the SD dataset, the contribution of base pairs between rRNA and SD sequences could not be detected when α = 106 (Supplementary Figure S8).
obtained with various α values (from 0 to 106) for the translation initiation, twister ribozyme, SD, GU donor sites, and GC donor sites datasets, respectively. As expected, the smaller α was, the larger the absolute values of the optimized parameters became. When α ≤ 1, optimized parameters were more dispersed and less interpretable. On the other hand, use of α ≥ 104 tended to give similar and interpretable results. However, in the translation initiation dataset, the secondary structure shown in Figure 3D could not be obtained when α = 106 (Supplementary Figure S6). In the SD dataset, the contribution of base pairs between rRNA and SD sequences could not be detected when α = 106 (Supplementary Figure S8).
In general, α is determined based on cross-validation tests. Table 2 shows the prediction accuracy (Pearson’s r) obtained by 10-fold cross-validation tests in which all data were randomly divided into 10 bins, and one bin was used as test data, with the remaining 9 bins used as training data. As shown in Table 2, the prediction accuracy was the highest when α = 0 or 1, which are values much smaller than we used in this study (the last column in Table 1). Even if we divided all data such that similar RNA sequences were not included in both test and training data, as in the cross-validation tests used previously (12), the best performing α was 0 for the translation initiation dataset (parentheses in Table 2). As described above, the optimized parameters 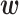 obtained with α ≤ 1 were more disordered and difficult to interpret than those obtained with larger α values. Thus, the α values determined by the cross-validation tests did not produce results with clear interpretability, although they showed high prediction accuracy.
obtained with α ≤ 1 were more disordered and difficult to interpret than those obtained with larger α values. Thus, the α values determined by the cross-validation tests did not produce results with clear interpretability, although they showed high prediction accuracy.
Table 2.
Prediction accuracy of cross validation
| Dataset | |||||
|---|---|---|---|---|---|
| α | TIS | Ribo | SD | GU | GC |
| 0 | 0.79 (0.73) | 0.74 | 0.89 | 0.85 | 0.80a |
| 1 | 0.78 (0.72) | 0.73 | 0.86 | 0.83 | 0.80 b |
| 101 | 0.78 (0.72) | 0.69 | 0.85 | 0.80 | 0.77 |
| 102 | 0.78 (0.72) | 0.64 | 0.83 | 0.76 | 0.70 |
| 103 | 0.77 (0.72) | 0.53 | 0.79 | 0.68 | 0.63 |
| 104 | 0.75 (0.72) | 0.36 | 0.75 | 0.63 | 0.60 |
| 105 | 0.70 (0.68) | 0.29 | 0.72 | 0.62 | 0.59 |
| 106 | 0.65 (0.63) | 0.25 | 0.70 | 0.62 | 0.59 |
Values shown are Pearson’s correlation coefficient r. The best accuracy for each dataset is shown in bold. α = 0 means that we did not use the regularization term. r values in parenthesis were obtained by cross validation considering sequence similarity (see the main text for details). TIS, translation initiation; Ribo, twister ribozymes; SD, Shine–Dalgarno; GU, GU; GC, GC donor sites. a 0.795, b 0.802.
In addition, we also examined the prediction accuracy when we used the position-specific structural features obtained from the minimum free energy structure. The cross-validation procedure is the same as that used to generate the results summarized in Table 2. For all the datasets, the prediction accuracy decreased (Supplementary Table S1). The decrease in the prediction accuracy was especially pronounced for the translation initiation dataset. It is possible that the secondary structure prediction based on the minimum free energy structure did not work well when the length of RNAs was long, as in the translation initiation dataset, for example. The minimum free energy structures were obtained using the Vienna RNA package (32).
Incorporating chemical probing data
The development of chemical probing experiments such as icSHAPE and DMS-seq enabled us to obtain information on secondary structure of many RNAs simultaneously. The result of these experiments is typically represented by reactivity values assigned to each base. High reactivity indicates a base does not interact with other bases. By incorporating these data, the prediction of RNA secondary structure should be more accurate.
We incorporated the chemical probing data into the QRNAstruct framework by calculating the position-specific structural features that take into account the probing reactivity values. We adopted the approach proposed by Deigan et al. (33) to incorporate the SHAPE probing data. Briefly, the SHAPE reactivity value of each base is converted to the pseudo-free energy and incorporated into the calculation of the position-specific features. The pseudo-free energy is applied twice to internal base pairs, and once to edge base pairs. We modified the CapR program (21) such that it could calculate the position-specific structural features considering the reactivity values and integrated it to the QRNAstruct.
As an example, we applied our method to the data obtained by Mustoe et al. (34). They conducted the SHAPE experiment to transcriptome in E.coli and obtained the reactivity data for 407 protein coding genes. RNA secondary structure around the start codon has shown to affect translation efficiency. Therefore, we used RNA sequences around the start codon (from upstream 30 nt to downstream 90 nt) of the 407 genes as input RNA sequences and their translation efficiency data measured by Li et al. (35) as bioactivity values. The ‘slope’ and ‘intercept’ parameters for the pseudo-free energy calculation were set to 1.8 and −0.6 kcal/mol, respectively, according to (34).
Figure 7 compares the optimized parameters with and without the SHAPE reactivity data (α = 104). The values of 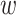 E around the start codon (from −30 to +25) have high positive values (Figure 7A), indicating that translation efficiency becomes high when the region is in external loops. This structural tendency is consistent with that found in Figure 3. If we did not use the SHAPE reactivity data, we found that the optimized parameter values were more dispersed and their interpretation was difficult (Figure 7B). The pearson’s correlation coefficients based on the 10-fold cross-validation were 0.37 and 0.05 with and without the SHAPE data, respectively. The low correlation coefficient of 0.37 even with the use of the SHAPE reactivity data can be attributed to the use of data on endogenous genes that are individually regulated and the integration of two sets of data obtained under different experimental conditions (i.e. those of Mustoe et al. (34) and Li et al. (35)). Importantly, however, by using the SHAPE data, we succeeded in obtaining plausible trends in RNA secondary structure.
E around the start codon (from −30 to +25) have high positive values (Figure 7A), indicating that translation efficiency becomes high when the region is in external loops. This structural tendency is consistent with that found in Figure 3. If we did not use the SHAPE reactivity data, we found that the optimized parameter values were more dispersed and their interpretation was difficult (Figure 7B). The pearson’s correlation coefficients based on the 10-fold cross-validation were 0.37 and 0.05 with and without the SHAPE data, respectively. The low correlation coefficient of 0.37 even with the use of the SHAPE reactivity data can be attributed to the use of data on endogenous genes that are individually regulated and the integration of two sets of data obtained under different experimental conditions (i.e. those of Mustoe et al. (34) and Li et al. (35)). Importantly, however, by using the SHAPE data, we succeeded in obtaining plausible trends in RNA secondary structure.
Figure 7.

Comparison of optimized parameter values with and without SHAPE reactivity data. RNA sequences around the start codon and their translation efficiency in E.coli were used to optimize parameters. The top and bottom matrix show parameter values optimized (A) with and (B) without the SHAPE reactivity data, respectively. Columns represent the relative position from the start codon. Rows represent the type of parameter: L, 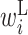 ; R,
; R,  ; H,
; H, 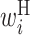 ; B,
; B,  ; I,
; I, 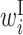 ; E,
; E,  .
.
DISCUSSION
We have proposed a method for extracting secondary structural features from RNA sequence and bioactivity data that considers the thermodynamic fluctuation of the underlying secondary structure. As shown in Equation (1), the proposed regression model consists of two functions, P(ϕ|x) and  . P(ϕ|x) represents the stochastic behavior of the RNA secondary structure formed by RNA sequence x, while
. P(ϕ|x) represents the stochastic behavior of the RNA secondary structure formed by RNA sequence x, while  is a function that evaluates the effect of structure ϕ on bioactivity and is learned from the training data. Computational prediction of RNA secondary structures has a long history, having been developed and used since the 1980s (13,15,36). Previous studies have shown that nearest neighbor models are useful for predicting RNA secondary structures (13,15). By using a previously developed nearest neighbor model as the function P(ϕ|x), our method can incorporate the accumulated knowledge of parameters used to predict RNA secondary structures as prior knowledge for learning the structure–activity relationship.
is a function that evaluates the effect of structure ϕ on bioactivity and is learned from the training data. Computational prediction of RNA secondary structures has a long history, having been developed and used since the 1980s (13,15,36). Previous studies have shown that nearest neighbor models are useful for predicting RNA secondary structures (13,15). By using a previously developed nearest neighbor model as the function P(ϕ|x), our method can incorporate the accumulated knowledge of parameters used to predict RNA secondary structures as prior knowledge for learning the structure–activity relationship.
In this study, we applied our method to different types of biological data and revealed more detailed insights into structure–activity relationships than previously reported. For example, in the analysis of translation initiation sites, we extracted the specific shapes of RNA secondary structures that inhibit or promote protein expression. In our previous study, we showed that the accessibility around the start codon (i.e. the probability that the region around a start codon is single-stranded) has a significant impact on the protein expression level (12). In the current analysis, we were able to find more specific secondary structures, as shown in Figure 3B–D. In the analysis of twister ribozyme mutants, we were able to identify changes in RNA secondary structure that significantly reduce self-cleavage activity but have not been previously noted. In the analysis of the interaction between U1 RNAs and GC donor sites, our method clarified that there are two types of secondary structures that promote splicing in training data (Figure 6D,E).
In previous studies, the position-specific structural features employed here were used to investigate structural propensities around protein binding sites (21,37). We extended their study and showed that these features can be used to clarify the structural features affecting bioactivity by combining them with Ridge regression. Ridge regression was found to handle multicollinearity among the position-specific features well and provided highly interpretable regression models.
In general, the regularization parameter α can be determined based on cross-validation tests. However, α values determined by cross-validation tests did not provide results with clear interpretability. In general, computational models inevitably have some disparity from reality. Ridge regression strives to limit such differences by forcibly adjusting model parameters. We infer that this can somewhat increase the prediction accuracy, while sometimes reducing interpretability of the model parameters. Therefore, we suggest that in order to obtain good interpretability, α values larger than those determined based on the cross-validation accuracy should be used.
A previous study has shown that the sites involved in RNA intermolecular and intramolecular interactions can be predicted from RNA sequence alignments (38). Two other studies have proposed methods to predict the interface of interactions with other molecules in RNA by combining RNA sequence alignment with RNA 3D structure information (39) or with the structural probing data from RNA mutants (40). Although the methods used in these studies use algorithms and input data that are different from ours, they share the same goal of finding functionally important sites in RNA sequences. Therefore, these methods are complementary to ours, and there is value in comparing their results with ours.
Variation and extension of position-specific parameters
There are many possible variations of the position-specific parameters that we have proposed in this study. For example, we can use a new parameter to estimate the contribution of two consecutive base pairs in a specific position to bioactivity, reminiscent of the stacking energy of the Turner model (41,42). We can also introduce parameters corresponding to bases in the left and right side of a bulge or internal loop and estimate their contributions separately. In this study, we have considered the position of a base and its type of RNA secondary structure, but not the type of base (i.e. A, C, G or U). However, we can consider types of bases by setting different parameters for different bases. For example, it is possible to set different parameters for each type of base pair and estimate their contributions separately. This could be useful, for example, in the analysis of microRNA binding sites, because GU base pairs in microRNA binding sites are known to reduce the inhibitory effect of microRNAs (43). However, by setting different parameters for each type of base, the number of parameters increases. As the number of parameters increases, more training data should be required. Additionally, the interpretation of the optimized parameter values may become more complicated. When considering the types of bases, a balance must be struck between the negative impact of increasing the number of parameters and the positive impact of making the regression model more precise.
Future works
Our method, as it is, cannot be used for the analysis of structural features that are not position specific. However, it can be extended for the analysis of features that are not position specific, provided that their expected occurrences can be calculated. For example, suppose that the existence of the kink-turn motif, a common RNA structural motif, is expected to affect bioactivity. In such a case, we can use a parameter representing the contribution of the motif located anywhere in each RNA sequence and investigate its effect on bioactivity. However, we need to develop a new algorithm to calculate the expected occurrences of the motif anywhere in each RNA. The use of non-position specific features is an important future direction, because it enables us to analyze RNA sequences that are of different lengths and unaligned and thus expand the applicability of our method.
Currently, our method does not consider the presence of pseudoknot structures. Therefore, the accuracy of the analysis of RNA sequences with pseudoknots is likely reduced. However, in our analysis of twister ribozyme mutants, we were able to extract biologically interpretable and thus plausible structure–bioactivity relationships. Therefore, our method could be used to analyze RNA sequences with pseudoknots as long as secondary structures other than pseudoknots were correctly predicted, as in the case of twister ribozyme mutants. However, our method could potentially incorporate a probability distribution of RNA secondary structures considering pseudoknots. Although such a probability distribution is currently difficult to obtain, its incorporation would make our method more accurate for the analysis of RNA sequences with pseudoknots.
As noted above, our method does not take into account the intramolecular base pairing of a pair of interacting RNAs. For longer RNAs, it may be important to consider the competition between intra- and intermolecular base pair. If these two types of interactions are considered simultaneously, O(L6) computational time is required to obtain the position-specific structural features (where L is the length of RNA). However, we should be able to reduce the computational complexity by imposing constraints on the secondary structure to be considered.
In our method, we adopted the CONTRAfold model, but other RNA-folding models can be used as well. We have examined the effect of using the widely used Turner model. However, we have not obtained better prediction accuracy in cross-validation tests than that obtained with CONTRAfold model. Although the results so far suggest that CONTRAfold model is a better choice between the two models, further analyses are needed to obtain more reliable conclusion.
CONCLUSION
In this study, we have proposed a new method for extracting position-specific secondary structural features from RNA sequence and bioactivity data that considers all possible secondary structures formed by each RNA sequence in training data. By applying our method to translation initiation, twister ribozyme, SD, and GU and GC donor site datasets, we were able to reveal more detailed insights into the structure–activity relationships than previously reported. The datasets analyzed here vary in size, diversity, and the RNA molecules involved. Thus, the results obtained here demonstrate that our method can be used to analyze various types of data consisting of RNA sequences and bioactivity values.
DATA AVAILABILITY
The training data for the translation initiation, twister ribozyme, Shine–Dalgarno, and GU and GC donor site datasets and the code implementing our method are available from GitHub (https://github.com/gterai/QRNAstruct).
Supplementary Material
ACKNOWLEDGEMENTS
We thank the members of the Asai and Frith laboratories for useful discussions. Computations were partially performed on the NIG supercomputer at the ROIS National Institute of Genetics.
Contributor Information
Goro Terai, Department of Computational Biology and Medical Sciences, Graduate School of Frontier Sciences, University of Tokyo, Kashiwanoha 5-1-5, Kashiwa, Chiba 277-8561, Japan.
Kiyoshi Asai, Department of Computational Biology and Medical Sciences, Graduate School of Frontier Sciences, University of Tokyo, Kashiwanoha 5-1-5, Kashiwa, Chiba 277-8561, Japan.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Japan Society for the Promotion of Science [JP21H04912 to K.A., JP16H06279 to K.A., JP21K15075 to G.T.]; Japan Science and Technology Agency (JST) CREST [JPMJCR18S1 to K.A.]. Funding for the open access charge: Japan Society for the Promotion of Science [JP21K15075 to G.T.].
Conflict of interest statement. None declared.
REFERENCES
- 1. Serganov A., Nudler E.. A decade of riboswitches. Cell. 2013; 152:17–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Guil S., Esteller M.. RNA-RNA interactions in gene regulation: the coding and noncoding players. Trends Biochem. Sci. 2015; 40:248–256. [DOI] [PubMed] [Google Scholar]
- 3. Doherty E.A., Doudna J.A.. Ribozyme structures and mechanisms. Annu. Rev. Biochem. 2000; 69:597–615. [DOI] [PubMed] [Google Scholar]
- 4. Ray-Soni A., Bellecourt M.J., Landick R.. Mechanisms of bacterial transcription termination: all good things must end. Annu. Rev. Biochem. 2016; 85:319–347. [DOI] [PubMed] [Google Scholar]
- 5. Staley J.P., Guthrie C.. Mechanical devices of the spliceosome: motors, clocks, springs, and things. Cell. 1998; 92:315–326. [DOI] [PubMed] [Google Scholar]
- 6. Kudla G., Murray A.W., Tollervey D., Plotkin J.B.. Coding-sequence determinants of gene expression in Escherichia coli. Science. 2009; 324:255–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Thisted T., Gerdes K.. Mechanism of post-segregational killing by the hok/sok system of plasmid R1. J. Mol. Biol. 1992; 223:41–54. [DOI] [PubMed] [Google Scholar]
- 8. Henkin T.M. Riboswitch RNAs: using RNA to sense cellular metabolism. Genes Dev. 2008; 22:3383–3390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Cambray G., Guimaraes J.C., Arkin A.P.. Evaluation of 244,000 synthetic sequences reveals design principles to optimize translation in Escherichia coli. Nat. Biotechnol. 2018; 36:1005–1015. [DOI] [PubMed] [Google Scholar]
- 10. Wong M.S., Kinney J.B., Krainer A.R.. Quantitative activity profile and context dependence of all human 5’ splice sites. Mol. Cell. 2018; 71:1012–1026.e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Kobori S., Yokobayashi Y.. High-throughput mutational analysis of a twister ribozyme. Angew. Chem. Int. Ed. Engl. 2016; 55:10354–10357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Terai G., Asai K.. Improving the prediction accuracy of protein abundance in Escherichia coli using mRNA accessibility. Nucleic Acids Res. 2020; 48:e81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Do C.B., Woods D.A., Batzoglou S.. CONTRAfold: RNA secondary structure prediction without physics-based models. Bioinformatics. 2006; 22:e90–e98. [DOI] [PubMed] [Google Scholar]
- 14. Hamada M., Kiryu H., Sato K., Mituyama T., Asai K.. Prediction of RNA secondary structure using generalized centroid estimators. Bioinformatics. 2009; 25:465–473. [DOI] [PubMed] [Google Scholar]
- 15. Zuker M., Stiegler P.. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res. 1981; 9:133–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Sankoff D. Simultaneous solution of the RNA folding, alignment and protosequence problems. SIAM J. Appl. Math. 1985; 45:810–825. [Google Scholar]
- 17. Klein R.J., Eddy S.R.. RSEARCH: finding homologs of single structured RNA sequences. BMC Bioinformatics. 2003; 4:44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Nawrocki E.P., Eddy S.R.. Infernal 1.1: 100-fold faster RNA homology searches. Bioinformatics. 2013; 29:2933–2935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Gruber A.R., Findei S., Washietl S., Hofacker I.L., Stadler P.F.. RNAz 2.0: improved noncoding RNA detection. Pac. Symp. Biocomput. 2010; 69–79. [PubMed] [Google Scholar]
- 20. Hoerl A.E., Kennard R.W.. Ridge regression: biased estimation for nonorthogonal problems. Technometrics. 1970; 12:55–67. [Google Scholar]
- 21. Fukunaga T., Ozaki H., Terai G., Asai K., Iwasaki W., Kiryu H.. CapR: revealing structural specificities of RNA-binding protein target recognition using CLIP-seq data. Genome Biol. 2014; 15:R16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Kalvari I., Nawrocki E.P., Ontiveros-Palacios N., Argasinska J., Lamkiewicz K., Marz M., Griffiths-Jones S., Toffano-Nioche C., Gautheret D., Weinberg Z.et al.. Rfam 14: expanded coverage of metagenomic, viral and microRNA families. Nucleic Acids Res. 2021; 49:D192–D200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Goodman D.B., Church G.M., Kosuri S.. Causes and effects of N-terminal codon bias in bacterial genes. Science. 2013; 342:475–479. [DOI] [PubMed] [Google Scholar]
- 24. de Smit M.H., van Duin J.. Secondary structure of the ribosome binding site determines translational efficiency: a quantitative analysis. Proc. Natl. Acad. Sci. U.S.A. 1990; 87:7668–7672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Ingolia N.T., Ghaemmaghami S., Newman J.R.S., Weissman J.S.. Genome-wide analysis in vivo of translation with nucleotide resolution using ribosome profiling. Science. 2009; 324:218–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Tibshirani R. Regression shrinkage and selection via the lasso: a retrospective. J. R. Stat. Soc. Ser. B (Statistical Methodol.). 2011; 73:273–282. [Google Scholar]
- 27. Liu Y., Wilson T.J., McPhee S.A., Lilley D.M.J.. Crystal structure and mechanistic investigation of the twister ribozyme. Nat. Chem. Biol. 2014; 10:739–744. [DOI] [PubMed] [Google Scholar]
- 28. Shine J., Dalgarno L.. Determinant of cistron specificity in bacterial ribosomes. Nature. 1975; 254:34–38. [DOI] [PubMed] [Google Scholar]
- 29. Steitz J.A., Jakes K.. How ribosomes select initiator regions in mRNA: base pair formation between the 3’ terminus of 16S rRNA and the mRNA during initiation of protein synthesis in Escherichia coli. Proc. Natl. Acad. Sci. U.S.A. 1975; 72:4734–4738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Bonde M.T., Pedersen M., Klausen M.S., Jensen S.I., Wulff T., Harrison S., Nielsen A.T., Herrgad M.J., Sommer M.O.A.. Predictable tuning of protein expression in bacteria. Nat. Methods. 2016; 13:233–236. [DOI] [PubMed] [Google Scholar]
- 31. Chen H., Bjerknes M., Kumar R., Jay E.. Determination of the optimal aligned spacing between the Shine-Dalgarno sequence and the translation initiation codon of Escherichia coli mRNAs. Nucleic Acids Res. 1994; 22:4953–4957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Lorenz R., Bernhart S.H., Höner zu Siederdissen C., Tafer H., Flamm C., Stadler P.F., Hofacker I.L.. ViennaRNA Package 2.0. Algorithms. Mol. Biol. 2011; 6:26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Deigan K.E., Li T.W., Mathews D.H., Weeks K.M.. Accurate SHAPE-directed RNA structure determination. Proc. Natl. Acad. Sci. U.S.A. 2009; 106:97–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Mustoe A.M., Busan S., Rice G.M., Hajdin C.E., Peterson B.K., Ruda V.M., Kubica N., Nutiu R., Baryza J.L., Weeks K.M.. Pervasive regulatory functions of mRNA structure revealed by high-resolution SHAPE probing. Cell. 2018; 173:181–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Li G.W., Burkhardt D., Gross C., Weissman J.S.. Quantifying absolute protein synthesis rates reveals principles underlying allocation of cellular resources. Cell. 2014; 157:624–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Nussinov R., Jacobson A.B.. Fast algorithm for predicting the secondary structure of single-stranded RNA. Proc. Natl. Acad. Sci. U.S.A. 1980; 77:6309–6313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Cook K.B., Vembu S., Ha K.C.H., Zheng H., Laverty K.U., Hughes T.R., Ray D., Morris Q.D.. RNAcompete-S: combined RNA sequence/structure preferences for RNA binding proteins derived from a single-step in vitro selection. Methods. 2017; 126:18–28. [DOI] [PubMed] [Google Scholar]
- 38. Weinreb C., Riesselman A.J., Ingraham J.B., Gross T., Sander C., Marks D.S.. 3D RNA and functional interactions from evolutionary couplings. Cell. 2016; 165:963–975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Su H., Peng Z., Yang J.. Recognition of small molecule-RNA binding sites using RNA sequence and structure. Bioinformatics. 2021; 37:36–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Reinharz V., Ponty Y., Waldispühl J.. Combining structure probing data on RNA mutants with evolutionary information reveals RNA-binding interfaces. Nucleic Acids Res. 2016; 44:e104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Mathews D.H., Sabina J., Zuker M., Turner D.H.. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999; 288:911–940. [DOI] [PubMed] [Google Scholar]
- 42. Mathews D.H., Disney M.D., Childs J.L., Schroeder S.J., Zuker M., Turner D.H.. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl. Acad. Sci. U.S.A. 2004; 101:7287–7292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Bartel D.P. MicroRNAs: target recognition and regulatory functions. Cell. 2009; 136:215–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The training data for the translation initiation, twister ribozyme, Shine–Dalgarno, and GU and GC donor site datasets and the code implementing our method are available from GitHub (https://github.com/gterai/QRNAstruct).





