A Mechanism for Nitrogenase Including Loss of a Sulfide

Abstract

Nitrogenase is the only enzyme in nature that can fix N₂ from the air. The active cofactor of the leading form of this enzyme contains seven irons and one molybdenum connected by sulfide bridges. In several recent experimental studies, it has been suggested that the cofactor is very flexible, and might lose one of its sulfides during catalysis. In this study, the possible loss of a sulfide has been investigated by model calculations. In previous studies, we have shown that there should be four activation steps before catalysis starts, and this study is based on that finding. It was found here that, after the four reductions in the activation steps, a sulfide will become very loosely bound and can be released in a quite exergonic step with a low barrier. The binding of N₂ has no part in that release. In our previous studies, we suggested that the central carbide should be protonated three times after the four activation steps. With the new finding, there will instead be a loss of a sulfide, as the barrier for the loss is much lower than the ones for protonating the carbide. Still, it is suggested here that the carbide will be protonated anyway, but only with one proton, in the E₃ to E₄ step. A very complicated transition state for H₂ formation involving a large structural change was obtained. The combined step, with a loss of H₂ and binding of N₂, is calculated to be endergonic by +2.3 kcal mol⁻¹; this is in excellent agreement with experiments in which an easily reversible step has been found.

Lost property: The possible loss of a sulfide mechanism for the Mo‐nitrogenase has been investigated by hybrid DFT using a cluster model. The calculations show that, after four reductions, a sulfide can be released as a H₂S group. After another four reductions, the central carbon is protonated with one proton in E4, from where the loss of H₂ and binding of N₂ is reversible.

Introduction

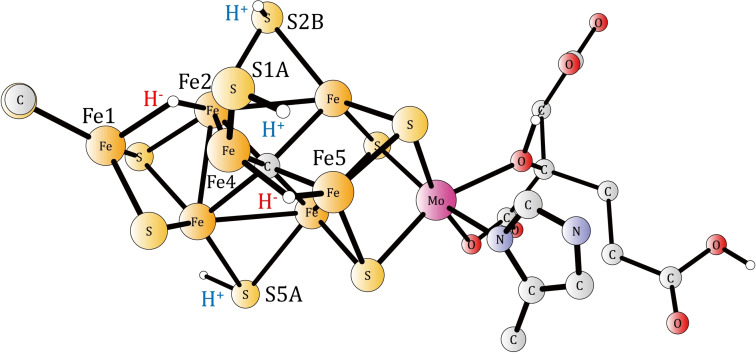
Nitrogen atoms are present in all biological systems. As a source for nitrogen, N₂ in the air is mostly used, which is very difficult to activate due to its strong triple bond. Nitrogenase is the major enzyme in nature that is able to transform N₂ from air to ammonia, which can then be used in the biological synthesis of amino acids, for example. An X‐ray structure of the enzyme was obtained almost 30 years ago. ^[1] The active cofactor, termed FeMoco has seven irons and one molybdenum linked by sulfide bridges. There is also an unusual ligand on molybdenum, a homocitrate. Higher resolution structures have since then been repeatedly reported. A major surprise has been that a central carbide was found in the cofactor. ^[2] The present investigation of the mechanism is based on the high‐resolution structure of the FeMo cofactor ^[2b] (PDB ID: 3U7Q contains the supplementary crystallographic data for this paper. These data are provided free of charge by the Protein Date Bank). The active site of the enzyme obtained here after four reductions is shown in Figure 1. Even though a structure was obtained at a resolution of 1 Å, the mechanism for N₂ activation is still not known. Important early work, reviewed in 1996, ^[3] showed that N₂ is activated after four reductions in the catalytic cycle. The states are termed E₀ to E₄. The most important and detailed finding concerning the mechanism was obtained by a set of EPR measurements. ^[4] It was found that the binding of N₂ in the E₄ state was accompanied by a loss of two bridging hydrides, forming H₂. It had long been known that one H₂ was formed for every N₂ that is activated, but the EPR study showed that the loss was obligatory for activating N₂.

Figure 1.

The core structure of the active site obtained from calculations after four reductions of the cofactor (here termed the A₄ state). The numbering follows the one given in the X‐ray structure (PDB ID: 3 U7Q). ^[2b]

X‐ray structures have so far been determined only for the ground state E₀ (here termed A₀ for reasons discussed below). The lack of structures for the other E‐intermediates has, of course, severely hampered the understanding of the mechanism. From the EPR study, mentioned above, a structure for the active E₄ state has been assumed. Starting from the X‐ray crystal structure for the ground state, assumed to be E₀, E₄ should be formed after four reductions. From the assumed E₀, four hydrogens should be added. Two of them should form the two bridging hydrides observed, and the remaining two should therefore protonate two sulfides. This meant that E₄ should have four Fe^III. ^[4]

A quite different E₄ structure was suggested in our previous studies. ^[5] It was found that it was not energetically possible to activate N₂ already after four reductions from the ground state. This was not a surprising finding since the E₄ structure suggested by experiments has quite high oxidations states for the irons. Instead, the conclusion from the calculations was that FeMoco needed to be reduced four times to reach E₀, which is the beginning of the catalytic cycle. These reductions are needed in order to make all irons Fe^II, and are made only once before catalysis. The activation states were termed A₀ to A₄. After the first four reductions in the catalytic cycle, altogether eight reductions from the ground state A₀, the E₄ state was reached with a structure that was in very good agreement with the EPR analysis. ^[4] The optimized structure had two hydrides which could form H₂ prior to the activation of N₂. The reason for this type of activation of N₂ was easy to understand from the computed results, since the loss of H₂ led to a very low oxidation state of FeMoco with two Fe^I and five Fe^II. ^[5] With such a low oxidation state, the required transfer of electrons to N₂ was significantly enhanced. The idea of an activation of the cofactor, as a part of suggested mechanisms for nitrogenase, has become more and more common. ^[6]

Three years ago, an X‐ray crystallography study for vanadium nitrogenase showed a structure where there was a loss of a sulfide. ^[6c] Furthermore, the analysis of the density showed that the sulfide was replaced by a ligand, suggested to be a nitrogen containing intermediate from the catalytic cycle. However, theoretical studies indicated that the intermediate instead was most probably an OH, which is a very unlikely intermediate for nitrogenase. ^[7] Quite recently, in another X‐ray crystallography study, structures were obtained where sulfides were again lost. ^[6e] Very interestingly, a bound protonated nitrogen containing intermediate was detected. The intermediate, which was found to be bridging between two irons, was identified as N₂H₂. A bound N₂ was also suggested from another structure in the same study. The present study was inspired by those findings. It should be noted that the experimental interpretations of the X‐ray structure have been strongly criticized in two recent papers. ^[8] The density suggested to be coming from N₂ was instead identified as coming from a sulfide. A reply from the authors has also been given. ^[9] The methodology used here in the present theoretical study is the same as the one used in our previous studies. The first part of the study was focused on investigating possibilities to lose a sulfide from the cofactor. In all previous studies, it has been suggested that N₂ replaces the sulfide ligand, but our previous study indicated that this should not be energetically possible. ^[5a] The search for a loss of a sulfide, was here combined with our previous findings that four activation steps are needed before the catalytic cycles start. ^[5]

Computational Methods

The methods used here are the same as the ones used in our previous studies on nitrogenase, ^[5] and on many other redox enzymes. ^[10] The results from those studies have been shown to be in excellent agreement with available experimental findings in all cases investigated. ^[10b] The starting point is the use of the standard hybrid DFT method with the B3LYP functional. ^[11] For the geometry optimization a medium size basis set, LACVP*, has been found to be adequate for obtaining reliable energies. Transition states have been obtained from computed Hessians. The final energies demand more care and are obtained with a large basis set (cc‐pvtz(‐f) and LACV3P*). It has been found that for redox systems, the energies are quite sensitive to the amount of exact exchange used in the functional.[ ^10b , ¹² ] In most cases a fraction of 15 % has been found optimal, and that is what has been used here for the energies reported. In order to obtain an estimate of the errors in the energies, the energies were calculated also with 10 and 20 %.[ ¹⁰ , ¹² ] In most cases, that type of estimate of the energy error suggests that it is not larger than 3 kcal mol⁻¹ for 15 %. The same dependence on the fraction of exact exchange has been noted in our previous study on the E₄ state of nitrogenase. ^[12] Dispersion was added using the D2 correction. ^[13] For the large basis set, the energies have to be computed without the pseudo‐spectral approach. Solvation effects were obtained using a Poisson‐Boltzmann solver, ^[14] with a dielectric constant of 4.0. The programs used were Jaguar ^[15] and Gaussian. ^[16]

It can be added that the high accuracy of B3LYP is strongly connected with the absence of multireference effects. Stable molecules like H₂O, CH₄ are single reference molecules and B3LYP therefore works fine, as shown by all experience obtained so far. The high accuracy obtained for the present type of enzyme mechanisms shows that also these systems are basically single reference systems, at least at room temperature. As the temperature is raised, multireference effects should start to appear. The high accuracy also for transition states indicates that the results stay accurate up to at least 20 kcal mol⁻¹ from the ground state of these systems. On the other hand, problems may appear for excited states higher than 30 kcal mol⁻¹, but they are not studied here. A significant number of tests have been made concerning the accuracy of the present approach. It has recently been tested on Photosystem II, nitrogenase, cytochrome c oxidase, NiFe and FeFe hydrogenases, NiFe‐CO dehydrogenase, multi‐copper oxidases and acetyl‐CoA synthase. The results in all cases are excellent. ^[10a]

The active site is modeled as a cluster ^[17] that is similar to the one used in our most recent study on nitrogenase but somewhat smaller. Because a very large number of investigations had to be performed, the previous model with around 270 atoms ^[5b] was found to be impractical. Instead, a model with around 170 atoms was used, more like the one used in our first study. ^[5a] The present model includes, besides the FeMoco ligands also His195, Arg96, Arg359, Glu380, Phe381 and Gln191. The region outside His195 was previously found to be important for an accurate pKa value for this residue, but that should have no affect for the present investigations and was therefore left out. The region outside the homocitrate was found to be important for the rearrangements of this ligand, ^[18] but as those structural changes do not appear in this study, this region was also left out.

In order to obtain the energetics for the different transitions, an energy value for the addition of a (H⁺, e⁻) is needed. The same value as in our previous studies of 348.6 kcal mol⁻¹ was used. That value was based on the redox potential for the donating P cluster of −1.6 V, which is obtained after the activation of the enzyme by two ATP. The value for obtaining a proton from the medium at pH 7 was 279.8 kcal mol⁻¹. ^[19] The sum of these values used for (H⁺, e⁻) addition has been found to be much more accurate than the individual values in enzyme surroundings. The reason is that adding (H⁺, e⁻) does not change the charge and therefore, long‐range enzyme effects can safely be neglected.

Many different spin‐coupling schemes were investigated. At the end, only one of them, (+−−−+++, the order of the labels for the spins follows the order of irons in the X‐ray structure), was used in all cases but one. That exception occurs for the case in which H₂ is released in E₄, where a coupling (−+−−+++) was found to be somewhat better. The difference in energies between the best couplings is not large and not decisive for the present study. The odd E‐states are triplets, while the even ones are doublets. It can be noted that the preferred spin‐coupling is different from the one of the ground state. ^[20] The reason is that as more and more Fe^II are created, the anti‐ferromagnetic coupling between the different irons decreases in strength and the anti‐ferromagnetic coupling between Mo and Fe dominates.

Results

A major point of the previous study of the mechanism for nitrogenase, was that there are four initial activation steps before the catalytic cycling starts. That was found to be necessary in order to form a state which has sufficiently low redox states for the irons to eventually be able to activate N₂. The initial activation states were termed A₀ to A₄. The present study starts at A₄, with a structure in which the carbide is not protonated. In the previous study, there were one bridging hydride between Fe2 and Fe6, and three protonated belt sulfides (S2B, S3 A and S5 A). ^[5b] A better structure has now been obtained, which is −7.3 kcal mol⁻¹ lower in energy. The structure is shown in Figure 1. There is now one bridging hydride between Fe4 and Fe5, which forces S3 A to take a terminal position. There are three protonated sulfides on S2B, S3 A and S1B. S3 A forms a hydrogen bond with the proton on S1B. There are five Fe^II and two Fe^III. The spins are delocalized, with all irons having populations in the range 3.5 to 3.6. The spin on Mo is about 2.6, and it stays at about the same level throughout the mechanism, indicating an oxidation state of Mo^III.

For the protonations of the cofactor described below, the protons are assumed to be delivered by organized hydrogen bonded chains that end at the cofactor region at, for example His195. After that, there should be nearly freely movable water molecules around the cofactor that could deliver the protons further to the desired ligands of the cofactor. It can be added that for nitrogenase, the rate of proton transfer does not need to be much faster than the rate‐limiting step of electron delivery occurring in seconds. In other enzymes, where proton transfer is required to be fast it can occur on the order of microseconds.

Release of H₂S

The first critical step of the present mechanism is the release of a sulfide. After some investigation, it was found that the protonated terminal S3 A was able to abstract the proton from S1B. The barrier for the release of H₂S is quite low with +7.2 kcal mol⁻¹. The transition state is shown in Figure 2. The loss of H₂S is found to be exergonic by −12.3 kcal mol⁻¹ assuming that the binding of H₂S outside the FeMoco is similar to the corresponding one of H₂O, since the hydrogen bonds should be similar. Even with a much less favorable hydrogen bonding, the loss of H₂S would be quite exergonic. With such a low barrier and large exergonicity, it is difficult to see how the loss of H₂S can be avoided in the reduction process. As a comparison, the protonation of the carbide calculated in the previous study had to pass a barrier of +16.3 kcal mol⁻¹ to become exergonic; ^[5b] this shows that the previously suggested mechanism for nitrogenase is kinetically less favorable than the present one, even though the thermodynamics for carbide protonation is more exergonic. A position where H₂S can bind outside the cofactor has been suggested in some of the recent X‐ray structural studies.[ ^6a , ^6e ] The presence of at least one hydride is necessary for the release mechanism, and it can therefore not occur before A₄. The hydride is needed to take the place of the sulfide that is released. As catalysis is over, due to lack of ATP or N₂, the cluster becomes oxidized from its highly reduced states during catalysis, and the rebinding of the sulfide becomes favorable again.

Figure 2.

The core structure for the transition state for H₂S release.

The release of a sulfide leads to large structural changes. The frozen coordinates for the surrounding residues is a guarantee that these structural changes can be accommodated in the enzyme surrounding. The question of contributions from residues outside the model has also been investigated. Backbone NH‐groups from Gly356, Gly357 and Ile358 can potentially form hydrogen bonds to S3 A. However, at the TS the hydrogens of these NH groups have distances between 3 and 4 Å from S3 A and are therefore very unlikely to affect the TS.

The mechanism given here for the release of the sulfide is quite different from the suggestions in all other previous studies, experimental and theoretical ones.[ ^6a , ^6b , ^6d , ²¹ ] In those studies it was assumed that the sulfide was replaced by the binding of N₂. That replacement has previously been found in our studies to be very endergonic and therefore not possible. ^[5a] Instead, we suggest here that the sulfide is reduced away in A₄. N₂ can still not bind and be activated at this stage. In the position between Fe4 and Fe5, there is a bridging hydride that binds strongly and compensates for the loss of the bridging sulfide. To release the S2B or S5 A sulfides in the other belt positions would require that the bridging hydride is moved to those positions. That is possible for S2B but leads to a barrier which is higher by +5.3 kcal mol⁻¹ than the one for the loss of S3 A described above. The structure of the TS is shown in Figure S2. To release the S5 A sulfide is less favorable energetically as the binding of a hydride between Fe3 and Fe7 is significantly higher in energy than for the other positions.

It is interesting to compare the present scenario in A₄, with the one suggested in our previous studies. In those studies it was instead found to be energetically possible to protonate the carbide. With the lack of experimental information at that time, the loss of a sulfide was never considered. Even though the protonation of the carbide is possible, both thermodynamically and kinetically, it is shown here that the barrier for the loss of a sulfide is much lower than the ones for protonating the carbide, as discussed above. To clarify further, to protonate the carbide would have to be preceded by the loss of the sulfide since the barrier is lower, and the barrier to protonate the carbide after that loss requires going back +12.3 kcal mol⁻¹ before the carbide protonation, leading to a total barrier of +28.6 kcal mol⁻¹, which therefore becomes prohibitive.

In order to test the accuracy of the calculations, the barrier was recalculated by varying the fraction of exact exchange which has been shown to be the by far most sensitive parameter for the present type of systems.[ ¹⁰ , ¹² ] For the case of the barrier for the H₂S loss, the variation is rather small with 0.4 kcal mol⁻¹ for each percent. For the exergonicity the variation is also small with 0.2 kcal mol⁻¹.

The E₀ and E₁ states

The first state in the catalytic cycle is E₀, which is reached after the loss of S3 A in A₄, as described above. Because A₄ has one bridging hydride and three protonated sulfides, E₀ still has the bridging hydride between Fe4 and Fe5, but only one protonated sulfide, the one on S2B bridging between Fe2 and Fe6. This means that there will be many sulfide sites for further protonations, required for the reductions in the subsequent E‐states. It was found in our previous studies that every reduction is accompanied by a protonation, in order not to change the charge of the FeMoco cofactor. The effect of the loss of H₂S has a similarity to our previous suggestion with a protonated carbide, which also allowed many remaining sulfide sites for the subsequent protonations, as three protons were placed on the carbide. The present E₀ state is a doublet, with the quartet +14.3 kcal mol⁻¹ higher in energy (lacvp*). In contrast, the A₀ state is a quartet in agreement with experiments.

Many sulfide sites were investigated for the best protonation in the first reduction to E₁. One more hydride was also tried, but the energy was too high. The best protonation was found for the S5 A belt sulfide. The structure is shown in Figure 3. In E₁ there are now two protonated sulfides, the ones on S2B and S5 A. The oxidation state has six Fe^II and one Fe^III and the spin state is a triplet. The spin populations on the irons vary between 3.3 and 3.6. Fe4 has the lowest spin and Fe1 the highest one. The exergonicity of the E₀ to E₁ transition is −6.3 kcal mol⁻¹, which is enough for allowing the catalysis to avoid losses. Every transition should have an exergonicity of at least −3.0 kcal mol⁻¹ to secure turnover. The exergonicity is hardly changed by varying the fraction of exact exchange.

Figure 3.

The core structure for the E₁ state.

The E₂ state

In the next reduction, the E₂ state is reached. The lowest energy is obtained when another hydride is added in between Fe1, Fe2 and Fe4. At the same time, S5 A becomes deprotonated and S1 A protonated. There are two alternative structures with almost the same energy. In the first one, the carbide remains unprotonated (Figure 4). In that structure, there are five Fe^II and two Fe^III irons. The lowest spin‐population is found on Fe5 with 3.3. All the other irons have spins between 3.5 and 3.6. The spin on the carbide is 0.05. In the second structure, which is only +0.2 kcal mol⁻¹ higher, the bridging hydride between Fe4 and Fe5 has moved to the carbide in a redox step (Figure 5). In that structure all irons are Fe^II. The spin populations vary between 3.5 and 3.6. The spin on the carbide is 0.15. A TS between these structures has been obtained and the barrier for the redox transition was found to be +19.3 kcal mol⁻¹. The C−H distance in the TS is 1.66 Å. The protonation of S1 A makes it rather easy to move, which is of importance in the later E‐states. The exergonicity of the E₁ to E₂ transition is −9.5 kcal mol⁻¹. The dependence on the fraction of exact exchange is 0.5 kcal mol⁻¹ for every percent. Our findings for the E₂ state is interesting in relation to EPR studies that showed two E₂ states close in energy. ^[22] It is tempting to suggest that the states observed are the ones shown in Figures 4 and 5. However, the two states observed were assigned as quartets while the present states are doublets. For the structure in Figure 5, the quartet state is more than 10 kcal mol⁻¹ higher, but for the structure in Figure 4, it is only 5 kcal mol⁻¹ higher, which means that a quartet state cannot be definitely ruled out since the sensitivity to exact exchange is rather high.

Figure 4.

The core structure for the first E₂ state. There are two hydrides, one bridging Fe4 and Fe5, the other one in the Fe1, 2, 4 region. The carbide is unprotonated.

Figure 5.

The core structure for the second E₂ state. The carbide is protonated. There is one hydride in the Fe1, 2, 4 region.

The E₃ state

The next reduction leads to the E₃ state. The E₃ structure in Figure 6 is very similar to the one of the first E₂ state in Figure 4. All that is required is a protonation on S5 A. Therefore, a reasonable conclusion is that the second E₂ structure in Figure 5 never enters into the mechanism, and the carbide remains unprotonated all the way to the E₃ state.

Figure 6.

The core structure for the best E₃ state. One hydride is bridging Fe4 and Fe5, the other one is in the Fe1, 2, 4 region.

In E_3, there are two bridging hydrides and three protonated sulfides, S1 A, S2B and S5 A. The hydride distances to the three irons are 1.92, 1.83 and 1.96 Å. The protonated S1 A has moved towards a terminal position on Fe4. There are now six Fe^II and one Fe^III. The spins on six of the irons are rather close in the range 3.4–3.6. The spin is lower on Fe2 with only 3.2, probably because of the short distance of 1.83 Å to the hydride. There is a small spin of 0.20 on the carbide. There are two low‐lying states just as for the E₂ state, discussed above. The lowest energy is found for the one in Figure 6, with two hydrides and an unprotonated carbide. The E₂ to E₃ transition is exergonic by −5.1 kcal mol⁻¹. The structure with one hydride and a protonated carbide (E₃‐CH, Figure S3) is +7.2 kcal mol⁻¹ higher in energy. However, it is that structure that is able to proceed to the E₄ state, see below. A TS for the redox transition between the two structures has been located, E₃‐TS (Figure S4) with a barrier of +17.9 kcal mol⁻¹, counted from the unprotonated carbide structure. The C−H distance in E₃‐TS is 1.69 Å. The two states are in thermal equilibrium during catalysis, which occurs on the time‐scale of a second. Varying the fraction of exact exchange has rather small effects, for the barrier of only 0.3 kcal mol⁻¹ for each percent and for the energy difference between the two states of 0.5 kcal mol⁻¹.

The E₄ state

It is known from experiments that a formation of H₂ from two hydrides is necessary for nitrogen activation,[ ^4b , ^5b ] see below. For that reason, a broad investigation was performed to find a region where two hydrides could come close to each other and form H₂. That investigation was made before the reactions in E₄ were studied, actually before many of the results described above were obtained. The hydrides were randomly moved around on the cofactor, without considering the pathways for the hydrides. The best possibility to form H₂ from two hydrides was found in the Fe1, 2, 4 region. That is the region in which a hydride became bound in E₂, as described above. A major surprising finding in all of our studies has been that if the hydride is placed in the wrong region, the barriers are prohibitively large to reach the active region. In other words, it is important that the energetically best position for the hydride is in that region in E₂, otherwise the hydride will be bound in a region where H₂ cannot be formed from two hydrides.

There are two possibilities to reach an E₄ state from E₃. The first one is to add an (H⁺, e⁻) to the ground state of E₃ with an unprotonated carbide. The second one is to add an (H⁺, e⁻) to the E₃ state with a protonated carbide. The two E₃ states are in thermal equilibrium, so both are possible starting points for the reduction. It turns out that the second possibility is strongly preferred by −8.5 kcal mol⁻¹. Adding the proton as a hydride is very unfavorable in the case of the E₃ state with an unprotonated carbide, since there are already two hydrides in that E₃. Therefore, the best position for the proton in that case is on S4 A, which is not a belt sulfide, since those are already protonated. There are two problems with the protonation of S4 A. The first one is the poor proton binding energy (pK _a). The second one is even more problematic. S4 A is close to the active region for H−H bond formation, where the two hydrides should eventually be. That would imply a big danger for forming an unproductive H₂, from the proton on S4 A and one of the hydrides. If that happens, catalysis would just go back to E₂, and not proceed to nitrogen activation.

For the second possibility with a protonated carbide, the best position for the added proton is a hydride bridging between Fe1 and Fe4 (Figure 7). It can reach that position directly from the medium, just as for the case of the first hydride, which enters in E₂. In that structure, there are three protons bound to the belt sulfides. The fourth proton is bound to the carbide, as described above. In that position the proton is well hidden from the hydrides with high barriers, and cannot form any unproductive H₂. Still, there are three protons bound to the belt sulfides, but those positions are the best ones for avoiding unproductive H₂ formation, as they are rather far from the two hydrides and also since those sulfides have the highest pK _a values and the protons are difficult to move. The structure with a protonated carbide is better than the other one by −8.5 kcal mol⁻¹. The E₃ to E₄ transition is exergonic by −13.2 kcal mol⁻¹. It turns out that this value has the largest uncertainty of the results reported here with a variation of 1.6 kcal mol⁻¹ for each percent of exact exchange. However, the exact value is of limited importance for the mechanism. The results for 10, 15 and 20 % agree that the E₃ to E₄ transition is exergonic by more than 5 kcal mol⁻¹.

Figure 7.

The core structure for the E₄ state. One hydride is bridging Fe1 and Fe4, the other one is in the Fe1, 2, 4 region. The carbide is protonated.

The next step in the nitrogenase mechanism is to form H₂ from the two bridging hydrides. One hydride is bound in the Fe1, 2, 4 region, which is the position taken already in E₂. The second one is bridging between Fe1 and Fe4. Moving the hydrides closer to each other, in a linear search, led to very high barriers. A detailed analysis was therefore needed. Comparing the best E₄ structure with the best one obtained when H₂ has been released, see below, showed that a significant structural change of the cluster would be needed to reach the desired product. The most important structural change found concern the distance between Fe4 and S4 A, which is 4.12 Å for the E₄ reactant, but only 2.32 Å after the release of H₂. Another one is the distance between Fe1 and S2 A, which changes from 4.48 to 2.38 Å. Finally, the distance between Fe7 and S5 A changes from 2.50 to 4.50 Å, but that one is not very energy sensitive. A problem in finding the TS was that these distances are not strongly coupled. Taking any one of them as a single reaction coordinate did not lead to the region of the TS. At the end, the four distances, H−H, Fe4−S4 A, Fe1−S2 A and Fe7−S5 A, were changed together in a four‐dimensional grid. A plausible region for a TS was eventually found that way. A Hessian was calculated with that starting point, and could be used to fully converge a TS (Figure 8). At the TS, the H−H distance is 2.16 Å, the Fe4−S4 A distance 2.85 Å, the Fe1−S2 A distance 3.02 Å, and the Fe7−S5 A distance 3.77 Å. The hydrogens forming H₂ have short distances of 1.74 and 1.93 Å to Fe4, and one of them a distance of 1.79 Å to Fe2. The computed barrier for H₂ formation is +18.2 kcal mol⁻¹. The imaginary frequency at the TS of 82 i cm⁻¹ is unusually low for a formation of H₂ because the frequency also involves several sulfide movements. To make certain that the structure obtained is indeed a TS for H−H bond formation, energies were calculated by going with small steps of H−H in both directions from the TS, and the energy was found to go down in both directions. There are significant effects from dispersion and solvation, raising the barrier. The dispersion effect of +4.0 kcal mol⁻¹ is expected because the cluster has to open up in order for the hydrides to approach each other. The solvation effect is +3.4 kcal mol⁻¹. Together the effects change H−H formation from being very fast in less than a millisecond to one that approaches a second. However, the reaction is still possible at the time scale of catalysis. In this context, it can be noted that barriers of this type are always overestimated by a few kcal mol⁻¹ using the present methods. That could be due to increasing multireference effects at higher energies.

Figure 8.

The core structure of the TS for H₂ formation in the E₄ state (E₄‐TS). The carbide is protonated.

In order to test the accuracy of the calculations, the barrier was recalculated with a fraction of exact exchange of 10 and 20 %, just as for the case of the barrier for losing a sulfide in A₄. The barrier in the case for H−H formation in E₄ is quite insensitive to this fraction. The variation is linear, as usual, with a change of only 0.2 kcal mol⁻¹ for each percent. The barrier should therefore be quite accurate.

After the E₄‐TS in Figure 8, H₂ is released and the structure in Figure 9 is obtained. The critical distances in the E₄‐TS have now changed dramatically as described above. All structures in the mechanism previous to the one in Figure 9, were done with the spin‐coupling (+−−−+++). However, after the large structural change when H₂ is formed and released, the optimal spin‐coupling changes to (−+−−+++).The energy gain by the shift of spin‐coupling is −3.5 kcal mol⁻¹. That difference is not large, but is consistent with the small differences found for the other structures in the mechanism, for which (+−−−+++) instead was found to be slightly superior. After the release of H₂, there are two Fe^I and five Fe^II. The smallest spins are found on Fe4 and Fe7 with about 3.2, indicating the most Fe^I character. Releasing H₂ leads to a large gain of entropy, here estimated to be −9.3 kcal mol⁻¹. Without that gain, the release would be strongly endergonic but with it, the release is almost thermoneutral, here calculated to be slightly endergonic by +0.9 kcal mol⁻¹ counted from the energy for the best E₄ state in Figure 7. This result is consistent with the experimental finding that the release of H₂ and the binding of N₂ are reversible and pressure dependent. ^[4b] It should be added that in all of our investigations so far, the binding of N₂ has been found to be at most very weak in E₄, see further below.

Figure 9.

The core structure after the release of H₂ in the E₄ state (E₄‐H₂).

For the release of H₂, the exergonicity is rather sensitive to the fraction of exact exchange. The variation is linear with 2.8 kcal mol⁻¹ for every percent. The accuracy for the exergonicity is therefore much lower than for the barrier of H₂ formation. This may not be so surprising since much more happens when the hydrides are released. For 15 %, the release of H₂ is endergonic by +0.9 kcal mol⁻¹, while for 10 % it is exergonic by −5.2 kcal mol⁻¹ and for 20 % endergonic by +7.2 kcal mol⁻¹. As usual, the result for 15 % appears to be most in line with the experimental results.

In the process of the H₂ loss, N₂ binds. Many possible sites for N₂ binding were investigated and the lowest energy was found for an end on binding of N₂ on Fe4, which after the loss of H₂, is one of the two irons with most Fe^I character. Another reason Fe4 binds N₂ best is that it leads to the smallest steric strain. The Fe4−N₂ distance is 1.91 Å, and the N−N distance 1.13 Å. An important structural change as N₂ binds is that Fe4 sticks out from the cluster. The distance between Fe4 and Fe3 trans to N₂ increases by 0.5 Å. The structure is shown in Figure 10. The only other iron site that shows some activation of N₂ is Fe2 with an Fe−N₂ distance of 2.1 Å, but the energy is much higher than for the one on Fe4. Trying to bind N₂ to Fe1, Fe6 and Fe7, gave essentially no activation of N₂ with long distances to the irons of 2.3 Å. The result for Fe7 is interesting since that iron has about the same Fe^I character as Fe4, but the steric strain is larger. Some structures with N₂H₂ were also tried, but the energies were high. In the recent experiments, ^[6e] a bridging N₂ was found, suggested to replace a sulfide. In our previous study, ^[5a] we showed that such a replacement is very endergonic. Structures with bridging N₂ were studied here, but they were found to be much higher in energy than the one in Figure 10. With the presence of two Fe^I, the cofactor is quite electron donating. As a measure of the electron donation, the spin on N₂ on Fe4 is 0.18, with most spin (0.16) on the outer nitrogen. The carbide gets a minor spin of 0.09. In the binding of N₂, there is a large loss of translational entropy of 9.9 kcal mol⁻¹. This means that, even though the computed enthalpic binding of N₂ is rather large with −8.5 kcal mol⁻¹, the binding becomes endergonic with +1.4 kcal mol⁻¹. The overall reaction energy when H₂ is lost and N₂ binds is therefore +2.3 kcal mol⁻¹, which is in very good agreement with experiments, indicating an energy difference of about zero. For a fraction of exact exchange of 10 %, the reaction is exergonic by −4.1 kcal mol⁻¹ and for 20 % it is endergonic by +8.6 kcal mol⁻¹. Again, the result with 15 % shows the best agreement with experiments.

Figure 10.

The core structure for the E₄ state with a bound N₂ (E₄‐H₂+N₂).

The energies calculated for the nitrogenase mechanism can finally be described in a diagram. The early transitions from A₄ to E₃ are shown in Figure 11, the later ones from E₃ to the binding of N₂ in Figure 12. The requirement that all E‐transitions are exergonic is fulfilled. E₀ to E₁ is exergonic by −6.3 kcal mol⁻¹, the one from E₁ to E₂ by −9.5 kcal mol⁻¹, the one from E₂ to E₃ by −5.1 kcal mol⁻¹, and the one from E₃ to E₄ by −13.2 kcal mol⁻¹. The first three steps in the activation of the cofactor are also exergonic as shown in our previous study, with −12.3 kcal mol⁻¹ for A₀ to A₁, with −10.0 kcal mol⁻¹ from A₁ to A₂, and with −7.6 kcal mol⁻¹ from A₂ to A₃. ^[5b] With the finding of a better A₄ in this study, the A₃ to A₄ transition is also exergonic, by −3.4 kcal mol⁻¹. In A₄ there is an exergonic release of H₂S by −12.3 kcal mol⁻¹. The barrier for the release is +7.2 kcal mol⁻¹. The formation of the protonated carbide in E_3, which is necessary before the E₃ to E₄ transition, has a barrier of +17.9 kcal mol⁻¹ and is endergonic by +7.2 kcal mol⁻¹. The barrier for formation of H₂ in E₄ is 18.2 kcal mol⁻¹. The diagrams for 10 % and 20 % exact exchange are given in the Supporting Information.

Figure 11.

The energetics for the first part of the present mechanism for nitrogenase.

Figure 12.

The energetics for the second part of the present mechanism for nitrogenase.

It is interesting to compare the energetics for moving the hydride in this case, where a sulfide is lost from the cluster, to the one in the previous study without that loss. In the previous case, moving the hydrides was found to be easy with small barriers, whereas in this case there are very high barriers. It is clear that the bridging hydrides play a different role when the sulfide is lost. They are evidently important for the stability of the cluster. Already when the sulfide was lost in A₄, it was found to be very important that the hydride takes the bridging position of the lost sulfide to keep the cluster stable and the energy low.

Conclusions

In this study, the mechanism of nitrogenase has been reinvestigated for the case in which a sulfide is lost from the cofactor. There are several recent experimental studies that have indicated that the cofactor should be very flexible, and a sulfide might be lost in the process.[ ^6a , ^6c , ^6d , ^6e ] In all those studies, and also in some theoretical ones,[ ^6b , ²¹ ] it has been assumed that the binding of N₂ causes the loss of the sulfide. That scenario was already tested in our first study of the mechanism, and it was concluded to be quite impossible, leading to a very endergonic step. ^[5a] N₂ is much too weakly bound to force the loss of a sulfide. For the case of binding CO, the situation is quite different. CO is much more strongly bound than N₂ and is actually able to push away a sulfide in a nearly thermoneutral step, in agreement with experimental findings. ^[6a] In the reinvestigation of the mechanism, the experimental suggestions of the loss of a sulfide is combined with our previous findings that catalysis should be preceded by four reduction steps, A₀ to A_4. The reason for the necessary extra activation steps is that a structure in which the oxidation state of all iron atoms is no higher than Fe^II was found to be needed to activate N₂. In the experimentally suggested mechanism, four Fe^III atoms are present. That state is much more oxidized than the P cluster, and it would be very surprising if it could activate N₂. It has been found here that after the four activation steps, in A₄ a sulfide is indeed very weakly bound and can be released in a rather strongly exergonic step, estimated to be −12.3 kcal mol⁻¹. The barrier for the release was found to be very low at only +7.2 kcal mol⁻¹. Therefore, it is hard to imagine that the sulfide would not be lost in A₄. That finding rules out our previous suggestion that the carbide should be protonated three times in A₄. The present conclusion is made because the barrier for the protonation of the carbide is much higher than the barrier for losing a sulfide.

After the loss of the sulfide, the E‐steps of catalysis begin. The cofactor now behaves very differently from before. For example, in the previous studies it was found that the hydrides, which are of key importance for the mechanism, ^[4b] were very easy to move around on the cofactor. After the sulfide loss, the hydrides become an important part of the stability of the cofactor and can hardly move. In A₄, where the release of the sulfide occurs, the presence of a hydride is very important for replacing the lost sulfide. Therefore, the loss of the sulfide cannot occur before A₄, as no hydrides are then present. ^[5b]

The positioning of the hydride in A₄ becomes very important, because the hydride cannot easily move to another position after the sulfide loss. The lowest‐energy position was found to be bridging between Fe4 and Fe5. As it turns out, that hydride is not one of the hydrides that will form H₂. Instead, the hydride is ideally placed to move to the carbide in the E₃ to E₄ transition.

By randomly scanning hydride positions in E₄, it was found that H₂ should energetically best be formed in the Fe1, 2, 4 region. The first of these hydrides becomes bound in E₂ in the middle of the Fe1, 2, 4 region. Again, that is the position that is energetically best at that stage, and the hydride does not need to move to another place later in the process. The second hydride that should form H₂ becomes bound in the E₃ to E₄ transition. It cannot be bound directly in the Fe1, 2, 4 region, but the energetically best position is rather close to that region, bridging between Fe1 and Fe4. At the same time as the second hydride becomes bound, the bridging hydride from A₄ between Fe4 and Fe5 moves to the carbide. The three positions for the other protons are all on belt sulfides, which are the best ones energetically. In that way, loosely bound protons, which could otherwise form H₂ with a hydride, are avoided as much as possible. That kind of H₂ formation would otherwise just lead back to E₂ from E₄, and no activation of N₂ would occur.

The transition state for H₂ formation was very difficult to locate. Rather than the usual one‐ or sometimes two‐dimensional search to locate the region of the TS, a four‐dimensional search was needed. Besides the H−H distance, there are three Fe−S distances that change dramatically as the TS region is reached. Once the TS region had been found, a Hessian could be constructed that led to the final fully optimized TS. The barrier was found to be +18.2 kcal mol⁻¹, which is high, but not too high. The H₂ release is endergonic by +0.9 kcal mol⁻¹.

After the loss of H₂, the cofactor has two Fe^I atoms, and the cluster is able to donate electrons to N₂. The enthalpic binding of N₂ is fairly large at −8.5 kcal mol⁻¹, but with a loss in entropy of +9.9 kcal mol⁻¹, the binding becomes endergonic by +1.4 kcal mol⁻¹. Experimentally, the combined loss of H₂ and binding of N₂ is easily reversible and pressure dependent. Therefore, the present results for this critical step with an endergonicity of +2.3 kcal mol⁻¹ is in very good agreement with experiments.

Supporting Information

Coordinates for all structures and energy diagrams for 10 and 20 % are given as Supporting Information.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

W.-J. Wei, P. E. M. Siegbahn, Chem. Eur. J. 2022, 28, e202103745.

Data Availability Statement

The data that support the findings of this study are available in the supplementary material of this article.