Significance
The mechanosensitive ion channel Piezo1 plays many important physiological functions. This essential ion channel is selectively activated by a synthetic small molecule called Yoda1. Despite current efforts to develop Yoda1 analogs with potential clinical value, the nature and extent of Piezo1 functions modulated by Yoda1 remain unknown. Here we performed a comprehensive biophysical characterization of the effects of Yoda1 and of its antagonist analog Dooku1. We show that Yoda1 activates Piezo1 by energetically stabilizing and destabilizing conducting and nonconducting Piezo1 conformations, respectively. We further discovered that the electrophysiological effects of Yoda1 strongly depend on membrane potential and temperature, two known physiological Piezo1 modulators. Our study illuminates the complexity by which Piezo1 integrates physical and chemical cues.
Keywords: mechanotransduction, Piezo1, Yoda1, temperature, membrane potential
Abstract
Piezo1 channels are essential mechanically activated ion channels in vertebrates. Their selective activation by the synthetic chemical activator Yoda1 opened new avenues to probe their gating mechanisms and develop novel pharmaceuticals. Yet, the nature and extent of Piezo1 functions modulated by this small molecule remain unclear. Here we close this gap by conducting a comprehensive biophysical investigation of the effects of Yoda1 on mouse Piezo1 in mammalian cells. Using calcium imaging, we first show that cysteine bridges known to inhibit mechanically evoked Piezo1 currents also inhibit activation by Yoda1, suggesting Yoda1 acts by energetically modulating mechanosensory domains. The presence of Yoda1 alters single-channel dwell times and macroscopic kinetics consistent with a dual and reciprocal energetic modulation of open and shut states. Critically, we further discovered that the electrophysiological effects of Yoda1 depend on membrane potential and temperature, two other Piezo1 modulators. This work illuminates a complex interplay between physical and chemical modulators of Piezo1 channels.
All living organisms must rapidly adapt to mechanical stress for their survival (1). Rapid transduction of mechanical stress into cellular signals is mainly achieved by mechanosensitive ion channels (MSCs). In eukaryotes, a large diversity of phylogenetically and structurally unrelated families of MSCs have been identified, including two-pore domain potassium channels (2), transient receptor potential channels (3), OSCA/TMEM63 channels (4), transmembrane-like channels (TMC) (5), and Piezo channels (6). Such a molecular diversity of eukaryotic MSCs suggests the existence of a comparable diversity of molecular mechanisms by which these proteins detect mechanical stimuli (7).
Piezo channels play important mechanotransduction functions in plants (8, 9), insects (10–12), and nematodes (13, 14). In vertebrates, two homologs named Piezo1 and Piezo2 participate in an astonishing diversity of physiological functions, including cell volume homeostasis (15), somatosensation (16, 17), vascular and lymphatic functions (7, 18), and proprioception (19). Piezo1 and Piezo2 share a large homotrimeric structure harboring a central cation-selective fenestrated pore topped by an extracellular cap domain (20–26). Their central pore region is surrounded by three curved transmembrane peripheral domains called blades, giving these channels an overall bowl-like shape anticipated to curve the surrounding lipid bilayer (27). A growing amount of evidence suggests that the curved Piezo blades act as elastic mechanotransduction domains sensitive to local membrane deformations (20, 28–34).
Beside mechanical stimuli, Piezo1 is selectively activated by Yoda1, a synthetic small molecule identified from high-throughput screening (35). Yoda1 has no modulatory effects on Piezo2 (35), making it an ideal tool to probe Piezo homolog-specific functions (15, 36–48). Despite the identification and characterization of novel Piezo1 activators (49) and Yoda1 analogs (50), Yoda1 remains the most potent Piezo1-selective modulator, making it a promising molecule to expand the currently limited Piezo channel pharmacome.
Electrophysiological assays in which mechanical stimuli are delivered through patch pipette pressurization or cellular indentations revealed that the presence of Yoda1 correlates with slower inactivation kinetics and with a shift of the peak ionic current vs. pipette pressure (I/P curve) toward lower pressure values (35, 49, 51). These effects are consistent with that of a so-called gating modulator, a molecular paradigm in which Yoda1 increases Piezo1’s sensitivity to mechanical stimuli. This pharmacological mechanism is supported by experimental and computational evidence for the existence of a Yoda1 binding site located in the putative mechanosensory blade domain (26, 49). Such a direct interaction between Yoda1 and Piezo1 is further consistent with bilayer electrophysiology experiments showing Yoda1 robustly activates Piezo1 channels reconstituted into symmetric bilayers in absence of other cellular factors (35). Unfortunately, since reconstituted Piezo1 channels did not open in absence of Yoda1, a comparative dwell time analysis could not be done to evaluate the energetic effects of Yoda1 on Piezo1 (35).
In this study, we first show that the effects of Yoda1 require protein motions associated with mechanical gating, consistent with the prevailing notion that Yoda1 acts as a gating modulator. We next perform a comprehensive electrophysiological characterization of the effects of Yoda1. We used single-channel dwell time analysis to show that Yoda1 increases open probability by both extending open dwell times and shortening nonconducting (shut) dwell times. Interestingly, the nonactive Yoda1 analog Dooku1 alters single-channel dwell times without affecting open probability, consistent with Dooku1 being unable to activate Piezo1 while being able to antagonize the effects of Yoda1 (50). Using macroscopic recordings, we show that Yoda1 slows down deactivation and inactivation kinetics and accelerates the rate of recovery from inactivation, whereas Dooku1 has no significant effects on macroscopic channel kinetics. We further discovered that the electrophysiological effects of Yoda1 are maximal at room temperature and negative voltages, dwindling near mammalian body temperature or upon depolarized potentials.
Results
Gating Motions Are Necessary for Piezo1 Activation with Yoda1.
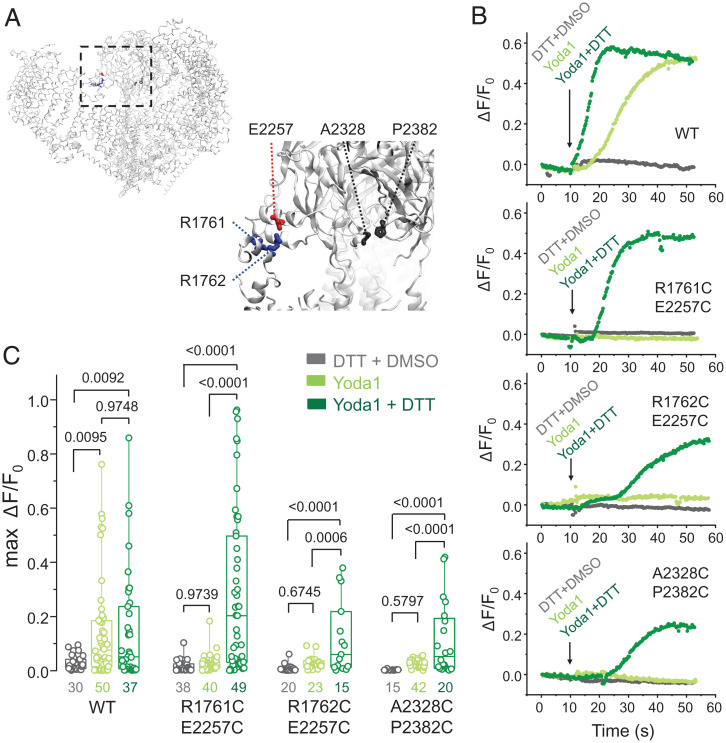
One way to test whether Yoda1 acts as a gating modulator is to test whether Yoda1 maintains its effects when the gating machinery of the channel is stalled. This test is feasible, thanks to an elegant study by Lewis and Grandl (52) showing that mechanically evoked currents in mouse Piezo1 (mPiezo1) are reversibly inhibited by the formation of intersubunit disulfide bridges within the cap (mPiezo1 residues A2328C/P2382C) or between the cap and blade (mPiezo1 residues E2257C/R1762C and E2257C/R1761C) (Fig. 1A).
Fig. 1.
Gating motions are required for Yoda1-mediated mPiezo1 activation. (A) mPiezo1 structure (Protein Data Bank ID 6B3R) highlighting the positions of cysteine substitutions reported by Lewis and Grandl (52) (R1761C, R1762C, E2257C, A2328C, and P2382C). (B) Representative calcium-dependent fluorescence time courses from individual cells expressing double cysteine mutants or WT mPiezo1 in response to acute incubation with a saline solution containing 100 µM Yoda1 and supplemented or not with 25 mM DTT (DMSO was kept at 1% in all experiments). (C) Maximal amplitude of calcium-dependent fluorescence changes (max ΔF/F0) from experiments illustrated in B. Numbers below box plots represent the number of independent cells measured from a minimum of 8 to 12 culture wells. Numbers above box plots indicate exact P values from one-way ANOVA and post hoc Tukey multiple comparisons tests. Boxes indicate first and third quartiles, and horizontal lines indicate medians.
To test whether these inhibitory disulfide bridges also inhibit the effects of Yoda1, we transfected Piezo1-deficient HEK293TΔPZ1 cells (53) with a plasmid encoding wild-type (WT) mPiezo1 or one of aforementioned double cysteine mutants and with a second plasmid encoding a calcium indicator. Fig. 1B shows exemplar time courses of relative fluorescence change (ΔF/F0) in transfected cells acutely exposed to 100 µM Yoda1, Yoda1 + 25 mM 1,4-dithiothreitol (DTT), or 25 mM DTT + 1% DMSO as vehicle control. As expected, cells expressing WT mPiezo1 exhibit robust calcium signals in both presence and absence of DTT, whereas our DTT + DMSO control treatment failed to elicit calcium responses in any tested channel construct. Interestingly, cells expressing any double cysteine mutants respond to Yoda1 but only in the presence of DTT.
For each transfection condition, we tested whether the maximal calcium responses (max ΔF/F0) significantly differ as a function of acute treatment using one-way ANOVA and post hoc Tukey multiple comparisons tests. For WT mPiezo1, calcium responses were significantly larger when Yoda1 was present (P ≤ 0.0095), regardless of the presence of DTT (P = 0.9748) (Fig. 1C). In all mutants, Yoda1 failed to elicit calcium responses in absence (P = 0.9739 for R1761C/E2257C; P = 0.6745 for R1762C/E2257C; P = 0.5797 for A2328C/P2382C) but not in the presence (P ≤ 0.0006) of DTT. Thus, experimental manipulations that inhibit the gating machinery of Piezo1 fully inhibit the effects of Yoda1. These data provide a line of evidence suggesting that Yoda1 acts as a gating modulator of Piezo1.
Modulation of Piezo1 Single-Channel Dwell Times by Yoda1.
If Yoda1 energetically modulates the gating machinery of mPiezo1, what are these modulations? To answer this question, we used cell-attached single-channel recordings, the ultimate approach to measure energetic parameters of ion channels in the physiological context of living cells. We transfected HEK293TΔPZ1 cells with a plasmid encoding WT mPiezo1 and patched these cells with pipettes filled with physiological solutions containing 30 µM Yoda1 [a concentration above the EC50 measured from calcium imaging (35)], 30 µM of the nonactive analog Dooku1 [a concentration above the reported IC50 for Dooku1 to antagonize the effects of Yoda1 (50)], or with 0.3% DMSO as a vehicle control.
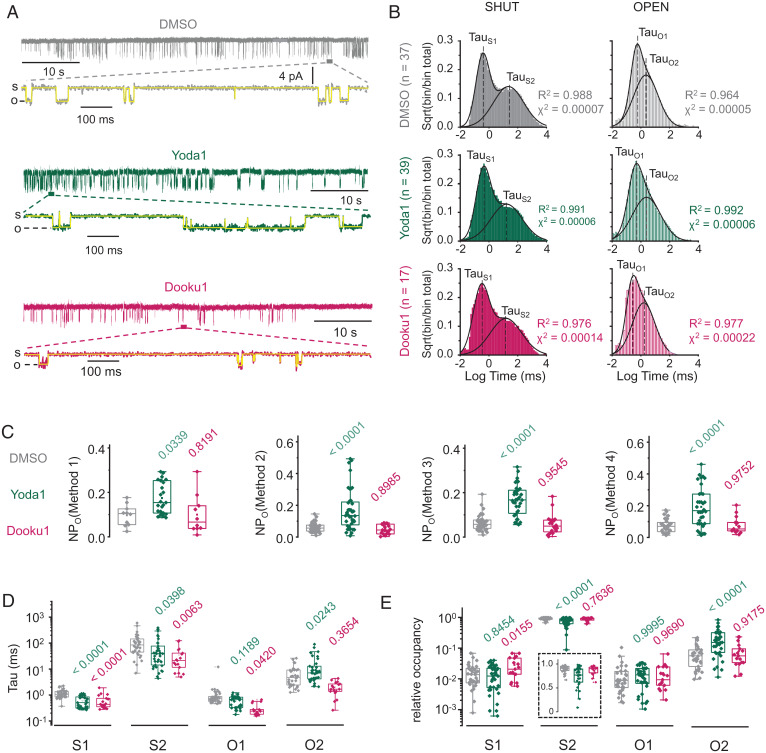
To increase sampling of open events, we applied a constant pipette pressure of −40 mm Hg to stimulate mPiezo1 via membrane stretch (30, 32). We clamped the membrane potential at −90 mV to increase the amplitude of unitary channel currents, facilitating the detection of discrete open and shut events. For our analysis, we only used current traces displaying no more than two current levels (open and shut) for at least 1 min because those traces are more likely to correspond to patches having a single functional channel (Fig. 2A).
Fig. 2.
Modulation of single-channel dwell times by Yoda1 and Dooku1. (A) Exemplar 60-s single-channel current traces of mPiezo1 expressed in HEK293TΔPZ1 cells in the presence of 0.3% DMSO (gray), 30 µM Yoda1 (green), or 30 µM Dooku1 (fuchsia) in the patch pipette (temperature, 23 °C; V = −90 mV; s, shut; o, open). A 1-s expanded view is shown below each trace with pClamp time series idealization (yellow). (B) Aggregated dwell time distribution for open and shut states and for each experimental group (DMSO, n = 37; Yoda1, n = 39; Dooku1, n = 17). Lines are Gaussian fits to the data. (C) Scatter box plot comparison of NPo calculated with the indicated method (Materials and Methods) for three experimental groups (DMSO, 32 ≤ n ≤ 36; Yoda1, 34 ≤ n ≤ 40; Dooku1, 13 ≤ n ≤ 20). (D) Scatter box plot comparison of Tau values obtained for each state (DMSO, 35 ≤ n ≤ 37; Yoda1, 38 ≤ n ≤ 39; Dooku1, n = 17). (E) Scatter box plot comparison of relative occupancy for each state (DMSO, 34 ≤ n ≤ 35; Yoda1, 38 ≤ n ≤ 39; Dooku1, n = 17). Numbers above plots in C–E indicate P values from one-way ANOVA with Dunnett’s multiple comparisons post hoc tests (green, DMSO vs. Yoda1; fuchsia, DMSO vs. Dooku1). Boxes indicate first and third quartiles, and horizontal lines indicate medians. Temperature is clamped at 23 °C for all recordings.
Open and shut dwell times were extracted by performing standard time series idealization in pClamp, refined by automated selection/rejection of open/shut events in MATLAB (Materials and Methods). We first tested whether our dataset was adequately sized for meaningful statistical analysis. To this aim, we first aggregated all binned dwell time data obtained from independent patches (DMSO, n = 37 patches/81,268 total events; Yoda1, n = 39 patches/169,180 total events; Dooku1, n = 17 patches/98,897 total events) and plotted the square root of frequency-normalized events as a function of binned log-transformed dwell times, a common representation that equalizes bin count variance across logarithmic time scale and transforms individual exponential components into clearly identifiable Gaussian peaks (54).
Aggregated histograms display bigaussian distributions, defining two identifiable populations (short-lived and long-lived) for both open and shut events (Fig. 2B). Similar dwell time distributions were previously reported from cell-attached and bilayer recordings (35, 55). In each experimental group, a Gaussian probability density function accurately recapitulates the bimodal dwell time distribution for both open and shut states. The temporal coordinate of each fitted Gaussian peak corresponds to a fitted mean dwell time (Tau) for the short-lived open (TauO1), short-lived shut (TauS1), long-lived open (TauO2), and long-lived shut (TauS2) events. The goodness of the fit was demonstrated by coefficient of determination values near unity (0.964 ≤ R2 ≤ 0.992) and low reduced χ2 values (0.00005 ≤ χ2 ≤ 0.00022).
We next calculated the apparent open probability (NPo) for each individual patch using four different methods: 1) by calculating the relative area under the curve from all-point histograms (method 1), 2) by dividing the sum of durations of individual open events by the total record duration (method 2), 3) by dividing the mean open duration by the sum of open and shut mean durations (method 3), and 4) by dividing TauO1 + TauO2 by the sum of all Tau values (method 4) (Materials and Methods).
We then asked whether NPo values change in the presence of Yoda1 or Dooku1 using one-way ANOVA and Dunnett’s multiple comparisons post hoc tests. Regardless of the method used, NPo was twofold to threefold higher in the presence of Yoda1 (0.06 < NPoDMSO < 0.07; 0.14 < NPoYoda1 < 0.19; P ≤ 0.039), consistent with the known agonist property of Yoda1 (Fig. 2C). In contrast, the presence of Dooku1 did not significantly change NPo (0.05 < NPoDMSO < 0.08; 0.8191 ≤ P ≤ 0.9752), consistent with the inability of this Yoda1 analog to activate Piezo1 (50).
We next tested whether the fitted mean dwell time of each microscopic state changes in presence of Yoda1 or Dooku1 using one-way ANOVA and Dunnett’s multiple comparisons post hoc tests. We compared the distribution of individual Tau values calculated for each patch rather than the aggregated Tau values shown in Fig. 2B to better consider experimental variability of event sampling in our statistical analysis (Fig. 2D and SI Appendix, Fig. S1). The presence of Yoda1 correlates with a significant decrease of all shut dwell times (TauS1, P < 0.0001; TauS2, P = 0.0398) and with a significant increase of the long-lived open dwell time (TauO2, P = 0.0243). In contrast, the presence of Dooku1 tends to decrease all dwell times, an effect which was significant for three of them (TauS1, P < 0.0001; TauS2, P = 0.0063; TauO1, P = 0.0420; and TauO2, P = 0.3654). This observation suggests that Dooku1 energetically interacts with Piezo1 but in different ways from Yoda1.
We next calculated the relative occupancy of each single-channel state by dividing the corresponding Tau values by the sum of all Tau values (Fig. 2E). One-way ANOVA with Dunnett’s post hoc tests shows that the presence of Yoda1 1) significantly decreased the relative occupancy of the long-lived shut state from 89.6 ± 1.2% to 74.6 ± 3.2% (P < 0.0001), 2) significantly increased the relative occupancy of the long-lived open state from 7.3 ± 1.0% to 22.5 ± 3.1% (P < 0.0001), and 3) did not significantly change the relative occupancy of short-lived states (0.8454 ≤ P ≤ 0.9995). Interestingly, although Dooku1 decreases Tau values for S1, S2, and O2 states, this effect only increased relative occupancy of the short-lived shut state (P = 0.0155) with no significant changes of relative occupancy for other states (0.7636 ≤ P ≤ 0.9690). Given the small relative occupancy of short-lived states in all our experimental conditions (∼1 to 3%), it is not surprising that Dooku1 does not appreciably change NPo (Fig. 2C).
Markov Chain Modeling.
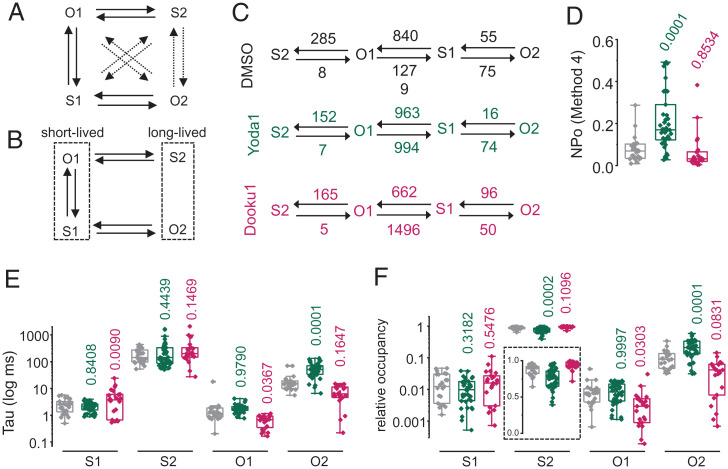
To study how the presence of Yoda1 and Dooku1 affects microscopic single-channel transitions, we performed continuous-time Markov chain modeling using the online program Quantify Unknown Biophysics (QUB) (56, 57). We first verified that the idealization step done by QUB does not distort our idealized single-channel trajectories (SI Appendix, Fig. S2). We then fitted our idealized trajectories using an unconstrained model, authorizing all 12 possible transitions between any two of the four states identified from our dwell time analysis (Fig. 3A).
Fig. 3.
Markov chain modeling of single-channel trajectories at 23 °C. Topological representations for the (A) unconstrained and (B) minimal Markov chain models (dotted arrows indicate near-zero fitted rates). (C) Linear representations of the minimal model showing fitted rate constants obtained from the QUB software for each experimental condition. Numbers indicate fitted rate values (in s−1) rounded to the nearest one. (D) NPo values (calculated using method 4) predicted for each experimental condition. Scatter box plots showing (E) mean dwell time and (F) relative occupancy for each individual idealized trajectory analyzed using the minimal model shown in B. Boxes indicate first and third quartiles, and horizontal lines indicate medians. Numbers above plots indicate P values from one-way ANOVA with Dunnett’s multiple comparisons post hoc tests.
Regardless of experimental treatment (DMSO/Yoda1/Dooku1), this unconstrained model systematically yielded near-zero (∼10−3 to ∼10−13 s−1) forward and reverse rates for the same set of microscopic transitions (O1↔O2, S1↔S2, and S2↔O2), suggesting that these specific transitions are rare enough to be practically ignored. This prompted us to refit our trajectories using a minimal six-parameter model (Fig. 3B). Both models converged satisfactorily, yielding identical or nearly similar log-likelihood, Bayesian information criterion values, and fitted values for the shared rate constants (Table 1 and SI Appendix, Figs. S1 and S2). Regardless of experimental conditions, the most frequent transitions occur between short-lived states (Table 1). According to the model topology, these rapid flickering between short-lived open and shut states may constitute a bursting mode exhibited when channels transit between their long-lived open and shut states (Fig. 3B and C).
Table 1.
Microscopic rate constants fitted using the minimal Markov model
| Transitions | DMSO | Yoda1 | Dooku1 |
|---|---|---|---|
| S1→O1 | 839.6 ± 0.027 | 963.2 ± 0.007 | 662.2 ± 0.031 |
| O1→S1 | 1279 ± 0.02 | 994.1 ± 0.037 | 1496 ± 0.004 |
| S1→O2 | 75.1 ± 0.003 | 74.3 ± 0.002 | 50.2 ± 8.9 × 10−4 |
| O2→S1 | 55.4 ± 6.8 × 10−5 | 16.3 ± 0.001 | 95.5 ± 0.002 |
| S2→O1 | 7.8 ± 1.1 × 10−4 | 7.3 ± 2.4 × 10−4 | 5.1 ± 1 × 10−5 |
| O1→S2 | 285.2 ± 4.4 × 10−4 | 151.6 ± 0.012 | 164.9 ± 3.7 × 10−4 |
Rates are in s−1; errors are SDs.
Markov chain modeling indicates that the largest effect of Yoda1 is a greater than threefold reduction of O2→S1 closure rate (∼16 vs. ∼55 s−1), consistent with increased dwell time for the long open state. Other changes are a reduction of O1→S1 and O1→S2 closure rates and an increase of S1→O1 opening rate (Fig. 3C). These changes are overall consistent with the effects of Yoda1, i.e., increased open probability, increased occupancy of the long-lived open state, and decreased occupancy of the long-lived shut state (Fig. 3D–F). However, the dwell time distribution carried out by the Bayesian-based Markov chain modeling did not exactly match that obtained by Gaussian fitting. In particular, Yoda1 no longer reduces the mean dwell time of the long shut state (Fig. 3E). This discrepancy could be due to differential allocations of single-channel events to specific states by the two different methods.
Markov chain modeling further shows that the presence of Dooku1 alters microscopic rates and dwell times but in a way that does not statistically alter open probability or the mean dwell time and relative occupancy for the long-lived open and shut states, as observed earlier (Fig. 3D–F).
Single-Channel Effects of Yoda1 Decrease at Physiological Temperatures.
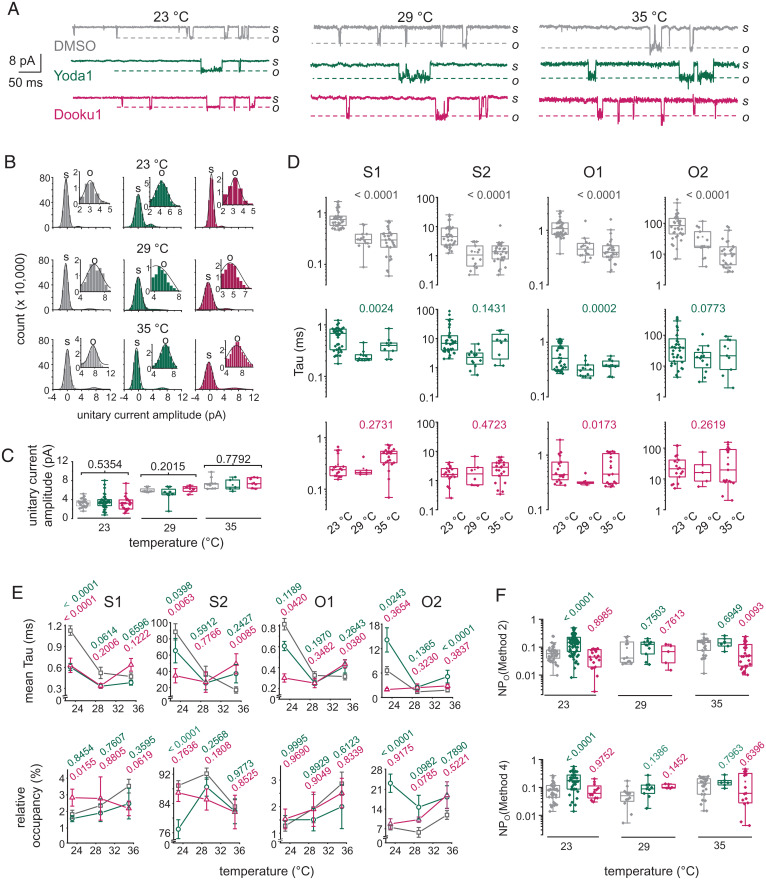
We next wondered whether the microscopic effects of Yoda1 are maintained at temperatures closer to that of mammalian physiology, in part because temperature inherently affects Piezo1 activity (58). To this aim, we performed single-channel measurements at 29 and 35 °C (Figs. 4A and SI Appendix, Figs. S3 and S4). All-point histogram analysis shows that the amplitude of unitary Piezo1 currents gradually increases upon increasing temperature (Fig. 4B and C), a known contributing factor to the thermal modulation of Piezo1 (58). The unitary current amplitude was not affected by the presence of Yoda1 or Dooku1 at any tested temperatures (0.2015 ≤ P ≤ 0.7792).
Fig. 4.
Heating decreases the extent of dwell time modulation by Yoda1. (A) Exemplar single-channel current traces obtained at indicated temperatures in presence of 0.3% DMSO (gray), 30 µM Yoda1 (green), or 30 µM Dooku1 (fuchsia) in the pipette (V = −90 mV; s, shut; o, open). (B) Exemplar all-point current histograms determined between time coordinates 10 and 15 s for current traces obtained at indicated temperatures and pharmacological treatments. (Insets) Open current distributions (s, shut; o, open). Lines are Gaussian fits to the data. (C) Scatter box plot comparison of unitary current amplitude at 23 °C (DMSO, n = 25; Yoda1, n = 36; Dooku1, n = 22), 29 °C (DMSO, n = 8; Yoda1, n = 8; Dooku1, n = 6), and 35 °C (DMSO, n = 10; Yoda1, n = 5; Dooku1, n = 7) calculated from all point histograms. (D) Scatter box plots showing Tau values obtained for each pharmacological treatment, state, and temperature (DMSO23°C, n = 35; DMSO29°C, n = 14; DMSO35°C, n = 29; Yoda123°C, n = 39; Yoda129°C, n = 12; Yoda135°C, n = 9; Dooku123°C, n = 17; Dooku129°C, n = 6; Dooku135°C, n = 21). Number above plots indicate P values from one-way ANOVA. (E) (Top) Mean Tau values from data shown in D plotted relative to temperature for each state. (Bottom) Relative occupancy of each state plotted as a function of temperature. (F) Scatter box plot comparing NPo values obtained using indicated methods for each experimental group and temperature (DMSO/Yoda1/Dooku1 at 23 °C, n = 35/40/19; DMSO/Yoda1/Dooku1 at 29 °C, n = 12/10/5; DMSO/Yoda1/Dooku1 at 35 °C, n = 25/7/30). Numbers above plots in C, E, and F indicate P values from one-way ANOVA with Dunnett’s multiple comparisons post hoc tests (green, DMSO vs. Yoda1; fuchsia, DMSO vs. Dooku1). Boxes indicate first and third quartiles, and horizontal lines indicate medians.
Increasing temperature shortened all dwell times in DMSO control patches (P < 0.0001), consistent with higher temperatures decreasing kinetic energy barriers (Fig. 4D). By contrast, heating only reduced mean dwell times of short-lived states in the presence of Yoda1 or Dooku1, leaving long-lived states statistically unaffected (0.0773 ≤ P ≤ 0.4723). Fig. 4E shows that the agonist effects of Yoda1 on mean dwell times and relative state occupancy decrease with increasing temperature. Indeed, whereas Yoda1 robustly modulates the relative occupancy of the two major Piezo1 states at room temperature (P < 0.0001), these effects are no longer statistically significant at warmer temperatures (0.7890 ≤ P ≤ 0.9773) (Fig. 2E). In addition, although open probability tends to increase in presence of Yoda1 at all tested temperatures, this effect is only statistically significant at room temperature (P < 0.0001 at 23 °C; 0.1386 ≤ P ≤ 0.7503 at 29 °C; 0.6949 ≤ P ≤ 0.7963 at 35 °C) (Figs. 2C and 4F).
The Kinetic Effects of Yoda1 Are Maximal at Room Temperature and Negative Voltages.
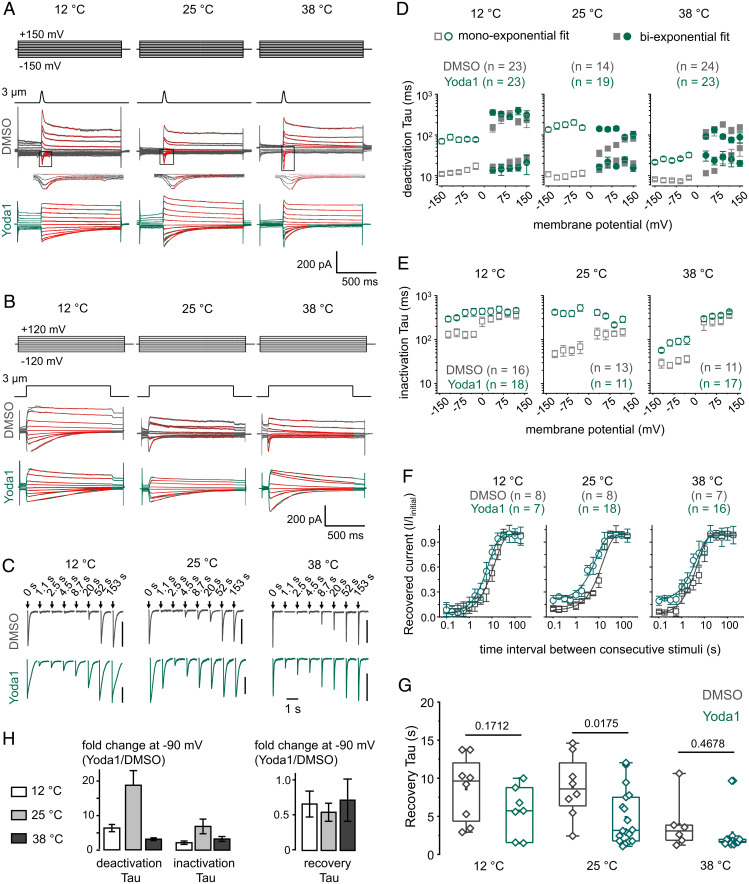
To further investigate the kinetic effects of Yoda1, we measured indentation-evoked macroscopic Piezo1 currents in mPiezo1-transfected HEK293TΔPZ1 cells under whole-cell voltage-clamp configuration at 12, 25, or 38 °C. We mechanically stimulated Piezo1-expressing cells using a poking stimulus (3 µm probe displacement) for a short (40 ms) or long (1 s) duration to measure the relaxation time course associated with macroscopic open→closed (deactivation) and open→inactivated (inactivation) transitions. Since the time course of deactivation and inactivation depends on membrane voltage, we performed these measurements over a wide range of membrane potentials (52, 59, 60). We also measured the time course of recovery from inactivation at −90 mV by measuring the fraction of current recovered after repeated poking stimuli, as described earlier (52) (Fig. 5A–C).
Fig. 5.
Temperature and voltage modulate the extent of Piezo1 modulation by Yoda1. (A) Exemplar Piezo1 deactivation whole-cell current evoked by 40 ms poke stimuli at indicated temperatures and voltages in presence of 30 µM Yoda1 (green) or 0.075% DMSO (gray) in the bath solution. Red lines are monoexponential or biexponential fits of deactivating currents. The fast kinetic component of deactivation is highlighted in the Insets underneath DMSO control traces. (B) Current traces obtained similarly to those described in A but using 1-s poke stimuli. Red lines are monoexponential fits of inactivating currents. (C) Exemplar Piezo1 currents evoked by 1-s poke stimuli repeated at indicated time (V = −90 mV; vertical bars indicate 300 pA). For clarity, not all time points are shown. (D) Deactivation Tau values plotted as a function of voltage and temperature in presence of Yoda1 or DMSO. (E) Inactivation Tau values plotted as function of voltage and temperature in presence of Yoda1 or DMSO. (F) Fraction of recovered peak negative current (I/Iinitial) plotted as a function of time between successive pokes at indicated temperatures in presence of Yoda1 or DMSO. Lines are single exponential fit from aggregated data points. (G) Scatter box plots showing recovery Tau values fitted from individual patches at indicated temperature and in the presence of Yoda1 or DMSO (V = −90 mV). (H) Bar graphs showing Yoda1-induced fold change of deactivation, inactivation, and recovery Tau values for indicated temperatures (V = −90 mV). Error bars = propagated SEM from data shown in D–F. Numbers above box plots in G indicate P values from two-tailed Student’s t tests. The number of independent patches (n) is indicated in D–F. In D–F, error bars indicate SEM. Boxes indicate first and third quartiles, and horizontal lines indicate medians.
For these whole-cell experiments, we diluted a higher-concentration Yoda1 stock (40 mM) to prepare our standard 30 µM working solutions with lower [DMSO] (0.075%) to reduce DMSO-induced cellular toxicity. In addition, to reduce calcium overload and subsequent cellular stress induced by acute exposure to 30 µM Yoda1, we patched only one cell per coverslip to limit Yoda1 incubations to the duration of our recordings. In DMSO control cells, the rate of mPiezo1 deactivation and inactivation slows down with membrane depolarization, an effect consistent with previous observations (59, 60) (Fig. 5D and E). At room temperature and negative voltages, the presence of Yoda1 is associated with an approximately eightfold slowing of inactivation kinetics, confirming previous observations (35), and with an ∼13- to ∼19-fold deactivation slowing, a previously undescribed pharmacological effect (Fig. 5D and E). These kinetic effects decrease in an exponential manner when the bath concentration of Yoda1 decreases, as expected if these effects are mediated through a direct Yoda1–Piezo1 interaction (SI Appendix, Fig. S5). Interestingly, the effects of Yoda1 on inactivation and deactivation kinetics decrease at positive voltages, i.e., potentials at which deactivation and inactivation are inherently slowed (59, 60).
In addition to slowing inactivation and deactivation, Yoda1 tends to accelerate the rate of recovery from inactivation, although this effect was only statistically significant at room temperature (Fig. 5F and G). By increasing the readiness of channels to open, this modulation constitutes with an agonist effect . Because recovery from inactivation necessarily involves transitions between nonconducting states, this macroscopic effect strongly suggests Yoda1 energetically modulates shut states, as predicted by Gaussian-fitting analysis of dwell time distribution (Fig. 2D).
Remarkably, all three kinetic effects of Yoda1 were maximal at room temperature, diminishing when the bath solution was cooled to 12 °C or warmed to 38 °C (Fig. 5H). The heating-induced reduction of macroscopic kinetic effects is consistent with the reduction of single-channel effects observed when temperature was raised from 23 to 35 °C (Fig. 4).
Although Dooku1 remains thermodynamically silent, it modulates mPiezo1 single-channel dwell times (Figs. 2–4) and, thus, could also modulate macroscopic kinetics. To test this possibility, we measured the rate of deactivation, inactivation, and recovery from inactivation in the presence of 30 µM Dooku1 or DMSO at −90 mV and at three temperatures (12, 25, and 38 °C). Our results show that the presence of Dooku1 does not appreciably modulate these kinetic properties in any tested condition (SI Appendix, Fig. S6).
Discussion
We first reveal that conformational rearrangements associated with mechanical gating are necessary for the activation of Piezo1 by Yoda1, supporting the prevailing notion that Yoda1 acts by interacting with, and energetically modulating, mechanosensory domains as previously suggested (26, 35, 49).
We next perform a comprehensive electrophysiological investigation to probe the nature and extent of these biophysical modulations, using a relatively high (near saturating) Yoda1 concentration of 30 µM. At room temperature and negative voltages, the presence of Yoda1 increases by approximately twofold the mean dwell time of a long-lived open state and decreases by ∼1.8-fold the mean dwell time of a long-lived shut state. Macroscopically, Yoda1 slows down inactivation (up to eightfold) and deactivation (up to 19-fold) kinetics and accelerates by about twofold the rate of recovery from inactivation. Together, these effects are consistent with an energetic stabilization of an open state and with a destabilization of either closed or inactivated state(s).
We further show that the nonactive analog Dooku1, like its parent molecule Yoda1, also energetically modulates single-channel dwell times but does so in a manner that does not appreciably affect open probability or macroscopic kinetics, consistent with a model in which Dooku1 acts as a silent binder. The ability of Dooku1 to antagonize the effects of Yoda1 could thus be simply explained by the ability of Dooku1 to compete with Yoda1 for the same binding site, a fair assumption considering the high structural similarity between these two molecules (50).
Although the effects of Yoda1 on inactivation and deactivation kinetics are unmistakable at negative voltages, these effects dwindle at depolarized potentials. How could membrane depolarizations reduce the kinetic effects of Yoda1? Since membrane depolarizations slow down both macroscopic transitions, the reduced effect of Yoda1 at positive potentials could be due to a saturation effect, preventing further slowing by Yoda1. Another hypothesis is that the kinetic effects of Yoda1 and membrane depolarization are inherently nonadditive. This could be the case, for instance, if the molecular pathways used by these stimuli converge onto the same molecular mechanism(s) to modulate inactivation and deactivation. For instance, a shared mechanism could involve a lysine residue which was recently shown indispensable to mediate the voltage dependence of Piezo1 inactivation kinetics (60).
Additionally, we cannot exclude the possibility that membrane depolarizations might inherently diminish Yoda1 binding affinity and/or efficacy. As Yoda1 is not electrically charged, this hypothetical scenario would involve electrically charged groups harbored by specific Piezo1 residues. Such a hypothesis could be tested using mutagenesis approaches, for instance, by mutating basic and/or acid residues located in the vicinity of our proposed binding site (26).
The biphasic temperature dependence of the effects of Yoda1 is puzzling considering the linear temperature dependence of chemical transformations predicted by the Van ‘t Hoff equation. Such nonlinear effects would nonetheless occur if the chemical changes associated with Piezo1 channel opening and/or Yoda1 binding were accompanied by significant changes of heat capacity (61). Indeed, thermodynamics laws imply that heat capacity changes lead to biphasic temperature modulations (62). These theoretical predictions have been rigorously validated through rational design of thermal sensitivity in a voltage-gated potassium channel (63). This hypothetical mechanism for the temperature dependence of the effects of Yoda1 seems plausible, considering that the binding of Yoda1, a hydrophobic ligand, and the opening of Piezo1, a membrane protein harboring >1,200 hydrophobic amino acids, likely involve hydration and/or dehydration of hydrophobic chemical groups, two robust drivers of heat capacity changes (61). Future studies will be needed to determine whether this mechanism contributes to the temperature dependence of the effects of Yoda1.
Last, the sharp amplitude reduction of the electrophysiological effects of Yoda1 near mammalian body temperatures or at low Yoda1 concentrations should, by no means, suggest that the effects of Yoda1 are necessarily small when it is used in these experimental conditions. Recent studies show that exposure of lymphatic cells to low micromolar, or even submicromolar, Yoda1 concentrations at physiological temperatures induces robust changes in cell morphology and gene expression consistent with Piezo1 activation (42, 44). Such robust biological effects occur most likely because these cells were exposed to Yoda1 for a relatively long time (1 to 24 h), which would compensate for small electrophysiological effects, giving enough time for slowly accumulating calcium ions to build up cytosolically and trigger downstream signaling.
Materials and Methods
Cell Culture, Reagents, and Transfection.
Piezo1 deficit HEK293TΔPZ1 cells, a generous gift from Dr. Ardèm Patapoutian (The Scripps Research Institute, La Jolla, CA), were cultured at 37 °C and 5% CO2 in Dulbecco’s Modified Eagle Medium (GIBCO) supplemented with Penicillin-Streptomycin and 10% fetal calf serum (Life Technologies). Yoda1 and Dooku1 were purchased from Sigma-Aldrich (SML1558 and SML2397, respectively). Dooku1 was dissolved in DMSO at 10 mM, and Yoda1 was dissolved in DMSO at 10 mM or 40 mM. All compounds were aliquoted and stored at −20 °C. Cells grown at low confluence on 5 × 5 mm glass coverslips were placed inside a 35-mm cell culture dish and transiently transfected with a pCDNA3.1-mPiezo1-IRES-mCherry plasmid with Lipofectamine 3000 Transfection Reagent (Life Technologies) using the manufacturer’s recommended instructions. For calcium imaging, HEK293TΔPZ cells were seeded in 96-well plates and cotransfected at 30 to 50% confluence with 100 ng of a pCDNA3.1-GcAMP6m plasmid encoding a calcium indicator as described previously (51) and 100 ng of WT pCDNA3.1-mPiezo1 or one of three double cysteine mutants cloned into pCDNA3.1-mPiezo1-IRES-GFP plasmids, generous gifts from Dr. Jörg Grandl (Duke University, Durham, NC) (52).
Calcium Imaging.
Three to four days after transfection, cells were washed with 100 µL Hank’s Balanced Saline Solution (HBSS) and returned to the incubator for 20 min. Cells were then placed on an inverted epifluorescence microscope (Nikon Eclipse 2000). GcAMP6m fluorescence was evoked by collimating the light of a 100 W mercury lamp through a standard green fluorescence cube and focusing it onto the sample through a 20× objective. Fluorescence images were acquired at 4 Hz using a DigitalSight camera and the Nikon Digital Element D software. Approximately 10 s after the start of the recording, 100 µL of a 2× HBSS solution containing either 200 µM Yoda1, 200 µM Yoda1 + 50 mM DTT, or 50 mD DTT + 2% DMSO was added to the cells. Final DMSO concentration after adding the solution was 1% in all conditions.
Single-Channel Recordings.
Cells were patched 12 to 24 h after transfection. Patch pipettes were pulled from thin-wall borosilicate capillaries with internal filament (GC 150TF-7.5; Harvard Apparatus) to a resistance of 5 to 6 MΩ using a vertical pipette puller PC-10 (Narishige). Pipettes were not fire-polished in order to reduce fluctuations of pipette tip geometry. Transfected cells were placed onto an inverted epifluorescence microscope (Olympus IX73) mounted on an air table ). mCherry-positive cells producing red fluorescence were selected for patch-clamping. Cell attached voltage-clamp experiments were performed at room temperature using an Axopatch 200B capacitor-feedback patch clamp amplifier (Molecular Devices) connected to a Digidata 1550B low-noise data acquisition system plus hum silencer (Molecular Devices) and controlled using the Clampex software (Molecular Devices). Negative pressure stimuli were delivered to the backside of patch pipettes using a Clampex-controlled high-speed pressure clamp (ALA Scientific Instruments). Pipettes were filled with 140 mM KCl, 10 mM Hepes, 10 mM TEA, and 2 mM EGTA (pH 7.4 with NaOH). HBSS (GIBCO) was used as bath solution. Resting membrane potential of the transfected cells was −28 ± 5 mV when measured using the above-mentioned saline solutions. Therefore, a +60 mV holding potential was applied through the pipette electrode to provide a −90 mV potential across the membrane patch. Currents were acquired as individual 1 to 3 min continuous gap-free recordings using a sampling rate of 500 kHz and a filtering frequency of 5 kHz. Data were subsequently filtered at 500 Hz for display. DMSO concentration in the patch pipette was kept at 0.3% for all experiments.
Macroscopic Patch Clamp Recordings.
Experiments were performed similarly to those described above for single-channel recordings but with the following differences. Cells were used 48 to 72 h after transfection. Recording pipettes were pulled to a resistance of 2 to 3 MΩ and fire polished using a microforge (MF2, Narishige). Blunt poking probes were made by fire-polishing the tip of glass pipettes to a size of ∼2 to 4 µm. Indentation stimuli were delivered by displacing poking probes angled at ∼70° with a piezoelectric actuator (P-841, Physik Instrumente) controlled by Clampex via an amplifier (E-625, Physik Instrumente). Before each experiment, the probe was slowly moved until visual deformation of the cell. The probe was then retracted ∼1 to 2 µm to set the initial probe position as close as possible to the cell surface without physical contact. A 40-mM Yoda1 stock in DMSO was diluted in HBSS to create a working bath solution containing 30 μM Yoda1 while keeping DMSO at 0.075% to maintain patch quality. Except for experiments measuring the time course of recovery from inactivation, all consecutive poking stimuli were delivered using 20-s time intervals to allow full recovery from inactivation. Exponential fitting of inactivation Tau, deactivation Tau, and recovery Tau was done by fitting data with the function
| [1] |
Current Histograms and Dwell Time Analysis.
All-point current histograms were generated using Clampfit software (Molecular Devices) and fitted with OriginPro2018s Multiple Peak Fit tool using the default Gauss function. Single-channel time series were idealized using Clampfit using a dead time of 10 µs. A MATLAB script posted to GitHub (https://github.com/LacroixLaboratory) was used to revert shut events with current amplitude >75% of the preceding open event to an open event and combined with the preceding open event. Open events with current amplitude <125% of the previous shut event were corrected to a shut event and combined with the previous shut event. Log dwell time histograms were fitted with OriginPro2018s Multiple Peak Fit tool using the default Gauss function.
Open Probability Calculations.
For method 1, NPo was calculated from all-point histograms data according to
| [2] |
where and are the area under the curve directly obtained from multiple peak Gaussian fitting (Current Histograms and Dwell Time Analysis). Method 2 uses the sum of channel open and shut times,
| [3] |
where is the duration of individual open events and is the total recording duration. For method 3, NPo was calculated using the mean open and mean shut times calculated using the following formula:
| [4] |
with and being the duration of individual open and shut events, respectively, while and are the total number of open and shut events, respectively. For method 4, NPo was calculated using the Gaussian fitting of dwell time histograms using the following formula:
| [5] |
Markov Chain Modeling.
QUB, a software suite for the idealization and analysis of Markovian processes, was used to determine transition rates between single-channel states. Current trajectories were idealized by pClamp and MATLAB as previously described prior to data input and further compressed 10-fold due to file size constraints (final sampling frequency = 1 kHz). For rate calculations, QUB requires input traces to first be idealized through a segmental k-means algorithm. In our case, no differences were present between input and QUB-idealized traces, showing that no loss of information occurs as a result of multiple idealization steps (SI Appendix, Fig. S2). An initial dwell time of 1 ms and initial rate of 1 s−1 were used for each of the 12 possible transitions between S1, S2, O1, and O2 states, and the model was optimized for 10,000 iterations with a step size of 10−6 s−1 and a maximum of 10,000 steps per iteration. Under this approach, three transitions (S1/S2, O1/O2, and S2/O2) consistently converged to near-zero values (SI Appendix, Table S1). Consequently, these transitions were omitted, and the new model (minimal model) was optimized for a further 10,000 iterations under the same parameters.
Data and Statistical Analyses.
The operators were not blinded to the manipulation of independent variables. Statistical tests and corresponding P values were determined using GraphPad and are reported in figures and in the text. The lowercase letter n indicates the exact number of independent cells analyzed.
Supplementary Material
Acknowledgments
This work was supported by NIH Grant GM130834 to J.J.L.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2202269119/-/DCSupplemental.
Data Availability
Excel tables and raw data have been deposited in Open Science Framework (DOI: 10.17605/OSF.IO/CBUQ3) (64).
References
- 1.Kloda A., Martinac B., Mechanosensitive channels in archaea. Cell Biochem. Biophys. 34, 349–381 (2001). [DOI] [PubMed] [Google Scholar]
- 2.Patel A. J., Lazdunski M., Honoré E., Lipid and mechano-gated 2P domain K(+) channels. Curr. Opin. Cell Biol. 13, 422–428 (2001). [DOI] [PubMed] [Google Scholar]
- 3.Mochizuki T., et al. , The TRPV4 cation channel mediates stretch-evoked Ca2+ influx and ATP release in primary urothelial cell cultures. J. Biol. Chem. 284, 21257–21264 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Murthy S. E., et al. , OSCA/TMEM63 are an evolutionarily conserved family of mechanically activated ion channels. eLife 7, e41844 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jia Y., et al. , TMC1 and TMC2 proteins are pore-forming subunits of mechanosensitive ion channels. Neuron 105, 310–321.e3 (2019). [DOI] [PubMed] [Google Scholar]
- 6.Coste B., et al. , Piezo proteins are pore-forming subunits of mechanically activated channels. Nature 483, 176–181 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kefauver J. M., Ward A. B., Patapoutian A., Discoveries in structure and physiology of mechanically activated ion channels. Nature 587, 567–576 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mousavi S. A. R., et al. , PIEZO ion channel is required for root mechanotransduction in Arabidopsis thaliana. Proc. Natl. Acad. Sci. U.S.A. 118, e2102188118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Radin I., et al. , Plant PIEZO homologs modulate vacuole morphology during tip growth. Science 373, 586–590 (2021). [DOI] [PubMed] [Google Scholar]
- 10.Wang P., Jia Y., Liu T., Jan Y. N., Zhang W., Visceral mechano-sensing neurons control drosophila feeding by using Piezo as a sensor. Neuron 108, 640–650.e4 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Oh Y., et al. , Periphery signals generated by Piezo-mediated stomach stretch and Neuromedin-mediated glucose load regulate the Drosophila brain nutrient sensor. Neuron 109, 1979–1995.e1976 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Min S., et al. , Control of feeding by Piezo-mediated gut mechanosensation in Drosophila. eLife 10, e63049 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bai X., et al. , Caenorhabditis elegans PIEZO channel coordinates multiple reproductive tissues to govern ovulation. eLife 9, e53603 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Millet J. R. M., Romero L. O., Lee J., Bell B., Vásquez V., C. elegans PEZO-1 is a mechanosensitive ion channel involved in food sensation. J. Gen. Physiol. 154, e202112960 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cahalan S. M., et al. , Piezo1 links mechanical forces to red blood cell volume. eLife 4, e07370 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ranade S. S., et al. , Piezo2 is the major transducer of mechanical forces for touch sensation in mice. Nature 516, 121–125 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schneider E. R., et al. , A cross-species analysis reveals a general role for Piezo2 in mechanosensory specialization of trigeminal ganglia from tactile specialist birds. Cell Rep. 26, 1979–1987.e1973 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Syeda R., Physiology and pathophysiology of mechanically activated PIEZO channels. Annu. Rev. Neurosci. 44, 383–402 (2021). [DOI] [PubMed] [Google Scholar]
- 19.Woo S. H., et al. , Piezo2 is the principal mechanotransduction channel for proprioception. Nat. Neurosci. 18, 1756–1762 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jiang W., et al. , Crowding-induced opening of the mechanosensitive Piezo1 channel in silico. Commun. Biol. 4, 84 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhao Q., et al. , Structure and mechanogating mechanism of the Piezo1 channel. Nature 554, 487–492 (2018). [DOI] [PubMed] [Google Scholar]
- 22.Saotome K., et al. , Structure of the mechanically activated ion channel Piezo1. Nature 554, 481–486 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Guo Y. R., MacKinnon R., Structure-based membrane dome mechanism for Piezo mechanosensitivity. eLife 6, e33660 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ge J., et al. , Architecture of the mammalian mechanosensitive Piezo1 channel. Nature 527, 64–69 (2015). [DOI] [PubMed] [Google Scholar]
- 25.Wang L., et al. , Structure and mechanogating of the mammalian tactile channel PIEZO2. Nature 573, 225–229 (2019). [DOI] [PubMed] [Google Scholar]
- 26.Botello-Smith W. M., et al. , A mechanism for the activation of the mechanosensitive Piezo1 channel by the small molecule Yoda1. Nat. Commun. 10, 4503 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Haselwandter C. A., MacKinnon R., Piezo’s membrane footprint and its contribution to mechanosensitivity. eLife 7, e41968 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lin Y. C., et al. , Force-induced conformational changes in PIEZO1. Nature 573, 230–234 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.De Vecchis D., Beech D. J., Kalli A. C., Molecular dynamics simulations of Piezo1 channel opening by increases in membrane tension. Biophys. J. 120, 1510–1521 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Cox C. D., et al. , Removal of the mechanoprotective influence of the cytoskeleton reveals PIEZO1 is gated by bilayer tension. Nat. Commun. 7, 10366 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Syeda R., et al. , Piezo1 channels are inherently mechanosensitive. Cell Rep. 17, 1739–1746 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lewis A. H., Grandl J., Mechanical sensitivity of Piezo1 ion channels can be tuned by cellular membrane tension. eLife 4, e12088 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Poole K., Herget R., Lapatsina L., Ngo H. D., Lewin G. R., Tuning Piezo ion channels to detect molecular-scale movements relevant for fine touch. Nat. Commun. 5, 3520 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Yang X., et al. , Structure deformation and curvature sensing of PIEZO1 in lipid membranes. Nature 604, 377–383 (2022). [DOI] [PubMed] [Google Scholar]
- 35.Syeda R., et al. , Chemical activation of the mechanotransduction channel Piezo1. eLife 4, e07369 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Passini F. S., et al. , Shear-stress sensing by PIEZO1 regulates tendon stiffness in rodents and influences jumping performance in humans. Nat. Biomed. Eng. 5, 1457–1471 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Deivasikamani V., et al. , Piezo1 channel activation mimics high glucose as a stimulator of insulin release. Sci. Rep. 9, 16876 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Caolo V., et al. , Shear stress activates ADAM10 sheddase to regulate Notch1 via the Piezo1 force sensor in endothelial cells. eLife 9, e50684 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Morley L. C., et al. , Piezo1 channels are mechanosensors in human fetoplacental endothelial cells. Mol. Hum. Reprod. 24, 510–520 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bosutti A., et al. , “Time window” effect of Yoda1-evoked Piezo1 channel activity during mouse skeletal muscle differentiation. Acta Physiol. (Oxf.) 233, e13702 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jetta D., Gottlieb P. A., Verma D., Sachs F., Hua S. Z., Shear stress-induced nuclear shrinkage through activation of Piezo1 channels in epithelial cells. J. Cell Sci. 132, jcs226076 (2019). [DOI] [PubMed] [Google Scholar]
- 42.Choi D., et al. , Piezo1 incorporates mechanical force signals into the genetic program that governs lymphatic valve development and maintenance. JCI Insight 4, e125068 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Romac J. M., Shahid R. A., Swain S. M., Vigna S. R., Liddle R. A., Piezo1 is a mechanically activated ion channel and mediates pressure induced pancreatitis. Nat. Commun. 9, 1715 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nonomura K., et al. , Mechanically activated ion channel PIEZO1 is required for lymphatic valve formation. Proc. Natl. Acad. Sci. U.S.A. 115, 12817–12822 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wang S., et al. , Endothelial cation channel PIEZO1 controls blood pressure by mediating flow-induced ATP release. J. Clin. Invest. 126, 4527–4536 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Holt J. R., et al. , Spatiotemporal dynamics of PIEZO1 localization controls keratinocyte migration during wound healing. eLife 10, e65415 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Desplat A., et al. , Piezo1-Pannexin1 complex couples force detection to ATP secretion in cholangiocytes. J. Gen. Physiol. 153, e202112871 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li X., et al. , Stimulation of Piezo1 by mechanical signals promotes bone anabolism. eLife 8, e49631 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang Y., et al. , A lever-like transduction pathway for long-distance chemical- and mechano-gating of the mechanosensitive Piezo1 channel. Nat. Commun. 9, 1300 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Evans E. L., et al. , Yoda1 analogue (Dooku1) which antagonizes Yoda1-evoked activation of Piezo1 and aortic relaxation. Br. J. Pharmacol. 175, 1744–1759 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lacroix J. J., Botello-Smith W. M., Luo Y., Probing the gating mechanism of the mechanosensitive channel Piezo1 with the small molecule Yoda1. Nat. Commun. 9, 2029 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lewis A. H., Grandl J., Inactivation kinetics and mechanical gating of Piezo1 ion channels depend on subdomains within the cap. Cell Rep. 30, 870–880.e2 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lukacs V., et al. , Impaired PIEZO1 function in patients with a novel autosomal recessive congenital lymphatic dysplasia. Nat. Commun. 6, 8329 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sigworth F. J., Sine S. M., Data transformations for improved display and fitting of single-channel dwell time histograms. Biophys. J. 52, 1047–1054 (1987). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Nosyreva E. D., Thompson D., Syeda R., Identification and functional characterization of the Piezo1 channel pore domain. J. Biol. Chem. 296, 100225 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Milescu L. S., Akk G., Sachs F., Maximum likelihood estimation of ion channel kinetics from macroscopic currents. Biophys. J. 88, 2494–2515 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Nicolai C., Sachs F., Solving ion channel kinetics with the QuB software. Biophys. Rev. Lett. 8, 191–211 (2013). [Google Scholar]
- 58.Zheng W., Nikolaev Y. A., Gracheva E. O., Bagriantsev S. N., Piezo2 integrates mechanical and thermal cues in vertebrate mechanoreceptors. Proc. Natl. Acad. Sci. U.S.A. 116, 17547–17555 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Coste B., et al. , Piezo1 and Piezo2 are essential components of distinct mechanically activated cation channels. Science 330, 55–60 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wu J., et al. , Inactivation of mechanically activated piezo1 ion channels is determined by the C-terminal extracellular domain and the inner pore helix. Cell Rep. 21, 2357–2366 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Prabhu N. V., Sharp K. A., Heat capacity in proteins. Annu. Rev. Phys. Chem. 56, 521–548 (2005). [DOI] [PubMed] [Google Scholar]
- 62.Clapham D. E., Miller C., A thermodynamic framework for understanding temperature sensing by transient receptor potential (TRP) channels. Proc. Natl. Acad. Sci. U.S.A. 108, 19492–19497 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Chowdhury S., Jarecki B. W., Chanda B., A molecular framework for temperature-dependent gating of ion channels. Cell 158, 1148–1158 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Wijerathne T.D., Ozkan A.D., Lacroix J.J., Yoda1’s energetic footprint on Piezo1 channels and its modulation by voltage and temperature. Open Science Framework. https://osf.io/cbuq3/. Deposited 2 February 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Excel tables and raw data have been deposited in Open Science Framework (DOI: 10.17605/OSF.IO/CBUQ3) (64).