Direct measuring of single–heterogeneous bubble nucleation mediated by surface topology

Significance

Although bubble nucleation has been recognized as highly stochastic and heterogeneous, it is still poorly understood how surface nanoscopic topologies quantitatively modulate the nucleation process. Here, we directly measure single-bubble nucleation on surfaces with silica nanoparticles of controlled size and surface chemistry as foreign nucleants using the scanning electrochemical cell microscopy technique. Unlike the conventional spectroscopic or optical microscopic methods, our approach not only provides both high temporal and spatial resolution but also, quantifies the corresponding chemical supersaturation ratio at single nucleation. Spatially resolved scanning mapping allows for convincing correlation with local surface topologies. Our study of single-bubble nucleation demonstrates the previously unseen dependence of heterogenous bubble nucleation on the surface topology at the single nucleation level.

Abstract

Heterogeneous bubble nucleation is one of the most fundamental interfacial processes ranging from nature to technology. There is excellent evidence that surface topology is important in directing heterogeneous nucleation; however, deep understanding of the energetics by which nanoscale architectures promote nucleation is still challenging. Herein, we report a direct and quantitative measurement of single-bubble nucleation on a single silica nanoparticle within a microsized droplet using scanning electrochemical cell microscopy. Local gas concentration at nucleation is determined from finite element simulation at the corresponding faradaic current of the peak-featured voltammogram. It is demonstrated that the criteria gas concentration for nucleation first drops and then rises with increasing nanoparticle radius. An optimum nanoparticle radius around 10 nm prominently expedites the nucleation by facilitating the special topological nanoconfinements that consequently catalyze the nucleation. Moreover, the experimental result is corroborated by our theoretical calculations of free energy change based on the classic nucleation theory. This study offers insights into the impact of surface topology on heterogenous nucleation that have not been previously observed.

Gas bubbles are ubiquitous and involved in various areas of nature (1, 2) and technology (3–8). As a prototype of phase transition, the study of bubble nucleation and its kinetics is fundamentally important but remains elusive due to its transient and nanoscale nature (9, 10). In the last decade, effective experimental techniques, including high-speed optical microscopy (11–13), ion conductance measurement (14, 15), and liquid–cell transmission electron microscopy (16), elucidated the bubble nucleation processes in aspects of where and when nucleation occurs with excellent spatiotemporal resolution. However, localized gas concentration and supersaturation for individual bubble nucleation are some of the most interesting but unexplored. Recently, nanoelectrodes have been employed as an innovative method to probe single-gas nanobubble nucleation, and insightful stochasticity and heterogeneity have been quantitatively characterized (17–21).

It has been suggested that surface topology is vitally important to the heterogeneous nucleation process (22). Previous experimental studies demonstrated that ice freezing can be promoted on surfaces with topological features of pits, cracks, steps, or foreign nucleants (23, 24), and protein crystallization is enhanced on polymer films with specific nanopore structure or cross-linked polymer microgels with optimum mesh size (25, 26). Although these macroscopic observations provide strong evidence for the surface topology on heterogeneous nucleation, it is still poorly understood how these nanoscopic surface features quantitatively dictate the heterogeneous liquid-to-gas bubble nucleation, especially at the single-entity level.

Scanning electrochemical cell microscopy (SECCM) is an emerging scanning probe technique that allows for unambiguous correlation of surface microstructure and electrochemical phenomenon at the nanoscale (27, 28). It has been applied to study intrinsic activities in (photo-)electrocatalysis by others and us from nanoparticles (29–33) to nanosheets (34–36) and metal films with grain boundaries (37–40), with only a few studies to observe nucleation (41). In a previous article (42), we established a reproducible SECCM method for the study of bubble nucleation on flat surfaces and determined that the local gas concentration at the surface is solely associated with the faradaic current in the voltammogram, opening the door to utilize critical nucleation current as a surrogate for local gas concentration (or supersaturation). In this article, we utilize the SECCM technique to further measure the single–heterogeneous bubble nucleation on a nanoparticle and clarify the unprecedented nanoscopic surface topological basis of bubble nucleation.

Here, electrochemically inert spherical silica nanoparticles with highly monodispersed size are immobilized on a flat glassy carbon surface to construct well-defined nanoconfinement geometry. By visualizing individual bubble nucleation at different positions across a surface, we discovered that positions with SiO₂ nanoparticles have preferential nucleation with a lower critical gas supersaturation. A nonmonotonous relationship between the critical gas concentration for nucleation and nanoparticles radii is revealed, and such an optimum particle radius is supported by theoretical calculation of free energy change based on the classic nucleation theory. Our study of heterogeneous nucleation on a nanoparticle at a single entity reveals unique insights to understand how surface topology directs the nucleation process.

Results and Discussion

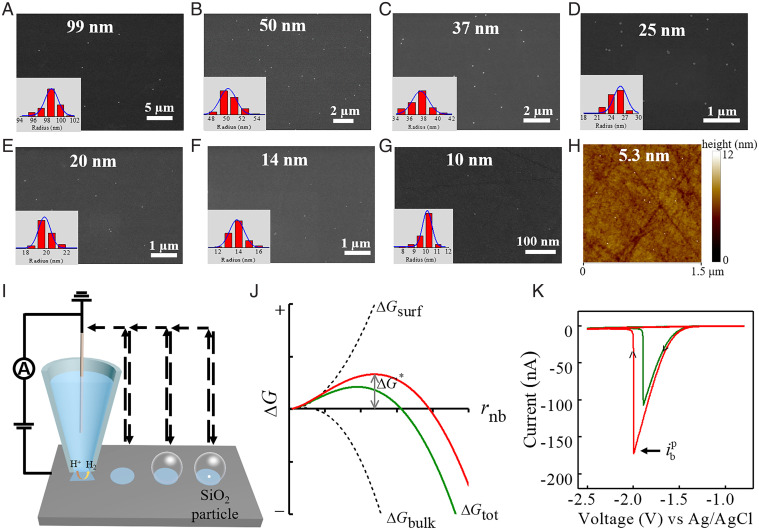
We chose spherical silica nanoparticles to study single–heterogeneous nanobubble nucleation for two reasons. First, the size and surface chemistry can be easily manipulated during synthesis, allowing for the construction of well-defined surface topology. Second, unlike the conventional single-particle electrocatalysis, the SiO₂ nanoparticles are electrochemically inert, acting only as surface nucleants for bubble nucleation but without bringing significant change of local mass transport configuration. Monodispersed SiO₂ nanoparticles with radii ranging from a few nanometers to 100 nm were synthesized through hydrolysis and polycondensation of tetraethoxysilane (43, 44). Both the small SiO₂ seeds (<10 nm) and colloids have identical surface chemistry (Si-OH group), and ζ-potential measurement reveals their charge neutrality in aqueous solution at pH = 7. Scanning electron microscopy (SEM) and transmission electron microscopy (TEM) characterization images show that the prepared SiO₂ nanoparticles exhibit extremely narrow size distribution, with average radii of 99 ± 2, 50 ± 2, 37 ± 2, 25 ± 1, 20 ± 1, 14 ± 1, 10 ± 0.8, 5.3 ± 0.8, and 3.4 ± 1.0 nm (SI Appendix, Fig. S1). Subsequently, individual SiO₂ nanoparticles were deposited on the precleaned smooth glassy carbon surface to achieve low coverage density without obvious aggregations (Fig. 1 A–G). Because of the limited spatial resolution of SEM, smaller SiO₂ nanoparticles below 10 nm were verified by atomic force microscopy (AFM) (Fig. 1H), while the bare glassy carbon surface possesses a local rms roughness of 1.35 nm (SI Appendix, Fig. S2).

Fig. 1.

(A–G) SEM images of synthesized SiO₂ nanoparticles sparsely dispersed on glassy carbon surface with radii of 99 ± 2, 50 ± 2, 37 ± 2, 25 ± 1, 20 ± 1, 14 ± 1, and 10 ± 0.8 nm. The Insets are the corresponding radius distributions of SiO₂ nanoparticles. (H) Tapping mode AFM height image (1.5 × 1.5 μm) of smooth glassy carbon surface deposited with individual 5.3-nm radius SiO₂ nanoparticles. Each size distribution is obtained from analyzing more than 50 SiO₂ nanoparticles from electron microscopy images. (I) Scheme of the SECCM measurement of single–H₂ gas bubble nucleation on an SiO₂ nanoparticle. (J) Schematic energetics of classic nucleation theory for bubble nucleation. The nucleation occurring on an SiO₂ nanoparticle is expected to exhibit different energetics with a lower free energy barrier (green line). (K) Typical cyclic voltammograms at 0.5 V/s for single–H₂ bubble formation on the bare glassy carbon (red line) and a 50-nm-radius SiO₂ nanoparticle (green line). In the experiment, a pipette with a 1.5-μm-radius tip opening filled with 2.0 M H₂SO₄ solution was used.

Fig. 1I shows the schematic for direct measurement of single-bubble nucleation on an SiO₂ nanoparticle using SECCM. A single-barrel glass micropipette with a 1.5-μm-radius tip opening filled with acidic solution and inserted with an Ag/AgCl wire as a quasireference/counterelectrode (QRCE) was used as the probe. Local gas supersaturation for bubble nucleation is triggered and controlled by the electrochemical generation of H₂ molecules from proton reduction on the smooth glassy carbon surface within the microdroplet. Further single-bubble nucleation mapping across surfaces with different local nanoscopic topologies is achieved using the “hopping” mode with a distance of 7 μm. Fig. 1J illustrates the energetics of heterogeneous bubble nucleation on a flat surface with and without a nanoparticle. The nanoparticles on the surface are expected to act as active nucleant sites for nucleation with lower free energy barrier. Presentative voltammograms for single-bubble nucleation are shown in Fig. 1K, where peak currents of –172.6 and –106.7 nA are observed for nucleation on the smooth surface and on a 50-nm-radius SiO₂ nanoparticle, respectively. According to previous theoretical and experimental studies, such peak features represented the formation of a gas bubble within the microdroplet (42, 45). At the peak current, $i_{\text{b}}^{\text{p}}$, the local H₂ concentration at the electrode surface reaches a critical value, causing a nanobubble to nucleate and quickly grow to block the proton transport toward the substrate electrode.

There are several important features of SECCM to validate its quantitative study of single-bubble nucleation. First, the peak-featured cyclic voltammetry of bubble nucleation was independent of scan rates (SI Appendix, Fig. S4), implying the very fast mass transport and bubble nucleation kinetics. Therefore, mass transport within the microdroplet can reach steady state, and local gas concentration at the electrode surface is readily derived from the faradaic current (46, 47). Bubble nucleation is naturally stochastic, occurring randomly either in time and space for a constant supersaturation or in supersaturation for the initial observation of nucleation. The histograms of nucleation current from independent voltammetric measurements at the same position show single-peak Gaussian distribution (SI Appendix, Fig. S5). Second, studies demonstrated that single-bubble nucleation voltammograms were not sensitive to small variations of meniscus droplet shape by slightly changing the tip–substrate distance after droplet contact (SI Appendix, Fig. S6). Third, the consistence of such criteria bubble nucleation current was further validated by a galvanostatic measurement, where constant current is applied to trigger gas supersaturation and bubble nucleation in a droplet (SI Appendix, Fig. S7). Unlike the conventional spectroscopic or optical microscopic methods, the SECCM approach of nucleation not only provides both high temporal and spatial resolution for single nanobubbles, but also, it extracts local chemical supersaturation and allows statistical analysis for nucleation from mapping across surfaces.

SECCM mapping of bubble nucleation is first performed on a smooth glassy carbon surface, and the perceived slight spatial nonuniformities in nucleation current could be caused by the stochasticity of nucleation as well as the surface heterogeneity (SI Appendix, Fig. S8). Fig. 2 presents a typical SECCM mapping of single-bubble nucleation on 50-nm-radius SiO₂ nanoparticles deposited on a glassy carbon surface. The dashed white circles in Fig. 2A indicate the footprints of individual microsized meniscus droplets left after voltammetric measurements, and the dimension is consistent with pipette tip opening. The position incorporated with SiO₂ nanoparticles, as confirmed by correlative SEM, shows a voltammogram with lower peak current (Fig. 2B). Zoomed-in SEM images of partial positions and corresponding cyclic voltammograms are presented in Fig. 2 C and D, respectively. Specifically, at spots I and II, where one 50-nm-radius SiO₂ nanoparticle is incorporated, the critical $i_{\text{b}}^{\text{p}}$ decreases significantly to –124.4 and –103.3 nA, respectively. At spots III and V, where two separated or connected 50-nm-radius SiO₂ nanoparticles are incorporated, the critical $i_{\text{b}}^{\text{p}}$ changes to –107.1 and –105.1 nA, respectively. Additional correlated SECCM and SEM imaging for single–gas bubble nucleation on 50-nm-radius SiO₂ nanoparticles shows consistent observations (SI Appendix, Figs. S11 and S12).

Fig. 2.

(A) SEM image of the glassy carbon surface with well-dispersed 50-nm-radius SiO₂ nanoparticles. Circles represent locations of droplets left from SECCM measurement, while colors stand for SiO₂ nanoparticle number within the droplet, with yellow for one, green for two, and red for three. (B) SECCM mapping of bubble nucleation current, $i_{\text{b}}^{\text{p}}$, across the same surface as in A. (C) Zoomed-in SEM images of partial locations with nanoparticles and (D) corresponding voltammograms for single–H₂ bubble formation. The Insets in C are the corresponding magnified SEM images of individual SiO₂ nanoparticles.The peak currents at locations I, II, III, and V are –124.4, –103.3, –107.1, and –105.1 nA, respectively. In the experiment, a pipette with a 1.5-μm-radius tip opening and 2.0 M H₂SO₄ solution was used. Voltammograms were recorded at 0.5 V/s with a step size of 7 μm.

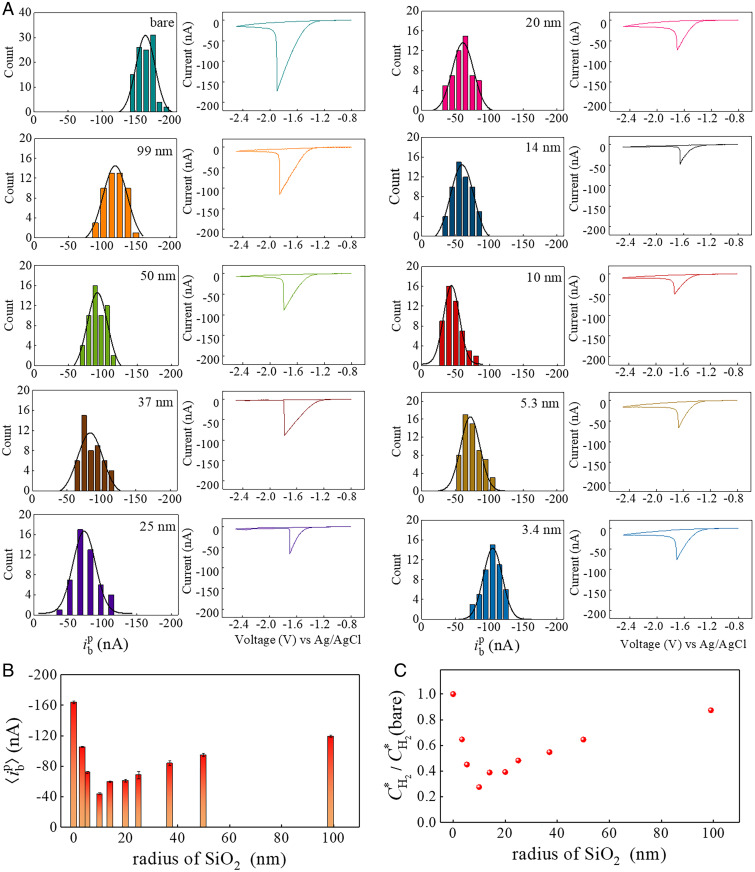
Having shown the capability of quantitative measurement of single-bubble nucleation on a nanoparticle, we then systematically explored SiO₂ nanoparticles with radii ranging from 99 to 3.4 nm. Correlated SEM and SECCM mapping of bubble nucleation on SiO₂ nanoparticles with radii of 99, 37, and 25 nm is illustrated in SI Appendix, Figs. S13–S18. It is explicitly observed that droplet spots containing SiO₂ nanoparticles exhibit distinct bubble nucleation currents compared with the adjacent bare glassy carbon surfaces. Occasional stain observed in the correlative SEM image most likely comes from contamination in the air after the SECCM experiment, and such data are excluded from further statistical analysis (SI Appendix, Fig. S19). The nucleation theory predicts that multiple nanoparticles (nucleation sites) within a droplet enable higher bubble nucleation rates; however, we measure the critical supersaturation at nucleation onset. Therefore, dependence of nucleation current on nanoparticle numbers within the droplet was not observed. Finally, it is worthwhile to note that for SiO₂ nanoparticles smaller than 20 nm in radius, SEM imaging offers poor colocalization with the SECCM mapping. Nevertheless, SECCM mapping of individual single-bubble nucleation throughout the nanoparticle-deposited surface displayed two distinct distributions of peak currents, one ascribed to the nucleation on a smooth glassy carbon surface and the other to that on small SiO₂ nanoparticles.

Fig. 3A summarizes the statistical results for bubble nucleation measurements that stringently count one SiO₂ nanoparticle within the meniscus droplet. All the histograms of nucleation currents display a typical Gaussian distribution, and corresponding typical peak-shaped voltammograms are presented aside, showing excellent consistence of bubble formation as well as hydrogen evolution reaction on glassy carbon. The mean bubble nucleation current, $\langle i_{\text{b}}^{\text{p}}\rangle$, was determined from statistical analysis using Gaussian fitting. Compared with the smooth glassy carbon surface with $\langle i_{\text{b}}^{\text{p}}\rangle$ at –164.1 ± 1.7 nA, the relative extent of reduction in $\langle i_{\text{b}}^{\text{p}}\rangle$ serves as a measure of the effectiveness of the SiO₂ nanoparticle in promoting heterogeneous bubble nucleation. Specifically, as the nanoparticle radius decreases from 99 to 25 and 10 nm, the $\langle i_{\text{b}}^{\text{p}}\rangle$ decreases monotonously from –119.2 to –73.2 and –43.9 nA. Surprisingly, further decreasing the radius to 5.3 and 3.4 nm leads to a rise of $\langle i_{\text{b}}^{\text{p}}\rangle$ to –72.0 and –105.3 nA, respectively. Fig. 3B shows such a nonmonotonic dependence of the mean bubble nucleation current on the radii of the SiO₂ nanoparticle, and the most effective nucleation promotion occurs at a radius of 10 nm.

Fig. 3.

(A) Histograms of single–H₂ bubble nucleation current, $i_{\text{b}}^{\text{p}}$, on just one SiO₂ nanoparticle as a function of nanoparticle radii. Each distribution contains about 50 independent measurements of bubble formation, and the distributions are fitted by Gaussian function with the mean nucleation current, $\langle i_{\text{b}}^{\text{p}}\rangle$, at –164.1 ± 1.7 nA for smooth glassy carbon surface; –119.2 ± 1.3 nA for 99 nm; –95.0 ± 2.1 nA for 50 nm; –83.9 ± 3.1 nA for 37 nm; –73.2 ± 1.4 nA for 25 nm; –61.1 ± 1.6 nA for 20 nm; –59.8 ± 1.0 nA for 14 nm; –43.9 ± 1.1 nA for 10 nm; –72.0 ± 1.5 nA for 5.3 nm; and –105.3 ± 0.8 nA for 3.4 nm. (B) The Gaussian peak position extracted from A, $\langle i_{\text{b}}^{\text{p}}\rangle$, as a function of SiO₂ nanoparticle radii. (C) The normalized critical local surface H₂ concentration, $C_{{\text{H}}_2}^{*}/C_{{\text{H}}_2}^{*}(\text{bare})$, obtained from the finite element simulation based on measurement results (B) as a function of SiO₂ nanoparticles radii. $C_{{\text{H}}_2}^{*}(\text{bare})$ stands for the local surface H₂ concentration at bubble nucleation in the absence of an SiO₂ nanoparticle, which is 119 mM from SI Appendix, Fig. S24A.

We now consider the conversion to local surface H₂ concentration from experimentally measured nucleation current using the finite element simulation. A meniscus geometry similar to the previous work by Unwin and coworkers (48) is adopted, with gas exchange occurring at the liquid–air interface. The current is calculated from proton reduction on the glassy carbon electrode across the droplet contact area using Butler–Volmer electrode kinetics, and mass conservation is applied to study H₂ transport within the droplet and pipette. SI Appendix, Fig. S24A shows the H₂ concentration distribution within the meniscus droplet, where it is highest at the center and decreases gradually along the radial direction due to gas leakage. When an electrochemically inert 50-nm-radius SiO₂ nanoparticle is incorporated at the center of the droplet, a slightly higher local concentration at the particle–electrode interface is revealed (SI Appendix, Fig. S24B). Interestingly, simulations with a particle sitting at different positions within the droplet demonstrate that the particle–electrode interface possesses the highest local H₂ concentration, and this magnitude is largely insensitive to the particle position (SI Appendix, Figs. S22 and S24C), justifying our speculation that gas nuclei form at the crevice between the particle and glassy carbon surface. Therefore, local gas concentration at the particle–electrode interface, $C_{{\text{H}}_2}^{*}$, with different radii nanoparticles can be obtained (SI Appendix, Fig. S23), and Fig. 3C summarizes the normalized local surface concentration by the scenario of bare and smooth surface, $C_{{\text{H}}_2}^{*}/C_{{\text{H}}_2}^{*}(\text{bare})$, where a consistent nonmonotonic relationship is illustrated.

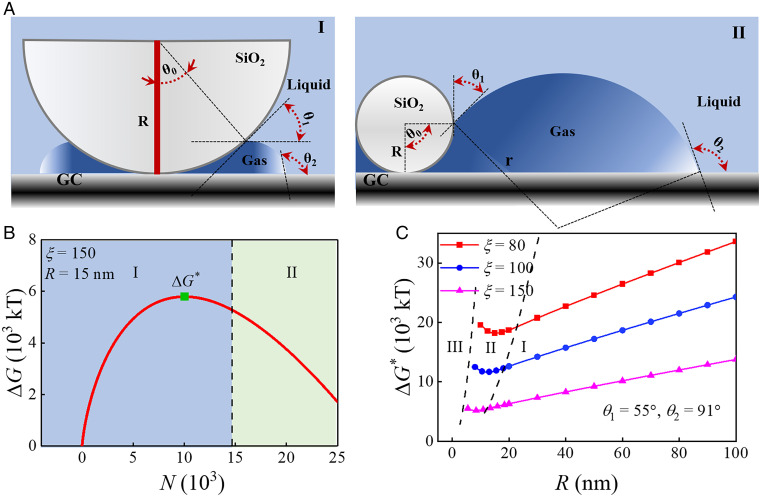
We speculate that such an optimum nanoparticle radius for bubble nucleation is related with the special nanoconfinement geometry between the SiO₂ nanosphere and the substrate. Previously, using Monte Carlo or molecular dynamics simulation, Page and Sear (49) and Li and coworkers (50), respectively, found that crystal nucleation in wedges is many orders faster than on a flat surface, and there exists an optimum wedge angle at which the overall free energy for crystal growing is most favorable. We carry out the calculation of free energy barrier of gas nanobubble nucleation on an SiO₂ nanosphere based on the classic nucleation theory (51). Since gas molecules are electrogenerated from the electrode surface, we use a model for bubble nucleation occurring at the crevice between nanosphere and substrate (Fig. 4A and SI Appendix, Fig. S25). We identify the growing of the bubble nucleus into three regimes: regime I when the bubble nucleus is of a smaller size compared with the particle (i.e., θ₀ ≤ θ₁), regime II when the nucleus has a comparable size to the particle (i.e., θ₁ < θ₀ < θ₁ + 90°), and regime III when the nucleus is substantially larger than the particle (i.e., θ₀ ≥ 180°). During the nucleus evolution, the total free energy barrier can be calculated from energy differences of volume, chemical potential, and interface (52). With experimentally measured surface tension (γ), Young contact angle of electrolyte solution on SiO₂ surface (θ₁) and on glassy carbon surface (θ₂) (SI Appendix, Fig. S20), and assumed supersaturation for the initial gas nucleus (ζ), we can obtain the free energy profile as the bubble nucleus grows. Fig. 4B shows a typical free energy change profile during the growing of the bubble nucleus on a specific nanoparticle with a radius of 15 nm, where the nucleation occurs in regime I and the free energy barrier, ΔG*, for the nucleation process can be deduced. Additional free energy change profiles with a different particle radius show that as the particle radius decreases to less than 12.075 nm, the bubble nucleation with a ΔG* will occurs in regime II (SI Appendix, Fig. S26). Satisfactorily, over a reasonable initial gas nucleus supersaturation range (53), the calculated free energy barrier predicts that the nonmonotonic behavior from the experiment with the optimum bubble nucleation occurs at a nanoparticle radius between 9 and 15 nm (Fig. 4C). Further analysis of free energy contribution reveals that at small nanospheres, the gas–liquid interface free energy at the slit confinement (γ_lA₃) dominates the total free energy, and increasing the SiO₂ radius causes smaller slit angle and stronger nanoconfinement, thus promoting the bubble nucleation (SI Appendix, Fig. S27). On the other hand, at large nanospheres, the gas–SiO₂ interface free energy (γ_lA₁cosθ₁) dominates, and increasing the radius of hydrophilic SiO₂ leads to an increase in the nucleation barrier.

Fig. 4.

(A) Thermodynamic model of bubble nucleation and growth pathway on an SiO₂ nanoparticle. (A, I) Small gas nucleus within the crevice. (A, II) Comparable gas nucleus size as the nanosphere_. (B) Typical free energy changes as a gas nucleus grows calculated from classic nucleation theory, where ΔG* stands for the free energy barrier for bubble nucleation at the green symbol. The SiO₂ nanoparticle radius, R, is set as 15 nm, and the solution supersaturation, ζ, is set as 150. θ₁ = 55° and θ₂ = 91°. (C) Overall free energy barriers at bubble nucleation as a function of SiO₂ nanoparticle radius at assumed supersaturation (ζ = 80, 100, and 150) and contact angles (θ₁ = 55° and θ₂ = 91°).

In addition, the effect of the interaction of gas–SiO₂ and gas–carbon to bubble nucleation is discussed via tuning Young contact angles θ₁ and θ₂. Calculation results show that increasing the hydrophobicity of the carbon surface (increasing θ₂) brings down the free energy barrier, while an optimum nanosphere radius within a similar range still exists (SI Appendix, Fig. S28). Increasing the hydrophobicity of the SiO₂ surface (increasing θ₁) causes a similar enhanced bubble nucleation with a slightly decreased free energy barrier. More interestingly, calculations using broader contact angle ranges (θ₁ = 15°, 20°, 30°, θ₂ = 140°) show the consistent nonmonotonic behavior of the free energy barrier, justifying the soundness of our energy calculation model (SI Appendix, Fig. S29). Future efforts employing nanoparticles with various surface chemistry and film electrode with controllable surface roughness are highly favorable to comprehensively understand the structural basis of heterogeneous nucleation phenomenon.

Conclusion

In summary, we have demonstrated an SECCM coordinated with SEM method to map the bubble nucleation on a single-nanoparticle nucleant. In contrast to previous methods that measure heterogenous ice freezing (23) or vapor bubble nucleation (12, 54) on nanostructure-patterned surfaces using high-speed optical microscopy, the present approach not only can allow the measurement of single nucleation events one at a time, but also, it can provide quantitative local gas supersaturation and synchronously obtain correlated surface nanostructures. While the heterogeneous bubble nucleation process is significantly promoted by the local surface nanoconfinment, the critical gas concentration for nucleation shows a nonmonotonic relation with the radius of the nanoparticle. Such an optimum nanoparticle geometry is predicted from our theoretical calculation of the free energy barrier from classic nucleation theory. This study advances our understanding of how surface nanoscale defects can quantitatively trigger and control the heterogeneous nucleation process. We believe that this result offers alternative and complementary opportunities to manipulate surface bubbles for implications in gas-evolved energy conversion (55) and fine chemical engineering (4). The approach using a nanoparticle as a nucleation site will open many surface chemistry perspectives and can be facilely extended to a wide range of surface nucleation and electroplating processes.

Materials and Methods

Chemicals and Materials.

All chemicals were used as received. Sulfuric acid (H₂SO₄; 98%) and hydrochloric acid (37%) were purchased from Adamas-Beta. Tetraethyl orthosilicate (TEOS), n-hexyltriethyoxysilane, and sodium dodecyl sulfate (SDS) were purchased from Sinoreagent Chemistry. Ethanol, isopropanol, and (3-mercaptopropyl)triethoxysilane were purchased from Aladdin. Triethanolamine (TEA) was purchased from Alfa Aesar. Glassy carbon (10 × 10 × 2 mm) was purchased from Gaoss Union. Ultrapure water (18.2 MΩ cm, total organic carbon < 3 ppm) was used throughout this work.

SiO₂ Nanoparticle Synthesis.

SiO₂ colloids with radii of 5.3 and 3.4 nm were prepared according to a previously reported method (43). Specifically, in a 500-mL flask equipped with a reflux condenser, 10.40 g (or 2.75 g) TEOS was added to a 200 mL water solution under stirring, and the pH of the solution was adjusted to 9.5 using TEA. Then, the mixture was heated to 80 °C and kept for 12 h under mechanical stirring with a speed of 450 rpm.

SiO₂ colloids with radii larger than 5.3 nm were prepared using a two-step seeded growth from 5.3-nm-radius seed particles; 2.0 g SiO₂ seed particles aqueous dispersion (40 wt %) was diluted to 200 mL by aqueous solution with SDS concentration of 0.05 mg/mL. Then, TEA was added to adjust the pH to 9.5. Subsequently, the mixture was heated to 80 °C, and then, 9.7 g TEOS was added to initiate the first step of the seeded growth. The reaction solution was maintained at 80 °C for 12 h under mechanical stirring with a speed of 450 rpm. Vacuum distillation was performed to remove the ethanol generated from TEOS hydrolysis. Afterward, additional TEA was used to adjust the pH back to 9.5, and an extra 9.7 g TEOS was added into the mixture with another 12 h of mechanical stirring at 80 °C to complete growth. The obtained spherical SiO₂ nanoparticles were characterized by SEM or TEM (SI Appendix, Fig. S1).

Nanoparticles Deposition on Smooth Glassy Carbon.

The glassy carbon plates were first carefully polished prior to the deposition of SiO₂ nanoparticles. Typically, a glassy carbon substrate was soaked in ethyl alcohol solution and ultrapure water for 10 min to remove impurities followed by mechanical polishing with alumina powder of 30-nm nanoparticle size for 1 h. Afterward, the polished substrate was sonicated in a 1:1 (vol/vol) mixture of water and isopropanol followed by acetone for 10 min each. Then, the glassy carbon substrate was polished against a clean wet polishing pad to remove residual alumina particles. The substrate was sonicated in ethyl alcohol solution and ultrapure water for 10 min to ensure thorough cleaning. Finally, the substrate was dried with N₂ flow, and SEM was used to inspect that the cleaned surface was free of alumina particles. A tapping mode atomic force microscope (Bruker Multimode 8) confirmed that the polished surface has a local rms roughness of ∼1.35 nm (SI Appendix, Fig. S2).

A sparse loading of SiO₂ nanoparticles on the glassy carbon substrate is important for the subsequent single-entity bubble nucleation study. Before deposition, the SiO₂ nanoparticles were centrifuged six to eight times to remove surfactants on the surface. After the SiO₂ nanoparticle solution (∼10¹⁰/mL) was diluted to a number density about ∼10⁶/mL, a 20-μL droplet was deposited on the cleaned glassy carbon surface and left to dry at ∼40 °C. Finally, the dried glassy carbon was immersed into a clean acidic solution for ∼2 min to remove remaining SDS surfactant. SEM (HITACHI S-400) was used to inspect that SiO₂ nanoparticles are sparsely dispersed on the smooth surface and that obvious aggregation is not observed. For small SiO₂ nanoparticles, tapping mode AFM was used to confirm their dispersion on the glassy carbon surface (SI Appendix, Fig. S2).

Micropipettes Preparation.

Micropipettes were fabricated from borosilicate glass capillaries (1.0 mm outer diameter, 0.55 mm inner diameter) using a puller (Sutter Instruments P-1000). Micropipettes with tip opening radius of 1.5 μm were prepared with the parameters of heat = 535, pull = 0, velocity = 150, delay = 0, and PRESSURE = 200 and cut by a quartz knife for the target tip size. The dimension of micropipettes was characterized with SEM.

SECCM Procedure.

The SECCM experiments were carried out by a homebuilt SECCM instrument, as previously developed by Unwin and coworkers (29, 56), and controlled by Warwick Electrochemical Scanning Probe Microscopy software. A single-barrel glass pipette with tip opening radius of 1.5 μm prepared from the puller was used as the scanning probe and mounted to a pipette holder (SI Appendix, Fig. S3). The pipette was filled with 2.0 M H₂SO₄ aqueous solution as the electrolyte, and an Ag/AgCl wire was inserted as QRCE. In the experiment, the scanning probe was first slowly brought down to the substrate by a piezoelectric motor (P-622.1CD; Physik Instrumente) in the z direction, while the position of the substrate was controlled by a xy piezoelectric motor (P-542.2CD; Physik Instrumente). During the approach, the current flows through the circuit at appropriate potential (–1.5 V vs. Ag/AgCl) are monitored using a Heka EPC-10 amplifier. Once the meniscus droplet at the pipette tip ending contacts the conducting substrate, the piezoelectric motor will simultaneously stop, and a microsized electrochemical cell is formed. Electrochemical measurements, such as potentiostatic and galvanostatic method, are performed to study the local electrochemical bubble nucleation, and the scanning hopping mode is conducted to achieve electrochemical mapping across the substrate (57–59).

Theoretical Calculation of Free Energy.

According to the classic nucleation theory, the bubble nucleation rate is controlled by the gas supersaturation and the energy barrier. The gas molecules from electrogeneration are assumed to be entrapped within the nanoconfinement between the SiO₂ nanoparticle and the glassy carbon surface. There are three nucleation paths according to the geometric size of the bubble nucleus (Fig. 4A and SI Appendix, Fig. S25). Considering a constant volume closed system of uniform and constant temperature containing a gas nucleus surrounded by liquid, the change in the free energy during gas nucleus growing can be calculated from the volume, chemical potential, and interface:

$$\mathrm{\Delta }G=-\mathrm{\Delta }PV+N\mathrm{\Delta }\mu +{\displaystyle \sum \gamma A}.$$ [1]

Assume that the contact angles of the bubble with SiO₂ and glassy carbon surface are the Young contact angles and H₂ is the only gas. For an SiO₂ nanoparticle with a given radius, the bubble nucleus follows the nucleation path, and a nucleation barrier, $\mathrm{\Delta }{G}^{*}$, can be calculated as a function of nanoparticle radius.

Data Availability

All study data are included in the article and/or SI Appendix.