Anomalous metals: From “failed superconductor” to “failed insulator”

Significance

A ubiquitous observation of robust metallic ground states arising from “failed superconductors” has attracted much attention in recent years because it presents a fundamental challenge to the standard theory of electron fluids. Meanwhile, observations of analogous metallic phases arising from “failed insulators” are often overlooked in analysis of similar data. Aiming to reconcile observations of both regimes in strongly granular In/InO_x two-dimensional films, we propose a unified understanding of these seemingly different anomalous metallic phases by drawing connections to resistive-capacitive-shunted Josephson junction arrays. Effects of quantum phase/charge fluctuations and macroscopic quantum tunneling are invoked to understand the anomalous metallic phase, thus advancing fundamental understandings of metals beyond the standard Fermi liquid theory.

Abstract

Resistivity saturation is found on both superconducting and insulating sides of an “avoided” magnetic-field-tuned superconductor-to-insulator transition (H-SIT) in a two-dimensional In/InO_x composite, where the anomalous metallic behavior cuts off conductivity or resistivity divergence in the zero-temperature limit. The granular morphology of the material implies a system of Josephson junctions (JJs) with a broad distribution of Josephson coupling E_J and charging energy E_C, with an H-SIT determined by the competition between E_J and E_C. By virtue of self-duality across the true H-SIT, we invoke macroscopic quantum tunneling effects to explain the temperature-independent resistance where the “failed superconductor” side is a consequence of phase fluctuations and the “failed insulator” side results from charge fluctuations. While true self-duality is lost in the avoided transition, its vestiges are argued to persist, owing to the incipient duality of the percolative nature of the dissipative path in the underlying random JJ system.

An increasing number of recent experiments on disordered superconducting films, initially searching for a superconductor-to-insulator transition (SIT), end up instead with an “avoided” transition, where scaling about a putative zero-temperature quantum critical point fails in the limit $T\to 0$, giving way to a phase characterized by a resistance that levels off to a constant value independent of temperature (1–8). This “anomalous metallic state” (AMS) seems to exhibit electronic properties that cannot be understood on the basis of the standard paradigms for transport in disordered two-dimensional (2D) metals (for a recent review, see ref. 9). While extensive efforts have been devoted to understanding AMSs on the superconducting side, termed a “failed superconductor,” (9) and its transition to a “true” superconducting state (10), the complementary leveling of resistance on the insulating side of the same avoided SIT is often overlooked. Here, an initial resistivity divergence trend for $T\to 0$ is replaced with distinct saturation, exhibiting resistivity values that can be orders-of-magnitude higher than quantum of resistance for Cooper pairs $R_Q=h/4e^2\sim 6.45\hspace{0.17em}\text{k}\mathrm{\Omega }$. This ubiquitous behavior of a “failed insulator” can be found in studies of ultrathin granular metal films (11), amorphous metal-insulator films (3, 12), and Josephson junction (JJ) arrays (13).

In this paper, we propose a unified phenomenology for the emergence of AMSs from an avoided SIT in disordered superconducting films. Focusing on the magnetic-field-tuned SIT (H-SIT) in a strongly granular system of In-on-InO_x composites, we show that vestiges of the self-duality observed in a true H-SIT (14, 15) are still pronounced in the AMS on both sides of the avoided H-SIT (8), including the resistance saturation. Bearing in mind that, from its nature, the critical point of any SIT yields an anomalous metal, we propose that the broadening of the metallic phase on both sides of the H-SIT has the same origin modulo the dual relation between phase of the order parameter (or vortices) and charge (both Cooper pairs and single electrons). Specifically, we argue that the low-temperature resistance can be interpreted as a sum of a temperature-dependent activation term and a temperature-independent term associated with quantum fluctuations, leading to macroscopic quantum tunneling (MQT) of the phase and/or the charge. On the superconducting side, a superconductor-to-quantum-metal transition (SQMT) appears with the destruction of global phase coherence (9, 16, 17), while on the insulating side, quantum charge fluctuations prevent the establishment of a Coulomb-blockade-driven insulating state (13, 18, 19) driving a quantum-metal-to-insulator transition (QMIT).

The robustness of the anomalous metallic phase in the In/InO_x system (8) further enforces these expanded observations, while strongly contending interpretations solely based on nonequilibrium effects and responses to extrinsic effects of the electronic system (20) (see also Materials and Methods). At the same time, the temperature-independent term associated with MQT depends delicately on the details of the distribution of grains and junctions, which may be controlled by external effects leading to different saturation values of the resistance, emphasizing its nonuniversal value in the anomalous metal regime. This, in turn, leads us to propose the phase diagram of Fig. 1 and suggest a unified understanding of AMSs in disordered superconducting films. Excluding the regime where pairs are no longer present, this phase diagram has strong resemblance to that of 2D electron gas about half-filled Landau levels (21).

Fig. 1.

Zero-temperature phase diagram of a 2D granular superconductor with two controlling parameters. In the present study, X1 is magnetic field and X2 is intergrain coupling. The shaded area represents the region in parameter space where anomalous metal appears. The thick solid line represents a true H-SIT (15), while the other solid lines represent the transition from a superconductor to a quantum anomalous metal (SQMT) and from a quantum anomalous metal to an insulator (QMIT). Dashed lines represent cross-overs from a Bose-dominated system, where superconducting In islands provide the source of pairing, to a normal-electrons insulator. The dash-dotted line represents the cross-over from phase to charge-dominated quantum anomalous metal state. Full circles represent a quantum critical point for a particular realization of the control parameters, while an open circle is a cross-over point. See Discussion for further explanations.

Whether samples are inherently inhomogeneous, such as arrays of Josephson junctions (JJs), or morphologically uniform, such as amorphous films, superconducting pairing interaction tends to “amplify” mesoscopic fluctuations of the disorder and its associated Coulomb interaction, resulting in an effective granular morphology (22–25). Such puddle morphology was also argued to be a consequence of the competition between the local potential of randomly distributed charged impurities and screening by holes or by strongly bound Cooper pairs, yielding a similar phase diagram to our Fig. 1 (26). Therefore, it is reasonable to assume that the superconducting transition in 2D disordered metallic films is dominated by phase fluctuations (16, 17, 27), and the material can be modeled as superconducting grains embedded in a tunable intergrain coupling matrix. Here, we emphasize the truly 2D granular morphology of our indium-on-indium–oxide (In/InO_x) system, as shown in Fig. 2, which will be a key to our understanding of the data.

Fig. 2.

Morphology of the In/InO_x system. (A) Scanning electron microscopy image of the In/InO_x sample. Bright grains are metallic In islands, while the dark background is a uniform underlying layer of weakly insulating amorphous InO_x. Note the broad distribution of grain sizes, including the interstitial ones. (Scale bar: 1 µm.) (B) Distribution of grain size. Note the two broad peaks at $\sim 0.03$ µm and $\sim 0.5$ µm. See SI Appendix for details in our image analysis (28).

While local pair amplitude fluctuations depend on the grain size (29), global superconductivity is achieved via the establishment of a percolating path of phase coherence (30–33) through Josephson coupling of pairs of adjacent grains. For a given pair {ij}, $E_J^{ij}$ is a function of the local gaps Δ_i and Δ_j and the intergrain normal-state resistance $R_n^{ij}$. However, the granular nature of 2D disordered films also requires that we consider the capacitance (both intergrain and self) involved and the associated charging energy $E_C^{ij}$, which is a function of the local density at the grains n_i and n_j, and the dielectric constant of the intergrain material ${\chi }_n^{ij}$. An insulating phase is the result of Coulomb blockade, which prevents Cooper pairs tunneling between adjacent grains. For a granular film with typical Josephson energy E_J and charging energy E_C, the ratio $\gamma \equiv E_J/E_C$ determines the occurrence of SIT (19, 34, 35). Besides the initial film morphology, other external parameters, such as an applied magnetic field or carrier density modulation through an applied gate, can be used to control γ.

Results

In Fig. 3, we plot temperature dependence of resistivity in varying perpendicular magnetic fields across three annealing stages, S0, S1, and S2, of the same initial sample. Low-temperature annealing ($<50{\hspace{0.17em}}^{°}$C) is well-known (36) to irreversibly reduce sample resistance, yet maintain an amorphous nature of the underlying InO_x, thus altering the dielectric response in the poorly conducting matrix that couples superconducting grains. We restrict the range of magnetic field in this analysis to under 600 Oe to ensure robust superconductivity within the single grain (15).

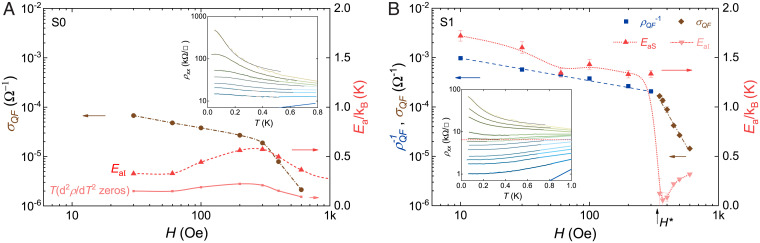
Fig. 3.

Temperature dependence of resistivity. $\rho (T)$ in varying magnetic field for three successive annealing stages S0 through S2 is shown. The dotted lines in S0 connect cooling data $<0.7$ K with a field sweep at 1.1 K.

Annealing stage S0 shows the most salient signatures of resistivity saturation on the insulating side of an avoided SIT. In zero field, as temperature is lowered, resistivity decreases and saturates at around 6.2 k$\mathrm{\Omega }/\square$ as a failed superconductor. A magnetic field as low as 30 Oe flips the temperature coefficient of resistance to negative, as in an insulator. However, the resistivity upturn gives way to saturation at around 0.2 K, eventually settling at a finite value as $T\to 0$. In higher fields, the features are qualitatively similar, until at 600 Oe, where resistivity strongly diverges, and no saturation is found above our base temperature. In a broad range of magnetic field, we identify an insulator where resistivity fails to diverge as $T\to 0$, dubbed as a failed insulator.

In contrast, annealing stage S1 or S2 develops a superconducting ground state in zero field, where the T_c is just below our base temperature for S1, while $T_c\approx 0.4$ K for S2. Nevertheless, in low field, $\lesssim 400$ Oe, the ground state is a failed superconductor and has been discussed extensively (8). For S1, at 400 Oe, the system is right on the insulating side of the transition, yet the resistivity saturates as $T\to 0$, despite an upturn at $\sim 0.2$ K. In higher field, $\gtrsim 400$ Oe for both S1 and S2, resistivity saturation is substantially reduced, and the temperature dependence can be fitted by a logarithmic divergence with a large prefactor (8). Such logarithmic divergence is in stark contrast with the saturated resistivity in S0. Resistivity of insulators typically has exponential (hopping) or weak granularity-induced divergence persisting to zero temperature, meaning that their curvature $d^2\rho /d{T}^2$ remains positive as $T\to 0$. However, in S0, the resistivity divergence is cut off by a saturation, marked by a sign change in the curvature in the temperature dependence at around 0.2 K (Fig. 4A).

Fig. 4.

Evolution of resistivity saturation in magnetic field. (A) Temperature-independent term σ_QF (left axis) and activation temperature $E_a/k_B$ (right axis) extracted from the fits. Also shown are the zeros (light red) in the curvatures of $\rho (T)$. (A, Inset) Temperature dependence of resistivity in S0 fitted by empirical law Eq. 1. (B) Temperature-independent term ${\rho }_{QF}^{-1}$ ($■$) or σ_QF ($♦$) (left axis) and activation temperature $E_a/k_B$ (right axis) extracted from the fits. (B, Inset) Temperature dependence of resistivity in S1 fitted by empirical laws Eq. 2 for $H\le H^{*}$ and Eq. 1 for $H\ge H^{*}$. Also shown is Cooper-pair quantum of resistance $R_Q=h/4e^2\sim 6.5\hspace{0.17em}\text{k}\mathrm{\Omega }/\square$ as the red separatrix. Dotted and dashed lines are guidance to the eye.

To quantitatively analyze the evolution of resistivity behavior as a function of magnetic field on the insulating side, we adopt an empirical functional form Eq. 1, which satisfactorily fits S0 data, as shown in Fig. 4A. This empirical law was previously employed (13) to describe an analogous conductivity saturation in insulating JJ arrays. The saturation was modeled as a consequence of a temperature-independent quantum fluctuation term σ_QF, in addition to thermally activated conductivity on the insulating side with activation energy E_aI and a proportionality constant σ₀. In writing this equation, we assume that the Hall conductivity is zero:

$$\rho (T)={[{\sigma }_{QF}+{\sigma }_0·\exp (-E_{aI}/k_{B}T)]}^{-1}.$$ [1]

Fig. 4A shows an overlay of the extracted quantum fluctuation contribution σ_QF (left axis) and activation temperature $E_a/k_B$ (right axis) as a function of magnetic field. Since σ_QF is intimately related to the saturation, it decreases as the field increases until around 600 Oe, where the divergence is restored and the saturation disappears. Meanwhile, the activation temperature starts off at around 0.3 K, peaks at just below 0.6 K near 300 Oe, and subsequently decreases before leveling off at high fields. Since the overall tendency for an insulating behavior is governed by the charging energy, we may estimate $E_{aI}\approx \alpha E_C$, where $\alpha \approx 1/\langle z\rangle$ and $\langle z\rangle \approx 6$ is the average coordination number of the random array of indium grains of average size $\sim 0.1$ µm (8). Taking a dielectric constant of $\sim 10$ for the InO_x and average distance between grains of $\sim 10$ nm, we obtain E_aI in the range that we find experimentally in Fig. 4A. The corresponding ${({\sigma }_{QF})}^{-1}$ increases in the high-field limit to the order of $\sim 1$ MΩ, emphasizing the fact that this saturated resistance is much larger than the quantum of resistance R_Q.

To quantitatively analyze resistivity saturation on the superconducting side, we adopt a similar empirical law by exchanging the role of resistivity ρ and conductivity σ, justified as a manifestation of charge-phase correspondence (or particle-vortex duality) near either a direct SIT or an avoided SIT—a cross-over between failed superconductors and failed insulators (8, 14).

$$\rho (T)={\rho }_{QF}+{\rho }_0·\exp (-E_{aS}/k_{B}T),$$ [2]

where ρ_QF is an analogous temperature-independent contribution to resistivity and E_aS is activation energy on the superconducting side. Fits of this form to resistivity of S1 are shown in Fig. 4B, where Eq. 1 is used for $H\ge 350$ Oe and Eq. 2 for $H\le 300$ Oe. The left y axis shows ${\rho }_{QF}^{-1}$ from low field and σ_QF from high field in the same plot. Quantum fluctuation contribution ρ_QF grows (or, equivalently, ${\rho }_{QF}^{-1}$ shrinks) upon increasing field, while quantum fluctuation contribution σ_QF shrinks in higher fields. The field dependence for either branch is a power law with ${\rho }_{QF}^{-1}\propto H^{-0.45}$ and ${\sigma }_{QF}\propto H^{-4.7}$. Activation temperature on the low-field side is around 1.5 K and gradually decreasing, until a sharp drop at $H^{*}\sim 300$ Oe, where the sample switches to insulating behavior. Besides a factor of ∼4 difference between activation temperatures in the two regimes, the qualitative trend in the field is consistent with those in S0. The dome-shaped presence of ρ_QF and σ_QF suggests that quantum fluctuations play important roles in both regimes of anomalous metallic phase.

Discussion

The evolution of zero-temperature behaviors of resistivity in S0 and S1 leads us to a holistic understanding of the T = 0 phase diagram in Fig. 1. We identify the blue trace (SQMT) as a magnetic-field-tuned (or annealing-tuned) quantum superconductor–anomalous-metal transition (solid line), followed by a transition to an insulating ground state (solid line). The anomalous metallic regime can be further divided into failed-superconductor and failed-insulator regimes, separated by an avoided SIT (dash-dot line) representing a wide cross-over regime. We also identify the green trace as an annealing-tuned failed-insulator–failed-superconductor transition (QMIT), similar to the magnetic-field-controlled scenario, despite a fundamental difference in the nature of these two control parameters. As an example, universal anomalous metallic behaviors under different tuning parameters were recently discussed in ref. 37. Finally, a direct SIT that is typically found in homogeneous films or granular materials with stronger coupling is shown as the red trace (SIT), while transition to a disordered 2D metallic phase appears when Cooper pairs are broken (dashed line). Within our granular system of In/InO_x composite, a true H-SIT (15) can be tuned to unveil an avoided H-SIT, which was previously shown to exhibit vestiges of self-duality around the putative quantum critical point (8).

The analysis presented in Results explores the duality idea in a wider temperature range, which includes the resistance saturation associated with the AMS, thus providing further insight into the possible origin of this enigmatic phase. The fact that the data show a continuous evolution from an AMS with very low sheet resistance to one with very large sheet resistance that far exceeds even the fermion quantum of resistance, $h/e^2$, suggests that the superconducting grains and the intergrain tunneling play the key role in determining the saturation value—that is, ${({\sigma }_{QF})}^{-1}$ in Eq. 1 smoothly connects to ρ_QF in Eq. 2. Focusing on Fig. 4B, it shows that the separating saturation resistance between the two regimes is $\sim 6.5$ k$\mathrm{\Omega }/\square$ at the field of $H^{*}\approx 300$ Oe, where the curves change character as a result of the avoided H-SIT. The drop in activation energy between $|E_a{|}_{H\lesssim H^{*}}$ and $|E_a{|}_{H\gg H^{*}}$ is a factor of 4. Since $H^{*}$ marks an avoided transition, where we expect $E_J\sim E_C$, then, we conclude that E_aI saturates to $\frac{1}{4}{E}_C$, as was previously observed for ordered arrays of JJs (13, 38). This further suggests that for $H\gg H^{*}$, the saturation is associated with charge fluctuations. From examination of the samples in the reverse direction of annealing (S2 to S1 to S0), we suggest that we observe a smooth cross-over of macroscopic quantum effect from a regime dominated by Josephson coupling to a regime dominated by Coulomb interaction, which, for each realization of coupling (annealing) and magnetic field, could be attributed to a single junction behavior in the respective regime.

Starting from a single resistively-capacitively-shunted JJ with $E_J\gg E_C$, for a small bias current, a phase difference is established along the junction, resulting in a zero-voltage supercurrent. However, at very low temperatures, where activation is exponentially small, quantum fluctuations of the phase induce quantum tunneling of the phase variable (39) and, thus, a finite voltage (40, 41). With increasing charging energy, and in the limit $E_J\ll E_C$, a dual situation is expected, where the electric charge on the junction capacitance, which conjugates to the junction’s phase, results in Coulomb blockade and, thus, an insulating state. For a small bias voltage, quantum fluctuations of the charge may give rise to a coherent current of Cooper pairs and to dissipation due to single-electron tunneling (42). The latter is also a macroscopic quantum effect due to the participation of the collective electron system in the process (43, 44).

To rationalize the analogy with a single resistively-capacitively-shunted JJ, we follow Fisher (45), assuming that junctions in the $E_J\gg E_C$ regime (samples S2 and S1) are resistively shunted with a wide distribution of shunt resistors. While, in general, the idea of a normal conductance channel was challenged in the limit of $T\ll T_c$ for an ordered array of JJs (46), we believe that it is natural to expect normal regions in a random array of grains, such as in our In/InO_x composite, especially in the presence of magnetic field (8, 15). Using an Ambegaokar–Halperin–Langer (AHL) approach (47), we assume that there exists a set of junctions that are coupled to shunt resistors large enough to allow phase slips and are connected to form an infinite network that spans the system. By the nature of the effect where the phase slips span the size of the sample for a magnetic field $H_{SM}\ll H_c^{*}$, we can map it on a random-resistor network (RRN) percolation problem, which at very low temperature, for a given tuning parameter (here, the magnetic field), is self-organized to be at criticality. Note that, as such, our approach is fully quantum mechanical in a similar way that AHL describes variable range hopping on the insulating side of Anderson localization (see, e.g., ref. 48). A well-known result for percolation theory is that the resistance above percolation is bounded from below by the total resistance of the so-called “singly connected bonds” (49–51)—that is, the bonds that, if cut, will disrupt the integrity of the infinite network. Near criticality, for a system of size L, the average conductance is given by $\langle G\rangle =L^{d-1}\langle g_1\rangle$, where d is the dimensionality and g₁ is the linear conductance of the chain of singly connected bonds estimated here as $\langle g_1\rangle \sim 1/L{r}_s$, where r_s is the limiting shunt resistance (52). In two dimensions, the value of the saturated resistivity within this RRN-percolation model is easily estimated as ${\rho }_s\approx {\langle G\rangle }^{-1}\approx r_s$. Thus, the regime of anomalous metal is a consequence of MQT through junctions characterized by $r_s\ll R_Q$.

Turning to the more insulating samples (S0 and high-field S1), the intergrain-mediating InO_x layer is insulating enough (single-junction resistance $\gg R_Q$) to prevent an infinite cluster of percolating phase-coherent superconducting grains, even at zero magnetic field. At a finite field, $E_C/E_J\gg 1$, and with mesoscopic fluctuations in local conductance, dissipation may arise from a shunt resistor, or discrete tunneling of quasiparticles and shot noise, irrespective of the otherwise macroscopic effect of localization in the 2D InOx system (42). In this regime, the small grains, which appear interstitially between the larger superconducting islands, become the bottleneck for continuous conduction due to their large charging energy, satisfying $E_C\gg E_J$. This situation is amplified with increasing magnetic field, where more of the weaker junctions between large superconducting islands lose phase coherence. At the same time, a true insulating state as a consequence of Coulomb blockade may fail because of MQT of charge (13, 44). This dual behavior to the phase-MQT suggests to extend the percolation description according to Ambegaokar, Halperin, and Langer results (47) to the insulating side, where a saturated resistivity is expected with limiting junction shunt resistance $r_s\gg R_Q$ and $E_C\gg E_J$.

The phase-charge duality is further understood by the intrinsic duality of the RRN of the randomly distributed shunt resistances underlying the JJ array. Indeed, there is an exact relation between the bulk effective conductivity of a 2D continuing composite made of two isotropic components and that of the dual composite (51, 53–57). For a rectangular array of JJs representing bonds with resistances $\left\{r_i\right\}$ and conductances $\left\{g_i\right\}$ (where $g_i^D=1/g_i\equiv r_i$), the dual total conductance $G_x^D(g_1^D,g_2^D\dots .\hspace{0.17em}{g}_N^D)$ along the x direction is related to the conductance along the y direction $G_y(g_1,g_2,\dots g_N)\equiv 1/R_y(r_1,r_2,\dots r_N)$ as: $G_x^D=1/G_y$. The same average behavior is expected for the random system, which is manifested in our random In/InO_x composite (51, 53, 54): $\langle G_x^D\rangle =\langle R_y\rangle$. The charge-phase correspondence maps onto the RRN duality and further reinforces the vestiges of duality that originate from the H-SIT, as suggested by Shimshoni et al. (22).

A further consequence of the above model is the realization of the fragility of the superconducting or insulating states, from which the failed superconductor and failed insulator emerge. Besides the annealing and magnetic field, any perturbation applied to the system strongly affects the distribution of junction properties, thus leading to a shift in the potential barrier for the MQT process, resulting in a shift of the saturated resistance. For example, external radiation can work to enhance the quantum fluctuations, and, thus, AMS will emerge with larger saturated resistance as $T\to 0$ (20), or reduce them and thus pin the superconducting state (8). Similarly, a ground plane near a sample can provide another dissipation channel to pin the superconducting state, as well as alter the charging energies to modify the saturation on the insulating side; both effects were observed in JJ arrays (58) and in highly disordered films (59).

In summary, we identify two regimes in anomalous metallic phase—a failed superconductor and a failed insulator, as clearly suggested by resistivity saturation on both sides of an avoided SIT. The close connection between our granular composite and JJ arrays is revealed by a set of empirical fits to the temperature dependence of resistivity. Quantum fluctuations of phase drive the transition from superconductor to anomalous metal when superconductors fail to establish global phase coherence, while quantum fluctuations of charge number drive the transition from insulator to anomalous metal when charge localization gives way to dissipative transport. A duality picture is strongly justified in our discussions by interchanging the roles of N and $\varphi$ and corroborated by the resemblance of transport behaviors when exchanging the roles of ρ and σ.

Materials and Methods

InO_x/In granular composites were grown by electron-beam evaporation of In₂O₃ in oxygen partial pressure, followed by that of In under high vacuum. Consecutive in situ depositions of the two components resulted in a clean interface that is crucial for optimal interface coupling. The uniform underlying amorphous InO_x was specifically prepared to be weakly insulating to mediate couplings among the In grains and nearby proximitized regions. Details of the sample preparation process were provided in ref. 8.

Resistivity was measured on a patterned Hall-bar sample using standard four-point lock-in technique. Current excitation was provided by reference alternating-current voltage source in series with a 1-GΩ resistor that was much more resistive than any measured sample resistance in this study. The current intensity ranged from 0.1 nA to 1 nA, while the frequency varied between 0.7 and 7 Hz, depending on sample resistance. Linear response to excitation current was confirmed at the highest resistance. Temperature ramps were sufficiently slow compared to the prolonged time constant.

In our dilution refrigerator, all measurement wires were filtered at both room temperature and mixing-chamber temperature ($T\gtrsim 10$ mK) using commercial in-line pi filters and cryogenic filters, achieving over 100-dB attenuation throughout the 100-MHz to 5-GHz range. Sample phonon temperature was measured by a calibrated on-chip RuO₂ thermometer subject to the same mounting and wiring as the sample. Data were not considered in our analysis when sample temperature differed more than 10% from mixing-chamber temperature. The refrigerator was operating at the highest cooling power with an extra circulation pump running, despite at the cost of a higher base (mixing chamber) temperature.

Data Availability

Some study data are available. The data that support the findings of this study are accessible upon reasonable request on Zenodo (DOI: 10.5281/zenodo.6622148) (60). Previously published data were used for this work. A small portion of the data has been published (though plotted differently) in ref. 8. In that paper, we focused on sample S2 and the robustness of the failed superconductor state. In this paper, we focus on samples S0 and S1, the possible mechanism behind the metallic states, and introduce the idea of a failed insulator that connects to the failed superconductor state.