Emergency medical resource allocation among hospitals with non-regressive production technology: A DEA-based approach

Abstract

This paper proposes an approach for medical resource allocation among hospitals under public health emergencies based on data envelopment analysis (DEA). First, the DEA non-regressive production technology is adopted to ensure that the DMU can always refer to the most advanced production technology throughout all production periods. Based on the non-regressive production technology, two efficiency evaluation models are presented to calculate the efficiencies of DMUs before and after resource allocation. Our theoretical analysis shows that all the DMUs can be efficient after medical resource allocation, and thus a novel resource allocation possibility set is developed. Further, two objectives are considered and a bi-objective resource allocation model is developed. One objective is to maximize the output target realizability of the DMUs, while the other is to ensure the allocated resource to each DMU fits with its operation size, preperformance, and operation practice (i.e., proportion of critically ill patients). Additionally, a trade-off model is proposed to solve the bi-objective model to obtain the final resource allocation results. The proposed approach contributes by ensuring that the medical resources are allocated in such a way that they can all be efficiently used as well as considering multiple objectives and practical constraints that make the approach more fitted with the practical application scenarios. Finally, a case study of 30 hospitals in Wuhan during the COVID-19 epidemic is applied to illustrate the proposed approach.

1. Introduction

The outbreak of COVID-19 has caused massive casualties and incalculable economic loss. Until May 1, 2021, 152,014,757 confirmed cases and 3,191,540 deaths had been reported worldwide.1 In the early stage of the COVID-19 epidemic, Wuhan was the most severely affected area in the world. Demand for medical resources surged, the market-led supply mechanism was malfunctioning, the shortage of medical materials was severe, and medical materials were difficult to dock in time. Owing to the sudden outbreak of the epidemic, commonly used personal protective equipment (PPE), such as protective clothing, medical-surgical masks, N95 masks, and rubber gloves, were severely insufficient to meet the demand of patients and medical personnel in hospitals. To help Wuhan fight against COVID-19, people from all walks of life have donated medical supplies. Donations, general supplies, and medical supplies were concentratedly received by the Wuhan Municipal Charity Federation and the Red Cross Society. Furthermore, to address the shortage of hospital beds and the difficulty of attending fever clinics, Wuhan announced the 55 designated hospitals (e.g., Hankou Hospital). The outpatient departments of these hospitals all serve as fever clinics and provide beds to centralize the treatment of fever patients in Wuhan. Moreover, medical teams were dispatched nationwide to support Wuhan. According to the National Health and Wellness Commission, as of February 17, 2020, more than 30,000 medical staff had been sent to support Wuhan, mainly from respiratory, infection, critical care, and other specialties. Although medical materials donations and medical staff had been sent to Wuhan to overcome the problem of medical resource shortages, the government institutions lacked the professional experience to quickly and adequately allocate and dispatch these resources to the hospitals. Additionally, during the early stage of the epidemic, the consumption of medical resources was much greater than that supplied, leaving the front-line medical supplies in the epidemic-affected hospitals still highly scarce. As a result, the response to the epidemic was extremely inefficient, and social panic ensued. Therefore, the quick and efficient allocation of emergency medical resources during public health emergencies is essential to save lives and reduce loss during public health emergencies. The issue of emergency medical resource allocation is worthy of further investigation.

Data envelopment analysis (DEA), developed initially by Charnes et al. (1978), is a data-driven and non-parametric approach. This method is usually applied to evaluate a group of homogenous decision-making units’ (DMUs) performances. It is widely used in operations management and economics because of its unique advantages in dealing with multiple inputs and outputs. Scholars have extended the DEA models for fixed cost/resource allocation and investigated the health system’s performance. However, few studies have investigated the problem of allocating limited medical resources allocation among hospitals under public health emergencies (Yang, 2017, Sun and Luo, 2017, Nepomuceno et al., 2020, Liu and Liu, 2021). Under the context of public health emergencies, the medical resources should be appropriately allocated among the hospitals to ensure the efficient use of the medical resources and regular operation. Additionally, to better fit the reality, several inevitable constraints cannot be ignored in specific scenarios (for instance, setting a lower boundary limitation of patients’ admission capacity for each hospital and considering the structural characteristics of patients in various hospitals). In addition, when establishing a medical resources allocation strategy, multiple factors such as the operation size, preperformance, and the proportion of critically ill patients are taken into account from the standpoint of fairness and efficiency. Therefore, when allocating medical resources under public health emergencies, it is necessary to consider the efficient utilization of medical resources and achievement of multiple goals. However, the existing DEA-based resource allocation methods are not sufficient to solve this problem.

To fill the research gap discussed above, this study presents a DEA-based approach for emergency medical resource allocation among hospitals under public health emergencies (e.g., the COVID-19 epidemic). We first adopt the non-regressive production technology in DEA to ensure that the hospitals (called decision-making units, DMUs, in DEA) can always refer to the most advanced production technology over production periods. Then, two models are developed to evaluate DMUs’ efficiencies before and after resource allocation. Based on theoretical analysis, we point out that there is always a feasible resource allocation result that can make all the DMUs efficient after resource allocation. According to this finding, we propose the resource allocation possibility set, which ensures that all the DMUs are efficient and some essential medical requirements are fulfilled after resource allocation. Further, two objectives are considered, and a bi-objective resource allocation model is developed. One objective aims to maximize the output target realizability of the DMUs. The other guarantees the resource allocation results fit with each DMU’s operation size, preperformance, and operation practice. Furthermore, a trade-off model is adopted to solve the bi-objective model and further obtain the final resource allocation solutions. Finally, we illustrate the proposed approach with a case study of 30 hospitals in Wuhan during the COVID-19 epidemic.

This paper has at least four theoretical contributions. First, our approach guarantees that all the DMUs are efficient after resource allocation, which means efficient utilization of limited resources is realized. Second, a resource allocation possibility set with a non-regressive production frontier is proposed by adopting current and historical data, ensuring continuous optimization of production technology throughout the whole period. Third, to cope with the practical and managerial requirements, our approach considers pre-performance, operation size, and the proportion of critically ill patients when determining the final resource allocation results. Additionally, we have added some constraints of patients’ admission capacity of hospitals when setting output targets. Such settings have made our approach more fitted to managerial practices. Finally, we consider the output target realizability of the DMUs when making resource allocation decisions so that the output targets in the new production period can be realized more easily.

The remainder of this paper is organized as follows. Related literature is reviewed in Section 2. Section 3 proposes two models for the efficiency evaluation of DMUs before and after resource allocation. Section 4 provides a dynamic bi-objective resource allocation approach. In Section 5, a case study of 30 hospitals in Wuhan is carried out to illustrate the proposed method. Finally, Section 6 presents the conclusions and offers several ideas for future work.

2. Literature review

This section reviews previous relevant studies in terms of DEA-based fixed cost/resource allocation and DEA applications in the medical field and emergency management.

2.1. DEA-based fixed cost/resource allocation

Generally, DEA-based fixed cost/resource allocation research can be characterized into two types.

The first category adopts the principle of efficiency invariance, which was first proposed by Cook and Kress (1999). According to efficiency invariance, all DMUs’ efficiencies remain unchanged after fixed cost/resource allocation. Cook and Kress (1999) put forward one more principle, namely “Pareto-minimality,” which indicates that the fixed cost cannot be moved from one DMU to any of the other DMUs in the fixed cost allocation result. Cook and Zhu (2005) pointed out that Cook and Kress (1999)’s approach is only applicable in the single-dimensional case (i.e., only one input resource in the DMU). Hence, they extended Cook and Kress (1999)’s work to handle multi-dimensional cases. To seek a fair allocation of resources among competing entities, Jahanshahloo et al. (2005) proposed a DEA-based allocation method, where efficiency invariance and output “Pareto-maximality” were preserved. Output “Pareto-maximality” means no resource (or fixed cost) is allowed to be adjusted from one DMU to another without breaking the rule of efficiency invariance. Lin (2011a) proved that the approach of Cook and Zhu (2005) might not find a feasible solution once a few specific constraints are attached. To this end, non-negative variables were introduced to prevent inefficient DMUs from sharing all resources, ensuring the feasibility of the approach even when constraints are imposed. Then, an output-oriented DEA resource allocation model was proposed on the premise of the minimal deviation principle, which guarantees that the distance between the target resources and the proportion of resources can be reduced as much as possible. Lin (2011b) claimed that Jahanshahloo et al. (2005)’s model only utilizes the output proportions of DMUs, whereas other relevant factors (e.g., sizes of DMUs) are excluded. Therefore, Lin (2011b) developed a DEA-based resource allocation approach reflecting the DEA efficiency and the sizes of individual DMUs under the premise of the efficiency invariance principle. Specifically, the final results of the allocation are proportional to the sizes and efficiencies of DMUs. Lin and Chen (2016) explicitly explained that applying the “Pareto-minimality” principle is inappropriate because it does not guarantee a unique resource allocation result when only the efficiency invariance principle is adopted. Therefore, they proposed a super CCR-based method, which ensures obtaining a unique solution. Efficiency invariance and common weights were applied simultaneously by Li et al. (2017) for resource allocation. Their approach minimized the deviation between the plans generated by the common-weight principle and those by the efficiency invariance principle.

The second category uses the principle of efficiency maximization, which assumes that all DMUs are efficient and produce on the efficient frontier after fixed cost/resource allocation. It also indicates that we allocate the resource (or fixed cost) so that every part of it is used most efficiently. By maximizing the average efficiency of all DMUs, Beasley (2003) first presented a non-linear DEA model for resource allocation. However, Lozano and Villa (2004) pointed out that Beasley (2003)’s approach cannot guarantee that all DMUs are projected on the efficient frontier after allocation. A radial DEA-based resource allocation model was presented in a centralized pattern to address this issue. In this model, all DMUs can ensure that they can project onto the efficient frontier by minimizing the total inputs on the premise of a non-decrease in total outputs. They then extended their method to the non-radial scenario. Avellar et al. (2007) developed a spherical frontier DEA model by assuming that the DEA production frontier is concave under the constant returns to scale assumption. To do this, a smooth frontier was used to substitute for the initial piece-wise DEA frontier. Afterward, a simple constraint that defines the post-allocation efficiency of each DMU as equal to unity was added to ensure that all DMUs are efficient after reallocation. Guedes et al. (2012) extended Avellar et al. (2007)’s model to an adjusted spherical frontier model. They further illustrated that the new model could provide a resource allocation result that is more consistent with the result of Beasley (2003) compared with Avellar et al. (2007)’s model. Under the framework of centralized decision-making, Lotfi et al. (2013) provided a mechanism regarding a common-weight principle for allocating resources. Their approach minimizes the changes in resource and output targets and maximizes the post-allocation efficiency of DMUs. Similarly, from a centralized perspective, Wu et al. (2016) developed a resource allocation approach for the allocation of discretionary inputs considering the satisfaction degree of all evaluated DMUs on the premise of common-weight efficiency maximization. Sadeghi and Dehnokhalaji (2019) extended Lozano and Villa (2004)’s approach by assuming that the total resource to be allocated could be changed compared with the amount consumed in the last production period. Their approach further ensured that all evaluated DMUs could simultaneously be projected onto the efficient frontier. Zhang et al. (2018) pointed out that previous studies neglect the operation size growth of DMUs while allocating fixed costs. Thus, they developed a resource allocation approach that maximizes the global technical efficiency of DMUs while keeping the pure technical efficiency of each DMU unchanged after resource allocation.

Additionally, several studies investigate the DEA-based approaches for allocating resources while assuring the efficiency of DMUs is non-deteriorated after allocation (Bi et al., 2011, Hatami-Marbini et al., 2015, Ding et al., 2018, Yang et al., 2019, Kiaei and Matin, 2020, Bernardo et al., 2020, Dai et al., 2021).

Apart from the above-discussed studies, scholars have considered the DEA-based resource allocation problem from other aspects, for instance, setting more realizable output targets for DMUs (Yang et al., 2018, Jiang et al., 2020) and considering various relationships among DMUs using DEA cross-efficiency evaluation (Chen et al., 2020, Pendharkar, 2020).

Table 1 presents a summary of the existing DEA-based resource allocation approaches.

Table 1.

Comparison of resource allocation references.

Studies	Allocation principles			Weights
	Efficiency Invariance	Efficiency Maximization	Efficiency Non-deteriorated	Common	Variable
Cook and Kress (1999)	√				√
Beasley (2003)		√		√
Lozano and Villa (2004)		√			√
Jahanshahloo et al. (2005)	√				√
Avellar et al. (2007)		√			√
Bi et al. (2011)			√	√
Lin(2011a)	√				√
Lin(2011b)	√				√
Guedes et al. (2012)		√
Lotfi et al. (2013)		√		√
Hatami-Marbini et al. (2015)			√	√
Wu et al. (2016)		√		√
Lin and Chen (2016)	√				√
Li et al. (2017)	√			√
Ding et al. (2018)			√		√
Sadeghi and Dehnokhalaji (2019)		√			√
Yang et al. (2018)		√			√
Zhang et al. (2018)		√			√
Yang et al (2019)			√		√
Chen et al. (2020)	√				√
Jiang et al. (2020)		√		√
Kiaei and Matin (2020)			√	√
Bernardo et al. (2020)			√		√
Pendharkar (2020)		√			√
Dai et al. (2021)			√		√

2.2. DEA-based allocation of medical resources

In this sub-section, we first introduce the health indicators commonly chosen in research of medical and health resources. Further, some DEA-based medical resources allocation studies are reviewed. Finally, literature on emergency medical resource allocation is provided.

Medical and health resources are special kinds of resources characterized by scarcity. Health resource scarcity exists in many countries, especially in low and middle-income countries (Yang, 2017). To address this issue, scholars are devoted to exploring how to improve the efficiency of medical and health resource allocation. The most common input indicators considered in modeling the production technology of health systems usually are human capital, financial and material inputs, such as physicians, nurses, and other staff, the number of beds for hospitalizations, personal protective equipment (PPE), drugs, hospital infrastructure, and funding. Medical prescriptions, number of hospitalizations, outpatient procedures, inverse mortality rate, patients discharged, number of surgeries, and bed utilization rate are adopted as outputs (Clement et al., 2008, Yang, 2017, Sun and Luo, 2017, Ibrahim and Sahand, 2018, Zare et al., 2019, Yi et al., 2020, Nepomuceno et al., 2020).

Bastian et al., 2014, Lai et al., 2018 presented DEA-based models to realize that the DMUs are efficient after reallocating medical resources. Yazdian et al. (2017) suggested that medical resource allocation should match the initial efficiency (pre-performance) of DMUs. In contrast to younger people, Yang (2017) indicated that older people could share more medical resources, which is in line with our social norm. Similarly, several studies suggested that vaccines should be prioritized for people by age and risk, also taking population structure into account (Lee et al., 2010, Sah et al., 2018, Zhou et al., 2021).

Recently, scholars have adopted DEA for performance evaluation and emergency medical resource allocation under the background of the COVID-19 pandemic. Nepomuceno et al. (2020) proposed a two-step approach for hospital bed evacuation and reallocation during the COVID-19 pandemic. The optimal number of beds to be reallocated was prioritized according to various complex needs for each medical apartment. In addition, a branch of the studies (Zhang et al., 2020, Liu and Liu, 2021, Xu et al., 2021, Hamzah et al., 2021) adopted DEA-based approaches to evaluate the COVID-19 response efficiency and medical resource allocation efficiency.

In other emergency management scenarios, several studies (Liu and Liu, 2014, Yang et al., 2016, Hong, 2020) developed DEA models (i.e., cross DEA and multiple criteria DEA) to seek optimization of resources allocation in emergency response.

2.3. Non-regressive production technology in DEA

Non-regressive production technology means that the production frontier does not worsen using sequential (panel) data. Specifically, the production data of the DMUs during all the past production periods are included in the production possibility set to ensure that the DMUs could always refer to the most advanced production technology throughout all the production periods. Diewert (1980) as well as Diewert and Parkan (1983) were the early studies that considered the non-regressive technical change in non-parametric measurement of productivity and efficiency. When technical change is non-regressive, any input–output combination found in any previous period is also feasible in a subsequent period, but not necessarily the other way around (Ray and Kim, 1995). Since then, a branch of research has explored non-regressive technological changes based on the DEA approach and applied it to analyze technological changes in various industries, such as manufacturing (Mukherjee, 2008, Mukherjee, 2010, Kalai, 2019), healthcare (Bekaroglu and Heffley, 2018), agriculture (Aldaz and Millán, 2003), education (Foltz et al., 2012), and other fields (Millán and Aldaz, 2004, Ray et al., 2008).

Under the context of public health emergencies, the allocation of medical resources needs to assure the efficient utilization of the medical resources, the regular operation of hospitals, and the fairness of the allocation strategy. However, some existing studies are based on the principle of efficiency invariance, and cannot cope with the problem of efficient utilization of medical resources, especially in the scenario where medical resources are extremely scarce. Although a branch of the existing resource allocation studies adopts the principle of efficiency maximization, which can achieve the efficient use of medical resources, however, most of them cannot meet essential requirements for the regular operation of hospitals, nor can they guarantee the fairness of the allocation results.

Motivated by this investigation, we propose a DEA-based resource allocation approach to address the above issues. In addition to the efficient utilization of limited resources, output target realizability, fairness, and practical fitness are all considered. Specifically, to efficiently utilize medical resources under public health emergencies, our model is established based on the principle of efficiency maximization while adopting the non-regressive production technology. In this way, all the DMUs can be efficient after resource allocation. Meanwhile, the production technology is optimized continuously over the whole period. Additionally, to cope with some practical and managerial requirements under public health emergencies, we take pre-performance, operation size, and the structure of patients into account, ensuring the allocation results’ fairness. Moreover, some constraints are added to limit the patient admission capacity of each hospital to better fit with the practical requirements.

3. Efficiency evaluation models and resource allocation possibility set

This section introduces the research problem and proposes two models for the efficiency evaluation of DMUs before and after resource allocation. Further, based on some theoretical analysis, we build the resource allocation possibility set, which will be further used as the basis to develop the resource allocation model in Section 4.

Under public health emergencies, the contradiction between the scarcity of medical resources and their growing demand becomes prominent. For instance, with the increase in confirmed cases in Wuhan at the beginning of COVID-19, there was a severe shortage of medical staff in local hospitals in Wuhan. Both hospitals and medical staff were on overload. In addition, due to the lack of effective treatments, more and more patients developed into critically ill patients, resulting in highly insufficient ICU beds to provide treatment services. Moreover, personal protective equipment such as protective clothing and surgical masks was also in severe shortage during the breakout of COVID-19. Under such a situation and within the DEA framework, each hospital is regarded as a decision-making unit (DMU) that uses inputs to produce outputs. The inputs for each DMU are doctors and nurses, ICU beds, PPE, and fixed assets, where doctors and nurses, ICU beds, and PPE are resource inputs that can be reallocated among the DMUs, and fixed assets are fixed inputs that cannot be changed in the short run. The outputs contain the number of admitted patients, the number of discharged patients, and the number of deaths. The number of admitted patients and the number of discharged patients are desirable outputs, and the number of deaths is regarded as undesirable output. To facilitate our modeling part, the notations used in the paper are described as follows:

General parameters:$n$: Number of DMUs;$m$: Number of fixed inputs;$s$: Number of desirable outputs;$p$: Number of undesirable outputs; $q$: Number of resource inputs to be allocated. Data parameters: $X_j$: Vector of fixed inputs $x_{\mathit{ij}}\left(i=1,\cdots ,m\right)$ of DMU j; $Y_j$: Vector of outputs $y_{\mathit{rj}}\left(r=1,\cdots ,s\right)$ of DMU j; $Z_j$: Vector of undesirable outputs $z_{\mathit{hj}}\left(h=1,\cdots ,p\right)$ of DMU j; $F_j$: Vector of resources $f_{\mathit{lj}}\left(l=1,\cdots ,q\right)$ of DMU j; $\beta$: Maximum change ratio of resources; $\omega$: Relative importance of fairness ${\omega }_1$, efficiency ${\omega }_2$, and humanitarianism ${\omega }_3$. Decision variables: $W$: Weight attached to the fixed input; $U$: Weight attached to the output; $\phi$: Weight attached to the undesirable output; $\pi$: Weight attached to the resource input; $\mathrm{\Delta }{F}_j$: Adjustment of resource inputs $\mathrm{\Delta }{f}_{\mathit{lj}}\left(l=1,\cdots ,q\right)$ for each DMU j.

As has been carefully discussed in the introduction, medical resources should be appropriately allocated among hospitals to ensure their efficient use under public health emergencies. Additionally, some practical constraints cannot be ignored (for instance, a limitation is set on the least amount of admitted patients for each hospital to ensure the regular operation and the prioritization of patients with varying degrees of illness). Moreover, the allocated medical resources to each hospital fit with the operation size, preperformance, and the proportion of critically ill patients. Therefore, to cope with the above goals and requirements, in the modeling part, we will give some theoretical analysis and propose several assumptions and principles (for instance, being efficient after resource allocation, maximizing output target realizability, and adding lower bounds of output target) accordingly.

3.1. Efficiency evaluation before resource allocation

Model (1) is given for the efficiency evaluation of the DMUs where undesirable outputs and fixed inputs are considered simultaneously.

$$\mathrm{m}\mathrm{a}\mathrm{x}\frac{U·Y_d^T+\phi ·\left(M-Z_d^T\right)-u_0}{W·X_d^T+\pi ·F_d^T}$$ (1)

$$s.t.\frac{U·Y_j^t+\phi ·\left(M-Z_j^t\right)-u_0}{W·X_j^t+{\pi ·F}_j^t}\le 1,\forall j\in J,\forall t\in \mathcal{T}$$ (1a)

$$W\ge 0\in {\mathbb{R}}_{+}^m,U\ge 0\in {\mathbb{R}}_{+}^{\mathit{s}},\phi \ge 0\in {\mathbb{R}}_{+}^{\mathit{p}},\pi \ge 0\in {\mathbb{R}}_{+}^q$$ (1b)

$$u_{0}free$$ (1c)

In model (1), $\mathcal{T}=\{1,\cdots ,T\}$ is the set of production period indexes. The time unit of the production period could be a day, week, month, year, etc. Model (1) is under the assumption of variable returns to scale (VRS). The monotone decreasing transformation method is adopted to handle the undesirable outputs. Specifically, the undesirable outputs are transformed using the equation $M-Z_j^t$, where $M$ is a large enough vector that ensures that the undesired outputs are positive after transformation. A similar approach was also used by Seiford and Zhu, 2002, Wu et al., 2016, and Jiang et al. (2020).

Non-regressive of the production technology: Unlike previous papers, historical and current data are considered in (1a) to develop the production possibility set. This approach assures the non-regressive of production technology (Diewert, 1980, Tulkens and Eeckaut, 1995, Ray and Kim, 1995). Specifically, using the data of DMUs in all the production periods to build the production possibility set ensures that the DMUs with the most advanced production technology in history are always included. Therefore, when a DMU is evaluated and projected on the efficient frontier, it will always take the DMUs with the most advanced production technology in history as the reference set. Such a property is essential when allocating medical resources. The DMUs could be assumed to produce with the most advanced production technology after resource allocation, ensuring that the medical resources are used efficiently.

Model (1) is a non-linear program that can be easily transformed into the following linear model (2) by using Charnes–Cooper transformation (Charnes and Cooper, 1962).

$$\mathrm{m}\mathrm{a}\mathrm{x}U·Y_d^T+\phi ·\left(M-Z_d^T\right)-u_0$$ (2)

$$s.tW·X_d^T+\pi ·F_d^T=1$$ (2a)

$$U·Y_j^t+\phi ·\left(M-Z_d^t\right)-W·X_j^t-\pi {·F}_j^t\le 0,\forall j\in J,\forall t\in \mathcal{T}$$ (2b)

$$W\ge 0\in {\mathbb{R}}_{+}^m,U\ge 0\in {\mathbb{R}}_{+}^{\mathit{s}},\phi \ge 0\in {\mathbb{R}}_{+}^{\mathit{p}},\pi \ge 0\in {\mathbb{R}}_{+}^q$$ (2c)

$$u_{0}free$$ (2d)

3.2. Efficiency evaluation considering resource allocation

Considering resource allocation among the DMUs, we further propose model (3) for efficiency evaluation of DMU $d$ ($\forall d\in J$) after resource allocation.

$$E_d^{\mathit{re}}=\mathrm{m}\mathrm{a}\mathrm{x}\frac{U·Y_d^T+\phi ·\left(M-Z_d^T\right)-u_0+{\mathrm{\Phi }}_d^T}{W·X_d^T+\pi ·(F_d^T+\mathrm{\Delta }{F}_d^T)}$$ (3)

$$s.t\frac{U·Y_j^T+\phi ·\left(M-Z_j^T\right)-u_0+{\mathrm{\Phi }}_j^T}{W·X_j^T+\pi ·(F_j^T+\mathrm{\Delta }{F}_j^T)}\le 1,\forall j\in J$$ (3a)

$$\frac{U·Y_j^t+\phi ·\left(M-Z_j^t\right)-u_0}{W·X_j^t+\pi ·F_j^t}\le 1,\forall j\in J,\forall t\in \mathcal{T}$$ (3b)

$${\sum }_{j\in J}\mathrm{\Delta }{F}_j^T=\mathrm{\Delta }F$$ (3c)

$$\mathrm{\Delta }{F}_j^T+\beta F_j^T\ge 0,\forall j\in J$$ (3d)

$$\mathrm{\Delta }{F}_j^T-\beta F_j^T\le 0,\forall j\in J$$ (3e)

$$u_1·Y_{1j}^T+{\mathrm{\Phi }}_j^T\ge u_1{Y}_{1j}^{\mathit{ts}},\forall j\in J$$ (3f)

$$W\ge 0\in {\mathbb{R}}_{+}^m,U\ge 0\in {\mathbb{R}}_{+}^{\mathit{s}},\phi \ge 0\in {\mathbb{R}}_{+}^{\mathit{p}},\pi \ge 0\in {\mathbb{R}}_{+}^q$$ (3g)

$$u_{0}free$$ (3h)

$$\mathrm{\Delta }{F}_j^T\in {\mathbb{R}}^q,{\mathrm{\Phi }}_j^T\ge 0,\forall j\in J$$ (3i)

In model (3), $u_1$ is the first element in the output weight vector, therefore we have $u_1\ge 0$ because we restrict $U\ge 0\in {\mathbb{R}}_{+}^{\mathit{s}}$. Note that $\mathrm{\Delta }{F}_j^T$ ($\forall j\in J$) is free in sign (i.e., we let $\mathrm{\Delta }{F}_j^T\in {\mathbb{R}}^q$), which means that each resource input of a DMU j can be higher, equal to, or lower than its current level after allocating the resource for the new production period. Similar to the efficiency evaluation model (i.e., model (2)), the objection function of model (3) maximizes the efficiency of DMU $d$ considering its input and output after resource allocation. Constraint (3a) guarantees that all the DMUs’ efficiencies are no larger than one after resource allocation. In the numerator of (3a), ${\mathrm{\Phi }}_j^T$ denotes the output target that is set for DMU j ($\forall j\in J$) when making resource allocation. ${\mathrm{\Phi }}_j^T$ is calculated as the weighted sum of desirable and undesirable outputs. Such a setting was used by Jiang et al. (2020). In constraint (3b), all the observed productions of the DMUs before resource allocation are considered to form the production possibility set. This consideration assures the non-regressive of production technology of the DMUs. Thus, DMUs with the most advanced production technology are maintained to construct the production technology. Any DMU that wishes to improve its production can refer to the observed DMUs with the most advanced production technology. Constraint group (3c) ensures that the total resources are fully allocated among all DMUs. In managerial practice, changing resources in large proportions is inappropriate. Therefore, (3d), (3e) jointly ensure that the maximum change ratio of resources of a DMU does not exceed $\beta$. Because the total amount of resources should be fully allocated among the DMUs (i.e., the existence of constraint group (3c)), it should be noted that when setting the value for $\beta$, we must ensure that $\beta \ge \frac{\left|\mathrm{\Delta }F\right|}{{\sum }_{j\in J}{F}_j^T}$. This indicates that we should allow the amount of resources of each DMU to be changed to a certain extent so that the total resource change (i.e., $\mathrm{\Delta }F$) can be attained.

When considering emergency medical resource allocation, we should also ensure that the allocated resources fulfill the requirements of the DMUs (or the hospitals) so that each DMU can at least admit a certain number of patients. Therefore, in constraint (3f), we set a lower bound for the target of the first output of each DMU, where $Y_{1j}^{\mathit{ts}}(\forall j\in J)$ is a constant value set by a decision-maker.

Theorem 1

There is a feasible solution of model(3)that could make all the DMUs efficient after resource allocation.

Proof

Let $\left(U^{\ast },{\phi }^{\ast },W^{\ast },{\pi }^{\ast },u_0^{\ast }\right)$ be the optimal solution of model (1) when solving it to DMU d. Let $U^{\prime }=U^{\ast }$, ${\phi }^{\prime }={\phi }^{\ast }$, $u_0^{\prime }=u_o^{\ast }$ and $\mathrm{\Delta }{F_j^T}^{\prime }=\mathrm{\Delta }F\ast \frac{F_j^T}{{\sum }_{d\in J}{F}_d^T},\forall j\in J$. Let ${{\mathrm{\Phi }}_j^T}^{\prime }=\eta \ast \left(W^{\ast }·X_j^T+{\pi }^{\ast }·\left(F_j^T+\mathrm{\Delta }{F}_j^{T^{\prime }}\right)\right)-\left(U^{\ast }·Y_j^T+{\phi }^{\ast }·\left(M-Z_j^T\right)-u_o^{\ast }\right),\forall j\in J$, where $\eta$ is a parameter. There must be a large enough $\eta ={\eta }^{\prime }\ge 1$ such that ${{\mathrm{\Phi }}_j^T}^{\prime }={\eta }^{\prime }\ast \left(W^{\ast }·X_j^T+{\pi }^{\ast }·\left(F_j^T+\mathrm{\Delta }{F}_j^{T^{\prime }}\right)\right)-\left(U^{\ast }·Y_j^T+{\phi }^{\ast }·\left(M-Z_j^T\right)-u_o^{\ast }\right)>u_1^{\ast }{Y}_{1j}^{\mathit{ts}}-u_1^{\ast }·Y_{1j}^T,\forall j\in J$ (a). Then, let $W^{\prime }={\eta }^{\prime }\ast W^{\ast }$, ${\pi }^{\prime }={\eta }^{\prime }\ast {\pi }^{\ast }$. Then, for the solution $\left(U_d^{\prime },{\phi }_d^{\prime },W_d^{\prime },{\pi }_d^{\prime },u_{0d}^{\prime },{{\mathrm{\Phi }}_{\mathit{jd}}^T}^{\prime }\right)$, we have: $\frac{U^{\prime }·Y_j^T+{\phi }^{\prime }·\left(M-Z_j^T\right)-u_0^{\prime }+{{\mathrm{\Phi }}_j^T}^{\prime }}{W^{\prime }·X_j^T+{\pi }^{\prime }·\left(F_j^T+\mathrm{\Delta }{F}_j^{T^{\prime }}\right)}=\frac{U^{\ast }·Y_j^T+{\phi }^{\ast }·\left(M-Z_j^T\right)-u_0^{\ast }+\left(\eta \ast \left(W^{\ast }·X_j^T+{\pi }^{\ast }·\left(F_j^T+\mathrm{\Delta }{F}_j^{T^{\prime }}\right)\right)-\left(U^{\ast }·Y_j^T+{\phi }^{\ast }·\left(M-Z_j^T\right)-u_o^{\ast }\right)\right)}{\eta \ast \left(W^{\ast }·X_j^T+{\pi }^{\ast }·\left(F_j^T+\mathrm{\Delta }{F}_j^{T^{\prime }}\right)\right)}=1,\forall j\in J$, $\frac{U^{\prime }·Y_j^t+{\phi }^{\prime }·\left(M-Z_j^t\right)-u_0^{\prime }}{W^{\prime }·X_j^t+{\pi }^{\prime }·F_j^t}=\frac{U^{\ast }·Y_j^t+{\phi }^{\ast }·\left(M-Z_j^t\right)-u_0^{\ast }}{\eta \prime \ast \left(W^{\ast }·X_j^t+{\pi }^{\ast }·F_j^t\right)}\le 1,\forall j\in J,\forall t\in \mathcal{T}$ (because $\left(U^{\ast },{\phi }^{\ast },W^{\ast },{\pi }^{\ast },u_0^{\ast }\right)$ is the optimal solution of model (1) (see constraint group (1a)) and ${\eta }^{\prime }\ge 1$), ${\sum }_{j\in J}\mathrm{\Delta }{F}_j^{T\prime }={\sum }_{j\in J}\left(\mathrm{\Delta }F\ast \frac{F_j^T}{{\sum }_{d\in J}{F}_d^T}\right)=\mathrm{\Delta }F$, $\mathrm{\Delta }{F}_j^{T^{\prime }}+\beta F_j^T=\mathrm{\Delta }F\ast \frac{F_j^T}{{\sum }_{d\in J}{F}_d^T}+\beta F_j^T=F_j^T(\frac{\mathrm{\Delta }F}{{\sum }_{j\in J}{F}_j^T}+\beta )\ge 0,\forall j\in J$ (because we have $\beta \ge \frac{\left|\mathrm{\Delta }F\right|}{{\sum }_{j\in J}{F}_j^T}$), $\mathrm{\Delta }{F}_j^{T^{\prime }}-\beta F_j^T=\mathrm{\Delta }F\ast \frac{F_j^T}{{\sum }_{d\in J}{F}_d^T}-\beta F_j^T=F_j^T(\frac{\mathrm{\Delta }F}{{\sum }_{j\in J}{F}_j^T}-\beta )\le 0,\forall j\in J$(because we have $\beta \ge \frac{\left|\mathrm{\Delta }F\right|}{{\sum }_{j\in J}{F}_j^T}$), and $u_1^{\prime }·Y_{1j}^T+{{\mathrm{\Phi }}_j^T}^{\prime }=u_1^{\ast }·Y_{1j}^T+{{\mathrm{\Phi }}_j^T}^{\prime }\ge u_1^{\ast }{Y}_{1j}^{\mathit{ts}}\left(see\left(a\right)\right)$. Therefore, $\left(U^{\prime },{\phi }^{\prime },W^{\prime },{\pi }^{\prime },u_0^{\prime },{{\mathrm{\Phi }}_j^T}^{\prime },\forall j,\mathrm{\Delta }{F_j^T}^{\prime },\forall j\right)$satisfies all the constraints in model (3) and we have $\frac{U^{\prime }·Y_j^T+{\phi }^{\prime }·\left(M-Z_j^T\right)-u_0^{\prime }+{{\mathrm{\Phi }}_j^T}^{\prime }}{W^{\prime }·X_j^T+{\pi }^{\prime }·\left(F_j^T+\mathrm{\Delta }{F}_j^{T^{\prime }}\right)}=1,\forall j$. Therefore, there is a feasible solution that could make all the DMUs efficient after resource reallocation. Q.E.D.

Corollary 1

There is a feasible solution of model(3)that could make the DMU under evaluation efficient.

Theorem 1 says that there is a feasible solution of model (3) that makes all the DMUs efficient after resource allocation. This solution must make the DMU under evaluation efficient after resource allocation. Thus, Corollary 1 is true accordingly.

3.3. Resource allocation possibility set

As illustrated in Theorem 1, a feasible solution that could make all the DMUs efficient after resource allocation always exists. To improve the utilization efficiency of limited resources, we hope that all DMUs could be efficient after resource allocation. Hence, the following Resource allocation possibility set (RAPS) is built based on the above observations to pursue the most efficient use of resources for decision-makers.

$$\mathit{RAPS}=\left\{\left(\mathrm{\Delta }{F}_j^T,\forall j\in J\right)\right)\left|\frac{U·Y_j^T+\phi ·\left(M-Z_j^T\right)-u_0+{\mathrm{\Phi }}_j^T}{W·X_j^T+\pi ·(F_j^T+\mathrm{\Delta }{F}_j^T)}=1,\forall j\right)\in J$$ (4a)

$$\frac{U·Y_j^t+\phi ·\left(M-Z_j^t\right)-u_0}{W·X_j^t+\pi ·F_j^t}\le 1,\forall j\in J,\forall t\in \mathcal{T}$$ (4b)

$${\sum }_{j\in J}\mathrm{\Delta }{F}_j^T=\mathrm{\Delta }F$$ (4c)

$$\mathrm{\Delta }{F}_j^T+\beta F_j^T\ge 0,\forall j\in J$$ (4d)

$$\mathrm{\Delta }{F}_j^T-\beta F_j^T\le 0,\forall j\in J$$ (4e)

$$u_1·Y_{1j}^T+{\mathrm{\Phi }}_j^T\ge u_1{Y}_{1j}^{\mathit{ts}},\forall j\in J$$ (4f)

$$W\ge 0\in {\mathbb{R}}_{+}^m,U\ge 0\in {\mathbb{R}}_{+}^{\mathit{s}},\phi \ge 0\in {\mathbb{R}}_{+}^{\mathit{p}},\pi \ge 0\in {\mathbb{R}}_{+}^q$$ (4g)

$$u_{0}free$$ (4h)

$$\mathrm{\Delta }{F}_j^T\in {\mathbb{R}}^q,\left({\mathrm{\Phi }}_j^T\ge 0,\forall j\in J\right\}$$ (4i)

In model (4), constraint group (4a) indicates that all DMUs are efficient after resource allocation, which ensures that the medical resources are allocated among the hospitals in such a way that all the resources are efficiently used. As mentioned above, a production frontier with non-regressive production technology is constructed by using all the historical production data of the DMUs. In this way, the production frontier is not only composed of the most efficient DMUs in the current period but also the DMUs with the most advanced production technology in the whole period. The current DMUs can learn from the most advanced DMUs, thus providing more meaningful guidance and management implications for DMUs in the current period.

Overall, the suggested RAPS is characterized by several properties. First, it ensures that each DMU is efficient after resource allocation. This property means that every part of the resource is used in an efficient production system, efficiently utilizing the input resources to produce outputs. Second, the historical data of the DMUs are adopted to develop the production possibility set, which assures the non-regressive of the production technology. Further, limitations have been included on the variation of resources of each DMU to fit the managerial practice. Finally, a lower bound has been set on the output target, which ensures that each DMU could at least admit a certain number of patients. Such a condition is fit with the practical requirement to confront the public health emergencies.

4. A bi-objective allocation model

In Section 3.3, the resource allocation possibility set (RAPS) is defined. However, multiple allocation results can satisfy all Set (4) constraints. A novel bi-objective resource allocation model based on the RAPS is proposed in this section to obtain the final allocation result. First, we consider defining two objective functions in terms of the principle of fairness, the realizability of output targets, and humanitarianism. On this basis, a bi-objective model is provided to seek the unique allocation result. Finally, we apply a trade-off model to calculate the bi-objective model and further obtain the final allocation solutions.

4.1. Two objective functions

Some objective functions based on the RAPS need to be added to seek a final allocation result. This subsection defines two objective functions to search for a final resource allocation result. The following part will present specific explanations on how to set the objective functions.

From the decision maker’s rational perspective, searching for an efficient allocation plan for all DMUs is essential in the background of emergency resource allocation. Note that some restrictive factors, such as the level of production technology, should be considered when reallocating limited resources. When the output targets are too far from the production practice, DMUs may not be able to achieve them due to limited management capabilities. It is important in public health emergencies because if hospitals cannot realize the output targets in the new production period, then the required number of patients is unable to be admitted, which will lead to severe consequences. From this viewpoint, objective function 1 is put forward for output target setting.

$$\min \underset{j\in J}{\max }{\mathrm{\Phi }}_j^T$$ (5)

${\mathrm{\Phi }}_j^T$ is the output target of DMU j, which is denoted as the weighted outputs (including desired and undesired outputs) that need to be increased when the target is set in period $T$. The smaller the value of ${\mathrm{\Phi }}_j^T$, the fewer variations that DMU j needs to make to its outputs to realize the output targets. Objective function 1 aims to minimize the maximum output target among all DMUs. Thus, objective function 1 intends to seek the closest output targets for the DMUs while ensuring that all DMUs are efficient after allocation. In this way, all targets are easily achieved by the DMUs.

A hospital’s production efficiency in the previous production period indicates the hospital’s ability to transform medical resources into outputs. Generally, hospitals with high pre-performance can better utilize medical resources. Therefore, more resources should be allocated to these hospitals. Jiang et al. (2020) and Dai et al. (2020) emphasized the same viewpoint. Additionally, the operation sizes of hospitals should not be ignored. Li et al., 2019, Jiang et al., 2020 believed that allocating more resources to DMUs with small inputs and outputs is unreasonable. Given that hospitals are homogenous, a hospital with a large operation size reasonably consumes more resources, which is in line with managerial practice. In addition, some practical situations need to be considered, for instance, how to allocate ICU beds among patients with different degrees of infection. From this perspective, the proportion of critically ill patients is taken into account, which can better meet the practical requirements.

Based on the above analysis, to derive the final resource allocation result, we propose finding the one with a minimum deviation from the allocation result determined by considering each DMU’s pre-performance, operation size, and proportion of critically ill patients. Therefore, the following objective function is used.

$$\min \underset{j\in J,\mathcal{q}\in Q}{\max }\left|\mathrm{\Delta }{F}_{\mathcal{q}j}^T-\mathrm{\Delta }{\widehat{F}}_{\mathcal{q}j}^T\right|$$ (6)

The objective function (6) aims to find the indicator with the largest deviations between the reallocated value $\mathrm{\Delta }{F}_{\mathcal{q}j}^T$ and the ideal value $\mathrm{\Delta }{\widehat{F}}_{\mathcal{q}j}^T$ among the Q reallocated resources. Then, the maximum deviation is minimized. Note that some indicators have large dimensions, and others have small dimensions. Given the dimensional difference between indicators, comparing the deviations directly is not appropriate. For instance, for the two indicators of PPE and ICU beds, their reallocated and ideal values are 10,000 and 9,990, 1 and 0.5, respectively. Owing to the large absolute deviation of the former, the indicator PPE plays a restrictive role in the objective function (6). However, the relative deviation of the latter is relatively large. The latter should be adopted for optimization. To solve this issue, the relative deviations of the indicators are taken into account, which is achieved by standardizing reallocated indicators. Before calculating the reallocated values, the ratios of the corresponding indicators of each DMU to the total amount of the indicators in all DMUs ($F_{\mathcal{q}j}^T/{\sum }_{\forall j\in J}{F}_{\mathcal{q}j}^T$) are calculated to substitute for the initial values ($F_{\mathcal{q}j}^T$).

$$\mathrm{\Delta }{\widehat{F}}_{\mathcal{q}d}^T=\left({\omega }_1·{\alpha }_d^T+{\omega }_2·E_d^T/{\sum }_{\forall j\in J}{E}_j^T+{\omega }_3·p_d^T\right)·\left({\sum }_{\forall j\in J}{F}_j^T+\mathrm{\Delta }F\right)-F_d^T$$ (7)

${\alpha }_d^T$ denotes the operation size of DMU $d$ during period $T$, where$\sum {\alpha }_j^T$ = 1.${\alpha }_d^T$ is evaluated by experts according to the scale of outputs and inputs of DMU $d$. $E_d^T$ denotes the efficiency of DMU d in production period $T$. Using the proposition $E_d^T/{\sum }_{\forall j\in J}{E}_j^T(\forall d\in J)$ indicates that more resources are required to be allocated to DMUs with high performance. $p_d^T$ is the proportion of critically ill patients with DMU $d$ in all DMUs during period $T$. Specifically, for DMU $d$, $p_d^T=Y_{1d}^T/{\sum }_{\forall j\in J}{Y}_{1j}^T,$ where $Y_{1d}^T$ denotes the amount of critically ill patients of DMU $d$. More medical equipment like ICU beds should be allocated to critically ill patients rather than mildly ill patients in all hospitals. Note that ${\omega }_1,{\omega }_2,{\omega }_3>0$, where ${\omega }_1+{\omega }_2+{\omega }_3=1$, denotes the relative importance of the size of operation, efficiency, and the proportion of critically ill patients, respectively.

Objection function (6) is put forward from the point of view of fairness, the realization of the targets, and humanitarianism. First, resources should adhere to the principle of fair allocation. Allocating more resources to DMUs with a small operation size is unreasonable. Second, during the outbreak of the COVID-19 epidemic, medical resources were severely short in supply. DMUs with high efficiencies in the previous production period were more likely to utilize the limited medical resources better than DMUs with low efficiencies. Therefore, the better a DMU performs in the last period, the more resources are considered to be allocated to it. Third, humanitarianism should not be ignored when allocating emergency medical resources (i.e., CPU beds and ventilators). Hospitals aim to prolong the lives of critically ill patients to the greatest extent. Hence, more medical equipment should be allocated to hospitals with a high proportion of critically ill inpatients.

4.2. The bi-objective resource allocation model

Based on the two objective functions and the resource allocation possibility set (please see Formula (4)) discussed above, we present a bi-objective resource allocation model as follows:

$$\min \underset{j\in J}{\max }{\mathrm{\Phi }}_j^T$$ (8)

$$\min \underset{j\in J,\mathcal{q}\in Q}{\max }\left|\mathrm{\Delta }{F}_{\mathcal{q}j}^T-\mathrm{\Delta }{\widehat{F}}_{\mathcal{q}j}^T\right|$$ (8a)

$$s.t\frac{U·Y_j^T+\phi ·\left(M-Z_j^T\right)-u_0+{\mathrm{\Phi }}_j^T}{W·X_j^T+\pi ·(F_j^T+\mathrm{\Delta }{F}_j^T)}=1,\forall j\in J$$ (8b)

$$\frac{U·Y_j^t+\phi ·\left(M-Z_j^t\right)-u_0}{W·X_j^t+\pi ·F_j^t}\le 1,\forall j\in J,\forall t\in \mathcal{T}$$ (8c)

$${\sum }_{j\in J}\mathrm{\Delta }{F}_j^T=\mathrm{\Delta }F$$ (8d)

$$\mathrm{\Delta }{F}_j^T+\beta F_j^T\ge 0,\forall j\in J$$ (8e)

$$\mathrm{\Delta }{F}_j^T-\beta F_j^T\le 0,\forall j\in J$$ (8f)

$$u_1·Y_{1j}^T+{\mathrm{\Phi }}_j^T\ge u_1{Y}_{1j}^{\mathit{ts}},\forall j\in J$$ (8g)

$$W·{\sum }_{j\in J}{X}_j^T+\pi ·\left({\sum }_{j\in J}{F}_j^T+\mathrm{\Delta }F\right)=n$$ (8h)

$$W\ge 0\in {\mathbb{R}}_{+}^m,U\ge 0\in {\mathbb{R}}_{+}^{\mathit{s}},\phi \ge 0\in {\mathbb{R}}_{+}^{\mathit{p}},\pi \ge 0\in {\mathbb{R}}_{+}^q$$ (8i)

$$u_{0}free$$ (8j)

$$\mathrm{\Delta }{F}_j^T\in {\mathbb{R}}^q,{\mathrm{\Phi }}_j^T\ge 0,\forall j\in J$$ (8k)

Compared with the constraints listed in the resource allocation possibility set, we have added a new constraint $W·{\sum }_{j\in J}{X}_j^T+\pi ·\left({\sum }_{j\in J}{F}_j^T+\mathrm{\Delta }F\right)=n$ to avoid trivial solutions. Additionally, the non-regressive of production technology is considered. That is, the construction of the production frontier for period $T$ is based on all historical data ($t$ from 1 to$T$ − 1). For instance, $T=1$ only involves the original data of the first production period, and no other historical data are used as a reference. When $T=2$, both data of production periods 1 and 2 of the DMUs are used to establish the production possibility set. With the increase of periods, an increasing number of DMU production data are included in the production possibility set. The most advanced DMU among all the periods is chosen as the benchmark. In such a way, the production technology of DMUs will be improved continually due to the non-regressive of the production frontier.

Let $\mathrm{\Phi }=\underset{j\in J}{\max }{\mathrm{\Phi }}_j^T$ and $F=\underset{j\in J,\mathcal{q}\in Q}{\max }\left|\mathrm{\Delta }{F}_{\mathcal{q}j}^T-\mathrm{\Delta }{\widehat{F}}_{\mathcal{q}j}^T\right|$. Then, we convert model (8) into model (9).

$$\min \mathrm{\Phi }$$ (9)

$$\min F$$ (9a)

$$s.t\frac{U·Y_j^T+\phi ·\left(M-Z_j^T\right)-u_0+{\mathrm{\Phi }}_j^T}{W·X_j^T+\pi ·(F_j^T+\mathrm{\Delta }{F}_j^T)}=1,\forall j\in J$$ (9b)

$$\frac{U·Y_j^t+\phi ·\left(M-Z_j^t\right)-u_0}{W·X_j^t+\pi ·F_j^t}\le 1,\forall j\in J,\forall t\in \mathcal{T}$$ (9c)

$${\sum }_{j\in J}\mathrm{\Delta }{F}_j^T=\mathrm{\Delta }F$$ (9d)

$$\mathrm{\Delta }{F}_j^T+\beta F_j^T\ge 0,\forall j\in J$$ (9e)

$$\mathrm{\Delta }{F}_j^T-\beta F_j^T\le 0,\forall j\in J$$ (9f)

$$u_1·Y_{1j}^T+{\mathrm{\Phi }}_j^T\ge u_1{Y}_{1j}^{\mathit{ts}},\forall j\in J$$ (9g)

$${\mathrm{\Phi }}_j^T\le \mathrm{\Phi },\forall j\in J$$ (9h)

$$\left|\mathrm{\Delta }{F}_{\mathcal{q}j}^T-\mathrm{\Delta }{\widehat{F}}_{\mathcal{q}j}^T\right|\le F,\forall j\in J,\forall \mathcal{q}\in Q$$ (9i)

$$W\ge 0\in {\mathbb{R}}_{+}^m,U\ge 0\in {\mathbb{R}}_{+}^{\mathit{s}},\phi \ge 0\in {\mathbb{R}}_{+}^{\mathit{p}},\pi \ge 0\in {\mathbb{R}}_{+}^q$$ (9j)

$$u_{0}free$$ (9k)

$$\mathrm{\Delta }{F}_j^T\in {\mathbb{R}}^q,{\mathrm{\Phi }}_j^T\ge 0,\forall j\in J$$ (9l)

Model (9) is a non-linear model which cannot be solved directly. Let $\mathrm{\Delta }{F}_{\mathcal{q}j}^{T\prime }={\pi }_{\mathcal{q}}\mathrm{\Delta }{F}_{\mathcal{q}j}^T,\forall \mathcal{q}\in Q,\forall j\in J$, $\mathrm{\Delta }{F}_j^{T\prime }={\left(\mathrm{\Delta }{F}_{\mathcal{q}j}^{T^{\prime }},\forall \mathcal{q}\in Q\right)}^T$, and $\mathrm{\Delta }{F}^{\prime }=\left({\pi }_{\mathcal{q}}\mathrm{\Delta }{F}_{\mathcal{q}},\forall \mathcal{q}\in Q\right)$. Model (9) can be transformed into the linear model (10).

$$\min \mathrm{\Phi }$$ (10)

$$\min F$$

$$s.tU·Y_j^T+\phi ·\left(M-Z_j^T\right)-W·X_j^T-\pi ·F_j^T-{\sum }_{\mathcal{q}\in Q}\mathrm{\Delta }{F}_{\mathcal{q}j}^{T^{\prime }}-u_0+{\mathrm{\Phi }}_j^T=0,\forall j\in J$$ (10a)

$$U·Y_j^t+\phi ·\left(M-Z_j^t\right)-W·X_j^t-\pi ·F_j^t-u_0\le 0,\forall j\in J,\forall t\in \mathcal{T}$$ (10b)

$${\sum }_{j\in J}\mathrm{\Delta }{F}_{\mathcal{q}j}^{T\prime }={\pi }_{\mathcal{q}}\mathrm{\Delta }{F}_{\mathcal{q}},\mathcal{q}\in Q$$ (10c)

$$\mathrm{\Delta }{F_{\mathcal{q}j}^T}^{\prime }+\beta {\pi }_{\mathcal{q}}{F}_{\mathcal{q}j}^T\ge 0,\forall j\in J,\forall \mathcal{q}\in Q$$ (10d)

$$\mathrm{\Delta }{F_{\mathcal{q}j}^T}^{\prime }-\beta {\pi }_{\mathcal{q}}{F}_{\mathcal{q}j}^T\le 0,\forall j\in J,\forall \mathcal{q}\in Q$$ (10e)

$$u_1·Y_{1j}^T+{\mathrm{\Phi }}_j^T\ge u_1{Y}_{1j}^{\mathit{ts}},\forall j\in J$$ (10f)

$${\mathrm{\Phi }}_j^T\le \mathrm{\Phi },\forall j\in J$$ (10g)

$$\left|\mathrm{\Delta }{F}_{\mathcal{q}j}^{T\prime }-\pi \mathrm{\Delta }{\widehat{F}}_{\mathcal{q}j}^T\right|\le F,\forall j\in J,\mathcal{q}\in Q$$ (10h)

$$W·{\sum }_{j\in J}{X}_j^T+\pi ·\left({\sum }_{j\in J}{F}_j^T+\mathrm{\Delta }F\right)=n$$ (10i)

$$W\ge 0\in {\mathbb{R}}_{+}^m,U\ge 0\in {\mathbb{R}}_{+}^{\mathit{s}},\phi \ge 0\in {\mathbb{R}}_{+}^{\mathit{p}},\pi \ge 0\in {\mathbb{R}}_{+}^q$$ (10j)

$$u_{0}free$$ (10k)

$$\mathrm{\Delta }{F}_j^{T\prime }\in {\mathbb{R}}^q,{\mathrm{\Phi }}_j^T\ge 0,\forall j\in J$$ (10l)

4.3. A trade-off model

The bi-objective model (10) cannot be solved directly. Therefore, we adopt a trade-off model to calculate a non-dominated solution of this model to compute the final resource allocation results.

Before implementing tradeoffs, we need to obtain the intervals for the optimal results of two objective functions (i.e., min $\mathrm{\Phi }$ and $\min F$). To do this, we need to optimize the two objective functions sequentially. First, we optimize the first objective function (i.e., min $\mathrm{\Phi }$) to obtain the minimum value that $\mathrm{\Phi }$ could reach. We denote this lower bound of $\mathrm{\Phi }$ as ${\mathrm{\Phi }}_L$. Then, under the premise that $\mathrm{\Phi }$ is at the lower bound level, we optimize the second objective function (i.e., $\min F$), which obtains the upper bound of $F$ among all the non-dominated solutions of model (10). We denote this upper bound of $F$ as $F_U$. Similarly, by optimizing the objective function $\min F$ first and then the objective function $\min \mathrm{\Phi }$, we obtain the lower bound (denoted as $F_L$) of $F$ and the upper bound (denoted as ${\mathrm{\Phi }}_U$) of $\mathrm{\Phi }$. Thus, the optimal results of $\mathrm{\Phi }$ and $F$ are located in the intervals [${\mathrm{\Phi }}_L$, ${\mathrm{\Phi }}_U$] and [$F_L$, $F_U$], respectively.

Model (11) is given based on the intervals we discussed above. It uses a trade-off considering to optimize the two objective functions simultaneously.

$$\min I-∊\times (I_1+I_2)$$ (11)

$$s.tU·Y_j^T+\phi ·\left(M-Z_j^T\right)-W·X_j^T-\pi ·F_j^T-{\sum }_{\mathcal{q}\in Q}\mathrm{\Delta }{F}_{\mathcal{q}j}^{T^{\prime }}-u_0+{\mathrm{\Phi }}_j^T=0,\forall j\in J$$ (11a)

$$U·Y_j^t+\phi ·\left(M-Z_j^t\right)-W·X_j^t-\pi ·F_j^t-u_0\le 0,\forall j\in J,\forall t\in \mathcal{T}$$ (11b)

$${\sum }_{j\in J}\mathrm{\Delta }{F}_{\mathcal{q}j}^{T\prime }={\pi }_{\mathcal{q}}\mathrm{\Delta }{F}_{\mathcal{q}},\mathcal{q}\in Q$$ (11c)

$$\mathrm{\Delta }{F_{\mathcal{q}j}^T}^{\prime }+\beta {\pi }_{\mathcal{q}}{F}_{\mathcal{q}j}^T\ge 0,\forall j\in J,\forall \mathcal{q}\in Q$$ (11d)

$$\mathrm{\Delta }{F_{\mathcal{q}j}^T}^{\prime }-\beta {\pi }_{\mathcal{q}}{F}_{\mathcal{q}j}^T\le 0,\forall j\in J,\forall \mathcal{q}\in Q$$ (11e)

$$u_1·Y_{1j}^T+{\mathrm{\Phi }}_j^T\ge u_1{Y}_{1j}^{\mathit{ts}},\forall j\in J$$ (11f)

$${\mathrm{\Phi }}_j^T\le {\mathrm{\Phi }}_{\mathrm{L}}+I\times \left({\mathrm{\Phi }}_U-{\mathrm{\Phi }}_L\right)+I_1,\forall j\in J$$ (11g)

$$\left|\mathrm{\Delta }{F}_{\mathcal{q}j}^{T\prime }-\pi \mathrm{\Delta }{\widehat{F}}_{\mathcal{q}j}^T\right|\le F_L+I\times \left(F_U-F_L\right)+I_2,\forall j\in J,\mathcal{q}\in Q$$ (11h)

$$W·{\sum }_{j\in J}{X}_j^T+\pi ·\left({\sum }_{j\in J}{F}_j^T+\mathrm{\Delta }F\right)=n$$ (11i)

$$W\ge 0\in {\mathbb{R}}_{+}^m,U\ge 0\in {\mathbb{R}}_{+}^{\mathit{s}},\phi \ge 0\in {\mathbb{R}}_{+}^{\mathit{p}},\pi \ge 0\in {\mathbb{R}}_{+}^q$$ (11j)

$$u_{0}free$$ (11k)

$$\mathrm{\Delta }{F}_j^{T\prime }\in {\mathbb{R}}^q,{\mathrm{\Phi }}_j^T\ge 0,\forall j\in J$$ (11l)

In model (11), parameter I is introduced to address the trade-off of the optimal values between two objective functions. Specifically, $I\in$[0, 1] denotes the increment proportion of the two objective function values with both of them considered. Thus, when the optimal value of $\mathrm{\Phi }$ decreases from ${\mathrm{\Phi }}_U$ to ${\mathrm{\Phi }}_{\mathrm{L}}+I\times ({\mathrm{\Phi }}_U-{\mathrm{\Phi }}_L)$, the optimal value of $F$ needs to be increased by proportion I accordingly. In addition, $I=1$ or $I=0$ corresponds to the extreme values of two objective functions.

In the objective function of model (11), $∊$ is a small positive value. $I_1$ and $I_2$ are the slacks corresponding to the two objective functions. Such a setting means that the slacks are maximized under the condition that $I$ is minimized. This setting ensures that model (11) always obtains a non-dominated solution for model (10).

Assume the optimal solution of model (11) is $\left(W^{\ast },U^{\ast },{\phi }^{\ast },{\pi }^{\ast },u_0^{\ast },{{\mathrm{\Phi }}_j^T}^{\ast },\mathrm{\Delta }{F_{\mathcal{q}j}^T}^{\prime },\forall q\in Q,\forall j\in J,I^{\ast },I_1^{\ast },I_2^{\ast }\right)$, then final resource allocated to DMU j $(\forall j\in J)$ is calculated as follows:

$$F_{\mathit{qj}}^{T\ast }=F_{\mathit{qj}}^T+{{\mathrm{\Delta }F}_{\mathit{qj}}^T}^{\ast },\forall q\in Q$$ (12)

where ${\mathrm{\Delta }F}_{\mathit{qj}}^{\ast }={\mathrm{\Delta }{F_{\mathcal{q}j}^T}^{\prime }}^{\ast }/{\pi }_{\mathit{qj}}^{\ast }$.

Further, to obtain the output target for the output indicators, we propose increasing desirable outputs proportionally and reducing undesirable outputs. Therefore, the following equation is used.

$$U^{\ast }·Y_j^T+{\phi }^{\ast }·\left(M-Z_j^T\right)+{{\mathrm{\Phi }}_j^T}^{\ast }\triangleq U^{\ast }\bullet \left(1+{\beta }_j\right)\bullet Y_j^T+{\phi }^{\ast }\bullet \left(M-\left(1-{\beta }_j\right)\right)\bullet Z_j^T,\forall j\in J$$ (13)

In formula (13), ${\beta }_j$ denotes the proportion that the desirable (undesirable) outputs need to be increased (decreased) to achieve the output targets. By simple mathematical transformation, we can derive that ${\beta }_j={{\mathrm{\Phi }}_j^T}^{\ast }/\left(U^{\ast }·Y_j^T+{\phi }^{\ast }\bullet Z_j^T\right)$. Then, for DMU $j$, the optimal results of desired outputs ${Y_j^T}^{\ast }$ and undesired outputs ${Z_j^T}^{\ast }$ after adjustment can be denoted respectively as:

$${Y_j^T}^{\ast }=\left(1+{\beta }_j\right)\bullet Y_j^T$$ (14)

$${Z_j^T}^{\ast }=\left(1-{\beta }_j\right)\bullet Z_j^T$$ (15)

In practice, the resource indicators may be integers, for instance, the number of doctors. However, model (11) does not necessarily ensure obtaining an integer resource allocation result. To solve this problem, we suggest ranking DMUs in decreasing order according to their corresponding decimal parts of the number of resources. The number of resources constructed by the decimal parts is then allocated to the top-ranked DMUs. For instance, assume we have five hospitals labeled as H1, H2, H3, H4, and H5, respectively. A total amount of 100 doctors needs to be allocated among these hospitals. Assume that model (11) obtains the resource allocation result as (18.8, 20.4, 19.6, 21.2, 20.0). Note that the decimal parts construct two doctors. We can then rank the hospitals by the decimal parts as H1, H3, H2, H4, and H5. Therefore, the two doctors constructed by the decimal parts are allocated to H1 and H3. Thus, the final resource allocation result is obtained as (19, 20, 20, 21, 20).

4.4. Feature comparison of our approach with existing approaches

In this section, we compare our approach with some existing approaches (Bastian et al., 2014, Yang, 2017, Yazdian et al., 2017, Wang and Gao, 2017, Lai et al., 2018, Nepomuceno et al., 2020), which also investigated the problem of medical resource allocation. These approaches are compared from the following 6 aspects:

• A1: Whether the approach ensures the DMUs are efficient after resource allocation;

• A2: Whether the non-regressive production technology is used;

• A3: Whether the output target realizability is considered;

• A4: Whether operation size of the DMU is considered;

• A5: Whether pre-performance of the DMU is considered;

• A6: Whether practical medical constraints are added.

The comparison results are listed in Table 2 . It is noted that each of the existing approaches intends to focus on only a single feature while our approach takes into account all six of the features listed above. Therefore, our approach is more in line with the practical requirements for medical resource allocation. Additionally, it should be noted that the existing approaches have not considered adopting fixed inputs or undesirable outputs. Some of them have neither considered the practical medical constraints. Therefore, they are not applicable in the case study discussed in Section 5. Due to such a limitation, we cannot compare our approach with the existing ones by numerical analysis.

Table 2.

Feature comparison of alternative approaches.

Studies	A1	A2	A3	A4	A5	A6
Bastian et al. (2014)	√
Yang (2017)						√
Yazdian et al. (2017)					√
Wang and Gao (2017)			√
Lai et al. (2018)	√
Nepomuceno et al. (2020)						√
Our study	√	√	√	√	√	√

5. A case study of 30 hospitals in Wuhan

In this part, we apply the proposed approach for a case study of emergency medical resource allocation among 30 hospitals in Wuhan during the early stage of COVID-19.

5.1. Input and output indicators and data

According to the existing studies (Clement et al., 2008, Yang, 2017, Sun and Luo, 2017, Ibrahim and Sahand, 2018, Zare et al., 2019, Yi et al., 2020, Nepomuceno et al., 2020) that have investigated health systems, the input and output indicators used in this study are selected. The number of doctors and nurses is adopted in terms of human capital inputs. For financial input, fixed assets are chosen. The number of ICU beds and personal protective equipment is selected for material inputs. Additionally, since fixed assets are difficult to adjust in the short term, we consider them as fixed inputs and the rest of the easily changeable indicators as resources. Outputs can be divided into desirable outputs and undesirable outputs, where desirable outputs include the number of inpatients and the number of discharges. The number of deaths is treated as an undesirable output. However, in public health emergencies such as COVID-19, the structure of inpatients should be further considered. Persad et al., 2009, Laventhal et al., 2020, and Yip (2021) argued that critical-ill patients and non-critical ill patients should be distinguished because the principles of giving priority to the worst off, greatest need, and the sickest first need to be emphasized. Therefore, in our indicator system, the outputs of inpatients are further subdivided into two categories: critical-ill patients and non-critical-ill patients. Table 3 lists the final evaluation indicators selected.

Table 3.

Description of indicators.

Type	Indicators	Notation
Fixed input	Fixed assets	X1
Resource input	The number of doctors	F1
	The number of nurses	F2
	The number of ICU beds	F3
	The number of personal protective equipment	F4
Desirable output	The number of non-critically admitted patients	Y1
	The number of critically admitted patients	Y2
	The number of discharged patients	Y3
Undesirable output	The number of death patients	Z1

According to COVID-19 epidemic data from January 21, 2020, to March 3, 2020, released by the Health Commission of Hubei Province, the related data (i.e., the numbers of admitted, discharged, and dead patients) of the epidemic in Wuhan are obtained. Other data (i.e., PPEs) which is hard to collect is simulated using Monte Carlo simulation. Jiang et al. (2020) and Dai et al. (2020) emphasized that DMUs with high pre-performance have a better ability to utilize resources and thus prioritize receiving the resources. Similarly, several studies hold the view that it is prominent to provide the greatest benefit to the greatest number of individuals while the fewest resources are used for allocating scarce resources (Biddison et al., 2014, Yazdian et al., 2017, Vergano et al., 2020, Laventhal et al., 2020). Additionally, Li et al., 2019, Jiang et al., 2020 also emphasized the significance of the operation sizes of DMUs when allocating resources. Moreover, Grover et al. (2020) argued that the importance of the degree of patients’ needs is less of a priority than the performance of utilizing the scarce resource. Accordingly, we assign similar importance (i.e., ${\omega }_1={\omega }_2=0.4$) to preperformance and operation size, both of which are higher than the weight assigned to the proportion of critically ill patients (i.e., ${\omega }_3=0.2$). To ensure the realizability of allocation plans, the maximum adjustment ratio $\beta$ is equal to 20 %. Note that this specific simulation is for the threshold period of the outbreak, thus, the setting of period $T$ will not be too large. Hence, we assume the allocation strategy is adjusted every 7 days. Assuming that in period $T$ ($T=5$), a group of medical staff is dispatched from hospitals of other provinces and some medical supplies are raised by society to support Wuhan, where [$\mathrm{\Delta }{F}_1$ , $\mathrm{\Delta }{F}_2$ , $\mathrm{\Delta }{F}_3$ , $\mathrm{\Delta }{F}_4$] = [500,900, 20,15000]. Table 4 shows the final generated data for hospitals with different sizes.

Table 4.

Data of hospitals with different sizes.

	DMU	Y1	Y2	Y3	Z1	X1	F1	F2	F3	F4	Q	$\mathit{s}\mathit{i}\mathit{z}\mathit{e}$
Large Hospital	1	531	120	74	30	28	878	1096	87	7318	591	0.058
	2	511	102	54	25	30	512	1123	99	5331	528	0.063
	3	603	107	94	29	15	651	967	92	5305	606	0.062
	4	634	149	68	21	16	583	915	89	5450	713	0.071
	5	507	148	86	20	27	782	902	70	7781	508	0.054
Medium Hospital	6	324	86	40	9	14	246	276	28	3528	372	0.040
	7	215	68	20	24	8	279	315	29	2376	261	0.034
	8	204	79	29	12	7	269	286	22	2025	215	0.041
	9	273	91	18	20	11	155	372	24	2225	318	0.039
	10	296	76	27	16	9	161	322	18	3267	352	0.029
	11	347	45	32	17	9	203	369	25	3920	352	0.031
	12	320	76	38	7	7	157	376	27	2566	334	0.039
	13	250	67	34	15	8	286	492	25	2264	287	0.033
	14	257	100	22	19	10	179	423	15	2369	260	0.034
	15	333	91	18	13	6	236	488	28	3980	354	0.041
	16	231	80	40	18	5	206	291	26	2104	285	0.041
	17	319	62	36	20	11	209	340	22	2683	352	0.038
	18	269	79	28	22	5	220	398	17	3223	272	0.036
	19	286	91	27	14	6	154	439	27	2587	293	0.040
	20	256	90	36	18	14	292	278	25	2962	260	0.035
Small Hospital	21	140	20	12	0	2	135	113	3	631	155	0.014
	22	115	15	4	5	4	109	144	2	968	119	0.011
	23	139	0	5	12	3	131	145	1	760	151	0.010
	24	115	14	7	11	4	57	109	0	859	135	0.004
	25	62	14	10	6	4	88	113	5	521	79	0.020
	26	125	17	0	2	2	164	160	3	570	134	0.017
	27	141	37	8	10	4	53	158	2	653	150	0.013
	28	52	2	14	8	3	97	115	1	610	59	0.009
	29	129	19	7	2	4	138	184	6	991	149	0.020
	30	75	25	11	7	4	75	112	8	491	86	0.021

5.2. Results and analysis

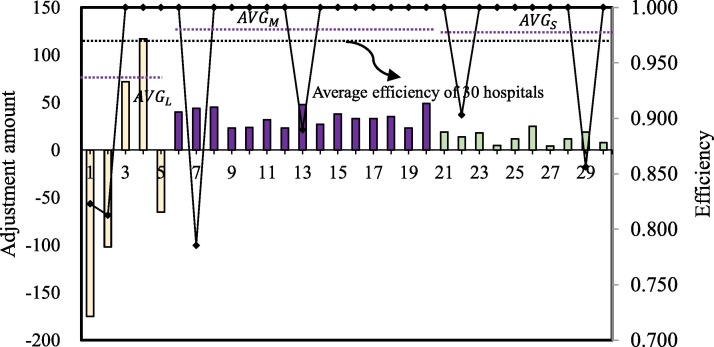
Model (12) is applied to obtain resource allocation results in Table 5 , where ${\alpha }_j$ denotes the change proportion of each resource. Table 5 demonstrates specific information on efficiency performance scores of 30 hospitals and adjustments of four kinds of medical resources. Fig. 1 is further derived from Table 5.

Table 5.

Efficiency evaluation and final resource allocation adjustments.

	DMU	$E^b$	$E^a$	$\mathrm{\Delta }{F}_1$	${\alpha }_1$	$\mathrm{\Delta }{F}_2$	${\alpha }_2$	$\mathrm{\Delta }{F}_3$	${\alpha }_3$	$\mathrm{\Delta }{F}_4$	${\alpha }_4$
Large	1	0.823	1	−175	−0.20	−211	−0.19	−10	−0.11	1464	0.20
	2	0.813	1	−102	−0.20	−224	−0.20	−19	−0.19	207	0.04
	3	1	1	72	0.11	−38	−0.04	−10	−0.11	1061	0.20
	4	1	1	117	0.20	118	0.13	0	0.00	1090	0.20
	5	1	1	−65	−0.08	10	0.01	7	0.10	1351	0.17
Average/Total		0.927	1	−153	−0.03	−345	−0.06	−32	−0.06	5173	0.16
Medium	6	1	1	40	0.16	51	0.18	4	0.14	706	0.20
	7	0.785	1	44	0.16	57	0.18	4	0.14	475	0.20
	8	1	1	45	0.17	52	0.18	3	0.14	405	0.20
	9	1	1	23	0.15	69	0.19	3	0.13	445	0.20
	10	1	1	24	0.15	60	0.19	2	0.11	653	0.20
	11	1	1	32	0.16	69	0.19	4	0.16	784	0.20
	12	1	1	23	0.15	70	0.19	4	0.15	513	0.20
	13	0.890	1	48	0.17	93	0.19	4	0.16	453	0.20
	14	1	1	27	0.15	80	0.19	2	0.13	474	0.20
	15	1	1	38	0.16	93	0.19	4	0.14	796	0.20
	16	1	1	33	0.16	54	0.19	4	0.15	421	0.20
	17	1	1	33	0.16	63	0.19	3	0.14	537	0.20
	18	1	1	35	0.16	75	0.19	2	0.12	645	0.20
	19	1	1	23	0.15	83	0.19	4	0.15	517	0.20
	20	1	1	49	0.17	51	0.18	4	0.16	592	0.20
Average/Total		0.978	1	517	0.16	1020	0.19	51	0.14	8416	0.20
Small	21	1	1	19	0.14	18	0.16	0	0.00	126	0.20
	22	0.903	1	14	0.13	24	0.17	0	0.00	194	0.20
	23	1	1	18	0.14	24	0.17	0	0.00	152	0.20
	24	1	1	5	0.09	17	0.16	0	0.00	172	0.20
	25	1	1	12	0.14	19	0.17	0	0.00	104	0.20
	26	1	1	25	0.15	28	0.18	0	0.00	114	0.20
	27	1	1	4	0.08	27	0.17	0	0.00	131	0.20
	28	1	1	12	0.12	18	0.16	0	0.00	122	0.20
	29	0.856	1	19	0.14	32	0.17	0	0.00	198	0.20
	30	1	1	8	0.11	18	0.16	1	0.13	98	0.20
Average/Total		0.976	1	136	0.12	225	0.17	1	0.01	1411	0.20
Average/Total		0.969	1	500		900		20		15,000

Fig. 1.

Allocation adjustment amounts of resource $F_1$ and pre-efficiencies of 30 hospitals. Note:${\mathit{AVG}}_L,{\mathit{AVG}}_M,{\mathit{AVG}}_S$ denotes the average efficiency of large, medium, and small hospitals, respectively.

Table 5 shows that the efficiency of all hospitals is equal to 1 after resource adjustment, which indicates that our model can guarantee the efficient utilization of limited medical resources. Furthermore, we take resource $F_1$ as an example and draw Fig. 1 to help explain the results intuitively. It can be seen that large hospitals need to make relatively larger adjustments on $F_1$ compared to the adjustments on medium and small hospitals. For some large hospitals (i.e., DMUs 3 and 4), the $F_1$ level needs to be increased, and the others (i.e., DMUs 1, 2, and 5) need to decrease the $F_1$ level. However, for all the medial and small hospitals, their $F_1$ levels are suggested to be increased. Overall, medium hospitals need to increase the $F_1$ level more than small hospitals. Additionally, the average efficiency of the large hospitals before resource allocation is much smaller than those of the medium and small hospitals. Therefore, the differences and redundancy of medical resources in large hospitals lead to the ineffective use of medical resource $F_1$; the shortage of medical resources faced by medium hospitals is more serious than in small hospitals. Similar results can be seen in the analysis of the allocation results of $F_2$, $F_3,$ and $F_4$.

Further, we can derive more details of the redundancy for each hospital from Fig. 2, Fig. 3, Fig. 4, Fig. 5 . The redundancy of medical staff in large hospitals is the most serious, followed by ICU beds. Thus, to improve the efficiency of hospitals, the reductant medical staff and ICU beds in large hospitals should be transferred to small and medium-sized hospitals. The increase in the number of medical staff in small and medium-sized hospitals will enhance the capacity of hospitals to admit and treat patients. The COVID-19 outbreak has exposed the fact that the team of public health professionals was not strong enough. From 2009 to 2018, the number of Center for Disease and Prevention Control (CDC) personnel nationwide decreased by 10.2 %, lower than the standard CDC (1.75/10,000 of the resident population).2 The weak reserve force of full-time hospital infection management personnel, as well as the lack of homogenization of the medical ability and level of critical care professionals, led to the overload of hospitals and medical staff during the outbreak.

Fig. 2.

Allocation adjustments of $F_1$ for 30 hospitals.

Fig. 3.

Allocation adjustments of $F_2$ for 30 hospitals.

Fig. 4.

Allocation adjustments of $F_3$ for 30 hospitals.

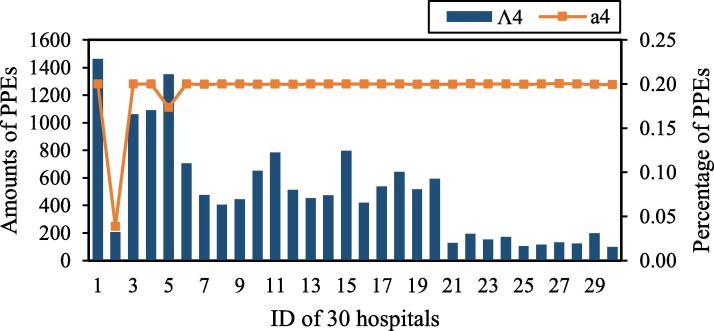
Fig. 5.

Allocation adjustments of $F_4$ for 30 hospitals.

Additionally, as indicated in Fig. 2, Fig. 3, Fig. 4, Fig. 5, medium and small hospitals are the recipients of resources in allocation, and only large hospitals are the distributors of resources. From the perspective of the proportion of adjustments, for $F_4$, the adjustment ratio of all DMUs (except for DMU 2 and DMU 5) reached the highest threshold of 0.2. This result indicates that the demand for PPE such as masks is urgent in the early stage of the outbreak, and hospitals’ reserves could hardly meet the current demand of increasing patients, which also reveals the insufficient of a normalized anti-epidemic material guarantee mechanism. Hospitals do not do a good job of stocking medical resources (i.e., PPEs) in advance. Materials for epidemic prevention and control are in severe shortage. Additionally, it is too difficult for manufacturers to produce PPEs in a short time to meet the sharply increased needs of the whole society, which leads to a severe mismatch between the supply and demand of medical resources during the outbreak. Except for DMU 30, the adjustment amount of ICU beds in small hospitals is 0. Moreover, ICU beds are reallocated among large and medium-sized hospitals. There may be two reasons behind the results. On the one hand, due to the lack of effective treatments and prevention, more and more patients have developed into critically ill patients, resulting in insufficient ICU beds to provide treatment services. On the other hand, it is significantly related to the fact that large and medium-sized hospitals can provide more kinds of high-quality medical monitoring and treatment technology for patients in time. Thus, small hospitals lack priority for ICU beds allocation compared to medium-sized hospitals.

Hospitals with different sizes have various adjustment ranges in resources. The adjustment of large hospitals is the most significant among all hospitals of different sizes. Specifically, both resource redundancy and resource shortage have appeared. Overall, the resource adjustment of medium hospitals is the most stable, especially for the adjustment proportions of $F_1$ and $F_2$, which maintains 15 %−17 % and 18 %−19 %. It also exposes the insufficient of public health professionals in medium hospitals.

6. Conclusion and implications

Under the efficiency analysis framework, a novel bi-objective DEA model with a non-regressive production technology for emergency resource allocation is presented. DEA non-regressive production technology assures that DMUs can always choose the most advanced production technology over entire production periods as reference. In addition, on the premise of the efficient maximization principle, all the DMUs can achieve DEA efficient after resource allocation. Moreover, two objectives jointly ensure output target realizability and the fairness of resource allocation results. Additionally, some essential constraints are added to our model to fit with the management practice in the context of public health emergencies. To solve the bi-objective model, a trade-off approach is further adopted. Finally, a case study is given to allocate emergency medical resources among 30 hospitals of different sizes in Wuhan during the COVID-19 outbreak.

The results indicate that the initial medical resource allocation is irrational. Specifically, medium hospitals have the highest efficiency performance, followed by small hospitals, and large hospitals perform worst. Further, the adjustment values indicated that the large hospitals were inefficient due to redundant input resources, including medical and nursing staff and ICU beds. In contrast, the inefficiency of small and medium-sized hospitals was caused by insufficient resources. The structure of healthcare resources should be optimized to formulate a new resource allocation strategy. To this end, redundant medical resources of large hospitals should be transferred to small and medium-sized hospitals. Note that ICU beds in large hospitals are assisted by medium hospitals rather than small ones, likely related to the hierarchical diagnosis and treatment, where there is a division of labor and collaboration mechanism among the different sizes of hospitals. Large and medium-sized hospitals have an advantage in treating critically ill patients due to the greater specialization of healthcare workers.

Our empirical analysis has also brought some policy implications. First, coordinate and optimize the beds and personnel within the hospital. Accordingly, healthcare staff within the hospital can be deployed to support the front-line departments (e.g., fever clinics). Second, a unified real-time system of epidemic prevention material reserves and demand warning can be established so that the professional team can reasonably deploy medical resources to respond to public health emergencies quickly and efficiently. Collaborative relationships among hospitals, government, medical equipment suppliers, expert teams, and institutions can be built to shorten the decision-making time and reduce casualties and property losses. Besides, Internet medical treatment, health medical big data, and artificial medical intelligence also play a crucial role in epidemic prevention. Telemedicine through the Internet relieves the pressure on medical institutions and avoids unnecessary cross-infection. Finally, optimization of medical and health resources and balanced regional distribution. Policy support for small hospitals and primary health institutions is expected to be implemented. For primary health institutions, the quality and efficiency of medical services need to be enhanced.

Nevertheless, our study has several limitations that may be explored in future research. First, more detailed parameters can be considered to make the allocation more reasonable and realistic. Second, the allocation in this article is based on existing and occurred data, which may lead to obstacles to the real-time allocation of emergency supplies. To solve this problem, a spreading epidemic model such as SEIR can be introduced to predict future epidemic situations to provide a scientific and reliable reference basis for the rapid response to resource allocation. Furthermore, it is sometimes difficult to obtain all the precise data information under public health emergencies. Therefore, scholars may adopt the DEA robust optimization methods (Salahi et al., 2019, Salahi et al., 2021, Toloo et al., 2021) and further extend our approach to consider the resource allocation problem under uncertainty.

Acknowledgements

The authors are sincerely grateful for the suggestions and comments given by the anonymous reviewers. The research is supported by the National Natural Science Foundation of China (No. 71901225) and the Natural Science Foundation of Hunan Province (No. 2020JJ5778).

CRediT authorship contribution statement

Junfei Chu: Conceptualization, Methodology, Supervision, Writing – review & editing, Funding acquisition. Xiaoxue Li: Methodology, Software, Writing – original draft. Zhe Yuan: Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.