Mechanism of Spatial and Temporal Control in Precision Cyclic Vinyl Polymer Synthesis by Lewis Pair Polymerization

Abstract

In typical cyclic polymer synthesis via ring‐closure, chain growth and cyclization events are competing with each other, thus affording cyclic polymers with uncontrolled molecular weight or ring size and high dispersity. Here we uncover a mechanism by which Lewis pair polymerization (LPP) operates on polar vinyl monomers that allows the control of where and when cyclization takes place, thereby achieving spatial and temporal control to afford precision cyclic vinyl polymers or block copolymers with predictable molecular weight and low dispersity (≈1.03). A combined experimental and theoretical study demonstrates that cyclization occurs only after all monomers have been consumed (when) via conjugate addition of the propagating chain end to the specific site of the initiating chain end (where), allowing the cyclic polymer formation steps to be regulated and executed with precision in space and time.

Spatiotemporal control in cyclic polymer synthesis: Lewis pair polymerization controls where and when cyclization takes place to afford precision cyclic vinyl homo and block copolymers.

Introduction

Cyclic polymers have gained increased attention in recent years.[ ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ ] This excitement is partly due to availability of more diverse classes of cyclic polymers made possible by emerging methodologies, such as zwitterionic ring‐opening polymerization,[ ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ ] ring‐expansion polymerization,[ ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ ] Lewis pair polymerization (LPP),[ ²² , ²³ , ²⁴ , ²⁵ , ²⁶ ] and coordinative insertion/back‐biting ring closure.[ ²⁷ , ²⁸ , ²⁹ ] Added to this development are the advances in more traditional techniques such as unimolecular and bimolecular coupling reactions used for ring closure, most notably the click reactions.[ ² , ³⁰ , ³¹ , ³² , ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ ] Additionally, materials properties unique to cyclic polymers (with respect to linear analogues), such as lower intrinsic viscosity (η),[ ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ , ⁴² ] faster crystallization kinetics,[ ⁴³ , ⁴⁴ , ⁴⁵ ] and sometimes higher resistance to chemical[ ⁴⁶ , ⁴⁷ ] and thermal degradation, can be exploited. Perhaps most intriguing is the role of cyclic block copolymers (BCPs) in self‐assembly where the dynamics of phase segregation differ from their linear counterparts in their degree of entanglement and degrees of rotational and translational freedom.[ ³⁷ , ⁴⁷ , ⁴⁸ , ⁴⁹ , ⁵⁰ ]

The principal synthetic challenge in precision synthesis of cyclic polymers lies in the cyclization or ring‐closure step, where a chemical path is necessary to bond the two termini. If the cyclization step is available during the polymerization (propagation), then the ring‐closing event will be in competition with propagation and will thus occur statistically over a broad range of molecular weights (Scheme 1), usually in the form of a chain transfer.[ ¹⁰ , ¹³ , ¹⁴ , ¹⁷ ] On the other hand, the ring closing event can be reserved until a later step, and triggered by an exogenous reagent. For example, polymerizations can be executed by controlled radical methods while installing a coupling node (such as an alkyne) on the initiating molecule and installing a second node (such as an azide) on the opposite terminus either with a functionalized quenching molecule or an additional post‐functional step. ^[31] Then, in a final step, a click reaction can be triggered to bond the termini together.[ ³⁰ , ³¹ , ³² , ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ ] Although these methods afford more control over number‐average molecular weight (M _n) and dispersity (Đ), they require multiple steps and privileged chemistries restricting them to largely academic interests. A more ideal methodology, in our opinion, is to make available the potential for ring‐closing during the polymerization step, while installing some chemo‐ or spatial and temporal control ^[51] that allows the polymerization to achieve full conversion (i.e., monomer depletion) and only then execute the cyclization event to occur at the specific site of the chain (Scheme 1).

Scheme 1.

Schematic illustration of spatial and temporal control that regulates where and when cyclization takes place to achieve precision cyclic polymers with predictable M _n and low Đ values as well as high structural fidelity.

In this context, Takasu and co‐workers recently disclosed a facile route to cyclic polar polyolefins from LPP of the biorenewable monomer class of alkyl sorbates. ^[26] The sorbate monomer is a conjugated diene involving a complex electron system with complicated regio‐ and stereochemistry associated with its polymerization. Anionic routes were first explored on this monomer class by Takasu and Hirabayashi[ ⁵² , ⁵³ , ⁵⁴ ] where much of the regio and stereochemistry was defined spectroscopically. Those reports showed that employment of the bulky Lewis acid (LA) methyl aluminum‐di(2,6‐di‐tert‐butyl‐4‐methyl‐phenoxy) (MAD) can restrict the regiochemistry of the resulting polysorbates to the 1,4‐addition structure, while cold temperatures and various other conditions could yield more stereoselective polymers. When Takasu and Hayashi employed an organic Lewis base (LB), 1,3‐di‐tert‐butylimidazolin‐2‐ylidene (I ^t Bu), instead of traditional alkyl lithium bases, the resulting polymers were found to be cyclic, as determined by matrix‐assisted laser desorption ionization time‐of‐flight mass spectrometry (MALDI‐TOF‐MS), viscometry, ^[26] and later by direct observation with transmission electron microscopy (TEM) upon thiol‐ene click post‐functionalization. ^[55]

The proposed mechanism (Scheme 2) was that nucleophilic conjugate addition of the initiating LB (I ^t Bu) to the electrophilic alkyl sorbate δ‐carbon results in the formation of a zwitterionic enolate, which then after repeated conjugate additions to other sorbate molecules (aided by MAD) a polysorbate is produced with an imidazolium cationic α‐terminus and an anionic enolaluminate ω‐terminus. This nucleophilic‐initiation‐based mechanistic hypothesis then afforded the enticing nuance that the two termini electrostatically draw each other into proximity, where an S_N2‐type ring‐closure can occur to regenerate the neutral I ^t Bu and yield a neutral cyclic polysorbate.

Scheme 2.

Originally proposed path to cyclic polysorbates (top) and more generalized route to cyclic poly(methacrylate)s (bottom), with both mechanisms operating through a zwitterionic propagating species and an S_N2‐type ring‐closure.

This method was later utilized by Takasu to render a more generalized method to synthesize cyclic poly(methacrylate)s by simply preforming the sorbate‐derived active species (presumed at the time to be the zwitterionic 1‐mer, Scheme 2) by premixing MAD, methyl sorbate (MS), and I ^t Bu together at a 1/1/1 molar ratio followed by addition of methyl methacrylate (MMA) with some additional MAD catalyst. ^[56] Polymerization then proceeded from the sorbate 1‐mer to grow polymethacrylate chains that would eventually ring‐close presumably via the same S_N2 step, displacing the I ^t Bu⁺ leaving group and forming a bond between the once methacrylic enolate ω‐terminus and the sorbate δ‐carbon. The result was indeed cyclic poly(methyl methacrylate) (c‐PMMA), as judged by the MALDI‐TOF‐MS and viscometry. Later, allyl methacrylate was employed so that 1‐octadecanethiol (1‐ODT) chains could be clicked onto the pendant allyl groups to make cyclic‐brush‐polymethacrylates which can be directly observed by TEM.[ ⁵⁵ , ⁵⁷ ]

Intrigued by this hypothesized mechanism, we most recently adapted Takasu's methodology for our compounded sequence control (CSC) LPP method[ ⁵⁸ , ⁵⁹ ] to make cyclic di‐BCPs of n‐butyl acrylate ( ⁿ BA) and MMA in one pot and one step. ^[22] By utilizing this unique strategy, we successfully synthesized high molecular weight (M _n up to 267 kDa) cyclic P ⁿ BA‐b‐PMMA with narrow dispersity (Đ=1.03) at room temperature (RT) and without highly dilute conditions. By several lines of evidence including hydrodynamic radius (V _h), radius of gyration (R _g), solution viscometry, bulk viscometry, and TEM, we supported the cyclic topology of these di‐BCPs.

However, when we checked the proton NMR of the preformed sorbate initiating species (generated by 1/1/1 mixing of ethyl sorbate (ES), MAD, and I ^t Bu), we noticed that the 1‐mer was not a zwitterionic product of nucleophilic attack, but rather an ion pair product of basic deprotonation (Figures 1 and S1). After rigorously assigning the structure of the [I ^t Bu⋅H]⁺[MAD⋅ES]⁻ ion pair 1 using ¹H and HH‐COSY NMR techniques as well as mass spectrometry, we concluded that the mechanism first proposed by Takasu et al. needed to be revisited and revised. If an ion pair is the species initiating polymerization of sorbates and (meth)acrylates, then there is no leaving group to facilitate S_N2 ring‐closure. Hence, without that enticing S_N2 ring‐closure event, the fundamental question is: how does the cyclization actually take place to form the cyclic polymer?

Figure 1.

Deprotonative mechanism by which the initiating species 1 is generated via the basic pathway (top) and ¹H NMR (C₆D₆) of ion pair 1, showing two geometric isomers.

After reviewing all of the evidence again, including MALDI‐TOF‐MS, viscometry, R _g and V _h, differential refractive index, glass transitions, TEM, and most convincingly the MALDI‐TOF‐MS evidence from the original report ^[26] featuring mass calculations before and after hydrogenation of cyclic polysorbates, we were convinced that this method produces cyclic polymers by an unknown mechanism of which we needed to elucidate. Herein we disclose the results of this investigation and present what we believe is a strong case for an alternative mechanism.

Results and Discussion

Distinguishing Basic vs. Nucleophilic Initiation Pathways by I ^t Bu

As mentioned in the Introduction we first noticed by ¹H NMR that 1 was not a zwitterion but rather an ion pair. This ion pair was prepared by mixing MAD/ES/I ^t Bu together in C₆D₆, toluene, or dichloromethane (DCM) at a molar ratio of 1/1/1. We generally premix MAD and the sorbate molecule together first, and only then add the mixture to I ^t Bu. Solubilities are best in DCM, which is what we used for most polymerization runs. However, due to side reactions between I ^t Bu and DCM, we took precautions to not expose I ^t Bu to DCM unless the MAD/ES adduct was already present. Figure 1 shows the ¹H NMR spectrum of this ion pair 1 as a mixture of some E/Z isomer pair. Although there are technically two alkenes that could express geometric isomerism (α and γ), the α (enolate) alkene is the one assumed to be expressing isomerism. This assumption is based on a similar ion pair formed when methyl crotonate (MC) is reacted with MAD/I ^t Bu, which also forms an analogous E/Z ion pair. However, the crotonate ion pair only has one alkene from which geometric isomerism can exist and it is the enolate. Thus, we assume the same for the more ambiguous sorbates. When 1 was synthesized in DCM (Figure S4), the compositional ratio of the isomer pair was 1/1. When 1 was synthesized in C₆D₆, the ratio was 2/1. When the E/Z=1/1 solution in DCM was diluted into C₆D₆, the E/Z ratio remained 1/1 indefinitely vs. time and did not drift towards 2/1. Thus, it seems as though when I ^t Bu deprotonates the ES ⋅ MAD adduct, the reaction is irreversible.

The 1 synthesized in DCM (Figure S4) clearly showed the I ^t Bu⁺‐H proton peak at 7.51 ppm. Additionally, the terminal ϵ‐protons of the deprotonated ES can be correlated to the rest of the structure with the HH‐COSY (Figures S4 and S3), and as one would expect, both protons have their own peaks since it is an asymmetric alkene. The fact that two unique doublets for these terminal ϵ‐methyl protons can be observed, as well as two unique nuclear overhauser effect (NOE) signals with the δ‐proton on the HH‐COSY, strongly supports the deprotonative mechanism. And since Takasu et al. ran the polymerizations at −20 °C, we checked to ensure that the synthesis of 1 at −20 °C would give the same product, and it does (Figure S5). We also want to point out that Takasu et al. mainly used MS in their studies while we used ES. We chose ES as it has a lower boiling point (making purification by distillation more convenient), and it might better stabilize the ion pair 1, making it more durable for our studies. In any case, we made sure MS behaves the same as ES and synthesized the MAD/MS/I ^t Bu ion pair (Figure S6), and it gave an identical set of ¹H NMR peaks (with the exception of a slightly different E/Z ratio) indicating that it forms the ion pair just like ES and does not form the zwitterion by the nucleophilic initiation. Additionally, we found further evidence for this ion pair 1 structure when we performed time of flight mass spectrometry on this molecule (Figure S7). In the absence of any ionizing agent, we found that the imidazolium cation was the major m/z peak observed in positive mode (m/z=181.17), while the MAD capped sorbate was the only peak observed in negative mode (m/z=619.43).

Determining Initiation and Termination Chain Ends

Next, we ensured that the deprotonative initiation pathway was in fact the real mechanism in a polymerization scenario. Here, we initiated polymerization on 200 equiv of ES simply by using I ^t Bu as the initiator so that the deprotonation (or conjugate addition) would occur in situ. The ES/MAD/I ^t Bu ratio used was 200/2/1 with [ES]₀=0.60 M in toluene. However, we quenched aliquots of the reaction at various time points. An aliquot quenched at 27 % conversion yielded a poly(ethyl sorbate) (PES) with the degree of polymerization (DP) equal to approximately 54. Crucially here, the PES chains are still growing and would not have cyclized yet. Therefore, one of two outcomes is expected. First, if the polymerization is initiating nucleophilically (according to Takasu's mechanism) and cyclizes by S_N2 attack on the carbon bearing the I ^t Bu⁺, premature quenching of the reaction should yield a polymer with the I ^t Bu⁺ initiating group still attached, the weight of which would be detectable via MALDI‐TOF‐MS and most likely represented by an end group mass near m/z=181 (I ^t Bu⁺+H). Alternatively, if the initiation step is basic, no end groups should be detected and the MALDI‐TOF‐MS would give an intercept of near 23 (the mass of Na⁺, Scheme 3). The polymer we gathered after premature quenching at 27 % conversion gave a MALDI‐TOF‐MS spectrum which had one set of peaks characterized by a m/z=140n+23 (Figure 2). Thus, the deprotonative mechanism is experimentally supported.

Scheme 3.

Premature quenching of an ES/MAD/I ^t Bu LPP hypothesized to yield a binary result to distinguish between basic/nucleophilic initiation.

Figure 2.

MALDI‐TOF‐MS spectrum of PES initiated by ion pair 1 but quenched prematurely at 27 % conversion. One set of peaks with an intercept of 23 reveals the basic initiation pathway. Note that the shown chemical structures only represent one of several regiochemical possibilities.

Next, we chose some other LBs that we know from our prior and literature work have higher tendencies to operate through the nucleophilic path rather than the basic initiation pathway and conducted similar LPP on ES attempting to observe the S_N2 ring closing step. In our earlier report on the LPP of MC, ^[60] which also has both nucleophilic and basic pathways available, we found that 1,3,4‐triphenyl‐4,5‐dihydro‐1H‐1,2,4‐triazol‐5‐ylidene (TPT) exclusively operates through the nucleophilic path, while I ^t Bu exclusively operates through the basic path. Additionally, we and others have observed TPT acting as a leaving group in several umpolung‐type coupling reactions.[ ⁶¹ , ⁶² , ⁶³ , ⁶⁴ , ⁶⁵ ] We hypothesized that this same behavior might be expressed in the sorbate system. When we attempted to synthesize the TPT/ES/MAD 1/1/1 zwitterionic species in C₆D₆, we obtained an extremely convoluted ¹H NMR that was inconclusive (Figure S8). We surmised that the complicated NMR spectrum was a product of the number of possible regio‐ and stereoisomers that could be obtained when there are two points of attack (β and δ) and two alkenes with E/Z isomers available for ES. Accordingly, we added this presumed non‐selective cocktail of isomeric zwitterions (2) to an MMA/MAD solution in toluene so that the calculated MMA/MAD/2 concentration was 40/1/1 with [MMA]₀=0.60 M. We acquired an aliquot after 1 h which showed full monomer conversion but left the reaction to stir for a full 24 h so that if the S_N2‐type cyclization step was at all accessible, the step had plenty of time to execute (Scheme 4). After 24 h, the reaction was quenched and isolated, then prepped for MALDI‐TOF‐MS analysis. The resulting polymer yielded a mass spectrum (Figure 3) with one set of peaks that correlated to m/z=100.19n+438.7, with 100.19 accounting for an MMA repeat unit and 438.7 accounting for an end group involving TPT⁺ (297.4 Da), ES (140.2 Da) and a proton (1.0 Da). The fact that a Na⁺ was not accounted for in the mass of the intercept implies that the TPT initiating group was still cationic after 24 h so it can be assumed that the commonly observed proton exchange, which yields a neutral enamine, is not operative here.[ ⁶⁶ , ⁶⁷ ] Although inconclusive, this experiment demonstrates that (in accordance with many other LPP studies) of vinyl monomers when an N‐heterocyclic carbene (NHC) initiates LPP along the nucleophilic path, the NHC bond is rather strong and not readily susceptible to substitution reactions and ES is not an exception. We performed a similar experiment wherein ES was polymerized by tricyclohexyl phosphine (PCy₃) at an ES/MAD/PCy₃ ratio of 40/2/1 with [ES]₀=0.60 M in toluene and a full 24 h of stirring before quenching. Similarly, cationic PCy₃ ⁺ end groups were exclusively found in the MALDI‐TOF‐MS spectrum as an intercept of m/z=281.4 (PCy₃ ⁺+H) was detected (Figure S10).

Scheme 4.

Investigation into the true nucleophilic path using the uniquely nucleophilic but less basic TPT.

Figure 3.

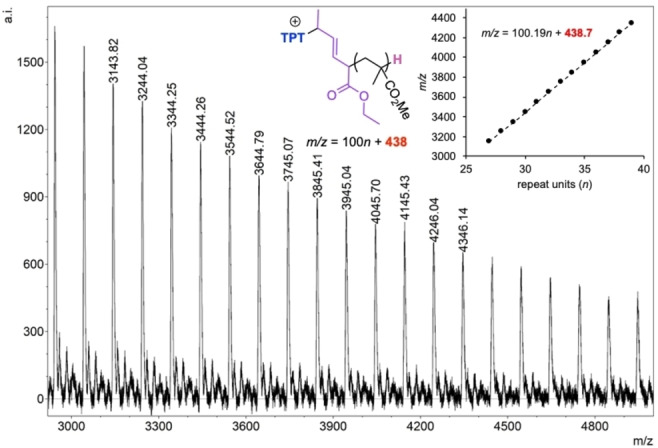
MALDI‐TOF‐MS spectrum of linear PMMA (l‐PMMA) initiated by species 2, quenched after 24 h, showing one dominant set of peaks with an end group mass correlating to the expected mass of TPT, and ES unit, and a proton, supporting our claim that S_N2‐type ring closure is improbable for the nucleophilic pathway. Shown chemical structures only represent one of several regiochemical possibilities.

Elucidating Mechanism of Ring Closure

Guided by the above‐described results, we then formulated a few alternative hypotheses. First, if sorbate ion pair 1 initiated LPP by attack of monomer from either the nucleophilic γ or ϵ carbon of the enolate in 1, there would be an alkene conjugated to the sorbate carbonyl which might act as an electrophile for eventual conjugate addition from the enolate at the opposite terminus. This hypothesis seems promising especially when considering the effect of MAD coordination to the conjugated sorbate unit providing additional activation. This hypothesis would yield a cyclic polymer bearing an enolate on the sorbate unit (Scheme 5). We reasoned that this enolate might be detected if we quenched the reaction with a deuterated acid. Importantly, an ES LPP initiated by I ^t Bu normally gives a set of MALDI‐TOF‐MS peaks with an intercept of m/z=23 (the mass of just Na⁺). The cyclic PES hypothetically generated by Takasu's original mechanism (Scheme 2) would also have an intercept of m/z=23. However, Takasu's S_N2 ring‐closing step gives a neutral polymer that should not even react with the quenching acid. Therefore, when a deuterium is used as the acid quench, an intercept of m/z=24 would be additional evidence that the S_N2 mechanism is improbable as it implies that the product interacts with the quenching medium and is thus basic, as well as a strong piece of evidence that the ring‐closing step is indeed a conjugate addition since any other ring closing step would not result in a basic (enolate) product. We performed a LPP of ES at an ES/MAD/I ^t Bu ratio of 40/2/1 with [ES]₀=0.60 M and gave a full 24 h for cyclization to occur. We then partitioned the reaction solution into two different vials. One of the vials was quenched with benzoic acid/MeOH, while the other was quenched with D₂O/MeOD. Both samples were analyzed by MALDI‐TOF‐MS. The sample quenched with benzoic acid/MeOH gave an intercept of m/z=23 while the sample quenched with D₂O/MeOD gave an intercept of m/z=24 (Figure 4), thus supporting our hypothesis.

Scheme 5.

Deuterium‐labeling experiment used to determine the chemical nature of the post‐cyclized product.

Figure 4.

MALDI‐TOF‐MS spectra of presumably cyclic PES initiated by ion pair 1 and given 24 h to react before quenching by benzoic acid (top) and D₂O/MeOD (bottom) supporting the enolate product of ring‐closure by conjugate addition. Shown chemical structures only represent one of several regiochemical possibilities.

While the conjugate addition mechanism in Scheme 5 is viable if initiation is either γ‐ or ϵ‐selective, we questioned whether the first addition is regioselective. Our work on the related crotonate system ^[60] and Waymouth's similar work ^[68] of the dimerization of crotonates was highly suggestive of α‐addition, and several small molecule synthesis reports[ ⁶⁹ , ⁷⁰ ] also gave convincing evidence that the Li⁺ enolate of alkyl sorbates yielded an α‐addition product. Thus, it is reasonable to suspect a mixture of both ϵ‐ and α‐ initiation with the ϵ‐initiated cyclic polymer accounted for within the current mechanism. Therefore, it is necessary for us to deal with the possibility of α‐initiation which would render a pendant diene that is not conjugated to the carbonyl, thus preventing it from being a target for conjugate addition from the opposite enolaluminate terminus. We then considered the possibility of an α‐proton migration to the ϵ‐carbon which would then put the diene into conjugation with the carbonyl.

We considered this possibility after recalling an observation in Waymouth's previous work ^[68] on the dimerization of crotonates, wherein a similar isomerization is observed (Scheme 6). In this example, a terminal alkene is repositioned to into conjugation, presumably by a base‐catalyzed proton exchange. Since the conjugated alkene is clearly thermodynamically favored over the terminal alkene due to conjugation, similar logic would suggest the sorbate analogue would be equally, if not more, disposed to this type of transformation if there is a path to overcome the energy barrier for such a proton exchange.

Scheme 6.

Necessary proton shifts required to reposition terminal alkenes into conjugation if α‐initiation prevails.

Accordingly, we designed an experiment to study the evolution of the alkenyl protons constituting the sorbate end group vs time. We set up a polymerization with an MMA/MAD/1 molar ratio of 25/0.50/1.00 where [MMA]₀=0.45 M in toluene. We quenched half of the reaction at 1 min and found that the conversion was 99 %. The other half of the reaction was quenched at 24 h and interestingly the reaction was still at 99 % conversion, while a normal LPP at this point would have gone to completion. Our hypothesis here is that the residual 1 % of MMA is a result of competitive MAD coordination by the ester carbonyl on the sorbate initiating group which becomes prohibitively dominant once [MMA] _t gets very low. More interesting is that at 1 min, there was an abundance of peaks in the alkenyl region (Figure 5, top; also see Figures S11 and S14). The pair of doublets at 5.05 and 5.2 ppm are indicative of terminal alkenyl protons since they have similar integration, different J‐coupling constants, and both couple to the multiplet at 6.25 ppm on the HH‐COSY (Figure S12). Thus, we can speculate that the presence of a terminal alkene is suggestive of either α‐ or γ‐initiation but not ϵ. We might also speculate that these peaks represent an extent of the reaction before the proton exchange proposed in Scheme 6 has occurred. After 24 h all of these peaks disappeared except for one clump of peaks at 5.4 ppm, in accordance with Takasu's data. ^[56] We then obtained MALDTI‐TOF‐MS spectra for both these samples and found the m/z trend to be identical at m/z=100n+163 (Figures S13 and S15). Thus, to account for the loss of unsaturation while maintaining the exact same molecular weight (Figure 5, bottom; Figures S11–S15), ring closure by conjugate addition seems the most reasonable.

Figure 5.

A) ¹H NMR (CDCl₃) of isolated PMMA initiated by 1 quenched after 1 min and 24 h (both at 99 % conversion), expanded to the alkenyl region, showing the presence of many alkene peaks after 1 min and disappearance of those peaks after 24 h. B) Overlaid MALDI‐TOF‐MS spectra for l‐PMMA quenched at 1 min and c‐PMMA quenched after 24 h, showing nearly identical spectra for both polymers.

Furthermore, we repeated the experiment but tracked the vinyl peaks over time, taking aliquots every few hours and could gradually observe the disappearance of vinyl peaks over the course of 24 h (Figure S11). The lack of any convincing new peaks led us to think that the proton exchange intermediate (Scheme 6) is transient and quickly undergoes cyclization once it is formed. We interrogated the possibility of a LA‐catalyzed proton shift by mixing a model small molecule, ethyl 2‐(cyclohex‐1‐en‐1‐yl)butanoate, which should have considerable thermodynamic incentive to undergo proton shift by a similar path, with 10 mol% MAD in toluene but no proton shift was observed. Thus, our favorite hypothesis is a proton shift that involves cooperative effort from the LA and basic enolates (see below).

Considerations Regarding Spatial and Temporal control

We mentioned in our previous work[ ²² , ⁵⁹ ] on this topic that many comparable cyclization strategies (especially those related to zwitterionic polymerization) contain an internal limitation in that the cyclization step will become competitive with propagation, thereby yielding cyclic polymers with broad molecular weight distributions. Our latest work seemed to overcome this limitation by providing cyclic di‐BCPs of MMA and ⁿ BA with M _n up to 267 kg mol⁻¹ and Đ as low as 1.03. ^[22] It is now quite clear that this exquisite control is the consequence of a temporal control (i.e., when cyclization occurs) that arises from the necessity for LA activation during the proton transfer/cyclization steps. When there is a considerable amount of free monomer present in the system, the monomer will outcompete the sorbate terminus for control over the LA and thus propagation will continue. Only when monomer is depleted (or near depletion) can the sorbate terminus begin to control the LA. Thus, the cyclization step must wait for propagation to finish before it becomes appreciable. One caveat here is that the ES sorbate 1 might not be the optimal initiator for obtaining temporal control. Since MMA is a weak donor and its coordination to MAD is less competitive than most monomers, ^[22] it is not unreasonable to suspect the sorbate terminus will become active for cyclization earlier than expected, thus generating some broadening of Đ. To test this limit, the LPP at a high MMA/MAD/1 ratio of 2000/10/1 and [MMA]₀=0.45 M in toluene led to PMMA with M _n=201 kg mol⁻¹ and Đ=1.61. After 24 h, the reaction remained at 98.6 % conversion, suggesting that cyclization occurred with some monomer still present. To optimize temporal control and thus reclaim narrow Đ during high MMA ratio polymerizations, it might be necessary to further tune the sorbate molecule (perhaps by tuning the sterics of the ester). On the other hand, optimal temporal control can be achieved by copolymerizing MMA with ⁿ BA. ^[22]

The mechanism by which spatial control (i.e., where cyclization takes place) is achieved by the MAD/I ^t Bu/sorbate system is more subtle to explain. It would be convenient if the zwitterionic mechanism by nucleophilic initiation could be invoked, which would give the termini electrostatic attraction and put the electrophilic carbon in line with the leaving I ^t Bu⁺ to guide the point of attack by the terminal enolate (Scheme 2). However, since we must now consider the revised ion‐pair mechanism, the spatial control arises from conjugate addition of the terminal enolate to the initiating sorbate terminus (Scheme 6) at the δ‐site (see below). A possible side reaction of this preferential intramolecular addition (ring‐closing) is intermolecular addition (linear chain coupling). The intermolecular chain coupling product (most likely followed up by another ring‐closure) can be ascertained by MALDI‐TOF‐MS and can be seen in Figure 5 (the small set of peaks near the baseline that appeared in the c‐PMMA spectrum) according to m/z=100n+303 (Figure S15; y‐intercept corresponds to ES+ES+Na⁺), but this side product seems quite negligible for polymerizations ran even at a relatively high concentration of [MMA]₀=0.45 M.

Achieving Spatiotemporal Cyclization Beyond Sorbates

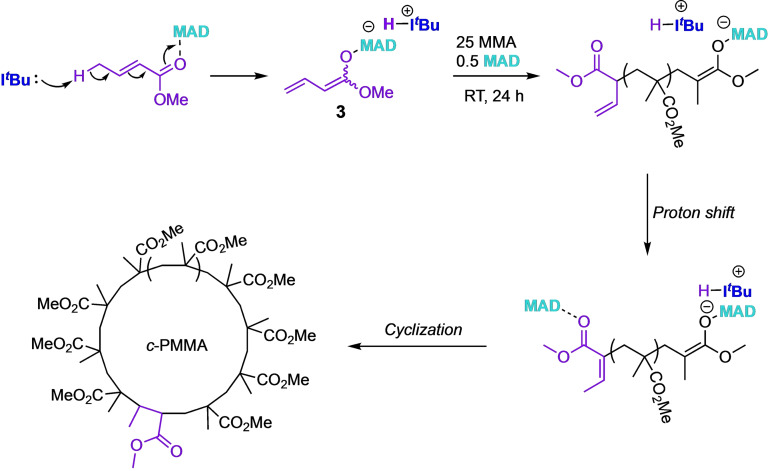
In light of these new mechanistic insights, we decided to revisit our aforementioned crotonate chemistry to investigate whether similar structure and reactivity of crotonates with respect to sorbates would render a similar cyclization pathway. Previously, we showed that the homopolymerization of crotonates by MAD/I ^t Bu produced linear polymers with a vinyl chain end due to the acidic protons on the γ‐methyl which render the homopolymerization more predisposed to chain transfer. ^[60] However, if the discretely synthesized crotonate ion pair 3 is used to initiate polymerization of methacrylates, then the deprotonative chain transfer is no longer available, thus preserving the potential for a ring‐closing step analogous to the sorbate system. Guided by this hypothesis, we isolated ion pair 3 and concluded based on ¹H NMR characterization that it was a fairly even mixture of geometric isomers based on the asymmetric enolate alkene (Figure S9). Our previous study provided evidence that 3 initiates from the α‐ carbon of the enolate giving a polymer with a vinyl end group. ^[60] Thus, a similar proton shift would be needed to move the terminal alkene into conjugation with the crotonate carbonyl before cyclization can take place (Scheme 7).

Scheme 7.

Proposed route to c‐PMMA by crotonate ion pair 3, involving a proton shift which generates a conjugated ester followed by cyclization via conjugate addition.

With the above hypotheses formulated, we attempted MMA polymerization by applying an MMA/MAD/3 ratio of 25/0.50/1.0 with [MMA]₀=0.87 M in toluene. This reaction was partitioned into two equal volume reactors, with one of the reactors being completely quenched after 1 min. This quenched polymer was isolated and characterized by ¹H NMR and HH COSY to define the vinyl end group peaks (≈5.2 ppm and ≈5.7–5.9 ppm in CDCl₃). Meanwhile, the unquenched reactor was monitored vs time via ¹H NMR to track the disappearance of the vinyl end groups (Figure 6).

Figure 6.

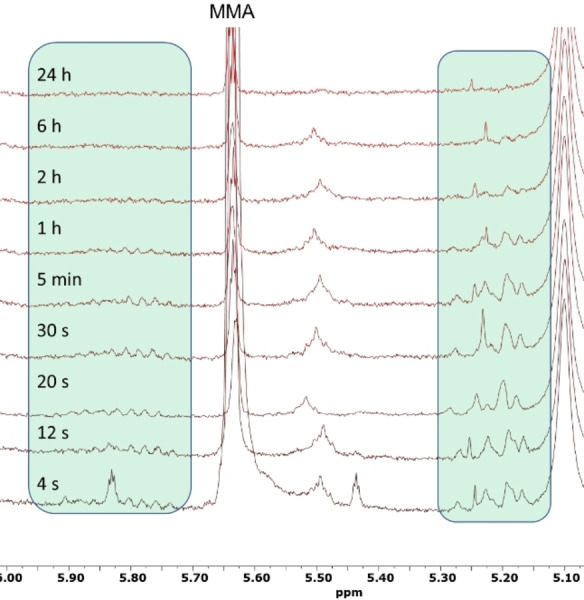
¹H NMR (CDCl₃) of the MMA polymerization by 3 at various time points, showing gradual disappearance of vinyl end groups over time, indicating ring‐closing.

As expected, the vinyl peaks disappeared over time and vanished after 24 h. This is consistent with the mechanistic scenario outlined in Scheme 7 and strikingly similar to the analogous experiment performed by the sorbate ion pair 1. Another important clue here is that the MMA was never completely consumed but concluded at 98.6 % conversion after 24 h. Again, this contrasts drastically from a typical LPP of methacrylates to linear polymers wherein monomer will generally convert quantitatively. The incomplete monomer conversion is highly indicative of a scenario such as that shown in Scheme 7, where the conjugated product following the proton shift has a stronger affinity for MAD relative to MMA. Thus, at low monomer concentrations, the conjugated crotonate end group outcompetes the residual MMA for MAD coordination and propagation stops shy of full conversion as a consequence.

To confirm that 3 does indeed produce cyclic polymers, we substituted allyl methacrylate (AMA) for MMA and performed a polymerization using a ratio AMA/MAD/3=200/2/1 with [AMA]₀=0.45 M in toluene and gave 24 h of reaction time to produce cyclic PAMA (c‐PAMA) with M _n=45.3 kg mol⁻¹ and Đ=1.08. The isolated c‐PAMA was subjected to post‐functionalization by the thiol‐ene click reaction using 1‐ODT as the substrate to quantitatively convert the allyl pendant groups into long alkyl chains, affording grafted c‐PAMA (c‐PAMA _g , theoretical M _n=148 kg mol⁻¹), which might make the ring polymers large enough to be directly observable by TEM. To our satisfaction, we directly observed the cyclic structures by TEM and obtained several example images of c‐PAMA _g (Figure 7; see also Figures S24–S26), strongly supporting our conclusion that crotonates, like sorbates, are capable of spatio‐temporally controlled macrocyclization via a proton transfer/conjugate addition mechanism.

Figure 7.

Synthesis of c‐PAMA _g and corresponding TEM images of the resulting cyclic polymers showing singular and clustered cyclic polymers that average 100 nm in diameter.

Understanding Active Species Generation, Chain Initiation, and Cyclization by a Density Functional Theory (DFT) Study

As discussed in the previous sections, the nature of LB (i.e., I ^t Bu vs. TPT) employed in the polymerization allows different mechanistic pathways (i.e., basic vs. nucleophilic pathway) to proceed in the polymerization of MMA by the LB/sorbate/MAD system. To assist the DFT discussion, Scheme 8 compares the basic pathway, which involves the abstraction of an ϵ‐methyl proton of the activated MS by the LB to generate the corresponding ion pair active species, with the nucleophilic pathway that proceeds through conjugate addition of the LB to the δ (or β) carbon of the MS⋅MAD adduct to form the corresponding zwitterionic active species. As showed in Scheme 8, for the sterically hindered, strong base I ^t Bu, the basic pathway is kinetically favored over the nucleophilic pathway, judged by a 2.4 kcal mol⁻¹ lower kinetic barrier [16.6 vs. 19.0 kcal mol⁻¹ transition state (TS) energy]. On the other hand, the nucleophilic addition product, the zwitterionic species, is thermodynamically favored by 2.5 kcal mol⁻¹ with respect to the ion pair, afforded via the basic pathway (−5.7 vs. −3.2 kcal mol⁻¹ product energy). Nevertheless, the key competition occurs at the TS level since, once the active species is generated, it will quickly react with the MMA present in abundance in the reaction environment, shifting the reaction towards the overall downhill chain growth to form thermodynamically stable polymer products (see below). Moreover, experimental evidence implies that this deprotonation is irreversible.

Scheme 8.

Energetic profiles of basic vs nucleophilic pathway in generation of active species as a function of LB. Free energies reported in toluene and kcal mol⁻¹.

In contrast, in the case of the uniquely nucleophilic but less basic TPT, the preferred reaction pathway is reversed, resulting in an inversion of selectivity. In fact, the nucleophilic addition is now almost 10 kcal mol⁻¹ more favored than the proton abstraction barrier (10.6 vs. 19.9 kcal mol⁻¹ TS energy). This strong kinetic preference for the nucleophilic pathway by TPT is also synergistically coupled with its resulting zwitterionic species being thermodynamically favored by almost 20 kcal mol⁻¹ relative to the basic pathway product, thus ruling out the basic pathway for TPT (−14.8 vs. +5.1 kcal mol⁻¹ product energy). These DFT results on the opposite selectivity between I ^t Bu and TPT for the active species generation step are consistent with, and provide a better understanding of, the above described, experimentally observed selectivity inversion.

Focusing on the kinetically favored basic pathway by I ^t Bu, the system that actually produces the cyclic polymer, we examined the next fundamental step of the polymerization reaction, which is the monomer initiation to generate the propagating enolate species that undergoes repeated conjugate addition in the chain propagation cycle. In this monomer (MMA) initiation step involving nucleophilic addition of the sorbate enolate 1 (MS) to the MMA⋅MAD adduct, three possible regioselectivity scenarios must be considered (Scheme 9): the nucleophilic attack of the MMA⋅MAD adduct by the α, γ, and ϵ‐carbon sites of enolate 1.

Scheme 9.

Regioselectivity considerations for the monomer initiation step to generate the propagating enolate. Free energies reported in toluene and kcal mol⁻¹.

From a kinetic standpoint, both γ and ϵ‐site attacks need to overcome a relative energy barrier of 8–9 kcal mol⁻¹ with the ϵ‐carbon addition product being thermodynamically much more favored (by more than 10 kcal mol⁻¹). However, the α‐site attack is clearly kinetically controlled with a relative energy barrier of only 5.6 kcal mol⁻¹, about 3 kcal mol⁻¹ lower than the other two pathways. In addition, the α‐selectivity also produces the initiated MMA enolate propagation species with good stability, 10 kcal mol⁻¹ lower in energy with respect to the ion pair and the MMA⋅MAD adduct considered at infinite distance (Scheme 9). However, the above computed initiation regioselectivity brought about an intriguing question: since the preferred α‐selectivity generates the active propagating species that contains neither the conjugated Michael acceptor terminus (c.f., Scheme 9) required for cyclization via conjugate addition ring closure nor a leaving group required for S_N2 type ring‐closure, how does the cyclization actually take place to form the cyclic polymer?

To address this question while avoiding complex conformation issues when modeling the cyclization step of the favored “α‐initiated” growing chain, we computed this step by using two separated fragments simulating the two chain ends, the same approach we had used in our previous work. ^[67] One fragment in Scheme 10 represents the initiation chain‐end with the methyl group at the α‐carbon simulating the polymer chain, and the other fragment is the ion pair formed by the protonated LB and the anionic chain end representing the last enchained MMA unit. To generate the diene conjugated with the ester carbonyl (i.e., the Michael acceptor), we considered a proton transfer from the α‐carbon to the ϵ‐carbon of the sorbate chain end fragment. Since the direct 1,6‐H transfer requires an energy barrier of 26.4 kcal mol⁻¹, which is much higher than those required in the other steps of the scenarios considered, we focused on a two‐step pathway involving the anionic chain end fragment. At first, the proton at the α‐carbon transfers from the initiation fragment to the α‐carbon of the enolate fragment, forming an anionic sorbate unit paired with the positively charged [I^tBu−H]⁺ moiety and a neutral MMA‐MAD chain‐end. Next, a further H‐transfer from the α‐carbon of the neutral fragment to the ϵ‐carbon of the anionic sorbate unit leads to a new conjugated Michael acceptor terminus (Scheme 10).

Scheme 10.

Cyclization considerations for the ring‐closure step leading to the cyclic polymer formation. Free energies reported in toluene and kcal mol⁻¹.

The energies reported in Scheme 10 indicate the H‐transfer steps as energetically feasible, requiring ≈12 and ≈15 kcal mol⁻¹ for the first and the second step, respectively, with the transient intermediate and the final isomerization conjugate product being ≈12 and ≈5 kcal mol⁻¹ more stable than the starting species, respectively. Noteworthy here is that the barrier of 12–15 kcal mol⁻¹ for H‐transfer is considerably higher than the propagation step (5–8 kcal mol⁻¹); thus, these events that lead to cyclization have to wait until essentially all monomer is consumed, thus the temporal control of cyclization. The final cyclization step involving the conjugate addition to the δ‐carbon is almost 7 kcal mol⁻¹ more kinetically favored than the one involving the β‐carbon, leading to a strong kinetic selectivity towards the formation of the c‐PMMA with an endocyclic double bond, consistent with the above‐described experimental result. The overall reaction is about 20 kcal mol⁻¹ downhill relative to the starting species, providing a strong thermodynamic driving force for the ring closure. It is worth noting that the cyclization scenarios computed along the nucleophilic pathway occurring via S_N2 type ring‐closure by back‐biting attack of the enolate chain end at either the δ‐ or β‐carbon of the sorbate unit, with concomitant elimination of I ^t Bu, are considered as energetically inaccessible, with energy barriers higher than 49 or 41 kcal mol⁻¹ (Scheme 10).

Conclusion

Key takeaways and conclusions drawn from the herein combined experimental and theoretical study towards establishing the highly demanding spatial and temporal control for the precision synthesis of cyclic polymers with predictable M _n and low Đ values as well as high structural fidelity by the LPP methodology, here represented by a prototype system comprising [LB (I ^t Bu, TPT)+LA (MAD)+substrate (sorbates, crotonates, methacrylates)], are summarized as follows:

1. For the active species generation step, the nature of the LB determines the mechanistic pathway by which the LPP operates on monomers and thus ultimately the topology of the resulting polymers. While the steric hindered, strong base I ^t Bu activates the sorbate⋅LA adduct via the basic pathway to produce the ion pair propagating species leading to cyclic polymers, the less basic TPT proceeds with the nucleophilic pathway to afford the zwitterionic species leading to linear polymers.

2. For the monomer initiation step along the cyclic‐polymer‐forming basic pathway to generate the ion‐pair propagating species, the regioselectivity is confirmed to be the attack from the α‐site of the sorbate enolate to generate an unconjugated terminus. The surprise here is largely due to the follow‐up question of how the subsequent cyclization could occur since the α‐initiated terminus contains neither the conjugated Michael acceptor terminus required for cyclization via conjugate‐addition ring closure, nor a leaving group required for S_N2 type ring‐closure.

3. The cyclization step to form cyclic polymers is also surprising and counterintuitive. The realization of isomerization of the non‐conjugated initiating terminus to the conjugated one via a two‐step H‐transfer is significant in twofold. First, this process provides the suitable motif for cyclization to occur and complete ring‐closure. Second, the considerably higher energy barrier for the isomerization than the chain propagation encourages temporal control of cyclization—it does not occur until after essentially all monomers have been consumed. Convincing lines of evidence also show that the nucleophilic pathway does not lead to cyclic polymers because the S_N2 type ring‐closure proposed in literature are considered as energetically inaccessible, with energy barriers higher than 41 kcal mol⁻¹.

4. LPP is uniquely equipped for achieving spatiotemporal control in the precision cyclic polymer synthesis, such as cyclic homopolymers c‐PES and c‐PMMA, as well as cyclic BCP P ⁿ BA‐b‐PMMA with M _n up to 267 kDa and Đ as narrow as 1.03. The key features of LPP that enabled such exquisite control include CSC, selective K _eq binding of the LA to specific sites for activation to trigger programmable chemical events, and largely differentiated kinetic barriers between chain propagation and cyclization, thus allowing the polymerization to achieve essentially full monomer conversion and only then execute the cyclization event to occur at the specific site of the chain. Overall, the discrete, individual roles of the LA and LB, as well as their synergy and cooperativity, are essential for the successful implementation of LPP for precision cyclic polymer synthesis.

5. A mechanistic understanding of LPP for precision cyclic polymer synthesis enabled us to expand the built‐in initiating/ring‐closing moiety from sorbates to crotonates. However, under high monomer to initiator ratio conditions, the polymerization of MMA stops at ≈99 % monomer conversion, a result of the isomerized conjugated sorbate or crotonate initiating terminus that outcompetes the residual MMA for MAD coordination. These results suggest that cyclization occurred with a trace amount of monomer still present, shy of the ideal, complete MMA conversion under such conditions.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

M. L. McGraw, L. T. Reilly, R. W. Clarke, L. Cavallo, L. Falivene, E. Y.-X. Chen, Angew. Chem. Int. Ed. 2022, 61, e202116303; Angew. Chem. 2022, 134, e202116303.

Data Availability Statement

The data that support the findings of this study are available in the Supporting Information of this article.