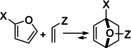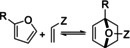The Interplay between Kinetics and Thermodynamics in Furan Diels–Alder Chemistry for Sustainable Chemicals Production

Abstract

Biomass‐derived furanic platform molecules have emerged as promising building blocks for renewable chemicals and functional materials. To this aim, the Diels–Alder (DA) cycloaddition stands out as a versatile strategy to convert these renewable resources in highly atom‐efficient ways. Despite nearly a century worth of examples of furan DA chemistry, clear structure–reactivity–stability relationships are still to be established. Detailed understanding of the intricate interplay between kinetics and thermodynamics in these very particular [4+2] cycloadditions is essential to push further development and truly expand the scope beyond the ubiquitous addend combinations of electron‐rich furans and electron‐deficient olefins. Herein, we provide pertinent examples of DA chemistry, taken from various fields, to highlight trends, establish correlations and answer open questions in the field with the aim to support future efforts in the sustainable chemicals and materials production.

The furan Diels–Alder (DA) cycloaddition is a powerful green methodology to upgrade bio‐derived resources into valuable, renewable chemical products. The intricate interplay between kinetics and thermodynamics often complicates the understanding of this chemistry. In this review we provide simple structure–reactivity–stability relationships to guide future efforts in the design of efficient new synthesis routes based on furan DA reactions.

1. Introduction

The Diels–Alder (DA) [4+2] cycloaddition is one of the most powerful and versatile reactions in the toolbox of the synthetic organic chemist, allowing complex architectures to be constructed from simple building blocks. Recently, the use of furan heterocycles as dienes is again receiving particular attention, as furanics are key renewable platform molecules with tremendous potential for the more sustainable production of chemical building blocks and materials. Indeed, bio‐derived furanics such as furfural (FA) and its 5‐hydroxymethyl homologue (5‐HMF), accessed from lignocellulosic carbohydrates, play a central role in many biorefinery operations. DA chemistry features very prominently in the efforts aimed at valorization of the renewables‐based furanic building blocks, as it offers a strategic opportunity for truly sustainable chemistry. Indeed, DA cycloaddition is 100 % atom‐efficient, adhering to a core principle of green chemistry.[ ¹ , ² , ³ ] Moreover, cycloaddition reactions are highly selective and convergent synthetic tools for the rapid generation of molecular complexity, offering control over regio‐ and stereochemistry. This contributes to other green chemistry objectives, such as improved step‐economy, prevention of waste and avoiding derivatization. Importantly, the DA adducts are versatile synthons en route to a slate of valuable products that feature the ubiquitous six‐membered (aromatic) carbocycle motif. The various research efforts in the design and implementation of novel synthetic applications of furanic building blocks clearly build on the wealth of prior knowledge on general cycloaddition chemistry; however, as we will showcase here, in many ways furans behave atypically compared to other types of dienes and understanding their reactivity (or lack thereof) is far from trivial.

What distinguishes the furan–diene DA reactions from other [4+2] cycloadditions is the reaction's reversibility at near ambient temperatures. Indeed, the position of the DA equilibrium can generally be shifted in a controlled, predictable, and tunable manner, at temperatures ideally suited for e.g., material science applications. For this reason, the furan DA coupling has been extensively exploited in various macromolecular applications built around reversibility, such as responsive materials[ ⁴ , ⁵ , ⁶ , ⁷ ] and drug delivery systems.[ ⁸ , ⁹ ] In contrast, other important areas of application require stability rather than reversibility, as generally seen for instance in bioconjugation, ^[10] natural product synthesis,[ ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ ] drug discovery ^[16] and the synthesis of renewables‐based chemical commodities (Figure 1).[ ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ ] In such cases, further synthetic elaboration of the relatively labile DA adduct is in competition with the kinetically accessible cycloreversion pathway, posing a major challenge (Figure 2 A).

Figure 1.

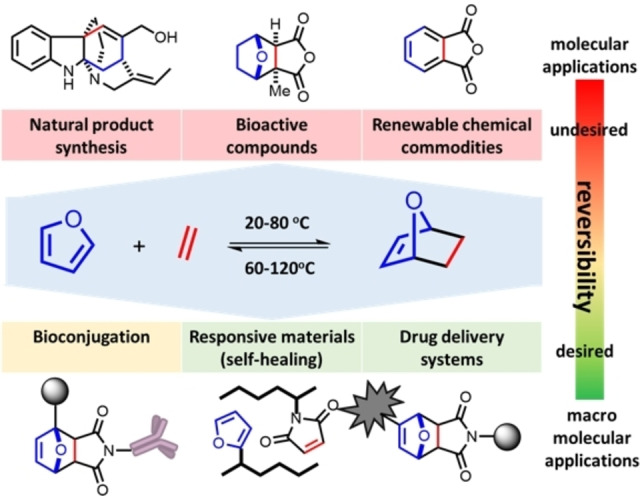
Synthetic applications of furan DA reactions.

Figure 2.

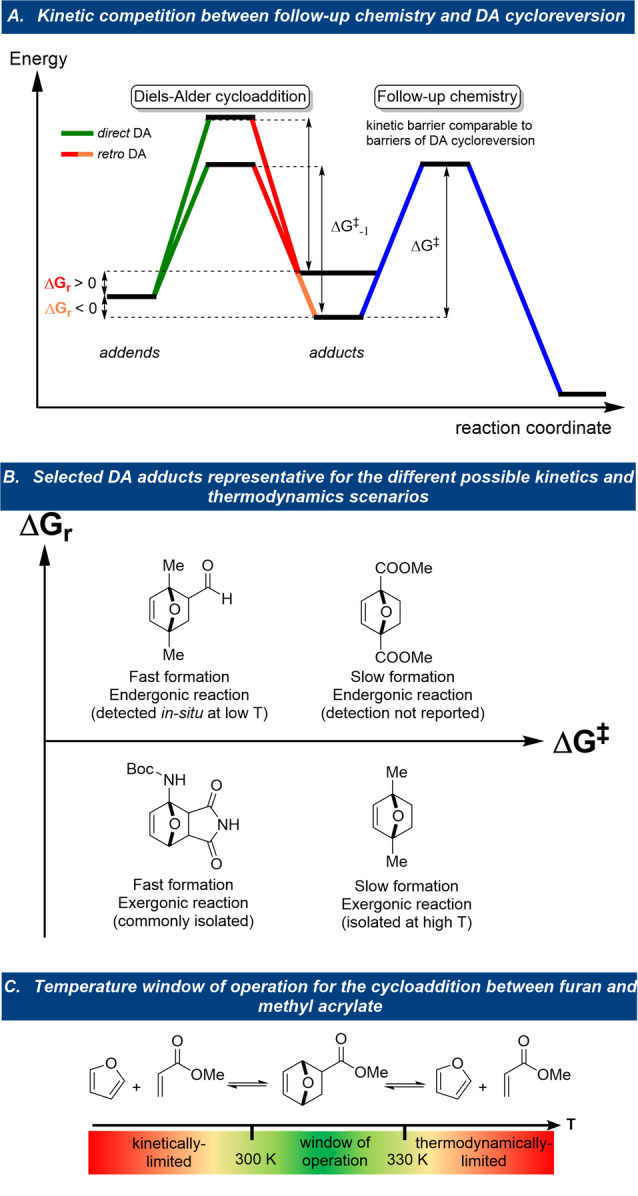
Furan DA‐based synthetic routes: success depends on intrinsic structural features of the diene/dienophile pair, external conditions and the control over the cycloreversion process.

Either way, whether reversibility is a blessing or a curse, correct understanding of both the kinetic and thermodynamic aspects of the DA equilibrium is of pivotal importance for any DA‐based molecular design. While the well‐established principles of frontier molecular orbital (FMO) theory have been successfully applied to explain the kinetics of the cycloaddition in terms of various structural elements of the diene/dienophile pair, establishing a unified set of rules that captures the (trends in) reaction thermodynamics is much less straightforward (Figure 2 B). Indeed, because of its overwhelming popularity and success in the field of cycloaddition reactions in general, there is a certain bias towards relying mainly on FMO theory arguments when it comes to interpreting observations in furan DA couplings, while the thermodynamics of the reaction is often overlooked. Moreover, the contradicting effects that electronic and steric factors (can) have on kinetics and thermodynamics can result in unexpected outcomes (e.g. ethylene adducts are slow to form but surprisingly thermodynamically stable). These subtleties are insufficiently appreciated, complicating predictions and clouding the interpretation of experimental results. Notably, as kinetics and thermodynamics are intertwined and as ΔG _r is characteristically ±0 kcal mol⁻¹, reactions that seem kinetically feasible may only produce small amounts of adduct (if at all). Similarly, reactions anticipated to be slow might seem not to proceed altogether, regardless of operating temperature; as this key process parameter has opposite effects on the rate and equilibrium constants, the window for the successful operation of the chemistry is often narrow (Figure 2 C). Thus, together with intrinsic properties of the adducts, reaction conditions (particularly temperature) critically impact the chances of detecting an appreciable amount of adduct formation to serve as starting point in any route selection or optimization campaign.

Here, we aim to provide an overview of the most important factors governing the kinetics and thermodynamics of formation of furan DA adducts and emphasize the interplay between them, to guide the design of sustainable synthesis routes towards renewable chemicals. Examples of structurally diverse 7‐oxabicyclo[2.2.1]hept‐2‐ene (7‐oxanorbornene) adducts abound in the nearly century‐old DA chemistry ^[22] and our intention herein is to provide a selection thereof, highlighting trends, categorizing and generalizing the sometimes scattered observations in the literature. Various aspects of this rich area of research have been reviewed before. For instance, Vardon and co‐workers discussed the opportunities to produce renewable chemical commodities by heterogeneous DA catalysis, with furans featuring as prominent biobased dienes. ^[17] Ananikov et al. recently provided an extensive overview of the scope of the furan DA cycloaddition, highlighting the most frequently employed diene/dienophile combinations;[ ¹⁸ , ²³ ] notably, furfurals and other related oxygen‐rich furans emerged from this overview as notoriously unreactive dienes, and the recent progress in developing strategies to overcome these reactivity challenges have been briefly summarized by Gomes and Ravasco. ^[24]

A comprehensive analysis of the structure–reactivity–stability relationships that underly furan DA reactions is currently not available, however, and is the topic of this review. Thus, furan DA cycloadditions will be discussed from the FMO viewpoint as well as beyond, to provide a more general understanding of the possibilities and limitations of this chemistry, with emphasis on renewable building blocks and sustainable chemistry applications.

Thus, we start with a brief overview of furan diene and dienophile scope, emphasizing the opportunities available for the conversion of the most readily accessible bio‐derived inputs into value‐added chemicals. Next, the vast literature on furan DA cycloadditions is surveyed to establish generic structure–reactivity–stability relationships, looking at kinetic and thermodynamic aspects independently as well as at their interplay. Examples of and opportunities for one of the most general approaches to overcome an all too often encountered unfavorable DA equilibrium, that is, coupling DA cycloaddition to an exergonic, kinetically accessible secondary reaction, are next discussed in detail. In the second part of this review, the focus is on the (tandem) dehydration of DA adducts into aromatics (Figure 1, top right corner), a highly topical and industrially relevant showcase area of furan DA chemistry.

Progress in the field is discussed in terms of substituent effects on the reaction rate and thermal stability of the adduct, as well as ease of adduct dehydration, and placed into the context of the (in)availability of the prerequisite biobased furanics. The selected examples thus highlight the (mis)match between bioresource accessibility/reactivity/end‐product value, which is key to the development of efficient and cost‐competitive manufacturing processes and eventual adoption of this technology by the chemical industry.

2. DA Chemistry with Renewables: Diene/Dienophile Scope

2.1. Biobased Furanic Dienes: Typical Substitution Patterns

The synthesis of the most prominent bio‐derived furans, furfural and 5‐HMF, and their (catalytic) conversion to value‐added (functionalized) derivatives is a major focus of biorefining and has been extensively reviewed.[ ²⁵ , ²⁶ , ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ³² ] The most industrially relevant C5 furans, furfural and furfuryl alcohol, are already produced at large scale, via well‐established and fairly robust processes. Comparatively, the C6 homologues are clearly lagging behind, mainly due to 5‐HMF stability issues, ^[33] with current production efforts now being at pilot scale. Nonetheless, the tremendous recent interest in molecules such as 5‐HMF and 2,5‐furandicarboxylic acid (FDCA) is a major incentive for the further development of scalable manufacturing processes. Indeed, AVA Biochem, the largest current producer of 5‐HMF, intends to upscale manufacturing from its present 300 tpa level to a 10 ktpa scale in the near future; ^[31] similarly, Avantium, pioneer in commercial FDCA manufacturing, expects to deliver up to 5 ktpa of this product by 2023. ^[32] In any case, the formylated furans furfural and 5‐HMF are and will certainly remain key branching points in (future) biorefinery efforts (Scheme 1). Although less frequently investigated than 5‐HMF, 5‐chloromethylfurfural (5‐CMF) is another versatile furan of considerable potential (see for example Scheme 34),[ ³⁴ , ³⁵ , ³⁶ ] together with ethers of 5‐HMF. ^[37]

Scheme 1.

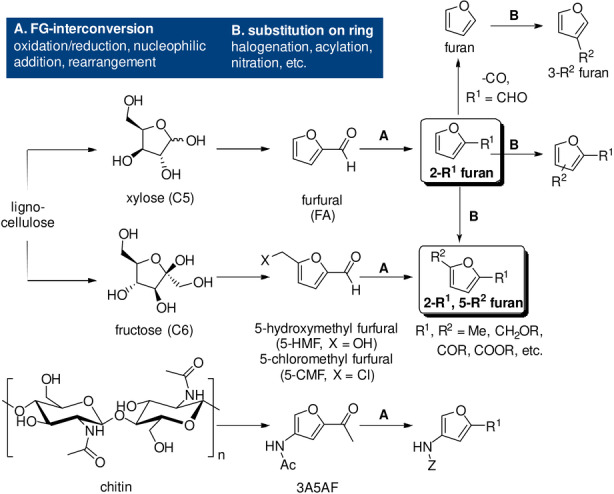
Bioderived furan dienes: directly accessible platform molecules and typical conversions to other derivatives.

Scheme 34.

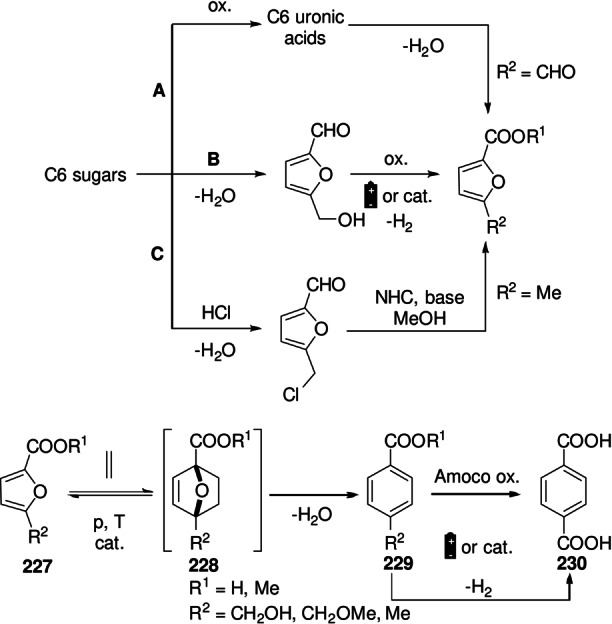
Synthesis of renewable terephthalic acid by cycloaddition/dehydration of furoic acids and ethylene; sourcing of furoic acids from biomass: route A: from uronic acids; route B: from C6 sugars via 5‐HMF; route C: from C6 sugars via CMF.

The carbohydrate origin of the renewable furans is reflected in the substitution pattern of the most readily available derivatives (Scheme 1) with 2‐monosubstituted furans stemming from the C5 sugars and 2,5‐disubstituted furans from the C6 carbohydrates. The synthesis of furans with alternative substitution patterns is considerably more elaborate and often implies forging the furan ring from acyclic (fossil‐derived) precursors. There is one exception: amine‐functionalized furans such as 3‐amino‐5‐acetylfuran (3A5AF) and derivatives thereof can be synthesized directly from chitin, another cheap and abundant natural resource. These furans have, however, not yet been investigated in DA chemistry, to the best of our knowledge. ^[38]

2.2. Biobased Furanic Dienes: (Avoiding) the Redox Detour

Many transformations that convert furfural and 5‐HMF into other furan building blocks involve redox reactions (Scheme 1). There is, however, a striking imbalance between the two directions of oxidation state change and, as a result, the current scope of furan dienes for DA chemistry applications. Indeed, the vast majority of DA cycloaddition studies involve the reduced derivatives (e.g. R=H, Me, CH₂X, etc.), while the direct use of the formylated derivatives themselves or their oxidized variants (e.g. R=CHO, COR, COOR, etc.) is the exception.[ ¹⁸ , ²⁴ , ²⁵ ] This presents an unfortunate limitation in scope, as formyl or carboxyl substituents provide versatile reactivity handles and are as such highly desirable in advanced intermediates. Moreover, these functional groups are often essential for application of the building blocks in polyesters, polyamides, thermosets, lubricants, adhesives, resins, etc.

That the most readily available oxygenated furans are underutilized in DA cycloadditions is arguably the result of the widespread idea that, in terms of diene reactivity, electron‐withdrawing substituents are highly detrimental for the reaction rate, often to the extent that product formation is deemed impossible. While this FMO theory‐derived kinetic argument certainly has validity, it is important not to overlook the thermodynamics of the reaction. Indeed, a small but significant number of recent studies suggest that the DA cycloaddition with electron‐poor furans is not just relatively slow, but also relatively endergonic. This makes efficient DA reactions with these substrates indeed impossible, but for a more serious reason than sluggish conversion: the intrinsically unfavorable thermodynamics. Not surprisingly, the current approaches towards the synthesis of oxygenated furan DA adduct derivatives typically rely on a series of atom‐inefficient and wasteful redox reactions, that is, proceed via a so‐called “redox detour”: initial chemical activation of the furan diene for DA cycloaddition by hydrogenation (e.g. to methylated furans) and late‐stage, downstream oxidation of the oxygen‐poor intermediates. Evidently, this negatively impacts the overall atom‐, energy‐ and process efficiency. The production of (highly oxidized) terephthalic acid through DA cycloaddition of 2,5‐dimethylfuran and ethylene with p‐xylene as intermediate is a typical example of this approach (Scheme 2, red arrow). Clearly, truly sustainable synthetic routes require expansion of the diene scope to include also the electron‐poor furans and for this reason in this review we will particularly emphasize recent success in this direction.

Scheme 2.

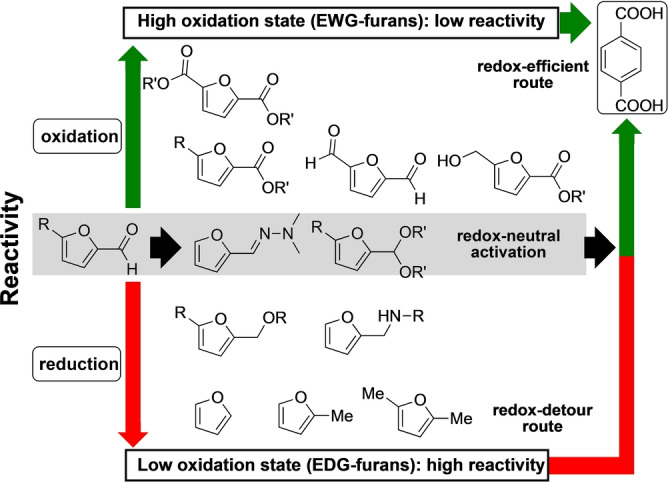
Redox conversions of biobased furfurals and routes towards oxygenated aromatics, exemplified for terephthalic acid formation.

2.3. Biobased Dienophiles: Scope and Potential

The most frequently employed dienophiles in cycloadditions with furan dienes are listed in Scheme 3. As further detailed in Section 4.3, dienophile reactivity can be linked in a relatively predictable manner to certain structural parameters, such as the number and type of substituents on the olefinic bond, as well as their cyclic/acyclic nature. As with the furan dienes, a large variety of dienophiles can be sourced from biomass with current technology (Scheme 3, highlighted in green). This paves the way towards DA‐based products with 100 % renewable carbon, an important prerequisite of green and circular chemistry.[ ³⁹ , ⁴⁰ , ⁴¹ ] However, a mismatch between reactivity and dienophile accessibility can again be noted, which becomes a relevant issue for scale‐up of the chemistry. For instance, maleimides, acetylenedicarboxylic acid esters and activated acrylates (e.g. fluorinated esters, p‐nitrophenyl acrylate) are excellent dienophiles but their synthesis from renewable sources is tedious and costly (Scheme 3, highlighted in red).

Scheme 3.

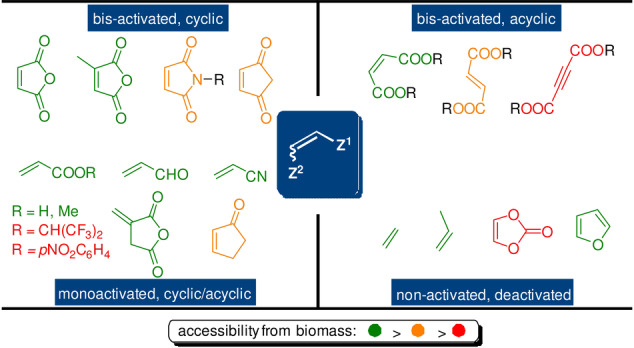
Four categories of dienophiles with representative examples.

In addition, it is important to note that for the readily accessible bio‐derived dienophiles, there are marked differences in the theoretical carbon yields of the manufacturing routes (Scheme 4). Biobased maleic anhydride and derivatives (e.g. maleate esters) are produced by the oxidation of furfural or 5‐HMF with carbon yields of 80 % and 67 %, respectively.[ ²⁶ , ⁴² , ⁴³ ] Similarly, the production of bioethylene by sugar fermentation has a carbon yield of 67 %. ^[44] On the other hand, no carbon atoms are wasted in the production of acrylate derivatives such as acrylic acid, acrolein, or acrylonitrile;[ ⁴² , ⁴³ , ⁴⁵ ] from a sustainability point of view, these are the most attractive dienophiles.

Scheme 4.

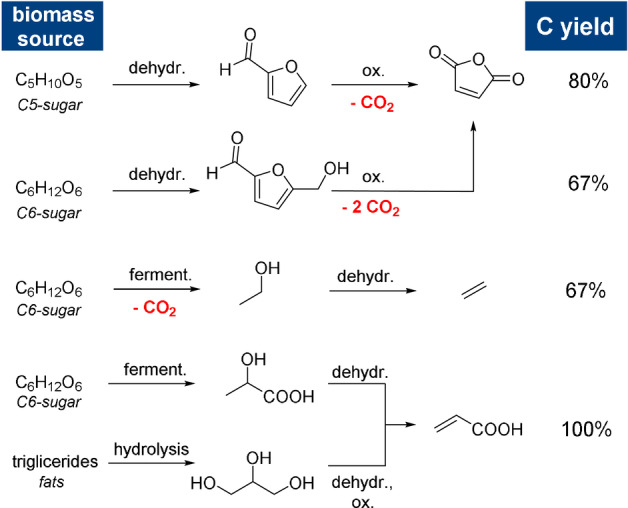
Synthesis routes and carbon yields for some typical bioderived dienophiles.

3. Some General Aspects of Furan DA Reactions

While the mechanism of the (furan) [4+2] cycloaddition is still being debated, most often a (synchronous or asynchronous) concerted pathway is proposed; however, depending on the particularities of the addends, stepwise mechanisms (radical‐based, ionic) are also possible. ^[46] While certain general aspects of DA cycloadditions also hold for furans, ^[17] several elements distinguish them in the pool of dienes. First, the aromatic nature of furan (albeit significantly lower than that of the prototypical aromatic molecule, benzene) provides an additional stabilization to the addends’ side of approximately −14 to −15 kcal mol⁻¹; ^[47] this has tremendous consequences for the kinetics and thermodynamics of the cycloaddition. For example, in comparison to structurally related cyclopentadiene (CpH), a prototypical nonaromatic cyclic diene, the differences are significant: furan DA reactions are relatively slower, less favored thermodynamically and characteristically under thermodynamic control. The [4+2] cycloaddition of furan with maleic anhydride serves as a classical example. According to Svatoš et al., ^[48] the reactions with furan as diene are considerably less exergonic than those with CpH, with the difference being comparable to the furan resonance energy (ΔΔG _r 12 kcal mol⁻¹ for the exo product and 16 kcal mol⁻¹ for the endo isomer, respectively); the activation energies are 3–6 kcal mol⁻¹ higher for furan (Figure 3 top). The barriers for cycloreversion are, however, much lower for the furan adducts (with approximately 10 kcal mol⁻¹), allowing equilibration at near ambient temperatures. In contrast, under typical experimental conditions, the reaction with CpH is not reversible and the outcome is dictated by the kinetic preference for the endo isomer (the Alder rule). On the other hand, in most examples, furan DA reactions are under thermodynamic control, with the exo stereoisomer ultimately prevailing (although the endo product may also be detected in the initial stages of the experiment, Figure 3 bottom). Kinetic control with furan addends is rather exceptional, and involves the use of catalysis at low temperatures (e.g. <−50 °C) ^[49] or strongly electron‐donating substituents at the furan 3‐position (see for example, Scheme 5). ^[50]

Figure 3.

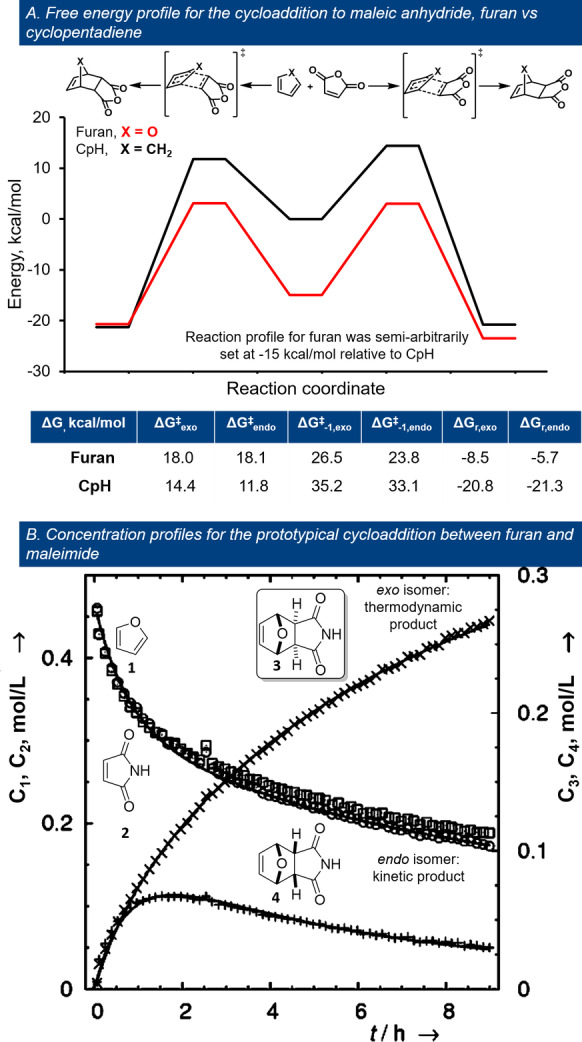
Particularities of the furan DA cycloaddition highlighted by prototypical reactions with maleic acid derivatives; reproduced with permission from ref. [48].

Scheme 5.

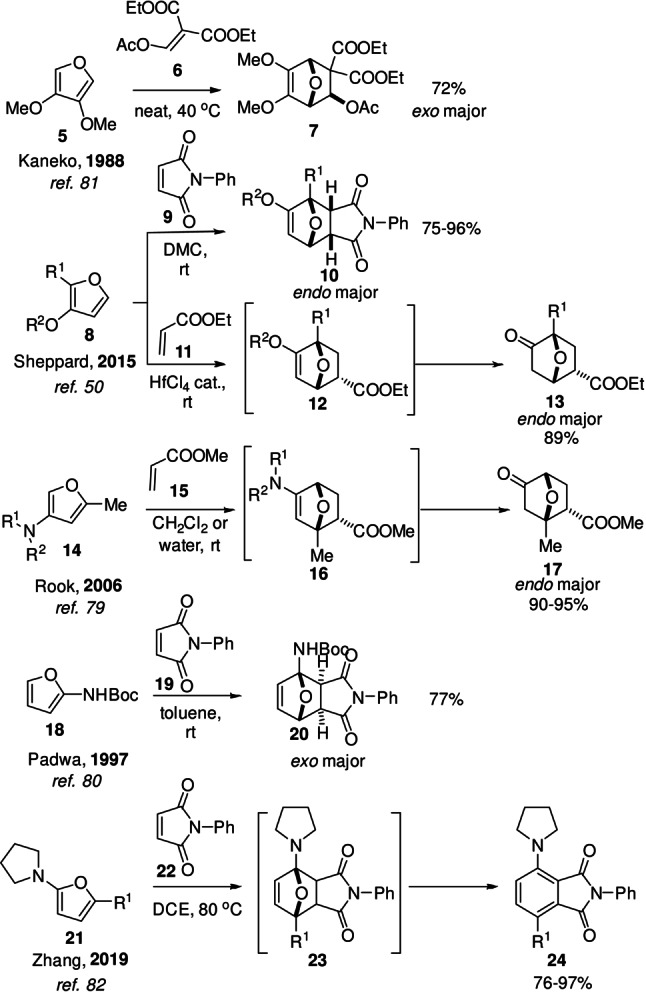
Selection of cycloadditions with electron‐rich furan dienes: reactions proceed at relatively low temperatures; secondary reaction channels are accessible and can limit selectivity towards the DA cycloadduct.

These furan‐specific characteristics can lead to confusion or misinterpretation of experimental results. For instance, almost invariably, researchers benchmark experimental findings against FMO predictions. ^[51] These principles allow for the reliable interpretation of reaction kinetics but, as furan DA cycloadditions operate under thermodynamic rather than kinetic control, FMO theory‐based arguments should be used with care. In the next section we will provide many examples to showcase the strengths and limitations of FMO theory in understanding the performance of furan DA reactions.

4. Kinetics

4.1. Furan DA Reactions and FMO Theory: Utility and Limitations

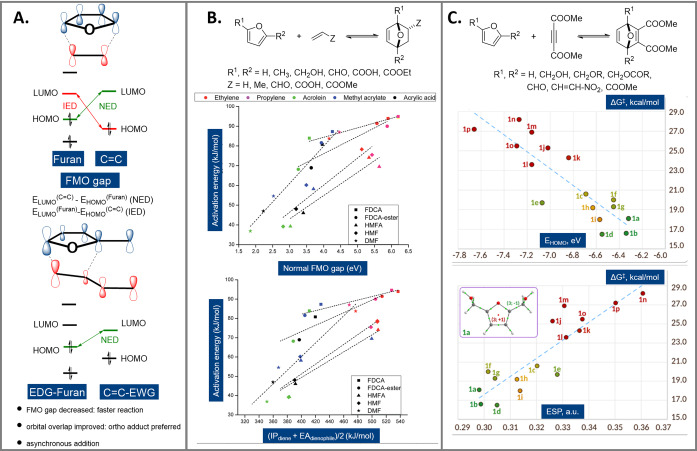
According to FMO theory, during cycloaddition new bonds are formed through interactions of the HOMO (highest occupied molecular orbital) and the LUMO (lowest unoccupied molecular orbital) of the addends. The reaction rate is highest when this orbital interaction is maximized, that is, when the shapes and energies of these FMOs of the addends are similar. The FMO theory has traditionally been used with great success to rationalize relative rates in cycloaddition chemistry and the particular case of furan dienes is no exception. Two types of DA cycloadditions can be distinguished: normal‐electron‐demand reactions (NED), involving the interaction between the diene HOMO and the dienophile LUMO, and inverse‐electron‐demand cycloadditions (IED), which involve the LUMO of the diene and the HOMO of the dienophile (Figure 4 A).

Figure 4.

FMO interpretation of furan DA reactions (A); correlations of rate/activation energy with the FMO gap and other related descriptors (B) and (C); IP=ionization potential, EA=electron affinity, ESP=electrostatic potential; see Figure 9 for structures 1 a–p; reproduced with permission from refs. [52, 53].

Regardless of the electron flow, the smaller the energy gap between the FMO orbitals, the faster the reaction. In terms of structural features, electron‐donating substituents on the diene and electron‐withdrawing groups on the dienophile accelerate NED reactions, the opposite being true for IED cycloadditions. Since the oxygen atom in the furanic ring already destabilizes the diene HOMO, the vast majority of furan DA reactions can be classified as NED ones. Indeed, as noted above, the long‐standing tradition of employing electron‐rich furans in DA chemistry, typically in combination with electron‐deficient dienophiles, is rationalized by these FMO considerations. ^[18] IED mechanisms are much less accessible, and generally imply the presence of several, strongly electron‐withdrawing groups on the furan, aided by activating Lewis acids, and the use of ethylene as dienophile (see for instance Section 8.4).

In general, orbital/bond polarization in the addends as a consequence of electronic properties of substituents not only implies faster cycloaddition, but it also sometimes tightens the regioselectivity control, according to the geometry that allows for the maximal orbital overlap in the (now asynchronous) transition state (Figure 4 A). Such regioselectivity control only holds under conditions of kinetic control, that is, in reactions run at low temperatures.

Typical correlations between rate/ΔG ^≠ and FMO energy gap are frequently reported for furan DA cycloadditions: two such examples are provided in Figure 4 B, C. Alternatively, other related reactivity descriptors are also useful, for instance the average of the diene ionization potential and dienophile electron affinity ((IP_diene+EA_dienophile)/2) ^[54] or the value of the electrostatic potential (ESP) at the ring critical point of the furan cycle. ^[52] Mapping rate parameters vs. orbital energies is quite likely to be of limited use in understanding the thermodynamically controlled furan DA reactions, however. In this respect, as will be showcased in Section 6, Bell–Evans–Polanyi relationships or complete reaction energy profiles, which look at both kinetic and thermodynamic barriers, have much higher practical utility.

Next, FMO theory is frequently used to explain catalytic effects in enhancing the rate of furan DA cycloadditions. Catalysis, in the form of Lewis acid coordination to heteroatom‐containing functional groups in the addends, particularly the dienophile, further enhances the productive polarization of the FMOs (i.e. by lowering dienophile LUMO energy and improving the orbital overlap). A recent computational study challenges this traditional view, however, by proposing that diminished Pauli repulsion between the electron clouds of the two approaching addends upon binding of the catalyst is instead responsible for the rate enhancement: ^[55] this work showed that coordination of the Lewis acid to the dienophile does lead to a stabilization of the LUMO^dienophile, but not to an overall enhancement of the orbital interactions between the addends. While very popular in DA chemistry in general, the use of Lewis acid catalysis with furan dienes is much more challenging, as the Lewis acid may also bind to the furan, deactivating it or promoting undesirable side reactions (i.e. humin formation). Therefore, success is very often case specific and accordingly the overall scope of catalysts quite broad, ranging from simple metal salts (see a selection of references[ ⁴⁹ , ⁵⁶ , ⁵⁹ ]) to organocatalysts ^[60] and zeolites. ^[17]

The many factors that influence the kinetics of the cycloaddition are depicted schematically in Figure 5. In the following sections, we will look in more detail at how furan and dienophile structure relate to reactivity.

Figure 5.

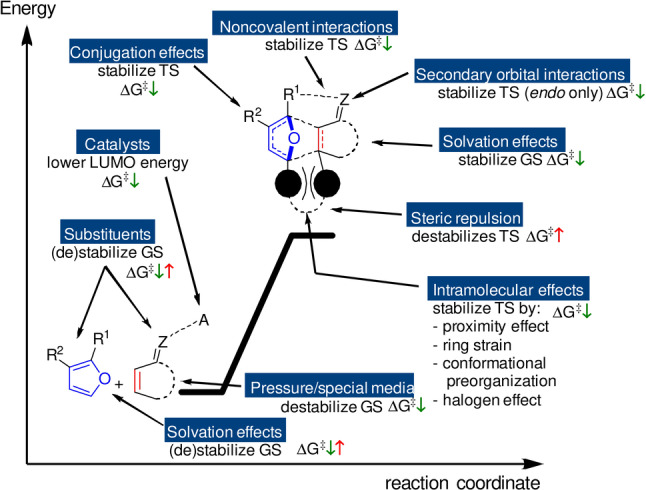
Factors influencing the kinetics in furan DA reactions; GS=ground state; TS=transition state.

4.2. Furan Dienes: Reactivity Is Predictably Modulated by the Electronic Properties of Substituents

Understanding the reactivity of furans has been the object of numerous experimental and computational studies. For instance, Qiu computed the free energy of activation ΔG ^≠ (but not ΔG) for the coupling of various 2‐ and 3‐substituted furans with maleic anhydride (X=O, Figure 6). ^[61] The general reactivity trend in the series was: OMe >Me >H >Cl >CF₃ >CHO >NO₂ >CN, with the barrier for the 3‐isomers being consistently lower than for the 2‐substituted isomers. Obviously, substituent mesomeric properties (either positive or negative) were found to have a greater impact than inductive effects, as suggested by the Hammett plot (Figure 6), in line with numerous experiments. In absolute terms, the range of values obtained for ΔG ^≠ was approximately 20–30 kcal mol⁻¹. Notably, even in the case of the least reactive furans in the series (R=CN or NO₂), the reaction is predicted to be kinetically feasible at reasonable temperatures (85–110 °C); to the best of our knowledge, however, the respective adducts have not yet been evidenced experimentally. ^[62]

Figure 6.

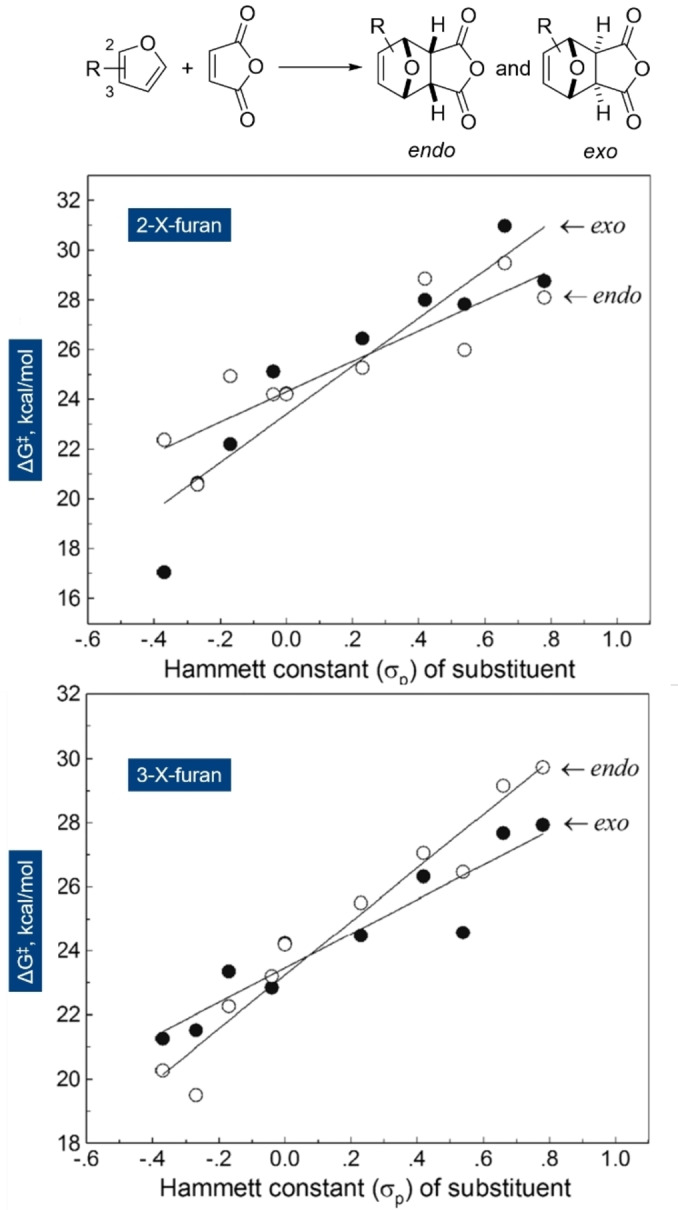
Hammett plots for the reaction between substituted furans (top: 2‐substituted furans; bottom: 3‐substituted ones) and maleic anhydride (MA); reproduced with permission from ref. [61].

Northrop and Boutelle reported similar results for the furan/maleimide cycloaddition (R=OMe, Me, H and CHO, and X=NH). ^[63] While calculated barriers for the activated furans are expectedly low, so are those predicted for the reluctant furfural derivatives (in the range of 24–26 kcal mol⁻¹). This would imply a cycloaddition to be kinetically accessible at 50–60 °C. Interestingly, the authors could experimentally detect the formation of some (5–10 %) of the adduct of 3‐formylfuran and maleimide (CD₃CN, 0.5 M, 75 °C, 10 days), but the 2‐regioisomer remained elusive. Relatedly, Jérôme et al. investigated the coupling between 2‐furfural and acrylonitrile and concluded based on both experimental and computational evidence that disruption of the conjugation between the formyl substituent and the furan ring is key to lowering the activation barrier for the process, as highlighted in Table 1. Indeed, alkyl‐, hydroxyalkyl‐ or acetal‐substituted furans readily formed adducts at relatively low temperatures (60 °C), whereas no reaction was observed for furfural itself, regardless of conditions tested, even though the ΔG ^≠ seems to be only 1–3 kcal mol⁻¹ higher (the computed FMO gap is accordingly 0.5–0.6 eV higher). ^[57] A similar conclusion was reached by Ananikov et al. for the related 5‐HMF/maleimide couple. ^[64] These studies highlight the kinetic challenges (and subtleties) of employing electron‐poor furan dienes in DA cycloadditions; as will be discussed in Section 5.1, these reactions are problematic from a thermodynamic point of view as well.

Table 1.

Cycloaddition of 2‐substituted furans with acrylonitrile: furfural adducts remain experimentally elusive. ^[57]

Entry	R	HOMO [eV][a]	ΔG ≠ [kcal mol−1][a]	Observed (>60 °C)
1	CH=O	−9.16	31–32	no
2	CH2OMe	−8.63	29–31	yes
3	CH(OCH2CH2O)[b]	−8.58	28–30	yes
4	Me	−8.32	29–31	yes
5	CH2OH	−8.67	28–30	yes
6	H	−8.66	n.d.	n.d.

[a] Range for the four possible adduct isomers. [b] Acetal of furfural with ethylene glycol. n.d.=not determined

Next to furfurals, COOH‐substituted furans are another class of kinetically challenging dienes. For instance, in reaction with maleimides, conversion of 2‐furoic acid is approximately two orders of magnitude slower than 3‐(2‐furyl)propionic acid; ^[65] the 3‐regioisomer is somewhat in between. Remarkably, this system is highly responsive to solvent effects, with a nearly 200‐fold rate acceleration seen for 2‐furoic acid when the cycloaddition was performed in water instead of dimethyl formamide. This observation could be generalized to a broad selection of organic solvents. ^[66] While the rate‐enhancing capabilities of water are well‐known in DA chemistry ^[67] and typically explained in terms of the hydrophobic effect, ^[68] in this system hydrogen bonding may play a more critical role. Since water is an excellent hydrogen‐bond acceptor, its interaction with the COOH group reduces the electron‐withdrawing effect of the latter, raising the diene HOMO. In line with this, complete proton transfer (to a base) enhances the reactivity even further, not only in water but also in various organic solvents. Remarkably, this approach activates even the most notoriously unreactive dienes, for example, FDCA. Similarly, furoic acid esters or amides are generally poor dienes,[ ⁶⁵ , ⁶⁹ , ⁷⁰ , ⁷¹ , ⁷² , ⁷³ ] unless the reactions are run neat or “on water”, conditions that allow for good adduct yields (50–70 %). ^[66] Under neat conditions, the reaction rate benefits from the high concentration effect, while activation by hydrogen‐bond formation is likely again involved when the reaction is run on water. Notably, only a handful of other studies describe the use of furoic acid esters, namely in macromolecular applications, in contrast to the abundant literature on the related furfuryl alcohol esters; this is again testament to the relative ease of cycloaddition in the latter systems.[ ⁷⁴ , ⁷⁵ , ⁷⁶ , ⁷⁷ ]

At the other end of the spectrum, substituents with positive mesomeric effects (‐OR, OCOR, ‐NR₂, NHCOR, etc.) lead to the most notable rate enhancements, as exemplified in Scheme 5; increased reactivity due to inductive effects is much less frequently observed and typically involves rather exotic functional groups (e.g. ‐BF₃K). ^[78] Such substituents destabilize the HOMO of the diene; however, this not only leads to higher reactivity but also to greater sensitivity towards oxidation. Accordingly, furans bearing alkoxy or amino functionalities are challenging to access synthetically, more so from bio‐derived precursors, except for chitin‐derived 3‐amino furans (Scheme 1).

As showcased in Scheme 5, strongly electron‐donating furan substituents decidedly impact the rate (i.e. reactions proceed at near ambient temperatures) and may also alter the (stereochemical) outcome of the reaction. For example, a shift is noted from the typical regime of thermodynamic control to the kinetic products with 3‐substituted amino and alkoxy furans (Scheme 5, second ^[50] and third ^[79] example), but not with Boc 2‐aminofuran 18 ^[80] or 3,4‐dimethoxyfuran 5. ^[81] In addition, these substituents readily open up channels for subsequent irreversible reactions such as hydrolysis or dehydration, ^[82] a topic that will be discussed in greater detail in the coming sections.

Interestingly, for furans with both electron‐donating and electron‐withdrawing substituents, activation generally prevails over deactivation and tandem adduct dehydration is very facile. For instance, 5‐dialkylamino‐2‐formyl furans 29 react with maleimides at temperatures around 70 °C (Scheme 6), whereas 2‐furfural does not. ^[83] The so‐called “push–pull” substitution pattern leads to a reduction of the furan aromaticity and an increase in its diene character, something that is already apparent from the ¹H NMR spectra. The HOMO levels are increased with respect to the parent furan 25 (albeit not as much as in the case of an exclusive substitution by an electron‐donating group, that is, 28, Scheme 6) and correlate well with the relative reactivity. ^[80]

Scheme 6.

Push–pull furan dienes and DA applications.[ ⁸⁰ , ⁸³ ]

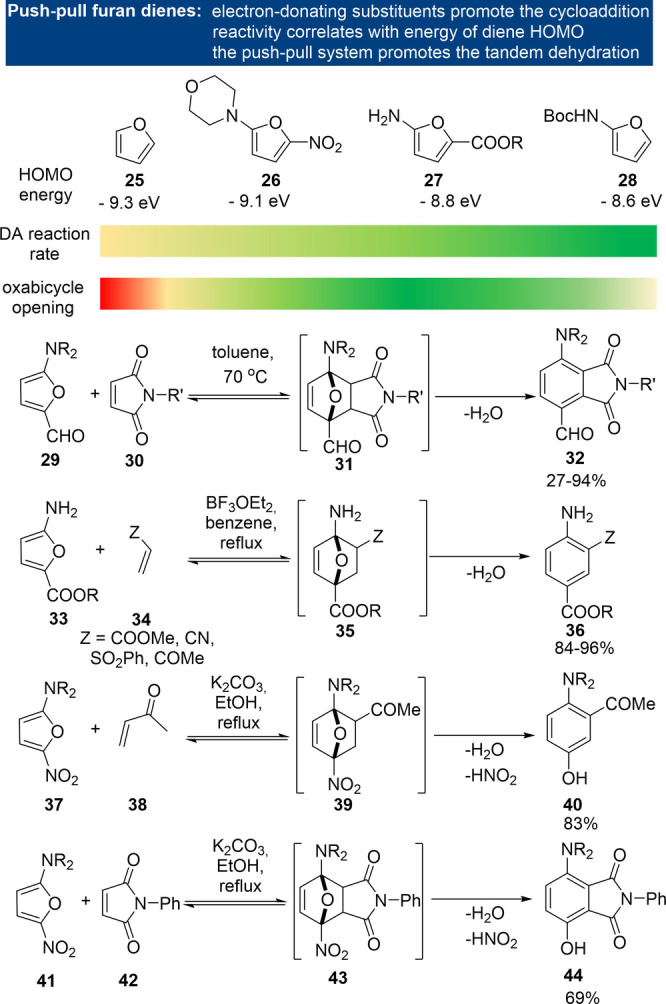
A notable exception to the generally FMO theory‐consistent DA cycloaddition kinetic behavior of substituted furans is provided by the so‐called “halogen effect”: the rate (and exergonicity) of intramolecular DA reactions increases upon introduction of electron‐withdrawing halogens (Scheme 7). ^[84] Various explanations have been provided, including conformational or steric effects, a shift in regime towards an IED reaction, and electronic reasons (improved stabilization of the halogen at the more electron‐rich bridgehead position in the TS, the mesomeric effect of halogens, dipolar interactions, etc.).

Scheme 7.

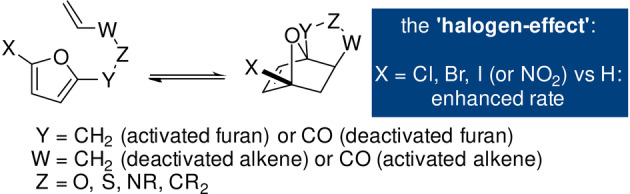
The “halogen effect”: the presence of halogen substituents on the furan diene increases the reaction rate and exergonicity.

Consensus on the matter has not yet been reached, however, particularly since the effect is observed regardless of the electronic nature of the other furan substituents, ^[85] their position on the ring ^[86] or the nature of the (tethered) dienophile nature (Scheme 7); intriguingly, a nitro group seems to induce a similar result. ^[87] This property has been exploited almost exclusively in intramolecular DA furan reactions, with intermolecular versions being very rare. ^[88] While the presence of halogen groups opens up many possibilities for further synthetic upgrading of the adducts, the methodologies to introduce and substitute halogens are often not in line with the green chemistry principles, making halogenated furans less suitable for sustainable synthesis of chemical building blocks.

Finally, next to electronic effects, the substituents on the furan ring can influence diene reactivity also by engaging in noncovalent interactions, for example with a maleimide counterpart. ^[89] For instance, reactivity was found to increase in the series: furan <furfuryl alcohol ≈2,5‐bis(hydroxymethyl)furan <2,5‐bis(hexylurethane)furan. ^[90] The significant rate enhancement induced by the carbamate groups was explained by the stabilization of the transition state by means of hydrogen bonding to the dienophile in this case.

4.3. Dienophiles: Relative Reactivity and Main Structural Factors Influencing It

The nature of the dienophile is the second critical factor impacting the rate of the DA reaction. Again, based on FMO theory, it is well accepted that olefin conjugation with electron‐withdrawing substituents stabilizes the LUMO and thus leads to faster cycloaddition, but other structural factors are also important (Figure 5). In order of decreasing reactivity, typical furan diene partners can be grouped into four categories: bis‐activated cyclic, bis‐activated acyclic, mono‐activated, nonactivated/deactivated, as shown in Scheme 3.

Maleic anhydride is perhaps the most reactive dienophile while maleimides follow closely. Unsubstituted maleimide seems to be the least reactive, but N‐substitution generally does not lead to great changes in rate. ^[63] For instance, in reaction with furfuryl alcohol, k ₁ was found to be approximately five times greater for N‐hydroxymaleimide than for N‐(hydroxyethyl)maleimide, ^[91] but typical alkyl/aryl substituents led to less pronounced differences in rate (see also Figure 11 top). The fully carbocyclic analogue, cyclopentene‐3,5‐dione, is approximately four times less reactive than maleic anhydride; in addition, applications based on this dienophile are hampered by its poor chemical stability.[ ⁹² , ⁹³ ] The extent to which confinement of the alkene bond in a ring activates the dienophile for cycloaddition is surprisingly high, as evidenced by the comparison of maleic anhydride and imide derivatives with maleic acid. Although the picture is not completely clear, there are several factors that may play a role, such as antiaromaticity, ^[94] maximization of conjugation between the C=C bond and the two C=O bonds (due to perfect planarity and the reduced carbonyl stabilization by mesomeric effects in the anhydride structure relative to the bis‐acid), as well as ring strain. ^[95] The latter is likely a significant contribution, as suggested by the remarkable kinetic stability of the (saturated) imide ring in (hydrogenated) DA adducts (45) with respect to hydrolysis in comparison to fully planar maleimide 49 and phthalimide 47 (Scheme 8). ^[66] Exocyclic substituents, such as in 2,3‐dimethylmaleic anhydride, citraconic anhydride, etc., lead to a drastic reduction of the rate, primarily due to steric congestion in the transition state. As a result, such DA adducts can only be observed under high pressures (>10 kbar) or special conditions (5 M LiClO₄ in Et₂O). ^[96]

Figure 11.

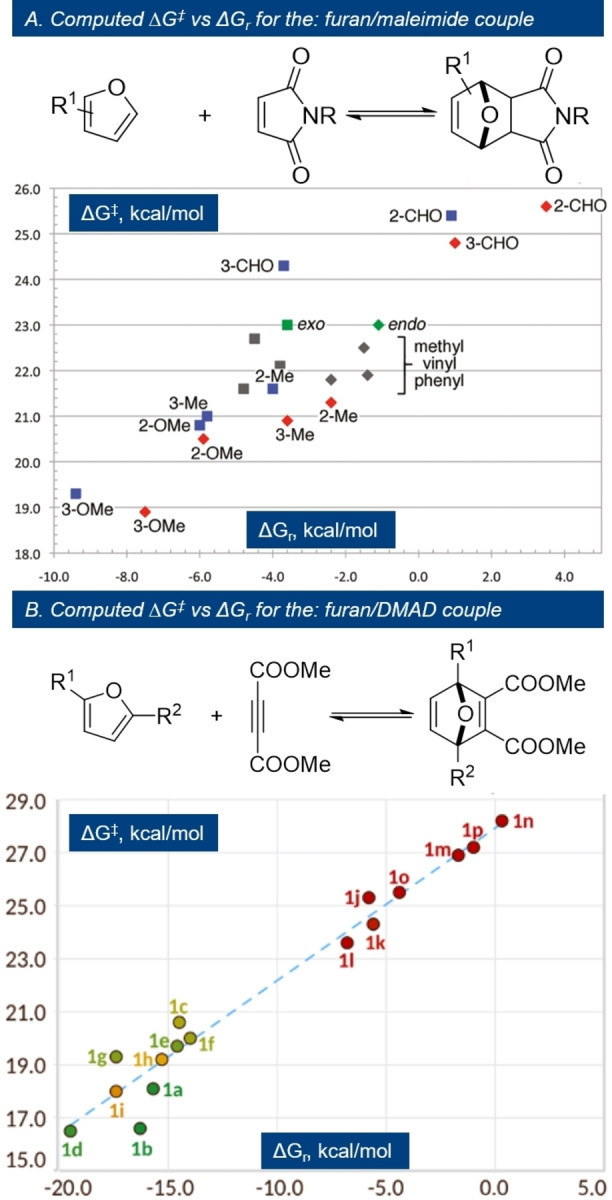
Bell–Evans–Polanyi relationships in furan DA cycloadditions; A) endo=diamonds, exo=squares; substituted furans: red (endo) or blue (exo); substituted maleimides (gray); unsubstituted inputs (green); B) see Figure 9 for structures; reproduced with permission from ref. [52, 63].

Scheme 8.

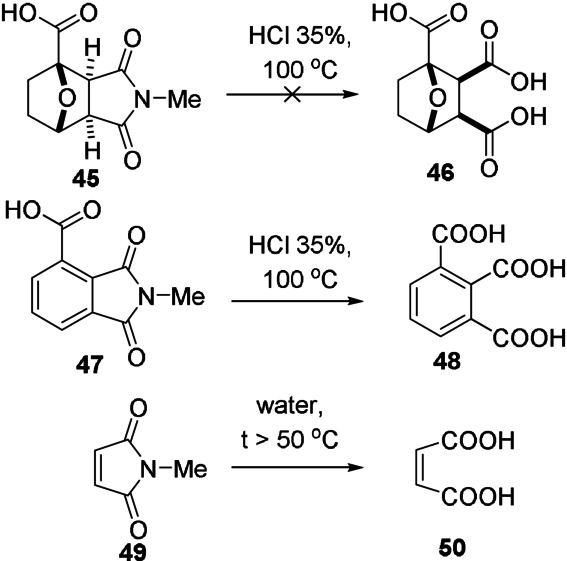
Relative ease of hydrolysis of several imide derivatives suggesting a difference in ring strain between maleimide dienophiles and corresponding DA adducts; accordingly, strain release may contribute to reactivity. ^[66]

Acetylene dicarboxylic acid and its esters are also excellent dienophiles, having a low‐lying and sterically accessible LUMO. Their application is, unsurprisingly, quite common at laboratory scale, but their non‐renewable origin hampers more widespread use in green synthesis. ^[18] As explained before, a significant drop in reactivity occurs upon going further in the series to acyclic, bis‐activated dienophiles such as maleic and fumaric acid derivatives. Generally, the latter are more reactive, presumably as a result of diminished conjugation through deviations from planarity, resulting in the anticipated changes in LUMO energies. ^[97] Curiously, in reaction with furan, fumaric acid reportedly reacts more slowly than its cis‐isomer, whereas the respective diethyl esters show opposite reactivity. ^[98] Fumaroyl chloride is expectedly the most reactive dienophile in the series, but chemoselectivity control is challenging. ^[99] Other bis‐activated dienophiles include fumaronitrile, ^[100] methyl 3‐nitroacrylate, and 1,2‐bis‐(phenylsulfonyl)ethylene, ^[101] but examples are rare.

Importantly, in unsymmetrical systems FMO interactions dictate regioselectivity (Figure 4 A), but also the extent of side reactions: particularly when both the diene and dienophile are highly polarized, Michael addition prevails over the DA pathway. ^[102] For instance, in the reaction between symmetrical, unsubstituted furan 51 a with methyl 3‐nitroacrylate 52, equilibration towards the two stereoisomeric DA adducts was achieved in approximately 20 days at ambient temperatures (Scheme 9); no Michael addition products were detected. In contrast, with the highly polarized 2‐methoxyfuran 51 b, Michael addition prevailed. Only upon cooling to −10 °C, DA adducts 53 and 54 could be detected by ¹H NMR spectroscopy, but facile cycloreversion (in a matter of minutes) precluded their isolation. The Michael adducts 55 and 56 preserve the aromaticity of furan and are therefore thermodynamically favored; in polarized systems where the kinetics of this side reaction is highly favorable, it is thus very challenging to steer the chemoselectivity toward the cycloadduct. ^[103]

Scheme 9.

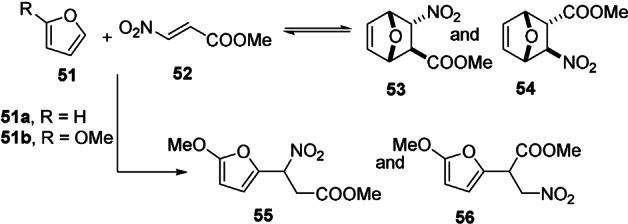
Competition between furan DA and Michael addition in polarized systems. ^[102]

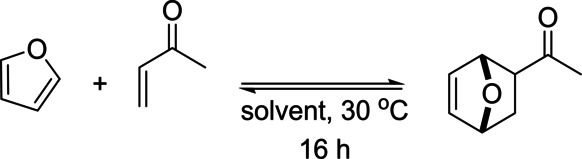
As expected, monoactivated dienophiles such as acrylates are considerably less reactive; often, they require catalysis or special conditions to entice reactivity. Alternatively, as we will elaborate on later, enals (e.g. acrolein) and enones (e.g. methyl vinyl ketone) are fairly reactive dienophiles but the formation of the corresponding adducts is not thermodynamically favorable (see for instance Table 2 and Scheme 13); the Michael addition products are often observed instead. ^[100]

Table 2.

DA cycloaddition between furan and methyl vinyl ketone: product is only formed in unconventional solvents (formamide, ethylene glycol), water and/or under ultrahigh pressures. ^[126]

Entry	Solvent	Yield [%] 1 bar	Yield [%] 3 kbar
1	dichloromethane	0	17
2	methanol	0	18
3	ethylene glycol	18	86
4	formamide	23	97
5	water	23	87

Scheme 13.

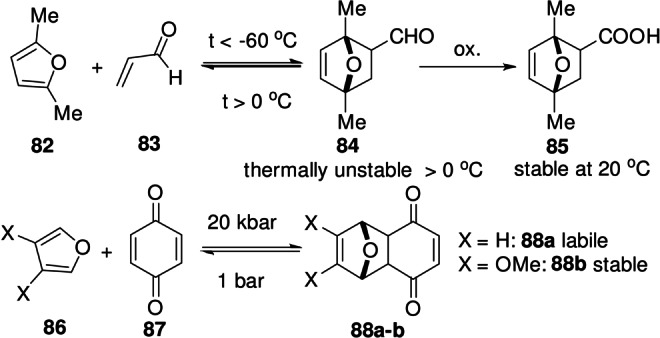
Fast but thermodynamically disfavored DA reactions.[ ¹²⁹ , ¹³⁰ ]

Next, simple alkenes like ethylene, propylene or allyl alcohol only add to furan under harsh (catalytic) conditions or if tethered. For example, the computed free energy of activation for the couple furan/ethylene was 37.5 kcal mol⁻¹. ^[104] In practice, these DA adducts are rarely detected, ^[105] and most typically conditions are chosen such that they evolve towards more stable structures via tandem reactions, as discussed in Section 8.

Expectedly, only very few reports are available that describe DA reactions between furan and deactivated alkenes such as vinylene carbonate 58 (LUMO −0.25 eV vs. −3.2 eV for maleic anhydride ).[ ¹⁰⁶ , ¹⁰⁷ ] These reactions are slow and require elevated temperatures, prolonged times and high excess of one of the addends; oligomerization reactions are competitive and often limit yields. Notably, a confirmed side reaction is the coupling between furan and the primary DA adduct 59 functioning as dienophile; this highlights the deactivated nature of the C=C bond in vinylene carbonate (Scheme 10 A). Only in rare examples furans are seen to act as dienophiles themselves (at least formally, Scheme 10 B), as exemplified by the catalytic furan DA dimerization and subsequent dehydration to benzofuran 62, proposed as a relevant pathway in the conversion of furan to renewable aromatics by catalytic fast pyrolysis. ^[108] Electron‐poor furans served as dienophiles in cycloadditions with classical dienes such as isoprene 63 and 1,3‐butadiene 66, although reactions rates were low. ^[109] The 1,3‐butadiene/2‐furfural pair actually led to a trimeric product 69 (in low yield), where the furan acted as a bis‐dienophile in two tandem [4+2] reactions; ^[109] expulsion of HNO₂ followed the cycloadditions employing 2‐nitrofurans 71 as dienophiles. ^[110] Finally, furans acted as the 2π‐component in reactions with masked ortho‐benzoquinones 74. ^[111] Contrary to the previous examples, the rate of this reaction benefited from electron‐donating substituents on the furan, suggesting the operation of an IED mechanism. However, experimental ^[112] and theoretical ^[113] investigations instead supported a two‐stage mechanism going through a zwitterionic intermediate, with the furan acting as a formal dienophile in this case.

Scheme 10.

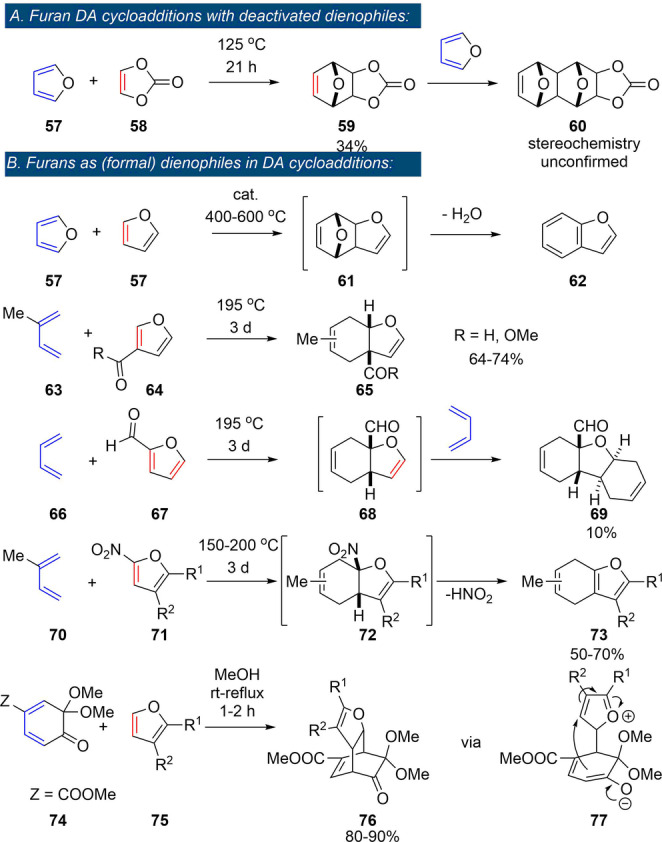
Rare examples of furan DA reactions: deactivated dienophiles (A);[ ¹⁰⁶ , ¹⁰⁷ ] furans as (formal) dienophiles (B).[ ¹⁰⁸ , ¹⁰⁹ , ¹¹⁰ , ¹¹¹ ]

5. Thermodynamics

5.1. Relevant Structural Factors in the Adduct/Addends and Their (Often) Unpredictable Impact on ΔG _r

Aromaticity is the key structural element that distinguishes furan from the other typical dienes, but other factors also influence the overall thermodynamics of the cycloaddition, as schematically depicted in Figure 7.

Figure 7.

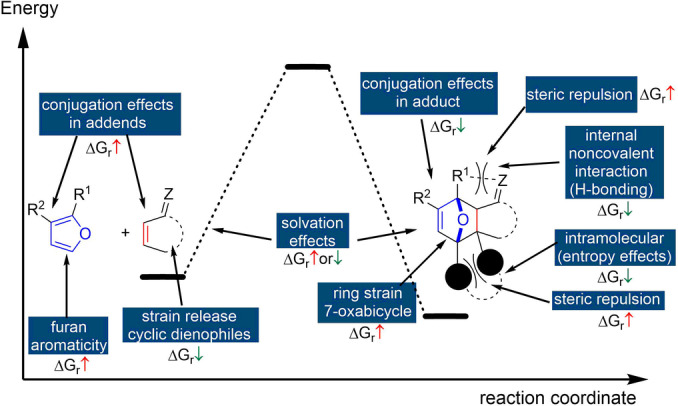
Correlation of reaction thermodynamics with structural features in the addends and cycloadduct.

Some of these aspects have been discussed elsewhere ^[11] and will not be further elaborated here. The strain energy in the 7‐oxanorbornene scaffold was estimated to be about 22 kcal mol^−1 [114] and thus represents a significant contribution to the overall energetics of the cycloaddition (this value is, however, not substantially different for nonaromatic cyclopentadiene). Conjugation between the furan ring and substituents has a profound effect on the overall thermodynamics of the reaction as well. In this respect, substitution at the furan 3‐position leads to relatively more exergonic reactions compared to 2‐substitution, as (part of) the conjugation energy is retained in the adducts. This trend holds for both electron‐donating or withdrawing substituents.[ ⁵⁰ , ⁶³ , ⁶⁵ ] On the other hand, relative to the parent unsubstituted furan, the effect of substituents on the reaction thermodynamics does depend on its nature. Generally, provided steric effects are not predominant, the presence of electron‐donating substituents on the furan increases the exergonicity of the reaction, while electron‐withdrawing groups show the opposite effect. This trend is nicely illustrated by the in silico investigation by Haider et al. on a series of DA reactions between five diversely substituted furans and four representative dienophiles (acrylic acid, ethylene, methyl acrylate and acrolein). The cycloadditions were found to be exothermic (ΔH _r as low as −4 kcal mol⁻¹) only in the case of DMF and HMFA (5‐hydroxymethyl 2‐furoic acid). In all other examples, particularly when FDCA and its ethyl ester were investigated as dienes, the reactions were considerably less thermodynamically favorable (ΔH _r up to 11 kcal mol⁻¹) (Figure 8). ^[53]

Figure 8.

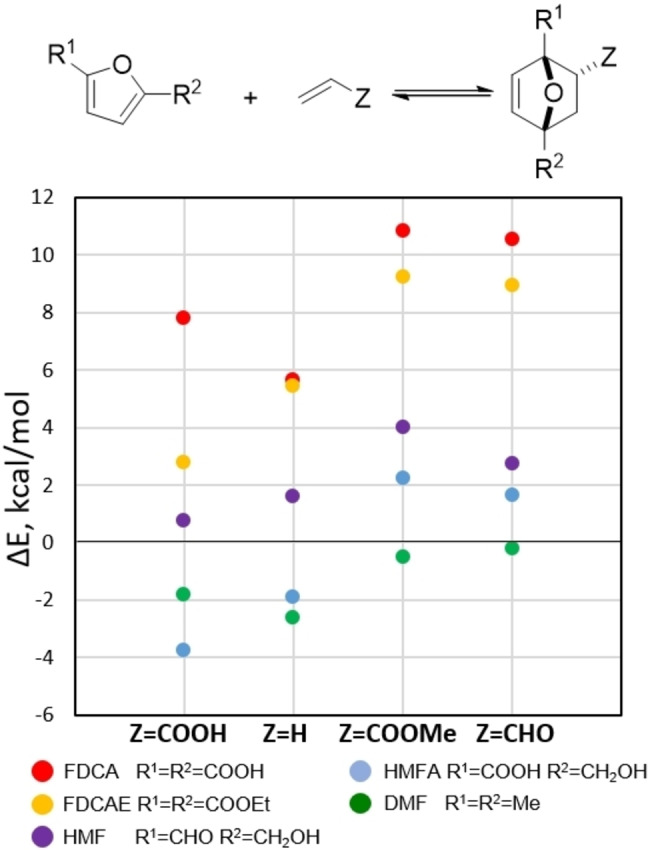
In silico thermodynamics data on the furan DA reaction. ^[53]

Many experimental observations, for instance on the relative thermal stability of DA adducts, confirm this trend. For example, the formation of the adduct 20 between Boc 2‐aminofuran and maleimide (Scheme 5) is very exergonic (the molecule is fully stable in solution at 80 °C), ^[80] this in contrast to DA products of the furfural/maleimide ^[115] or furoate/maleimide couples, which are prone to thermal cycloreversion. ^[66] Another illustrative example is provided by Dumesic et al. who showed that the corresponding DA adducts 80 of 5‐HMF acetals 78 and maleimides 79 form readily at 50 °C, but upon acidic hydrolysis, the putative formyl‐substituted adducts 81 rapidly cyclorevert (Scheme 11). ^[116]

Scheme 11.

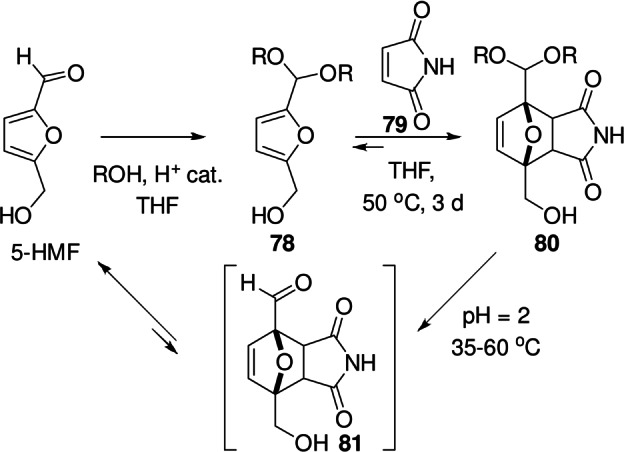
Stabilization of 5‐HMF/maleimide adducts by acetalization; upon hydrolysis, the formyl adducts undergo cycloreversion. ^[116]

The trends in cycloaddition thermodynamics highlighted above are arguably much less known and appreciated than the trends in kinetics, that is, in relative reactivity, discussed in the previous section. How reaction exergonicity varies as function of the electronic properties of furan substituents is also less obvious. Ananikov et al. recently suggested that answer lies in the aromaticity of the furan, with more extensive conjugation of the furan ring with electron‐withdrawing substituents having a stabilizing effect on the 6π electron system. This renders the furan more aromatic, causing a higher penalty in terms of resonance energy loss, making cycloaddition more endergonic. The reported correlation between aromaticity (expressed as the Harmonic Oscillator Model of Aromaticity index, HOMA ^[117] ) and ΔG _r for the reaction between a series of furans and dimethyl acetylene dicarboxylate (DMAD) is given in Figure 9. ^[52]

Figure 9.

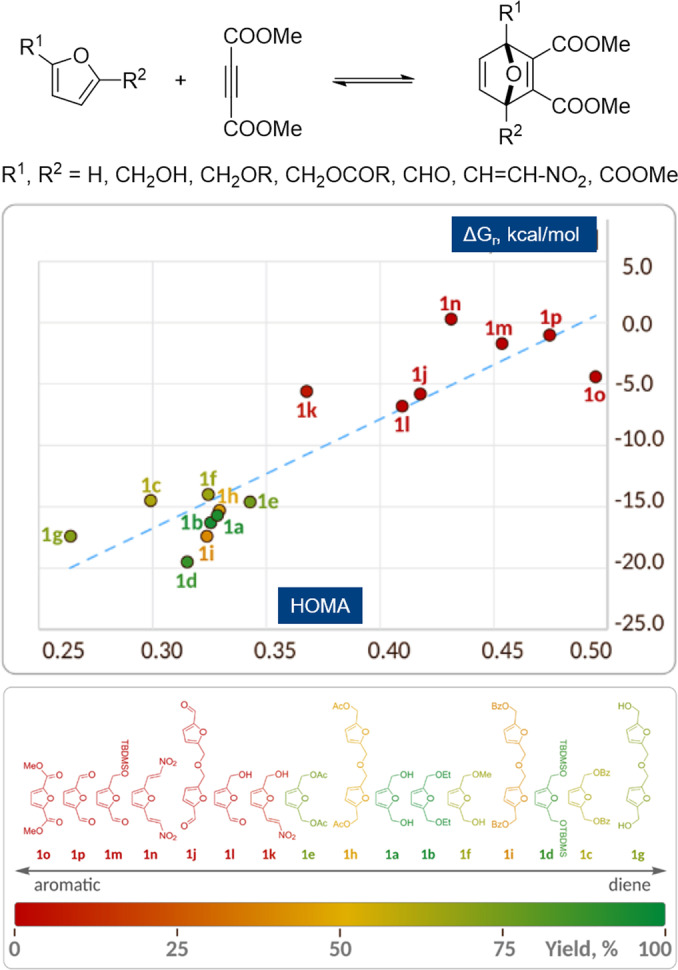
Correlation of the cycloaddition ΔG _r with the aromaticity (HOMA index) of the furan diene; HOMA is a geometrical parameter reflecting the deviations of chemical bond lengths from the values corresponding to a perfectly aromatic molecule: cf., the HOMA of benzene is by definition 1; reproduced with permission from ref. [52].

Steric factors can override electronic effects, for example, when steric congestion limits the thermodynamic stability of the DA adduct (Scheme 12). This is illustrated by the equilibrium conversions for methylated furans and itaconic anhydride, which decrease counter to expectation based on electronics: furan >2‐methylfuran (MF) >2,5‐dimethylfuran (DMF); ^[118] the trend is similar with maleic anhydride as dienophile. ^[119] In reaction with maleimide, unsubstituted furan and the 2‐methylated derivative show the same equilibrium conversion, as demonstrated in a competition experiment. ^[63] On the other hand, with fumaronitrile, the equilibrium constants for a series of 2,5‐disubstituted furans follows the trend: Me >Et >Bu >Hex >H, evidently balancing both effects. ^[120] Another clear manifestation of sterics is the superior stability of the exo adduct over the endo diastereoisomer: in the former, the oxanorbornene substituents are oriented anti to the bulkier bridge of the bicycle, which leads to a thermodynamic benefit of 2–3 kcal mol⁻¹.[ ⁴⁸ , ¹²¹ ] In reactions between 2‐monosubstituted furans and nonsymmetrical dienes, distal (meta) regioisomers generally prevail at equilibrium over the proximal (ortho) isomers, for similar reasons.[ ¹¹⁸ , ¹²² ] Finally, the absence of steric repulsions in the adduct between furan and ethylene presumably contributes significantly to its high stability relative to other typical furan DA adducts (e.g. with maleic anhydride, maleates or fumarates, etc., as dienophiles). ^[11] The reaction of furan with ethylene is slow, elevated temperatures are mandatory, and at equilibrium (155 °C, under approximately 80 bar pressure), 7‐oxabicyclo[2.2.1]hept‐2‐ene is present only in low amount, 5–8 %. ^[105] However, estimation of the equilibrium constant at low temperatures (40 °C) based on simple thermodynamic calculations gives a surprisingly high value (in the order of 10³ L mol⁻¹). ^[11] Remarkably, this parent furan DA adduct can even be isolated by distillation at 119 °C at which most substituted derivatives would undergo retro‐cycloaddition. Similar behavior is reported for the DMF adduct of ethylene. ^[123] This somewhat counterintuitive, enhanced stability of ethylene adducts has direct implications in the development of biobased routes towards renewable aromatics via DA chemistry (see Section 8).

Scheme 12.

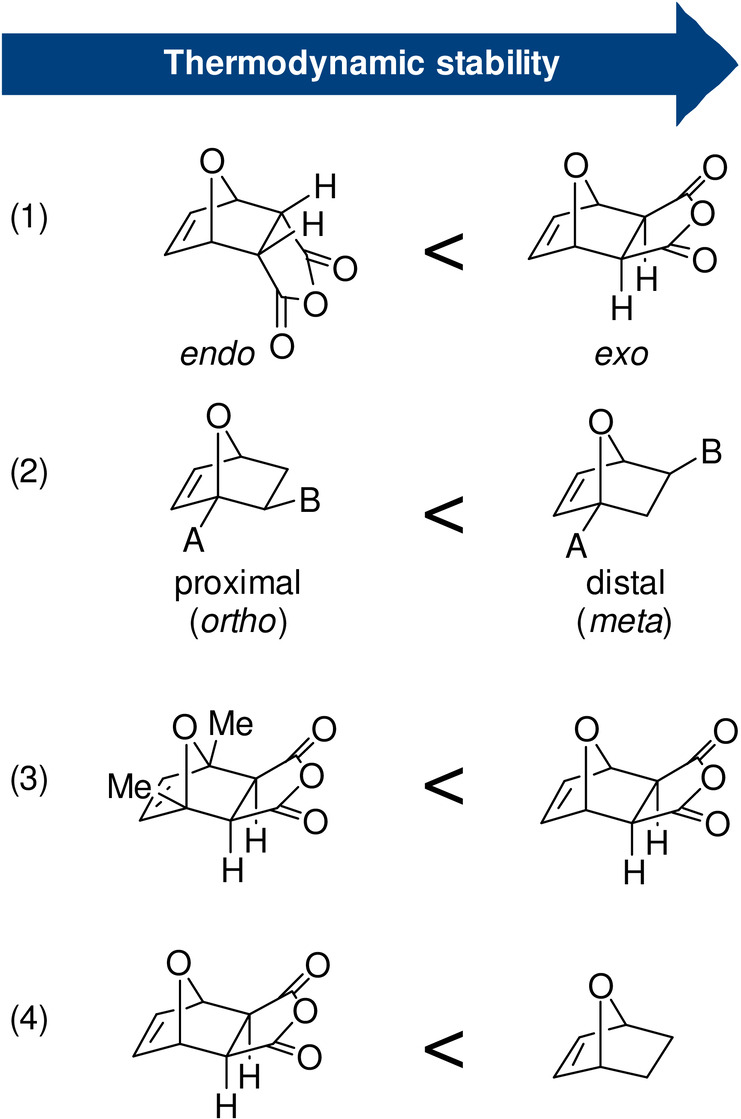
Influence of steric factors on the thermodynamic stability of DA adducts: general trends.

Lastly, the thermodynamic stability of furan DA adducts is also influenced by noncovalent interactions. This feature has been made particularly evident in macromolecular applications: the thermal lability of polymer networks based on the furan/maleimide couple was shown to depend on the nature of the linker connecting the furan diene to the polymer backbone. Namely, in the case of acylated furfuryl amine, that is, with amide or urethane linkers, the crosslinking degree was higher than with ester‐linked furfuryl alcohol based polymers.[ ⁹⁰ , ¹²⁴ ] The difference was attributed to the ability of ‐NH‐CO‐ and ‐NH‐COO‐ functionalities to participate in stabilizing hydrogen bonds with the maleimide carbonyls. Relatedly, the Stoichet group designed a hyalouran/furan/maleimide‐based hydrogel in which a nonclassical hydrogen bond present in the furan diene provided additional stabilization to the addends’ side; macroscopically, this led to a reduction in the extent of crosslinking. ^[125]

5.2. Reaction Conditions as a Straightforward Way to Leverage the Equilibrium Position

Since the Gibbs free energy change for DA cycloadditions typically lies between −2 and +2 kcal mol⁻¹, the corresponding equilibrium constants are in the range of 10⁻² to 10². It is therefore not unusual that the equilibrium conversion is generally well below 100 %; furthermore, this value is highly dependent on experimental parameters (concentration, stoichiometry, temperature, pressure, etc.) as qualitatively captured by Le Chatelier's principle.

The effect that initial reactant concentration C₀ has on the equilibrium conversion (maximum yield η) is shown in Figure 10 as function of ΔG _r (or K). Thus, for a reaction with ΔG _r=0 kcal mol⁻¹, the equilibrium conversion would be about 65 % under neat conditions versus ≈38 % in solution and only 10 % under more dilute conditions. In the case of a moderately endergonic reaction (ΔG _r=2–3 kcal mol⁻¹), there is a high chance that the formation of the DA adduct will go undetected (η<3 %) unless run neat (η=5–10 %). Illustrative examples would be the addition of maleimide to furfural or furoate esters, respectively. In solution, the equilibrium conversion is very low and the adducts fall under the detection limit of the analytical technique (typically NMR spectroscopy),[ ⁶³ , ⁷³ ] but when the reactions are run neat, conversions of around 10 % are expected, which is sufficient for unambiguous characterization. ^[115]

Figure 10.

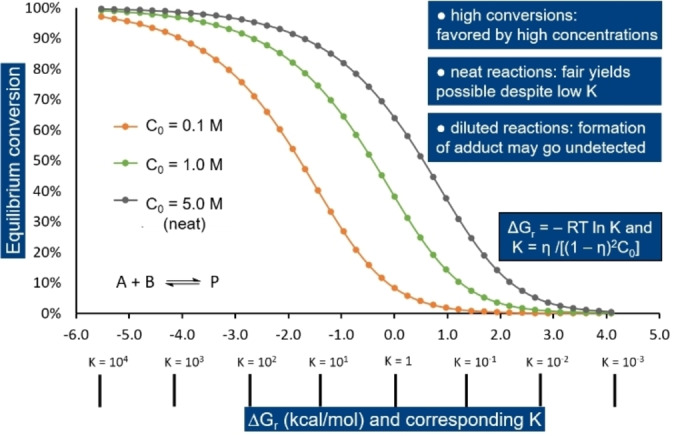
Theoretical equilibrium conversion as a function of ΔG _r and C₀.

Next, the DA equilibrium is strongly impacted by temperature. The reaction is exothermic which implies that, according to Van't Hoff's law [Eq. 1], the equilibrium constant and thus maximum yield decrease upon heating. Vogel estimated that for the parent reaction between furan and ethylene the equilibrium constant at 40 °C is about 4–5 orders of magnitude higher than at 155 °C, the temperature where the reaction is kinetically feasible. ^[11] In Gibbs free energy terms, as ΔS _r <0 for the bimolecular DA coupling, the reaction becomes more endergonic at elevated temperatures. The kinetic explanation of the temperature effect on the DA equilibrium would be the differential increase in reaction rate constants k ₁ and k ₋₁ upon heating: the rate constant of the reverse reaction k ₋₁ shows a stronger temperature dependence and thus the ratio K= k ₁/k ₋₁ decreases with temperature.[ ⁴⁸ , ⁹⁶ ]

$${\displaystyle (\partial \ln \mathrm{K}/\partial T){}_{\mathrm{p}}=\Delta H{}_{\mathrm{r}}/\mathrm{RT}{}^2}$$ (1)

Finally, the DA equilibrium can be shifted to the product side by applying pressure. This effect is particularly important in the gas phase, where the equilibrium responds even to relatively low variations in total pressure. In the condensed phase, the pressure influence is exerted only in the kbar regime [Eq. 2], pressures that have little practical significance for large scale applications.

$${\displaystyle (\partial \ln K/\partial P){}_{\mathrm{T}}=-\Delta V/\mathrm{RT}\mathrm{with}\Delta V<0}$$ (2)

Similarly, in some cases, remarkable adduct stabilization (as well as cycloaddition rate acceleration) was observed in unconventional reaction media (Table 2); this was attributed to a compression effect exerted by solvent molecules, in a manner comparable to the macroscopic application of external pressures.[ ¹²⁶ , ¹²⁷ ]

6. Interplay between Kinetics and Thermodynamics

An important conclusion of the above is that while kinetics depends in a fairly straightforward manner on diene structural features, as demonstrated by various correlation graphs and in line with FMO theory, the impact of structure variation on thermodynamics is much more intricate and difficult to anticipate. In fact, careful consideration of the interplay between kinetic and thermodynamic factors is essential for a correct understanding of furan DA reactions.

Correlations between kinetic and thermodynamic parameters are seldom reported in the DA literature, however. Those that are available provide valuable insight into the furan DA chemistry. Northrop et al. for example have determined computationally the activation barriers and the Gibbs free energies for a series of reactions between furans and maleimides. ^[63] When plotted against one another in a BEP‐type chart, it became apparent that substituents influence both ΔG ^≠ and ΔG _r in a comparable manner (Figure 11).

A similar picture was provided by Ananikov's group ^[52] in the cycloaddition between furans and DMAD (Figure 14 B) and Jérôme et al. in their study of the furan/acrylonitrile system, ^[57] the former reporting a strong linear correlation. Notably, in all these examples, the data acquired in silico accurately predicted the success/performance of the cycloadditions in practice. The reactions with electron‐poor furans are thus not only relatively slow, but also endergonic, and the corresponding adducts are therefore very unlikely to be detected experimentally. Indeed, the only such adducts that could be evidenced spectroscopically in these studies (in very low yields) were the products of the 3‐furfural/maleimide and 2‐(2‐nitrovinyl)furan (1 k)/DMAD reactions, both corresponding to the least electron‐poor furans in the respective series.

Figure 14.

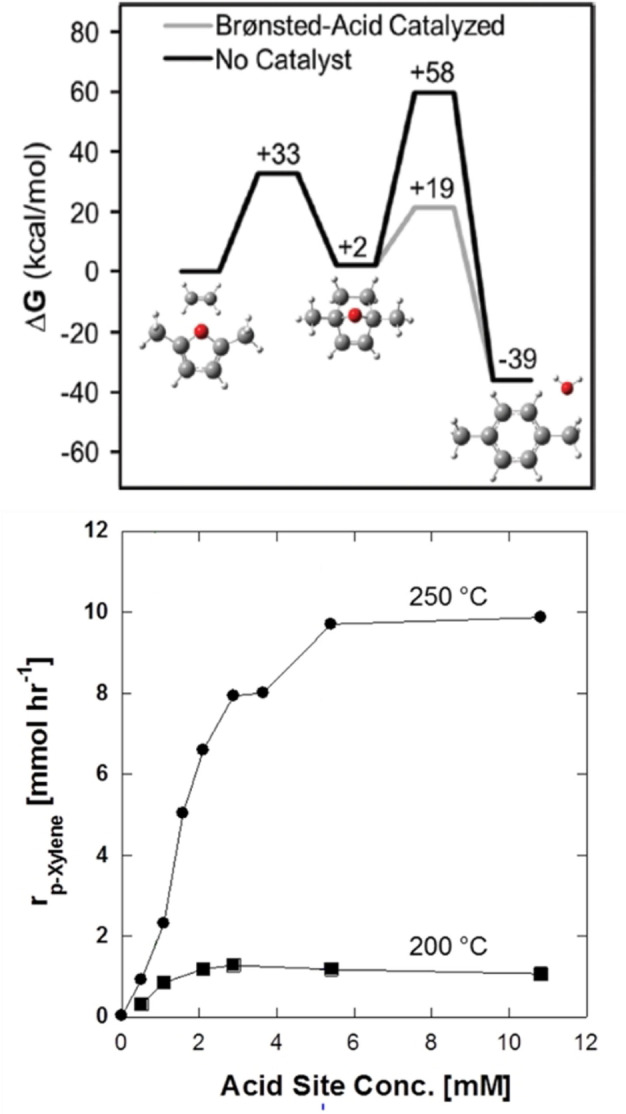
Computed ΔG _r (300 °C) for the cycloaddition between DMF and ethylene towards TA: the cycloaddition is mildly endergonic, the dehydration is very exergonic (top); catalysis determines the rate‐limiting step at low acid‐site concentration (bottom); reproduced with permission from ref. [192] (https://pubs.acs.org/doi/10.1021/cs5020783; further permissions related to the material excerpted should be directed to the ACS) and ref. [193].

At least qualitatively, this type of analysis suggest that substituents which lower ΔG ^≠ also lead to a decrease in ΔG _r; concomitantly, it appears that reactions with deactivated furans such as furfural are not just relatively slow but also more endergonic. ^[115] This suggests that the main effects of substituents on the furan diene seem to be the stabilization/destabilization of the ground state, whereas the impact on the transition state and the product is less pronounced. Indeed, the barrier of the forward reaction, ΔG ^≠, seems to be more sensitive to variations in ΔG _r compared to ΔG ^≠ ₋₁ (i.e. the slope of the BEP charts in Figure 11 is approximately 0.6 vs. −0.4 for the correlation of ΔG ^≠ ₋₁ with ΔG _r). Functional groups profoundly influence the electronic properties of the furan ring and ultimately its positioning on the diene/aromatic molecule continuum (Figure 9). Substituents with positive mesomeric effects (electron‐donating heteroatoms, ‐X) destabilize furan, enhancing its diene character, and thus the kinetic and thermodynamic feasibility of the cycloaddition. At the other end of the spectrum, substituents with negative mesomeric effects (containing X=Y bonds) attached to the ring render furan more aromatic, which translates into an additional energy penalty to crossing barriers, together with a less thermodynamically favorable cycloaddition.

These apparent structure–reactivity–stability correlations (summarized in Table 3) are reflected in the widespread use of furans from classes [1] and [2] in applications, while class [3] is very much underrepresented.

Table 3.

Classes of furan DA reactions according to electronic properties of substituents on the furan diene.

Class	[1]	[2]	[3]
DA cycloaddition equilibrium
Substituents	X=OR, NR2	R=H, alkyl, aryl, halogens, CH(OR)2, etc.	X, Y=heteroatoms
Electronic effects	Positive mesomeric	Positive/negative inductive	Negative mesomeric
Kinetics	Fast	Intermediate	Slow
Thermodynamics	Exergonic, ▵G r<0	Reversible, ▵G r≈0	Endergonic, ▵G r>0
Diene/aromatic character

While generalizing the observations to formulate the rule “more reactive systems also form more stable adducts” is tempting, it is crucial to note that there are other relevant factors to consider, making it often challenging to predict (relative) yields in furan DA cycloadditions. As already mentioned, sterics can sometimes override electronics: in the series of methylated furans, reactivity increases upon methylation but stability of the adducts generally decreases. ^[118] Next, the nature of the dienophile also plays a role. Maleic anhydride reacts faster than maleimide derivatives but the reactions of the latter are more exergonic. ^[48] Similarly, ethylene is a poorly reactive diene, but the stability of its adduct with furan is greater than that of the corresponding maleic anhydride adduct, which readily forms at ambient temperature. ^[11]

Finally, reaction conditions are evidently important, as the equilibrium conversion is critically dependent on external parameters, particularly for reactions in classes [2] and [3] (Table 3). Moreover, under certain conditions, yields can be pushed beyond the intrinsic thermodynamic limit of the reaction, for instance by the selective crystallization of the product.[ ⁷⁸ , ¹²⁸ ] It is also worth mentioning that some adducts that would be expected to form rapidly (e.g. low FMO gap for addends) are in fact very unstable at ambient conditions (k ₁ is indeed high, but k ₋₁ is even higher). Representative examples would be the adduct of 2,5‐dimethylfuran with acrolein (unstable above 0 °C)[ ⁵⁹ , ¹²⁹ ] and the adduct between furan and benzoquinone, which is pressure labile (decomposes rapidly in the absence of high pressures) (Scheme 13); ^[130] replacing the furan diene with its 3,4‐dimethoxy derivative alleviates the problem in this case (this reaction belongs to class [1], fast and exergonic cycloadditions). ^[131]

7. Overcoming Unfavorable Thermodynamics: Tandem Reactions

While dealing with slow kinetics is fairly straightforward, that is, one can optimize temperature and solvent, or apply catalysis, overcoming unfavorable thermodynamics/preventing the retro DA reaction is inherently a much more challenging task. Several strategies can be applied on a case‐by‐case basis, for example, the use of high pressures (kbar) or unconventional reaction media (see for instance Table 2). Kinetically blocking the reverse DA process is also a commonly employed strategy that suits certain synthetic applications. Methods include hydrogenation of the alkene bond in the adducts (92),[ ⁶⁴ , ¹³² ] or alkene epoxidation/dihydroxylation (93).[ ¹³³ , ¹³⁴ ] In addition, synthetic manipulation of the oxanorbornene exocyclic groups is another means to tune the cycloreversion rate (Scheme 14). ^[135] This can be conveniently done for instance via redox transformations, for example by reduction of the anhydride functionality in the adduct 89 and functionalization to 94 a–c as shown in the example in Scheme 14.

Scheme 14.

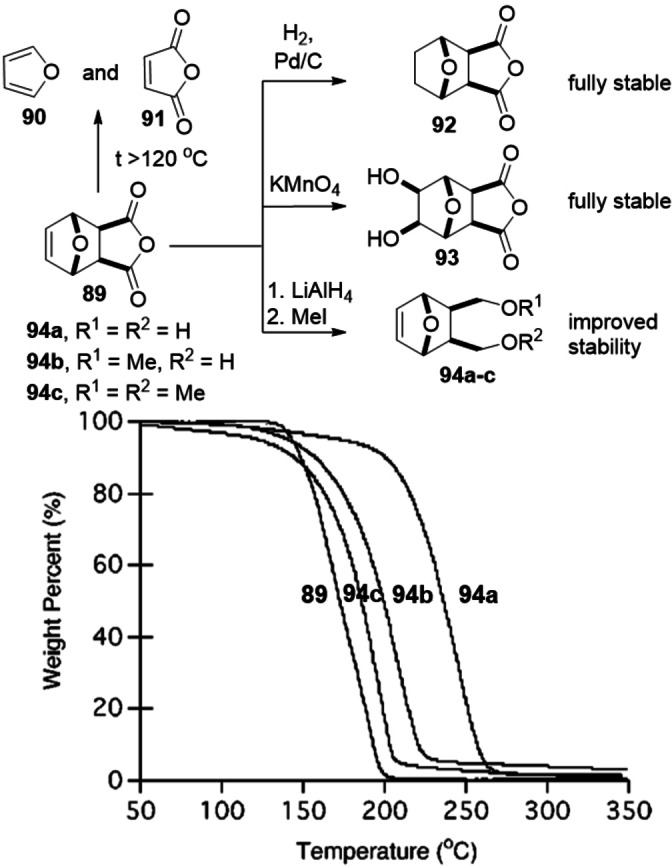
Chemical modifications used to thermally stabilize the DA adduct/block the cycloreversion channel; reproduced with permission from ref. [135].

Alternatively, going up the oxidation scale may also provide additional stabilization to certain thermally labile cycloadducts. In the coupling between 2,5‐dimethylfuran and acrolein (Scheme 13), the in situ Pinnick oxidation of the aldehyde adduct 84 to the more thermally stable carboxylic acid 85 allowed a substantial improvement in adduct yield; the DA reaction was performed under kinetic control at −60 °C using Sc(OTf)₃ as catalyst. ^[59]

Next to these rather straightforward adduct derivatization strategies, the coupling of the DA equilibrium to a tandem, exergonic secondary reaction is another robust and general approach to boost thermodynamically limited conversions/prevent adduct cycloreversion. Notably, even when the Gibbs free energy that is achieved in this way is relatively small, for example, in the order of 1–2 kcal mol⁻¹, the effect on equilibrium conversion can still be substantial (see Scheme 15). Secondary reactions employed for this purpose range from elementary molecular changes such as enolization or hydration to entropically favored intramolecular cyclizations and more profound, highly exothermic transformations such as oxabridge opening and dehydration to an aromatic ring (Section 8).

Scheme 15.

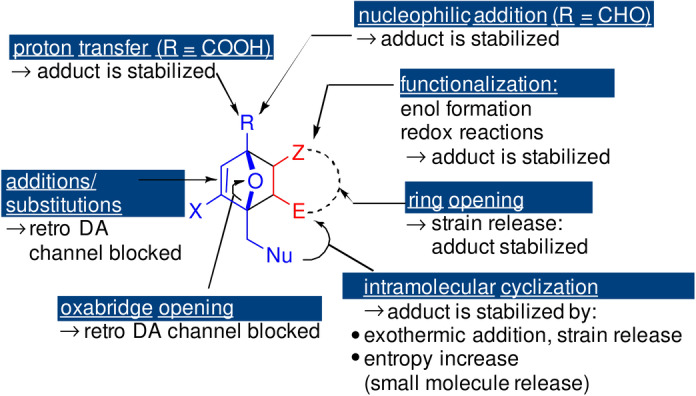
Options for stabilization of the DA adduct by tandem conversion.

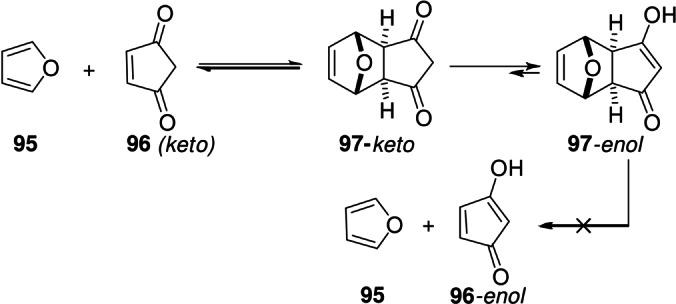
To begin with, the DA adduct between furan and cyclopentene‐3,5‐dione is an enol, ^[136] whereas the dienophile is found exclusively in the ketonic form (as 96‐enol would be antiaromatic). ^[92] This is likely the simplest example of coupling the DA equilibrium to a secondary exergonic reaction; this relatively minor additional stabilization of the adduct (and implicit destabilization of the corresponding addends) translates into a reduced tendency of the adduct to cyclorevert (Scheme 16).

Scheme 16.

Enolization as tandem reaction. ^[136]

The efficiency of the DA reaction between 2‐furoic acids, another prominent example of a class [3] furan (Scheme 17), and maleimides was found to be significantly improved in the presence of 1 equiv of base. Both rate and equilibrium conversion benefited from the additive effect: the reactivity of 98‐Na is increased relative to 98 in accordance to the FMO theory (deprotonation of 98 raises the diene HOMO energy level as explained in Section 4.2), whereas the thermodynamic gain is related to relative acidity. Indeed, the DA adduct 100 was found to be more acidic than the 2‐furoic acid diene 98; as illustrated by the Hess cycle shown in Scheme 17, this results in an estimated thermodynamic gain of ΔΔG _r,323K=2.303 RT ΔpK _a=−0.9 kcal mol⁻¹. ^[66]

Scheme 17.

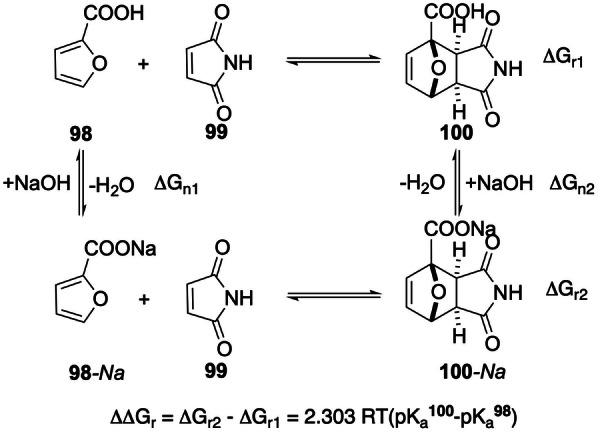
The thermodynamics of the DA reaction between furoic acid 98 and maleimide 99 is improved in the presence of basic additives, due to the differences in acidity between the adduct 100 and the furan diene. ^[66]

A small but crucial improvement in the overall thermodynamics was credited to a carbonyl hydration reaction in the furfural/maleimide couple (Figure 12 A). ^[115] When water was employed as solvent, the highly electrophilic aldehyde adducts 103 readily underwent hydration towards solution‐stable geminal diols. This effectively pulled the otherwise unfavorable equilibrium to the product side, as corroborated by DFT results (Figure 12 B). Without this tandem hydration, the equilibrium conversion was very low: 2–5 % in organic solvents and up to 10 % under neat conditions. Thus, the yield in the DA cycloaddition of electron‐poor furans such as furfurals is proven to be primarily limited by unfavorable thermodynamics rather than slow kinetics.

Figure 12.

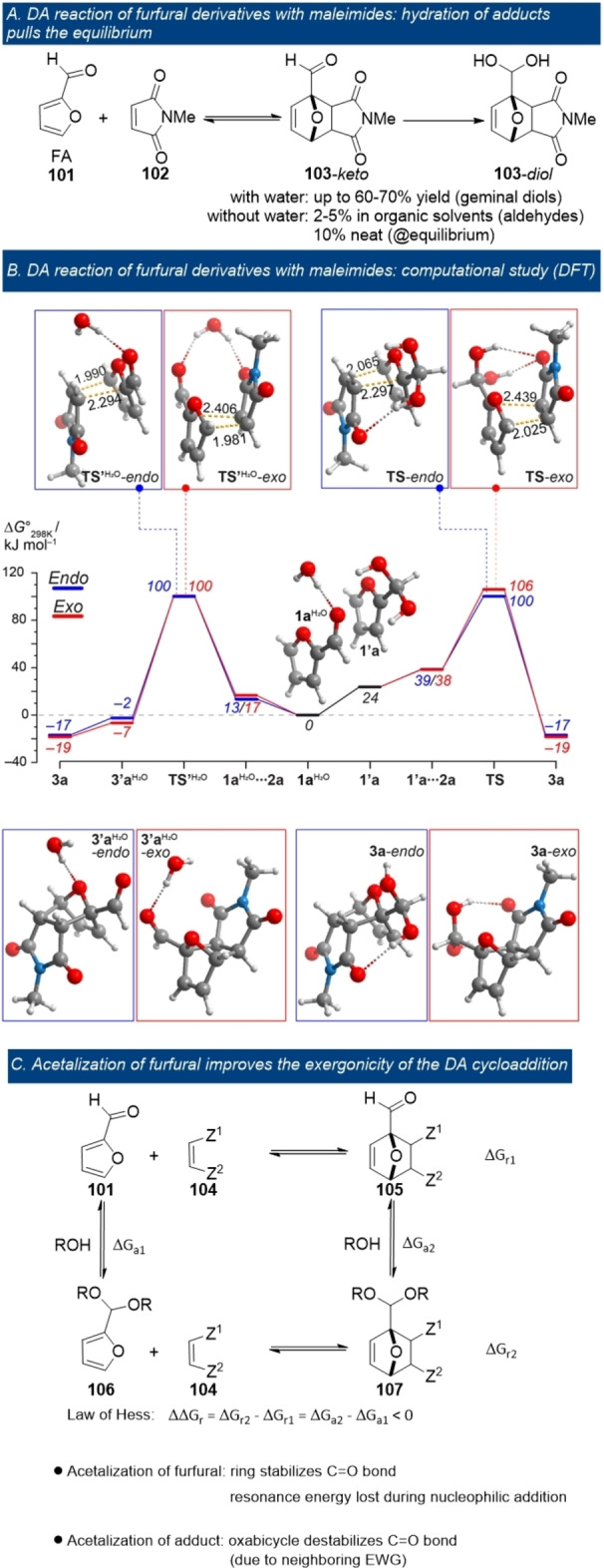
Overcoming unfavorable thermodynamics of DA cycloadditions with furfurals; reproduced with permission from ref. [115].

The intriguing formation of geminal diol products in this study suggests that the formyl substituent in furfural‐derived DA adducts is highly electron‐deficient; likely, this is due to the presence of the neighboring electron‐withdrawing ether bridge. Thus, the C=O bond in the adduct 105 is relatively destabilized, whereas in the corresponding diene, furfural 101, the formyl group is, in contrast, stabilized by conjugation with the ring. This rationale also provides an explanation for the reportedly improved thermodynamics of DA reaction upon acetalization of furfural (Figure 12 C). Accordingly, DA adducts (107) of furfural acetals 106 are commonly reported in the literature[ ⁵⁷ , ⁵⁸ , ¹¹⁶ , ¹²⁸ ] in contrast with those of underivatized formyl‐furans 101. This striking difference between the electronic properties of functional groups in the addends vs. the adduct (as also seen in the previous examples) can be thus exploited to design novel strategies for more efficient cycloaddition; this control over stability and cycloreversion by orthogonal modification can furthermore be exploited in functional molecules/materials. ^[116]

Intramolecular cyclizations constitute another important category of stabilizing secondary reactions; notably, the combination of reversible DA reactions with tandem intramolecular ring formation processes is also a highly effective strategy to direct an otherwise stereo‐ and regio‐unselective coupling towards a single isomeric adduct. The contribution to the overall Gibbs free energy can be enthalpic (e.g. quenching of reactive functionalities, strain release), entropic (release of a small molecule) or both. Reactions involving anhydride‐based dienophiles fall into the first category. An illustrative example is provided by Hoye and co‐workers who investigated various furan/itaconic anhydride combinations. ^[118] 2‐Substituted furans 108 lead to the formation of two pairs of exo/endo adducts 110, the distal and proximal isomers (Scheme 18). The authors interestingly found that when moving from ‐Me and ‐CH₂OAc substituents to a ‐CH₂OH group on the furan (112), the equilibrium conversion increased from 10–20 % to >95 %. Furthermore, instead of the distribution of the four isomeric adducts (in which the sterically preferred distal isomers predominated) a single component crystallized out, namely the product of prox/exo adduct lactonization 111 (Scheme 18). The driving force in this system is the opening of the high‐energy anhydride bond; crystal lattice energy may also contribute as the reaction is heterogeneous. ^[137]

Scheme 18.

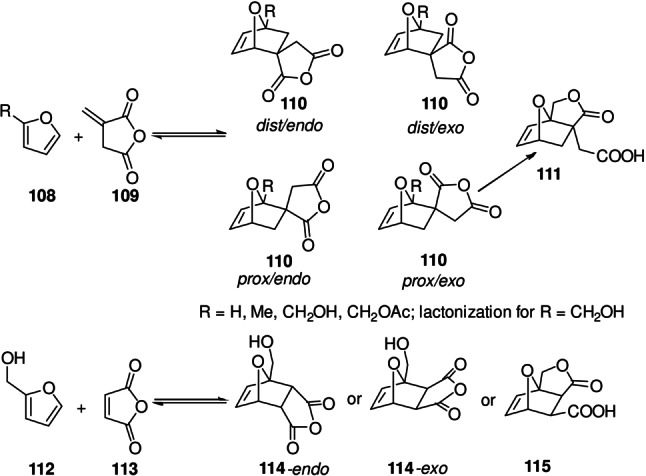
Lactonization/anhydride opening as secondary reaction.[ ¹³⁷ , ¹⁴¹ ]

Importantly, the mechanism was convincingly shown computationally to consists of a DA‐lactonization sequence rather than the other way around (as is operative for instance in the case of furfuryl amine‐based dienes[ ¹³⁸ , ¹³⁹ ]), although it may seem surprising that acylation of the alcohol only takes place intramolecularly. ^[140] A similar phenomenon occurs in the furfuryl alcohol 112/maleic anhydride 113 couple; in this system, however, the reaction mechanism and outcome (anhydride 114 or lactone product 115) seem to strongly depend on the reaction conditions. ^[141]

The lactonization strategy was also recently successfully applied in DA reactions between furfuryl alcohol and acrylate esters.[ ¹²² , ¹⁴² ] Nonactivated ester groups are not electrophilic enough to undergo lactonization: in such cases, the DA equilibrium conversion was low and a mixture of all four isomeric adducts was formed. The use of activated esters (hexafluoroisopropanolate, p‐nitrophenolate) or acrylic anhydride enabled not just an increase in the reaction rate but also a much‐improved selectivity towards a single isomer resulting from the lactonization of the prox/exo adduct. In these systems, the thermodynamic gain is both enthalpic (exothermic lactone formation) and entropic (release of a second molecule, for example, (CF₃)₂CHOH); the additional ring‐strain penalty seems to be minor. Importantly, the stability of the lactone against cycloreversion facilitated follow‐up chemistry, in this case aromatization.

Next, extensive efforts have focused on pulling the DA reaction equilibrium by ring‐opening of the oxabicycle ether bridge (Scheme 19). The significant release of strain energy contained in the oxabicyclic ring system of the adducts ^[114] can be used to render even fairly endergonic DA reactions irreversible, particularly since most of the times the initial ring‐opened intermediate rapidly evolves towards very stable molecules (aromatic molecules, ketones, polycycles, etc.). However, this process is very slow in the absence of activation; this can be provided either externally, for example, with acid or base catalysis, or promoted internally by groups with positive mesomeric effects at the oxanorbornene 1‐ or 4‐positions, as depicted in Scheme 19.

Scheme 19.

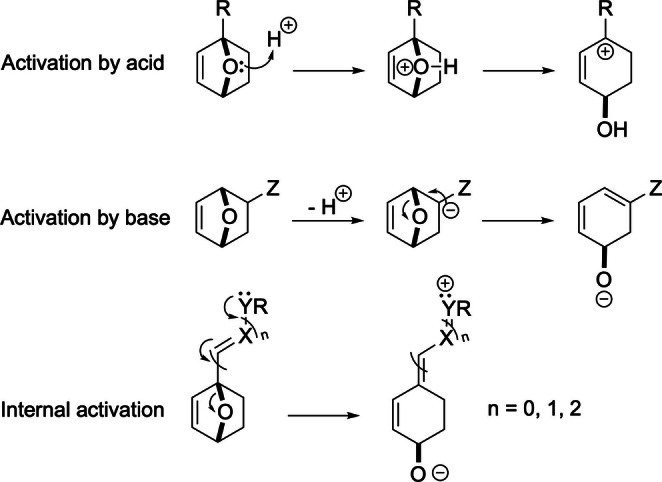
Activation of DA adducts towards oxabridge opening reactions.

Depending on adduct structure and reaction conditions, the initial ring opening can be followed by dehydration, transpositions or cyclization events, as depicted in Scheme 20. For example, oxanorbornene opening occurs spontaneously if the bridgehead position is occupied by amino or methoxy substituents. This process can be very facile, as in the case of 2‐methoxyfuran adducts of maleic anhydride or maleimides (118, R=OMe), which aromatize upon standing at room temperature. ^[143] In contrast, the corresponding N‐Boc 2‐aminofuran ^[80] and 2‐acetoxyfuran ^[144] adducts required relatively harsher conditions (>100 °C). Curiously, the ring‐opening/aromatization is particularly fast in adducts of push–pull dienes[ ⁸⁰ , ⁸³ ] or when there is an aryl substituent at the diene 5‐position (120, R=Ar). ^[82] The nature of the dienophile is also important. Frederich and Borger reported that dehydration of adducts of 2‐pyrrolidino‐5‐aryl furans 125 does not follow ring opening when the dienophile is acrylonitrile; ^[145] instead, tandem cyclizations can occur if proper reactivity handles (XH‐ on the neighboring aryl ring) are embedded in the scaffold. Lastly, intramolecular DA reactions of 2‐aminofurans can produce a wide range of structures (i.e. 134, 136) via transformations initiated by the oxabicycle opening. ^[146] This strategy has been extensively employed in alkaloid synthesis. ^[15]

Scheme 20.

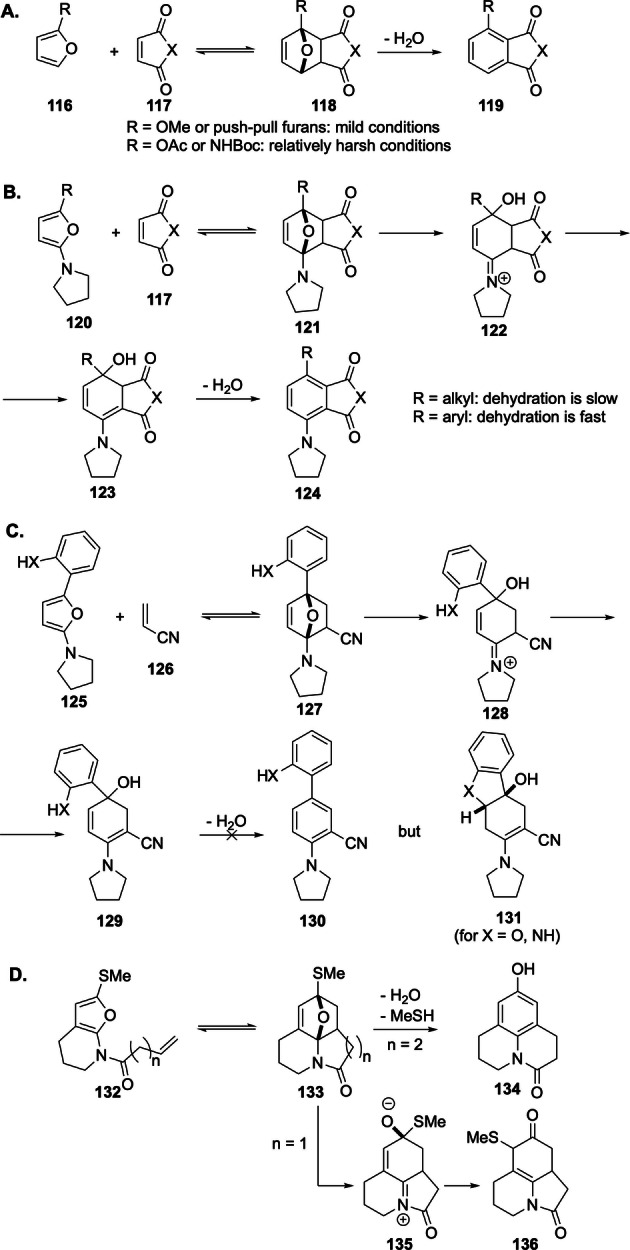
Spontaneous oxabicycle ring‐opening triggered by bridgehead electron‐donating substituents.

The concept of facilitating oxabicycle ring fission by placing electron‐donating substituents adjacently can be readily extended by vinylogy (Scheme 21), as shown in the DA chemistry of furfural hydrazones 137. Kinetically, hydrazone formation leads to activation of the furan diene due to donation of electron density from the hydrazone group, raising the diene HOMO level relative to furfural. ^[147] In addition, the adducts 139 nearly always aromatize, making the overall transformations strongly exergonic and thus irreversible. Initially disclosed in typical organic solvents,[ ¹⁴⁷ , ¹⁴⁸ ] DA reactions with furfural hydrazones proved more efficient and more economical when ran “on water”; ^[149] moreover, hydrazone formation was found to be water compatible, making one‐pot transformations also possible. ^[100] Notably, the ease of aromatization of the primary adducts was shown to subtly depend on structural elements: the adducts between furfural N,N‐dimethylhydrazone 137 and substituted maleimides 138 are stable up to 65 °C when R=Ph (aromatization required heating to 100 °C), while for R=Et the phthalimide was surprisingly formed already at ambient temperature. ^[149] Synthetically, the value of this method is to provide quick access to 1,2,3(,4)‐polysubstituted benzene derivatives 140 with full regioselectivity control; potential areas of application are the synthesis of bioactive molecules[ ¹⁰⁰ , ¹⁵⁰ , ¹⁵¹ ] and production of renewable chemical commodities (see Section 8). ^[152] When hydrazine is used as a chemical auxiliary, its efficient release and recycling is essential, for toxicity and economic reasons. Remarkably, the vinylogous reactivity can even be taken a step further: the hydrazone of 3‐furylacrolein 141 also readily undergoes the cycloaddition/dehydration cascade. ^[100] The interesting case of terfuran 145, which only forms terminal, aromatic adducts 148 with maleimides can also be included in this category. ^[153]

Scheme 21.

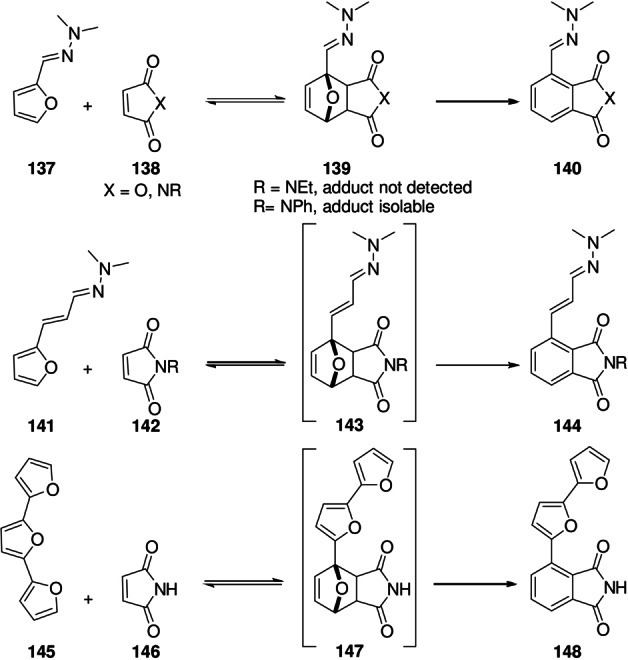
Vinylogous reactivity in DA/aromatization reactions.[ ¹⁰⁰ , ¹⁵³ ]

Oxabicycle ring‐opening and dehydration has been extensively investigated in the last decade in the context of renewable aromatics production. This topic will be the focus of the next section of this review. But before discussing this approach in detail, it is important to again emphasize the underrepresentation of electron‐poor furans in the scope of synthetically useful dienes. ^[24] In addition to the very few successful examples of reactions with furfural or furoic acid derivatives detailed earlier, a number of interesting transformations initiated by DA additions to N=N‐based dienophiles 150 have also been reported (Scheme 22). The particularity of the dienophile is key to the success of these reactions, both from the kinetic point of view (these dienophiles are highly reactive) and also with respect to thermodynamics (the resulting hydrazine adduct 151 has various options to evolve towards more exergonic structures). Thus, in reaction with phthalazine‐1,3‐dione, furfural or furoic acid derivatives form a DA adduct that readily undergoes ring scission and recyclization towards [5,6]benza‐3a,7a‐diazaindane 154. ^[154] In combination with azodicarboxylates, the reaction of 2‐furfural and 2‐acetylfuran follows initially a similar pathway but the ring‐opened intermediate 152 is stabilized by an alternative mode of ring closure. ^[155] These reactions have been mechanistically shown to proceed via the classical concerted DA pathway, despite the presence of the electron‐withdrawing substituents on the diene. ^[156]

Scheme 22.

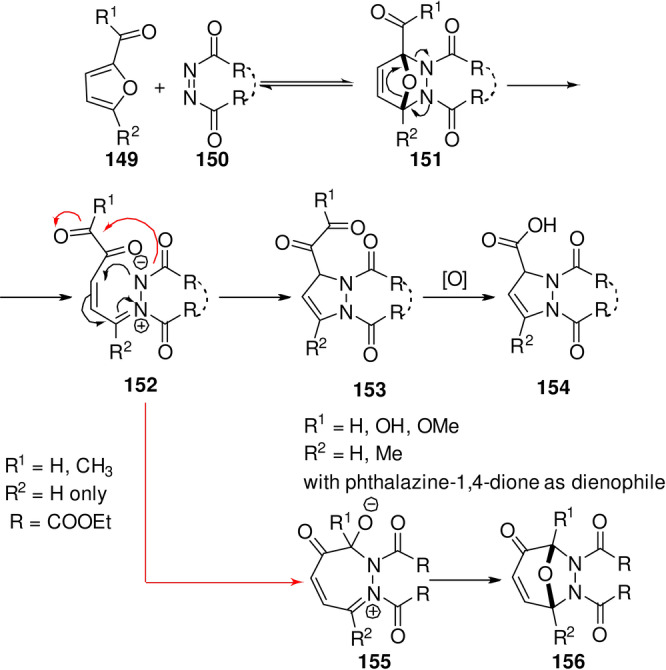
DA cycloaddition‐based reaction sequences with electron‐poor furans and N=N‐based dienophiles.[ ¹⁵⁴ , ¹⁵⁵ , ¹⁵⁶ ]

8. Selected Application: Renewable Aromatics

In the last decade, the furan DA/dehydration has been much explored as a route to renewable aromatics, with functionalized benzene derivatives finding widespread use as solvents, plastics monomers, lubricants, adhesives, plasticizers, intermediates for fine chemicals, etc. Aromatic compounds are presently produced nearly exclusively from petrochemical resources, on a massive scale and with steady market growth predictions, so there is both an environmental as well as commercial incentive to develop improved manufacturing processes.

The range of products synthesized via furan DA chemistry is shown in Scheme 23. The structures are fairly diverse, ranging from simple hydrocarbons (benzene, toluene, p‐xylenes, ethyl benzene) to highly functionalized molecules, such as m‐xylylene diamine or trimellitic acid. Most of the research in the field targets bio‐derived drop‐in replacements for well‐known products with established markets. These range from bulk chemical commodities produced on multimillion ton scale (e.g. phthalic anhydride, terephthalic acid, benzoic acid, ethyl benzene, etc.) to specialty chemicals such as the mellitic acids. In addition, there is also interest in developing renewable functional alternatives for valuable aromatics, including near drop‐ins such as 3‐methylphthalic anhydride. Notably, new technologies to introduce bio‐derived drop‐in substitutes for bulk products would obviously be most impactful from an environmental point of view, but they unfortunately can only compete on price with the highly optimized and cost‐effective petrochemical‐based processes. In the current socio‐economic context, this represents a tremendous challenge, as the market price of many of these bulk chemical commodities is presently lower than that of the cheapest and most readily available furan, furfural; moreover, the balance is considerably less favorable for 5‐HMF and its downstream products (DMF, FDCA). The integration of the furan‐to‐aromatics DA‐based technologies with the on‐site refining of lignocellulose into the required precursors thus seems a mandatory prerequisite for commercial success (see also discussion at the end of Section 8.2). Alternatively, specialty chemicals/functional replacements could be more economically competitive as they feature greater flexibility in accommodating process costs; the lower tonnage implies a correspondingly reduced contribution to meeting sustainability goals.

Scheme 23.

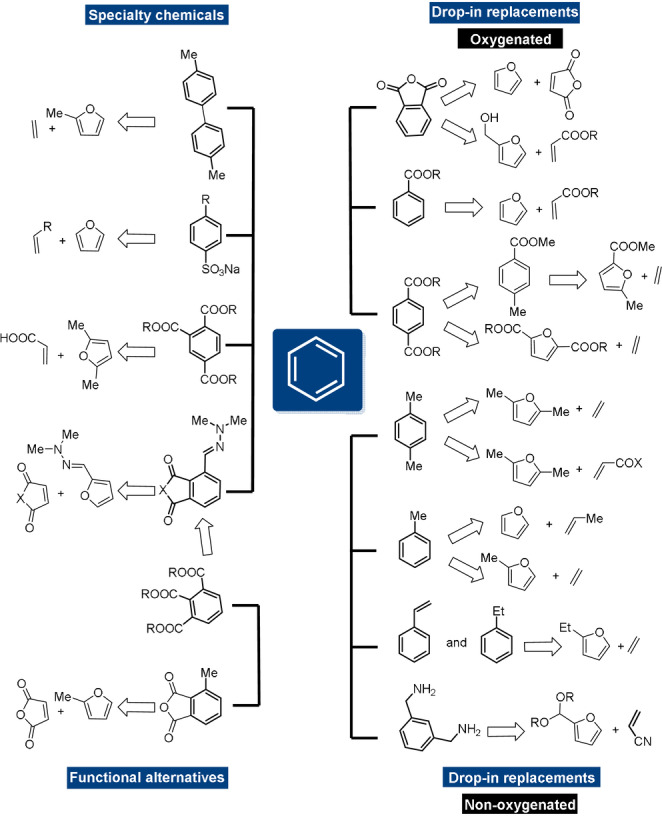
Scope of renewable aromatics accessible via the furan DA cycloaddition/dehydration route.

The DA/aromatization cascade can be performed either sequentially or, ideally, in tandem; for many addend combinations the route would in fact not be possible otherwise (e.g. with isolation of the intermediate adduct), as the DA cycloaddition is endergonic. The furan diene scope is very broad, ranging from the highly reactive 2,5‐dimethylfuran to the other extreme, 2,5‐furandicarboxylic acid; the same goes for the dienophiles, where maleic anhydride, ethylene and many olefins in between are well represented. In the next section, we will showcase the utility of the furan DA chemistry in the production of renewable aromatics, with an emphasis on the interplay between kinetic and thermodynamic considerations that impact process development and optimization. To better reflect the specific reactivity challenges, the examples are grouped in four categories, depending on the nature of the diene/dienophile couple, as indicated in Figure 13.

Figure 13.

Categories of furan DA cycloaddition reactions for the production of renewable aromatics.

8.1. Category I: Activated Furan/Activated Dienophile

The furan/maleic anhydride couple serves as the prototype of this category of fast and relatively exergonic DA reactions. Processes characteristically capitalize on the fair thermal stability of the adducts and separate the cycloaddition and aromatization stages to maximize chemoselectivity and productivity. Maleic anhydride is widely used as a highly reactive dienophile, and the cycloadditions typically occur noncatalytically, at near‐ambient temperatures. The use of monoactivated dienophiles such as acrylates is kinetically more challenging. On the other hand, acrylates are ideal building blocks because their production via biomass‐based routes has 100 % carbon economy and high atom‐efficiency in general (see Scheme 4). ^[157] Therefore, considerable efforts have been devoted to the development of efficient systems for the (catalytic) DA coupling between furans and acrylates, particularly based on Lewis acid activation. While molecular Lewis acids such as HfCl₄ ^[49] have shown high activity in the furan/acrylate cycloaddition, heterogeneous options are clearly more desirable from a process point of view and in this respect silica‐supported Lewis acids (for instance AlEt₂Cl, TiCl₄, ZnCl₂),[ ¹⁵⁸ , ¹⁵⁹ ] Lewis acidic zeolites (Hf‐, Zr‐, Sn‐Beta)[ ¹⁶⁰ , ¹⁶¹ ] and band‐gap metal oxides (HfO₂, ZrO₂) ^[162] were proposed as promising candidates for further development.

While the kinetics is typically fast for this category of addends, it is important to note that the cycloreversion reaction may also be fast, particularly under the action of the (acid) catalysts employed in the aromatization stage. Moreover, such conditions are generally incompatible with the addends and often result in their subsequent degradation. This is particularly true for the furan dienes, especially in the absence of alkyl substituents at the 2‐ and 5‐positions, which generally confer the furan protection against acids. To prevent such highly detrimental side reactions, research is focused around two main, complementary strategies: 1) the development of mild, near‐ambient‐temperature aromatization methodologies and 2) the obstruction/closure of the retro‐cycloaddition channel by a chemical transformation of the adduct.

A typical example of the former approach was disclosed by Lobo et al., who made use of mixed sulfonic‐carboxylic acid anhydrides for dehydrating DA adducts, mainly targeting products such as phthalic anhydride and benzoic acid (Scheme 24 A). ^[163] Ring‐opening of the DA adducts occurred readily at ambient temperature at which the cycloreversion rate was low; the resulting mono‐ and diacetate intermediates require subsequent heating to approximately 80 °C to aromatize. An interesting feature of this approach is that water is actually not formed during the reaction, mitigating the risk of deleterious hydrolysis side reactions (albeit at the expense of stoichiometric acetic anhydride consumption).

Scheme 24.

Acid/base mediation of dehydration of DA adducts and selected products.[ ¹⁶³ , ¹⁶⁴ ]

Alternatively, mild aromatization of DA adducts of this category can also be achieved by the action of strong bases, although this approach is mechanistically more challenging (Scheme 19) and its application is very specific.[ ¹⁶⁵ , ¹⁶⁶ ] For example, adducts of 2‐substituted furans (R=Me, CH₂OEt) with maleic anhydride afford substituted o‐phthalic acids 165 in fair yields by treatment with sodium methoxide in methanol at ambient temperature (Scheme 24 C). ^[164] The main drawback of this methodology is the use of stoichiometric base and the need to neutralize the sodium phthalate during work‐up and isolation. This considerably reduces the process economics; however, it may be an interesting option to produce value‐added chemicals, such as hemimellitic acid.

On the other hand, catalytic amounts of base were shown to be sufficient for the aromatization of furan DA adducts of acrylonitrile, as reported by the Jérôme group (Scheme 25).[ ⁵⁷ , ⁵⁸ , ¹⁶⁷ ] Interestingly, there is a pronounced difference in the acidity of the CH‐CN protons for the meta and ortho pairs of adducts 169. This difference was exploited and with proton abstraction being more favorable in the former adduct (169 ‐meta); this elegantly allowed for the kinetic resolution of these regioisomers and the meta‐substituted benzonitrile 170 was selectively produced (with 20 mol % NaOMe in DMSO at 30 °C). After separation, the ortho adducts could be thermally cycloreversed (at 80 °C) to regenerate the addends (furfural ethylene glycol acetal 167 and 168). In this manner, despite the lack of regioselectivity of the DA reaction, a single aromatic product could be obtained. This intermediate can be efficiently elaborated further into meta‐xylylenediamine 171, an industrial curing agent for epoxy resins and coatings. The methodology could be extended to the homologue 2,5‐diformylfuran, providing access to trisubstituted benzene derivatives, such as 1,2,4‐tri(aminomethyl)benzene and trimellitic acid 173. ^[168]

Scheme 25.

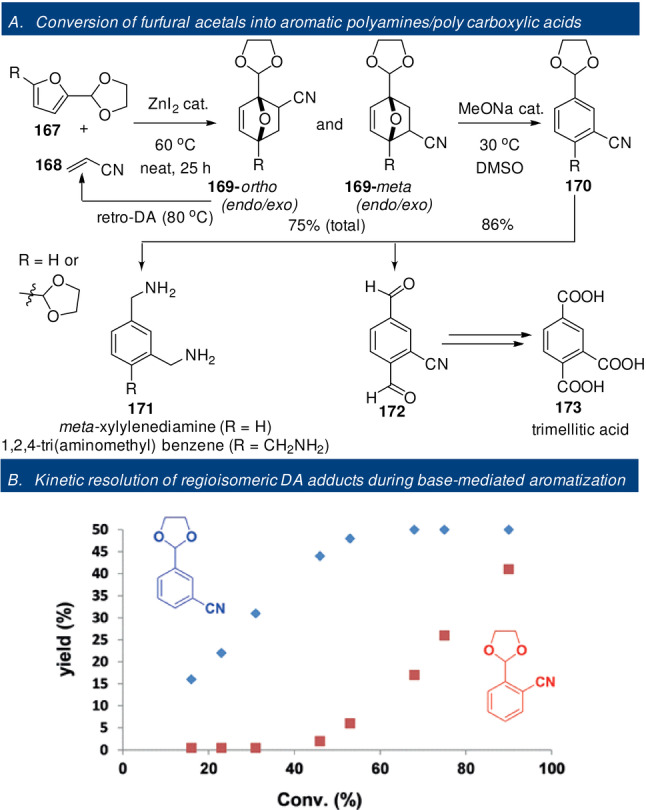
Regioselective synthesis of aromatic benzonitriles makes use of C−H acidity differences in the ortho and meta adducts; reproduced with permission from ref. [57].

The second option to mitigate the risks of retro‐DA reactions during the dehydration of the adducts towards aromatics is to completely obstruct or disable the cycloreversion pathway. A convenient way to achieve this is by hydrogenation of the adducts to form stable oxanorbornanes. This does introduce an additional step in the route and consumes 1 equiv of H₂ but the gain in aromatization efficiency offsets the disadvantage (and the hydrogen is ultimately regenerated).

A catalytic system able to promote both dehydration and dehydrogenation is required for the success of this approach: a combination of solid acid H‐VUSY and Pd/C (either a physical mixture or a bifunctional material) was found to be active in this transformation applied to adducts 176 of methylated furans to maleic anhydride (Scheme 26).[ ¹³² , ¹⁶⁹ ] Interestingly, lactone 178 formed by acid‐catalyzed isomerization of 177 was identified as the key intermediate in the dehydration process. This chemistry is also amenable to solid‐phase (neat) conditions, which remarkably afforded comparable results in shorter reaction times and in the absence of the Pd dehydrogenation catalyst (dehydrogenation occurred thermally). ^[170]

Scheme 26.

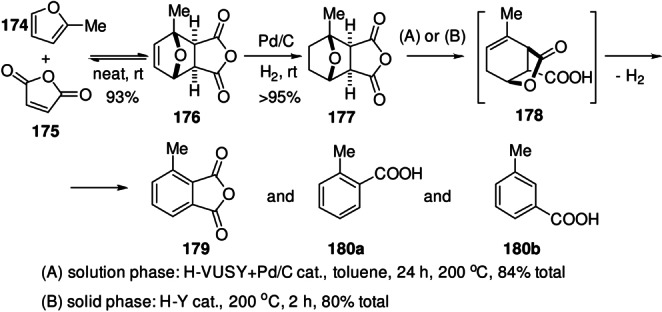
Synthesis of oxygenated aromatics by catalytic dehydration of hydrogenated adducts: this detour blocks the cycloreversion channel, allowing high levels of selectivity.[ ¹³² , ¹⁶⁹ , ¹⁷⁰ ]

As already mentioned, the ease of selective aromatization is critically linked to the kinetic lability of the DA adduct. This was recently evidenced in a study targeting phthalide 184 (Scheme 27 A). ^[122] Lactone 183 (see Section 7 for its formation) was shown to exhibit significantly improved thermal stability compared to the related intermolecular adducts 186 and 187: the energy barrier for its cycloreversion was calculated to be at least 5 kcal mol⁻¹ higher in the former case (Scheme 27 B). Thus, the aromatization of 183 could be performed with high selectivity in a variety of acidic conditions. The product phthalide 184 is a valuable intermediate towards phthalic anhydride, this route offering a high carbon efficiency.

Scheme 27.

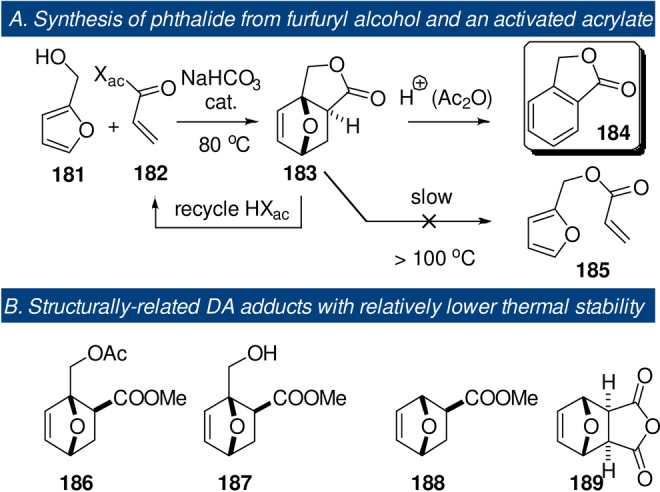
Synthesis of renewable phthalide starting from furfuryl alcohol and activated acrylates. ^[122]

Within this category of inputs, tandem DA/aromatization routes are relatively rare. As noted in Sections 4 and 7, the one‐pot transformation is facile with 2‐amino‐ or 2‐alkoxy‐substituted furans, but these building blocks are not readily accessible from biomass sources, limiting their relevance to the synthesis of renewable bulk aromatics.

An illustrative, successful example of tandem DA/aromatization is the coupling of the 2,5‐dimethylfuran 190 and acrylic acid 191, en route to p‐xylene (Scheme 28). This system is closely related to the amply investigated DMF/ethylene pair, which also yields p‐xylene directly, ^[171] although generally with the cogeneration of 2,5‐dimethylbenzoic acid (DMBA 194, R¹=R²=Me), in various amounts; this byproduct can serve as intermediate either to boost the p‐xylene yield by decarboxylation, ^[59] or as precursor for trimellitic acid. In comparison to the use of ethylene as dienophile, monoactivated acrylic acid is considerably more reactive, ^[53] allowing for a much faster reaction at convenient temperatures (near 25 °C, compared to 150–250 °C for ethylene), and its higher boiling point obviates the need for high gas pressures. Importantly, the theoretical carbon yield is similar for the two options, as in the ethylene‐based route 1 equivalent of CO₂ per mol of p‐xylene produced is also lost (but early on, at the fermentation stage, see Scheme 4).

Scheme 28.

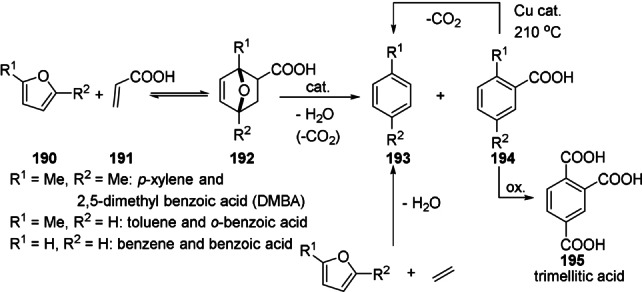
Synthesis of renewable p‐xylene starting from DMF and acrylic acid: reactions proceed under much milder conditions compared to the use of pressurized ethylene as dienophile.[ ¹⁷² , ¹⁷³ , ¹⁷⁴ ]

Thus, Zhang and co‐workers showed that 2,5‐dimethylfuran can be converted into aromatics in a single stage by reaction with acrylic acid at 15 °C in (1‐ethyl‐3‐methylimidazolium bis(trifluoromethylsulfonyl)imide, [Emim]NTf₂), under Lewis acid catalysis (Sc(OTf)₃). ^[172] The reaction time is very short, in the order of hours. The authors found that the selectivity for aromatics could be improved up to 92 % by the addition of acid additives like H₃PO₄, which presumably catalyze the oxabicycle 192 dehydration; DMBA was formed up to 25 %. With scale‐up in mind, the Al‐Naji group devised a continuous flow approach for p‐xylene synthesis from DMF and acrylic acid. ^[173] By exploiting zeolite catalysis under liquid phase flow (H‐Beta, 200 °C, 30 bar), transformation towards aromatics was fully selective, with a p‐xylene/DMBA ratio of approximately 5:1; these two products can be readily separated by distillation. Importantly, the very short residence time (10 min) ensures that the process is energy efficient. Wu et al. ^[174] also reported a heterogeneous catalyst system for this conversion. A bismuth/trimesic acid‐based MOF catalyst enabled significantly milder conditions for the synthesis of p‐xylene (batch conditions, acetone solvent, 160 °C, ca. 10 bar) from DMF and acrylic acid (albeit with a relatively long reaction time, 24 h). The total selectivity for aromatics was 96 % at full conversion of DMF, with a p‐xylene/DMBA ratio of 23:1. The catalyst could be recycled and no leaching of Bi was detected. Importantly, less substituted furan dienes were also well tolerated in this reaction, with 2‐methylfuran and furan giving 88 % (65 % toluene) and 80 % (37 % benzene) yields; the co‐products, o‐toluic acid and benzoic acid, respectively, have high commercial value as well. This feature distinguishes the use of acrylic acid as an ethylene surrogate from the ethylene use itself, for which, as shown in the next section, the acceptance of dienes other than DMF is generally poor.

Finally for this category, the Hoz group described the selective (80–90 %) tandem DA aromatization reaction between 2,5‐dimethylfuran and methyl acrylate, catalyzed by Lewis acid functionalized silica gel (e.g. with TiCl₄);[ ¹⁵⁸ , ¹⁵⁹ ] most likely, both steps benefit from the action of the catalyst.

8.2. Category II: Activated Furan/Nonactivated Dienophile

The reaction of bio‐derived furans with simple olefins such as ethylene has received tremendous attention in the last decade, as it provides access to drop‐in replacements for the most important aromatic building blocks: benzene, toluene, xylene(s) (BTX) and ethyl benzene (a styrene precursor). With a yearly production scale >80 million tons, ^[175] terephthalic acid (TA) is definitely the most important functionalized aromatic product. The current route towards terephthalic acid (the Amoco process) ^[176] requires pure p‐xylene which is tedious to source from crude oil. ^[17] The oxidation of p‐xylene to TA, although high‐yielding and utilizing the ideal oxidant, air, suffers from some drawbacks. These include for instance harsh conditions, loss of AcOH solvent by burning, corrosive catalysts, co‐generation of ozone‐depleting off‐gases (MeBr), troublesome removal of problematic impurities (4‐formylbenzoic acid, a polyester chain‐growth inhibitor), etc. ^[176] The furan DA/dehydration approach thus provides the opportunity not only to substitute petrochemical resources with renewable feedstocks, but also to circumvent the costly purification of p‐xylene and potentially improve on the downstream oxidation (see also Section 8.4). Importantly, the production of the requisite dienophile, ethylene, from biomass is already a mature and scalable technology. ^[44]

Production of p‐xylene from DMF and ethylene via tandem catalytic DA/aromatization has received much attention, following a patent by Brandvold (Honeywell/UOP) from 2010. ^[177] Without disclosing the details, Brandvold claimed p‐xylene yields higher than 30 % in the acid‐catalyzed conversion of DMF and ethylene, sparking a quest towards highly active, selective and stable catalysts for this transformation. Various hetero‐ and homogeneous Brønsted and Lewis acids have been studied for p‐xylene production: (transition‐)metal oxides[ ¹⁷⁸ , ¹⁷⁹ ] and phosphates,[ ¹⁸⁰ , ¹⁸¹ ] (acid‐functionalized) silica,[ ¹⁸² , ¹⁸³ ] heteropolyacids, ^[184] and molecular Brønsted and Lewis acids;[ ¹⁸⁵ , ¹⁸⁶ ] zeolite catalysis is particularly popular. ^[17] The most selective zeolite catalyst to date is a phosphorous‐containing zeolite, P‐Bea, which delivers p‐xylene in yields as high as 97 %. ^[187] These comprehensive studies have constructed a detailed picture of the mechanistic pathways that operate in the DMF/ethylene system. In the absence of catalysis, the reaction barriers are computationally estimated to be ≈40 kcal mol⁻¹ and 60 kcal mol⁻¹ for the DA and dehydration steps, respectively. ^[188] The second barrier is prohibitively high and p‐xylene is generally not detected in the absence of reaction activators. Catalysis achieves dramatic improvements in the dehydration step with Brønsted acids unquestionably outperforming Lewis acids.[ ¹⁸⁸ , ¹⁸⁹ ] This trend is reversed in the first stage, the DA cycloaddition between DMF and ethylene. Brønsted acids are ineffective at catalyzing this step, as demonstrated both computationally and experimentally. Indeed, three Brønsted acid activation modes have been investigated for the DA step (Scheme 29, A=H⁺): 1) ethylene activation; 2) DMF activation at the oxygen atom; 3) DMF activation at an endocyclic carbon atom. None of these pathways are believed to have kinetic relevance.[ ¹⁸⁹ , ¹⁹⁰ , ¹⁹¹ , ¹⁹² ]

Scheme 29.

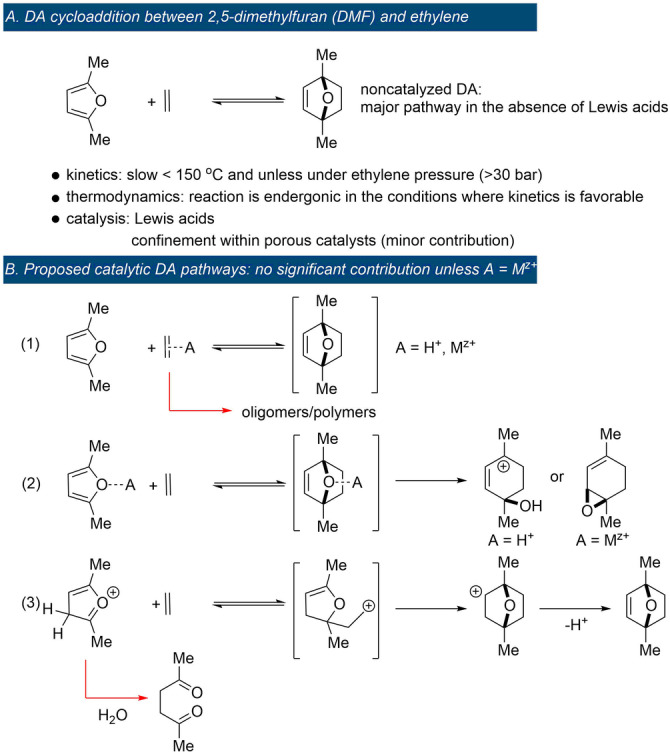
Brønsted/Lewis acid activation modes in the cycloaddition between DMF and ethylene.

Although activation of the dienophile would be expected to lower the reaction barrier according to the general FMO theory, this appears not to happen in the ethylene/proton system. Moreover, due to its higher polarity, DMF is more likely to occupy the catalytic sites. In addition, protonation of ethylene would be expected to initiate detrimental oligomerization side reactions. DA cycloaddition via DMF O‐protonation does display a reduced activation barrier according to DFT calculations (the mechanism is probably an IED demand cycloaddition) but can be excluded since protonation at the endocyclic carbons (C2/C3) is much more preferred.[ ¹⁸⁸ , ¹⁸⁹ ] However, this third activation mode would break the diene symmetry and thus prohibit cycloaddition. An alternative pathway consisting of stepwise adduct formation after initial DMF C3‐protonation was proposed, ^[190] but is likely not viable since it involves a high‐energy primary carbocation intermediate. These computational insights have been validated experimentally. At a high concentration of acid sites, the rate is no longer dependent on the number of acid sites (Figure 14, bottom). ^[192] Indeed, in this kinetic regime, the cycloaddition is rate‐limiting and acid‐activation is not observed. The DA reaction is mainly promoted by thermal activation (typically temperatures above 200 °C are employed). While not being essential, ^[190] confinement effects in the catalyst pores may also play a minor role. ^[193]

Lewis acid catalysis (Scheme 29, A=M^z+) is important for the DMF/ethylene cycloaddition, however. Activation can occur either at the dienophile or the diene (to give a NED or IED mechanism, respectively);[ ¹⁸⁸ , ¹⁸⁹ , ¹⁹⁴ , ¹⁹⁵ ] pathways in which the metal ion binds to ethylene were generally shown to be more favorable (Scheme 29 B, (1), A=M^z+). ^[188] To sum up, p‐xylene synthesis via the furan DA route benefits from Lewis catalysis in the cycloaddition step and Brønsted catalysis in the dehydration step. Accordingly, recent catalyst development has strived to match the optimal balance of the two types of acid sites, which indeed seems a promising direction for the next generation of catalysts. ^[196]

The cycloaddition and the dehydration stages of the tandem p‐xylene synthesis are also notably distinct when it comes to thermodynamics: the former is endergonic while the latter is highly exergonic. The strongly exothermic and entropically favored aromatization thus compensates for the unfavorable DA equilibrium, providing the thermodynamic driving force for p‐xylene formation. The endergonic nature of the cycloaddition is a somewhat overlooked and to some extent controversial aspect of this chemistry. The quantification of the impact of the unfavorable DA equilibrium on the overall process rate is a relevant topic but challenging to assess. At the typically high operating temperatures (200–300 °C), the entropic penalty of this bimolecular reaction is considerable. On the other hand, as discussed in a Section 5.1, DA reactions with ethylene are predicted to be fairly exothermic (especially relative to the use of other, substituted dienophiles) due to the absence of steric repulsions in the adduct. Given these contrasting effects, the Gibbs free energy of reaction can be expected to have a low, positive value. Dauenhauer et al. report a theoretical value for ΔG _r of +2.3 kcal mol⁻¹ at 300 °C (Figure 14 top). ^[193] Since all these studies are performed under high ethylene pressures (20–50 bar) and generally concentrated solution, fairly decent equilibrium conversions can be expected. Indeed, the consistently observed positive correlation of the p‐xylene formation rate with temperature suggests that the thermal lability of the adduct is not a major limitation for the overall transformation. ^[190] Interestingly, in nearly all studies, the DMF/ethylene adduct has not been isolated nor spectroscopically characterized; a number of investigations do report its detection as a component in the crude reaction mixture,[ ¹⁷⁸ , ¹⁷⁹ , ¹⁸³ , ¹⁹⁷ ] at levels of a few percent (and as high as 10 % ^[196] ). However, the typically employed analytical technique (GC/MS) does not allow the unambiguous structural distinction of this critical intermediate from other isomeric molecules. ^[197]

In this respect, a rather unique patent from 1955 describing not the tandem, but the sequential synthesis of p‐xylene from DMF and ethylene has been somewhat overlooked. ^[123] Although limited experimental details are provided, it seems that it takes 4 h at 180–200 °C and 40 atm to reach equilibrium in this system. The adduct can be isolated by distillation under reduced pressure and subsequently aromatized with HBr in acetic acid. The methods described in this old study can be more elaborately exploited to further advance the field. Access to 1,4‐dimethyl‐1,4‐epoxy‐2‐cyclohexene would not only allow the unambiguous identification of this intermediate, for example, in GC traces, but also the independent study of the catalytic dehydration, decoupled from the cycloaddition.

While p‐xylene is the preferred target, many studies have attempted to extend the application of the DA/dehydration route towards other valuable aromatics. Benzene and toluene are obviously important synthetic goals, but unfortunately the selectivity seems to critically depend on the degree of methylation in the furan diene. Indeed, methyl groups at the furan 2,5‐positions positively impact the overall transformation by 1) increasing the furan diene reactivity; 2) improving the thermodynamics (oxabicycle ring strain is reduced upon methylation at bridgehead positions ^[114] ); 3) increasing the acid‐catalyzed dehydration rate; and 4) suppressing deleterious side reactions (alkylations, dimerization to benzofuran, furan hydrolysis and polycondensation, etc.).

In all reported studies, the selectivity consistently decreased in the order DMF >2‐methylfuran >furan. Very few groups have attempted to optimize these results and the process is indeed less efficient than with DMF (maximum yields 65–70 %).[ ¹⁹⁸ , ¹⁹⁹ ] In the series of ethylated furans, the same observations hold. Tsang and co‐workers investigated the production of ethylbenzene 200 (R′=H) from furan and ethanol; ^[200] yields up to 45 % of ethylbenzene could be obtained at 70 % furan conversion over a HUSY‐type zeolite. The process involves parallel furan alkylation with ethanol and ethanol dehydration to ethylene to generate the addends for cycloaddition/dehydration (Scheme 30). The most important side product, p‐diethylbenzene, is valuable in its own right as a precursor to p‐divinylbenzene, a widely used crosslinking monomer. Alternatively, renewable p‐diethylbenzene can be obtained by applying the standard cycloaddition/dehydration methodology to 2,5‐diethylfuran and ethylene; the former building block is accessed by sequential acylation/hydrodeoxygenation of furan. ^[201]

Scheme 30.

Synthesis of renewable styrene and p‐divinylbenzene.[ ²⁰⁰ , ²⁰¹ ]

Another interesting recent development in Category II of furan DA reactions is the synthesis of biphenyl derivatives from 2‐methylfuran 202.[ ²⁰² , ²⁰³ ] Oxidative dimerization of 202 to 5,5′‐dimethylbifuran 203 is followed by bis‐DA cycloaddition with ethylene and dehydration (Scheme 31). The sustainability of this approach benefits not only from the renewable character of the precursor, but also from the high atom‐efficiency of the route, in contrast with the classical metal‐based strategies for the cross‐coupling of substituted benzenes. In addition, the 4,4′‐dimethylbiphenyl product 205 can be readily functionalized into various added‐value molecules with potential use in polymer applications.

Scheme 31.

Synthesis of bio‐derived 4,4′‐biphenyl derivatives via 2‐methylfuran dimerization and bis‐DA cycloaddition/dehydration.[ ²⁰² , ²⁰³ ]

Regarding the dienophile scope, higher ethylene homologues present additional reactivity and selectivity challenges, as substitution of the olefinic bond with electron‐donating groups (alkyl) destabilizes its LUMO and diminishes reactivity. ^[53] Nonetheless, this route would provide access to aromatic intermediates with commercial value, such as linear alkylbenzenes used in the surfactant industry. ^[204]

While the DMF/ethylene route to TA has been extensively investigated in the last decade, it is important to note that the adoption of this technology in industry is hampered by the still harsh reaction conditions (200–250 °C, 20–40 bar) and long reaction times. Accordingly, the sustainability advantage of employing renewable resources is offset by the high energy demand of the chemistry and the intensive processing of biomass to produce the requisite intermediates (e.g. 5‐HMF and DMF), to the extent that the biobased route is no longer more environmentally friendly that the petrochemical one. ^[205] Intuitively, this techno‐economic analysis result should not come as a big surprise, given the fact that the intrinsic resource capital of the biomass is completely lost in a route that connects a highly oxygenated raw material (5‐HMF, 38 wt % O) to an oxygen‐rich product (TA, 39 wt % O) via a simple hydrocarbon (p‐xylene, 0 wt % O). In other words, even under perfect conditions, approximately 3 kg of C6‐carbohydrate would still be required to produce 1 kg of p‐xylene, whereas the classical oil‐refining approach typically features very low levels of waste and is unidirectional in terms of redox changes. This critical issue is well acknowledged in the field and various strategies have been considered to address it (see also Section 8.4). For example, the overall process can be simplified by combining several reaction steps in a cascade transformation, reducing the number of unit operations and purifications. In this context, the Tsang group disclosed the use of ethanol as an ethylene surrogate, enabling the p‐xylene synthesis from DMF to take place under lower pressures and shorter reaction times. ^[206] Similarly, Cao et al. developed a catalytic system capable of combining the hydrogenation of 5‐HMF to DMF with the cycloaddition to ethylene and adduct dehydration. ^[207] Notably, by using 5‐chloromethyl furfural as key (integrated) intermediate in the conversion of sugars towards DMF, U.S.‐based Origin Materials is currently advancing the furan DA technology towards renewable p‐xylene from pilot phase to commercial scale. ^[186] Alternatively, the energy intensity of the process can be significantly improved by substituting ethylene for the more reactive acrylic acid, without compromising the overall carbon yield of the route, as discussed previously (Category I reaction).

8.3. Category III: Deactivated Furan/Activated Dienophile

Examples of DA‐based methodologies employing deactivated (oxygenated) furans like furfurals and furoic acids are scarce, ^[24] which is unfortunate given their ready accessibility from biomass (Section 2.1). Moreover, many of the valuable aromatic targets are oxygenated molecules (e.g. terephthalic acid, phthalic anhydride, benzoic acid, mellitic acids, etc., Scheme 23) but the lack of reactivity of these oxygenated furans does not allow one to fully capitalize on this excellent match between resource and product structure. A single study discloses the direct observation of DA adducts of furfurals (with reactive maleimides as dienophiles), albeit in minor amounts (see also previous section). ^[115] Chemical derivatization (either by redox reactions as discussed or nucleophilic addition to the C=O group) is required to enable diene reactivity in formyl furans, essentially turning these reactions into ones of Category I type. The main redox‐neutral approach to access aromatics from furfural derivatives is via hydrazone activation (see also Section 7).[ ¹⁴⁷ , ¹⁴⁸ ] The hydrazone functional group enhances diene reactivity and also allows for a facile (typically spontaneous) adduct dehydration. In this manner, the otherwise recalcitrant DA process is promoted both kinetically and thermodynamically. In combination with activated dienophiles (e.g. maleic anhydride and maleimides in particular), this route provides quick access to 1,2,3‐trisubstituted or 1,2,3,4‐tetrasubstituted benzene derivatives with complete regiocontrol. ^[100] Unfortunately, the efficiency of the transformation drops considerably when monoactivated dienophiles are employed (acrylates, acrylonitrile) and accessing disubstituted benzene derivatives via this methodology is troublesome. The optimization of these reactions is furthermore challenging due to the fairly high instability of furfural hydrazones.[ ¹⁰⁰ , ¹⁴⁷ , ¹⁵² ]

The use of furoic acids as dienes in the synthesis of renewable aromatics is also rather exceptional (Scheme 32). For instance, furoic acid 207 (R¹=R²=H) combined with highly reactive cyclopentadienone 208 to give a cycloadduct that upon treatment with base led to the formation of 4‐hydroxyindanone 210; the yield of the DA reaction was, however, very low (Scheme 32 top). ^[208] Furoic acid also reacted fairly quickly with maleimides in aqueous medium (at near ambient temperatures), but the conversion was thermodynamically limited to 50–60 %. ^[66] In this case, both the rate and equilibrium conversion benefited from the addition of stoichiometric base to neutralize the acid functionality, in water but also in organic solvents (the reactions essentially become Category I cycloadditions). Other carboxylic acid derivatives (esters, amides) showed comparable behavior; the DA coupling performed reasonably well in neat conditions while aqueous conditions improved the yields and rates (due to “on‐water” activation mechanisms ^[67] ). The aromatization of this type of adducts is troublesome due to their high thermal lability (cycloreversion already occurs at 40–50 °C) and the reduced basicity of the ether bridge; HBr in AcOH seems to be a specifically useful reagent in this regard. ^[62]

Scheme 32.

The use of furoic acids in combination with activated dienophiles in the synthesis of renewable aromatics.[ ⁶⁶ , ²⁰⁸ , ²⁰⁹ ]

A final example is provided by the coupling of 2,5‐furandicarboxylic acid bismethyl ester with benzyne 214 (Scheme 32 bottom). ^[209] While this chemistry might not necessarily be interesting for scale‐up (due to the difficulty in generating/handling benzyne and the limited commercial utility of the naphthalene end products), it suggests that in combination with the right partner, DA reactions proceed even with bis‐deactivated furan dienes (see also next section). Importantly, in this system, the cycloaddition with the highly electrophilic benzyne is not only very fast but also irreversible. As for the aromatization, it is interesting to note that the single‐step transformation of the adduct (deoxygenation in the presence of TMSI) was significantly less efficient than a two‐step, hydrogenation and dehydration approach, a strategy analogous to that in Scheme 26. Remarkably, despite the presence of two strongly electron‐withdrawing groups at the adduct bridgehead positions, the acid‐mediated dehydration still proceeded readily.

8.4. Category IV: Deactivated Furan/Nonactivated Dienophile

The DA coupling of poorly reactive dienes (furfural, furoic acids) with nonactivated dienophiles is obviously a major scientific challenge in view of the slow kinetics and strongly unfavorable thermodynamics. Furfurals 218 are likely unsuitable substrates: the direct DA coupling to ethylene is simply too unfavorable and under forcing conditions these formyl‐furans rapidly decompose (e.g. via oligomerization/humin formation).[ ³³ , ²¹⁰ ] Alternatively, a positive development in this direction would be the redox‐neutral derivatization of furfural as N,N‐dimethyl hydrazone 220 (Scheme 33). Under copper catalysis, the DA reaction with ethylene afforded up to 22 % yield of aromatic product 222 (250 °C, 35 bar, in dioxane), providing access to useful molecules, such as benzaldehyde, benzoic acid, benzonitrile and phenol. The 5‐HMF‐derived hydrazone afforded the expected aromatic product in a slightly lower yield. ^[152] These examples serve as proof‐of‐concept and additional optimization efforts are required (including the recycling of the hydrazine auxiliary).

Scheme 33.

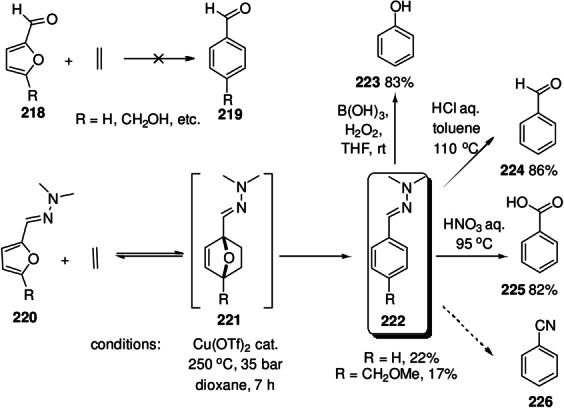
Activation of furfurals as N,N‐dimethyl hydrazones in reaction with ethylene towards substituted benzenes. ^[152]

On the other hand, furoic acid based dienes are less prone to decomposition and show greater promise in DA cycloadditions to ethylene. These alternative routes ultimately targeting terephthalic acid involve several oxidations stages (namely the generation of the furoic acid precursor from the biomass and the late‐stage oxidation of the aromatic intermediate towards TA (Scheme 34), but they are clearly more redox‐efficient and potentially more sustainable than the approaches discussed in Section 8.2. Indeed, such stagewise oxidation can be more beneficial than the direct conversion of methyl substituents to COOH. As already mentioned, the Amoco process presents various challenges, while the oxidation of functional groups that are already oxygenated (CH₂OH, CHO) is generally much more facile. ^[211] Moreover, this conversion could be achieved by electrochemical means/catalytic dehydrogenation, co‐generating valuable H₂ in the process, instead of consuming it (e.g. in the 5‐HMF to DMF conversion). ^[212] Alternatively, furoic acids can also be obtained from uronic acids, bypassing the notoriously unstable 5‐HMF (Scheme 34 top, route A vs. route B). ^[213]

Pacheco and Davis were the first to demonstrate the utility of furoic acids as dienes in DA reactions with ethylene (Scheme 34 bottom).[ ²¹⁴ , ²¹⁵ ] The use of Lewis acidic zeolites (Sn‐Beta, Zr‐Beta, Zn‐Beta ^[216] ) was key to success: the Lewis acid center is involved in catalyzing both the DA step as well as the subsequent dehydration of the adduct 228. This process can be performed at a temperature as low as 190 °C, which is somewhat counterintuitively lower that what is typically observed in the previously discussed DMF/ethylene‐based routes (200–250 °C). Brønsted acidic zeolites led mostly to coke formation, confirming the essential role of Lewis acid catalysis.

The mechanism of this rather unexpected DA aromatization reaction was studied in detail in silico by Bell et al., ^[217] with particular attention on the rate‐limiting DA step in the sequence. Six different pathways were investigated for the cycloaddition of 5‐hydroxymethylfuroic acid (227, R¹=H, R²=CH₂OH) to ethylene in Sn‐BEA: four different activation modes of the furan by the Sn center, one pathway involving ethylene binding to Sn and a pathway involving a Si site. The binding of Sn to the COOH group of the substrate was found to lead to the fastest cycloaddition; this effect was particularly strong when compared to the classical FMO‐theory‐predicted Lewis acid activation of the dienophile (Figure 15). Importantly, the role of the Sn site seems to be the electrostatic stabilization of the DA transition state rather than the facilitation of a charge transfer between the furan diene and ethylene. The configuration in which the Sn atom binds to the carboxyl group maximizes this electrostatic interaction and thus corresponds to the preferred reaction pathway; compared to the uncatalyzed reaction, the cycloaddition energy barrier is considerably lower (−23 kcal mol⁻¹).

Figure 15.

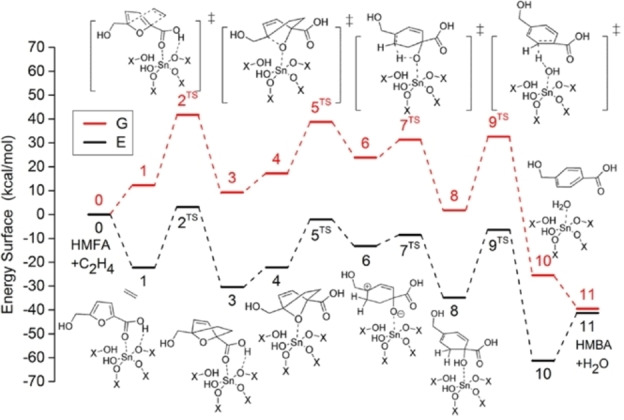
Energy (E) and free energy (G) surfaces for the most favorable path for formation of p‐hydroxymethylbenzoic acid from 5‐hydroxymethylfuroic acid and ethylene mediated by Sn‐BEA; reproduced with permission from ref. [217].

Regarding the scope of this approach, methylated (esters/ethers) furoic acid derivatives consistently showed improved selectivity; ^[218] methyl 5‐methylfuroate (227, R¹=R²=Me) is a distinctly promising diene in this respect,[ ¹⁸⁵ , ²¹⁴ , ²¹⁵ , ²¹⁸ ] particularly given its ready production from hexoses, by the HCl treatment of fructose to form 5‐chloromethyl furfural followed by an overall redox‐neutral NHC‐catalyzed rearrangement (Scheme 34 top, route C). ^[219]

A final interesting option to renewably produce terephthalic acid would be the combination of ethylene with 2,5‐furandicarboxylic acid or its esters (FDCA 76; Scheme 35). FDCA has recently received a great deal of attention in the context of the production of (novel) bio‐derived polymers (e.g. polyethylene furanoate, PEF ^[220] ) and commercial scale‐up of this compound has been announced.[ ³² , ²²¹ ] An FDCA‐based DA/aromatization route would be concise, atom‐ and redox efficient and would avoid the challenges of the Amoco oxidation. Unfortunately, the presence of two electron‐withdrawing substituents on the furan ring not only nearly completely suppresses its diene character but also renders the cycloaddition highly endergonic (see Figure 11); moreover, it diminishes the propensity of the corresponding ethylene cycloadduct to undergo acid‐activation towards dehydration.

Scheme 35.

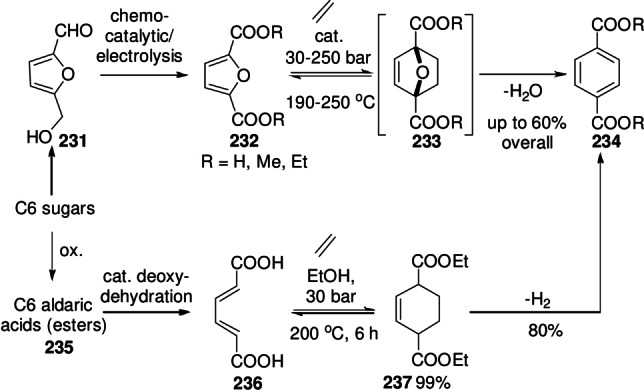
FDCA[ ²²⁵ , ²²⁷ ] vs. muconic acid ^[229] as prototypical bis‐deactivated dienes in the synthesis of TA via the DA/dehydration route.

Not surprisingly, attempts to develop routes based on this idea first met with little success: a BP patent (2008) initially reported a maximum yield of 0.14 % of terephthalic acid. ^[222] Since then, considerable progress has been made, albeit in small incremental steps. The use of Lewis acidic zeolites such as Zn‐Beta increased the maximum yield to about 5 % (from FDCA‐methyl ester). ^[216] A patent by Furanix disclosed the production of TA starting from FDCA and ethylene in 17 % yield and noncatalytic conditions: AcOH/benzoic anhydride, 240 °C, 30 bar. ^[223] In another patent by UOP (2016), yields of TA up to 22 % were reported (with a WOx/ZrOx catalyst at 225 °C). ^[224] Finally, recent studies demonstrated a step‐change in the yield of terephthalates obtained from FDCA esters (methyl or ethyl): the Clark group achieved yields above 50 % (at 250 °C, 60 bar) using an aluminum‐pillared montmorillonite catalyst[ ²²⁵ , ²²⁶ ] whereas Jae et al. reported approximately 60 % yield of the desired product by means of a silica‐supported heteropolyacid catalyst (HPW/SiO₂) at 225 °C and 35 bar. ^[227] Generally, the use of FDCA esters leads to better results, as issues with the low solubility of FDCA and side reactions arising from decarboxylation are circumvented.

That product formation could be detected for these unreactive addends at temperatures as low as 190 °C is remarkable. Vlachos et al. ^[228] investigated the mechanism of the Zn‐Beta catalyzed process ^[216] by DFT calculations and concluded that most likely the catalyst is not involved in the cycloaddition step, except for a minor confinement (entropic) contribution; despite the presence of the strongly electron‐withdrawing substituents on the furan and the nonactivated nature of the dienophile, the reaction most likely still proceeds via the NED pathway. This noncatalytic nature of the cycloaddition is also suggested by the experimental conditions of the Furanix process, in which metal‐based Lewis acids were not at all employed. Presumably, these unusual reactions are rendered possible by the highly efficient coupling of the endergonic DA reaction with the fast catalytic dehydration towards the very stable aromatic core. It thus seems that with the proper understanding of the kinetics/thermodynamics dichotomy, essentially any type of (tandem) furan DA cycloaddition can be optimized.

A comparison of the use of FDCA and structurally related muconic acid 236 for TA synthesis highlights the particularities of the furan DA cycloaddition (Scheme 35). Both dienes bear two electron‐withdrawing substituents and are thus strongly deactivated, requiring high temperatures for the cycloaddition. However, the aromatic character of the furan (enhanced by the COOR groups) renders the FDCA reaction endergonic; the adduct 233 is presumably present in only small amounts at equilibrium (undetected to date) and tandem, catalytic dehydration to TA is critical for conversion. In contrast, with muconic acid the DA equilibrium can be completely shifted to the adduct 237 side under high ethylene pressure. The resulting cyclohexene is thermally stable and can be isolated in nearly quantitative yield (albeit as mixture of isomers). ^[229] Dehydrogenation can be performed in a subsequent step to yield TA (as its diethyl ester). In terms of atom‐economy and other sustainability metrics, the two routes compare well; ^[225] however, the availability of muconic acid from biomass is currently still a major challenge (particularly in the stereopure trans,trans‐236 form), ^[230] and progress is lagging behind research on FDCA. Finally, from a business point of view, it is fair to note that the synthesis of renewable PET from FDCA competes with its direct conversion to high‐performance, novel polycondensation polymers (PEF), which might have stronger economic incentives. ^[231]

9. Conclusions

The furan DA reaction is an extremely valuable synthetic tool for (macro)molecular applications and to produce sustainable chemical building blocks in particular. Unfortunately, despite (or perhaps because of) a tremendously large body of literature, proper understanding of this particular class of cycloaddition reactions is still clouded by ambiguities and some confusion. Indeed, with examples of furan DA chemistry being scattered over different disciplines (organic chemistry/material science/heterogenous catalysis, etc.), structure–reactivity relationships have been slow to emerge.

For example, that the general, FMO‐derived theory of [4+2] cycloadditions is not always the most suitable framework to explain furan DA reactions may not have been sufficiently acknowledged in the field. Indeed, the aromaticity of the furan diene profoundly impacts many aspects of its DA chemistry: kinetics, thermodynamics, and stereoselectivity. While the general conclusions of the FMO theory do hold, e.g., that the rate of the cycloaddition is highest when electron‐donating groups are present on the diene, its predictions are less powerful, as control in furan DA chemistry is often thermodynamic and reversibility is highly relevant, even at near‐ambient temperatures.

The chemistry is also particularly sensitive to small structural variations, with the modulation of the furan ring aromaticity by substituents playing a major role in moving the reactions up and down the Gibbs free energy (of activation) scale. In addition, external factors are highly critical: often, there is only a narrow window of temperatures in which kinetics and thermodynamics are concomitantly favorable; some adducts can only be synthesized under ultrahigh pressures, or in unconventional reaction media. Appreciation of the interplay between thermodynamics and kinetics for each category of diene/dienophile combination is essential in guiding the choice of experimental conditions most likely to produce a hit and facilitate further reaction optimization. To this aim, the coupling of the DA equilibrium with an exergonic secondary transformation, however simple, can make the difference between a “possible” and an “impossible” reaction.

In this Review, we aimed to provide a fresh, critical look at a nearly complete century of furan DA chemistry, highlighting general trends in structure–reactivity–stability relationships (Figure 16), as well as emphasizing subtleties and exceptions. Thus, the classical, FMO theory suggested that the combination of electron‐rich furans with electron‐poor olefins generally features concomitantly favorable ΔG _r and ΔG ^≠ for the reaction to proceed at near ambient temperatures; steric constraints might limit the stability of the adduct in certain systems. Importantly, the cycloreversion channel is kinetically accessible and might pose selectivity issues in downstream processing. Secondly, the use of nonactivated dienophiles such as ethylene features high activation barriers that can only be crossed at temperatures above 150 °C (above 200 °C if the furan is also deactivated). At these temperatures, due to unfavorable entropic contributions, the reactions are endergonic and the adduct yields are modest. However, given the absence of steric encumbrance, the formation of ethylene adducts is the most exothermic in the series and thus the propensity of such DA products to cyclorevert is relatively low. This property can be (and has been) exploited in the design of tandem transformations. Next, the presence of electron‐withdrawing substituents on the furan diene negatively impacts both ΔG ^≠ and ΔG _r since this enhances its aromatic character. Nonetheless, in combination with activated dienophiles, adduct formation is still kinetically feasible at temperatures below 100 °C; the equilibrium conversion is generally low, and creative solutions are required to overcome these thermodynamic impediments. Finally, the combination of electron‐poor furans with nonactivated olefins, a potentially IED cycloaddition on the basis of FMO considerations, is in practice both very slow and endergonic. While these DA adducts have never been detected/reported in the literature, tandem transformations leading to more stable products (i.e. aromatics) can be designed.

Figure 16.

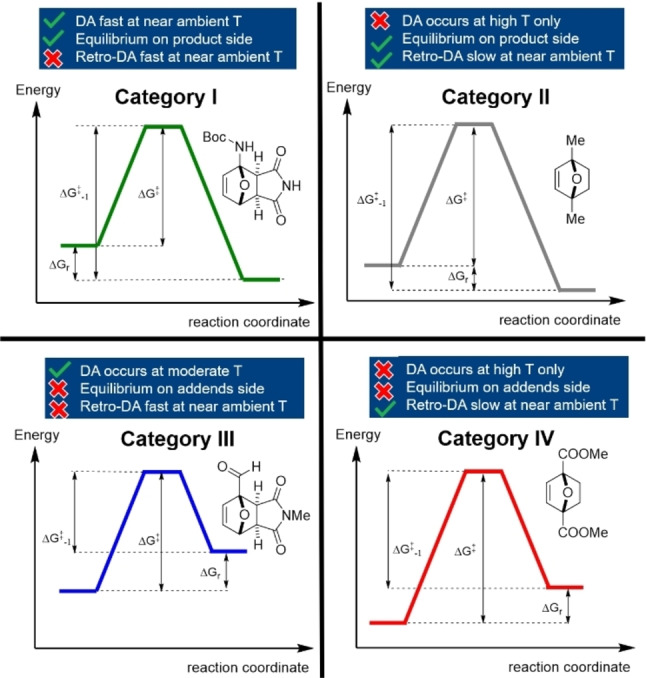
Generic structure–reactivity–stability relationship in furan DA chemistry.

The examples we showcase herein are meant to equip chemists with an updated set of tools and troubleshooting tips (i.e. analysis of kinetic plots, solvent‐free conditions, Bell–Evans–Polanyi correlations, tandem secondary transformations, etc.) to use in both drawing up new synthesis routes and optimizing them in the lab; in this way, we hope to give an impetus to the design and efficient production of the renewable chemicals of the future.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Răzvan C. Cioc obtained his PhD (2017) from Vrije Universiteit Amsterdam (The Netherlands). After gaining industrial experience in the pharmaceutical industry as a process chemist, he transitioned back to academia as a postdoctoral researcher in the group of Pieter Bruijnincx (Utrecht University), pursuing his interest in sustainable organic chemistry. His current research focuses on the conversion of biomass (primarily furans) to (novel) chemical building blocks.

Biographical Information

Marc Crockatt obtained his BSc (Hons) in Chemistry at Heriot‐Watt University, Edinburgh (Scotland). After working for 13 years in the pharmaceutical industry, he transferred to the Netherlands Organization for Applied Scientific Research (TNO), where he focuses on the development of new, sustainable technologies for the chemical industry. He is currently the Technical Lead for the Biorizon program, which is utilizing DA technology for the production of bio‐aromatics from 2nd generation feedstock streams and scaling these processes up.

Biographical Information

Jan C. van der Waal has a PhD (1998) in the catalytic application of zeolite beta titanium and other materials from the University of Delft (The Netherlands). Following a postdoctoral stay at the Shell Research and Technology Center (Amsterdam), he co‐founded Avantium Technologies (2000) and worked as an assistant professor at Delft University of Technology. He is Senior Scientist in the Sustainable Processes and Energy Systems group at TNO specializing in heterogeneous catalysis and process development for novel biomass conversions.

Biographical Information

Pieter C. A. Bruijnincx obtained his PhD degree from Utrecht University (The Netherlands) on bio‐inspired oxidation catalysis in 2007 (cum laude). After a postdoctoral stay at the University of Warwick (UK, with Prof. Sadler), he returned to Utrecht to work on catalysis for renewables. Currently, he holds the Chair of Sustainable Chemistry and Catalysis and is interested in developing new conversions and catalysts for the production of sustainable and circular chemical building blocks and materials, for example, from biomass, CO₂ or waste.

R. C. Cioc, M. Crockatt, J. C. van der Waal, P. C. A. Bruijnincx, Angew. Chem. Int. Ed. 2022, 61, e202114720; Angew. Chem. 2022, 134, e202114720.