Mapping of solar energy potential in Fiji using an artificial neural network approach

Abstract

The concerned stakeholders have been pursuing renewable energy seriously due to its overwhelming benefits. Countries that receive less solar radiation are not lagging behind as they are working to optimize the available radiation let alone of countries that receive sufficient solar radiation over long durations such as Fiji. In view of the abundancy of this energy in Fiji, the country has been working intensely on tapping the full potential of this energy, thus proposed that by 2030; more than 50% of its energy will come from renewable energy. The accurate estimation of global solar radiation determines the reliability of performance evaluation of solar energy systems. Therefore, the key interest of this study is in respect of accurate mapping of solar radiation to aid reliable solar energy design especially in siting and sizing of photovoltaic power systems. In the light of this, this work modelled solar radiation on the earth of Fiji from common meteorological and geographical data in all locations in Fiji using Artificial Neural Networks (ANN). There are different configurations of ANN but in this study, Levenberg-Marquardt (LM) and Scaled Conjugate Gradient (SCG) were selected as the learning algorithms due to the data size, speed of computation and the success of these algorithms in solar radiation modelling. Similarly, a tangent sigmoid transfer function was used in the network. In total, twelve different configurations of ANN were considered and the best configuration was selected to predict the solar radiation potential in Fiji. Since ANN requires input data to train the network, meteorological data covering 36 years (1984–2019) and geographical data from NASA database were supplied to the network. All the locations considered were distributed evenly throughout Fiji and thus covered all the four regions and 14 provinces in Fiji. The geographical and meteorological data used to train the network are month, latitude, longitude, altitude, mean temperature, relative humidity, precipitation and solar radiation. The mean squared error of 0.118838 and correlation coefficient of 0.9402 were obtained between the ANN predicted and measured solar radiation for the entire dataset. These correlation coefficients and mean squared error showed that ANN model of solar radiation in Fiji is satisfactory and thus can be used as an alternative where solar radiation data are not available. Similarly, the network produced satisfactory solar radiation result for the locations where there are no solar radiation data. To ease solar radiation assessment of all places in Fiji, the iso-lines of the solar radiation were presented in the form of monthly maps. It is believed that this prediction will aid energy stakeholders in making best decision concerning solar energy potential in Fiji thus boosting optimal utilization of the scarce resource.

Artificial neural network; ANN learning algorithms; Activation function; Solar radiation mapping; Coefficient of correlation.

1. Introduction

It is no more an illusion that renewable energy is the way as many researches have proven beyond reasonable doubt its overwhelming benefit especially its sustainability and eco-friendliness (Oyewola et al., 2022; Prasad, 1991; Woodruff, 2007; Dornan and Frank, 2011; Svantesson and Linder, 2012; Chen et al., 2015). Climate depletion and difficulty in transporting the nonrenewable energies led to sourcing of other energies that can solve these current challenges (Prasad. 1991; Bhikabhai, 2005; Woodruff, 2007; Chen et al., 2015; SPC, 2020). It is well known and established that renewable energy; reduces greenhouse gas emission such as CO₂, consolidates the insufficient non-renewable energies, eases accessibility and reduces maintenance (FREPP, 2014; Podder et al., 2015). Solar energy is not only available abundantly all over the world with less maintenance but 100% green (Fadare et al., 2010; Sofiu et al., 2011; Svantesson and Linder, 2012; Podder et al., 2015). Furthermore, the solar energy receives in 1 h on the earth is more than the total energy used by the whole population in one year which indicate that solar energy is far sufficient for human consumption. These merits can only be fully tapped if reliable knowledge of this energy technologies and resources, especially its variability are available. The absence of the knowledge of its variability with location, time, terrain and human activities makes it difficult to rely on it with total certainty, even though it is proven that the solar energy received is sufficient on the average. It should be noted that knowledge of global solar radiation is used in the design and installation of solar energy, solar still, agricultural greenhouse, drying processes and many others (Cooper, 1969). While the solar radiation received on the earth varies with time, it is also absorbed, reflected, and transmitted as it passes through the planet earth. It is worth to note that ozone, water vapour, carbon dioxide, oxygen, nitrogen and others absorb about 16% of the extraterrestrial solar radiation in the atmosphere which worsen the variability of the solar radiation (Black, 1956; Sofiu et al., 2011). Besides, terrain, human activities, nature and many other things affect the amount and quality of solar radiation received on the earth. Summarily, to make best decision in solar energy installation as well as making it widely available, satisfactory mapping and prediction of it is required for almost all regions and all year round.

Almost all nations have been gathering weather data from meteorological stations, many of these locations are without solar radiation data and in some cases, the pyranometer has stopped working which make many locations without this meteorological data (Prasad 1991; Sofiu et al., 2011). In the light of this, the solar radiation of other locations is projected from the nearby meteorological stations using this data. This has led to modelling of this meteorological data to offset the unavailability of solar radiation. It is worth noting that modelling involves finding mathematical relationship between one (univariate) or more (multivariate) dependent variable(s) with one or more independent variable(s). In order to achieve this, many methods have been explored in the past. For instance, right from the early days, empirical method has been explored which were found to be reasonably accurate in the absence of solar radiation data (Black 1956; Hargreaves and Allen, 2003; Adaramola, 2012). One of the early works of Black (1956) correlated solar radiation with cloud amount using quadratic regression fit and plotted the isopleths of solar radiation based on data collected from five continents. Based on this, it was discovered that global solar radiation on the sea is lower than on the land. This finding was attributed to the high relative humidity above the sea. Similarly, George et al. (1966) generated world daily means distribution of solar radiation but concluded that due to scarcity of data in many locations, the map cannot be said to be very accurate. Thus, it can be said that regional analysis is required for reliable solar radiation mapping. Fortunately, due to the availability of computer nowadays, computer aided methods such as ANN and even complex analysis of the early known methods are used leading to improved accuracy with less effort and time. In the early days, Kalogirou (2001) reviewed the application of artificial neural networks in renewable energy systems and concluded that ANN is useful in system modelling such as complex renewable energy resources mappings. In addition, this work showed that errors from using ANN are within tolerant limit.

Furthermore, tackling the stochastic nature of this resource, Barrera et al. (2020) with the help of improved machine learning algorithm made use of open data and ANN in the solar energy prediction. They concluded that their approach produced better result than others with MSE of 0.04 as compared to others of 0.05. In Nigeria, Fadare (2009) modelled solar energy potential using ANN with the aid of MatLab®. The work resulted in correlation coefficient of 90% indicating that ANN can be used with good accuracy and relative certainty in solar radiation mapping. Similarly, for the whole Africa, Fadare et al. (2010) used ANN in the modelling of solar energy potential using data from 172 locations spanning 22 years. Their result shows that MSE ranged from 0.002 to 0.004, which indicate the applicability of ANN in solar radiation modelling in Africa. In addition, in Algeria, Mellit et al. (2006) combined wavelet theory with ANN in the forecasting of daily total solar-radiation. The result of this study is approximately 97% accurate and the MAPE is not more than 6%, which indicate the applicability of ANN in solar radiation forecasting. It should be noted that 19 years data were used and they asserted that their design was the best in comparison with other ANN networks. In turkey, Sozen et al. (2004) obtained R² of 99.893% for solar potential mapping using ANN. Moreover, in Europe, Barrera et al. (2020) applied ANN and open data to predict solar energy. Their result gives MSE of 0.04, thus indicating higher reliability to other proposed methods with MSE 0.055. It is also worth noting that in India, Krishnaiah et al. (2007) obtained average MBE, RMSE and R-squared of 0.3133%, 4.61% and 0.999954, respectively for global solar radiation estimation using ANN and concluded that ANN is capable of generalization over unseen data and produce accurate prediction. Benkaciali et al. (2016) estimated global solar radiation in Algeria using ANN techniques. Their result showed that ANN (R² = 98%) is better than the quadratic model (R² = 97.22%). It is worth to note that other studies such as Hontoria et al. (2002), Hassan and Ali (2017) and Notton et al. (2019) have used ANN in one form or the other to estimate global solar radiation for specific region or country. The consensus that stemmed out from the afore-mentioned works is that accurate mapping and prediction of solar radiation is one of the most important factors in siting and sizing solar PV array.

Fiji comprises of more than 330 islands with the island of Viti Levu and Vanua Levu as the main island having 87% of the inhabited areas. However, being one of the pacific countries where more than 55% of the population except Papua New Guinea lives within 1 km from the sea, the climatic impact is high and even worse due to less diversification of their economy (World Bank, 2017). For instance, Agrawala et al. (2003) carried out the effect of development and climate change in Fiji. They inferred that based on current climatic trend, mean temperature is projected to increase by 0.9 and 1.5 by 2050 and 2100, respectively. Present assessment of this impact shows that climate change has already been felt in the food and water security, reef and fisheries productivity and many more as it is been felt all around the world. Furthermore, as at present, the hydropower is the main source of electricity in Fiji but due to high cost of grid extension, most other areas could not be connected to the grid because they are highly dispersed islands. It is worth to note that the energy issue is complicated because Fiji do not produce fuel (diesel, petrol and kerosene) thus rely on fuel importation that fluctuate in price. This has led Fiji to look into renewable energy as a substitute since over three decades ago (Siwratibau, 1982; Prasad, 1991). Prasad (1991) who carried out an overview of renewable energy resources in the South Pacific Island countries with biasness for Fiji conducted one of the early works on renewable energy assessment in Fiji. The work showed that renewable energy resources are abundant in the south pacific countries. However, due to the limited number of field studies and state of technology as at then, best decision could not be reached, since other potential locations for renewable energy are not assessed. Therefore, literature are sparse on the mapping of solar radiation for all locations in Fiji despite its importance. This work is timely and important, as it will aid energy stakeholders in decision making in the face of scare resources. In the light of this, this present study, which extend the work of Oyewola et al. (2022) that used empirical models to predict global solar radiation in Fiji Islands, models solar energy resource in Fiji using ANN. This study fills both local and academic gaps. To the best of the authors' knowledge, no literature has investigated the solar radiation resource of the entire Fiji using ANN. Besides, this study investigates the used of the readily available meteorological data in Fiji for solar radiation prediction using ANN. This is important because Fiji is an island surrounded by body of waters thus it is under the effect of this water bodies. In addition, this study will generate iso-rad maps (solar radiation map of every coordinate in Fiji) with the associated statistics, which will aid assessment of solar energy potential of every region in Fiji with their level of reliability.

2. Materials and method

2.1. ANN model description

Based on the results from different applications, Artificial neural networks (ANNs) has been proven to be a good tool in modelling complex problems such as data fitting, pattern recognition, identification, classification, speech, vision, control systems and thus it has been extended to other areas. It has been extensively applied in the study and installation of renewable energies (Hontoria et al., 2002; Sozen et al., 2003; Krishnaiah et al., 2007; Fadare, 2009; Notton et al., 2018; Benali et al., 2018). The ANNs has proved to be more versatile than human brains and other mathematical methods such as regression analysis. It is an offset of biological neurons, which get information and then process the information non-linearly before responding to the stimulus. The complexity of this biological system leads to the theory of ANN. Similarly, the basic processing function of the ANN is the neuron. As biological system requires input, processing neuron and output so as the ANN, thus the ANN consists of an input layer, hidden layers consisting of neurons, and an output layer. The internal processing of this network is termed ‘black-box’ because it is not explicit and thus it can perform non-linear complex analysis by relating a multidimensional input onto another multidimensional output without prior information about their relationship. In view of this capability, ANN finds successfully application in the field of renewable energy and climate changes for modelling.

Constituently, ANN consists of weight, input and biases, output, summing junction and transfer function. The neuron is the main building block of ANN consisting of input, hidden, and output layers. Training process build up the knowledge of the network learning by fine-tuning the weights. The network weights are updated until the network build a satisfactory set target by the user based on the input. Out of the many ANN algorithms, the success of the back-propagation in many applications has led to its adoption. The backpropagation algorithm updates the weights in feedforward neural nets consisting of several layers. In Feedforward neural network, the information moves from the preceding layer to the next layer. In the back-propagation algorithm, the network weights adjust along the negative of the Jacobian of the mean squared error to reduce the error between the output and target. These linkages have unique weights that enforce some relation between the connections. Back-propagation is a supervised training algorithm with multiple-layer networks. ANN is said to be supervised learning if the target is supplied, while it is unsupervised if the target is not supplied to the network. Data assembling/collection, network creation, network configuration, weight and biases initialization, network training, network validation and network simulation are the six basic steps in ANN training processes. The essence of training the network is to get a network that map an output state, called target states, to each of several input states. Sufficient training is required for the network to solve complex problem. Despite the black-box process of ANN, it is known to be capable and time saving in modelling of complex systems compared to other mathematical models. Figure 1 shows an ANN schematic diagram that consist of input, hidden and output layers in which the input with the biases transformed by its corresponding weight and further processed with the transfer functions within each layer before the final output. The bias, which is usually constant serve as a buffer to the model and thus offset error in the input elements. Similarly, transfer function, which is either a linear, or a non-linear function transforms the input to a form. The weights may be randomly chosen or uniquely supplied. A carefully selected weights network converges faster than a randomly chosen weight though it requires great deal of work to identify the best initial weights.

Figure 1.

ANN schematic diagram showing its components.

All networks have unique learning algorithm. One in which the gradient and Jacobian with respect to network weights are computed backward through the network is called back-propagation. All of the algorithms have their pros and cons. For Instance, Levenberg-Marquardt (LM) is the best for data fitting/function approximation but for a fewer than 100 weights, while Scaled Conjugate Gradient (SCG) is not as good as LM but produce better result when the weights are larger than 100 (Sozen et al., 2004; Beale et al., 2010). Some are good for pattern recognition but perform woefully for function approximation. Most often, LM and SCG are mainly used for function approximation because of their accuracy and speed (Sozen et al., 2004; Fadare, 2009). The inputs and outputs to the net are usually scaled into the range ±1. The input layer has no processing neurons but only to store the scaled input values. The hidden and the output layers neurons multiply the input with the weight and sum all the results, then transform by the transfer function.

2.2. Data collection and locations

The meteorological data consisting of mean temperature, relative humidity, precipitation, monthly mean daily solar radiation as well as geographical data consisting of latitude, longitude and altitude are the input parameters used for this present model. The meteorological and geographical data used for this work were extracted from NASA surface meteorology website (NASA, 2021). Table 1 shows the cities/towns in Fiji with their latitude, longitude and altitude used in this model. The map in Figure 2 shows the geographical locations used in this work.

Table 1.

Cities/Towns in Fiji with their information used for this study.

S/N	City	Lat.(deg)	Long.(deg)	Altitude(m)
1	Tavuki	−19.1253	178.1317	5.51
2	Serua	−18.0563	177.8717	88.8
3	Nakelo	−18.055	178.6241	12.13
4	Suva	−18.1248	178.4501	105.92
5	Malomalo	−18.1249	177.3581	37.07
6	Wainimala	−17.8371	178.0235	177.39
7	Nawaka	−17.8114	177.4338	54.39
8	Ovalau	−17.6799	178.7874	28.77
9	Ba	−17.5382	177.6878	140.09
10	Rakiraki	−17.3454	178.1789	95.09
11	Koro	−17.3012	179.408	14.73
12	Cakaudove	−16.9009	179.9523	41.89
13	Yasawa	−16.7881	177.5074	2.43
14	Bua	−16.7598	178.7106	35.89
15	Labasa	−16.4271	179.3683	45.2
16	Itutiu	−12.5035	177.0827	0.08
17	Macuata	−16.4865	179.2847	45.2
18	Vuya	−16.9317	178.6916	35.89
19	Nakorotubu	−17.5536	178.3402	177.39
20	Malolo	−17.7414	177.1694	54.39
21	Lomaivuna	−17.9705	178.421	177.39
22	Sawakasa	−17.7266	178.5508	28.77
23	Navosa	−17.9865	177.6581	140.09
24	Tavuki	−19.1253	178.1317	5.51
25	Nuku	−18.0993	178.044	105.92
26	Baravi	−18.1412	177.7354	88.8
27	Veivatuloa	−18.1973	178.216	105.92
28	Lakeba	−18.2147	178.7941	12.13
29	Bega	−18.3828	178.1194	105.92
30	Wainikoroiluva	−18.0693	178.0287	105.92
31	Nadi	−17.8	177.4356	54.39

Figure 2.

Locations of the cities/towns used in this model on the Map of Fiji.

2.3. Design of the artificial neural network model

The aim of this work is to model solar radiation resource across Fiji using ANN. Out of the many ANN methods; feed forward back propagation was adopted for this work due to its popularity and applicability in solar radiation estimation (Sujan et al., 2019; Shboul et al., 2021). Feed-forward back-propagation (FFBP) neural network is composed of neuron processes. The output of any neuron is equal to the activation function transformation of the summation of the weights multiply by the neuron inputs, plus the biases. The neuron processes structure is shown in Figure 3.

Figure 3.

Structure of Neuron processes.

Eq. (1) gives the mathematical description of this neuron processes,

$$\theta =\phi \left(b+\sum _{i=1}^n{w}_i{a}_i\right)$$ (1)

where, θ = neuron output value, w_i = weights of inter-neurons connection, b = neuron bias value, a_i = output values of the previous neurons, n = the total number of input neurons, φ = the activation function. The sigmoid function (log and tan) is good for pattern recognition while linear function is good for function approximation. In view of this, the tan-sigmoid and pure linear were used for the hidden layer and the output layer respectively in this study.

The training of the network involves identification of the appropriate weights that will produce satisfactory result. The optimized weight is arrived through comparison of the network output with the target output using mean squared error as the criteria (Eq. (2)). This process is cumbersome without the use of training algorithm, thus, training algorithms such as Conjugate Gradient, Levenberg-Marquardt (LM), and Newton's method are devised.

$$F=mse=\frac{1}{N}\sum _{i=1}^N{\left(e_i\right)}^2=\frac{1}{N}\sum _{i=1}^N{(t_i-{\theta }_i)}^2$$ (2)

where F = mean squared error (MSE) function, ti = target value, θi = network output value. Sometimes the initial configuration may not produce satisfactory result, so the configuration is modified through addition/removal of neurons and layers and using different training algorithm until satisfactory result is obtained or the network cannot be further optimized.

Artificial neural network of the multi-layer feed-forward back-propagation with different architecture were used for this work. As shown in Figure 1, the network consists of input layer, hidden layer and output layer with seven elements supplied at the input as well as one element as the target (output). The number of input elements is fixed, while the size of hidden layer was varied from 1 to 2 with number of neurons varied from 10 to 20 with a step of 5. The hidden layer and the output layer have tangent sigmoid (tansig) and linear (purelin) transfer functions, respectively, while the input is without transfer function.

2.4. Training and testing of the model

Tangent Sigmoid (tansig) transfer function requires the input and target data sets to be normalized to the range −1 to +1, in view of this; these data sets were normalized to this range. The size of the hidden layer and neurons in the hidden layers were set. Also, based on both the report of ANN Toolbox documentation and previous applications, Levenberg–Marquardt (LM) and Scaled Conjugate Gradient (SCG) learning algorithms were said to be the best for this type of data modelling and in the light of this, the training algorithm was limited to this two (Hassan and Ali, 2017). Early stopping was automatically provided to avoid overfitting for these two supervised networks (network with target). It is important to note that the combinations of these two algorithms resulted into 12 networks with variation in the numbers of hidden layers and neurons. These 12 networks were simulated and their results determine the most suitable network for this model. All the networks were tested 10 times and their statistics are used to select the best architecture. The training dataset takes 70%, testing data takes 15%, while validation dataset takes the remaining 15% of all the data (55,296 data from 16 locations, 36 years, 12 months and 8 other meteorological and geographical information). Coefficient of correlation and Mean Squared Error (MSE) were used as the performance evaluation of all the networks. The different resulting networks and their results are given in Table 2.

Table 2.

Statistics of neural network performance for the dataset.

Training algorithm	Size of hidden layer	Size of neuron in the hidden layer	Coefficient of correlation (R-value)								Mean squared error (MSE)
			Training data				All data
			Mean	std	Max	Min	Mean	std	Max	Min	Mean	std	Max	Min
LM	1	20	0.94055	0.001279	0.94246	0.93819	0.939135	0.000748	0.94047	0.93784	0.118962	0.004079	0.12507	0.11161
		15	0.939863	0.001341	0.94201	0.93713	0.938104	0.000677	0.93904	0.9369	0.122699	0.007997	0.13602	0.10816
		10	0.937476	0.001164	0.93964	0.93545	0.936163	0.000934	0.93758	0.93413	0.127499	0.003904	0.13295	0.11952
	2	20 by 20	0.94319	0.00064	0.94451	0.94238	0.94084	0.000596	0.94186	0.93982	0.120795	0.005911	0.13084	0.11182
		15 by 15	0.942289	0.001785	0.94571	0.93993	0.940412	0.000978	0.94267	0.93884	0.122108	0.004781	0.1301	0.11279
		10 by 10	0.941227	0.000832	0.94295	0.93967	0.939821	0.000606	0.94099	0.93897	0.118838	0.002941	0.12354	0.11267
SCG	1	20	0.917034	0.007736	0.93144	0.9006	0.916749	0.007709	0.93091	0.90041	0.157926	0.01696	0.19535	0.12816
		15	0.912231	0.006038	0.91826	0.89643	0.912168	0.005652	0.91843	0.89734	0.164146	0.010635	0.18692	0.14858
		10	0.908912	0.00523	0.9206	0.9027	0.908901	0.004398	0.91851	0.90297	0.169053	0.01151	0.19026	0.15578
	2	20 by 20	0.919298	0.004164	0.92506	0.91062	0.918904	0.003736	0.92508	0.91201	0.15345	0.006737	0.1685	0.14288
		15 by 15	0.912044	0.013226	0.92305	0.87585	0.911392	0.012733	0.92134	0.87728	0.165776	0.02495	0.23228	0.14435
		10 by 10	0.910744	0.007895	0.92179	0.89556	0.909868	0.008372	0.92073	0.89374	0.168445	0.013742	0.19757	0.1536

2.5. Evaluation criteria

Eqs. (3) and (4) are the two statistical parameters used in evaluating the accuracy of the different network configuration of this present model. These provide information about measure of accuracy of the model. The smaller the MSE, the better the model, while the higher the correlation coefficient, the better the model.

Mean Squared Error (MSE)

$$MSE=\frac{1}{P}\sum {(H_{m-mes}-H_{m-est})}^2$$ (3)

Coefficient of Correlation (R)

$$R=\frac{\sum (H_{m-est}^i-{\overline{H}}_{m-est}^i)(H_{m-mes}^i-{\overline{H}}_{m-mes}^i)}{\sqrt{\sum {(H_{m-est}^i-{\overline{H}}_{m-est}^i)}^2\sum {(H_{m-mes}^i-{\overline{H}}_{m-mes}^i)}^2}}$$ (4)

Where;

$$H_{m-est}=estimatedvalueoftheglobalsolarradiation$$

$$H_{m-mes}=measuredvalueoftheglobalsolarradiation$$

P = number of the data.

3. Results and discussion

3.1. Network optimization

Twelve different configurations were investigated for the optimization of the network. The twelve configurations are six variations of LM and six variations of SCG. The differences in these configurations are training algorithms (LM and SCG), number of hidden layers and number of neurons in the hidden layers. The number of hidden layers is a function of complexity of the problem. Similarly, the number of neurons improves the accuracy of the modelling. The computational resources, accuracy of the modelling and marginal changes in the result with increasing the hidden layers and neurons dictated the limit on the number of the hidden layers and neurons. The twelve configurations are shown in the rows of Table 2. The first configuration, LM with 1 hidden layer and 20 neurons, is shown in row 1 of Table 2. The second configuration, LM with 1 hidden layer and 15 neurons, is shown in row 2 of Table 2. The third configuration, LM with 1 hidden layer and 10 neurons, is shown in row 3 of Table 2. The fourth configuration, LM with 2 hidden layer and 20 by 20 neurons in the two hidden layers, is shown in row 4 of Table 2. The fifth configuration, LM with 2 hidden layer and 15 by 15 neurons in the two hidden layers, is shown in row 5 of Table 2. The sixth configuration, LM with 2 hidden layers and 10 by 10 neurons in the two hidden layers, is shown in row 6 of Table 2. The seventh configuration, SCG with 1 hidden layer and 20 neurons, is shown in row 7 of Table 2. The eighth configuration, SCG with 1 hidden layer and 15 neurons, is shown in row 8 of Table 2. The ninth configuration, SCG with 1 hidden layer and 10 neurons, is shown in row 9 of Table 2. The tenth configuration, SCG with 2 hidden layer and 20 by 20 neurons in the two hidden layers, is shown in row 10 of Table 2. The eleventh configuration, SCG with 2 hidden layer and 15 by 15 neurons in the two hidden layers, is shown in row 11 of Table 2. The twelfth configuration, SCG with 2 hidden layers and 10 by 10 neurons in the two hidden layers, is shown in row 12 of Table 2.

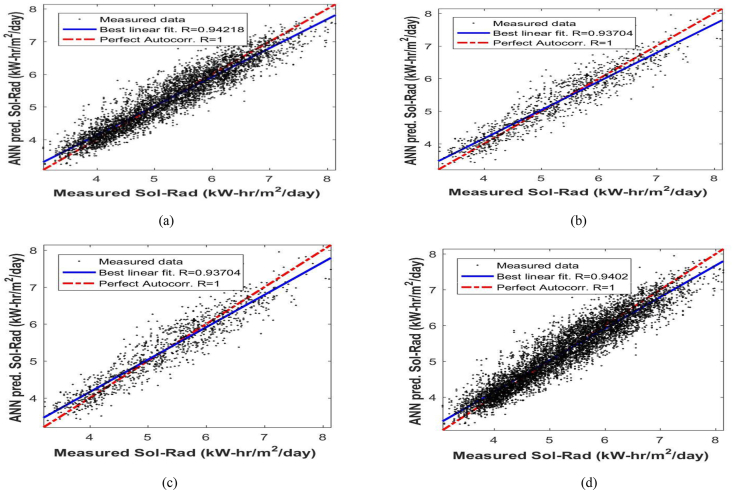
Table 2 shows the results of the optimization of the networks with different configurations. The LM training algorithm network with 10 by 10 neurons in the two hidden layers produced the best prediction based on the correlation coefficient (R-value) and Mean Squared Error (MSE). Similarly, the correlation coefficient (R-value) between the measured and ANN predicted monthly mean global solar radiation for training, validation, testing and entire dataset are presented in Figure 4 for the optimized configuration. It should be noted that 0.94218, 0.93704, 0.93704 and 0.9402 were obtained for the R-values of the training, validation, testing and the entire dataset, respectively, while the MSE for this network is 0.118838 (kW-hr/m²/day)². These results prove that ANN can be used to model solar radiation with satisfactory result in the absent of field data in Fiji despite being a pacific island with high influence of water bodies.

Figure 4.

Performance result of the best training network for prediction of solar radiation in Fiji a) Training dataset, b) Validation dataset, c) Testing dataset and d) Entire dataset.

Table 3 shows the effect of training, testing, and validation data ratio on the network performance for the best configuration selected in Table 2. The table shows that training ratio has the highest effect on the accuracy of the network because as the training data ratio increase the accuracy increase. In addition, the table shows that training data ratio above 0.25 gives reasonable result.

Table 3.

Effect of training, testing and validation data ratio on the R and MSE.

No.	% of Training data	% of testing data	% of Validation data	R	MSE
1	5	50	45	0.89518	0.0634
2	15	45	40	0.92527	0.105
3	25	40	35	0.93334	0.109
4	35	35	30	0.9374	0.106
5	45	30	25	0.9371	0.109
6	55	25	20	0.9388	0.110
7	65	20	15	0.9402	0.110
8	75	15	10	0.9391	0.110
9	85	10	5	0.9407	0.110

3.2. Mapping of solar radiation in Fiji

After certifying the reliability of the network, the ANN was used to predict (map) the monthly average daily solar radiation for other locations in Fiji. It is worth to note that the monthly solar radiation maps for Fiji were plotted from the input of the meteorological data to the ANN. The monthly mean solar radiation and the comparison between the measured and ANN predicted solar radiation for all the month of the year (January to December) were plotted as iso-lines as shown in Figures 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, and 15 using ArcMap®.

Figure 5.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of January in Fiji.

Figure 6.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of February in Fiji.

Figure 7.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of March in Fiji.

Figure 8.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of April in Fiji.

Figure 9.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of May in Fiji.

Figure 10.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of June in Fiji.

Figure 11.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of July in Fiji.

Figure 12.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of August in Fiji.

Figure 13.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of September in Fiji.

Figure 14.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of October in Fiji.

Figure 15.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of November in Fiji.

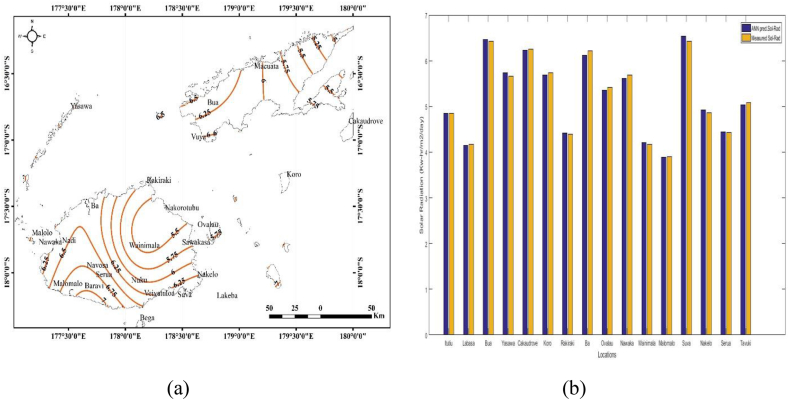
Figure 5a shows the monthly mean of daily solar radiation map for the month of January, while Figure 5b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of January. Figure 5a shows that solar radiation decreases from 7 kW-hr/m²/day in the southwestern region to 5.5 kW-hr/m²/day in the northeastern region of Viti Levu (main island at the bottom of the map). While, the solar radiation decreases from 6.6 kW-hr/m²/day in the southwestern region to 5 kW-hr/m²/day in the northeastern region of Vanua Levu (Main Island at the top of the map). These indicate that the southwestern region receives more sunlight than the northeastern region. This is because sun rises in the east and takes an arc through the northern direction to set in the west for location in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 5b is 0.003 (kW-hr/m²/day)².

Figure 6a shows the monthly mean of daily solar radiation map for the month of February, while Figure 6b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of February. Figure 6a shows that solar radiation decreases from 6.75 kW-hr/m²/day in the southwestern region to 5.25 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decreases from 6.25 kW-hr/m²/day in the southwestern region to 4.75 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the southwestern region receives more sunlight than the northeastern region. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 6b is 0.0028 (kW-hr/m²/day)².

Figure 7a shows the monthly mean of daily solar radiation map for the month of March, while Figure 7b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of March. Figure 7a shows that solar radiation decrease from 6 kW-hr/m²/day in the southwestern region to 4.75 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decrease from 5.75 kW-hr/m²/day in the southwestern region to 4.75 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the southwestern region receives more sunlight than the northeastern region. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 7b is 0.0035 (kW-hr/m²/day)².

Figure 8a shows the monthly mean of daily solar radiation map for the month of April, while Figure 8b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of April. Figure 8a shows that solar radiation decrease from 5 kW-hr/m²/day in the western region to 4.25 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decrease from 5 kW-hr/m²/day in the southwestern region to 4.5 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the western region receives more sunlight than the northeastern region. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 8b is 0.00056271 (kW-hr/m²/day)².

Figure 9a shows the monthly mean of daily solar radiation map for the month of May, while Figure 9b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of May. Figure 9a shows that solar radiation decrease from 4.5 kW-hr/m²/day in the northwestern region to 4 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decrease from 4.5 kW-hr/m²/day in the northwestern region to 4 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the northwestern region receives more sunlight than the northeastern region. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 9b is 0.0025 (kW-hr/m²/day)².

Figure 10a shows the monthly mean of daily solar radiation map for the month of June, while Figure 10b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of June. Figure 10a shows that solar radiation decrease from 4.25 kW-hr/m²/day in the northwestern region to 3.75 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decrease from 4.25 kW-hr/m²/day in the northeastern region to 3.75 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the northwestern region receives more sunlight than the northeastern region. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 10b is 0.0017 (kW-hr/m²/day)².

Figure 11a shows the monthly mean of daily solar radiation map for the month of July, while Figure 11b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of July. Figure 11a shows that solar radiation decrease from 4.5 kW-hr/m²/day in the northwestern region to 4 kW-hr/m²/day in the eastern region of Viti Levu while the solar radiation decrease from 4.5 kW-hr/m²/day in the northeastern region to 4 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the northwestern region receives more sunlight than the northeastern region. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 11b is 0.0018 (kW-hr/m²/day)².

Figure 12a shows the monthly mean of daily solar radiation map for the month of August, while Figure 12b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of August. Figure 12a shows that solar radiation decrease from 4.75 kW-hr/m²/day in the southeastern region to 4.25 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decrease from 5 kW-hr/m²/day in the northeastern region to 4.25 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the southeastern region receives more sunlight than the northeastern region. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 12b is 0.0024 (kW-hr/m²/day)².

Figure 13a shows the monthly mean of daily solar radiation map for the month of September, while Figure 13b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of September. Figure 13a shows that solar radiation decrease from 5.5 kW-hr/m²/day in the western region to 4.75 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decrease from 5.75 kW-hr/m²/day in the northwestern region to 4.75 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the eastern region receives more sunlight than the western. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 13b is 0.0029 (kW-hr/m²/day)².

Figure 14a shows the monthly mean of daily solar radiation map for the month of October, while Figure 14b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of October. Figure 14a shows that solar radiation decrease from 6.5 kW-hr/m²/day in the southwestern region to 5.25 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decrease from 6.25 kW-hr/m²/day in the northwestern region to 5.5 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the eastern region receives more sunlight than the western. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 14b is 0.0027 (kW-hr/m²/day)².

Figure 15a shows the monthly mean of daily solar radiation map for the month of November, while Figure 15b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of November. Figure 15a shows that solar radiation decrease from 6.75 kW-hr/m²/day in the southwestern region to 5.5 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decrease from 6.5 kW-hr/m²/day in the northwestern region to 5 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the eastern region receives more sunlight than the western. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 15b is 0.0036 (kW-hr/m²/day)².

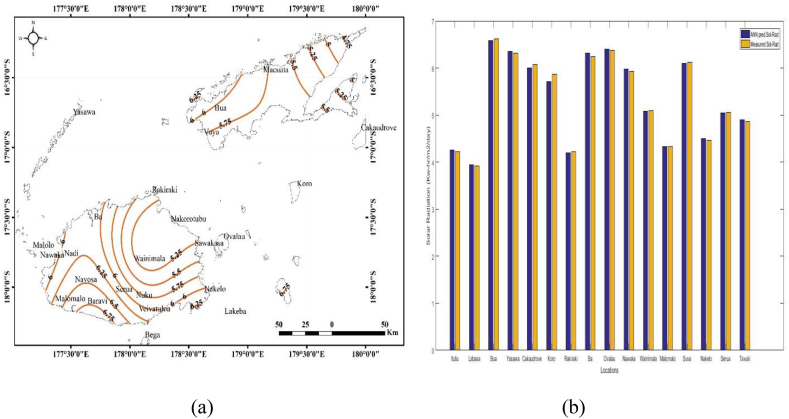
Figure 16a shows the monthly mean of daily solar radiation map for the month of December, while Figure 16b shows the comparison between the ANN predicted and measured monthly mean of daily solar radiation of some selected locations in Fiji for the month of December. Figure 16a shows that solar radiation decrease from 7 kW-hr/m²/day in the southwestern region to 5.5 kW-hr/m²/day in the northeastern region of Viti Levu while the solar radiation decrease from 6.75 kW-hr/m²/day in the northwestern region to 5 kW-hr/m²/day in the northeastern region of Vanua Levu. These indicate that the eastern region receives more sunlight than the western region. This is because sun rises in the east and takes an arc through the northern direction to set in the west in the southern hemisphere. Besides, the earth revolution and tilt angle contribute to this variation. Also, the MSE of the comparison between the ANN predicted value and measured value of Figure 16b is 0.0016 (kW-hr/m²/day)².

Figure 16.

a) Solar radiation map and b) Comparison between measured and ANN predicted solar radiation (kW-hr/m²/day); for the month of December in Fiji.

Summarily, the maps show that solar radiation varies significantly across the regions as well as on a monthly basis. Table 4 shows the maximum, minimum, average and standard deviation of solar radiation for all the twelve months in Fiji. The highest value of 7 kW-hr/m²/day was obtained in the month of December, while minimum value of 3.6972 kW-hr/m²/day was obtainable in the month of June. The mean squared errors of all the months for the sampled locations vary from 0.000556271 to 0.0036, which indicate that ANN is satisfactory for solar radiation mapping.

Table 4.

Statistics of Solar radiation in Fiji from 1984-2019.

Month	Solar radiation kW-hr/m2/day
	Max	Min	Average	std
January	6.6239	5.6658	6.1659	0.3627
February	6.3358	5.3619	5.8905	0.3553
March	5.7078	4.9944	5.4452	0.2578
April	5.0886	4.3989	4.7766	0.2291
May	4.625	4.0008	4.259	0.2059
June	4.3411	3.6972	3.9449	0.2317
July	4.61	3.9058	4.1703	0.2505
August	5.11	4.3244	4.6717	0.2717
September	5.6978	4.8886	5.2802	0.2761
October	6.2558	5.42	5.8953	0.2925
November	6.4853	5.6069	6.1372	0.3421
December	6.6953	5.7206	6.2409	0.3811

Furthermore, the maps show that southwestern region has the highest solar radiation, while the northeastern region has the lowest solar radiation. For instance, the solar radiation ranges from 6.75 (kW-hr/m²/day) in the western region to 5 (kW-hr/m²/day) in the north eastern region of Vanua Levu in December, while it ranges from 7 (kW-hr/m²/day) in the south-western region to 5.5 (kW-hr/m²/day) in the north-eastern region of Viti Levu in the month of December. In addition, it ranges from 4.25 (kW-hr/m²/day) in the southwestern region to 3.75 (kW-hr/m²/day) in the northeastern region of Vanua Levu in June, while it ranges from 4.25 (kW-hr/m²/day) in the western region to 3.75 (kW-hr/m²/day) in the northeastern region of Viti Levu in the month of June. These two months of December and June served as the upper boundary and lower boundary when solar radiation is at maximum and minimum respectively.

4. Conclusions

The present study adopted Levenberg-Marquardt (LM) and Scaled Conjugate Gradient (SCG) learning algorithms of Artificial Neural Network (ANN) to model solar radiation using common meteorological and geographical data in all locations in Fiji. This multilayered, feed-forward, back-propagation ANN with different configurations were used for this model. In general, the result of this study is satisfactory. Therefore, solar radiation can be predicted (mapped) from common meteorological data and geographical information such as temperature, elevation, month of the year, relative humidity, precipitation, longitude and latitude using ANN approach. The result showed that the monthly mean solar radiation potential in Fiji ranges from maximum in the month of December with 7 kW-hr/m²/day to minimum of 3.6972 kW-hr/m²/day in the month of June. Similarly, the solar radiation ranges from 6.75 kW-hr/m²/day in the western region to 5 kW-hr/m²/day in the north eastern region of Vanua Levu in December, while it ranges from 7 kW-hr/m²/day in the south-western region to 5.5 kW-hr/m²/day in the north-eastern region of Viti Levu in the month of December. In addition, it ranges from 4.25 kW-hr/m²/day in the southwestern region to 3.75 kW-hr/m²/day in the northeastern region of Vanua Levu in June, while it ranges from 4.25 (kW-hr/m²/day) in the western region to 3.75 (kW-hr/m²/day) in the northeastern region of Viti Levu in the month of June. These two months of December and June served as the upper boundary and lower boundary when solar radiation is at maximum and minimum, respectively. Therefore, the model can be easily used for estimation of solar radiation for preliminary design of solar applications. Summarily, the result showed that ANN can be used to predict solar radiation from other common meteorological data and this makes solar radiation potential assessment of other location within Fiji possible thus, aids energy stakeholders in taking best decision leading to optimal utilization of the scarce resource in the face of numerous wants.

Declarations

Author contribution statement

Olanrewaju M. Oyewola: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Olawale S. Ismail: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Malik O. Olasinde: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Olusegun O. Ajide: Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data included in article/supplementary material/referenced in article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.