Abstract
Health insurance markets with community‐rated premiums typically include risk adjustment (RA) to mitigate selection problems. Over the past decades, RA systems have evolved from simple demographic models to sophisticated morbidity‐based models. Even the most sophisticated models, however, tend to overcompensate people with persistently low spending and undercompensate those with persistently high spending. This paper compares three methods that exploit spending‐level persistence for improving health plan payment systems: (1) implementation of spending‐based risk adjustors, (2) implementation of high‐risk pooling for people with multiple‐year high spending, and (3) indirect use of spending persistence via constrained regression. Based on incentive measures for risk selection and cost control, we conclude that a combination of the last two options can substantially outperform the first, which is currently used in the health plan payment system in the Netherlands.
Keywords: health insurance, risk adjustment, risk selection, risk sharing
1. INTRODUCTION
Several health insurance systems rely on premium‐rate restrictions to promote fairness and/or mitigate reclassification risk. Examples include mandatory health insurance schemes in Belgium, Germany, Israel, the Netherlands, and Switzerland; voluntary health insurance markets in Ireland and Australia; and Medicare Advantage and the Marketplaces in the United States (McGuire & van Kleef, 2018). A well‐known problem of premium‐rate restrictions, however, is that they confront insurers with predictable profits and losses, which generate incentives for risk selection. Though insurers in the aforementioned systems are not allowed to deny coverage, selection can take place indirectly, for example, via design of the insurance plans.
Most health insurance systems with rate restrictions rely on risk adjustment (RA) to compensate insurers for predictable profits and losses. Over the past decades, the RA formulas used for this purpose have evolved from simple demographic models to sophisticated morbidity‐based models using indicators based on diagnostic information (Ellis et al., 2018). Even morbidity‐based models, however, are unlikely to fully eliminate predictable profits and losses. The simple explanation is that these models are subject to limitations. For example, morbidity classifications are typically based on diagnoses from “just” 1 year (i.e., either the current year or the previous year). Moreover, they generally do not include diagnostic codes that are ambiguous and/or vulnerable to upcoding.
For several reasons, remaining predictable profits and losses can be problematic. First, to the extent that profitable and unprofitable people sort into different insurance plans, the premiums for these plans will not only reflect “plan value” but also the effect of selection. This can lead consumers to choose the “wrong” plans (Akerlof, 1970; Einav & Finkelstein, 2011). Second, insurers have disincentives to be responsive to the preferences of unprofitable risk groups (Glazer & McGuire, 2000; Rothschild & Stiglitz, 1976).
An effective indicator for identifying predictable profits and losses net of RA is “spending in prior years.” Empirical research has shown that high spending is to some extent persistent (Monheit, 2003; van Veen, 2016). Other papers have shown how morbidity‐based RA undercompensates people with multiple‐year high spending (van Kleef & van Vliet, 2012) and overcompensates those with multiple‐year low spending (Eijkenaar et al., 2019). These findings indicate that spending persistence has indeed potential to identify predictable profits and losses net of RA and thus provides a starting point for reducing these profits and losses. A key question, however, is how to use this information in the payment system?
One way to exploit the predictiveness of “spending persistence” in the health plan payment system is to implement risk adjustors that explicitly flag persistently low and/or persistently high spenders. This procedure is applied in the Netherlands where an indicator for “persistently high spending” was introduced in the RA model in 2014 and an indicator for “persistently low spending” was introduced in 2018. Though this approach mitigates predictable profits/losses, it also has a downside: it reduces incentives for insurers to contain costs, since lower costs can lead to lower (future) RA payments.
Health insurance literature offers two interesting alternatives for the Dutch approach: high‐risk pooling and constrained regression. The first alternative involves cost‐based compensation for a group of high‐risk people identified ex‐ante (e.g., van Barneveld et al., 1996). The second alternative involves implementation of “constraints” in the regression model for deriving RA payment weights. Prior research has shown that such constraints can form a powerful tool to move funds from low‐risk people to high‐risk people (e.g., van Kleef et al., 2017). As will be explained in Section 3 of the present paper, high‐risk pools can be an interesting alternative for risk adjustors based on persistently high spending. Constrained regression on the other hand can be a promising alternative for risk adjustors based on persistently low spending. The goal of this paper is to empirically simulate these alternative methods and compare their outcomes with the approach of “implementing variables for persistently low/high spending in the RA model.” For these simulations we have access to administrative cost data covering the entire Dutch population (N = 16.7 m).
When it comes to the design of health plan payment systems, the primary challenge for regulators is to mitigate risk selection while maintaining incentives for insurers to control costs (van de Ven & Ellis, 2000). The abovementioned modalities are expected to have different impacts on selection incentives and incentives for cost control. In order to compare the different modalities in the light of these incentives, we develop a series of quantitative metrics. To approximate selection incentives we identify two sets of groups that are particularly relevant in the light of possible “selection actions” in the Dutch basic health insurance: groups based on the presence (or absence) of specific medical conditions and groups based on the level of the voluntary deductible. The first set is identified from electronic patient records (N = 1.4 m). The second set is identified in administrative data (N = 16.7 m). To approximate insurers' incentives for cost control we simulate the change in “plan payment” as a result of a (hypothetical) change in “plan costs.” A stronger link between payments and costs implies weaker incentives for cost control. For example,: in systems where 1 euro (in)efficiency results in 1 euro lower (higher) payment, incentives for cost control are absent; the opposite is true for systems in which (in)efficiency has no effect on payments.
This paper is structured as follows. The next section describes the Dutch context including the specification of the RA model and the indicators based on persistently low/high spending. It also describes the “choice options” for consumers and “instruments” for insurers, which define the scope for risk selection in the Netherlands and guide our choice of incentive metrics. Section 3 describes the alternative approaches and summarizes applications of these approaches in previous papers. Sections 4 and 5 introduce the data and methods and Section 5 presents the findings of our simulations. Section 6 discusses our main findings.
2. REGULATED COMPETITION AND RISK ADJUSTMENT IN THE NETHERLANDS
The Netherlands has organized its basic health insurance scheme according to the model of regulated competition (van de Ven et al., 2013). This model combines competition among health insurers and among healthcare providers with specific regulation to protect public objectives such as individual accessibility and affordability of coverage (Enthoven, 2012). In this model, competition is driven by free consumer choice of insurance plan (which puts insurers in competition) and freedom for insurers to decide where and by whom medical treatments are provided (which puts healthcare providers in competition). In this system, insurers fulfill a key role in improving social welfare: at the insurance market, they are supposed to respond to consumer preferences; at the healthcare market they are supposed to improve the efficiency of care by applying managed care tools such as selective contracting of providers, innovative provider payment methods and utilization management.
On the “regulation” side, the basic health insurance scheme is subject to a standardized benefits package in terms of medical services (such as primary care and pharmaceutical care), an insurance mandate, open enrollment, community‐rating per health plan, and an RA system. Given the community‐rated premium, the primary goal of the RA system is to reduce selection incentives while maintaining incentives for insurers to control costs. An appropriate RA system is crucial to the overall functioning of the healthcare system: as long as specific groups of consumers (e.g., those with pre‐existing conditions such as diabetes or cancer) are predictably unprofitable, insurers face disincentives to meet specific preferences of these groups. At the same time, the RA compensation for predictable losses should be (sufficiently) independent of realized costs in order to maintain incentives for insurers to control costs (Newhouse, 1996). (A simple way to eliminate predictable profits and losses is to fully compensate insurers for realized spending; such cost‐based compensation, however, would also eliminate incentives for insurers to control costs.)
In 2018, the Dutch RA system includes three different models, one for each of the following types of spending: somatic care, mental care and out‐of‐pocket spending due to the mandatory deductible of 385 Euros per adult per year. Each of these three models leads to a prediction of medical spending per individual, which forms the basis for the RA payment. In this paper, we focus on the RA model for somatic care. An early version of this model was implemented in the sickness fund insurance in 1993. Over the course of time, a large number of risk adjustors has been added to the model based on the following characteristics: age interacted with gender (1993), zip‐code clusters based on regional factors (1995), source of income interacted with age (1995), pharmacy‐based cost groups (2002; PCG's), hospital diagnosis‐based cost groups (2004; DCG's), socioeconomic status interacted with age (2008), multiple‐year high cost groups (2012; MYHC), durable medical equipment groups (2014; DMEG), prior spending on home care (2016), institutional status and household size interacted with age (2017), and physiotherapy diagnosis groups (2016; PDG's). Based on these characteristics, the RA model 2018 distinguishes 193 risk adjustors (van Kleef et al., 2018). van Kleef et al. (2020) show that the RA model of 2018 substantially compensates insurers for predictable variation in medical spending, but not completely. Net of RA, groups of healthy people tend to be profitable while groups of chronically ill tend to be unprofitable. These predictable profits and losses confront insurers with incentives for risk selection.
By risk selection we mean “Actions by consumers and insurers to exploit unpriced risk heterogeneity and break pooling arrangements” (Newhouse, 1996). In the Dutch context, there are at least four types of “actions” that can lead to risk selection. First, insurers have flexibility with respect to network design, coverage for out‐of‐network spending, utilization management and provider payment methods. Although these “instruments” are meant to improve the efficiency of care, they can also lead to risk selection. For example, an insurer contracting with doctors who have a good reputation in managing diabetes care, can expect to attract relatively many diabetes patients compared to insurers that do not contract these doctors. This can discourage all insurers to contract these doctors, which would have negative consequences for the functioning of the health insurance system (Glazer & McGuire, 2000). Ultimately, insurance plans might not cover healthcare providers preferred by unprofitable patients, which would discourage providers to specialize in the diseases of these patients.
A second type of selection actions is that consumers can choose a voluntary deductible. Given the community‐rated premiums and rebates for deductibles, this deductible option is more attractive for low‐risk people than for high‐risk people, which results in sorting of these risk types into different deductible options. This type of self‐selection is exacerbated by the fact that consumers can change their deductible each year. Consequently, premium rebates do not only reflect differences in coverage and moral hazard between deductible options, but also the effect of selection (to the extent that RA does not correct for selection effects). Selection‐driven premium variation can lead to a distortion of consumers” price‐quality tradeoff when choosing a plan (Einav & Finkelstein, 2011). Moreover, society might consider it unfair when, on average, people in good health pay lower premiums than those in poor health.
A third type of selection actions is that insurers can target profitable enrollees via marketing and customer service. For example, the Dutch regulation allows insurers to offer “group arrangements.” People joining a group arrangement must have an individual contract with the insurer, but can enjoy specific benefits such as a premium discount on the basic health insurance (max. 5%) and/or on other insurance products. To the extent that these premium discounts reflect selection rather than efficiency, they can distort health plan prices and might be considered unfair. Another example of a marketing action is selective advertisement. Resources used for selection‐driven marketing do not add any social value.
A fourth type of selection actions has to do with the supplementary health insurance. Though basic and supplementary insurance must be contractually separated by law, consumers tend to perceive these as one product: of all people with supplementary insurance (about 85% of the population), 99% obtains basic insurance from the same insurer. This implies that insurer‐actions regarding supplementary insurance can lead to selection in the basic insurance (Duijmelinck & van de Ven, 2014). Apart from standard insurance regulation, the supplementary health insurance operates as a “free market,” implying that insurers can risk‐rate their premiums, decide on the coverage of their plans and reject applicants. When the supplementary health insurance is used as a tool for risk selection in the basic health insurance, negative welfare effects might occur. First, people who are unprofitable for the basic health insurance might not be able to obtain supplementary insurance. Second, people with supplementary insurance might not switch insurer for the basic health insurance (because they are afraid to be rejected for a new supplementary insurance). Such frictions distort the functioning of a health insurance market, with generally negative welfare effects.
3. THREE OPTIONS TO DEAL WITH PERSISTENTLY HIGH/LOW SPENDERS IN PAYMENT SYSTEMS
As discussed in the introduction, the literature offers three interesting options to exploit the predictiveness of “persistently high/low spending” in health plan payment systems: (1) implementation of spending‐based risk adjustors, (2) implementation of high‐risk pooling for people identified on the basis of spending persistence, and (3) indirect use of spending persistence via constrained regression. Below we describe these options in more detail.
3.1. Option 1: Spending‐based risk adjustors
An intuitive strategy to exploit the predictiveness of multiple‐year high/low spending is the implementation of spending‐based risk adjustors. In an earlier study, van Kleef and van Vliet (2012) developed a series of risk classes on the basis of multiple‐year high spending. More recently, Eijkenaar et al. (2019) supplemented this set with an explicit risk class for people with multiple‐year low spending. The classification used in the RA model of 2018 includes nine mutually exclusive classes shown in the first column of Table 1. People are assigned to the highest class applicable. For example, someone in the top‐0.5% of spending in each of the three prior years is classified in the group “3x top‐0.5%,” but not in the other groups. Someone in the top‐0.5% in year t‐1 and year t‐2, and in the top‐1.5% (but not in the top‐0.5%) in year t‐3 is classified in the group “3x top‐1.5%.” Table 1 shows the spending thresholds corresponding to the relevant quantiles in each of the prior years.
TABLE 1.
Risk classes based on multiple‐year low/high spending
| Risk class in year t | Thresholds in Euros corresponding to quantiles of spending | ||
|---|---|---|---|
| t‐3 | t‐2 | t‐1 | |
| 3x in bottom‐70% | 1058 | 1070 | 1099 |
| 2x in top‐10% | ‐ | 4157 | 4305 |
| 3x in top‐15% | 2632 | 2706 | 2789 |
| 3x in top‐10% | 3998 | 4157 | 4305 |
| 3x in top‐7% | 5514 | 5751 | 5980 |
| 3x in top‐4% | 8627 | 9095 | 9508 |
| 3x in top‐1.5% | 16,524 | 17,772 | 18,610 |
| 3x in top‐0.5% | 30,682 | 34,186 | 35,584 |
Note: Risk classes are defined as in the Dutch risk adjustment model for somatic care in 2018. Overall mean per person spending equals 2227 Euros for t‐1, 1946 Euros for t‐2, and 1848 for t‐3.
The classification in Table 1 serves as a starting point for our empirical simulation, meaning that risk adjustors for multiple‐year high/low spending will be defined as in Table 1. For detailed descriptions of how these risk classes were constructed and a discussion of the tradeoffs involved we refer to van Kleef and van Vliet (2012) and Eijkenaar et al. (2019).
To the extent that persistently high/low spending in prior years is predictive of under/overcompensation by the RA model, the implementation of risk adjustors based on this information is expected to improve payment fit and to mitigate selection incentives. Spending‐based risk adjustors, however, also come with a downside: they reduce incentives for cost control (Marchand et al., 2003; van de Ven & Ellis, 2000; van Kleef & van Vliet, 2012). More specifically, such risk adjustors create a link between (prior) spending and (future) payments and thereby reduce incentives for insurers to contain costs. This can be illustrated with the threshold values in Table 1: if an insurer succeeds in reducing spending, then some individuals will move to a lower “top‐X%” group or even to the “3x bottom‐70%” group, resulting in a lower RA payment in later years (under the reasonable assumption that RA payments go up with higher thresholds – which has indeed been proven to be the case).
3.2. Option 2: Pooling of multiple‐year high spenders
The second option is high‐risk pooling. This option has been proposed by van Barneveld et al. (1996, 2001) and basically means that insurers receive a cost‐based compensation for a risk group that is identified ex‐ante. The latter implies that people are assigned to the “high‐risk pool” before the start of the contract period. Assignment can be done by the regulator and/or the insurers themselves. The cost‐based compensation for people in the high‐risk pool can take a variety of forms, for example, X% compensation of actual spending or X% compensation of actual spending above a threshold. In this paper the concept proposed by van Barneveld et al. (1996, 2001) will be combined with the concept of “residual‐based reinsurance” proposed by Schillo et al. (2016) and further developed by McGuire, Schillo, and van Kleef (2020). The latter two studies argue that reinsurance payments (i.e., cost‐based payments for individual‐level spending above a threshold) should be targeted at residual spending from the RA model instead of actual spending. Residual‐based reinsurance compensates for payment gaps net of RA and avoids reinsurance payments for high spenders that are sufficiently compensated by RA. In our empirical analysis, we examine modalities of high‐risk pooling in which people with multiple‐year high spending (i.e., the seven top‐X% groups in Table 1) are assigned to the pool. For these people insurers then receive a 100% compensation for residual spending above a threshold. The threshold is determined such that the mean undercompensation of those in the pool is eliminated. Cost‐based compensations in the pool are financed by a reduction of RA payments; more specifically RA payment weights are estimated net of spending in the high risk pool. Since the threshold for the high risk pool depends on the RA payments, and vice versa, an iterative procedure is needed to optimize both the threshold and RA coefficients. During this iterative procedure, both the RA payments and threshold for high‐risk pooling decrease, resulting in a larger high‐risk pool, both in terms of enrollees and spending.
As with spending‐based risk adjustors, high‐risk pooling reduces incentives for insurers to control costs. Given that payments are partly based on actual spending, total payments will—on average—increase (decrease) with higher (lower) spending. So, like option 1, option 2 also comes with a tradeoff between incentives for selection and cost control (Newhouse, 1996).
3.3. Option 3: Constraints based on spending persistence
Another strategy to exploit the predictiveness of spending persistence is “constrained regression.” This method allows for indirect use of predictive information by implementing a (set of) constraints on the coefficients of the existing risk adjustors (Layton et al., 2018; van Kleef et al., 2017, 2020; Withagen‐Koster et al., 2020). In the context of this paper a constraint could mean that “mean predicted spending” for a group in Table 1 equals “mean actual spending” for that group. More technically, this constraint can be written as
| (1) |
where is the mean predicted spending in group g, is the regression coefficient of risk adjustor j, is the mean value of for the individuals in g and is the mean actual spending in g. Implementation of (1) requires an initial pass through the data to calculate and . Obviously, can be replaced by any other target value (van Kleef et al., 2017).
Constrained regression returns the set of estimated coefficients (i.e., the betas) that minimize the residual sum of squares, given the constraint. To satisfy the constraint, the regression will exploit correlations between the risk adjustors included in the model and group g, which itself is not explicitly included as a dummy in the model. The extent to which coefficients move because of a constraint depends on these correlations and the specification of the constraint. Compared to an unconstrained model, a constrained RA model programmed to reduce under/overcompensation for groups of interest tends to shift RA payments from people “flagged” as “healthy” by risk adjustor variables (e.g., no DCG) to those flagged as “unhealthy” (e.g., at least one DCG). Previous empirical simulations have shown that constrained regression can improve payment fit for some groups, but worsen it for others (van Kleef et al., 2017; Withagen‐Koster et al., 2020). Given a certain choice of “relevant” groups, however, well‐specified constraints can improve the performance of RA models. When relevant groups include a combination of groups flagged by “risk adjustors” and groups flagged by “constraints,” previous studies show that constraints requiring a <100% reduction in the initial under/overcompensation on group g tend to lead to better outcomes than a constraint requiring a 100% reduction. For example, Withagen‐Koster et al. (2020) find that for a cross tabulation of yes/no morbidity flag (according to morbidity indicators included in the Dutch RA model) and yes/no (very) poor or moderate self‐reported health (as used by the researchers to define constraints in their alternative RA model), the absolute weighted mean under/overcompensation on the four combinations is lowest for constraints that reduce the undercompensation on the group of people with (very) poor or moderate self‐reported health by 20%–80%. The optimal percentage reduction, however, is not a universal constant, but depends on the specification of the RA model, the characteristics of subgroups used for evaluation, and the weighting of under/overcompensations for subgroups of interest.
In our payment system alternatives we include a constraint based on the group with multiple‐year low spending. Our motivation for selecting this particular group, is that forms of cost‐based compensation (as in option 2) are inappropriate for exploiting persistently low spending since this group hardly incurs (substantial) spending. Our expectation is that option 2 (high‐risk pooling for people with multiple‐year high spending) and option 3 (constrained regression based on multiple‐year low spending) are complementary tools for improving plan payment systems. In theory, however, option 2 could be extended with a series of constraints for groups based on multiple‐year high spending, for example, seven constraints that require a specific reduction in under/overcompensation for each of the top‐X% groups presented Table 1. Such use of multiple constraints allows exploiting the risk heterogeneity within the group of people with multiple‐year high spending. It is unclear, however, what these constraints should look like. For example, should they reduce under/overcompensation of the groups in Table 1 by the same percentage? Should a constraint be included for each of the eight groups or would fewer constraints on a selection of groups lead to better outcomes? If so, which groups should serve as a basis for constraints, and which not? To avoid an overload of models and comparisons in the present paper, we decided to leave the option of multiple constraints for future research.
As mentioned above, constrained regression comes with a tradeoff: while it might improve payment fit for some groups, it can worsen payment fit for others. This implies that, for our empirical analyses, it is crucial to think about the selection of groups for determining payment fit. Ideally, this selection is guided by the possible selection actions in the system of interest (in our case: the Dutch basic health.
4. DATA
For the purpose of this study we obtained permission to use individual‐level data on medical spending and risk adjustors for the entire Dutch population with basic health insurance in 2015 (N = 16.7 m). Originally, this information came from various sources, including insurers, the tax collector and the registration service for social benefits. Individual‐level spending originates from 2015, but is made representative for 2018. More specifically, individual‐level spending for services included (removed) from the benefits package between 2015 and 2018 were included (removed) from the data set. Risk adjustors include those actually applied in the RA model for somatic care in 2018 and are based on the following information: age, gender, region, source of income, socioeconomic status, institutional status, household size, PCGs, DCGs, DMEGs, PDGs, and multiple‐year prior spending. More specifically, the latter comprises a classification of people according to multiple‐year high/low spending, based on spending levels in the years 2012, 2013, and 2014, conform Table 1. In addition, this data set includes information on the chosen level of the voluntary deductible for 2015.
In addition, we obtained permission to use morbidity data from Nivel Primary Care Database (Nivel‐PCD). Nivel‐PCD routinely collects data from electronic health record systems of general practitioners, including information about consultations, morbidity, prescriptions and diagnostic tests, in a sample of about 400 general practices serving 1.4 million registered patients. Diagnoses are coded according to the International Classification of Primary Care which distinguishes nearly 700 diagnoses (Lamberts & Wood, 1987). For each of the 1.4 million registered patients, the data set indicates whether or not a diagnosis was present in a patient in the period 2012–2014. Nivel‐PCD developed an algorithm to construct episodes of illness, based on recorded diagnoses by the general practitioner (GP), and to determine whether a patient has a certain condition at a specific point in time. In the current study, we only use the 109 conditions that Nivel‐PCD labeled as “chronic.” Roughly speaking, Nivel‐PCD considers a condition as “chronic” when—according to medical experts—it is unlikely that people suffering from that disease will fully recover. For more information about the Nivel‐PCD, we refer to Nielen et al. (2019). A crucial feature of this data set is that it provides a complete overview of a person's health status. The reason is threefold. First, in the Netherlands, all outpatient drug prescriptions are done by GPs. Second, the GP functions as a gatekeeper to specialized care, meaning that any person in need of specialized care will first have to see his GP to obtain a referral. Moreover, the medical specialist always informs the GP about the patient afterwards. Third, 99% of Dutch inhabitants are registered with a GP. Because of these features, it is very likely that when a person is (not) suffering from a certain condition her GP patient record does (not) make mention of that condition. Therefore, this sample provides a more complete overview of a person's health status than any other data source in the Dutch healthcare system. We will use this sample to identify people with specific medical conditions in order to quantify selection incentives regarding these groups.
5. METHODS
Our empirical analysis consists of four steps. First, we specify and estimate alternative payment systems that exploit the predictiveness of persistently high/low spending in different ways. Second, we merge—at the individual level—actual spending, plan payments, and risk adjustors with the GP data, and check the representativeness of the sample for which GP patient records are available. Third, we specify and calculate a series of ex‐ante measures to quantify incentives for risk selection and incentives for cost control under the alternative payment systems. Below we describe these steps in more detail.
5.1. Step 1: Estimating alternative payment systems
Table 2 describes the seven payment systems simulated in this paper. Our starting point is the “base model,” which mimics the Dutch RA model for somatic care in 2018, though without the risk adjustors for multiple‐year high/low spending. In addition, there are two other differences with the actual model. First, on the spending side, we exclude “home care spending.” Second, on the side of risk adjustors, we exclude “prior‐year spending on home care.” The reason for keeping this information out of the simulations is that this “home care” risk adjustor correlates strongly with our multiple‐year spending variables. Including “prior‐year spending on home care” would complicate the interpretation of the results. Moreover, we believe that by excluding this information, the analysis becomes more relevant for an international audience. The simulations can now be framed as: suppose you have an RA model based on demographic, socioeconomic, and morbidity information. To what extent does multiple‐year high/low spending explain spending variation net of RA?
TABLE 2.
Payment systems included in the empirical simulations
| Abbreviation | Description |
|---|---|
| Base model | Risk adjustment (RA) with risk adjustors based on age/gender; socioeconomic variables; and morbidity indicators based on prior use of: prescribed drugs, inpatient and outpatient hospital treatments, durable medical equipment and physiotherapy. |
| MYHC adjustor | Base model + dummy variables for groups based on multiple‐year high spending. Groups defined on the basis of the threshold values in Table 1. |
| MYHC pooling | Base model + pooling of residual spending above a threshold for people in the top‐15% of spending in each of 3 prior years. RA coefficients are optimized for the presence of the high‐risk pool, and vice versa. |
| MYLC adjustor | Base model + dummy variables based on the group with multiple‐year low spending. Groups defined on the basis of the threshold values in Table 1. |
| MYLC constraint | Base model + constraint on the estimated RA coefficients that reduces the overcompensation for people with multiple‐year low spending by 50%. |
| MYHC adjustor & MYLC adjustor | Base model + dummy variables for groups based on multiple‐year high/low spending. Groups defined on the basis of the thresholds in Table 1. |
| MYHC pooling & MYLC constraint | Base model + pooling of residual spending above a threshold for people in the top‐15% of spending in each of 3 prior years + constraint on the estimated RA coefficients that reduces the overcompensation for people with multiple‐year low spending by 50%. RA coefficients are optimized for the presence of the high‐risk pool, and vice versa. |
In the next six models, we supplement the base model with options to exploit the information on spending persistence. In the models “MYHC adjustor,” “MYLC adjustor,” and “MYHC adjustor & MYLC adjustor,” we enrich the base model with risk adjustors (in the form of dummy variables) corresponding to the risk classes in Table 1. More specifically, the MYLC classification splits the population in two groups: yes/no 3x bottom‐70% of spending. The MYHC classification splits the population in eight groups: the seven top‐X% groups shown in Table 1 and a separate risk class for “other.” A combination of MYLC and MYHC comprises nine groups (i.e., the eight groups in Table 1 plus a separate risk class for “other”).
“MYHC pooling” comprises a form of high‐risk pooling in which people with multiple‐year high spending (i.e., those in one of the seven top‐X% groups in Table 1) are assigned to the pool. As a supplement to the RA payment, insurers receive a cost‐based compensation for those with the highest residual spending in this group. More specifically, the insurer receives a compensation of 100% of residual spending above a threshold. The threshold is chosen such that the mean payments for those with multiple‐year high spending exactly equal their mean actual spending. A challenge with this combination of RA and high‐risk pooling is that these two payment system components interact: in a zero‐sum payment system, higher payments via high‐risk pooling implies lower payments via RA. Lower RA payments, however, imply higher residual spending, which requires a lower threshold to eliminate undercompensation of the high‐risk pool. We solve for the “optimal” RA coefficients and pooling threshold by estimating these parameters iteratively. In the 15th iteration, the change in threshold value turns out to be less than 2 euros. In the “MYHC pooling” system, the threshold value equals 3420 euro of residual spending in the high‐risk pool. In the “MYHC pooling & MYLC constraint” the threshold value equals 7003 euro of residual spending in the high‐risk pool.
In the “MYLC constraint” systems, the base model is extended with a constraint on the estimated coefficients. This constraint takes the form of Equation (1) with g specified as “3x in bottom 70%.” A difference with (1), however, is that we do not require a 100% reduction in overcompensation of this group. As will be shown below, the “base model” overcompensates this group by on average 237 euro per person per year. Guided by the aforementioned study of Withagen‐Koster et al. (2020), we specify the constraint such that the overcompensation of people with multiple‐year low spending is reduced by 50% compared to the base model.
5.2. Step 2: Rebalancing GP data
In a next step, we combine the individual‐level information on spending and payments with the GP morbidity data. For the purpose of this research, we are able to merge the two data sources on the basis of a unique, individual‐level identification code (which for privacy reasons was anonymized by a trusted third party). The initial sample with GP data from 2014 covers 1,425,541 individuals. For 1,398,748 (i.e., 98.1%) of these we find a successful match with the spending data from 2015. Reasons for an unsuccessful match are death and migration (before 2015), non‐enrollment in the Dutch basic health insurance of 2015 (e.g., small groups of defaulters, military servants, and detained people) and invalid identification codes.
Table 3 compares the sample with the population in terms of mean spending and prevalence, both for the entire population and for subgroups defined by risk adjustor variables. It turns out that elderly people are slightly overrepresented in the sample. The same is true for people with at least one PCG, DCG, and/or DMEG. Consequently, mean spending is somewhat higher than in the population: 2095 versus 2043 Euros. To improve the representativeness of the sample we applied an iterative proportional fitting procedure. This procedure rebalances the sample in such a way that the weighted frequencies of risk adjustor variables in the sample exactly equal those in the population (Battaglia, 2009). For a detailed description of this procedure, we refer to van Kleef et al. (2019). After rebalancing, relative frequencies of subgroups in the rebalanced sample exactly match those in the population. As shown in Table 3, the mean per person costs in these groups are very similar in the two data sets.
TABLE 3.
Prevalence and mean costs by individual characteristics: (rebalanced) sample versus population
| Sample (GP data) | Rebalanced sample | Population | ||||
|---|---|---|---|---|---|---|
| Prevalence | Mean costs | Prevalence | Mean costs | Prevalence | Mean costs | |
| Total | 100% | 2095 | 100% | 2043 | 100% | 2043 |
| Men, 1–17 years | 10.0% | 939 | 10.0% | 956 | 10.0% | 970 |
| Men, 19–34 years | 9.8% | 722 | 10.4% | 710 | 10.4% | 702 |
| Men, 35–44 years | 6.2% | 1045 | 6.3% | 1011 | 6.3% | 1005 |
| Men, 45–54 years | 7.7% | 1538 | 7.7% | 1532 | 7.7% | 1548 |
| Men, 55–64 years | 6.9% | 2708 | 6.6% | 2669 | 6.6% | 2667 |
| Men, 65 years or over | 8.7% | 5131 | 8.4% | 5054 | 8.4% | 5066 |
| Women, 1–17 years | 9.5% | 850 | 9.5% | 851 | 9.5% | 849 |
| Women, 19–34 years | 9.7% | 1512 | 10.3% | 1487 | 10.3% | 1486 |
| Women, 35–44 years | 6.5% | 1536 | 6.5% | 1562 | 6.5% | 1566 |
| Women, 45–54 years | 7.8% | 1815 | 7.7% | 1813 | 7.7% | 1813 |
| Women, 55–64 years | 6.9% | 2565 | 6.7% | 2553 | 6.7% | 2550 |
| Women, 65 years or over | 10.3% | 4550 | 10.0% | 4463 | 10.0% | 4444 |
| No PCG | 79.2% | 1258 | 80.1% | 1240 | 80.1% | 1240 |
| At least one PCG | 20.8% | 5282 | 19.9% | 5268 | 19.9% | 5269 |
| No DCG | 87.7% | 1346 | 88.2% | 1327 | 88.2% | 1324 |
| At least one DCG | 12.3% | 7440 | 11.8% | 7379 | 11.8% | 7409 |
| No DMEG | 96.4% | 1853 | 96.6% | 1813 | 96.6% | 1811 |
| At least one DMEG | 3.6% | 8642 | 3.4% | 8518 | 3.4% | 8576 |
| No PDG | 98.2% | 2002 | 98.2% | 1953 | 98.2% | 1952 |
| At least one PDG | 1.8% | 7117 | 1.8% | 6915 | 1.8% | 6984 |
Note: spending is presented in euros per person per year. Prevalence is calculated as a percentage of total insured years in the population and (rebalanced) sample.
Abbreviations: DCG, diagnosis‐based cost groups; DMEG, durable medical equipment groups; GP, general practitioner; PCG, pharmacy‐based cost groups.
5.3. Step 3: Calculating incentive measures for selection and cost control
As a final step, we compare the alternative payment systems in terms of their expected effects on incentives for cost control and incentives for risk selection.
5.3.1. Incentives for cost control
When it comes to incentives for cost control, we apply a series of simulations to approximate the change in “plan payments” in response to a change in “plan spending.” Our simulations are in the spirit of the “power” metric proposed by Geruso and McGuire (2016):
| (2) |
where N is the number of enrollees in an insurance plan, and is the derivative of payment R for person i with respect to a marginal change in spending Y for person i.
Our simulations can be framed as follows. Imagine two insurers—A and B—who both have a representative share of the market and whose risk portfolios are identical in terms of the risk adjustor in the base model. Assume, however, that insurer B is less successful in cost control and therefore has 10% higher spending per enrollee than insurer A. In our simulation, we approximate the effect of B's higher spending level on B's payment.
Under the base model the payments for insurer A and insurer B are the same (since their portfolios are identical in terms of the risk adjustor in the base model). Systems with “MYHC pooling” are expected to lead to higher payments for B than for A, since B's enrollees are more likely to enter the high‐risk pool. By dividing the euro difference in payment between A and B by the euro difference in spending (and by multiplying the outcome by 100%) we obtain a “ratio” that can be interpreted as the “% reduction in cost control incentives compared to the base model.” We assume that under the base model (which does not include any form of cost‐based payments or risk adjustors) incentives for cost control are 100%.
Systems with “MYHC adjustor” and/or “MYLC adjustor” are also expected to lead to higher payments for B than for A. The reason is that B's enrollees are more likely to have a MYHC‐flag (and are less likely to have a MYLC‐flag). Again, we approximate the “% reduction in incentives for cost control compared to the base model” by dividing the euro difference in payment between A and B by the euro difference in spending (multiplied by 100%).
An important difference between the simulation of cost control incentives for “MYHC pooling” and those for “MYHC adjustor” and/or “MYLC adjustor” is that the former looks at the relationship between spending and payments in the current year while the latter look at the relationship between spending in prior years and payments in the current year. To effectively compare the outcomes of these simulations we assume that consumers stay with the same insurance plan from year to year. As more consumers switch plans from year to year, the relationship between spending and payments as a result of the introduction of “MYHC adjustor” and/or “MYLC adjustor” will be weaker, resulting in a smaller impact of these modalities on the incentives for insurers to control costs. In the Dutch basic health insurance, about 6% of the population changes insurance plan each year.
5.3.2. Effects on incentives for risk selection
Incentives for risk selection under payment system alternatives will be quantified by the fit between payments and spending at the individual level and the level of relevant groups. In the Dutch context, individual‐level fit is relevant since selection actions via supplementary health insurance can take place at the individual level: insurers can discourage unprofitable individuals to enroll in basic insurance by denying them supplementary insurance (see Section 2). Following Layton et al. (2017), we apply two common measures for individual‐level fit:
| (3) |
| (4) |
with the spending for individual i, the mean spending in the population and the payments (revenues) that an insurer receives for individual i. The difference between these two measures is that (4) takes the absolute value of differences between spending and payments, while (3) takes the squared value of these differences. In other words, measure (3) puts more weight on larger difference than measure (4).
In Section 2, we have distinguished three other dimensions through which selection can take place in the Dutch basis health insurance: provider network design, voluntary deductibles and marketing. These forms of risk selection typically take place at the group level assuming that some groups (i.e., risk types) come with predictable profits while others come with predictable losses. This brings us to the following measure for group‐level payment fit:
| (5) |
with the payment an insurer receives for individual i in group g, the insurer's spending on i and the number of people in g. In the light of the possible selection actions, we focus on two sets of relevant groups. The first set classifies the population according to specific conditions, assuming insurers can attract (deter) people with a specific condition, for example, by (not) contracting healthcare providers who have a good reputation in managing that condition. The second set classifies the population according to the chosen level of deductible.
6. RESULTS
This section presents and compares the outcomes of the seven payment systems. We first present some outcomes of the base model to indicate the predictiveness of spending‐level persistence net of the base model. After that, we compare the effects of the alternative payment systems in three steps: “MYHC adjustor versus MYHC pooling,” “MYLC adjustor versus MYLC constraint,” and “MYHC/MYLC adjustors versus MYHC pooling and MYLC constraint.”
6.1. Predictiveness of spending persistence net of morbidity‐based risk adjustment
Figure 1 shows the mean financial result per person per year for the groups with multiple‐year low/high spending defined on the basis of Table 1. Under the base model, the group of people with “3x spending in the bottom‐70%” (53.2% of the population) is overcompensated by on average 237 euro per person per year. For people with persistently high spending the base model generates undercompensations up to 27,576 euro per person per year.
FIGURE 1.
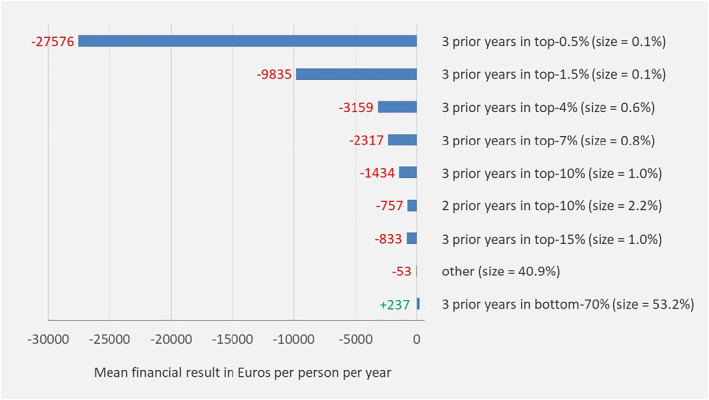
Mean financial result under the “base model” for mutually exclusive groups based on spending levels in prior years. Outcomes are based on the total population (N = 16.7 m). “size” refers to the prevalence in the current year. People are categorized in the highest group applicable. For example, those with 2 prior years in the top‐0.5% and 1 year in the top‐1.5% (but not in the top‐0.5%) are classified in the group “3 prior years in top‐1.5%”
The mean financial result in Figure 1 might suggest that selection incentives under the base model are mainly driven by undercompensation of high‐risk people rather than overcompensation of low‐risk people. The total financial result, however, as portrayed in Figure 2, gives a different perspective. For the group with multiple‐year low spending, the total financial result exceeds 2 billion euros per year. For the groups with multiple‐year high spending the total financial result varies from about 100 to 400 million per year.
FIGURE 2.
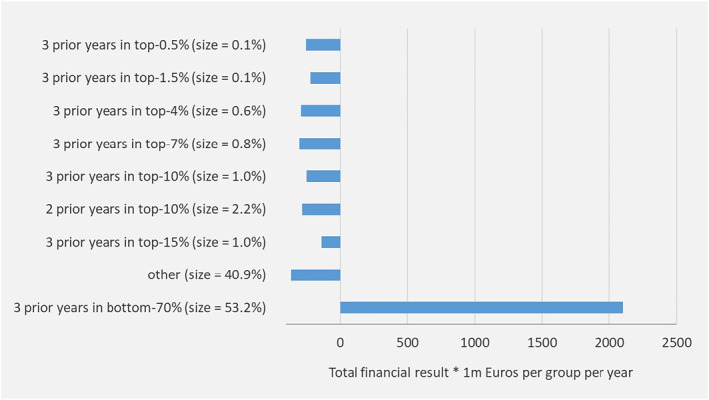
Total financial result under the “base model” for mutually exclusive groups based on spending levels in prior years. Outcomes are based on the total population (N = 16.7 m). “size” refers to the prevalence in the current year. People are categorized in the highest group applicable. For example, those with 2 prior years in the top‐0.5% and 1 year in the top‐1.5% (but not in the top‐0.5%) are classified in the group “3 prior years in top‐1.5%”
The results in Figures 1 and 2 imply that spending persistence in prior years is indeed predictive of spending in the current year, even after applying a sophisticated RA model with risk adjustors based on demographic, socioeconomic, and morbidity information.
6.2. Comparison of payment system alternatives
Figure 3 provides an indication of the redistribution of payments under each of the alternative payment systems compared to the base model. More specifically, it presents the mean per person payment for people in the bottom‐80% and those in the top‐20% of actual spending (in the current year). All alternative payment systems trigger a shift in payments from “low” spenders to “high” spenders. The only exception is the system with the risk adjustor for multiple‐year low spending; apparently, this system results in a redistribution of revenues among low spenders rather than between low and high spenders. The shift in revenues is largest for the payment system with both MYHC‐pooling and MYLC‐constraint.
FIGURE 3.
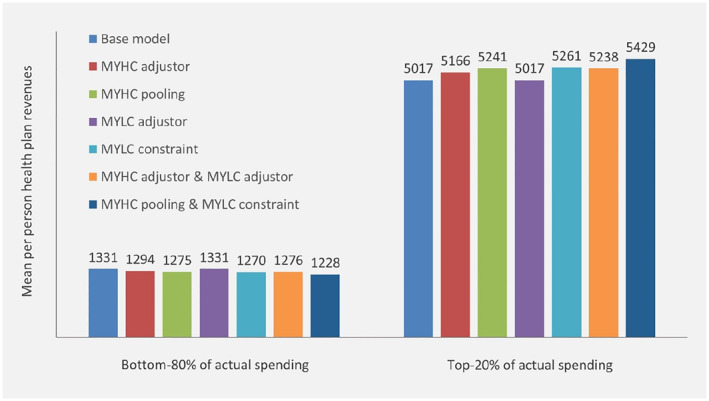
Mean per person health plan revenues from seven alternative payment systems for people in the bottom‐80% and those in the top‐20% of actual spending respectively. Outcomes are based on total population (N = 16.7 m). Revenues in Euros
The crucial question is what the redistribution of revenues means for selection incentives and to what extent alternative payment systems reduce incentives for cost control. Table 4 presents the outcome measures for both the base model and the six alternative systems. A complete list of the outcomes for the 109 chronic conditions identified by Nivel‐PCD is given in Table A1 in Appendix; for Table 4, we selected the five groups with the highest mean undercompensation and the five groups with the highest total undercompensation under the base model. In addition, the table shows the mean financial result for five groups based on the chosen deductible. To summarize the group‐level under/overcompensations, Table 4 also shows the mean absolute financial result for the 15 groups weighted by their size (WMAR).
TABLE 4.
Outcome measures under alternative payment systems
| Base model | MYHC adjustor | MYHC pooling | MYLC adjustor | MYLC constraint | MYHC adjustor & MYLC adjustor | MYHC pooling & MYLC constraint | |||
|---|---|---|---|---|---|---|---|---|---|
| Reduction in incentives for cost control compared to base model | ‐ | 17.2% | 22.9% | 8.1% | 0% | 25.3% | 18.9% | ||
| Payment System Fit (PSF) | 0.249 | 0.268 | 0.493 | 0.250 | 0.248 | 0.270 | 0.480 | ||
| Cummings Prediction Measure (CPM) | 0.249 | 0.268 | 0.371 | 0.258 | 0.246 | 0.277 | 0.339 | ||
| Prev. | Mean costs | Mean financial result in Euros per person per year | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Malignant neoplasm blood other | 0.07% | 20,674 | −6427 | −6141 | −2996 | −6522 | −5985 | −6109 | −2843 |
| Leukemia | 0.12% | 14,983 | −3942 | −3969 | −2644 | −3980 | −3610 | −3920 | −2523 |
| Malignancy NOS | 0.04% | 12,963 | −3212 | −2823 | −1910 | −3245 | −2856 | −2786 | −1842 |
| Limited function/disability (d) | 0.03% | 8779 | −2300 | −1354 | −290 | −2302 | −2029 | −1281 | −317 |
| Congen.anom. blood/lymph other | 0.04% | 7145 | −2175 | −1802 | −1282 | −2146 | −2038 | −1726 | −1245 |
| Hypertension uncomplicated | 13.68% | 4182 | −159 | −158 | −174 | −151 | 82 | −128 | 80 |
| Osteoarthrosis of knee | 2.97% | 5344 | −580 | −466 | −461 | −569 | −253 | −426 | −156 |
| Cardiovascular disease other | 1.75% | 6550 | −932 | −792 | −548 | −964 | −612 | −765 | −297 |
| Diabetes | 6.10% | 5915 | −255 | −205 | −206 | −274 | 130 | −185 | 180 |
| Chronic obstructive pulmonary disease | 2.72% | 6955 | −569 | −520 | −517 | −696 | −178 | −495 | −135 |
| Voluntary deductible = 100 euro | 0.78% | 1182 | 157 | 154 | 161 | 131 | 77 | 105 | 76 |
| Voluntary deductible = 200 euro | 0.77% | 863 | 250 | 256 | 256 | 208 | 145 | 187 | 143 |
| Voluntary deductible = 300 euro | 0.45% | 821 | 270 | 276 | 283 | 217 | 160 | 197 | 163 |
| Voluntary deductible = 400 euro | 0.13% | 821 | 296 | 311 | 316 | 238 | 187 | 226 | 196 |
| Voluntary deductible = 500 euro | 5.34% | 602 | 317 | 327 | 333 | 257 | 182 | 238 | 186 |
| Weighted mean absolute result (WMAR) of 15 groups shown above | 343 | 313 | 295 | 343 | 188 | 273 | 156 | ||
Note: Spending is presented in euros per person per year. Prevalence is calculated as a percentage of total insured years in the population and (rebalanced) sample.
6.2.1. “MYHC adjustor” versus “MYHC pooling”
Compared to the “base model,” both “MYHC adjustor” and “MYHC pooling” reduce selection incentives: PSF and CPM are higher and the WMAR for the 15 subgroups presented in Table 4 is smaller. Overall, “MYHC pooling” leads to a larger reduction in selection incentives than “MYHC adjustor.” As expected, both systems also reduce incentives for cost control. This reduction is larger for “MYHC pooling” than for “MYHC adjustor”: 22.9% versus 17.2%.
6.2.2. “MYLC adjustor” versus “MYLC constraint”
Compared to the “base model,” both “MYLC adjustor” and “MYLC constraint” hardly increase PSF and CPM. “MYLC constraint” even leads to a slight reduction in PSF; the explanation is that the constraint leads estimated coefficients to deviate from those under the least squares criterion. At the group level, however, the “MYLC constraint” substantially outperforms the “MYLC adjustor” for all 15 subgroups. While “MYLC adjustor” does not improve the WMAR compared to the base model, “MYLC constraint” reduces the WMAR by almost 50%.
Remarkably, the improvements under “MYLC constraint” do not only come from the (healthy) deductible groups, but also from the (unhealthy) groups with chronic conditions. These effects can be explained as follows. To satisfy the constraint, the regression model generates lower coefficients for the non‐morbidity classes in the RA model such as the risk class “no DCG” (because people with multiple‐year low costs are concentrated in precisely those classes and the constraint forces the model to lower RA payments for them in order to better match actual costs). Consequently, coefficients for the morbidity classes (e.g., at least one DCG) increase. Given the positive correlation of the deductible groups with the non‐morbidity classes and the positive correlation of the disease groups with the morbidity classes, payment fit improves for both the deductible groups and the disease groups.
Since the constraint on MYLC is linear in the coefficients of the RA model, one can easily compute the effects of alternative percentage reductions on the undercompensation of MYLC compared to the base model. For example, with a 100% reduction of the undercompensation of MYLC the change in mean financial result for group g compared to the base model is twice the change from the “Base model” to “MYLC constraint” observed for group g in Table 4. So, the reduction in mean financial result for the group with Leukemia from −3942 (Base model) to −3610 (MYLC constraint) implies a reduction to −3278 for a constrained regression that requires a 100% reduction in overcompensation on the group with MYLC. In an additional analysis, we found that the WMAR for “MYLC constraint” would be lowest (169 euros) for a constraint requiring a 33% reduction in overcompensation of the group with MYLC. This indicates that a refined version of “MYLC constraint” can result in even bigger improvements over “MYLC adjustor” than the improvements presented in Table 4.
Compared to the base model, “MYLC adjustor” reduces incentives for cost control by about 8%. The “MYLC constraint” system does not explicitly link RA payments to spending. Instead, RA payments are redistributed by changes in the coefficients of the existing risk adjustors in the base model, meaning that incentives for cost control (as measured here) remain untouched.
6.2.3. “MYHC adjustor & MYLC adjustor” versus “MYHC pooling & MYLC constraint”
Compared to the base model, “MYHC adjustor & MYLC adjustor” improves payment fit, both at the individual and group level. For all selection metrics in Table 4, however, “MYHC pooling & MYLC constraint” comes with bigger improvements. At the same time, the decrease in incentives for cost control is smaller for “MYHC pooling & MYLC constraint” than for “MYHC adjustor & MYLC adjustor”: 18.9% versus 25.3%. This brings us to the observation that spending‐based risk adjustors (the current Dutch approach) is not necessarily the best strategy to exploit the predictiveness of spending persistence in payment systems.
7. DISCUSSION
Our empirical findings lead us to two conclusions. First, persistently high/low spending in prior years is substantially predictive of spending in the current year, also net of sophisticated morbidity‐based RA. This finding indicates that health plan payment systems with morbidity‐based RA—such as those applied in health insurance schemes in Germany and Switzerland, and in Medicare Advantage and the Marketplaces in the United States—might benefit from taking into account “spending persistence.” Our second conclusion is that the method for taking into account spending persistence matters for selection incentives and incentives for cost control. In this paper we compared three distinct methods: (1) implementation of spending‐based risk adjustors, (2) implementation of high‐risk pooling for people with multiple‐year high spending and (3) indirect use of spending persistence via constrained regression. In our simulation, a combination of methods 2 and 3 results in smaller incentives for selection and greater incentives for cost control than method 1.
There is a growing literature showing that insurers respond to selection incentives. Bauhoff (2012), Carey (2017a, 2017b), Decoralis and Guglielmo (2017), Geruso et al. (2019), Han and Lavetti (2017), and Lavetti and Simon (2018) provide evidence of how health insurers engage in actions to selectively attract predictable profitable groups. When it comes to measurement of selection incentives in a specific setting it is important to take into account the “actions” that insurers can take in that setting. In this paper, we described four possible dimensions through which selection can take place in the mandatory health insurance in the Netherlands (i.e., network design and coverage for out‐of‐network care, voluntary deductibles, marketing and supplementary insurance). Based on these dimensions, we defined a meaningful set of individual‐ and group‐level incentive metrics. We acknowledge that in other countries/settings risk selection can take place through other dimensions, implying that research in these settings might require a different set/specification of evaluation metrics than applied in this paper.
To identify incentives for cost control we quantified the link between an insurer's spending and revenues. We have shown how both “spending‐based risk adjustors” and “high‐risk pooling” introduce a positive correlation between spending and revenues and thereby reduce incentives for cost control. Although our metrics give a general idea of the direction in which incentives for cost control move, they are also incomplete. First, our metrics assume that insurers take general decisions about spending levels, for example, whether or not to invest in cost control overall. In practice, insurers are more likely to make decisions at the level of health care services (e.g., hospital care, pharmaceutical care and primary care). It is an empirical question whether the link between spending and revenues differs across services. If it does, however, this should be taken into account when quantifying incentives for cost control (in line with our consideration of selection metrics). A second limitation of our incentive metrics for cost control is that they do not take into account the indirect effects of our alternative payment systems on incentives for “upcoding.” Geruso and Layton (2020) and Bauhoff (2017) have provided evidence of health insurers taking actions to get more people “flagged” by a morbidity adjustor to pursue higher revenues from the payment system. Since our alternative payment systems all affect RA coefficients for morbidity adjusters—with different magnitudes and in different directions (not presented in this paper)—it might be necessary to take into account incentives for “upcoding” as well. In the Netherlands, the possibilities for upcoding are relatively limited since the payment systems for insurers and providers are unconnected. Taking into account incentives for upcoding might be more important when these payment systems are connected or even integrated. Appropriate incentive metrics for “upcoding” are likely to be different than those for “cost control.” We consider the development of both types of metrics as an important topic for future research.
In sum, our paper shows that policymakers have multiple options for exploiting “spending persistence” in health plan payment systems. In line with McGuire, Zink, and Rose (2020), we conclude that the conventional method of “adding variables to the RA model” is not necessarily the best strategy. In the light of the tradeoff between selection and efficiency, a combination of constrained regression and high‐risk pooling can lead to better outcomes. The exact specification of such a model, however, requires further research. For example, our choice for a “50% reduction of the overcompensation on the group with multiple‐year low spending” is somewhat arbitrary. We found that—for the 15 subgroups used for evaluation of our models—a reduction of 33% would be optimal. With another set of subgroups and/or a different specification of the RA model, a different percentage reduction may be optimal. The same may be true for the parameters of our high‐risk pooling modality, and for the definitions of “multiple‐year low spending” and “multiple‐year high spending”.
Finally, we would like to mention two other interesting directions for future research. The first is the design and evaluation of “multiple” constraints based on different subgroups of spending persistence (e.g., the eight groups in Table 1). It would be interesting to examine what an appropriate specification of multiple constraints looks like and how the outcomes compare to those of “MYHC adjustor & MYLC adjustor” and “MYHC pooling & MYLC constraint.” Another interesting question for further research is how the approach of “exploiting spending‐level persistence” compares to other strategies for improving payment systems such as “improving/extending morbidity classifications.” A potential advantage of the latter is that “morbidity” might be a better indicator for future healthcare needs than “spending.” However, given the substantial under/overcompensations under our “base model” (which already includes rich morbidity classifications), a key question is whether morbidity–based indicators alone can sufficiently reduce selection incentives for insurers.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the valuable comments on earlier versions of this paper by Thomas McGuire, Sonja Schillo, Wynand van de Ven, Suzanne van Veen, two anonymous reviewers, the participants of the Risk Adjustment Network meeting in Portland and the participants of the Dutch advisory board for scientific research on insurer data. The authors are also grateful to the Dutch Ministry of Health, Welfare and Sports and the Association of Health Insurers for access to (anonymized) claims data. They also thank the Netherlands Institute for Health Services Research (NIVEL) for access to morbidity information from General Practitioners. This study has been approved according to the governance code of NIVEL Primary Care Database, under number NZR–00317.059. Dutch law allows the use of electronic health records for research purposes under certain conditions. According to this legislation, neither obtaining informed consent from patients nor approval by a medical ethics committee is obligatory for this type of observational studies containing no directly identifiable data (Dutch Civil Law, Article 7:458). This research did not receive any specific grant from funding agencies in the public, commercial, or not–for–profit sectors.
TABLE A1.
Prevalence, mean costs and mean financial result under alternative payment systems for 109 chronic conditions identified by NIVEL‐PCD
| Prev. | Mean costs | Mean financial result in Euros per person per year | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Base model | MYHC adjustor | MYHC pooling | MYLC adjustor | MYLC constraint | MYHC adjustor & MYLC adjustor | MYHC pooling & MYLC constraint | ||||
| A28 | Limited function/disability NOS | 0.10% | 5065 | −141 | 55 | −237 | −224 | 120 | 98 | 17 |
| A79 | Malignancy NOS | 0.04% | 12,963 | −3212** | −2823** | −1910** | −3245** | −2856** | −2786** | −1842** |
| A90 | Congenital anomaly OS/multiple | 0.18% | 4446 | −502* | −150 | −443** | −509* | −382 | −14 | −416** |
| B28 | Limited function/disability blood and/or blood forming organs | 0.01% | 5052 | −306 | 66 | 229 | −308 | −104 | 138 | 383 |
| B72 | Hodgkin's disease/lymphoma | 0.18% | 8004 | 1136** | 1162** | 407 | 1135** | 1449** | 1217** | 863** |
| B73 | Leukemia | 0.12% | 14,983 | −3942** | −3969** | −2644** | −3980** | −3610** | −3920** | −2523** |
| B74 | Malignant neoplasm blood other | 0.07% | 20,674 | −6427** | −6141** | −2996** | −6522** | −5985** | −6109** | −2843** |
| B78 | Hereditary hemolytic anemia | 0.21% | 2539 | −137 | −96 | −71 | −66 | −99 | −36 | −39 |
| B79 | Congen.anom. blood/lymph other | 0.04% | 7145 | −2175** | −1802* | −1282* | −2146** | −2038** | −1726* | −1245* |
| B83 | Purpura/coagulation defect | 0.55% | 5805 | −754** | −591** | −512** | −709** | −601** | −521** | −416** |
| B90 | HIV‐infection/aids | 0.11% | 15,569 | −1571** | −1014** | −1075** | −1541** | −1107** | −984** | −737** |
| D28 | Limited function/disability (d) | 0.03% | 8779 | −2300** | −1354 | −290 | −2302** | −2029* | −1281 | −317 |
| D74 | Malignant neoplasm stomach | 0.05% | 8793 | 294 | 48 | −524 | 244 | 667 | 84 | −49 |
| D75 | Malignant neoplasm colon/rectum | 0.61% | 8443 | −341* | −350* | −390** | −340* | 73 | −313* | 47 |
| D76 | Malignant neoplasm pancreas | 0.02% | 12,048 | −514 | −1240 | −993 | −480 | −77 | −1216 | −471 |
| D77 | Malig. neoplasm digest other/NOS | 0.16% | 8865 | −446 | −494 | −763** | −447 | −115 | −440 | −419 |
| D81 | Congen. anomaly digestive system | 0.27% | 1981 | −435** | −350** | −355** | −360** | −487** | −248** | −437** |
| D92 | Diverticular disease | 1.51% | 5140 | −469** | −310** | −311** | −435** | −177** | −241** | −65 |
| D94 | Chronic enteritis/ulcerative colitis | 0.75% | 6120 | −525** | −432** | −411** | −467** | −233* | −370** | −158* |
| D97 | Liver disease NOS | 0.55% | 5317 | −766** | −649** | −538** | −727** | −527** | −579** | −335** |
| F28 | Limited function/disability eye | 0.16% | 3899 | −450* | −317 | −164 | −460* | −299 | −256 | −68 |
| F81 | Congenital anomaly eye other | 0.17% | 2222 | −383** | −299** | −245** | −341** | −383** | −245* | −290** |
| F83 | Retinopathy | 0.58% | 7685 | −702** | −486** | −292** | −732** | −271 | −468** | 76 |
| F84 | Macular degeneration | 0.52% | 6552 | −898** | −476** | −498** | −897** | −519** | −429** | −243** |
| F91 | Refractive error | 2.79% | 2213 | −195** | −157** | −177** | −172** | −208** | −117** | −201** |
| F93 | Glaucoma | 1.27% | 4255 | −34 | −21 | −55 | −36 | 253** | 2 | 247** |
| F94 | Blindness | 0.20% | 5103 | −821** | −613** | −596** | −835** | −612** | −576** | −441* |
| H28 | Limited function/disability ear | 0.09% | 4433 | −1078* | −912 | −399* | −1010* | −929 | −824 | −280 |
| H80 | Congenital anomaly of ear | 0.11% | 2468 | −643** | −509** | −491** | −559** | −671** | −419** | −553** |
| H83 | Otosclerosis | 0.08% | 3122 | −93 | −44 | −174 | −21 | 24 | 32 | −62 |
| H84 | Presbyacusis | 1.44% | 5489 | −249** | −150* | −185** | −245** | 91 | −95 | 142** |
| H85 | Acoustic trauma | 0.29% | 3650 | −298* | −179 | −185* | −252* | −163 | −117 | −80 |
| H86 | Deafness | 1.75% | 4138 | −452** | −342** | −334** | −405** | −278** | −266** | −189** |
| K28 | Limited function/disability cardiovascular | 0.12% | 4535 | −565 | −534 | −311 | −548 | −342 | −497 | −84 |
| K73 | Congenital anomaly cardiovascular | 0.32% | 3275 | −195 | −90 | −172* | −161 | −119 | −11 | −109 |
| K74 | Ischemic heart disease w. angina | 2.36% | 6407 | −458** | −290** | −342** | −462** | −68 | −250** | 8 |
| K76 | Acute myocardial infarction | 1.07% | 6735 | −564** | −383** | −330** | −582** | −165 | −353** | 20 |
| K77 | Heart failure | 1.10% | 10,023 | −836** | −569** | −368** | −964** | −310** | −586** | 55 |
| K82 | Pulmonary heart disease | 0.05% | 14,304 | −1767 | −1071 | −432 | −1953* | −1317 | −1065 | −179 |
| K86 | Hypertension uncomplicated | 13.68% | 4182 | −159** | −158** | −174** | −151** | 82** | −128** | 80** |
| K87 | Hypertension complicated | 1.96% | 6427 | −594** | −510** | −404** | −634** | −226** | −477** | −57 |
| K90 | Stroke/cerebrovascular accident | 1.64% | 6627 | −367** | −245** | −258** | −602** | 38 | −219** | 142** |
| K91 | Atherosclerosis [ex. K76,K90] | 1.13% | 5387 | −467** | −396** | −341** | −495** | −156 | −357** | −46 |
| K92 | Cardiovascular disease other | 1.75% | 6550 | −932** | −792** | −548** | −964** | −612** | −765** | −297** |
| L28 | Limited function/disability musculoskeletal | 0.29% | 5095 | −331* | −159 | −303** | −425** | −85 | −113 | −104 |
| L82 | Congenital anomaly musculoskeletal | 0.93% | 1957 | −202** | −156** | −188** | −198** | −226** | −101 | −229** |
| L84 | Back syndrome w/o radiating pain | 1.39% | 4990 | −470** | −329** | −321** | −460** | −177** | −284** | −70 |
| L85 | Acquired deformity of spine | 0.76% | 2873 | −126* | −84 | −172** | −158** | −61 | −44 | −112* |
| L88 | Rheumatoid/seropositive arthritis | 1.29% | 6396 | −229** | −124 | −170** | −228** | 101 | −89 | 160** |
| L89 | Osteoarthrosis of hip | 2.11% | 5577 | −624** | −509** | −463** | −617** | −287** | −468** | −167** |
| L90 | Osteoarthrosis of knee | 2.97% | 5344 | −580** | −466** | −461** | −569** | −253** | −426** | −156** |
| L91 | Osteoarthrosis other | 2.53% | 4445 | −381** | −272** | −271** | −358** | −120** | −228** | −30 |
| L95 | Osteoporosis | 2.34% | 5563 | −567** | −403** | −395** | −587** | −249** | −348** | −123** |
| L98 | Acquired deformity of limb | 3.30% | 2724 | −201** | −155** | −183** | −164** | −134** | −107** | −127** |
| N28 | Limited function/disability neurological system | 0.03% | 4578 | −38 | 62 | −240 | −186 | 166 | 98 | −88 |
| N70 | Poliomyelitis | 0.04% | 5022 | −684* | −568 | −700** | −931** | −462 | −501 | −508 |
| N74 | Malignant neoplasm nervous system | 0.05% | 9548 | −1172 | −1183 | −551 | −1220 | −873 | −1115 | −311 |
| N85 | Congenital anomaly neurological | 0.11% | 6137 | −233 | 519* | −273 | −404 | −51 | 619** | −254 |
| N86 | Multiple sclerosis | 0.17% | 9356 | −594** | −402* | −469** | −1312** | −251 | −348 | −250* |
| N87 | Parkinsonism | 0.26% | 8810 | −99 | −15 | 36 | −1047** | 382 | −6 | 545** |
| N88 | Epilepsy | 0.98% | 4523 | −281** | −189* | −192** | −308** | −65 | −130 | −1 |
| P28 | Limited function/disability psychological | 0.08% | 3724 | −448 | −375 | −431 | −453 | −305 | −351 | −267 |
| P70 | Dementia | 0.56% | 4465 | 1361** | 1376** | 1051** | 1304** | 1764** | 1415** | 1555** |
| P72 | Schizophrenia | 0.27% | 3201 | −84 | −154 | −123 | −67 | 141 | −146 | 137 |
| P80 | Personality disorder | 0.90% | 3062 | −377** | −286** | −299** | −333** | −271** | −243** | −232** |
| P85 | Mental retardation | 0.46% | 3007 | −194* | −142 | −164** | −198* | −93 | −92 | −72 |
| R28 | Limited function/disability respiratory system | 0.07% | 6401 | −544 | −415 | −498* | −676* | −300 | −370 | −272 |
| R84 | Malignant neoplasm bronchus/lung | 0.18% | 12,973 | −1291** | −1537** | −1569** | −1459** | −814* | −1538** | −1049** |
| R85 | Malignant neoplasm respiratory, other | 0.07% | 9020 | −727 | −484 | −605 | −725 | −352 | −439 | −295 |
| R89 | Congenital anomaly respiratory | 0.03% | 5248 | −1358 | −1052 | −539 | −1407 | −1289 | −956 | −503 |
| R91 | Chronische bronchitis/bronchiëctasieën | 0.76% | 4901 | −391** | −285** | −322** | −427** | −153 | −254** | −121 |
| R95 | Chronic obstructive pulmonary disease | 2.72% | 6955 | −569** | −520** | −517** | −696** | −178** | −495** | −135** |
| R96 | Asthma | 8.56% | 2618 | −160** | −144** | −159** | −126** | −90** | −100** | −89** |
| S28 | Limited function/disability skin | 0.03% | 3193 | 14 | 85 | −91 | 7 | 143 | 146 | −16 |
| S77 | Malignant neoplasm of skin | 2.78% | 4657 | −357** | −259** | −254** | −314** | −120* | −188** | −34 |
| S81 | Hemangioma/lymphangioma | 0.65% | 2297 | −129 | −96 | −45 | −88 | −99 | −46 | −22 |
| S83 | Congenital skin anomaly other | 0.25% | 2334 | −154 | −132 | −230** | −113 | −129 | −84 | −206* |
| S87 | Dermatitis/atopic eczema | 8.12% | 1856 | −116** | −108** | −103** | −95** | −137** | −81** | −130** |
| S91 | Psoriasis | 2.18% | 3661 | −197** | −171** | −173** | −182** | −48 | −142** | −27 |
| T28 | Limited function/disability endocrine system | 0.01% | 11,386 | −5738 | −4970 | −703 | −5863 | −5520 | −4945 | −732 |
| T71 | Malignant neoplasm thyroid | 0.05% | 4967 | −32 | 112 | 111 | −26 | 315 | 143 | 430* |
| T78 | Thyroglossal duct/cyst | 0.08% | 2698 | −428 | −393 | −182 | −370 | −413 | −331 | −169 |
| T80 | Congenital anom endocrine/metab | 0.09% | 5999 | −1652** | −870* | −672** | −1591** | −1536** | −753 | −747** |
| T81 | Goiter [ex. T85,T86] | 0.45% | 3750 | −243** | −170 | −235** | −213* | −31 | −117 | −27 |
| T86 | Hypothyroidism/myxedema | 2.46% | 3939 | −77 | −78 | −92** | −80 | 189** | −60 | 183** |
| T90 | Diabetes | 6.10% | 5915 | −255** | −205** | −206** | −274** | 130** | −185** | 180** |
| T92 | Gout | 2.19% | 5363 | −492** | −421** | −352** | −492** | −243** | −390** | −134** |
| T93 | Endocrine/metab/nutrit. dis. other | 7.05% | 3915 | −75** | −75** | −105** | −73** | 169** | −56* | 148** |
| U28 | Limited function/disability urinary | 0.06% | 11,980 | −1566* | −396 | −416 | −1838* | −1139 | −370 | −266 |
| U75 | Malignant neoplasm of kidney | 0.10% | 10,288 | −1160** | −1051* | −702** | −1188** | −734 | −1020* | −339 |
| U76 | Malignant neoplasm of bladder | 0.25% | 8422 | −483* | −247 | −307* | −524* | −3 | −252 | 137 |
| U77 | Malignant neoplasm urinary other | 0.02% | 7065 | 392 | 507 | −160 | 364 | 854 | 531 | 344 |
| U85 | Congenital anomaly urinary tract | 0.17% | 3994 | −248 | −134 | −309** | −164 | −165 | −48 | −239* |
| U88 | Glomerulonephritis/nephrosis | 0.14% | 6549 | −521 | −352 | −223 | −500 | −320 | −300 | −71 |
| W28 | Limited function/disability due to pregnancy | 0.08% | 2029 | −27 | 42 | −159 | 138 | 68 | 193 | −63 |
| W72 | Malignant neoplasm relate to pregnancy | 0.00% | 3689 | 362 | 1165 | 359 | 565 | 506 | 1344 | 393 |
| W76 | Congenital anomaly complicate pregnancy | 0.01% | 3762 | −2067 | −2003 | −2093 | −2019 | −2034 | −1950 | −2081 |
| X28 | Limited function/disability female genital | 0.01% | 3784 | −685 | −542 | −638 | −546 | −533 | −400 | −612 |
| X75 | Malignant neoplasm cervix | 0.21% | 3719 | −406** | −337* | −263* | −370* | −246 | −284 | −124 |
| X76 | Malignant neoplasm breast female | 1.20% | 5923 | −34 | −17 | −254** | −72 | 298** | 40 | 126* |
| X77 | Malignant neoplasm female genital other | 0.23% | 5786 | −247 | −166 | −249* | −228 | 63 | −115 | 44 |
| X83 | Congenital anomaly female genital | 0.05% | 2132 | −173 | −180 | −31 | −108 | −141 | −124 | −14 |
| X88 | Fibrocystic disease breast | 1.25% | 2447 | −173** | −153** | −181** | −112** | −91* | −97* | −98** |
| Y28 | Limited function/disability male genital | 0.07% | 4366 | −350 | −228 | −231 | −327 | −158 | −185 | −60 |
| Y77 | Malignant neoplasm prostate | 0.52% | 8006 | −728** | −706** | −427** | −753** | −305* | −683** | −70 |
| Y78 | Malign neoplasm male genital other | 0.10% | 3600 | 262 | 136 | −156 | 341 | 339 | 224 | 20 |
| Y82 | Hypospadias | 0.08% | 1713 | −251 | −171 | −80 | −231 | −328 | −124 | −189 |
| Y84 | Congenital genital anomaly male other | 0.04% | 1980 | −571* | −442 | −377* | −467 | −696* | −341 | −539** |
| Z28 | Limited function/disability social | 0.32% | 3116 | −80 | −27 | −47 | −92 | 10 | −13 | 32 |
| Weighted mean absolute result (WMAR) of all groups presented above | 326 | 263 | 254 | 328 | 192 | 228 | 141 | |||
Note: See Nielen et al. (2019) for the construction of disease groups.
* Statistically significantly different from zero (p < 0.05).
** Statistically significantly different from zero (p < 0.01).
van Kleef, R. C. , & van Vliet, R. C. J. A. (2022). How to deal with persistently low/high spenders in health plan payment systems? Health Economics, 31(5), 784–805. 10.1002/hec.4477
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the Dutch Ministry of Health, Welfare, and Sports and the Dutch Association of Health Insurers. Restrictions apply to the availability of these data, which were used under license for this study.
REFERENCES
- Akerlof, G. A. (1970). The market for “lemons”: Quality uncertainty and the market mechanism. Quarterly Journal of Economics, 84, 488–500. [Google Scholar]
- Battaglia, M. P. , Hoaglin, D. C. , & Frankel, M. R. (2009). Practical considerations in raking survey data. Survey Practice, 2–5, 1–10. [Google Scholar]
- Bauhoff, S. (2012). Do health plans risk‐select? An audit study on Germany's social health insurance. Journal of Public Economics, 96, 750–759. [Google Scholar]
- Bauhoff, S. , Fischer, L. , Göpffarth, D. , & Wuppermann, A. C. (2017). Plan responses to diagnosis‐based payment: Evidence from Germany's morbidity‐based risk adjustment. Journal of Health Economics, 56, 397–413. [DOI] [PubMed] [Google Scholar]
- Carey, C. (2017a). Technological change and risk adjustment: Benefit design incentives in Medicare Part D. American Economic Journal: Economic Policy, 9, 38–73. [Google Scholar]
- Carey, C. (2017b). A time to harvest: Evidence on consumer choice frictions from a payment revision in Medicare Part D [Working Paper]. [Google Scholar]
- Decoralis, F. , & Guglielmo, A. (2017). Insurers' response to selection risk: Evidence from Medicare enrollment reforms. Journal of Health Economics, 56, 383–396. [DOI] [PubMed] [Google Scholar]
- Duijmelinck, D. M. I. D. , & Van de Ven, W. P. M. M. (2014). Choice of insurer for basic health insurance restricted by supplementary insurance. European Journal of Health Economics, 15, 737–746. [DOI] [PubMed] [Google Scholar]
- Eijkenaar, F. , Van Vliet, R. C. J. A. , & Van Kleef, R. C. (2019). Risk equalization in competitive health insurance markets: Identifying healthy individuals on the basis of multiple‐year low spending. Health Services Research, 54, 455–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Einav, L. , & Finkelstein, A. (2011). Selection in insurance markets: Theory and empirics in pictures. Journal of Economic Perspectives, 25, 115–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis, R. P. , Martins, B. , & Rose, S. (2018). Risk adjustment for health plan payment. In McGuire T. G. & Van Kleef R. C. (Eds.), Risk adjustment, risk sharing and premium regulation in health insurance markets: Theory and practice (pp. 55–104). Elsevier. [Google Scholar]
- Enthoven, A. C. (2012). Health care, the market and consumer choice. Edward Elgar Publishing Limited. [Google Scholar]
- Geruso, M. , & Layton, T. J. (2020). Upcoding: Evidence from Medicare on squishy risk adjustment. Journal of Political Economy, 128(3), 984–1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geruso, M. , Layton, T. J. , & Prinz, D. (2019). Screening in contract design: Evidence from the ACA health insurance exchanges. American Economic Journal: Economic Policy, 11(2), 64–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geruso, M. , & McGuire, T. G. (2016). Tradeoffs in the design of health plan payment systems: Fit, power and balance. Journal of Health Economics, 47, 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glazer, J. , & McGuire, T. G. (2000). Optimal risk adjustment of health insurance premiums: An application to managed care. American Economic Review, 90, 1055–1071. [Google Scholar]
- Han, T. , & Lavetti, K. (2017). Does part D abet advantageous selection in Medicare advantage? Journal of Health Economics, 56, 368–382. [DOI] [PubMed] [Google Scholar]
- Lamberts, H. , & Wood, M. (1987). International classification of primary care. Oxford University Press. [Google Scholar]
- Lavetti, K. , & Simon, K. (2018). Strategic formulary design in Medicare Part D plans. American Economic Journal: Economic Policy, 10, 154–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton, T. J. , Ellis, R. P. , McGuire, T. G. , & van Kleef, R. C. (2017). Measuring efficiency of health plan payment systems in managed competition health insurance markets. Journal of Health Economics, 56, 237–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton, T. J. , McGuire, T. G. , & van Kleef, R. C. (2018). Deriving risk adjustment weights to maximize efficiency of health insurance markets. Journal of Health Economics, 61, 93–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchand, M. , Sato, M. , & Schokkaert, E. (2003). Prior health expenditures and risk sharing with insurers competing on quality. The RAND Journal of Economics, 34, 647–669. [PubMed] [Google Scholar]
- McGuire, T. G. , Schillo, S. , & van Kleef, R. C. (2020). Reinsurance, repayments, and risk adjustment in individual health insurance: Germany, the Netherlands and the U.S. Marketplaces. American Journal of Health Economics, 6, 139–168. [Google Scholar]
- McGuire, T. G. , & van Kleef, R. C. (2018). Regulated competition in health insurance markets: Paradigms and ongoing issues. In McGuire T. G. & van Kleef R. C. (Eds.), Risk adjustment, risk sharing and premium regulation in health insurance markets: Theory and practice (pp. 55–104). Elsevier. [Google Scholar]
- McGuire, T. G. , Zink, A. L. , & Rose, S. (2020). Simplifying and improving the performance of risk adjustment systems [NBER Working Paper 26736]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monheit, A. C. (2003). Persistence in health expenditures in the short run: Prevalence and consequences. Medical Care, III53–III64. [DOI] [PubMed] [Google Scholar]
- Newhouse, J. P. (1996). Reimbursing health insurers and health providers: Efficiency in production versus selection. Journal of Economic Literature, 34, 1236–1263. [Google Scholar]
- Nielen, M. , Spronk, I. , Davids, R. , Korevaar, J. C. , Poos, M. J. J. C. , Hoeymans, N. , Opstelten, W. , van der Sande, M. A. B. , Biermans, M. C. J. , Schellevis, F. G. , & Verheij, R. A. (2019). A new method for aggregating large number of encoded patient records from heterogeneous sources to estimate morbidity rates. JMIR Medical Informatics. Forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothschild, M. , & Stiglitz, J. (1976). Equilibrium in competitive insurance markets: An essay on the economics of imperfect information. Quarterly Journal of Economics, 90, 629–649. [Google Scholar]
- Schillo, S. , Lux, G. , Wasem, J. , & Buchner, F. (2016). High‐cost pool or high‐cost groups? How to handle the high(est) cost cases in a risk adjustment mechanism. Health Policy, 120(2), 141–147. [DOI] [PubMed] [Google Scholar]
- van Barneveld, E. M. , Lamers, L. M. , van Vliet, R. C. J. A. , & van de Ven, W. P. M. M. (2001). Risk sharing as a supplement to imperfect capitation: A tradeoff between selection and efficiency. Journal of Health Economics, 20, 147–168. [DOI] [PubMed] [Google Scholar]
- van Barneveld, E. M. , van Vliet, R. C. J. A. , & van de Ven, W. P. M. M. (1996). Mandatory high‐risk pooling: An approach to reducing incentives for cream skimming. Inquiry, 33, 133–143. [PubMed] [Google Scholar]
- Van de Ven, W. P. M. M. , Beck, K. , Buchner, F. , Schokkaert, E. , Schut, F. T. , Shmueli, A. , & Wasem, J. (2013). Preconditions for efficiency and affordability in competitive healthcare markets: Are they fulfilled in Belgium, Germany, Israel, the Netherlands and Switzerland? Health Policy, 109, 226–245. [DOI] [PubMed] [Google Scholar]
- van de Ven, W. P. M. M. , & Ellis, R. P. (2000). Risk adjustment in competitive health insurance markets. In Culyer A. J. & Newhouse J. P. (Eds.), Handbook of health economics (Chapter 14, pp. 755–845). Elsevier. [Google Scholar]
- van Kleef, R. C. , Eijkenaar, F. , & van Vliet, R. C. J. A. (2019). Selection incentives for health insurers in the presence of sophisticated risk adjustment. Medical Care Research and Review, 77, 584–595. 10.1177/1077558719825982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Kleef, R. C. , Eijkenaar, F. , van Vliet, R. C. J. A. , & Nielen, M. (2020). Exploiting incomplete information in risk adjustment using constrained regression. American Journal of Health Economics, 6(4), 477–497. [Google Scholar]
- van Kleef, R. C. , Eijkenaar, F. , van Vliet, R. C. J. A. , & van de Ven, W. P. M. M. (2018). Health plan payment in the Netherlands. In McGuire T. G. & van Kleef R. C. (Eds.), Risk adjustment, risk sharing and premium regulation in health insurance markets. Elsevier Publishing. [Google Scholar]
- van Kleef, R. C. , McGuire, T. G. , van Vliet, R. C. J. A. , & van de Ven, W. P. M. M. (2017). Improving risk equalization with constrained regression. The European Journal of Health Economics, 18, 1137–1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Kleef, R. C. , & van Vliet, R. C. J. A. (2012). Improving risk equalization using multiple‐year high cost as a health indicator. Medical Care, 50, 140–144. [DOI] [PubMed] [Google Scholar]
- van Veen, S. H. C. M. (2016). Evaluating and improving the predictive performance of risk equalization models in health insurance markets [Dissertation]. Erasmus University Rotterdam. https://repub.eur.nl/pub/79939 [Google Scholar]
- Withagen‐Koster, A. A. , van Kleef, R. C. , & Eijkenaar, F. (2020). Incorporating self‐reported health measures in risk equalization through constrained regression. The European Journal of Health Economics, 21, 513–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the Dutch Ministry of Health, Welfare, and Sports and the Dutch Association of Health Insurers. Restrictions apply to the availability of these data, which were used under license for this study.


