Thermodynamically Favourable States in the Reaction of Nitrogenase without Dissociation of any Sulfide Ligand

Abstract

We have used combined quantum mechanical and molecular mechanical (QM/MM) calculations to study the reaction mechanism of nitrogenase, assuming that none of the sulfide ligands dissociates. To avoid the problem that there is no consensus regarding the structure and protonation of the E₄ state, we start from a state where N₂ is bound to the cluster and is protonated to N₂H₂, after dissociation of H₂. We show that the reaction follows an alternating mechanism with HNNH (possibly protonated to HNNH₂) and H₂NNH₂ as intermediates and the two NH₃ products dissociate at the E₇ and E₈ levels. For all intermediates, coordination to Fe6 is preferred, but for the E₄ and E₈ intermediates, binding to Fe2 is competitive. For the E₄, E₅ and E₇ intermediates we find that the substrate may abstract a proton from the hydroxy group of the homocitrate ligand of the FeMo cluster, thereby forming HNNH₂, H₂NNH₂ and NH₃ intermediates. This may explain why homocitrate is a mandatory component of nitrogenase. All steps in the suggested reaction mechanism are thermodynamically favourable compared to protonation of the nearby His‐195 group and in all cases, protonation of the NE2 atom of the latter group is preferred.

The reaction mechanism of nitrogenase from N₂H₂ to 2 NH₃ without any dissociated sulfide ligands has been studied by QM/MM methods. The calculations suggest an alternating mechanism in which the substrate binds to Fe6. Homocitrate functions as a proton buffer, stabilising H₂NNH₂ and NH₃ intermediates. The two NH₃ products dissociate at the E₇ and E₈ levels. His‐195 prefers protonation on the NE2 atom and proton transfer from this residue is favourable for all steps.

Introduction

Nitrogen is an essential element of all lifeforms, being a component of all amino acids and nucleic acids. Although the atmosphere of Earth contains 78 % of N₂, nitrogen is still a limiting element for plant growth and a prominent component of fertilizers. The reason for this is the strong triple bond in N₂, which makes it chemically inert.[ ¹ , ² ] Industrially, N₂ is converted to ammonia through the Haber–Bosch process, which requires high temperature and pressure. ^[2] Only a single group of enzymes can cleave the N−N bond in N₂, the nitrogenases (EC 1.18/19.6.1), which work at ambient temperature and pressure.[ ¹ , ³ , ⁴ ]

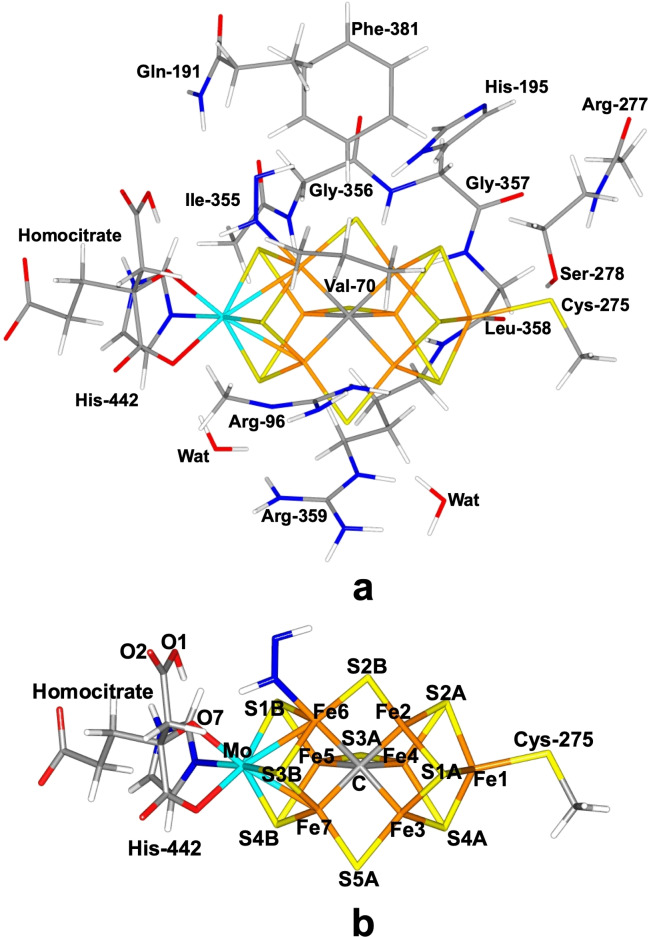
Crystallographic studies have shown that the most active type of nitrogenase contains a MoFe₇S₉C(homocitrate) cluster (the FeMo cluster) in the active site, connected to the protein by a histidine and a cysteine residue at the opposite ends of the cluster (Figure 1).[ ⁵ , ⁶ , ⁷ , ⁸ , ⁹ ] There also exist alternative nitrogenases with the Mo ion replaced with either vanadium or iron, which have lower activities towards N₂. ^[10]

Figure 1.

Structure of the FeMo cluster (with trans‐HNNH bound to Fe6), illustrating also the QM system used in all calculations, as well as the names of the nearby residues (a). (b) shows only the FeMo cluster with atom names indicated.

The nitrogenases catalyse the reaction

$${\displaystyle \mathrm{N}{}_2+8e{}^{-}+8\mathrm{H}{}^{+}+16\mathrm{ATP}\to 2\mathrm{NH}{}_3+\mathrm{H}{}_2+16\mathrm{ADP}+16\mathrm{P}{}_{\mathrm{i}}}$$ (1)

The mechanism is normally discussed in terms of nine intermediates E₀–E₈, differing in the number of added electrons and protons, according to the Lowe–Thorneley scheme. ^[11] Thorough biochemical, kinetic and spectroscopic studies have indicated that the resting E₀ state needs to be reduced to the E₄ state before N₂ may bind.[ ¹ , ³ , ⁴ , ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ ] It has also been suggested that H₂ formation through reductive elimination is a prerequisite for the binding of N₂, explaining why H₂ is a compulsory byproduct in the reaction. It is normally assumed that N₂ is directly reduced and protonated to N₂H₂ upon binding to the enzyme.[ ¹ , ¹⁸ ]

It has long been debated whether the nitrogenases follow a sequential or alternating reaction mechanism. In the sequential mechanism, the first three protons bind to the same N atom of N₂, which then dissociates as NH₃ from the E₅ intermediate, before the second N atom starts to be protonated. This mechanism was originally suggested by Chatt and has gained support from inorganic model complexes.[ ¹⁹ , ²⁰ , ²¹ , ²² , ²³ ] In the alternating mechanism, the protons are instead added alternatively to the two N atoms, so that HNNH and H₂NNH₂ (hydrazine) are intermediates and the first NH₃ product does not dissociate until the E₇ state. It is supported by the fact that nitrogenase can use hydrazine as a substrate and that hydrazine is released upon acid or base hydrolysis of the enzyme during turnover.[ ¹ , ³ , ²⁴ , ²⁵ ] Moreover, it has been shown that N₂, N₂H₂, CH₃NH₂ and N₂H₄ all react via a common intermediate.[ ¹ , ²⁶ ]

The nitrogenases have been thoroughly studied also by computational methods.[ ¹ , ¹³ , ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ³² , ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ , ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ , ⁴² ] Unfortunately, these studies have given very diverging and disparate suggestions. In fact, there is not even any consensus about the structure of the key E₄ intermediate. Important reasons for this are that different density‐functional theory (DFT) methods give very different predictions of the relative stability of various intermediates, with differences of 600 kJ/mol ^[43] and that there are very many possibilities for the structures and electronic states of the intermediates.[ ⁴⁴ , ⁴⁵ ]

Hoffman and coworkers have suggested a structure of the E₄ intermediate with two hydride ions bridging the Fe2 and Fe6 ions, as well as the Fe3 and Fe7 ions, and with two protons on the S2B and the S5A sulfides, all positioned on the same face of the FeMo cluster[ ¹⁵ , ⁴⁶ ] (the name of the various Fe and sulfide ions are shown in Figure 1b). They have shown that this structure is lower in energy than a few other structures and that it may bind N₂ after reductive elimination of the two hydride ions, leaving the cluster in a doubly reduced state.[ ¹⁵ , ⁴¹ , ⁴⁷ , ⁴⁸ ]

On the other hand, Siegbahn has suggested that the FeMo cluster needs to be reduced by four electrons from the resting state before the true E₀ state is reached, which involves a triply protonated central carbide and a strongly distorted cluster. ^[49] Then, this state is reduced by another four electrons to reach the E₄ state, from which H₂ dissociates and N₂ binds, bridging two Fe ions. It is successively protonated in a manner that is a mixture of the alternating and sequential mechanism, involving NNH₂, HNNH₂, H₂NNH₂, but also HNNH₃. The first NH₃ dissociates at the E₇ level.

Dance has presented a mechanism in which E₄ contains two terminal hydride ions on Fe2 and Fe6, and two protons on S2B and S3B. N₂ then binds side‐on to Fe6, without any dissociation of H₂ and is alternatively protonated to H₂NNH₂, at which level the N−N bond is cleaved, forming two NH₂ fragments on Fe2 and Fe6.[ ²⁷ , ⁵⁰ , ⁵¹ ]

On the other hand, Nørskov and coworkers have suggested a mechanism in which the E₀ state is doubly protonated and a sulfide ligand dissociates from the cluster during the reaction mechanism. ^[37] This forms a binding site, where N₂ binds in an end‐on fashion, bridging two Fe ions and it is then sequentially protonated on the outer N atom. The dissociation of the sulfide ion was inspired by several crystallographic studies of both Mo and V nitrogenase, showing that the S2B group can be replaced by several other ligands, for example CO, OH⁻ and Se.[ ⁸ , ⁵² , ⁵³ , ⁵⁴ , ⁵⁵ , ⁵⁶ ]

Recently, we studied a similar mechanism, involving dissociation of S2B. ^[57] We used a larger and more realistic model system, which was studied with the combined quantum mechanical and molecular mechanics (QM/MM) approach. Our study indicated that the conversion of N₂H₂ to two NH₃ molecules is thermodynamically favourable, but it follows a mainly alternating pathway (although the first intermediate involved a bridging NNH₂ group, which is normally connected to a sequential mechanism).

Naturally, such studies do not prove that the nitrogenase mechanism actually involves a dissociated S2B group. To that end, it must be shown that the replacement of S2B by N₂ is energetically favourable, which has been questioned by Dance. ^[58] Moreover, it should be shown that a reaction without replacement of S2B is not possible or at least is less favourable. Here, we make an investigation of the latter reactions, that is, the formation of ammonia from bound N₂ for Mo nitrogenase without dissociation of S2B. We show that also such a reaction is possible and thermodynamic favourable, following an alternating mechanism.

Methods

The protein

The calculations were based on the 1.0‐Å crystal structure of Mo nitrogenase from Azotobacter vinelandii (PDB code 3U7Q). ^[7] The setup of the protein is identical to that of our previous studies.[ ⁴³ , ⁵⁹ , ⁶⁰ , ⁶¹ ] The entire heterotetramer was considered in the calculations, because the various subunits are entangled without any natural way to separate them. The quantum mechanical (QM) calculations were concentrated on the FeMo clusters in the C subunit because there is a buried imidazole molecule from the solvent rather close to the active site (∼11 Å) in the A subunit. The two P‐clusters and the FeMo cluster in subunit A were modelled by MM in the fully reduced and resting states, respectively, using a QM charge model. ^[59]

The protonation states of all residues were the same as before: ^[59] All Arg, Lys, Asp and Glu residues were assumed to be charged, except Glu‐153, 440 and 231D (a letter “D” after the residue number indicates that it belongs to that subunit; if no letter is given, it belongs to subunit C; subunits A and B are identical to the C and D residues). Cys residues coordinating to Fe ions were assumed to be deprotonated. His‐274, 451, 297D, 359D and 519D were assumed to be protonated on the ND1 atom, His‐31, 196, 285, 383, 90D, 185D, 363D and 457D were presumed to be protonated on both the ND1 and NE2 atoms (and therefore positively charged), whereas the remaining 14 His residues were modelled with a proton on the NE2 atom. The homocitrate ligand was modelled in the singly protonated state with a proton shared between the hydroxy group (which coordinates to Mo) and the O1 carboxylate atom. This protonation state was found to be the most stable one in an extensive QM/MM, molecular dynamics and quantum‐refinement study ^[59] and this protonation state is also supported by another QM/MM study. ^[62]

The protein was solvated in a sphere with a radius of 65 Å around the geometrical centre of the protein. 160 Cl⁻ and 182 Na⁺ ions were added at random positions (but not inside the protein ^[59] ) to neutralise the protein and give an ionic strength of 0.2 M. ^[63] The final system contained 133 915 atoms. The added protons, counter ions and water molecules were optimised by a simulated annealing calculation (up to 370 K), followed by a minimisation, keeping the other atoms fixed at the crystal‐structure positions. ^[59]

All MM calculations were performed with the Amber software. ^[64] For the protein, we used the Amber ff14SB force field ^[65] and water molecules were described by the TIP3P model. ^[66] For the metal sites, the MM parameters were the same as in our previous investigation. ^[59] The metal sites[ ⁴⁵ , ⁵⁹ ] were treated by a non‐bonded model ^[67] and charges were obtained with the restrained electrostatic potential method, obtained at the TPSS/def2‐SV(P) level of theory[ ⁶⁸ , ⁶⁹ ] and sampled with the Merz–Kollman scheme. ^[70]

The FeMo cluster was modelled by MoFe₇S₉C(homocitrate)(CH₃S) (imidazole), where the two last groups are models of Cys‐275 and His‐442. In addition, all groups that form hydrogen bonds to the FeMo cluster were also included in the QM model, viz. Arg‐96, Gln‐191 and His‐195 (sidechains), Ser‐278 and Arg‐359 (both backbone and sidechain, including the Cα and C and O atoms from Arg‐277), Gly‐356, Gly‐357 and Leu‐358 (backbone, including the Cα and C and O atoms from Ile‐355), as well as two water molecules. Finally, Phe‐381 and Val‐70 were also included because they are close to the putative N₂ binding site and therefore may affect the binding of the substrate. The QM system involved 183–190 atoms in total (depending on the number of added protons and N atoms) and is shown in Figure 1a. The net charge of QM region was −3.

QM calculations

All QM calculations were performed with the Turbomole software (version 7.5). ^[71] All structures were studied with both the TPSS ^[68] and B3LYP[ ⁷² , ⁷³ , ⁷⁴ ] functionals with def2‐SV(P) basis set. ^[69] The most stable states were examined also with the larger def2‐TZVPD basis set. The calculations were sped up by expanding the Coulomb interactions in an auxiliary basis set, the resolution‐of‐identity (RI) approximation.[ ⁷⁵ , ⁷⁶ ] Empirical dispersion corrections were included with the DFT‐D4 approach, ^[77] as implemented in Turbomole. All minima were fully optimized without any restraints. Transition states (for N−N cleavage and NH₃ dissociation) were determined as the highest point on the potential energy surface along the reaction coordinates, which were scanned with a step of 0.1 Å near the transition states.

Experiments have shown that the ground spin state of E₄ is a doublet,[ ¹ , ⁷⁸ ] and we used this state for E₄ models. For the other E _n states, we used mainly the doublet or triplet states, but for the most interesting structures, we checked which of the two or three lowest spin states has the most favourable energy at the TPSS and B3LYP/def2‐SV(P) levels of theory.

The electronic structure of all QM calculations was obtained with the broken‐symmetry (BS) approach: ^[79] Each of the seven Fe ions were modelled in the high‐spin state, with either a surplus of α (four Fe ions) or β (three Fe ions) spin. Such a state can be selected in 35 different ways $\left(\frac{7!}{3!4!}\right)$ . ^[60] The various BS states were obtained either by swapping the coordinates of the Fe ions ^[80] or with the fragment approach by Szilagyi and Winslow. ^[81] The various BS states are named by listing the number in the Noodleman nomenclature (BS1—10), ^[79] followed by the numbers of the three Fe ions with minority spin (however, in the tables, only the latter three numbers are given). Most structures were studied in the BS10‐147 state, i. e. with β spin on Fe1, Fe4 and Fe7, because it was found to be lowest in both this and in our previous study. ^[57] However, sometimes the calculations converged to other states (especially BS7‐235). For twelve of the most stable structures, the relative stabilities of all 35 states were examined (with structures fully optimised for each BS state). Moreover, for all structures within 20 kJ/mol of the most stable structure at each E _n level, the BS7‐235 state was also studied.

As have been discussed before,[ ⁴³ , ⁶⁰ ] TPSS/def2‐SV(P) calculations give geometries that reproduce the crystal structure of the resting state of nitrogenase excellently with average and maximum deviations of 0.05 and 0.09 Å for the metal–metal distances, and 0.02 and 0.06 Å for metal—ligand distances, and a root‐mean‐squared‐deviation (RMSD) of 0.06 Å for the metals and the first‐sphere ligands. This is similar to the results obtained with the TPSSh ^[62] approach and appreciably better than with the B3LYP/def2‐SV(P) method, which gives average and maximum deviations of 0.08 and 0.12 Å for the metal–metal and 0.04 and 0.11 Å metal–ligand distances, respectively and a RMSD of 0.08 Å. Therefore, we discuss primarily the TPSS/def2‐SV(P) results.

QM/MM calculations

QM/MM calculations were performed with the comqum software.[ ⁸² , ⁸³ ] In this approach, the protein and solvent are split into three subsystems: System 1 (the QM region) was relaxed by QM methods. System 2 contained all residues and water molecules with at least one atom within 6 Å of any atom in system 1 and it was optionally relaxed by MM. It included residues 49, 59–74, 92, 95–98, 189–199, 226–231, 234, 235, 253–255, 273–282, 300, 353–355, 358–364, 377–383, 385, 386, 401 422–427, 438, 440–444, 450 and 451 from subunit C and residues 93, 97, 98, 101 and 105 from subunit D, in total 94 residues and 39 water molecules). Finally, system 3 contained the remaining part of the protein and the solvent, and it was kept fixed at the original coordinates (equilibrated crystal structure to avoid the risk that different calculations end up in different local minima). The total system was spherical and non‐periodic with 133 915 atoms. Most calculations were performed without relaxing system 2, but for the most interesting structures, calculations with relaxed surroundings were also performed. The effect of the relaxed surroundings are described in the Supporting Information.

In the QM calculations, system 1 was represented by a wavefunction, whereas all the other atoms were represented by an array of partial point charges, one for each atom, taken from the MM setup. Thereby, the polarisation of the QM system by the surroundings is included in a self‐consistent manner (electrostatic embedding). When there is a bond between systems 1 and 2 (a junction), the hydrogen link‐atom approach was employed: The QM system was capped with hydrogen atoms (hydrogen link atoms, HL), the positions of which are linearly related to the corresponding carbon atoms (carbon link atoms, CL) in the full system.[ ⁸² , ⁸⁴ ] All atoms were included in the point‐charge model, except the CL atoms. ^[85]

The total QM/MM energy in ComQum is calculated as[ ⁸² , ⁸³ ]

$${\displaystyle E_{\mathrm{QM}/\mathrm{MM}}=E_{\mathrm{QM}1+\mathrm{ptch}23}^{\mathrm{HL}}+E_{\mathrm{MM}123,q_1=0}^{\mathrm{CL}}-E_{\mathrm{MM}1,q_1=0}^{\mathrm{HL}}}$$ (2)

in which $E_{\mathrm{QM}1+\mathrm{ptch}23}^{\mathrm{HL}}$ is the QM energy of the QM system truncated by HL atoms and embedded in the set of point charges modelling systems 2 and 3 (but excluding the self‐energy of the point charges). $E_{\mathrm{MM}1,q_1=0}^{\mathrm{HL}}$ is the MM energy of the QM system, still truncated by HL atoms, but without any electrostatic interactions. Finally, $E_{\mathrm{M}\mathrm{M}123,q_1=0}^{\mathrm{C}\mathrm{L}}$ is the classical energy of all atoms in the system with CL atoms and with the charges of the QM region set to zero (to avoid double‐counting of the electrostatic interactions). Thus, ComQum employs a subtractive scheme with van der Waals link‐atom corrections. ^[86] No cut‐off is used for any of the interactions in the three energy terms in Equation (3).

The geometry optimisations were continued until the energy change between two iterations was less than 2.6 J/mol (10⁻⁶ a.u.) and the maximum norm of the Cartesian gradients was below 10⁻³ a.u.

QM/MM calculations give comparable energies only if they contain exactly the same number of electrons and atoms of each element in both the QM and MM systems. Therefore, we compare only structures within the same E _n level. On the other hand, it means that we can study proton transfers within the QM system, for example from the homocitrate ligand or from His‐195 to the substrate. For each transition from E _n to E _n+1, an electron and a proton is added to the QM system, and we compare the energies of structures with this proton in different positions.

Result and Discussion

In this investigation, we study the later part of the reaction mechanism of nitrogenase, assuming that the S2B ligand does not dissociate. We describe in separate sections states at different oxidation levels, from E₄ to E₈.

N₂‐bound E₄ structures

We start with the N₂‐bound E₄ state. As in our previous study of the reaction mechanism with a dissociated S2B ligand, ^[57] we avoid the problem there is no consensus regarding the protonation of the E₄ state[ ²⁷ , ³⁸ , ⁴³ , ⁵⁹ , ⁶¹ , ⁸⁷ , ⁸⁸ , ⁸⁹ ] by starting from a state where N₂ has already bound to the cluster and is protonated to N₂H₂. The immediate protonation of the substrate upon binding is normally assumed,[ ¹ , ¹⁸ ] although it has not been experimentally observed. Mutations and other studies have shown that the substrate most likely bind either the Fe2 or Fe6 ions of the FeMo cluster[ ¹ , ⁹⁰ , ⁹¹ ] and this is also supported by a systematic scan of all possible N₂H₂ binding positions. ^[45] Therefore, we look for the best structure with N₂H₂ bound to either Fe2 or Fe6, or to both. In the latter case, the substrate may bind on two different sides of the bridging S2B ligand and we call these structures Fe2/6(3) and Fe2/6(5), depending on whether it is on the same side as S3A or S5A. Likewise, when N₂H₂ binds only to Fe2, the non‐bonding N atom point either to the S3A or S5A sides of the cluster, which will be called Fe2(3) or Fe2(5) (and similar for binding to Fe6). We have considered three isomers of N₂H₂, viz. NNH₂, cis‐HNNH or trans‐HNNH (the latter two are abbreviated cHNNH or tHNNH in the following). Moreover, we have tested three protonation states of His‐195: with protons on either ND1 (HID) or NE2 (HIE) or on both (HIP; but this adds an extra proton to the system and was therefore studied for the next higher E _n level). The results are collected in Table 1 and are shown Figure S1.

Table 1.

Energies (in kJ/mol), N−N and Fe−N distances (in Å) of the various structures of the E₄ states. All states were studied in the S=$1/2$ state unless otherwise stated. His is the protonation state of His‐195. The BS state is identified by the Fe ions with minority spin (e. g. 147=BS10‐147). Up to four different energies are listed: TPSS‐D4/def2‐SV(P) (TP), B3LYP‐D4/def2‐SV(P) (B3), TPSS‐D4/def2‐TZVPD (TZ), all based on TPSS‐D4/def2‐SV(P) structures obtained with fixed surroundings, as well as TPSS‐D4/def2‐SV(P) with relaxed surroundings (Rlx). When multiple Fe−N distances are given, Fe2 comes before Fe6.

Structure	His	BS	TP	B3	TZ	Rlx	N‐N	Fe‐N
Fe2‐cHNNH(3)	HID	147	139	126			1.26	1.92
	HIE	147	35	21	55	28	1.26	1.92
Fe2‐cHNNH(5)	HIE	147	91	75			1.25	1.92
		235	124	97			1.25	1.98
Fe6‐cHNNH(3)	HID	147	182	186			1.26	1.91
	HIE	147	55	54			1.25	1.91
		235	54	52			1.26	1.86
Fe6‐cHNNH(5)	HID	147	133	125			1.25	1.95
	HIE	147	48	37	58	78	1.26	1.92
Fe2/6‐cHNNH(3)	HID	147	227	222			1.31	1.88,1.90
	HIE	147	206	239			1.38	1.97,1.90
Fe2/6‐cHNNH(5)	HID	147	220	229			1.30	1.92,1.88
	HIE	147	161	199			1.35	1.98,1.89
Fe2/6‐cHNNH[a]	HIE	147	204	237			1.36	1.91,1.88,2.05
Fe2/6‐cHNNH[b]	HIE	147	152	139			1.36	1.94,1.93,1.95
Fe2‐tHNNH(3)	HID	147	108	94			1.26	1.94
	HIE	147	20	5	22	34	1.25	1.95
		235	51	30			1.25	2.01
Fe2‐tHNNH(5)	HID	147	176	94			1.25	1.95
	HIE	147	61	48			1.25	1.93
Fe6‐tHNNH	HID	147	86	86			1.26	1.91
	HIE	147	0	0	0	0	1.26	1.91
		235	10	10			1.26	1.87
S=3/2		147	30	−7			1.26	1.94
Fe2‐NNH2(3)	HID	147	194	192			1.27	1.83
	HIE	147	66	42			1.26	1.89
Fe2‐NNH2(5)	HID	147	222	211			1.25	1.91
	HIE	147	99	82			1.25	1.89
		235	129	119			1.25	1.91
Fe2/6‐NNH2(3)[c]	HID	235	244	275			1.32	1.83,1.77
	HIE	235	113	166			1.38	1.82,1.79
Fe2/6‐NNH2(5)[c]	HID	147	255	217			1.30	1.85,1.80
	HIE	147	108	195			1.36	1.80,1.77
Fe6‐HNNH2	HID	147	87	75			1.29	1.85
	HIE	147	4	‐6	4	3	1.29	1.85
		235	18	3			1.29	1.84

[a] S2B has dissociated from Fe6; One atom of N₂ bridges Fe2/6, the other binds to Fe6. [b] S2B has dissociated from Fe2; One atom of N₂ bridges Fe2/6, the other binds to Fe2. [c] S2B has dissociated from Fe6.

It can be seen that in nearly all structures, the HIE protonation state was more favourable than HID protonation by 21–132 kJ/mol. The only exception was the Fe2/6(3)‐cHNNH state with B3LYP. All structures were studied in the BS10‐147 state, but sometimes it shifted to the BS7‐235 state (the spin on Fe6 is often small and may change sign; the latter state was also studied for all low‐energy structures). However, BS10‐147 was always 9–37 kJ/mol lower in energy than BS7‐235 when both states were found, except for the Fe6‐cHNNH(3) state, for which BS7‐235 was 1 kJ/mol more stable at both the TPSS and B3LYP levels).

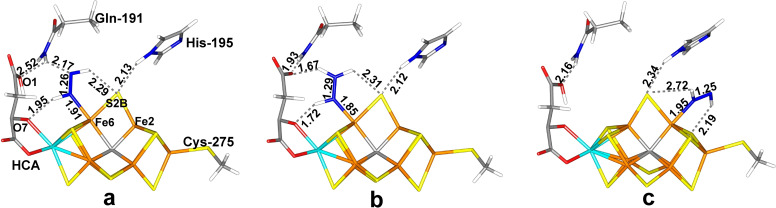
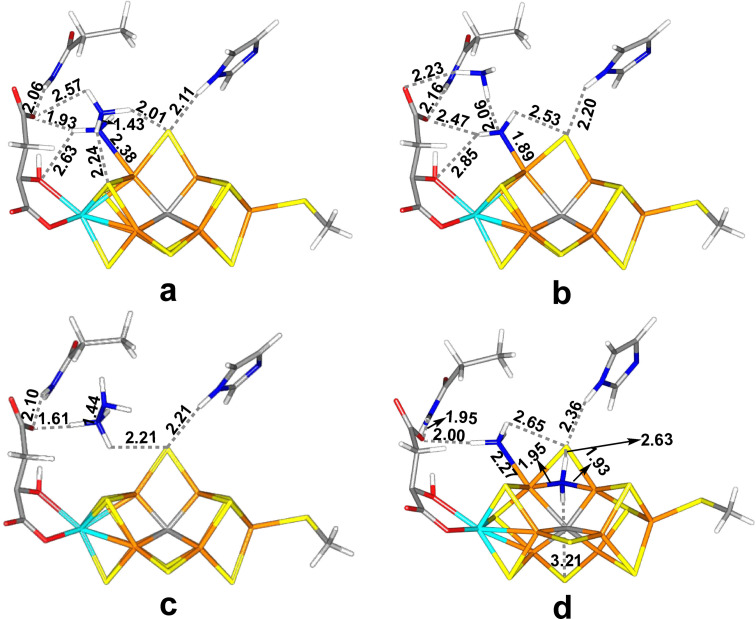
The most favourable structure has trans‐HNNH end‐on bound to Fe6 (Figure 2a). The Fe6‐N distance is 1.91 Å and the N−N bond length is 1.26 Å, which is slightly longer than in isolated trans‐HNNH, optimised with the same level of theory, 1.25 Å. The Mulliken spin populations are (in absolute terms) 3.2–2.7 e on the seven Fe ions, except Fe6, which has only 1.6 e (cf. Table S1 in the Supporting Information). Mo has a population of −0.3 e. This structure is stabilised by a hydrogen bond from the HN group bound to Fe6 to the alcohol O7 atom of homocitrate (which coordinates to Mo), with a H⋅⋅⋅O distance of 1.95 Å (cf. Figure 2a). The other N atom of the substrate receives a hydrogen bond from the HE1 atom of Gln‐191 (the HE1⋅⋅⋅N distance is 2.17 Å) and the other H atom of the substrate is directed towards S2B, with a H⋅⋅⋅S distance of 2.29 Å, but the N‐H⋅⋅⋅S angle is only 124°. S2B receives another hydrogen bond from the HE2 atom of His‐195 (2.13 Å, with a more ideal geometry). The corresponding structure in the quartet state is 30 kJ/mol less stable with the TPSS functional, but 7 kJ/mol more stable with the B3LYP. A full investigation of all 35 BS states, collected in Table S2, shows that the BS10‐147 state is indeed the most stable BS state, 10–67 kJ/mol more stable than the other BS states (BS7‐235 second lowest).

Figure 2.

The best E₄ structures: (a) Fe6‐tHNNH, (b) Fe6‐HNNH₂ and (c) Fe2‐tHNNH(3), all with the HIE state of His‐195.

A structure with NNH₂ bound end‐on to Fe6 is only 4 kJ/mol less stable with TPSS (also with the larger def2‐TZVPD basis set and 3 kJ/mol with relaxed surroundings) and it is actually 6 kJ/mol more stable with B3LYP. In this structure, the substrate has abstracted the alcohol proton from homocitrate, giving HNNH₂ (Figure 2b). It has a Fe6‐N distance of 1.85 Å and a N−N bond length of 1.29 Å (1.21 Å in neutral NNH₂ and 1.23 Å in HNNH₂ ⁺ optimised with the same method). It is stabilised by hydrogen bonds from the Fe6‐bound NH group to the alcohol O7 atom of homocitrate (H⋅⋅⋅O7=1.72 Å), from the NH₂ to one of the carboxylic groups of homocitrate (H⋅⋅⋅O1=1.67 Å) and from the other atom of NH₂ group to S2B (H⋅⋅⋅S2B=2.31 Å; Figure 2b). The S2B atom also receives a hydrogen bond from His‐195 (HE2⋅⋅⋅S2B=2.12 Å) and the O1 atom of homocitrate receives another hydrogen bond from Gln‐191 (HE1⋅⋅⋅O1=1.93 Å). This structure has also a low spin population on Fe6 (1.8 e). Again, a full investigation of all 35 BS states showed that BS10‐147 is the most favourable BS (Table S2), although it is only 4 kJ/mol more stable than BS10‐135 (14 kJ/mol more stable than BS7‐235).

A structure with trans‐HNNH binding to Fe2, directed to the S3A side (Figure 2c), is 20 kJ/mol less stable than Fe6‐tHNNH structure (22 kJ/mol with the larger basis set, 34 kJ/mol with relaxed surroundings and 5 kJ/mol with B3LYP). The Fe2‐N distance is 1.95 Å and the N−N bond length is 1.25 Å. The two H atoms of the substrate point towards S2B (H⋅⋅⋅S2B=2.72 Å) and S1A (H⋅⋅⋅S1A=2.19 Å), but the N−H⋅⋅⋅S angles are far from straight (83° and 131°, respectively). The Fe spin population on Fe2 (2.1 e) is only slightly less than on the other Fe ions (3.2–2.4 e in absolute terms). A full investigation of all 35 BS (Table S2) shows that BS10‐147 indeed is the most stable state. The structure with the substrate directed to the S5A side is 41 kJ/mol less stable.

Other structures studied are appreciably less stable. Structures with cis‐HNNH bound side‐on to Fe2 and Fe6 are 161–239 kJ/mol less stable than Fe6‐tHNNH, structures with cis‐HNNH bound end‐on to either Fe2 or Fe6 are 35–182 kJ/mol less stable and structures with NNH₂ bound to Fe2 are 66–255 kJ/mol less stable.

We also considered structures with S2B dissociated from either Fe2 or Fe6 (but still bound to the other ion), because such structures have been suggested to be competitive by other authors.[ ³⁵ , ⁴² , ⁴⁸ , ⁵⁸ ] However, with our methods, such structures were always high in energy, by 108–255 kJ/mol for structures with NNH₂ bridging Fe2 and Fe6 with the terminal N atom and by 152–204 kJ/mol for structures with cis‐HNNH bridging Fe2 and Fe6.

The present results are somewhat different from those obtained in our previous study of the binding of N₂H₂ to the FeMo cluster. ^[45] In that study, we found that the structure with trans‐HNNH bound to Fe2 was 10 kJ/mol more stable than the Fe6‐tHNNH state and 9 kJ/mol more stable than the Fe6‐HNNH₂ state (19 and 3 kJ/mol with the larger def2‐TZVPD basis set). The difference is most likely connected to the larger QM system used in the present study (models of Val‐70, Gln‐191 and Phe‐381, all situated around the binding site, were not included in the previous study). The present results should be more reliable.

The results also differ from those obtained with a dissociated S2B ligand (and a rotated conformation of Gln‐191), ^[57] for which a structure with NNH₂ bridging Fe2 and Fe6 was found to be most favourable. Such structures were at least 108 kJ/mol less stable than Fe6‐tHNNH in this study and led to half‐dissociation of S2B. Clearly, the active site with a bridging S2B group is so crowded that it disfavours structures with N₂H₂ simultaneously bridging Fe2 and Fe6.

Bjornsson and coworkers studied structures with trans‐HNNH bound to the FeMo cluster in the E₄ state. ^[42] They also found that binding to Fe6 was more favourable than to Fe2, in agreement with our results, but the difference was larger, 69 kJ/mol. In their models, S5A was protonated and one of the protons on HNNH was abstracted from homocitrate.

E₅ structures

Next, we added an electron and a proton to the FeMo cluster (i. e. to the QM system) to obtain structures at the E₅ level. They were studied in the triplet state with BS10‐147. The structures are described in Table 2 and the best are shown in Figures 3 and S2. As for the E₄ structures, HIE structures were always more stable than the corresponding HID structures, by 16–173 kJ/mol.

Table 2.

Energies (in kJ/mol), N−N and Fe−N distances (in Å) of the various structures of the E₅ states. All states were studied in the S=1 state unless otherwise stated. The entries are the same as in Table 1.

Structure	His	BS	TP	B3	TZ	Rlx	N‐N	Fe‐N
Fe2‐HNNH2(3)	HID	147	209	209			1.37	1.92
	HIE	147	80	76	94	54	1.36	1.94
Fe2‐HNNH2(5)	HID	147	272	186			1.34	1.95
	HIE	147	131	126			1.35	1.94
Fe6‐HNNH2	HID	147	205	152			1.38	1.39
	HIE	147	75	82	84	66	1.38	1.88
S=0		147	86	123			1.39	1.59
S=2		147	122	115			1.38	1.88
Fe2/6‐HNNH2(3)	HID	147	320	303			1.42	1.98,1.90
	HIE	147	247	250			1.45	1.95,2.00
Fe2/6‐HNNH2(5)	HID	147	305	324			1.44	2.08,1.90
	HIE	147	248	291			1.45	2.06,1.93
Fe2/6‐H2NNH(3)	HID	167	272	298			1.44	1.93,1.98
	HIE	147	223	217			1.45	2.02,1.98
Fe2/6‐H2NNH(5)	HID	147	337	366			1.43	1.90,2.04
	HIE	147	182	193			1.45	2.00,2.02
Fe6‐H2NNH2(3)	HID	147	130	129			1.43	2.10
	HIE	147	0	0	0	0	1.43	2.09
		235	−9	−3			1.43	2.08
S=0		147	−16	38			1.43	2.11
		235	15	37			1.43	2.06
S=2		147	33	4			1.43	2.09
Fe6‐H2NNH2(5)	HID	147	128	121			1.43	2.14
	HIE	147	1	−6	−1	38	1.43	2.13
		235	0	−1			1.43	2.15
Fe2‐NNH3	HID	147	344	334			1.45	1.86
	HIE	147	196	184			1.44	1.84
Fe2/6‐NNH3(5)	HID	147	407	471			1.46	1.92,1.91
	HIE	147	301	367			1.47	1.93,1.91
Fe6‐HNNH3(3)	HID	147	215	213			1.43	1.93
	HIE	147	80	75	87	72	1.43	1.92
Fe6‐HNNH3(5)	HID	147	151	148			1.44	1.93
	HIE	147	67	65	68	54	1.44	1.93
Fe2‐cHNNH(5)	HIP	147	333	344			1.25	1.91
Fe6‐cHNNH(3)	HIP	147	300	290			1.27	1.91
Fe6‐cHNNH(5)	HIP	147	279	273			1.27	1.88
Fe2‐tHNNH(3)	HIP	147	259	76			1.28	1.99
Fe2‐tHNNH(5)	HIP	147	295	322			1.25	1.93
Fe6‐tHNNH	HIP	147	239	236			1.25	1.89
Fe2‐NNH2(3)	HIP	147	323	353			1.32	1.90
Fe2‐NNH2(5)	HIP	147	353	363			1.26	1.88
Fe2/6‐NNH2(3)	HIP	147	379	265			1.42	1.82,1.89
Fe2/6‐NNH2(5)	HIP	147	430	417			1.30	1.85,1.81
Fe6‐HNNH2	HIP	147	233	170			1.30	1.87

Figure 3.

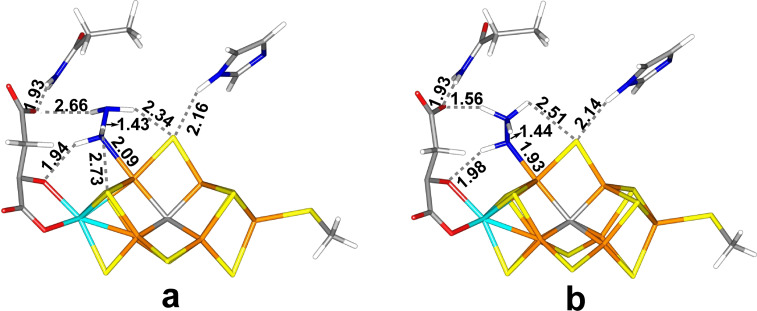
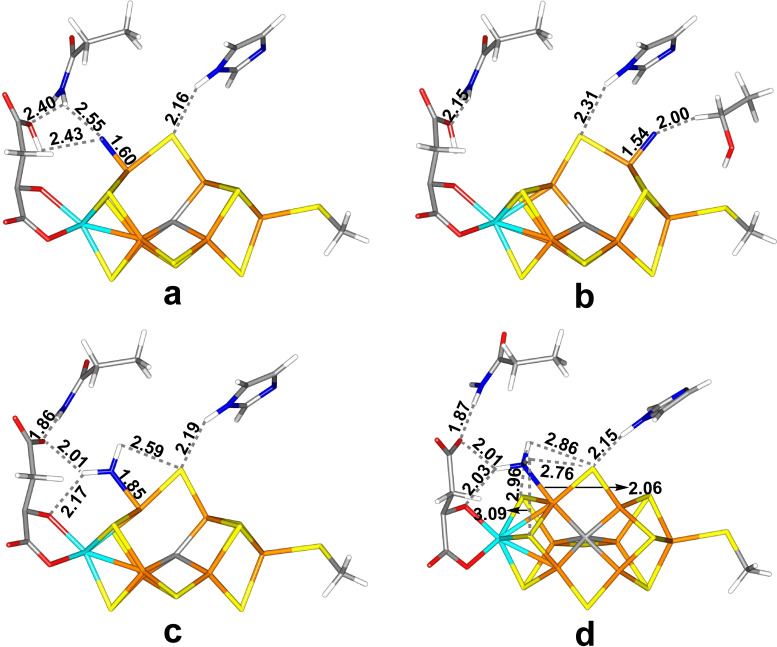
The best E₅ structures: (a) Fe6‐H₂NNH₂(3) and (b) Fe6‐HNNH₃(5) both with the HIE state of His‐195.

The most favourable state has H₂NNH₂ (hydrazine) bound to Fe6, where the extra proton is abstracted from the hydroxy group of homocitrate (Figure 3a). The Fe6‐N distance is 2.09 Å and the N−N bond length is 1.43 Å, which is the same as for isolated hydrazine, optimised at the same level of theory. The non‐coordinating NH₂ group is directed to the S3A side of the cluster. The two H atoms of the Fe‐bound NH₂ group forms hydrogen bonds to O7 of homocitrate (H⋅⋅⋅O7=1.94 Å) and S3B (H⋅⋅⋅S3B=2.73 Å). The other two H atoms of hydrazine point towards O1 of homocitrate (H⋅⋅⋅O1=2.66 Å) and S2B (H⋅⋅⋅S2B=2.34 Å). The spin density on Fe6 is 2.1 e (Table S3). The singlet state was 16 kJ/mol more stable than the triplet state with TPSS, but 38 kJ/mol less stable with B3LYP. The quintet was 4–33 kJ/mol less stable than the triplet. A full investigation of all BS states (Table S2) showed that BS7‐235 is actually 9 kJ/mol lower in energy than BS10‐147. In fact, nine different BS states were found within 11 kJ/mol of the lowest state. There are several structures with similar energies with slight variations in the hydrogen‐bond lengths and the relative conformations of the two NH₂ groups. For example, a structure with the non‐bonded NH₂ group directed towards S5A is only 1 kJ/mol less stable (6 kJ/mol more stable by B3LYP, but 38 kJ/mol less stable with relaxed surroundings).

Other structures are appreciably less stable. The second‐best structure had HNNH₃ bound end‐on to Fe6 with the NH group and with the NH₃ group directed toward S5A (Figure 3b; again with a proton abstracted from homocitrate). It is 54–68 kJ/mol less stable than the Fe6‐H₂NNH₂ structure at the various levels of theory. A similar structure with the NH₃ group directed towards S3A is 10–18 kJ/mol less stable. A structure with HNNH₂ bound end‐on to Fe6 with the NH group (i. e. without the proton transfer from homocitrate) is 66–84 kJ/mol less stable than the Fe6‐H₂NNH₂ structure. A structure with HNNH₂ bound to Fe2 with the NH₂ group directed towards S3A is 54–94 kJ/mol less stable than the best structure. The structure with the NH₂ group pointing in the opposite direction is 50 kJ/mol less stable. Structures with NNH₃ bound to Fe2 are 184–196 kJ/mol less stable than the best Fe6‐HNNH₃ structure.

We also studied a number of structures with HNNH₂ or NNH₃ bridging Fe2 and Fe6 on either side of S2B, but all of them were high in energy (182–471 kJ/mol less favourable than Fe6‐HNNH₃). Moreover, we studied structures with a proton on His‐195, instead of on the substrate, giving the HIP state. These structures were at least 233–430 kJ/mol higher than Fe6‐H₂NNH₂‐HIE, with Fe6‐HNNH₂ lowest, 6 kJ/mol lower than Fe6‐tHNNH. This may illustrate a possible path for the transfer of protons to the substrate and it is apparently strongly downhill.

For the best Fe6‐HNNH₃ structure, we tested to cleave the N−N bond. However, this reaction turned out to prohibitive with an activation barrier of 119 kJ/mol and a reaction energy of 78 kJ/mol to a product with NH bound to Fe6 and NH₃ dissociated from the cluster, but forming hydrogen bonds to O1 of homocitrate, S2B and S3B. This indicates that nitrogenase does not follow a sequential reaction mechanism. On the other hand, the N−N bond can be cleaved in Fe2‐NNH₃, with a barrier of 49 kJ/mol, but the reactant and the Fe2‐N product are 196 and 149 kJ/mol less stable than the Fe6‐H₂NNH₂ structure, showing that they are not expected to form during the reaction mechanism.

E₆ structures

Adding a proton and an electron to the previous structures gives intermediates at the E₆ level. These were studied primarily in the doublet BS10‐147 state. The results are collected in Table 3 and the best structures are shown in Figures 4 and S3. As for the E₄ and E₅ structures, HIE protonation was found also to be 1–138 kJ/mol more favourable than HID, except for Fe2/6(3)‐H₂NNH₂ with TPSS (2 kJ/mol), where His‐195 accepts a hydrogen bond from H₂NNH₂ in the HID state.

Table 3.

Energies (in kJ/mol), N−N and Fe−N distances (in Å) of the various structures of the E₆ states. All states were studied in the S=1/2 state unless otherwise stated. The entries are the same as in Table 1.

Structure	His	BS	TP	B3	TZ	Rlx	N‐N	Fe‐N
Fe2‐H2NNH2(3)	HID	147	163	163			1.43	2.10
	HIE	147	33	29	31	28	1.43	2.12
		157	17				1.43	2.11
Fe2‐H2NNH2(5)	HID	147	163	161			1.42	2.10
	HIE	147	60	55			1.42	2.06
Fe6‐H2NNH2(3)	HID	147	83	84			1.45	2.10
	HIE	147	0	0	0	0	1.45	2.10
		235	51	9			1.45	2.05
[a]		147	43	−38			1.43	2.27
S=3/2		147	16	−53			1.45	2.12
Fe6‐H2NNH2(5)	HID	147	93	87			1.45	2.15
	HIE	147	2	−33	19	9	1.45	2.15
		235	17	−18			1.45	2.09
Fe2/6‐H2NNH2(3)	HID	235	245	213			1.46	2.10,1.99
	HIE	235	247				1.46	2.15,1.98
Fe2/6‐H2NNH2(5)	HID	147	226	76			1.47	2.12,2.02
	HIE	147	201				1.45	2.36,2.06
Fe2‐HNNH3(3)	HID	147	232	177			1.44	2.09
	HIE	147	109	82			1.45	2.07
Fe2‐HNNH3(5)	HID	147	282	246			1.44	2.13
	HIE	147	150	108			1.44	2.09
Fe6‐HNNH3(3)	HID	147	243	197			1.44	2.02
	HIE	147	105	108			1.44	2.02
Fe6‐HNNH3(5)	HID	147	200	204			1.44	2.11
	HIE	147	119	122			1.44	2.11
Fe2/6‐NH(3)+NH3	HID	147	220	179				1.81,1.88
	HIE	147	117	194				1.87,1.90
Fe2/6‐NH(5)+NH3	HID	147	309	286				1.91,1.87
	HIE	147	265	285				1.92,1.87
Fe6‐H2NNH3(5)	HID	147	110	116			1.44	2.11
	HIE	147	28	31	29	43	1.44	2.11
Fe2‐HNNH2(5)	HIP	147	342	345			1.37	1.96
Fe2/6‐HNNH2(3)	HIP	147	478	547			1.45	1.95,2.01
Fe2/6‐HNNH2(5)	HIP	147	445	501			1.46	1.97,1.99
Fe6‐HNNH2	HIP	147	285	249			1.42	1.89
Fe6‐H2NNH2(3)	HIP	147	156	167			1.44	2.09
Fe6‐H2NNH2(5)	HIP	147	164	169			1.45	2.15
Fe2‐NNH3	HIP	147	409	409			1.45	2.05
Fe2/6‐NNH3(5)	HIP	147	502	537			1.47	1.91,1.91
		235	469	533			1.46	1.91,1.92
Fe6‐HNNH3(5)	HIP	147	254	267			1.45	1.99

[a] A structure with a H−N−N−H torsion of 98–99°.

Figure 4.

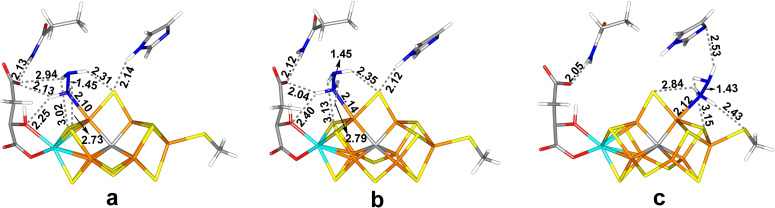
The best E₆ structures: (a) Fe6‐H₂NNH₂(3), (b) Fe6‐H₂NNH₂(5) and (c) Fe2‐H₂NNH₂(3), all with the HIE state of His‐195.

The best structure at the TPSS level has H₂NNH₂ bound end‐on to Fe6, with the non‐coordinating NH₂ group pointing towards S3A (thus, the new proton in the E₆ state is added to homocitrate and not the substrate; Figure 4a). It has a Fe6‐N distance of 2.10 Å and a N−N bond length of 1.45 Å, which is slightly longer than for the E₅ structures and the same molecule optimised in vacuum, 1.43 Å. The Fe ions have spin populations of 2.2–3.2 e, but 2.0 e on Fe2 and 1.4 e on Fe6 (Table S4). The spin on Mo is minor and slightly positive, 0.1 e. It is stabilised by a hydrogen bond from the Fe6‐bound NH₂ group to the hydroxy O7 atom of homocitrate (H⋅⋅⋅O7=2.25 Å) and by a hydrogen bond from the other NH₂ group to S2B (H⋅⋅⋅S2B=2.31 Å). The other H atom of the latter NH₂ group points in the direction of S1B, but the distance is long, 3.02 Å. It is also 2.94 Å from O1 of homocitrate. The fourth H atom of the substrate is 2.73 Å from S3B, but the geometry is far from ideal. It is also close to a methyl group of Val‐70 (1.83 Å H−H distance). The quartet state was 16 kJ/mol less stable at the TPSS level, but 53 kJ/mol more stable with B3LYP. An investigation of all BS states (Table S2) showed that BS10‐147 is most stable, 6 kJ/mol better than BS10‐135. With B3LYP, a structure in which the two NH₂ groups are twisted with respect to each other (H−N−N−H torsion of 99°), as in the structure for the free hydrazine, is 38 kJ/mol more stable than the structure in Figure 4a, but at the TPSS level, the other structure is 43 kJ/mol more stable.

The corresponding structure with the non‐coordinating NH₂ group pointing towards S5A (Figure 4b) is only 2–19 kJ/mol less stable with TPSS but 33 kJ/mol more stable B3LYP. It is stabilised by a hydrogen bond to the O1 atom of homocitrate (H⋅⋅⋅O1=2.04 Å), whereas the other H atoms interact with S2B, S3B and S1B as for the other conformation (H⋅⋅⋅S distances of 2.35, 3.13 and 2.79 Å). With B3LYP, this structure is further stabilised by 62 kJ/mol when studied in the BS7‐235 state, whereas with TPSS the BS10‐147 state is 48 kJ/mol more stable.

The corresponding structure with hydrazine bound end‐on to Fe2 (Figure 4c) is 17–33 kJ/mol less stable. The two H atoms of the NH₂ group bound to Fe2 form hydrogen bonds to SG of Cys275 (H⋅⋅⋅SG=2.43 Å) and S2B (H⋅⋅⋅S2B=2.84 Å). The other two H atoms interact with ND1 of His‐195 and S1A (H⋅⋅⋅ND1=2.53 and H⋅⋅⋅S1A=3.15 Å), but with poor geometries. A full investigation of all BS states (Table S2) showed that this structure is most stable in the BS6‐157 state, which is 16 kJ/mol more stable than the BS10‐147 state. End‐on bound HNNH₃ structures are 105–282 kJ/mol less stable, whereas side‐on (Fe2/6) structures are 117–309 kJ/mol less stable and those with HNNH₃ dissociate to NH and NH₃.

We have also studied the same structures as for E₅, but with HIP and an extra electron. They were all high in energy, 156–547 kJ/mol less stable than the best Fe6‐H₂NNH₂ structure, showing that proton transfer from His‐195 is strongly favourable. In several of this type of structures, the substrate automatically abstracts a proton from His‐195, forming HID states instead (which are less stable than the HIE structures, as has already been discussed).

E₇ structures

After adding yet another proton and electron, we reach the E₇‐level intermediates. They were studied in the triplet BS10‐147 state. The structures are listed in Table 4 and the most stable structures are shown in Figures 5 and S4. As usual, the HID structures were less stable than the corresponding HIE structures by 3–176 kJ/mol.

Table 4.

Energies (in kJ/mol), N−N and Fe−N distances (in Å) of the various structures of the E₇ states. All states were studied in the S=1 state unless otherwise stated. The entries are the same as in Table 1. Fe−N distances of NH₂ precede those of NH₃.

Structure	His	BS	TP	B3	TZ	Rlx	N‐N	Fe‐N
Fe2‐H2NNH3(3)	HID	147	277	297			1.42	2.14
	HIE	147	137	162			1.43	2.05
Fe2‐H2NNH3(5)	HID	147	248	256			1.43	2.17
	HIE	147	143	159			1.43	2.14
Fe6‐H2NNH3(3)	HID	147	193	216			1.43	2.28
Fe6‐H2NNH3(5)	HID	147	217	237			1.43	2.26
	HIE	147	133	−12	28	132	1.43	2.38
		234	97				1.42	2.43
H2NNH3 dissociated	HIE	147	50				1.44
Fe2‐NH2(3)‐Fe6‐NH3	HID	147	94	109				1.84,2.06
	HIE	147	61	68				1.88,2.08
Fe6‐NH2(3)‐Fe2‐NH3	HID	147	76	147				1.98,1.91
	HIE	147	73	57				2.06,1.92
Fe6‐NH2(5)‐Fe2‐NH3	HID	147	85	154				2.01,1.91
	HIE	147	88	126				2.03,1.93
Fe2/6‐NH2(3)‐Fe2‐NH3	HID	147	104	166				1.93,1.95,2.01
	HIE	147	0	110				1.93,1.95,2.00
Fe2/6‐NH2(3)‐Fe6‐NH3	HID	147	61	86				1.94,1.97,2.09
	HIE	147	36	51				1.96,2.02,2.27
Fe2/6‐NH2(5)‐Fe2‐NH3	HID	147	107	188				1.95,1.94,2.05
	HIE	147	26	38				1.93,1.96,2.05
Fe2/6‐NH2(5)‐Fe6‐NH3	HID	147	83	105				1.93,1.97,2.24
	HIE	147	0	0	0	0		1.93,1.95,2.27
		14	−50					1.92,1.94,2.09
S=0		147	−31	37				1.92,1.95,2.16
S=2		147	20	97				1.92,1.95,2.21
Fe2/6‐NH3(3)‐Fe2‐NH2	HID	147	110	85				2.57,2.03,1.89
	HIE	147	83	75				2.70,2.03,1.88
Fe2/6‐NH3(3)‐Fe6‐NH2	HIE	147	132	145				2.45,2.13,2.02
Fe2/6‐NH3(5)‐Fe2‐NH2	HID	147	135	169				2.04,2.95,2.00
	HIE	147	43	−7				2.02,2.95,1.98
Fe2/6‐NH3(5)‐Fe6‐NH2	HID	147	198	231				2.86,2.04,2.01
	HIE	147	136	200				2.64,2.01,2.02
Fe6‐NH2+NH3	HIE	147	−21					1.89
Fe2‐H2NNH2(3)	HIP	147	210	224			1.45	2.16
Fe2‐H2NNH2(5)	HIP	147	240	252			1.42	2.08
Fe6‐H2NNH2(3)	HIP	147	183	202			1.45	2.09
Fe6‐H2NNH2(5)	HIP	147	191	206			1.46	2.15
Fe2/6‐H2NNH2(3)	HIP	235	424	426			1.46	2.12,1.99
Fe2/6‐H2NNH2(5)	HIP	147	374	205			1.48	2.15,2.03
Fe2‐HNNH3(5)	HIP	147	368	229			1.43	2.14
Fe6‐HNNH3(3)	HIP	147	292	313			1.44	2.02
Fe6‐HNNH3(5)	HIP	147	307	326			1.44	2.10
Fe6‐H2NNH3(5)	HIP	147	217	239			1.44	2.10

Figure 5.

The best E₇ structures: (a) Fe6‐H₂NNH₃(5), (b) Fe6‐NH₂+NH₃, (c) H₂NNH₃ dissociated and (d) Fe2/6‐NH₂(5)‐Fe6‐NH₃, all with the HIE state of His‐195.

Only a few structures were obtained with H₂NNH₃ bound to the FeMo cluster. They had a N−N distance of 1.42–1.43 Å. The most stable one had H₂NNH₃ bound end‐on to Fe6, with the NH₃ directed towards the S5A side (Figure 5a), but binding to Fe2 was only 4 kJ/mol less favourable with TPSS (30 kJ/mol by B3LYP). An investigation of all BS states (Table S2) showed that this complex is most stable in the BS2‐234 state, which is actually 36 kJ/mol more stable than the BS10‐147 state. The N−N bond can readily be cleaved in this structure with an activation barrier of only 32 kJ/mol and an exothermic reaction energy of −154 kJ/mol. The product has NH₂ bound end‐on to Fe6 and NH₃ dissociated, but hydrogen bonded to the cluster (Figure 5b). The two H atoms of NH₂ form hydrogen bonds to O1 of homocitrate (H⋅⋅⋅O1=2.47 Å) and S2B (H⋅⋅⋅S2B=2.53 Å). The dissociated NH₃ molecule forms hydrogen bonds to NH₂ (H⋅⋅⋅N=2.06 Å) and O2 of homocitrate (H⋅⋅⋅O2=2.23 Å), whereas the third H atom does not form any favourable interaction, but instead is quite close to a methyl group of Val‐70 (2.03 Å H−H distance). A structure with H₂NNH₃ dissociated from the Fe ions, but still hydrogen‐bonded to the cluster is 83 kJ/mol more stable than the bound Fe6‐H₂NNH₃ structure (Figure 5c). When it is dissociated, it is appreciably harder to cleave the N−N bond – the calculated barrier is 91 kJ/mol.

Structures with a cleaved N−N bond and both NH₂ and NH₃ coordinated to the cluster are up to 84 kJ/mol more stable than the bound Fe6‐H₂NNH₃ structure, but 21 kJ/mol less stable than the structure with NH₃ dissociated. The best one has NH₂ bridging Fe2 and Fe6 on the side facing S5A, whereas NH₃ binds to Fe6 (Figure 5d). The two Fe–NH₂ distances are 1.93 and 1.95 Å, whereas the Fe6—NH₃ distance is 2.27 Å. S2B has moved considerably, but it still binds to Fe2 and Fe6, and it receives a hydrogen bond from His‐195 (HE2⋅⋅⋅S2B=2.36 Å). NH₃ forms a hydrogen bond to O1 of homocitrate (H⋅⋅⋅O1=2.00 Å), whereas the second H atom points towards S2B (H⋅⋅⋅S2B=2.65 Å). The third H atom does not form any favourable interactions. The two H atoms of NH₂ point towards S3A and S2B (H⋅⋅⋅S3A=3.21 and H⋅⋅⋅S2B=2.63 Å). The spin populations on Fe2 and Fe6 are relatively low, 2.1 and 2.2 e, respectively, but that on Fe7 is even lower, 1.5 e (Table S5). NH₃ may dissociate from this structure, but the activation barrier is rather high, 78 kJ/mol.

There are several other structures with comparable energies (cf. Table 4), for example with NH₂ bridging Fe2 and Fe6 on either side of S2B and with NH₃ either on Fe2 or Fe6. The relative energies sometimes differ rather much between TPSS and B3LYP.

As for the other E _n states, we tested also structures with HIP protonated, but all these were at least 183 kJ/mol less stable.

E₅–E₈ structures with only one N atom

We studied also structures with only a single N atom, i. e. after N−N bond cleavage and dissociation of a NH₃ product. These were studied at four levels of oxidation and protonation (E₅–E₈), even if the results in the previous subsections indicate that only the E₇ and E₈ states are involved in the reaction mechanism. The results are collected in Table 5 and the best structures are shown in Figures 6, 7 and S5.

Table 5.

Energies (in kJ/mol), N−N and Fe−N distances (in Å) of the various structures of the E₅‐E₈ states with a single N atom. All states were studied in the S=1 (E₅ or E₇) or S=$1/2$ (E₆ or E₈) state unless otherwise stated. The entries are the same as in Table 1.

State	Structure	His	BS	TP	B3	TZ	Rlx	Fe‐N
E5	Fe2‐N	HID	147	124	157			1.53
		HIE	147	2	35	−1	−41	1.54
			235	−5	87			1.52
	Fe6‐N	HID	147	126	126			1.60
		HIE	147	0	0	0	0	1.60
			235	−37	−13			1.52
	S=0		147	−39	11			1.52
	S=2		147	38	33			1.60
	Fe2/6‐N(3)	HID	147	155	309			1.69,1.79
			235	134	256			1.71,1.72
		HIE	147	57	23			1.69,1.81
	Fe2/6‐N(5)	HID	43	111	302
		HIE	127	30	199
			14	64	−64
	Fe6‐NH	HID	147	117	16			1.77
		HIE	147	2	38	−14	−9	1.72
			235	−17	28			1.62
E6	Fe2‐NH	HID	147	226	199			1.85
		HIE	147	132	118	139	69	1.83
	Fe6‐NH	HID	147	204	196			1.89
		HIE	147	126	90	131	69	1.79
	S=3/2		147	154	133			1.77
	Fe2/6‐NH(3)	HID	147	239	328			1.80,1.87
		HIE	147	129	107	149	79	1.84,1.86
	S=3/2		147	124	167			1.86,1.87
	Fe2/6‐NH(5)	HID	147	250	302			1.85,1.90
		HIE	147	138	188	175	116	1.85,1.89
	Fe6‐NH2	HID	147	86	113			1.86
		HIE	147	0	0	0	0	1.85
			235	26	−48			1.84
	Fe6‐N	HIP	147	305	273			1.53
	Fe2/6‐N(3)	HIP	147	373	288			1.72,1.85
	Fe6‐NH	HIP	147	319	296			1.78
E7	Fe2‐NH2	HID	147	207	201			1.89
		HIE	147	117	107	119	95	1.87
	Fe6‐NH2	HID	147	200	195			1.86
		HIE	147	112	109	113	99	1.85
	S=0		147	118	150			1.87
	S=2		147	149	101			1.85
	Fe2/6‐NH2(3)	HID	147	242	213			1.97,1.96
		HIE	147	224	240			1.98,2.03
	Fe2/6‐NH2(5)	HID	147	281	350			1.94,1.95
		HIE	147	191	263			1.92,1.94
	Fe6‐NH3	HID	147	89	85			2.06
		HIE	147	0	0	0	0	2.06
			156	−8				2.09
	S=0		147	−13	47			2.08
	S=2		147	33	−37			2.06
	Fe6‐NH	HIP	147	418	394			1.82
	Fe6‐NH2	HIP	147	283	281
E8	Fe2‐NH3	HID	147	126	128			2.06
		HIE	147	11	8	14	−28	2.06
			235	35	−2			2.13
	Fe6‐NH3	HID	147	88	81			2.12
		HIE	147	0	0	0	0	2.13
			235	17	12			2.07
	S=3/2		147	23	−35			2.20
	Fe2/6‐NH3(3)	HID	147	326	336			2.09,2.51
		HIE	147	324	301			2.11,2.34
	Fe2/6‐NH3(5)	HID	147	273				2.10,3.14
	NH4 dissociated	HID	147	88	74			3.04
		HIE	147	−2	6	1	−32	3.03
			235	17	−20			3.09
	Fe6‐NH2	HIP	147	292	228			1.88
	Fe6‐NH3	HIP	147	152	146			2.06

Figure 6.

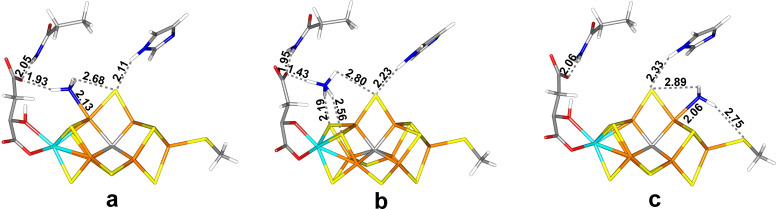
The best structures with only one N atom: (a) E₅‐Fe6‐N, (b) E₅‐Fe2‐N, (c) E₆‐Fe6‐NH₂, (d) E₇‐Fe6‐NH₃, all with the HIE state of His‐195.

The best E₅ structure has N bound end‐on to Fe6 with a Fe−N distance of 1.60 Å (Figure 6a). The N atom receives a hydrogen bond from HE1 of Gln‐191 (2.55 Å, but this hydrogen also forms a hydrogen bond to O1 of homocitrate with a H⋅⋅⋅O1 distance of 2.40 Å). We tested also the singlet and quartet states for this structure. The latter was 38 kJ/mol less stable at the TPSS level (33 kJ/mol with B3LYP). However, the singlet was 39 kJ/mol more stable with TPSS, but 11 kJ/mol less stable with B3LYP. A structure with NH bound to Fe6 (with the proton abstracted from homocitrate) is only 2 kJ/mol less stable (38 kJ/mol by B3LYP), but it is 14 kJ/mol more stable with the larger basis set and 9 kJ/mol more stable if the surroundings are relaxed.

The corresponding structure with N bound end‐on to Fe2 (Figure 6b) is also 2 kJ/mol less stable (35 kJ/mol with B3LYP), but 1 kJ/mol more stable with the larger basis set, 41 kJ/mol more stable if the surroundings are relaxed. It has an even shorter Fe2–N bond length of 1.54 Å. The N atom does not receive any polar hydrogen bond, but it is 2.00 Å from a HB atom of Ser‐278. The corresponding structures with N bridging Fe2 and Fe6 are 30 kJ/mol (on the S3A side) and 57 kJ/mol (S5A side) less stable. In both cases, S2B moves to a position where it interacts with more Fe ions than Fe2 and Fe6. Moreover, N receives the hydrogen bond from His‐195 (instead of S2B; 2.44 and 2.50 Å, respectively). The corresponding HID structures are 78–126 kJ/mol less stable. Interestingly, for the three most stable structures BS7‐235 was found to be 5–37 kJ/mol more stable than the BS10‐147 state. However, the Fe6‐N structure was still the best structure.

The most stable E₆ structure has NH₂ bound end‐on to Fe6 with the extra proton on the substrate abstracted from homocitrate (Figure 6c). It has a Fe6–N bond length of 1.85 Å and the H atoms of NH₂ point toward O1 and O7 of homocitrate (H⋅⋅⋅O1=2.01 Å, H⋅⋅⋅O7=2.17 Å) and S2B (H⋅⋅⋅S2B=2.59 Å). The spin population on Fe6 (2.0 e) is slightly lower than that on Fe2 (2.1 e; Table S6). This structure is 126 kJ/mol more stable (63–90 kJ/mol with B3LYP, the larger basis set or relaxed surroundings) than a structure with NH binding end‐on to Fe6 (Fe6–N bond length of 1.73 Å). The corresponding HID structures are 51–221 kJ/mol higher in energy. Structures with HIP are 305–373 kJ/mol higher in energy, showing that proton transfer from His‐195 is favourable.

The most stable E₇ structure has NH₃ bound end‐on to Fe6 (with a proton abstracted from homocitrate). The Fe6–N bond length is 2.06 Å (Figure 6d). One of the three H atoms forms hydrogen bonds to both O1 and O7 of homocitrate (H⋅⋅⋅O1=2.01 and H⋅⋅⋅O7=2.03 Å). The other two are rather close to S2B (H⋅⋅⋅S2B=2.76 and 2.86 Å), but also to S1B and S3B (H⋅⋅⋅S1B=2.96 Å and H⋅⋅⋅S3B=3.09 Å). The spin population of Fe6 is 2.1 e (Table S6). NH₃ cannot dissociate from this structure (the energy keeps rising by more than 120 kJ/mol when the Fe6–N bond is elongated). A full investigation of all BS states (Table S2) showed that BS6‐156 is actually lowest, but the BS10‐147 state is only 8 kJ/mol higher in energy and there are five BS states within 10 kJ/mol of BS6‐156.

This Fe6‐NH₃ structure is 99–113 kJ/mol more stable than a structure with NH₂ bound to Fe6 (and a proton on homocitrate). The structure with NH₂ bound to Fe2 is 95–119 kJ/mol less stable. Structures with NH₂ bridging Fe2 and Fe6 are 191–350 kJ/mol higher in energy than the best structure. Structures with HID are ∼90 kJ/mol less stable than the corresponding HIE structures. Structures with HIP are 281–418 kJ/mol less stable, again indicating that proton transfer from His‐195 is strongly favourable.

Finally, we studied also E₈ states. Again, the most stable structure has NH₃ bound to Fe6 with a Fe−N distance of 2.13 Å (Figure 7a). NH₃ forms a hydrogen bond to O1 of homocitrate with a H−O distance of 1.93 Å. One of the other H atoms is 2.68 Å from S2B, but the last atom does not form any favourable interactions. The Fe spin populations are 2.2–3.2 e, but 2.0 e on Fe6 (Table S6). The structure was studied in the doublet state and the corresponding quartet state is 23 kJ/mol less stable with TPSS, but 35 kJ/mol more stable with B3LYP. A full investigation of all possible BS states (Table S2) showed that the BS10‐147 state is best, but there are four other BS states within 10 kJ/mol. NH₃ can dissociate from this structure with a barrier of 42 kJ/mol. The dissociation energy of NH₃ (compared to the quartet BS7‐235 E₀ state and NH₃ in a water‐like continuum solvent with a dielectric constant of 80) is 16 kJ/mol (−20 kJ/mol with B3LYP), which can easily be overcome by the gain in translational and rotational entropy of the released NH₃ ligand, ∼60 kJ/mol).[ ⁹² , ⁹³ ]

Figure 7.

The E₈ structures: (a) Fe6‐NH₃, (b) NH₄ dissociated and (c) Fe2‐NH₃, all with the HIE state of His‐195.

A structure, in which NH₃ has abstracted the proton from O7 of homocitrate, forming NH₄ ⁺, is actually 2 kJ/mol more stable than the Fe6‐NH₃ structure. NH₄ ⁺ has dissociated from Fe6 and the four H atoms form hydrogen bonds to O1 of homocitrate (H⋅⋅⋅O1=1.43 Å), S2B (H⋅⋅⋅S2B=2.80 Å), S1B (H⋅⋅⋅S1B=2.19 Å) and S3B (H⋅⋅⋅S3B=2.56 Å; Figure 7b).

A structure with NH₃ bound to Fe2 is 8–11 kJ/mol less stable than the Fe6‐NH₃ structure (but 28 kJ/mol more stable with relaxed surroundings). It has a slightly shorter Fe−N bond (2.06 Å; cf. Figure 7c). Two of the H atoms of NH₃ points approximately towards SG of Cys‐275 and S2B (H⋅⋅⋅SG=2.75 Å and H⋅⋅⋅S2B=2.89 Å). A full investigation of all BS states showed that BS10‐147 indeed is the most stable state, but only 2 kJ/mol more stable than the BS6‐157 state. We also tried to find structures with NH₃ bridging Fe2 and Fe6, but they were at least 326 kJ/mol less stable. Structures with HID were 81–120 kJ/mol less stable than the corresponding HIE structures. Structures with HIP were 152–292 kJ/mol less stable, showing that proton transfer from His‐195 is strongly favourable.

Conclusions

In this investigation, we have studied possible reaction intermediates of nitrogenase, assuming that the S2B remains bound to the FeMo cluster. To avoid the problem that the structure of the E₄ intermediate is not known and that different DFT functionals give very different relative stabilities of various protonation states,[ ⁴³ , ⁴⁴ ] we started our study after H₂ has dissociated and N₂ has bound to the cluster and has become doubly protonated to N₂H₂,[ ¹ , ¹⁸ ] so that no protons remain bound to the cluster. Based on the accumulated experimental evidence,[ ¹ , ⁹⁰ , ⁹¹ ] as well a systematic study of the binding of N₂H₂ to the FeMo cluster, ^[45] and in agreement with most previous computational studies, ^[27] we have assumed that N₂H₂ binds either to Fe2 or Fe6.

Our study has led to the following conclusions:

• For the E₄ state, Fe6‐tHNNH, Fe2‐tHNNH and Fe6‐HNNH₂ structures are all competitive (within 5 kJ/mol with at least one of the four levels of theory included in Table 1).

• For the E₅ state, Fe6‐H₂NNH₂ is lowest in energy. Fe6‐NNH₃ is 54–68 kJ/mol higher and the N−N bond in cannot be cleaved.

• For the E₆ state, Fe6‐H₂NNH₂ structure is lowest in energy, 28–43 kJ/mol lower than Fe6‐H₂NNH₃. Cleavage of N−N in the latter has a barrier of 95 kJ/mol.

• The N−N bond in the H₂NNH₃ E₇ complexes can easily be cleaved, the reaction is exothermic and NH₃ moves spontaneously into the second coordination sphere of the cluster, whereas NH₂ binds with similar affinities to both Fe2 and Fe6. However, the most stable structure is obtained if NH₂ abstracts the hydroxy proton from homocitrate, forming NH₃ bound to Fe6, which cannot dissociate at this level of reduction.

• In the E₈ state, NH₃ binds preferably to Fe6 (binding to Fe2 is 8–11 kJ/mol higher in energy). It can readily dissociate from the FeMo cluster.

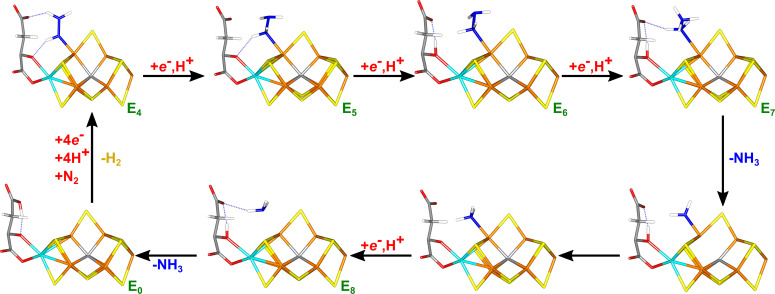
Based on these results, we suggest the reaction mechanism in Figure 8. In this mechanism, the substrate binds to Fe6. In the E₅ state, it is protonated to H₂NNH₂, whereas in E₆, the proton is added to homocitrate, so that the ligand remains H₂NNH₂. In the E₇ state, the substrate is protonated to H₂NNH₃, in which the N−N bond is readily cleaved and NH₃ automatically dissociates. The resulting NH₂ group remains bound to Fe6 and is protonated to NH₃. In the E₈ state, NH₃ dissociates and the resting E₀ state is formed.

Figure 8.

Suggested reaction mechanism for nitrogenase, assuming that S2B remains bound to the cluster.

It has been much discussed whether the reaction mechanism of nitrogenase follows a sequential or alternating reaction mechanism. ^[1] Our results suggest that the enzyme follows an alternating mechanism, with HNNH and H₂NNH₂ as intermediates (although the former may be protonated by homocitrate to HNNH₂). Moreover, the N−N bond is cleaved in the E₇ state and that the NH₃ products dissociate at the E₇ and E₈ levels, in accordance with an alternating mechanism.

Between the various E _n levels in Figure 8, we have assumed that an electron and a proton are delivered to the FeMo cluster. The electrons are provided by the Fe protein, via the P‐cluster.[ ¹ , ⁴ ] The protons ultimately come from the solvent. Dance has investigated different proton paths from the solvent to the FeMo cluster. He suggested that protons are transferred from the surface via a chain of water molecules to a water molecule close to homocitrate and the S3B atom.[ ⁹⁴ , ⁹⁵ , ⁹⁶ , ⁹⁷ ] He has also studied how the proton may be transferred within the FeMo cluster, starting on the S3B atom and ultimately ending up close to the substrate‐binding sites. ^[96] His‐195 may also provide protons to the substrate, as has often been assumed.[ ³⁸ , ⁴⁹ ] In fact, our calculations show that such a transfer (via the HIP state of His‐195) is always downhill. However, this gives the HID state of His‐195, which is nearly always unfavourable. Moreover, Dance has shown that rotation of the sidechain of His‐195 is unlikely in the protein.[ ⁹⁴ , ⁹⁸ ] Therefore, His‐195 can probably not provide more than one proton to the substrate (at the most).

However, it should be remembered that QM studies of nitrogenase are extremely complicated. Our survey of the most stable structures at the various E₄–E₈ levels have indicated that several structures often have quite similar energies and that here are many conformations of the bound intermediates, depending on the direction of the non‐coordinated N‐group, the H−N−N−H dihedral angle and the formation of hydrogen bonds and other polar interactions. Moreover, sometimes other BS states than BS10‐147 are most stable and a full BS investigation of every structure is currently too demanding. This makes it harder to settle the most stable structures and it cannot be excluded that we might have overlooked some low‐energy structures.

For all states, we have optimised structures with both TPSS and B3LYP. In general, the two methods give relative energies that agree reasonably. However, in some cases, differences >50 kJ/mol are observed, without any significant differences in the geometry. This is often observed for the various spins states (B3LYP typically prefers higher spin states than TPSS, as expected). However occasionally, such differences also occur for structures with differences only in the hydrogen‐bond pattern or coordination mode, making interpretation of the results harder.

For the most interesting states, we have also recalculated energies with the larger def2‐TZVPD basis set. As in our previous studies,[ ⁴³ , ⁵⁹ , ⁶⁰ , ⁶¹ ] this has typically only a minor effect on the energies, <20 kJ/mol. However, calculations with relaxed surroundings occasionally have larger effects, up to 26 kJ/mol, which may indicate that the structure need to relax more than is allowed in the rather large QM system or problems with local minima in the surroundings. However, a more detailed study of the relaxation of the surroundings (in the Supporting Information) indicates that the large energy differences are connected to major movements of water molecules and other groups far from the substrate‐binding site, suggesting that it reflects more occurrences of multiple local minima, rather than important relaxation of the surroundings.

For many of the E _n states, we have observed that a transfer of the hydroxy proton of homocitrate to the N₂‐intermediate is favourable. This indicates homocitrate may constitute a proton buffer, which can be used to stabilise certain intermediates of the reaction, especially H₂NNH₂ and NH₃. This provides an attractive explanation why homocitrate is mandatory for the function of nitrogenase.[ ⁸⁸ , ⁹⁹ ] Bjornsson and coworkers have also suggested that the hydroxy proton of homocitrate is employed to form trans‐HNNH from N₂ in the E₄ intermediate, although the reaction was uphill. ^[42]

For all E _n levels, binding of the intermediates to Fe6 seems to be preferred and therefore we have suggested such binding in the mechanism in Figure 8. This site has more hydrogen‐bond possibilities (besides sulfide ions), involving His‐195, Gln‐191 and the homocitrate ligand. It can also employ the suggested proton buffer of homocitrate and it is also closer to the end of the suggested proton‐transfer path, involving a chain of water molecules, ending close to homocitrate and S3B.[ ⁹⁴ , ⁹⁵ , ⁹⁶ , ⁹⁷ ] However, for the E₄ and E₈ states, binding of the N₂‐intermediates to Fe2 are competitive. Moreover, it has been suggested that a likely N₂‐binding channel ends at Fe2. ^[27]

We have previously studied the reaction mechanism of nitrogenase, assuming that S2B dissociates from the FeMo cluster, opening up for an obvious binding site of the substrate. ^[57] This gave rise to a mainly alternating reaction mechanism, in which the substrate and the intermediates bound in a bridging mode (with one or both N atoms) between Fe2 and Fe6. In the present study, bridging intermediates were always found to be much less stable than end‐on intermediates, except for E₇ structures with both NH₂ and NH₃. The reason for this is that the FeMo cluster is too crowded if both the substrate and S2B bridges Fe2 and Fe6. In fact, it is often observed that S2B moves to other positions or reacts with the substrate or other sulfide ions in such high‐energy structures with a bridging substrate. Thus, it seems clear that bridging substrate structures are unlikely when S2B remains bound.

In conclusion, this study shows that the second part of the nitrogenase reaction (after binding of N₂) is possible also if the S2B ligand has not dissociated. Such a reaction follows an alternating mechanism with the substrate and intermediates binding to Fe6. It has also pointed out an important role for the homocitrate ligand as a proton buffer. In future studies, we study the binding of N₂ and dissociation of H₂ to the E₄ state of the cluster.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

H. Jiang, U. Ryde, Chem. Eur. J. 2022, 28, e202103933.

Data Availability Statement

The data that support the findings of this study are available in the supplementary material of this article.