Chiral Phosphoric Acid Catalyzed Conversion of Epoxides into Thiiranes: Mechanism, Stereochemical Model, and New Catalyst Design

Abstract

Computations and experiments leading to new chiral phosphoric acids (CPAs) for epoxide thionations are reported. Density functional theory calculations reveal the mechanism and origin of the enantioselectivity of such CPA‐catalyzed epoxide thionations. The calculated mechanistic information was used to design new efficient CPAs that were tested experimentally and found to be highly effective. Bulky ortho‐substituents on the 3,3′‐aryl groups of the CPA are important to restrict the position of the epoxide in the key transition states for the enantioselectivity‐determining step. Larger para‐substituents significantly improve the enantioselectivity of the reaction.

DFT calculations have clarified the mechanism and origin of the enantioselectivity of the chiral phosphoric acid (CPA) catalyzed thionation of epoxides with thiolactam by kinetic resolution. Bulky ortho groups are important to restrict the position of the epoxide group in the key transition states of the enantioselectivity‐determining step, while increasing the size of the para‐substituents also increases the enantioselectivity significantly.

Introduction

Chiral phosphoric acids are arguably the best known class of acidic organocatalysts in the literature, ^[1] with many reports on their efficient activity as catalysts for a wide range of organic transformations with potential applications in both industry and academia. ^[2] The success of this privileged motif relies in part on its bifunctional character, where the hydroxy group is a Brønsted acid, ^[3] while the phosphoryl oxygen atom acts as a Brønsted base. ^[4] This balance of Brønsted acidity/basicity as well as the steric demands of the catalyst can be finely tuned by careful choice of the substituents attached to the phosphoric acid moiety.[ ⁵ , ⁶ ] Chiral phosphoric acid (CPA) catalysis has become an important field in enantioselective synthesis. ^[7]

Among the several chiral backbones available in the literature, 1,1′‐bi‐2‐naphthol (BINOL) stands out, as Brønsted acids derived therefrom have become a prominent group of catalysts, with high catalytic activity under mild reaction conditions. ^[8] The binaphthyloxyl group can be further functionalized by attaching substituents, which provides a variety of catalysts for enantioselective synthesis. ^[9] Small changes to the properties (steric and/or electronic) of these substituents can lead to significant differences in the observed enantioselectivities. ^[10] The development of a particular transformation in a highly enantioselective fashion generally involves the preparation and testing of a large number of CPAs. ^[11] Increasingly, theoretical calculations have proven to be a useful tool to design and computationally screen CPAs, and this approach can potentially reduce the experimental workload. ^[12]

The efficiency and robustness of chiral CPAs can also be applied to the kinetic resolution of racemic reactants. ^[13] Recently, the List group reported a highly efficient method for the synthesis of thiiranes by epoxide thionation through kinetic resolution using CPA (R)‐C1 as the catalyst and thiolactam 3  a as the sulfur donor (Scheme 1). ^[14] Considering the importance of enantiopure epoxides as building blocks in chemical synthesis, we were motivated to further understand this underdeveloped transformation. To clarify the mechanism and chirality transfer process of this reaction, we resorted to density functional theory (DFT) calculations. Ultimately, these calculations led to several designed CPAs that were predicted to perform the target kinetic resolution in a highly selective fashion. These predictions were confirmed experimentally.

Scheme 1.

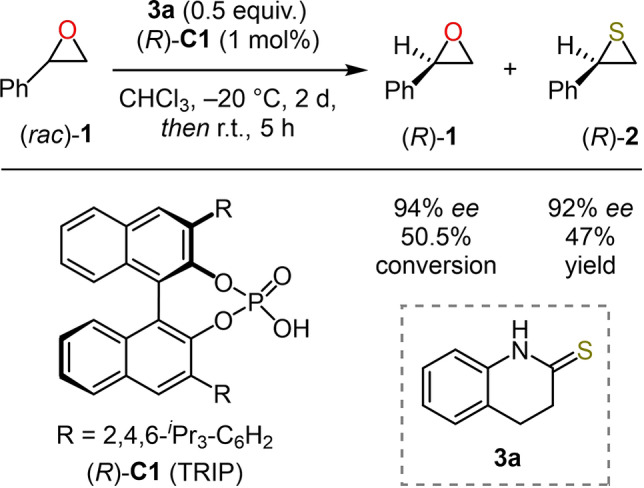
CPA‐catalyzed epoxide thionation with thiolactam 3  a by kinetic resolution.

Computational Methods. Geometry optimizations and frequency calculations were performed using the B3LYP functional with the 6‐31G(d) basis set.[ ^4a , ^7a , ¹⁵ ] Normal vibrational mode analysis was carried out for all stationary points to confirm them as local minima or saddle points, and to derive the thermochemical corrections for the enthalpies and free energies. Single‐point energies and solvent effects in chloroform were computed with the SMD solvation model at the M06‐2X/6‐311+G(d,p) level of theory using the gas‐phase‐optimized structures. ^[16] A variety of other functionals were tested to verify the calculated selectivities. All calculations were performed using Gaussian 09. ^[17]

Results and Discussion

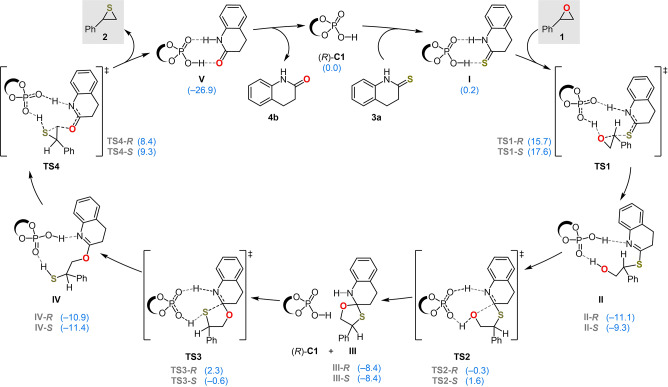
Computational Investigations. Previous experimental observations led to the proposed general catalytic cycle for the CPA‐catalyzed epoxide thionation shown in Figure 1. CPA (R)‐C1 interacts with thiolactam 3  a to give heterodimer I; this association process is slightly endergonic by 0.2 kcal mol⁻¹. Complex I reacts with the epoxide by intermolecular nucleophilic substitution reaction via transition state TS1, which is activated by the hydrogen bond with the phosphoric acid. The reaction is a backside S_N2 process, but at the substituted carbon atom of the epoxide, partially resembling an S_N1 process. Ring‐opened iminothioate intermediate II irreversibly forms, but can reversibly form the isomer IV via cyclic intermediate III. This isomerization proceeds by intramolecular nucleophilic addition of the hydroxy group to the imido moiety, which occurs via transition state TS2 to give oxathiaazaspirodecane species III. Proton transfer from the CPA to the imido moiety induces an intramolecular S_N2 substitution to yield thiirane product 2. The regenerated catalyst associates with another molecule of thiolactam 3  a, releasing the corresponding side‐product lactam 4  b.

Figure 1.

Proposed catalytic cycle for the CPA‐catalyzed epoxide thionation. The DFT‐calculated free energies, in kcal mol⁻¹, are shown in parentheses. The stereochemical indicators R/S for all intermediates and transition states refer to the enantiomer of the thiirane obtained for each pathway.

DFT calculations revealed that the enantioselectivity‐determining step of this kinetic resolution is the CPA‐assisted nucleophilic ring‐opening of the epoxide by the thiolactam via the transition states TS1‐R or TS1‐S . The calculated relative free energy of ring‐open transition state TS1‐S with R‐epoxide 1 is 1.9 kcal mol⁻¹ higher than that of transition state TS1‐R with the S‐epoxide. Based on this energy difference, the calculated ee value is 92 %, in agreement with the experimental observation (92 % ee).

The distortion (ΔE _dist) and interaction (ΔE _int) energies of the key transition states TS1‐R and TS1‐S were calculated to analyze the origin of the stereoselectivity of the reaction (Table S1). ^[18] In this analysis, transition states TS1‐R and TS1‐S were divided into three parts: catalyst, epoxide, and thiolactam. The calculated E _dist values of the catalyst and epoxide components in TS1‐S are 5.9 and 1.0 kcal mol⁻¹ higher than those in TS1‐R (57.9 and 24.6 kcal mol⁻¹), respectively. The E _dist value of the thiolactam segment in TS1‐R (1.0 kcal mol⁻¹) is almost the same as that in TS1‐S (1.2 kcal mol⁻¹). The calculated difference in E _int between TS1‐R (−102.2 kcal mol⁻¹) and TS1‐S (−107.2 kcal mol⁻¹) is 5.0 kcal mol⁻¹. These results suggest that the difference in the reactivity of the two epoxide enantiomers is a consequence of the larger ΔE _dist value of the catalyst in TS1‐S .

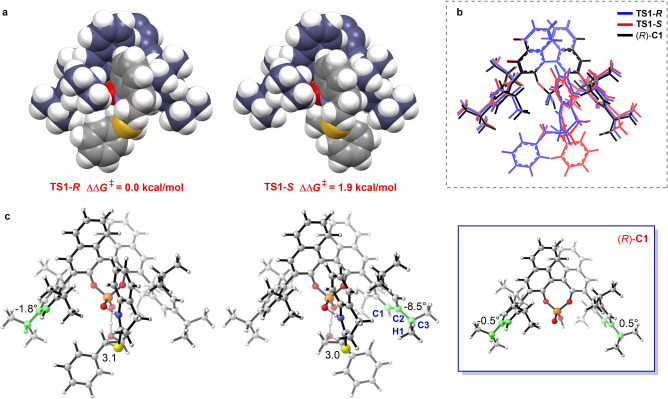
The origins of the different distortion energies for transition states TS1‐R and TS1‐S can be visualized from the corresponding calculated geometries (Figure 2). In TS1‐S , the phenyl group from the reacting epoxide group is oriented toward the bulky isopropyl substituent of the catalyst (Figure 2(a,c)). Therefore, the dihedral angle C1‐C2‐C3‐H1 of the CPA catalyst moiety in TS1‐S rotates to −8.5°, which is significantly different from the original position (almost 0°), and suggests that the catalyst changes to an unfavorable conformation due to steric repulsion with the phenyl group of the reacting epoxide.

Figure 2.

a) Space‐filling models of TS1‐R and TS1‐S . b) Superimposition of the axial projections of (R)‐C1 (black), TS1‐R (blue), and TS1‐S (red). c) Axial projections of TS1‐R , TS1‐S , and (R)‐C1. The key bond lengths and angles are shown.

To better demonstrate this twisting of the catalyst structure, the axial projections of (R)‐C1, TS1‐R , and TS1‐S are overlaid in Figure 2(b). This shows that the catalyst moiety in TS1‐S is distorted from the original position, leading to a visible difference between the TS1‐S (red) and (R)‐C1 (black) structures. Moreover, the unfavorable transition state TS1‐S is also shifted further along the reaction coordinate, as reflected by the forming C−S bond being shorter. This causes a relatively large interaction with a larger unstable distortion in TS1‐S than that in TS1‐R . Therefore, distortion of the catalyst is responsible for the observed enantioselectivities.

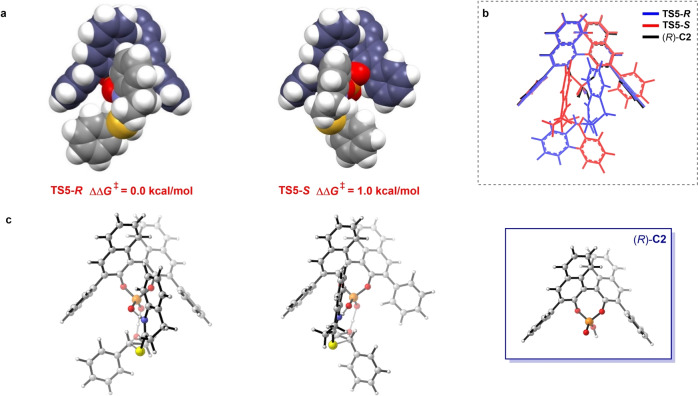
These theoretical calculations indicate that the isopropyl group plays a key role in the determination of the enantioselectivity in the first S_N2‐type ring opening of the epoxide (Figure 3). Therefore, the unsubstituted CPA (R)‐C2 was also computed as a catalyst to reveal the effect of substituents on the CPA. In the absence of ortho‐isopropyl groups on the 3,3′‐phenyl rings of (R)‐C2, the key step (CPA‐induced S_N2‐type ring opening of the thiolactam to the epoxide) becomes less selective. The calculated energy difference between the two key transition states (TS5‐S and TS5‐R ) decreases to 1.0 kcal mol⁻¹, indicating significantly lower enantioselectivity for the reaction. The predicted ee value decreases to 69 %, which shows the same trend as the experimental observation (31 %). Notably, the reacting epoxide in TS5‐S has a favorable conformation, which can be attributed to the absence of the isopropyl groups in CPA leading to a vacancy for the incoming epoxide. Therefore, modification of the bulky groups on the phenyl substituent of the CPA causes the change in the enantioselectivity of the epoxide thionation.

Figure 3.

a) Space‐filling models of TS5‐R and TS5‐S . b) Superimposition of the axial projections of (R)‐C2 (black), TS5‐R (blue), and TS5‐S (red). c) Axial projections of TS5‐R , TS5‐S , and (R)‐ C2.

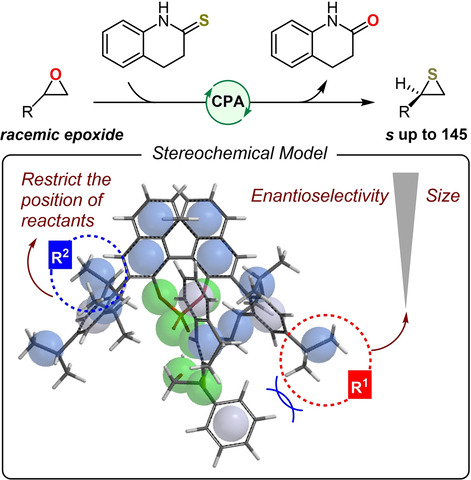
Based on our calculations, the enantioselectivity‐determining models for the S_N2‐type ring opening of the epoxide are summarized in Figure 4. In the first model (Figure 4a), the isopropyl groups at the ortho‐positions fix the orientations of substrates in both possible transition states for activation of the racemic epoxide. As a result, the phenyl ring of the epoxide is much closer to the isopropyl groups of the catalyst in the unfavorable transition state TS1‐S . Hence, increasing the size of the para‐substituent groups should enhance the enantioselectivity. In contrast, in the second model (Figure 4b), the absence of ortho‐isopropyl groups leads to a suitable vacancy for the incoming epoxide in the unfavorable transition state TS5‐S . The phenyl group of the epoxide is forced to move away to avoid steric repulsion with the para‐substituents of the CPA. In this case, the presence of bulky para‐substituent groups on the CPA should not improve the enantioselectivity.

Figure 4.

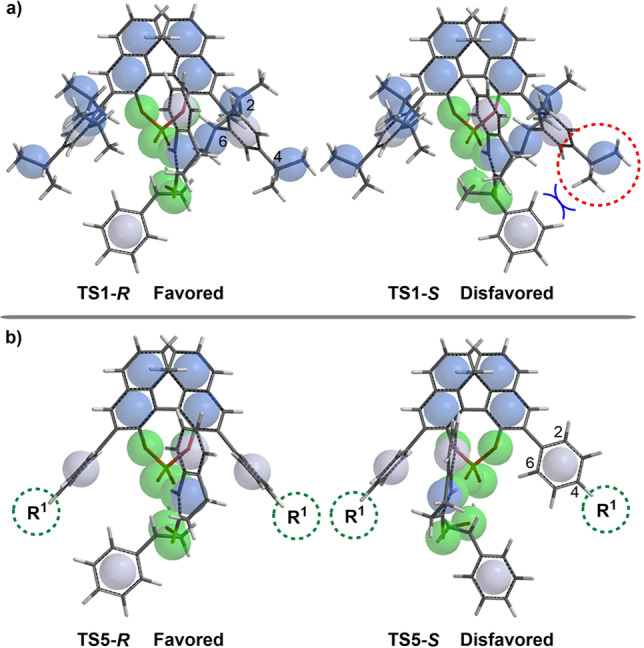
Enantioselectivity‐determining models for the key step of S_N2 attack leading to ring opening of the epoxide in the CPA‐catalyzed epoxide thionation when the ortho‐substituents of the 3,3′‐phenyl rings are: a) isopropyl groups or b) hydrogen atoms.

To test these assumptions from the enantioselectivity‐determining models, we undertook the computational prediction of the performances of a set of CPA catalysts in epoxide thionation reactions (Figure 5). For CPA (R)‐C1, the first enantioselectivity‐determining model is valid because of the presence of ortho‐isopropyl groups. By contrast, CPAs (R)‐C2, (R)‐C3, and (R)‐C4 all contain hydrogen atoms at the ortho positions of their 3,3′‐phenyl groups and, therefore, they were analysed with the second model shown in Figure 4.

Figure 5.

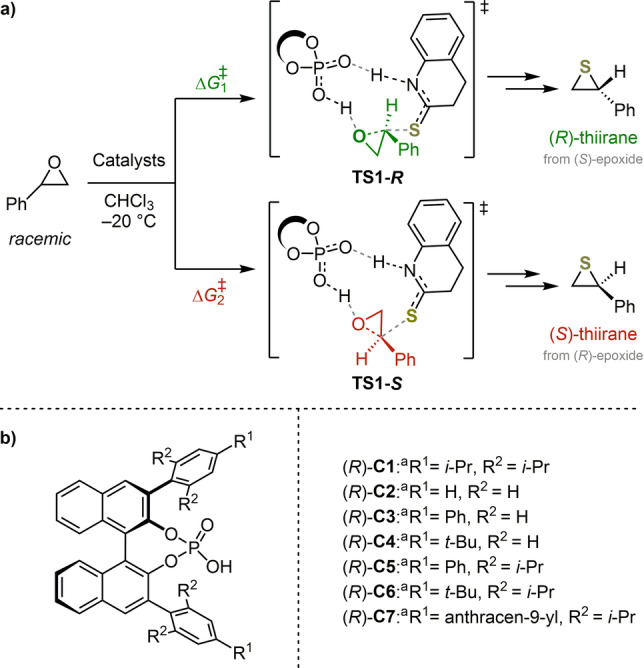
a) Transition states considered for the enantioselectivity‐determining step of the epoxide thionation. b) Set of CPAs used for the predictive analysis.

The theoretically predicted and available experimentally observed enantioselectivities for the thionation of epoxides catalyzed by various CPAs are given in Table 1. When R¹ and R² are both isopropyl groups ((R)‐C1), the calculated ΔΔG ^≠ value is 1.9 kcal mol⁻¹ (entry 1), indicating an ee value of 92 %. When the R¹ (para) and R² (ortho) groups are changed to hydrogen atoms ((R)‐C2), the calculated ΔΔG ^≠ value decreases to 1.0 kcal mol⁻¹ (entry 2). Furthermore, when R² is a hydrogen atom and R¹ is either a phenyl or a tert‐butyl group (entries 3 and 4, respectively), the calculated ΔΔG ^≠ values are only 0.7 or 0.4 kcal mol⁻¹. These results agree reasonably well with the experimental observations, thus confirming that the R² group is the most influential, and that simply increasing the size of R¹ in the absence of a large R² does not improve the enantioselectivity. Other density functionals gave similar predictions, and are described later as well as in the Supporting Information.

Table 1.

Theoretically predicted and experimentally observed enantioselectivities for the thionation of rac‐1, catalyzed by various CPAs.

Entry	Catalyst	ΔΔG ≠ calc [a]	ΔΔG ≠ exp [b]	ee calc [c]	ee exp [d]
1	(R)‐C1	1.9	1.9	92	92
2	(R)‐C2	1.0	0.4	69	31
3	(R)‐C3	0.7	0.3	53	24
4	(R)‐C4	0.4	0.1	33	7
5	(R)‐C5	3.1	2.1	99	94
6	(R)‐C6	3.6	2.3	>99	96
7	(R)‐C7	4.2	2.1	>99	94

[a] ΔΔG ^≠ _calc=ΔG ^≠ ₂−ΔG ^≠ ₁, where ΔG ^≠ ₁ and ΔG ^≠ ₂ were obtained by theoretical calculations. [b] ΔΔG ^≠ _exp is extrapolated from the experimentally observed ee values (ΔΔG ^≠=−RTln[(1−ee)/(1+ee)]). [c] ee value predicted by theoretical calculations. [d] ee values experimentally observed. Energy differences are given in kcal mol⁻¹.

Based on the first enantioselectivity‐determining model, some new CPA catalysts ((R)‐C5, (R)‐C6, and (R)‐C7) were designed to further improve the enantioselectivity. The key idea is that the ortho‐isopropyl groups should be maintained. As shown in Table 1 (entry 5), changing R¹ to a phenyl group increases the calculated ΔΔG ^≠ value to 3.1 kcal mol⁻¹. If the size of R¹ is further increased (tert‐butyl group, entry 6), the corresponding energy difference ΔΔG ^≠ is 3.6 kcal mol⁻¹. Moreover, when R¹ is a 9‐anthracenyl ring, the calculated ΔΔG ^≠ value goes up to 4.2 kcal mol⁻¹. These calculations confirm that increasing the size of the R¹ group leads to higher enantioselectivity in the presence of ortho‐isopropyl groups. The calculated free energy barriers of the rate‐determining step (ΔG _rds) with (R)‐C5, (R)‐C6, and (R)‐C7 as catalysts are 19.0, 20.4, and 22.9 kcal mol⁻¹, respectively. This suggests that bulky groups at the para position should not inhibit reactivity.

Experimental Tests. To test the predicted improvement in enantioselectivity, the thionation of rac‐styrene oxide (rac‐ 1) was examined using the chiral phosphoric acids (R)‐C5, (R)‐C6, and (R)‐C7 as catalysts under the previously reported conditions, ^[14] where (R)‐TRIP ((R)‐C1) performed excellently. The (R)‐BINOLs required for the synthesis of (R)‐C5 and (R)‐C6, containing 2,6‐diisopropyl‐4‐substituted phenyl rings in the 3,3′‐positions, were prepared following reported procedures based on Kumada cross‐coupling reactions (see the Supporting Information). It is worth mentioning that, for the case when R¹ is 9‐anthracenyl (towards (R)‐C7), an approach based on a Negishi cross‐coupling led to a more reproducible synthesis, as well as a higher yield of the desired (R)‐BINOL.

By using (R)‐C5 as the catalyst, the reaction of rac‐1 with thiolactam 3  a provided thiirane (R)‐2 with slightly higher enantioselectivity compared to (R)‐C1 (94 % ee, entry 5). In line with the predictions, when (R)‐C6 acted as the catalyst, thiirane (R)‐2 was obtained with 96 % ee (entry 6). Finally, catalyst (R)‐C7 also matched the predicted trend, producing (R)‐2 with 94 % ee. This experimental validation further supports that the ortho‐substituents on CPAs play a significant role in determining the position of the epoxide, and also that increasing the size of the para‐substituents can lead to higher enantioselectivity. The results obtained with the set of CPAs show a good correlation between the corresponding free energy differences derived from the experiment and from the calculations (R ²=0.85, Figure 6). We also further evaluated the reactions of several aliphatic epoxides with thiolactam 3  a in the presence of the new CPA catalysts. Unfortunately, both computational and experimental results agreed that the reactions proceed with low enantioselectivity (see Table S2).

Figure 6.

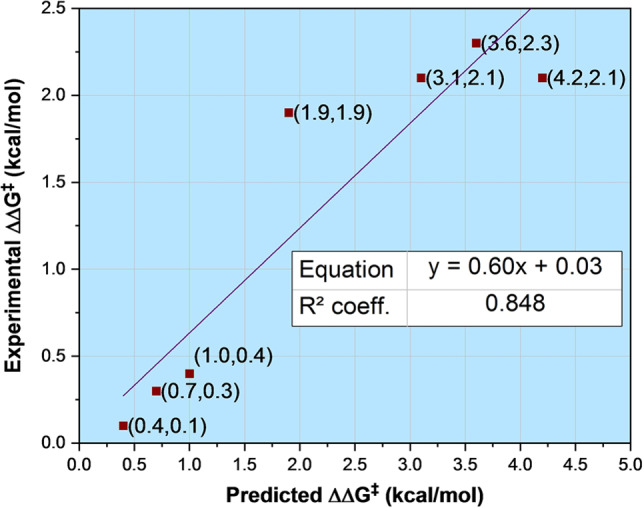
Correlation between the experimental and predicted ΔΔG ^≠ values.

To test the accuracy of our computational results on the performance of various catalysts, single‐point energies were evaluated with the popular density functionals as well as higher accuracy density functionals: ωB97X‐D3, ωB97M‐V, ωB97M‐D3BJ, ωB97M‐D4, and PWPB95‐D3BJ using the ORCA 5.1.0 program for a comparison of the stereoselectivities (Table S3). ^[19] The trends in enantioselectivities are consistent with each of the five DFT methods. For example, with (R)‐C5, (R)‐C6, and (R)‐C7, our standard method predicted energetic preferences for the formation of one stereoisomer of 3.1, 3.6, and 4.2 kcal mol⁻¹, respectively, while the higher accuracy methods gave 2.0–2.5, 3.1–3.4, and 3.6–4.7, respectively. Geometry optimizations were also performed on enantioselectivity‐determining steps with the SMD solvation model at the M06‐2X/6‐31G(d) level of theory to determine the influence of dispersion and solvent effects on geometries. The detailed energy differences are summarized in Table S4; the results are consistent with the methods originally used for the predictions described here.

Conclusion

The mechanism and origin of the enantioselectivity of the CPA‐catalyzed epoxide thionation with thiolactam by kinetic resolution have been explored with DFT calculations. The catalytic cycle involves two main steps of nucleophilic ring opening of epoxide and carbonyl elimination. The enantioselectivity‐determining step is the first S_N2 ring opening of the epoxide by CPA‐activated thiolactam. The observed enantioselectivities result from the steric interaction between the epoxide group and the substituents of the CPA catalyst. Two enantioselectivity‐determining models were observed depending on the ortho‐substituents of the phenyl group attached to the CPAs. The ortho‐isopropyl groups restrict the position of the epoxide group, leading to alteration of the enantioselectivity as a result of the size of the para‐substituents. On the basis of this model, some new CPA catalysts were designed and found to improve the enantioselectivity of this reaction.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Supporting Information

M. Duan, C. D. Díaz-Oviedo, Y. Zhou, X. Chen, P. Yu, B. List, K. N. Houk, Y. Lan, Angew. Chem. Int. Ed. 2022, 61, e202113204; Angew. Chem. 2022, 134, e202113204.